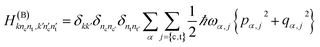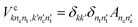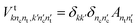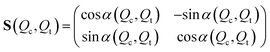Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dissipative dynamics at conical intersections: simulations with the hierarchy equations of motion method
Lipeng
Chen
a,
Maxim F.
Gelin
b,
Vladimir Y.
Chernyak
c,
Wolfgang
Domcke
b and
Yang
Zhao
a
aDivision of Materials Science, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798
bDepartment of Chemistry, Technische Universität München, Garching D-85747, Germany
cDepartment of Chemistry, Wayne State University, Detroit, USA
First published on 10th May 2016
Abstract
The effect of a dissipative environment on the ultrafast nonadiabatic dynamics at conical intersections is analyzed for a two-state two-mode model chosen to represent the S2(ππ*)–S1(nπ*) conical intersection in pyrazine (the system) which is bilinearly coupled to infinitely many harmonic oscillators in thermal equilibrium (the bath). The system–bath coupling is modeled by the Drude spectral function. The equation of motion for the reduced density matrix of the system is solved numerically exactly with the hierarchy equation of motion method using graphics-processor-unit (GPU) technology. The simulations are valid for arbitrary strength of the system–bath coupling and arbitrary bath memory relaxation time. The present computational studies overcome the limitations of weak system–bath coupling and short memory relaxation time inherent in previous simulations based on multi-level Redfield theory [A. Kühl and W. Domcke, J. Chem. Phys. 2002, 116, 263]. Time evolutions of electronic state populations and time-dependent reduced probability densities of the coupling and tuning modes of the conical intersection have been obtained. It is found that even weak coupling to the bath effectively suppresses the irregular fluctuations of the electronic populations of the isolated two-mode conical intersection. While the population of the upper adiabatic electronic state (S2) is very efficiently quenched by the system–bath coupling, the population of the diabatic ππ* electronic state exhibits long-lived oscillations driven by coherent motion of the tuning mode. Counterintuitively, the coupling to the bath can lead to an enhanced lifetime of the coherence of the tuning mode as a result of effective damping of the highly excited coupling mode, which reduces the strong mode–mode coupling inherent to the conical intersection. The present results extend previous studies of the dissipative dynamics at conical intersections to the nonperturbative regime of system–bath coupling. They pave the way for future first-principles simulations of femtosecond time-resolved four-wave-mixing spectra of chromophores in condensed phases which are nonperturbative in the system dynamics, the system–bath coupling as well as the field-matter coupling.
I. Introduction
The nonequilibrium dynamics of quantum systems which are interacting with a large (macroscopic) environment in thermal equilibrium is a problem with a long history in condensed-matter physics and chemistry, see, e.g.,1–7 and references therein. In the present work, we are addressing the question of how the complex nonadiabatic dynamics occurring at conical intersections of electronic potential-energy (PE) surfaces of polyatomic molecules8–11 is affected by weak to moderate coupling to a condensed-phase environment. Conical intersections are hypersurfaces of exact degeneracy of adiabatic PE surfaces and are universally encountered in polyatomic molecules.12–15 The simplest model of a conical intersection involves two electronic states and two vibrational modes which span the so-called branching space of the conical intersection.16 In the case of a symmetry-allowed conical intersection, these vibrational modes can be classified as coupling and tuning modes.17 The singularity of the non-Born–Oppenheimer coupling elements at the seam of intersection and the pronounced local anharmonicity of the adiabatic PE surfaces cause exceptionally strong electronic inter-state couplings as well as vibrational mode–mode couplings. The interplay of these couplings gives rise to ultrafast radiationless relaxation processes following preparation of the upper electronic state by optical excitation.8–11In most applications explored in the physics literature, the quantum system of interest is simple and exhibits trivial dynamics when being isolated, such as a nuclear spin1,2 or a harmonic oscillator.3 Conical intersections, on the other hand, are multi-level systems with a complex internal dynamics. Even for minimal two-state two-mode models of conical intersections, the Hilbert space required for the description of the photoinduced dynamics can be quite large and the numerical diagonalization of the Hamiltonian can be challenging. Due to the intricate internal dynamics of conical intersections, the physics of energy and phase relaxation due to coupling to an environment can be much richer than the physics of a few-level system or a harmonic oscillator coupled to the same environment.
Early studies of the effects of an external bath on the photoinduced dynamics of two-mode and three-mode conical intersections were performed by Gerdts and Manthe,18 Kühl and Domcke19,20 and Baltzer and Stock,21,22 assuming bilinear coupling of the active modes of the conical intersection to a harmonic bath with ohmic spectral density. The dissipative dynamics of these systems was numerically simulated with multi-level Redfield theory23,24 which is valid within the limits of weak system–bath coupling and short memory relaxation time of the bath. Kosloff, Ratner and coworkers performed similar computational studies of conical intersections coupled to a bath, considering Lindblad-type relaxation operators or a bath of two-level systems.25,26 Starting from multi-mode conical intersection Hamiltonians in the diabatic representation, Gindensperger, Burghardt and Cederbaum developed an effective-mode formalism which leads to a hierarchy of system–bath couplings.27–31 In this approach, the short-time dynamics of the multi-mode conical intersection can be accurately reproduced with the inclusion of just a few effective bath modes. Burghardt and Hynes32 and Malhado and Hynes33,34 studied the effect of a dissipative solvent mode, described by a generalized Langevin equation, on the dynamics of a conical intersection related to retinal photoisomerization.
Herein, we employed the hierarchy equation of motion (HEOM) method developed by Tanimura and coworkers35–38 to simulate the dynamics of a conical intersection in a dissipative environment. The HEOM method is a numerical technique for the solution of the Liouville equation of motion for the reduced density matrix of system–bath models. It is based on the construction and numerical solution of a hierarchy of master equations.38 An alternative formulation of the HEOM method is based on Fokker–Planck equations.39 The HEOM method is the most powerful method currently available for the numerically exact solution of master equations for a certain type of system–bath models.38 In practical applications of the HEOM method, it is convenient to model the bath and the system–bath coupling by the Drude spectral function7 or linear combination thereof.40 The Drude bath is characterized by a system–bath coupling parameter λ and a memory relaxation time γ−1. We will focus here on models with weak to moderate system–bath coupling, assuming that the strongly active modes of the conical intersection are included in the system Hamiltonian. Duan and Thorwart recently adopted an alternative strategy to simulate the dynamics of a two-state two-mode conical intersection coupled to a Drude bath.41 By transforming the coupling and tuning modes of the conical intersection into the bath, they obtained an electronic two-level system which is coupled to a structured bath. The resulting master equation was solved with the HEOM method.
II. Theoretical framework
A. Hamiltonian
We partition the total Hamiltonian into the system Hamiltonian, the bath Hamiltonian, and their coupling| H = H(S) + H(B) + H(SB) | (1) |
We adopt a minimal model of a conical intersection which involves two excited electronic states |φ1〉, |φ2〉 and two vibrational modes, the coupling mode and the tuning mode. Keeping only the leading (linear) terms in the electronic–vibrational couplings, the system Hamiltonian is written in the diabatic representation as17
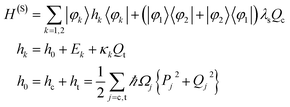 | (2) |
We assume that the coupling mode Qc and the tuning mode Qt are bilinearly coupled to an external bath. Due to the different symmetry of the two system modes in the present model of a symmetry-allowed conical intersection, it makes sense to assume that each of the two modes is coupled to its own bath. The Hamiltonian of the environment is thus written as
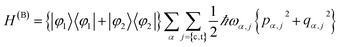 | (3) |
We assume that the coupling and tuning vibrational modes are bilinearly coupled to the respective bath. The corresponding system–bath coupling Hamiltonian reads
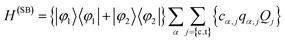 | (4) |
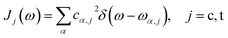 | (5) |
The system–bath Hamiltonians specified as above can be used for deriving master equations in two different ways.39–43 One can either retain the strongly coupled high-frequency vibrational modes in the system Hamiltonian or move the modes to the bath, resulting in a structured bath. The two descriptions are, in principle, equivalent and connected via a canonical transformation.39–44 In the context of the HEOM method, the inclusion of all vibrational modes in the bath is the common choice.40,41,45 In the present study we prefer to keep the strongly coupled high-frequency vibrational modes in the system Hamiltonian (cf.ref. 46). This way, we can treat fairly general system Hamiltonians (e.g., beyond the harmonic approximation for the system vibrational modes).
Introducing a basis set |nc〉, |nt〉 for the coupling mode and the tuning mode, respectively, we can construct the matrix representation of the total Hamiltonian
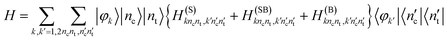 | (6) |
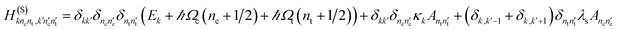 | (7) |
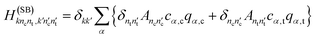 | (8) |
with
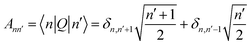 | (9) |
In matrix form:
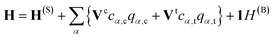 | (10) |
The total (system + bath) dynamics is described by the Liouville–von Neumann equation
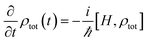 | (11) |
The dynamics of the relevant system is described by the reduced density matrix ρ(t), defined as the trace over the bath degrees of freedom of the full density matrix ρtot(t)
| ρ(t) = trB{ρtot(t)} | (12) |
We assume instantaneous electronic excitation of the system from the electronic ground state |φ0〉 to the diabatic state |φ2〉 by an ideally short laser pulse. This corresponds to the preparation of the density matrix
| ρ(0) = |φ2〉|0〉〈0|〈φ2| | (13) |
We model the bath by the Drude spectral density,7
| Jj(ω) = 2λjγjω/(ω2 + γj2), j = c, t | (14) |
B. HEOM method
The HEOM method is a numerically exact method which allows the computation of the time evolution of the reduced density matrix ρ(t) beyond the Markovian approximation and for arbitrary system–bath coupling strength.35–38Using the matrix representation of the Hamiltonian (6) and adopting the high-temperature approximation (βħγj < 1, where β = (kBT)−1 is inverse temperature) which is fulfilled in our simulations, one obtains the following hierarchy of coupled equations of motion for the reduced density matrix
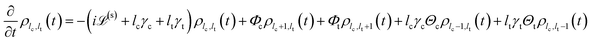 | (15) |
![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (s), and the relaxation operators Φ and Θ are defined as
(s), and the relaxation operators Φ and Θ are defined as| Φj = iV×j | (16) |
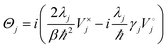 | (17) |
The system of eqn (15) represents an infinite number of coupled master equations. It can be shown that the condition for the termination of the hierarchy is N = lc + lt ≫ ω(S)/min(γ1, γ2), where ω(S) is a characteristic frequency of ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (s).47 In this case, the last term in the infinite hierarchy of eqn (15) can be replaced by
(s).47 In this case, the last term in the infinite hierarchy of eqn (15) can be replaced by
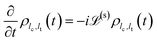 | (18) |
Low-temperature correction terms have to be included in eqn (15) when the condition βħγj < 1 is not satisfied (see ref. 37 and 38). The low-temperature correction results in the replacements
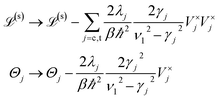 | (19) |
C. Physical observables
Once the reduced density matrix ρ(t) is given, the time evolution of system observables can straightforwardly be calculated. The most important observables for monitoring radiationless decay dynamics are the time-dependent populations of the electronic states. The population of the kth diabatic electronic state is defined as10| Pdik(t) = trS{|φk〉〈φk|ρ(t)} | (20) |
The population of the adiabatic electronic states is given by
Padk(t) = trS{|![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) k〉〈 k〉〈![[small variant phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e12c.gif) k|ρ(t)} k|ρ(t)} | (21) |
The adiabatic electronic states are related to the diabatic states via
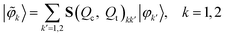 | (22) |
and α(Qc, Qt) is the diabatic-to-adiabatic mixing angle. The adiabatic population Pad2 is the observable which directly reflects the radiationless electronic decay dynamics from the upper to the lower adiabatic energy surface. The diabatic electronic population Pdi2, on the other hand, is directly related to spectroscopic signals, e.g. to the total (frequency-integrated) spontaneous emission signal.48 Note that the system modes Qc and Qt are traced out in the definition of Pad2 and Pdi2 and therefore can be considered as part of the bath.
The coherence of vibrational motion of the system is monitored by the expectation values of the position and momentum operators of the system vibrational modes, which are defined as10
| 〈Qj〉t = trS{Qjρ(t)} | (23) |
| 〈Pj〉t = trS{Pjρ(t)} | (24) |
For the nontotally symmetric coupling mode νc of the conical intersection, the expectation values of position and momentum operators vanish by symmetry. To visualize the coupled electronic-vibrational dynamics of the system, we consider the reduced probability densities of the coupling and tuning modes in the adiabatic electronic representation, defined as10
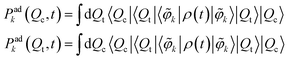 | (25) |
Under certain conditions, these probability densities are related to the time- and frequency-resolved fluorescence spectrum.49
D. Parametrization of the Hamiltonian and computational details
The S2[1B2u(ππ*)]–S1[1B3u(nπ*)] conical intersection in pyrazine is a well-known example for ultrafast electronic relaxation via a conical intersection.50–53 Various models of this conical intersection, comprising from 2 to 24 vibrational modes, have been constructed.54–59 These models have served as testbeds for the benchmarking of novel methods for the theoretical description of electronically nonadiabatic dynamics.60–72 The out-of-plane normal mode ν10a of B1g symmetry is the only normal mode which can couple the 1B2u and 1B3u electronic states in first order. The mode ν6a of A1g symmetry is the dominant tuning mode of this conical intersection. For the present purposes, a two-mode model of the S2–S1 conical intersection including the normal modes ν10a and ν6a is suitable as a simple and generic model of a conical intersection.The numerical values of the parameters of the model Hamiltonian H(S) of eqn (2) are taken from ref. 55. The frequencies of the coupling and tuning modes are ħωc = 952 cm−1 (2π/ωc = 35 fs) and ħωt = 597 cm−1 (2π/ωt = 56 fs). The intra-state electron-vibration coupling constants are κ1 = −847 cm−1 and κ2 = 1202 cm−1. The inter-state vibronic coupling constant is λs = 2110 cm−1. The vertical excitation energies are E1 = 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1 and E2 = 39
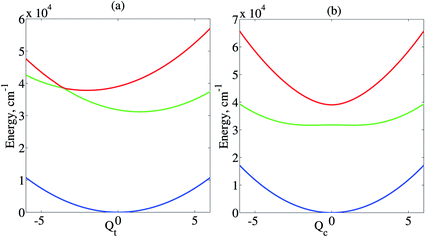
800 cm−1 and E2 = 39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. Cuts through the potential-energy surfaces along the normal coordinates Qt and Qc are shown in Fig. 1. The bath temperature is set to 300 K.
000 cm−1. Cuts through the potential-energy surfaces along the normal coordinates Qt and Qc are shown in Fig. 1. The bath temperature is set to 300 K.
The numerical calculation of the system dynamics is based on the representation of the Hamiltonian H(S) in a direct product basis of diabatic electronic states and harmonic-oscillator basis functions for the coupling and tuning modes. We have employed a basis set of 20 harmonic-oscillator functions for each mode, resulting in a dimension of 800 of the system Hamiltonian matrix H(S). The numerical evaluation of ρ(t) via the HEOM method requires the propagation of a large number of coupled equations of motion for auxiliary matrices of large dimension, which is computationally demanding. We overcame the computational challenge by using a GPU (Graphic Processing Unit) implementation of the ArrayFire package which provides an easy-to-use API (application programming interface) and an array-based function set that facilitates GPU programming.73 The numerical integration of the equations of motion for the auxiliary density matrices are performed on a NVIDIA Tesla M2050 GPU with 448 processors and 2 GB ECC-protected on-board memory. The HEOM eqn (15) has been solved via a fourth-order Runge–Kutta method with a time step of 0.2 fs. Depending on the value of system–bath coupling strength λj, j = c, t, the truncation threshold N of the hierarchy was varied from 6 to 12, which was found to be sufficient for obtaining converged results. With this efficient algorithm implemented on GPU hardware, the propagation of ρ(t) up to 1000 fs on a single GPU requires from several hours to 10 hours, depending on the truncation number N. The matrix–matrix multiplications in eqn (15) are carried out by the ArrayFire function matmul. The adiabatic populations Padk are obtained by evaluating the expectation values of the projection operators on the lower and upper adiabatic electronic states in the diabatic representation, as described in ref. 74. The vibrational probability densities (25) are calculated by using a discrete variable representation (DVR) scheme. In this DVR scheme, a transformation between the harmonic-oscillator basis and a grid in coordinate space is performed to represent operators in coordinate space (see ref. 75 for details).
III. Results
A. Electronic population probabilities and vibrational coherences
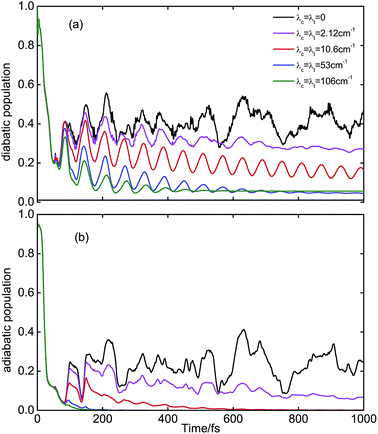
Fig. 2(a) shows the time-dependent population Pdi2(t) of the diabatic ππ* state for different system–bath coupling strengths on a time scale of 1 ps. The time evolution of Pdi2(t) for the isolated system (λc = λt = 0, black line) exhibits an initial decay on a timescale of ≈30 fs, followed by a few quasi-periodic recurrences with the period of the tuning mode. Beyond about 400 fs, the ππ* population probability exhibits irregular fluctuations. The long-time average of Pdi2(t) is ≈0.4. For the system–bath coupling strengths considered here, the coupling to the bath does not affect the fast initial decay of Pdi2(t) which is driven by the strong nonadiabatic coupling at the conical intersection. On the other hand, the irregular fluctuations of Pdi2(t) for t ≥ 400 fs are wiped out by even very weak system–bath coupling (λc = λt = 2.1 cm−1, magenta line). With increasing, but still weak, system–bath coupling (λc = λt = 10.6 cm−1, red line), Pdi2(t) exhibits, counterintuitively, a revival of the coherent oscillations driven by the tuning mode which extends now well beyond 1 ps. With further increasing system–bath coupling, the coherent oscillations of Pdi2(t) are damped out on a time scale of a few hundred femtoseconds, see Fig. 2(a), blue and green lines. The long-time limit of Pdi2(t) decreases with increasing system–bath coupling and is seen to converge to a small, but nonzero, value.The time evolution of the population Pad2(t) of the adiabatic S2 state is shown in Fig. 2(b). The initial decay of Pad2(t) of the isolated conical intersection (black line) occurs on a time scale of ≈20 fs and is somewhat faster than the initial decay of Pdi2(t). Pad2(t) approaches an asymptotic value of ≈0.2 at 1 ps. The system–bath coupling does not affect the short-time dynamics within the first ≈100 fs. As observed for the diabatic population probability, the irregular fluctuations of Pad2(t) are efficiently damped out by even very weak system–bath coupling (λc = λt = 2.1 cm−1, magenta line). With increasing system–bath coupling, the population of the S2 state quickly drops to zero, see Fig. 2(b). For the strongest system–bath coupling considered (λc = λt = 106.0 cm−1), all recurrences of Pad2(t) are quenched (green line). It should be noted that the long-lasting coherent oscillations of Pdi2(t) observed for λc = λt ≥ 10.6 cm−1 are absent in Pad2(t). Overall, Pad2(t) reveals a bimodal relaxation dynamics. The ultrafast initial decay on a time scale of a few tens of femtoseconds originates from the nonadiabatic dynamics of the conical intersection itself. The coupling to the environment leads to a complete transfer of the population of the S2 state to the S1 state on sub-picosecond time scales for even weak system–bath coupling.
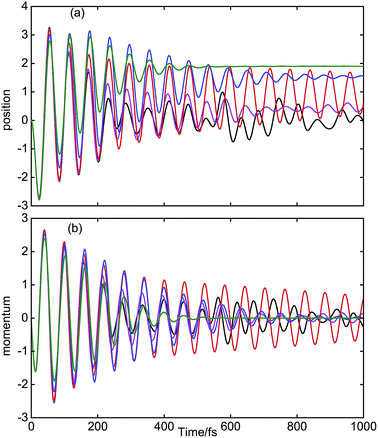
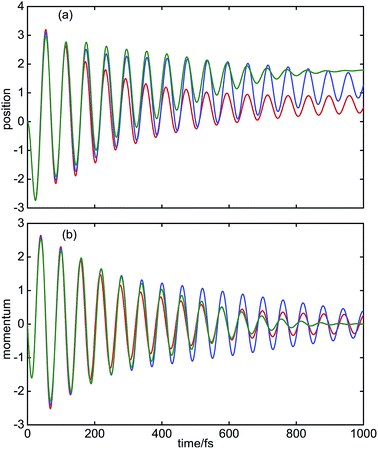
The expectation values of the position operator, 〈Qt〉t, and the momentum operator, 〈Pt〉t, of the tuning mode are shown in Fig. 3(a) and (b), respectively. For the coupling mode, these expectation values vanish by symmetry. For the isolated conical intersection (black line), 〈Qt〉t and 〈Pt〉t exhibit oscillations which are damped on a time scale of ≈300 fs. The mechanisms of this intrinsic vibrational dephasing of the conical intersection has been discussed in detail for the three-mode model of the S2–S1 conical intersection of pyrazine in ref. 55. A very weak system–bath coupling (λc = λt = 2.1 cm−1 magenta line) effectively damps residual fluctuations of 〈Qt〉t and 〈Pt〉t for t ≥ 500 fs. For stronger, but still weak, system–bath coupling (λc = λt = 10.6 cm−1, red line), a significant enhancement of the amplitude of the tuning mode is observed. This “dedamping” of the tuning mode is the reason for the long-lived coherent oscillations of Pdi2(t) in Fig. 2(a). The mechanism of this effect will be discussed in Section IV. With further increasing system–bath coupling (blue and green lines in Fig. 3), the oscillations of 〈Qt〉t and 〈Pt〉t are damped on time scales of a few hundred femtoseconds. Moreover, the long-time limit of 〈Qt〉t is seen to shift towards an asymptotic value, which corresponds to the minimum of the adiabatic S1 PE surface, see Fig. 1. This reflects the flow of excess vibrational energy from the conical intersection into the environment.
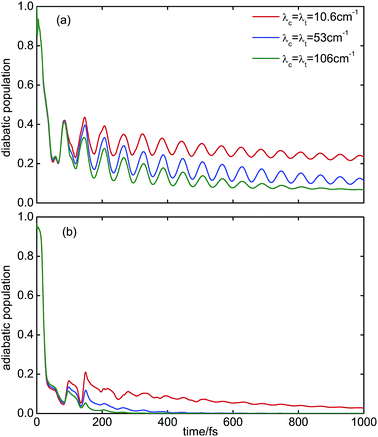
Next we consider the effect of the bath relaxation time γ−1 on the electronic populations and vibrational coherences. Fig. 4 shows the time-dependent population probabilities of the diabatic ππ* state (a) and the adiabatic S2 state (b), calculated for a longer bath relaxation time (γc−1 = γt−1 = 166 fs) and three different system–bath coupling strengths. Compared to Fig. 2 (bath relaxation time γc−1 = γt−1 = 50 fs), the coherent beatings of Pdi2(t) last longer in Fig. 4(a). The adiabatic populations Pad2(t) in Fig. 4(b) also decay more slowly than those in Fig. 2(b). The bath with longer relaxation time is less effective in draining coherence and energy from the dynamics of the system.
The corresponding expectation values of 〈Qt〉t and 〈Pt〉t are shown in Fig. 5(a) and (b), respectively. The damping of the oscillations of 〈Qt〉t and 〈Pt〉t due to system–bath coupling is less pronounced than in Fig. 3. The effect of dedamping of 〈Qt〉t and 〈Pt〉t occurs for a higher value of the system–bath coupling strength, λc = λt = 53.0 cm−1 (blue line in Fig. 5). For strong system–bath coupling (λc = λt = 106.0 cm−1 (green line)), the oscillations of 〈Qt〉t and 〈Pt〉t are completely quenched at ≈900 fs, while they were quenched already at ≈500 fs for the shorter bath relaxation time (Fig. 3).
B. Vibrational probability densities
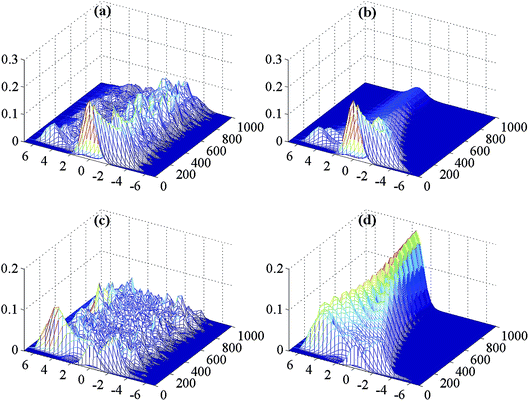
The most detailed insight into the dynamics of the ultrafast internal-conversion process in the present model of a dissipative conical intersection is provided by the time-dependent probability densities Padk(Qc,t), Padk(Qt,t) defined in eqn (25). In what follows we call Padk(Qj,t), j = c, t, probability densities of Qc and Qt, but it should be kept in mind that they are reduced probability densities, that is, the respective other vibrational mode is integrated out.Fig. 6 shows the probability densities Pad2(Qt,t) (upper panels) and Pad1(Qt,t) (lower panels) of the tuning mode for zero system–bath coupling (left column) and system–bath coupling of intermediate strength (λc = λt = 53.0 cm−1, right column). Let us consider the isolated conical intersection first (panels (a) and (c)). The localized wave packet prepared at t = 0 on the S2 surface propagates to the right (towards negative Qt) following the gradient of the S2 surface (see Fig. 1(a)). Within half of a vibrational period, the wave packet reaches the conical intersection and partially transfers to the S1 surface, where it experiences a gradient in the opposite direction. This results in coherent wave-packet dynamics in the tuning mode at short times, see panels (a) and (c). For the isolated two-mode conical intersection, the S2 → S1 radiationless transition is incomplete. Beyond ≈200 fs, the structure of the probability density becomes more and more chaotic, especially on the S1 surface. The coupling of the conical intersection to the environment results in a qualitatively different picture (panels (b) and (d)). The probability densities are smoothed and exhibit rather regular quasi-periodic behavior. The transfer of energy to the bath assists in the relaxation of the wave packet from the upper adiabatic surface to the lower adiabatic surface. Recurrences of the probability density to the upper surface are strongly suppressed. For the dissipative conical intersection, the probability density of the tuning mode on the S1 surface at t = 1 ps is peaked at Qt ≈ 1.8 (panel (d)), which is not the case for the isolated conical intersection (panel (c)). This illustrates that the vibrational excess energy available after the S2 → S1 radiationless transition is effectively drained into the environment, allowing relaxation of the system to a stationary state.
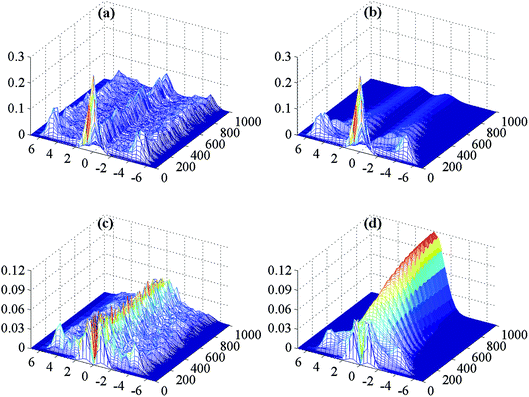
The probability densities Pad2(Qc,t) (upper panels) and Pad1(Qc,t) (lower panels) of the coupling mode are shown in Fig. 7. As in Fig. 6, the left column shows the bath-free dynamics, while the right column displays the dynamics of the conical intersection coupled to a bath with λc = λt = 53.0 cm−1. For the isolated conical intersection (panels (a) and (c)) the probability density in Qc spreads very rapidly in a symmetric manner. The probability density on the upper surface exhibits three “ridges” at Qc = 0 and Qc = ±5 (the outer turning point in Qc). The wave packet on the lower surface exhibits a symmetry-required node at Qc = 0 and the width of the probability density shrinks with time. Beyond ≈200 fs, the probability densities on both surfaces are quite noisy. Panels (b) and (d) of Fig. 7 illustrate the effect of the system–bath coupling on the probability densities Pad2(Qc,t) and Pad1(Qc,t). The peak of Pad2(Qc,t) at Qc = 0 rapidly disappears, while the peaks near the turning points decrease in height and move inwards, reflecting the loss of vibrational energy from the coupling mode. On the lower adiabatic surface, the width of the vibrational distribution narrows even more rapidly and the zero of Pad1(Qc = 0, t = 0) develops into a pronounced peak centered at Qc = 0, see Fig. 7(d). As observed for the tuning mode, the probability densities of the coupling mode are much smoother than for the isolated two-mode conical intersection.
IV. Discussion
Considering the population dynamics of the diabatic ππ* state, it is eye-catching how sensitive the electronic population dynamics is to the coupling of the system modes to an environment (Fig. 2(a) and 4(a)). Even the weakest system–bath coupling considered here (λc = λt = 2.1 cm−1), completely quenches the irregular fluctuations of Pdi2(t) beyond 400 fs (Fig. 2(a), magenta line). With somewhat larger, but still weak, system–bath coupling (λc = λt = 10.6 cm−1), a qualitatively different behavior of Pdi2(t) is observed: the diabatic population probability exhibits completely regular coherent beatings with the frequency of the tuning mode (Fig. 2(a), red line). With further increases in system–bath coupling, these coherent beatings are damped out on time scales of a few hundred femtoseconds. For a longer bath relaxation time (γc−1 = γt−1 = 166 fs), the coherent oscillations live longer.It is interesting to compare these numerically exact results with earlier results obtained with multi-level Redfield theory for the same two-state two-mode conical intersection coupled in the same manner to an ohmic bath.19 In this earlier work, the secular approximation4,24 to multi-level Redfield theory was employed. For a very weak system–bath coupling (η = 0.003 in ref. 19, λc = λt = 2.1 cm−1 in Fig. 2(a)), the diabatic population probabilities are essentially identical. It can be concluded that for very weak system–bath coupling the spectral function of the bath does not matter and multi-level Redfield theory gives correct results even with the secular approximation. For somewhat stronger system–bath coupling (η = 0.015 in ref. 19, λc = λt = 10.6 cm−1 in Fig. 2(a)), on the other hand, secular Redfield theory fails dramatically. The pronounced coherent beatings of Pdi2(t) (red line in Fig. 2(a)) are completely absent in the simulations with secular Redfield theory.19 A later study performed with non-secular multi-level Redfield theory for a three-mode model of the S2–S1 conical intersection in pyrazine20 reproduces the coherent oscillations of Pdi2(t), albeit somewhat less pronounced and less regular than in Fig. 2(a), which may be a consequence of the additional tuning mode or the different spectral densities employed. A very similar result was obtained by Gelman et al.26 for the two-mode model with a modified (Lindblad-type) Redfield theory. It can be concluded that non-secular multi-level Redfield theory gives a qualitatively correct description of the diabatic electronic population dynamics for weak coupling of a conical intersection to a bath (see also ref. 22). The mechanism of the dedamping of the tuning mode for intermediate system–bath coupling strength, which leads to the pronounced coherent beatings in Pdi2(t), was qualitatively explained in ref. 20. The coupling mode becomes particularly highly excited during the ultrafast internal conversion process at the conical intersection (see below) and is therefore highly susceptible to environmental damping. The efficient damping of the amplitude of the coupling mode reduces the intrinsic mode–mode coupling of the conical intersection, thus “liberating” the tuning mode to perform long-lived oscillations which in turn drive the diabatic electronic population dynamics. In addition, the center of the vibrational wave packet migrates towards the minimum of the S1 PE surface at Qt ≈ 1.4 and thus away from the conical intersection at Qt ≈ −3.5 (see Fig. 2(a)) to a region where the PE surface is more harmonic than in the vicinity of the conical intersection.
These phenomena are further illustrated by the dynamics of the expectation values of Qt and Pt in Fig. 3 and 5. Fig. 3 shows that a very weak system–bath coupling (λc = λt = 2.1 cm−1, magenta line) causes a damping of the oscillations of 〈Qt〉t and 〈Pt〉t of the isolated conical intersection (black line), whereas a stronger system–bath coupling (λc = λt = 10.6 cm−1) leads to a pronounced increase of the oscillations of 〈Qt〉t and 〈Pt〉t and a suppression of their damping (red line in Fig. 3), which is the dedamping effect discussed above. With further increase of the system–bath coupling, the coherent oscillation of the tuning mode is damped by the environment. For the strongest system–bath coupling considered here (λc = λt = 106.0 cm−1, green line in Fig. 3), the wave packet becomes stationary at Qt ≈ 2.0 at 500 fs. For a bath with longer memory time (γc−1 = γt−1 = 166 fs), the dedamping of 〈Qt〉t and 〈Pt〉t is more pronounced at λc = λt = 53.0 cm−1 and the coherent oscillations of the tuning mode extend to longer times (blue line in Fig. 5).
Let us now consider the time evolution of the population probability Pad2(t) of the S2 state. Again, a very weak system–bath coupling, λc = λt = 2.1 cm−1, is remarkably efficient in suppressing the irregular fluctuations of Pad2(t) of the isolated conical intersection (Fig. 2(b), magenta line). With increasing system–bath coupling, the decay of Pad2(t) is significantly enhanced. For λc = λt ≥ 53.0 cm−1, Pad2(t) decays within less than 200 fs. It is noteworthy that the long-lived coherent oscillations of Pdi2(t) are completely absent in Pad2(t). This observation underlines that the long-lived coherent wave-packet motion occurs exclusively on the lower adiabatic PE surface away from the conical intersection. With longer bath memory time, γc−1 = γt−1 = 166 fs, the quenching of Pad2(t) by the environment is less pronounced, see Fig. 2(b).
The reduced probability densities of the coupling mode and the tuning mode in Fig. 6 and 7, respectively, provide additional insight. The probability densities in panels (a) and (c) clearly exhibit the irregular, chaotic character of the dynamics of the isolated two-state two-mode conical intersection. These irregularities are the time-domain signatures of the dense eigenvalue spectrum with incommensurable energy-level spacings which arise from the exceptionally strong nonadiabatic coupling at the conical intersection and the pronounced local anharmonicity of the adiabatic PE surfaces. These chaotic features of the dynamics at the conical intersection, which are reflected in various level spacing distributions,17 are highly sensitive to perturbations and are therefore eliminated by even very weak coupling to a dissipative environment. In contrast, the probability densities obtained for λc = λt = 53.0 cm−1 and shown in panels (b) and (d) of Fig. 6 and 7 are completely smooth and regular. The chaotic character of the dynamics was not observed in previous simulations for a three-mode model of the S2–S1 conical intersection in pyrazine,20,55 presumably because the second tuning mode of the conical intersection (the ν1 normal mode of pyrazine) already acts as a quencher of the chaotic dynamics.
The vibrational probability densities Padk(Qc,t) and Padk(Qt,t) of the dissipative conical intersection in Fig. 6(b) and (d) and 7(b) and (d) illustrate how the large excess energy in the tuning mode and the coupling mode, which is generated within ≈30 fs after excitation, is drained out of the system dynamics, resulting in a nearly stationary wave packet at ≈1 ps. Comparing panels (a) and (b) of Fig. 7, it can be seen that the ridge of the density surviving on the S2 surface at Qc = 0 in panel (a) is turned into a valley by the coupling with the bath (panel (b)). The recurrences of the wave packet to the S2 surface are strongly suppressed and occur near the minimum geometry of the S1 PE surface in the Qc coordinate (see Fig. 1(b)), opposed to the isolated conical intersection, where the recurrences to the S2 surface occur at Qc = 0 and at the outer turning points of the motion in Qc, see Fig. 7(a).
V. Conclusions
We performed extensive simulations of the electronic and vibrational dynamics of a two-state two-mode conical intersection which is weakly to moderately coupled to a dissipative environment. The bath oscillators are bilinearly coupled to the coupling mode and the tuning mode of the conical intersection. The chaotic features of the intrinsic dynamics of the conical intersection, which are clearly visible in the electronic population dynamics and the reduced vibrational probability densities, are completely wiped out by even very weak system–bath coupling. While the ultrafast nonadiabatic dynamics within the first ≈30 fs is unaffected by the coupling to the environment, the population probability of the upper adiabatic state is effectively quenched on sub-picosecond time scales by weak to moderate system–bath coupling. On the other hand, a counterintuitive dedamping of the dynamics of the tuning mode is observed for specific values of the system–bath coupling strength which depend on the bath memory time. This effect is a signature of the exceptionally pronounced nonseparability of the dynamics of the coupling and tuning modes of the conical intersection, to an extent that damping of the coupling mode liberates the dynamics of the tuning mode. Overall, the results confirm that the nonadiabatic wave-packet dynamics at a conical intersection is unusually sensitive to weak coupling to a thermal environment with the exception of the first few tens of femtoseconds. Due to the complexity of the intrinsic dynamics of the conical intersection, the simulations exhibit phenomena which are quite different from the familiar scenarios of the optical Bloch equations or the Brownian oscillator. Our calculations show, in particular, that dissipative conical intersections not only can maintain vibrational wave-packets revealing the tuning modes, but also can create vibrational wavepackets featuring the coupling mode(s). Related effects have been observed in recent time and frequency resolved experiments on β-carotene and rhodopsin.76,77The present study extends earlier simulations of the dynamics of conical intersections coupled to an environment, which were based on multi-level Redfield theory or similar models that are restricted to weak system–bath coupling and short bath relaxation time.19–22,25,26 With the HEOM method, we were able to explore system–bath couplings in the nonperturbative regime. With this method, system–bath couplings of arbitrary strength can be investigated for complex systems such as conical intersections, as demonstrated recently also by Duan and Thorwart.41 In future extensions of the present work, the coupling of the material system with femtosecond pulsed laser fields will be included in a nonperturbative manner. While a nonperturbative treatment of the laser-matter interaction may not be a necessity for the laser fields typically employed in spectroscopy, the inclusion of the laser–matter interaction in the equation of motion of the density matrix may be more straightforward and computationally efficient than the calculation of higher-order multi-time response functions and multiple nested integrals over the laser fields, which are required in the perturbative theory of nonlinear optics.78 The calculation of femtosecond time-resolved four-wave-mixing signals from laser-driven equations of motion has been demonstrated, for example, for pump-probe and photon-echo spectroscopy,46,79–81 two-dimensional electronic spectroscopy82 or femtosecond resonant Raman spectroscopy.83 The combination of nonperturbative HEOM simulations of dissipative nonadiabatic dynamics with the calculation of spectroscopic signals directly from field-driven equations of motion will become a powerful tool for the analysis and/or prediction of state-of-the-art time and frequency resolved nonlinear spectra.
Acknowledgements
Support from the Singapore National Research Foundation through the Competitive Research Programme (CRP) under Project No. NRF-CRP5-2009-04 is gratefully acknowledged. M.F.G. and W.D. acknowledge support from the Deutsche Forschungsgemeinschaft through a research grant and through the DFG-Cluster of Excellence “Munich-Centre for Advanced Photonics” (http://www.munich-photonics.de). M.F.G. thanks the members of the Zhao group for hospitality and numerous stimulating discussions. Fruitful discussions with Akihito Ishizaki are also thankfully acknowledged.References
- F. Bloch, Rev. Mod. Phys., 1957, 105, 1206 CrossRef CAS.
- A. G. Redfield, Adv. Magn. Opt. Reson., 1965, 1, 1 Search PubMed.
- G. W. Ford, M. Kac and P. Mazur, J. Math. Phys., 1965, 6, 504 CrossRef.
- W. H. Louisell, Quantum Statistical Properties of Radiation, Wiley, New York, 1973 Search PubMed.
- A. J. Leggett, S. Chakravarty, A. T. Dorsey, M. P. A. Fischer, A. Garg and W. Zwerger, Rev. Mod. Phys., 1987, 59, 1 CrossRef CAS.
- N. G. van Kampen, Stochastic Processes in Physics and Chemistry, North-Holland, Amsterdam, 1992 Search PubMed.
- U. Weiss, Quantum Dissipative Systems, World Scientific, Singapore, 1993 Search PubMed.
- W. Domcke, D. R. Yarkony and H. Köppel, Conical Intersections: Electronic Structure, Dynamics and Spectroscopy, World Scientific, Singapore, 2004 Search PubMed.
- W. Domcke, D. R. Yarkony and H. Köppel, Conical Intersections: Theory, Computation and Experiment, World Scientific, Singapore, 2011 Search PubMed.
- W. Domcke and G. Stock, Adv. Chem. Phys., 1997, 100, 1 CrossRef CAS.
- G. A. Worth and L. S. Cederbaum, Annu. Rev. Phys. Chem., 2004, 55, 127 CrossRef CAS PubMed.
- W. Domcke and D. R. Yarkony, Annu. Rev. Phys. Chem., 2012, 63, 325 CrossRef CAS PubMed.
- M. Klessinger and J. Michl, Excited States and Photochemistry of Organic Molecules, VCH, Weinheim, 1995 Search PubMed.
- M. A. Robb, F. Bernardi and M. Olivucci, Pure Appl. Chem., 1995, 67, 783 CrossRef CAS.
- D. R. Yarkony, Rev. Mod. Phys., 1996, 68, 985 CrossRef CAS.
- D. R. Yarkony, in Conical Intersections: Electronic Structure, Dynamics and Spectroscopy, World Scientific, Singapore, 2004, ch. 2, p. 41 Search PubMed.
- H. Köppel, W. Domcke and L. S. Cederbaum, Adv. Chem. Phys., 1984, 57, 59 CrossRef.
- T. Gerdts and U. Manthe, Chem. Phys. Lett., 1998, 295, 167 CrossRef CAS.
- A. Kühl and W. Domcke, Chem. Phys., 2000, 259, 227 CrossRef.
- A. Kühl and W. Domcke, J. Chem. Phys., 2002, 116, 263 CrossRef.
- B. Balzer and G. Stock, J. Phys. Chem. A, 2004, 108, 6464 CrossRef CAS.
- B. Baltzer and G. Stock, Chem. Phys., 2005, 310, 33 CrossRef.
- W. T. Pollard, A. K. Felts and R. A. Friesner, Adv. Chem. Phys., 1996, 93, 77 CrossRef CAS.
- K. Blum, Density Matrix Theory and Applications, Plenum Press, New York, 1981 Search PubMed.
- G. Katz, R. Kosloff and M. A. Ratner, Isr. J. Chem., 2004, 44, 53 CrossRef CAS.
- D. Gelman, G. Katz, R. Kosloff and M. Ratner, J. Chem. Phys., 2005, 123, 134112 CrossRef PubMed.
- L. S. Cederbaum, E. Gindensperger and I. Burghardt, Phys. Rev. Lett., 2005, 94, 113003 CrossRef PubMed.
- E. Gindensperger, I. Burghardt and L. S. Cederbaum, J. Chem. Phys., 2006, 124, 144103 CrossRef PubMed.
- E. Gindensperger, I. Burghardt and L. S. Cederbaum, J. Chem. Phys., 2006, 124, 144104 CrossRef PubMed.
- E. Gindensperger, H. Köppel and L. S. Cederbaum, J. Chem. Phys., 2007, 126, 034106 CrossRef PubMed.
- E. Gindensperger and L. S. Cederbaum, J. Chem. Phys., 2007, 127, 124107 CrossRef PubMed.
- I. Burghardt and J. T. Hynes, J. Phys. Chem. A, 2006, 110, 11411 CrossRef CAS PubMed.
- J. P. Malhado, R. Spezia and J. T. Hynes, J. Phys. Chem. A, 2011, 115, 3720 CrossRef CAS PubMed.
- J. P. Malhado and J. T. Hynes, J. Chem. Phys., 2012, 137, 22A543 CrossRef PubMed.
- Y. Tanimura and R. Kubo, J. Phys. Soc. Jpn., 1989, 58, 101 CrossRef.
- Y. Tanimura and P. G. Wolynes, Phys. Rev. A, 1991, 43, 4131 CrossRef CAS.
- A. Ishizaki and Y. Tanimura, J. Phys. Soc. Jpn., 2005, 74, 3131 CrossRef CAS.
- Y. Tanimura, J. Phys. Soc. Jpn., 2006, 75, 082001 CrossRef.
- V. Chernyak and S. Mukamel, J. Chem. Phys., 1996, 105, 4565 CrossRef CAS.
- K.-B. Zhu, R.-X. Xu, H. Y. Zhang, J. Hu and Y. J. Yang, J. Phys. Chem. B, 2011, 115, 5678 CrossRef CAS PubMed.
- H.-G. Duan and M. Thorwart, J. Phys. Chem. Lett., 2016, 7, 382 CrossRef CAS PubMed.
- M. F. Gelin, D. Egorova and W. Domcke, J. Chem. Phys., 2012, 136, 034507 CrossRef PubMed.
- A. W. Chin, J. Prior, R. Rosenbach, F. Caycedo-Soler, S. F. Huelga and M. B. Plenio, Nat. Phys., 2013, 9, 113 CrossRef CAS.
- A. Garg, J. N. Onuchic and V. Ambegaokar, J. Chem. Phys., 1985, 83, 4491 CrossRef CAS.
- Y. Tanimura, J. Chem. Phys., 2012, 137, 22A550 CrossRef PubMed.
- M. F. Gelin, Y. Tanimura and W. Domcke, J. Chem. Phys., 2013, 139, 214302 CrossRef CAS PubMed.
- A. Ishizaki and G. R. Fleming, J. Chem. Phys., 2009, 130, 234111 CrossRef PubMed.
- A. V. Pisliakov, M. F. Gelin and W. Domcke, J. Phys. Chem. A, 2003, 107, 2657 CrossRef CAS.
- D. Egorova, M. F. Gelin and W. Domcke, J. Chem. Phys., 2005, 122, 134504 CrossRef PubMed.
- V. Stert, P. Farmanara and W. Radloff, J. Chem. Phys., 2000, 112, 4460 CrossRef CAS.
- T. Horio, T. Fuji, Y.-I. Suzuki and T. Suzuki, J. Am. Chem. Soc., 2009, 131, 10392 CrossRef CAS PubMed.
- Y.-I. Suzuki, T. Fuji, T. Horio and T. Suzuki, J. Chem. Phys., 2010, 132, 174302 CrossRef PubMed.
- T. Suzuki, Molecules, 2014, 19, 2410 CrossRef PubMed.
- R. Schneider and W. Domcke, Chem. Phys. Lett., 1988, 150, 235 CrossRef CAS.
- R. Schneider, W. Domcke and H. Köppel, J. Chem. Phys., 1990, 92, 1045 CrossRef CAS.
- C. Woywod, W. Domcke, A. L. Sobolewski and H. J. Werner, J. Chem. Phys., 1994, 100, 1400 CrossRef CAS.
- G. Stock, C. Woywod, W. Domcke, T. Swinney and B. S. Hudson, J. Chem. Phys., 1995, 103, 6851 CrossRef CAS.
- S. Krempl, H. Winterstetter and W. Domcke, J. Chem. Phys., 1995, 102, 6499 CrossRef CAS.
- A. Raab, G. A. Worth, H. D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1999, 110, 936 CrossRef CAS.
- G. S. Latha and M. D. Prasad, J. Chem. Phys., 1996, 105, 2972 CrossRef CAS.
- U. Müller and G. Stock, J. Chem. Phys., 1997, 107, 6230 CrossRef.
- G. A. Worth, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 1998, 109, 3518 CrossRef CAS.
- J. Y. Fang and S. Hammes-Schiffer, J. Phys. Chem. A, 1999, 103, 9399 CrossRef CAS.
- M. Thoss, W. H. Miller and G. Stock, J. Chem. Phys., 2000, 112, 10282 CrossRef CAS.
- M. Ben-Nun and T. J. Martínez, Adv. Chem. Phys., 2002, 121, 439 CrossRef CAS.
- D. V. Shalashilin and M. S. Child, J. Chem. Phys., 2004, 121, 3563 CrossRef CAS PubMed.
- P. Puzari, B. Sarkar and S. Adhikari, J. Chem. Phys., 2006, 125, 194316 CrossRef PubMed.
- R. Martinazzo, K. H. Hughes, F. Martelli and I. Burghardt, Chem. Phys., 2010, 377, 21 CrossRef CAS.
- T. Grinev, M. Shapiro and P. Brumer, J. Chem. Phys., 2012, 137, 094302 CrossRef PubMed.
- T. Zimmermann and J. Vanićek, J. Chem. Phys., 2014, 141, 134102 CrossRef PubMed.
- M. Kanno, Y. Ito, N. Shimokura, S. Koseki, H. Kono and Y. Fujimura, Phys. Chem. Chem. Phys., 2015, 17, 2012 RSC.
- U. Werner, R. Mitrić, T. Suzuki and V. Bonačić-Kouteckỳ, Chem. Phys., 2008, 349, 319 CrossRef CAS.
- http://arrayfire.com/ .
- U. Manthe and H. Köppel, J. Chem. Phys., 1990, 93, 345 CrossRef CAS.
- W. Domcke, H. Köppel and L. S. Cederbaum, Mol. Phys., 1981, 43, 851 CrossRef CAS.
- M. Liebel, C. Schnedermann and P. Kukura, Phys. Rev. Lett., 2014, 112, 198302 CrossRef CAS PubMed.
- P. J. M. Johnson, A. Halpin, T. Morizumi, V. I. Prokhorenko, O. P. Ernst and R. J. D. Miller, Nat. Chem., 2015, 7, 980 CrossRef CAS PubMed.
- S. Mukamel, Principles of Nonlinear Optical Spectroscopy, Oxford University Press, New York, 1995 Search PubMed.
- L. Seidner, G. Stock and W. Domcke, J. Chem. Phys., 1995, 103, 3998 CrossRef CAS.
- M. F. Gelin, D. Egorova and W. Domcke, J. Phys. Chem. Lett., 2011, 2, 114 CrossRef CAS PubMed.
- M. F. Gelin, D. Egorova and W. Domcke, Acc. Chem. Res., 2009, 42, 1290 CrossRef CAS PubMed.
- J. Krčmář, M. F. Gelin and W. Domcke, J. Chem. Phys., 2015, 143, 074308 CrossRef PubMed.
- B. J. Rao, M. F. Gelin and W. Domcke, J. Phys. Chem. A, 2016, 120, 3286 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |