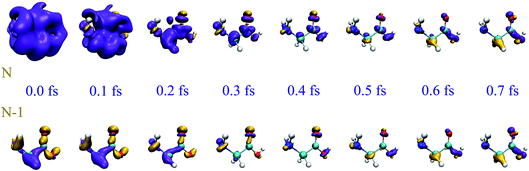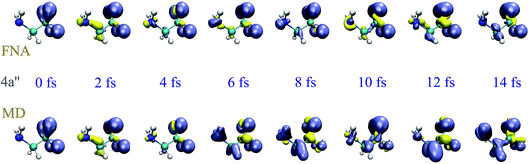Decoherence, control and attosecond probing of XUV-induced charge migration in biomolecules. A theoretical outlook
Received
11th April 2016
, Accepted 1st June 2016
First published on 1st June 2016
Abstract
The sudden ionization of a molecule by an attosecond pulse is followed by charge redistribution on a time scale from a few femtoseconds down to hundreds of attoseconds. This ultrafast redistribution is the result of the coherent superposition of electronic continua associated with the ionization thresholds that are reached by the broadband attosecond pulse. Thus, a correct theoretical description of the time evolution of the ensuing wave packet requires the knowledge of the actual ionization amplitudes associated with all open ionization channels, a real challenge for large and medium-size molecules. Recently, the first calculation of this kind has come to light, allowing for interpretation of ultrafast electron dynamics observed in attosecond pump–probe experiments performed on the amino acid phenylalanine [Calegari et al., Science 2014, 346, 336]. However, as in most previous theoretical works, the interpretation was based on various simplifying assumptions, namely, the ionized electron was not included in the description of the cation dynamics, the nuclei were fixed at their initial position during the hole migration process, and the effect of the IR probe pulse was ignored. Here we go a step further and discuss the consequences of including these effects in the photoionization of the glycine molecule. We show that (i) the ionized electron does not affect hole dynamics beyond the first femtosecond, and (ii) nuclear dynamics has only a significant effect after approximately 8 fs, but does not destroy the coherent motion of the electronic wave packet during at least few additional tens of fs. As a first step towards understanding the role of the probe pulse, we have considered an XUV probe pulse, instead of a strong IR one, and show that such an XUV probe does not introduce significant distortions in the pump-induced dynamics, suggesting that pump–probe strategies are suitable for imaging and manipulating charge migration in complex molecules. Furthermore, we show that hole dynamics can be changed by shaping the attosecond pump pulse, thus opening the door to the control of charge dynamics in biomolecules.
1 Introduction
Imaging electron dynamics in biomolecules with few-femtosecond or sub-femtosecond time resolutions is the first step towards achieving control of biologically relevant processes.1–8 The rapid progress in attosecond technology9–13 has already permitted the control of electron dynamics in atoms14,15 and hydrogen molecules,16,17 and recent experimental efforts aim at doing so in more complex molecules.4,7 So far two different approaches have been used to visualize electron dynamics in such systems. The first one is high-harmonic spectroscopy, where the light emitted after the round trip of an IR-driven molecular electron carries information about the cation dynamics with sub-fs temporal and sub-Å spatial resolutions.18–20 The other one is pump–probe spectroscopy,4,16,17,21 where an attosecond XUV pump pulse ionizes the molecule and a time-delayed fs IR pulse probes the dynamics generated in the molecular cation. The two approaches imply that an electron is ionized, by a strong IR field in the first case or a weak XUV field in the second case, but differ in the way the dynamics is probed in the cation: by the returning an electron itself or by another ultrashort pulse, respectively.
In either case, the sudden ionization of the molecule creates a hole that subsequently migrates on a time scale ranging from a few femtoseconds down to hundreds of attoseconds. The migration is due to a coherent superposition of electronic states generated by the pump pulse. This coherent superposition can be the result of the broad band of the ionizing pulse, which covers several ionization thresholds, or of the appearance of a dense manifold of ionic states due to rearrangements in the electronic structure of the molecular cation induced by electron correlation. In both cases the charge is expected to move from one molecular site to another or to fluctuate all along the molecular backbone. Depending on the initial wave packet that is created, the interplay between the electronic and nuclear dynamics can lead to the final localization of the charge on a specific molecular site.
A fully ab initio theoretical description of the correlated motion of electrons and nuclei that follows ionization by laser pulses is still very challenging, even for the simplest molecule H2,22 and practically out of reach for many-electron polyatomic molecules. Besides the intrinsic limitations associated with the large number of electronic and nuclear degrees of freedom, which are also applicable to calculations involving molecular bound states, there is the additional limitation of dealing with the electronic continuum. For this reason, most theoretical approaches to large molecules have ignored the ionization step and have only described the cation dynamics that arises from arbitrarily chosen initial wave packets.1–3 Notably a “sudden ionization” ansatz, corresponding to the creation of a Koopman's hole,23,24i.e. the removal of an electron from a ground state Hartree–Fock orbital, generating a wave packet through electron correlation in the final ion, has been largely employed in earlier studies. Alternatively, the evaluation of ionization amplitudes employing Coulomb waves located in the molecular center of mass25–28 have permitted the gap to be reduced between completely ignoring ionization and fully describing it, but with variable success.29 The first theoretical calculation that fully accounts for the ionization induced by an attosecond pulse in a large molecule, namely phenylalanine, has been reported very recently.4 At variance with earlier calculations, in this work the initial wave packet was built from actual ionization amplitudes, which were obtained from the solution of the scattering equations in the framework of the static exchange DFT method.30–32
The first experimental evidence of ultrafast charge migration has been reported by Calegari et al.4 for the case of the amino acid phenylalanine. In this work, a sub-300-as XUV pulse was used to ionize the molecule and a controlled time-delayed 4 fs IR pulse to probe the dynamics induced by the former. The measured yields for the production of doubly-charged immonium fragments exhibit few-fs oscillations superimposed on a typical smooth decreasing background associated with the much slower dissociation dynamics. The unusually fast oscillations were interpreted as the signature of the coherent electron dynamics generated by the attosecond pulse on the remaining molecular cation. This interpretation was supported by the good agreement between the observed frequencies and those resulting from the above-mentioned theoretical calculations,4,32 in which the actual transition amplitudes associated with the different ionization channels were accurately evaluated. Evaluation of these amplitudes is essential to obtain a realistic description of the electronic wave packet motion, which is dictated by the relative value of the corresponding moduli and phases associated with the different ionization channels.
In spite of the significant advance provided by such calculations, the comparison with the actual experimental measurements was somewhat indirect. First, following common practice for the subject,1,3,8,29,33,34 the evolution of the charge density in the cation was described by assuming that the ionized electron leaves the system instantaneously (sudden ionization), so that it does not interact with the remaining electrons at all. In other words, as soon as the interaction of the attosecond pulse with the neutral molecule is over, the theory described the evolution of an (N − 1)-electron system instead of that of the original N-electron one. This looks like a reasonable approximation when the ejected electron is far away from the remaining cation, i.e., long after the interaction with the attosecond pulse. But what about the early stages of the wave packet evolution when the ionized electron is still close to the cation? Second, due to the complexity of the chosen molecule, charge dynamics was studied by assuming that the nuclei remain fixed during the whole process. As in existing literature,1,3,4,29,33,34 it was argued that nuclear motion should have a negligible effect at the early stages of this evolution, typically during the first tens of fs, since the shortest vibrational periods in this kind of molecules are around 10 fs and usually correspond to peripheral X–H bonds (X = C, N, O), which are barely involved in charge delocalization processes. However, recent theoretical studies have shown that coherence between two electronic states can be lost in less than 10 fs when the nuclei move across a conical intersection.35 Furthermore, the quantum distribution of geometries inherent to any nuclear wave packet introduces additional dephasing in a similar time scale.8 Since conical intersections are a common feature in large molecules, can we really assume that nuclear motion does not play any role in the early stages of the charge migration process? Third, as mentioned above, the charge dynamics is mostly determined by the ionization amplitudes associated with all open channels, i.e. by the initial electron wave packet created in the cation. So, in principle, one would expect that by changing those amplitudes one should also change the electron wave packet dynamics. But is this feasible in practice, e.g., by modifying the pump pulse characteristics? The latter question is relevant because, if answered positively, it would open the way to control the charge dynamics in biomolecules. The fourth and final remark is that the effect of the probe pulse was completely ignored. In principle, the role of the probe pulse is to project, at a given time (the pump–probe delay), the dynamics induced by the attosecond pump onto specific observables. Ideally, the probe pulse should not distort the dynamics induced by the pump pulse, but in practice it does. As explained in earlier work,36 the ideal probe pulses are those containing UV or XUV photons, since, due to their short wavelength, distortion of the molecular potential, and hence of the pump induced dynamics, is reduced to a minimum. Nevertheless, even such a “gentle” probe pulse will further ionize the system, thus leading to a molecular dication that can subsequently break leading to different neutral, singly- and doubly-charged fragments. In fact, the mass and energy of these ions are the actual observables in most pump–probe experiments. The same occurs with IR probe pulses, with the additional complication that, due to their longer wavelengths, they also affect the pump-induced dynamics.16 The question is then: how does the dynamics generated by the XUV attosecond pulse reflect in the actual pump–probe signal?
In this paper we partially address the previous questions for the case of the glycine molecule. First, we have included the ionized electron in the description of the wave packet dynamics that follows the interaction with the attosecond pulse. We show that the ionized electron only leaves its trace during approximately the first femtosecond. Second, we have made use of Ehrenfest non-adiabatic dynamics to include the effect of nuclear motion on the charge migration process. We show that the latter process is not affected by the nuclear motion during the first 8 fs, but has a significant effect at later times. Nevertheless, modifications of electron dynamics at these later times do not destroy the coherent motion of the electronic wave packet during a few tens of fs. Third, we have employed three different XUV attosecond pulses, all of them generated in recent experiments,4,37 covering different spectral ranges and with different envelopes, to show that the charge dynamics induced in each case is substantially different. Finally, by means of a simple model that makes use of realistic ionization amplitudes within the fixed-nuclei approximation, we show how the XUV-induced dynamics manifests in the computed double ionization yields after interaction with a “gentle” probe pulse, namely, another XUV pulse, which apart from further ionizing the molecular cation, barely perturbs the molecular potential. This is a first step towards understanding the role of less “gentle” probe pulses, such as the IR one used in earlier experiments.
2 Theoretical methods
A theoretical description of laser–matter interactions using attosecond light sources requires of a time-dependent treatment. We work with two different approaches, both based on the density functional theory (DFT) formalism: (i) the static-exchange DFT method plus time-dependent perturbation theory, and (ii) the time-dependent Kohn–Sham (TDKS) method combined with Ehrenfest molecular dynamics (TDDFT-MD). The former will be used to evaluate the ionization amplitudes and the second one to describe the evolution of the ionic system when nuclear motion is included. The static-exchange DFT method30,31,38,39 has been successfully applied to describe ionization of many molecules, from the simple N2 or CO molecules40 to biomolecules such as the amino acid phenylalanine.4 The strength of this method lies in the accurate description of the continuum electron wave function, which allows for an accurate evaluation of photoionization amplitudes and cross sections of molecular systems. The combination of this method with first-order time-dependent perturbation theory has recently provided the first reliable description of the electronic wave packet created in the ionization of a biomolecule by a broadband attosecond pulse.4,32 Previous applications of this method have either ignored the nuclear motion (fixed-nuclei approximation, FNA) or have included at most a single nuclear degree of freedom, which is appropriate for diatomic molecules40,41 or for small polyatomic molecules in problems where a single vibrational mode is active.42,43 Here we go a step further and include nuclear motion by means of the TDDFT-MD method, which combines Ehrenfest molecular dynamics (MD) for the nuclear motion with a time-dependent DFT (TDDFT) description of the electronic dynamics as implemented in the CPMD package.44 In this section, we will first summarize the essence of the static-exchange DFT method and its implementation in the framework of first-order time-dependent perturbation theory, and then briefly describe the basic equations employed to describe the evolution of the N and N − 1 electron densities associated, respectively, with the full and the cationic system. Finally, we will explain our implementation of the TDDFT-MD method to account for the nuclear motion during the evolution of the electronic wave packet created in the ionization step.
2.1 The initial electronic wave packet
Attosecond pulses are mainly produced from high-harmonic generation. These pulses are typically of low intensity and contain frequencies in the XUV spectral domain. In this context, one can make use of first-order time-dependent perturbation theory to describe their interaction with matter. Thus, the wave packet created upon the interaction of the molecule with such pulses can be written in the basis of molecular eigenstates as| | 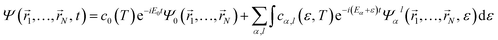 | (1) |
where Ψ0(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1,…,
1,…,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N) is the ground state of the neutral molecule and Ψαl(
N) is the ground state of the neutral molecule and Ψαl(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1,…,
1,…,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N, ε) describes the N-electron system where one electron is in the continuum with energy ε and angular momentum l, and the ion is left behind with a hole in the α orbital. The time evolution of the wave packet is given by the stationary phases in the absence of the field (t > T, where T is the pulse duration) and the corresponding amplitudes at the end of the pulse:
N, ε) describes the N-electron system where one electron is in the continuum with energy ε and angular momentum l, and the ion is left behind with a hole in the α orbital. The time evolution of the wave packet is given by the stationary phases in the absence of the field (t > T, where T is the pulse duration) and the corresponding amplitudes at the end of the pulse:| | 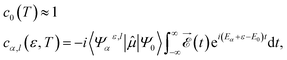 | (2) |
where 〈Ψαε,l|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |Ψ0〉 is the dipole transition matrix element connecting the ground and a continuum state,
|Ψ0〉 is the dipole transition matrix element connecting the ground and a continuum state, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) stands for the dipole operator (here we have used the length gauge form of this operator), the time integral is the Fourier transform of the electric field,
stands for the dipole operator (here we have used the length gauge form of this operator), the time integral is the Fourier transform of the electric field, 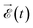 , and (Eα + ε − E0) is the energy absorbed by the system. The field is defined from 0 to T using experimental temporal envelopes, F(t), in the form
, and (Eα + ε − E0) is the energy absorbed by the system. The field is defined from 0 to T using experimental temporal envelopes, F(t), in the form 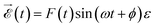 , with
, with ![[small epsilon, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e7.gif) being the polarization vector and ϕ the carrier-envelope phase, which is fixed to zero. Due to our definition of the field, the integral in eqn (2) can be identically evaluated in the interval [0, T].
being the polarization vector and ϕ the carrier-envelope phase, which is fixed to zero. Due to our definition of the field, the integral in eqn (2) can be identically evaluated in the interval [0, T].
The final continuum state is obtained by using the static-exchange DFT method as described in ref. 30, 31 and 39. In brief, we make use of the DFT formalism as implemented in the Amsterdam Density Functional (ADF) package45,46 to compute the ground state of the neutral molecule, employing the LB94 functional with a TZP basis. The first ionization potential of the molecule is computed using the outer-valence Green's function method and the DFT-LB94 eigenvalues are accordingly shifted. The calculated Kohn–Sham density and orbitals are used to represent the exchange and correlation potentials needed to solve the multichannel scattering equations that describe a continuum electron in the presence of an (N − 1)-electron molecular cation represented by a Slater determinant that includes the above-mentioned orbitals with the exception of that from which the electron has been ionized. Both the original Kohn–Sham orbitals and the continuum electron are written as a multicenter expansion in a basis of B-splines, which is particularly suitable to represent the continuum functions at any desired distance from the molecular center of mass. Evaluation of a continuum state associated with a particular electron energy is made by using the Galerkin approach.47,48 The multicenter expansion consists of a basis placed at the center of mass of the molecule, containing 111 B-splines enclosed in a sphere of 30 a.u. for the radial components and spherical harmonics with a maximum angular momentum of lmax = 20, and a smaller basis located at each atomic center containing B-splines in spheres ranging from 0.2 to 1.6 a.u. and with lmax = 2.
In this paper, we will present results for charge migration dynamics originating from two different ways: (i) by removing an electron from a given orbital of the neutral molecule, as it has been done in most extant theoretical works,1,3,29,49 and (ii) by creating a coherent superposition of one-hole states, as in the case of ionization by an attosecond pulse. It is in the second context where one cannot avoid evaluating the ionization amplitudes.4,32 The common feature in both scenarios, however, is the formation of a non-stationary cationic state, which induces the hole dynamics along the molecular skeleton.
2.2
N-Electron and (N − 1)-electron densities
A common theoretical practice to visualize charge migration in large molecules is to compute the electron density in the remaining ion, assuming that the dynamics of the photoelectron and that of the cation can be decoupled. This approximation will be valid as long as the interaction of the leaving photoelectron and the ion is negligible, for instance, if the electron is rapidly ejected. To validate this approximation within our DFT-based formalism, we have compared the electron densities of the N and (N − 1)-electron systems. In the first case, the effect of the continuum electron is explicitly included. In the second case, a common procedure is to make use of the reduced density matrix formalism to get rid of the ejected electron.
We compute the time-dependent one-particle electron density from the perturbed part of the N-electron wave function, as
| | 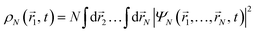 | (3) |
where
ΨN(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1
1,…,
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N
N,
t) is the
N-electron wave packet created by the XUV pulse, which can be written, as in
eqn (1), as an expansion over
N-electron continuum eigenstates:
| | 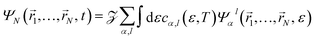 | (4) |
with
![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif)
being a normalization factor. The corresponding expression for the one-particle density in the basis of spin-orbitals is given by
| | 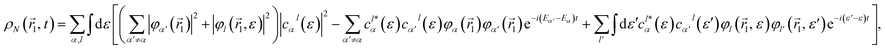 | (5) |
where
φα(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1
1) is a Kohn–Sham spin-orbital and
φl(
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1
1,
ε) is a continuum spin orbital. The above expression has a stationary part, the first term, and two other terms that lead to variations of the electron density with time. We will see oscillations in the density with a periodicity dictated by the energy differences between cationic states (second term) and between continuum orbitals themselves (third term). The former are possible because electrons can be ejected with the same energy and angular momentum from different orbitals. The third term is expected to vanish in the neighborhood of the molecule if one waits long enough until the ejected electron is far away from the molecule. When this limit is reached, it is legitimate to ignore this electron and define a one-particle electron density from an (
N − 1)-electron system. For this purpose, we rely on the reduced density matrix formalism, where the
N-electron wave function is first projected into the continuum wave functions and then integrated over all continuum energies, thus leading to an
N − 1 ionic electron density
| | 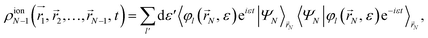 | (6) |
in which the brackets indicate an integral over the
N-th spatial coordinate. We then define the ion one-particle electron density as
| | 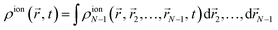 | (7) |
where one now has an integral over the spatial coordinates of
N − 2 instead of
N − 1 electrons. Introducing
(4) in the above equation results in the following expression for the electron density of the ion:
| | 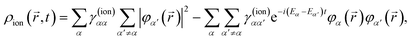 | (8) |
where we have introduced the reduced density matrix,
γ(ion)αα′, in the form
| | 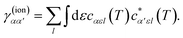 | (9) |
For illustrative purposes, it is common to define the hole density as the difference between the electron density that corresponds to the initial state of the neutral target and that of the cation, ρhole(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t) = ρneutral(
, t) = ρneutral(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) − ρion(
) − ρion(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t). For consistency, in the case of the N-electron system we will use a similar expression, where ρion(
, t). For consistency, in the case of the N-electron system we will use a similar expression, where ρion(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t) is now replaced by ρN(
, t) is now replaced by ρN(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t) given in eqn (5). The electron density of the neutral molecule is simply given by the sum of the squares of the occupied Kohn–Sham orbitals,
, t) given in eqn (5). The electron density of the neutral molecule is simply given by the sum of the squares of the occupied Kohn–Sham orbitals, 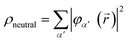 , and thus the hole density is simply given by
, and thus the hole density is simply given by
| | 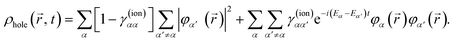 | (10) |
2.3 Classical Ehrenfest nuclear dynamics
To account for non-adiabatic effects in the evolution of inner-shell vacancies created by XUV light, we have performed first-principles calculations within the so-called Ehrenfest molecular dynamics (MD) approximation where the mean field potential energy surface driving the nuclear dynamics is computed at the TDDFT level. In earlier work,35,49 Ehrenfest MD has also been combined with an ab initio CASSCF methodology to study charge migration processes involving a reduced number of electronic states. A detailed description of our TDDFT MD method can be found in ref. 44, 50 and 51. Briefly, an isolated glycine molecule was placed in a tetragonal box of dimensions 30 × 20 × 20 Å. Both the Kohn–Sham orbitals and the electronic density were expanded in a plane wave basis set using an energy cutoff of 70 Ry. Core electrons were replaced by pseudo-potentials (PP) of the standard Troullier–Martins form52 and PP energies and forces were evaluated using the Kleinman–Bylander scheme.53 The exchange correlation energy was calculated using the PBE functional.54 The orbitals of the neutral glycine molecule were optimized using a convergence threshold of 10−8. In TDDFT-based Ehrenfest MD, the electronic density evolves according to the time-dependent Kohn–Sham (TDKS) equations.55 The propagation of the electronic degrees of freedom was started from a non-equilibrium electronic structure in which an electron is removed from a previously occupied KS orbital of neutral glycine. This initial electron density, which does not correspond to a specific state of Gly+, was then propagated by numerical integration of the unrestricted TDKS equations using an iterative Crank–Nicolson algorithm combined with a two-step Runge–Kutta scheme to maintain the δt3 order accuracy (for more details on the implementation, see a recent review56). A time-step of 0.01 a.u. was chosen to ensure energy conservation within 1% over the entire simulation length (25 fs). The initial atomic configuration was taken from a geometry optimization of the uncharged system at 0 K. The forces on the nuclei were computed according to the Hellmann–Feynman theorem as the analytic derivative of the expectation value of the energy. Due to the fact that the number of α and β electrons is unbalanced in the cation, the hole density at each instant of the propagation is given by the difference between the α and β spin densities.44
3 Effect of the ionized electron on the cation dynamics
We explore the signature of the emitted photoelectron on the cationic dynamics right after the ionization event. As mentioned before, most extant works in this field consider a sudden electron emission and simply capture the dynamics of the remaining cation. Alternatively, we calculate here the expected value of the one-particle density operator for the N-electron system in order to trace in time the photoelectron ejection and assess its effect in the remaining cationic density. To that end, we have chosen a realistic case in which the most stable conformer of the glycine molecule is ionized upon the interaction with the experimentally available sub-300-as pulse reported in,4 with a spectral energy bandwidth covering photon energies from 18 to 35 eV. The selected glycine conformer is the most abundant one at room temperature (≃60%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57)), so in line with the results of ref. 32 for the phenylalanine molecule, one can expect that the hole dynamics observed in a real experiment should not differ significantly from the one reported here. For consistency, the same conformer has been used in all calculations reported in the forthcoming sections. To avoid spurious reflections of the photoelectron at the box boundaries, we have used a rather large simulation box of 100 a.u. for the radial grid. The XUV pulse is sufficiently energetic to eject an electron from the 15 outer orbitals of glycine, leading to the formation of a coherent superposition of ionic states, as described in eqn (1), including all those 15 states with their associated electronic continua. One can then extract the one-particle electron density as given in eqn (8) for the (N − 1)-electron system, i.e. by first projecting into the continuum states as shown in expression (6), or instead, extract it directly from the N-electron target as defined in eqn (3).
57)), so in line with the results of ref. 32 for the phenylalanine molecule, one can expect that the hole dynamics observed in a real experiment should not differ significantly from the one reported here. For consistency, the same conformer has been used in all calculations reported in the forthcoming sections. To avoid spurious reflections of the photoelectron at the box boundaries, we have used a rather large simulation box of 100 a.u. for the radial grid. The XUV pulse is sufficiently energetic to eject an electron from the 15 outer orbitals of glycine, leading to the formation of a coherent superposition of ionic states, as described in eqn (1), including all those 15 states with their associated electronic continua. One can then extract the one-particle electron density as given in eqn (8) for the (N − 1)-electron system, i.e. by first projecting into the continuum states as shown in expression (6), or instead, extract it directly from the N-electron target as defined in eqn (3).
In Fig. 1 we show the early evolution of the hole density, ρhole(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = ρneutral(
,t) = ρneutral(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) − ρion(
) − ρion(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t), in both scenarios, i.e., by including (top row) and excluding (bottom row) the ionized electron, respectively. As can be seen, the ejected electron spreads around the whole molecule when t < 0.2 fs, so that one cannot ignore its presence in the evaluation of the hole density. Later on, the ionized electron vanishes from the vicinity of the molecular skeleton, but the correlation effects induced on the dynamics of the remaining cation are still visible, up to t ∼ 0.7 fs. At longer times, the evolution of the hole density is practically the same as that resulting from ignoring the ionized electron, as shown in Fig. 2. This figure provides a more quantitative information about the role of the ionized electron, by comparing the actual electron densities integrated around different molecular sites. Fig. 2 shows again that the effect of the ionized electron is only appreciable during the first half of femtosecond. The precise value of this elapsed time will strongly depend on the kinetic energy of the photoelectron and, consequently, it will depend on the energy spectrum of the pulse employed to ionize the molecule. In the present case, the broad pulse bandwidth ranges from ∼15–35 eV, leading to the emission of relatively slow electrons, since the ionization potential (IP) from the highest-occupied molecular orbital (HOMO) of glycine is around 11 eV, while for the lowest valence orbital reached by the pulse (6a′) it is close to 32 eV. The resulting electronic wave packet is thus built from components of relatively low kinetic energy, giving a lower bound for this elapsed time. The general conclusion is that in the very early stages of the process, the observed dynamics will be exactly the same as that of the residual cation in the absence of the photoelectron, thus proving that, although one has to account for ionization in order to obtain a realistic description of the electronic wave packet generated by the XUV pulse, one can safely ignore the ionized electron in the subsequent evolution of the electronic wave packet in the cation.
, t), in both scenarios, i.e., by including (top row) and excluding (bottom row) the ionized electron, respectively. As can be seen, the ejected electron spreads around the whole molecule when t < 0.2 fs, so that one cannot ignore its presence in the evaluation of the hole density. Later on, the ionized electron vanishes from the vicinity of the molecular skeleton, but the correlation effects induced on the dynamics of the remaining cation are still visible, up to t ∼ 0.7 fs. At longer times, the evolution of the hole density is practically the same as that resulting from ignoring the ionized electron, as shown in Fig. 2. This figure provides a more quantitative information about the role of the ionized electron, by comparing the actual electron densities integrated around different molecular sites. Fig. 2 shows again that the effect of the ionized electron is only appreciable during the first half of femtosecond. The precise value of this elapsed time will strongly depend on the kinetic energy of the photoelectron and, consequently, it will depend on the energy spectrum of the pulse employed to ionize the molecule. In the present case, the broad pulse bandwidth ranges from ∼15–35 eV, leading to the emission of relatively slow electrons, since the ionization potential (IP) from the highest-occupied molecular orbital (HOMO) of glycine is around 11 eV, while for the lowest valence orbital reached by the pulse (6a′) it is close to 32 eV. The resulting electronic wave packet is thus built from components of relatively low kinetic energy, giving a lower bound for this elapsed time. The general conclusion is that in the very early stages of the process, the observed dynamics will be exactly the same as that of the residual cation in the absence of the photoelectron, thus proving that, although one has to account for ionization in order to obtain a realistic description of the electronic wave packet generated by the XUV pulse, one can safely ignore the ionized electron in the subsequent evolution of the electronic wave packet in the cation.
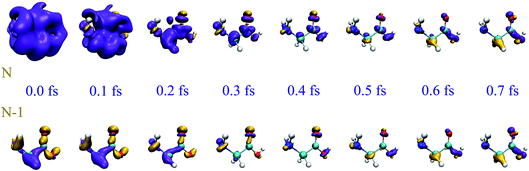 |
| | Fig. 1 Comparison of hole densities corresponding to N and N − 1 electron systems right after the action of a sub-300-as XUV pulse. For the sake of clarity, the hole density has been referenced to its time-averaged value, so that yellow and purple colors indicate, respectively, excess and default of charge with respect to the average hole density. Upper rows: N-electron system (see text). Lower rows: (N − 1)-electron system. Isosurfaces with values 8 × 10−4 and −8 × 10−4 a.u. are plotted in yellow and purple, respectively. Zero time is taken right at the end of the XUV pulse. | |
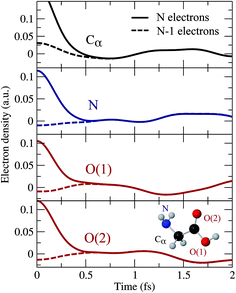 |
| | Fig. 2 Variation of the hole density obtained around different molecular sites as a function of time with respect to its time-averaged value. Full lines: N-electron system. Dashed lines: (N − 1)-electron system. Zero time is taken right at the end of the XUV pulse. | |
4 Effect of nuclear motion on the cation dynamics
To investigate the effect of the nuclear motion on the XUV induced dynamics, we have compared the results of the TDDFT-MD method described in section 2.3, in which the nuclear motion is described in the framework of a semiclassical Ehrenfest approach, with those obtained from TDDFT calculations in which the nuclear positions remain fixed (fixed-nuclei approximation, FNA). For a meaningful comparison, both types of calculations have been performed by using the same code and the same set of parameters (initial wave packet, basis set, integration steps, exchange-correlation functional, box, etc.), the only difference being the turning on or off of the nuclear dynamics, respectively. To simplify the analysis, we have considered one-hole initial states resulting from single-electron removal from specific Kohn–Sham orbitals, instead of initial states that result from the coherent superposition of one-hole states as those arising in ionization by attosecond pulses. As an illustration, we have considered electron removal from the 4a′′ and 14a′ orbitals. Fig. 3 and 4 show the corresponding hole densities as functions of time. As can be seen, the effect of nuclear motion is negligible within the first 6–8 fs, whereas it is noticeable at longer times, up to the point that it leads to an entirely different dynamics. The time interval within which nuclear motion can be ignored is significantly shorter than the typical periods of the glycine vibrational modes. This is likely due to the relatively rapid non-adiabatic transitions between different electronic states. This result is compatible with the time scales found by Vacher et al.8,35 for benzene and its derivatives. Since our TDDFT calculations account for non-adiabatic effects involving a large manifold of molecular states, the conclusion is that nuclear motion starts to affect electron dynamics right after the first non-adiabatic transition.
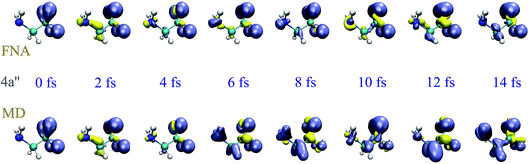 |
| | Fig. 3 Time evolution of the spin density, defined as ρα − ρβ, after removing an electron with α-spin from the 4a′′ orbital. The isosurfaces enclose charge densities larger than 0.005 a.u. of β (blue) and α (yellow) electrons. | |
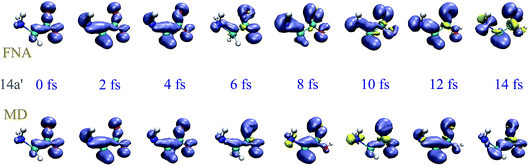 |
| | Fig. 4 Same as Fig. 3 for the 14a′ orbital. | |
As shown in previous work,4 coherent hole motion can lead to rapid oscillations in the measured ion yields as a function of the pump–probe delay. These oscillations reflect the typical frequencies of such coherent motion. To analyze the effect of nuclear motion on the measured frequencies, we have calculated the Fourier transform of the hole density around different molecular sites, namely the Cα atom, the two oxygen atoms, and the N atom. Since, in current experiments, ultrafast oscillations have only been observed for time delays shorter than 20 or 30 fs, we have limited our study to the time interval 0–25 fs. The results are shown in Fig. 5 and 6. As a result of the limited time interval used in our analysis, the peaks associated with the different frequencies exhibit a width. As in the case of the phenylalanine molecule,4 a striking feature of the calculated frequency spectra is the appearance of very few peaks, typically two or three in the interval from 0.1 to 1.5 PHz. These frequencies correspond to energy differences between the cationic states that compose the electronic wave packet generated in the ionization process. However, among all possible energy differences, only a few ones are actually observed, not necessarily involving the state in which the vacancy was initially created. Inclusion or not of the nuclear motion does not alter this general picture. However, the actual values of the frequencies can be significantly affected by the presence of the nuclear motion. As can be seen, some frequencies are slightly shifted, and others can even appear or disappear. This is the consequence of non-adiabatic transitions between the initially populated cationic states and cationic states that were initially empty. The fact that the values of the frequencies do not differ too much from those obtained in the fixed-nuclei approximation would suggest that non-adiabatic transitions are likely to occur between neighboring states.
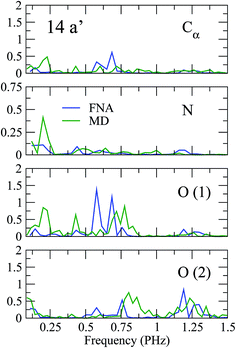 |
| | Fig. 5 Fourier transforms of the spin density around the Cα atom, the two oxygen atoms, and the N atom of glycine for ionization from the 14a′ orbital. | |
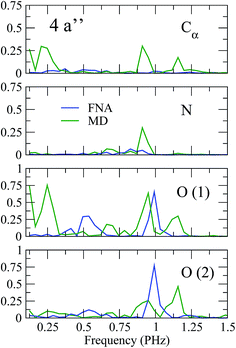 |
| | Fig. 6 Same as Fig. 5 for the 4a′′ orbital. | |
5 Control of hole dynamics through attosecond pulse shaping
Hole dynamics reflects the time evolution of the initially created electronic wave packet, which is a coherent superposition of cationic states. Thus different initial electronic wave packets must evolve differently. Here we show that one can indeed modify such dynamics by changing the pulse characteristics. To prove it, we have chosen three different pulses whose frequency spectra are identical to three attosecond pulses produced in recent experiments.4,37 These frequency spectra are shown in Fig. 7. Two of the pulses cover a similar frequency region, around 20 eV, but have very different envelopes. The third one has a very simple spectral shape but covers a range of higher frequencies, around 90 eV. Fig. 7 also shows the photoionization cross sections of the glycine molecule associated with electron removal from different molecular orbitals. As can be seen, for all pulses, there is a substantial number of ionization channels that are open. Obviously this number is larger for the pulse containing the higher photon energies. All ionization probabilities are comparable in magnitude. However their relative values change significantly with photon energy. Similarly, the relative phases between the different ionization amplitudes change with photon energy. Therefore, one can expect that, by using pulses with different spectral shapes or covering different frequency ranges, different coherent superpositions of cationic states will be generated. Fig. 7 shows the frequency spectra associated with the hole dynamics around the Cα atom, the two oxygen atoms, and the N atom of glycine. As can be seen, the frequency spectra, or in other words the hole dynamics, can indeed be very different, but not always. Surprisingly the largest differences are observed for the two pulses that cover a similar range of photon energies. These two pulses, however, have a very different spectral shape. Since the ionization probabilities exhibit the largest relative variations at low photon energies, it is thus clear that the actual shape of the pulse matters. This is because spectral peaks strategically placed at specific photon energies may favor ionization in specific channels, in detriment of ionization in the other channels. Selectivity is much less pronounced at higher energies, where ionization probabilities and their corresponding relative values vary slowly with photon energy. In this case, the calculated frequency spectra are different from those obtained by using the other two pulses, although they exhibit some similarities to those obtained from the pulse with the largest spectral width.
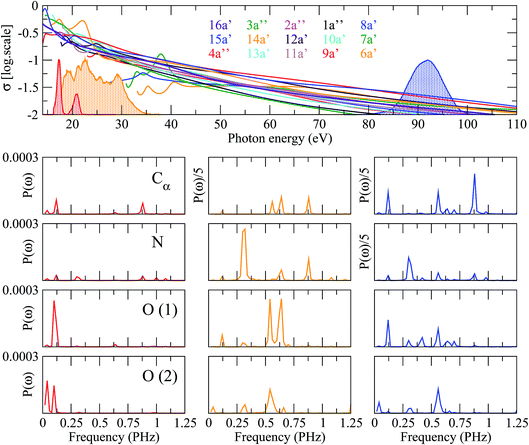 |
| | Fig. 7 Upper panel: photoionization cross sections of glycine from the molecular orbitals indicated in the colored labels. The shadowed lines correspond to the experimental energy distributions of three different attosecond pulses centered at 20 eV (red), 18–35 eV (orange) and 90 eV (blue), respectively. Lower panels: Fourier power spectra of the time-dependent spin density integrated around various molecular centers, computed for the three pulses (left column: 20 eV; middle column: 18–35 eV; right column: 90 eV). Each row corresponds to a given atom as labeled in the first column. | |
These results show that, in general, a large degree of control can only be achieved in regions of the ionization spectrum where the relative ionization probabilities change significantly with photon energies. In large molecules, this usually occurs close to the ionization threshold, within the first 10 to 40 eV, where specific tuning of shape resonances or broad autoionizing states can play an important role. In this region, the optimum way to exert such control is by introducing peaks in different regions of the pulse spectrum.
6 Role of the probe pulse on the cation dynamics
In pump–probe experiments, common observables employed to capture ultrafast electron dynamics in molecules are total or partial ionization yields as functions of the time delay between the pulses.4,16 A complete calculation that includes both electron and nuclear dynamics, in conjunction with ionization of a second electron and the eventual dissociation induced by a probe pulse is currently out of reach. For this reason, as a first step to explore the role of the probe pulse, we have ignored the nuclear motion and we have assumed that the second ionization step can be described by using the same Kohn–Sham orbitals as for ionization of the pump pulse. This is equivalent to assume that electron correlation in our Kohn–Sham description of the neutral, singly- and doubly-charged species is the same. Therefore, our analysis can only have a qualitative value. Nevertheless, it will already allow us to understand if the hole dynamics initiated by the pump pulse is captured after the additional ionization produced by the probe pulse. The general expression for the two-photon double ionization amplitude can be written as:| | 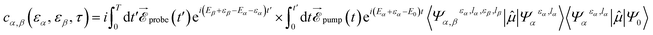 | (11) |
where the two indices α and β are used to denote the final dicationic states, indicating the Kohn–Sham orbitals from which the two electrons have been ejected, first by the pump pulse, leading to the α vacancy, and then by the probe pulse, leading to the β vacancy. For the reasons explained in the introduction, we consider an XUV probe pulse identical to the pump probe, 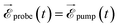 , with a time delay of τ between them such that they never overlap. Hence the double integral in time is separable and the time-dependence can be factored out. Eqn (11) has been evaluated for the sub-300-as pulse of ref. 4. The resulting total double ionization yield as a function of the pump–probe delay is shown in Fig. 8 together with its Fourier transform. We observe that the double ionization yield exhibits rapid oscillations superimposed to a slower one of period ∼10 fs. These are the main frequencies seen in Fig. 7 (central panels) for this same pulse. Notice, however, that beatings corresponding to different atoms appear all at once in the double ionization yield, although their relative intensities are no longer modulated by the orbitals' overlap as for the hole densities shown in Fig. 7 [see also eqn (10)]. These findings are in agreement with the conclusion of ref. 36 for the case of the XUV-pump/XUV-probe ionization of H2, although, in the latter case, only the single ionization channel is open due to the large energy separation between the electronic states of the molecule. The present results show that, as in ref. 36, the use of a “gentle” XUV pulse allows us to uncover the pump-induced dynamics without introducing additional distortions. That such a conclusion is still valid when IR probe pulses are used or when the nuclear degrees of freedom are taken into account remains to be seen.
, with a time delay of τ between them such that they never overlap. Hence the double integral in time is separable and the time-dependence can be factored out. Eqn (11) has been evaluated for the sub-300-as pulse of ref. 4. The resulting total double ionization yield as a function of the pump–probe delay is shown in Fig. 8 together with its Fourier transform. We observe that the double ionization yield exhibits rapid oscillations superimposed to a slower one of period ∼10 fs. These are the main frequencies seen in Fig. 7 (central panels) for this same pulse. Notice, however, that beatings corresponding to different atoms appear all at once in the double ionization yield, although their relative intensities are no longer modulated by the orbitals' overlap as for the hole densities shown in Fig. 7 [see also eqn (10)]. These findings are in agreement with the conclusion of ref. 36 for the case of the XUV-pump/XUV-probe ionization of H2, although, in the latter case, only the single ionization channel is open due to the large energy separation between the electronic states of the molecule. The present results show that, as in ref. 36, the use of a “gentle” XUV pulse allows us to uncover the pump-induced dynamics without introducing additional distortions. That such a conclusion is still valid when IR probe pulses are used or when the nuclear degrees of freedom are taken into account remains to be seen.
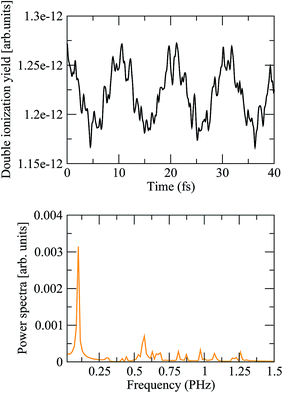 |
| | Fig. 8 (Upper panel) Double ionization yields as a function of the pump–probe time delay, computed from eqn (11) using the static exchange DFT method. (Lower panel) Power spectrum of the above signal. | |
7 Conclusion
We have theoretically investigated, by means of the static-exchange DFT and TDDFT-MD methods, the effect of different factors that have hitherto been ignored in the description of charge migration induced by attosecond XUV pulses in biologically relevant molecules, namely, (i) the role of the ionized electron in the electron wave packet dynamics that follows the interaction with a XUV attosecond pulse, (ii) the effect of nuclear motion on the charge migration process, (iii) the possibility to control such dynamics by shaping the attosecond pulse that ionizes the molecule, and (iv) the role of the probe pulse on the pump-induced electron dynamics. By using the glycine molecule as a benchmark, we have shown that (i) the ionized electron only affects these dynamics during approximately the first femtosecond, (ii) nuclear dynamics has a significant effect after approximately 8 fs, but does not destroy the coherent motion of the electronic wave packet during a few tens of fs, (iii) charge dynamics can indeed be changed by modifying the pump pulse characteristics, thus opening the door to the control of charge dynamics in biomolecules, and (iv) a weak XUV probe pulse does not introduce significant distortions in the pump-induced dynamics, suggesting that pump–probe strategies are suitable for imaging and manipulating charge migration in complex molecules.
Acknowledgements
We acknowledge allocation of computer time at Mare Nostrum BSC and CCC-UAM. This work was supported by the European Research Council Advanced Grant No. XCHEM 290853, the MINECO Project No. FIS2013-42002-R, the European COST Action XLIC CM1204, and the CAM project NANOFRONTMAG. A. P. gratefully acknowledges the “Ramón y Cajal” program from the Spanish Ministry of Economy and Competitiveness.
References
- L. Cederbaum and J. Zobeley, Chem. Phys. Lett., 1999, 307, 205–210 CrossRef CAS.
- H. Hennig, J. Breidbach and L. S. Cederbaum, J. Phys. Chem. A, 2005, 109, 409–414 CrossRef CAS PubMed.
- F. Remacle and R. D. Levine, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 6793–6798 CrossRef CAS PubMed.
- F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. De Camillis, S. Anumula, F. Frassetto, L. Poletto, A. Palacios, P. Decleva, J. B. Greenwood, F. Martín and M. Nisoli, Science, 2014, 346, 336–339 CrossRef CAS PubMed.
- F. Lépine, M. Y. Ivanov and M. J. J. Vrakking, Nat. Photonics, 2014, 8, 195–204 CrossRef.
- S. R. Leone, C. W. McCurdy, J. Burgdörfer, L. S. Cederbaum, Z. Chang, N. Dudovich, J. Feist, C. H. Greene, M. Ivanov, R. Kienberger, U. Keller, M. F. Kling, Z.-h. Loh, T. Pfeifer, A. N. Pfeiffer, R. Santra, K. Schafer, A. Stolow, U. Thumm and M. J. J. Vrakking, Nat. Photonics, 2014, 8, 162–166 CrossRef CAS.
- P. M. Kraus, B. Mignolet, D. Baykusheva, A. Rupenyan, L. Horny, E. F. Penka, G. Grassi, O. I. Tolstikhin, J. Schneider, F. Jensen, L. B. Madsen, A. D. Bandrauk, F. Remacle and H. J. Worner, Science, 2015, 350, 790–795 CrossRef CAS PubMed.
- M. Vacher, L. Steinberg, A. J. Jenkins, M. J. Bearpark and M. A. Robb, Phys. Rev. A, 2015, 92, 040502 CrossRef.
- M. Hentschel, R. Kienberger, C. Spielmann, G. A. Reider, N. Milosevic, T. Brabec, P. B. Corkum, U. Heinzmann, M. Drescher and F. Krausz, Nature, 2001, 414, 509–513 CrossRef CAS PubMed.
- P. M. Paul, E. S. Toma, P. Breger, G. Mullot, F. Auge, P. Balcou, H. G. Muller and P. Agostini, Science, 2001, 292, 1689–1692 CrossRef CAS PubMed.
- M. Drescher, M. Hentschel, R. Kienberger, M. Uiberacker, V. Yakovlev, A. Scrinzi, T. Westerwalbesloh, U. Kleineberg, U. Heinzmann and F. Krausz, Nature, 2002, 419, 803–807 CrossRef CAS PubMed.
- M. F. Kling and M. J. Vrakking, Annu. Rev. Phys. Chem., 2008, 59, 463–492 CrossRef CAS PubMed.
- F. Krausz and M. Ivanov, Rev. Mod. Phys., 2009, 81, 163–234 CrossRef.
- M. Uiberacker, T. Uphues, M. Schultze, a. J. Verhoef, V. Yakovlev, M. F. Kling, J. Rauschenberger, N. M. Kabachnik, H. Schröder, M. Lezius, K. L. Kompa, H.-G. Muller, M. J. J. Vrakking, S. Hendel, U. Kleineberg, U. Heinzmann, M. Drescher and F. Krausz, Nature, 2007, 446, 627–632 CrossRef CAS PubMed.
- M. Schultze, M. Fiess, N. Karpowicz, J. Gagnon, M. Korbman, M. Hofstetter, S. Neppl, A. L. Cavalieri, Y. Komninos, T. Mercouris, C. A. Nicolaides, R. Pazourek, S. Nagele, J. Feist, J. Burgdorfer, A. M. Azzeer, R. Ernstorfer, R. Kienberger, U. Kleineberg, E. Goulielmakis, F. Krausz and V. S. Yakovlev, Science, 2010, 328, 1658–1662 CrossRef CAS PubMed.
- G. Sansone, F. Kelkensberg, J. F. Pérez-Torres, F. Morales, M. F. Kling, W. Siu, O. Ghafur, P. Johnsson, M. Swoboda, E. Benedetti, F. Ferrari, F. Lépine, J. L. Sanz-Vicario, S. Zherebtsov, I. Znakovskaya, A. L'Huillier, M. Y. Ivanov, M. Nisoli, F. Martín and M. J. J. Vrakking, Nature, 2010, 465, 763–766 CrossRef CAS PubMed.
- P. Ranitovic, C. W. Hogle, P. Riviére, A. Palacios, X.-M. Tong, N. Toshima, A. González-Castrillo, L. Martin, F. Martín, M. M. Murnane and H. Kapteyn, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 912–917 CrossRef CAS PubMed.
- O. Smirnova, Y. Mairesse, S. Patchkovskii, N. Dudovich, D. Villeneuve, P. Corkum and M. Y. Ivanov, Nature, 2009, 460, 972–977 CrossRef CAS PubMed.
- A. Ferré, D. Staedter, F. Burgy, M. Dagan, D. Descamps, N. Dudovich, S. Petit, H. Soifer, V. Blanchet and Y. Mairesse, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124023 CrossRef.
- A. Ferré, C. Handschin, M. Dumergue, F. Burgy, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, L. Merceron, E. Mével, L. Nahon, S. Petit, B. Pons, D. Staedter, S. Weber, T. Ruchon, V. Blanchet and Y. Mairesse, Nat. Photonics, 2015, 9, 93–98 CrossRef.
- L. Belshaw, F. Calegari, M. J. Duffy, A. Trabattoni, L. Poletto, M. Nisoli and J. B. Greenwood, J. Phys. Chem. Lett., 2012, 3, 3751–3754 CrossRef CAS PubMed.
- A. Palacios, J. L. Sanz-Vicario and F. Martín, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 242001 CrossRef.
- B. T. Pickup, Chem. Phys., 1977, 19, 193–208 CrossRef CAS.
- Y. Öhrn and G. Born, Adv. Quantum Chem., 1981, 13, 1–88 CrossRef.
- B. Mignolet, R. D. Levine and F. Remacle, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124011 CrossRef.
- N. V. Golubev and A. I. Kuleff, Phys. Rev. A, 2015, 91, 051401 CrossRef.
- A. Marciniak, V. Despré, T. Barillot, A. Rouzée, M. Galbraith, J. Klei, C.-H. Yang, C. Smeenk, V. Loriot, S. N. Reddy, A. Tielens, S. Mahapatra, a. I. Kuleff, M. Vrakking and F. Lépine, Nat. Commun., 2015, 6, 7909 CrossRef CAS PubMed.
- A. Trabattoni, M. Klinker, J. González-Vázquez, C. Liu, G. Sansone, R. Linguerri, M. Hochlaf, J. Klei, M. J. J. Vrakking, F. Martín, M. Nisoli and F. Calegari, Phys. Rev. X, 2015, 5, 041053 Search PubMed.
- A. I. Kuleff and L. S. Cederbaum, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124002 CrossRef.
- M. Stener and P. Decleva, J. Chem. Phys., 2000, 112, 10871–10879 CrossRef CAS.
- G. F. D. Toffoli, M. Stener and P. Decleva, Chem. Phys., 2002, 276, 25–43 CrossRef.
- F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. De Camillis, F. Frassetto, L. Poletto, A. Palacios, P. Decleva, J. B. Greenwood, F. Martin and M. Nisoli, IEEE J. Sel. Top. Quantum Electron., 2015, 21, 1–12 CrossRef.
- J. Breidbach and L. S. Cederbaum, J. Chem. Phys., 2003, 118, 3983 CrossRef CAS.
- J. Breidbach and L. S. Cederbaum, Phys. Rev. Lett., 2005, 94, 033901 CrossRef CAS PubMed.
- M. Vacher, D. Mendive-Tapia, M. J. Bearpark and M. A. Robb, J. Chem. Phys., 2015, 142, 094105 CrossRef PubMed.
- A. Palacios, A. González-Castrillo and F. Martín, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 3973–3978 CrossRef CAS PubMed.
- D. Fabris, T. Witting, W. Okell, D. Walke, P. Matia-Hernando, J. Henkel, T. Barillot, M. Lein, J. Marangos and J. Tisch, Nat. Photonics, 2015, 9, 383 CrossRef CAS.
- M. Stener, A. Lisini and P. Decleva, Int. J. Quantum Chem., 1995, 53, 229–244 CrossRef CAS.
- M. Stener, G. Fronzoni and P. Decleva, J. Chem. Phys., 2005, 122, 234301 CrossRef CAS PubMed.
- S. E. Canton, E. Plesiat, J. D. Bozek, B. S. Rude, P. Decleva and F. Martin, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 7302–7306 CrossRef CAS.
- E. Kukk, D. Ayuso, T. D. Thomas, P. Decleva, M. Patanen, L. Argenti, E. Plésiat, A. Palacios, K. Kooser, O. Travnikova, S. Mondal, M. Kimura, K. Sakai, C. Miron, F. Martín and K. Ueda, Phys. Rev. A, 2013, 88, 033412 CrossRef.
- K. Ueda, C. Miron, E. Plésiat, L. Argenti, M. Patanen, K. Kooser, D. Ayuso, S. Mondal, M. Kimura, K. Sakai, O. Travnikova, A. Palacios, P. Decleva, E. Kukk and F. Martín, J. Chem. Phys., 2013, 139, 124306 CrossRef CAS PubMed.
- D. Ayuso, M. Kimura, K. Kooser, M. Patanen, E. Plésiat, L. Argenti, S. Mondal, O. Travnikova, K. Sakai, A. Palacios, E. Kukk, P. Decleva, K. Ueda, F. Martín and C. Miron, J. Phys. Chem. A, 2015, 119, 5971–5978 CrossRef CAS PubMed.
-
CPMD, Copyright IBM Corp 1990-2015, Copyright MPI für Festkörperforschung Stuttgart 1997-2001, http://www.cpmd.org/, 2014 Search PubMed.
-
A. S. Computing and Modeling, Vrije Universiteit, Amsterdam, Netherlands, http://www.scm.com Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. F. Fischer and M. Idrees, J. Phys. B: At., Mol. Opt. Phys., 1990, 23, 679 CrossRef CAS.
- H. Bachau, E. Cormier, P. Decleva, J. E. Hansen and F. Martín, Rep. Prog. Phys., 2001, 64, 1815 CrossRef CAS.
- D. Mendive-Tapia, M. Vacher, M. J. Bearpark and M. A. Robb, J. Chem. Phys., 2013, 139, 044110 CrossRef PubMed.
- I. Tavernelli, U. F. Röhrig and U. Rothlisberger, Mol. Phys., 2005, 103, 963–981 CrossRef CAS.
- I. Tavernelli, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094204 CrossRef.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS.
- L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48, 1425–1428 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- B. F. E. Curchod, U. Rothlisberger and I. Tavernelli, ChemPhysChem, 2013, 14, 1314–1340 CrossRef CAS PubMed.
- T. F. Miller III and D. C. Clary, Phys. Chem. Chem. Phys., 2004, 6, 2563–2571 RSC.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1,…,
1,…,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N) is the ground state of the neutral molecule and Ψαl(
N) is the ground state of the neutral molecule and Ψαl(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1,…,
1,…,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N, ε) describes the N-electron system where one electron is in the continuum with energy ε and angular momentum l, and the ion is left behind with a hole in the α orbital. The time evolution of the wave packet is given by the stationary phases in the absence of the field (t > T, where T is the pulse duration) and the corresponding amplitudes at the end of the pulse:
N, ε) describes the N-electron system where one electron is in the continuum with energy ε and angular momentum l, and the ion is left behind with a hole in the α orbital. The time evolution of the wave packet is given by the stationary phases in the absence of the field (t > T, where T is the pulse duration) and the corresponding amplitudes at the end of the pulse: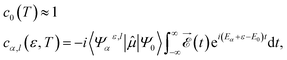
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |Ψ0〉 is the dipole transition matrix element connecting the ground and a continuum state,
|Ψ0〉 is the dipole transition matrix element connecting the ground and a continuum state, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) stands for the dipole operator (here we have used the length gauge form of this operator), the time integral is the Fourier transform of the electric field,
stands for the dipole operator (here we have used the length gauge form of this operator), the time integral is the Fourier transform of the electric field, 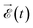 , and (Eα + ε − E0) is the energy absorbed by the system. The field is defined from 0 to T using experimental temporal envelopes, F(t), in the form
, and (Eα + ε − E0) is the energy absorbed by the system. The field is defined from 0 to T using experimental temporal envelopes, F(t), in the form 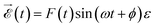 , with
, with ![[small epsilon, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e7.gif) being the polarization vector and ϕ the carrier-envelope phase, which is fixed to zero. Due to our definition of the field, the integral in eqn (2) can be identically evaluated in the interval [0, T].
being the polarization vector and ϕ the carrier-envelope phase, which is fixed to zero. Due to our definition of the field, the integral in eqn (2) can be identically evaluated in the interval [0, T].
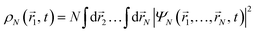
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1,…,
1,…,![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) N, t) is the N-electron wave packet created by the XUV pulse, which can be written, as in eqn (1), as an expansion over N-electron continuum eigenstates:
N, t) is the N-electron wave packet created by the XUV pulse, which can be written, as in eqn (1), as an expansion over N-electron continuum eigenstates: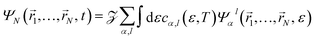
![[scr Z, script letter Z]](https://www.rsc.org/images/entities/char_e14b.gif) being a normalization factor. The corresponding expression for the one-particle density in the basis of spin-orbitals is given by
being a normalization factor. The corresponding expression for the one-particle density in the basis of spin-orbitals is given by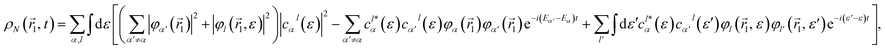
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1) is a Kohn–Sham spin-orbital and φl(
1) is a Kohn–Sham spin-orbital and φl(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1, ε) is a continuum spin orbital. The above expression has a stationary part, the first term, and two other terms that lead to variations of the electron density with time. We will see oscillations in the density with a periodicity dictated by the energy differences between cationic states (second term) and between continuum orbitals themselves (third term). The former are possible because electrons can be ejected with the same energy and angular momentum from different orbitals. The third term is expected to vanish in the neighborhood of the molecule if one waits long enough until the ejected electron is far away from the molecule. When this limit is reached, it is legitimate to ignore this electron and define a one-particle electron density from an (N − 1)-electron system. For this purpose, we rely on the reduced density matrix formalism, where the N-electron wave function is first projected into the continuum wave functions and then integrated over all continuum energies, thus leading to an N − 1 ionic electron density
1, ε) is a continuum spin orbital. The above expression has a stationary part, the first term, and two other terms that lead to variations of the electron density with time. We will see oscillations in the density with a periodicity dictated by the energy differences between cationic states (second term) and between continuum orbitals themselves (third term). The former are possible because electrons can be ejected with the same energy and angular momentum from different orbitals. The third term is expected to vanish in the neighborhood of the molecule if one waits long enough until the ejected electron is far away from the molecule. When this limit is reached, it is legitimate to ignore this electron and define a one-particle electron density from an (N − 1)-electron system. For this purpose, we rely on the reduced density matrix formalism, where the N-electron wave function is first projected into the continuum wave functions and then integrated over all continuum energies, thus leading to an N − 1 ionic electron density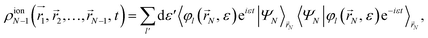
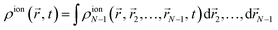
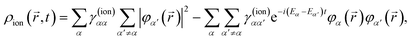
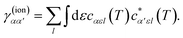
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t) = ρneutral(
, t) = ρneutral(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) − ρion(
) − ρion(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t). For consistency, in the case of the N-electron system we will use a similar expression, where ρion(
, t). For consistency, in the case of the N-electron system we will use a similar expression, where ρion(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t) is now replaced by ρN(
, t) is now replaced by ρN(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t) given in eqn (5). The electron density of the neutral molecule is simply given by the sum of the squares of the occupied Kohn–Sham orbitals,
, t) given in eqn (5). The electron density of the neutral molecule is simply given by the sum of the squares of the occupied Kohn–Sham orbitals, 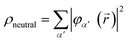 , and thus the hole density is simply given by
, and thus the hole density is simply given by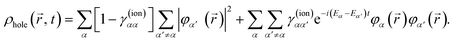
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 57)), so in line with the results of ref. 32 for the phenylalanine molecule, one can expect that the hole dynamics observed in a real experiment should not differ significantly from the one reported here. For consistency, the same conformer has been used in all calculations reported in the forthcoming sections. To avoid spurious reflections of the photoelectron at the box boundaries, we have used a rather large simulation box of 100 a.u. for the radial grid. The XUV pulse is sufficiently energetic to eject an electron from the 15 outer orbitals of glycine, leading to the formation of a coherent superposition of ionic states, as described in eqn (1), including all those 15 states with their associated electronic continua. One can then extract the one-particle electron density as given in eqn (8) for the (N − 1)-electron system, i.e. by first projecting into the continuum states as shown in expression (6), or instead, extract it directly from the N-electron target as defined in eqn (3).
57)), so in line with the results of ref. 32 for the phenylalanine molecule, one can expect that the hole dynamics observed in a real experiment should not differ significantly from the one reported here. For consistency, the same conformer has been used in all calculations reported in the forthcoming sections. To avoid spurious reflections of the photoelectron at the box boundaries, we have used a rather large simulation box of 100 a.u. for the radial grid. The XUV pulse is sufficiently energetic to eject an electron from the 15 outer orbitals of glycine, leading to the formation of a coherent superposition of ionic states, as described in eqn (1), including all those 15 states with their associated electronic continua. One can then extract the one-particle electron density as given in eqn (8) for the (N − 1)-electron system, i.e. by first projecting into the continuum states as shown in expression (6), or instead, extract it directly from the N-electron target as defined in eqn (3).
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) = ρneutral(
,t) = ρneutral(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) − ρion(
) − ρion(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) , t), in both scenarios, i.e., by including (top row) and excluding (bottom row) the ionized electron, respectively. As can be seen, the ejected electron spreads around the whole molecule when t < 0.2 fs, so that one cannot ignore its presence in the evaluation of the hole density. Later on, the ionized electron vanishes from the vicinity of the molecular skeleton, but the correlation effects induced on the dynamics of the remaining cation are still visible, up to t ∼ 0.7 fs. At longer times, the evolution of the hole density is practically the same as that resulting from ignoring the ionized electron, as shown in Fig. 2. This figure provides a more quantitative information about the role of the ionized electron, by comparing the actual electron densities integrated around different molecular sites. Fig. 2 shows again that the effect of the ionized electron is only appreciable during the first half of femtosecond. The precise value of this elapsed time will strongly depend on the kinetic energy of the photoelectron and, consequently, it will depend on the energy spectrum of the pulse employed to ionize the molecule. In the present case, the broad pulse bandwidth ranges from ∼15–35 eV, leading to the emission of relatively slow electrons, since the ionization potential (IP) from the highest-occupied molecular orbital (HOMO) of glycine is around 11 eV, while for the lowest valence orbital reached by the pulse (6a′) it is close to 32 eV. The resulting electronic wave packet is thus built from components of relatively low kinetic energy, giving a lower bound for this elapsed time. The general conclusion is that in the very early stages of the process, the observed dynamics will be exactly the same as that of the residual cation in the absence of the photoelectron, thus proving that, although one has to account for ionization in order to obtain a realistic description of the electronic wave packet generated by the XUV pulse, one can safely ignore the ionized electron in the subsequent evolution of the electronic wave packet in the cation.
, t), in both scenarios, i.e., by including (top row) and excluding (bottom row) the ionized electron, respectively. As can be seen, the ejected electron spreads around the whole molecule when t < 0.2 fs, so that one cannot ignore its presence in the evaluation of the hole density. Later on, the ionized electron vanishes from the vicinity of the molecular skeleton, but the correlation effects induced on the dynamics of the remaining cation are still visible, up to t ∼ 0.7 fs. At longer times, the evolution of the hole density is practically the same as that resulting from ignoring the ionized electron, as shown in Fig. 2. This figure provides a more quantitative information about the role of the ionized electron, by comparing the actual electron densities integrated around different molecular sites. Fig. 2 shows again that the effect of the ionized electron is only appreciable during the first half of femtosecond. The precise value of this elapsed time will strongly depend on the kinetic energy of the photoelectron and, consequently, it will depend on the energy spectrum of the pulse employed to ionize the molecule. In the present case, the broad pulse bandwidth ranges from ∼15–35 eV, leading to the emission of relatively slow electrons, since the ionization potential (IP) from the highest-occupied molecular orbital (HOMO) of glycine is around 11 eV, while for the lowest valence orbital reached by the pulse (6a′) it is close to 32 eV. The resulting electronic wave packet is thus built from components of relatively low kinetic energy, giving a lower bound for this elapsed time. The general conclusion is that in the very early stages of the process, the observed dynamics will be exactly the same as that of the residual cation in the absence of the photoelectron, thus proving that, although one has to account for ionization in order to obtain a realistic description of the electronic wave packet generated by the XUV pulse, one can safely ignore the ionized electron in the subsequent evolution of the electronic wave packet in the cation.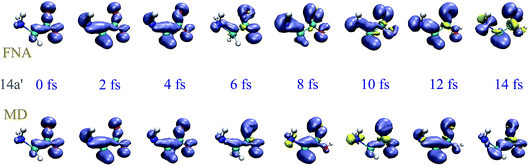


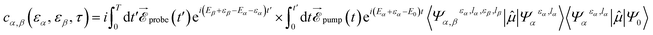
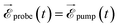 , with a time delay of τ between them such that they never overlap. Hence the double integral in time is separable and the time-dependence can be factored out. Eqn (11) has been evaluated for the sub-300-as pulse of ref. 4. The resulting total double ionization yield as a function of the pump–probe delay is shown in Fig. 8 together with its Fourier transform. We observe that the double ionization yield exhibits rapid oscillations superimposed to a slower one of period ∼10 fs. These are the main frequencies seen in Fig. 7 (central panels) for this same pulse. Notice, however, that beatings corresponding to different atoms appear all at once in the double ionization yield, although their relative intensities are no longer modulated by the orbitals' overlap as for the hole densities shown in Fig. 7 [see also eqn (10)]. These findings are in agreement with the conclusion of ref. 36 for the case of the XUV-pump/XUV-probe ionization of H2, although, in the latter case, only the single ionization channel is open due to the large energy separation between the electronic states of the molecule. The present results show that, as in ref. 36, the use of a “gentle” XUV pulse allows us to uncover the pump-induced dynamics without introducing additional distortions. That such a conclusion is still valid when IR probe pulses are used or when the nuclear degrees of freedom are taken into account remains to be seen.
, with a time delay of τ between them such that they never overlap. Hence the double integral in time is separable and the time-dependence can be factored out. Eqn (11) has been evaluated for the sub-300-as pulse of ref. 4. The resulting total double ionization yield as a function of the pump–probe delay is shown in Fig. 8 together with its Fourier transform. We observe that the double ionization yield exhibits rapid oscillations superimposed to a slower one of period ∼10 fs. These are the main frequencies seen in Fig. 7 (central panels) for this same pulse. Notice, however, that beatings corresponding to different atoms appear all at once in the double ionization yield, although their relative intensities are no longer modulated by the orbitals' overlap as for the hole densities shown in Fig. 7 [see also eqn (10)]. These findings are in agreement with the conclusion of ref. 36 for the case of the XUV-pump/XUV-probe ionization of H2, although, in the latter case, only the single ionization channel is open due to the large energy separation between the electronic states of the molecule. The present results show that, as in ref. 36, the use of a “gentle” XUV pulse allows us to uncover the pump-induced dynamics without introducing additional distortions. That such a conclusion is still valid when IR probe pulses are used or when the nuclear degrees of freedom are taken into account remains to be seen.