In situ evaluation of DGT techniques for measurement of trace metals in estuarine waters: a comparison of four binding layers with open and restricted diffusive layers†
Amir Houshang
Shiva
,
William W.
Bennett
,
David T.
Welsh
and
Peter R.
Teasdale
*
Environmental Futures Research Institute, Griffith University, Gold Coast Campus, QLD 4215, Australia. E-mail: p.teasdale@griffith.edu.au; Fax: +61 7555 28067; Tel: +61 7555 28358
First published on 9th December 2015
Abstract
Four different DGT binding layers were used to make selective measurements of trace metals in coastal waters within The Broadwater (Gold Coast, Queensland). Chelex and PAMPAA (polyacrylamide-polyacrylic acid) binding layers were used to measure cations (Cd, Co, Cu, Mn, Ni, Pb, Zn), and Metsorb was used to measure anions (Al, As, Mo, Sb, V, W). A mixed binding layer (MBL) containing both Chelex and Metsorb was used to measure each of the trace metals and determine diffusive boundary layer (DBL) thicknesses. DGT measurements that were not corrected for the DBL thickness (0.049–0.087) were underestimated by 70% on average. Good agreement was observed between DGT-MBL and DGT-Chelex for measurement of Cd, Co, Cu, Ni, Pb and Zn, and between DGT-MBL and DGT-Metsorb for As, Sb and V. DGT-MBL measured significantly higher concentrations for Mn (compared with DGT-Chelex) and Al (compared with DGT-Metsorb). DGT-Chelex measured only 6–8% of Al species measured by either DGT-MBL or DGT-Metsorb. DGT-PAMPAA measurements of Cu, Pb and Al were lower than those of either DGT-MBL or DGT-Chelex varying from 74–81% for Cu to 54–70% for Pb and 51–55% for anionic Al(OH)4−, suggesting that this binding layer may make more selective measurements. All measured trace metal concentrations were well below ANZECC water quality guidelines, except for Cu which was 2 to 10 times higher than trigger values. Each of the DGT techniques was deployed using both open and restricted diffusive layers (ODL and RDL). Most trace metal measurements were not significantly different with ODL and RDL for all binding layers. However, concentrations of Cu (CRDL/CODL = 0.68–0.75) and Al (CRDL/CODL = 0.73–0.79) were significantly different with DGT-MBL, DGT-Chelex and DGT-Metsorb.
Environmental impactThe diffusive gradients in thin films (DGT) is a highly effective technique for selectively measuring trace metals concentrations in natural waters, providing information on the environmental health of waterways and understanding key processes. DGT is a monitoring tool for which the selectivity can be modified by use of different components, especially the diffusive and binding layers. In this study, we have evaluated DGT measurements of trace metals using four binding layers and two diffusive layers in waters adjacent to an urbanised coast. The choice of DGT measurements with differing selectivity will be important for future studies. |
1. Introduction
Trace metals are one of the major contaminants of concern in many coastal and estuarine waters as a result of inputs from anthropogenic sources.1,2 Elevated concentrations of essential (e.g. Cu, Mn, Ni and Zn) and non-essential (e.g. Cd, Pb and As) trace metals can have detrimental impacts on the environment and may cause toxicity to aquatic organisms.3 Trace metals often exhibit complex speciation in seawater with the free metal cations or oxyanions, especially, and labile inorganic/organic complexes considered to be bioavailable through environmental exposure.4 Therefore, in order to assess environmental health and potential biological impacts of trace metals, there is a need for methods that are able to make selective measurements of the most bioavailable metal species.The diffusive gradients in thin films (DGT) technique is a passive sampler that measures the free ions and labile inorganic/organic complexes in water, sediment and soil,5–7 allowing inferences to be made on metal bioavailability and toxicity.6,8,9 DGT techniques are based on the diffusional transport of analytes across a layer of known thickness (diffusive layer) and their accumulation on a binding layer, which is usually a resin or metal oxide material embedded in a polyacrylamide hydrogel.10 Depending on the target analyte, various binding materials with differing selectivity have been used for metal cations or oxyanions. Chelex-100 has been the most commonly used binding material for measurement of trace metals11–13 and is suitable for coastal waters.14–17 Polyacrylamide-polyacrylic acid (PAMPAA) is another type of binding layer for measurement of metal species, which is prepared from the polyacrylamide hydrogels, typically used for diffusive layers, through a hydrolysis reaction in an alkaline solution.18 This binding layer has been validated for Cu and Cd measurements in the laboratory and compared with DGT-Chelex and other novel DGT binding layers in natural waters.18,19 On the other hand, several binding materials have been used for oxyanion species including zirconium oxide,20,21 mercaptopropyl-silica,22 ferrihydrite23,24 and Metsorb25,26 (a commercially available titanium dioxide-based resin).
Binding materials have also been combined to allow simultaneous measurement of cationic and oxyanionic metal species by DGT. A mixture of Chelex-100 and zirconium oxide has been used to measure phosphorous and iron.27 Mason et al.28 and Huynh et al.29 combined Chelex-100 and ferrihydrite for measurement of Mn, Cu, Zn, Cd, Pb, As, Mo and P in water and soils. Recently, Panther et al.30 developed a Chelex–Metsorb mixed binding layer (MBL) for simultaneous measurement of a wide range of cations and oxyanions (Cd, Co, Cu, Mn, Ni, Pb, Zn, As, Mo, Sb, V, W) in water. Additionally, Shiva et al.31 evaluated the capability of DGT-MBL for measurement of Al at different pH, based on the findings of another study32 that DGT-Chelex and DGT-Metsorb accurately measure Al only in weakly acidic and slightly basic waters, respectively. Although the previous study30 has evaluated the capability of DGT-MBL in synthetic freshwater and seawater, the performance of this binding layer has not yet been evaluated in natural waters.
DGT techniques are therefore able to make selective measurements of trace metals in natural waters, either by using binding layers with differing selectivity22 or by using diffusive layers (polyacrylamide hydrogels) with differing pore sizes.33 It has been demonstrated that the smaller pore size and greater tortuosity of the restricted diffusive layers (RDL) results in retarded diffusion of trace metals compared to the open diffusive layers (ODL) that have normally been used with DGT.31,34 Therefore, DGT techniques employing a RDL will exclude or diffusionally retard the organic complexes, and preferentially measure smaller species such as free metals and inorganic complexes, compared to the same DGT techniques employing ODL.33 Since these smaller species are considered to be the most bioavailable,4 measurements with RDL may better represent the bioavailable metal concentrations in the environment. The performance of DGT as a speciation tool has been evaluated by comparison with other speciation techniques for selective measurement of trace metals;35–37 however, none of these investigations have evaluated DGT measurements with different binding and diffusive layers in coastal waters.
The purpose of this study was to systematically evaluate the selectivity of DGT measurements using several DGT binding layers selective for trace metals and/or oxyanions combined with ODL and RDL in coastal waters. Chelex, Metsorb, mixed Chelex–Metsorb and PAMPAA binding layers were used, with particular interest on evaluating the performance of the mixed biding layer (MBL) in natural saline waters. Further characterization of the PAMPAA binding layer was done, measuring uptake and elution efficiencies for aluminium and cationic metals. All DGT measurements were compared with filterable metal concentrations at two estuarine sites within The Broadwater, Gold Coast City, Queensland.
2. Experimental section
2.1. General procedures
All equipment, including DGT devices, were soaked in 10% nitric acid (AR grade, Merck) for at least 24 hours and were rinsed with deionised water (Milli-Q Element, Millipore, >18.2 MΩ cm−1) prior to use. Deionised water also was used for preparing the reagent solutions and for processing all samples. All preparation and experiments were done in an ISO class 5 (ISO 14644-1) laminar flow hood within an ISO class 6 (ISO 14644-1) clean room. Powder free latex gloves (Microtouch Dermaclean, Ansell) were used. Diffusive and binding layers were cast in a fume hood.2.2. Preparation of hydrogels and DGT samplers
PAMPAA binding layers were prepared according to Li et al.18 Briefly, polyacrylamide hydrogel sheets were placed at 80 °C for 5 h within sealed flasks containing 40 mL of 10% (w/v) NaOH. The hydrolysis reaction that occurs results in amide groups within the polyacrylamide gel being converted into carboxylic acid groups. However, as the ammonia produced by this reaction is trapped within the sealed flask the reaction cannot proceed to completion, resulting in an equilibrium and formation of the PAMPAA copolymer. Following hydration for 24 h in deionised water, the gels were placed in 0.1 M HNO3 for a further 24 h to remove unreacted alkali and ammonia, and then stored in 0.1 M NaNO3 at <4 °C to remove stickiness. Further information on the characteristics of the different binding layers used in this study is provided in Table S1 in the ESI.†
2.3. DGT deployment and DBL calculations
DGT deployments were performed at two sites in The Broadwater, a coastal lagoon on the Gold Coast, southeast Queensland, connected to the Pacific Ocean by the Seaway (Fig. 1). The first site was The Spit, a popular boat anchorage in a well flushed area on the seaward side of the Broadwater, immediately south of the Seaway. The second site was within Runaway Bay Marina, on the landward side of the Broadwater, north of the Seaway. Runaway Bay Marina has a hardstand and also receives urban stormwater from the surrounding urban area. These sites were selected as they have different influences and have previously been reported to have measurable concentrations of filterable trace metals.14,15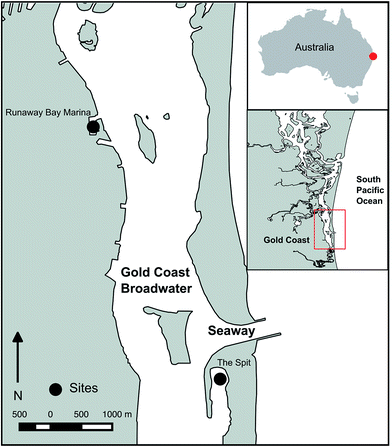 | ||
| Fig. 1 Map of the Broadwater (Gold Coast, Queensland, Australia) showing the location of The Spit anchorage and Runaway Bay Marina. | ||
Three replicates of each DGT type (DGT-MBL, DGT-Chelex, DGT-Metsorb and DGT-PAMPAA) with ODL and three replicates with RDL were deployed from 18th to 21st November 2013 at each site for approximately 72 h (exact time recorded). An additional set of triplicate acid-washed DGT-Metsorb were also deployed for Al measurements.32 pH, salinity and temperature were monitored in situ every day using a Mettler-Toledo pH meter (FiveGo, FG2) and a TPS conductivity-TDS meter (model MC-84). The respective values for average pH, salinity and temperature were 8.02 ± 0.05, 37.33 ± 0.25 and 25.5 ± 0.72 °C at Runaway Bay Marina, and 8.23 ± 0.10, 30.70 ± 1.57 and 26.5 ± 0.89 °C at The Spit. Filtered (0.45 μm, Millex®-HA, Millipore) grab water samples were collected daily, acidified (pH <2) immediately and stored at <4 °C.
To measure the thickness of the diffusive boundary layer (DBL), a quiescent layer of water that forms at the interface of DGT samplers and bulk water, two additional sets of triplicate DGT-MBL with ODL thicknesses of 0.04 and 0.12 cm were deployed at each site.39 The average DBLs determined were applied to all DGT-Chelex, DGT-Metsorb and DGT-PAMPAA measurements (see Section 2.4).
2.4. Sample analysis and DGT calculations
Following removal of the binding layers from the DGT samplers, Metsorb and MBL gels were rinsed in 5 mL of deionised water for 1 h to remove the salts present in the gel, which can interfere with the elution procedure.32,40 The additional set of DGT-Metsorb used for Al measurements, was immersed in 50 mL of 0.0001 mol L−1 HNO3 for 1 h, prior to rinsing with deionised water. This process has been reported to increase the elution efficiency for Al.32 In this study, we also investigated the effect of an acid wash on DGT-Metsorb measurements for oxyanions, as Al and oxyanions accumulate on the Metsorb gel at the same time (see ESI†).The elements retained by binding layers were eluted using different eluents. Chelex and PAMPAA binding layers were eluted for 24 h in 1 mL of 1 mol L−1 HNO3 (Baseline) and 5 mL of 2 mol L−1 HNO3 (Baseline),18 respectively. MBL gels were eluted in 1 mL of 1 mol L−1 HNO3 (Baseline) for 24 h, rinsed with deionised water to remove excess acid and then eluted in 1 mL of 1 mol L−1 NaOH, for a further 24 h.30 Then, to elute Sb, the MBL gels were immersed in 1 mL of 1 mol L−1 NaOH/1 mol L−1 H2O2 for another 24 h.30 These eluents were combined before analysis. Metsorb binding layers were eluted in 1 mL of 1 mol L−1 NaOH for 24 h, and then for elution of Sb, the gels were immersed in 1 mL of 1 mol L−1 NaOH/1 mol L−1 H2O2 for another 24 h.40 The eluents for Chelex, Metsorb and MBL were diluted 10-fold (using 2% HNO3, Baseline), and for PAMPAA diluted 2-fold prior to analysis. 0.45 μm filtered grab samples were diluted 20-fold with 2% HNO3 prior to analysis.
All elemental analyses were carried out using an inductively coupled plasma mass spectrometer (ICP-MS, Agilent 7500a). Analytical standards for ICP-MS analysis were prepared in 2% (v/v) HNO3 (Baseline) using a multi-element standard (High Purity Standards). A quality control blank (QCB) followed by a 10 μg L−1 quality control (QC, High Purity Standards) were run every 15–20 samples to ensure there was no change in ICP-MS sensitivity. Sc, Y and In were added to each sample as internal standard (100 μg L−1, High Purity Standards) to account for any instrument drift and all recoveries were in the range of 91–102%.
The accumulated mass of each analyte (M, ng) on each binding layer was calculated from analyte concentration in the eluent (Ce) using eqn (1);11 where Ve is the volume of the eluent, Vgel is the volume of the gel (0.2 mL) and fe is the elution efficiency for the element.
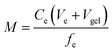 | (1) |
The elution efficiencies used in this study (except for Al) were those reported for MBL, Chelex and Metsorb by Panther et al.30 For Al, the elution efficiencies measured for Chelex and Metsorb binding layers by Panther et al.32 were used and an elution factor of 0.845 (average of Chelex and Metsorb) was utilized for MBL. For the PAMPAA binding layer, a separate experiment was carried out to determine uptake and elution efficiencies for the complete range of cations and Al (see Table S2, ESI†). The results showed that only Al, Cu and Pb have reasonable uptake efficiencies (ranged 75.51 to 94.99%), and therefore only these three elements and Cd (which has been more thoroughly evaluated previously18) were selected for comparison with other binding layers.
The DGT-measured concentrations (CDGT, μg L−1) were determined using eqn (2);11 where Dgel (cm2 s−1) represents the diffusion coefficient of analytes through the diffusive layer (Δg, cm) and DBL (δ, cm), t (s) is the deployment time, and A (cm2), is the area of the gel exposed to the water. Diffusion coefficients of all the analytes in both open and restricted diffusive layers (Dgel) were obtained from Shiva et al.,31 corrected for temperature using the Stokes–Einstein equation,11 and values of 0.9 × Dgel were used as the medium was seawater.5
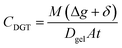 | (2) |
The thickness of the DBL (δ) was calculated as described by Warnken et al.39 using eqn (3); where, Dw represents the diffusion coefficient of analytes in the water.41 A plot of 1/M (ng−1) accumulated by the binding layer versus the diffusive layer thickness (Δg, cm) is a straight line with a slope (m) of 1/(DgelCDGTAt) and an intercept (b) of δ/(DwCDGTAt). Therefore, the DBL thickness can be calculated using eqn (4).39
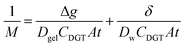 | (3) |
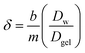 | (4) |
Since the DBL thickness is incorporated into all DGT calculations, a value of 3.8 cm2 (instead of 3.14 cm2) was used as the effective sampling area (A) in the DGT equation (see Warnken et al.39 for more information on determination of this value).
2.5. DGT blanks and method detection limits (MDL)
To monitor for any contamination during synthesis, DGT blanks were prepared in the same way as the deployed DGT samplers and subjected to all procedures except for deployment in the water; however the blanks were transported to the field and exposed to the air for several minutes to detect contamination associated with dust or handling. Blanks were conducted in triplicate for each DGT type and mass measurements were calculated using eqn (1). The average blank mass was subtracted from the accumulated mass for each analyte to obtain corrected mass values (ng). A set of triplicate filtration blanks were also collected in the field with daily grab samples using deionised water.Method detection limits (MDL, ng) were calculated for each element for the Chelex, Metsorb, MBL and PAMPAA binding layers as three times the standard deviation of the blanks.28,40 The detection limits were converted to concentrations (μg L−1) using the DGT equation with the diffusion thickness, Δg of 0.09 cm (diffusive layer and filter membrane), deployment time, t of ∼72 h (in seconds), an available gel area, A of 3.14 cm2 and diffusion coefficients obtained from Shiva et al.31 for open (DODL) and restricted (DRDL) diffusive layers corrected for temperature.
2.6. Statistical analysis and interpretation of metal risks to the environment
A one-way ANOVA followed by a Tukey's post-hoc test at a significance level of 0.05 was used to determine the statistical differences between DGT-MBL, DGT-Chelex, DGT-Metsorb and DGT-PAMPAA measurements of each element at each site. Measurements for each DGT type with ODL and RDL were compared using an independent t-test. All filterable and DGT-measured concentrations of metals were compared to the water quality guidelines determined by the Australian and New Zealand Environment and Conservation Council (ANZECC)42 for the 95% level of ecosystem protection in marine waters to assess the ecological risks of metals to the Gold Coast Broadwater.3. Results and discussion
3.1. DGT blanks and method detection limits (MDL)
Table 1 shows the method detection limits (MDL, μg L−1) calculated for DGT-MBL, DGT-Chelex, DGT-Metsorb and DGT-PAMPAA with both ODL and RDL. To lower the blank values, Metsorb adsorbents were cleaned with 1 mol L−1 HNO3 and 1 mol L−1 NaOH prior to use32 as higher detection limits have been reported for Mn, Ni, Cu, Zn and V when using unwashed Metsorb.30 All detection limits in our study (except for Al and Zn) were below 0.112 μg L−1 and in most cases ≤0.045 μg L−1, indicating low-level contamination of binding layers. The estimated detection limits in our study are in line with previously reported values for DGT-MBL,30 DGT-Chelex,30,43 DGT-Metsorb,25,40 DGT-PAMPAA.19 Values were quite similar for ODL and RDL, and were all considerably below the ANZECC water quality guidelines for each trace metal.42 Relatively high detection limits for Al and Zn have also been reported by other investigators17,28 and may be due to the presence of these elements in the Metsorb adsorbent; however, the calculated MDLs are generally acceptable for these elements. Theoretically, DGT detection limits can be lowered by increasing the deployment time.| Metal | DGT-MBL | DGT-Chelex | DGT-Metsorb | DGT-PAMPAA | ANZECC trigger values for marine waters | ||||
|---|---|---|---|---|---|---|---|---|---|
| MDLODL | MDLRDL | MDLODL | MDLRDL | MDLODL | MDLRDL | MDLODL | MDLRDL | 95% protection | |
| Cd | 0.010 | 0.013 | 0.005 | 0.006 | — | — | 0.016 | 0.022 | 5.5 |
| Co | 0.035 | 0.045 | 0.002 | 0.003 | — | — | — | — | 1 |
| Cu | 0.087 | 0.112 | 0.022 | 0.028 | — | — | 0.015 | 0.020 | 1.3 |
| Mn | 0.023 | 0.030 | 0.010 | 0.013 | — | — | — | — | — |
| Ni | 0.062 | 0.081 | 0.025 | 0.032 | — | — | — | — | 70 |
| Pb | 0.008 | 0.010 | 0.008 | 0.011 | — | — | 0.013 | 0.018 | 4.4 |
| Zn | 2.05 | 2.71 | 1.83 | 2.42 | — | — | — | — | 15 |
| Al | 0.461 | 0.672 | 0.177 | 0.257 | 1.32 | 1.93 | 0.323 | 0.470 | — |
| As | 0.014 | 0.020 | — | — | 0.011 | 0.016 | — | — | — |
| Mo | 0.001 | 0.002 | — | — | 0.003 | 0.004 | — | — | — |
| Sb | 0.004 | 0.006 | — | — | 0.004 | 0.006 | — | — | — |
| V | 0.028 | 0.037 | — | — | 0.018 | 0.023 | — | — | 100 |
| W | 0.020 | 0.029 | — | — | 0.027 | 0.039 | — | — | — |
3.2. Diffusive boundary layer (DBL) measurements
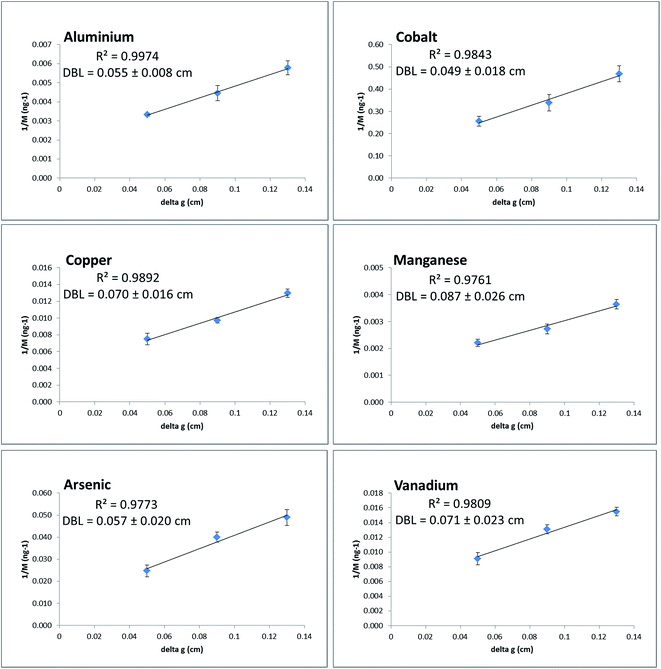
To accurately determine dissolved analyte concentrations using DGT techniques, it is important that the total diffusive path-length (Δg plus DBL) is known.39,44 In order to determine the DBL at the sampling sites, DGT-MBL samplers with varying diffusive layer thicknesses (0.05, 0.09 and 0.13 cm, including filter membrane) were deployed in triplicate. Regression lines from plots of 1/M vs. Δg were used to calculate the thickness of the DBL for each element (eqn (4)). Good linearity (R2 = 0.9761–0.9974) was observed for Al, Co, Cu, Mn, As and V at Runaway Bay Marina with an average DBL thickness of 0.065 ± 0.014 cm determined (Fig. 2). This average DBL thickness was quite similar for cations (0.065 ± 0.017 cm) and oxyanions (0.064 ± 0.010 cm), and is in excellent agreement with previously reported DBL thicknesses at the same locations (0.072 cm,32 0.067 cm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25 and 0.068 cm
25 and 0.068 cm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26). Good linearity (R2 = 0.9581–0.9999) was also observed for Al, Co, Cu, Mn, As and V at The Spit with an average DBL thickness of 0.060 ± 0.010 cm determined (Fig. S2, ESI†). This average DBL was also very similar for cations (0.059 ± 0.005 cm) and oxyanions (0.063 ± 0.019 cm). While varying DBL values for different cationic metals have been previously shown to reflect kinetic effects related to the lability of organic complexes,6,45,46 the relatively low standard deviations for the DBL thicknesses and the similarity between cations and oxyanions, indicates that such kinetic effects were not important in this study. Therefore, the average DBL thickness was used to determine the concentrations for all trace metals in this study. These DBL values are higher than those that have been reported in rivers previously,47 but this is consistent with the fact that water movement at these coastal sites will largely be due to tidal exchange, which will produce both strong currents and virtually no current at different times over the tidal cycle.
26). Good linearity (R2 = 0.9581–0.9999) was also observed for Al, Co, Cu, Mn, As and V at The Spit with an average DBL thickness of 0.060 ± 0.010 cm determined (Fig. S2, ESI†). This average DBL was also very similar for cations (0.059 ± 0.005 cm) and oxyanions (0.063 ± 0.019 cm). While varying DBL values for different cationic metals have been previously shown to reflect kinetic effects related to the lability of organic complexes,6,45,46 the relatively low standard deviations for the DBL thicknesses and the similarity between cations and oxyanions, indicates that such kinetic effects were not important in this study. Therefore, the average DBL thickness was used to determine the concentrations for all trace metals in this study. These DBL values are higher than those that have been reported in rivers previously,47 but this is consistent with the fact that water movement at these coastal sites will largely be due to tidal exchange, which will produce both strong currents and virtually no current at different times over the tidal cycle.
The effect of the DBL was investigated by comparing DGT measurements, with each binding layer, with and without correction for the DBL thickness. The DGT concentrations for all metals at Runaway Bay Marina and The Spit when the DBL was not corrected for were 70% and 73%, respectively, of the values obtained when the DBL was corrected for. This highlights the degree of underestimation associated with not accounting for the DBL. Example results for Al are shown in Table 2, which allow comparison of the differences in concentrations when corrected for the DBL thickness. These results are described in more detail in Section 3.4.
| Field site | Binding layers | Measured Al with DBL (μg L−1) | Measured Al without DBL (μg L−1) | C without DBL/CDBL |
|---|---|---|---|---|
| Runaway Bay Marina | DGT-MBL | 7.52 ± 0.22 | 5.29 ± 0.16 | 0.70 |
| DGT-Metsorb | 6.13 ± 0.42 | 4.31 ± 0.29 | ||
| DGT-Chelex | 0.49 ± 0.08 | 0.35 ± 0.05 | ||
| DGT-PAMPAA | 3.81 ± 0.67 | 2.68 ± 0.47 | ||
| The Spit | DGT-MBL | 6.50 ± 0.45 | 4.72 ± 0.33 | 0.73 |
| DGT-Metsorb | 4.88 ± 0.25 | 3.54 ± 0.18 | ||
| DGT-Chelex | 0.37 ± 0.11 | 0.27 ± 0.08 | ||
| DGT-PAMPAA | 3.56 ± 0.42 | 2.58 ± 0.30 |
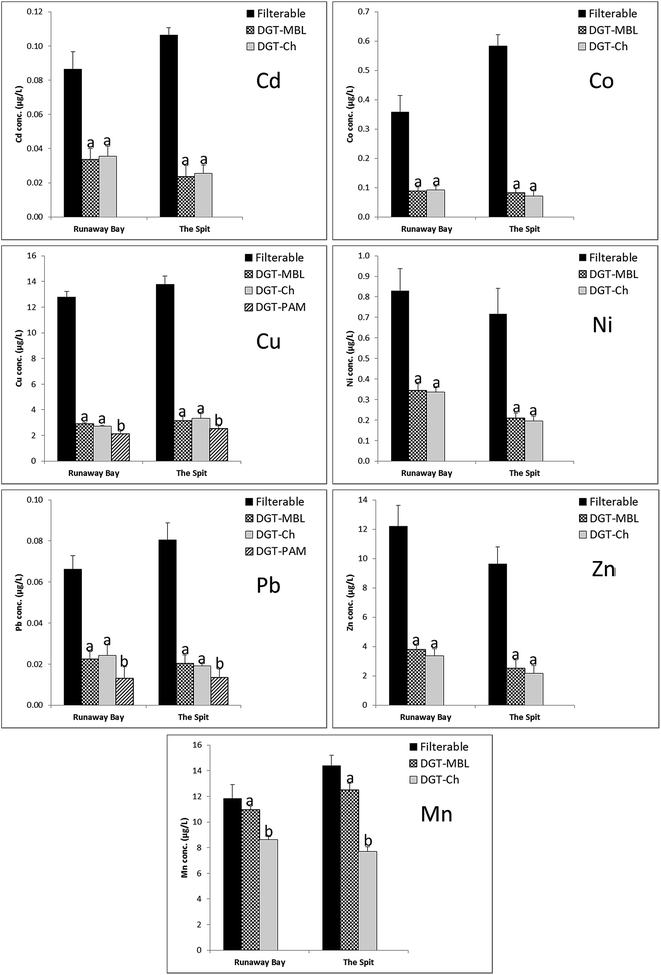
3.3. Comparison of DGT-labile and filterable concentrations for cationic metals
DGT-labile concentrations for cations (Cd, Co, Cu, Mn, Ni, Pb, Zn) measured by DGT-MBL and DGT-Chelex, and the mean filterable concentrations over 3 days at Runaway Bay Marina and The Spit are summarised in Fig. 3. DGT-PAMPAA measurements for Cu and Pb are also in Fig. 3. Mean concentrations of filterable metals, collected over the course of the DGT deployments, were substantially greater than the DGT labile concentrations measured by all DGT binding layers for all cations at both sampling sites, with the exception of Mn by DGT-MBL. The DGT-labile concentrations represented only 24–41% of Cd, 12–26% of Co, 17–24% of Cu, 27–41% of Ni, 17–37% of Pb and 23–31% of Zn filterable concentrations measured at the field sites. This observation suggests the majority of these metals existed as colloids and/or non-labile complexes which are generally not measured by DGT.35,48Natural waters typically contain a wide range of complexes with different diffusion and dissociation rates. Organic complexes can dominate the speciation of many cationic metals, and the fact that DGT-labile concentrations are >10% of the filterable concentrations implies that a sizeable fraction of organic complexes are measurable. Most inorganic complexes are considered to be labile to DGT measurements, although there are some inorganic complexes that need longer times than the duration of the DGT deployments to dissociate, and are therefore non-labile46,49 (see reviews by Davison and Zhang,6 and Galceran and Puy,45 for more details). Since non-labile complexes have a low bioavailability via exposure, the DGT-labile concentrations are considered to better represent bioavailable fractions of metals than filterable concentrations in natural waters. However, it should be noted that the measured DGT-labile concentrations use the diffusion coefficients of the free metal ions, even though labile inorganic and/or organic complexes may dominate the metal speciation; this is an aspect of DGT measurements that are highly operational, especially for cationic metals. In this study, all the DGT measured metal concentrations were calculated based on the diffusion coefficients of the respective free metal ions measured by Shiva et al.31 in open or restricted diffusive gels, as appropriate; due to their larger size, organic metal complexes have lower diffusion coefficients than free metal ions and consequently these species contribute less to DGT-measured concentrations than highly labile smaller species (free metal ions and inorganic complexes). DGT measured concentrations using ODL and RDL are compared in Section 3.5, as use of RDL is operationally considered to exclude or further diminish the contribution of organic complexes.
Although the Gold Coast Broadwater is an important coastal lagoon in southeast Queensland, the number of studies conducted on the environmental health of this estuary is limited.14 To assess the risk of metals to the health of the environment at each of the field sites, all DGT measured and filterable trace metal concentrations were compared to the ANZECC water quality guidelines42 for the 95% level of ecosystem protection in marine waters, where such data exist (Table 1). Results indicated that Cd, Co, Ni and Pb concentrations with all measurement techniques were well below trigger values at both sites. Concentration of Zn measured by the DGT techniques were also well below the guidelines, however, filterable concentrations of Zn were only marginally below the trigger values. Cu had concentrations above the guidelines at both sampling sites with all measurement methods (approximately 10 times higher for grab measurements and 2 times higher for DGT measurements). Dunn et al.14 also reported Cu concentrations above the ANZECC guidelines at different locations within the Broadwater, indicating anthropogenic inputs of Cu in the urban waterways of The Broadwater. These inputs are likely due to the presence of a large number of boats, used for recreational activities that use Cu-based antifouling paints.15,50
There were no significant differences (p >0.05) between concentrations measured by DGT-MBL (CMBL) and DGT-Chelex (CChelex) for Cd, Co, Cu, Ni, Pb and Zn at both sampling locations; CMBL/CChelex values ranged from 0.92 to 1.16 for all elements at both sampling sites. These results indicate that DGT-Chelex and DGT-MBL measured similar ranges of metal species. Panther et al.30 reported a similar correspondence between measurements of cationic metals by DGT-Chelex and DGT-MBL during laboratory deployments in synthetic seawater. Concentrations for DGT-PAMPAA were also determined for Cd, Cu and Pb, although Cd was below the detection limit (Fig. 3). DGT-PAMPAA measured concentrations represented only 17–18% and 17–20% of the filterable concentrations of Cu and Pb, respectively. CPAMPAA concentrations were between 74 and 81% for Cu, and 54 and 70% for Pb of CChelex and CMBL concentrations at both sites and were significantly different (p <0.05; values between 0.001 and 0.047). These data are in accordance with the results obtained by Li et al.,19 where DGT-PAMPAA and DGT-Chelex were compared in coastal waters for Cd and Cu. The stability constant of Cu is reported to be higher for Chelex than for PAMPAA,19 and it is therefore possible that DGT-PAMPAA measures a more selective fraction of Cu species (e.g. weaker labile complexes). Lehto et al.51 have discussed the effect of the stability constant of binding sites and metal–ligand complex lability on DGT metal uptake using numerical models. This is a potentially interesting result that warrants further investigation, but DGT-PAMPAA needs to be more thoroughly validated for a range of cations, especially in seawater, to ensure that the lower concentrations measured are not due to the effects of competition.
The relationship of filterable, DGT-Chelex and DGT-MBL data for Mn were different to those of other cations. Independent t-tests revealed that there was no statistical difference (p >0.05) between CMBL and Cfilterable at both sites, while CChelex and Cfilterable were significantly different (p <0.05; values between 0.014 and 0.026). CDGT/Cfilterable ratios of 0.87–0.93 were observed for DGT-MBL and 0.53–0.73 for DGT-Chelex. Ratios close to 1, especially for DGT-MBL, are not surprising as Mn tends not to readily form organic complexes and the dominant species in seawater is Mn2+ with some hydr(oxide) forms likely to be present as neutral species or as colloids.52,53 DGT-MBL measured significantly different (p <0.001) and considerably higher Mn concentrations compared to DGT-Chelex (CMBL/CChelex = 1.27 and 1.63 at Runaway Bay Marina and The Spit, respectively). This difference in the Mn concentrations measured by DGT-MBL and DGT-Chelex may be due to Metsorb accumulating a species that Chelex does not. However, this explanation is unlikely based on the known speciation of Mn in seawater which is dominated by free metal ions;53 the possibility of neutral or colloidal species binding to the MBL is discussed further in Section 3.5 using the DGT measurements with RDL. Alternatively, previous research30,54 has observed underestimation of Mn in seawater with DGT-Chelex with deployment times >24 h, and proposed that this may be due to competition by Mg2+ and Ca2+, which are present at high concentrations in seawater. Therefore, another explanation for the higher concentration measured by DGT-MBL is that Metsorb also binds Mn2+ quite strongly and with less interference from Mg2+ and Ca2+. It is not possible to consider the relative contributions of the Chelex and Metsorb to MBL measurements of Mn without separate DGT-Metsorb measurements; however the DGT-MBL technique measurements appear to largely overcome the known limitations of DGT-Chelex for Mn.
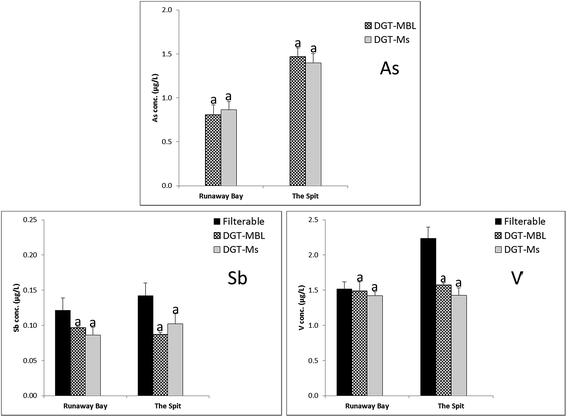
3.4. Comparison of DGT-labile and filterable concentrations for oxyanionic metals
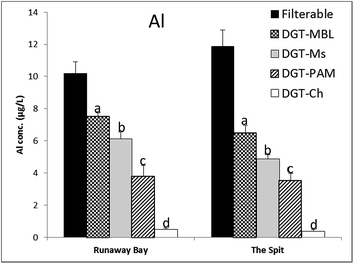
DGT-MBL and DGT-Metsorb labile concentrations of oxidized As, Sb and V, along with filterable concentrations of Sb and V, measured at Runaway Bay Marina and The Spit are summarised in Fig. 4. Filterable concentrations could not be measured for As in seawater by ICP-MS due to the spectral interference with polyatomic ArCl (m/z 75),55 whereas these interferences are effectively diluted by the DGT measurements. Mo and W concentrations were below the method detection limits of DGT-MBL and DGT-Metsorb at both sampling sites. Additionally, DGT-Metsorb has been reported to be incapable of measuring Mo in synthetic seawater due to the competition between major anions and Mo ions.40 DGT measured concentrations for Sb and V were generally more similar to the mean filterable concentrations than observed with cations, as 61–79% of total filterable Sb, and 70–98% of total filterable V in both estuarine waters was DGT labile. This is consistent with these elements having a simpler speciation than cationic metals in seawater;56,57 the difference in concentrations may be due to the presence of these elements adsorbed onto colloids in the filterable samples. DGT-MBL and DGT-Metsorb measured concentrations were consistent for As, Sb and V with no significant differences (p >0.05) recorded and all ratios of CMBL/CMetsorb in the range of 0.85 to 1.12. These results support those of Panther et al.,30 who recorded no significant differences in the concentrations of As, Sb and V determined by DGT-Metsorb and DGT-MBL in synthetic seawater, and further validate the use of DGT-MBL for measurement of these oxidized oxyanion species in natural seawaters.Filterable and DGT-labile concentrations of Al measured by DGT-MBL, DGT-Metsorb, DGT-PAMPAA and DGT-Chelex at Runaway Bay Marina and The Spit are shown in Fig. 5. Filterable Al concentrations were higher than all of the DGT labile concentrations (CDGT/Cfilterable ranged from 0.03 to 0.05 for Chelex, and 0.30 to 0.55 for the other binding layers, although DGT-MBL measured up to 70% of the filterable Al at Runaway Bay Marina). Al is known to associate with colloids and natural dissolved organic matter in natural waters,58 which would explain the higher filterable concentrations.
However, the dominant soluble form of Al in waters at pH >8 is Al(OH)4(aq.)−, which makes interpretation of the various DGT measurements interesting, as they all measured significantly different concentrations at both sites. DGT-MBL measured significantly (p ≤0.036) higher concentrations of Al compared to DGT-Metsorb at both sampling sites, with ratios of CMBL/CMs between 1.23 and 1.33, even though DGT-Metsorb had previously been shown to accurately determine Al in synthetic seawater.32 DGT-Chelex measurements were very low (6% of DGT-MBL) and significantly different (p <0.001) from the measurements of other DGT binding layers, consistent with the fact that Chelex-100 is a cation exchange resin and therefore not expected to work for Al in seawater,32 where the dominant species is Al(OH)4(aq.)−. The slight DGT-Chelex response may be due to the uptake of Al3+ and labile organic complexes, or due to a partial uptake of the dissociated anionic and minor neutral species. The DGT-MBL measurement, however, does not appear to be simply the sum of the DGT-Chelex and DGT-Metsorb measurements. DGT-PAMPAA measured significantly lower (p = 0.002 at Runaway Bay Marina and p = 0.031 at The Spit) concentrations of Al compared to DGT-Metsorb (CPAMPAA/CMs 0.62 and 0.73 at Runaway Bay Marina and The Spit, respectively). Although this DGT technique has not been validated for Al, the large difference with DGT-Chelex and relatively high uptake efficiency of PAMPAA for Al (Table S2†) indicates that this technique merits further investigation and validation in various waters, especially seawater, using a range of Al species.
3.5. Further evaluation of the speciation of trace metals using DGT techniques
The DGT measurements using various binding layers described previously in this study used open diffusive layers (ODL). This section discusses the additional insights into selective DGT measurements of metals available by using restricted diffusive layers (RDL), something that has not been done often in natural waters. The pore sizes of ODL and RDL are different and the application of DGTs with both diffusive layer types at the same time has been reported to be useful for discriminating between organic and inorganic species of analytes in laboratory studies.33 The measured concentrations were used to determine the ratio of CRDL/CODL for each analyte and DGT binding type. The results are summarised in Fig. 6 for Runaway Bay Marina and Fig. S3 (ESI†) for The Spit, and the full range of data is provided in Tables S3 and S4 (ESI†) for comparison.The data for Runaway Bay Marina (Fig. 6) indicate that CRDL/CODL values for several metals (Mn, Ni, Pb, V, As, Sb) were within the range of 0.9–1.1 for all binding layers, suggesting that these metals do not have substantial labile organic complexes in this coastal water and the majority of the analyte masses accumulated by the DGTs were due to the binding of free ions and very small labile complexes.52,59 Similar outcomes were observed for Mn, Pb, V and As at The Spit (Fig. S3†). Co, Zn and Cd at Runaway Bay Marine (Fig. 6) and Co, Ni, Zn, Cd and Sb at The Spit (Fig. S3†) had ratios in the range 0.8–0.9, perhaps signifying that labile organic complexes were contributing slightly more to the DGT measurements with ODL for these metals.
Our results are in general agreement with those of the other DGT studies in natural waters, where ratios of CRDL/CODL ranged from 0.6 to 1.1 for a wide range of cations35 and were between 0.80 and 0.89 for Cu and Ni.60 While the situation in the field is more complex than for laboratory studies, these interpretations seem reasonable and are generally consistent with what is known about the speciation of these metals in coastal waters, although variation in measurements should also be considered to be a factor in some instances (e.g. Sb at The Spit). Furthermore, the differences between these ratios (standard deviations not shown) for different binding layers were not significant (p >0.05) for any of these metals, indicating that the DGTRDL measurements with the various binding layers were also equivalent.
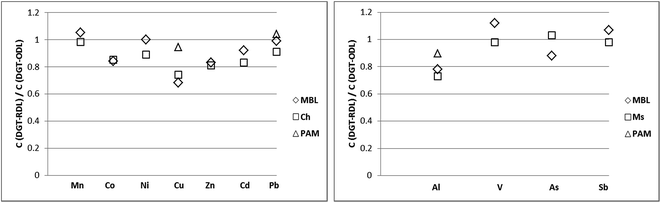
Significant differences (p <0.05; values between 0.001 and 0.037) were only observed between RDL and ODL concentrations for Cu measured by DGT-Chelex and DGT-MBL (CRDL/CODL ratio of 0.68–0.75), and Al measured by DGT-Metsorb and DGT-MBL (CRDL/CODL ratio of 0.73–0.79) (Fig. 7). These observations suggest that DGT measurements of Al and Cu in coastal waters using ODL include some labile organic species that are excluded or significantly retarded when using RDL. While Cu is well known to bind to organic matter in coastal waters,48,61 these observations may provide new insights into speciation of Al in coastal waters, especially as determined by DGT. The greater complexity of results for Al with the various binding and diffusive layers suggests that species in addition to (or perhaps even instead of) organic complexes may be contributing to some measurements, such as colloids.35 For instance, the Chelex present in MBL may solubilize lattice or counterion Al3+ ions from very fine aluminosilicates that pass though the diffusive layers. These will then hydrolyse to Al(OH)4− at the pH of these coastal waters and bind to Metsorb in the MBL. The relationship between DGT-Chelex, DGT-Metsorb and DGT-MBL measurements of Al with the different diffusive layers therefore requires further evaluation.
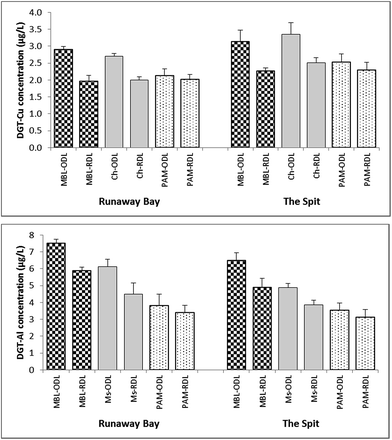 | ||
| Fig. 7 Comparison of labile concentrations of Cu and Al measured by DGT-MBL, DGT-Chelex (Ch), DGT-Metsorb (Ms) and DGT-PAMPAA (PAM) with open (ODL) and restricted (RDL) diffusive layers. | ||
In contrast, there were no significant differences (p >0.05) in the ODL and RDL concentrations of Cu and Al measured by DGT-PAMPAA, with CRDL/CODL ratios being between 0.91–0.94 for Cu and 0.88–0.90 for Al. This demonstrates that the exclusion/retardation of organic/inorganic complexes by RDL, which significantly influenced the Cu and Al concentrations measured by the other DGT binding layers, had no significant effect on the measurements of DGT-PAMPAA, although the ODL measurements of PAMPAA were slightly higher than RDL for both metals. Furthermore, there were no differences between the RDL measurements for Cu with DGT-MBL and DGT-Chelex and either of the DGT-PAMPAA measurements. This suggests that DGT-PAMPAA may largely measure free ions or inorganic complexes of Cu; therefore perhaps PAMPAA binding layer provides a more selective measurement, with only highly labile Cu complexes being measured, as suggested previously.19 The DGT-PAMPAA technique is therefore worth investigating further as a measure of bioavailable Cu in particular.
4. Conclusion
It is of great importance to evaluate any new DGT binding layer in saline waters, which is one of the most difficult and challenging matrixes in the environment. This complex matrix is characterised by the presence of high concentrations of potentially competing ions and natural ligands, both of which can affect DGT measurements. This study provides the first evaluation of DGT-MBL (Chelex–Metsorb) in natural seawaters for simultaneous measurement of cations and oxyanions. The results obtained were also compared with three other DGT types (DGT-Chelex, DGT-Metsorb and DGT-PAMPAA).The concentrations obtained for DGT-MBL agreed very well with DGT-Chelex for cationic trace metals (Cd, Co, Cu, Ni, Pb and Zn), and with DGT-Metsorb for oxyanionic metals (As, Sb and V), as reported by Panther et al.30 for laboratory evaluations in synthetic seawater. This consistency between binding layers was observed regardless of the diffusive layer used. However, significant differences were observed between DGT-MBL and DGT-Chelex for Mn, with the most likely explanation being that use of MBL overcomes the known limitations of DGT-Chelex for Mn. The fact that DGT-MBL measurements were very close to the filterable Mn concentrations supports this interpretation. Al also gave different results between DGT-MBL and other binding layers (see below). Overall, these findings validate use of the DGT-MBL technique in natural saline waters and confirm that the DGT-MBL method provides a more versatile alternative to DGT-Chelex and DGT-Metsorb due to its ability to simultaneously measure both cationic and anionic trace metal species using a single sampler. DGT-PAMPAA, measured lower concentrations of Al, Cu and Pb compared to DGT-MBL and DGT-Chelex. We propose that DGT-PAMPAA may have the capability to measure selectively the fraction of metals that are not bound to other organic/inorganic complexes, especially for Cu. Since carboxylic acid functional groups play a significant role for metal complexation in PAMPAA binding layers,18 and these functional groups are often present at sites of biological uptake, it might be useful to compare DGT-PAMPAA measurements with metal bioaccumulation in future studies to determine whether it provides better information on metal bioavailability in the environment, compared to other DGT techniques.
This study also investigated the capability of DGT techniques as a speciation tool in coastal waters by using different binding and diffusive layers to vary the selectivity of measurements. The overall results suggest that although the use of DGT samplers with a restricted diffusive layer (DGTRDL) will theoretically result in accumulation of mostly free ions and inorganic complexes, the situation is more complicated with in situ deployments. The ratio of RDL to ODL measurements was effectively 1 for Mn, Pb, V and As at both sites, indicating the presence of no labile organic ligands. Cd, Co and Zn had ratios of 0.8–0.9 at both sites suggesting that labile organic ligands were present and contributing to the DGT measurement with ODL. The results for Ni and Sb varied with ratios of about 1 at Runaway Bay Marine and ratios of 0.8–0.9 at The Spit. A ratio of about 0.7 between RDL and ODL measurements was found for Cu using DGT-MBL and DGT-Chelex, and Al using DGT-MBL and DGT-Metsorb, which suggests that labile organic complexes make a substantial contribution to ODL measurements of these metals. These results were generally consistent with what is known about the speciation of these metals in coastal waters and therefore do not contradict the previous operational observations that DGT measurements using RDL are mostly of free metals and inorganic complexes, while measurements using ODL can also include labile organic complexes.
A ratio of about 1 was obtained between ODL and RDL measurements of DGT-PAMPAA for Cu though, with the concentrations similar to the RDL measurements for the other binding layers. This suggests that DGT-PAMPAA measures only inorganic complexes and free Cu, which would be an important finding and needs to be investigated further. The results for Al were also very interesting with significant differences observed between measurements with MBL, Metsorb, PAMPAA and Chelex binding layers, with concentrations decreasing in this order, and often between ODL and RDL also. These results indicate that selective Al measurements by DGT are very complex and require further detailed investigation.
Acknowledgements
The authors would like to thank the School of Environment, Griffith University, for the provision of a PhD scholarship for A.H. Shiva. We also thank Graver Technologies (http://www.gravertech.com) for providing the Metsorb product used in this study.References
- S. N. Luoma and P. S. Rainbow, Metal contamination in aquatic environments: science and lateral management, Cambridge University Press, Cambridge, UK, 2008 Search PubMed.
- M. J. Kennish, Practical handbook of estuarine and marine pollution, CRC Press, Boca Raton, Florida, 1997 Search PubMed.
- P. S. Rainbow, Mar. Pollut. Bull., 1995, 31, 183–192 CrossRef CAS.
- P. G. C. Campbell, in Metal speciation and bioavailability in aquatic systems, ed. A. Tessier and D. R. Turner, Wiley Chichester, UK, 1995, vol. 3, pp. 45–102 Search PubMed.
- W. Davison, G. Fones, M. Harper, P. Teasdale and H. Zhang, in In situ monitoring of aquatic systems: chemical analysis and speciation, ed. J. Buffle and G. Horvai, John Wiley & Sons Ltd., Chichester, 2000, pp. 495–569 Search PubMed.
- W. Davison and H. Zhang, Environ. Chem., 2012, 9, 1–13 CrossRef CAS.
- W. J. G. M. Peijnenburg, P. R. Teasdale, D. Reible, J. Mondon, W. W. Bennett and P. G. C. Campbell, Integr. Environ. Assess. Manage., 2014, 10, 179–196 CrossRef CAS PubMed.
- E. D. Amato, S. L. Simpson, C. V. Jarolimek and D. F. Jolley, Environ. Sci. Technol., 2014, 48, 4485–4494 CrossRef CAS PubMed.
- C. Zhang, S. Ding, D. Xu, Y. Tang and M. Wong, Environ. Monit. Assess., 2014, 186, 7367–7378 CrossRef CAS PubMed.
- W. Davison and H. Zhang, Nature, 1994, 367, 546–548 CrossRef CAS.
- H. Zhang and W. Davison, Anal. Chem., 1995, 67, 3391–3400 CrossRef CAS.
- S. Denney, J. Sherwood and J. Leyden, Sci. Total Environ., 1999, 239, 71–80 CrossRef CAS PubMed.
- J. Gimpel, H. Zhang, W. Davison and A. C. Edwards, Environ. Sci. Technol., 2003, 37, 138–146 CrossRef CAS PubMed.
- R. J. K. Dunn, P. R. Teasdale, J. Warnken and R. R. Schleich, Environ. Sci. Technol., 2003, 37, 2794–2800 CrossRef CAS PubMed.
- R. J. K. Dunn, P. R. Teasdale, J. Warnken, M. A. Jordan and J. M. Arthur, Environ. Pollut., 2007, 148, 213–220 CrossRef CAS PubMed.
- V. I. Slaveykova, I. B. Karadjova, M. Karadjov and D. L. Tsalev, Environ. Sci. Technol., 2009, 43, 1798–1803 CrossRef CAS PubMed.
- J. E. Sherwood, D. Barnett, N. W. Barnett, K. Dover, J. Howitt, H. Ii, P. Kew and J. Mondon, Anal. Chim. Acta, 2009, 652, 215–223 CrossRef CAS PubMed.
- W. Li, H. Zhao, P. R. Teasdale, R. John and S. Zhang, React. Funct. Polym., 2002, 52, 31–41 CrossRef CAS.
- W. Li, H. Zhao, P. R. Teasdale, R. John and F. Wang, Anal. Chim. Acta, 2005, 533, 193–202 CrossRef CAS.
- Q. Sun, J. Chen, H. Zhang, S. Ding, Z. Li, P. N. Williams, H. Cheng, C. Han, L. Wu and C. Zhang, Anal. Chem., 2014, 86, 3060–3067 CrossRef CAS PubMed.
- S. Ding, D. Xu, Q. Sun, H. Yin and C. Zhang, Environ. Sci. Technol., 2010, 44, 8169–8174 CrossRef CAS PubMed.
- W. W. Bennett, P. R. Teasdale, J. G. Panther, D. T. Welsh and D. F. Jolley, Anal. Chem., 2011, 83, 8293–8299 CrossRef CAS PubMed.
- J. Luo, H. Zhang, J. Santner and W. Davison, Anal. Chem., 2010, 82, 8903–8909 CrossRef CAS PubMed.
- H. Österlund, S. Chlot, M. Faarinen, A. Widerlund, I. Rodushkin, J. Ingri and D. C. Baxter, Anal. Chim. Acta, 2010, 682, 59–65 CrossRef PubMed.
- W. W. Bennett, P. R. Teasdale, J. G. Panther, D. T. Welsh and D. F. Jolley, Anal. Chem., 2010, 82, 7401–7407 CrossRef CAS PubMed.
- J. G. Panther, P. R. Teasdale, W. W. Bennett, D. T. Welsh and H. Zhao, Environ. Sci. Technol., 2010, 44, 9419–9424 CrossRef CAS PubMed.
- D. Xu, Y. Chen, S. Ding, Q. Sun, Y. Wang and C. Zhang, Environ. Sci. Technol., 2013, 47, 10477–10484 CAS.
- S. Mason, R. Hamon, A. Nolan, H. Zhang and W. Davison, Anal. Chem., 2005, 77, 6339–6346 CrossRef CAS PubMed.
- T. Huynh, H. Zhang and B. Noller, Anal. Chem., 2012, 84, 9988–9995 CrossRef CAS PubMed.
- J. G. Panther, W. W. Bennett, D. T. Welsh and P. R. Teasdale, Anal. Chem., 2014, 86, 427–434 CrossRef CAS PubMed.
- A. H. Shiva, P. R. Teasdale, W. W. Bennett and D. T. Welsh, Anal. Chim. Acta, 2015, 888, 146–154 CrossRef CAS PubMed.
- J. G. Panther, W. W. Bennett, P. R. Teasdale, D. T. Welsh and H. Zhao, Environ. Sci. Technol., 2012, 46, 2267–2275 CrossRef CAS PubMed.
- H. Zhang and W. Davison, Anal. Chem., 2000, 72, 4447–4457 CrossRef CAS PubMed.
- S. Scally, W. Davison and H. Zhang, Anal. Chim. Acta, 2006, 558, 222–229 CrossRef CAS.
- R. Liu, J. R. Lead and H. Zhang, Geochim. Cosmochim. Acta, 2013, 109, 14–26 CrossRef CAS.
- I. J. Allan, J. Knutsson, N. Guigues, G. A. Mills, A.-M. Fouillac and R. Greenwood, J. Environ. Monit., 2007, 9, 672–681 RSC.
- S. Meylan, N. Odzak, R. Behra and L. Sigg, Anal. Chim. Acta, 2004, 510, 91–100 CrossRef CAS.
- H. Zhang and W. Davison, Anal. Chim. Acta, 1999, 398, 329–340 CrossRef CAS.
- K. W. Warnken, H. Zhang and W. Davison, Anal. Chem., 2006, 78, 3780–3787 CrossRef CAS PubMed.
- J. G. Panther, R. R. Stewart, P. R. Teasdale, W. W. Bennett, D. T. Welsh and H. Zhao, Talanta, 2013, 105, 80–86 CrossRef CAS PubMed.
- Y.-H. Li and S. Gregory, Geochim. Cosmochim. Acta, 1974, 38, 703–714 CrossRef CAS.
- ANZECC and ARMCANZ, National Water Quality Management Strategy Paper 4, 2000 Search PubMed.
- N. Odzak, D. Kistler, H. Xue and L. Sigg, Aquat. Sci., 2002, 64, 292–299 CrossRef CAS.
- Ø. A. Garmo, K. R. Naqvi, O. Røyset and E. Steinnes, Anal. Bioanal. Chem., 2006, 386, 2233–2237 CrossRef PubMed.
- J. Galceran and J. Puy, Environ. Chem., 2015, 12, 112–122 CrossRef CAS.
- K. W. Warnken, W. Davison and H. Zhang, Environ. Sci. Technol., 2008, 42, 6903–6909 CrossRef CAS PubMed.
- G. S. Turner, G. A. Mills, M. J. Bowes, J. L. Burnett, S. Amos and G. R. Fones, Environ. Sci.: Processes Impacts, 2014, 16, 393–403 CAS.
- M. R. Twiss and J. W. Moffett, Environ. Sci. Technol., 2002, 36, 1061–1068 CrossRef CAS PubMed.
- J. Puy, J. Galceran, S. Cruz-González, C. A. David, R. Uribe, C. Lin, H. Zhang and W. Davison, Anal. Chem., 2014, 86, 7740–7748 CrossRef CAS PubMed.
- J. Warnken, R. J. K. Dunn and P. R. Teasdale, Mar. Pollut. Bull., 2004, 49, 833–843 CrossRef CAS PubMed.
- N. J. Lehto, W. Davison, H. Zhang and W. Tych, Environ. Sci. Technol., 2006, 40, 6368–6376 CrossRef CAS PubMed.
- J. Forsberg, R. Dahlqvist, J. Gelting-NystrÖm and J. Ingri, Environ. Sci. Technol., 2006, 40, 3901–3905 CrossRef CAS PubMed.
- G. Glasby and H. Schulz, Aquat. Geochem., 1999, 5, 227–248 CrossRef CAS.
- S. Tankéré-Muller, W. Davison and H. Zhang, Anal. Chim. Acta, 2012, 716, 138–144 CrossRef PubMed.
- E. McCurdy and D. Potter, Spectrosc. Eur., 2001, 13, 14–21 CAS.
- R. Michalski, S. Szopa, M. Jabłońska and A. Łyko, Sci. World J., 2012, 2012, 902464 CrossRef PubMed.
- G. Abbasse, B. Ouddane and J. Fischer, Anal. Bioanal. Chem., 2002, 374, 873–878 CrossRef CAS PubMed.
- G. Alberti, G. D'Agostino, G. Palazzo, R. Biesuz and M. Pesavento, J. Inorg. Biochem., 2005, 99, 1779–1787 CrossRef CAS PubMed.
- S. Scally, H. Zhang and W. Davison, Aust. J. Chem., 2004, 57, 925–930 CrossRef CAS.
- H. Österlund, J. Gelting, F. Nordblad, D. C. Baxter and J. Ingri, Mar. Chem., 2012, 132–133, 34–43 CrossRef.
- M. Wallner-Kersanach, C. F. F. d. Andrade, H. Zhang, M. R. Milani and L. F. H. Niencheski, J. Braz. Chem. Soc., 2009, 20, 333–340 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5em00550g |
| This journal is © The Royal Society of Chemistry 2016 |