Biradical character in the ground state of [Mn@Si₁₂]⁺: a DFT and CASPT2 study

Abstract

Both density functional theory and multi-configurational ab initio (CASPT2) calculations are used to explore the potential energy surface of the hexagonal prismatic cluster [Mn@Si₁₂]⁺. Unlike isoelectronic Cr@Si₁₂, the ground state is a biradical, with triplet and open-shell singlet states lying very close in energy. The results are discussed in the context of recent experimental studies using infra-red multiple photon dissociation spectroscopy and X-ray MCD spectroscopy.

---

Introduction

The study of small clusters containing both silicon and a transition element can be traced back to two papers published by Beck in the late 1980s^1,2 which described the formation of M@Si_n clusters in a supersonic beam. Hiura, Miyazaki and Kanayama later used a quadrupole ion trap to isolate [M@Si_nH_x]⁺ and show that the tungsten series [W@Si_nH_x]⁺, for example, terminates at n = 12.³ Moreover, high-resolution spectra showed that the hydrogen content of the clusters, x, is reduced as n increases, and in the limit of n = 12 the most abundant tungsten cluster was completely devoid of hydrogens. The interpretation of this data is that the metal atom is completely encapsulated in M@Si₁₂, binding to all twelve silicon atoms and hence eliminating the need for additional hydrogens to saturate their valence. In the same paper, Hiura and co-workers also used density functional theory to explore the structure of W@Si₁₂, initially reporting a ‘basketlike’ structure where the metal is encapsulated within the cluster and each silicon atom is bonded to three others. However, a note added in proof identified a more stable hexagonal prismatic structure (D_6h point symmetry, see Fig. 1), which Khanna, Rao and Jena subsequently confirmed to be the global minimum for Cr@Si₁₂.⁴ Experimental support for this proposal came from the photo-detachment spectrum of the corresponding anion, [Cr@Si₁₂]⁻,⁵ which shows a peak at 3.18 eV compared to Khanna's computed value of 3.11 eV. Later scanning tunneling microscopy experiments by Uchida and co-workers showed features consistent with intact hexagonal prismatic Ta@Si₁₂ clusters on reconstructed Si(111) surfaces.⁶ XANES and EXAFS spectroscopy at the W L3 edge of W@Si_x clusters deposited on silica also suggest that the hexagonal prismatic structure is retained.⁷ The structure of Cr@Si₁₂ and W@Si₁₂ is remarkable, simply because it is so very different from the deltahedral geometries that dominate the cluster chemistry of electron-deficient species such as the boranes (icosahedral [B₁₂H₁₂]²⁻, for example). These deltahedra typically have 4- or 5-connected vertices: 3-connected structures such as the hexagonal prism, in contrast, are typically the preserve of electron-precise clusters such as tetrahedral P₄ or prismane, the unstable isomer of benzene. Over the past decade, however, a number of 3-connected structures have emerged in the cluster chemistry of germanium, including pentagonal prismatic [Co/Fe@Ge₁₀]^{3− 8–12} and D_2d-symmetric [Ru@Ge₁₂]³⁻.¹³ The fact that the endohedral metals are all from the middle of the transition series suggests that 3-connected structural motifs require filled metal d orbitals that are relatively high in energy. The origin of the stability of Cr@Si₁₂ has been debated by a number of groups including our own. One explanation is that the Cr or W atom is simply too large to fit inside an icosahedral Si₁₂ cage, and so the prismatic structure, with its larger volume, is preferred.^14,15 Jellium-type models can also be applied in this context, and configurations of 1s²1p⁶1d¹⁰ (18 electrons) and 1s²1p⁶1d¹⁰2s² (20 electrons) have been invoked to account for the relatively high dissociation energies of Cr@Si₁₂ and isostructural Fe@Si₁₂.^16–18 In their initial report,³ Hiura et al. suggested that the stability of W@Si₁₂ could be rationalised in terms of an 18-electron rule: donation of 12 electrons from the Si₁₂ cage to the metal raises the electron count to 18, leaving three electrons per Si center to form the three Si–Si bonds. The consensus now, however, is that the electronic configuration about the metal is best described as 16-electron, with a vacant d_z² orbital directed towards the centre of the two 6-membered rings (11a_1g in Fig. 1).^8,18 Despite the debate about the qualitative description of bonding in Cr@Si₁₂, the fact that it is a singlet with a perfectly D_6h-symmetric structure, as proposed by Hiura and Khanna, has not been seriously questioned in the literature. The apparently conflicting results of recent experimental observations on the isoelectronic cationic manganese cluster cation, [Mn@Si₁₂]⁺, therefore appear rather surprising. Ngan et al. have reported the infra-red multiple photon dissociation spectroscopy of [Mn@Si₁₂]⁺·Xe, and based on comparison of their spectrum to DFT-computed values (with the B3P86 functional), have argued that the ground state is in fact a triplet rather than a singlet. Moreover, the structure is not perfectly hexagonal prismatic, but rather distorted to C_i point symmetry, suggesting that it is descended from a state which is orbitally degenerate in D_6h symmetry.¹⁹ Silicon-based clusters which retain some or all of the characteristic magnetic moment of the endohedral transition metal have potential applications in the spintronics field,^20–22 and so the apparent emergence of a triplet state represents a significant finding. In direct contrast, however, Lau and co-workers have measured the X-ray MCD spectrum of [Mn@Si₁₂]⁺ and concluded that the cluster is in fact diamagnetic.²³ Their DFT calculations (using the PBE0 functional) identified a D_6h-symmetric singlet ground state, although more recent computational work from the same group suggests that a distorted triplet is in fact more stable.²⁴ The purpose of this work is to explore the potential energy surface using a variety of theoretical tools, and hence to establish the factors that lead to the close proximity of singlet and triplet states in [Mn@Si₁₂]⁺ but not in isoelectronic Cr@Si₁₂. We also address the relationship between structure and spin state, and how this impacts on the vibrational spectrum. We touched briefly on related issues in a previous paper⁸ which focused on the energy landscape for a range of M@E₁₂ clusters. Specifically, we showed that the relative stabilization of the metal d orbitals in [Mn@Si₁₂]⁺ compared to Cr@Si₁₂ stabilises a charge-transfer state where an electron is promoted from the 8a_2u orbital localised exclusively on the Si₁₂ cage (Fig. 1) into the 11a_1g LUMO with dominant Mn d_z² character. For reasons that we discuss in detail below, this charge transfer state is a singlet rather than a triplet and moreover is not orbitally degenerate, and so on both counts appears inconsistent with Ngan et al.'s interpretation of the IR data.¹⁹ What we did not consider previously is the fact that the 8a_2u orbital is almost degenerate with another orbital localised primarily on the Si₁₂ cluster, 8e_2g in Fig. 1, and so the manifold of charge transfer states is in fact much richer than previously suspected. Moreover, the degeneracy of the 8e_2g orbital provides a natural driving force for distortions from the hexagonal prismatic limit in charge transfer states where it is partially occupied.

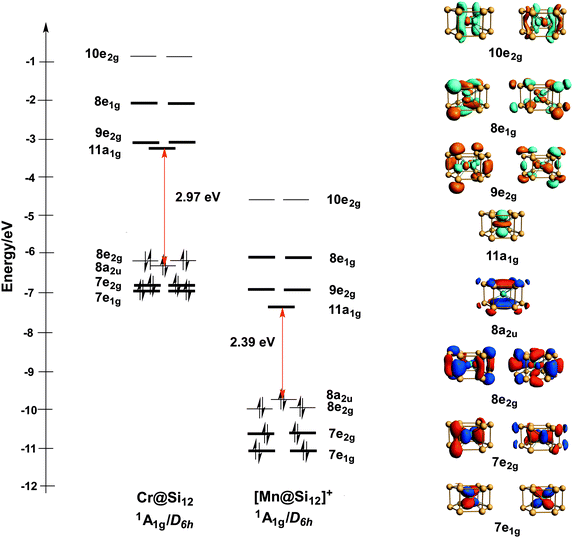Fig. 1 Comparison of the Kohn–Sham MO diagrams for Cr@Si₁₂ and [Mn@Si₁₂]⁺ (B3LYP functional, isosurface value = 0.04 (e a.u.⁻³)^1/2). Orbitals with substantial metal 3d character are shown in bold.

Computational methods

All DFT calculations described in this paper were performed with the Amsterdam Density Functional package (ADF2013.01)^25–27 using the gradient-corrected (GGA) functional proposed by Becke and Lee, Yang and Parr (BLYP)^28,29 and the hybrid functional B3LYP.^30,31 An all electron Slater-type basis sets of triple-ζ quality, extended with a single polarisation function (TZP), was used to describe all the atoms (Cr, Mn and Si). All structures were optimised using the gradient algorithm of Versluis and Ziegler.³² For numerical frequency calculations the number of fit functions was increased by adding the subkey ‘FitType QZ4P’ of the key BASIS and a fine grid was used for numerical integration (keyword ‘Becke good’). Single point CASSCF/CASPT2 calculations were performed with the MOLCAS 8.0 package.³³ Atomic natural orbitals optimised for relativistic corrections and core correlation (ANO-RCC) basis sets were used to expand the orbitals.³⁴ The large primitive set of functions is contracted to [5s4p2d1f] for Si, [7s6p5d3f2g1h] and [7s7p5d3f2g1h] for Mn and Cr, respectively. Scalar relativistic effects were included using the Douglas–Kroll–Hess Hamiltonian. The computational cost of evaluating the two-electron integrals was reduced by the Cholesky decomposition technique (threshold 10⁻⁶ a.u.).³⁵ We used the standard zeroth-order Hamiltonian and an imaginary shift of 0.1 a.u. to avoid the appearance of weak intruder states in the CASPT2 calculations.

Results and discussion

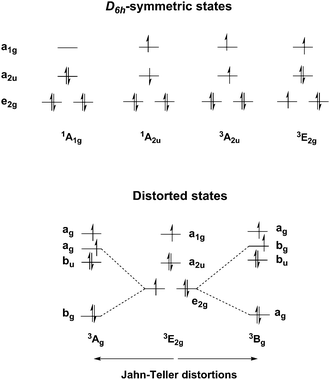
Symmetry considerations and the manifold of states

To set the scene for the quantitative discussion to follow, we first consider the symmetries of low-lying states that could, in principle, be candidates for the ground state of [Mn@Si₁₂]⁺. The single determinant configuration shown in Fig. 1 (for both [Mn@Si₁₂]⁺ and Cr@Si₁₂) and also in Scheme 1 corresponds to a closed-shell singlet with ¹A_1g symmetry. The charge transfer states alluded to in the introduction all involve the promotion of a single electron into the 11a_1g orbital (which carries dominant metal 3d_z² character), the donor orbital being either the 8a_2u orbital or 8e_2g. Within this charge-transfer manifold, both singlet and triplet configurations are possible, giving rise to states of ^1/3A_2u and ^1/3E_2g symmetry (we note from the outset that the open-shell singlets are intrinsically multi-determinantal in nature). The orbitally degenerate ^1/3E_2g states are necessarily unstable with respect to low-symmetry distortions, and indeed imaginary frequencies always appear for these states. In principle, any distortion that removes the 3-fold rotation axis will lift the degeneracy of the ^1/3E_2g states, and here we have considered two possibilities: a C_2h-symmetric distortion leading to puckering of the hexagonal prism in states of ^1/3A_g/B_g symmetry and a C_s-symmetric distortion where one edge of the hexagonal prism is elongated, giving states of ^1/3A′/A′′ symmetry. The former is closely related to the C_i-symmetric structure reported by Ngan et al.¹⁹ while the latter is similar to the structure of Hf@Si₁₂ reported by Uchida et al.³⁶ In practice, it seems that the precise nature of the distortion has little impact on the computed energies (vide infra). Before moving to a discussion of these energies, we note one further symmetry-related issue that has significant implications for the subsequent discussion. The two donor orbitals of interest here are 8a_2u and 8e_2g, Fig. 1. The former is localised rigorously on the Si₁₂ cage, the only contribution from the metal coming from 4p_z. In contrast the 8e_2g orbital retains some residual contribution from metal 3d_x²−y²/xy (∼15% in the ¹A_1g state), and this difference proves to be important when we consider the exchange interaction between the two unpaired electrons, and hence the singlet/triplet separation (vide infra).

Scheme 1 Manifold of single-determinant configurations for [Mn@Si₁₂]⁺ and Cr@Si₁₂.

Energy landscape using density functional theory

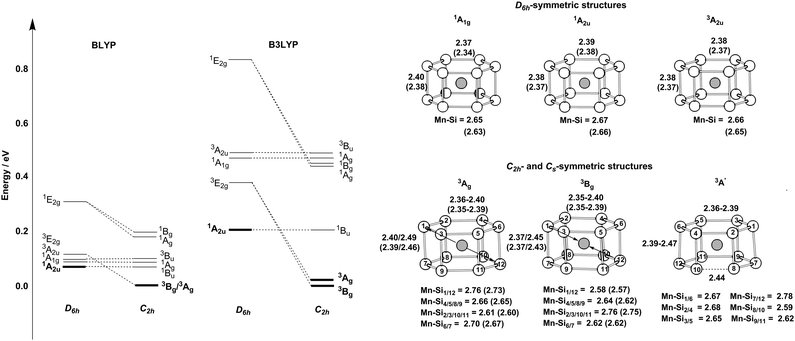
The relative energies and optimised structures of the various configurations summarised in Scheme 1 are collected in Fig. 2: full details of the energies and Mulliken spin densities are summarised in Table 1. Given the well-known dependence of spin states on the chosen functional, we report values for two distinct and contrasting functionals – a typical GGA functional, BLYP and its hybrid analogue, B3LYP. Corresponding data for isoelectronic Cr@Si₁₂ are presented in ESI† (Table S1). Before discussing [Mn@Si₁₂]⁺ in detail, we note first that the identity of the ground state in Cr@Si₁₂ is not in doubt: the ¹A_1g state lies substantially (∼0.8 eV) below any other, irrespective of functional, precisely as has been reported by Khanna,^4,16,18 us,⁸ and others.¹⁴ In [Mn@Si₁₂]⁺, however, the relative stabilization of the metal-based orbitals closes the HOMO–LUMO gap (2.39 eV vs. 2.97 eV in Cr@Si₁₂ in Fig. 1) and as a result the ¹A_2u state is in fact more stable than ¹A_1g, only marginally so with the BLYP functional but substantially (0.26 eV) with the hybrid B3LYP. The values of 〈S²〉 in the ¹A_2u state (1.22/2.11 for BLYP/B3LYP) are indicative of strong spin contamination, and the Mulliken spin densities, ρ(Mn) = +1.62/+2.69 and ρ(Si₁₂) = −1.62/−2.69, confirm a high degree of biradical character. The fact that the ¹A_2u state is more stable than the corresponding triplet, ³A_2u, is at first sight surprising as it is apparently in conflict with Hund's rule. The preference for the singlet stems from the fact alluded to earlier that the two singly occupied orbitals, 11a_1g and 8a_2u, are localised in completely different regions of the molecule: 11a_1g is almost entirely Mn d_z² in character while 8a_2u is almost entirely localised on the silicon cage. The direct exchange interaction between the electrons in these two singly occupied orbitals, which would favour a triplet, is therefore very small. The dominant exchange interaction is instead between the single electron in 11a_1g and those in the Mn–Si bonding orbitals (7e_1g, 7e_2g in Scheme 2). Within the unrestricted Kohn–Sham ansatz, the result is that the spin-α electrons in these orbitals are polarised towards the metal, giving Mulliken spin densities far in excess of 1.0 (+1.62/+2.69 for BLYP/B3LYP). As a corollary, the spin-β electrons are polarised in the opposite direction, towards the Si₁₂ cage, stabilizing the ¹A_2u state, where the electron in the 8a_2u orbital is also spin-β, over the triplet (³A_2u) where the spin densities arising from the two orbitals are opposed. This is certainly a relatively minor effect simply because repulsions between electrons delocalised over the Si₁₂ cage are in any case not severe, but it is clearly just large enough to tip the balance in favour of the singlet.

Fig. 2 The energy landscape for [Mn@Si₁₂]⁺ obtained with both BLYP and B3LYP functionals and the corresponding optimised structural parameters (bond lengths obtained with B3LYP are shown in parentheses).

Table 1 Relative energies, structural data, Mulliken spin densities and values of 〈S²〉 for various states of [Mn@Si₁₂]⁺ computed at the BLYP level of theory. Data for B3LYP are shown in parenthesis

	D 6h-symmetric states					C 2h-symmetric states		C s-symmetric states
	^1A1g	^1A2u	^3A2u	^1E2g	^3E2g	^3Ag	^3Bg	^3A′
a The degenerate ^3E2g state is defined using fractional occupation numbers: 0.5 electrons in each of the two spatial components of the 8e2g orbital with spin-β. The value of 〈S^2〉 is therefore not defined.
DFT:BLYP (B3LYP energies in parenthesis)
Energy/eV	+0.09 (+0.47)	+0.07 (+0.21)	+0.10 (+0.49)	+0.31 (+0.84)	+0.12 (+0.38)	0.00 (+0.02)	0.00 (+0.00)	0.00
Mn–Si/Å	2.65 (2.63)	2.67 (2.66)	2.66 (2.65)	2.65 (2.64)	2.66 (2.65)	2.61–2.76 (2.60–2.73)	2.58–2.76 (2.57–2.75)	2.59–2.78
ρ(Mn)	0.00 (0.00)	1.62 (2.69)	1.66 (2.56)	1.51 (2.70)	2.14 (3.13)	2.11 (3.00)	2.10 (3.09)	2.09
ρ(Si12)	0.00 (0.00)	−1.62 (−2.69)	0.34 (−0.56)	−1.51 (−2.70)	−0.14 (−1.13)	−0.11 (−1.00)	−0.10 (−1.09)	−0.09
〈S^2〉	0.00 (0.00)	1.22 (2.11)	2.10 (2.62)			2.17 (2.65)	2.17 (2.74)	2.16
CASPT2@BLYP geometry (CASPT2@B3LYP geometry in parenthesis)
Energy/eV	+0.17 (+0.14)	+0.07 (+0.09)	+0.16 (+0.13)			+0.06 (0.05)	0.00 (0.00)
ρ(Mn)			1.15 (1.15)			2.43 (2.42)	2.41 (2.44)
ρ(Si12)			0.85 (0.85)			−0.43 (−0.42)	−0.41 (−0.44)

---

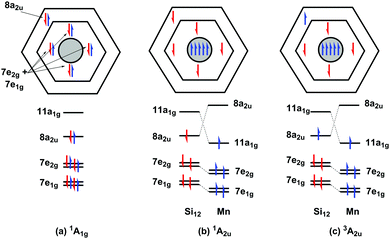Scheme 2 Qualitative picture of the polarization of the Mn–Si electrons in the ¹A_2u and ³A_2u states as a result of promotion of one electron into the d_z² orbital.

The tendency of hybrid functionals to stabilise states of high local spin density is well known, and it is therefore no surprise that the B3LYP functional favors the ¹A_2u state over ¹A_1g and also amplifies the biradical character as measured both by the value of 〈S²〉 and also the spin densities. The limit of complete localization of all four spin-α electrons in the 7e_1g and 7e_2g orbitals would correspond to formation of a half-filled 3d shell at the Mn center, and the B3LYP functional clearly approaches this limit much more closely than does BLYP. Finally, we note in passing that the polarization of the electrons in the Mn–Si bonding orbitals is, in principle, possible even without the preceding transfer of an electron into the d_z² orbital (i.e. in the ¹A_1g state). We have been unable to locate such a broken-symmetry state with the BLYP functional or even B3LYP, but the BHandHLYP functional, with 50% Hartree Fock exchange, does lead to symmetry breaking. The greater ease of symmetry breaking in the ¹A_2u state can be viewed as ‘seeding’ of the polarization by the unpaired electron in the d_z² orbital.

Turning now to the orbitally degenerate D_6h-symmetric states, ^1/3E_2g, we note first that the electron density distribution shown in Table 1 is qualitatively rather similar to that in ^1/3A_2u: both singlet and triplet have spin densities at the metal far in excess of 1.0, particularly with the hybrid B3LYP functional. The key difference between the ^1/3A_2u and ^1/3E_2g pairs is that in the latter it is the triplet that lies lowest (i.e. the normal Hund order is restored). We emphasised above the point that the stability of the ¹A_2u state can be traced, ultimately, to the almost complete localization of the two singly-occupied orbitals in different regions of physical space which causes the direct exchange interaction between them to become negligibly small. In the ^1/3E_2g pair the situation is subtly different because the donor orbital (8e_2g) carries some residual Mn 3d_x²−y²/xy character, as a result of which the direct exchange interaction with the electron in 11a_1g is non-negligible, favouring the triplet. Regardless of the chosen functional, however, the ¹A_2u state lies below ³E_2g, so the most stable D_6h-symmetric structure is a singlet, not a triplet, although the energies are close.

The Jahn–Teller theorem tells us that the ³E_2g states must necessarily be unstable with respect to a low-symmetry distortion, and given the proximity of ¹A_2u and ³E_2g, only a relatively small stabilization would be required to invert the singlet/triplet ordering. As noted in the discussion of symmetry-related features, any distortion that annihilates the 3-fold rotation axis will lift the degeneracy of the ³E_2g state, and we have considered explicitly two possibilities, a puckering of the 6-membered rings (C_2h symmetry) and an elongation of one Si–Si edge (C_s). With the BLYP functional, we can locate three distinct states of this type, C_2h-symmetric ³A_g and ³B_g‡ and C_s-symmetric ³A′, which differ subtly in the distribution of Mn–Si bond lengths (Fig. 2). With B3LYP, we have been able to locate only the C_2h-symmetric structures, ³A_g and ³B_g. These low-symmetry triplet states are, however, almost degenerate, suggesting that the precise nature of the distortion is not critical. More important in the context of the singlet/triplet debate is the fact that the distorted triplet states now lie below the singlet, ¹A_2u, albeit only marginally, irrespective of the functional. Thus the emergence of a triplet ground state for [Mn@Si₁₂]⁺ is intimately linked to the distortion from perfect D_6h symmetry: without this distortion, which is rather minor in structural terms and rather ill defined (in the sense that C_2h- and C_s-symmetric structures are almost identical in energy), the singlet would be more stable.

CASSCF/CASPT2 studies

In light of the functional dependence of the spin state energetics, and also the strong spin contamination in the open-shell states indicated by the values of 〈S²〉, we have turned to multi-configurational SCF methodologies (CASPT2) for an alternative perspective on the bonding. In all cases we used a (10,15) active space (10 electrons in 15 orbitals). The active space includes the two singly occupied orbitals in the ¹A_2u state (one of a_2u symmetry, the other a_1g symmetry), the M–Si bonding orbitals of e_2g and e_1g symmetries, their antibonding counterparts and the five 4d orbitals. A qualitatively similar (14,15) active space was used by Pierloot and co-workers In their study of the closely-related [Mn@Si₁₄]⁺ cluster.³⁷ The importance of the 4d ‘double shell’ in complexes of the first transition series has been demonstrated on numerous occasions,^38,39 but in this case they have very small natural occupation numbers and a parallel series of calculations without the 4d orbitals (a (10,10) active space) yields very similar results – see ESI† (Table S2). Full geometry optimisations at the CASPT2 level of theory are not feasible in systems of this size, and so we have considered the energies of the key states at both the BLYP and B3LYP-optimised structures. The B3LYP functional gives Mn–Si bond lengths that are ∼0.01–0.02 Å shorter than their BLYP analogues, and this difference leads to an ∼0.1 eV lowering of the CASPT2 energies of all states at the B3LYP geometries. Manual optimizations where all twelve Mn–Si bond lengths are uniformly decreased in 0.01 Å steps has allowed us to locate approximate minima for the ¹A_2u and ³B_g states a further 0.07–0.09 eV lower in energy with Mn–Si bond lengths ∼0.02 Å shorter than the B3LYP-optimised ones (see ESI† for a full discussion). However, in the context of the present discussion the key point is that the singlet–triplet separation (¹A_2u–³B_g) is essentially independent of the chosen geometry, with the triplet lying lower by 0.07–0.09 eV. The CASPT2 results therefore concur with both BLYP and B3LYP in identifying a distorted triplet ground state.§ The dispersion of energies at the CASPT2 level is relatively narrow, with the ¹A_1g, ¹A_2u and ³B_g states separated by only 0.17 eV: the results are therefore more consistent with the BLYP functional than B3LYP, which appears to overestimate the stability of the open-shell states, and of the triplets in particular. In the discussion of the DFT spin densities we highlighted the significance of the polarisation of the Mn–Si bonding electrons, particularly in the charge-transfer states where the presence of an unpaired electron in the d_z² orbital ‘seeds’ the localisation. We can identify related phenomena in the occupation numbers of the natural orbitals in the CAS wavefunction, which are summarised in Fig. 3 for five key states of [Mn@Si₁₂]⁺: D_6h-symmetric ¹A_1g, ¹A_2u and ³A_2u and C_2h-symmetric ³B_g and ³A_g (using the corresponding B3LYP geometry in each case). In the closed-shell singlet (¹A_1g), the d_z² orbital is vacant (natural orbital occupation = 0.05) while in the ¹A_2u state it is singly occupied (0.99), as is the a_2u orbital (1.00). These changes are accompanied by more subtle but nevertheless significant variations in the occupations of the e_1g- and e_2g-symmetric Mn–Si bonding and antibonding orbitals. The occupations of the bonding orbitals decrease from ∼1.86 in the ¹A_1g state to ∼1.78 in ¹A_2u, while the occupations of the antibonding orbitals show the opposite trend: ∼0.12 in ¹A_1g but ∼0.22 in ¹A_2u. The correlation of the Mn–Si bonding electrons is clearly significantly enhanced by the transfer of an electron into the a_1g orbital. Thus the ‘seeding’ effect that leads to polarisation of the spin density in the unrestricted density functional ansatz also emerges as enhanced multi-configurational character in the CASSCF wavefunction.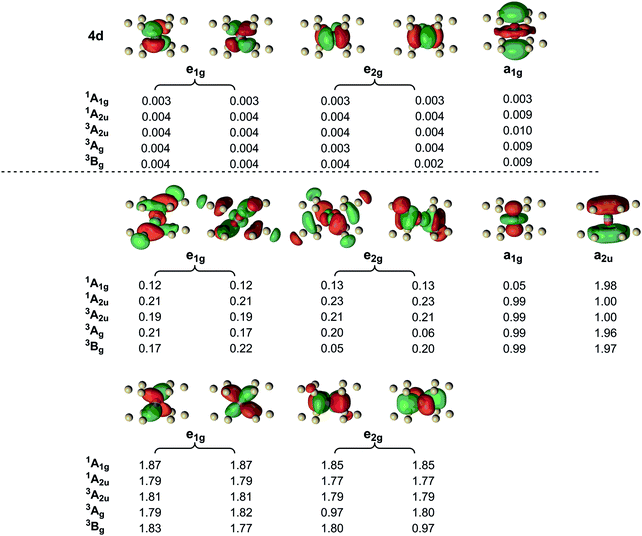

Fig. 3 Orbitals in the (10,15) active space and their occupations in the various states of [Mn@Si₁₂]⁺ (B3LYP geometry). Orbitals were generated for the ¹A_1g state using an isosurface value of 0.04.

Analysis of the vibrational spectrum

Ngan et al. have argued that their measured vibrational spectrum, which shows two broad absorptions centered at ∼260 cm⁻¹ and ∼330 cm⁻¹ (Fig. 4, top), is consistent with a distorted C_i-symmetric triplet state.¹⁹ In order to establish the degree to which we can confidently exclude the D_6h-symmetric singlets (¹A_1g or ¹A_2u) based on a poorer match to experiment, we have computed vibrational spectra for the three key, closed-shell ¹A_1g, open-shell ¹A_2u (D_6h symmetry) and ³B_g (C_2h symmetry). We have used the B3LYP functional as it is in generally good agreement with experimental frequencies for transition metal compounds.^40,41 The computed spectrum of the ¹A_1g state (Fig. 4a) shows an intense feature at 222 cm⁻¹ (e_1u symmetry) corresponding to motion of the Mn atom in the xy plane and a weaker one at 333 cm⁻¹ (a_2u) corresponding to motion along the 6-fold axis (coupled to an a_2u-symmetric vibration of the Si₁₂ cage). This spectrum compares rather poorly with the experimental one: the separation of the two most intense bands is 111 cm⁻¹ (222 and 333 cm⁻¹) compared to a measured separation of only ∼70 cm⁻¹. In the open-shell singlet state (¹A_2u), the same two intense bands (e_1u and a_2u) are apparent in the spectrum, but the e_1u band is shifted 16 cm⁻¹ to higher frequency, appearing at 238 cm⁻¹, while the a_2u mode is shifted to lower frequency, 310 cm⁻¹. We note immediately that this spectrum affords a qualitatively better match to experiment in so much as the separation of the two dominant features is now only ∼70 cm⁻¹. We can relate these shifts in vibrational frequencies to the very clear differences in electronic structure between the closed-shell ¹A_1g state on one hand and the open-shell ¹A_2u on the other. In the former, the electron density about the metal is highly anisotropic: the occupied Mn–Si bonding orbitals (7e_1g and 7e_2g) are localised primarily in the xy plane while the d_z² orbital is vacant. The result is that the metal can move in the xy plane with little energetic penalty (i.e. the frequency is low) but motion along the z axis is less facile. In the ¹A_2u state, in contrast, the d_z² orbital is singly occupied, as are, to a first approximation, d_x²−y², d_xy, d_xz and d_yz due to the strong polarization of the bonding orbitals. The more isotropic electron density distribution in the ¹A_2u state is reflected in the smaller separation between vibrational modes corresponding to motion in the xy plane (e_1u) and along the z axis (a_2u). All our results (DFT and CASPT2) suggest that the electron density distributions in the ³B_g and ¹A_2u states are qualitatively very similar (both can be regarded as biradicals) and the general features of the vibrational spectra are also strikingly similar, Fig. 4b and c (we also note that our computed spectrum for ³B_g state is almost identical to that reported by Ngan et al.¹⁹). In particular, the two intense features remains centered around 240 cm⁻¹ and 310 cm⁻¹, and on this basis we believe that the separation of the e_1u and a_2u bands in the infra-red spectrum distinguishes clearly between closed-shell (¹A_1g) and biradical (¹A_2u/³B_g) configurations (we note that unfortunately no spectrum of Cr@Si₁₂ has been reported to test this prediction). The distinction between open-shell singlet (¹A_2u) and triplet (³B_g) is, however, more difficult to make simply because the electron density distributions are so very similar, as are the computed vibrational spectra. The only clear difference between the two comes from the splitting of the e_1u band in the ³B_g state, which should give rise to a shoulder to high frequency of the intense band at 250 cm⁻¹. The resolution of the spectrum is, however, insufficient to establish whether such a band is present or not. Moreover, it is important to emphasise that the IRMPD experiment relates not to the cluster in isolation but rather to one with a Xe tag ([Mn@Si₁₂]⁺·Xe), and the reduction in symmetry associated with the weak binding of the tag could also lead to a small splitting of the e_1u peak, in either singlet or triplet. The IR spectrum therefore appears to be equally consistent with either the ¹A_2u or the ³B_g state, and the former cannot be dismissed as a candidate for the ground state based on this data alone.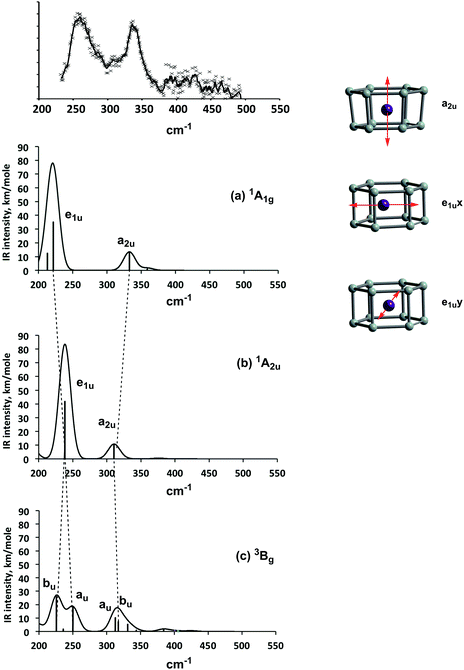

Fig. 4 Experimental Infra-red multi-photon dissociation (IRMPD) spectrum of [Mn@Si₁₂]⁺ and simulated vibrational spectra of the ¹A_1g, ¹A_2u and ³B_g states.

Conclusions and the relationship between theory and experiment

Our interest in the [Mn@Si₁₂]⁺ cluster was originally driven by the conflicting claims for singlet and triplet ground states in the experimental literature. A detailed exploration of the potential energy surface has confirmed that open-shell singlets and triplets are indeed very close in energy, in marked contrast to isoelectronic Cr@Si₁₂ where the closed-shell singlet is energetically isolated. The triplet is found to be the ground state of [Mn@Si₁₂]⁺ at all levels of theory considered here (DFT and CASPT2), and so, on face value, our calculations appear consistent with Ngan et al.'s interpretation of the IRMPD experiments: i.e. that the ground state is a triplet. Our analysis in the previous section, however, suggests that whilst the IR data do eliminate the closed-shell ¹A_1g state as a candidate for the ground state, they do not effectively discriminate between the ¹A_2u and ³B_g states, both of which are biradicals – certainly not to the extent that we could confidently eliminate the former. Meanwhile the XMCD data is clearly in favour of a singlet, so there appears to be no compelling evidence from experiment alone to support a triplet ground state. A closer analysis of the computational data shows that it is only the hybrid B3LYP functional that strongly favours the triplet (ΔE = 0.21 eV), and we must treat this number with caution as the tendency of hybrids to over-stabilise high spin states is well established. The gap is much smaller for the gradient-corrected functional BLYP (ΔE = 0.07 eV) and also at the CASPT2 level of theory (ΔE = 0.07–0.09 eV), values that lie below the threshold where we could confidently make a definitive assignment of the ground state. The case for a triplet from theory is therefore certainly not overwhelming. What is not in doubt, however, is that the ground state of [Mn@Si₁₂]⁺ is fundamentally different from that of isoelectronic Cr@Si₁₂: the former is a biradical (either triplet or singlet) while the latter has a closed-shell singlet ground state, and this difference manifests itself in characteristic shifts in the vibrational spectrum.

Acknowledgements

We thank the EPSRC for financial support (JEM, VA, EP/K021435/1) and also for the TMCS CDT programme (DF, EP/L015722/1). We also acknowledge the Spanish Administration (CdG, Project CTQ2014-51938-P), the Generalitat de Catalunya (CdG, Project 2014SGR199) and the European Union (JEM, CdG, COST Action ECOSTBio CM1305) for financial support. Finally, we thank Professor André Fielicke, Professor Tobias Lau and Dr Linn Leppert for helpful discussions and the former for providing the original spectroscopic data shown in Fig. 4.

Notes and references

1. S. M. Beck, J. Chem. Phys., 1987, 87, 4233–4234.
2. S. M. Beck, J. Chem. Phys., 1989, 90, 6306–6312.
3. H. Hiura, T. Miyazaki and T. Kanayama, Phys. Rev. Lett., 2001, 86, 1733–1736.
4. S. N. Khanna, B. K. Rao and P. Jena, Phys. Rev. Lett., 2002, 89, 016803.
5. W. Zheng, J. M. Nilles, D. Radisic and K. H. Bowen, Jr., J. Chem. Phys., 2005, 122, 071101.
6. N. Uchida, L. Bolotov, T. Miyazaki and T. Kanayama, J. Phys. D: Appl. Phys., 2003, 36, L43–L46.
7. Z. Sun, H. Oyanagi, N. Uchida, T. Miyazaki and T. Kanayama, J. Phys. D: Appl. Phys., 2009, 42, 015412.
8. J. M. Goicoechea and J. E. McGrady, Dalton Trans., 2015, 44, 6755–6766.
9. T. Krämer, J. C. Duckworth, M. D. Ingram, B. Zhou, J. E. McGrady and J. M. Goicoechea, Dalton Trans., 2013, 42, 12120–12129.
10. B. B. Zhou, M. S. Denning, D. L. Kays and J. M. Goicoechea, J. Am. Chem. Soc., 2009, 131, 2802–2803.
11. S. Scharfe, F. Kraus, S. Stegmaier, A. Schier and T. F. Fässler, Angew. Chem., Int. Ed., 2011, 50, 3630–3670.
12. J. Q. Wang, S. Stegmaier and T. F. Fässler, Angew. Chem., Int. Ed., 2009, 48, 1998–2002.
13. G. Espinoza-Quintero, J. C. Duckworth, W. K. Myers, J. E. McGrady and J. M. Goicoechea, J. Am. Chem. Soc., 2014, 136, 1210–1213.
14. R. B. King, Struct. Bonding, 2011, 140, 1–24.
15. R. B. King, I. Silaghi-Dumitrescu and M. M. Uta, Dalton Trans., 2007, 364–372.
16. J. Ulises Reveles and S. N. Khanna, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 165413.
17. J. Ulises Reveles and S. N. Khanna, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035435.
18. M. B. Abreu, A. C. Reber and S. N. Khanna, J. Phys. Chem. Lett., 2014, 5, 3492–3496.
19. V. T. Ngan, E. Janssens, P. Claes, J. T. Lyon, A. Fielicke, M. T. Nguyen and P. Lievens, Chem. – Eur. J., 2012, 18, 15788–15793.
20. J. U. Reveles, P. A. Clayborne, A. C. Reber, S. N. Khanna, K. Pradhan, P. Sen and M. R. Pederson, Nat. Chem., 2009, 1, 310–315.
21. R. Robles and S. N. Khanna, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115414.
22. J. Zhao, X. Huang, P. Jin and Z. Chen, Coord. Chem. Rev., 2015, 289–290, 315–340.
23. V. Zamudio-Bayer, L. Leppert, K. Hirsch, A. Langenberg, J. Rittmann, M. Kossick, M. Vogel, R. Richter, A. Terasaki, T. Möller, B. v. Issendorff, S. Kümmel and J. T. Lau, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 115425.
24. L. Leppert and J. T. Lau, personal communication.
25. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
26. C. F. Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403.
27. E. J. Baerends, SCM, Theoretical chemistry, Vrije Universiteit, Amsterdam, The Netherlands, ADF2013, http://www.scm.com.
28. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
29. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
30. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
31. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
32. L. Versluis and T. Ziegler, J. Chem. Phys., 1988, 88, 322–328.
33. F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. X. Ma, P. A. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. L. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Marti, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541.
34. O. B. Roos, V. Veryazov and P. O. Widmark, Theor. Chem. Acc., 2003, 111, 345–351.
35. F. Aquilante, P. A. Malmqvist, T. B. Pedersen, A. Ghosh and B. O. Roos, J. Chem. Theory Comput., 2008, 4, 694–702.
36. N. Uchida, T. Miyazaki and T. Kanayama, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 205427.
37. V. T. Ngan, K. Pierloot and M. T. Nguyen, Phys. Chem. Chem. Phys., 2013, 15, 5493–5498.
38. K. Andersson and B. O. Roos, Chem. Phys. Lett., 1992, 191, 507–514.
39. K. Pierloot, Int. J. Quantum Chem., 2011, 111, 3291–3301.
40. B. Y. Liang and L. Andrews, J. Phys. Chem. A, 2002, 106, 6945–6951.
41. Y. I. Ishikawa and K. Kawakami, J. Phys. Chem. A, 2007, 111, 9940–9944.

---

Footnotes

† Electronic supplementary information (ESI) available: Table S1: Relative energies, structural data, Mulliken spin densities and values of 〈S²〉 for various states of Cr@Si₁₂. Table S2: relative energies for various states of [Mn@Si₁₂]⁺ obtained with CASPT2 (10,10) (no 4d orbitals) and (10,15) (with 4d orbitals) active spaces. Tables S3–S5: analysis of potential energy surfaces using CASPT2. Table S6: Cartesian coordinates and total energies of all stationary points for [Mn@Si₁₂]⁺ and Cr@Si₁₂. See DOI: 10.1039/c6cp03534e

‡ The C_2h-symmetric ³A_g and ³B_g states are conceptually related to the familiar tetragonal elongation and compression modes in octahedral complexes.

§ The corresponding CASPT2 energies for Cr@Si₁₂ are listed in Table S1: the closed-shell ¹A_1g state is clearly the most stable (by 0.72–0.78 eV) just as predicted by DFT.

---