Open Access Article
Open Access ArticleQuantitative diffusion and swelling kinetic measurements using large-angle interferometric refractometry†
John E.
Saunders
,
Hao
Chen
,
Chris
Brauer
,
McGregor
Clayton
,
Weijian
Chen
,
Jack A.
Barnes
and
Hans-Peter
Loock
*
Department of Chemistry, Queen's University, Kingston, Ontario, Canada. E-mail: hploock@queensu.ca
First published on 1st October 2015
Abstract
The uptake and release of sorbates into films and coatings is typically accompanied by changes of the films' refractive index and thickness. We provide a comprehensive model to calculate the concentration of the sorbate from the average refractive index and the film thickness, and validate the model experimentally. The mass fraction of the analyte partitioned into a film is described quantitatively by the Lorentz–Lorenz equation and the Clausius–Mosotti equation. To validate the model, the uptake kinetics of water and other solvents into SU-8 films (d = 40–45 μm) were explored. Large-angle interferometric refractometry measurements can be used to characterize films that are between 15 μm to 150 μm thick and, Fourier analysis, is used to determine independently the thickness, the average refractive index and the refractive index at the film–substrate interface at one-second time intervals. From these values the mass fraction of water in SU-8 was calculated. The kinetics were best described by two independent uptake processes having different rates. Each process followed one-dimensional Fickian diffusion kinetics with diffusion coefficients for water into SU-8 photoresist film of 5.67 × 10−9 cm2 s−1 and 61.2 × 10−9 cm2 s−1.
1 Introduction
Understanding the diffusion of liquids and gases out of thin polymer films is an important concern in many industrial processes. This includes, for example, the application and curing of paints and coatings and of protective layers for electronic components. Diffusion of gases and solvents into polymer films affects the chemical resistance of these films and is similarly important. In analytical chemistry analyte diffusion into thin films governs solid phase microextraction (SPME) and partitioning of the analyte between the mobile and stationary phase in chromatographic separations. The uptake and release of sorbates can frequently be modelled using Fick's laws of diffusion with boundary conditions that imply an impermeable substrate on one side of the film and an infinite, homogenous supply (or sink) on the other.1 In chromatographic separations, this infinite layer is the known as the “mobile phase”.A large number of methods exist for the measurement of diffusion constants. They typically exploit either the change in mass or the change in film thickness upon uptake or release of an analyte. For example, the resonance frequency changes of a Quartz Crystal Microbalance (QCM) or thickness shear mode resonator give accurate values for diffusion coefficients from effective mass changes.2,3 These methods work well for some thin films (<100 nm), but require correction terms to account for the elasticity and damping of thicker films.4
Measurements of the optical properties of films such as absorption, bulk refractive index and fluorescence are sensitive, “non-contact” forms of interrogation that are well-suited for many diffusion kinetics measurements. These changes are related to the average concentrations of analytes within the film. For example, using attenuated total-internal reflection Fourier transform infrared spectroscopy (ATR-FTIR) diffusion coefficients can be measured in real time from the absorption lines characteristic of the diffusing target species.5–7
The refractive index is arguably the most universal optical property of a film that changes with analyte uptake. It can be measured over a very large wavelength range but provides the least information about the identity of the molecule. The specificity can be recovered by synthesizing coating materials that are selective to a target group of analytes. Refractive index is often measured using Abbé-type refractometers, where a sample is placed between an illumination and a refraction prism.8 An alternative arrangement involves measuring the refraction of light when shone through sample liquids inside a V-block prism refractometer.9,10 Other approaches involve placing the prism on a goniometer to probe the refraction of a sample at a range of incident angles.11 Sensitive measurements were performed by sandwiching liquid samples between a prism and a diffraction grating and then measuring changes to the diffraction peaks.12 Refractive index can also be measured using surface plasmon resonance (SPR) and has been used to measure, for example, the diffusion of aromatic solvent vapour into a Teflon AF1600 coating.13 More recently, refractive index measurements have been demonstrated from the intensity of Fresnel reflection at the end of a fibre14 or reflection from fibre Fabry–Perot cavities formed using fibre Bragg gratings.15 They have also been demonstrated using fibre bundles16 and lensed photonic crystal fibres (PCF) with micromirrors.17 However, refractive index measurements on their own are not sufficient to characterize the uptake or release of compounds into thin films. For example, the uptake of an analyte into a film frequently leads to a refractive index increase, but if the film also swells upon analyte uptake and the liquid analyte's refractive index is lower than that of the film, the refractive index may actually decrease.
For the simultaneous measurement of refractive index and thickness of thin films (10 nm–1 μm), ellipsometry is usually the preferred technique. While it is difficult to beat the resolution and accuracy offered by this technique, it can be complicated to measure the film's index and thickness in situ, since ellipsometry typically requires unobstructed optical access to the top surface of the film.18,19 In this regard, “conventional” refractometry has demonstrated potential for determining the in situ refractive index of liquids and films.8,20,21 Typically, thin film interference cannot provide independent measurements of thickness and refractive index but can only measure the optical path length, i.e. the product of these two values. Hence, it remains difficult to use these measurements for accurate uptake analysis.
Alternatively, film thickness, surface roughness, density and refractive index profiles can be measured for thin films (1–500 nm) using either X-ray or neutron reflectometry.22–25 Here, collimated X-ray or neutron beams are reflected by a film at glancing angles and the film profile is extracted from the angular reflection pattern. Neutron reflection has the added advantage that it is sensitive to the nuclear mass allowing it to distinguish between different isotopes contained in either the films or the diffusing analytes.22 These techniques have been used to study the swelling of polyacrylamide24,25 and polystyrene polymers.23 While both reflectometry techniques provide better than nanometer resolution, they require highly specialized and expensive equipment. Both techniques are conceptually quite similar to the optical method presented in this article.
Here, we demonstrate the use of a specifically designed large-angle interferometric refractometer for independent measurements of (a) the film's thickness, (b) its bulk index and (c) the refractive index at the film/substrate interface. The instrument permits measurements at a rate that is currently limited by the frame rate of our camera to 1 Hz, with a refractive index resolution of 1 to 5 × 10−4 and a thickness resolution of <1% on a 40 μm thick film. This technique is suitable for characterization of smooth, and homogeneous, transparent films with a thickness in the range of 15–150 μm. In a previous letter we described the application of this method to measurements of gas diffusion into a siloxane-type polymer.26 Herein, the technique is validated by observing the time-resolved diffusion of water into SU-8 photoresist films (40–45 μm thick). The uptake of methanol, isopropanol and other solvents into SU-8 is also described.
SU-8 was selected as a test material because of the extensive literature and well-understood physical properties of this photoresist. The structure of SU-8 is a tetramer glycidylether of a Bisphenol A Novolac resin shown in Fig. 1. SU-8 is a popular photoresist for electronic and photonic circuitry and for micromechanical and microelectro-mechanical systems (MEMS). Photo-activated resists, including SU-8, Novolac™ and EPON™ resins, are commonly used to template high aspect ratio structures.27,28 Using photolithography, SU-8 can be made into complex structures including pillars, microcantilevers, microfluidic channels and micromechanical valves in lab-on-a-chip applications (e.g.ref. 29 and 30). SU-8 is also used for the fabrication of microfluidics on top of optical nanodevices (e.g. silicon, silicon nitride and silica photonic devices), and as a protective overcoat for photonic and electronic chips.31–33 In these applications it is important to understand the diffusion of water and other solvents through SU-8. Previous studies on water diffusion into photoresist films found that water causes SU-8 and other photoresists to swell slightly.3,34–37 Exposure to other solvents can also result in film cracking, delamination and damage to microstructures.38–41
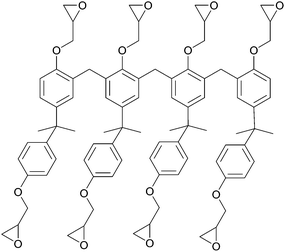 | ||
| Fig. 1 Structure of uncured SU-8 photoresist containing eight epoxy groups. These groups are responsible for cross-linking the resist. | ||
In this study, we use interferometric refractometry at large incidence angles to demonstrate real-time kinetic measurements of refractive index and thickness of films. The diffusion of water and other solvents into SU-8 photoresist is used to highlight the sensitivity and accuracy of the technique. Comprehensive models for both the diffusion kinetics and the quantification of the water mole fraction and mass fraction in the film complete the study.
This article provides first a brief description of the interferometric refractometer, its operating principle and a detailed description of the data analysis procedure. The change in thickness and refractive index of a thin SU-8 film during the uptake of water is presented. The mole fraction of water in the SU-8 film is then calculated using an equation derived from the Lorenz–Lorentz and Clausius–Mosotti equations. The average bulk refractive index, and the refractive index near the film–substrate interface are both used to obtain the diffusion coefficients of water from a simple, but accurate, kinetic model based on Fick's laws of diffusion. The interactions of SU-8 with other solvents including methanol, isopropanol, acetone, acetonitrile and m-xylene are also described.
2 Experimental methods
The glancing-angle interferometric refractometer and Fourier transform-based data analysis were briefly described in a letter.26 The following provides details on the data acquisition and processing. A theoretical interpretation of the results in terms of the analytes' mole fraction and the Fickian diffusion constants is given in Section 3.2.1 Experimental setup
A refractometer was constructed using a 1550 nm diode laser (Thorlabs LPS-1550-FC, 1.5 mW) as a high coherence length light source. A fibre polarization controller and polarization filter was used to select only p-polarized light. Two lenses were used as a Galilean beam expander to increase the laser beam diameter to approximately 1 cm. The light was then focused onto the top surface of a 25 mm high-density flint glass equilateral prism (Schott N–SF11, n1550 = 1.7434) using a cylindrical lens (f = 2.50 cm). A second cylindrical lens (f = 5.00 cm) was used to focus the reflected light onto a near-IR CCD camera (Edmund Optics, NIR Camera # 56-567) as shown in Fig. 2A. Cylindrical lenses are preferred over spherical lenses to reduce aberration of the fringes in the images.The intensity of the reflected light at the film–substrate interface is governed by the Fresnel reflection of p-polarized light:
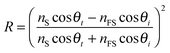 | (1) |
Below the critical angle the Fresnel reflected light interferes with light reflected from the top surface of the film resulting in a fringe pattern. One would expect this fringe pattern to extend all the way to the angle of total internal reflection, but instead a dark band is observed at glancing angles that are very close to the critical angle. At these angles the light is reflected over considerable lengths within the film and is then spatially separated from the reflection at the bottom of the film. Interference is then no longer possible (see ESI† for details). The cross-sections of the images were obtained by averaging the intensities of each pixel column using a custom Matlab™ protocol (Fig. 3A). Performing Fourier analysis on the cross-sections allows for extraction of the associated phase, ϕ.26 After “unwrapping” the phase (Fig. 3B), the average refractive index of the film, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) F, and its thickness, d, can be extracted from a fit to
F, and its thickness, d, can be extracted from a fit to
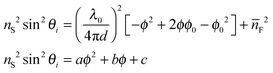 | (2) |
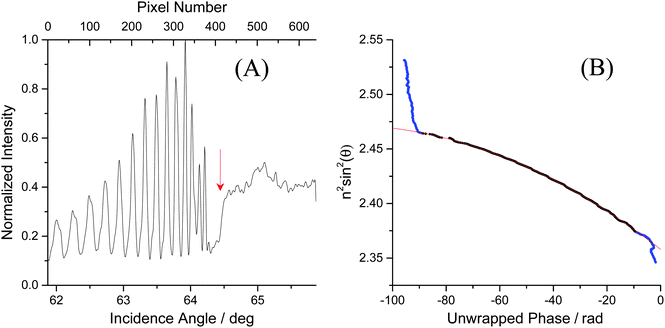 | ||
Fig. 3 (A) The cross section of the image shown in Fig. 2B. The fringes are due to thin film interference whereas the step marks the transition to total internal reflection. The critical angle was determined from a Gaussian fit to the derivative of this curve and is marked by an arrow. (B) The unwrapped phase was obtained after Fourier analysis of the left graph. Standard refractive index solutions with known refractive index were used for calibration. A selection of the phase data that correspond to the fringe region (black dots) were fit with eqn (2) (red line). This fit yields a film thickness of d = 43.41 μm and an average refractive index of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) F = 1.5722. F = 1.5722. | ||
The fitting parameters a, b, and c, are used to obtain the film thickness, d, and the average refractive index, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) F.
F.
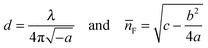 | (3) |
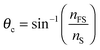 | (4) |
2.2 Data processing
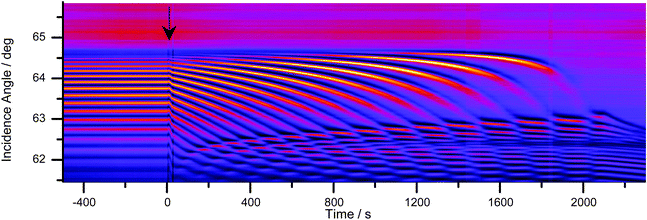
Baseline measurements were taken for 20 minutes before approximately 5 mL of either water or another solvent was pipetted on top of the SU-8 film. To visualize the uptake, the cross-sections – obtained as in Fig. 3A – were stacked as columns of an image (Fig. 4A). This image was then Fourier filtered (Fig. 4B) using Image-J software42 to remove periodic features smaller than 10 pixels and larger than 640 pixels. Fourier filtering also removed vertical stripes which were attributed to intensity fluctuations between images. Finally, an edge-finding algorithm, based on the first derivative, was used to obtain the critical angle (Fig. 4C). The critical angle was determined by fitting a Gaussian function to the highlighted band (arrow in Fig. 4C).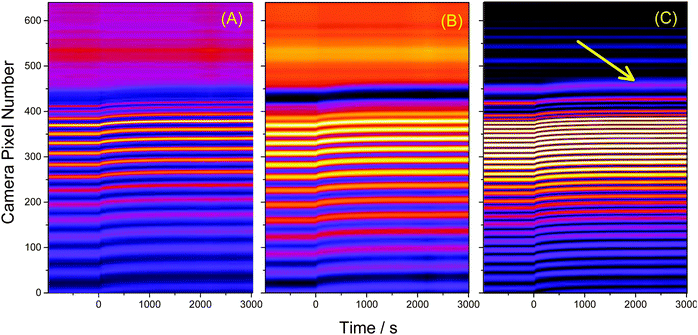 | ||
| Fig. 4 (A) 4000 image cross sections similar to Fig. 3A were taken in 1 s intervals and stacked as pixel columns. At t = 0 s water was placed above the SU-8 film. (B) A Fourier filter was applied to the image to reduce the noise. (C) An edge finding routine was used to help locate the critical angle (arrow). This image has been contrast-enhanced to emphasize the interface position. | ||
The cross-sections of the original data (Fig. 3A) were also processed by Fourier analysis as described by Chen et al.26 Here, the Fourier transform was taken of each intensity cross-sections (Fig. 3A) and windowed to select only the positive spatial frequency component. The inverse Fourier transform was then taken and the phase was extracted as a function of incident angle (Fig. 3B). After unwrapping the phase, the film thickness, d, and the average refractive index, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) film were extracted using eqn (2) where the limits of the fitted region were defined dynamically using the previously obtained critical angle, θc. To increase the robustness of our measurements the refractive index and thickness were obtained from over 600 slightly different fitting regions on each image and then averaged to compensate for any image anomalies.
film were extracted using eqn (2) where the limits of the fitted region were defined dynamically using the previously obtained critical angle, θc. To increase the robustness of our measurements the refractive index and thickness were obtained from over 600 slightly different fitting regions on each image and then averaged to compensate for any image anomalies.
2.3 SU-8 film preparation
Five SU-8 films were prepared using SU-8 50 resin (Microchem, Newton, MA) which was spin-coated onto high density flint glass slides (Schott Glass N-SF11, thickness ∼1 mm; n1550 = 1.7434) according to the manufacturer's instructions.The slides were cleaned with isopropanol, dried using compressed air and then heated to 65 °C. To obtain films with thicknesses between 30 to 45 μm, the slides were spin coated at 500 rpm for 15 seconds with an acceleration of ∼50 rpm s−1 to uniformly spread the resin on the substrate, then at 3000 rpm for 35 seconds with an acceleration of ∼250 rpm s−1 to achieve the desired thickness. The films were then prebaked at 65 °C for 5 minutes followed by a soft bake at 95 °C for 15 minutes. Three of the slides were exposed to UV light (P = 10 mW cm−2, λ = 350 nm) for 40 seconds. The other two slides were exposed for an additional 2 minutes and 20 seconds (total: 3 minutes) to test whether the UV curing time affected the film properties. After the curing step, the slides were post-baked at 65 °C for 1 minute and then at 95 °C for 4 minutes. The slides were left on the hot plate for 15 minutes as the hot plate cooled down to prevent cracking from rapid cooling. Between experiments, the slides were stored in a vacuum desiccator containing activated Drierite (Sigma Aldrich). The desiccator was evacuated using an oil-free membrane pump. To contain the liquid solvents on top of the films, a glass cylinder was glued to the top of the SU-8 films using commercially available “5 minute” epoxy adhesive. The coated slides were then placed on top of the prism using refractive index matching liquid (nd = 1.7250, Cargille Labs).
3 Theoretical methods
3.1 Calculation of mole fraction
In the following paragraphs, calculations are presented to correlate the experimentally observed change in thickness and refractive index of a polymer film to the unknown mass fraction and mole fraction of an analyte within the film. As will be shown, the mole fraction of a compound absorbed by a polymer film, X, is unambiguously related to thickness and refractive index of a film.The polarizability, P, of a material can be related to its density, ρ, molar mass, M, and refractive index, n. Within the assumptions of the Clausius–Mosotti equation, the polarizabilities of the polymer, PP, and the analyte, PA, are treated as independent of each other, i.e. the small contribution of intermolecular interactions to the polarizability is neglected.
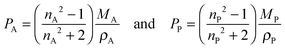 | (5) |
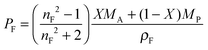 | (6) |
| PF = XPA + (1 − X)PP | (7) |
This equation corresponds to the well-established Lorentz–Lorenz equation.43–45 Insertion of eqn (5) and (6) into (7) gives after rearrangement:
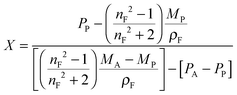 | (8) |
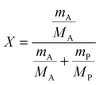 | (9) |
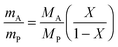 | (10) |
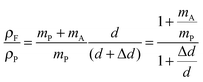 | (11) |
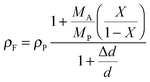 | (12) |
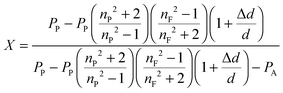 | (13) |
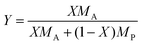 | (14) |
3.2 Diffusion kinetics
The mole fractions calculated in the previous section are obtained by analysis of a large number of interferograms taken in 1 second intervals. Fitting to the mole fractions as a function of time allows for determination of the diffusion rate of a analyte through a polymer film. In the following section we derive two equations that permit the determination of the diffusion constant from either the average mole fraction of the analyte in the polymer film or from the mole fraction near the film–substrate interface.We assume that the uptake of an analyte (liquid or gas) into a polymer film (or membrane) can be modelled using Fick's second law for one-dimensional diffusion:
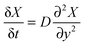 | (15) |
With the appropriate boundary conditions one can find solutions, X(y, t), for eqn (15). Since our films are open to the analyte at one face and impermeable at the opposite face, we can treat the problem as one-dimensional diffusion through a plane of finite thickness within an infinite reservoir of analyte.
The interferometric refractometer provides two different methods of determining the film's refractive index. When using the critical angle of reflection, θc, to determine the film's index, we probe the refractive index, nFS, close to the glass substrate. This index is therefore related to the mole fraction at the bottom of the film (film–substrate interface) X(y = 0, t). On the other hand, the fringes apparent in Fig. 3A depend on the average bulk index of the film, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) F, a property that is related to the average concentration of the analyte which is obtained by integrating over the entire film thickness.
F, a property that is related to the average concentration of the analyte which is obtained by integrating over the entire film thickness.
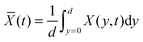 | (16) |
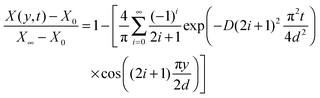 | (17) |
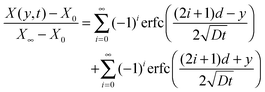 | (18) |
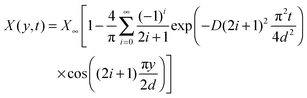 | (19) |
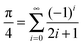 | (20) |
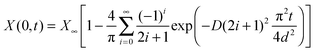 | (21) |
The average mole fraction of the film can be calculated from ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) F using the thin film interference pattern and eqn (13). To obtain an expression for the uptake, eqn (19) is integrated across the film thickness, d, to obtain:
F using the thin film interference pattern and eqn (13). To obtain an expression for the uptake, eqn (19) is integrated across the film thickness, d, to obtain:
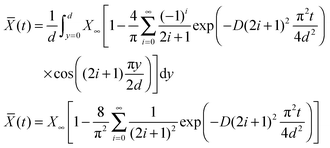 | (22) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) F from which the mole fraction
F from which the mole fraction ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) (t) is obtained with eqn (13).
(t) is obtained with eqn (13).
It is now apparent that one can determine the diffusion coefficient from two different measurements, i.e. using either the local analyte mole fraction at the film–substrate interface or the average analyte mole fraction in the bulk film.
Fig. 5A shows the simulated mole fraction of the analyte, X(y, t), in a film with an impermeable wall for different times, t. The diffusion coefficient was set to D = 1 × 10−8 cm2 s−1 and the thickness of the film to d = 40 μm. The red traces show the concentration profile in the film at t = 5 s then from 10 s to 100 s in 10 second increments and finally from 100–1500 s in 100 second increments using eqn (19). The dashed black lines in Fig. 5A show the concentration profile calculated using a sum of complementary error functions from the approximate eqn (18). Fig. 5B shows the mole fraction near the substrate, X(0,t), from eqn (21) and the average mole fraction, ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) (t) from eqn (22). Ten exponential terms were included in the calculation of X(0, t) and in the calculation of
(t) from eqn (22). Ten exponential terms were included in the calculation of X(0, t) and in the calculation of ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) (t).
(t).
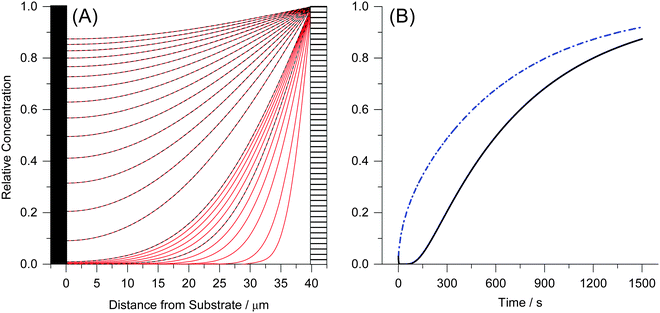 | ||
| Fig. 5 (A) The concentration profile as a function of time and depth into a 40 μm film on an impermeable wall at d = 0 μm. The concentration gradients are shown at t = 5 s then from 10 s to 100 s in 10 second increments and finally from 100–1500 s in 100 second increments. Curves calculated using eqn (19) are shown as red solid lines and those calculated using eqn (17) are given as dashed black lines. (B) The concentration change at the film–substrate interface (black solid line) is calculated using eqn (21). It shows an initial lag due to the time required for the analyte to diffuse through the material. The average concentration inside the film is given by eqn (22) (dashed blue line). | ||
4 Experimental results and discussion
4.1 Mole fraction and diffusion of water through SU-8
The diffusion of water through an SU-8 film was recorded by taking images of the interference patterns in one-second intervals. Fourier analysis was performed on each image profile to extract the film thickness and average refractive index. A sudden jump in the average film refractive index was observed when water was deposited on top of the films (Fig. 6). This step was followed by a much slower change in thickness and refractive index, which is consistent with the expected diffusion dynamics. The film thickness values of similar coatings obtained by large angle interferometry were found to be within 3% of the values obtained using a stylus profilometer (Dektak 8 Stylus Profiler, Veeco Instruments Inc.).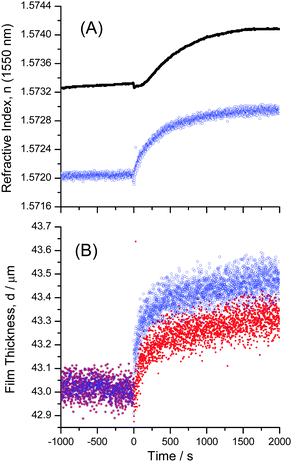 | ||
Fig. 6 (A) The average refractive index ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) film obtained by fitting the unwrapped phase with eqn (2) (blue open circles) and the refractive index near the film–substrate interface nFS, (black dots) during the uptake of water. The refractive index near the film–substrate interface, nFS, is obtained from the critical angle (see Fig. 4). The Goos–Hänchen effect causes only a small step in the bulk refractive index curve, film obtained by fitting the unwrapped phase with eqn (2) (blue open circles) and the refractive index near the film–substrate interface nFS, (black dots) during the uptake of water. The refractive index near the film–substrate interface, nFS, is obtained from the critical angle (see Fig. 4). The Goos–Hänchen effect causes only a small step in the bulk refractive index curve, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) film. (B) Thickness of an SU-8 film obtained by fitting the unwrapped phase with eqn (2) (blue empty circles). The much larger Goos–Hänchen effect in the thickness measurement was corrected by subtracting 160 nm from all measurements after t = 0 (red dots). film. (B) Thickness of an SU-8 film obtained by fitting the unwrapped phase with eqn (2) (blue empty circles). The much larger Goos–Hänchen effect in the thickness measurement was corrected by subtracting 160 nm from all measurements after t = 0 (red dots). | ||
The initial step is attributed to the Goos–Hänchen effect. The optical environment above the film changes rapidly from air to water resulting in a sudden extension of the evanescent field's permeation depth, and an increase of the effective index of the film. For large incidence angles this causes a small spatial shift of the reflected beam. Since the shift occurs between two consecutive images (<1 s) it can be assumed that it is not a result of diffusion into the film and can be subtracted from the data set. After subtraction of the Goos–Hänchen effect, both the bulk (average) refractive index and the film's thickness were found to increase immediately. Conversely, the Goos–Hänchen effect is not observed at the film–substrate interface (critical angle) as the surrounding environment, the bulk film, did not change significantly. Instead we observe a delayed response as analytes must first diffuse through the film to the film–substrate interface (Fig. 6). The large data set allows for an estimate of the precision of the relative refractive index and thickness measurements as δnFS = 1.5 × 10−5, δ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) F = 2.6 × 10−5 and δd = 0.04 μm based on the standard deviations of the 900 s before the uptake experiment.
F = 2.6 × 10−5 and δd = 0.04 μm based on the standard deviations of the 900 s before the uptake experiment.
In our case, eqn (13) and (19) are valid at any location in the film and can be applied to calculate either the local concentration at the film–substrate interface using nF = nFS and eqn (21), or the average concentration throughout the film using nF = ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) F and eqn (22). In the calculation of the water mole fraction we use as a reference the molar mass of a single tetramer unit of SU-8, MSU-8 = 1399.7 g mol−1, as well as MH2O = 18.0153 g mol−1, ρSU-8 = 1.19 g mL−1, and ρH2O = 0.99704 g mL−1.
F and eqn (22). In the calculation of the water mole fraction we use as a reference the molar mass of a single tetramer unit of SU-8, MSU-8 = 1399.7 g mol−1, as well as MH2O = 18.0153 g mol−1, ρSU-8 = 1.19 g mL−1, and ρH2O = 0.99704 g mL−1.
When a film begins to swell, the density does not change uniformly, i.e. the uppermost portions of the film will swell before the lower portions. This spatially distributed swelling in non-equilibrated films is expected to generate refractive index gradients which may complicate the interpretation of the interferograms. While light rays will bend towards the higher refractive index region of the film, the interferograms only contain information about the “effective” refractive index of the bulk film, (i.e. nF = ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) F). Using a ray model we have examined whether the effective index obtained for an index gradient is indeed close to the average refractive index and found that for incidence angles that are at least 0.5 degrees below the critical angle the refractive index is accurate within 5 × 10−4 (see ESI† for a detailed discussion). Most of the fringes are observed at incidence angles that are more than 1 degree below the critical angle (Fig. 3A) and the refractive index gradient in the film is then well-approximated with the film's spatially averaged index. The lack of sensitivity to the refractive index gradient simplifies our mathematical treatment on one hand, but also points to a shortcoming of our method when compared with ellipsometry, and neutron- and X-ray reflectometry, i.e. techniques that permit measurements of index gradients.
F). Using a ray model we have examined whether the effective index obtained for an index gradient is indeed close to the average refractive index and found that for incidence angles that are at least 0.5 degrees below the critical angle the refractive index is accurate within 5 × 10−4 (see ESI† for a detailed discussion). Most of the fringes are observed at incidence angles that are more than 1 degree below the critical angle (Fig. 3A) and the refractive index gradient in the film is then well-approximated with the film's spatially averaged index. The lack of sensitivity to the refractive index gradient simplifies our mathematical treatment on one hand, but also points to a shortcoming of our method when compared with ellipsometry, and neutron- and X-ray reflectometry, i.e. techniques that permit measurements of index gradients.
Fig. 7A shows the mole fraction and mass fraction of water in the bulk SU-8 film as obtained from ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) F in Fig. 6A and from d in Fig. 6B. The data cannot be fit using a simple 1-D diffusion model, but instead reflects independent contributions from two diffusion processes having different rates. We fit the data using a sum of two uptake curves as in eqn (21) – each having ten terms in the sum. The fit is remarkably good and yields two limiting values, X∞ and diffusion coefficients, D. We obtain X∞,1 = 0.176, D1 = 5.67 × 10−9 cm2 s−1 for the slower process and X∞,2 = 0.348, D2 = 61.2 × 10−9 cm2 s−1 for the faster process. The mass fractions are calculated from eqn (14) as Y∞ = 2730 ppmw and 6810 ppmw, respectively. A mole fraction of 0.176 (0.348) implies that on average there is approximately one water molecule per 5.7 (2.9) SU-8 tetramer units (see Fig. 1).
F in Fig. 6A and from d in Fig. 6B. The data cannot be fit using a simple 1-D diffusion model, but instead reflects independent contributions from two diffusion processes having different rates. We fit the data using a sum of two uptake curves as in eqn (21) – each having ten terms in the sum. The fit is remarkably good and yields two limiting values, X∞ and diffusion coefficients, D. We obtain X∞,1 = 0.176, D1 = 5.67 × 10−9 cm2 s−1 for the slower process and X∞,2 = 0.348, D2 = 61.2 × 10−9 cm2 s−1 for the faster process. The mass fractions are calculated from eqn (14) as Y∞ = 2730 ppmw and 6810 ppmw, respectively. A mole fraction of 0.176 (0.348) implies that on average there is approximately one water molecule per 5.7 (2.9) SU-8 tetramer units (see Fig. 1).
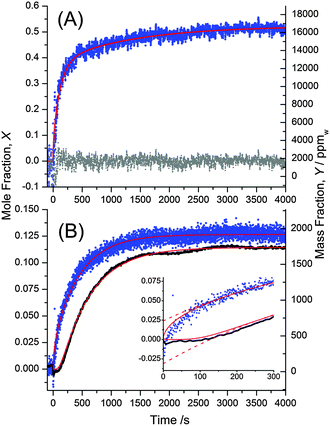 | ||
Fig. 7 (A) The mole fraction of water in SU-8 is calculated using the data in Fig. 6 and eqn (13). The data are fit using a sum of two uptake curves each described by eqn (21). The residual of the fit is shown with grey points. (B) Mole fractions as in (A) but neglecting the swelling of the polymer. The uptake near the film–substrate interface (black circles), X(0, t), is delayed compared to the average concentration within the film (blue circles), ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) (t). A fit of X(0, t) to eqn (21) and a fit of (t). A fit of X(0, t) to eqn (21) and a fit of ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) (t) to eqn (22) requires only one diffusion process. When using only a single term in eqn (21) and (22) compared with 10 terms, the agreement is less satisfactory at early times (dashed red line in the inset), but the fit yields comparable parameters. (t) to eqn (22) requires only one diffusion process. When using only a single term in eqn (21) and (22) compared with 10 terms, the agreement is less satisfactory at early times (dashed red line in the inset), but the fit yields comparable parameters. | ||
We speculate that the observed rapid change in thickness (Fig. 6A) is due to a restructuring of the SU-8 surface layers and is therefore a local phenomenon. The bulk density and the local density at the substrate interface would then be much less affected. Liu et al. made a similar qualitative observation when they found that water predominantly absorbs in the uppermost part of a 5.6 μm thick cantilever.34 In our experiment the mole fraction of adsorbed water near the top of the film is about twice as high as in the rest of the film. The slower process then clearly corresponds to the diffusion of the remaining adsorbed water throughout the film. Only the slower process affects the refractive index below the surface of the film and would be observable in critical angle measurements. This process leads to the observed delayed change in refractive index at the film–substrate interface (Fig. 7B).
The mole fraction of water near the film–substrate interface cannot be calculated in the same manner, since the density change at this interface and the associated term Δd/d is unknown. However, since only about one water molecule per 5.7 SU-8 tetramer units is present, the local fractional density change (1 + Δd/d) (see eqn (13)) at the substrate interface is likely small. We found that neglecting the change of density entirely, i.e. setting Δd = 0 in eqn (13) produces an uptake curve that is remarkably well described using a 1-D Fickian diffusion model (Fig. 7B), lending support to the hypothesis that the density of the lower portion of the films does not change as much as the change in overall film thickness would suggest, and, furthermore, that this thickness change is largely a surface phenomenon. The diffusion coefficient obtained by fitting to eqn (21) is found to be D = 13.98(2) × 10−9 cm2 s−1, and X∞ = 0.11440(4) (Y∞ = 1660 ppmw). The uncertainty in the last digit reflects the fit error. The similarity of the fit parameters to those of Fig. 7A supports our hypothesis that the slower process (D = 5.67 × 10−9 cm2 s−1) describes the diffusion of the adsorbed water throughout the film, and is accompanied by only a small change in density.
Fig. 7B also presents the mole fraction of water in the bulk film calculated from the phase analysis with eqn (13) as in Fig. 7A but setting again Δd = 0. The fit to eqn (22), is excellent and furthermore yields fitted parameters (X∞ = 0.12656(9) (Y∞ = 1861.5 ppmw) and D = 16.42(8) × 10−9 cm2 s−1) that are very similar to the data obtained from the critical angle measurement.
We note that diffusion coefficients are often calculated from similar data but only with the first term in the series of exponential terms of eqn (22).48 While this is adequate at late times or for sparse data sets49 the fits may deviate substantially at early times of the uptake curve (inset in Fig. 7). When fitting only the early data, the diffusion coefficient from a single exponential fit differs by a factor of two compared to the fit including ten exponential terms. Of course, the additional terms in our eqn (22) do not introduce extra fitting parameters and therefore do not complicate the fit.
4.2 Comparison to previous work
The preparation of SU-8 is a multistep process involving spin coating, a two-step soft bake, exposure to light (UV or X-ray), a two-step post-bake, development to remove the uncured resist, and an optional hard-bake for added stability of complex structures. There are a large number of parameters that may be adjusted, and, accordingly, the properties of SU-8 films can vary drastically depending on the protocol used.In all our experiments the diffusion constant for the slow process D = 5.67 × 10−9 cm2 s−1 was slightly larger than those in the literature (1.25–3.00 × 10−9 cm2 s−1).3,34,35 This is not unexpected as our SU-8 curing conditions were somewhat different from those reported earlier. Diffusion of water through EPON 828, a closely related material, has similarly been shown to exhibit a large range of diffusion rates (4 × 10−10–1 × 10−8 cm2 s−1).36 The large range of diffusion coefficients is a result of mechanical differences from the preparation procedures of the epoxies. For example, high concentrations of solvents gamma-butyrolactone, in SU-8, or cyclopentanone in SU-8 2000, at the time of UV irradiation allows for enhanced diffusion of photo-acids generated within the film. This results in denser cross-linked materials that form stronger films, with less internal stress and cracking during film preparation.35,50 If the concentration of solvent is too high, photo-acids may diffuse into unexposed portions of the SU-8 causing unwanted cross-linking and defects in complex structures.51 As the degree of cross-linking increases, the affinity to water decreases due to increased rigidity of the material.52 In the present work the SU-8 films were not optimized to increase their resistance to water and others solvents, and it is therefore not surprising that the measured diffusion rate was found to be slightly higher compared to the previously reported rates.3,34,35
Finally, two of the previously reported methods calculated diffusion rates from swelling of SU-8, and ignored any density effects from the incorporation of water within the film. This would lead to an underestimate of the diffusion coefficients.34,35 Especially, for somewhat porous films the diffusion rates would be underestimated at early times, as analytes fill voids but not necessarily swell the film. Refractive index measurements would be more appropriate in this situation.
In any case, the affinity of SU-8 to water and the swelling that can occur during water uptake may represent substantial challenges when using SU-8 for microfluidic applications or photonic sensor overcoats. In these types of applications, care must be taken when establishing SU-8 coating protocols to ensure that highly cross-linked films are produced which are more resistant to water and humidity.
4.3 Uptake of other solvents by SU-8
To further understand the chemical compatibility of SU-8, the uptake and swelling of the SU-8 films when exposed to other common organic solvents were explored. Using the same procedure outlined above, we measured the changes of refractive indices and thicknesses as the films were exposed to six different solvents. In none of the cases was it possible to accurately determine diffusion rates from the data. Instead, uptake experiments were allowed to proceed to equilibrium, if the film remained intact, or were terminated when the film disintegrated. When the SU-8 films were exposed to isopropanol and m-xylene the thickness and refractive index changes were too small to reliably calculate diffusion coefficients. After these experiments the SU-8 films were dried in a vacuum desiccator with activated Drierite (Sigma Aldrich) to minimize moisture uptake into the film. When small polar solvents – methanol, acetone and acetonitrile – were placed on of SU-8 films, rapid dissolution and eventual delamination of the SU-8 polymer was observed. It is expected that SU-8 curing conditions can be optimized to prevent dissolution and delamination, although significant swelling might still be expected.In the case of methanol, one of the SU-8 films that was UV-cured for 40 seconds, began to dissolve almost instantaneously. This was observed by the appearance of a second set of interference fringes. The fringes of the emerging layer at low incidence angles became more closely spaced as time proceeds – indicating that the new layer was becoming thicker (Fig. 8). The fringes at larger angles of incidence and the position of the critical angle remain unaffected until approximately 1600 seconds into the experiment, suggesting that the new layer was formed on the top surface of the film – likely due to top-down dissolution of SU-8 by methanol.
Additionally, the boundary between the SU-8 film and the new layer rapidly shifted to larger angles of incidence indicating that the refractive index of this new layer increased as more of the SU-8 was dissolved. The original fringes of the film spread out as the remaining SU-8 film becomes thinner, until it delaminated from the substrate at around t = 2000 s. Delamination was also observed with SU-8 films that were exposed to UV exposure for 3 minutes, although on a much slower time scale. From these experiments it is apparent that SU-8 has a strong affinity to methanol.
The films used in our experiments were not hard baked, so it is likely that they were not fully cross-linked. Hard baking is essential when fabricating complex structures out of SU-8, and would also have provided additional chemical resistance.
The chemical compatibility of a polymer can be predicted using solubility parameters. Neither the Hildebrand nor the Hansen solubility parameters are readily available for any formulation of SU-8 photoresist, so similar epoxy photoresists such as EPON 1001, have been previously used as stand-ins in the literature.53 The Hansen solubility parameters for EPON 1001 are given as (δD = 17 MPa1/2, δP = 9.6 MPa1/2, δH = 7.8 MPa1/2, R0 = 7.1 MPa1/2).54 From these values, it would be expected that EPON 1001 and likely SU-8 would be soluble in acetone and acetonitrile. These epoxy polymers should also be somewhat soluble in methanol and isopropanol, and not soluble in m-xylene. All these predictions for EPON 1001 agree quite well with our experimental observations for SU-8 and with those by Ford and co-workers.53 A more detailed discussion including the solubility parameters of many common organic solvents is included in the ESI.†
5 Conclusions
Using Fourier analysis of images taken using a large-angle interferometric refractometer, it is possible to simultaneously extract the changes in average refractive index,![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) film, and thickness, d, of thin transparent films (15–150 μm). Additionally, from changes to the critical angle of total internal reflection, the refractive index at the interface with the substrate, nFS, was extracted. In combination with the Lorentz–Lorenz model and a Fickian diffusion model, all three measurements allow for a precise calculation of the average analyte mole fraction and mass fraction in a film with a high time resolution.
film, and thickness, d, of thin transparent films (15–150 μm). Additionally, from changes to the critical angle of total internal reflection, the refractive index at the interface with the substrate, nFS, was extracted. In combination with the Lorentz–Lorenz model and a Fickian diffusion model, all three measurements allow for a precise calculation of the average analyte mole fraction and mass fraction in a film with a high time resolution.
Diffusion expressions derived from those presented by Crank1 were used to model the changes of both the average concentration and the film-interface concentration during the uptake process. Despite its simplicity, the model described the experimental data very well. One might have anticipated complications, as concentration and refractive index gradients are present within the film prior to reaching equilibrium. The refractive index gradient is expected to deflect the light rays from a straight path, somewhat complicating the analysis of the interference pattern (see Fig. 2). In our analysis, however, these effects were not apparent and the data was fit remarkably well (see Fig. 7 and ESI†). The data is of such high quality that two parallel uptake processes can be readily distinguished and quantified.
Many groups have previously studied the uptake of volatile organic compounds into common polymeric materials including polydimethylsiloxanes, polystyrenes and polymethylmethacrylate.2,5,55 Diffusion of molecules into polymeric films is also the principle behind Solid Phase Micro-Extraction (SPME), a common analytical technique used for sampling of volatile compounds in the head space above solutions.56 The model we present here is applicable in these situations as long as the system can be described by Fickian diffusion. Moreover, our theoretical model may be used to understand the time-response of a variety of other optical devices – including coated silicon-on-insulator devices (SOI)31,57,58 and Fabry–Perot interferometers.57,58
Using ∼40 μm thick spin-coated SU-8 50 photoresist films as a model system, the uptake of common solvents was measured. Diffusion of water into SU-8 was accompanied by changes in ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) film and nFS of 0.0009 and 0.0008 respectively and a thickness change of 0.7%. Kinetic analysis of one of these processes gave evidence for two diffusion processes that happened with different rates (D1 = 5.67 × 10−9 cm2 s−1 and D2 = 61.2 × 10−9 cm2 s−1) with equilibrium mole fractions of X∞,1 = 0.176, (mass fraction, Y = 2230 ppmw) and X∞,2 = 0.348 (4420 ppmw) which were calculated from the concentration change in the bulk film. As was suggested previously34 the surface of an SU-8 film has a stronger affinity to water than the bulk of the film. We propose that the faster process corresponds to restructuring of the top layers of the SU-8 film and the slower process corresponds to the diffusion of water throughout the entire film. Since the second process is accompanied by only a very small change of density the slower diffusion process can also be quantified using refractive index changes at the film–substrate interface and neglecting density changes. The constants D = 1.398(2) × 10−8 cm2 s−1, X∞ = 0.11440(4); Y = 1452 ppmw are consistent with a lower permeability of the bulk film compared to the surface. The diffusion constants reported here are higher than those in the literature for the SU-8 2000 series, firstly because some of the previous reported values measure diffusion constants from only the swelling of the SU-8 film and neglect solvent contributions to density changes, and, secondly, because the two materials are prepared from precursors in different solvents.
film and nFS of 0.0009 and 0.0008 respectively and a thickness change of 0.7%. Kinetic analysis of one of these processes gave evidence for two diffusion processes that happened with different rates (D1 = 5.67 × 10−9 cm2 s−1 and D2 = 61.2 × 10−9 cm2 s−1) with equilibrium mole fractions of X∞,1 = 0.176, (mass fraction, Y = 2230 ppmw) and X∞,2 = 0.348 (4420 ppmw) which were calculated from the concentration change in the bulk film. As was suggested previously34 the surface of an SU-8 film has a stronger affinity to water than the bulk of the film. We propose that the faster process corresponds to restructuring of the top layers of the SU-8 film and the slower process corresponds to the diffusion of water throughout the entire film. Since the second process is accompanied by only a very small change of density the slower diffusion process can also be quantified using refractive index changes at the film–substrate interface and neglecting density changes. The constants D = 1.398(2) × 10−8 cm2 s−1, X∞ = 0.11440(4); Y = 1452 ppmw are consistent with a lower permeability of the bulk film compared to the surface. The diffusion constants reported here are higher than those in the literature for the SU-8 2000 series, firstly because some of the previous reported values measure diffusion constants from only the swelling of the SU-8 film and neglect solvent contributions to density changes, and, secondly, because the two materials are prepared from precursors in different solvents.
Thickness or refractive index changes were not measurable when SU-8 was exposed to isopropanol and m-xylene, but rapid film dissolution and delamination was observed when SU-8 was exposed to acetone, acetonitrile and methanol. This suggests that SU-8 has a strong affinity to polar solvents. The chemical resistance of SU-8 films can likely be increased by more strongly cross-linking the polymer. Since SU-8 fabrication involves a multi-step process, the mechanical properties of SU-8 are substantially altered for different fabrication protocols. Ultimately, care must be taken to optimize the fabrication conditions when using SU-8 as overcoats for photonic sensors and for microfluidic applications to reduce analyte partitioning into and swelling of films.
The optical measurements described in this report provide rapid, high-quality, non-contact information about the diffusion of a mobile phase into a film of finite thickness. The instrument developed in our lab permits measurements of film thickness with a <0.1% resolution and is thus sensitive to swelling of the film. The thickness range is currently limited to 15–150 μm by the number of fringes visible in the image and may be changed by either recording images with higher resolution or by changing the distance between the prism and the camera. The refractive index range is fundamentally limited by the requirement of total internal reflection at the film–substrate interface, and requires, for the present high-density flint glass substrate, that the film has an index of n < 1.74. Other substrates that exhibit transparency at the interrogation wavelength can also be used. For low index polymers regular soda-lime glass microscope slides (n = 1.50 at 1550 nm) and a matching prism would be sufficient. Silicon (n = 3.47 at 1550 nm) may be used as a substrate for very high index films.
Ongoing uptake studies on a softer siloxane polymer show that the instrument is also well-suited for quantitative characterization of faster partitioning processes involving much larger changes of refractive index and thickness.
Acknowledgements
The authors thank Robert Knobel and members of the Kingston Nano-Fabrication Lab (KNFL) for access to their facility and Jeff Crouse for help with the data analysis. Financial support from the Natural Sciences and Engineering Research Council (NSERC) of Canada is gratefully acknowledged.References
- J. Crank, The Mathematics of Diffusion, Oxford University Press, New York, 2nd edn, 2011 Search PubMed.
- R. Patel, R. Zhou, K. Zinszer, F. Josse and R. Cernosek, Anal. Chem., 2000, 72, 4888 CrossRef CAS.
- J. Hossenlopp, L. Jiang, R. Cernosek and F. Josse, J. Polym. Sci., Part B: Polym. Phys., 2004, 42, 2373 CrossRef CAS PubMed.
- D. Johannsmann, Phys. Chem. Chem. Phys., 2008, 10, 4516 RSC.
- I. Linossier, F. Gaillard, M. Romand and J. F. Feller, J. Appl. Polym. Sci., 1997, 66, 2465 CrossRef CAS.
- K. Ichikawa, T. Mori, H. Kitano, M. Fukuda, A. Mochizuki and M. Tanaka, J. Polym. Sci., Part B: Polym. Phys., 2001, 39, 2175 CrossRef CAS PubMed.
- T. P. Skourlis and R. L. McCullough, J. Appl. Polym. Sci., 1994, 52, 1241 CrossRef CAS PubMed.
- J. Rheims, J. Köser and T. Wriedt, Meas. Sci. Technol., 1997, 8, 601 CrossRef CAS.
- E. Moreels, C. de Greef and R. Finsy, Appl. Opt., 1984, 23, 3010 CrossRef CAS.
- P. R. Cooper, Appl. Opt., 1983, 22, 3070 CrossRef CAS.
- G. H. Meeten and A. N. North, Meas. Sci. Technol., 1995, 6, 214 CrossRef CAS.
- Y. Sarov, S. Sainov, I. Kostic, V. Sarova and S. Mitkov, Rev. Sci. Instrum., 2004, 75, 3342 CrossRef CAS PubMed.
- R. P. Podgorsek and H. Franke, Appl. Phys. Lett., 1998, 73, 2887 CrossRef CAS PubMed.
- C.-B. Kim and C. B. Su, Meas. Sci. Technol., 2004, 15, 1683 CrossRef CAS.
- S. Silva, O. Frazão, J. L. Santos and F. X. Malcata, Sens. Actuators, B, 2012, 161, 88 CrossRef CAS PubMed.
- D. Sengupta, M. Sai Shankar, P. S. Reddy, R. L. N. Sai Prasad and K. Srimannarayana, Optoelectron. Adv. Mater., Rapid Commun., 2010, 4, 128 CAS.
- G. Mudhana, K. S. Park, S. Y. Ryu and B. H. Lee, IEEE Sens. J., 2011, 11, 1178 CrossRef CAS.
- H. Elbs and G. Krausch, Polymer, 2004, 45, 7935 CrossRef CAS PubMed.
- W. L. Chen, K. R. Shull, T. Papatheodorou, D. A. Styrkas and J. L. Keddie, Macromolecules, 1999, 32, 136 CrossRef CAS.
- S. Kedenburg, M. Vieweg, T. Gissibl and H. Giessen, Opt. Mater. Express, 2012, 2, 1588 CrossRef CAS.
- K. Moutzouris, M. Papamichael, S. C. Betsis, I. Stavrakas, G. Hloupis and D. Triantis, Appl. Phys. B: Lasers Opt., 2014, 116, 617 CrossRef CAS.
- T. P. Russell, Mater. Sci. Rep., 1990, 5, 171 CrossRef CAS.
- P. Müller-Buschbaum, E. Bauer, E. Maurer, A. Nelson and R. Cubitt, Phys. Status Solidi RRL, 2007, 1, R68 CrossRef PubMed.
- W. Wang, G. Kaune, J. Perlich, C. M. Papadakis, A. M. Bivigou Koumba, A. Laschewsky, K. Schlage, R. Röhlsberger, S. V. Roth, R. Cubitt and P. Müller-Buschbaum, Macromolecules, 2010, 43, 2444 CrossRef CAS.
- M. Mukherjee, A. Singh, J. Daillant, A. Menelle and F. Cousin, Macromolecules, 2007, 40, 1073 CrossRef CAS.
- W. J. Chen, J. E. Saunders, J. A. Barnes, S. S. H. Yam and H. P. Loock, Opt. Lett., 2013, 38, 365 CrossRef CAS PubMed.
- H. Lorenz, M. Despont, N. Fahrni, N. LaBianca, P. Renaud and P. Vettiger, J. Micromech. Microeng., 1997, 7, 121 CrossRef CAS.
- J. M. Shaw, J. D. Gelorme, N. C. LaBianca, W. E. Conley and S. J. Holmes, IBM J. Res. Dev., 1997, 41, 81 CrossRef CAS.
- S. Balslev, A. M. Jorgensen, B. Bilenberg, K. B. Mogensen, D. Snakenborg, O. Geschke, J. P. Kutter and A. Kristensen, Lab Chip, 2006, 6, 213 RSC.
- P. Abgrall, V. Conedera, H. Camon, A.-M. Gue and N.-T. Nguyen, Electrophoresis, 2007, 28, 4539 CrossRef CAS PubMed.
- D. X. Xu, A. Densmore, A. Delage, P. Waldron, R. McKinnon, S. Janz, J. Lapointe, G. Lopinski, T. Mischki, E. Post, P. Cheben and J. H. Schmid, Opt. Express, 2008, 16, 15137 CrossRef CAS.
- J. H. Schmid, P. J. Bock, P. Cheben, W. Sinclair, J. Garcia, S. Janz, J. Lapointe, G. C. Aers, D. Poitras, Y. Li, G. Lopinski, A. Delage, A. Densmore, B. Lamontagne, R. Ma and D.-X. Xu, Silicon Photonics V, 2010, 7606, 76060F Search PubMed.
- D. Duval, A. Belen Gonzalez-Guerrero, S. Dante, J. Osmond, R. Monge, L. J. Fernandez, K. E. Zinoviev, C. Dominguez and L. M. Lechuga, Lab Chip, 2012, 12, 1987 RSC.
- C. Liu, Y. Liu, M. Sokuler, D. Fell, S. Keller, A. Boisen, H.-J. Butt, G. K. Auernhammer and E. Bonaccurso, Phys. Chem. Chem. Phys., 2010, 12, 10577 RSC.
- K. Wouters and R. Puers, J. Micromech. Microeng., 2010, 20, 095013 CrossRef.
- M. R. Vanlandingham, R. F. Eduljee and J. W. Gillespie, J. Appl. Polym. Sci., 1999, 71, 787 CrossRef CAS.
- Y. Diamant, G. Marom and L. J. Broutman, J. Appl. Polym. Sci., 1981, 26, 3015 CrossRef CAS PubMed.
- C. M. Berger and C. L. Henderson, Polymer, 2003, 44, 2101 CrossRef CAS.
- V. M. Blanco Carballo, J. Melai, C. Salm and J. Schmitz, Microelectron. Eng., 2009, 86, 765 CrossRef CAS PubMed.
- J. Park and D.-S. Shin, Mater. Chem. Phys., 2006, 98, 309 CrossRef CAS PubMed.
- L. Yi, W. Xiaodong, L. Chong, L. Zhifeng, C. Denan and Y. Dehui, Microsyst. Technol., 2005, 11, 1272 CrossRef CAS.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671 CrossRef CAS PubMed.
- V. Rouessac, A. van der Lee, F. Bosc, J. Durand and A. Ayral, Microporous Mesoporous Mater., 2008, 111, 417 CrossRef CAS PubMed.
- M. R. Baklanov, K. P. Mogilnikov, V. G. Polovinkin and F. N. Dultsev, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct. – Process., Meas., Phenom., 2000, 18, 1385 CrossRef CAS.
- R. Mehra, Proceedings of the Indian Academy of Sciences-Chemical Sciences, 2003, 115, 147 CrossRef CAS.
- S. M. Sirard, P. F. Green and K. P. Johnston, J. Phys. Chem. B, 2001, 105, 766 CrossRef CAS.
- L. Masaro and X. X. Zhu, Prog. Polym. Sci., 1999, 24, 731–775 CrossRef CAS.
- M. C. D. Carter, C. D. Sorrell and M. J. Serpe, J. Phys. Chem. B, 2011, 115, 14359 CrossRef CAS PubMed.
- C. S. Brazel and N. A. Peppas, Polymer, 1999, 40, 3383–3398 CrossRef CAS.
- S. Keller, G. Blagoi, M. Lillemose, D. Haefliger and A. Boisen, J. Micromech. Microeng., 2008, 18, 125020 CrossRef.
- C. Becnel, Y. Desta and K. Kelly, J. Micromech. Microeng., 2005, 15, 1249 CrossRef CAS.
- R. Feng and R. J. Farris, J. Micromech. Microeng., 2003, 13, 80 CrossRef CAS.
- J. Ford, S. R. Marder and S. Yang, Chem. Mater., 2009, 21, 476 CrossRef CAS.
- C. M. Hansen, Hansen Solubility Parameters A User's Handbook, CRC Press, Taylor & Francis Group, Boca Raton, Florida, USA, 2nd edn, 2007 Search PubMed.
- J. N. Lee, C. Park and G. M. Whitesides, Anal. Chem., 2003, 75, 6544 CrossRef CAS PubMed.
- A. Saraullo, P. A. Martos and J. Pawliszyn, Anal. Chem., 1997, 69, 1992 CrossRef CAS PubMed.
- J. B. Smiley-Wiens and M. J. Serpe, Colloid Polym. Sci., 2013, 291, 971 CAS.
- R. St-Gelais, G. Mackey, J. Saunders, J. Zhou, A. Leblanc-Hotte, A. Poulin, J. A. Barnes, H.-P. Loock, R. S. Brown and Y.-A. Peter, Sens. Actuators, B, 2013, 182, 45 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Propagation of light through materials with a refractive index gradient and discussion of solubility parameters for similar epoxy materials to SU-8. See DOI: 10.1039/c5sm02170g |
| This journal is © The Royal Society of Chemistry 2015 |