Exotic hexagonal NaCl atom-thin layer on methylammonium lead iodide perovskite: new hints for perovskite solar cells from first-principles calculations

Abstract

Alkali halides are simple inorganic compounds extensively used as surface modifiers in optoelectronic devices. In perovskite solar cells (PSCs), they act as interlayers between the light absorber material and the charge selective layers improving their contact quality. They introduce surface dipoles that enable the fine tuning of the relative band alignment and passivate surface defects, a well-known drawback of hybrid organic–inorganic perovskites, that is responsible for most of the issues hampering the long-term performances. Reducing the thickness of such salt-based insulating layer might be beneficial in terms of charge transfer between the perovskite and the electron/hole transport layers. In this context, here we apply density functional theory (DFT) to characterize the structure and the electronic features of atom-thin layers of NaCl adsorbed on the methylammonium lead iodide (MAPI) perovskite. We analyze two different models of MAPI surface terminations and find unexpected structural reconstructions arising at the interface. Unexpectedly, we find an exotic honeycomb-like structuring of the salt, also recently observed in experiments on a diamond substrate. We also investigate how the salt affects the perovskite electronic properties that are key to control the charge dynamics at the interface. Moreover, we also assess the salt ability to improve the defect tolerance of the perovskite surface. With these results, we derive new hints regarding the potential benefits of using an atom-thin layer of alkali halides in PSCs.

---

Efficiencies and long-term stability of perovskite solar cells (PSCs) go along with the selection and the development of proper charge selective layers and interfacial control. The insertion of a thin salt interlayer can help the bonding of the charge transport layer (CTL) with the light active material, improving the quality of the contact and preventing charge recombination at the interface that affects the device performance, lowering the open circuit voltage.^1,2 The different species electronegativity in these binary compounds results in dipole moments that make it possible to tune the work function of the charge transport layers for a convenient alignment with the perovskites.³ Alkali halides have also been exploited as passivating interlayers in several electronic devices and in PSCs.^4,5 They represent a good choice since both alkali and halogens are often components of the perovskites or are employed as doping species to improve their stability. Among them, sodium chloride, table salt, is probably the most common. Despite its apparent simplicity, the interfacial properties of sodium chloride deposited as an atom-thin layer on different substrates are far from being completely understood. In the work by Kvashnin et al.,⁶ a graphitization of (111)-oriented nanofilms of NaCl with rock salt structure is predicted via ab initio DFT calculations. This is a common tendency of other materials like cubic diamond, boron nitride and other cubic compounds, which is driven by surface energy reduction, since the atomic rearrangement contrasts the surface dipole normal to the highly polar (111) surface.^7,8 Several studies have investigated the synthesis of NaCl films on different substrates and assessed the correlation between both the type and the orientation of the substrate with the NaCl film properties.^9,10 In a recent work, Tikhomirova et al.¹¹ have theoretically predicted and experimentally confirmed an exotic two-dimensional hexagonal structure that has been observed when thin salt films are grown on a diamond (110) surface. Such a kind of effect has been ascribed to both the strength of the interaction and the strain effects due to lattice mismatch. In particular, a subtle balance between chemical interactions and confinements seems to be responsible for other observed hexagonal geometries of nano-confined NaCl: L. Wang et al.¹² found a peculiar hexagonal structure when crystallizing NaCl from solutions confined between graphene; and very recently, in 2022, Zhao et al.¹³ reported a graphitic-like phase of NaCl at ambient conditions, spontaneously formed by unsaturated NaCl solution in the quasi-2D confined space between reduced graphene oxide layers.

Motivated by these findings and by the relevance of using alkali halides in PSCs, here we report the formation of similar exotic NaCl structuring on a perovskite film by means of state of the art density functional theory calculations. In particular, we consider the prototypical methylammonium lead tri-iodide (MAPI) perovskite, the first used in PSCs.^14,15 We investigate the modifications of MAPI electronic properties due to the presence of the salt layer and we consider the formation of an iodine vacancy defect at the perovskite surface so as to assess the role played by the salt in improving the perovskite defect tolerance. Such defects are likely or not to form depending on the specific synthesis conditions and are often associated with the presence of a shallow donor state in the band structure that can be responsible for an undesired doping of the absorber material.¹⁶ Moreover, the diffusion of iodine defects has been considered among the most important degradation mechanisms of methylammonium lead iodine in solar cells as it can lead to the formation and release of I₂. Our calculations reveal that the salt layer can contribute to limiting the formation of surface vacancies and preventing the presence of shallow states in the band structure.

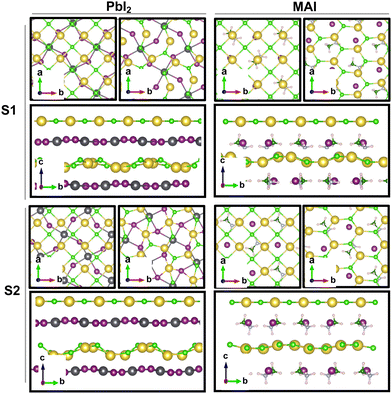
Our theoretical model consists of a full coverage of the¹⁷ (010)-MAPI surface with an atom-thin layer of sodium chloride cut along the most energetically favorable NaCl (001)-surface.¹⁸ We consider the orthorhombic low temperature MAPI phase (Pnma group)¹⁹ with methyl-ammonium molecules oriented according to the work by Lee et al.²⁰ We account for the two distinct possible surface terminations, namely the PbI₂- and the methyl-ammonium iodine (MAI-) ones, to both assess their role on the electronic features of the slab and to investigate the different local environment interaction with the salt layer. The model consists in a 7-layer perovskite slab sandwiched between two atom-thin salt layers to avoid net dipole moments. Each interface model is approximatively ∼2 nm thick and contains a vacuum layer of about 2 nm. Structural models are depicted in the ESI,† Fig. S1. We stack the salt layer in two different configurations, S1 and S2, differing from a translation of the salt of a ¼ of the unit cell along the a direction. This choice is motivated by the interest in assessing the local chemical interactions between the salt and the perovskite that can depend on the stacking. The lattice constants of MAPI are calculated through bulk structure geometrical minimization performed within the PBE-D3BJ level of theory. Their values (a = 8.844 Å, b = 12.592 Å, and c = 8.563 Å) show a good agreement with those measured by both X-ray²¹ and NPD.²² We calculate the minimum energy NaCl lattice constant within the same level of theory used for MAPI calculations. Its value is 5.59 Å and agrees with the experimental one of 5.64 Å.²³ We realize the perovskite/salt interface by covering a 1 × 1 slab of MAPI with a ½ monolayer of the 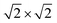NaCl supercell. The interface lattice constants are fixed to those of the MAPI slab, thus resulting in a NaCl stretching in both in-plane directions. The strain experienced by the salt can be quantified through the lattice mismatch defined as:

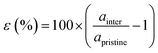and is about 12% and 8% along the a and b directions, respectively.

Optimized structures of the PbI₂- and MAI-terminated MAPI/NaCl interfaces are a result of relaxing all atom positions without freezing any coordinates nor imposing symmetry constraints during the structural optimizations. Vibrational frequency calculations confirm that the optimized structures correspond to potential energy surface minima. We conduct supplementary phonon band structure calculations along the U–Γ–V Brillouin path, and the corresponding density of states computed using the Phonopy code. These additional analyses provide further confirmation of the stability of the examined structure and contribute to a comprehensive assessment of frequency dispersion (see frequency analysis section of the ESI†).

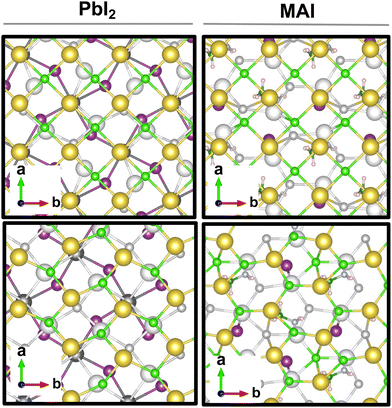
The result is a massive structural reconstruction that occurs in the salt layer as depicted by Fig. 1. The top views of both stackings in the PbI₂-terminated interface show a similar reconstruction in which closed irregular chains of alternating Na and Cl atoms are visible, resembling a distorted cubic structure. In the MAI-terminated interface, sodium and chlorine atoms reorganize to form a pseudo-hexagonal arrangement independently from the stacking. In both stackings and terminations, the lateral views of the interfaces show a corrugation that has a wavy fashion in the MAI system, while it is less regular for the PbI₂. Such an effect has been previously reported for a (001)-oriented NaCl monolayer on the Cu(110)²⁴ surface and on diamond¹¹ and, in both cases, ascribed to epitaxial mismatch. To assess the role of strain in our system we have relaxed the salt monolayer starting from its interface geometry minimum without the perovskite film. The salt layer becomes flat after optimization while conserving its atomic arrangement in the x–y plane (ESI,† Fig. S2). Such behavior suggests a non-innocent role of the perovskite in driving the observed structural reconstruction. We simulate a layer-by-layer growth, by adding a second rock salt monolayer on top of the optimized one and then we relax the whole system (full interface's models are depicted in ESI,† Fig. S3). Pictures of both the top (nearest to the vacuum region) and the bottom layers (atoms in white) are shown in Fig. 2 before and after the optimization. In both cases after relaxation, we observe a behavior similar to the one reported by ref. 11 with the second layer retaining the pattern of the underlying one.

Fig. 1 Top views before (left) and after (right) the geometrical optimization for the PbI₂- and the MAI-terminated MAPI/NaCl interfaces corresponding to stackings S1 and S2. Lateral views before (upper) and after (lower) the optimization for the PbI₂- and the MAI-terminated MAPI/NaCl interfaces corresponding to stackings S1 and S2. Only the outermost layer of the MAPI slab is shown. Color code: Pb – dark gray; I – violet; C – green; N – light blue; H – light pink; Na – yellow; Cl – light green.

Fig. 2 Top views of the top (closest to vacuum) and the bottom salt layers (atoms in white) shown before (up) and after (down) the optimization at the PBE-D3BJ level of theory, for the PbI₂ and the MAI systems. Only the perovskite layer nearest to the salt is depicted. Color code: Pb – dark gray; I – violet; Na – yellow; Cl – light green.

We quantify the interaction between the MAPI and the salt buffer via calculation of the adhesion energy per unit area given by:

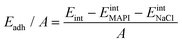where E_int is the total interface energy, while E^int_MAPI and E^int_NaCl are, respectively, the total energies of the isolated perovskite film and the salt at the interface geometry, while A is the contact area between them. Results for both 1L and 2L are listed in Table 1.

Table 1 Adhesion energies per unit area for 1L (S1 and S2 stacking) and 2L (S1 stacking)

Adhesion energy (eV Å^−2)
	1L		2L
	S1	S2	S1
PbI2	−0.072	−0.077	−0.056
MAI	−0.040	−0.021	−0.046

---

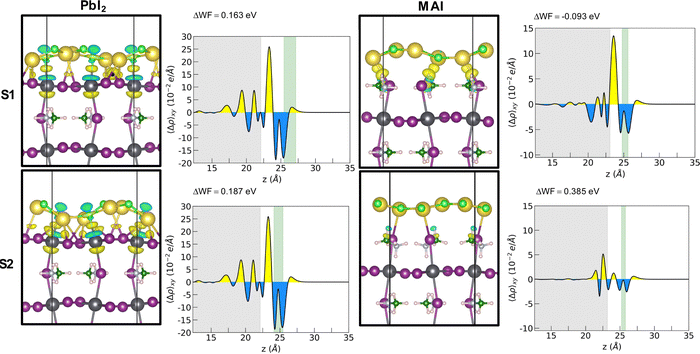
Adhesion energies reveal that both heterostructures are favorable to form and suggest a van der Waals mediated interaction between the two materials. The larger absolute values of the adhesion energy per unit area obtained in the case of PbI₂ termination suggests a stronger interaction both for 1L and 2L. The energies for the 1L systems are not dependent on the stacking for the PbI₂ systems while they seem to favor S1 stacking for the MAI system. A cross comparison with the charge density difference plot is depicted by Fig. 3 for the 1L systems.

Fig. 3 Electron density differences for the interaction between the PbI₂- and the MAI-terminated MAPI film and the NaCl layer (left). Yellow denotes increased electronic density and light blue indicates decreased electronic density. Isosurface value: 0.0025. Planar average charge density difference for each system (right). Color code: Pb – dark gray; I – violet; C – green; N – light blue; H – light pink; Na – yellow; Cl – light green.

In the PbI₂ case, we observe a charge reorganization of the same entity for the two stackings, with alternating accumulation and depletion regions along the Pb–Cl bonds and a slight charge accumulation along the Na–I bonds. Conversely, for the MAI system, the different stacking gives rise to different interactions that reflect the obtained adhesion energy values. In the most interacting S1 configuration a strong charge accumulation occurs along the Na–I bonds suggesting the formation of covalent-like bonding between the two ions. It is important here to point out a difference with respect to the case of NaCl on a diamond substrate.¹¹ We observe the exotic reshaping of the salt layer even for energies lower than the ones obtained by Tikohmirova et al. (about 0.4 eV Å⁻²); our values are instead closer to those that they obtain for metallic substrates.

The geometrical reorganization of the salt atoms also impacts on the electric properties of the perovskite. We explore here the modification in the MAPI work function (WF). Such a quantity can be calculated by means of the following equation:

WF = E_Vacuum − E_VBM (3)

where E_Vacuum is the value of the planar average potential in the vacuum region of the cell and E_VBM is the energy of the last occupied Kohn–Sham state. Results obtained for S1 and S2 stackings on PbI₂ - and MAI-terminated 1L systems are reported in Fig. 3 together with the planar averaged charge density difference. In the PbI₂ case, the WF increases with similar values for both S1 and S2 stackings. On the contrary, in MAI systems the stacking S1 shows a WF decrease about three times smaller than the WF increase for stacking S2.

The WF variation is important to account for designing new interfaces with optimized charge transport features. A WF increase means a lower energy position for both the VB and CB edges (within a rigid band model picture) that influences the band alignment at the interfaces, setting the thermodynamic conditions for hole and electron transfer across junctions. A non-optimal band ordering at the interfaces with the CTLs causes insufficient driving force for charge injection defined as ΔE_h-inj = E_VBM-HTL − E_VBM-MAPI and ΔE_e-inj = E_CBM-MAPI − E_CBM-ETL for holes and electrons, respectively. It is widely agreed that an optimal band offset is at least ∼0.2 eV,²⁵ since such value results in a suitable driving force without compromising the final open circuit voltage V_oc ≈ E_CBM-ETL − E_VBM-HTL. The WF increase (decrease) observed for both PbI₂ stackings and for the S2 stacking of MAI (stacking S1 of MAI) corresponds to a downward (upward) band bending of both the VBM and CBM of the MAPI that pushes its experimental band edges (VBM = −5.43 eV and CBM = −3.88 eV)²⁶ to the values reported in Table 2.

Table 2 VBM and CBM energies for both PbI₂ and MAI terminations and stackings, accounting for the WF variations reported for each system in Fig. 3. Values reported in the below are calculated from the experimental references (VBM = −5.43 eV and CBM = −3.88 eV).²⁶

Energies (eV)	PbI2		MAI
	S1	S2	S1	S2
VB maximum	−5.59	−5.62	−5.34	−5.82
CB minimum	−4.04	−4.07	−3.79	−4.26

---

Data reported in Table 2 suggest a beneficial role of the NaCl layer that increasing the WF gives an optimal band offset (about 0.2 eV) for both stackings of PbI₂-terminated systems with some HTLs such as CuZnSn₂ (−5.4 eV),²⁷ Cu₂O (−5.38 eV),²⁸ and MoS₂ (−5.3 eV),²⁹ that do not match well with the pristine MAPI VB level. The WF decrease, experienced by the S1 stacking of the MAI-termination, improves the band offset with the most used P3HT (−5.10 eV)³⁰ and PEDOT:PSS (−5.10 eV).³¹ On the ETL side, the WF variation for the S2 stacking of the MAI-terminated model results in a proper band alignment with the ZnO (−4.4 eV).²⁹

We also investigate the presence of an iodine vacancy for the S1 configuration of both terminations. The vacancy is simulated by removing a neutral iodine atom from the topmost perovskite layer, closer to the salt buffer, and relaxing the geometry of the system without any constraints on atoms. We then compute the vacancy formation energies (listed in Table 3) as:

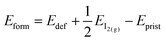Table 3 Vacancy formation energies calculated at the PBE-D3BJ level of theory according to eqn (4), for stacking S1 of both –PbI₂ and –MAI terminations of the pristine and the salt covered perovskite

Iodine vacancy formation energy (eV)
	Pristine	NaCl covered
PbI2	2.44	2.78
MAI	2.96	3.01

---

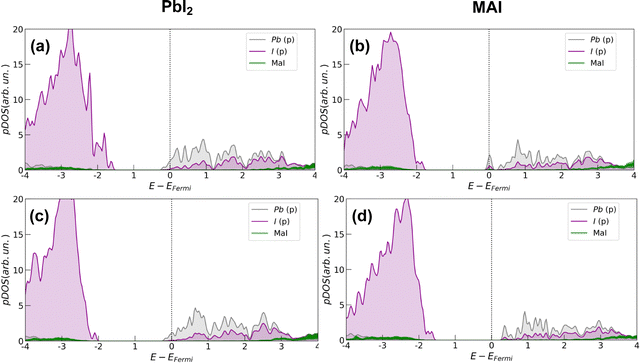
In all cases, the presence of the salt slightly inhibits the defect formation with a more pronounced effect on the PbI₂ system for which the energy is increased by about 0.35 eV (∼8 kcal mol⁻¹). The corresponding effects on the electronic structure are analyzed through projected density of states (pDOS), depicted by Fig. 4. In agreement with previous works,³² we find that iodine vacancies form shallow defects in the conduction band proximity. In the case of PbI₂ a n-type doping behavior appears in the pDOS and is retained even upon salt coverage. In the MAI case, a more localized state appears just below the conduction band in the pristine perovskite layer. In this case, the effect of the salt buffer is more evident since such a state disappears upon salt coverage.

Fig. 4 Projected density of states (pDOS) calculated at the PBE level of theory for the S1 configuration of both surface terminations. Upper plots (a) and (b) refer only to the perovskite with an iodine vacancy. In pictures (c) and (d), the same analysis is shown for the same systems with the salt coverage.

In conclusion, we investigate a system composed by a MAPI film with two different terminations, namely MAI and PbI₂, and covered with an atom-thin layer of NaCl. The formation of both interfaces is thermodynamically favored and leads to a strong structural reorganization of the salt atoms. In the case of the MAI-terminated slab we find a regular honeycomb-like hexagonal structure of the salt layer. A similar observation has been recently reported by Tykhomirova et al.¹¹ on a diamond substrate and has been ascribed by the authors to the strong interaction arising between the two interfacing compounds. Our results confirm that such singular structuring of the salt atom is a consequence of the interactions and bonds formed between the salt ions and the substrate, here the perovskite. In both the MAI and PbI₂ cases the formation of covalent-like bonding between Na and I, and a general charge redistribution between Pb and Cl atoms in the PbI₂-terminated model is observed. The comparable adhesion energy values obtained for the two terminations suggest that the final configuration depends not only on the strength of the interaction itself, but also on the specific local chemical environment and the substrate/covering reciprocal symmetry. We assess the electronic modifications caused in the MAPI film due to the salt coverage in terms of WF. We find that the PbI₂ has a higher WF when it is covered by NaCl in both stacking configurations, while the MAI-terminated system shows different behaviors for the two stackings, with a small decrease of the WF for S1 balanced by the large increase of WF for stacking S2. An overall increase of the WF in the presence of the salt layer would lead to a downward shift of the VB and CB band edge potentials for the MAPI. Such variations make the MAPI perovskite suitable for use in cells involving usually not-well-matching CTLs.

We also investigate the formation and the electronic effects of an iodine vacancy in the MAPI surface, since this kind of defect is often responsible for low efficiencies in perovskite solar cells. We find that surface iodine defects cause unintentional n-type doping in both the MAI and the PbI₂ cases. Our calculations reveal that the salt buffer can contribute to inhibiting their formation and – in the case of MAI termination – can prevent the vacancy induced doping effect in the perovskite absorber. Overall, our findings highlight how relevant the possible structural rearrangements are at the interface between the photoactive lead halide perovskite and the salt buffer layer, thus paving a route to future studies on alkali halides and different perovskite compositions and terminations.

Methods and computational details

We performed periodic spin-polarized density functional theory (DFT)-calculations with projector-augmented wave (PAW) potentials^33,34 and a plane wave (PW) basis set with the Vienna Ab Initio Simulation Package (VASP, version 5.4.4) and the Perdew–Burke–Ernzerhof (PBE) exchange–correlation density functional.³⁵ Dispersion has been accounted within the Grimme's D3 framework with the damping scheme by Becke and Johnson (D3BJ).^36,37 Plane wave energy cutoff has been set to 600 eV in all calculations. We use a Γ-centered Monkhorst–Pack k-point sampling grid of 4 × 3 × 4, 4 × 4 × 4 for orthorhombic MAPI, and cubic NaCl. The k-point sampling for the surface slabs and heterojunctions has been scaled accordingly. We set a SCF energy threshold of 10⁻⁵ eV, and a total forces threshold of 0.03 eV Å⁻¹ for all structural minimizations. All atoms of bulks, surface slabs and heterojunctions have been allowed to relax without freezing coordinates or imposing symmetry during geometry optimizations.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the Italian Ministry of Environment and Energy Security in the framework of the Operating Agreement with ENEA for Research on the Electric System. The computing resources and the related technical support used for this work have been provided by CRESCO/ENEA-GRID High Performance Computing infrastructure and its staff.³⁸ CRESCO/ENEAGRID High Performance Computing infrastructure is funded by ENEA, Italy, the Italian National Agency for New Technologies, Energy and Sustainable Economic Development and by Italian and European research programs; see https://www.cresco.enea.it for information. A. P. acknowledges the PON R&I 2014–2020-Asse IV “Istruzione e ricerca per il recupero-REACT-EU” for funding.

References

1. J. Dagar, K. Hirselandt, A. Merdasa, A. Czudek, R. Munir, F. Zu, N. Koch, T. Dittrich and E. L. Unger, Sol. RRL, 2019, 3, 1900088.
2. D. Di Girolamo, N. Phung, M. Jošt, A. Al-Ashouri, G. Chistiakova, J. Li, J. A. Márquez, T. Unold, L. Korte, S. Albrecht, A. Di Carlo, D. Dini and A. Abate, Adv. Mater. Interfaces, 2019, 6, 1900789.
3. S. Apergi, G. Brocks and S. Tao, Phys. Rev. Mater., 2020, 4, 085403.
4. E. Ahlswede, J. Hanisch and M. Powalla, Appl. Phys. Lett., 2007, 90, 163504.
5. L. S. Hung, C. W. Tang and M. G. Mason, Appl. Phys. Lett., 1997, 70, 152–154.
6. A. G. Kvashnin, P. B. Sorokin and D. Tománek, J. Phys. Chem. Lett., 2014, 5, 4014–4019.
7. P. B. Sorokin, A. G. Kvashnin, Z. Zhu and D. Tománek, Nano Lett., 2014, 14, 7126–7130.
8. A. G. Kvashnin, E. Y. Pashkin, B. I. Yakobson and P. B. Sorokin, J. Phys. Chem. Lett., 2016, 7, 2659–2663.
9. A. Riemann, S. Fölsch and K. H. Rieder, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 125423.
10. Q. Guo, Z. Qin, C. Liu, K. Zang, Y. Yu and G. Cao, Surf. Sci., 2010, 604, 1820–1824.
11. K. A. Tikhomirova, C. Tantardini, E. V. Sukhanova, Z. I. Popov, S. A. Evlashin, M. A. Tarkhov, V. L. Zhdanov, A. A. Dudin, A. R. Oganov, D. G. Kvashnin and A. G. Kvashnin, J. Phys. Chem. Lett., 2020, 11, 3821–3827.
12. L. Wang, J. Chen, S. J. Cox, L. Liu, G. C. Sosso, N. Li, P. Gao, A. Michaelides, E. Wang and X. Bai, Phys. Rev. Lett., 2021, 126, 136001.
13. Y. Zhao, Q. Zhang, Y. Li, L. Chen, R. Yi, B. Peng, D. Nie, L. Zhang, G. Shi, S. Zhang and L. Zhang, ACS Nano, 2022, 16, 2046–2053.
14. A. Pecoraro, A. D. Maria, P. D. Veneri, M. Pavone and A. B. Munoz-Garcia, Phys. Chem. Chem. Phys., 2020, 22, 28401–28413.
15. Y. Li, R. L. Z. Hoye, H.-H. Gao, L. Yan, X. Zhang, Y. Zhou, J. L. MacManus-Driscoll and J. Gan, ACS Appl. Mater. Interfaces, 2020, 12, 7135–7143.
16. J. M. Ball and A. Petrozza, Nat. Energy, 2016, 1, 1–13.
17. J. H. Heo, S. H. Im, J. H. Noh, T. N. Mandal, C.-S. Lim, J. A. Chang, Y. H. Lee, H. Kim, A. Sarkar, M. K. Nazeeruddin, M. Grätzel and S. I. Seok, Nat. Photonics, 2013, 7, 486–491.
18. P. W. Tasker, Philos. Mag. A, 1979, 39, 119–136.
19. P. S. Whitfield, N. Herron, W. E. Guise, K. Page, Y. Q. Cheng, I. Milas and M. K. Crawford, Sci. Rep., 2016, 6, 35685.
20. J.-H. Lee, N. C. Bristowe, P. D. Bristowe and A. K. Cheetham, Chem. Commun., 2015, 51, 6434–6437.
21. T. Baikie, Y. Fang, J. M. Kadro, M. Schreyer, F. Wei, S. G. Mhaisalkar, M. Graetzel and T. J. White, J. Mater. Chem. A, 2013, 1, 5628–5641.
22. M. T. Weller, O. J. Weber, P. F. Henry, A. M. D. Pumpo and T. C. Hansen, Chem. Commun., 2015, 51, 4180–4183.
23. J. E. Nickels, M. A. Fineman and W. E. Wallace, J. Phys. Chem., 1949, 53, 625–628.
24. M. Wagner, F. R. Negreiros, L. Sementa, G. Barcaro, S. Surnev, A. Fortunelli and F. P. Netzer, Phys. Rev. Lett., 2013, 110, 216101.
25. F. Cao, M. Wang and L. Li, Nano Sel., 2020, 1, 152–168.
26. C. Zhang, W. Luan and Y. Yin, Energy Procedia, 2017, 105, 793–798.
27. A. S. Nazligul, M. Wang and K. L. Choy, Sustainability, 2020, 12, 5138.
28. A. M. Elseman, S. Sajid, A. E. Shalan, S. A. Mohamed and M. M. Rashad, Appl. Phys. A: Mater. Sci. Process., 2019, 125, 476.
29. S. Li, Y.-L. Cao, W.-H. Li and Z.-S. Bo, Rare Met., 2021, 40, 2712–2729.
30. Y. Chen, L. Zhang, Y. Zhang, H. Gao and H. Yan, RSC Adv., 2018, 8, 10489–10508.
31. S. Rafique, S. M. Abdullah, M. M. Shahid, M. O. Ansari and K. Sulaiman, Sci. Rep., 2017, 7, 39555.
32. J. L. Miller, Phys. Today, 2014, 67, 13–15.
33. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
34. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
35. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
36. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
37. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101.
38. G. Ponti, F. Palombi, D. Abate, F. Ambrosino, G. Aprea, T. Bastianelli, F. Beone, R. Bertini, G. Bracco, M. Caporicci, B. Calosso, M. Chinnici, A. Colavincenzo, A. Cucurullo, P. Dangelo, M. De Rosa, P. De Michele, A. Funel, G. Furini, D. Giammattei, S. Giusepponi, R. Guadagni, G. Guarnieri, A. Italiano, S. Magagnino, A. Mariano, G. Mencuccini, C. Mercuri, S. Migliori, P. Ornelli, S. Pecoraro, A. Perozziello, S. Pierattini, S. Podda, F. Poggi, A. Quintiliani, A. Rocchi, C. Sciò, F. Simoni and A. Vita, 2014 International Conference on High Performance Computing & Simulation (HPCS), 2014, pp. 1030–1033.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02712k

---