The hydrogen evolution reaction: from material to interfacial descriptors

Abstract

The production of sustainable hydrogen with water electrolyzers is envisaged as one of the most promising ways to match the continuously growing demand for renewable electricity storage. While so far regarded as fast when compared to the oxygen evolution reaction (OER), the hydrogen evolution reaction (HER) regained interest in the last few years owing to its poor kinetics in alkaline electrolytes. Indeed, this slow kinetics not only may hinder the foreseen development of the anionic exchange membrane water electrolyzer (AEMWE), but also raises fundamental questions regarding the parameters governing the reaction. In this perspective, we first briefly review the fundamentals of the HER, emphasizing how studies performed on model electrodes allowed for achieving a good understanding of its mechanism under acidic conditions. Then, we discuss how the use of physical descriptors capturing the sole properties of the catalyst is not sufficient to describe the HER kinetics under alkaline conditions, thus forcing the catalysis community to adopt a more complex picture taking into account the electrolyte structure at the electrochemical interface. This work also outlines new techniques, such as spectroscopies, molecular simulations, or chemical approaches that could be employed to tackle these new fundamental challenges, and potentially guide the future design of practical and cheap catalysts while also being useful to a wider community dealing with electrochemical energy storage devices using aqueous electrolytes.

---

Introduction

Storing electricity in the form of a chemical fuel is critical for the penetration of renewable energies into the energy mix and into the chemical industry. To do so, hydrogen (H₂), which is of prime importance for the production of ammonia (NH₃) by the Haber–Bosch process, the production of steel and aluminum as well as for CO₂ transformation, appears as the ideal fuel and has thus gained a lot of interest over the past few years. However, over 95% of the current production of hydrogen is based on the reforming of fossil-fuels,¹ a process which emits CO₂. This realization pushes us to urgently develop water electrolysis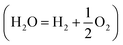 , which to date represents no more than 4% of the H₂ production, mainly as a side product of the chloroalkali process, as a greener solution.^1,2 Indeed, with the price of electricity generated with renewable technologies (wind turbines or photovoltaics) falling down, water electrolysis could seize this opportunity and generate cheap and sustainable H₂ at a large scale. One of the main hurdles to increase the penetration of water electrolysis in the H₂ production share is the low efficiency of this process and the absence of cheap and earth-abundant catalysts for the hydrogen evolution reaction (HER: 2H⁺ + 2e⁻ = H₂) and for the oxygen evolution reaction (OER: 2H₂O = O₂ + 4H⁺ + 4e⁻).

Since its discovery in 1789,³ and because it simply consists of two consecutive proton–electron transfers with no side reactions, the HER has probably been the most studied reaction in electrocatalysis.⁴ Until recently, numerous studies have been devoted to understanding from the material point of view how the physical properties of metallic surfaces govern the HER kinetics, as largely discussed in recent reviews.^5,6 This large body of research led to a good understanding of the chemical nature of the active sites and its correlation with the HER activity.^5,6 Furthermore, realizing that the HER kinetics is drastically affected by a change of pH from acidic to alkaline, the field has recently seen a regain of interest for fundamental studies on the HER, with the overall goal to master the HER activity by a fine tuning of the active site–electrolyte interactions. In light of these recent studies, questions regarding the role of the solvent structure and dynamics at the electrode–electrolyte interface, the effective nature of the reactants, and the use of spectator-additives in the HER kinetics arose and are now at the edge of the research focus. Moreover, not only such an understanding of the structure of the electrolyte in the vicinity of the active site became of prime importance for the HER, but a complete understanding of such fine effects will surely benefit unlocking the massive development of various electrochemical processes such as those involving CO₂/N₂/O₂ reduction^7–9 and their selectivity as well as developing aqueous electrolytes for Li-ion batteries.^10–13

In order to reflect this past development in the field of the HER, we will first recall how the hydrogen binding energy (HBE) has emerged as a physical descriptor to rationalize the HER activity on the surface of a wide variety of catalysts in acid. We will then emphasize how recent observations highlight that some discrepancies exist regarding the universality of the HBE as a descriptor for the HER, before discussing new models that recently emerged to explain the pH/electrolyte dependence of the HER as well as new physical descriptors capturing the catalyst–electrolyte interactions. Finally, we will discuss how new experimental and computational techniques combined with strategies relying on a better understanding of interfacial interactions could unravel the factors controlling the HER kinetics.

Fundamentals of the HER

Mechanistic understanding under acidic conditions on model materials

In acidic media, the cathodic reaction of the water electrolysis is the reduction of hydronium ions (H₃O⁺) to gaseous dihydrogen (H₂). From a thermodynamic point of view, this multi-step electrode reaction should occur at the potential of the reference hydrogen electrode (RHE). The first step of this reaction is the reduction of a proton on an active site of the catalyst surface (Volmer step, eqn (1.1)), followed by the evolution of molecular H₂, either through a second proton/electron transfer (Heyrovsky step, eqn (1.2)) or through the recombination of two adsorbed protons (Tafel step, eqn (1.3)):¹⁴

(Volmer) H₃O⁺ + e⁻ + * = H* + H₂O (1.1)

(Heyrovsky) H* + H₃O⁺ + e⁻ = H₂ + H₂O (1.2)

(Tafel) 2H* = H₂ (1.3)

where * denotes an active site on the catalyst surface, and H* a hydrogen atom adsorbed on an active site. Usually, one step kinetically limits the electrochemical reaction and is called the rate-determining step (rds). The HER kinetics is strongly dependent on the electrode material, for instance a mercury (Hg) electrode exhibits slow kinetics while the HER on platinum is one of the fastest electrocatalytic processes known.⁴ It is notable that the kinetics is subject to variations of parameters such as the nature of the electrolyte or the crystalline nature and orientation of the electrode (single-crystal, polycrystalline, amorphous, etc.).

Owing to its outstanding electrocatalytic activity, most of the studies therefore focus on the HER mechanism on the surface of Pt in acidic media. A typical cyclic voltammogram (CV) recorded for a polycrystalline platinum (Pt(pc)) electrode in acidic media is shown in Fig. 1.

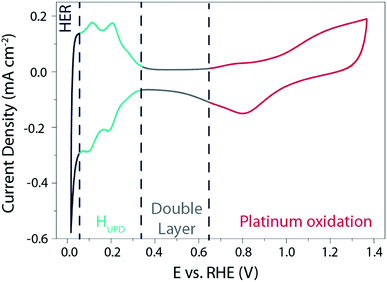Fig. 1 Cyclic voltammogram recorded on a Pt(pc) electrode at 50 mV s⁻¹ in a 0.5 M H₂SO₄ solution degassed with argon.

This typical cyclic voltammogram exhibits 4 regions. At high potentials (>0.65 V vs. RHE), the Pt surface is oxidized/reduced with the subsequent formation of Pt–OH and/or Pt-oxide that can be concomitant with the specific adsorption of anions on the surface of the platinum. The second region at potentials comprised between 0.35 V and 0.65 V vs. RHE is referred to as the “double layer region” as no faradaic process occurs. At potentials between 0.05 V and 0.35 V vs. RHE, the third region is usually denoted as the hydrogen underpotential deposition (H_UPD) region and is characterized by the discharge of protons on the Pt surface following the reaction: H⁺ + e⁻ + Pt* = Pt − H_UPD. Note that the precise nature of this phenomenon was recently reviewed, and may involve cation adsorption as well as OH desorption, which will be discussed later on.^15–17 Finally, at more negative potentials, H₂ is evolved in the HER region.

Three main features can be seen in the H_UPD region: one broad envelope, a couple of redox peaks at ∼0.20 V vs. RHE followed by a third peak at ∼0.10 V vs. RHE. While these phenomena were already described by comparing CVs recorded on single-crystal surfaces in the 60's and tentatively assigned to the hydrogen UPD on different facets of platinum,¹⁸ this assignment was confirmed in the 80's owing to the development by Clavilier of new methods for preparing high-quality surface single crystals.¹⁹ Hence, the large envelope is related to the H_UPD on Pt(111) facets, while the peaks at ∼0.10 V vs. RHE and ∼0.20 V vs. RHE are related to H_UPD on the Pt(110) and the Pt(100) sites, respectively. It should be noted that the underpotential deposition of hydrogen is not unique to platinum and is known to occur on other metallic surfaces.²⁰ Due to the ultra-fast kinetics of the HER on platinum electrodes, the faradaic current is often limited by the mass-transport of H₂ generated during the HER, even when a rotating-disk electrode (RDE) apparatus is employed.^21,22 This limitation hinders a proper fitting with microkinetic models¹⁴ and has thus prevented the catalysis community from achieving a fine understanding of the HER mechanisms under acidic conditions. Despite this limitation, by measuring the HER and hydrogen oxidation reaction (HOR) currents in the micropolarization zone (small potential window across the RHE potential) at low temperature, Marković et al. were able to discriminate different activation energies for the HER on different Pt-single crystal facets, with the activation energy ranging from 9.5 kJ mol⁻¹ for Pt(110) to 18 kJ mol⁻¹ for Pt(111) (Fig. 2a).²¹

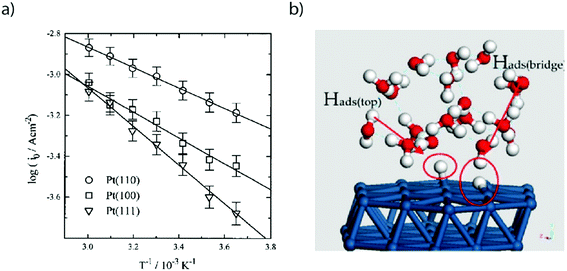Fig. 2 (a) Arrhenius plot of exchange current densities for Pt(110) (circle), Pt(100) (square) and Pt(111) obtained by cyclic voltammetry in a 50 mM H₂SO₄ solution (reproduced from ref. 21 with permission from the American Chemical Society, Copyright (1997)). (b) Snapshot of a MD-DFT simulation showing the presence of two types of adsorbed hydrogen on a Pt(111) electrode. Reproduced from ref. 23 with permission from Elsevier, Copyright (2007).

From the Tafel slope measurements, which are themselves subject to practical limitations (ohmic drop correction, gas saturation, impurities, fitting parameters, etc.), the recombination step (Tafel step with a slope of ∼30 mV per decade) was determined to be the rds for Pt(110) while the Heyrovsky (Tafel slope of ∼40 mV per decade) step is believed to be the rds for Pt(100). For Pt(111), the value obtained (74 mV per decade) does not match any of the expected values from microkinetics analysis. For polycrystalline platinum, Tafel slope values of around 30 mV per decade are usually measured, which match well with the expected values for the Tafel step being the rds.⁴

While the growth of high quality single crystals has been tremendous for the understanding of the HER on Pt, the development of computational methods has also brought a deeper understanding for the HER/HOR. For instance, combining molecular dynamics (MD) with density-functional theory (DFT), the HOR was predicted to follow a Heyrovsky–Volmer mechanism on Pt(111) (Fig. 2b).²³ Furthermore, these calculations also confirmed the presence of two types of hydrogen atoms adsorbed on the Pt(111) surface. The first one is directly adsorbed from the H₂ molecule on the bridge sites of the Pt slab and is found not to be reactive, thus its tentative assignment to the H_UPD. The second one, adsorbed on top of the Pt(111) slab corresponds to a proton in solution being reductively adsorbed on the femtosecond time scale on the electrode surface. While theoretical insights help the understanding of the mechanism in a very short timescale, they must be validated with experimental results to assess their validity. Toward that goal, femto spectro-electrochemical techniques were recently used to correlate the activation energies measured by Marković et al.²¹ with the rate of electron transfer along the Pt–H_UPD bond, showing that this transfer occurs at the fs timescale.²⁴ Doing so, the interfacial solvent reorganization which is taking place at a greater timescale prior to any electron transfer was also shown to be critical for the H_UPD kinetics.²⁴

From a physical descriptor to the discovery of practical catalysts

While these fundamental investigations on platinum model single-crystal electrodes started in the 80's, numerous other polycrystalline electrodes were historically investigated aiming to correlate kinetic parameters with the physical properties of different metals. Hence, inspired by the pioneering work of Conway and Bockris,²⁵ the exchange current densities for numerous sp metals and transition metals were measured by Trasatti.²⁶ From this investigation, a linear relationship between the exchange current density of the HER on metallic surfaces and their work-function was shown and was ascribed to a different orientation of water molecules at the surface of the electrode depending on the nature of the metal. However, this classification does not provide insights on the intermediates of the HER. Thus, comparing the hydrogen binding energy (HBE) on the metal with the exchange current density, a typical volcano shape was later found (Fig. 3a), suggesting that the Sabatier principle can apply to the HER. Indeed, an ideal catalyst for the HER should bind hydrogen strong enough to adsorb protons from the electrolyte (Volmer step). However, if the binding is too strong, it slows down the desorption of H* necessary to evolve H₂ (either through the Heyrovsky or the Tafel step), thus limiting the HER kinetics. Inspired by these experimental studies, Nørskov et al. computed using DFT the free energy of formation (ΔG_H*) of the H* intermediate on several metallic surfaces and obtained a similar volcano shape (Fig. 3b), confirming the HBE to be a good physical descriptor for the HER.²⁷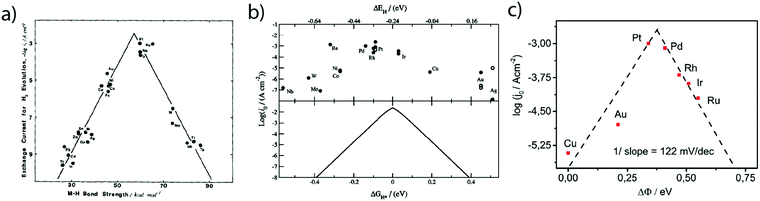

Fig. 3 Dependence of the exchange current density of the HER on the (a) measured (reproduced from ref. 26 with permission from Elsevier, Copyright (1972)) and (b) calculated (reproduced from ref. 23 with permission from Electrochemical Society, Inc., Copyright (2005)) metal hydrogen binding energy and (c) difference of work-function between a hydrogenated and a wetted surface (reproduced from ref. 28 with permission from PCCP Owner Societies, Copyright (2017)).

Nevertheless, as mentioned by Trasatti, one of the challenges pertaining to this approach is the reliability in measuring the physical properties of pure metals omitting the presence of the electrolyte and adsorbed species, alike in the work of Trasatti, or even of a passivation layer (e.g. Mo or W are covered by an oxide layer while platinum is covered by the H_UPD). In light of these limitations and thanks to recent advances in ultra-high vacuum (UHV) techniques, the work-function of realistic surfaces was recently reinvestigated by Zeradjanin et al. as a physical descriptor for the HER including the role of adsorbed water.²⁸ Considering that the free energy of activation ΔG* for proton adsorption is a combination of (1) the work to transfer a proton from the Outer-Helmholtz plane (OHP) to the Inner-Helmholtz Plane (IHP), (2) the proton desolvation and the energy resulting from the difference of potential between the metal and the IHP and (3) the energy to transfer electrons from the metal (at its Fermi level) to the IHP, it was thus qualitatively predicted that the proton adsorption energy becomes more endergonic (weaker E(M − H)) when the electrode (with an interfacial water layer) work function is increased.²⁸ As a direct consequence, increasing the work function should increase ΔG* and thus decrease the exponential term of the electron transfer rate constant, usually described within the framework of the transition-state theory (TST) as: 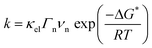where κ_el is the electronic transmission coefficient (0 ≤ κ_el ≤ 1) which accounts for the tunneling-probability of the electron increasing with the electrode–reactant coupling, Γ_n is the nuclear tunneling factor (Γ_n ≥ 1) which corrects the rate expression taking into account molecules/ions that react without entirely surmounting the classical electrochemical free energy barrier, ν_n is the nuclear frequency factor which represents the frequency at which the reacting species approach the transition state thanks to the solvent and bond coordinate motions and ΔG* is the activation free energy.²⁸ However, as deduced from this expression, increasing the work function not only affects the activation free energy but also results in an increase of the pre-exponential constant (greater reactant–electrode coupling resulting in larger values of both κ_el and Γ_n), which is often omitted but counterbalances the increase in activation energy. Thus, a more precise volcano plot is obtained when plotting the exchange current density versus the difference of work functions between hydrogenated and non-hydrogenated metals in the presence of an interfacial water layer (Fig. 3c). Finally, it is worth mentioning that this discussion on the work function stands only to assess the ease with which hydrogen binds to a given material. Nevertheless, it does not capture the effect of other parameters such as modification of the electrolyte and/or interfacial interactions which can control the HER kinetics for the best catalysts.

Interestingly, despite some approximations and limitations, the HBE theory remains largely used by the catalysis community since it can easily act as a guide for the discovery of new catalysts. For instance, it was used to explain the great performances of new cheap catalysts, such as MoS₂ for the HER,^29,30 and helped to clarify the nature of active sites which led to the design of new chalcogenide compounds enriched in active sites.³¹

Hence, the HER under acidic conditions is now relatively well understood. Nevertheless, when increasing the pH of the electrolyte from acidic to alkaline conditions, the HER and HOR performances of numerous catalysts were reported to dramatically decrease. For instance, platinum is known to undergo a decrease from 2 to 3 orders of magnitude of the HER exchange current density from pH = 0 to pH = 13.^32,33 This pH effect thus renders the use of the HBE theory to find a simple activity descriptor based on a sole material's properties difficult. The second part of this perspective will therefore focus on recent studies discussing the preponderant role of other adsorbed species, such as cations or hydroxide anions, as well as the reorganization of the electrolyte on the surface of the electrode in the HER kinetics.

The HBE descriptor and its limits

Inspired by the seminal work on the HBE,^26,27 Sheng et al. recently correlated the HER activities of several monometallic surfaces in 0.1 M KOH solutions with computed HBE.³⁴ Similar to the results obtained by Nørskov in acidic media,²⁷ they could show that the HER activity of the selected metals follows a volcano trend in alkaline media, with Pt being the most efficient catalyst. Following this finding, the authors subsequently focused on the behavior of Pt(pc)³⁵ and found a pH-dependence for the H_UPD potentials on (110) and (111) facets. Using the relationship ΔH_HBE = −FE_peak (Fig. 4a), H_HBE values experimentally determined were then compared with the HER overpotential at a fixed current density. Doing so, a linear decrease of the HER activity with the experimentally determined HBE was found (Fig. 4b). This methodology was then tentatively generalized for different carbon supported platinoid metals³⁶ and while a similar trend was found (decrease of the activity while the HBE increases in absolute value), the initial findings were tempered when observing that the HBE values evaluated by electrochemistry in alkaline electrolytes are far from those measured by UHV techniques for Pt(pc). This realization led to the conclusion that the orientation of adsorbed water should be taken into account.³⁶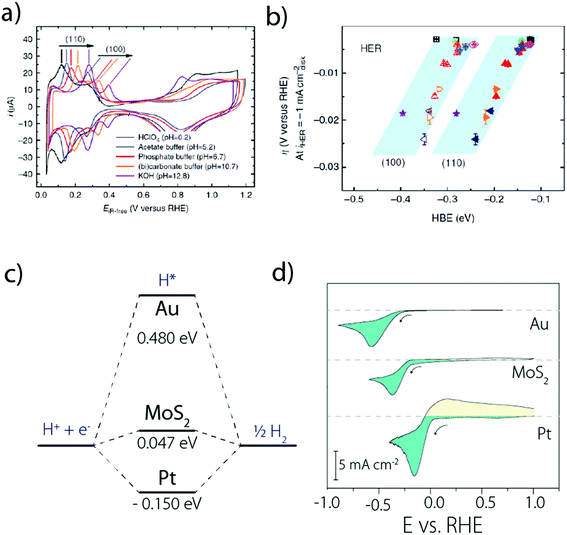

Fig. 4 (a) CVs recorded at different pH values on a polycrystalline platinum electrode (reproduced from ref. 35 with permission from Springer Nature, Copyright (2015)) from which the hydrogen binding energy is extracted, (b) overpotential for the HER at −1 mA cm⁻² on a polycrystalline platinum electrode in different buffered electrolytes, plotted versus the HBE obtained from electrochemical measurements (reproduced from ref. 35 with permission from Springer Nature, Copyright (2015)), (c) calculated free energy diagram for the HER at pH = 0 and no overpotential for Pt, MoS₂ and Au surfaces (data are from ref. 27) and (d) cyclic-voltammogram at pH = 2 (H₂SO₄ 18 mM + K₂SO₄ 82 mM degassed with Ar) on Pt, amorphous MoS₂ and Au electrodes with a scan rate of 50 mV s⁻¹ with oxidation currents in yellow and reduction current in blue, dashed lines indicating the j = 0 axis.

While being attractive, some concerns have thus been recently raised about the HBE theory.³⁷ Indeed, as the H⁺/H₂ couple is found to be reversible on the Pt surface for instance,²¹ all the HER elementary steps are reversible and the HOR intermediates are certainly identical.³² Therefore, the HBE should control the HER and the HOR in a similar fashion. However, exploring other materials with relatively good HER performances and a small HBE value such as MoS₂ (ref. 29 and 38) (Fig. 4c), it is observed that MoS₂ poorly catalyzes the HOR (Fig. 4d). Hence, the absence of reversibility on a low-HBE material suggests that the energy and the nature of the intermediates for the HOR and HER reactions are not identical, which may originate from changes of some material properties (defects, electronic properties, etc.) or of the double-layer structure/composition as a function of the applied potential, thus preventing the use of HBE as a sole descriptor of the HER kinetics.

Furthermore, as previously mentioned, HBE measurement by either UHV or electrochemical measurements (H_UPD) involves hydrogen atoms that are likely to be different from those involved as reactive intermediates in the HER. One obvious manifestation of this difference is that while the H_UPD deposition potential on Pt(111) follows a Nernstian behavior with pH (60 mV per unit) and so the HBE determined from electrochemical measurements is not expected to change with pH, the HER activity drastically decreases by 2–3 orders of magnitude changing from pH = 0 to pH = 13 for the same surface.³³ Finally, the effect of buffer solution should also be investigated when performing measurements at intermediate pH values, as it can also impact the proton transfer kinetics.³⁹

At this point, we have shown how the identification of reaction intermediates on single-crystal model electrodes has triggered the quest for finding universal descriptors for the HER activity. While the HBE was initially seen as a good candidate, this theory cannot predict how the electrode–electrolyte interfacial structure impacts the performances of a given surface. Indeed, puzzled by the severe loss of activity of Pt when used under neutral or alkaline conditions, the electrocatalysis community recently investigated questions previously overlooked: what is the rate determining step for the HER under alkaline conditions? Which is the proton donor? What is the role of spectator species? How is the catalyst surface modified?

Interfacial interactions: how to rationalize them?

Unlike in acidic media, the Tafel slope measured for Pt electrodes in alkaline solutions is around 120 mV per decade, indicating that the Volmer or the Heyrovsky step is the rds.¹⁴ Nevertheless, one of the main differences between alkaline and acidic HER is that the proton concentration is drastically diminished, so that the Volmer and Heyrovsky steps are likely to include a water-dissociation step^5,33 as detailed below:

(Volmer) H₂O + e⁻ + * = H* + OH⁻ (1.4)

(Heyrovsky) H₂O + e⁻ + H* = H₂ + OH⁻ (1.5)

Moreover, it was observed that the HER kinetics over Pt(111) under alkaline conditions is drastically enhanced by the presence of oxophilic groups, such as Pt-islands (defects) and Ni(OH)₂ on the catalyst surface (Fig. 5a),³³ which could be explained as originating from an easier H₂O dissociation. Following this observation, it was confirmed that the HER activity for Pt(111) decorated by different 3d transition metal hydroxides M(OH)₂ follows the Brønsted–Evans–Polanyi principle and the oxophilic groups' affinity to OH_ads should be neither too strong (surface poisoning) nor too weak (no binding) to promote the HER kinetics.⁴⁰

Fig. 5 (a) HER activity in alkaline solutions measured on a Pt(111) single crystal electrode, customized with different oxophilic groups and (b) “bi-functional” mechanism responsible for the enhanced activity when groups that promote water dissociation are present on the Pt(111) surface (reproduced from ref. 33 with permission from AAAS, Copyright (2011)).

Thus, in alkaline electrolytes, the cleavage of water O–H bond and the transport of OH⁻ from the catalyst surface to the bulk of the electrolyte are likely to be part of the limiting step for this so-called bi-functional mechanism. A similar conclusion was recently made for copper electrodes for which a larger HER activity was measured with more oxophilic surface created by applying a mechanical or electrochemical surface treatment.⁴¹ Overall, switching from H₃O⁺ to H₂O as a proton donor could simply hamper the Volmer step,^42–44 explaining the difference in activity between acidic and alkaline conditions. Indeed, as stated earlier, the Volmer step in alkaline electrolytes includes a water O–H bond dissociation step, while it is not true for acidic electrolytes. If this dissociation is in a fast equilibrium, the HER kinetics should only be determined by the proton–electron transfer rate. Nevertheless, as the activation energy for water auto-ionization (around 75 kJ mol⁻¹ at 300 K^5,45) is found to be larger when compared to the one for the HER in alkaline electrolytes (around 30–45 kJ mol⁻¹ for Pt catalysts^5,32), this could suggest that the water auto-ionization step is coupled with the electron transfer (as recently supported by DFT calculations⁴⁶), and thus is partly responsible for the slow HER kinetics measured in alkaline electrolytes.

Alike for the HBE, recent studies however interrogate the importance of the surface oxophilicity and of the bi-functional mechanism in the HER kinetics.^36,47,48 Indeed, comparing the HER activity of Pt/C, PtNi/C and PtNi/C treated in acid to remove Ni from the surface of the nanoparticles revealed that while the presence of nickel increases the HER kinetics in alkaline media when compared to Pt/C,⁴⁷ removing it from the surface does not hinder the HER and HOR kinetics for PtNi/C. Thus, the role of the 3d metal was rather assigned to a modification of the HBE. Additionally, it was demonstrated that in unbuffered solutions, the two reduction events previously attributed to a different kinetics for the H₃O⁺ and the H₂O reduction⁴² may simply arise from the modification of the surface pH with the applied potential.⁴⁹ Hence, assuming that the surface pH is solely determined by the applied potential on Pt electrodes (Nernst equation), the peculiar electrochemical response observed at large current densities is well explained by the modification of the surface pH. However, this peculiar shape has been observed for a wide variety of surfaces on which the H⁺/H₂ couple is not reversible.^38,42 Also, it may not explain the role of spectator species observed in the study of alkaline HER kinetics.

Indeed, even more revealing than the surface decoration of Pt with M(OH)₂, the addition of Li⁺ cations in the electrolyte was found to be beneficial for the HER in the presence of surface oxophilic groups (Fig. 5a).³³ This effect was initially rationalized by the anchoring of Li⁺ to the M(OH)₂ moieties promoting the water-dissociation through non-covalent interactions (Fig. 5b).³³ While the role of these “interfacial” interactions was previously discussed for the oxygen reduction reaction (ORR) and the HOR,⁵⁰ this first observation for the HER highlighted the role of “spectator” species from the electrolyte and prompted novel fundamental studies.⁵ In particular, unlike the previous model which was based on non-specific adsorption of cations,⁵⁰ recent DFT and electrochemical measurements on Pt single crystal electrodes revealed that cation specific adsorption can occur.^16,17,51 Hence, both computational and experimental studies were carried out on Pt(111), Pt(100) and Pt(110) to tentatively explain the unusual non-Nernstian shift of 50 mV (vs. SHE) for the UPD peak observed for the two latter facets¹⁶ and revealed that considering the sole adsorption of hydrogen in the H_UPD region cannot reproduce the experimental cyclic voltammograms recorded for Pt(110) and Pt(100).^15,16 Rather, OH adsorption should also be taken into account (or in fact the co-adsorption with H₂O, as discussed later), resulting in the equation

xOH^δ+_ad + (x + 1)H⁺ + [(1 + δ)x + 1]e⁻ = H* + xH₂O, (1.6)

where δ is the partial charge on the adsorbed OH group that can be negative, which satisfies a non-Nernstian behavior if δ ≠ 0.¹⁵

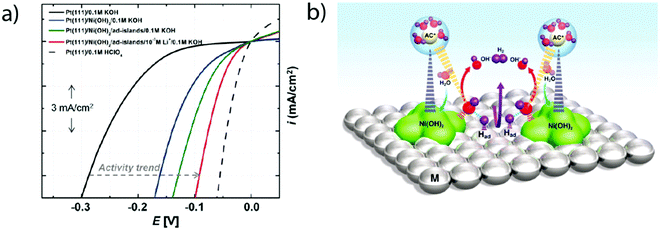
Later on, the effect of the specific adsorption of cations onto the Pt(100) and Pt(110) was investigated to explain the remaining charge on OH_ad. Indeed, K⁺ adsorption was found to shift the OH⁻/H₂O adsorption (and so desorption) to a higher potential by destabilizing OH_ad on the surface of the electrode.¹⁶ This destabilization was ascribed to an increase of the Pt–O bond lengths (Fig. 6a) as well as to a partial charge retention by the adsorbed cation, which is compensated by the presence of a negative charge on the adsorbed OH_ad and H₂O_ad (eqn (1.6) and Fig. 6b). Both of these effects eventually lead to a more positive potential for the adsorption of OH from the bulk of the electrolyte as the concentration of K⁺ is increased, explaining the non-Nernstian shift of the “hydrogen” peaks with the KOH concentration. This hypothesis was further generalized to more complex Pt surfaces such as Pt(533) that contains Pt(111) terraces and (100) steps.¹⁷ Finally, the role of the cation has been investigated on Pt(110) steps for which a non-Nernstian positive shift of the “UPD peaks” was only observed for pH > 3 following the ionic radius trend in the alkali series: Li⁺ < Na⁺ < K⁺ < Cs⁺ (Fig. 6c).¹⁷ The absence of the cation effect at low pH was explained as the consequence of the potential of zero charge (pzc) being more negative than the potentials of the UPD region for Pt(110), so no cation is expected to be adsorbed in the steps.¹⁷ In contrast, at higher pH the influence of the cation was explained by a size effect: the larger the cation, the more charge it retains (as the charge retained is proportional to the change in surface-normal dipole moment) and the more OH_ad is destabilized.^17,51

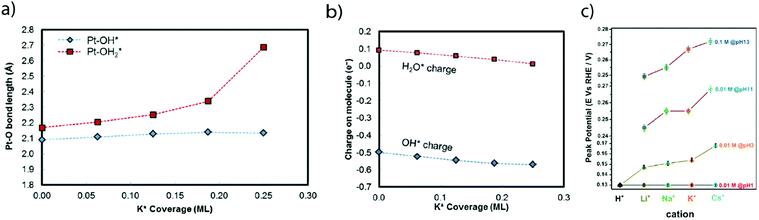Fig. 6 (a) Pt–O bond lengths and (b) Bader charge for adsorbed OH and H₂O molecules on Pt(100) calculated using DFT at different adsorbed potassium coverages (reproduced from ref. 16 with permission from the American Chemical Society, Copyright (2016)), and (c) experimental position of the OH_ad/H* peak on Pt(533)_ad at different pH values with different alkali cation contents (reproduced from ref. 17 with permission from John Wiley and Sons, Copyright (2017)).

Unfortunately, for most of these fundamental studies, the impact of the H*/OH_ad exchange on the HER kinetics is not discussed. The few studies focusing on the role of alkali concentration and pH in the HER performances of Pt or PtNi^52,53 could show that even if modest, the nature of the cation impacts the HER kinetics as follows: Li⁺ > Na⁺ > K⁺. This trend corresponds to a smaller destabilization of the OH_ad and so virtually a greater interfacial oxophilicity (and easier water dissociation, as shown by the group of Marković^40,41) of the surface when the cation is specifically adsorbed, as stated by Koper's group.^17,51 If not specifically adsorbed, the cation effect could be rationalized by the formation of an OH_ad–(H₂O)–AM⁺ adduct, as discussed above, as the cation would promote the removal of OH_ad from this adduct and its transport out of the double-layer. This effect is expected to be enhanced in the presence of more acidic cations which would also explain the greater HER activity measured in the presence of smaller alkali cations. Overall, further studies will be necessary to better understand this interfacial structure–reactivity dependence.

While most of the research studies carried out recently have been focusing on the role of the cationic species at the solid/liquid interface, the seminal work conducted by Trasatti more than 50 years ago suggested that the water orientation at the interface could be responsible for the discrepancies in activity over different metallic surfaces.²⁶ Pitfalls exist in experimentally assessing such sensitive effects and the accuracy of theoretical calculations suffers as well from the high computational cost of including explicit solvent molecules.⁵⁴ However, while it was shown by UHV and DFT calculation that interfacial water does not drastically affect the H_UPD energetics,^15,16 it is expected to largely influence the alkali cations and hydroxide adsorption.¹⁶ Therefore, investigating the water structure (orientation, chemical environment) and dynamics (lifetime in the IHP, structure reorganization along charge transfer) at the electrode–electrolyte interfaces will be key to unravel the mechanisms by which interfacial interactions impact the HER activity. These observations on the role of the spectator species lead us to speculate that the use of bare physical descriptors such as the HBE cannot fully capture the HER kinetics which requires inclusion of dynamic effects occurring at the electrochemical interface. We believe that, within the experimental framework developed by Zeradjanin et al.,²⁸ it would be critical to reinvestigate, using different electrolytes, physical descriptors such as work function difference between non-hydrogenated and hydrogenated wetted surfaces.

Interfacial reorganization: role of the solvent

Only a few experimental characterizations of the water structure at the electrode–electrolyte interface during the HER have been carried out, the main reason being the ambivalent role of water as the solvent and active molecule so that reactive water molecules are often masked by their environment. Consequently, indirect measurements such as laser-jump measurements⁵⁵ or in situ spectroscopies⁵⁶ have been so far used to gain insights on the water interfacial structure. For instance, the use of laser-jump experiments revealed that Ni(OH)₂ addition on Pt(111) lowers its pzcf^57–59 which eventually reduces the interfacial electric field at the HER operating potential, and softens the double-layer to facilitate the OH⁻ and H⁺ transport.⁵⁷ Similarly, this can explain the sluggish activity of Pt(111) in the alkaline electrolyte as its potential of zero free charge (pzfc) remains unchanged with the pH while the operating potential (referred vs. the SHE) for the HER is much more negative, which rigidifies the double-layer and hampers the transport of charged reactants/products (Fig. 7a).^57,60 Nevertheless, such an explanation goes against the initial observations made by Trasatti^26,61 and more recently by Zeradjanin et al.²⁸ who noticed an increase of the HER activity with the catalyst work-function as well as found a positive linear correlation between the work-function value and the catalyst pzc, resulting in poor activity for low pzc materials (Fig. 7b).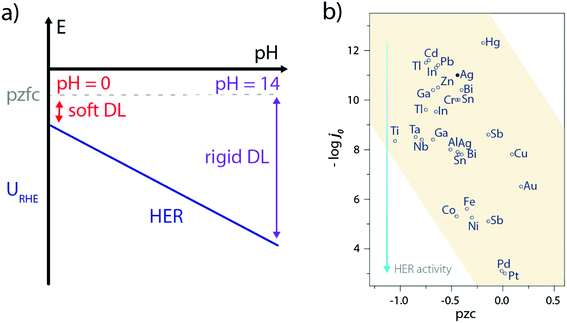

Fig. 7 (a) Effect of the pH and pzfc on the double-layer rigidity during the HER, (b) plot of HER exchange current density as a function of the potential of zero charge for several metallic electrodes (pzc values are taken from ref. 61 and exchange current densities under acidic conditions from ref. 26).

While the pzfc model should properly work for surfaces having similar properties (i.e. similar active sites), a more precise picture of the influence of the pzc on the proton-transfer kinetics for a given surface must also consider eventual modifications of the pre-exponential factor of the kinetic constant which can reflect a modification of the proton/electron tunneling or the H⁺ concentration at the interface, among numerous parameters.^28,60 Other models considering the double-layer ordering were thus developed to explain this pH-dependent activity. Hence, it was suggested that the activation energy for proton adsorption is mainly driven by a loss of entropy while protons are transferred from the bulk of the electrolyte to the OHP, a loss which increases with the pH.⁶² This entropy loss is compensated by the enthalpy term with a delay, so that the variation in the Gibbs free energy remains null, satisfying the equilibrium conditions.⁶² Such a proposition relies on the assumption that the liquid water structure between the OHP and the electrode is not affected by pH variations,⁶² which should be discussed in light of the study discussed above on the influence of interfacial water structure on the HER activity (pzfc theory).⁵⁷

Furthermore, some computational efforts attempting to explicitly model the electrode–electrolyte interface are worth highlighting. For instance, a seminal study on the water dissociation on a Pd surface by Filhol et al. proposed that at least three distinct water layers at the electrochemical interface are required for the H₂O reductive (resp. oxidative) dissociation: a layer with proton donors (resp. hydroxide donors), a layer to accept the generated hydroxide (resp. protons) by H-bonding and a layer to diffuse the as-generated species in solution.⁶³ Moreover, thanks to recent advances in DFT calculations, a reduced charge of +0.7e for protons located in the OHP at the Pt(111)–H₂O interface was found, which was explained by a charge transfer between the electrode and the interfacial solvent molecules.⁶⁴ Interestingly, a bulk behavior (protons exhibiting a unit charge) was found for protons located in the third layer of water. These differences in charge highlight the importance of understanding the electrode–electrolyte interface at the molecular scale to precisely assess the charge transfer energetics. Finally, we should recall that all these models share the same assumption: water self-ionization is in a fast equilibrium and H₃O⁺ should be considered as the reactant at every pH. However, since the H₂O self-ionization activation energy exceeds by a factor of ∼2 the one measured for the HER on Pt,⁴⁶ the validity of this hypothesis has to be demonstrated. Overall, both water-dissociation (bifunctional mechanism) and interfacial electric field (pzfc theory) can simultaneously play a role in the HER kinetics in alkaline media.

Naively speaking, considering all the parameters reviewed above, an ideal catalyst should possess the following properties. First, the active site must be able to bind H neither too strongly nor too weakly (HBE theory). Regarding its pzc, it should be high enough to enhance the pre-exponential factor of the rate constant (more protons at the interface and more coupled to the electrode), but low enough to minimize the double-layer rigidity and facilitate charge transport through the double layer. With these properties presumably competing with each other, finding an optimal catalyst with a single active site might prove difficult. Rather combining with the help of synthesis routes such as (de)alloying, surface decoration, etc. different active sites with different functionalities is probably a more promising strategy to follow, bearing in mind that some species contained in the electrolyte are taking part in the reaction mechanism. Taking into account the surface properties, non-reactive species such as Lewis acids can help tune the energies of the intermediates by for instance promoting the H₂O self-ionization and reducing the overall HER activation energy. Nevertheless, these effects have mostly been overlooked till recently, the reason being the relative lack of experimental and theoretical studies that could draw a molecular understanding of the catalyst–electrolyte structure. Thus, in the last part of this perspective, in situ spectroscopic techniques and computational methods recently developed and that could prove useful to probe the impact of water interfacial structure on its reactivity will be highlighted.

Water at charged interfaces: toward a structure–reactivity descriptor?

Insights from in situ spectroscopies

As previously discussed, the nature of the double-layer has a tremendous influence on the faradaic processes encountered at the electrode–electrolyte interface.^65,66 However, due to its narrow thickness (∼30 nm in diluted aqueous electrolytes),⁶⁷ its precise characterization is challenging. In order to overcome this difficulty, new tools were recently developed to investigate the physical properties of the aqueous double layer. For instance, ambient-pressure X-ray photoelectron spectroscopy (APXPS) was used to probe the potential drop across the Gouy–Chapman layer in diluted alkaline solutions in contact with a gold electrode.⁶⁷ Furthermore, owing to the linear dependence of the core-level binding energy with the local potential (referred to the working electrode), this technique also gives access to the pzc of the electrode. However, the measured signal is concentration dependent and thus the very thin Stern layer cannot be distinguished from the diffuse layer. This low resolution also hinders the investigation of concentrated solutions, in which the double-layer thickness is further decreased.

Thus, the determination of the water structure (density, orientation, etc.) in the first molecular layers at the surface of the electrode, and especially in the IHP, requires the use of other in situ analytical techniques. Among them, surface X-ray scattering was employed to determine the potential-dependent density and orientation of water molecules in NaF aqueous solution at the Ag(111)–electrolyte interface. Doing so, it was demonstrated that under polarization, the first layer of water at the interface exhibits a larger density than in the bulk of the electrolyte, which implied a disruption of the hydrogen bonding network.⁶⁸ Additionally, this observation was correlated with the presence of a large electric field (∼10⁷ V cm⁻¹) which attracts and orientates water molecules at the interface, switching from hydrogen pointing toward the electrode (H-down) at potentials more negative than the pzc to oxygen pointing toward the surface (H-up) at potentials above the pzc. This potential-dependent orientation of water molecules at the interface was also confirmed by laser-jump measurements on Pt single crystals.⁵⁵ Furthermore, combining X-ray absorption spectroscopy (XAS) measurements at the oxygen K-edge in total fluorescence yield (TFY, bulk sensitive) and total electron yield (TEY, surface sensitive) modes with ab initio simulations, useful information about the water structure at a gold interface upon polarization could be gained.⁵⁶ Hence, at potentials more negative than the pzc, the H-down orientation was confirmed and the amount of dangling bonds was found to increase, leading to a disruption of the water H-bond network (Fig. 8a and b).⁵⁶ Finally, a very recent study employing in situ Raman spectroscopy in the presence of shiners confirmed the decrease of hydrogen-bond donor water molecules at decreasing potential for a gold electrode (Fig. 8b),⁶⁹ as well as the densification of the interface and the favored “one H-down” orientation toward the surface upon negative polarization, while 2H-down water molecules could be spotted only at very negative potentials.

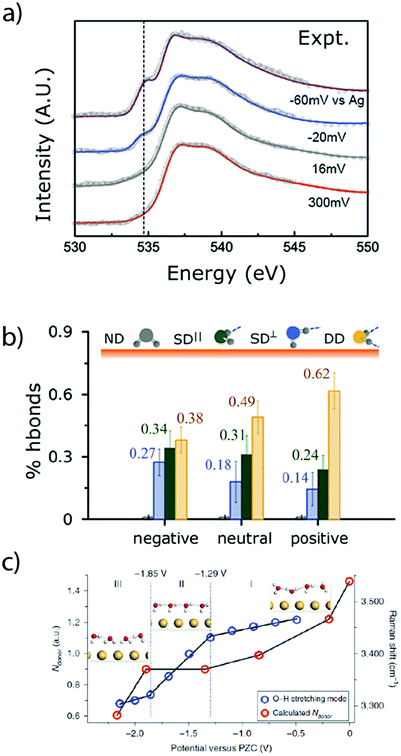Fig. 8 (a) Experimental O K-edge total electron yield XAS spectra of water, collected at a gold electrode under polarization and (b) population of H-bonded water molecules deduced from these spectra at different polarization (adapted from ref. 56 with permission from AAAS, Copyright (2014)). (c) Number of hydrogen-bond donors of interfacial water molecules at different potentials on a gold electrode calculated from in situ Raman measurement (reproduced from ref. 69 with permission from Springer Nature, Copyright (2019)).

While being very useful, these techniques often require the use of model non-reactive electrodes, as in the examples cited above. Nevertheless, it is worth mentioning that similar techniques were also employed on more practical systems attempting to probe the presence/absence of chemical transformations of the catalyst surface. Hence, using in situ XAS experiments on a platinum electrode in sulfuric acid, doubts were raised about the nature of the phenomena occurring in the oxidation region for the Pt electrochemistry.⁷⁰ Unlike the commonly accepted explanation that the anodic current in this region is, at least partly, related to the formation of Pt–O or Pt–OH groups on the surface, results obtained by in situ XAS experiments suggest that the change observed in the oxygen K-edge XAS spectra upon positive polarization is rather due to the specific adsorption of sulfates.⁷⁰ This conclusion was further confirmed by in situ APXPS measurements which revealed the specific adsorption of anions onto platinum which is only oxidized at potentials higher than +1 V vs. SHE.⁷¹ In addition to these measurements focusing on Pt under anodic polarization, a recent operando study on Pt in alkaline electrolytes⁷² confirmed the absence of PtO or PtO₂ species during the HER. Rather, the formation of Pt–H bonds that are not stripped in the UPD region was observed. Unfortunately, in the presence of faradaic electrochemical processes, information about the solvent structure is often difficult to obtain and emphasis was paid to the modifications occurring on the surface of the electrodes.

The help of computational chemistry: toward a molecular understanding?

While these operando techniques proved very powerful, their investigative power is often strongly reinforced when coupled with ab initio calculations which can predict the spectroscopic signature of different interfacial configurations. Hence, the theoretical framework for water structure at the metal–electrolyte interface is quite extended, with for instance the use of classical MD investigating the dynamics of water molecules at the Pt–electrolyte interface.^73,74 Interestingly, the binding energy of a water molecule onto a Pt surface was found greater than a typical H-bond (<0.25 eV).⁷³ Moreover, while the interaction of a single water molecule with a Pt surface is not sensitive to the Pt surface orientation, the collective interaction of the water–adlayer with the Pt surface and bulk electrolyte is drastically influenced by the Pt surface orientation. For instance, Pt(100) promotes adlayer self-organization, leading to the absence of H-bond donation from the adlayer to the bulk of the electrolyte, thus forming a hydrophobic interface. In contrast, Pt(111) surface creates vacancies into the H-bond network of the adlayer, resulting in a reduced contact angle of this layer with the bulk of the electrolyte (Fig. 9a).⁷³

Moreover, the dynamics observed for the defect reorganization in the adlayer is much slower than in the bulk electrolyte (∼1 ns vs. ∼5 ps), which is very likely to impact electrocatalytic reactions. Indeed, it can result in a larger concentration of hydronium ions in the first adlayer and can also hinder the diffusion of adsorbed species on the Pt surface, thus explaining that the Tafel step is the rds for the HER on Pt in acidic media.⁷³ Furthermore, conducting similar simulations, the same group also revealed that the transfer of a water molecule from the bulk of the electrolyte to the adlayer requires a reorganization of the adlayer. Hence, this reorganization results in slow dynamics for the exchange of water molecules from the bulk to the interface, with a lifetime of ∼40 ns for water molecules in the adlayer.⁷⁴ While these solvent reorganization phenomena happen at timescales (ps/ns) faster than the HER in alkaline media, it was recently observed that even if the “pure electron transfer” timescale for the HER (under acidic conditions) is less than 3 ps, it requires a pre-organized solvent–electrolyte interfacial structure to occur,²⁴ which advocates that faster solvent reorganization kinetics would increase the HER rate. Altogether, these results highlight the importance of considering entropic effects when transition-state energies are calculated for electrochemical processes.

Fig. 9 (a) Snapshots from MD simulation showing water structure at Pt(100) and Pt(111) interfaces (reproduced from ref. 73 with permission from the National Academy of Sciences, Copyright (2013)) and (b) hydrogen-bond lifetime at the Pt(111) surface (blue) compared to bulk water (red) obtained by ab initio MD simulations (reproduced from ref. 75 with permission from the National Academy of Sciences, Copyright (2017)).

Computational chemistry also proves useful to investigate ion-separation dynamics at the interface and more specifically the kinetics of the Grotthuss OH⁻/H₃O⁺ shuttling mechanism. Using ab initio calculations for water–ions, while regular MD was used for cation–anion (Na⁺/I⁻) interactions, and considering the Madelung potential as the water collective contribution to the electric potential, Kattirtzi et al. showed that these two families of ions do not respond similarly at the electrode/electrolyte interface.⁷⁵ Indeed, the activation energy for ion recombination at the interface is larger in the case of water–ions than for classical Na⁺/I⁻ ions and the charge separation rate for classical ions is slower by more than one order of magnitude at the interface compared to the bulk, while water–ion separation remains equally fast. Interestingly, the activation energy for both systems is found to be about 1.5 k_BT greater at the interface than in the bulk of the electrolyte. Nevertheless, in the case of water–ions, the flux of reactants is increased thanks to a larger lifetime for hydrogen bonds (Fig. 9b), which results in a neutral effect on the water–ion recombination kinetics.⁷⁵ We believe that such a fine understanding of the water structure at the electrode–electrolyte interface would help to rationalize experimental observations from a molecular point of view. For instance, following the evolution of the hydrogen bond structure and dynamics upon polarization may provide a better understanding of the pzfc theory previously discussed. Moreover, these calculations so far limited to Pt and other model electrodes could be extended to other materials to provide new descriptors (H-bond lifetime at the catalyst surface, Grotthuss kinetics at the interface, etc.) for the HER.

Outlook: water in a constrained environment, a new tool to study the HER?

Realizing the importance of water structuration at the electrochemical interface in the electrocatalytic activity of metals, new strategies based on constraining the H₂O molecule environment can be envisioned to tune and understand the HER kinetics independently of the nature of the electrocatalyst. This could be done by the use of physical confinement, alike for studies beyond the scope of electrocatalysis which recently pointed out that water molecules can adopt unusual properties at a material–electrolyte interface, resulting from a drastic change in their environment. For instance, it was recently proposed that water molecules constrained in nanoslits in the presence of Li⁺ cations have a negative dielectric constant.^76,77 Furthermore, it was proposed that under confinement, the activation energy for water self-dissociation could be decreased.⁴⁵ Both observations confirm that studying how the water environment relates to its physical properties could be a critical point to understand how water interfacial structure governs its reactivity. Another strategy to constraint the environment of H₂O molecules is to use non-reactive chemical matrices such as organic solvents or ionic liquids (ILs). Such a chemical strategy was not widely explored and only a few studies focused on the HER activity and the effect of the water structure in aprotic media such as ILs or organic electrolytes. However, doing so, different proton donors can be used and the concentrations of ions and water were modulated to constraint the water–electrolyte interactions.

Among the few studies carried out on ILs, most of them were focusing on the impact of moisture contamination on the cathodic stability of these ILs,^78–80 with the aim to generate H₂ through H₂O reduction with low-cost catalysts^81,82 or to construct a hydrogen-based reference electrode for ILs.⁸³ Interestingly, following this strategy it was found that electrochemical interfaces are enriched in water upon polarization, following the hydrophilicity of the ions in solution (more water molecules at the positive electrode as IL anions are more hydrophilic).⁷⁹ Furthermore, alike for aqueous electrolytes, the redox couple H⁺/H₂ was found to be reversible on a Pt electrode in TFSI-based ILs.⁸³ However, under these conditions, the Volmer step was identified as the rds which differs from the step usually found to be rate determining in acidic aqueous electrolytes.⁸³ Similarly, using H₂O as a proton donor, the activity of non-precious low carbon steel electrodes was found to outweigh that of Pt in BF₄-based ILs.⁸² Altogether, these observations confirm the strong dependence of the proton donor structure on the HER mechanism and activity and certainly open further experimental explorations.

In contrast with ILs, a deeper understanding on the HER mechanism was developed in organic electrolytes. Interestingly, when using a strong acid such as HClO₄ in acetonitrile, the proton reduction occurs at less negative potentials than water reduction on Au and Pt as well as remains independent of the water content,^84,85 unlike for the HOR on Pt which is impacted by the water concentration.^85,86 Rather, when water is used as the source of protons in an organic electrolyte, its reduction can be observed at more negative potentials (<−0.8 V vs. SHE on Pt(pc)) and strongly depends on the nature of the cation employed: the stronger the cation–H₂O interactions (Li⁺ > Na⁺ for instance), the less negative the onset potential for water reduction is.^84,85,87 It is no surprise that in the presence of large hydrophobic cations such as organic-ammonium, the water reduction can be nearly suppressed.^84,87 Furthermore, in these organic–H₂O electrolytes, the reduction of water follows on the different facets of Pt the same trend as in aqueous alkaline solutions, suggesting that the HER kinetics is controlled by the cleavage of the O–H in the Volmer step.⁸⁷ Moreover, measuring the ¹H NMR spectra of H₂O in these electrolytes helped reveal the role of alkali cations in the proton acidification following the strength of the cation–water interaction, Li⁺ being the strongest.⁸⁴ As previously discussed, in situ techniques such as sum frequency generation⁸⁸ (SFG), Raman spectroscopy,^89,90 FTIR spectroscopy,^85,86 or surface X-ray diffraction⁹¹ (XRD) are currently employed to appreciate how these constraints on the water structure in the bulk of the electrolyte translate to the electrochemical interface. While all these techniques converge to the fact that polarizing the electrode negatively results in an enrichment of water at the interface, some discrepancies about the role of the cation,^85,88 or water orientation^88,91 remain.

Finally, working in organic electrolytes has enabled researchers not only to tune the nature and the amount of cation–water and water–water interactions, but also helped unravel the impact of the nature of the proton donor on the proton reduction (Fig. 10, left). Indeed, comparing two different proton donors possessing similar pK_a values but different geometries, Jackson et al. demonstrated that the use of a bulkier proton donor slows down the HER in acetonitrile, while in an aqueous environment no such steric effect was observed for the HER, highlighting the critical role of water in the overall proton transfer,⁹² as later on rationalized by theoretical calculations.⁹³ Similarly, adding crown-ethers known for their ability to chelate alkali cations to organic electrolytes has been shown to allow fine tuning of water–cation interactions and thus the water reactivity in organic electrolytes (Fig. 10, right).⁸⁴ Interestingly, other electrocatalytic reactions such as the OER are already taking benefit of this approach to isolate reaction-intermediates that could not be observed in aqueous electrolytes due to their short lifetime.^94,95 We thus believe that characterizing water-involving electrochemical reactions out-of-water could bring a wider comprehension on how water reacts. For instance, the role of the Grotthuss mechanism in the HER could be tested by comparing the reactivity of “single” water molecules isolated by working at low H₂O content with molecules undergoing water–water interactions simply by increasing the H₂O concentration in organic electrolytes (Fig. 10, bottom). Similarly, the influence of the proton donor structure (hydronium vs. water, or buffered electrolyte)^33,42,49 could be studied (Fig. 10, top).

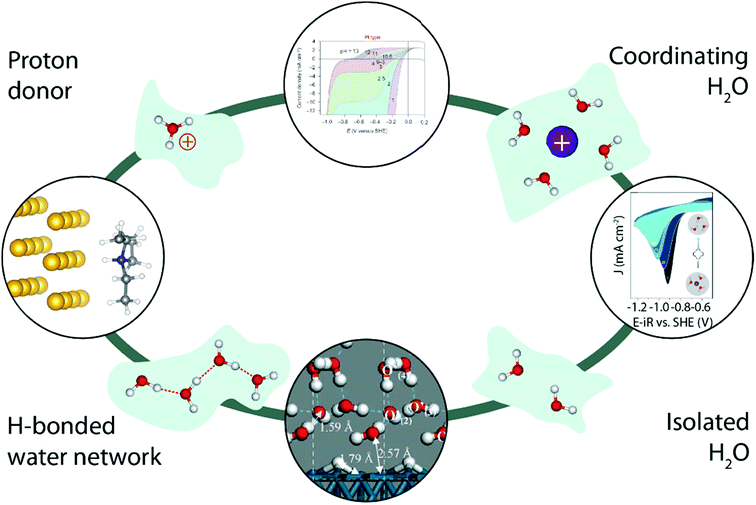Fig. 10 Illustration of how water structure could be constrained by using an inert matrix (light green), and how the study of the water reactivity in all these cases could bring a fundamental understanding of several parameters in the HER kinetics. The top image is reproduced from ref. 42 with permission from Springer Nature, Copyright (2013). The image on the right is reproduced from ref. 84 with permission from the American Chemical Society, Copyright (2018). The bottom image is reproduced from ref. 63 with permission from John Wiley and Sons, Copyright (2006). The image on the left is reproduced from ref. 92 with permission from the American Chemical Society, Copyright (2016).

Conclusion

Driven by the so-far ill understood observation that the HER is slower under alkaline conditions than under acidic conditions on the surface of Pt, numerous studies were recently dedicated to reveal the physical origin of such an effect. Historically, the role of hydrogen binding energy on the surface of a given catalyst was proposed as a descriptor for the HER, and led to the discovery of new promising materials such as transition metal phosphides or sulfides. However, experimentally assessing the reaction enthalpy and entropy formation for H_UPD on Pt, let alone for the initial proton discharge Volmer step, remains challenging.⁵ Furthermore, it was recently realized that the HBE theory may not be sufficient to explain the pH-dependence of the HER and the slow kinetics measured in alkaline aqueous electrolytes. Thus, since the introduction of a new “bifunctional” mechanism in which non-covalent interactions play a critical role in the HER kinetics, novel studies focusing on the effect of non-covalent interactions, adsorbed species, etc. on model electrodes were carried out. These studies as well as the emergence of high-resolution operando spectroscopies or laser-based techniques combined with theoretical/computational studies made possible an in-depth understanding of the water structure at the electrode–electrolyte interface, and demonstrated the influence of the double-layer structure and rigidity on surface adsorption properties. However, a direct correlation with water reactivity is yet to be reached.

In addition to these operando and theoretical studies, simple chemical strategies can be designed to gain deeper understandings at the molecular level.⁹⁶ For that, decoupling all the different interactions at the interface (water–catalyst, water–water, ion–water, ion–catalyst) is critical. While challenging in aqueous solutions, the difficulty of decoupling these interactions can be alleviated by studying the HER under “non-usual” conditions such as in aprotic solvents or confined structures. This new comprehension could help understand the dynamic role of the water structure in the HER and pave the way towards the design of more efficient and stable HER catalysts. Moreover, not only this understanding is critical for the design of better water electrolyzers but, in light of recent studies on aqueous superconcentrated electrolytes for batteries^{10–12,97,98} or the role of water and proton impurities on the growth of solid–electrolyte interphases (SEI),^13,99 this knowledge will certainly benefit the field of energy storage and conversion devices as a whole. Finally, achieving an in depth understanding of water structure and interfacial interactions is critical for other electrochemical reactions such as the OER,¹⁰⁰ ORR,⁹ and CO₂ (ref. 7) and N₂ (ref. 8) reduction. In conclusion, the field is only at its infancy regarding the control at a molecular level of the water structure at the electrochemical interfaces, and no doubt that major achievements/understandings will be accomplished toward that goal in the near future.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The authors would like to thank Claudio Cometto for helpful discussions and comments. N. D. acknowledges the Ecole normale supérieure for his Ph.D. scholarship. The authors thank the French National Research Agency for its support through the Labex STORE-EX project (ANR-10LABX-76-01).

References

1. IRENA, Hydrogen from Renewable Power: Technology Outlook for the Energy Transition, International Renewable Energy Agency, Abu Dhabi, 2018.
2. A. Kumar, K. R. Phillips, G. P. Thiel, U. Schröder and J. H. Lienhard, Direct Electrosynthesis of Sodium Hydroxide and Hydrochloric Acid from Brine Streams, Nat. Catal., 2019, 2(2), 106–113,  DOI:10.1038/s41929-018-0218-y.
3. A. Paets van Troostwijk and J. R. Deiman, Sur Une Manière de Décomposer l'Eau En Air Inflammable et En Air Vital, Obs. Phys., 1789, 369–384.
4. E. Gileadi, Physical Electrochemistry, Wiley-VCH Verlag GmbH & Co. KGaA, 2011.
5. Y. Zheng, Y. Jiao, A. Vasileff and S.-Z. Qiao, The Hydrogen Evolution Reaction in Alkaline Solution: From Theory, Single Crystal Models, to Practical Electrocatalysts, Angew. Chem., Int. Ed., 2018, 57(26), 7568–7579,  DOI:10.1002/anie.201710556.
6. C. Hu, L. Zhang and J. Gong, Recent Progress Made in the Mechanism Comprehension and Design of Electrocatalysts for Alkaline Water Splitting, Energy Environ. Sci., 2019, 12(9), 2600–2645,  10.1039/c9ee01202h.
7. J. Resasco, L. D. Chen, E. Clark, C. Tsai, C. Hahn, T. F. Jaramillo, K. Chan and A. T. Bell, Promoter Effects of Alkali Metal Cations on the Electrochemical Reduction of Carbon Dioxide, J. Am. Chem. Soc., 2017, 139(32), 11277–11287,  DOI:10.1021/jacs.7b06765.
8. S. Z. Andersen, V. Čolić, S. Yang, J. A. Schwalbe, A. C. Nielander, J. M. McEnaney, K. Enemark-Rasmussen, J. G. Baker, A. R. Singh and B. A. Rohr, et al., A Rigorous Electrochemical Ammonia Synthesis Protocol with Quantitative Isotope Measurements, Nature, 2019, 570(7762), 504–508,  DOI:10.1038/s41586-019-1260-x.
9. T. Kumeda, H. Tajiri, O. Sakata, N. Hoshi and M. Nakamura, Effect of Hydrophobic Cations on the Oxygen Reduction Reaction on Single-crystal Platinum Electrodes, Nat. Commun., 2018, 9(1), 4378,  DOI:10.1038/s41467-018-06917-4.
10. L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, “Water-in-Salt” Electrolyte Enables High-Voltage Aqueous Lithium-Ion Chemistries, Science, 2015, 350(6263), 938–943,  DOI:10.1126/science.aab1595.
11. Y. Yamada, K. Usui, K. Sodeyama, S. Ko, Y. Tateyama and A. Yamada, Hydrate-Melt Electrolytes for High-Energy-Density Aqueous Batteries, Nat. Energy, 2016, 1(10), 16129,  DOI:10.1038/nenergy.2016.129.
12. N. Dubouis, P. Lemaire, B. Mirvaux, E. Salager, M. Deschamps and A. Grimaud, The Role of the Hydrogen Evolution Reaction in the Solid–Electrolyte Interphase Formation Mechanism for “Water-in-Salt” Electrolytes, Energy Environ. Sci., 2018, 11(12), 3491–3499,  10.1039/C8EE02456A.
13. D. Strmcnik, I. E. Castelli, J. G. Connell, D. Haering, M. Zorko, P. Martins, P. P. Lopes, B. Genorio, T. Østergaard and H. A. Gasteiger, et al., Electrocatalytic Transformation of HF Impurity to H₂ and LiF in Lithium-Ion Batteries, Nat. Catal., 2018, 1(4), 255–262,  DOI:10.1038/s41929-018-0047-z.
14. T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Insight on Tafel Slopes from a Microkinetic Analysis of Aqueous Electrocatalysis for Energy Conversion, Sci. Rep., 2015, 5, 13801,  DOI:10.1038/srep13801.
15. M. J. T. C. van der Niet, N. Garcia-Araez, J. Hernández, J. M. Feliu and M. T. M. Koper, Water Dissociation on Well-Defined Platinum Surfaces: The Electrochemical Perspective, Catal. Today, 2013, 202, 105–113,  DOI:10.1016/j.cattod.2012.04.059.
16. I. T. McCrum and M. J. Janik, pH and Alkali Cation Effects on the Pt Cyclic Voltammogram Explained Using Density Functional Theory, J. Phys. Chem. C, 2016, 120(1), 457–471,  DOI:10.1021/acs.jpcc.5b10979.
17. X. Chen, I. T. McCrum, K. A. Schwarz, M. J. Janik and M. T. M. Koper, Co-Adsorption of Cations as the Cause of the Apparent pH Dependence of Hydrogen Adsorption on a Stepped Platinum Single-Crystal Electrode, Angew. Chem., Int. Ed., 2017, 56(47), 15025–15029,  DOI:10.1002/anie.201709455.
18. F. G. Will, Hydrogen Adsorption on Platinum Single Crystal Electrodes I. Isotherms and Heats of Adsorption, J. Electrochem. Soc., 1965, 112(4), 451–455,  DOI:10.1149/1.2423567.
19. J. Clavilier, R. Faure, G. Guinet and R. Durand, Preparation of Monocrystalline Pt Microelectrodes and Electrochemical Study of the Plane Surfaces Cut in the Direction of the (111) and (110) Planes, J. Electroanal. Chem. Interfacial Electrochem., 1980, 107(1), 205–209,  DOI:10.1016/S0022-0728(79)80022-4.
20. A. Zolfaghari, M. Chayer and G. Jerkiewicz, Energetics of the Underpotential Deposition of Hydrogen on Platinum Electrodes I. Absence of Coadsorbed Species, J. Electrochem. Soc., 1997, 144(9), 3034–3041,  DOI:10.1149/1.1837955.
21. N. M. Marković, B. N. Grgur and P. N. Ross, Temperature-Dependent Hydrogen Electrochemistry on Platinum Low-Index Single-Crystal Surfaces in Acid Solutions, J. Phys. Chem. B, 1997, 101(27), 5405–5413,  DOI:10.1021/jp970930d.
22. J. Durst, C. Simon, F. Hasché and H. A. Gasteiger, Hydrogen Oxidation and Evolution Reaction Kinetics on Carbon Supported Pt, Ir, Rh, and Pd Electrocatalysts in Acidic Media, J. Electrochem. Soc., 2015, 162(1), F190–F203,  DOI:10.1149/2.0981501jes.
23. Y. Ishikawa, J. J. Mateo, D. A. Tryk and C. R. Cabrera, Direct Molecular Dynamics and Density-Functional Theoretical Study of the Electrochemical Hydrogen Oxidation Reaction and Underpotential Deposition of H on Pt(111), J. Electroanal. Chem., 2007, 607(1), 37–46,  DOI:10.1016/j.jelechem.2006.10.011.
24. G. Zwaschka, Y. Tong, M. Wolf and R. K. Campen, Probing the Hydrogen Evolution Reaction and Charge Transfer on Platinum Electrodes on Femtosecond Timescales, ChemElectroChem, 2019, 6(10), 2675–2682,  DOI:10.1002/celc.201900336.
25. B. E. Conway and J. O. Bockris, Electrolytic Hydrogen Evolution Kinetics and Its Relation to the Electronic and Adsorptive Properties of the Metal, J. Chem. Phys., 1957, 26(3), 532–541,  DOI:10.1063/1.1743339.
26. S. Trasatti, Work Function, Electronegativity, and Electrochemical Behaviour of Metals, J. Electroanal. Chem. Interfacial Electrochem., 1972, 39(1), 163–184,  DOI:10.1016/S0022-0728(72)80485-6.
27. J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, Trends in the Exchange Current for Hydrogen Evolution, J. Electrochem. Soc., 2005, 152(3), J23,  DOI:10.1149/1.1856988.
28. A. R. Zeradjanin, A. Vimalanandan, G. Polymeros, A. A. Topalov, K. J. J. Mayrhofer and M. Rohwerder, Balanced Work Function as a Driver for Facile Hydrogen Evolution Reaction – Comprehension and Experimental Assessment of Interfacial Catalytic Descriptor, Phys. Chem. Chem. Phys., 2017, 19(26), 17019–17027,  10.1039/C7CP03081A.
29. B. Hinnemann, P. G. Moses, J. Bonde, K. P. Jørgensen, J. H. Nielsen, S. Horch, I. Chorkendorff and J. K. Nørskov, Biomimetic Hydrogen Evolution:  MoS₂ Nanoparticles as Catalyst for Hydrogen Evolution, J. Am. Chem. Soc., 2005, 127(15), 5308–5309,  DOI:10.1021/ja0504690.
30. T. F. Jaramillo, K. P. Jørgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Identification of Active Edge Sites for Electrochemical H₂ Evolution from MoS₂ Nanocatalysts, Science, 2007, 317(5834), 100–102,  DOI:10.1126/science.1141483.
31. D. Voiry, H. Yamaguchi, J. Li, R. Silva, D. C. B. Alves, T. Fujita, M. Chen, T. Asefa, V. B. Shenoy and G. Eda, et al., Enhanced Catalytic Activity in Strained Chemically Exfoliated WS2 Nanosheets for Hydrogen Evolution, Nat. Mater., 2013, 12(9), 850–855,  DOI:10.1038/nmat3700.
32. W. Sheng, H. A. Gasteiger and Y. Shao-Horn, Hydrogen Oxidation and Evolution Reaction Kinetics on Platinum: Acid vs Alkaline Electrolytes, J. Electrochem. Soc., 2010, 157(11), B1529,  DOI:10.1149/1.3483106.
33. R. Subbaraman, D. Tripkovic, D. Strmcnik, K.-C. Chang, M. Uchimura, A. P. Paulikas, V. Stamenkovic and N. M. Markovic, Enhancing Hydrogen Evolution Activity in Water Splitting by Tailoring Li⁺–Ni(OH)₂–Pt Interfaces, Science, 2011, 334(6060), 1256–1260,  DOI:10.1126/science.1211934.
34. W. Sheng, M. Myint, J. G. Chen and Y. Yan, Correlating the Hydrogen Evolution Reaction Activity in Alkaline Electrolytes with the Hydrogen Binding Energy on Monometallic Surfaces, Energy Environ. Sci., 2013, 6(5), 1509–1512,  10.1039/C3EE00045A.
35. W. Sheng, Z. Zhuang, M. Gao, J. Zheng, J. G. Chen and Y. Yan, Correlating Hydrogen Oxidation and Evolution Activity on Platinum at Different PH with Measured Hydrogen Binding Energy, Nat. Commun., 2015, 6, 5848,  DOI:10.1038/ncomms6848.
36. J. Zheng, W. Sheng, Z. Zhuang, B. Xu and Y. Yan, Universal Dependence of Hydrogen Oxidation and Evolution Reaction Activity of Platinum-Group Metals on PH and Hydrogen Binding Energy, Sci. Adv., 2016, 2(3), e1501602,  DOI:10.1126/sciadv.1501602.
37. M. J. Janik, I. T. McCrum and M. T. M. Koper, On the Presence of Surface Bound Hydroxyl Species on Polycrystalline Pt Electrodes in the “Hydrogen Potential Region” (0–0.4 V-RHE), J. Catal., 2018, 367, 332–337,  DOI:10.1016/j.jcat.2018.09.031.
38. N. Dubouis, C. Yang, R. Beer, L. Ries, D. Voiry and A. Grimaud, Interfacial Interactions as an Electrochemical Tool To Understand Mo-Based Catalysts for the Hydrogen Evolution Reaction, ACS Catal., 2018, 8(2), 828–836,  DOI:10.1021/acscatal.7b03684.
39. M. N. Jackson, O. Jung, H. C. Lamotte and Y. Surendranath, Donor-Dependent Promotion of Interfacial Proton-Coupled Electron Transfer in Aqueous Electrocatalysis, ACS Catal., 2019, 3737–3743,  DOI:10.1021/acscatal.9b00056.
40. R. Subbaraman, D. Tripkovic, K.-C. Chang, D. Strmcnik, A. P. Paulikas, P. Hirunsit, M. Chan, J. Greeley, V. Stamenkovic and N. M. Markovic, Trends in Activity for the Water Electrolyser Reactions on 3d M(Ni,Co,Fe,Mn) Hydr(Oxy)Oxide Catalysts, Nat. Mater., 2012, 11(6), 550–557,  DOI:10.1038/nmat3313.
41. P. F. B. D. Martins, P. P. Lopes, E. A. Ticianelli, V. R. Stamenkovic, N. M. Markovic and D. Strmcnik, Hydrogen Evolution Reaction on Copper: Promoting Water Dissociation by Tuning the Surface Oxophilicity, Electrochem. Commun., 2019, 100, 30–33,  DOI:10.1016/j.elecom.2019.01.006.
42. D. Strmcnik, M. Uchimura, C. Wang, R. Subbaraman, N. Danilovic, D. van der Vliet, A. P. Paulikas, V. R. Stamenkovic and N. M. Markovic, Improving the Hydrogen Oxidation Reaction Rate by Promotion of Hydroxyl Adsorption, Nat. Chem., 2013, 5(4), 300–306,  DOI:10.1038/nchem.1574.
43. V. Grozovski, S. Vesztergom, G. G. Láng and P. Broekmann, Electrochemical Hydrogen Evolution: H+ or H₂O Reduction? A Rotating Disk Electrode Study, J. Electrochem. Soc., 2017, 164(11), E3171–E3178,  DOI:10.1149/2.0191711jes.
44. B. You, Y. Zhang, Y. Jiao, kenneth Davey and S. Qiao, Negative Charging of Transition-Metal Phosphides via Strong Electronic Coupling for Destabilization of Alkaline Water, Angew. Chem., Int. Ed., 2019, 58(34), 11796–11800,  DOI:10.1002/anie.201906683.
45. D. Muñoz-Santiburcio and D. Marx, Nanoconfinement in Slit Pores Enhances Water Self-Dissociation, Phys. Rev. Lett., 2017, 119(5), 056002,  DOI:10.1103/PhysRevLett.119.056002.
46. P. S. Lamoureux, A. R. Singh and K. Chan, pH Effects on Hydrogen Evolution and Oxidation over Pt(111): Insights from First-Principles, ACS Catal., 2019, 6194–6201,  DOI:10.1021/acscatal.9b00268.
47. S. Lu and Z. Zhuang, Investigating the Influences of the Adsorbed Species on Catalytic Activity for Hydrogen Oxidation Reaction in Alkaline Electrolyte, J. Am. Chem. Soc., 2017, 139(14), 5156–5163,  DOI:10.1021/jacs.7b00765.
48. S. Intikhab, J. D. Snyder and M. H. Tang, Adsorbed Hydroxide Does Not Participate in the Volmer Step of Alkaline Hydrogen Electrocatalysis, ACS Catal., 2017, 7(12), 8314–8319,  DOI:10.1021/acscatal.7b02787.
49. M. Auinger, I. Katsounaros, J. C. Meier, S. O. Klemm, P. U. Biedermann, A. A. Topalov, M. Rohwerder and K. J. J. Mayrhofer, Near-Surface Ion Distribution and Buffer Effects during Electrochemical Reactions, Phys. Chem. Chem. Phys., 2011, 13(36), 16384,  10.1039/c1cp21717h.
50. D. Strmcnik, K. Kodama, D. van der Vliet, J. Greeley, V. R. Stamenkovic and N. M. Marković, The Role of Non-Covalent Interactions in Electrocatalytic Fuel-Cell Reactions on Platinum, Nat. Chem., 2009, 1(6), 466–472,  DOI:10.1038/nchem.330.
51. I. T. McCrum, X. Chen, K. A. Schwarz, M. J. Janik and M. T. M. Koper, Effect of Step Density and Orientation on the Apparent pH Dependence of Hydrogen and Hydroxide Adsorption on Stepped Platinum Surfaces, J. Phys. Chem. C, 2018, 122(29), 16756–16764,  DOI:10.1021/acs.jpcc.8b03660.
52. E. Liu, J. Li, L. Jiao, H. T. T. Doan, Z. Liu, Z. Zhao, Y. Huang, K. M. Abraham, S. Mukerjee and Q. Jia, Unifying the Hydrogen Evolution and Oxidation Reactions Kinetics in Base by Identifying the Catalytic Roles of Hydroxyl-Water-Cation Adducts, J. Am. Chem. Soc., 2019, 141(7), 3232–3239,  DOI:10.1021/jacs.8b13228.
53. D. J. Weber, M. Janssen and M. Oezaslan, Effect of Monovalent Cations on the HOR/HER Activity for Pt in Alkaline Environment, J. Electrochem. Soc., 2019, 166(2), F66–F73,  DOI:10.1149/2.0301902jes.
54. E. Santos, A. Lundin, K. Pötting, P. Quaino and W. Schmickler, Model for the Electrocatalysis of Hydrogen Evolution, Phys. Rev. B, 2009, 79(23), 235436,  DOI:10.1103/PhysRevB.79.235436.
55. N. Garcia-Araez, V. Climent and J. Feliu, Potential-Dependent Water Orientation on Pt(111), Pt(100), and Pt(110), As Inferred from Laser-Pulsed Experiments. Electrostatic and Chemical Effects, J. Phys. Chem. C, 2009, 113(21), 9290–9304,  DOI:10.1021/jp900792q.
56. J.-J. Velasco-Velez, C. H. Wu, T. A. Pascal, L. F. Wan, J. Guo, D. Prendergast and M. Salmeron, The Structure of Interfacial Water on Gold Electrodes Studied by X-Ray Absorption Spectroscopy, Science, 2014, 346(6211), 831–834,  DOI:10.1126/science.1259437.
57. I. Ledezma-Yanez, W. D. Z. Wallace, P. Sebastián-Pascual, V. Climent, J. M. Feliu and M. T. M. Koper, Interfacial Water Reorganization as a PH-Dependent Descriptor of the Hydrogen Evolution Rate on Platinum Electrodes, Nat. Energy, 2017, 2(4), 17031,  DOI:10.1038/nenergy.2017.31.
58. F. J. Sarabia, P. Sebastián-Pascual, M. T. M. Koper, V. Climent and J. M. Feliu, Effect of the Interfacial Water Structure on the Hydrogen Evolution Reaction on Pt(111) Modified with Different Nickel Hydroxide Coverages in Alkaline Media, ACS Appl. Mater. Interfaces, 2019, 11(1), 613–623,  DOI:10.1021/acsami.8b15003.
59. J. M. Feliu, F. J. Sarabia and V. Climent, Interfacial Study of Nickel Modified Pt(111) Surfaces in Phosphate Containing Solutions. Effect on the Hydrogen Evolution Reaction, ChemPhysChem, 2019 DOI:10.1002/cphc.201900543.
60. O. Pecina and W. Schmickler, A Model for Electrochemical Proton-Transfer Reactions, Chem. Phys., 1998, 228(1), 265–277,  DOI:10.1016/S0301-0104(97)00299-1.
61. S. Trasatti, Work Function, Electronegativity, and Electrochemical Behaviour of Metals, J. Electroanal. Chem. Interfacial Electrochem., 1971, 33(2), 351–378,  DOI:10.1016/S0022-0728(71)80123-7.
62. J. Rossmeisl, K. Chan, E. Skúlason, M. E. Björketun and V. Tripkovic, On the PH Dependence of Electrochemical Proton Transfer Barriers, Catal. Today, 2016, 262, 36–40,  DOI:10.1016/j.cattod.2015.08.016.
63. J.-S. Filhol and M. Neurock, Elucidation of the Electrochemical Activation of Water over Pd by First Principles, Angew. Chem., Int. Ed., 2006, 45(3), 402–406,  DOI:10.1002/anie.200502540.
64. L. D. Chen, M. Bajdich, J. M. P. Martirez, C. M. Krauter, J. A. Gauthier, E. A. Carter, A. C. Luntz, K. Chan and J. K. Nørskov, Understanding the Apparent Fractional Charge of Protons in the Aqueous Electrochemical Double Layer, Nat. Commun., 2018, 9(1), 3202,  DOI:10.1038/s41467-018-05511-y.
65. N. M. Markovic, Electrocatalysis: Interfacing Electrochemistry, Nat. Mater., 2013, 12(2), 101–102.
66. V. R. Stamenkovic, D. Strmcnik, P. P. Lopes and N. M. Markovic, Energy and Fuels from Electrochemical Interfaces, Nat. Mater., 2016, 16(1), 57–69,  DOI:10.1038/nmat4738.
67. M. Favaro, B. Jeong, P. N. Ross, J. Yano, Z. Hussain, Z. Liu and E. J. Crumlin, Unravelling the Electrochemical Double Layer by Direct Probing of the Solid/Liquid Interface, Nat. Commun., 2016, 7(1), 12695,  DOI:10.1038/ncomms12695.
68. M. F. Toney, J. N. Howard, J. Richer, G. L. Borges, J. G. Gordon, O. R. Melroy, D. G. Wiesler, D. Yee and L. B. Sorensen, Voltage-Dependent Ordering of Water Molecules at an Electrode–Electrolyte Interface, Nature, 1994, 368(6470), 444–446,  DOI:10.1038/368444a0.
69. C.-Y. Li, J.-B. Le, Y.-H. Wang, S. Chen, Z.-L. Yang, J.-F. Li, J. Cheng and Z.-Q. Tian, In Situ Probing Electrified Interfacial Water Structures at Atomically Flat Surfaces, Nat. Mater., 2019, 18(7), 697–701,  DOI:10.1038/s41563-019-0356-x.
70. C. H. Wu, T. A. Pascal, A. Baskin, H. Wang, H.-T. Fang, Y.-S. Liu, Y.-H. Lu, J. Guo, D. Prendergast and M. B. Salmeron, Molecular-Scale Structure of Electrode–Electrolyte Interfaces: The Case of Platinum in Aqueous Sulfuric Acid, J. Am. Chem. Soc., 2018, 140(47), 16237–16244,  DOI:10.1021/jacs.8b09743.
71. R. Mom, L. Frevel, J.-J. Velasco-Vélez, M. Plodinec, A. Knop-Gericke and R. Schlögl, The Oxidation of Platinum under Wet Conditions Observed by Electrochemical X-Ray Photoelectron Spectroscopy, J. Am. Chem. Soc., 2019, 141(16), 6537–6544,  DOI:10.1021/jacs.8b12284.
72. K. A. Stoerzinger, M. Favaro, P. N. Ross, J. Yano, Z. Liu, Z. Hussain and E. J. Crumlin, Probing the Surface of Platinum during the Hydrogen Evolution Reaction in Alkaline Electrolyte, J. Phys. Chem. B, 2018, 122(2), 864–870,  DOI:10.1021/acs.jpcb.7b06953.
73. D. T. Limmer, A. P. Willard, P. Madden and D. Chandler, Hydration of Metal Surfaces Can Be Dynamically Heterogeneous and Hydrophobic, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(11), 4200–4205,  DOI:10.1073/pnas.1301596110.
74. D. T. Limmer, A. P. Willard, P. A. Madden and D. Chandler, Water Exchange at a Hydrated Platinum Electrode is Rare and Collective, J. Phys. Chem. C, 2015, 119(42), 24016–24024,  DOI:10.1021/acs.jpcc.5b08137.
75. J. A. Kattirtzi, D. T. Limmer and A. P. Willard, Microscopic Dynamics of Charge Separation at the Aqueous Electrochemical Interface, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(51), 13374–13379,  DOI:10.1073/pnas.1700093114.
76. A. Sugahara, Y. Ando, S. Kajiyama, K. Yazawa, K. Gotoh, M. Otani, M. Okubo and A. Yamada, Negative Dielectric Constant of Water Confined in Nanosheets, Nat. Commun., 2019, 10(1), 850,  DOI:10.1038/s41467-019-08789-8.
77. K. Kim, Y. Ando, A. Sugahara, S. Ko, Y. Yamada, M. Otani, M. Okubo and A. Yamada, Dense Charge Accumulation in MXene with Hydrate Melt Electrolyte, Chem. Mater., 2019, 31(14), 5190–5196,  DOI:10.1021/acs.chemmater.9b01334.
78. A. M. O'Mahony, D. S. Silvester, L. Aldous, C. Hardacre and R. G. Compton, Effect of Water on the Electrochemical Window and Potential Limits of Room-Temperature Ionic Liquids, J. Chem. Eng. Data, 2008, 53(12), 2884–2891,  DOI:10.1021/je800678e.
79. G. Feng, X. Jiang, R. Qiao and A. A. Kornyshev, Water in Ionic Liquids at Electrified Interfaces: The Anatomy of Electrosorption, ACS Nano, 2014, 8(11), 11685–11694,  DOI:10.1021/nn505017c.
80. S. Bi, R. Wang, S. Liu, J. Yan, B. Mao, A. A. Kornyshev and G. Feng, Minimizing the Electrosorption of Water from Humid Ionic Liquids on Electrodes, Nat. Commun., 2018, 9(1), 5222,  DOI:10.1038/s41467-018-07674-0.
81. R. F. de Souza, J. C. Padilha, R. S. Gonçalves and J. Rault-Berthelot, Dialkylimidazolium Ionic Liquids as Electrolytes for Hydrogen Production from Water Electrolysis, Electrochem. Commun., 2006, 8(2), 211–216,  DOI:10.1016/j.elecom.2005.10.036.
82. R. F. de Souza, J. C. Padilha, R. S. Gonçalves, M. O. de Souza and J. Rault-Berthelot, Electrochemical Hydrogen Production from Water Electrolysis Using Ionic Liquid as Electrolytes: Towards the Best Device, J. Power Sources, 2007, 164(2), 792–798,  DOI:10.1016/j.jpowsour.2006.11.049.
83. Y. Meng, L. Aldous, S. R. Belding and R. G. Compton, The Hydrogen Evolution Reaction in a Room Temperature Ionic Liquid: Mechanism and Electrocatalyst Trends, Phys. Chem. Chem. Phys., 2012, 14(15), 5222–5228,  10.1039/C2CP23801B.
84. N. Dubouis, A. Serva, E. Salager, M. Deschamps, M. Salanne and A. Grimaud, The Fate of Water at the Electrochemical Interfaces: Electrochemical Behavior of Free Water Versus Coordinating Water, J. Phys. Chem. Lett., 2018, 9(23), 6683–6688,  DOI:10.1021/acs.jpclett.8b03066.
85. I. Ledezma-Yanez, O. Díaz-Morales, M. C. Figueiredo and M. T. M. Koper, Hydrogen Oxidation and Hydrogen Evolution on a Platinum Electrode in Acetonitrile, ChemElectroChem, 2015, 2(10), 1612–1622,  DOI:10.1002/celc.201500341.
86. I. Ledezma-Yanez and M. T. M. Koper, Influence of Water on the Hydrogen Evolution Reaction on a Gold Electrode in Acetonitrile Solution, J. Electroanal. Chem., 2017, 793, 18–24,  DOI:10.1016/j.jelechem.2016.08.018.
87. M. F. Suárez-Herrera, M. Costa-Figueiredo and J. M. Feliu, Voltammetry of Basal Plane Platinum Electrodes in Acetonitrile Electrolytes: Effect of the Presence of Water, Langmuir, 2012, 28(11), 5286–5294,  DOI:10.1021/la205097p.
88. S. Baldelli, G. Mailhot, P. N. Ross and G. A. Somorjai, Potential-Dependent Vibrational Spectroscopy of Solvent Molecules at the Pt(111) Electrode in a Water/Acetonitrile Mixture Studied by Sum Frequency Generation, J. Am. Chem. Soc., 2001, 123(31), 7697–7702,  DOI:10.1021/ja016063e.
89. P. Cao and Y. Sun, On the Occurrence of Competitive Adsorption at the Platinum–Acetonitrile Interface by Using Surface-Enhanced Raman Spectroscopy, J. Phys. Chem. B, 2003, 107(24), 5818–5824,  DOI:10.1021/jp027834j.
90. P. Cao, Y. Sun and R. Gu, Investigations of Chemisorption and Reaction at Non-Aqueous Electrochemical Interfaces By in Situ Surface-Enhanced Raman Spectroscopy, J. Raman Spectrosc., 2005, 36(6–7), 725–735,  DOI:10.1002/jrs.1341.
91. G. S. Harlow, I. M. Aldous, P. Thompson, Y. Gründer, L. J. Hardwick and C. A. Lucas, Adsorption, Surface Relaxation and Electrolyte Structure at Pt(111) Electrodes in Non-Aqueous and Aqueous Acetonitrile Electrolytes, Phys. Chem. Chem. Phys., 2019, 21(17), 8654–8662,  10.1039/C9CP00499H.
92. M. N. Jackson and Y. Surendranath, Donor-Dependent Kinetics of Interfacial Proton-Coupled Electron Transfer, J. Am. Chem. Soc., 2016, 138(9), 3228–3234,  DOI:10.1021/jacs.6b00167.
93. Z. K. Goldsmith, Y. C. Lam, A. V. Soudackov and S. Hammes-Schiffer, Proton Discharge on a Gold Electrode from Triethylammonium in Acetonitrile: Theoretical Modeling of Potential-Dependent Kinetic Isotope Effects, J. Am. Chem. Soc., 2018, 141(2), 1084–1090,  DOI:10.1021/jacs.8b11826.
94. B. M. Hunter, N. B. Thompson, A. M. Müller, G. R. Rossman, M. G. Hill, J. R. Winkler and H. B. Gray, Trapping an Iron(VI) Water-Splitting Intermediate in Nonaqueous Media, Joule, 2018, 2(4), 747–763,  DOI:10.1016/j.joule.2018.01.008.
95. P. E. Pearce, C. Yang, A. Iadecola, J. Rodriguez-Carvajal, G. Rousse, R. Dedryvère, A. M. Abakumov, D. Giaume, M. Deschamps and J.-M. Tarascon, et al., Revealing the Reactivity of the Iridium Trioxide Intermediate for the Oxygen Evolution Reaction in Acidic Media, Chem. Mater., 2019, 31(15), 5845–5855,  DOI:10.1021/acs.chemmater.9b01976.
96. J. Ryu and Y. Surendranath, Tracking Electrical Fields at the Pt/H ₂ O Interface During Hydrogen Catalysis, J. Am. Chem. Soc., 2019 DOI:10.1021/jacs.9b05148.
97. W. Li, J. R. Dahn and D. S. Wainwright, Rechargeable Lithium Batteries with Aqueous Electrolytes, Science, 1994, 264(5162), 1115–1118,  DOI:10.1126/science.264.5162.1115.
98. M. McEldrew, Z. A. H. Goodwin, A. A. Kornyshev and M. Z. Bazant, Theory of the Double Layer in Water-in-Salt Electrolytes, J. Phys. Chem. Lett., 2018, 9(19), 5840–5846,  DOI:10.1021/acs.jpclett.8b02543.
99. I. E. Castelli, D. Strmcnik, M. Zorko, T. Østergaard, P. F. B. D. Martins, P. P. Lopes, B. K. Antonopoulos, F. Maglia, N. M. Markovic and J. Rossmeisl, The Role of Interface in Stabilizing Reaction Intermediates for Hydrogen Evolution in Aprotic Li-Ion Battery Electrolyte, Chem, 2019 DOI:10.26434/chemrxiv.8246771.v1.
100. C. Yang, O. Fontaine, J.-M. Tarascon and A. Grimaud, Chemical Recognition of Active Oxygen Species on the Surface of Oxygen Evolution Reaction Electrocatalysts, Angew. Chem., Int. Ed., 2017, 56(30), 8652–8656,  DOI:10.1002/anie.201701984.

---