Open Access Article
Open Access ArticleOn the unsuspected role of multivalent metal ions on the charge storage of a metal oxide electrode in mild aqueous electrolytes†
Yee-Seul
Kim
a,
Kenneth D.
Harris
bc,
Benoît
Limoges
 *a and
Véronique
Balland
*a and
Véronique
Balland
 *a
*a
aUniversité de Paris, Laboratoire d'Electrochimie Moléculaire, UMR 7591, CNRS, F-75013 Paris, France. E-mail: limoges@univ-paris-diderot.fr; veronique.balland@univ-paris-diderot.fr
bNRC Nanotechnology Research Centre, Edmonton, Alberta T6G 2M9, Canada
cDepartment of Mechanical Engineering, University of Alberta, Edmonton, Alberta T6G 2V4, Canada
First published on 10th August 2019
Abstract
Insertion mechanisms of multivalent ions in transition metal oxide cathodes are poorly understood and subject to controversy and debate, especially when performed in aqueous electrolytes. To address this issue, we have here investigated the reversible reduction of nanostructured amorphous TiO2 electrodes by spectroelectrochemistry in mild aqueous electrolytes containing either a multivalent metal salt as AlCl3 or a weak organic acid as acetic acid. Our results show that the reversible charge storage in TiO2 is thermodynamically and kinetically indistinguishable when carried out in either an Al3+- or acetic acid–based electrolyte, both leading under similar conditions of pH and concentrations to an almost identical maximal charge storage of ∼115 mA h g−1. These observations are in agreement with a mechanism where the inserting/deinserting cation is the proton and not the multivalent metal cation. Analysis of the data also demonstrates that the proton source is the Brønsted weak acid present in the aqueous electrolyte, i.e. either the acetic acid or the aquo metal ion complex generated from solvation of Al3+ (i.e. [Al(H2O)6]3+). Such a proton-coupled charge storage mechanism is also found to occur with other multivalent metal ions such as Zn2+ and Mn2+, albeit with a lower efficiency than Al3+, an effect we have attributed to the lower acidity of [Zn(H2O)6]2+ and [Mn(H2O)6]2+. These findings are of fundamental importance because they shed new light on previous studies assuming reversible Al3+-insertion into metal oxides, and, more generally, they highlight the unsuspected proton donor role played by multivalent metal cations commonly involved in rechargeable aqueous batteries.
1 Introduction
Intercalation batteries based on the pairing of a multivalent metallic conversion anode (Mg, Zn, Al, etc.) with a multivalent metal ion-insertion cathode (i.e., electrode materials able to accommodate the reversible insertion of Mg2+, Zn2+, Al3+, etc.) are an attractive alternative to rechargeable Li-ion batteries for grid-scale applications. These intercalation batteries have the potential for high-energy density (because of the multiple electrons involved at the anode), low cost (many multivalent metal ions are earth-abundant and relatively inexpensive to mine), and possibly long cycle life.1–4 Moreover, if operating in aqueous electrolytes, these intercalation batteries can offer additional advantages of sustainability, eco-compatibility, safety, and ease of fabrication at large scale.To date, a variety of aqueous batteries based on naturally-abundant multivalent metal ions (Zn2+, Mg2+, Al3+…) have been proposed (still in the experimental stage) and significant milestones have been achieved over the past few years.1,3–6 For instance, remarkably high energy densities (ranging from 150 to 200 W h kg−1) with excellent capacity retentions (>80% over a few thousands cycles) and rate capabilities have been obtained for a range of rechargeable aqueous zinc-ion batteries paired with different intercalation metal oxide cathodes in mild aqueous electrolyte conditions (from near neutral to slightly acidic pHs).7–13 In these studies, the soluble metal ion (Zn2+) present in the electrolyte has been shown to be responsible for the reversible faradaic processes at the host electrode material, as evidenced by well-defined reversible waves in cyclic voltammetry (CV) and plateaus in galvanostatic experiments. The exact mechanism of charge storage, however, remains obscure and a matter of debate. By analogy with Li-ion batteries, it is often claimed that the charge storage arises from reversible intercalation/insertion of the aqueous multivalent metal cation within the metal oxide cathode.1 However, despite numerous attempts to establish the presence of intercalated multivalent cations via structural characterization, none of the studies to date have unambiguously demonstrated the intercalation/insertion mechanism. Additionally, in contrast to the high-charge storage capacities persistently achieved in aqueous electrolytes for a range of metal oxides hosts (i.e., manganese oxides, vanadium oxides, titanium oxides, and tungsten oxides) with different soluble multivalent metal cations (Zn2+, Mg2+ and even Al3+), for unknown reasons, tiny capacities were systematically retrieved for the same systems in water-free organic electrolytes.7,14–20 These poor electrochemical performances in non-aqueous electrolytes support the assumption that multivalent cations cannot readily insert in metal oxides because of their excessively strong coulombic interactions with the oxide host lattices. Difficulties are also imposed as the oxidation state of the solid structure changes to redistribute the charge of the inserted multivalent cations; this process is presumed to result in a drastic local deformation in the host crystal structure concomitant with a sudden adjustment in the coordination environment and bond lengths.21,22
Among the multivalent ions, the Al3+ ion is a particularly intriguing case. The benefit of Al3+-based electrolytes on the charge storage capacity of many metal oxide cathodes has been unequivocally revealed.15,23–33 This was first reported in 2012 by Gao and colleagues23 for anatase TiO2 nanotubes in a 1 M AlCl3 aqueous electrolyte. The reversible CV peaks as well as the significant capacity (75 mA h g−1 at 4 mA cm−2) recovered from galvanostatic experiments were attributed to the reversible formation of the Al0.076TiO2 intercalation compound.23 Similar observations were also made by other groups (see Table 1).26–28 The capacity was thereafter significantly improved using composite electrode materials incorporating black anatase TiO2 nanoleaves or anatase TiO2 nanospheres, reaching maximal capacities > 200 mA h g−1 in 1 M Al(NO3)3 or 1 M AlCl3 aqueous electrolytes (attributed thus to the formation of Al>0.2TiO2).29,30,34 Furthermore, along with these high gravimetric capacities, high rate capability (141 mA h g−1 at 6C) with reasonably good cyclability (>300 cycles) were found.29 In order to demonstrate Al3+ insertion in the TiO2 structure, different structural analyses have been undertaken, however, the results were generally inconclusive: the XPS peak of Al3+ in the reduced phase of TiO2 is barely discernable,23,26,27 and no significant differences between the XRD spectra of the oxidized and reduced TiO2 were observed.23,29 Besides TiO2, the advantageous effect of Al3+-based aqueous electrolytes has also been reported with other metal oxide electrodes such as WO3 nanowire films,15,31 MnO2,32,33 conductive polymer-coated MoO3,24 and V2O5 xerogels,25 but again, insertion of Al3+ within the metal oxide matrix has yet to be conclusively established.
| Film morphology | TiO2 crystallinity | Electrolyte | pHa | E 0′ (V) | Maximal capacity (mA h g−1) | Charging rate (A g−1) | Charging cut-off potential (V) | Ref. |
|---|---|---|---|---|---|---|---|---|
| a nr = not reported. b Formal potential of the reversible insertion wave in CV. c Composite electrodes with acetylene black. d Composite electrodes with graphene. e Composite electrodes with carbon nanotubes. f Data recovered from galvanostatic experiments at GLAD-TiO2/Ti electrodes. | ||||||||
| Nanotubes | Anatase | 1 M AlCl3 | nr | −1.05 | 75 | 4 mA cm−2 | −1.2 | 23 |
| Nanotubes | Anatase | Up to 0.5 M AlCl3 or Al2(SO4)3 | 2.5 | −1.1 | 75 | 4 mA cm−2 | −1.15 | 26 |
| Nanoleavesc | Black anatase | 1 M Al(NO3)3 | nr | −1.05 | 278 | 0.05 | −1.4 | 29 |
| 141 | 2 | |||||||
| Nanospheresc | Anatase | 1 M AlCl3 | nr | −1.06 | 183 | 0.05 | −1.2 | 30 |
| Nanotubesd | Anatase | 1 M AlCl3 | 3 | −1.13 | 33 | 6.25 | −1.075 | 28 |
| 0.25 M AlCl3 | 3.8 | 50 | 6.25 | |||||
| Nanoparticlese | Anatase | 1 M AlCl3 | ≤3 | −1.07 | 225 | 0.05 | −1.2 | 34 |
| 135 | 2 | |||||||
| Nanocolumnsf | Amorphous | 0.25 AlCl3 | 3 | −0.75 | 115 | 1.6 | −1.12 | This work |
| 0.25 M KCl | 3 | 25 | 1.6 | −1.12 | This work | |||
| 0.25 M acetic acid + 0.3 M KCl | 3 | −0.75 | 118 | 1.6 | −1.12 | This work | ||
| 8 M acetic acid | 5 | −1.0 | 155 | 0.8 | −1.24 | This work | ||
One argument frequently used to support the insertion of Al3+ in metal oxide cathodes is the smaller ionic radius of Al3+ (54 pm) compared to Li+ (76 pm). This argument, however, does not take into account the strong desolvation energy associated with the highly positively charged Al3+ ion, especially in water.35 Also, it does not consider the particularly strong coulombic interactions between the highly charged Al3+ and the surrounding metal oxide lattice, an effect that is assumed to considerably impede solid-state diffusion. By computing the theoretical migration energy barriers of multivalent ions such as Al3+, Mg2+, Zn2+, Ca2+ in Mn2O4 or V2O5, Ceder and colleagues concluded that there is little hope of intercalating Al3+ in common metal oxide hosts at room temperature.36 An additional possibility is competitive proton intercalation, which can occur naturally in aqueous environments upon dissolution of aluminum salts at molar concentrations (pH < 3),27 or be easily triggered from side reactions (e.g., electrolysis of water) or deprotonation of Brønsted weak acids.37
All of this shows that many unanswered fundamental questions remain to be elucidated if one wants to better understand the role played by multivalent ions in the storage of charges in metal oxides, especially in aqueous electrolytes. The particularly striking case posed by Al3+ (i.e., can be inserted into a three-dimensional crystalline structure such as TiO2) has pushed us to carry out an in-depth study of this system in aqueous media. In this study, we seek to draw knowledge that can then be transposed to other multivalent ion/metal oxide systems. The additional advantage of working with TiO2 is its rather simple solid-state redox chemistry, centered on a single reversible redox transition from TiIV and TiIII. Its excellent chemical stability in aqueous media over a wide range of pHs is a further advantage, avoiding many complications commonly encountered with electrodissolution and/or electrodeposition of metal oxides such as manganese oxides or vanadium oxides in aqueous electrolytes.38 The main objective of this work is therefore to elucidate and rationalize the role played by an Al3+-based aqueous electrolyte on the charge accumulated in model mesoporous TiO2 electrodes and to decipher the chemical nature of the inserting cation. As will be shown, the present results strongly support a charge storage mechanism exclusively based on proton insertion in TiO2, wherein the hexaaquo complex [Al(H2O)6]3+ (generated upon solvation of the Al3+ inorganic salt in the aqueous electrolyte) behaves as a proton donor at the metal oxide/electrolyte interface. This reactivity is also demonstrated for other multivalent metal ions such as Zn2+ and Mn2+, which in their hexahydrated forms, can play the role of a proton donor in water. This original result demonstrates that the Brønsted acidity of [M(H2O)6]n+ complexes can play a fundamental role in the charge storage of metal oxide electrode materials and that it must be taken into account when analyzing the charge storage mechanisms at rechargeable batteries combining metal salts and water molecules.
2 Materials and methods
2.1 Chemicals and materials
Aluminum chloride hexahydrate (AlCl3·6H2O) and zinc chloride tetrahydrate (ZnCl2·4H2O) were purchased from Sigma-Aldrich. Manganese chloride tetrahydrate (MnCl2·4H2O) was purchased from Alfa Aesar. Potassium hydroxide, acetic acid (100%, AnalaR NORMAPUR®) and hydrochloric acid (37 wt%) were obtained from VWR Prolabo. Potassium chloride (Merck & Co., puriss. p.a.) was used as received. All aqueous solutions were made with deionized water (18.2 MΩ cm) from a TKA MicroPure UV purification system.2.2 Mesoporous GLAD-TiO2 electrodes
Nanostructured electrodes were prepared by physical vapor deposition of a mesoporous amorphous TiO2 film using a glancing angle deposition (GLAD) approach. Two different electrode types, denoted GLAD-TiO2/TiO2/ITO and GLAD-TiO2/Ti, were prepared. In the first case, the conductive side of tin-doped indium oxide (ITO) coated glass (Delta Technologies, 8–12 Ω □−1) was coated with a thin layer of bulk TiO2 (15 nm-thick) by conventional (i.e., non-GLAD) e-beam evaporation, followed by GLAD-TiO2. For GLAD-TiO2/Ti, clean glass substrates were coated with 250 nm of bulk Ti, followed by GLAD-TiO2. In each case, the GLAD-TiO2 process was performed at a fixed oblique angle of 72° while continuously rotating the substrate at a rate of one complete rotation for every 10 nm of TiO2 film growth until the mesoporous TiO2 film was 1 μm-thick. GLAD-TiO2/TiO2/ITO electrodes were thermally annealed at 100 °C for 24 hours in order to increase the oxygen content and improve transparency. Prior to use, electrodes were cleaned in an ultraviolet ozone cleaner (UV/O3 Procleaner™ plus, Bioforce Nanosciences) for 15 min to remove surface contaminants and subsequently soaked at room temperature in acetone and then ethanol for 15 and 30 min, respectively. The electroactive TiO2 surface was delimited by depositing nail vanish to define a rectangular working electrode area of 0.5 ± 0.05 cm2 (evaluated from a set of N = 15 independent electrodes).2.3 Spectroelectrochemical and electrochemical experiments
Spectroelectrochemical experiments were performed with an Autolab PGSTAT-12 potentiostat (operated by GPES-4 software) synchronized through an input trigger signal to a fiber-coupled TORUS UV-visible spectrophotometer (Ocean Optics). This setup allows simultaneous monitoring of the electrochemical current and optical absorbance at a GLAD-TiO2 electrode during any type of electrochemical experiment. A balanced deuterium tungsten source (Micropack) was used for illumination, and an integration time of 3 ms was used for UV-vis spectral acquisition. The spectroelectrochemical cell (Fig. S2†) was thermostated at a temperature of 25 °C using a dedicated Peltier-heater (Quantum Northwest). In order to avoid faradaic contribution arising from O2 reduction, the electrolyte solution was thoroughly deaerated by argon bubbling (for at least 10 min) before each experiment, and a constant flux of argon was maintained above the solution during experiments. An Ag/AgCl electrode filled with an internal saturated KCl solution (WPI, Dri-Ref, +0.2 V vs. NHE at 25 °C) and a Pt wire were used as the reference and counter electrodes, respectively. An average ohmic drop compensation of 41 ± 4 Ω (N = 24) was applied to the electrochemical experiments (except for the potential step experiments, vide infra).In cyclic voltabsorptometry experiments, a satisfactory absorbance signal-to-noise ratio was obtained by averaging 12 scans for the experiments performed at 50 mV s−1, 6 scans for those at 100 mV s−1, and 4 scans for those at 200 mV s−1. The extinction coefficient of the charges accumulated in TiO2 at λ = 780 nm was recovered from the following relationship (expressed here in flux density, ϕ, or mol cm−2 s−1) relating the measured current to the absorbance change:
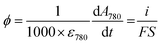 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1), S the geometric electroactive surface area (in cm2) and ε780 is the extinction coefficient (in M−1 cm−1) of the stored charges. As a function of the electrode used, ε780 values ranging from 900 to 1200 M−1 cm−1 were obtained, which is in agreement with the values previously reported by us and others.37,39–41
485 C mol−1), S the geometric electroactive surface area (in cm2) and ε780 is the extinction coefficient (in M−1 cm−1) of the stored charges. As a function of the electrode used, ε780 values ranging from 900 to 1200 M−1 cm−1 were obtained, which is in agreement with the values previously reported by us and others.37,39–41
Galvanostatic experiments were performed with current densities ranging from 0.4 mA cm−2 to 2 mA cm−2 and cut-off charge voltages ranging from +0.24 V to −1.12 V vs. Ag/AgCl at pH 3.
Whatever the electrochemical technique used, the charge density Q (in mC cm−2) accumulated in the GLAD-TiO2 film was determined from the maximal absorbance change monitored at 780 nm using the following expression:
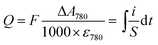 | (2) |
From the values determined for Q, the corresponding gravimetric capacity (in mC g−1 or mA h g−1) was calculated by taking into account the volumetric mass density of the GLAD-TiO2 film (i.e. 2.5 × 10−4 g cm−2 for the 1 μm-thick GLAD-TiO2 film).42 The gravimetric capacity arising exclusively from ion intercalation in TiO2 was determined after correcting for the amount of capacitive charges stored at the TiO2/electrolyte interface in an inert 0.3 M KCl aqueous electrolyte (adjusted to pH 3.0).
3 Results and discussion
3.1 Model GLAD-TiO2 electrodes
Model mesoporous metal oxide electrodes were composed of a 1 μm thick nanostructured amorphous TiO2 film. In contrast with the composite electrode materials commonly used for batteries (i.e., mixtures of active material, binder and conductive additives), these TiO2 electrodes are exclusively composed of active material. The nanostructured TiO2 film was obtained by glancing angle deposition (GLAD),42,43 a physical vapor deposition technique that leads to highly reproducible nanostructured metal oxide films of vertically aligned nanocolumns with well-controlled porosity and thickness. We have recently shown that protons can be rapidly and massively inserted/disinserted in these GLAD-TiO2 electrodes, negatively polarized in a neutral aqueous buffer.37 In this previous work, we also demonstrated that the inserted protons originate from the weak conjugate acid of the organic buffer present in solution at neutral pH. This is markedly different from proton insertion in a strongly acidic aqueous electrolyte (typically pH < 2) where free protons (or more rigorously hydronium ions) naturally serve as a proton source.37,44For the present study, two different types of 1 μm-thick GLAD-TiO2 electrodes were used (Fig. S1†): (i) 1 μm-thick amorphous TiO2 mesoporous film deposited by GLAD (using a deposition angle of 72°) over flat transparent conductive ITO-coated glass surfaces (GLAD-TiO2/TiO2/ITO electrodes), and (ii) the same 1 μm-thick GLAD TiO2 film deposited over a non-transparent conductive Ti-coated glass surfaces (GLAD-TiO2/Ti electrodes) (see Materials and methods for details). In the case of the GLAD-TiO2/TiO2/ITO electrodes, before the GLAD mesoporous TiO2 film deposition, a thin layer of bulk TiO2 (∼15 nm) was deposited over the ITO surface to protect the underlying ITO layer from the electrolyte. Without this TiO2 shielding, the ITO suffers an irreversible loss of conductivity under excessively negative potentials37 (see ESI† for additional comments). The GLAD-TiO2/TiO2/ITO electrodes are optically transparent, allowing spectroelectrochemical investigation of storage properties, while the GLAD-TiO2/Ti electrodes exhibit better stability under strongly reducing conditions, allowing investigation of charge storage at more negative potentials. As an illustration, Fig. 1 shows SEM images (top and side views) of a 1 μm-thick GLAD-TiO2/Ti electrode. The surface area enhancement and volumetric mass density of the GLAD TiO2 film are the same as previous reports, i.e. 540 per μm of film thickness and 2.5 g cm−3, respectively.42
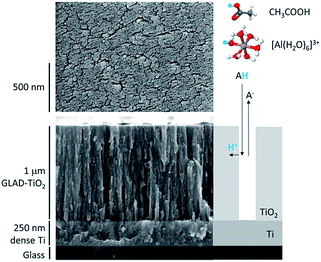 | ||
| Fig. 1 SEM images (top and side views) of the 1 μm-thick GLAD-TiO2/Ti film. At the right of the side view is a schematic representation of the two-step proton insertion mechanism within the nanostructured GLAD TiO2 film.37 In this two-step reaction scheme, the proton is provided at the TiO2/electrolyte interface by either the acetic acid or [Al(H2O)6]3+, followed by solid-state diffusion/migration throughout the bulk TiO2 lattice. The acidic proton is highlighted in blue. | ||
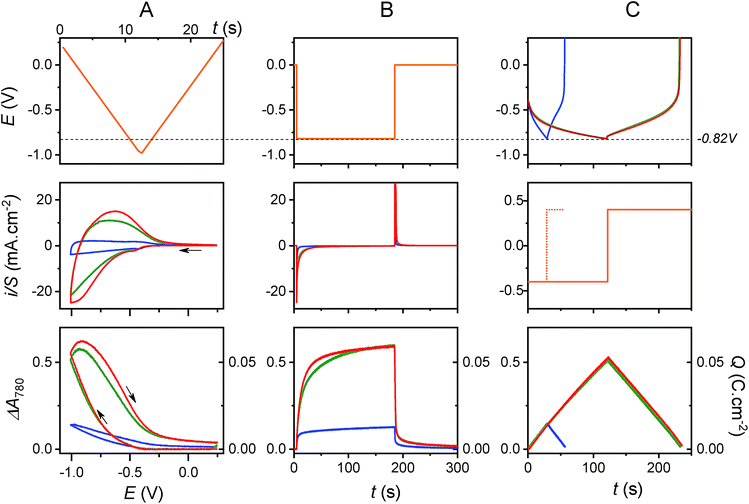
3.2 Charge storage in the presence of 0.3 M KCl, pH 3.0
The electrochemical charge storage properties of the transparent electrodes were characterized by real-time spectroelectrochemistry, a technique which allows absorbance changes (or electrochromic properties) of the TiO2 film to be monitored as a function of cathodic or anodic polarization in a mild aqueous electrolyte (see Materials and methods and Fig. S1 and S2†). The electronic properties of amorphous TiO2 are characterized by a bandgap of ∼3.2 eV and a pH-dependent conduction band potential of ECB = −0.36–0.06 × pH (V vs. Ag/AgCl),40,45 and therefore, the GLAD-TiO2/TiO2/ITO electrodes exhibit good transparency in the visible range and poor electronic conductivity as long as the applied potential E ≫ ECB. As the applied potential E is negatively increased and approaches ECB, light absorbance at the electrode increases concomitant with a rise in conductivity. This behavior is attributed to progressive filling of localized electronic states within the bandgap until E < ECB is reached and a degenerate state characteristic of a metal-like conductive film is formed.46,47In a 0.3 M KCl aqueous electrolyte (adjusted to pH 3.0), cyclic voltammograms (CVs) and cyclic voltabsorptograms (CVAs, monitored at 780 nm) at a GLAD-TiO2/TiO2/ITO electrode show, as expected, a typical transition from an insulating to a conductive state as the Fermi level of electrons in the TiO2 film increases toward the conduction band potential (a transition which starts here at ∼−0.3 V vs. Ag/AgCl) (Fig. S1† and 2). This process is associated with a simultaneous increase of the TiO2 film absorbance at 780 nm, which is characteristic of electrons accumulating in the electronic states of the semiconductive material (an increase that is proportional to the amount of charge accumulated within the semiconductive film).39,41,48 Once the applied potential lies within the potential window where TiO2 behaves as a metal-like conductive film (i.e., at E < −0.5 V vs. Ag/AgCl at pH 3.0), the CV displays a rectangular-shaped current response (Fig. 2A) almost independent of the applied potential and scaling linearly with the scan rate v (Fig. S1†). Such a behavior, corroborated by an almost linear and symmetric absorbance change during the forward and backward potential scans in the CVA (Fig. 2A), is characteristic of electrical charging of the double layer capacitance arising from simple ion adsorption at the metal-like-TiO2/electrolyte interface.49 The current density under these conditions is directly proportional to the high surface area of the mesoporous film.37 As attested by the complete restoration of the initial metal oxide transparency upon scanning back the potential in the anodic direction, the capacitive charging process is fully reversible.
The maximal amount of charge (Q) that can be stored through the capacitive charging process can be easily inferred from the maximal absorbance change (ΔAmax) of the GLAD-TiO2/TiO2/ITO electrode at 780 nm (see Materials and methods). As illustrated in Fig. 2, a maximal Q value of 15 mC cm−2 at −1.0 V (i.e., 15 mF cm−2, which is equivalent to 60 F g−1 or 17 mA h g−1) can be determined from the cyclic voltabsorptometry experiment, a value that matches those extracted from chronoabsorptometry or galvanostatic experiments (i.e., ∼13–14 mC cm−2 at the applied voltage of −0.82 V, which corresponds to ∼16–17 mF cm−2) (see blue curves on the bottom graphs of Fig. 2). That the same maximum Q values are obtained, regardless of the technique used, suggests a fast charging process. This is further confirmed by the shape of the chronoabsorptogram in Fig. 2B where the maximal Q value is reached within a few seconds, i.e., on a much shorter time scale than that required to perform CV or galvanostatic experiments. This behavior fully agrees with that expected for fast charging of the double layer electrical capacitance of a high surface area electrode.
3.3 Charge storage in the presence of 0.25 M AlCl3, pH 3.0
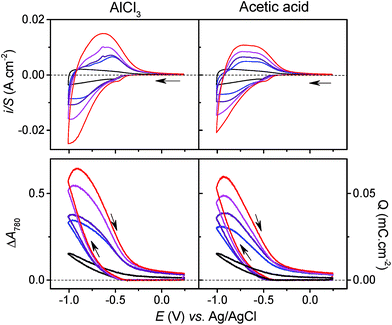
In the presence of AlCl3 electrolyte (0.25 M, pH 3), the magnitude and shape of the cyclic voltammogram at GLAD-TiO2/TiO2/ITO electrodes is strongly modified. On top of the above-mentioned capacitive current, a broad reversible wave appears, centered on a formal potential of E0′ ∼ −0.75 V, and this reversible wave appears together with a large increase in TiO2 film absorbance (Fig. 2). The magnitude of the reversible wave (or reversible absorbance change in CVA) increases with increasing Al3+ concentration in solution (Fig. 3), thus confirming that Al3+ directly contributes to the reversible charge accumulation. Analysis of the cathodic and anodic waves in CV as a function of the scan rate shows that the current is no longer proportional to the scan rate, and that once corrected from the capacitive current (by subtracting the CV recorded at the same scan rate in the KCl electrolyte), current is instead proportional to the square root of v over the entire range of Al3+ concentrations investigated (i.e., from 0.025 to 0.25 M, see Fig. S3† – higher concentrations of Al3+ were not examined because they lead to pH values below 3, which cannot easily be adjusted to higher values without aluminum salt precipitation).‡ Such behavior strongly supports a reversible charging/discharging process that is rate-controlled by diffusional mass transport of aluminum ions in solution.As illustrated with the chronoabsorptometry or galvanostatic experiments in Fig. 2, when enough time is given for the charge storage process to take place, the electrode absorbance reaches an equilibrium value that depends only on the applied potential (suggesting conditions entirely governed by thermodynamics). From the magnitude of the equilibrium absorbance change (indicative of an equilibrium amount of electrons stored within the material) recorded here at −0.82 V, a gravimetric capacity of 65 mA h g−1 can be estimated, which is 5-fold more than in the absence of AlCl3 at the same pH and potential (i.e., ∼13 mA h g−1). Additionally, under the selected experimental conditions, the charging process is fully reversible as attested by the complete restoration of the initial absorbance. All of these observations clearly suggest the occurrence of a reversible faradaic process, rate-limited by a diffusional mass transport involving Al3+. These results also confirm what has previously been obtained by other groups (see Table 1).23,26–30,34
At first sight, it is tempting to attribute this reversible charging process to the reversible faradaic reduction of the TiIV sites coupled with intercalation of Al3+ into TiO2 (to locally compensate the loss of charge within the metal oxide lattice) according to the following global reaction:
| TiO2 + 3xe− + xAl3+ ⇆ AlxTiO2 | (3) |
This reaction mechanism was proposed by several groups23,26,28–30,34 (see Table 1), arguing that the small radius of Al3+ as compared to Li+ (0.053 nm vs. 0.069 nm, see Table S1†) facilitates intercalation and migration within the solid phase of TiO2. On the basis of eqn (3), experimental x values ranging from 0.076 to 0.27 were thus proposed,23,29 which for the highest values, is near the maximal theoretical value (i.e., 0.33) assuming that all the TiIV atoms in TiO2 can be reduced into TiIII and that 3TiIII atoms are involved for each Al3+ ion inserted. This, however, does not take into consideration that dissolution of Al3+ salts in aqueous solutions leads to the formation of [Al(H2O)6]3+, a hexaaquo ion complex characterized by a rather large molecular size (diameter > 0.38 nm according to the Al–O internuclear distance of 0.19 nm (ref. 50)), in which the coordinated water molecules are strongly bonded because of the high charge and small size of Al3+ (ΔG0hydration = −4525 kJ mol−1, which is 10-fold higher than Li+).35 Accordingly, insertion of the unsolvated Al3+ ion into TiO2 must be thermodynamically more difficult (i.e., shifted to more negative potentials) than insertion of a monovalent cation of similar size and lower solvation energy (for instance Li+). In other words, insertion of Al3+ into TiO2 is expected to be penalized by the high energy cost associated with desolvation of its hydration shell (corresponding to a high change in Gibbs free energy for the ion insertion potential, i.e. ΔEi = −ΔGi/nF). Additionally, as already mentioned in the introduction, the strong coulombic interaction that is presumed to occur between the highly charged Al3+ and the surrounding TiO2 lattice should strongly hinder the solid-state cation diffusion.36
An additional aspect that has not previously been sufficiently taken into account is the weak acidity of the [Al(H2O)6]3+ complex, resulting from the Lewis acidity of Al3+ that strongly polarizes the coordinated water molecules in the hexaaquo complex. This polarization is sufficient to make the hydrogen atoms of the bonded water molecules more acidic than normal water molecules. For this reason, the [Al(H2O)6]3+ complex is characterized by a weak Brønsted acidity of pKa = 4.97.51 Accordingly, the dissolution of 0.25 AlCl3 in water leads to the following equilibrium mixture of ionic species in solution: 0.249 M [Al(H2O)6]3+, 1 mM [Al(H2O)6(OH)]2+, 1 mM H3O+ (pH 3.0) and 0.75 M Cl−. The electrolyte therefore consists of a large amount of [Al(H2O)6]3+ which, due to its weakly acidic properties, can be considered as an abundant latent source of protons. This source is much more abundant than the free proton concentration, which at pH 3.0 can be considered negligible. This means that the aluminum hexaaquo complex, rather than acting as an intercalating cation, can serve as a proton source to locally compensate the negative charge generated by reduction of TiO2, a process that can be formally described by the following interfacial reaction scheme:
| TiO2 + xe− + x[Al(H2O)6]3+ ⇆ TiOOHx + x[Al(H2O)5(OH)]2+ | (4) |
This proposed mechanism is also based on our recent finding that a weak organic acid such as the conjugate acid form of the zwitterionic HEPES buffer (i.e., 4-(2-hydroxyethyl)-1-piperazineethanesulfonate, pKa,2 = 7.5) can be an efficient proton donor to assist the proton insertion-coupled charge transfer generated at a negatively biased GLAD-TiO2 electrode in a neutral aqueous buffer (pH 7.0).37 By extension, we can postulate that a similar charge storage mechanism is at work in the presence of an Al3+-based electrolyte, wherein [Al(H2O)6]3+ is recruited as a source of protons at the metal oxide/electrolyte interface to promote the insertion of protons within the metal oxide lattice.
The first item in favor of this proton insertion mechanism is the remarkably fast charging/discharging rate evidenced by: (i) the reversible wave in CV, which remains particularly well-defined despite the unusually high scan rate used here (v = 0.1 V s−1 in Fig. 2, which is much higher than that ordinarily used to characterize Li-ion insertion in TiO2 (v < 10 mV s−1)),52 (ii) the chronoabsorptometry experiment of Fig. 2 which demonstrates rapid charging to a gravimetric capacity as high as 61 mA h g−1 in less than 1 min at −0.82 V, (iii) the galvanostatic experiments at different rates in Fig. S4† from which remarkably high charging efficiencies could be estimated (i.e., values as high as 70% at 1.6 A g−1, i.e. 45 mA h g−1 at 0.4 mA cm−2, or 40% at 8 A g−1, i.e. 27 mA h g−1 at 2 mA cm−2 at a cut-off potential of −0.82 V).§
This fast charging/discharging rate clearly supports fast uptake/release of the charge compensating cation. Uptake/release is fast enough that charge/discharge is almost always fully controlled by the mass transport of [Al(H2O)6]3+ in solution (Fig. 3 and S3†), a behavior that is supported by the close-to-linear dependence of the peak current in CV as a function of [AlCl3] (see Fig. S3 and its comment in ESI†). This observation argues in favor of proton insertion rather than Al3+ intercalation, which considering the ionic size argument, makes sense because the ionic radius of a proton is ∼6 × 104-fold smaller than Al3+ (see Table S1†).
3.4 Charge storage in the presence of 0.25 M acetic acid, pH 3.0
If we assume that, because of its weakly acidic character, [Al(H2O)6]3+ only acts as a donor to promote proton insertion at the TiO2/electrolyte interface, then by extrapolation, we can expect that other weak acids could support the same H+ insertion process. If this assumption is true, then it is reasonable to anticipate that under similar concentration and pH conditions, it should be impossible to differentiate the electrochemical experiments performed in an electrolyte containing [Al(H2O)6]3+ from those performed in an electrolyte containing an organic weak acid of similar pKa. To test this hypothesis, the spectroelectrochemical experiments performed with Al3+ were repeated with acetic acid, a monoprotic organic acid having a pKa of 4.76, almost identical to [Al(H2O)6]3+ (pKa = 4.97). To replicate the proton donor concentration and ionic strength of the Al3+-based experiments, an aqueous solution containing 0.25 M acetic acid and 0.3 M KCl, adjusted to pH 3.0, was used. The experimental data obtained with the acetic acid electrolyte at a GLAD-TiO2/TiO2/ITO electrode are reported in Fig. 2 and 3. Whatever the electrochemical technique used, it immediately emerges from Fig. 2 that the experimental data recorded in the presence of acetic acid are highly similar to those obtained in the Al3+-based electrolyte. In the presence of acetic acid, the CV and CVA show the appearance of an intense and broad reversible wave, whose shape, current intensity (or absorbance change), and potential positioning are almost overlaid with those obtained using the Al3+-based electrolyte. The absence of a potential shift in the position of the reversible wave is a strong indication that, thermodynamically, the same cationic species is involved in the faradaic transformation of TiO2. This observation is again consistent with proton insertion rather than Al3+ insertion (it is indeed hard to envision that the reducing potential of TiO2 does not depend on the nature of the inserted cation, a dependence that has been well-identified for the insertion of alkali-ions in solid metal hexacyanometalates and mainly attributed to a difference in the solvation energy of the cations53,54). Also, similar to the results found with Al3+, the magnitude of the reversible wave and absorbance change was observed to increase with the concentration of acetic acid (Fig. 3 and S5†), confirming that acetic acid is directly involved in the charge storage mechanism. Furthermore, once corrected for the contribution of the capacitive current, the magnitude of the cathodic and anodic peak currents in CV were observed to vary proportionally with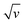 over the entire range of acetic acid concentrations investigated (Fig. S5†).
over the entire range of acetic acid concentrations investigated (Fig. S5†).
Again, this behavior is analogous to that obtained with the Al3+-based electrolyte, clearly suggesting a faradaic charging mechanism rate-controlled by diffusional mass transport, which here can unambiguously be attributed to the mass transport of the acetic acid in solution.
Other striking similarities in Fig. 2 are the charging and discharging rates which, in light of the chronoamperometry or chronoabsorptometry experiments, lead to almost identical kinetic traces for the two electrolytes. This is also the case for the galvanostatic experiments, which show very similar charging/discharging curves in each electrolyte. Additionally, the maximal equilibrium amount of charge reached at the end of the chronoamperometric or chronoabsorptometric experiments (i.e., at −0.82 V) are the same in both electrolytes (i.e., 67–68 mA h g−1). The similarities in the charging/discharging rates and in the amounts of accumulated charge with both electrolytes strongly suggest that the same cationic species is involved in the charge storage mechanism, and that the cation common to the two electrolytes is the proton, not Al3+.
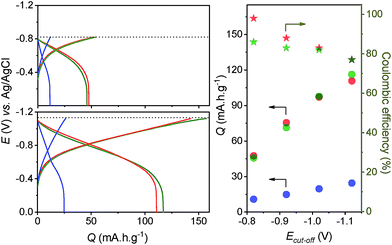
Because of their much higher stability under strongly reducing conditions, we examined the influence of an increasingly negative cut-off potential (ranging from −0.82 V up to −1.12 V) on the galvanostatic charging of GLAD-TiO2/Ti electrodes. This was done both in the presence and the absence of a proton donor. The resulting galvanostatic charging/discharging curves reported in Fig. 4 show that in the presence of AlCl3 or acetic acid, the amount of charge reversibly stored in the mesoporous film at a charging rate of 1.6 A g−1 is steadily increased as the negative cut-off potential is progressively shifted to more negative values, reaching a gravimetric capacity as high as 115 mA h g−1 at the most negative cut-off potential of −1.12 V in both electrolytes.¶ The main factor that impedes a more extensive reduction of the GLAD-TiO2 film is the competitive hydrogen evolution reaction that becomes progressively more dominant with application of increasingly negative potentials (and which leads to the obvious release of dihydrogen bubbles at the electrode interface). This is well-evidenced in Fig. 4 through the charge storage coulombic efficiency which decreases as the cut-off potential is raised to more negative values.
Despite the competitive hydrogen evolution, we found that the reversible gravimetric capacity could be improved to 155 mA h g−1 at a GLAD-TiO2/Ti electrode by further increasing the acetic acid-based electrolyte concentration to 8 M (Fig. S6†). This charge storage capacity is not far from the maximal theoretical value of 167 mA h g−1 assuming by analogy to Li+,55 that only half of the bulk TiIV sites in TiO2 can be reduced into TiIII (x = 0.5).
3.5 Interpretation in terms of proton-coupled electron storage
As acetic acid cannot itself insert within the TiO2 structure, and the free proton concentration at pH 3.0 is quite low, the only way to explain the faradaic response observed in the presence of this weak acid is that the latter behaves as a proton donor (i.e., a Brønsted weak acid, AH) at the TiO2 interface, exactly as we have previously shown at neutral pH with the HEPES buffer.37,56 This type of proton-coupled electron charge storage can be formally expressed as follows:| TiO2 + xe− + xAH ⇆ TiOOHx + xA− | (5) |
| TiIVO2 + e− + AH ⇆ TiIII(O)(OH) + A− | (6) |
| TiIVO2 + TiIII(O)(OH) ⇆ TiIII(O)(OH) + TiIVO2 | (7) |
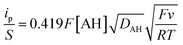 | (8) |
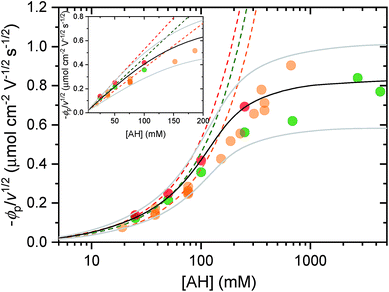 | ||
| Fig. 5 Cathodic peak potential (expressed in flux density and normalized to v1/2) as a function of AH concentration in the electrolyte (adjusted to pH 3.0), where AH is (red) [Al(H2O)6]3+, (green) acetic acid, and (orange) the weak acid conjugate of the HEPES buffer. The dashed lines correspond to the linear regression fits of eqn (8) to the low concentration range of the experimental data, from which the following diffusion coefficients of the proton donor in solution, i.e. DAH, were recovered: (red) 4 × 10−6 cm2 s−1, (green) 3 × 10−6 cm2 s−1, and (orange) 2 × 10−6 cm2 s−1. HEPES data (pH 7.0) are reproduced from (ref. 37). The black and gray plain lines are the numerical simulations of the model reported in (ref. 56) using a DAH value of (3 ± 1.5) × 10−6 cm2 s−1 and a solid-state diffusion coefficient of (5 ± 2.5) × 10−16 cm2 s−1. The grey simulated curves that bookend the black have been calculated by taking into account the confidence range on the diffusion coefficients. Inset: magnification of the lower concentration range (linear scale). | ||
3.6 Extension to other multivalent metallic ions
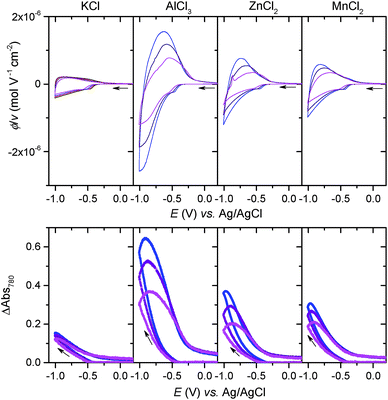
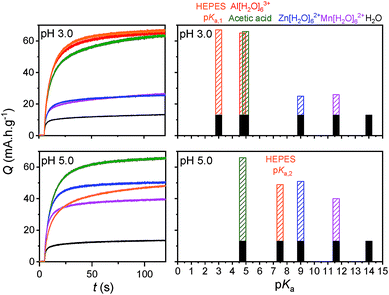
If [Al(H2O)6]3+ serves as an efficient proton source due to its Brønsted acidity, one can presume that this effect can also extend to other multivalent hexaaquo metal ions exhibiting weak acid properties in aqueous solution.51 We have thus investigated the electrochemical charging of GLAD TiO2/TiO2/ITO electrodes in aqueous electrolytes (adjusted to pH 3.0) containing either 0.25 M ZnCl2 or 0.25 M MnCl2, two divalent metal ions that are commonly present in a wide range of aqueous zinc-ion batteries.1,3,7,9–11 As for AlCl3, once ZnCl2 and MnCl2 are dissolved in aqueous solution, they form hexaaquo complexes [Zn(H2O)6]2+ and [Mn(H2O)6]2+, characterized by pKa values of 9.0 and 10.6, respectively (Table S1†). The resulting CVs and CVAs reported in Fig. 6 show a net increase in current density and absorbance change (monitored at 780 nm) at potentials lower than −0.5 V as compared to the same electrode scanned in a pure 0.3 M KCl electrolyte. Also similar to [Al(H2O)6]3+, this increase is proportional to v1/2 and a function of the metal ion concentration in solution, behaviors which attest to a charge storage process kinetically governed by the solution mass transport of metal ions toward the electrode surface. It is interesting to note that Zn2+ and Mn2+ have much larger ionic radii than Li+ and Al3+ (see Table S1†), so that the cation size argument can no longer explain the increase of capacity by uptake of these divalents ions within the 3D structure of TiO2. Hence, the increase of capacity can again be unambiguously attributed to the reversible insertion of protons provided by the hexaaquo metal ion complexes during the reversible reduction of TiO2.The main difference that become apparent in side-by-side comparison of the CVs and CVAs recorded in the various electrolytes is the somewhat lower charging/discharging current densities and absorbance changes when using [Zn(H2O)6]2+ and [Mn(H2O)6]2+, indicating a lower charge storage efficiency with these metal ions as compared to [Al(H2O)6]3+. We attribute this effect to the lower Brønsted acidity of [Zn(H2O)6]2+ and [Mn(H2O)6]2+, which indicates that protons are donated less easily than the aluminum complex. This effect is also most likely accompanied by a shift of the reversible proton-insertion wave to more negative potentials, which makes sense if we consider the higher energetic cost required to dissociate the acidic proton from [Zn(H2O)6]2+ and [Mn(H2O)6]2+ as compared to [Al(H2O)6]3+ (suggesting that the pKa of the proton donor is involved in the thermodynamics of the reversible proton-insertion process). In an attempt to better resolve the reversible proton-insertion wave in CV for each of the metal ions and to assess their formal potentials, we attempted to push the CV scans to more negative potentials. Unfortunately, these experiments were unsuccessful due to both the interference of hydrogen evolution and recurrent electrode failures at excessively negative potentials.
In order to better compare the equilibrium amount of charge that can be stored at pH 3.0 within GLAD-TiO2/TiO2/ITO electrodes as a function of the chemical nature of the electrolyte, potential step chronoabsorptometric experiments were performed by applying a charging potential (i.e., −0.82 V) close to the formal potential of the reversible proton insertion wave measured for acetic acid- and Al3+-based electrolytes (Fig. 7). After less than 2 min of charging, an almost constant absorbance value was systematically attained for all of the electrolytes but with different magnitudes, indicative of different charging equilibria. In the presence of Zn2+- and Mn2+-based electrolytes, the absorbance increase at 780 nm is equivalent to a charge storage of ∼25 mA h g−1, a value which is significantly higher than that obtained in a pure aqueous KCl electrolyte at the same pH (i.e. 13 mA h g−1). Even if this increase of capacity remains lower than with the acetic acid- or Al3+-based electrolytes, it demonstrates the advantageous effect of these metal ion electrolytes on proton-insertion charge storage. This effect was also observed to depend on pH as illustrated by the chronoabsorptometric experiments repeated for the same electrolytes at pH 5.0 and at an applied potential adjusted to −0.94 V (Fig. 7) (the potential was adjusted to a 120 mV more negative value in order to take into account the −60 mV shift of the conduction band potential per unit of pH,37 and through this to have comparable equilibrium charge storage conditions as at pH 3.0). This is particularly true for the weak acid [Zn(H2O)6]2+ and [Mn(H2O)6]2+ complexes which upon increasing the pH from 3.0 to 5.0 show a net gain in proton storage capacity. This, however, is not the case with acetic acid which remains nearly unchanged whatever the pH. Independent of the proton storage capacities, the gravimetric capacities at pH 5.0 rapidly reach equilibrium whatever the nature of the electrolyte, and this proceeds with kinetics similar to those at pH 3.0.
In Fig. 7, the results of earlier studies in HEPES buffer adjusted to either pH 3.0 or 5.0 were also added. The peculiarity of HEPES is its weak acidity characterized by two pKa values (i.e., pKa,1 = 3.0 and pKa,2 = 7.5). At pH 3.0, the diprotic acidic form of HEPES is predominantly involved as a proton donor, while at pH 5.0 the less acidic zwitterionic form of HEPES dominates the proton charge storage.
The equilibrium amounts of charge reversibly stored either at pH 3.0 and 5.0 were plotted for each electrolyte as a function of the pKa of the proton donor in solution (Fig. 7). We also added water to the plot (i.e., the H2O/OH− couple with a pKa value of 14) because of its potential involvement as a proton donor, although this effect is more likely to be observed in a pure KCl electrolyte under our experimental conditions. The results gathered in Fig. 7 clearly demonstrate that the proton storage efficiency at GLAD-TiO2 films strongly depends on both the pH of the electrolyte and the pKa of the proton donor. In agreement with our previous finding,37 water is inefficient in delivering protons under the present experimental conditions (aqueous KCl electrolyte of pH 3.0 or 5.0) and this is in spite of its very high concentration (i.e. ∼55 M). This behavior is clearly related to the low acidity of water (pKa = 14). Likewise, at pH 3.0, the lower efficiency of Zn2+- and Mn2+-based electrolytes as compared to Al3+, acetic acid or HEPES can also be attributed to the lower acidity (or higher pKa values) of [Zn(H2O)6]2+ and [Mn(H2O)6]2+ relative to [Al(H2O)6]3+, acetic acid or HEPES. This effect is partially countered upon raising the pH to 5.0, wherein the weak acids [Zn(H2O)6]2+ and [Mn(H2O)6]2+ complexes become more efficient proton donors, but at the expense of a more negative applied potential value (or higher energy) than at pH 3.0.
3.7 Comments on the discharging mechanism
It is interesting to note that if we compare the discharging process to the charging process in chronopotentiometric experiments (Fig. 2), the former clearly appears to be much faster than the latter. This is a behavior we observed whatever the nature of the electrolyte. While a thermodynamic equilibrium is typically reached within ∼60 s of application of a reductive potential close to the formal potential of the reversible proton insertion (E < ECB), the subsequent discharge of the electrode upon applying a positive bias (E ≫ ECB) occurs within a significantly shorter time, i.e. <10 s. If we assume that eqn (4) is a fully reversible process at the microscopic level, then one would assume that the discharging process also depends on the amount of conjugate base available at the metal oxide/electrolyte interface. Since the present experiments were all performed at pH ≪ pKa, the amount of base is low relative to the weak acid. The discharging process should thus be a priori slower than the charging process, however, this is not what we observed. This behavior thus raises fundamental questions on the mechanism of proton disinsertion from TiO2 that will be addressed in future work.4 Conclusions
By comparing the electrochemical reversible charge storage at model GLAD-TiO2 electrodes in mild aqueous electrolytes containing either AlCl3 or acetic acid, we demonstrate that an identical faradaic charge storage mechanism occurs in both electrolytes. Contrary to the general belief that Al3+ ions insert within TiO2, we reveal rather that its hexaaquo ion complex acts as a proton donor at the TiO2/electrolyte interface, similar to acetic acid. This allows for fast and massive proton-coupled electron storage even under conditions with a negligible concentration of free protons. These results are of great significance because the role of proton donor played by metal aquo complexes on the charge/discharge of TiO2 in an aqueous electrolyte can a priori extend to many other metal oxide electrode materials immersed either in aqueous electrolytes containing multivalent metal ions or in organic electrolytes containing multivalent metal ions and a small amount of water. Additionally, the present results shed new light on mechanisms that may lead to systematically improved battery performances (i.e., higher gravimetric capacities as well as better rates) when the so-called rechargeable multivalent ion-insertion batteries operate in aqueous electrolytes7–13 rather than in a water-free organic electrolyte.14,16,18–20Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
K. D. H. thanks Jeremy Sit for access to the GLAD evaporator, and the NRC Nanotechnology Initiative GIANNT project for partial funding support.Notes and references
- R. Guduru and J. Icaza, Nanomaterials, 2016, 6, 41 CrossRef PubMed.
- P. Canepa, G. Sai Gautam, D. C. Hannah, R. Malik, M. Liu, K. G. Gallagher, K. A. Persson and G. Ceder, Chem. Rev., 2017, 117, 4287–4341 CrossRef CAS PubMed.
- Z. Xing, S. Wang, A. Yu and Z. Chen, Nano Energy, 2018, 50, 229–244 CrossRef CAS.
- V. Verma, S. Kumar, W. Manalastas, R. Satish and M. Srinivasan, Adv. Sustainable Syst., 2018, 3, 1800111 CrossRef.
- Z. Chang, Y. Yang, M. Li, X. Wang and Y. Wu, J. Mater. Chem. A, 2014, 2, 10739–10755 RSC.
- J. Liu, C. Xu, Z. Chen, S. Ni and Z. X. Shen, Green Energy & Environment, 2018, 3, 20–41 Search PubMed.
- H. Pan, Y. Shao, P. Yan, Y. Cheng, K. S. Han, Z. Nie, C. Wang, J. Yang, X. Li, P. Bhattacharya, K. T. Mueller and J. Liu, Nat. Energy, 2016, 1, 16039 CrossRef CAS.
- D. Kundu, B. D. Adams, V. Duffort, S. H. Vajargah and L. F. Nazar, Nat. Energy, 2016, 1, 16119 CrossRef CAS.
- N. Zhang, F. Cheng, J. Liu, L. Wang, X. Long, X. Liu, F. Li and J. Chen, Nat. Commun., 2017, 8, 405 CrossRef PubMed.
- W. Sun, F. Wang, S. Hou, C. Yang, X. Fan, Z. Ma, T. Gao, F. Han, R. Hu, M. Zhu and C. Wang, J. Am. Chem. Soc., 2017, 139, 9775–9778 CrossRef CAS PubMed.
- W. Qiu, Y. Li, A. You, Z. Zhang, G. Li, X. Lu and Y. Tong, J. Mater. Chem. A, 2017, 5, 14838–14846 RSC.
- N. Zhang, Y. Dong, M. Jia, X. Bian, Y. Wang, M. Qiu, J. Xu, Y. Liu, L. Jiao and F. Cheng, ACS Energy Lett., 2018, 3, 1366–1372 CrossRef CAS.
- F. Wan, L. Zhang, X. Dai, X. Wang, Z. Niu and J. Chen, Nat. Commun., 2018, 9, 1656 CrossRef PubMed.
- K. W. Nam, S. Kim, S. Lee, M. Salama, I. Shterenberg, Y. Gofer, J.-S. Kim, E. Yang, C. S. Park, J.-S. Kim, S.-S. Lee, W.-S. Chang, S.-G. Doo, Y. N. Jo, Y. Jung, D. Aurbach and J. W. Choi, Nano Lett., 2015, 15, 4071–4079 CrossRef CAS PubMed.
- Y. Tian, W. Zhang, S. Cong, Y. Zheng, F. Geng and Z. Zhao, Adv. Funct. Mater., 2015, 25, 5833–5839 CrossRef CAS.
- X. Sun, V. Duffort, B. L. Mehdi, N. D. Browning and L. F. Nazar, Chem. Mater., 2016, 28, 534–542 CrossRef CAS.
- T. Koketsu, J. Ma, B. J. Morgan, M. Body, C. Legein, W. Dachraoui, M. Giannini, A. Demortière, M. Salanne, F. Dardoize, H. Groult, O. J. Borkiewicz, K. W. Chapman, P. Strasser and D. Dambournet, Nat. Mater., 2017, 16, 1142–1148 CrossRef CAS PubMed.
- X. Ji, J. Chen, F. Wang, W. Sun, Y. Ruan, L. Miao, J. Jiang and C. Wang, Nano Lett., 2018, 18, 6441–6448 CrossRef CAS PubMed.
- F. Wang, W. Sun, Z. Shadike, E. Hu, X. Ji, T. Gao, X.-Q. Yang, K. Xu and C. Wang, Angew. Chem., Int. Ed., 2018, 57, 11978–11981 CrossRef CAS PubMed.
- D. Kundu, S. Hosseini Vajargah, L. Wan, B. Adams, D. Prendergast and L. F. Nazar, Energy Environ. Sci., 2018, 11, 881–892 RSC.
- E. Levi, M. D. Levi, O. Chasid and D. Aurbach, J. Electroceram., 2009, 22, 13–19 CrossRef CAS.
- E. Levi, Y. Gofer and D. Aurbach, Chem. Mater., 2010, 22, 860–868 CrossRef CAS.
- S. Liu, J. J. Hu, N. F. Yan, G. L. Pan, G. R. Li and X. P. Gao, Energy Environ. Sci., 2012, 5, 9743 RSC.
- F. Wang, Z. Liu, X. Wang, X. Yuan, X. Wu, Y. Zhu, L. Fu and Y. Wu, J. Mater. Chem. A, 2016, 4, 5115–5123 RSC.
- J. R. González, F. Nacimiento, M. Cabello, R. Alcántara, P. Lavela and J. L. Tirado, RSC Adv., 2016, 6, 62157–62164 RSC.
- Y. Liu, S. Sang, Q. Wu, Z. Lu, K. Liu and H. Liu, Electrochim. Acta, 2014, 143, 340–346 CrossRef CAS.
- S. Sang, Y. Liu, W. Zhong, K. Liu, H. Liu and Q. Wu, Electrochim. Acta, 2016, 187, 92–97 CrossRef CAS.
- H. Lahan, R. Boruah, A. Hazarika and S. K. Das, J. Phys. Chem. C, 2017, 121, 26241–26249 CrossRef.
- Y. J. He, J. F. Peng, W. Chu, Y. Z. Li and D. G. Tong, J. Mater. Chem. A, 2014, 2, 1721 RSC.
- M. Kazazi, P. Abdollahi and M. Mirzaei-Moghadam, Solid State Ionics, 2017, 300, 32–37 CrossRef CAS.
- K. Li, Y. Shao, S. Liu, Q. Zhang, H. Wang, Y. Li and R. B. Kaner, Small, 2017, 13, 1700380 CrossRef PubMed.
- T. Chen and E. Peled, J. Solid State Electrochem., 2017, 21, 3325–3331 CrossRef CAS.
- C. Wu, S. Gu, Q. Zhang, Y. Bai, M. Li, Y. Yuan, H. Wang, X. Liu, Y. Yuan, N. Zhu, F. Wu, H. Li, L. Gu and J. Lu, Nat. Commun., 2019, 10, 73 CrossRef PubMed.
- M. Kazazi, Z. A. Zafar, M. Delshad, J. Cervenka and C. Chen, Solid State Ionics, 2018, 320, 64–69 CrossRef CAS.
- Y. Marcus, J. Chem. Soc., Faraday Trans., 1991, 87, 2995–2999 RSC.
- Z. Rong, R. Malik, P. Canepa, G. Sai Gautam, M. Liu, A. Jain, K. Persson and G. Ceder, Chem. Mater., 2015, 27, 6016–6021 CrossRef CAS.
- Y.-S. Kim, S. Kriegel, K. D. Harris, C. Costentin, B. Limoges and V. Balland, J. Phys. Chem. C, 2017, 121, 10325–10335 CrossRef CAS.
- M. Pourbaix, Atlas of electrochemical equilibria in aqueous solutions, National Association of Corrosion Engineers, Houston, Texas, 2d English, 1974 Search PubMed.
- T. Berger, J. A. Anta and V. Morales-Florez, J. Phys. Chem. C, 2012, 116, 11444–11455 CrossRef CAS.
- G. Rothenberger, D. Fitzmaurice and M. Graetzel, J. Phys. Chem., 1992, 96, 5983–5986 CrossRef CAS.
- G. Boschloo and D. Fitzmaurice, J. Phys. Chem. B, 1999, 103, 7860–7868 CrossRef CAS.
- K. M. Krause, M. T. Taschuk, K. D. Harris, D. A. Rider, N. G. Wakefield, J. C. Sit, J. M. Buriak, M. Thommes and M. J. Brett, Langmuir, 2010, 26, 4368–4376 CrossRef CAS PubMed.
- M. J. Brett and M. M. Hawkeye, Science, 2008, 319, 1192–1193 CrossRef CAS PubMed.
- A. Ghicov, H. Tsuchiya, R. Hahn, J. M. MacAk, A. G. Munoz and P. Schmuki, Electrochem. Commun., 2006, 8, 528–532 CrossRef CAS.
- L. A. Lyon and J. T. Hupp, J. Phys. Chem. B, 1999, 103, 4623–4628 CrossRef CAS.
- F. Fabregat-Santiago, I. Mora-Seró, G. Garcia-Belmonte and J. Bisquert, J. Phys. Chem. B, 2003, 107, 758–768 CrossRef CAS.
- T. Berger, D. Monllor-Satoca, M. Jankulovska, T. Lana-Villarreal and R. Gomez, ChemPhysChem, 2012, 13, 2824–2875 CrossRef CAS PubMed.
- D. Mandal and T. W. Hamann, Phys. Chem. Chem. Phys., 2015, 17, 11156–11160 RSC.
- C. Costentin and J.-M. Saveant, Chem. Sci., 2019, 5656–5666 RSC.
- Y. Marcus, Chem. Rev., 1988, 88, 1475–1498 CrossRef CAS.
- S. J. Hawkes, J. Chem. Educ., 1996, 73, 516 CrossRef CAS.
- H. Lindström, S. Södergren, A. Solbrand, H. Rensmo, J. Hjelm, A. Hagfeldt and S.-E. Lindquist, J. Phys. Chem. B, 1997, 101, 7717–7722 CrossRef.
- F. Scholz and A. Dostal, Angew. Chem., Int. Ed., 1995, 34, 2685–2687 CrossRef CAS.
- H. W. Lee, M. Pasta, R. Y. Wang, R. Ruffo and Y. Cui, Faraday Discuss., 2014, 176, 69–81 RSC.
- R. J. Cava, D. W. Murphy, S. Zahurak, A. Santoro and R. S. Roth, J. Solid State Chem., 1984, 53, 64–75 CrossRef CAS.
- Y. S. Kim, V. Balland, B. Limoges and C. Costentin, Phys. Chem. Chem. Phys., 2017, 19, 17944–17951 RSC.
- CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, FL, Internet V., 2005 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc02397f |
| ‡ The problem of working at a pH well below 3.0 is that the concentration of free protons becomes high enough to contribute significantly to charge storage via proton insertion, which therefore makes it more difficult to properly interpret the results we observed with the aluminum ion. |
| § Similar results were also obtained with the GLAD-TiO2/Ti electrodes under the same experimental conditions, confirming that the mesoporous TiO2 films behave similarly whether the GLAD TiO2 film has been deposited over an underlying ITO or Ti conductive substrate. |
| ¶ It is important to note that this gravimetric capacity also includes the charges stored in the double layer capacitance of the high-surface area TiO2 film, which as shown in Fig. 4 corresponds to 25 mA h g−1 at −1.12 V in the absence of a proton donor (i.e., in a pure KCl electrolyte). Accordingly, the capacity of the electrode resulting exclusively from the bulk faradaic reduction of TiIV into TiIII can be estimated to be 90 mA h g−1 when working in acetic acid–based or Al3+-based electrolytes. This corresponds to the reduction of ∼27% of the total amount of TiIV sites present in the mesoporous TiO2 film (i.e. 3.13 × 10−6 mol cm−2 estimated from the film density of 2.5 g cm−3 and a film thickness of 1 μm). |
| This journal is © The Royal Society of Chemistry 2019 |