Controlling fine touch sensations with polymer tacticity and crystallinity†
Abigail
Nolin
a,
Kelly
Pierson
a,
Rainer
Hlibok
a,
Chun-Yuan
Lo
b,
Laure V.
Kayser
 ab and
Charles
Dhong
ab and
Charles
Dhong
 *ac
*ac
aDepartment of Materials Science and Engineering, University of Delaware, Newark, DE, USA. E-mail: cdhong@udel.edu
bDepartment of Chemistry and Biochemistry, University of Delaware, Newark, DE, USA
cDepartment of Biomedical Engineering, University of Delaware, Newark, DE, USA
First published on 6th May 2022
Abstract
The friction generated between a finger and an object forms the mechanical stimuli behind fine touch perception. To control friction, and therefore tactile perception, current haptic devices typically rely on physical features like bumps or pins, but chemical and microscale morphology of surfaces could be harnessed to recreate a wider variety of tactile sensations. Here, we sought to develop a new way to create tactile sensations by relying on differences in microstructure as quantified by the degree of crystallinity in polymer films. To isolate crystallinity, we used polystyrene films with the same chemical formula and number averaged molecular weights, but which differed in tacticity and annealing conditions. These films were also sufficiently thin as to be rigid which minimized effects from bulk stiffness and had variations in roughness lower than detectable by humans. To connect crystallinity to human perception, we performed mechanical testing with a mock finger to form predictions about the degree of crystallinity necessary to result in successful discrimination by human subjects. Psychophysical testing verified that humans could discriminate surfaces which differed only in the degree of crystallinity. Although related, human performance was not strongly correlated with a straightforward difference in the degree of crystallinity. Rather, human performance was better explained by quantifying transitions in steady to unsteady sliding and the generation of slow frictional waves (r2 = 79.6%). Tuning fine touch with polymer crystallinity may lead to better engineering of existing haptic interfaces or lead to new classes of actuators based on changes in microstructure.
Introduction
Fine touch is the ability to localize and perceive the shape, size, and texture of objects, and is a critical source of information for people with low vision or blindness. When a finger slides across an object, mechanical forces are generated on the finger through friction and adhesion phenomena.1 These mechanical forces on the finger form the basis for tactile stimuli and give rise to tactile perception.Haptic devices are technologies that generate tactile sensations and have applications including virtual reality, robotics, and assistive communication devices. Currently, haptic devices are limited in the types of sensations they can create. Haptic devices typically generate tactile stimuli by changing physical features, such as mechanical vibrations, or physical pins and bumps (e.g. braille), to generate mechanical forces on the user's finger.2–5 To form more immersive environments in virtual reality, or higher quality assistive devices for people with low vision or blindness, haptic devices have increasing demands to recreate realistic tactile sensations or widen the variety of tactile sensations which can be generated.6,7 Technologies based on mechanical actuators have been developed extensively and therefore may not yield a breakthrough in creating new types of tactile sensations. In addition, while electrical stimulation—electrotactiles—are a common non-mechanical haptic actuator, the precise microscale control over electrodes has not translated to precise recreation of tactile stimuli due to indiscriminate depolarization of all mechanosensitive neurons.8 Indeed, electrotactiles can feel unpleasant.9 An alternate approach taken here is to control tactile sensations by using chemical properties, which encompasses materials phenomenon like surface energy, phase behavior, chemical structure, and microscale morphology.10–14 These chemical properties also impact adhesion and friction phenomena8 and could provide a new range of techniques in haptic interfaces. However, it is not known how to connect molecular scale effects, like polymer tacticity or crystallinity with human tactile perception. The challenge of connecting molecular scale effects with human performance is the inability to sufficiently describe friction with simple material properties such as a constant coefficient of friction, the human variability in applied force and sliding velocity, the contact mechanics of the finger, and the lack of established relationships between friction and tactile percepts.15–17
Here, we used polystyrenes with the same molecular formulas and similar number averaged molecular weights, which varied primarily in their tacticity, i.e., the relative stereochemistry of monomer units, and degree of polymer crystallinity, i.e., the regular packing of polymer chain segments into a molecularly ordered conformation. While increasing the degree of crystallinity is commonly known to increase bulk elastic modulus, increasing crystallinity also lowers frictional forces.11,12 Through dynamic friction testing with a mock finger and custom signal analysis, we predicted that humans are sensitive to as low as a difference of 11% in the degree of polymer crystallinity and verified our mechanical testing analysis with human psychophysical testing. Our findings show that even with identical chemical formulas and relatively smooth, rigid thin films, differences in the microstructure of polystyrene films can be used to generate distinctive tactile sensations. More broadly, these microstructures and morphologies extend to other types of polymers and could identify new material systems for use in haptic technologies.
Background
As a finger touches an object, mechanical stimulation originating from friction and adhesion forces activates afferent mechanosensory neurons in the fingertips. Mechanosensory neurons in the fingertips terminate into four primary end organs (Pacinian corpuscles, Ruffini endings, Meissner corpuscles, Merkel disks),1 each of which respond to a subset of frequencies and magnitudes of mechanical stimuli. The friction between the contacted surface and glabrous skin of the finger is dynamic and complex, varying both spatially and temporally across the finger during a touch event.16 To study the role of friction in touch, tactile discrimination has been explored by controlling surface texture and asperities through micropatterning techniques.18 Skedung et al. used elastomers with patterned wrinkles formed by surface buckling to identify a minimum feature size of 13 nm for discriminating objects purely by surface roughness.4 Sahli et al. designed randomly rough 3-D printed surfaces with an average RMS value of 0.4 mm and varied the Hurst roughness exponent and topographic shape to probe the ability of humans to discriminate randomly rough surfaces.19,20 They found that tactile discrimination was dominated by the microscale roughness, specifically differences in Hurst exponent as low as 0.2, rather than topographical resemblance. Higher microscale roughness contributed to higher frictional forces and subjects were able to notice differences in friction coefficients as small as 0.035.19In contrast to physical approaches like micropatterning, chemical approaches have also been used to probe frictional forces to elicit tactile discrimination. Previous work from Carpenter et al. compared a hydrophobic fluorinated self-assembled monolayer (SAM) deposited on a silicon wafer with a hydrophilic plasma-oxidized silicon wafer. Despite both surfaces being smoother than the physical limits of human perception of surface roughness as determined by Skedung,4 the two surfaces were discriminable to human subjects due to differences in friction traces originating from surface chemistry properties, most notably surface energy.21 Our previous work compared nine different SAMs deposited onto the silicon wafers and found that humans were able to discriminate monolayers which differed only by single or several atom differences due to a phase transition between a disordered and ordered monolayer.15 Humans were able to discriminate surface monolayers, even if the surfaces had similar surface energies. The mechanism of human discriminability was that disordered monolayers increase energy dissipation, resulting in additional frictional and adhesion forces compared to an ordered-like monolayer.15,22,23 A common feature in both these studies was that the frictional forces, i.e., tactile stimuli, were not derived from topography or physical roughness, but rather from chemical structure. These studies demonstrated the ability to design surfaces differentiable to fine touch with molecular level differences. In this work, we aimed to demonstrate that materials with the same chemical structure but different tacticity and degree of crystallinity, could be a new route to generate tactile sensations in haptic interfaces.
While silanes are a model system due to monolayer formation and systematic variation in functional groups, polymers are ubiquitous in industrial manufacturing24 and are often already present in haptic interfaces.7,25 It is common to tune the bulk properties, like stiffness, of a polymer, but polymer films have not been used to directly influence fine touch via nanoscale friction. Prior studies have showed that the chemical structure and morphology of polymers influences friction. Satyanarayana et al. compared differences in macroscale frictional forces of linear polymer, polyethylene, which is a molecularly flexible chain, and polystyrene, which is more molecularly rigid from the presence of bulky side-groups. Polyethylene films showed lower coefficients of friction, stiction, and wear than those of polystyrene. The more flexible molecular chain of polyethylene had more efficient molecular relaxation and energy dissipation under shear. In addition to chemical structure, the degree of crystallinity, also influences nanoscale frictional forces.10,12 Through atomic force microscopy, Gracias et al. compared frictional forces of isotactic (crystallinity = 63%) polypropylene with atactic polypropylene (crystallinity < 2%) and found that a higher degree of crystallinity increased molecular stiffness and lowered friction by allowing energy to more efficiently dissipate.11,12,14 Furthermore, crystalline polymers demonstrated a lower modulation of friction with applied loads than its amorphous counterpart due to higher shear strengths in crystalline polymers.12
While relationships between crystalline structure and frictional forces have been investigated at the nanoscale, our goal is to connect polymer crystallinity and mesoscale frictional forces to human tactile discrimination. However, the following three challenges remain between connecting materials phenomena to tactile discrimination in human subjects as described in previous work.15,16,21
Fine touch is not predicted with simple material properties
Developing a general relationship between tactile discrimination and polymer crystallinity is difficult because friction is not a material property but rather a dynamic property dependent on applied force and sliding velocity, both of which are variable when humans touch objects.16,17,21,26 Friction phenomena take place at multiple length scales and depend on the force applied and real contact area at the interface, which is influenced by both nanoscopic properties (i.e., van der Waals, lubrication, microscale roughness) and macroscopic properties (i.e., roughness, geometry, compliance of material).10 Thus, the frictional properties of a material cannot be fully described by a single value such as the coefficient of friction.A key limitation in using a constant coefficient to describe friction is that it does not explain how two materials with similar average friction forces (i.e., pressing harder on one surface to achieve the same overall friction force) can be routinely distinguished by humans. Instead of a constant friction force, oscillations in friction forces are generated when a finger slides across a surface. These oscillations arise from a mechanical phenomenon known as stick-slip friction.16,27 Stick-slip friction originates from a transient trapping of a portion of the finger (stick) and then subsequent energetic release (slip) as a finger slides across an object.16,21,27 This stick-slip occurs at multiple locations across the finger, but are linked through the elasticity of the finger.28,29 In addition to material properties, the magnitude and type of oscillation is dependent on the loading and velocity at the surface.30 While oscillations from stick-slip originate from microscale processes, the forces generated are apparent on the mesoscale and perceptible by humans (μ > 0.035).15,19
Contact mechanics of a finger and variability of human exploration
In “free exploration”, humans typically touch objects at a range of sliding velocities and pressures to arrive at a tactile perception.31 To account for this human variability, a common approach is to apply a restraint or apparatus on the subject's finger to control for the velocities and pressures applied during the tactile experience.32,33 However, this approach does not replicate how humans explore everyday objects, which lowers “ecological validity”, i.e., lowering the relevance of lab studies to real world conditions.8 Another approach which preserves free exploration is to track the tactile exploration with a camera and/or force plate.31 However, this approach is limited as it is unclear at which moment, or exploration condition, the tactile judgement was made, limiting the ability to connect the exploration conditions with tactile perception.8 In this study, we use an alternative approach established in our prior work15,21 which still permits free human exploration and accounts for human variability. During mechanical testing, we test across a range of pressures and velocities relevant to human exploration. Human exploration of a sliding finger occurs at velocities ∼1 mm s−1 to 100 mm s−1 and downward forces up to ∼1 N for fine texture discrimination.21,34,35 The friction traces produced across this range are then analyzed to provide the total amount of tactile stimulus available, i.e., the total differences in friction forces, across the expected range in human exploration. Our approach provides a method to quantify the potential tactile stimuli when subjects explore a surface without restricting the finger, accounts for human variability, and is independent of currently unresolved relationships between friction and human perception.15To predict tactile stimuli typically available to subjects, the mock finger mimics key parameters of a real human finger while keeping the mechanical testing within a feasible parameter space. The human finger is a multi-layered structure consisting of a rigid bone surrounded by soft tissue layers, with an overall effective modulus of ∼100 kPa.16,36 While soft, it is not sticky and sebum excretion makes the skin of the finger moderately hydrophilic (∼60° by water contact angle).15,37 While the shape of a finger is rounded, in a sliding motion the interface of the finger during contact rapidly approaches saturation in contact area (at ∼1 N force 90% contact area of the fingertip is achieved), providing an approximately planar, opposed to spherical interface.21,31,35,38 This straight edge interface is consistent with residue patterns left by human subjects.39 Finally, while a human finger typically possess fingerprints, these fingerprints vary from person to person. Our prior work showed that while fingerprints amplify differences in friction,16 surfaces which contained differences in friction for patterned mock fingers were qualitatively similar to flat fingers.21 This mock mechanical finger, even with a flat interface, was previously successful in predicting combinations out of a set of 36 possible pairs of silane monolayers which were both discriminable and not discriminable to human subjects.15
Unestablished relationships between friction and tactile perception
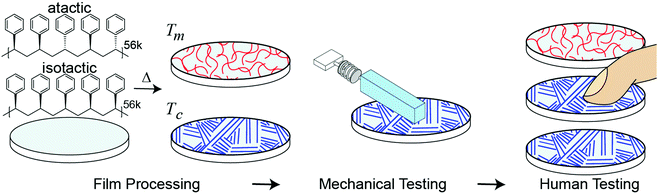
Separate from applications to touch or haptics, developing a relationship between molecular structure and mesoscale sliding friction is a historic challenge due to friction phenomena taking place at multiple lengths scales (atomistic to microscale) and the dependence of single asperity dynamics on both applied force and contact area.10,29,30,40,41 In addition to challenges in accurately modeling mesoscale friction, it is unclear which specific differences in frictional mechanical stimuli contribute to tactile discrimination. The appearance and shape of stiction spikes in friction has previously been suggested as important in encoding tactile discirmination.27,42 Gueorguiev et al.48 correlated human discrimination performance between commercial glass and PMMA with the force traces at the transitory phase leading to initial slip, but the correlation was relatively low and for a fixed applied load and velocity. Furthermore, these stick-slip events occur frequently and at multiple locations across a finger during human exploration. However, slips, or the incipient start of motion are an important aspect of tactile perception and are known to form a minimal unit of stimulation in the sensory cortex in experiments on mice by Schwartz et al.33Considering these challenges, our goal is to create a new way of generating tactile sensations by connecting a materials phenomenon, polymer crystallinity, with tactile perception. Fig. 1 outlines our approach. We spin-coated amorphous (atactic) and semi-crystalline (isostatic) polystyrene stereoisomers with similar molecular weights to generate thin and smooth (relative to human tactile sensitivity) films. The degree of crystallinity is further tuned through isothermal annealing at the crystallization temperature (Tc). As humans use friction to discriminate between surfaces,15,21,43 we quantify how much difference in macroscopic friction is present between the different surfaces through mechanical testing with a mock finger and custom analysis. To account for human variability, mechanical testing is performed at a range of applied forces and sliding velocities which encompasses typical human exploration. As two surfaces which show larger differences in friction across a relevant range of masses and velocities are likely to be easier for subjects to discriminate, we use mechanical testing to form predictions of human performance, which is validated with human psychophysical testing. Our approach addresses the previously identified challenges by measuring friction as a dynamic quantity, opposed to using a constant coefficient of friction, and accounts for the human variability of free exploration.
Experimental methods and rationale
Controlling the degree of crystallinity and surface preparation
The degree of crystallinity of polymer films can be tuned through tacticity and processing conditions. The stereoregularity of the phenyl side groups of isotactic polystyrene (iPS) provides a more flexible chain, enhancing chain mobility and allowing the chains to pack into a regular unit cell leading to the formation of crystalline structures known as lamallae.44,45 In contrast, the random stereochemistry of atactic polystyrene (aPS) prevents formation of a regular unit cell, resulting in a more energetically favorable amorphous state.44 As a result, iPS, unlike aPS, is a semi-crystalline polymer capable of forming crystalline regions.Polymer processing through spin-coating results in polymer films smoother (Ra < 7 nm) than the limits of human tactile discrimination of roughness,46 produces well-controlled thicknesses, and also induces a strain alignment of polymer chains parallel to the substrate.47,48 After initial deposition by spin-coating, crystalline growth can be further controlled through isothermal annealing—heating the polymer to a temperature between the melt and glass transition temperature.44,49 Isothermal annealing of iPS films has been well studied and this crystallization process is dependent on many factors including deposition technique, annealing temperature, length of exposure, molecular weight of polymer, and film thickness, all of which were controlled for in this study.46,49–52
Isotactic polystyrene (tacticity: 95%, PDI: 2.1, MW = 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) and atactic polystyrene (PDI: 1.2, MW = 58
000 g mol−1) and atactic polystyrene (PDI: 1.2, MW = 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) with matching number averaged molecular weights (Mn = 56
000 g mol−1) with matching number averaged molecular weights (Mn = 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) were purchased from Polymer Source, Inc. and dissolved in cyclohexanone. Films were prepared by spin-coating 1.0 wt% iPS or 1.4 wt% aPS cyclohexanone solutions onto polished silicon wafers. Prior to polymer coating, the silicon wafers were exposed to air plasma (Glow Plasma System, Glow Research) for one minute to provide some affinity to the surface, and the solutions were spun onto the wafers at 2000 rpm for 35 seconds. Film thicknesses were determined to be 45 nm ± 2.8 nm through ellipsometry. This thickness was chosen to limit solvent entrapment during the drying phase (thicknesses > 50 nm require extensive drying),49 while also be thick enough to permit the diffusion of polymer molecules during the crystallization of the polymer film (polymer films become kinetically trapped as thickness approaches the radius of gyration of a single polymer chain).49,53 As the film thickness was kept constant, the annealing time could be standardized across samples to control the degree of crystallization. Films were placed in a vacuum desiccator heated to 90 °C overnight (∼24 hours) to dry. To generate amorphous films, atactic polystyrene (aPS) and isotactic polystyrene (iPS) were melted at 230 °C (Tm: 222 °C) and quenched at room temperature using a cold metal plate to below the glass transition temperature (Tg ∼ 98 °C). Tm and Tg were verified by differential scanning calorimetry. For annealing crystallized films, isostatic polystyrene was melted, quenched, and then annealed at 175 °C for either 2 h (iPSA1) or 5 h (iPSA2) to induce varying degrees of crystallinity.49,54
000 g mol−1) were purchased from Polymer Source, Inc. and dissolved in cyclohexanone. Films were prepared by spin-coating 1.0 wt% iPS or 1.4 wt% aPS cyclohexanone solutions onto polished silicon wafers. Prior to polymer coating, the silicon wafers were exposed to air plasma (Glow Plasma System, Glow Research) for one minute to provide some affinity to the surface, and the solutions were spun onto the wafers at 2000 rpm for 35 seconds. Film thicknesses were determined to be 45 nm ± 2.8 nm through ellipsometry. This thickness was chosen to limit solvent entrapment during the drying phase (thicknesses > 50 nm require extensive drying),49 while also be thick enough to permit the diffusion of polymer molecules during the crystallization of the polymer film (polymer films become kinetically trapped as thickness approaches the radius of gyration of a single polymer chain).49,53 As the film thickness was kept constant, the annealing time could be standardized across samples to control the degree of crystallization. Films were placed in a vacuum desiccator heated to 90 °C overnight (∼24 hours) to dry. To generate amorphous films, atactic polystyrene (aPS) and isotactic polystyrene (iPS) were melted at 230 °C (Tm: 222 °C) and quenched at room temperature using a cold metal plate to below the glass transition temperature (Tg ∼ 98 °C). Tm and Tg were verified by differential scanning calorimetry. For annealing crystallized films, isostatic polystyrene was melted, quenched, and then annealed at 175 °C for either 2 h (iPSA1) or 5 h (iPSA2) to induce varying degrees of crystallinity.49,54
Surface characterization
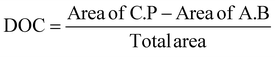 | (1) |
Mock finger preparation
The mock finger is made by curing a polydimethylsiloxane (PDMS) slab with dimensions of 1 cm × 1 cm × 5 cm around a 3-D printed acrylic cylindrical “bone” at 60 °C for one hour providing a finger with a dead weight of 5.6 g. The rectangular geometry ensures consistent nominal contact area even under different loading conditions, and as stated earlier, human subjects tend to leave residues with consistent width and straight edges even at low loads (∼1 N).15,16,31,39 The 3D printed bone provides mechanical rigidity and mechanical stiffness similar to the distal phalange within a human finger, and the elastic modulus of the PDMS is controlled by the ratio of base to crosslinker (30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to achieve 100 kPA, similar to the effective modulus of real fingertips.15,21 A real finger is deformable, but not sticky so the PDMS slab is then treated with UV/Ozone for four hours to remove viscoelastic tack to obtain a tackiness and surface energy similar to that of human skin (60° by water contact angle)14,15 While the rectangular, finite size of our mock finger means there could be edge effects and uneven pressure distributions, these conditions are also present in a real human finger, and we aim to recreate real scenarios in human touch, even if the scenarios are non-ideal for precision mechanical testing. Our goal with mechanical testing is to find differences in friction traces robust enough to be felt by most humans under many conditions. This simplified finger model controls for all the critical material properties of a real human finger to sufficiently measure frictional forces (i.e., tactile stimuli) present in tactile exploration.15,16,21
1) to achieve 100 kPA, similar to the effective modulus of real fingertips.15,21 A real finger is deformable, but not sticky so the PDMS slab is then treated with UV/Ozone for four hours to remove viscoelastic tack to obtain a tackiness and surface energy similar to that of human skin (60° by water contact angle)14,15 While the rectangular, finite size of our mock finger means there could be edge effects and uneven pressure distributions, these conditions are also present in a real human finger, and we aim to recreate real scenarios in human touch, even if the scenarios are non-ideal for precision mechanical testing. Our goal with mechanical testing is to find differences in friction traces robust enough to be felt by most humans under many conditions. This simplified finger model controls for all the critical material properties of a real human finger to sufficiently measure frictional forces (i.e., tactile stimuli) present in tactile exploration.15,16,21
Mechanical testing
To collect stick-slip friction traces of materials for predictions of human performance, a custom mechanical apparatus setup was used to measure the friction of our elastic, but not sticky, mock finger at added masses (relative to the dead weight, 5.6 g of the finger), M = 0, 25, 75, and 100 g, and velocities, v = 5, 10, 25, and 45 mm s−1, conditions which are consistent with human exploration.15,21 The mock finger was loaded with the desired mass and brought into a contact length of 1 cm, resulting in a contact area of 1 cm × 1 cm. The finger was slid for a distance of 4 mm using a motorized stage (V-508 PIMag Precision Linear stage, Physikinstumente) across the surface while friction force was measured with a Futek 250 g force sensor (k = 13.9 kN m−1, peak-to-peak noise of 0.1 mN), sampling at 800 Hz (Keithley 7510 DMM), sufficient to capture signals important to mechanoreceptors in fine touch (∼40–400 Hz).57 The finger was slid four separate times, where the first slide was discarded to eliminate erroneous effects due to aging from testing setup. We obtained these three slides on three fresh spots for each condition. In sum, each surface was tested under 16 combinations of masses and velocities, with nine friction traces at each combination.Results
Surface characterization
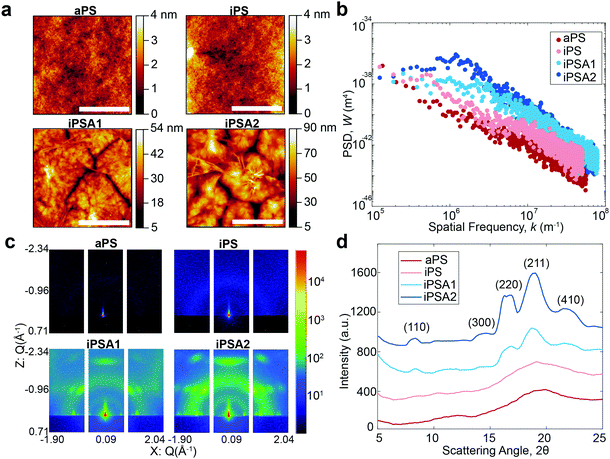
A summary of surface characterization of the polystyrene films is shown in Table 1. Water contact angle measurements have a similar value for all films, and the low hysteresis indicates a relatively homogeneous surface. Film uniformity as measured by roughness parameters and Hurst exponent was measured via AFM and the degree of crystallinity was obtained by GIWAXS.| Polymer film | Annealing (hours) | Water contact angle (°) | Roughness (Ra, nm) | Roughness (Rpm, nm) | Hurst exponent (H) | Degree of crystallinity |
|---|---|---|---|---|---|---|
| aPS (atactic Polystyrene) | None | (89.4–86.4) ± 1.82 | 0.20 | 1.3 | 0.17 | 0% |
| iPS (isotactic Polystyrene) | None | (92.1–87.6) ± 1.85 | 0.34 | 2.6 | 0.71 | 4% |
| iPSA1 (isotactic Polystyrene) | 2 | (93.9–88.1) ± 3.34 | 3.1 | 12 | 0.98 | 15% |
| iPSA2 (isotactic Polystyrene) | 5 | (90.6–84.9) ± 2.40 | 4.7 | 19 | 0.96 | 35% |
AFM height images shown in Fig. 2a revealed lamellar crystals in the form of multilayer assemblies for the annealed films, iPSA1 and iPSA2. Annealing at 175 °C resulted in the growth of flat-on lamellae with overgrowth terraces resulting from a profusion of screw dislocations as well as some branched lamellae.46,49–52,54 This morphology was consistent across all sections of the wafer which is shown in Fig. S2 of ESI.† In contrast, the unannealed films, iPS and aPS, did not show these crystalline structures. iPS does show some small features, potentially some single lamellar structures, but is a predominantly amorphous film and looks more similar to aPS than the annealed films.
Annealed films resulted in an increase in roughness compared to unannealed films, but this was expected as isothermal annealing of polymers and subsequent crystallization is known to increase surface roughness.61,62 Isothermal annealing increases the nanoscale roughness of films due to the growth of higher-order structures, specifically lamellar crystal formations that become confined by grain boundaries with continued growth. The scale bar in the AFM height images for the annealed films shows this effect as the largest peak-to-peak height of the higher order structures is ∼50 nm for iPSA1 and ∼90 nm for iPSA2. AFM measurements provide high detail over microscale areas, but do not capture the average roughness of the film across meso- or macroscale. Ellipsometry which measures larger sample areas, confirmed an average thickness of 45 nm in all films after annealing.
Molecular roughness scaling behavior was quantified by taking a power spectrum density function (PSD) (Gwyddion software, Fig. 2b) of the larger area scan AFM height images (100 μm × 85 μm, Fig. S1 of ESI†). On a log(PSD) versus log(kspatial freq.) plot, the absolute value of the slope in the linear regime is related to the fractal dimension Df by Df = 0.5(7 − |slope|), and the roughness scaling factor, Hurst exponent (H), is determined by H = 0.5(|slope| − 1).20,63 The films iPS and aPS have one linear fit at all length scales with relatively small slopes, resulting in a small H and evidence of a single characteristic roughness at all length scales.63,64 iPSA1 and iPSA2 show a non-linear region at low frequencies, and a relatively large slope at high frequencies, resulting in a large H and evidence of changes in surface features upon scaling.63
The annealed films result in a non-linear PSD and large H, indicating heterogeneous contributions to roughness.64 This heterogeneity arises from the induced lamellae formations in individual ordered semicrystalline structures which have a roughness which differs from the roughness of the surface as a whole. In contrast, the unannealed films show relatively uniform roughness at all length scales evidenced by the linear PSD. Previously, in small molecule self-assembled monolayers (SAMs), we used the Hurst exponent to define the degree of ordering in a monolayer, where a non-linear PSD and large H described a disordered monolayer.15 The Hurst exponent in these polymer films has the opposite relationship with ordering because SAMs were a smaller length scale and these polymers have a new length scale of roughness originating from the microscale formation of lamellae crystals.
For the iPS films, the PSD also reveals a maximum which can be correlated to the characteristic spacing of semi-periodic height features (Fig. 2b). A maximum is seen for iPSA2 at 1.2 × 106 m−1 which indicates a characteristic spacing of 5.2 μm or 5200 nm. iPSA1 has a maximum appearing at 2.3 × 106 m−1 which indicates a characteristic spacing of 2.7 μm or 2700 nm. These spacings are an order of magnitude larger than the spacings cited in Skedung (760 nm) to differentiate small periodic structures through purely physical means. The iPS film also shows a maximum at 0.56 × 106 m−1 possibly due to uncontrolled small, scattered crystalline structures, which correlates to a characteristic spacing of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 nm or 10 μm. In contrast, no maximum or transition in slope is apparent in the aPS film's PSD indicating a featureless film and similar roughness at all length scales.
000 nm or 10 μm. In contrast, no maximum or transition in slope is apparent in the aPS film's PSD indicating a featureless film and similar roughness at all length scales.
For tactile perception, in all cases, the average roughness is lower than the detectable limit of perceived physical roughness, so we expect to attribute human performance on these films to molecular effects instead of straightforward differences in roughness. Yet, the PSD still quantifies and categorizes the molecular roughness and morphology of the surfaces.
The degree of crystallinity (DOC) in the semi-crystalline films (Table 1) was also quantified through the X-ray scattering using the atactic polystyrene as the amorphous baseline, i.e., a degree of crystallinity of 0%. Degree of crystallinity is calculated from the corresponding 1D graphs of signal intensity as a function of scattering angle (2θ) (Fig. 2d) with eqn (1). First, the amorphous background (aPS) is subtracted and the remaining crystalline peaks are integrated. The integral of the crystalline peaks is then divided by the total area of coherent scattering55 to calculate the degree of crystallinity. The Miller Indices of the crystalline reflections are indicated. aPS, amorphous polystyrene, provided two broad peaks indicating many short-range order interactions at the atomic scale, consistent with amorphous behavior.55,67 While a few structures were seen for iPS in AFM, scattering provides an average signal of microstructure across the entire film. iPS showed a small characteristic crystallinity peak forming at 2θ = ∼19. This resulted in a calculated degree of crystallinity of 4%, but iPS films could be considered practically amorphous. In contrast, the annealed films, iPSA1 and iPSA2, show the appearance of more pronounced peaks at characteristic scattering angles, demonstrating preferential atomic ordering, i.e., crystalline structure, resulting in a degree of crystallinity of 15% for iPSA1 and 35% for iPSA2. Additional details on the crystallinity calculation are shown in Fig. S3 of ESI.†
Through AFM and GIWAXS, we were able to quantify and control the crystallinity of the films and confirm that the surface roughness was sufficiently low as to make differences in crystallinity the dominant contributor to friction, i.e., tactile stimuli, for subsequent mechanical and human testing.
Mechanical testing
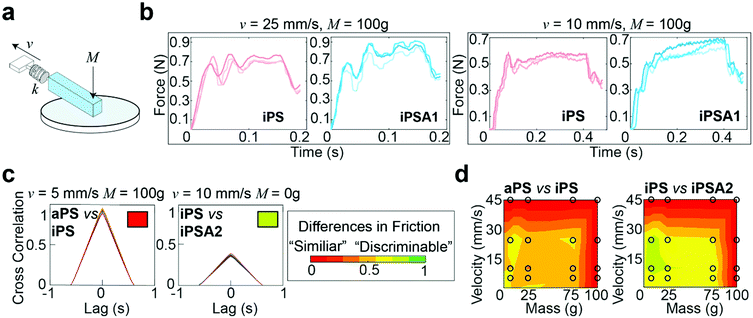
A custom mechanical testing apparatus (schematic shown in Fig. 3a) was used to measure the mesoscale friction between a mock finger and polymer films at a combination of 16 sliding velocities and applied masses relevant to human exploration conditions. To combine the experimental space of masses, velocities, and material surfaces into a prediction of tactile performance, we analyzed the presence of stick-slip friction and quantified the total similarities or differences between friction traces through cross-correlation.16,21 The underlying hypothesis was that humans use friction on the finger as a tactile cue, thus two surfaces which generate similar friction forces under most applied masses and velocities are probably more difficult for subjects to discriminate, whereas two surfaces which generate distinctive friction forces are probably easier for subjects to discriminate.15,19Fig. 3b shows representative friction traces generated on the mock finger sliding across the iPS and iPSA1 films. All films produced oscillations characteristic of stick-slip friction traces, and the magnitudes of these oscillations were in a perceptible range of friction forces (μ = F/Fn > 0.035), i.e., coefficients of friction (μ) were on average ∼0.1.19 For the iPS film at v = 25 mm s−1 and M = 100 g, the relatively large amplitude, low frequency oscillations are characteristic of slow frictional waves—elastic instabilities that occur as a competition between adhesion (via friction) and elasticity.68 Under the same conditions, the iPSA1 film also forms slow frictional waves. Forces generated by stick-slip friction have been suggested as a source of tactile stimuli to inform tactile discrimination.27,42 Thus, the lack of distinctive features in the friction traces from iPS and iPSA1 at v = 25 mm s−1 and M = 100 g suggest that these two surfaces may be non-discriminable to humans at these experimental conditions. However, the periodic waves disappear for iPSA1 at a lower velocity, v = 10 mm s−1, while the iPS film maintains at least two clear periodic waves. This gives rise to two observations. First, at v = 10 mm s−1 and M = 100 g, iPS and iPSA1 could now have sufficiently distinct friction traces to where humans can now discriminate the two surfaces, despite their similarities at v = 25 mm s−1 and M = 100 g. Second, as humans explore objects freely at multiple conditions, the condition-dependent appearance or disappearance of these distinctive oscillations means that examining a few isolated conditions may yield inaccurate predictions about human behavior. This second observation supports our approach for testing multiple velocities and masses.
To more rigorously quantify the similarity or dissimilarity between friction traces, we used cross-correlation analysis between the traces of different surfaces15,21 as shown in Fig. 3c. Two surfaces which generate similar friction traces, i.e., high correlations, under most human exploration conditions are likely more difficult for humans to discriminate, and surfaces which generate distinctive friction traces, i.e., low correlations, under most human exploration conditions are likely easier for humans to discriminate. The similarity was quantified by cross-correlating the friction traces of each film at each given applied mass and velocity. The cross-correlation is normalized by the absolute magnitude of both input vectors and calculated by eqn (2):15
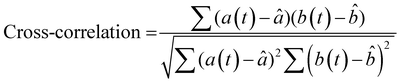 | (2) |
By combining the parameterized cross-correlation at each velocity and mass, a discriminability matrix can be constructed. The discriminability matrices shown in Fig. 3d summarize the differences in frictional trace parametric values by AUC between the films across all the experimental space where red is high similarity (i.e., likely less discriminable to humans) and green is low similarity (i.e., likely more discriminable by humans). Matrices which show more green regions indicate surfaces that are likely easier to discriminate under a wider range of exploration conditions. This discriminability matrix suggests that the polymer films, iPS vs. iPSA2, are likely more discriminable by human subjects compared to iPS vs. aPS.
Human subjects testing
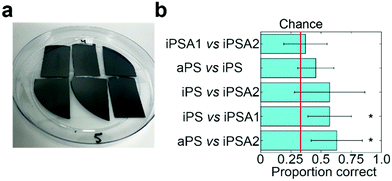
To verify if humans can tell apart the surfaces identified by friction trace analysis, we performed human psychophysical testing using the three-alternative forced choice test (Fig. 4a, IRB approval in acknowledgements).21 Subjects are presented three surfaces: two of the same surfaces and one of a different surface. The location and the material used as the single alternative is randomized across trials. Subjects are told to freely explore each surface and identify which is unlike the other two. This task is then repeated in five sequential trials. Subjects were untrained and did not touch the samples before testing. The annealed films had a slight blue hue when held under light at certain angles. While most participants did not notice this hue (samples are not visibly distinguishable in Fig. 4a), as a precaution, all tests were carried out inside a 1 ft × 1 ft dark photo light box as to block the lights and provide a visual barrier.Subjects successfully discriminated between two pairs of films (Fig. 4b). Subjects were able to discriminate between iPS vs. iPSA1 (accuracy = 57.1%, t = 3.51, Cohen's d = 1.24, p < 0.05) and aPS vs. iPSA2 (accuracy = 62.9%, t = 3.65, Cohen's d = 1.43, p < 0.05) with statistical significance. Subjects, on average, were able to discriminate between aPS vs. iPS, (accuracy = 45.7%, Cohen's d = 0.70, p > 0.05) and iPS vs. iPSA2 (accuracy = 57.1%, Cohen's d = 0.96, p > 0.05), but results were not statistically significant. iPSA1 vs. iPSA2 (accuracy = 37.1%, Cohen's d = 0.20, p > 0.05) was very close to chance (33%) and subjects were therefore not able to discriminate between these two surfaces.
Human testing showed that amorphous polystyrene and semi-crystalline polystyrene offers sufficient frictional difference for successful tactile discrimination. While aPS vs. iPS on average were discriminable above chance (45.7% vs. 33%), iPS vs. iPSA1 (57.1%) and aPS vs. iPSA2 (62.9%) had a higher accuracy. This follows a trend with increasing differences in crystallinity as both aPS vs. iPSA2 and iPS vs. iPSA1 have a larger difference in the degree of crystallinity than aPS vs. iPS (11% and 35%, respectively, vs. 4% see Table 1). However, the degree of crystallinity alone is not sufficiently predictive of human tactile performance. iPSA1 vs. iPSA2 also had a relatively large difference in degree of crystallinity (20%) but were not discriminable, and the difference in crystallinity between the discriminable iPS vs. iPSA1 and the non-discriminable aPS vs. iPS is only 7%. In the case of iPSA1 vs. iPSA2, both films exhibited crystalline structure, rather than one film being amorphous and the other semi-crystalline like the case of iPS vs. iPSA1 and aPS vs. iPSA2. Humans do not sense crystallinity directly. Rather, the ability for humans to distinguish the surfaces arises from differences in friction originating crystalline structure. Finally, the polymer films were also sufficiently robust to survive human touch, which supports the role of film crystallinity as the source of tactile contrast (Fig. 4a and Fig. S4 of ESI†).
Discussion
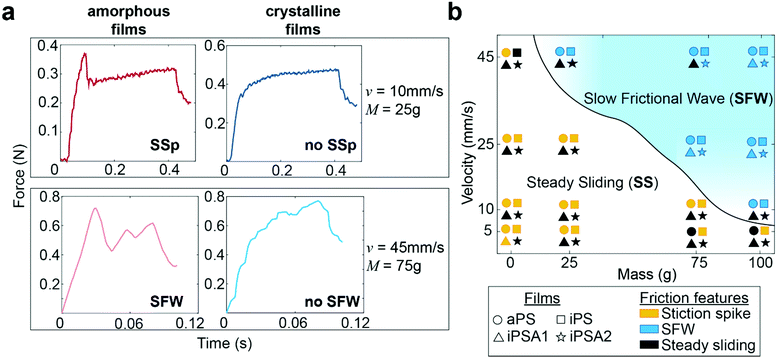
Human testing results indicate no difference in perception between the two crystalline films iPSA1 vs. iPSA2 (Fig. 4b) and no significant perception between the two amorphous films aPS vs. iPS. However, subjects successfully discriminated amorphous films, aPS and iPS, from crystalline films, iPSA2 and iPSA1, respectively. In correlating human testing results with the mechanical testing on mock fingers, described earlier in Fig. 3, the friction traces produced on the amorphous films not only had quantitative (parametric values from cross-correlation traces) but also qualitative differences in friction features compared to the crystalline films. These friction features are the presence of a stiction spike, transitions between steady and unsteady sliding, and the generation of slow frictional waves,68–70 as shown in Fig. 5a.The first friction feature is the appearance of stiction spikes (SSp, top row of Fig. 5a). A stiction spike71 is where the sliding finger overcomes an adhesive contact interface, and the energetic breaking or melting of this contact produces static friction forces larger than the kinetic friction forces produced once contact is broken.72 Stiction spikes are indicative of a slow molecular relaxation mechanism and are associated with polymer wear.73,74 These stiction spikes are due to increased frictional force dissipation and occur when surfaces are slid at a shear rate similar to the molecular relaxation of the interface.72 While aged, deformable interfaces are likely to generate prominent stiction spikes, samples were always pulled once prior to data acquisition to remove any artifacts from test preparation. Consequently, the generation or absence of prominent stiction spikes during sequential pulls indicates differences originating from the film's properties. At the conditions tested here, stiction spikes appeared much more frequently for aPS and iPS films than for iPSA1 and iPSA2 films. aPS films have previously shown high prevalence of stiction and wear in the literature due to their bulky chain and amorphous nature resulting in large chain entanglement and inefficient energy dissipation.11,72 iPS, while a more flexible chain than aPS, contains the same bulky side groups and also retains the chain entanglement of an amorphous state. In contrast, the annealed films, iPSA1 and iPSA2, are in a semi-crystalline state in which organized polymer chains can more quickly respond to shear, resulting in less frequent stiction.11,73
The second friction feature was the generation of slow frictional waves (SFW, bottom row of Fig. 5a). These distinct waves are due to instabilities formed at soft, adhesive interfaces (such as the human finger) from the competition between adhesion (i.e., friction) at the interface and elasticity of a sliding object.68,70 Slow frictional wave generation was defined here as two or more periodic peaks of an amplitude ≥ 0.03 N. With increasing velocities, there is a transition from steady sliding with or without stiction to unsteady sliding producing distinct waves.72 These slow frictional waves are visible at a sliding velocity of 10 mm s−1 and the largest applied load of 100 g (∼1 N) where the friction traces of aPS and iPS films begin to propagate larger amplitude, lower frequency oscillations. At 25 mm s−1, crystalline films iPSA1 and iPSA2, also propagate slow frictional waves, but slightly less prominently compared to the amorphous films. Transitions from steady sliding to slow frictional waves generation are known to occur with increasing velocity.69,70 During this transition, the interface dynamics change from smaller local detachments to large interface detachments, resulting in wave nucleation. The critical velocity for this transition and its range depends on the material and adhesion properties of the interface: an interface with low adhesive energy and high molecular stiffness is expected to decrease dissipation effects, thus requiring a larger critical velocity to initiate this friction instability.68,75 Therefore, the higher critical velocity required to produce slow frictional waves for iPSA1 and iPSA2 films is expected since crystalline structure can more quickly dissipate shear forces due to chain alignment and efficient molecular chain relaxation.13
At 45 mm s−1, amorphous films demonstrate steady sliding only at the lowest applied loads (0 g applied onto the deadweight of the finger) while crystalline films transition away from periodic waves to steady sliding even at higher applied loads (75 g, Fig. 5a bottom row). In other words, the crystalline films require relatively higher loads to achieve similar friction dynamics to the amorphous films. The relevance of this to human testing and touch perception is that the crystalline films would need to be pressed harder to achieve similar friction dynamics to the amorphous films. While these friction traces in the steady sliding regime retain some irregular instability peaks (Fig. 5a bottom row), overall, there was a disappearance in large scale periodic wave formation and a transition towards steady sliding at the highest velocity and low loads.
The phase diagram in Fig. 5b summarizes the differences in friction features amongst the films, where the solid line shows the transitions from steady sliding to slow frictional waves. Overall, polymer crystallinity appeared to affect the transitions to wave propagation at velocities 10 mm s−1 and 45 mm s−1 and applied loads at high velocity (0–75 g). As stated earlier, we expect that during free exploration, subjects would reasonably use this range of velocities and masses. Successful human discriminability verified that there was sufficient crystalline structure induced by iPSA1 at the interface to result in the characteristic transition in friction dynamics, and these could be important in distinguishing between amorphous films and crystalline films.
To quantify the relationship between the presence of friction features (Fig. 5b) and human testing results, the number of experimental conditions in which the two films resulted in different friction features, denoted as “phase differences,” was used as a predictor of subject's accuracy through linear regression analysis. Fitting the average accuracy in human testing yielded the linear model shown in eqn (3). p < 0.041, r2 = 79.6%. Fitting the effect size (Cohen's d) from human testing also yielded a predictive linear model shown in eqn (4). p < 0.08, r2 = 67.4%. The high correlation of human behavior by phase differences indicates that human discriminability may use these phase differences in fine touch.
| Accuracy = 0.396 + 0.0152 × ∑phase differences | (3) |
| Effect size = 0.377 + 0.0645 × ∑phase differences | (4) |
We also considered the parametric values quantified from the cross-correlations as predictors for linear regression analysis. In our prior work on silane monolayers,15 skew was a strong predictor of tactile performance. Here, skew alone had a lower, but positive correlation (r2 = 49.7% for averaged accuracy, r2 = 29.7% for effect size). This is not surprising as the polymers here are a different material system, with a different microstructure from AFM (Fig. 2a), and different mechanisms underlying the transitions in friction dynamics between samples. Given these differences, the fact that skew still correlates with human performance across two different material systems leads us to speculate that skew may be related to a basic mechanism behind tactile discriminability.
In the introduction, we stated that simple material properties do not necessarily predict human performance. Here also, we saw that accuracy and effect size were not highly correlated with material properties. Difference in degree of crystallinity had a low but positive correlation (r2 = 25.7% for averaged accuracy, r2 = 11.9% for effect size) and surface energy had a negative correlation. Roughness did have a high, positive correlation (r2 = 79.1% for averaged accuracy, r2 = 62.3% for effect size). This was expected because the presence of crystalline structure directly affected the nanoscale roughness, where the crystalline films had higher roughness than the amorphous films. Thus, in this case, roughness served as a predictor since crystalline vs. amorphous structure was the parameter which led to successful tactile discrimination. While there could be some contribution from roughness in our most successful pair (aPS vs. iPSA2) because our average peak-to-peak roughness is similar to the roughness distinguishable by purely physical means (Rpm > 13 nm), the average roughness remained lower than those distinguishable by purely physical means (Ra < 7 nm). Furthermore, these surfaces were isotropic and the effect of the peak-to-peak roughness would be lessened.59 Indeed, human subjects successfully discriminated between iPS vs. iPSA1 (Rpm = 2.6 nm vs. Rpm = 12, respectively) which is below the known limits of both Rpm and Ra. Therefore, roughness should be considered as a covariate with crystallinity.
The annealed films, iPSA1 and iPSA2, had nm-length height features over a characteristic length of 2.7 μm and 5.2 μm, respectively, which could conceivably influence friction force oscillations. To quantify the potential influence of the surface topography of the annealed films on friction oscillations, the period of the oscillations was evaluated using a Fast Fourier Transform (FFT) of the friction trace data (Fig. S5 of ESI†). The FFT on the slow frictional wave oscillations revealed a periodicity of 0.02–0.045 s depending on the conditions (i.e., velocity). Multiplying periodicity by the respective velocities resulted in characteristic lengths of ∼0.9–1.2 mm, or 900–1200 μm, a length scale much larger than the crystalline structures. Thus, these differences in oscillations between films are likely not related to the height structures formed by crystallinity, and rather through adhesion and friction phenomena originating from differences in polymer crystallinity.
While differences in frictional forces and tactile discrimination were observed between the amorphous and crystalline films, the differences were not as strong as some of our previous experiments comparing self-assembled monolayers15 likely due to the overall large stiffness of all the polymers films due to high confinement. Spin-coating as well as the thin films confines polymer chain movement increasing the stiffness of the polymer. This stiffening effect may have downplayed the role of crystalline structure on frictional forces and tactile discrimination. Future work could better exploit the effect of crystalline structure by processing thicker, less constrained films or melts, or polymers with a lower Tg.
Tactile discriminability was most strongly correlated with differences in friction features amongst these polymer films. Differences in these friction instabilities may serve as a better predictor across broader material systems, as these are established methods to categorize stick-slip friction behavior, opposed to skew or other values from our cross-correlation analysis. This analysis thus suggests that to create tactile contrast in polymer films, materials should promote differences in friction features, specifically stiction spikes and slow frictional waves, at multiple masses and velocities relevant to human exploration.
Conclusions
Through mechanical testing and human testing, we showed that humans can distinguish surfaces which differed only in the degree of crystallinity, even in smooth surfaces with the same chemical structure. Our mock finger and analysis yielded useful predictions of human performance, therefore minimizing the need for human testing. The mechanism of tactile discriminability originated from the reduced dissipation of friction in the more crystalline films. From an analysis of the friction traces, we found that human performance was strongly correlated with the number of transitions in friction features, specifically the absence or presence of a stiction spike, and the generation of slow frictional waves. This correlation suggests that humans may use transitions in friction features in fine touch. Consequently, it may be possible to generate higher tactile contrast between two surfaces by designing these transitions to occur at ranges of applied masses and velocities found in human exploration. Traditionally, crystallinity and microstructure morphology is widely used to engineer polymer performance in diverse applications and can now also be harnessed to engineer fine touch. The design of tactile interfaces through chemical and materials phenomenon may yield new classes of haptic actuators, provide greater variety in tactile devices, and provide a new toolkit to study basic aspects of tactile perception.Author contributions
A. N., K. P., R. P., and C. L. performed experiments. A. N., L. K., and C. D. conceptualized the study, performed analysis, and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Atomic force microscopy access was supported by grants from the NIH-NIGMS (P20 GM103446), the NSF (IIA-1301765) and the State of Delaware and conducted at the DBI Bio-Imaging Center at the University of Delaware. Xenocs GIWAXS measurements were conducted at the Advanced Materials Characterization Lab at the University of Delaware. This study was conducted and approved by the Institutional Review Board of the University of Delaware (Project #1484385-2). Data were collected from a total of 8 healthy volunteers between the ages of 18 and 40. Funding. We acknowledge support from the National Eye Institute of the NIH (R01EY032584-01) and the University of Delaware Research Foundation.References
- C. R. Noback, N. L. Strominger, R. J. Demarest and D. A. Ruggiero, The Human Nervous System Structure and Function, Humana Press Inc., 6th edn, 2005 Search PubMed.
- M. Ayyildiz, M. Scaraggi, O. Sirin, C. Basdogan and B. N.-J. Persson, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 12668–12673 CrossRef CAS PubMed.
- Y. Abe, M. Fujiwara, Y. Makino and H. Shinoda, IEEE Trans. Haptics, 2021, 14, 260–265 Search PubMed.
- L. Skedung, M. Arvidsson, J. Y. Chung, C. M. Stafford, B. Berglund and M. W. Rutland, Sci. Rep., 2013, 3, 2617 CrossRef PubMed.
- E. Jarocka, J. A. Pruszynski and R. Johansson, J. Neurosci., 2021, 41(16), 3622–3634 CrossRef CAS PubMed.
- F. Sorgini, R. Caliò, M. C. Carrozza and C. M. Oddo, Disabil. Rehabil. Assist. Technol., 2018, 13, 394–421 CrossRef PubMed.
- J. Yin, R. Hinchet, H. Shea and C. Majidi, Adv. Funct. Mater., 2021, 31, 2007428 CrossRef CAS.
- D. J. Lipomi, C. Dhong, C. W. Carpenter, N. B. Root and V. S. Ramachandran, Adv. Funct. Mater., 2019, 30, 1–15 Search PubMed.
- S. E. Root, C. W. Carpenter, L. V. Kayser, D. Rodriquez, D. M. Davies, S. Wang, S. T.-M. Tan, Y. S. Meng and D. J. Lipomi, ACS Omega, 2018, 3, 662–666 CrossRef CAS PubMed.
- A. Vanossi, D. Dietzel, A. Schirmeisen, E. Meyer, R. Pawlak, T. Glatzel, M. Kisiel, S. Kawai and N. Manini, Beilstein J. Nanotechnol., 2018, 9, 1995–2014 CrossRef CAS PubMed.
- N. Satyanarayana, S. K. Sinha and L. Shen, Tribol. Lett., 2007, 28, 71–80 CrossRef CAS.
- D. H. Gracias and G. A. Somorjai, Macromolecules, 1998, 31, 1269–1276 CrossRef CAS.
- N. K. Myshkin and A. V. Kovalev, Polymer Tribology, IMPERIAL COLLEGE PRESS, 2009, pp. 3–37 Search PubMed.
- D. Wang and H. Ishida, Comptes Rendus Chim., 2006, 9, 90–98 CrossRef CAS.
- A. Nolin, A. Licht, K. Pierson, C.-Y. Y. Lo, L. V. Kayser and C. Dhong, Soft Matter, 2021, 17, 5050–5060 RSC.
- C. Dhong, L. V. Kayser, R. Arroyo, A. Shin, M. Finn, A. T. Kleinschmidt and D. J. Lipomi, Soft Matter, 2018, 14, 7483–7491 RSC.
- O. Ben-David and J. Fineberg, Phys. Rev. Lett., 2011, 106, 1–4 CrossRef.
- A. Gedsun, R. Sahli, X. Meng, R. Hensel and R. Bennewitz, Adv. Mater. Interfaces, 2022, 9, 2101380 CrossRef.
- R. Sahli, A. Prot, A. Wang, M. H. Müser, M. Piovarči, P. Didyk and R. Bennewitz, Sci. Rep., 2020, 10, 1–12 CrossRef PubMed.
- T. D.-B. Jacobs, T. Junge and L. Pastewka, Surf. Topogr. Metrol. Prop., 2017, 5(1), 013001 CrossRef.
- C. W. Carpenter, C. Dhong, N. B. Root, D. Rodriquez, E. E. Abdo, K. Skelil, M. A. Alkhadra, J. Ramírez, V. S. Ramachandran and D. J. Lipomi, Mater. Horiz., 2018, 5, 70–77 RSC.
- A. Lio, D. H. Charych and M. Salmeron, J. Phys. Chem. B, 1997, 101, 3800–3805 CrossRef CAS.
- S. Watson, M. Nie, L. Wang and K. Stokes, RSC Adv., 2015, 5, 89698–89730 RSC.
- L. Benyahia, C. Verdier and J.-M. Piau, J. Adhes., 1997, 62, 45–73 CrossRef CAS.
- S. Biswas and Y. Visell, Adv. Mater. Technol., 2019, 4, 1900042 CrossRef.
- W. Tang, N. Chen, J. Zhang, S. Chen, S. Ge, H. Zhu, S. Zhang and H. Yang, Tribol. Lett., 2015, 58, 28 CrossRef.
- C. Waiblinger, D. Brugger, C. J. Whitmire, G. B. Stanley and C. Schwarz, Front. Integr. Neurosci., 2015, 9, 1–11 Search PubMed.
- J. H.-E. E. Cartwright, E. Hernández-García and O. Piro, Phys. Rev. Lett., 1997, 79, 527–530 CrossRef CAS.
- A. Ruina, J. Geophys. Res., 1983, 88, 10359–10370 CrossRef.
- A. Vanossi, N. Manini, M. Urbakh, S. Zapperi and E. Tosatti, Rev. Mod. Phys., 2013, 85, 529–552 CrossRef CAS.
- M. J. Adams, S. A. Johnson, P. Lefèvre, V. Lévesque, V. Hayward, T. André and J.-L. L. Thonnard, J. R. Soc., Interface, 2013, 10, 20120467 CrossRef.
- A. Moscatelli, M. Bianchi, A. Serio, A. Terekhov, V. Hayward, M. O. Ernst and A. Bicchi, Curr. Biol., 2016, 26, 1159–1163 CrossRef CAS.
- M. Farajian, R. Leib, H. Kossowsky, T. Zaidenberg, F. A. Mussa-Ivaldi, I. Nisky and E. Vaadia, eLife, 2020, 9, 1–38 CrossRef PubMed.
- K. Kuramitsu, T. Nomura, S. Nomura, T. Maeno and Y. Nonomura, Chem. Lett., 2013, 42, 284–285 CrossRef CAS.
- C. Dhong, R. Miller, N. B. Root, S. Gupta, L. V. Kayser, C. W. Carpenter, K. J. Loh, V. S. Ramachandran and D. J. Lipomi, Sci. Adv., 2019, 5, 5–7 Search PubMed.
- Y. Yuan and R. Verma, Colloids Surf., B, 2006, 48, 6–12 CrossRef CAS PubMed.
- A. Mavon, H. Zahouani, D. Redoulesc, P. Agache, Y. Gall and P. Humbert, Colloids Surf., B, 2001, 179, 131 CrossRef.
- G. J. Gerling, S. C. Hauser, B. R. Soltis, A. K. Bowen, K. D. Fanta and Y. Wang, IEEE Trans. Haptics, 2018, 11, 498–508 Search PubMed.
- B. M. Dzidek, M. J. Adams, J. W. Andrews, Z. Zhang and S. A. Johnson, J. R.Soc., Interface, 2017, 14(127), 20160935 CrossRef.
- N. Manini, O. M. Braun, E. Tosatti, R. Guerra and A. Vanossi, J. Phys.: Condens. Matter, 2016, 28(29), 293001 CrossRef CAS PubMed.
- J. Chen, A. R. Niemeijer and C. J. Spiers, J. Geophys. Res. Solid Earth, 2017, 122, 9627–9657 CrossRef.
- D. Gueorguiev, S. Bochereau, A. Mouraux, V. Hayward and J.-L. L. Thonnard, Sci. Rep., 2016, 6, 1–7 CrossRef PubMed.
- D. P. Vallette and J. P. Gollub, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1993, 47, 820 CrossRef PubMed.
- P. C. Hiemenz, Polymer Chemistry, CRC Press, 2007 Search PubMed.
- K. Grigoriadi, J. B.-H. M. Westrik, G. G. Vogiatzis, L. C.-A. Van Breemen, P. D. Anderson and M. Hütter, Macromolecules, 2019, 52, 5948–5954 CrossRef CAS PubMed.
- S. Sawamura, H. Miyaji, K. Izumi, S. J. Sutton and Y. Miyamoto, J. Phys. Soc. Jpn., 1998, 67, 3338–3341 CrossRef CAS.
- S. T. Hsu and Y. L. Yao, J. Manuf. Sci. Eng. Trans. ASME, 2014, 136, 1–38 Search PubMed.
- P. C. Sukanek, J. imaging Technol, 1985, 11, 184–190 CAS.
- K. L. Beers, J. F. Douglas, E. J. Amis and A. Karim, Langmuir, 2003, 19, 3935–3940 CrossRef CAS.
- K. Taguchi, H. Miyaji, K. Izumi, A. Hoshino, Y. Miyamoto and R. Kokawa, Polymer, 2001, 42, 7443–7447 CrossRef CAS.
- S. J. Sutton, K. Izumi, H. Miyaji, Y. Miyamoto and S. Miyashita, J. Mater. Sci., 1997, 32, 5621–5627 CrossRef CAS.
- K. Taguchi, H. Miyaji, K. Izumi, A. Hoshino, Y. Miyamoto and R. Kokawa, J. Macromol. Sci., Part B: Phys., 2002, 41 B, 1033–1042 CrossRef.
- J. M. Carr, D. S. Langhe, M. T. Ponting, A. Hiltner and E. Baer, J. Mater. Res., 2012, 27, 1326–1350 CrossRef CAS.
- J. J. Hernández, D. R. Rueda, M. C. García-Gutiérrez, A. Nogales, T. A. Ezquerra, M. Soccio, N. Lotti and A. Munari, Langmuir, 2010, 26, 10731–10737 CrossRef.
- H. Xu, B. S. Ince and P. Cebe, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 3026–3036 CrossRef CAS.
- H. Schnablegger and Y. Singh, Ant. Paar GmbH, 2013, 1–99 Search PubMed.
- R. S. Johansson and J. R. Flanagan, Nat. Rev. Neurosci., 2009, 10, 345–359 CrossRef CAS.
- D. Nečas and P. Klapetek, Cent. Eur. J. Phys., 2012, 10, 181–188 Search PubMed.
- I. Cesini, J. D. Ndengue, E. Chatelet, J. Faucheu and F. Massi, Tribol. Int., 2018, 120, 330–339 CrossRef.
- P. L. Menezes, S. V. Kailas and M. R. Lovell, Tribol. Lett., 2011, 41(1), 1–15 CrossRef CAS.
- W. Wang, G. Zhao, X. Wu and Z. Zhai, J. Appl. Polym. Sci., 2015, 132(46) DOI:10.1002/app.42773.
- Y. Uto, K. Mizobata, S. K. Maurya, T. Akiyama and T. Nakajima, Surf. Interface Anal., 2017, 49, 577–583 CrossRef CAS.
- X. Cui, J. F. Hetke, J. A. Wiler, D. J. Anderson and D. C. Martin, Sens. Actuators, A, 2001, 93, 8–18 CrossRef CAS.
- F. M. Mwema, O. P. Oladijo, T. S. Sathiaraj and E. T. Akinlabi, Mater. Res. Express, 2018, 5(4), 046416 CrossRef.
- S. Schott, E. Gann, L. Thomsen, S. H. Jung, J. K. Lee, C. R. McNeill and H. Sirringhaus, Adv. Mater., 2015, 27, 7356–7364 CrossRef CAS PubMed.
- K. Uchida, K. Mita, Y. Higaki, K. Kojio and A. Takahara, Polym. J., 2019, 51, 183–188 CrossRef CAS.
- C. Marega, V. Causin, A. Marigo, S. Chimiche and U. Padova, Macromol. Res., 2006, 14, 588–595 CrossRef CAS.
- M. Barquins, Mater. Sci. Eng., 1985, 73, 45–63 CrossRef CAS.
- S. Maegawa, F. Itoigawa and T. Nakamura, Tribol. Int., 2016, 96, 23–30 CrossRef CAS.
- K. Viswanathan, N. K. Sundaram and S. Chandrasekar, Soft Matter, 2016, 12, 5265–5275 RSC.
- D. W. Lee, X. Banquy and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E567–E574 CAS.
- S. Yamada, Langmuir, 2008, 24, 1469–1475 CrossRef CAS PubMed.
- M. C. Pooley and D. Tabor, Proc. R. Soc. London, Ser. A, 1972, 329, 251–274 Search PubMed.
- S. Yamada, J. Chem. Phys., 2009, 131, 184708 CrossRef PubMed.
- Y. zhong Hu, T. bao Ma and H. Wang, Friction, 2013, 1, 24–40 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm00264g |
| This journal is © The Royal Society of Chemistry 2022 |