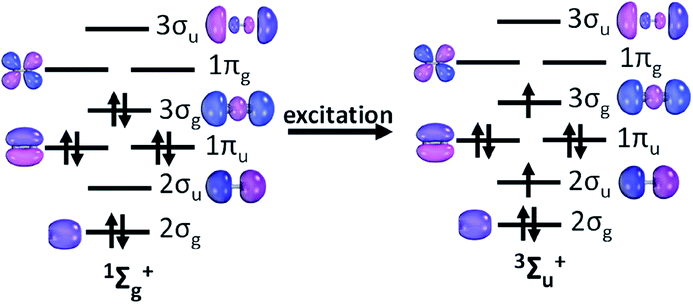Comprehending the quadruple bonding conundrum in C₂ from excited state potential energy curves

Abstract

The question of quadruple bonding in C₂ has emerged as a hot button issue, with opinions sharply divided between the practitioners of Valence Bond (VB) and Molecular Orbital (MO) theory. Here, we have systematically studied the Potential Energy Curves (PECs) of low lying high spin sigma states of C₂, N₂, Be₂ and HC≡CH using several MO based techniques such as CASSCF, RASSCF and MRCI. The analyses of the PECs for the ^2S+1Σ_g/u (with 2S + 1 = 1, 3, 5, 7, 9) states of C₂ and comparisons with those of relevant dimers and the respective wavefunctions were conducted. We contend that unlike in the case of N₂ and HC≡CH, the presence of a deep minimum in the ⁷Σ⁺ state of C₂ and CN⁺ suggests a latent quadruple bonding nature in these two dimers. Our investigations reveal that the number of bonds in the ground state can be determined for 2^nd row dimers by figuring out at what value of spin symmetry a purely dissociative PEC is obtained. For N₂ and HC≡CH the purely dissociative PEC appears for the septet spin symmetry as compared to that for the nonet in C₂. This is indicative of a higher number of bonds between the two 2^nd row atoms in C₂ as compared to those of N₂ and HC≡CH. Hence, we have struck a reconciliatory note between the MO and VB approaches. The evidence provided by us can be experimentally verified, thus providing the window so that the narrative can move beyond theoretical conjectures.

---

Introduction

Bonding in homodiatomic 2^nd period elements constitutes the bedrock of our understanding of chemical bonding.¹ Though bonding in many of these homodiatomic species is well understood, the bonding situation in C₂ presents an exceptionally enigmatic scenario. A routine inspection of molecular orbitals (Hartree Fock orbitals) of C₂ would suggest that the bond order of C₂ is 2.0 arising from the two π bonds.² However, decades back a typical Wiberg bond index computation conducted on C₂ indicated the presence of four bonds.³ The last few years have witnessed a steep spike in interest to comprehend the state of bonding in C₂.^4–12 This has led to intense debate on the aspect of quadruple bonding in C₂.¹³ Shaik and co-workers have investigated the electronic structure of C₂ within the VB manifold and have concluded that the bonding in C₂ is best described as a case of quadruple bond and have went on to predict that the strength of the fourth bond is approximately 12 kcal mol⁻¹.^4,5 These findings were contested by Frenking and co-workers who mainly disagreed on the approach adopted by Shaik of estimating the strength of the fourth bond.^7,10 There have been several attempts by different groups which either concur or refute the presence of a fourth bond in C₂. The incongruity in views from different corners arise from the multi-reference nature of the σ orbitals in C₂.¹⁴ Incidentally, MO based approaches have by and large refuted the case of quadruple bonding, with some exceptions.^7,10 Zhong and co-workers have tried to point out some similarities between the MO based and the VB approaches for C₂ regarding a key orbital which was achieved through unitary transformation of CASSCF orbitals.¹⁵ However, their final Effective Bond Order study with the same orbitals suggested that the dimer in question has a bond order of 2.15. Alternatively, magnetic shielding studies based on MO based approaches by Karadakov et al. suggested a “bulkier” bond compared to that of acetylene.¹¹ Nevertheless, it can be argued that there is no direct or definitive proof of the presence of four bonds in C₂ from a MO standpoint. The lack of existence of reconciliation on this issue between the VB and the MO approaches still has kept the debate wide open and given the conflicting views it may not be unfair to comment that the overall understanding is still nebulous. Here we report our view point on the bonding in C₂ by conducting extensive studies on potential energy curves of excited states of C₂, largely covering the cases of high spin states of C₂ along with similar investigations on N₂ and HC≡CH. Our findings provide clinching evidence in support of the presence of quadruple bonding in C₂ or rather the ability to form two bonds by electrons in orbitals in σ symmetry thus establishing reconciliation between MO and VB manifold of methods.

The quintessential signature of bonding between two atoms lies in the presence of a well-defined discrete minimum in the potential energy curve (PEC) plotted against the interatomic distance of the two atoms. For instance, in the case of H₂ ground electronic state the PEC shows the presence of a distinct minimum and has a significant dissociation energy. This is due to the presence of a σ bond arising from 1σ_g² in the H₂ molecule.¹⁶ If this electron pair in the bonding orbital is broken and one of the electrons is promoted to the corresponding 1σ_u one would find that the bonding stabilization is negated and as a result a dissociative PEC with no minimum is obtained for the ³Σ_u⁺ state. Hence one can create a high spin state corresponding to the rupture of a bond that generates a PEC without a minimum. This seemingly simple argument may be extended to multiply bonded species as well, albeit with some intrinsic limitations which are discussed later. Multiple bonding between two atoms in the ground state would certainly leave footprints on the excited state PECs. Unlike H₂, N₂ which is multiply bonded exhibits high spin triplet and quintet states with respective minima.¹⁷ This becomes more evident when one compares and contrasts spectra of diatomics with and without multiple bonding.¹⁸

Hence, in the multiply bonded diatomic species one may generate high spin states by breaking bonding electron pairs within the valence orbitals and promoting electrons from a particular bonding orbital to the corresponding antibonding orbital such that for a particular high spin state a set of bonding orbital/s and respective antibonding have single occupation with parallel spins. This would lead to high spin states of ^2S+1Σ⁺ states. A step by step procedure can be adopted such that particular types of bonding may be negated by the proper choice of orbital symmetry. If specific orbitals are chosen to generate high spin electronic states, one can gradually generate electronic states which eliminate bonds one by one and reach a high spin state which would correspond to the total absence of any bonds between the two atoms resulting to a purely dissociative state. The no. of bonds in the ground state of the diatomic species would determine at which high spin state the purely dissociative PEC would be reached. For instance, in H₂ which has only one bond the triplet state is purely dissociative, whereas for N₂ which is known to have three bonds the septet state is purely dissociative.^16,17

Results and discussion

As the bonding in C₂ is suspect, we decided to investigate the nature of the PECs of high spin states of C₂ and see at which spin state a purely dissociative state is obtained. A cursory estimate obtained from the primary Hartree Fock (HF) MO picture of the C₂ would suggest that C₂ has only two π bonds.² The four electrons in the σ orbitals would appear not to contribute to bonding as there are two electrons in a bonding orbital and two electrons in an antibonding orbital. It must be noted that the Be₂ dimer with the same σ electron population and no π electron shows a total absence of bonding at HF and CASSCF levels of theory.¹⁹ Hence, one is tempted to infer that C₂ will have just two π bonds arising from the two π electrons. A full valence CASSCF calculation on the ground electronic state of C₂ reveals the multireference character of C₂. The dominant configuration state functions (CSFs) are with 70.9% and 13.6% contributions. The 2^nd CSF may suggest that it can contribute two σ bonds in the ground electronic state of C₂ (see Table 1). The no. of bonds arising from σ orbitals is the bone of contention, whereas there is no debate as to the presence of two π bonds in the ground electronic state. VB theory predictions from Shaik and others suggest that indeed two σ bonds are present. Due to the multi-reference character of C₂, simple MO based electronic structure theories are inadequate to predict the no. of σ bonds. However, as discussed earlier the high spin state PECs can be investigated to gauge the bonding situation in the ground electronic state. Using a full valence CASSCF for C₂, N₂, CN⁺ and HC≡CH we have investigated the dissociation PECs for high spin Σ states (see Fig. 1(a), (b) and (c) for C₂, N₂ and CN⁺ and Fig S1 in ESI† for acetylene respectively). The high spin Σ states are created in such a way that it would have lesser number of electron pairs in bonding orbitals. Such an exercise immediately reveals that for N₂ (Fig. 1(b)) and HC≡CH (Fig S1†) the lowest lying ⁷Σ_u⁺ state is purely dissociative. This would suggest that only three electron pairs contribute to bonding in the ground electronic state and when all of them are disrupted to create a high spin state of septet symmetry it leads to a purely dissociative PEC. Intriguingly, the same exercise with C₂ reveals a purely dissociative PEC is obtained for the Σ state of nonet spin symmetry, with ⁷Σ_u⁺ displaying a distinct minimum. The trends immediately suggest that probably the no. of electron pairs contributing to the bonding in the ground state of C₂ is more compared to those for N₂ and HC≡CH. Our hypothesis is based on the fact that on promoting electrons to the high spin states eliminate bonds. With that one needs to go the nonet spin state (⁹Σ_g⁺) for the purely dissociative state. It suggests that four bonding pairs have to be disrupted to decimate any form of bonding between the two atoms.

Table 1 Percentage of the major contributing CSFs for the five spin states of C₂ at equilibrium

Spin multiplicity	Major contributing CSF	Percentage
^1Σg^+	|2σg^22σu^21πux^21πuy^2〉	70.9
	|2σg^23σg^21πux^21πuy^2〉	13.6
^3Σu^+	|2σg^22σu^11πux^21πuy^23σg^1〉	86.3
	|2σg^21πux^21πuy^12σu^21πgy^1〉 + |2σg^21πux^11πuy^22σu^21πgx^1〉	3.6
^5Σg^+	|2σg^22σu^11πux^11πuy^23σg^11πgx^1〉 + |2σg^22σu^11πux^21πuy^13σg^11πgy^1〉	81.7
	|2σg^22σu^21πux^11πuy^11πgx^11πgy^1〉	6.7
^7Σu^+	|2σg^22σu^11πux^11πuy^13σg^11πgx^11πgy^1〉	97.8
	|2σg^12σu^11πux^11πuy^13σg^21πgx^11πgy^1〉	0.5
^9Σg^+	|2σg^12σu^11πux^11πuy^13σg^11πgx^11πgy^13σu^1〉	100.0

---

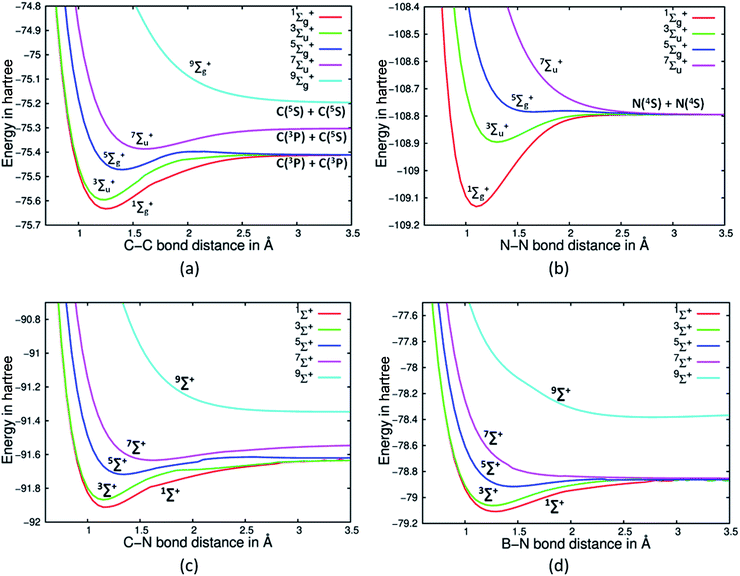Fig. 1 PECs corresponding to the (a) five spin states of C₂, (b) four spin states of N₂,^17a (c) five spin states of CN⁺ and (d) five spin states of BN.

Further inspection of the excited state PECs of C₂ along with the dominant CSF at the minimum at the PEC is instructive. The lowest lying ³Σ_u⁺ is dominated by a CSF which has the presence of two π bonds (see Table 1). The electron distribution in σ orbitals in ³Σ_u⁺ space avoids any significant participation from configurations which will have simultaneous double occupation in 2σ_g and 3σ_g orbital. Also, the dissociation energy of the ³Σ_u⁺ state is lower compared to that of the ¹Σ_g⁺ state by about 27 kcal mol (see ESI Table ST1†). The dominant CSF of ³Σ_u⁺ at the PEC minimum, |2σ_g²2σ_u¹1π_u⁴3σ_g¹〉 may be viewed as an excitation from the CSF |2σ_g²2σ⁰_u1π_u⁴3σ_g²〉 (the 2^nd most important CSF present in the ground state minimum) (see Fig. 2), which is essentially breaking a bonding pair of 3σ_g and putting parallel spins in 3σ_g and 2σ_u. It may be argued that ³Σ_u⁺ essentially maintains 2π bonds and eliminates plausibly one σ bond, which shows up in the decrease of the dissociation energy. The ⁵Σ_g⁺ is riddled with strong signatures of avoided crossings. State averaging by including four low lying ⁵Σ_g⁺ states were used to draw up the PECs (see ESI, Section S1†). The nature of the dominant CSF suggests the elimination of only one π bond and one σ bond w.r.t that of the ground state, using the same line of argument which was employed in the previous case. The dominant CSF at the minimum of the PEC for the lowest lying septet Σ state, ⁷Σ_u⁺ shows a total absence of π bonding but the presence of a deep minimum indicates stability conferred from the electron pair in 2σ_g orbital. The dominant septet state CSF at the ⁷Σ_u⁺ PEC minimum shows a marked absence of π bonding, yet this is the third state which has one σ bond w.r.t that of the ground electronic state as it has parallel spins in 3σ_g and 2σ_u akin to the dominant CSF in the PEC minima of ³Σ_u⁺ and ⁵Σ_g⁺ states. As mentioned earlier, all of the bonding interactions are annihilated at the ⁹Σ_g⁺ state leading to a purely dissociative PEC. This fact is in conjunction with the fact that ⁷Σ_u⁺ state PEC has a distinct minimum which strongly indicates that the ground electronic state of C₂ has four bonds, two σ and two π.

Fig. 2 Formation of the triplet state from the desired singlet state upon one electron excitation.

Though we have noted earlier that for N₂ and acetylene purely dissociative state appears only when one reaches the septet spin state (⁷Σ_u⁺), unfortunately the corresponding ⁵Σ_g⁺ state PECs do not show presence of distinct minima. Further investigations reveal that the situation for the ⁵Σ_g⁺ state is extremely complex as it involves significant contribution from CSFs which have partially filled π and σ orbitals. Moreover, some majorly contributing CSFs also show participation from 3σ_u orbital. State averaging does not alleviate the problem and such issues are well documented.^17b However, it must be noted that though the ⁵Σ_g⁺ state for N₂ does not show a distinct minimum, the PEC is certainly not purely dissociative in nature. Moreover, previous studies with MRCI and Multi-Reference Coupled Cluster suggested that the ⁵Σ_g⁺ state of N₂ does possess a shallow minimum.^17a,c Furthermore, the nature of bonding in diatomic systems BN and CN⁺ isoelectronic to C₂ were also investigated using the same stratagem. Interestingly, we do find that for CN⁺ the lowest four spin states display a distinct minimum on their respective PECs, while its nonet state is purely dissociative. Hence, by the extension of the same line of argument it can be suggested that CN⁺ has signature of quadruple bonding in agreement to the findings of Shaik and co-workers (see Fig. 1(c)).⁵ Contrary to the findings of Shaik et al. we find BN, which is also isoelectronic to C₂, does not have a quadruple bond as suggested by the purely dissociative PEC for ⁷Σ⁺ state (see Fig. 1(d)). Our strategy of counting bonds suggests it has three bonds which conforms to the usual Lewis structure prediction.² This difference may be ascribed to the electronegativity difference in the case of BN, which is completely absent in C₂ and quite reduced in CN⁺. After excitation in BN to ⁷Σ⁺ (with major contributing CSF: |[core]2σ²2σ^*11π_x¹1π_y¹3σ¹1π_x^*11π_y^*1〉), the fourth electron pair gets mostly localized as a lone pair on the nitrogen atom in contrast to C₂ where the excited electrons remain on each C atom. This may be the reason why ⁷Σ⁺ state of BN is unbound, even though VB theory shows a quadruple bond.⁵

One is disposed to question what happens if dynamic correlation is roped in. Does it change the scenario and the inferences derived from it? To address this question MRCI computations were conducted for C₂, BN and CN⁺ (see ESI Fig S3–S5†). The general trends of the PECs for the different Σ states for C₂ remain unaltered. The ⁷Σ_u⁺ state PEC still exhibited a distinct minimum and the dissociation energy was estimated to be 69 kcal mol⁻¹ and the ⁹Σ_g⁺ shows pristine dissociative character. Our MRCI results on BN also suggest that the ⁷Σ_u⁺ state is dissociative, indicating unlike C₂ it does not have a quadruple bond. Incidentally, the ⁷Σ⁺ states of C₂ and BN have not been studied experimentally. Our computations suggest that the ⁷Σ_u⁺ state of C₂ lies 9.4 eV above the ground state. Hence, the proof of existence of a minimum in the ⁷Σ_u⁺ for C₂ and the absence of such a minimum in the equivalent case for BN is likely to corroborate our findings on quadruple bonding in these two cases. Furthermore, CN⁺ being an ionic species can be investigated in an ion trap.²⁰ The case of presence of a bound ⁷Σ⁺ state can be verified experimentally.

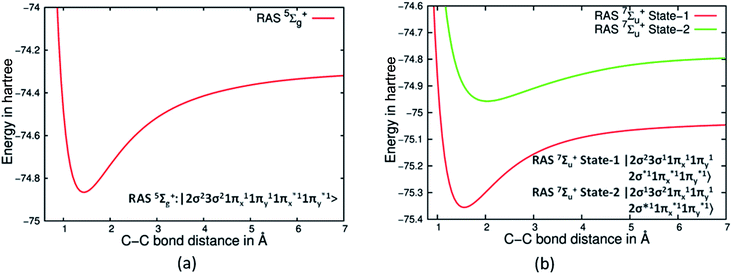
The most perplexing aspect of bonding in C₂ is the question of the presence of two σ bonds, while σ bonds are distinctly absent in Be₂ despite both having largely four electron population in σ orbitals (see ESI Section S2 and Fig S2†).¹⁹ We ventured to understand what would happen if we artificially prevent formation of π bonds in C₂, a situation akin to Be₂ where the electron population is zero in the π orbitals. We resorted to the use of the RASSCF technique which allowed us to restrict the population of π orbitals with one electron in each of them for C₂, thus negating the possibility of any π bonding. Whereas, for Be₂ we restricted the population of π orbitals to zero. This ensured that the dominant configurations both in Be₂ and C₂ would be restricted to four electrons in four σ orbitals. Such an approach helped us to examine the PECs of Be₂ and C₂ without any contribution to bonding from the π orbitals. Gratifyingly, we found that the RASSCF based PECs for ⁵Σ_g⁺ state of C₂ with dominant CSFs show a distinct deep minimum, whereas for ¹Σ_g⁺ Be₂ was totally dissociative (see Fig S2 in ESI† and Fig. 3(a)). RASSCF studies show that on imposition of similar restrictions on the two low lying ⁷Σ_u⁺ states the PECs have deep minimum in each state. Further analysis reveals that this is due to the presence of a single σ bond in each of these states (see Fig. 3(b)). The dominant CSFs of these two states are |2σ_g²3σ_g¹1π_u²1π_g²2σ_u¹〉 and |2σ_g¹3σ_g²1π_u²1π_g²2σ_u¹〉 respectively, indicating that indeed two sets of σ electron pairs do give rise to two σ bonds.

Fig. 3 (a) PEC corresponding to the RASSCF computation for the quintet spin state of C₂ and (b) PECs corresponding to the RASSCF computation for the two septet spin states of C₂ along with their dominant configurations.

Frenking and others have questioned the basis of quadruple bonding by comparing the force constants of the bond in C₂ with that of HC≡CH, with the bond in C₂ being weaker than that of HC≡CH.⁷ In the light of our findings this may stand as a contradiction. Here we must reiterate that the dominant determinant of the ground state of C₂ contributes only two π bonds. Hence, analysis of force constants is likely to reflect the attribute of primarily the dominant determinant of C₂ and may not serve as a good metric for this purpose. The latent quadruple nature of the bond in C₂ and CN⁺ can only be recognized through the PECs of the excited states.

Though our approach possibly brings in an avenue to understand the bonding situation in C₂, a probable question may arise that whether this hypothesis can be applied to comprehend the number of bonds in all diatomic systems and what are its intrinsic limitations. Naturally, one is inclined to ask whether this technique can be extended to molecules with triplet ground states like O₂ and B₂. Here we first discuss the case of O₂ to illustrate how this approach can be tailored to address cases where the ground state is ³Σ_g⁻ within the framework of traditional MO theory. In the case of the ³Σ_g⁻ ground state of O₂, a formal bond order of 2.0, one from σ and the other from π is assigned from the electronic distribution [core]2σ_g² 2σ_u²3σ_g²1π_u⁴1π_g². One can generate a higher spin state by breaking the bonding pair in the 3σ_g² bonding orbital and promoting an electron to 3σ_u, thus eliminating the σ bond. In order to disrupt the bonding arising from π orbitals one needs to excite a single electron from π to π* creating a configuration of the type π_u³π_g³ from π_u⁴π_g² of the ground state. This would eliminate the single π bond without ascending on the spin ladder. This is obviously different from the molecules with singlet ground state ¹Σ_g⁺ that has π bonds (consider the case of N₂ or HC≡CH). Armed with this simple information one would expect to obtain ³Σ_u⁺ with a minimum (conventional bond order = 1) and a ⁵Σ_g⁺ with a purely dissociative curve (conventional bond order = 0) (see Fig. S6(b) and S7(b) in ESI†). Indeed the findings from the previously reported CASSCF/MRCI PECs of high spin Σ states show that the approach holds good, it must be emphasized that for triplet ground state diatomic systems arising from π_u³π_g³ and π_u⁴π_g² configurations moving the bonding electron to the antibonding electron would not create a sigma state with higher spin symmetry.²¹ If this may seem confusing one may modify our strategy from a different viewpoint. Associated with these two configurations is a low-lying singlet ¹Δ_g configuration. From the lowest lying singlet state bonding pairs have to be broken to create high spin sigma states and the corresponding wavefunctions and their respective PECs have to be inspected to arrive at a proper conclusion regarding the number of bonds present in them (see Fig. S8 in ESI†). This tailored strategy would yield two bonds for O₂ and a single bond in B₂. While our approach appears to be simple it would be prudent to add a cautionary note, particularly for the quintet states of p-block elements. As has been discussed earlier, we find that for the p-block elements the quintet Σ state PECs are fraught with multiple avoided crossings as the dominating configurations can arise from electron bond pair breaking of the σ orbital or from π orbital. One has to ensure that adequate state-averaging is conducted to reveal the true nature of the state PECs of these dimers. Admittedly, the approach has to be tested further on metal dimer systems to see whether proper inferences can be drawn from analogous high spin state PECs regarding the number of bonds in their respective ground states.

Conclusions

In summary we provide overwhelming evidence which brings out the quadruple bonding nature in C₂ and CN⁺ with two σ and two π bonds. However, our approach indicates that BN, which is isoelectronic to C₂ at the most has three bonds. Additionally, we suggest that for both CN⁺ and C₂, a ⁷Σ⁺ state exists which has a clear distinct and deep minimum, which opens up a window for experimental verification.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

AP would like to thank Professor Debashis Mukherjee and Professor Eluvathingal D. Jemmis for enlightening discussions and thoughtful inputs. AP would like to acknowledge financial support from DST SERB CRG/2019/006685. DG would like to acknowledge DST-SERB grant EMR/2017/001054 for the financial support. IB would like to acknowledge financial support in the form of a research fellowship from CSIR, Govt. of India (Award Number: 09/080(1065)/2017-EMR-I).

References

1. (a) R. C. Fischer and P. P. Power, Chem. Rev., 2010, 110, 3877–3923; (b) P. R. Schreiner and H. P. Reisenauer, Angew. Chem., Int. Ed., 2009, 48, 8133–8136.
2. I. N. Levine, Quantum Chemistry, Allyn and Bacon, 2nd edn, 1974, p. 321, table 13.2.
3. P. V. R. Schleyer and P. Maslak, Tetrahedron Lett., 1993, 34, 6387–6390.
4. P. Su, J. Wu, J. Gu, W. Wei, S. Shaik and P. C. Hiberty, J. Chem. Theory Comput., 2011, 7, 121–130.
5. S. Shaik, D. Danovich, W. Wu, P. Su, H. S. Rzepa and P. C. Hiberty, Nat. Chem., 2012, 4, 195–200.
6. (a) S. Shaik, H. S. Rzepa and R. Hoffmann, Angew. Chem., Int. Ed., 2013, 52, 3020–3033; (b) D. Danovich, S. Shaik, H. S. Rzepa and R. Hoffmann, Angew. Chem., Int. Ed., 2013, 52, 5926–5928.
7. G. Frenking and M. Hermann, Angew. Chem., Int. Ed., 2013, 52, 5922–5925.
8. D. Danovich, P. C. Hiberty, W. Wu, H. S. Rzepa and S. Shaik, Chem. –Eur. J., 2014, 20, 6220–6232.
9. D. W. O. Sousa and M. A. C. Nascimento, J. Chem. Theory Comput., 2016, 12, 2234–2241.
10. M. Hermann and G. Frenking, Chem. –Eur. J., 2016, 22, 4100–4108.
11. P. B. Karadakov and J. Kirsopp, Chem. –Eur. J., 2017, 23, 12949–12954.
12. J. M. Matxain, F. Ruipérez, I. Infante, X. Lopez, J. M. Ugalde, G. Merino and M. Piris, J. Chem. Phys., 2013, 138, 151102.
13. (a) S. Shaik, H. S. Rzepa and R. Hoffmann, Angew. Chem., Int. Ed., 2013, 52, 3020–3033; (b) L. T. Xu and T. H. Dunning Jr, J. Chem. Theory Comput., 2014, 10, 195–201; (c) S. Shaik, D. Danovich, B. Braida and P. C. Hiberty, Chem. –Eur. J., 2016, 22(52), 18977–18980; (d) M. Piris, X. Lopez and J. M. Ugalde, Chem. –Eur. J., 2016, 22(12), 4109–4115.
14. P. F. Fougere and R. K. Nesbet, J. Chem. Phys., 1966, 1, 285–298.
15. R. Zhong, M. Zhang, H. Xu and Z. Su, Chem. Sci., 2016, 7, 1028–1032.
16. K. K. Lange, E. I. Tellgren, M. R. Hoffmann and T. Helgaker, Science, 2012, 337, 327–331.
17. (a) A. Engels-Putzka and M. Hanrath, Mol. Phys., 2009, 107, 143–155; (b) R. S. Mulliken, J. Chem. Phys., 1962, 37, 809–813; (c) H. Werner and P. J. Knowles, J. Chem. Phys., 1991, 94(2), 1264–1270.
18. (a) G. S. Scuseria, T. P. Hamilton and H. F. Schaefer III, J. Chem. Phys., 1990, 92, 568–573; (b) W. D. Laidig, P. Saxe and R. J. Bartlett, J. Chem. Phys., 1987, 86, 887–907.
19. J. M. Matxain, F. Ruipérez and M. Piris, J. Mol. Model, 2013, 19, 1967–1972.
20. A. L. Padellec, J. B. A. Mitchell, A. Al-Khalili, H. Danared, A. Källberg, Å. Larsen, S. Rosén, M. Ugglas, L. Vikor and M. Larsson, J. Chem. Phys., 1999, 110(2), 890–901.
21. (a) H. Liu, D. Shi, J. Sun, Z. Zhu and Z. Shulin, Spectrochim. Acta, Part A, 2014, 124, 216–229; (b) H. Partridge, C. W. Bauschlicher Jr, S. R. Langhoff and P. R. Taylor, J. Chem. Phys., 1991, 95(11), 8292–8300; (c) H. Lefebvre-Brion, H. P. Liebermann, J. M. Amero and G. J. Vázquez, J. Chem. Phys., 2016, 144(14), 144302.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc02336a

---