Open Access Article
Open Access ArticleConformationally adaptable macrocyclic receptors for ditopic anions: analysis of chelate cooperativity in aqueous containing media†
Stuart N.
Berry
 ,
Lei
Qin
,
Lei
Qin
 ,
William
Lewis
,
William
Lewis
 and
Katrina A.
Jolliffe
and
Katrina A.
Jolliffe
 *
*
School of Chemistry, The University of Sydney, NSW 2006, Australia. E-mail: Kate.Jolliffe@sydney.edu.au
First published on 18th June 2020
Abstract
The effect of chelate cooperativity on the binding of several ditopic anions to two tetrathiourea macrocycles has been analysed in competitive solvent mixtures (H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO 1
DMSO 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 v/v). The semi-flexible receptors bind dicarboxylates with high affinity dependent on the length and flexibility of the guest. Chemical double mutant cycle (DMC) analysis allowed the chelate cooperativity effects to be measured in detail and revealed both positive and negative cooperativity effects which were dependent on guest size, flexibility and spacer interactions between guest and macrocycle. 1H NMR and crystallographic studies confirmed the macrocycle hosts are adaptable, changing conformation to match their pore size to a selected guest.
9 v/v). The semi-flexible receptors bind dicarboxylates with high affinity dependent on the length and flexibility of the guest. Chemical double mutant cycle (DMC) analysis allowed the chelate cooperativity effects to be measured in detail and revealed both positive and negative cooperativity effects which were dependent on guest size, flexibility and spacer interactions between guest and macrocycle. 1H NMR and crystallographic studies confirmed the macrocycle hosts are adaptable, changing conformation to match their pore size to a selected guest.
Introduction
One of the key challenges in the selective discrimination of polyanionic species is the lack of chemical or structural differences between homologous series. For example, the linear aliphatic dicarboxylates (malonate–azelate) have similar chemical properties in terms of pKa and hydration enthalpies1,2 and differ only in terms of the length of the flexible aliphatic linker. Furthermore, polyanionic species exist preferentially in an aqueous environment, which adds further complications in the design of chemical entities for the selective discrimination of these species in their native environment. Because of their biological3–5 and industrial1,6,7 importance, the development of sensors which can selectively bind and detect polyanionic species is a significant challenge and has commanded special attention from the chemical community.In nature, succinate dehydrogenase selectively binds succinate via 5-hydrogen bonds to each carboxylate unit, with additional stabilisation of the anion achieved by exclusion of water molecules from the binding site.8,9 Malonate is a known competitive inhibitor of this enzyme,10 demonstrating that even for the naturally evolved systems in biology, selective discrimination of dicarboxylates is troublesome. Nonetheless, there are many excellent examples in the literature of receptors that utilise hydrogen,11–14 halogen15 and chalcogen bonds,16 ion-pairing interactions17,18 and metal–ligand interactions19,20 to discriminate di-(and multi)topic carboxylate species in competitive (and non-competitive) solvents with both macrocycles21–23 and cages24 used to achieve some levels of dicarboxylate discrimination. More recently, arrays have been utilised to selectively detect ditopic anionic species,25–27 although these often require complex calibration.
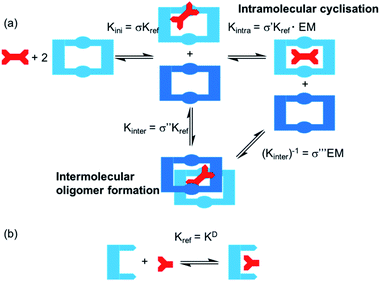
One potential strategy for achieving selective ditopic anion binding involves investigating and optimising the role of chelate (or intramolecular) cooperativity. Chelate cooperativity describes the likelihood of the formation of discrete complexes in preference to higher order oligomers (Fig. 1).28–30 In the case of a ditopic host binding to a ditopic guest, chelate cooperativity refers to the formation of the fully bonded 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex, where the initial binding event (Kini) at one ‘end’ of the complex brings the binding sites at the other ‘end’ into close proximity, thereby making the subsequent intramolecular binding event (Kintra) to give the 1
1 complex, where the initial binding event (Kini) at one ‘end’ of the complex brings the binding sites at the other ‘end’ into close proximity, thereby making the subsequent intramolecular binding event (Kintra) to give the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex more likely to occur than oligomerisation processes (Kinter). If both binding sites in the ditopic receptor are identical, the three microscopic binding constants Kini, Kintra and Kinter are deconvoluted into the monotopic reference binding constant (Kref) and appropriate statistical coefficients to account for the degeneracy of the systems, while Kintra is defined by eqn (1) where σ′ is the statistical coefficient and EM is the effective molarity; a correction factor to account for the intramolecular nature of the second binding step.
1 complex more likely to occur than oligomerisation processes (Kinter). If both binding sites in the ditopic receptor are identical, the three microscopic binding constants Kini, Kintra and Kinter are deconvoluted into the monotopic reference binding constant (Kref) and appropriate statistical coefficients to account for the degeneracy of the systems, while Kintra is defined by eqn (1) where σ′ is the statistical coefficient and EM is the effective molarity; a correction factor to account for the intramolecular nature of the second binding step.
| Kintra = σ′Kref × EM | (1) |
High EM and Kintra values ≫ 1 indicate positive cooperativity (i.e. favourable formation of the fully bonded 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex), whereas Kintra values ≪1 indicate negative cooperativity (i.e. favourable oligomer formation). While EM and Kintra cannot be measured directly, they can be determined using double mutant cycle (DMC) analyses, as described previously by Hunter,31–34 Schalley35–37 and others.38,39
1 complex), whereas Kintra values ≪1 indicate negative cooperativity (i.e. favourable oligomer formation). While EM and Kintra cannot be measured directly, they can be determined using double mutant cycle (DMC) analyses, as described previously by Hunter,31–34 Schalley35–37 and others.38,39
In recent years, several in-depth studies have revealed intriguing insights about the chelate cooperativity effect uncovering some of the range and limitations for which it may be utilised to design efficient supramolecular systems. Hunter and co-workers have shown that chelate cooperativity is enhanced in polar solvents over non-polar solvents due to sterically unfavourable interactions with competitive solvents which are relieved upon intramolecular ‘cyclisation’.33 In addition, studies have focused on the effect of pre-organisation and rigidity of both hosts and guests.32,34–36,38,40 While highly preorganised host/guest systems can yield very high EMs,41 often rigid host/guest systems with slight geometric mismatches suffer from much lower cooperative effects, as opposed to more flexible systems where the cooperative effect can remain strong over varied guest sizes due to the host undergoing a conformational change to adapt to guest size. This has led to the conclusion that often the synthetic effort required to produce highly pre-organised systems is not rewarded with strong cooperative effects, and more flexible systems may be useful in designing supramolecular motifs to achieve strong binding.
The majority of fundamental studies investigating chelate cooperativity to date have been conducted in relatively non-polar organic solvents, excluding potential competitive binding interactions arising from the solvent. Furthermore, most studies use charge or ion-pairing,17,42 in addition to hydrogen bonding to investigate the chelate effect. While these have provided valuable insights into the chelate effect, the application of the chelate effect in receptors designed for competitive solvent systems has been under explored. The aims of the study described herein were two-fold: firstly, to investigate chelate cooperativity in neutral receptors that rely solely on hydrogen bonding interactions with anionic guests and secondly, to investigate the chelate cooperativity contributions in a highly competitive aqueous containing solvent medium. We envisaged that full analysis of the chelate cooperativity for binding of ditopic anions in competitive solvent systems would provide valuable insight into how to maximise the chelate effect, thereby greatly enhancing the development of selective and specific receptors/sensors for ditopic anions with real-world applications.
Results and discussion
Strategy
We chose to investigate dicarboxylate guests because the inherent difficulties in designing receptors capable of discriminating between these species makes these challenging targets for selective recognition. In order to accommodate both linear and rigid dicarboxylate guests, we designed our receptors to be semi-flexible, maintaining a certain degree of adaptability to better encapsulate their guest. We employed the 1,8-diamino carbazole scaffold, which has previously exhibited strong binding to oxoanions and should allow analysis of the binding event by UV-vis and fluorescence spectroscopy,43–45 in the design of two ditopic tetrathiourea macrocyclic species dt1 (ditopic 1) and dt2 (ditopic 2) (Scheme 1). The bis-carbazole units are linked by either 1,3-xylyl (dt1) or 1,4-xylyl (dt2) groups to vary macrocycle pore shape and also to provide semi-flexibility wherein the macrocycle can flex about the 4 methylene units.46 As the reference compound for both macrocycles, we synthesised the open analogue mt3 (monotopic 3). All receptors were synthesised in moderate yields (see ESI† for details).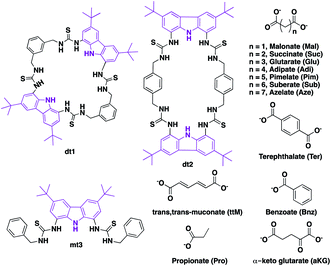 | ||
| Scheme 1 Carbazole tetrathiourea macrocycles dt1 (ditopic 1) and dt2 (ditopic 2) and open bisthiourea carbazole mt3 (monotopic 3) along with mono and dicarboxylate anions used in this study. | ||
As EM and Kintra cannot be measured experimentally, we employed the well-defined double mutant cycle (DMC) analysis to determine the individual components of each binding process (Fig. 2).30 This approach has been described in detail previously for similar ditopic host/ditopic guest binding35,47 and full details of the DMC analysis conducted in this study including derivation of the equations to calculate EM and Kintra are provided in the ESI.†
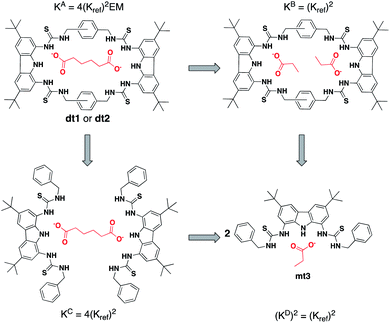 | ||
| Fig. 2 Double mutant cycle for dt1 or dt2 with Adi as a representative guest. Equations show how each macroscopic binding constant is related to the binding of the reference host/guest system (Kref). | ||
For this study, two cuts or chemical mutations were applied to the macrocycle–anion complex, first to the macrocycle to create receptor mt3, and secondly to the ditopic anion, in which we used the monotopic Pro or Bnz (as the cut for Ter) for all analysis in this study.
DMC analysis allows all individual components of the binding event to be measured experimentally and expressed in terms of EM, the monovalent reference Kref and statistical factors. By combining each mutation into an equilibrium (Fig. 3), the overall binding constant for the system can be calculated and subsequently EM (eqn (2)) and the apparent microscopic binding constant Kintra are derived (eqn (3)).
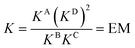 | (2) |
| Kintra = 1/2Kref × EM | (3) |
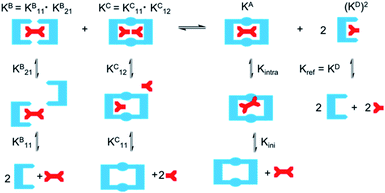 | ||
| Fig. 3 Application of DMC analysis to calculate the overall binding constants for the binding of a ditopic host to a ditopic guest in this study. | ||
Binding of ditopic hosts to guests
To initially investigate the spectroscopic responses of dt1 and dt2 to anions, fluorescence screening was carried out wherein 10 equivalents of various tetrabutylammonium anion salts (Cl−, Br−, I−, PF6−, SO42−, HCO3−, Bnz−, OAc−, Mal2−, Suc2−, Glu2−, Adi2−, Pim2−, Sub2−, Aze2−, Ter2−, ttM2− and aKG2−) were added to a 25 μM solution of dt1 or dt2 in aqueous DMSO solution (H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO 1
DMSO 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 v/v) (ESI Fig. S63–S66†). Following excitation at 300 nm, fluorescence spectra were obtained. Generally, significant quenching was observed with ditopic anions and SO42−, attributed to inhibition of the PET effect, whereas no or little quenching was observed with other anions, including monocarboxylates Bnz−, OAc− and HCO3− indicating that these ditopic receptors have a selective response for ditopic guests over monotopic guests.
9 v/v) (ESI Fig. S63–S66†). Following excitation at 300 nm, fluorescence spectra were obtained. Generally, significant quenching was observed with ditopic anions and SO42−, attributed to inhibition of the PET effect, whereas no or little quenching was observed with other anions, including monocarboxylates Bnz−, OAc− and HCO3− indicating that these ditopic receptors have a selective response for ditopic guests over monotopic guests.
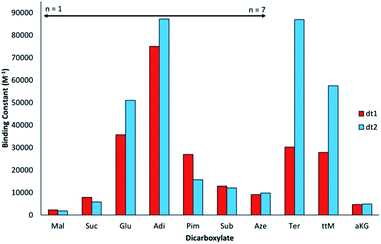
The binding affinities of dt1 and dt2 towards TBA (tetrabutylammonium) salts of linear unsaturated dicarboxylates Mal–Aze, the rigid Ter, the benzene exposure biomarker ttM and Kreb's cycle intermediate aKG were measured by UV-vis titration in aqueous DMSO solution (H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO 1
DMSO 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 v/v). Titration data was fitted to a 1
9 v/v). Titration data was fitted to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding model using a global fitting analysis on the Bindfit web app48 and are shown in Fig. 4 and Table 1 [fitted titration curves are provided in the ESI (Fig. S21–S41†)]. In all cases, data fitted better to a 1
1 binding model using a global fitting analysis on the Bindfit web app48 and are shown in Fig. 4 and Table 1 [fitted titration curves are provided in the ESI (Fig. S21–S41†)]. In all cases, data fitted better to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding model over other models tested (1
1 binding model over other models tested (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 2
2, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 etc.) suggesting this was the likely binding mechanism to ditopic anions (vide infra). Throughout this study all titration data was fitted to all possible binding models, with the best model selected by evaluation of quality of the fit using residual analysis.
1 etc.) suggesting this was the likely binding mechanism to ditopic anions (vide infra). Throughout this study all titration data was fitted to all possible binding models, with the best model selected by evaluation of quality of the fit using residual analysis.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO 1
DMSO 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 v/v) and data fitted to an appropriate model by conducting a global fitting analysis using Bindfit.48 Anions were added as tetrabutylammonium (TBA) or (TBA)2 salts
9 v/v) and data fitted to an appropriate model by conducting a global fitting analysis using Bindfit.48 Anions were added as tetrabutylammonium (TBA) or (TBA)2 salts
| mt3 | dt1 | dt2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Anion | n = | K 11 (M−1) | K A (M−1) | EMc (mM) | K intra (M−1) | K A (M−1) | EMc (mM) | K intra (M−1) |
a All errors ±15%. K11 as determined by UV-vis titration with data fitted to a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 statistical binding model.
b Macroscopic association constant as determined by fitting data to a 1 1 statistical binding model.
b Macroscopic association constant as determined by fitting data to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding model.
c Effective molarity determined by double mutant cycle (DMC) analysis. See ESI Section 5 for more information.
d
K
intra as determined by eqn (3) and by DMC analysis.
e Data fitted to a 1 1 binding model.
c Effective molarity determined by double mutant cycle (DMC) analysis. See ESI Section 5 for more information.
d
K
intra as determined by eqn (3) and by DMC analysis.
e Data fitted to a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 statistical model, K12 is shown in parenthesis.
f Data fitted to a full 1 2 statistical model, K12 is shown in parenthesis.
f Data fitted to a full 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 model, K12 is shown in parenthesis.
g Data fitted using single peak analysis at 360 nm.
h Not determined. 2 model, K12 is shown in parenthesis.
g Data fitted using single peak analysis at 360 nm.
h Not determined.
|
||||||||
| Pro | — | 600b | 3300 (830)e | — | — | 2300 (1200)f | — | — |
| Bnz | — | 1800b | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (480)f 000 (480)f |
— | — | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (200)f 000 (200)f |
— | — |
| Mal | 1 | 1600 | 2300 | 0.5 | 0.15 | 1900 | 0.4 | 0.12 |
| Suc | 2 | 550 | 7900 | 14 | 4.2 | 5800 | 10 | 2.9 |
| Glu | 3 | 1000 | 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
21 | 6.2 | 51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
28 | 8.5 |
| Adi | 4 | 660 | 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
91 | 27.4 | 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
102 | 30.7 |
| Pim | 5 | 1100 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
12 | 3.7 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
7 | 2.1 |
| Sub | 6 | 2100 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.6 | 0.5 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.5 | 0.5 |
| Aze | 7 | 1400 | 9000 | 2.5 | 0.8 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
2.6 | 0.8 |
| ttM | — | 680g | 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
32 | 9.7 | 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
64 | 19.3 |
| Ter | — | 1200 | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
19 | 17.4 | 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
210 | 191.4 |
| aKG | — | n/dh | 4600 | n/dh | n/dh | 5000 | n/dh | n/dh |
Interestingly, for the saturated linear dicarboxylate species (Mal–Aze), only minor discrepancies in binding affinity were observed between the two differently shaped receptors dt1 and dt2. Both macrocycles exhibit the highest affinity for Adi, with strong 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binding in the competitive aqueous solvent mixture used. In addition, both compounds display a similar selectivity pattern across the linear dicarboxylate series (Mal–Aze). This surprising result is attributed to the flexibility of m-xylyl linked (dt1) or p-xylyl linked (dt2) receptors. Although the two macrocycles have differing pore shapes, with saturated dicarboxylate guests both the host and guest are adaptable, and similar binding constants are observed for the two receptors. Adi (n = 4), with the highest binding affinity appears to be the optimal guest from the saturated dicarboxylate series for both macrocycles. With anions larger than Adi, the binding strength drops off sharply, presumably as the anion becomes too big to fit fully inside the macrocyclic pore. Notably, dt2 exhibits selectivity of almost one order of magnitude between anions two carbon chains smaller (Suc, n = 2) or larger (Sub, n = 6) than Adi.
1 binding in the competitive aqueous solvent mixture used. In addition, both compounds display a similar selectivity pattern across the linear dicarboxylate series (Mal–Aze). This surprising result is attributed to the flexibility of m-xylyl linked (dt1) or p-xylyl linked (dt2) receptors. Although the two macrocycles have differing pore shapes, with saturated dicarboxylate guests both the host and guest are adaptable, and similar binding constants are observed for the two receptors. Adi (n = 4), with the highest binding affinity appears to be the optimal guest from the saturated dicarboxylate series for both macrocycles. With anions larger than Adi, the binding strength drops off sharply, presumably as the anion becomes too big to fit fully inside the macrocyclic pore. Notably, dt2 exhibits selectivity of almost one order of magnitude between anions two carbon chains smaller (Suc, n = 2) or larger (Sub, n = 6) than Adi.
In contrast to the behaviour observed with flexible guests, when evaluating the binding to the rigid dicarboxylates the two macrocycles differ markedly in their binding affinities. The p-xylyl linked macrocycle dt2 binds Ter with a high affinity (Ka = 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1) in contrast to dt1, for which binding is three times weaker (Ka = 30
000 M−1) in contrast to dt1, for which binding is three times weaker (Ka = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1). This result suggests Ter, which is conformationally rigid, is a good geometric match to dt2 and a slight mismatch with the more ‘squashed’ pore of dt1. Likewise, a similar effect was observed with ttM, which is also conformationally restricted due to the restricted rotation around the double bonds. In this instance, dt2 (Ka = 58000 M−1) binds ttM twice as strongly as dt1 (Ka = 28000 M−1). It was hypothesised that the extra carbonyl group in aKG might provide an extra binding site for the hydrogen-bonding groups, however, for both macrocycles, the binding was considerably lower than binding to Glu, which has the same distance between the carboxylate groups. This may be due to unfavourable steric effects in accommodating the anion within the macrocyclic binding site.
000 M−1). This result suggests Ter, which is conformationally rigid, is a good geometric match to dt2 and a slight mismatch with the more ‘squashed’ pore of dt1. Likewise, a similar effect was observed with ttM, which is also conformationally restricted due to the restricted rotation around the double bonds. In this instance, dt2 (Ka = 58000 M−1) binds ttM twice as strongly as dt1 (Ka = 28000 M−1). It was hypothesised that the extra carbonyl group in aKG might provide an extra binding site for the hydrogen-bonding groups, however, for both macrocycles, the binding was considerably lower than binding to Glu, which has the same distance between the carboxylate groups. This may be due to unfavourable steric effects in accommodating the anion within the macrocyclic binding site.
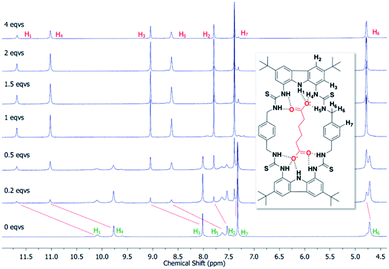
To confirm the binding mechanism, we performed 1H NMR titration experiments in DMSO-d6/0.5% H2O. For both macrocycles, with Adi we observed slow exchange up to 1 equivalent of guest and subsequently no further changes in 1H NMR spectra (Fig. 5 for dt2 and ESI Fig. S70† for dt1). Further, sharpening of the methylene protons (H6) which initially appear broad was observed, indicating a conformational change is occurring upon binding to Adi which brings all 8 methylene protons to a chemically equivalent environment in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. Interestingly, a similar effect was observed when investigating dt2 with the largest anion in the series, Aze (ESI Fig. S69†). Conversely however, with dt2 and the smallest anion, Mal, intermediate exchange was observed, suggesting a much weaker binding event, confirming the UV-vis titration results (ESI Fig. S67†). For dt1 with Mal, intermediate exchange was also observed up to addition of 1 equivalent of anion, with further peak splitting at higher guest concentrations, suggesting that higher order complexes (oligomers) may also be formed in this case (ESI Fig. S71†). Attempts to fit the UV-vis titration data to higher order binding models (2
1 complex. Interestingly, a similar effect was observed when investigating dt2 with the largest anion in the series, Aze (ESI Fig. S69†). Conversely however, with dt2 and the smallest anion, Mal, intermediate exchange was observed, suggesting a much weaker binding event, confirming the UV-vis titration results (ESI Fig. S67†). For dt1 with Mal, intermediate exchange was also observed up to addition of 1 equivalent of anion, with further peak splitting at higher guest concentrations, suggesting that higher order complexes (oligomers) may also be formed in this case (ESI Fig. S71†). Attempts to fit the UV-vis titration data to higher order binding models (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 models) for the titrations with Mal produced poor fits which were rejected. It is possible that the more competitive solvent used in UV-vis titration studies along with the much lower concentrations inhibits the formation of higher order complexes which could form in the NMR studies.
2 models) for the titrations with Mal produced poor fits which were rejected. It is possible that the more competitive solvent used in UV-vis titration studies along with the much lower concentrations inhibits the formation of higher order complexes which could form in the NMR studies.
Double mutant cycle analysis
Next, we performed full DMC analysis for receptors dt1 and dt2 by conducting UV-vis titrations in aqueous DMSO solution (H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO 1
DMSO 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 v/v) of mt3 and the full range of dicarboxylates, as well as of dt1 and dt2 with the monotopic guests, propionate and benzoate, as summarised in Table 1. In the DMC analysis, TBA propionate (Pro) was used as the monotopic guest mimic for all dicarboxylates with the exception of Ter, in which TBA benzoate (Bnz) was used. The chelate cooperativity effect becomes clear when the DMC analysis is assessed. Whereas the monotopic receptor mt3 binds the monotopic anion Pro with a low to moderate association constant in the order 103 M−1, the ditopic receptors can reach association constants approaching 105 M−1 with ditopic guests, more precisely, dt2 binds Adi 175 times stronger than mt3 binds Pro.
9 v/v) of mt3 and the full range of dicarboxylates, as well as of dt1 and dt2 with the monotopic guests, propionate and benzoate, as summarised in Table 1. In the DMC analysis, TBA propionate (Pro) was used as the monotopic guest mimic for all dicarboxylates with the exception of Ter, in which TBA benzoate (Bnz) was used. The chelate cooperativity effect becomes clear when the DMC analysis is assessed. Whereas the monotopic receptor mt3 binds the monotopic anion Pro with a low to moderate association constant in the order 103 M−1, the ditopic receptors can reach association constants approaching 105 M−1 with ditopic guests, more precisely, dt2 binds Adi 175 times stronger than mt3 binds Pro.
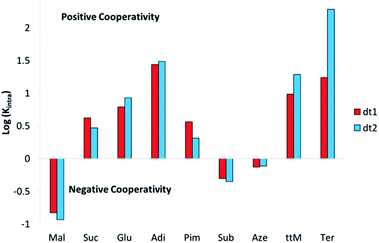
Analysis of the effective molarities (EM) and Kintra for this system allows several conclusions to be drawn. Interestingly, as with the initial binding constant analysis of dt1 and dt2 with ditopic anions, there are few discrepancies in the cooperativity trend between the two macrocycles. Fig. 6 shows a graphical representation of log(Kintra) whereby if log(Kintra) < 0, negative cooperativity is observed, and likewise if log(Kintra) > 0, positive cooperativity is observed.
For both macrocycles, with Mal, low Kintra values are obtained. This is because Mal is too short to span the width of both macrocycles and efficiently form a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex, therefore, oligomer formation is favourable. Likewise, with the largest two dicarboxylates Sub and Aze, Kintra values < 1 M−1 are observed indicating the formation of oligomers is favoured over the 1
1 complex, therefore, oligomer formation is favourable. Likewise, with the largest two dicarboxylates Sub and Aze, Kintra values < 1 M−1 are observed indicating the formation of oligomers is favoured over the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex. In this case, both anions are much too large for both hosts and therefore would have to bend significantly to bind both sides of the macrocycle, which would result in a significant entropic penalty resulting in favourable oligomer formation.
1 complex. In this case, both anions are much too large for both hosts and therefore would have to bend significantly to bind both sides of the macrocycle, which would result in a significant entropic penalty resulting in favourable oligomer formation.
For anions with intermediate binding strengths towards the macrocycle (Suc, Glu and Pim), Kintra values of less than 10 are observed, together with moderate EM values. This suggests modest positive cooperativity with equilibria shifted towards cyclised 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex formation, despite an imperfect size match. With the strongest binding linear dicarboxylate Adi, high Kintra values are observed, indicating strong positive cooperativity towards both macrocycles, along with EMs of ∼100 mM. Interestingly, the favourable chelate cooperativity drops away rapidly with increasing anion length above the optimal with KintraPim ∼ 7 (dt1) and 15 (dt2) times lower than KintraAdi. A possible reason for this rapid drop off in cooperativity above the optimal anion size could be due to favourable spacer effects arising from additional stabilisation gained if the alkyl spacer on the guest can be fully encapsulated by the host. If a longer guest has to bend or flex to induce a fit inside the macrocycle pore, some of the alkyl spacer will be exposed to the bulk solvent, which may destabilise the ditopically bound species resulting in less favourable cooperative effect.
1 complex formation, despite an imperfect size match. With the strongest binding linear dicarboxylate Adi, high Kintra values are observed, indicating strong positive cooperativity towards both macrocycles, along with EMs of ∼100 mM. Interestingly, the favourable chelate cooperativity drops away rapidly with increasing anion length above the optimal with KintraPim ∼ 7 (dt1) and 15 (dt2) times lower than KintraAdi. A possible reason for this rapid drop off in cooperativity above the optimal anion size could be due to favourable spacer effects arising from additional stabilisation gained if the alkyl spacer on the guest can be fully encapsulated by the host. If a longer guest has to bend or flex to induce a fit inside the macrocycle pore, some of the alkyl spacer will be exposed to the bulk solvent, which may destabilise the ditopically bound species resulting in less favourable cooperative effect.
Differences in cooperativity between the two differently shaped macrocycles are observed with rigid anions. With ttM, dt2 exhibits strong positive cooperativity, which is also reflected by a high binding constant. Conversely, for dt1 only moderate cooperativity is observed. For binding to Ter, in which Bnz was taken as the reference guest, dt2 shows the highest positive chelate cooperativity for the series with an EM value of 210 mM and Kintra approaching 200 M−1. This high positive cooperativity is attributed to a combination of excellent geometric match between dt2 and Ter, together with favourable π–π interactions between the central aromatic rings on the macrocycle and the aromatic guest. dt1 with Ter also exhibits reasonably strong positive cooperativity, which again could be a result of stabilisation through favourable π–π interactions. Further evidence for favourable aromatic stabilisation comes from closer examination of the DMC data. Whilst the monotopic mt3 binds Bnz with moderative affinity (Ka = 1800 M−1), both ditopic hosts exhibit a K11 binding constant an order of magnitude higher (K11 = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 for dt1 and 19
000 M−1 for dt1 and 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 M−1 for dt2), suggesting favourable stabilisation of this monotopic guest within the macrocycle. Nonetheless, dt2 exhibits an order of magnitude higher Kintra than dt1 towards Ter which can be attributed to a better geometric match of the receptor to the guest length.
000 M−1 for dt2), suggesting favourable stabilisation of this monotopic guest within the macrocycle. Nonetheless, dt2 exhibits an order of magnitude higher Kintra than dt1 towards Ter which can be attributed to a better geometric match of the receptor to the guest length.
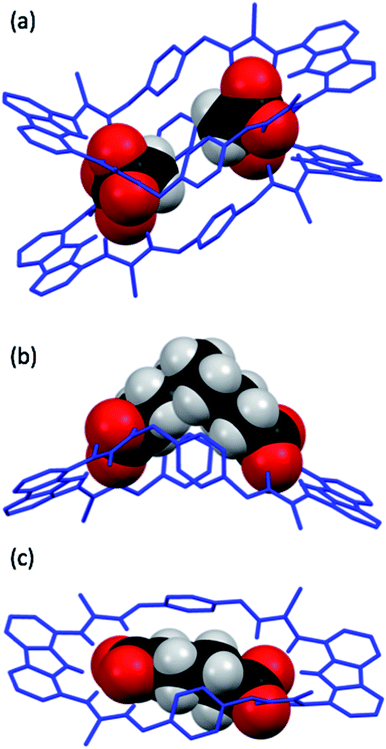
Crystal structure analysis
Single crystals of dt2 with three different dicarboxylates of various lengths suitable for X-ray crystal structure analysis were obtained (Fig. 7). The crystal structures confirmed the binding mode of the macrocycles, in which each carboxylate unit is bound by 5 hydrogen bonds stemming from the two thiourea groups and the central carbazole NH of each binding site.In the solid state, the complex of dt2 with Mal formed a [2+2] crystal structure (Fig. 7a), where each end of the dicarboxylate is bound to two different macrocycle molecules. A second dicarboxylate is bound to the other end of each macrocycle forming a cage. All eight thiocarbonyls on the macrocycles are pointing away from each other, along with the planar carbazole units. The xylyl aromatic rings on both macrocycles are arranged in a staggered, planar conformation, however, centroid–centroid distances of 4.993 Å and 4.819 Å suggest no π–π interactions are occurring between neighbouring macrocycles. This indicates that the cage is entirely held together by hydrogen bonding interactions from the macrocycles to the two dicarboxylate bridging units. It is clear that the Mal anion in this case is not large enough to span the distance between the two binding sites of an individual macrocycle. In this [2+2] complex, the two macrocycles in the structure are bent about their methylene units to accommodate both anions, the closest contact point between neighbouring macrocycles is from one thiourea NH to a second thiourea NH. This structure confirms the conclusions from the DMC analysis, indicating that oligomer formation is preferred in solution due to the anion being unable to span the two binding units of a single macrocycle.
The structure formed with dt2·Aze is quite different (Fig. 7b). Here, a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex was formed where the anion, which is much larger than the macrocyclic pore, contorts from its favourable conformation in order to bind to both ends of the macrocycle. The macrocycle is also significantly twisted with all thiocarbonyls pointing down and away from each other. The anion is forced to adopt an unfavourable conformation, as supported by the DMC analysis, to allow it to bind to the receptor in a 1
1 complex was formed where the anion, which is much larger than the macrocyclic pore, contorts from its favourable conformation in order to bind to both ends of the macrocycle. The macrocycle is also significantly twisted with all thiocarbonyls pointing down and away from each other. The anion is forced to adopt an unfavourable conformation, as supported by the DMC analysis, to allow it to bind to the receptor in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 manner. This conformational rearrangement from the preferred all-gauche conformer would be energetically unfavourable in solution. In addition, as the alkyl spacer on Aze is not encapsulated within the macrocycle pore, additional destabilisation may occur due to interactions between the non-polar alkyl chain and the polar solvent.
1 manner. This conformational rearrangement from the preferred all-gauche conformer would be energetically unfavourable in solution. In addition, as the alkyl spacer on Aze is not encapsulated within the macrocycle pore, additional destabilisation may occur due to interactions between the non-polar alkyl chain and the polar solvent.
Contrastingly, the crystal structure of dt2·Adi shows the anion is almost perfectly encapsulated by the macrocycle and the overall complex is relatively planar (Fig. 7c), with a slight twist in the macrocycle to better encapsulate the entirety of the anion. Table 2 shows the measured macrocycle pore sizes (N3⋯N8) for the three complexes dt2·Mal, dt2·Adi and dt2·Aze. In the structure for dt2·Aze, there are two macrocycle complexes in the unit cell, both showing similar geometry, only one complex is shown in Fig. 7b but both measured pore sizes are provided.
Interestingly, analysis of the macrocycle pore sizes shows that the complex with Adi has the largest N⋯N distance of the three crystals collected: 12.856 Å for dt2·Adiversus 12.285 Å for dt2·Aze (largest size) and 12.125 Å for dt2·Mal (largest size). This confirms the semi-flexibility of macrocycle and shows that the pore size and therefore binding pocket is malleable. In this case, the planarization of the macrocycle gives an increased pore size of ∼0.6 Å to better adapt to the added guest. The complimentary geometric matchup between Adi and dt2 is reflected in the high binding constant from titration studies and high positive cooperativity in DMC analysis. As a conformational change occurs upon binding, this is a clear indication of favourable energetics induced by increased cooperative effect towards forming the closed cyclic species.
Conclusions
To conclude, we have examined the anion binding of two differentially shaped ditopic macrocyclic receptors towards ditopic anionic guests in a competitive polar solvent. While surprisingly few discrepancies were observed between the binding affinities of the two hosts with flexible (unsaturated) guests, with rigid guests, larger differences in binding affinities between were observed due to geometric matches or mismatches. DMC analysis allowed the chelate cooperativity effects of these systems to be investigated. Negative cooperativity was observed in cases where the guest was too short to span the macrocycle pore. Negative cooperativity was also observed where the guest was much larger than the host pore, even though the guest can flex to bind both parts of the ditopic host as evidenced in the solid state; this is energetically unfavourable in solution. One reason for this may be due to a lack of favourable spacer interactions that occur when the host and guest fits are complimentary, which cannot occur if encapsulation of the guest is incomplete by the host. Conversely, positive cooperativity was observed where a flexible guest can span the length of the host and fit entirely within the macrocyclic pore. This cooperativity increases up to the optimal guest size and is rewarded with high EMs and binding constants and high selectivity over monotopic host/guest systems (selectivity for dt2 for adi over mt3 for pro is >175 times). Beyond the optimal guest size, the cooperative effect drops off rapidly. NMR and crystallographic studies have shown that the semi-flexible hosts can alter their pore size to better encapsulate guests and cooperativity analysis suggests that it is energetically favourable to do so. This work serves to further elucidate the subtle complexities between binding affinity and chelate cooperativity. While the ditopic binding of Aze was shown to be unfavourable, the binding constant is still an order of magnitude higher than the monotopic binding to the reference Pro. Furthermore, it serves to highlight how significant spacer interactions can stabilise or destabilise cooperative interactions, which will aid in future design for specific and selective supramolecular systems for multitopic receptors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Australian Research Council (DP170100118 to K. A. J.). L. Q. thanks the University of Sydney for a Lamberton Scholarship. This work was facilitated by access to Sydney Analytical, a core research facility at The University of Sydney.References
- B. Cornils and P. Lappe, in Ullmann's Encyclopedia of Industrial Chemistry, 2014, pp. 1–18 Search PubMed.
- D. Curiel, M. Más-Montoya and G. Sánchez, Coord. Chem. Rev., 2015, 284, 19–66 CrossRef CAS.
- A. M. Pajor, J. Membr. Biol., 2000, 175, 1–8 CrossRef CAS PubMed.
- K. S. Oyedotun and B. D. Lemire, J. Biol. Chem., 2004, 279, 9424–9431 CrossRef CAS PubMed.
- W. He, F. J. P. Miao, D. C. H. Lin, R. T. Schwandner, Z. Wang, J. Gao, J. L. Chen, H. Tlan and L. Ling, Nature, 2004, 429, 188–193 CrossRef CAS PubMed.
- I. Bechthold, K. Bretz, S. Kabasci, R. Kopitzky and A. Springer, Chem. Eng. Technol., 2008, 31, 647–654 CrossRef CAS.
- N. Werner and S. Zibek, World J. Microbiol. Biotechnol., 2017, 33, 1–9 CrossRef CAS PubMed.
- J. Ruprecht, V. Yankovskaya, E. Maklashina, S. Iwata and G. Cecchini, J. Biol. Chem., 2009, 284, 29836–29846 CrossRef CAS PubMed.
- V. Yankovskaya, R. Horsefield, S. Tornroth, C. Luna-Chavez, H. Miyoshi, C. Leger, B. Byrne, G. Cecchini and S. Iwata, Science, 2003, 299, 700–704 CrossRef CAS PubMed.
- L. Valls-Lacalle, I. Barba, E. Miró-Casas, J. J. Alburquerque-Béjar, M. Ruiz-Meana, M. Fuertes-Agudo, A. Rodríguez-Sinovas and D. García-Dorado, Cardiovasc. Res., 2016, 109, 374–384 CrossRef CAS PubMed.
- M. Más-Montoya, D. Curiel, C. Ramírez de Arellano, A. Tárraga and P. Molina, Eur. J. Org. Chem., 2016, 2016, 3878–3883 CrossRef.
- V. Korendovych, M. Cho, P. L. Butler, R. J. Staples and E. V. Rybak-Akimova, Org. Lett., 2006, 8, 3171–3174 CrossRef PubMed.
- T. Gunnlaugsson, A. P. Davis, J. E. O'Brien and M. Glynn, Org. Biomol. Chem., 2005, 3, 48–56 RSC.
- T. Gunnlaugsson, A. P. Davis, J. E. O'Brien and M. Glynn, Org. Lett., 2002, 4, 2449–2452 CrossRef CAS PubMed.
- J. Y. C. Lim, I. Marques, V. Félix and P. D. Beer, Angew. Chem., Int. Ed., 2018, 57, 584–588 CrossRef CAS PubMed.
- J. Y. C. Lim, I. Marques, V. Félix and P. D. Beer, Chem. Commun., 2018, 54, 10851–10854 RSC.
- A. D. Hughes and E. V. Anslyn, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6538–6543 CrossRef CAS PubMed.
- M.-P. Teulade-Fichou, J. Vigneron and J. Lehn, J. Chem. Soc., Perkin Trans. 2, 1996, 2, 2169–2175 RSC.
- M. Hu and G. Feng, Chem. Commun., 2012, 48, 6951–6953 RSC.
- P. Mateus, R. Delgado, V. André and M. T. Duarte, Inorg. Chem., 2015, 54, 229–240 CrossRef CAS PubMed.
- A. Ragusa, S. Rossi, J. M. Hayes, M. Stein and J. D. Kilburn, Chem.–Eur. J., 2005, 11, 5674–5688 CrossRef CAS PubMed.
- S. Rossi, G. M. Kyne, D. L. Turner, N. J. Wells and J. D. Kilburn, Angew. Chem., Int. Ed., 2002, 76, 4233–4236 CrossRef.
- W. Chen, C. Guo, Q. He, X. Chi, V. M. Lynch, Z. Zhang, J. Su, H. Tian and J. L. Sessler, J. Am. Chem. Soc., 2019, 141, 14798–14806 CrossRef CAS PubMed.
- Q. Q. Wang, V. W. Day and K. Bowman-James, Chem. Sci., 2011, 2, 1735–1738 RSC.
- C. Bravin, A. Guidetti, G. Licini and C. Zonta, Chem. Sci., 2019, 10, 3523–3528 RSC.
- M. Pushina, P. Koutnik, R. Nishiyabu, T. Minami, P. Savechenkov and P. Anzenbacher, Chem.–Eur. J., 2018, 24, 4879–4884 CrossRef CAS PubMed.
- S. L. Wiskur, P. N. Floriano, E. V. Anslyn and J. T. McDevitt, Angew. Chem., Int. Ed., 2003, 42, 2070–2072 CrossRef CAS PubMed.
- G. Ercolani and L. Schiaffino, Angew. Chem., Int. Ed., 2011, 50, 1762–1768 CrossRef CAS PubMed.
- C. A. Hunter and H. L. Anderson, Angew. Chem., Int. Ed., 2009, 48, 7488–7499 CrossRef CAS PubMed.
- L. K. S. Von Krbek, C. A. Schalley and P. Thordarson, Chem. Soc. Rev., 2017, 46, 2622–2637 RSC.
- A. Camara-Campos, D. Musumeci, C. A. Hunter and S. Turega, J. Am. Chem. Soc., 2009, 131, 18518–18524 CrossRef CAS PubMed.
- H. Adams, E. Chekmeneva, C. A. Hunter, M. C. Misuraca, C. Navarro and S. M. Turega, J. Am. Chem. Soc., 2013, 135, 1853–1863 CrossRef CAS PubMed.
- S. Henkel, M. C. Misuraca, Y. Ding, M. Guitet and C. A. Hunter, J. Am. Chem. Soc., 2017, 139, 6675–6681 CrossRef CAS PubMed.
- H. Sun, C. A. Hunter and E. M. Llamas, Chem. Sci., 2015, 6, 1444–1453 RSC.
- L. K. S. von Krbek, A. J. Achazi, S. Schoder, M. Gaedke, T. Biberger, B. Paulus and C. A. Schalley, Chem.–Eur. J., 2017, 23, 2877–2883 CrossRef CAS PubMed.
- W. Jiang, K. Nowosinski, N. L. Löw, E. V. Dzyuba, F. Klautzsch, A. Schäfer, J. Huuskonen, K. Rissanen and C. A. Schalley, J. Am. Chem. Soc., 2012, 134, 1860–1868 CrossRef CAS PubMed.
- K. Nowosinski, L. K. S. Von Krbek, N. L. Traulsen and C. A. Schalley, Org. Lett., 2015, 17, 5076–5079 CrossRef CAS PubMed.
- C. Montoro-García, J. Camacho-García, A. M. López-Pérez, M. J. Mayoral, N. Bilbao and D. González-Rodríguez, Angew. Chem., Int. Ed., 2016, 55, 223–227 CrossRef PubMed.
- G. Ercolani, J. Am. Chem. Soc., 2003, 125, 16097–16103 CrossRef CAS PubMed.
- M. C. Misuraca, T. Grecu, Z. Freixa, V. Garavini, C. A. Hunter, P. W. N. M. Van Leeuwen, M. D. Segarra-Maset and S. M. Turega, J. Org. Chem., 2011, 76, 2723–2732 CrossRef CAS PubMed.
- H. J. Hogben, J. K. Sprafke, M. Hoffmann, M. Pawlicki and H. L. Anderson, J. Am. Chem. Soc., 2011, 133, 20962–20969 CrossRef CAS PubMed.
- J. Raker and T. E. Glass, J. Org. Chem., 2002, 67, 6113–6116 CrossRef CAS PubMed.
- M. J. Chmielewski, M. Charon and J. Jurczak, Org. Lett., 2004, 6, 3501–3504 CrossRef CAS PubMed.
- M. Belén Jiménez, V. Alcázar, R. Peláez, F. Sanz, Á. L. Fuentes De Arriba and M. C. Caballero, Org. Biomol. Chem., 2012, 10, 1181–1185 RSC.
- D. E. Gross, V. Mikkilineni, V. M. Lynch and J. L. Sessler, Supramol. Chem., 2010, 22, 135–141 CrossRef CAS PubMed.
- L. Qin, A. Hartley, P. Turner, R. B. P. Elmes and K. A. Jolliffe, Chem. Sci., 2016, 7, 4563–4572 RSC.
- L. K. S. Von Krbek, A. J. Achazi, M. Solleder, M. Weber, B. Paulus and C. A. Schalley, Chem.–Eur. J., 2016, 27, 15475–15484 CrossRef PubMed.
- http://www.supramolecular.org, accessed March 2019.
Footnote |
| † Electronic supplementary information (ESI) available: Providing details of the compound synthesis and characterization, UV-vis binding studies and fitted titration data, DMC analysis and derivatization, fluorescence screening studies, NMR titration data and crystallography methods (PDF). Crystallographic data for dt2·Mal, dt2·Adi and dt2·Aze (cif). CCDC 1954830–1954832. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc02533j |
| This journal is © The Royal Society of Chemistry 2020 |