Nucleophilic substitution reactions of cyclic thiosulfinates are accelerated by hyperconjugative interactions

Abstract

Cyclic thiosulfinates are a class of biocompatible molecules, currently expanding our in vivo toolkit. Agar and co-workers have shown that they are capable of efficient cross-linking reactions. While strain energy has been shown to promote the nucleophilic substitution reactions of cyclic disulfides, the reactivities of cyclic thiosulfinate nucleophilic substitution is unexplored. We used density functional theory calculations [M06-2X/6-311++G(d,p)] to determine the activation and reaction free energies for the reactions of 3–10-membered cyclic thiosulfinates and cyclic disulfides with methyl thiolate. The nucleophilic substitution reaction of cyclic thiosulfinates was found to be strain-promoted, similar to the strain-promoted nucleophilic substitution reactions of cyclic disulfides. The origin of the nearly 100-fold rate enhancement of cyclic thiosulfinates over cyclic disulfides was understood using the distortion/interaction model and natural bond order analysis. The cyclic thiosulfinates benefit from a hyperconjugative interaction between an oxygen lone pair and the orbital . This interaction generally lengthens the reactant S₁–S₂ bond, which pre-distorts cyclic thiosulfinates to resemble their corresponding transition structures. The inductive effect of the oxygen in cyclic thiosulfinates lowers the orbital energies relative to cyclic disulfides and results in more stabiliizing transition state frontier molecular orbital interactions with methyl thiolate.

---

Introduction

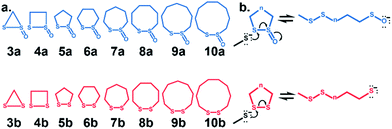
Cyclic disulfides are a privileged class of molecules that have long played important roles in energy metabolism and the modulation of cellular redox status.^1–6 Recently, they have been used for in vivo applications in biochemistry and biomaterials as building blocks for self-healing, biocompatible polymers, and hydrogels.^7,8 They can also serve as vehicles to shuttle large molecules and apoptosis-inducing substrates through cell membranes via the transferrin receptor.^9–12 In many cases, α-lipoic acid, a cyclic disulfide, has been used in a variety of functional assemblies at the gold surface.^13–15 Cyclic disulfides are one of the first known cross-linking-specific molecules; Agar and co-workers showed that they could selectively cross-link cysteine pairs while reversibly modifying lone cysteines in vivo.¹⁶ Our groups recently introduced a six-membered cyclic thiosulfinate (1,2-dithiane-1-oxide) capable of cross-linking free cysteine pairs up to 10⁴-fold faster than a six-membered cyclic disulfide (1,2-dithiane), by circumventing the rate-determining oxidation step.¹⁶ A covalent cross-link is efficiently formed between the sulfenic acid intermediate and a second thiolate. Whitesides and coworkers augmented their experiments with MM2 ¹⁷ calculations to show that the reactivities of cyclic disulfides towards biological thiolate-based nucleophiles were strain-promoted.^18,19 Bachrach and co-workers used DFT calculations to locate transition structures for the nucleophilic substitution reactions of a model thiolate to a series of cyclic disulfides.²⁰ This computational study builds on the results of Whitesides and Bachrach to determine the origin of the increased nucleophilic substitution reactivities of 3–10-membered cyclic thiosulfinates relative to cyclic disulfides (Scheme 1). A rigorous conformational search was employed to identify the global minima of reactants, ring-opened intermediates, and the lowest-energy transition structures. The DFT calculations are used to predict the reactivities of 3–10-membered cyclic thiosulfinates (3–10)a towards a model thiolate (methyl thiolate) by locating transition structures and disulfide-exchange intermediates. The corresponding activation free energies and reaction energies (ΔG^‡ and ΔG_rxn, respectively) were compared to those of an analogous series of cyclic disulfides to understand why cyclic thiosulfinates are more reactive than cyclic disulfides towards thiolates.

Scheme 1 (a) Series of cyclic thiosulfinates and cyclic disulfides examined in this manuscript. (b) Mechanism of thiol-disulfide exchange between nucleophilic methyl thiolate (MeS⁻) and a cyclic thiosulfinate (blue) or a cyclic disulfide (red).

Results and discussion

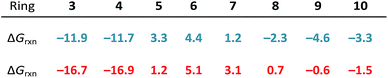
Ring strain is released upon nucleophilic addition of MeS⁻; as such, we defined strain energy as −ΔG_rxn. We computed reaction energies (ΔG_rxn) for the nucleophilic addition of MeS⁻ to (3–10)a and (3–10)b to assess the reversibilities of the nucleophilic substitution reactions. These energies are summarized in Table 1.

Table 1 ΔG_rxn of the nucleophilic attack of MeS⁻ on (3–10)a (blue) and (3–10)b (red). Computed using M06-2X/6-311++G(d,p) IEF-PMC^H₂O

---

For the most strained reactants, (3–4)a and (3–4)b, the reaction energies for the nucleophilic addition of MeS⁻ range from −11.9 to −11.7 and −16.9 to −16.7 kcal mol⁻¹, respectively. These reactions are exergonic because ring strain is released upon ring-opening. (5–7)a and (5–7)b lead to endergonic reaction energies ranging from 1.2 to 4.4 kcal mol⁻¹ and 1.2 to 5.1 kcal mol⁻¹, respectively. The larger cyclic structures, (8–10)a and (8–10)b have reaction free energies that range from −2.3 to −4.6 kcal mol⁻¹ and +0.7 to −1.5 kcal mol⁻¹, respectively.

The reaction energies of these series follow a similar trend to cycloalkanes in which (3–4)a and (3–4)b are significantly strained, (5–7)a and (5–7)b are relatively unstrained, and (8–10)a and (8–10)b are moderately strained.^20–22 The longer S₁–S₂ bond in the thiacycles relieves some strain compared the corresponding cycloalkanes (e.g., 1,2-dithiolane vs. cyclopentane).

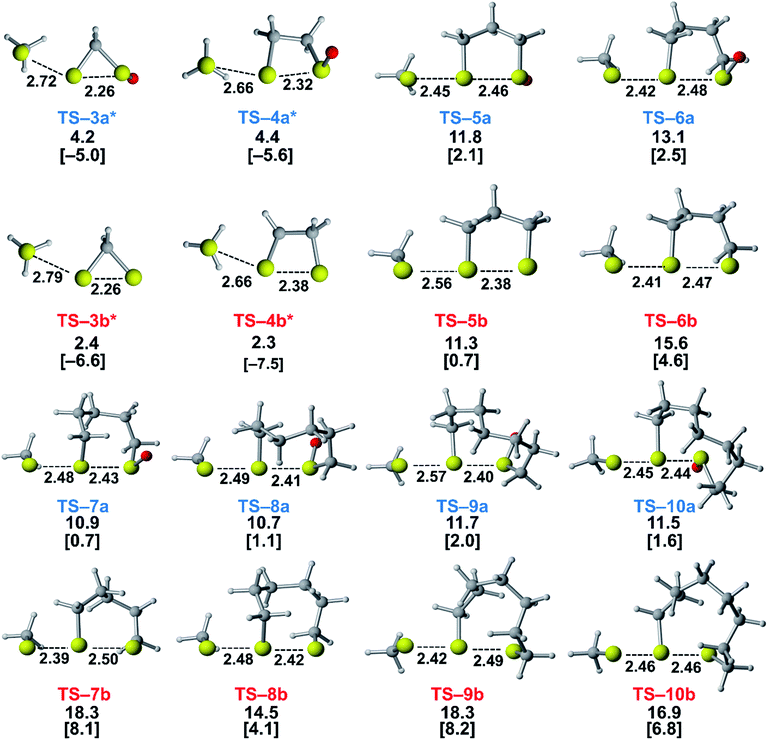
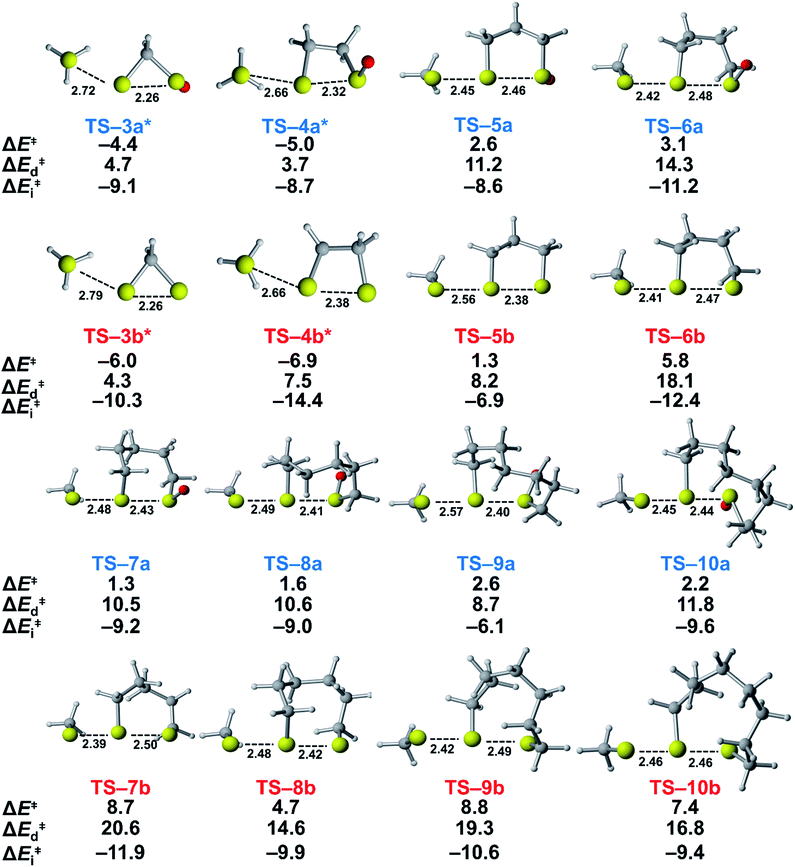
We assessed the reactivities of the cyclic thiosulfinates and cyclic disulfides towards methyl thiolate by locating transition structures and computing their corresponding activation free energies and enthalpies (Fig. 1). The transition structures shown in Fig. 1 generally have a nearly linear MeS⁻–S₁–S₂ angle; the transition states range from exactly synchronous to asynchronous. The breaking S₁–S₂ bonds of TS-(3–10)a and TS-(3–10)b range from 2.26–2.48 Å and 2.26–2.50 Å, respectively. The S–S₁ distance in TS-(3–10)a and TS-(3–10)b ranges from 2.42–2.72 Å and 2.39–2.79 Å, respectively. TS-10b is exactly synchronous (2.46 Å), while TS-5b is the most asynchronous (2.56 and 2.38 Å). The C–C and C–S σ bonds of (3–4)a and (3–4)b are well-described by Walsh orbitals due to the nearly 60° and 90° bonding angles, respectively. As such, incipient nucleophiles will interact with bent S₁–S₂ σ* orbitals, which results in the non-linear transition state geometries of TS-(3–4)a and TS-(3–4)b. The activation free energies of the smallest rings TS-(3–4)a and TS-(3–4)b are the lowest (2.3–4.4 kcal mol⁻¹). The low activation energies of (3–4)a and (3–4)b are consistent with the established strain-promoted reactions of cyclic disulfides. The activation free of energies of TS-(5–10)a are generally higher and range from 10.9 to 13.1 kcal mol⁻¹. The activation free energies of TS-(6–10)a are substantially lower than those of TS-(6–10)b; ΔΔG^‡ range from −2.5 to −7.4 kcal mol⁻¹, which corresponds to a 10²–10⁵-fold rate enhancement for cyclic thiosulfinates relative to cyclic disulfides.

Fig. 1 Transition structures for the reaction of MeS⁻ with cyclic thiosulfinates (3–10)a and cyclic disulfides (3–10)b. The ΔG^‡ and ΔH^‡ (in brackets) were computed with M06-2X/6-311++G(d,p) IEF-PCM^H₂O and provided for each transition structure. The bond lengths and energies are reported in Å and kcal mol⁻¹, respectively. *We were unable to locate transition states for (3–4)a and (3–4)b using B3LYP-D3BJ, M06-2X, or MP2 methods. Reported structures are energies for a constrained transition structure featuring one negative frequency corresponding to the substitution reaction using M06-2X/6-311++G(d,p).

Are these reactions strain promoted?

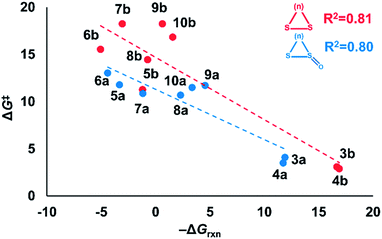
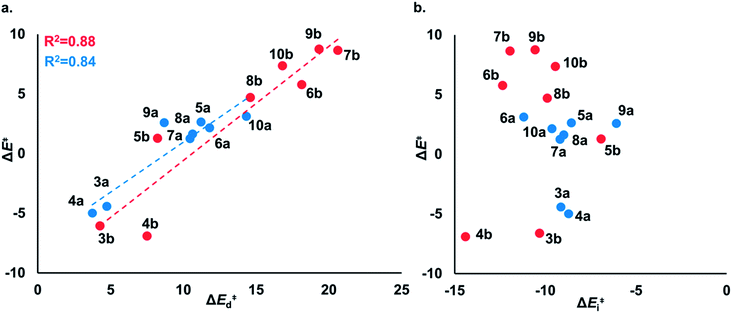
Nucleophilic substitution reactions of cyclic disulfides are often described as strain-promoted.^18,20,23 We assessed the role of strain energy on the reactivities of (3–10)a and (3–10)b by plotting ΔG^‡ against −ΔG_rxn (Fig. 2).

Fig. 2 Plot of ΔG^‡vs. −ΔG_rxn of series (3–10)a and (3–10)b. The linear equation for (3–10)a is ΔG^‡ = −0.53(−ΔG_rxn) + 11.33. The linear equation for (3–10)b is ΔG^‡ = −0.66(−ΔG_rxn) + 14.71. Computed using M06-2X/6-311++G(d,p) IEF-PCM^H₂O.

Fig. 2 shows a linear correlation between ΔG^‡ and −ΔG_rxn for the cyclic disulfide and cyclic thiosulfinate reactions (R² = 0.81 and 0.80, respectively). This suggests that strain energy controls the reactivities for a broad set of cyclic disulfides and establishes that the reactivities of cyclic thiosulfinates are also controlled by strain energy. The activation free energies of cyclic thiosulfinates are generally lower than those of cyclic disulfides; the y-intercept values are 11.3 and 14.7 kcal mol⁻¹, respectively.

Distortion/interaction model

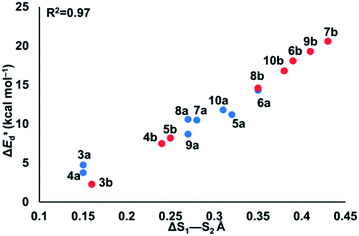
To understand the origin of generally lower activation barriers and strain energies of cyclic thiosulfinates relative to the cyclic disulfides, we turned to the distortion/interaction model.^24–26 The distortion/interaction model dissects activation barriers for bimolecular reactions into two terms: distortion and interaction energy [ΔE^‡ = ΔE^‡_d + ΔE^‡_i]. Distortion energy (ΔE^‡_d) is the energy required to deform reactants from their equilibrium structures to their distorted transition structure geometries without allowing them to interact. Interaction energy (ΔE^‡_i) results from the difference in ΔE^‡ and ΔE^‡_d and has been attributed to favorable intermolecular electrostatic, dispersion, and charge transfer interactions. The distortion/interaction model has been used to explain the reactivities and selectivities of pericyclic^27–30 and organometallic^31–33 reactions. The computed distortion and interaction energies of TS-(3–10)a and TS-(3–10)b are summarized in Fig. 3.

Fig. 3 Activation, distortion, and interaction energies of TS-(3–10)a and TS-(3–10)b. Computed using M06-2X/6-311++G(d,p) IEF-PCM^H₂O. The bond lengths and energies are reported in Å and kcal mol⁻¹, respectively. *Transition structures are constrained and have one negative frequency connecting reactants to product using M06-2X/6-311++G(d,p).

The distortion energies of cyclic thiosulfinates (3–10)a range from 3.7 to 14.3 kcal mol⁻¹ and the distortion energies of cyclic disulfides (3–10)b range from 4.3 to 20.6 kcal mol⁻¹. We plotted activation energies against distortion energies for the reactions of cyclic thiosulfinates (blue) and cyclic disulfides (red) in Fig. 4. These plots show that there is a linear relationship between ΔE^‡ and ΔE^‡_d for cyclic disulfides (R² = 0.88) and cyclic thiosulfinates (R² = 0.84). This suggests that the reactivities are controlled by distortion energy. The interaction energies of cyclic thiosulfinates (3–10)a and cyclic disulfides (3–10)b range from −6.1 to −11.2 kcal mol⁻¹ and −6.9 to −14.4 kcal mol⁻¹, respectively. There is no correlation between ΔE^‡ and ΔE^‡_i (R² = 0.001 for cyclic thiosulfinates and R² = 0.05 for cyclic disulfides), which implies that the interaction energies do not influence reactivities. We hypothesized that the strain energy would manifest itself as a structural pre-distortion of the reactants, an effect that results in distortion-accelerated reactions.³⁴ To this end, we analyzed (3–10)a and (3–10)b in their equilibrium and distorted transition state geometries; strained cyclic thiosulfinates and disulfides require less distortion to achieve their transition state geometries. This is demonstrated in Fig. 5, where we show the relationship between distortion energy and the difference in S₁–S₂ bond lengths in the reactant and transition state (ΔS₁–S₂).

Fig. 4 (a) ΔE^‡vs. ΔE^‡_d of the nucleophilic addition of MeS⁻ towards cyclic thiosulfinates (blue) and cyclic disulfides (red). The linear equation for (3–10)a is ΔE^‡ = 0.84ΔE^‡_d − 7.40. The linear equation for (3–10)b is ΔE^‡ = 0.96ΔE^‡_d − 10.12. (b) ΔE^‡vs. ΔE^‡_i of the nucleophilic addition of MeS⁻ towards cyclic thiosulfinates (blue, R² = 0.001) and cyclic disulfides (red, R² = 0.05). Computed using M06-2X/6-311++G(d,p) IEF-PCM^H₂O. The energies are reported in kcal mol⁻¹.

Fig. 5 ΔS₁–S₂ bond length between reactant and transition state of cyclic thiosulfinates (blue) and cyclic disulfides (red) vs. calculated distortion energy. The combined linear equation is ΔE^‡_d = 60.55(ΔS₁–S₂) − 6.39.

The reactions with the lowest activation energies resulted from reactants with the longest (pre-distorted) S₁–S₂ bonds at equilibrium. The linear relationship between ΔE^‡_d and ΔS₁–S₂ (R² = 0.97) confirms that the S₁–S₂ pre-distortion of cyclic thiosulfinates results in lower activation energies.

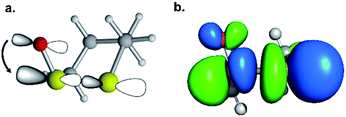
We then scrutinized the geometric and electronic structures of the cyclic thiosulfinates to understand why they are more pre-distorted than the cyclic disulfides. One of the oxygen lone pair orbitals adjacent to the S₁–S₂ bond is ideally positioned for a hyperconjugative interaction with the orbital, via the general anomeric effect, which stabilizes the developing electron deficiency in the breaking S₁–S₂ bond. There is a rich literature on this effect from the experimental and theoretical communities.^35–42Fig. 6 illustrates the possible orbital interaction.

Fig. 6 (a) Hyperconjugative orbital interaction. (b) Computed LUMO of 6a.

We quantified this effect with natural bond order (NBO)⁴³ calculations and second order perturbation theory analysis on the optimized structures of the cyclic thiosulfinates. Table 2 shows the hyperconjugative interaction energies, and the effect on S₁–S₂ bond lengths.

Table 2 Summary of S₁–S₂ bond lengths, n_O and energies, and the interaction energies between the n_O and orbitals

	S1–S2^a	Energy, nO^b	Energy, ^b
a S1–S2 bond lengths are reported in Å. b energies are reported in kcal mol^−1.
3a	2.12	−10.07	−0.54	−47.3
4a	2.17	−9.87	−0.17	−40.3
5a	2.14	−9.74	0.38	−35.8
6a	2.13	−9.74	0.47	−35.4
7a	2.15	−9.75	0.32	−36.9
8a	2.14	−9.77	0.45	−35.9
9a	2.13	−9.69	0.53	−33.9
10a	2.13	−9.70	0.53	−35.8

---

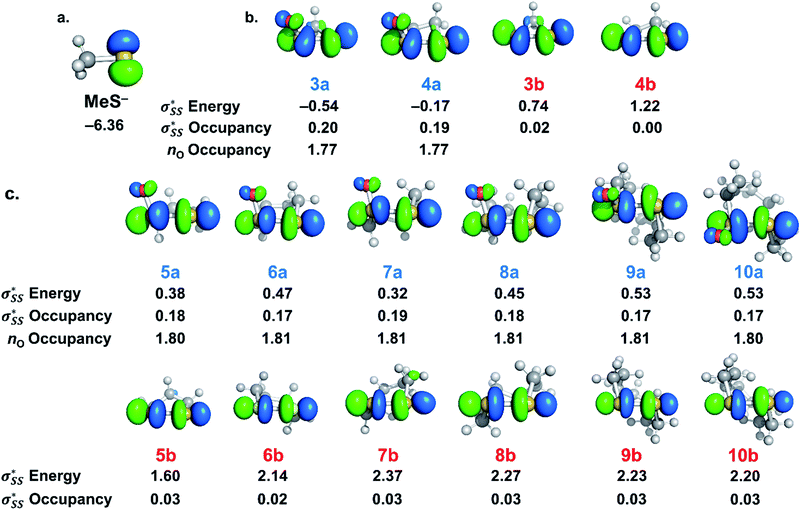
S₁–S₂ bond distances, energies for the n_O and orbitals participating in the hyperconjugative interaction, and the energies of the corresponding interactions are given in Table 2. The σ framework of 3a and 4a have relatively high-lying σ orbitals because of the increased p-character associated with the so-called banana bonds.⁴⁴ As such, 3a and 4a benefit from smaller energy gaps between the n_O and orbitals, which results in interaction energies of −47.3 and −40.3 kcal mol⁻¹, respectively. (5–10)a have smaller, but similar, orbital interaction energies (−33.9 to −36.9 kcal mol⁻¹), because of the larger energy gap between the n_O and orbitals and linear orbitals.

We then compared the orbital energies of cyclic thiosulfinates to those of cyclic disulfides to quantify the extent in which the hyperconjugative interaction contributes to nucleophilic substitution rate-enhancement. The HOMO energy of methyl thiolate, the orbital (LUMO) energies of (3–10)a and (3–10)b, and the occupancies of the and n_O orbitals are shown in Fig. 7.

Fig. 7 (a) Visual representation of MeS⁻ HOMO and corresponding orbital energy. (b) Visual representation of orbitals of (3–4)a and (3–4)b and the corresponding orbital energies and occupancies. (c.) Visual representation of orbitals of (5–10)a and (5–10)b and the corresponding orbital energies and occupancies. Computed M06-2X/6-311++G(d,p) IEF-PMC^H₂O. Energies are reported in eV.

The energies of cyclic thiosulfinates range from −0.54 to 0.53 eV; the energies of cyclic disulfides range from 0.74 to 2.37 eV. The orbitals of cyclic thiosulfinates are relatively low-lying because of the adjacent oxygen that is inductively electron withdrawing. The electron density of the sulfoxide oxygen disfavors nucleophilic attack of thiolates at S₁ because of substantial closed-shell repulsions with the incipient thiolate lone pair orbitals. (3–4)a and (3–4)b feature bent orbitals because of the small C–S–S bond angles in the three- and four-membered rings (54° and 78°, respectively). The n_O orbitals of cyclic thiosulfinates have reduced occupancies (1.77–1.81e) from the ideal value of 2.00e due to the hyperconjugative interaction; the orbitals of cyclic thiosulfinates have increased occupancies (0.17–0.20e) from the ideal value of 0.00e. The large stabilizing energies corroborate the proposed hyperconjugation between the n_O and the orbitals. Cyclic disulfides have a significantly lower occupancy of the orbitals ranging from 0.00–0.03e. The generally lower orbital energies of cyclic thiosulfinates, resulting from the interaction, lead to stronger frontier molecular orbital interactions with the MeS⁻ lone pair orbitals in the transition state. These more favorable interactions contribute to the general rate-enhancement of nucleophilic substitution towards cyclic thiosulfinates.

Methods

Initial conformational searches of all structures studied were performed within Maestro 11 (ref. 45) using low-mode sampling with a maximum atom deviation cutoff of 0.5 Å within the OPLS3e force field in the dielectric constant of water (ε = 78).⁴⁶ Each conformational search produced as maximum of 10 low energy conformations (energy cutoff = 100 kJ mol⁻¹). Each of these OPLSe-minimized structures were subjected to geometrical optimization using the hybrid density functional M06-2X/6-311++G(d,p) and the polarizable continuum model using the integral equation formalism variant (IEF-PCM) with the parameters for water.^47,48 Each stationary point was subjected to vibrational analysis from which exactly one negative frequency was identified for transition structures and an absence of negative frequencies for the minima. All DFT calculations were performed using the Gaussian 16 (ref. 49) program. All stationary points for (5–10)a and (5–10)b were optimized using M06-2X/6-311++G(d,p). Transition state scans of (3–4)a and (3–4)b were performed using the coupled cluster method (CCSD).⁵⁰ The distance between methyl thiolate and the cyclic disulfide/thiosulfinate was scanned between 2.3–2.8 Å. 9 steps at 0.04 Å per step were taken. Each result from this scan was optimized by constraining the forming MeS⁻–S₂ bond distance using the coupled cluster singles doubles method (CCSD) with the 6-31+G(d,p) basis set. Single point energy calculations were performed on the constrained transition structures with the same method and basis set [M06-2X/6-311++G(d,p)] as the unconstrained transition states to evaluate activation free energies. NBO analysis and second order perturbation theory analysis on the optimized cyclic thiosulfate reactants was performed to measure the interaction between the oxygen lone pair and the orbital and the corresponding orbital energies and occupancies. All chemical structures were prepared using CylView.⁵¹ The ESI† was prepared using ESIgen.⁵²

Conclusions

We used DFT calculations to predict the reactivities of a series of 3–10-membered cyclic thiosulfinates towards methyl thiolate for the first time. Similar to previous reports of cyclic disulfide reactivity, the reaction of thiolates towards cyclic thiosulfinates is strain-promoted. Our calculations suggest that the rate of nucleophilic substitution reactions of 6–10-membered cyclic thiosulfinates will be 10²–10⁵-fold faster than 6–10-membered cyclic disulfides. Our calculations show that (3–4)a and (3–4)b have bent orbitals that contribute to their significantly higher strain-dependence and lower activation barriers through increased p-character. The S₁–S₂ bonds in cyclic thiosulfinates (6–10)a are pre-distorted towards their transition structures and require less distortion energy (ΔE^‡_d) to deform reactants from their equilibrium geometries relative to corresponding cyclic disulfides (6–10)b. This results in generally lower activation barriers. A hyperconjugative interaction between the oxygen lone pair and the orbitals is responsible for the pre-distortion of cyclic thiosulfinates and was verified by decreased occupancies of n_O orbitals and increased occupancies of orbitals. The activation barriers are further lowered because the orbital energies are decreased by an inductive effect of the adjacent oxygen, which improves transition state frontier molecular orbital interactions. This effect is not observed in cyclic disulfides which have higher energy orbitals. These theoretical insights have begun to guide our development of new cross-linking tools that avoid toxic dead-end modifications and increase reaction rates in vitro and in vivo. We predict that cyclic thiosulfinate 7a will make the best cross-linking scaffold. Its relatively low strain energy results in a reversible nucleophilic substitution reaction, which will prevent off-target (dead-end) modification of cysteine residues. Additionally, the nucleophilic substitution towards 7a is 7.4 kcal mol⁻¹ lower in activation energy than 7b, resulting in a 10⁵-fold increase in reaction rate.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. A. L. thanks the NSF through the Extreme Science and Engineering Discovery Environment (TG-CHE170074), the Discovery HPC Cluster for computational resources, and NEU for financial support. D. P. D is funded by in part by the NIH R01NS065263, the Robert Johnston Foundation, and ALSA 18-IIA-420.

Notes and references

1. L. J. Reed, B. G. DeBusk, I. C. Gunsalus and C. S. Hornberger, Science, 1951, 114, 93–94.
2. A. Solmonson and R. J. DeBerardinis, J. Biol. Chem., 2018, 293, 7522–7530.
3. K. P. Shay, R. F. Moreau, E. J. Smith, A. R. Smith and T. M. Hagen, Biochim. Biophys. Acta, 2009, 1790, 1149–1160.
4. H. R. Rosenberg and R. Culik, Arch. Biochem. Biophys., 1959, 80, 86–93.
5. P. Ou, H. J. Tritschler and S. P. Wolff, Biochem. Pharmacol., 1995, 50, 123–126.
6. E. L. Feldman, J. Clin. Invest., 2003, 111, 431–433.
7. H. Ishida, A. Kisanuki and K. Endo, Polym. J., 2008, 41, 110.
8. H. Yu, Y. Wang, H. Yang, K. Peng and X. Zhang, J. Mater. Chem. B, 2017, 5, 4121–4127.
9. D. Abegg, G. Gasparini, D. G. Hoch, A. Shuster, E. Bartolami, S. Matile and A. Adibekian, J. Am. Chem. Soc., 2017, 139, 231–238.
10. P. Morelli and S. Matile, Helv. Chim. Acta, 2017, 100, e1600370.
11. L. Zong, E. Bartolami, D. Abegg, A. Adibekian, N. Sakai and S. Matile, ACS Cent. Sci., 2017, 3, 449–453.
12. N. Chuard, G. Gasparini, D. Moreau, S. Lorcher, C. Palivan, W. Meier, N. Sakai and S. Matile, Angew. Chem., Int. Ed. Engl., 2017, 56, 2947–2950.
13. Y. Dong, S. Abaci, C. Shannon and M. J. Bozack, Langmuir, 2003, 19, 8922–8926.
14. S. Roux, B. Garcia, J.-L. Bridot, M. Salomé, C. Marquette, L. Lemelle, P. Gillet, L. Blum, P. Perriat and O. Tillement, Langmuir, 2005, 21, 2526–2536.
15. J. M. Abad, S. F. L. Mertens, M. Pita, V. M. Fernández and D. J. Schiffrin, J. Am. Chem. Soc., 2005, 127, 5689–5694.
16. D. P. Donnelly, M. G. Dowgiallo, J. P. Salisbury, K. C. Aluri, S. Iyengar, M. Chaudhari, M. Mathew, I. Miele, J. R. Auclair, S. A. Lopez, R. Manetsch and J. N. Agar, J. Am. Chem. Soc., 2018, 140, 7377–7380.
17. N. L. Allinger, J. Am. Chem. Soc., 1977, 99, 8127–8134.
18. J. A. Burns and G. M. Whitesides, J. Am. Chem. Soc., 1990, 112, 6296–6303.
19. R. Singh and G. M. Whitesides, J. Am. Chem. Soc., 1990, 112, 6304–6309.
20. S. M. Bachrach, J. T. Woody and D. C. Mulhearn, J. Org. Chem., 2002, 67, 8983–8990.
21. P. Hanson, R. A. A. J. Hendrickx and J. R. Lindsay Smith, New J. Chem., 2010, 34, 65–84.
22. J. A. Boatz, M. S. Gordon and R. L. Hilderbrandt, J. Am. Chem. Soc., 1988, 110, 352–358.
23. É. Dumont, P.-F. Loos and X. Assfeld, Chem. Phys. Lett., 2008, 458, 276–280.
24. F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086.
25. D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187–10198.
26. W.-J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118–3127.
27. B. J. Levandowski, T. A. Hamlin, F. M. Bickelhaupt and K. N. Houk, J. Org. Chem., 2017, 82, 8668–8675.
28. P. H. Y. Cheong, R. S. Paton, S. M. Bronner, G. Y. J. Im, N. K. Garg and K. N. Houk, J. Am. Chem. Soc., 2010, 132, 1267–1269.
29. P. Yu, Z. Yang, Y. Liang, X. Hong, Y. Li and K. N. Houk, J. Am. Chem. Soc., 2016, 138, 8247–8252.
30. F. Liu, R. S. Paton, S. Kim, Y. Liang and K. N. Houk, J. Am. Chem. Soc., 2013, 135, 15642–15649.
31. A. G. Green, P. Liu, C. A. Merlic and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 4575–4583.
32. S. A. Lopez, M. Pourati, H.-J. Gais and K. N. Houk, J. Org. Chem., 2014, 79, 8304–8312.
33. T. Bura, S. Beaupré, M.-A. Légaré, J. Quinn, E. Rochette, J. T. Blaskovits, F.-G. Fontaine, A. Pron, Y. Li and M. Leclerc, Chem. Sci., 2017, 8, 3913–3925.
34. S. A. Lopez and K. N. Houk, J. Org. Chem., 2013, 78, 1778–1783.
35. I. V. Alabugin, M. Manoharan and T. A. Zeidan, J. Am. Chem. Soc., 2003, 125, 14014–14031.
36. I. V. Alabugin, J. Org. Chem., 2000, 65, 3910–3919.
37. M. P. Freitas, Org. Biomol. Chem., 2013, 11, 2885–2890.
38. C. J. Cramer, D. G. Truhlar and A. D. French, Carbohydr. Res., 1997, 298, 1–14.
39. Y. Mo, H. Jiao and P. von Rague Schleyer, J. Org. Chem., 2004, 69, 3493–3499.
40. I. V. Alabugin, J. Org. Chem., 2000, 65, 3910–3919.
41. E. Juaristi, G. dos Passos Gomes, A. O. Terent’ev, R. Notario and I. V. Alabugin, J. Am. Chem. Soc., 2017, 139, 10799–10813.
42. G. D. P. Gomes, V. Vil, A. Terent'ev and I. V. Alabugin, Chem. Sci., 2015, 6, 6783–6791.
43. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
44. K. B. Wiberg, Acc. Chem. Res., 1996, 29, 229–234.
45. Schrödinger Release 2019-1: Maestro, Schrödinger, LLC, New York, NY, 2018.
46. E. Harder, W. Damm, J. Maple, C. Wu, M. Reboul, J. Y. Xiang, L. Wang, D. Lupyan, M. K. Dahlgren, J. L. Knight, J. W. Kaus, D. S. Cerutti, G. Krilov, W. L. Jorgensen, R. Abel and R. A. Friesner, J. Chem. Theory Comput., 2016, 12, 281–296.
47. S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129.
48. J. L. Pascual-ahuir, E. Silla and I. Tuñon, J. Comput. Chem., 1994, 15, 1127–1138.
49. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, 2016.
50. G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918.
51. C. Legault, CYLview User Manual, 2012.
52. J. Rodriguez-Guerra Pedregal, P. Gomez-Orellana and J. D. Marechal, J. Chem. Inf. Model., 2018, 58, 561–564.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc01098j

---