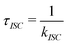Behind the scenes of spin-forbidden decay pathways in transition metal complexes
Torsha
Moitra
 a,
Pijush
Karak
b,
Sayantani
Chakraborty
b,
Kenneth
Ruud
a,
Pijush
Karak
b,
Sayantani
Chakraborty
b,
Kenneth
Ruud
 *c and
Swapan
Chakrabarti
*c and
Swapan
Chakrabarti
 *b
*b
aDTU Chemistry, Technical University of Denmark, Kemitorvet Bldg 207, DK-2800 Kongens Lyngby, Denmark
bDepartment of Chemistry, University of Calcutta, 92 A. P. C. Road, Kolkata-700009, West Bengal, India. E-mail: swcchem@caluniv.ac.in
cHylleraas Centre for Quantum Molecular Sciences, Department of Chemistry, University of Tromsø - The Arctic University of Norway, 9037 Tromsø, Norway. E-mail: kenneth.ruud@uit.no
First published on 10th November 2020
Abstract
The interpretation of the ultrafast photophysics of transition metal complexes following photo-absorption is quite involved as the heavy metal center leads to a complicated and entangled singlet–triplet manifold. This opens up multiple pathways for deactivation, often with competitive rates. As a result, intersystem crossing (ISC) and phosphorescence are commonly observed in transition metal complexes. A detailed understanding of such an excited-state structure and dynamics calls for state-of-the-art experimental and theoretical methodologies. In this review, we delve into the inability of non-relativistic quantum theory to describe spin-forbidden transitions, which can be overcome by taking into account spin–orbit coupling, whose importance grows with increasing atomic number. We present the quantum chemical theory of phosphorescence and ISC together with illustrative examples. Finally, a few applications are highlighted, bridging the gap between theoretical studies and experimental applications, such as photofunctional materials.
1 Introduction
The last decade can be unambiguously termed as the era of transition metal complexes. The advent of ultrafast spectroscopy has led to an improved understanding of the photophysics of transition metal complexes. The properties of transition metal complexes are fascinating not only because of their extensive use in opto-electronic materials, molecular electronics, biology, photochemistry and many more, but their photophysical properties also call for revisiting fundamental concepts.1–21Early studies of transition metal complexes were primarily confined to and dominated by photosubstitution reactions typical of ligand field (LF) excited-state reactivities of metal-carbonyl complexes.22,23 In 1971, Adamson and coworkers24 opened up a totally new and fascinating area of research on luminescent transition metal complexes and their photochemistry by studying the photoredox reactivities attributed to the metal-to-ligand charge transfer (MLCT) excited state of ruthenium(II) bipyridine complexes. This was followed by the emergence of a new branch of supra-molecular photochemistry.25–31 This rapidly growing field has been developed with the aid of sophisticated ligand-field theory and rigorous insight into electronic transitions and spectroscopic properties.25,32–39 The field has also benefited significantly from the state-of-the-art discovery of high-precision spectroscopic techniques.40 This prompted demand for the advancement of computational tools for unravelling the microscopic origin of experimentally observed phenomena.
Electronically excited states formed by photoabsorption are rather short-lived and decay within a small period of time through a variety of deactivation processes. If the excited molecule goes back to its original initial ground-state electronic configuration, the phenomenon is a photophysical process. In contrast, when a molecule undergoes chemical changes, the corresponding dissipative pathway is termed as a photochemical process. Physical relaxation processes can be broadly categorised as being either intramolecular or intermolecular. In this context, intramolecular deactivation mechanisms can be accompanied with or without the emission of light, called radiative and non-radiative processes, respectively. In addition, intermolecular processes, as the name suggests, occur due to interactions between two or more molecules, leading to vibrational relaxations, energy transfer or electron transfer. All these processes are triggered by modifications of the electronic structure upon excitation and are accompanied by geometrical changes.
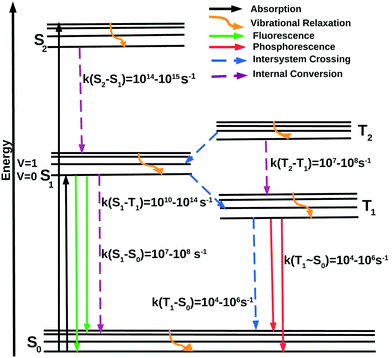
A schematic representation of the intramolecular photophysical events after excitation is shown by the modified Jablonski diagram41 in Fig. 1, named in honor of Aleksander Jablonski, who considered the metastable state as the origin of delayed emission. This metastable state is now recognized as the triplet state. The electronic ground state of a molecule is typically of singlet character (S0). Upon exposure to light, S0 → Sn absorption occurs, within a time-scale of a few femtoseconds. Nuclear changes are not feasible at such a short timescale and hence the molecule is usually excited to a higher vibrational level of the excited electronic state. The initially excited state has several possibilities for deactivation. It may undergo vibrational relaxation to the zero-point vibrational level of the Sn state or a spin-forbidden intersystem crossing (ISC) to a near isoenergetic triplet excited state (Tn) leading to population growth within the triplet manifold. These singlet and triplet higher-energy excited states undergo non-radiative deactivation to the lowest energy excited state, namely, S1 or T1. This is the origin of Kasha's rule, which states that due to the rapid rate of deactivation to the lowest vibrational level of the S1 (or T1) states, luminescence emission will originate from the lowest vibrational level of S1 and T1. Emission from the S1 and T1 states is referred to as fluorescence and phosphorescence, respectively.42 However, many instances of the breakdown of this rule have been documented.43–49
Due to spin conservation, transition between different spin states is spin-forbidden and thus phosphorescence is usually much less intense compared to its spin-allowed counterpart. Pioneering works by Terenin, Lewis and Kasha50,51 led to the understanding of the electronic origin of molecular phosphorescence.
The unique photophysical behavior of transition metal complexes is driven by the heavy atom-enhanced spin–orbit coupling (SOC) effect, which in a non-relativistic picture can be considered as leading to a mixing of different spin character into a spin-pure (singlet or triplet) state. This leads to a fast rate of ISC and hence highly efficient population of the lowest-lying triplet state (T1), followed by phosphorescence. This special characteristic has made these complexes promising candidates for a variety of applications.52–58
Transition metal complexes have several advantages from the stand-point of designing smart optical displays. First, the phosphorescence from d6, d8 or d10 electronic configurations usually leads to longer triplet-state lifetimes, allowing for their detection, and offers more sensitivity towards time-resolved studies. Second, in contrast to their fluorescent organic counterparts, these complexes rarely suffer from self-quenching and homo-fluorescence resonance energy transfer.59 Third, due to their ability to bind to a vast range of ligands, their photophysical characteristics can be fine-tuned more easily.
Heavy-metal complexes are a special class of compounds that has many different possibilities for excited-state character. These excited states include metal-to-ligand charge transfer (MLCT), ligand-to-metal charge transfer (LMCT), intra-ligand (IL), ligand-to-ligand charge transfer (LLCT), Sigma-bond-to-ligand charge transfer (SBLCT), metal–metal-to-ligand charge transfer (MMLCT) and ligand-to-metal–metal charge transfer (LTMMCT). Notably, these characteristics can be readily perturbed by various metal–ligand combinations and by changing the environment of the complexes.
A clear acumen from theory and computation is necessary for rationalising the origin of experimental observations. Indeed, theoretical studies based on rate constants calculated using perturbation theory have played a decisive role.60,61 More recently, simulations combining quantum chemistry with nuclear dynamic studies have been developed.62–66 Considerable attention has been paid to the study of ISC processes using non-adiabatic molecular dynamics involving SOC. Also, ISC dynamics have been studied using wave-packet dynamics in the past couple of years.67–77
In this perspective, we present the theory of molecular spin-forbidden transitions, namely, phosphorescence and ISC, which are the distinguishing characteristics of transition metal complexes. The concepts are further illustrated with specific examples demonstrating their wide-spread applicability.
2 Spin–orbit coupling
Spin–orbit coupling (SOC) is a relativistic effect emerging naturally from the full relativistic treatment of an electron,78 and it couples the orbital angular momentum of an electron with its spin magnetic moment. In the case of atoms, the coupling strength scales with the fourth power of the nuclear charge, making it more significant for heavy transition metal atoms. Its magnitude typically varies from a few meV for elements of the 2nd period to several eV for the valence shells of 6p elements. However, the nuclear charge is not the only parameter determining the SOC strengths, a large SOC can also result when two electronic states of different spin multiplicities are close in energy.The four-component electronic Dirac–Coulomb-Breit Hamiltonian is divided into a spin-free and a spin-dependent part.79,80 The latter accounts for the coupling of the electronic orbitals and spin degrees of freedom and leads to a mixing of states with different spin multiplicities. A fallacy of this separation approach is that the difference between the eigenfunctions of the electronic Hamiltonian based on multiplicity does not hold in the presence of spin–orbit coupling terms. However, for the sake of simplicity, we will in the following discussions assume that it is retained even when the SOC term is included.
The SOC operator is most often expressed in terms of the Breit–Pauli (BP) operator,
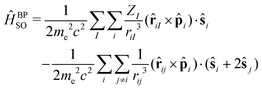 | (1) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) iI ×
iI × ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) i) and (
i) and (![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij ×
ij × ![[p with combining circumflex]](https://www.rsc.org/images/entities/b_char_0070_0302.gif) i) are the angular momenta of electron i with respect to nucleus I and electron j, respectively.
i) are the angular momenta of electron i with respect to nucleus I and electron j, respectively.
The first term in eqn (1) is the one-electron term describing the interaction of the spin magnetic moment of an electron with the magnetic moment induced by it while orbiting in the nuclear electrostatic field. This involves only spin-same-orbit coupling terms and arises from the electron–nuclear Coulomb attraction. The second term is the two-electron contribution and brings in contributions from both the spin-same-orbit and spin-other-orbit couplings. It relates to the interaction of the spin magnetic moment of the electron with the orbital magnetic moment of another electron. The spin-same-orbit part of the two-electron term originates from the transformation of the two-electron Coulomb interaction, whereas the spin-other-orbit term comes from the Gaunt interaction term. The Breit–Pauli spin–orbit operator has found widespread use, in particular in approaches based on perturbation or response theory. However, it is unbounded from below and can lead to a variational collapse in molecular calculations.
It is evident from eqn (1) that the one-electron term has a stronger dependence on the nuclear charge, and it surpasses the contribution from the two-electron term for high values of Z. In the case of 6d elements like Pt, the two-electron term reduces the magnitude of the one-electron term by approximately 10%. Thus, the second term can be neglected as an approximation to the BP operator for heavy elements. The two-electron term cannot, however, be neglected for lighter elements, where it leads to a significant screening of the one-electron part.
Various ways to approximate the one electron operator have been devised,81,82 the most rigorous being the spin–orbit-mean-field (SOMF) Hamiltonian, designed by Hess et al.83 In this method, the two-electron spin–orbit interaction of partially filled orbitals is averaged for α and β spin orientations before spin integration. This can be thought of as an extension of the frozen-core approximation to all-electron calculations. Benchmark calculations have shown that the accuracy of the SOMF operator corresponds closely to that of the full BP operator for heavy atoms. Several flavours of this approximation technique have been developed for use with internally contracted multireference configuration interaction (MRCI) and complete active space self-consistent field (CASSCF) wavefunctions.84 A partial two-electron (p2E) operator has also been defined by Fedorov and Gordon.85 Recently, another mean-field approach for the two-electron contribution has been developed by Pokhilko et al.,86 and in this approach, the elegant use of Wigner-Eckart's theorem helps to overcome the explicit evaluation of all the multiplet components and the formalism is implemented within the equation of motion coupled cluster method. Apart from the computational efficiency, this approach also resolves the phase issue arising upon separation of nuclear and electronic degrees of freedom within Born–Oppenheimer approximation.
If we consider the effect of the two-electron spin–orbit term as a form of screening, an empirical approach for constructing an effective one-electron spin–orbit coupling operator is to emulate the two-electron contributions by an effective nuclear charge (Zeff)
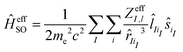 | (2) |
Here, iI denotes an electron occupying an orbital located at center I. Blume, Watson and Peierls showed that eqn (2) only partially accounts for the two-electron contribution.87 The use of this operator is limited by its dependence on the effective nuclear charge from a particular state, which varies considerably for dn configurations.88 Despite these fundamental deficiencies, ĤeffSO has been used extensively for studies of transition metal complexes by appropriate parameterization of Zeff to fit experimental fine-structure splittings of one or more electronic states of an atom.89–91
The concept of an effective spin–orbit coupling operator has been combined with the concept of the effective core potential (ECP). Here, Zeff has no physical meaning and is a purely empirical parameter.92,93 In the vicinity of a nuclear center, the amplitudes of pseudo-orbitals are small and the effective charge becomes very large. Most commonly, in the spin–orbit pseudo-potential approach, the 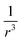 dependence is dropped and the SOC operator is shifted to the valence region. Teichteil et al. fitted the spin–orbit pseudo-operator such that its action on a pseudo-orbital appropriately reproduces the effect of the true spin–orbit operator of the corresponding all-electron orbital.94
dependence is dropped and the SOC operator is shifted to the valence region. Teichteil et al. fitted the spin–orbit pseudo-operator such that its action on a pseudo-orbital appropriately reproduces the effect of the true spin–orbit operator of the corresponding all-electron orbital.94
An alternative approach of including effects of inner shells on the valence properties is to use the ab initio model potential (AIMP) method.95 In contrast to the pseudo-orbitals, the AIMP orbitals retain the complete nodal structure of the all-electron operators. A combination of the SOMF Hamiltonian alongside ECP has also been used.96
SOC matrix elements are available for both quantum chemical methods and semi-empirical procedures. There are two main routes to calculate SOC matrix elements. One is to treat electron correlation and SOC simultaneously in a single step and the other is to evaluate the SOC on the basis of correlated molecular wavefunctions (two-step procedure). The utility of the two approaches depends on the system under study and the property to be determined. Variational perturbation theory, response theory and multi-reference spin–orbit configuration interaction (MRSOCI) are some of the one-step methods.97 These are beneficial for calculating second-order spin-dependent properties requiring an infinite summation over zero-order states within the Rayleigh–Schrödinger perturbation theory. The MRSOCI wavefunction for the calculation of phosphorescence is especially beneficial.98 Time-dependent Density functional theory (TD-DFT) coefficients are also used to calculate SOC matrix elements between singlet- and triplet-excited states.99 Two-step protocols offer the possibility of computing the diagonal matrix elements corresponding to spin-free excitation energies and the SOC matrix elements at different levels of theory.100,101
A popular method for computing relativistic effects of heavy-metal systems is the zeroth-order regular approximation (ZORA).102–105 The method transforms the four-component Dirac Hamiltonian to a two-component form, by replacing the expansion of the (E − V)/2c2 term by E/(2c2 − V) for a relativistic particle moving under Coulomb potential. This variationally stable and self-consistent ZORA method has further been simplified by Wang and Ziegler,106 where the lowest single-group excited states are evaluated at the scalar relativistic, time-dependent density functional theory (sr-TDDFT) level and spin–orbit coupling (SOC) is then included as a perturbation using the reference orbitals, obtained in a sr-TDDFT computation. The beauty of the method lies in the fact that the composition of the double-group excited states can automatically be evaluated from the single-group singlet and triplet excited states even though the relativistic wave functions are characterized by half-integral angular momentum quantum numbers and, in principle, it should have a point double-group symmetry.
The SOC operator must also be transformed according to the ZORA approximation and then becomes
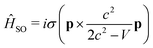 | (3) |
There has as of yet not been any systematic studies on phosphorescence at the four-component relativistic level of theory, despite this being computationally more straightforward than when non-relativistic reference wave functions are used. In four-component relativistic theory, transition moments and lifetimes are governed directly by dipole transition matrix elements, as the electronic states are no longer pure spin states. In a similar manner, ISCs are governed by transition dipole moments between excited states. The reasons for the lack of use of four-component relativistic methods in the study of transition metal complexes are three-fold: (1) relativistic four-component calculations of molecular properties have a much shorter history than non-relativistic molecular property calculations; (2) four-component relativistic calculations have until recently been significantly more computationally expensive than non-relativistic calculations; and (3) the noncollinear exchange–correlation kernels that have to be used because of the spin–orbit coupling.111
However, developments suggest that this picture is changing, suggesting that four-component and approximate two-component relativistic calculations, in which spin–orbit effects are included variationally, may become much more commonplace in future. The first four-component relativistic time-dependent density-functional theory (TDDFT) implementation was presented by Gao et al.,112,113 but limited to excitation energies only. Bast, Jensen and Saue later reported a noncollinear implementation of TDDFT in which transition moments could be obtained.114 However, all these papers reported results for atoms and fairly small molecular systems. Very recently, an implementation of four-component relativistic TDDFT for both open- and closed-shell systems was presented by Komorovsky, Cherry and Repisky.115 Although larger systems were studied in this article, the implementation was restricted to excitation energies only.
An alternative approach to address both excitation energies and transition moments is the complex polarization propagator theory. At the four-component level of theory, the first implementation was presented by Villaume, Saue and Norman116 and applied to, for instance, the phosphorescence of transition metal porphyrins.117 More recently, a similar approach was implementd by Konecny et al.118 and employed on some transition metal complexes ([M(phen)3]3+ (M = Fe, Ru, Os)). These developments suggest that four-component relativistic calculations of phosphorescence and ISC may soon be within reach for transition metal complexes also.
SOC constants for 5d elements are usually of the order of a few thousands of cm−1.119 One might naively assume that SOC is large in all transition metal complexes, but this is not the case. The singlet to triplet transition under study must have a large metal contribution in order to have a substantial amount of SOC.109,120 For instance, the 〈S1|ĤSO|T1〉 and 〈S1|ĤSO|T2〉 values for the (acetylacetonato)-bis(1-methyl-2-phenylimidazol)iridium(III) (aka N966) complex are 93 and 513 cm−1, respectively.108 This stark difference is reasonable as only the latter matrix element involves charge transfer from the 5d orbital of iridium to the acetylacetonato group. These different characteristics of the states are often used to preferentially select one transition pathway over another.
3 Phosphorescence
As per the IUPAC definition, phosphorescence can be defined phenomenologically as long-lived luminescence. According to mechanistic photochemistry, the term designates luminescence involving a change in spin multiplicity, typically from a triplet to a singlet state, or vice versa.121Historically, the term has been used somewhat uncritically, and was initially used for all long-lived emission processes. The phenomenological definition as a distinction of the time duration of afterglow compared with fluorescence was used until recently and was a source of ambiguity.122,123 The term has been used several times to describe luminescence phenomena arising due to completely different photophysical mechanisms.124 Here, we concentrate on the well established mechanistic definition of phosphorescence and thereby only look at radiative transitions between different spin states.
Theoretical understanding of the phenomenon requires analysis of the characteristics of the excited-state electronic structure. Typically, phosphorescence occurs from the lowest triplet state (T1) as a consequence of IC within the triplet manifold. The three triplet sublevels are degenerate within non-relativistic quantum theory, whereas the degeneracy is lifted in relativistic theory due to zero-field splitting effects.
In the following sections, we describe the theoretical methodologies developed for the calculation of phosphorescence within the framework of non-relativistic wavefunction and density–functional theories, focusing on perturbation theory and the quadratic response theory formalism. Finally, we discuss the basis for estimating phosphorescence lifetimes as well as transition moments and intensities.
3.1 Perturbation theory approach
SOC leads to a mixing of the pure singlet (Sn) and triplet (Tn) states by some contributions from the other spin state. In the limit when the contribution of the singlet state towards the triplet state (and vice versa) is small, the situation can be described by first-order perturbation theory.125–127 The total wave function of the triplet state (![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif) 1) can then be written as
1) can then be written as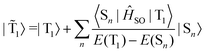 | (4) |
Similarly, the ground state is also perturbed by SOC and has some contributions from the triplet manifold.
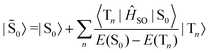 | (5) |
A smaller singlet–triplet energy separation and higher SOC between the opposite spin states increase the mixed nature of the states. In the case of phosphorescence from the lowest energy triplet state (![[T with combining tilde]](https://www.rsc.org/images/entities/char_0054_0303.gif) 1 →
1 → ![[S with combining tilde]](https://www.rsc.org/images/entities/char_0053_0303.gif) 0), the rate of population decay is given by the electric transition dipole moment between the two states.
0), the rate of population decay is given by the electric transition dipole moment between the two states.
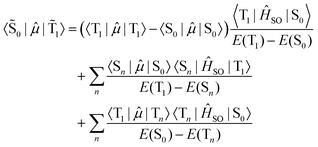 | (6) |
Recalling that the SOC matrix elements are imaginary, see eqn (1), one must also take into account the complex conjugate. The absolute value of the square of the transition moment is the same for both absorption and emission at a given geometry. The energy gap appearing in the denominator of eqn (6) does not depend on the spin sub-levels as zero-field splitting is much smaller than the singlet–triplet energy gap.
The first term in eqn (6) is a permanent dipole difference term of the pure spin states, while the second and third terms are guided by the spin-allowed transition moments. The dipole difference term plays a dominant role for heavy-metal complexes where the triplet state often has charge-transfer character. Metal-to-ligand charge-transfer states involve excitations from the heavy-atom center, leading to stronger SOC and thereby enhanced phosphorescence quantum yields.15,109,128 The second term in eqn (6) is important for purely organic molecules.
It is worth noting that the triplet state is composed of three sub-levels, each having a distinct decay rate with different polarization directions along the three Cartesian coordinate axes. Even though this is true for highly symmetric molecules, it is not so for systems with lower symmetry. For the latter, the quantization axes of the zero-field triplet sub-levels may not be the same as the symmetry axes, leading to emissions of mixed polarization.
3.2 Response theory approach
The response theory formalism129 is an alternative way of formulating the previously discussed time-dependent perturbation theory that allows exact- and approximate-state theories to be formulated in the same way, differing mainly in the explicit parameterization of these states. Specific molecular properties are obtained as response functions, identified in an order expansion with respect to time or frequency of an observable quantity in terms of an applied perturbation. The external time-dependent perturbing field (![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) t) generates a response for a molecular property
t) generates a response for a molecular property 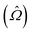 , which can be defined as the time-dependent expectation value of an observable, such as the electric dipole moment.
, which can be defined as the time-dependent expectation value of an observable, such as the electric dipole moment. | (7) |
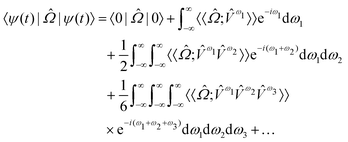 | (8) |
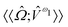 ,
, 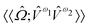 and
and 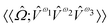 are the linear, quadratic and cubic response functions, respectively. These correspond to changes induced in the observable property
are the linear, quadratic and cubic response functions, respectively. These correspond to changes induced in the observable property 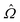 upon second-, third- or fourth-order perturbations of light–matter interactions.
upon second-, third- or fourth-order perturbations of light–matter interactions.
For the study of phosphorescence, the SOC operator acts as a perturbation to the electric dipole operator (![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) a) and hence the observable to be computed is associated with the residue of the quadratic response function:
a) and hence the observable to be computed is associated with the residue of the quadratic response function:
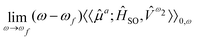 | (9) |
The response function (eqn (9)) corresponding to the transition moment is given by (using the Einstein summation convention for repeated indices)
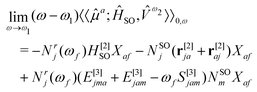 | (10) |
| Nr(ωf) = [(E[2] − ωfS[2])−1r[1]]* and NSO = (E[2])−1HSO[1] | (11) |
| (E[2] − ωfS[2])Xf = 0 | (12) |
We do not elaborate further here on the mathematical complexities of Eqs. 10 and 11 and refer to ref. 129 for more details. Instead, we highlight the advantage of quadratic response theory for calculations of phosphorescence. A key element of response theory is that the usual sum-over-excited-state algorithm is replaced by a set of linear equations that can be solved without prior knowledge of the excited states.130 This renders the method useful for treating large molecular systems described by approximate wave functions, and molecular properties can be calculated analytically.108,131–133 We note that several other strategies are also available for the computation of phosphorescence phenomena, such as the variational perturbation theory134 and spin–orbit coupling configuration interaction (SOC-CI)135,136 approaches. Some of these become particularly important for systems with nearly degenerate electronic ground states and where the spin–orbit contributions arise largely from within this manifold of nearly degenerate electronic states.
3.3 Lifetime
The phosphorescence lifetime τk from one of the three sublevels (k) of the lowest triplet state (T1) is given by the inverse of the rate of spontaneous emission (Ak→0).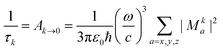 | (13) |
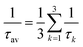 | (14) |
For transition metal complexes, eqn (14) is not strictly valid due to the potentially large zero-field splittings. This can be rectified by Boltzmann-weighted averaging over the individual spin sub-levels of the triplet state.
The lifetime of the triplet state is usually a few orders of magnitude larger than that of the singlet states, enabling a more detailed time-resolved study exploiting the triplet characteristics of the molecule. This has been extensively used in designing state-of-the-art molecular materials.125,137,138
3.4 Intensity
Due to the fact that spin is a good quantum number in non-relativistic theory, whereas the spin–orbit interaction leads to an inherent mixing of states of different spin multiplicity in variationally optimized relativistic calculations, the calculation of phosphorescence transition moments and intensities differs between the relativistic and non-relativistic realms. Within the former, there is no difference between fluorescence and phosphorescence and the electric transition dipole moments are obtained as residues of the linear response function.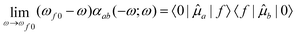 | (15) |
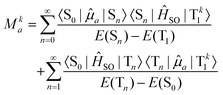 | (16) |
The summation over the intermediate triplet states runs over all the three sub-levels of the triplet state. The oscillator strength is thus given by
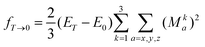 | (17) |
 | (18) |
3.5 Some examples
The success of prevalent phosphorescence from transition metal complexes is due to the comparable rate constants for radiative and non-radiative transitions from the T1 state. From Hund's rule, it follows that the triplet sub-levels are lower in energy than the first singlet state, and phosphorescence therefore occurs at lower energies in comparison to fluorescence. Also, in principle, phosphorescent molecules can achieve 100% [75% T1 → S0 + 25% S1 → S0] quantum efficiency.Extensive theoretical studies have been performed on Ir(III) complexes with organic ligands, and we refer to ref. 142 for more details. We instead focus our discussion on Pt complexes, as their phosphorescence properties can be fine-tuned to meet a variety of different requirements. Also, the thermal stability and charge neutrality of cyclometallated Pt(II) complexes render them good candidates as triplet emitters.143,144 The triplet state population rates of Pt(II) complexes are moderate and thus structure or environment alterations can swing the balance towards purely phosphorescence or dual emissive luminescence behavior.
Purely phosphorescent alkynyl cyclometalated Pt complexes (Fig. 2) have recently been investigated by Lázaro et al.139 These complexes exhibit a phosphorescence maximum at 625 nm with several vibrational fine structures, corresponding to C–C and C–N stretching modes. DFT and TDDFT calculations show that the transition is mediated by IL states mixed with MLCT character. The phosphorescence quantum efficiency and triplet lifetimes can be further enhanced by making the complex more rigid by ligating with aromatic ligands.145
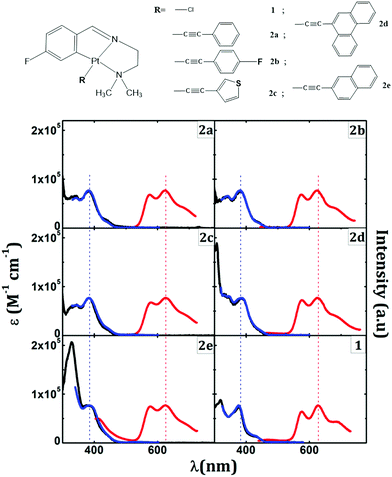 | ||
| Fig. 2 Chemical structures of alkynly cyclometalated Pt(II) complexes (top). Absorption (black) with phosphorescence excitation (blue) and phosphorescence (red) spectra are shown at the bottom. Adapted with permission from ref. 139. Copyright 2020 American Chemical Society. | ||
On the other hand, BODIPY and thioxanthonyl platinum(II) complexes show dual emissive behavior with fluorescence at 450–490 nm and phosphorescence at 510–650 nm, as shown in Fig. 3.140,141 The influence of the ligand is noticeable for the BODIPY ligand complex. The cis isomers have very low phosphorescence intensity in comparison to their trans counterparts. The calculations by Geist et al.140 show that the frontier molecular orbitals involved have the majority of their spin density on the BODIPY moiety with only a little contribution from the dπ orbital of Pt. This spin density distribution is a prototypical scenario favouring dual emission.
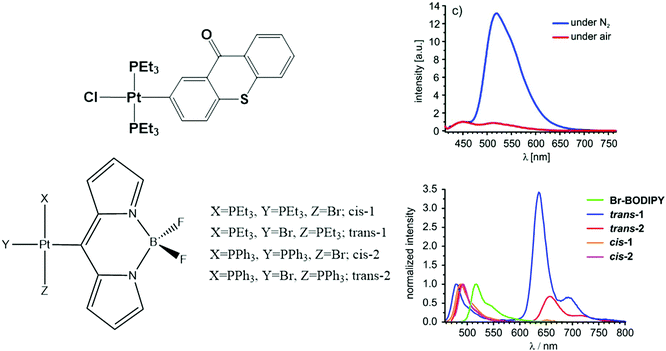 | ||
| Fig. 3 Chemical structure and photoluminescence spectra of Pt thioxanthonyl (top) and BODIPPY (bottom) complexes. Adapted with copyright from ref. 140 and 141. Copyright 2015 American Chemical Society and 2015 Royal Society of Chemistry. | ||
The cases discussed so far may lead one to think that phosphorescence wavelengths of transition metal complexes lie in the red and near infra-red regions of the optical spectra. However, more recently, a variety of blue phosphorescent Pt(II) complexes have been designed.146–148 Bidentate or tridentate Pt(II) complexes have low quantum efficiency and poor stabilities, and more rigid tetradentate complexes are therefore the usual choice. The tetradentate Pt(II) complexes are mainly of two types, metallochelates where the chelating ligands are linked by π-conjugation, and macrocylic complexes. The second class of complexes are very rigid and thus ensure high quantum efficiency and stability.146–152
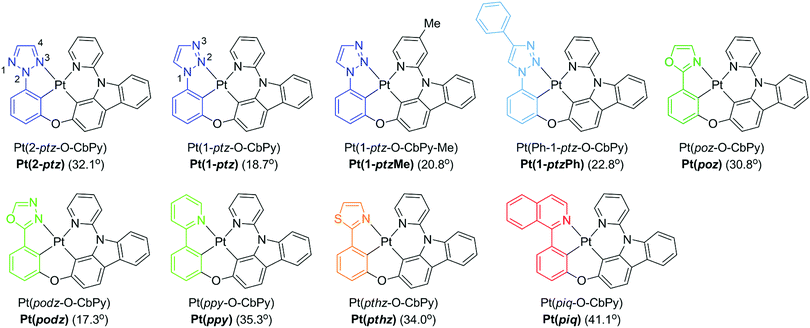
In order to demonstrate the generation of different visible light phosphorescent complexes, based purely on design, we used a series of tetradentate Pt(II) emitters having fused 5/6/6 metallocycles (Fig. 4).146 The photoluminescence spectra of these complexes at 77 K and room temperature are shown in Fig. 5. In comparison to Pt(2-ptz) complexes, these complexes display red shifts to varying degrees. Photoluminescence spectra at 77 K show a structured profile with a dominant peak followed by two or five fine-structure bands. However, at room temperature, a broad Gaussian type emission is seen. The strong rigidochromic shift of 8–52 nm exhibited by these molecules is a hallmark of significant 1MLCT/3MLCT characters in the lowest excited states.
 | ||
| Fig. 4 Chemical structures of tetradentate Pt(II) complexes. Adapted with permission from ref. 146. Copyright 2020 American Chemical Society. | ||
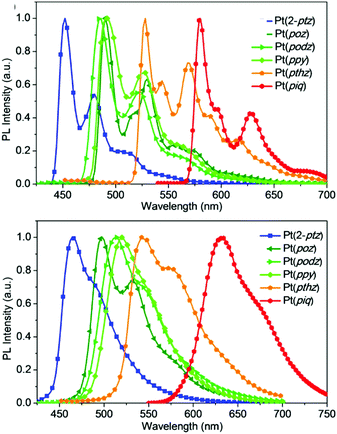 | ||
| Fig. 5 Photoluminescence spectra of tetradentate Pt(II) complexes shown in Fig. 4 at 77 K (top) and room temperature (bottom). Adapted with permission from ref. 146. Copyright 2020 American Chemical Society. | ||
4 Intersystem crossing
Intersystem crossing (ISC) is the near isoenergetic radiationless transition between two electronic states having different spin multiplicities. Even though it is described as a spin-forbidden singlet–triplet transition, like phosphorescence, the physical origin of the two is different. In particular, phosphorescence is guided by the transition dipole moment between the SOC perturbed singlet and triplet states, while ISC is fueled by the strength of the spin–orbit interaction between the initial and the final electronic states. ISC plays a key role in driving phosphorescence as it transfers population from the initially excited singlet state to the triplet manifold. Hence, we present here a detailed account of the developments of theoretical protocols for the calculation of the rate of ISC.The rate of population transfer between the initial and final states involved in an electronic transition can be studied by two approaches, nuclear dynamics based methods and perturbation theory-based approaches. The former involves considering the explicit nuclear motion over the potential energy surface, thereby following the nuclear dynamics of the molecule. This involves solving the time-dependent Schrödinger equation for multiple degrees of freedom. This becomes extremely expensive for large molecular systems unless strict selection criteria are imposed on the number of active modes under study. Multiconfiguration time-dependent Hartree (MCTDH)153 is a popular method where the time-dependent Schrödinger equation is solved by expanding the nuclear functions into a time-dependent basis set, with time-dependent co-efficients,
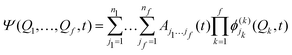 | (19) |
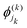 are the nk expansion functions for each degree of freedom k, known as the single particle functions. This method has the advantage that the time-dependent basis set ensures convergence with fewer basis functions. A more sophisticated version of the MCTDH method is the multi-layered variant, also known as ML-MCTDH,154 which has been used to study systems comprising over 1000 degrees of freedom. These approaches combine multiple degrees of freedom of a system under one single particle function, therefore reducing the effective number of degrees of freedom significantly. A more detailed discussion on these approaches is given in ref. 155.
are the nk expansion functions for each degree of freedom k, known as the single particle functions. This method has the advantage that the time-dependent basis set ensures convergence with fewer basis functions. A more sophisticated version of the MCTDH method is the multi-layered variant, also known as ML-MCTDH,154 which has been used to study systems comprising over 1000 degrees of freedom. These approaches combine multiple degrees of freedom of a system under one single particle function, therefore reducing the effective number of degrees of freedom significantly. A more detailed discussion on these approaches is given in ref. 155.
In order to overcome the requirement of grid-based nuclear dynamic methods to pre-compute the potential energy surface, on-the-fly dynamics has been developed. A wide range of on-the-fly methods are available, ranging from fully quantum approaches to mixed quantum-classical approaches like trajectory surface hopping (TSH). The electronic properties are computed at each time step, allowing for simulations to be performed in the full nuclear configuration space. Significant advances within this framework have been made by González et al., where they have taken into account SOC and non-adiabatic coupling to study the rate of ISC.69,70,73,76 The surface hopping formalism has recently been used in conjunction with the linear vibronic coupling method.156 The combined approach is computationally faster in comparison to on-the-fly dynamics and allows for inclusion of all degrees of freedom as opposed to quantum dynamics, without introducing any further additional approximations. A more advanced use of on-the-fly trajectory approaches is based on Gaussian wavepackets instead of independent point trajectories.157–159 A detailed description of these dynamic methods can be found in the recent review by Penfold et al.160 We therefore restrict our discussion of ISC to the perturbation theory-based methods.
In the limit of the coupling between the initial and final states involved in ISC being much smaller than the adiabatic energy difference, the rate of ISC can be described by perturbation theory. The common starting point is to approximate the initial and final state potentials by harmonic oscillators having vibrational frequencies, Ωi and Ωf, respectively. For electronic transitions between the initial (Qi) and final (Qf) potential energy surfaces, the Duschinsky transformation connects the two as
| Qf = JQi + D | (20) |
4.1 Qualitative rules
When the SOC integral between the initial and final states is much smaller than the adiabatic energy gap, a qualitative analysis of the rate of ISC (kISC) is possible by starting from the “Fermi's Golden Rule” approximation.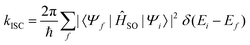 | (21) |
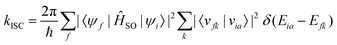 | (22) |
As is evident from eqn (22), the rate of ISC depends on two contributions: (i) purely electronic SOC and (ii) the vibrational density of states. These terms have enabled the qualitative estimation of the rate of ISC.
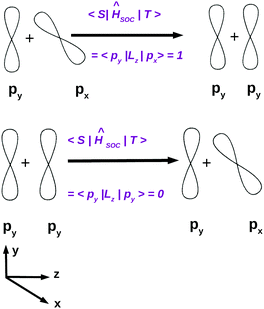
El-Sayed's rule was originally discussed in the context of purely organic chromophores. Angular momentum operators are purely imaginary and do not have diagonal matrix elements in a basis of real functions. As illustrated in Fig. 6, considering a molecule in the yz plane, the lz operator couples the out-of-plane π or π* type px orbitals with the non-bonding in-plane py orbitals while the spin operator sz changes the sign of the electron spin function, thus transforming the MS = 0 singlet state to a MS = 1 triplet state and vice versa.
The situation is more complicated for transition metal complexes. Naively, one can say that El-Sayed's rule is generally valid due to the Zeff4 dependence of SOC matrix elements. The SOC will be largest for transitions between states with d-electron contributions. Crystal field splitting effects play a crucial role towards the contribution of the d-electron to the MLCT state involved in ISC. For instance, in Au(I) complexes with metal-to-ligand charge transfer states, crystal field splitting is larger than for analogous Cu(I) complexes, and thus the d electron contribution to the low-lying excited state is smaller for the former, leading to a smaller SOC.
Despite the rule being relatively straightforward, it is based solely on electronic states of a single character. Mixing between states of different orbital character leads to a breakdown of the rule. Moreover, vibronic interactions are known to enhance ISC for El-Sayed forbidden transitions.160
4.2 Franck–Condon approximation
A Taylor expansion of eqn (22) about a chosen reference point (q0) gives a direct SOC term,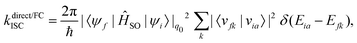 | (23) |
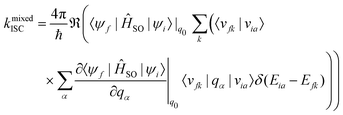 | (24) |
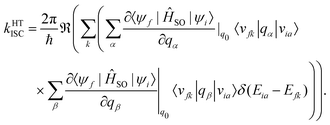 | (25) |
The reference point q0 is generally chosen to be the equilibrium geometry of the initial state or the crossing point of the two potential energy surfaces. Higher-order terms of the Taylor series expansion are usually negligible. It is further possible to compute the rate of ISC for transition to the individual levels of the triplet states. However, this involves going beyond first-order perturbation theory and requires knowledge about the composition of the triplet sub-states, and no such study has been performed either theoretically or experimentally.
Generally, the rate of ISC is approximated by the direct term (eqn (23)). However, under certain circumstances, it is essential to go beyond the Franck–Condon approximation and include higher order terms as in Eqs. 24 and 25. Higher-order terms of the Taylor series expansion account for vibronic SOC contributions.160 SOC matrix elements are complex valued, and only the real parts contribute to ISC, which is an observable quantity.
Focusing only on the direct contribution towards the rate of ISC, the task in hand boils down to approximating the Dirac δ distribution. Various methods have been developed to this end. These methods use one of two strategies for integration, an integration grid over either the energy domain or the time domain. We discuss these methods in further detail in the following sections.
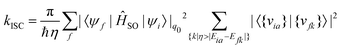 | (26) |
The applicability of this approach can be extended through the use of efficient pre-screening of the Franck–Condon factors, sum rules and mode selections.166–168 The limitations of this method lie in the fact that the computational cost grows significantly with increasing the number of normal modes and/or an increase in adiabatic energy separation between the states, both of which control the vibrational density of states (VDOS). Care must also be taken when choosing the finite step width. Moreover, the energy grid integration protocol gives a thorough insight into the vibrational modes contributing to the non-radiative transition.
Another time-independent approach is to consider the high-temperature limit and compute the transition rate as a sum over the Boltzmann-weighted rate constants kkISC, using a population distribution multiplier,
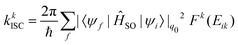 | (27) |
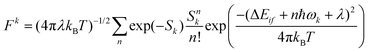 | (28) |
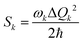 | (29) |
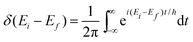 | (30) |
By employing properties of conjugation and resolution of identity, the rate of ISC can be expressed as
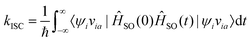 | (31) |
Eqn (31) is exact up to the first order in time-dependent perturbation theory, and the spin–orbit coupling operator in the Heisenberg picture is given by
| ĤSO(t) = eiĤ0t/ħĤSOe−iĤ0t/ħ | (32) |
The calculation of rate constants using this protocol is not restricted to harmonic potentials nor the Condon approximation for the spin–orbit matrix elements. Evaluation of the autocorrelation function nevertheless becomes simpler. The autocorrelation function (G(t)) was first established by Kubo and Lax,171–173 and it has been widely used to compute non-radiative rate constants both analytically and numerically.61,161,174,175 Etinski et al. employed the correlation function to arrive at an analytical expression for the rate of ISC within the Condon approximation for vibrationally cold molecules of
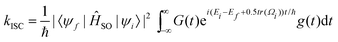 | (33) |
For the precise definition of the different quantities appearing in this equation, we refer to ref. 176. A carefully chosen Gaussian-type damping factor (g(t) = exp(−ηt2)) can be used to accelerate the convergence of the correlation function. This can be seen as accounting for all the additional possible damping that the vibronic states undergo, such as vibrational relaxation, radiative transition and coupling between normal modes. Recently, we modified this approach, incorporating the Boltzmann distribution function to calculate the rate of ISC both at finite temperatures and in the low-temperature limit,174
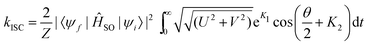 | (34) |
In the above simplified expression, we have used the same notation as in ref. 174.
An alternative procedure is to use the first- and second-order cumulant probability distribution for the time-ordered exponential functions,109
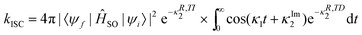 | (35) |
The same notations are used in eqn (35) as in ref. 109. Furthermore, Etinski et al.61 have derived a short-time expression that avoids numerical integration when calculating the rate of ISC. Both the exact expression and the cumulant expansion perform well and neither of them outperforms the other.
The methods described above are all computed using standard numerical integration procedures. Alternatively, analytical solutions are also possible by appropriately modelling the Hamiltonian by analytic functions, which are then evaluated by recursion formulas.161,177–179 The model Hamiltonian in use is the simple harmonic oscillator. In this case, the calculations are performed in the Fourier-transformed frequency space. Pioneering work in this field has been done by Borrelli and Peluso, with most application focusing on energy transfer mechanisms.175,180,181
4.3 Illustrative examples
Calculations of the rate of ISC within the Franck–Condon domain have been successfully used for various transition metal complexes.109,182–186 Here, we discuss representative 5d transition metal systems, with the aim to generate a better understanding of ISC processes based on the interplay of non-equilibrium excited-state dynamics and structural changes, and also the finer details brought to light by a detailed analysis of the effects of Duschinsky mixing.In order to demonstrate structure–dynamics relationships, we consider a set of analogous Os(II) complexes (Fig. 7), which exhibit changes in the luminescence behavior from purely phosphorescent (Os 1–4) to dual emissive (Os-5) to purely fluorescent (Os-6).128,187 These varying features are guided by the rate of ISC. The change in character of the lowest excited state dictates this behavior. The polyaromatic pendant introduces π conjugation at the β-diketonate, reducing the energy separation between the S1 and T1 states. Additionally, the very fast ISC for Os-1 can be rationalized from it having the strongest MLCT character in the ππ* orbital. (Table 1) The trend in the rate of ISC in these complexes follows the percentage mixing of ππ* by MLCT character.
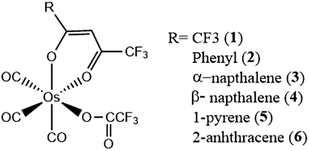 | ||
| Fig. 7 Chemical structure of Os(II) complexes. Adapted with permission from ref. 128. Copyright 2007 Royal Society of Chemistry. | ||
To further reinforce this concept, let us look at a pair of arylacetylide Au(I) (Au-1) and Au(III) (Au-2) complexes (Fig. 8). Experimentally, the rates of ISC are found to be 0.75 × 107 s−1 for Au-1 and 7.57× 1010 s−1 for Au-2. The large difference is explained in terms of El-Sayed's rule and the energy gap law. Fig. 9 shows that the available pathways for ISC are from the S1 state to the T2 and T4 states in Au-1 and to the T4 and T5 states in Au-2. For Au-1, transition is unfavourable to both of these triplet states as they compete with the T1 state and they all have the same orbital characteristics. In addition, for T4, even though one can observe efficient SOC, the energy separation (ΔE = 3180 cm−1) is too large to be overcome by thermal activation. On the other hand, in the Au-3 complex, facile S1 depopulation occurs to the T5 state, which is favoured by both a higher SOC (4100 cm−1) and thermally achievable small energy gaps.
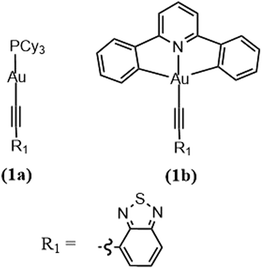 | ||
| Fig. 8 Chemical structure of Au(I) and Au(III) complexes. Adapted with permission from ref. 188. Copyright 2017 Royal Society of Chemistry. | ||
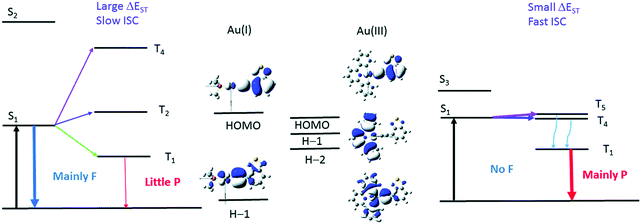 | ||
| Fig. 9 Illustration of the low-lying singlet and triplet excited states of Au(I) (left) and Au(III) (right) complexes that account for the different photophysical behavior. The d-orbitals involved in the T2 of Au-1 and T4 of Au-2 have the same orientations as their respective S1 excited state. F and P refer to fluorescence and phosphorescence, respectively. Adapted with permission from ref. 188. Copyright 2017 Royal Society of Chemistry. | ||
After establishing the success of semi-quantitative approaches, we now turn our attention to quantitative methods for computing rates of ISC. We will consider the photophysics of (acetylacetonato)-bis(1-methyl-2-phenylimidazol)iridium(III) (N966),108 which has a distinctive dual phosphorescence behavior leading to white light emission. N966 shows dual phosphorescence from both the T1 and T2 states. This anomalous behavior is due to a difference in nature of the T1 and T2 states, ensuring efficient S1 → T2 conversion, but a low rate of IC between the two triplet states. The T2 state is of dx2−y2 π → nπ character whereas the S1 and T1 states are of dxz π → pπ character.
As shown in Fig. 10, the smaller singlet–triplet energy gap and higher SOC for S1 → T2 lead to a more favourable ISC than for S1 → T1. However, the computed rate of ISC using the time-independent Marcus–Levich–Jortner theory predicts a comparably fast rate of ISC for both pathways. The authors attribute this to the Franck–Condon-weighted density of states, which compensates for the smaller SOC. The energy separation thus does not play a significant role as it appears in the decaying exponential term in eqn (28).
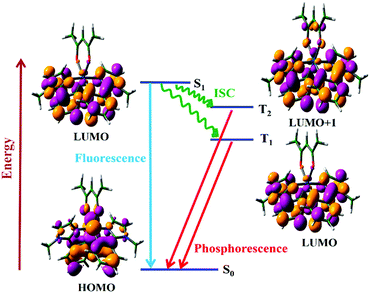 | ||
| Fig. 10 Jablonski diagram for the photophysical process of the N966 complex along with the frontier molecular orbitals involved in the transitions. Adapted with copyright from ref. 108. Copyright 2017 American Chemical Society. | ||
We next consider a pair of Pt(II) complexes (Fig. 11) containing acetylacetonate and extended cyclometalated 2-phenylpyridine (Pt-ppy) and 2-(2′-thienyl)pyridine ligands (Pt-thpy).109,189 Meticulous variation of Duschinsky rotation parameters gives great insight into the variation in the rates of ISC computed using the time-dependent correlation function and the cumulant expansion-based approach at both room temperature and 0 K.
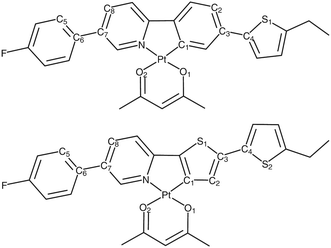 | ||
| Fig. 11 Chemical structure of Pt-ppy (top) and Pt-thpy (bottom) complexes. Adapted with copyright from ref. 109. Copyright 2018 Royal Society of Chemistry. | ||
The rates (see Table 2 and Fig. 12) of ISC suggest that in Pt-ppy complex, there is a rapid depopulation of the singlet-excited state, allowing for radiative emission only from the triplet manifold. In contrast, in Pt-thpy, the rate of ISC enables dual emission. It is worth noting that the rates calculated using the correlation function at 300 K is an order of magnitude smaller than that at 0 K. At finite temperatures, the excess vibrational energy in the S1 state reduced the ISC compared to that at 0 K.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 grid points, a damping factor of 2.0 and an upper limit of time integration of 20 ps. Data taken from ref. 109. Energy separation is in eV, SOC is in cm−1 and all rates are in s−1. a and b are for rates computed without J and D, respectively
000 grid points, a damping factor of 2.0 and an upper limit of time integration of 20 ps. Data taken from ref. 109. Energy separation is in eV, SOC is in cm−1 and all rates are in s−1. a and b are for rates computed without J and D, respectively
| Parameters | Temp. (K) | Pt-ppy S1 → T1 | Pt-ppy S1 → T2 | Pt-thpy S1 → T1 |
|---|---|---|---|---|
| ΔEST | 0.55 | 0.08 | 0.80 | |
| SOC | 75.27 | 329.62 | 1.04 | |
| k cumISC | 0 | 8.60 × 1010 | 4.59 × 1013 | 5.75 × 105 |
| k corrISC | 0 | 7.1 × 1010 | 1.07 × 1013 | 4.50 × 105 |
| k corISC r | 300 | 3.47 × 1010 | 6.87 × 1013 | 1.35 × 105 |
k
corrISC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
300 | 3.10 × 1010 | 5.02 × 1013 | 6.24 × 104 |
k
corrISC ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
300 | 8.51 × 109 | 2.74 × 1012 | 4.50 × 104 |
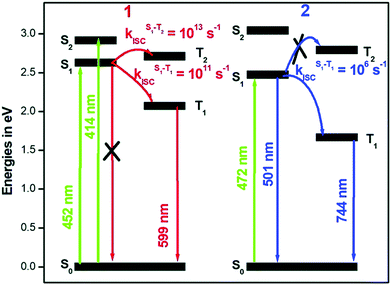 | ||
| Fig. 12 Modified Jablonski diagram describing the photophysics of Pt-ppy and Pt-thpy complexes. Adapted with copyright from ref. 109. Copyright 2018 Royal Society of Chemistry. | ||
We have also calculated the rates without including structural changes, that is, ignoring the J matrix and D vector of eqn (20). The dependence of the displacement vector on the rate of ISC in eqn (34) occurs through the K1 and K2 terms. The dependence on K2 enters in the cosine term, which varies between ±1. The most prominent feature is that the sign of K1 is negative, suggesting that a larger displacement vector contributes less to the net ISC value. In all cases, exclusion of the displacement vector reduces the rate by one order of magnitude.
The Duschinsky rotation matrix (shown in Fig. 13) couples the normal vibrational modes via the off-diagonal elements, enabling the ISC transition. In the case of the S1 → T2 transition for the Pt-thpy complex, the off-diagonal elements have comparable values to the diagonal elements, and the mixing is confined within a few normal modes. Therefore, neglecting the strong off-diagonal elements leads to a decrease in the rate of ISC by one order of magnitude.
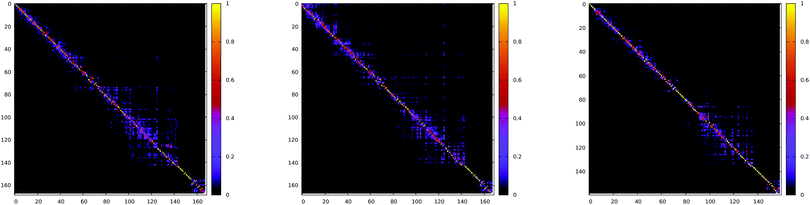 | ||
| Fig. 13 Absolute value of Duschinsky matrix for S1 → T1 (left) and S1 → T2 (middle) of Pt-ppy and S1 → T1 (right) of Pt-thpy. Taken from ref. 109. Copyright 2018 Royal Society of Chemistry. | ||
5 Recent advances
During the last 2–3 years, an enormous surge of research interest in the field of non-radiative decay process has been witnessed both at the experimental and the theoretical level. The experimental observations of the breakdown of Hund's rule or the inversion of the lowest singlet and triplet states vis-a-vis barrier free reverse intersystem crossing due to exciton–polariton interaction are ground breaking and, of course, demand the development of new theoretical tools to analyze such phenomena from first principles.190 Harvesting a triplet exciton via ISC in a transition metal complex, like platinum(II)-octaethyl-porphyrin (Pt-OEP), has been realized in a Fabry–Perot microcavity due to the formation of hybrid polariton states.191 It is worth noting that although the work of Li et al.192 is not related to the transition metal complexes, it still deserves a special mention since the combined experiment and multi-reference ab initio calculations suggest that ISC may even take place due to long-range dipole–dipole interactions between the radical fragments produced in a crossed-beam experiment. Recently, Monni et al.193 have tracked the vibrational coherence transfer during ultrafast ISC in the tetrakis(μ-pyrophosphito)diplatinate(II) complex. According to the authors, the solvent-induced stabilization of the triplet states facilitates the ISC process to the extent that the time taken for the non-radiative spin state transition is much shorter than the dephasing time of the vibrational wave packets. Besides, Mewes et al.194 performed a investigation on another platinum complex, namely [Pt(ppy)(μ-tBu2pz)]2, and found that the structural flexibility of this complex leads to the dephasing of the wave packet formed between the ground and the excited electronic states of the complex before the commencement of ISC. The role of ISC in therapeutics has also been explored a bit in the recent past. The efficient triplet state population gain in Ru, Ir, Pt, Pd and Sn based complexes has immense potential in photodynamic therapy (PDT) and photo-activated chemotherapy, and significant progress has already been made during the last few years.195 For example, phthalocyanine-assembled nanodots act as triplet photosensitizers that promote the generation of reactive oxygen species and thus allow the system to act as a good candidate for PDT.Impressive progress in the domain of theoretical non-radiative photodynamics has also been made in the past couple of years. Mai and Gonzalez gave an excellent review on the challenges in electronic structure theory and basis function vis-a-vis trajectory-based nuclear dynamics.196 The review also focuses on how to accelerate the in-silico photochemical and photophysical investigation of large molecular systems by invoking linear scaling, QM/MM and the Frenkel exciton model. Since the goal of the present perspective is to highlight all types of spin-forbidden transitions, we take the liberty of emphasizing some recent fundamental works that are in line with our objectives. Valentine and Li197 have recently proposed a new method for calculating the rate of ISC where the spin–orbit coupling is treated variationally, and the proposed method has been implemented in the framework of the exact-two component (X2C) method in combination with time-dependent density functional theory. This theoretical approach of calculating the rate of ISC will be particularly important when the strength of the spin–orbit coupling is large. Another new technique for estimating SOC based on El-Sayed's rule has been developed by Krylov and co-workers.86,198 They generated natural transition orbitals that allow the treatment of transitions between states with arbitrary spin multiplicities on an equal footing and the visualization and quantitative estimation of the contributions of specific orbital pairs to the overall SOC. Simulation of ISC dynamics at finite temperature using the thermal Schrödinger equation is challenging although such a thermo-field method is already available for studying non-radiative processes like energy transfer.199 The role of spin-vibronic interaction for the quantitative estimation of the rate of reverse intersystem crossing was shown to be well justified by Kim et al.200 The advances in trajectory-based dynamics are also quite remarkable. In particular, exploring internal conversion and ISC at the same level using exact factorization of the electron–nuclear wave function makes the generalized coupled-trajectory mixed quantum-classical algorithm very reliable.201 The use of machine learning in the study of nonadiabatic excited state dynamics is a recent development that reduces computational costs without compromising the accuracy of the calculations.202
6 Practical applications
The reasons for the wide-rang applicability of transition metal complexes are due to their high photostability, minimal self-quenching, wide range of photo-emission energies, and most importantly the fact that their luminescence properties can be readily modified by the use of a wide variety of ligands with different structural, electronic and coordinating properties.203–205For these reasons, the development of luminescent transition metal complexes as sensors, organic light emitting diodes (OLEDs) and dye-sensitized solar cells has received increasing attention in recent years. Applications of highly phosphorescent transition metal complexes as cellular reagents, such as biosensors and bioimaging reagents, also serve as a constant source of research. In the following sections, we give some examples of the use of transition metal complexes in OLEDs, light emitting electrochemical cells (LECs) and biological applications.
6.1 OLEDs
OLEDs consist of a cathode and an anode, with the region in between comprising electron and hole carriers, which combine to form excitons. These excitons undergo de-excitation, thereby emitting light.206 The excitons may either be singlet or triplet in configuration, in the ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, as predicted by spin statistics. SOC effects play a crucial role in maximizing the use of all singlet and triplet excitons and thus achieving 100% internal quantum efficiency, via provision of intense mixing of spin multiplets. Heavy-metal-containing phosphors such as Ir and Pt complexes can play a key role in OLEDs by efficiently harvesting all the electron-generated excitons and, hence, procuring high efficiency for the OLEDs.142,203,204
3, as predicted by spin statistics. SOC effects play a crucial role in maximizing the use of all singlet and triplet excitons and thus achieving 100% internal quantum efficiency, via provision of intense mixing of spin multiplets. Heavy-metal-containing phosphors such as Ir and Pt complexes can play a key role in OLEDs by efficiently harvesting all the electron-generated excitons and, hence, procuring high efficiency for the OLEDs.142,203,204
This approach has been studied since 1998 and its first successful commercial application was achieved in 2003, in the form of phosphorescent red OLEDs. Following this, OLED technology has been the subject of continuous research and improvement, which has led to the extensive use of OLEDs in the development of solid-state lighting (SSL),207 flat-panel displays and flexible screens. It has also led to red, green and blue (RGB) platforms206 of certain efficient phosphorescent dyes, which have been commercialized as displays in small hand-held devices and television sets. Also, white OLEDs have been found to be of immense importance with respect to lighting.208
Iridium(III) is the most commonly used transition metal in the design of OLEDs. Numerous mono-,bis-cyclometallated homo- and hetero-leptic iridium complexes are available,209,210 which can be used as phosphorescent emitters in OLEDs.211,212 Polymers containing Ir(III) complexes are also considered promising since they offer the appealing combination of a phosphor and a polymer in a single material. Moreover, ancilliary ligands, such as acetylacetonate (acac), picolinate (pic) and bipyridine (bpy) and their structural analogues, offer additional opportunities for tuning the electro-optical properties. For instance, Ir(III) acetylacetonates, with –OPh as a substituent at the cyclometallating ligand, emit a bluish-green color, whereas those with B(mesithyl)2 as a substituent give a red color.213 The devices, moreover, exhibit excellent power efficiencies (ηP = 26.8–28.6 lm W−1) and attain external quantum efficiencies of ηext = 10.3–11.1%.
In order to achieve enhanced thermal stability, increased solubility in solvents and polymer matrices, colour tunability, and high solid-state photoluminescence quantum efficiency, sterically hindered dendrons are often inserted at the periphery of an emitting core. Significant work on phosphorescent Ir(III) complexes with dendronic ligands has been carried out by the groups of Burn and Samuel.214,215 They were able to obtain very high device efficiencies from a series of dendrimer Ir(III) complexes, fastened with 2-ethylhexyloxy terphenyl dendrons, via the site isolation effect of the dendrimers. A maximum external device quantum efficiency of 10.4% was achieved for blue electrophosphorescence, highlighting the beneficial role of the dendrons.216,217
More recently, Pt(II), Zn(II), Cu(I) and other transition complexes have been used as materials for OLEDs.218–221 In the limited scope of this perspective, it is not possible to do justice to the wide range of transition metal complexes that are being explored in the world of OLEDs. Hence, we have restricted our discussion to a general description of design principles and a few specific examples of transition metal complexes incorporated in OLEDs.
6.2 LECs
Monolayered electroluminescent devices consisting of a luminescent material hosting the recombination of ionic charges, sandwiched between two electrodes, are regarded as Light-emitting Electrochemical Cells (LECs). The operational mechanism of LECs can be described by two models: the electrodynamical model (ED)222 and the electrochemical doping (ECD) model.223 Though there are certain differences in the assumptions of the two models, both models agree that the accumulation of ions at the two electrodes results in a sharp drop in the applied potential, resulting in charge reconstitution and, hence, triggering light emission, from the phosphorescent material clamped between the electrodes. LECs are easily engineered and their biggest advantage lies in their insensitivity towards the work function of the electrodes, unlike the highly sensitive and complexly structured OLEDs. This allows for the use of air-stable metals such as Au or Ag.206,224Pei et al.223 first introduced the concept of LECs in 1995, by coalescing an inorganic salt to a blend of a conjugated luminescent polymer and an ionic conductive polymer. Following this pioneering work, Maness et al.225 proposed an alternative pathway by incorporating a Ru(II) ionic transition metal complex (iTMC) as the only active component in the luminescent layer.
However, there is a constraint in color tunability for the Ru(II) chromophores, whose emission band is situated across the orange–red part of the visible spectrum. This hinders their application in lighting and display technologies, which demand extensive colour tunability. The entire color scale can be accessed by using luminescent iTMCs involving different metal centres. For example, on going from Ru to Ir, the enhanced metal–ligand bond strength and ligand field splitting energy promote better stability of the subsequent complexes, which in turn results in high quantum efficiency and satisfactory photochemical stability. Slinker et al. reported the first example of LECs consisting of a monolayer emitting yellow light and incorporating an Ir iTMC ([Ir(ppy)2(dtb-bpy)][PF6]),226 which displays a photoluminescence quantum yield of 23.5% in oxygen-free acetonitrile solution.
Several strategies have been adopted to design LECs with emissions across the entire visible spectrum.224 Ir(III) complexes have commonly been used for this purpose, with light-emitting complexes from red [Ir(ppy)2(qIbi)][PF6] to yellow [Ir(ppy)2(dtb-bpy)][PF6] and blue–green [Irdf-(CF3)ppy2 (dtb-bpy)][PF6] complexes.224
In short, LECs have made notable progress over the past few years, which when combined with their advantages over OLEDs, enable us to consider LECs as affordable, versatile and energy-efficient flat light sources.
6.3 Biological applications
The use of phosphorescent transition metal complexes in biology encompasses an extensive area of applications as sensing agents, bioimaging probes, therapeutic agents and theranostic agents.227Extensive studies of the photophysically enriched Ru(II)-diimine complexes have revealed that although [Ru(bpy)3]2+ did not show any enhancement in luminescence in the presence of duplex DNA, the more extended [Ru(bpy)2(dppz)]2+,230 and [Ru(phen)2(dppz)]2+,231 complexes displayed intensely amplified luminescence. This amplified luminescence can be attributed to the protection of the dppz moiety from solvent quenching upon intercalation into DNA, which ultimately triggered an effective emission from the MLCT excited state of the complex. Application of fluorescence lifetime imaging microscopy (FLIM)232 to the Δ and Λ isomers of Ru(II)-dppz complexes in live and fixed cells revealed that these complexes can serve as potential probes for biomolecular binding and cellular microenvironments.233
Due to these multiple roles successfully played by luminescent transition metal complexes, of which only a few have been discussed above, phosphorescent transition metal complexes can be widely used as dual-function metal complexes (possessing both diagnostic and therapeutic qualities in a single entity) in cancer theranostics.
7 Summary
We have in this perspective focused on the intersection of photophysical processes and transition metal complexes. Transition metal complexes are an interesting group of compounds with unique structure-bonding and luminescence properties. The metal centers are capable of bonding to a wide range of ligands and with varying coordination numbers. The formation and substition of metal–ligand bonds are easily accomplished. This allows their photophysical properties to be changed by altering the ligand numbers and types. The photophysics is mostly controlled by the characteristic large nuclear charge of the metal atom, which in turn gives rise to SOC between the singlet and triplet manifolds. The loss of pure spin states opens up new deactivation pathways, with ISC and phosphorescence being the two most important ones. We have in this perspective discussed the theoretical foundation as well as given examples of the three central quantities determining the photophysics of transition metal complexes, namely, SOC, ISC and phosphorescence.The demand for computational techniques to unravel the complexities behind photoluminescence spectroscopies has led to efficient implementations of these properties in quantum-chemical software packages such as the DALTON program,235 QChem software,236 Gaussian,237 DFT/MRCI,238 ADF,239 SPOCK136 and ReSpect.240 A number of programs can be used to perform frequency calculations and Franck–Condon analysis.237,239,241,242 However, the choice for computing rates of ISC is limited and is more often stand-alone codes developed by individual groups. Even though we have not discussed quantum dynamic methods explicitly, we note that SHARC and MCTDH are the two dominant programs in use for this purpose.153,243 In order to appropriately utilize these computational tools, an overall understanding of the theory is essential, and hopefully this contributed to it.
The novelty of transition metal complexes is far and wide. A variety of applications in the fields of opto-electronics and photobiology have been discussed. Ir(III) complexes are among the most popular candidates for this purpose. The field is growing rapidly and remains a hot research topic.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
T. M. acknowledges support from the Marie Skłodowska-Curie European Training Network “COSINE-Computational Spectroscopy in Natural sciences and Engineering”, Grant Agreement No. 765739. P. K. thanks the Council of Scientific and Industrial Research (CSIR) for granting him a Junior Research Fellowship. K. R. acknowledges support from the Research Council of Norway through a Centre of Excellence Grant (Grant No. 262695).References
- M. Fumanal, E. Gindensperger and C. Daniel, J. Phys. Chem. Lett., 2018, 9, 5189–5195 CrossRef CAS PubMed.
- B. A. McClure and J. J. Rack, Inorg. Chem., 2011, 50, 7586–7590 CrossRef CAS PubMed.
- Z. Guo, P. G. Giokas, T. P. Cheshire, O. F. Williams, D. J. Dirkes, W. You and A. M. Moran, J. Phys. Chem. A, 2016, 120, 5773–5790 CrossRef CAS PubMed.
- G. B. Shaw, C. D. Grant, H. Shirota, E. W. Castner, G. J. Meyer and L. X. Chen, J. Am. Chem. Soc., 2007, 129, 2147–2160 CrossRef CAS PubMed.
- N. Huse, T. K. Kim, L. Jamula, J. K. McCusker, F. M. F. de Groot and R. W. Schoenlein, J. Am. Chem. Soc., 2010, 132, 6809–6816 CrossRef CAS PubMed.
- R. M. van der Veen, A. Cannizzo, F. van Mourik, A. Vlček and M. Chergui, J. Am. Chem. Soc., 2011, 133, 305–315 CrossRef CAS PubMed.
- J. E. Monat and J. K. McCusker, J. Am. Chem. Soc., 2000, 122, 4092–4097 CrossRef CAS.
- Y. Zhang, K. Bennett and S. Mukamel, J. Phys. Chem. A, 2018, 122, 6524–6531 CrossRef CAS PubMed.
- G. J. Hedley, A. Ruseckas and I. D. W. Samuel, J. Phys. Chem. A, 2009, 113, 2–4 CrossRef CAS PubMed.
- M. L. Shelby, P. J. Lestrange, N. E. Jackson, K. Haldrup, M. W. Mara, A. B. Stickrath, D. Zhu, H. T. Lemke, M. Chollet, B. M. Hoffman, X. Li and L. X. Chen, J. Am. Chem. Soc., 2016, 138, 8752–8764 CrossRef CAS PubMed.
- M. Maiuri, M. Garavelli and G. Cerullo, J. Am. Chem. Soc., 2020, 142, 3–15 CrossRef CAS PubMed.
- C. N. Fleming, K. A. Maxwell, J. M. DeSimone, T. J. Meyer and J. M. Papanikolas, J. Am. Chem. Soc., 2001, 123, 10336–10347 CrossRef CAS PubMed.
- J. K. McCusker, Acc. Chem. Res., 2003, 36, 876–887 CrossRef CAS PubMed.
- M. Iwamura, H. Watanabe, K. Ishii, S. Takeuchi and T. Tahara, J. Am. Chem. Soc., 2011, 133, 7728–7736 CrossRef CAS PubMed.
- M. Chergui, Acc. Chem. Res., 2015, 48, 801–808 CrossRef CAS PubMed.
- M. Iwamura, S. Takeuchi and T. Tahara, Acc. Chem. Res., 2015, 48, 782–791 CrossRef CAS PubMed.
- C. Sousa, C. de Graaf, A. Rudavskyi, R. Broer, J. Tatchen, M. Etinski and C. M. Marian, Chem. – Eur. J., 2013, 19, 17541–17551 CrossRef CAS PubMed.
- W. Yang, B. Ashwood, J. Zhao, W. Ji, D. Escudero, D. Jacquemin and C. E. Crespo-Hernández, J. Phys. Chem. C, 2017, 121, 21184–21198 CrossRef CAS.
- J. Eng, C. Gourlaouen, E. Gindensperger and C. Daniel, Acc. Chem. Res., 2015, 48, 809–817 CrossRef CAS PubMed.
- G. Capano, U. Rothlisberger, I. Tavernelli and T. J. Penfold, J. Phys. Chem. A, 2015, 119, 7026–7037 CrossRef CAS PubMed.
- K. Li, G. S. Ming Tong, Q. Wan, G. Cheng, W.-Y. Tong, W.-H. Ang, W.-L. Kwong and C.-M. Che, Chem. Sci., 2016, 7, 1653–1673 RSC.
- A. D. Kirk, Chem. Rev., 1999, 99, 1607–1640 CrossRef CAS PubMed.
- M. S. Wrighton, Theoretical Inorganic Chemistry II, Berlin, Heidelberg, 1976, pp. 37–104 Search PubMed.
- A. W. Adamson and J. N. Demas, J. Am. Chem. Soc., 1971, 93, 1800–1801 CrossRef CAS.
- V. Balzani, N. Sabbatini and F. Scandola, Chem. Rev., 1986, 86, 319–337 CrossRef CAS.
- F. Scandola, M. T. Indelli, C. Chiorboli and C. A. Bignozzi, Photoinduced Electron Transfer II, Berlin, Heidelberg, 1990, pp. 73–149 Search PubMed.
- E. M. Kober, J. L. Marshall, W. J. Dressick, B. P. Sullivan, J. V. Caspar and T. J. Meyer, Inorg. Chem., 1985, 24, 2755–2763 CrossRef CAS.
- J. F. Endicott, Acc. Chem. Res., 1988, 21, 59–66 CrossRef CAS.
- H. Rensmo, S. Lunell and H. Siegbahn, J. Photochem. Photobiol., A, 1998, 114, 117–124 CrossRef CAS.
- S. Bonnet, J.-P. Collin and J.-P. Sauvage, Inorg. Chem., 2006, 45, 4024–4034 CrossRef CAS PubMed.
- S. Bonnet, J.-P. Collin and J.-P. Sauvage, Inorg. Chem., 2007, 46, 10520–10533 CrossRef CAS PubMed.
- H. Basch, A. Viste and H. B. Gray, J. Chem. Phys., 1966, 44, 10–19 CrossRef CAS.
- H. B. Gray and C. J. Ballhausen, J. Am. Chem. Soc., 1963, 85, 260–265 CrossRef CAS.
- V. Balzani and S. Campagna, Photochemistry and Photophysics of Coordination Compounds I, Springer-Verlag, Berlin Heidelberg, 2007 Search PubMed.
- T. J. Meyer and J. V. Caspar, Chem. Rev., 1985, 85, 187–218 CrossRef CAS.
- G. A. Crosby, Acc. Chem. Res., 1975, 8, 231–238 CrossRef CAS.
- R. J. Watts, J. Chem. Educ., 1983, 60, 834 CrossRef CAS.
- P. M. Kozlowski, B. D. Garabato, P. Lodowski and M. Jaworska, Dalton Trans., 2016, 45, 4457–4470 RSC.
- K. Kornobis, N. Kumar, P. Lodowski, M. Jaworska, P. Piecuch, J. J. Lutz, B. M. Wong and P. M. Kozlowski, J. Comput. Chem., 2013, 34, 987–1004 CrossRef CAS PubMed.
- A. Hauser and C. Reber, in 50 Years of Structure and Bonding - The Anniversary Volume. Structure and Bonding, ed. D. Mingos, Springer, Cham., 2016, ch. Spectroscopy and Chemical Bonding in Transition Metal Complexes Search PubMed.
- A. Jablonski, Nature, 1933, 131, 839–840 CrossRef CAS.
- M. Kasha, Discuss. Faraday Soc., 1950, 9, 14–19 RSC.
- L. Paul, T. Moitra, K. Ruud and S. Chakrabarti, J. Phys. Chem. Lett., 2019, 10, 369–374 CrossRef PubMed.
- D. Escudero and W. Thiel, Inorg. Chem., 2014, 53, 11015–11019 CrossRef CAS PubMed.
- Q. Zhang, X. Wang, Y. Zhang, L. Wang, J. Li and J. Zhang, J. Phys. Chem. C, 2016, 120, 27523–27532 CrossRef CAS.
- K. Veys and D. Escudero, J. Phys. Chem. A, 2020, 124, 7228–7237 CrossRef CAS PubMed.
- C. Feng, S. Li, L. Fu, X. Xiao, Z. Xu, Q. Liao, Y. Wu, J. Yao and H. Fu, J. Phys. Chem. Lett., 2020, 11, 8246–8251 CrossRef CAS PubMed.
- M. Röhrs and D. Escudero, J. Phys. Chem. Lett., 2019, 10, 5798–5804 CrossRef PubMed.
- A. P. Demchenko, V. I. Tomin and P.-T. Chou, Chem. Rev., 2017, 117, 13353–13381 CrossRef CAS PubMed.
- A. Terenin, Acta Physicochim. URSS, 1943, 28, 210–241 Search PubMed.
- G. N. Lewis and M. Kasha, J. Am. Chem. Soc., 1944, 66, 2100–2116 CrossRef CAS.
- F. Barigelletti, Photochemistry: Volume 38, The Royal Society of Chemistry, 2010, vol. 38, pp. 234–274 Search PubMed.
- K. K.-W. Lo, in Luminescent Transition Metal Complexes as Biological Labels and Probes, ed. V. W. W. Yam, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 205–245 Search PubMed.
- S. I. Pascu, P. A. Waghorn, T. D. Conry, H. M. Betts, J. R. Dilworth, G. C. Churchill, T. Pokrovska, M. Christlieb, F. I. Aigbirhio and J. E. Warren, Dalton Trans., 2007, 4988–4997 RSC.
- K. K.-W. Lo, S. P.-Y. Li and K. Y. Zhang, New J. Chem., 2011, 35, 265–287 RSC.
- K. K.-W. Lo, B. T.-N. Chan, H.-W. Liu, K. Y. Zhang, S. P.-Y. Li and T. S.-M. Tang, Chem. Comm., 2013, 49, 4271–4273 RSC.
- Q. Zhao, F. Li and C. Huang, Chem. Soc. Rev., 2010, 39, 3007–3030 RSC.
- Q. Zhao, C. Huang and F. Li, Chem. Soc. Rev., 2011, 40, 2508–2524 RSC.
- K. K.-W. Lo and S. P.-Y. Li, RSC Adv., 2014, 4, 10560–10585 RSC.
- V. Rai-Constapel, S. Salzmann and C. M. Marian, J. Phys. Chem. A, 2011, 115, 8589–8596 CrossRef CAS PubMed.
- M. Etinski, J. Tatchen and C. M. Marian, J. Chem. Phys., 2011, 134, 154105 CrossRef PubMed.
- S. Iuchi and N. Koga, Phys. Chem. Chem. Phys., 2016, 18, 4789–4799 RSC.
- I. Tavernelli, B. F. Curchod and U. Rothlisberger, Chem. Phys., 2011, 391, 101–109 CrossRef CAS.
- S. Mai, P. Marquetand and L. González, J. Chem. Phys., 2014, 140, 204302 CrossRef PubMed.
- M. Pederzoli and J. Pittner, J. Chem. Phys., 2017, 146, 114101 CrossRef PubMed.
- L. Martínez-Fernández, I. Corral, G. Granucci and M. Persico, Chem. Sci., 2014, 5, 1336–1347 RSC.
- M. Pápai, T. J. Penfold and K. B. Mø, J. Phys. Chem. C, 2016, 120, 17234–17241 CrossRef.
- M. Pápai, G. Vankó, T. Rozgonyi and T. J. Penfold, J. Phys. Chem. Lett., 2016, 7, 2009–2014 CrossRef PubMed.
- S. Mai, P. Marquetand and L. González, Int. J. Quantum Chem., 2015, 115, 1215–1231 CrossRef CAS.
- S. Mai, P. Marquetand and L. González, J. Phys. Chem. Lett., 2016, 7, 1978–1983 CrossRef CAS PubMed.
- A. Carlos Borin, S. Mai, P. Marquetand and L. González, Phys. Chem. Chem. Phys., 2017, 19, 5888–5894 RSC.
- G. Cui and W. Thiel, J. Chem. Phys., 2014, 141, 124101 CrossRef PubMed.
- S. Mai, M. Richter, P. Marquetand and L. González, Chem. Phys., 2017, 482, 9–15 CrossRef CAS.
- M. Fumanal, E. Gindensperger and C. Daniel, Phys. Chem. Chem. Phys., 2018, 20, 1134–1141 RSC.
- Y. Harabuchi, J. Eng, E. Gindensperger, T. Taketsugu, S. Maeda and C. Daniel, J. Chem. Theory Comput., 2016, 12, 2335–2345 CrossRef CAS PubMed.
- A. J. Atkins and L. González, J. Phys. Chem. Lett., 2017, 8, 3840–3845 CrossRef CAS PubMed.
- S. Gómez, M. Heindl, A. Szabadi and L. González, J. Phys. Chem. A, 2019, 123, 8321–8332 CrossRef PubMed.
- P. A. M. Dirac and R. H. Fowler, Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 1928, 117, 610–624 Search PubMed.
- K. G. Dyall, J. Chem. Phys., 1994, 100, 2118–2127 CrossRef CAS.
- W. Pauli, in Zur Quantenmechanik des magnetischen Elektrons, ed. C. P. Enz and K. V. Meyenn, Vieweg + Teubner Verlag, Wiesbaden, 1988, pp. 282–305 Search PubMed.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- G. Schreckenbach and T. Ziegler, Int. J. Quantum Chem., 1997, 61, 899–918 CrossRef CAS.
- B. A. Hess, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371 CrossRef CAS.
- A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823–1833 CrossRef CAS.
- D. G. Fedorov and M. S. Gordona, J. Chem. Phys., 2000, 112, 5611–5623 CrossRef CAS.
- P. Pokhilko, E. Epifanovsky and A. I. Krylov, J. Chem. Phys., 2019, 151, 034106 CrossRef PubMed.
- M. Blume, R. E. Watson and R. E. Peierls, Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1962, 270, 127–143 CAS.
- M. Blume, R. E. Watson and R. E. Peierls, Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1963, 271, 565–578 CAS.
- J. S. Cohen, W. R. Wadt and P. J. Hay, J. Chem. Phys., 1979, 71, 2955–2965 CrossRef CAS.
- C. Ribbing, M. Odelius and J. Kowalewski, Mol. Phys., 1991, 74, 1299–1314 CrossRef CAS.
- S. Koseki, M. W. Schmidt and M. S. Gordon, J. Phys. Chem., 1992, 96, 10768–10772 CrossRef CAS.
- S. Koseki, M. S. Gordon, M. W. Schmidt and N. Matsunaga, J. Phys. Chem., 1995, 99, 12764–12772 CrossRef CAS.
- S. Koseki, M. W. Schmidt and M. S. Gordon, J. Phys. Chem. A, 1998, 102, 10430–10435 CrossRef CAS.
- C. Teichteil, M. Pelissier and F. Spiegelmann, Chem. Phys., 1983, 81, 273–282 CrossRef CAS.
- L. Seijo and Z. Barandiarán, The Ab Initio Model Potential Method: A Common Strategy for Effective Core Potential and Embedded Cluster Calculations, 1999, pp. 55–152 Search PubMed.
- C. M. Marian and U. Wahlgren, Chem. Phys. Lett., 1996, 251, 357–364 CrossRef CAS.
- S. Yabushita, Z. Zhang and R. M. Pitzer, J. Phys. Chem. A, 1999, 103, 5791–5800 CrossRef CAS.
- S. R. Langhoff and C. W. Kern, in Molecular Fine Structure, ed. H. F. Schaefer, Springer US, Boston, MA, 1977, pp. 381–437 Search PubMed.
- S. G. Chiodo and N. Russo, Chem. Phys. Lett., 2010, 490, 90–96 CrossRef CAS.
- P. A. Malmqvist, B. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- F. Rakowitz, M. Casarrubios, L. Seijo and C. M. Marian, J. Chem. Phys., 1998, 108, 7980–7987 CrossRef CAS.
- E. v. Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- E. van Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953 CrossRef CAS.
- F. Wang and T. Ziegler, J. Chem. Phys., 2005, 123, 154102 CrossRef PubMed.
- K. Mori, T. P. M. Goumans, E. van Lenthe and F. Wang, Phys. Chem. Chem. Phys., 2014, 16, 14523–14530 RSC.
- L. Paul, S. Chakrabarti and K. Ruud, J. Phys. Chem. Lett., 2017, 8, 4893–4897 CrossRef CAS PubMed.
- T. Moitra, M. M. Alam and S. Chakrabarti, Phys. Chem. Chem. Phys., 2018, 20, 23244–23251 RSC.
- S. Mai, H. Gattuso, M. Fumanal, A. Muñoz Losa, A. Monari, C. Daniel and L. González, Phys. Chem. Chem. Phys., 2017, 19, 27240–27250 RSC.
- H. Eschrig and V. D. P. Servedio, J. Comput. Chem., 1999, 20, 23–30 CrossRef CAS.
- J. Gao, W. Liu, B. Song and C. Liu, J. Chem. Phys., 2004, 121, 6658–6666 CrossRef CAS PubMed.
- J. Gao, W. Zou, W. Liu, Y. Xiao, D. Peng, B. Song and C. Liu, J. Chem. Phys., 2005, 123, 054102 CrossRef PubMed.
- R. Bast, H. Jensen and T. Saue, Int. J. Quantum Chem., 2009, 109, 2091–2112 CrossRef CAS.
- S. Komorovsky, P. J. Cherry and M. Repisky, J. Chem. Phys., 2019, 151, 184111 CrossRef PubMed.
- S. Villaume, T. Saue and P. Norman, J. Chem. Phys., 2010, 133, 064105 CrossRef PubMed.
- T. Fransson, T. Saue and P. Norman, J. Chem. Theory Comput., 2016, 12, 2324–2334 CrossRef CAS PubMed.
- L. Konecny, M. Repisky, K. Ruud and S. Komorovsky, J. Chem. Phys., 2019, 151, 194112 CrossRef PubMed.
- S. Fraga, K. M. S. Saxena and J. Karwowski, Handbook of atomic data, Elsevier, Amsterdam, The Netherlands, 1976, vol. 5 Search PubMed.
- M. Gernert, L. Balles-Wolf, F. Kerner, U. Müller, A. Schmiedel, M. Holzapfel, C. M. Marian, J. Pflaum, C. Lambert and A. Steffen, J. Am. Chem. Soc., 2020, 142, 8897–8909 CrossRef CAS PubMed.
- G. Baryshnikov, B. Minaev and H. Ågren, Chem. Rev., 2017, 117, 6500–6537 CrossRef CAS PubMed.
- E. N. Harvey, A history of luminescence from the earliest times until 1900, American Philosophical Society, 1957, vol. 44 Search PubMed.
- B. Valeur and M. N. Berberan-Santos, J. Chem. Edu., 2011, 88, 731–738 CrossRef CAS.
- S. P. McGlynn, T. Azumi and M. Kinoshita, et al., 1969.
- B. Minaev, G. Baryshnikov and H. Agren, Phys. Chem. Chem. Phys., 2014, 16, 1719–1758 RSC.
- A. Messiah and L. I. Schiff, Quantum mechanics, McGraw-Hill College, 1968, vol. 643 Search PubMed.
- S. K. Lower and M. El-Sayed, Chem. Rev., 1966, 66, 199–241 CrossRef CAS.
- Y. Chi and P.-T. Chou, Chem. Soc. Rev., 2007, 36, 1421–1431 RSC.
- P. Norman, K. Ruud and T. Saue, Principles and Practices of Molecular Properties, John Wiley and Sons, Ltd, 1st edn, 2018 Search PubMed.
- Y. Luo, D. Jonsson, P. Norman, K. Ruud, O. Vahtras, B. Minaev, H. Ågren, A. Rizzo and K. Mikkelsen, Int. J. Quantum Chem., 1998, 70, 219–239 CrossRef CAS.
- E. Jansson, B. Minaev, S. Schrader and H. Ågren, Chem. Phys., 2007, 333, 157–167 CrossRef CAS.
- B. Minaev, V. Minaeva and H. Ågren, J. Phys. Chem. A, 2009, 113, 726–735 CrossRef CAS PubMed.
- K.-H. Kim, S. Lee, C.-K. Moon, S.-Y. Kim, Y.-S. Park, J.-H. Lee, J. W. Lee, J. Huh, Y. You and J.-J. Kim, Nat. Commun., 2014, 5, 1–8 Search PubMed.
- S. J. Havriliak and D. R. Yarkony, J. Chem. Phys., 1985, 83, 1168–1172 CrossRef CAS.
- V. Vallet, L. Maron, C. Teichteil and J.-P. Flament, J. Chem. Phys., 2000, 113, 1391–1402 CrossRef CAS.
- M. Kleinschmidt, J. Tatchen and C. M. Marian, J. Chem. Phys., 2006, 124, 124101 CrossRef PubMed.
- D. Jacquemin and D. Escudero, Chem. Sci., 2017, 8, 7844–7850 RSC.
- H. Yu, J. A. Sanchez-Rodriguez, M. Pollum, C. E. Crespo-Hernández, S. Mai, P. Marquetand, L. González and S. Ullrich, Phys. Chem. Chem. Phys., 2016, 18, 20168–20176 RSC.
- A. Lázaro, C. Cunha, R. Bosque, J. Pina, J. S. Ward, K.-N. Truong, K. Rissanen, J. C. Lima, M. Crespo, J. S. Seixas de Melo and L. Rodríguez, Inorg. Chem., 2020, 59, 8220–8230 CrossRef PubMed.
- F. Geist, A. Jackel and R. F. Winter, Inorg. Chem., 2015, 54, 10946–10957 CrossRef CAS PubMed.
- F. Geist, A. Jackel and R. F. Winter, Dalton Trans., 2015, 44, 3974–3987 RSC.
- Y. You and S. Y. Park, Dalton Trans., 2009, 1267–1282 RSC.
- A. Haque, L. Xu, R. A. Al-Balushi, M. K. Al-Suti, R. Ilmi, Z. Guo, M. S. Khan, W.-Y. Wong and P. R. Raithby, Chem. Soc. Rev., 2019, 48, 5547–5563 RSC.
- C. Song, J. Tang, J. Li, Z. Wang, P. Li and H. Zhang, Inorg. Chem., 2018, 57, 12174–12186 CrossRef CAS PubMed.
- S. Y.-L. Leung, E. S.-H. Lam, W. H. Lam, K. M.-C. Wong, W.-T. Wong and V. W.-W. Yam, Chem. – Eur. J., 2013, 19, 10360–10369 CrossRef CAS PubMed.
- G. Li, X. Zhao, T. Fleetham, Q. Chen, F. Zhan, J. Zheng, Y.-F. Yang, W. Lou, Y. Yang, K. Fang, Z. Shao, Q. Zhang and Y. She, Chem. Mater., 2020, 32, 537–548 CrossRef CAS.
- T. Fleetham, G. Li, L. Wen and J. Li, Adv. Mater., 2014, 26, 7116–7121 CrossRef CAS PubMed.
- C. Lee, R. Zaen, K.-M. Park, K. H. Lee, J. Y. Lee and Y. Kang, Organometallics, 2018, 37, 4639–4647 CrossRef CAS.
- M. Krause, D. Kourkoulos, D. González-Abradelo, K. Meerholz, C. A. Strassert and A. Klein, Eur. J. Inorg. Chem., 2017, 5215–5223 CrossRef CAS.
- P. J. G. Saris and M. E. Thompson, Org. Lett., 2016, 18, 3960–3963 CrossRef CAS PubMed.
- J. Soellner and T. Strassner, Organometallics, 2018, 37, 1821–1824 CrossRef CAS.
- J. D. Bullock, A. Salehi, C. J. Zeman, K. A. Abboud, F. So and K. S. Schanze, ACS Appl. Mater. Interfaces, 2017, 9, 41111–41114 CrossRef CAS PubMed.
- G. A. Worth, M. H. Beck, A. Jäckle and H.-D. Meyer, The MCTDH package, 2011, http://mctdh.uni-hd.de.
- H. Wang and M. Thoss, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef CAS.
- Multidimensional Quantum Dynamics: MCTDH Theory and Applications, ed. H. Meyer, F. Gatti and G. Worth, VCH, Weinheim, 2009 Search PubMed.
- F. Plasser, S. Gomez, M. F. S. J. Menger, S. Mai and L. Gonzalez, Phys. Chem. Chem. Phys., 2019, 21, 57–69 RSC.
- J. C. Tully and R. K. Preston, J. Chem. Phys., 1971, 55, 562–572 CrossRef CAS.
- T. J. Martinez, M. Ben-Nun and R. Levine, J. Phys. Chem., 1996, 100, 7884–7895 CrossRef CAS.
- E. J. Heller, J. Chem. Phys., 1975, 62, 1544–1555 CrossRef CAS.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025 CrossRef CAS PubMed.
- R. Borrelli and A. Peluso, J. Chem. Phys., 2003, 119, 8437–8448 CrossRef CAS.
- J. R. Reimers, J. Chem. Phys., 2001, 115, 9103–9109 CrossRef CAS.
- M. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS.
- R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164 CrossRef CAS.
- A. Toniolo and M. Persico, J. Comput. Chem., 2001, 22, 968–975 CrossRef CAS.
- J. Tatchen, N. Gilka and C. M. Marian, Phys. Chem. Chem. Phys., 2007, 9, 5209–5221 RSC.
- M. Dierksen and S. Grimme, J. Chem. Phys., 2005, 122, 244101 CrossRef PubMed.
- F. Santoro, A. Lami, R. Improta, J. Bloino and V. Barone, J. Chem. Phys., 2008, 128, 224311 CrossRef PubMed.
- K. Schmidt, S. Brovelli, V. Coropceanu, D. Beljonne, J. Cornil, C. Bazzini, T. Caronna, R. Tubino, F. Meinardi and Z. Shuai, et al. , J. Phys. Chem. A, 2007, 111, 10490–10499 CrossRef CAS PubMed.
- D. J. Tannor, Introduction to quantum mechanics: a time-dependent perspective, University Science Books, 2007 Search PubMed.
- R. Kubo, Phys. Rev., 1952, 86, 929–937 CrossRef CAS.
- M. Lax, J. Chem. Phys., 1952, 20, 1752–1760 CrossRef CAS.
- R. Kubo and Y. Toyozawa, Prog. Theor. Phys., 1955, 13, 160–182 CrossRef.
- P. Karak and S. Chakrabarti, Phys. Chem. Chem. Phys., 2020, 22, 24399–24409 RSC.
- R. Borrelli and A. Peluso, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 542–559 CAS.
- C. M. Marian, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 187–203 CAS.
- R. Borrelli and A. Peluso, J. Chem. Theory Comput., 2015, 11, 415–422 CrossRef CAS PubMed.
- A. Velardo, R. Borrelli, A. Peluso and A. Capobianco, J. Phys. Chem. C, 2016, 120, 24605–24614 CrossRef CAS.
- A. Landi, R. Borrelli, A. Capobianco, A. Velardo and A. Peluso, J. Phys. Chem. C, 2018, 122, 25849–25857 CrossRef CAS.
- R. Borrelli and A. Peluso, Phys. Chem. Chem. Phys., 2011, 13, 4420–4426 RSC.
- R. Borrelli, M. Thoss, H. Wang and W. Domcke, Mol. Phys., 2012, 110, 751–763 CrossRef CAS.
- N. Lüdtke, J. Föller and C. M. Marian, Phys. Chem. Chem. Phys., 2020, 22, 23530–23544 RSC.
- I. Lyskov and C. M. Marian, J. Phys. Chem. C, 2017, 121, 21145–21153 CrossRef CAS.
- J. Föller, M. Kleinschmidt and C. M. Marian, Inorg. Chem., 2016, 55, 7508–7516 CrossRef PubMed.
- A. Heil, K. Gollnisch, M. Kleinschmidt and C. M. Marian, Mol. Phys., 2016, 114, 407–422 CAS.
- M. Kleinschmidt, C. van Wüllen and C. M. Marian, J. Chem. Phys., 2015, 142, 094301 CrossRef PubMed.
- E. Yu-Tzu Li, T.-Y. Jiang, Y. Chi and P.-T. Chou, Phys. Chem. Chem. Phys., 2014, 16, 26184–26192 RSC.
- K. T. Chan, G. S. M. Tong, W.-P. To, C. Yang, L. Du, D. L. Phillips and C.-M. Che, Chem. Sci., 2017, 8, 2352–2364 RSC.
- M. Z. Shafikov, D. N. Kozhevnikov, M. Bodensteiner, F. Brandl and R. Czerwieniec, Inorg. Chem., 2016, 55, 7457–7466 CrossRef CAS PubMed.
- Y. Yu, S. Mallick, M. Wang and K. Borjesson, 2020.
- D. Polak, R. Jayaprakash, T. P. Lyons, L. A. Martínez-Martínez, A. Leventis, K. J. Fallon, H. Coulthard, D. G. Bossanyi, K. Georgiou, A. J. Petty, II, J. Anthony, H. Bronstein, J. Yuen-Zhou, A. I. Tartakovskii, J. Clark and A. J. Musser, Chem. Sci., 2020, 11, 343–354 RSC.
- H. Li, A. Kamasah, S. Matsika and A. G. Suits, Nat. Chem., 2019, 11, 123–138 CrossRef CAS.
- R. Monni, G. Capano, G. Auböck, H. B. Gray, A. Vlček, I. Tavernelli and M. Chergui, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6396–E6403 CrossRef CAS PubMed.
- L. Mewes, R. A. Ingle, S. Megow, H. Böhnke, E. Baranoff, F. Temps and M. Chergui, Inorg. Chem., 2020, 59, 14643–14653 CrossRef CAS PubMed.
- C. Imberti, P. Zhang, H. Huang and P. J. Sadler, Angew. Chem., Int. Ed., 2020, 59, 61–73 CrossRef CAS.
- S. Mai and L. Gonzalez, Angew. Chem., Int. Ed., 2020, 59, 16832–16846 CrossRef CAS PubMed.
- A. J. S. Valentine and X. Li, J. Chem. Phys., 2019, 151, 084107 CrossRef PubMed.
- P. Pokhilko and A. I. Krylov, J. Phys. Chem. Lett., 2019, 10, 4857–4862 CrossRef CAS PubMed.
- R. Borrelli and M. Gelin, Sci. Rep., 2017, 7, 9127 CrossRef PubMed.
- I. Kim, S. O. Jeon, D. Jeong, H. Choi, W.-J. Son, D. Kim, Y. M. Rhee and H. S. Lee, J. Chem. Theory Comput., 2020, 16, 621–632 CrossRef CAS PubMed.
- F. Talotta, S. Morisset, N. Rougeau, D. Lauvergnat and F. Agostini, J. Chem. Theory Comput., 2020, 16, 4833–4848 CrossRef CAS PubMed.
- P. O. Dral, M. Barbatti and W. Thiel, J. Phys. Chem. Lett., 2018, 9, 5660–5663 CrossRef CAS PubMed.
- J. Zhao, S. Ji, W. Wu, W. Wu, H. Guo, J. Sun, H. Sun, Y. Liu, Q. Li and L. Huang, RSC Adv., 2012, 2, 1712–1728 RSC.
- K. K.-W. Lo, S. P.-Y. Li and K. Y. Zhang, New J. Chem., 2011, 35, 265–287 RSC.
- A. Ahmad Warra, J. Chem. Pharm. Res., 2011, 3, 951–958 Search PubMed.
- C. Ulbricht, B. Beyer, C. Friebe, A. Winter and U. Schubert, Adv. Mater., 2009, 21, 4418–4441 CrossRef CAS.
- C. Humphreys, MRS Bull., 2008, 33, 459–470 CrossRef.
- K. Kamtekar, A. Monkman and M. Bryce, Adv. Mater., 2010, 22, 572–582 CrossRef CAS PubMed.
- I. M. Dixon, J.-P. Collin, J.-P. Sauvage, L. Flamigni, S. Encinas and F. Barigelletti, Chem. Soc. Rev., 2000, 29, 385–391 RSC.
- V. Marin, E. Holder, R. Hoogenboom and U. S. Schubert, Chem. Soc. Rev., 2007, 36, 618–635 RSC.
- J. D. Slinker, J. Rivnay, J. S. Moskowitz, J. B. Parker, S. Bernhard, H. D. Abruña and G. G. Malliaras, J. Mater. Chem., 2007, 17, 2976–2988 RSC.
- M. Thompson, MRS Bull., 2007, 32, 694–701 CrossRef CAS.
- W.-Y. Wong, Q. Wang, D. Ma, L. Wang, Z. Lin, T. B. Marder, C.-L. Ho and A. Beeby, Adv. Funct. Mater., 2008, 18, 499 CrossRef.
- K. A. Knights, S. G. Stevenson, C. P. Shipley, S.-C. Lo, S. Olsen, R. E. Harding, S. Gambino, P. L. Burn and I. D. W. Samuel, J. Mater. Chem., 2008, 18, 2121–2130 RSC.
- S. Vickers, H. Barcena, K. A. Knights, R. Thomas, J.-C. Ribierre, S. Gambino, I. Samuel, P. Burn and G. Fragneto, Appl. Phys. Lett., 2010, 96, 263302 CrossRef.
- A. W. Freeman, S. C. Koene, P. R. L. Malenfant, M. E. Thompson and J. M. J. Fréchet, J. Am. Chem. Soc., 2000, 49, 122 Search PubMed.
- S.-C. Lo, E. B. Namdas, C. P. Shipley, J. P. J. Markham, T. D. Anthopolous, P. L. Burn and I. D. W. Samuel, Org. Electron., 2006, 7, 85–98 CrossRef CAS.
- G. Cheng, G. K.-M. So, W.-P. To, Y. Chen, C.-C. Kwok, C. Ma, X. Guan, X. Chang, W.-M. Kwok and C.-M. Che, Chem. Sci., 2015, 6, 4623–4635 RSC.
- P. Pander, R. Bulmer, R. Martinscroft, S. Thompson, F. W. Lewis, T. J. Penfold, F. B. Dias and V. N. Kozhevnikov, Inorg. Chem., 2018, 57, 3825–3832 CrossRef CAS PubMed.
- G. Cheng, S. C. F. Kui, W.-H. Ang, M.-Y. Ko, P.-K. Chow, C.-L. Kwong, C.-C. Kwok, C. Ma, X. Guan, K.-H. Low, S.-J. Su and C.-M. Che, Chem. Sci., 2014, 5, 4819–4830 RSC.
- K. Li, G. Cheng, C. Ma, X. Guan, W.-M. Kwok, Y. Chen, W. Lu and C.-M. Che, Chem. Sci., 2013, 4, 2630–2644 RSC.
- J. C. deMello, J. J. M. Halls, S. C. Graham, N. Tessler and R. H. Friend, Phys. Rev. Lett., 2000, 85, 421–424 CrossRef CAS PubMed.
- Q. Pei, Y. Yang, G. Yu, C. Zhang and A. J. Heeger, J. Am. Chem. Soc., 1996, 118, 3922–3929 CrossRef CAS PubMed.
- R. D. Costa, E. Ortí, H. J. Bolink, F. Monti, G. Accorsi and N. Armaroli, Angew. Chem., 2012, 51, 8178–8211 CrossRef CAS.
- K. M. Maness, R. H. Terrill, T. J. Meyer, R. W. Murray and R. M. Wightman, J. Am. Chem. Soc., 1996, 118, 10609–10616 CrossRef CAS.
- J. D. Slinker, A. A. Gorodetsky, M. S. Lowry, J. Wang, S. Parker, R. Rohl, S. Bernhard and G. G. Malliaras, J. Am. Chem. Soc., 2004, 126, 2763–2767 CrossRef CAS PubMed.
- D.-L. Ma, H.-Z. He, K.-H. Leung, D. S.-H. Chan and C.-H. Leung, Angew. Chem., 2013, 52, 7666–7682 CrossRef CAS PubMed.
- H.-K. Liu and P. J. Sadler, Acc. Chem. Res., 2011, 44, 349–359 CrossRef CAS PubMed.
- M. Yu, Q. Zhao, L. Shi, F. Li, Z. Zhou, H. Yang, T. Yi and C. Huang, Chem. Commun., 2008, 2115–2117 RSC.
- A. E. Friedman, J. C. Chambron, J. P. Sauvage, N. J. Turro and J. K. Barton, J. Am. Chem. Soc., 1990, 112, 4960–4962 CrossRef CAS.
- C. Turro, S. H. Bossmann, Y. Jenkins, J. K. Barton and N. J. Turro, J. Am. Chem. Soc., 1995, 117, 9026–9032 CrossRef CAS.
- K. Suhling, P. M. W. French and D. Phillips, Photochem. Photobiol. Sci., 2005, 4, 13–22 CrossRef CAS PubMed.
- F. R. Svensson, M. Abrahamsson, N. Strömberg, A. G. Ewing and P. Lincoln, J. Phys. Chem. Lett., 2011, 2, 397–401 CrossRef CAS PubMed.
- L. Huynh, Z. Wang, J. Yang, V. Stoeva, A. Lough, I. Manners and M. A. Winnik, Chem. Mater., 2005, 17, 4765–4773 CrossRef CAS.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenaes, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjaergaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnaes, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Salek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 269–284 CAS.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. W. III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. D. Jr., H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. G. III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. S. III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. V. Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- C. M. Marian, A. Heil and M. Kleinschmidt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1394 Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- M. Repisky, S. Komorovsky, M. Kadek, L. Konecny, U. Ekström, E. Malkin, M. Kaupp, K. Ruud, O. L. Malkina and V. G. Malkin, J. Chem. Phys., 2020, 152, 184101 CrossRef CAS PubMed.
- D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108 CrossRef CAS PubMed.
- F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, J. Chem. Phys., 2007, 126, 084509 CrossRef PubMed.
- S. Mai, M. Richter, M. Heindl, M. Menger, A. Atkins, M. Ruckenbauer, F. Plasser, L. Ibele, S. Kropf, M. Oppel, P. Marquetand and L. González, SHARC2.1: Surface Hopping Including Arbitrary Couplings - Program Package for Non-Adiabatic Dynamics, 2019, sharc-md.org Search PubMed.
| This journal is © the Owner Societies 2021 |