Open Access Article
Open Access ArticleMachine-enabled inverse design of inorganic solid materials: promises and challenges
Juhwan
Noh
 ,
Geun Ho
Gu
,
Sungwon
Kim
and
Yousung
Jung
,
Geun Ho
Gu
,
Sungwon
Kim
and
Yousung
Jung
 *
*
Department of Chemical and Biomolecular Engineering, Korea Advanced Institute of Science and Technology (KAIST), 291, Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea. E-mail: ysjn@kaist.ac.kr
First published on 15th April 2020
Abstract
Developing high-performance advanced materials requires a deeper insight and search into the chemical space. Until recently, exploration of materials space using chemical intuitions built upon existing materials has been the general strategy, but this direct design approach is often time and resource consuming and poses a significant bottleneck to solve the materials challenges of future sustainability in a timely manner. To accelerate this conventional design process, inverse design, which outputs materials with pre-defined target properties, has emerged as a significant materials informatics platform in recent years by leveraging hidden knowledge obtained from materials data. Here, we summarize the latest progress in machine-enabled inverse materials design categorized into three strategies: high-throughput virtual screening, global optimization, and generative models. We analyze challenges for each approach and discuss gaps to be bridged for further accelerated and rational data-driven materials design.
1 Introduction
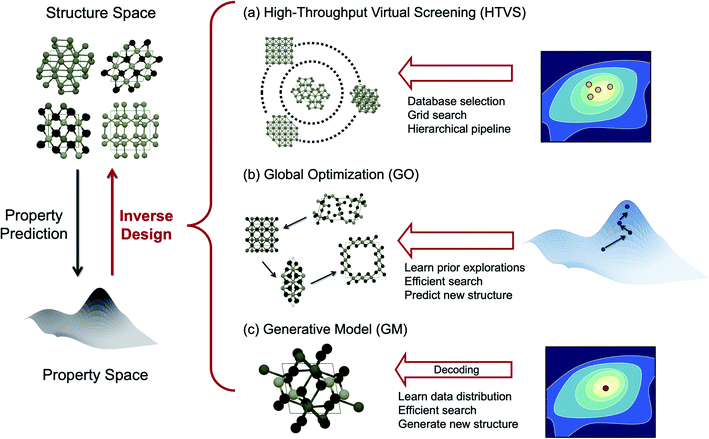
Technical demands for developing more advanced materials are continuing to increase, and developing improved functional materials necessitates going far beyond the known materials and digging deep into the chemical space.1 One of the fundamental goals of materials science is to learn structure–property relationships and from them to discover novel materials with desired functionalities. In traditional approaches, a candidate material is specified first using intuition or by slightly changing the existing materials, and their properties are scrutinized experimentally or computationally, and the process is repeated until one finds reasonable improvements to known materials (i.e. incremental improvement from the firstly discovered materials).2 This conventional approach is driven heavily by human experts' knowledge and hence the results vary person to person and can also be slow. Materials informatics deals with the use of data, informatics, and machine learning (ML, complementary to experts' intuitions) to establish structure–property relationships for materials and make a new functional discovery at a significantly accelerated rate. In materials informatics, human experts' knowledge is thus either incorporated into algorithms and/or completely replaced by data.There are two mapping directions (i.e. forward and inverse) in materials informatics. In a forward mapping, one essentially aims to predict the properties of materials using materials structures as input, encoded in various ways such as simple attributes of constituent atoms, compositions, structures in graph forms, etc. In an inverse mapping, by contrast, one defines the desired properties first and attempts to find materials with such properties in an inverse manner using mathematical algorithms and automations. While forward mapping mainly deals with property prediction given structures, inverse mapping focuses on the “design” aspect of materials informatics towards target properties. For effective inverse design, therefore, one needs (1) efficient methods to explore the vast chemical space towards the target region (“exploration”), and (2) fast and accurate methods to predict the properties of a candidate material along with chemical space exploration (“evaluation”).
The purpose of this mini-review is to survey exciting new developments of methods to perform inverse design by “exploring” the chemical space effectively towards the target region. We will particularly highlight the design of inorganic solid-state materials since there are excellent recent review articles in the literature for the molecular version of inverse design.3,4 To structure this review, we categorize the inverse design strategies of inorganic crystals as summarized in Fig. 1, namely, high-throughput virtual screening (HTVS), global optimization (GO), and generative ML models (GM), largely borrowing the classification of Sanchez-Lengeling and Aspuru-Guzik3 and Butler et al.5 Among them, HTVS may be regarded as an extended version of the direct approach since it goes through the library and evaluates its function one by one, but the data-driven nature of the automated, extensive, and accelerated search in the functional space makes it potentially included in the inverse design strategy.6
One of the drawbacks of HTVS, however, is that, the search is limited by the user-selected library (either the experimental database or substituted computational database) and experts' (sometimes biased) intuitions are still involved in selecting the database, and thus potentially high-performing materials that are not in the library can be missed out. Also, since the screening is run over the database blindly without any preferred directions to search, the efficiency can be low in HTVS. One way to expedite the brute-force search toward the optimal material is to perform global optimization (GO) in the chemical space. In evolutionary algorithms (EAs), one form of GO, for example, mutations and crossover allow effective visits of various local minima by leveraging the previous histories of configurational visits, and therefore can generally be more efficient and also go beyond the chemical space defined by known materials and their structural motifs unlike HTVS.7
The data-driven GM is another promising inverse design strategy.3 The GM is a probabilistic ML model that can generate new data from the continuous vector space learned from the prior knowledge on dataset distribution.3,21 The key advantage of GMs is their ability to generate unseen materials with target properties in the gap between the existing materials by learning their distribution in the continuous space. While both the EA and GM can generate completely new materials not in the existing database, they differ by the way each approach utilizes data. The EA learns the geometric landscape of the functionality manifold (energy and properties) implicitly as the iteration evolves, while the GM learns the distribution of the whole target functional space during training in an implicit (i.e. adversarial learning) or explicit (i.e. variational inference) manner.
Below we summarize the current status and successful examples of these three main strategies (HTVS, GO, and GM) of the data-driven inorganic inverse design approach. We also discuss several challenges for the practical application of accelerated inverse materials design and also offer some promising future directions.
2 Inverse design strategy
2.1 High-throughput virtual screening (HTVS)
The computational HTVS is a widely used discovery strategy in the field. Usual computational HTVS involves three steps: (1) defining the screening scope, (2) first principles-based (or sometimes empirical models) computational screening and (3) experimental verifications for the proposed candidates. Defining the screening scope involves field experts' heuristics, and the success of the screening highly depends on this step as the scope must contain promising materials, but it should not be so wide that the computational HTVS becomes too expensive. To save cost, computational funnels are often used where cheaper methods or easier-to-compute properties are used as initial filtering and more sophisticated methods or properties hierarchically narrow down candidates for a pool of final selections. Density functional theory (DFT) is usually used for the computational HTVS, but ML models for property predictions further accelerate the screening process significantly (evaluation aspect of materials informatics in Fig. 1a). For experimental verifications, the key step in the computational HTVS, high-throughput experimental methods such as sputtering can greatly help to survey a wide variety of synthesis conditions and activity.8 If activity is observed, more expensive characterization techniques are used to confirm the crystals.Using the computational HTVS going through the existing database, Reed and co-workers9 discovered 21 new Li-solid electrolyte materials by screening 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 Li-containing materials in the materials project (MP).10 Singh and co-workers11 newly identified 43 photocatalysts for CO2 conversion through the theory/experiment combined screening framework for 68
831 Li-containing materials in the materials project (MP).10 Singh and co-workers11 newly identified 43 photocatalysts for CO2 conversion through the theory/experiment combined screening framework for 68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860 materials available in MP. However, as discussed above, moving beyond the known materials is critical, and to address it, a new functional photoanode material has been discovered by enumerating hypothetical materials by substituting elements to the existing crystals.12 Recently, data mining-13 and deep learning-based14 algorithms for elemental substitution are proposed to effectively search through the existing crystal templates, and Sun et al.15 discovered a large number of metal nitrides using the data-mined elemental substitution algorithm which accelerated the experimental discovery of nitrides by a factor of 2 compared to the average rate of discovery listed on the inorganic crystal structure database, ICSD.16,17
860 materials available in MP. However, as discussed above, moving beyond the known materials is critical, and to address it, a new functional photoanode material has been discovered by enumerating hypothetical materials by substituting elements to the existing crystals.12 Recently, data mining-13 and deep learning-based14 algorithms for elemental substitution are proposed to effectively search through the existing crystal templates, and Sun et al.15 discovered a large number of metal nitrides using the data-mined elemental substitution algorithm which accelerated the experimental discovery of nitrides by a factor of 2 compared to the average rate of discovery listed on the inorganic crystal structure database, ICSD.16,17
Despite those successful results, the large computational cost for property evaluation using DFT calculations is still a main bottleneck in the computational HTVS, and to overcome the latter challenge, ML-aided property prediction has begun to be implemented (see Table 1 and ref. 18 and 19 for an extensive review on ML used in property predictions). Herein, we mainly focus on ML models predicting the stability of crystal structures since the stability represented by the formation energy is a widely used quantity, though crude, to approximate synthesizability in many materials designs.
| Representation | Invertibility | Invariance | Model | Application |
| Supervised learning (property prediction in HTVS) | ||||
| Atomic properties56,57 | No | Yes | SVR | Predicting melting temperature, bulk and shear modulus, bandgap |
| Crystal site-based representation20 | Yes | Yes | KRR | Predicting formation energy of ABC2D6 elpasolite structures |
| Average atomic properties22 | No | Yes | Ensembles of decision trees | Predicting the formation energy of inorganic crystal structures |
| Voronoi-tessellation-based representation58 | No | Yes | Random forest | Predicting the formation energy of quaternary Heusler compounds |
| Crystal graph24 | No | Yes | GCNN | Predicting formation enthalpy of inorganic compounds |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Unsupervised learning (GM) | ||||
| 3D atomic density59,79 | Yes | No | VAE | Generation of inorganic crystals |
| 3D atomic density and energy grid shape60 | Yes | No | GAN | Generation of porous materials |
| Lattice site descriptor61 | Yes | No | GAN | Generation of graphene/BN-mixed lattice structures |
| Unit cell vectors and coordinates36,62 | Yes | No | GAN | Generation of inorganic crystals |
Non-structural descriptor-based ML models have been proposed.20,22 For example, Meredig et al.22 proposed a formation energy prediction model for ∼15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 materials existing in the ICSD16,17 using both data-driven heuristics utilizing the composition-weighted average of corresponding binary compound formation energies (MAE = 0.12 eV per atom) and ensembles of decision trees which take average atomic properties of constituent elements as input (MAE = 0.16 eV per atom). The proposed models were used to explore ∼1.6 million ternary compounds, and 4500 new stable materials were identified with the energy above convex hull ≤100 meV per atom. With the latter examples considering compositional information only, Seko et al.23 have shown that the inclusion of structural information such as radial distribution function could further improve the prediction accuracy significantly from RMSE = 0.249 to 0.045 eV per atom for a cohesive energy of 18
000 materials existing in the ICSD16,17 using both data-driven heuristics utilizing the composition-weighted average of corresponding binary compound formation energies (MAE = 0.12 eV per atom) and ensembles of decision trees which take average atomic properties of constituent elements as input (MAE = 0.16 eV per atom). The proposed models were used to explore ∼1.6 million ternary compounds, and 4500 new stable materials were identified with the energy above convex hull ≤100 meV per atom. With the latter examples considering compositional information only, Seko et al.23 have shown that the inclusion of structural information such as radial distribution function could further improve the prediction accuracy significantly from RMSE = 0.249 to 0.045 eV per atom for a cohesive energy of 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 inorganic compounds with kernel ridge regression.
000 inorganic compounds with kernel ridge regression.
ML models that encode the structural information of crystals for the prediction of energies and properties have also been proposed. Notably, Xie et al.24 proposed the symmetry invariant crystal graph convolutional neural network (CGCNN) to encode periodic crystal structures which showed very encouraging predictions for various properties including formation energies (MAE = 0.039 eV per atom) and band gaps (MAE = 0.388 eV). An improved version of CGCNN was also proposed by incorporating explicit 3-body correlations of neighboring atoms and applied to identify stable compounds out of 132![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 structures obtained by tertiary elemental substitution of ThCr2Si2-structure prototype.25 Lately, the graph-based universal ML model that can treat both molecules and periodic crystals was proposed and demonstrated highly competitive accuracy across a wide range of 15–20 molecular and materials properties.24–27
600 structures obtained by tertiary elemental substitution of ThCr2Si2-structure prototype.25 Lately, the graph-based universal ML model that can treat both molecules and periodic crystals was proposed and demonstrated highly competitive accuracy across a wide range of 15–20 molecular and materials properties.24–27
While looking promising, one of the more practical challenges of ML-aided HTVS for crystals is that some property data is often limited in size to expect good predictive accuracy for model training across different chemistries.26,28 (A more general comparison between the inorganic crystal dataset and organic molecule database is discussed in more detail in a later section. See also Fig. 4) To address this small dataset size, algorithms such as transfer learning (i.e. using pre-trained parameters before training the model on the small-size of the database)29 and active learning (i.e. effectively sampling the training set from the whole database)30,31 could help. For example, one may build the ML model to predict computationally more difficult properties (e.g. band gap and bulk modulus) using model parameters trained on a relatively simple property (e.g. formation energy),26 and this would help prevent overfitting driven by using a smaller dataset for difficult properties.
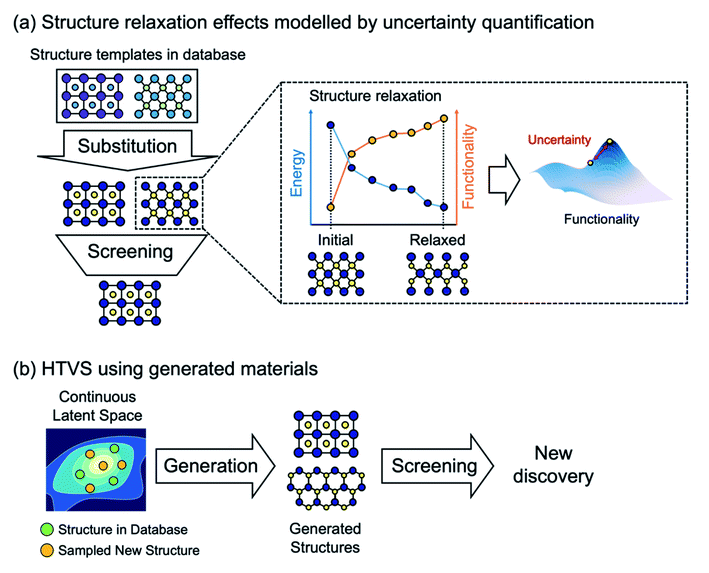
Furthermore, it is important to note that most current ML models to predict energies for crystals can only evaluate energies on relaxed structures, but cannot (or have not been shown to) calculate forces. Thus, when elemental substitution (which requires geometry relaxation) is used to expand the search space, one cannot use aforementioned ML models and still must perform costly DFT structure relaxations for every substituted structure as shown in Fig. 2a. To address this, data-driven interatomic potential models32–34 that can compute forces and construct a continuous potential energy surface are particularly promising, although they have not been widely used for HTVS of crystals yet since potentials are often developed for particular systems and so not applicable for the screening of widely varying systems. Or, still using the energy-only ML model but quantifying uncertainty caused by using unrelaxed structures could be an alternative way to increase the practical efficiency of HTVS.35 In addition, since the substitution-based enumeration limits the structural diversity of the dataset, generative models which will be discussed in detail below can effectively expand the diversity by sampling the hidden portion of the chemical space36 as shown in Fig. 2b.
2.2 Global optimization (GO)
Global optimization, including, but not limited to, quasi random search, simulated annealing, minima hopping, genetic algorithm, and particle swarm optimization, is an algorithm to find an optimal solution of target objective function, and thus it can be used for various inverse design problems.37 Many of these applications involve some form of crystal structure predictions. One of the earlier examples of GO applied to materials science is the work of Franceschetti and Zunger38 in which they used a simulated annealing approach to inversely design the optimal atomic configuration of the superlattice of AlxGa1−xAs alloys having the largest optical bandgap. Also, Doll et al.39 used a simulated annealing approach combined with ab initio calculations to predict the structure of boron nitride where various types of energetically favorable structures (e.g. layered structure, the wurtzite and zinc blende structure, β-BeO type and so on) were discovered showing the effectiveness of simulated annealing for crystal structure prediction. Random structure search, often constrained by a few chemical rules, is one of the simplest yet successful search strategies to find new phases of crystals, and Pickard and Needs combined it with first-principles calculations to predict the stable high-pressure phases of silane, for example.97Amsler and Goedecker40 proposed the minima hopping method to discover new crystal structures by adapting the softening process which modifies initial molecular dynamic velocities to improve the search efficiency. The latter minima hopping approach was extended to design transition metal alloy-based magnetic materials (FeCr, FeMn, FeCo and FeNi) by combining with additional steps evaluating magnetic properties (i.e. magnetization and magnetic anisotropy energy).41 FeCr and FeMn were predicted as soft-magnetic materials while FeCo and FeNi were predicted as hard-magnetic materials.
Evolutionary algorithms use strategies inspired by biological evolution, such as reproduction, mutation, recombination, and selection, and they can be used to find new crystal structures with optimized properties. The properties to optimize can be stability only (called convex hull optimization) or both stability and desired chemical properties (called Pareto or multi-objective optimization, see ref. 37 for more technical details). Two popular approaches include the Oganov-Glass evolutionary algorithm42 and Wang's version of particle swarm optimization.43 While the detailed updating process of each algorithm is different,37 the two key steps are commonly shared: (1) generating a population consisting of randomly initialized atomic configurations and (2) updating the population after evaluating stability (or/and property) of each configuration existing in the population, using DFT calculations or ML-based methods for an accelerated search. One of the major advantages of EA-based models is their capability to generate completely new materials beyond existing databases and chemical intuitions.
For convex hull optimization, Kruglov et al.44 proposed new stable uranium polyhydrides (UxHy) as potential high-temperature superconductors. Zhu et al.45 systematically investigated the (V,Nb)-(Fe,Ru,Os)-(As,Sb,Bi) family of half-Heusler compounds where 6 compounds were identified as stable and entirely new structures, and 5 of them were experimentally verified as stable with a half-Heusler crystal structure. Multi-objective optimization led to the inverse discovery of new crystal structures with various properties in addition to stability. Zhang et al.46 proposed 24 promising electrides with an optimal degree of interstitial electron localization where 18 candidates were experimentally synthesized that have not been proposed as electrides previously. Xiang et al.47 discovered a cubic Si20 phase, a potential candidate for thin-film solar cells, with a quasi-direct band gap of 1.55 eV. Bedghiou et al.48 discovered new structures of rutile-TiO2 with the lowest direct band gap of 0.26 eV under (ultra)high pressure conditions (i.e. up to 300 GPa) by simultaneously optimizing the stability and band gap during the evolutionary algorithm.
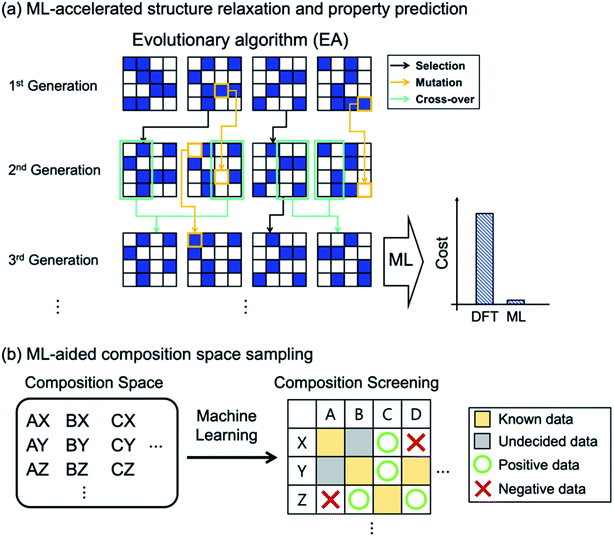
As in HTVS, the large computational cost for property evaluations is a major bottleneck (99% of the entire cost49) in EA (or GO in general) and ML models can greatly help. Of course, the same property prediction ML models or interatomic potentials described in HTVS can also be used in EAs, as shown in Fig. 3a. In specific examples, Jennings et al.50 proposed an ML-based genetic algorithm framework by adapting on-the-fly a Gaussian process regression model to rapidly predict target properties (energy in this case). Here, for PtxAu147−x alloy nanoparticles, the genetic algorithm was shown to reduce the number of configurational visits (or DFT energy calculations) from 1044 (brute force combinatorial possibilities) to 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and with the Gaussian process model described above, the required DFT calculations were further reduced to 300, representing 50-fold reduction in cost due to ML. Avery et al.51 constructed a bulk modulus prediction ML model, trained with the database existing in the Automatic FLOW (AFLOW)52 library, and used it to predict new 43 superhard carbon-phases in their EA-based materials design. Podryabinkin et al.49 used a moment tensor potential-based ML interatomic potential to replace expensive DFT structure relaxations in their crystal structure prediction of carbon and boron allotropes using EAs. The authors were able to find all the main allotropes as well as to find a hitherto unknown 54-atom structure of boron with substantially low cost.
000, and with the Gaussian process model described above, the required DFT calculations were further reduced to 300, representing 50-fold reduction in cost due to ML. Avery et al.51 constructed a bulk modulus prediction ML model, trained with the database existing in the Automatic FLOW (AFLOW)52 library, and used it to predict new 43 superhard carbon-phases in their EA-based materials design. Podryabinkin et al.49 used a moment tensor potential-based ML interatomic potential to replace expensive DFT structure relaxations in their crystal structure prediction of carbon and boron allotropes using EAs. The authors were able to find all the main allotropes as well as to find a hitherto unknown 54-atom structure of boron with substantially low cost.
Since most EA-based methods need a fixed chemical composition as input, one often needs to try many different compositions or requires experts' guess for the initial composition. To address this computational difficulty of searching through a large composition space, the recently proposed ML-based53 and tensor decomposition-based54 chemical composition recommendation models are noteworthy since those models could provide promising unknown chemical compositions from prior knowledge of experimentally reported chemical composition. Furthermore, Halder et al.55 combined the classification ML model with EAs, in which the classification model selected potentially promising compositions that would go into the EA-based crystal structure prediction as shown in Fig. 3b. The authors applied the method to find new magnetic double perovskites (DPs). They first used the random forest to select elemental compositions in A2BB′O6 (A = Ca/Sr/Ba, B/B′ = transition metals) as potentially stable DPs (finding 33 compounds out of 412 unexplored compositions), and using EA and DFT calculations they subsequently identified new 21 DPs with various magnetic and electronic properties.
2.3 Generative models (GM)
The generative model is an unsupervised learning that encodes the high-dimensional materials chemical space into the continuous vector space (or latent space) of low dimension, and generates new data using knowledge embedded in the latent space.3 However, unlike molecular generative models, there are only a few examples on crystal structure generative models due to the following difficulties: (1) invertibility of representations for periodic crystal structures, (2) symmetry invariance for translation, rotation, and unit cell repeat, and (3) low structural diversity (data) per element of inorganic crystal structures compared to the molecular chemical space. The first two issues (invertibility and invariance) correspond to the characteristics of representations (see Table 1) while the third (chemical diversity) is related to the data used for training.We first note that for organic molecules there are several string-based molecular representations that are symmetry-invariant and invertible as in SMILES63 and SELFIES,64 for which many language-based ML models such as RNN,65 Seq2Seq,66 and attention-based Transformer model67 can be applied.21,98 Furthermore, graph representation is another popular approach for organic molecules since chemical bonds between atoms in molecules can be explicitly defined and this can allow an inverse mapping from graph to molecular structure. Various implicit and explicit GMs68–70 have been proposed by adopting a graph convolutional network for organic molecules.71 However, in the case of crystal structures, currently there is no explicit rule to convert crystal structures into string-based representations, or vice versa. Although graph representation has been proposed with great success on property predictions, there is currently no explicit formulation on decoding the crystal graph back to the 3D crystal structure.
A low structural diversity (or data) per element for the inorganic crystal structure database is another critical bottleneck in establishing GMs (or in fact any ML models) for inorganic solids compared to organic molecules (see Fig. 4). This is because, for organic molecules, only a small number of main group elements can produce an enormous degree of chemical and structural diversity, but for inorganic crystals, the degree of structural diversity per chemical element is relatively low and not well balanced compared to molecules (for example, there are 2506 materials having ICSD-ids in MP that contain iron, but only 760 materials that contain scandium). This low structural diversity could bias the model during the training, and it may not able to generate so meaningful and very different new structures from existing materials. This makes a universal GM for inorganic crystals that covers the entire periodic table quite challenging.
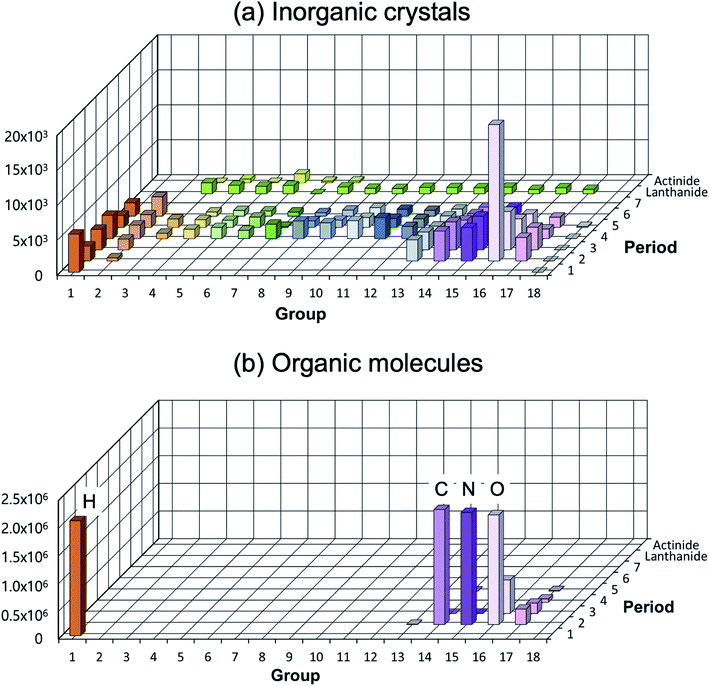 | ||
Fig. 4 Distribution of elements existing in the crystal/molecular database. (a) Experimentally reported inorganic materials (# of data = 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 567) taken from MP.10 They cover most elements in the periodic table (high elemental diversity), but the number of data per element is sparsely populated (low structural diversity). (b) Organic molecules taken from the subset of the ZINC database (# of data = 2 567) taken from MP.10 They cover most elements in the periodic table (high elemental diversity), but the number of data per element is sparsely populated (low structural diversity). (b) Organic molecules taken from the subset of the ZINC database (# of data = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 077 077![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 407).72 They cover very limited elements (low elemental diversity), but are densely populated (high structural diversity). 407).72 They cover very limited elements (low elemental diversity), but are densely populated (high structural diversity). | ||
Despite these challenges, there are some promising initial results for inorganic crystal generative models that addressed some of the aforementioned difficulties. Two concepts of GMs have been implemented for solid state materials recently (see Fig. 5a and b): variational autoencoder (VAE)73 and generative adversarial network (GAN).74 Here, we note that other generative frameworks (e.g. conditional VAE75/GAN,76 AAE,77 VAE-GAN,78etc.) derived from the latter two models can be applied depending on target objectives. VAE explicitly regularizes the latent space using known prior distributions such as Gaussian and Bernoulli distribution. Compared to VAE, the GAN implicitly learns the data distribution by iteratively checking the reality of the generated data from the known prior latent space distribution.
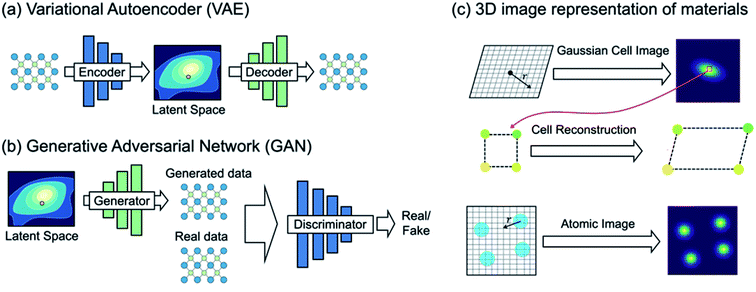 | ||
| Fig. 5 (a) Variational autoencoder (VAE) learns materials chemical space under the density reconstruction scheme by explicitly constructing the latent space. Each point in the latent space represents a single material, and thus one can directly generate new materials with optimal functionality. (b) Generative adversarial network (GAN), however, learns materials chemical space under the implicit density prediction scheme which iteratively discriminates the reality of the data generated from the latent space. (c) A VAE-based crystal generative framework proposed by Noh et al.59 using an invertible 3D image representation for the unit cell and basis (adapted with permission from ref. 59 Copyright 2019 Elsevier Inc. Matter). | ||
Noh et al.59 proposed the first GM for inorganic solid-state materials structures using a 3D atomic image representation (Fig. 5c). Here, the stability-embedded latent space was constructed under the VAE scheme,73 and used to generate stable vanadium oxide crystal structures. In particular, due to a low structural diversity of the current inorganic dataset described above, the authors used the virtual V–O binary compound space as a restricted materials space to explore (instead of learning the crystal chemistry across the periodic table). This image-based GM then discovered several new compositions and meta-stable polymorphs of vanadium oxides that have been completely unknown. Hoffmann et al.79 proposed a general purpose encoding-decoding framework for 3D atomic density under the VAE formalism. The model was trained with atomic configurations taken from crystal structures reported in the ICSD16,17 (which does not impose a constraint in chemical composition), and an additional segmentation network80 was used to classify the elements information from the generated 3D representation. However, we note that the proposed model is focused on generating valid atomic configurations only, and thus an additional network which generates a unit cell associated with the generated atomic configuration would be required to generate new ‘materials’.
Despite those promising results, 3D image-based representations have a few limitations, a lack of invariance under symmetry operations and heuristic post-processing to clean up chemical bonds, for example. The former drawback can be approximately addressed by data augmentation,60 and for example, Kajita et al.81 showed that 3D representations with data augmentation yielded a reasonable prediction of the various electronic properties of 680 oxide materials. For the latter problem, a representation which does not require heuristic post-processing would be desirable.
Rather than using computationally burdensome 3D representations, Nouira et al.62 proposed to use unit cell vectors and fractional coordinates as input to generate new ternary hydride structures by learning the structures of binary hydrides inspired by a cross-domain learning strategy. Kim et al.36 proposed a GAN-based generative framework which uses a similar coordinate-based representation with symmetry invariance addressed with data augmentation and permutation invariance with symmetry operation as described in PointNet,82 and used it to generate new ternary Mg–Mn–O compounds suitable for photoanode applications. There are also examples in which generative frameworks are used to sample new chemical compositions for inorganic solid materials.83,84 For these studies, adding concrete structural information would be a desirable further development, similar to the work of Halder et al.,55 which also highlights the importance of invertible representations in GMs to predict crystal structures.
We note that, while GMs themselves offer essential architectures needed to inversely design materials with target properties by navigating the functional latent space, many of the present examples shown above currently deal with generating new stable structures, and one still needs to incorporate properties into the model for a practical inverse design beyond stability embedding. One can use conditional GMs in which the target function is used as a condition,68,85 or perform the optimization task on a continuous latent space as described in Gómez-Bombarelli et al.21 for organic molecules. For example, Dong et al.61 used a generative model to design graphene/boron nitride mixed lattice structures with the appropriate bandgap by adding a regression network within the GAN in combination with the simple lattice site representation. A similar crystal site-based representation20 which satisfies both invertibility and invariance (Table 1) can be used to generate new elemental combinations for the fixed structure template. Also Kim et al.60 used an image-based GAN model to inversely design zeolites with user-defined gas-adsorption properties by adding a penalty function that guides the target properties. Furthermore, Bhowmik et al.86 provided a perspective on using a generative model for inverse design of complex battery interphases, and suggested that utilizing data taken from multiple domains (i.e. simulations and experiments) would be critical for the development of rationale generative models to enable accelerated discovery of durable ultra-high performance batteries.
3 Challenges and opportunities
Inorganic inverse design is an important key strategy to accelerate the discovery of novel inorganic functional materials, and various initial approaches have shown great promise as briefly summarized in the previous sections. To be used in more practical applications, there are several ongoing challenges. The grand challenge of inverse design is physical realization of newly predicted materials (i.e. reducing the gap between theory and experiment),2 and the importance of developing an experimental feedback loop for newly discovered materials cannot be overemphasized. From the materials acceleration point of view, as mentioned in several previous reviews,2,3,87 an experimental feedback loop can be significantly enhanced by robotic synthesis and characterization followed by AI making decisions for next experiments using Baysian optimization.88–91 P. Nikolaev et al.91 proposed an autonomous research system (ARES) which integrates autonomous robotics, artificial intelligence, data science (i.e. random forest model and genetic algorithm) and high-throughput/in situ techniques, and demonstrated its effectiveness for the case of carbon nanotube growth. More recently, MacLeod et al.92 demonstrated a modular self-driving laboratory capable of autonomously synthesizing, processing, and characterizing organic thin films that maximize the hole mobility of organic hole transport materials for solar cell applications. These studies clearly show that the closed-loop approach can give unprecedented extension of our understanding and toolkits for novel materials discovery in an accelerated and automated fashion.Another important missing ingredient is the lack of a model for synthesizability prediction for crystals. The screening and/or generation of hypothetical crystals produces a large number of promising candidates, but a significant number of them are not observed via experiments. Currently, hull energies (i.e. relative energy deviation from the ground state) are mostly used to evaluate the thermodynamic stability of crystals not because they are sufficient to predict synthesizability but mainly because they are simple quantities easily computable, but they are certainly insufficient to describe the complex phenomena of synthesizability of hypothetical materials.93 Developing a reliable model or a descriptor for synthesizability prediction is thus an urgent and essential area for accelerated inverse design of inorganic solid-state materials.
In the case of GMs, as mentioned in the ‘Generative models’ section, developing an invertible and invariant model is still of great challenge since there is currently no explicit approach that simultaneously satisfies the latter two conditions. There are several promising data-driven approaches along this direction. Thomas et al.94 proposed deep tensor field networks which have equivariance (i.e. generalized concept of invariance)95 under rotational and translational transformation for 3D point clouds. A recently proposed deep learning model, AlphaFold,96 predicting 3D protein structures from Euclidean distance geometry is also noteworthy since the distance between two atoms is an invariant quantity. Developing such invariant models and/or incorporating invariant features into 3D structures would thus be invaluable to develop more robust GMs for crystals.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We acknowledge generous financial support from NRF Korea (NRF-2017R1A2B3010176).References
- K. Alberi, M. B. Nardelli, A. Zakutayev, L. Mitas, S. Curtarolo, A. Jain, M. Fornari, N. Marzari, I. Takeuchi and M. L. Green, J. Phys. D: Appl. Phys., 2018, 52, 013001 CrossRef PubMed.
- A. Zunger, Nat. Chem., 2018, 2, 0121 CrossRef CAS.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- D. C. Elton, Z. Boukouvalas, M. D. Fuge and P. W. Chung, Mol. Syst. Des. Eng., 2019, 4, 828–849 RSC.
- K. T. Butler, J. M. Frost, J. M. Skelton, K. L. Svane and A. Walsh, Chem. Soc. Rev., 2016, 45, 6138–6146 RSC.
- E. O. Pyzer-Knapp, C. Suh, R. Gómez-Bombarelli, J. Aguilera-Iparraguirre and A. Aspuru-Guzik, Annu. Rev. Mater. Res., 2015, 45, 195–216 CrossRef CAS.
- A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227–237 CrossRef CAS PubMed.
- A. Ludwig, npj Comput. Mater., 2019, 5, 70 CrossRef.
- A. D. Sendek, Q. Yang, E. D. Cubuk, K.-A. N. Duerloo, Y. Cui and E. J. Reed, Energy Environ. Sci., 2017, 10, 306–320 RSC.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, APL Mater., 2013, 1, 011002 CrossRef.
- A. K. Singh, J. H. Montoya, J. M. Gregoire and K. A. Persson, Nat. Commun., 2019, 10, 1–9 CrossRef PubMed.
- J. Noh, S. Kim, G. ho Gu, A. Shinde, L. Zhou, J. M. Gregoire and Y. Jung, Chem. Commun., 2019, 55, 13418–13421 RSC.
- G. Hautier, C. C. Fischer, A. Jain, T. Mueller and G. Ceder, Chem. Mater., 2010, 22, 3762–3767 CrossRef CAS.
- K. Ryan, J. Lengyel and M. Shatruk, J. Am. Chem. Soc., 2018, 140, 10158–10168 CrossRef.
- W. Sun, C. J. Bartel, E. Arca, S. R. Bauers, B. Matthews, B. Orvañanos, B.-R. Chen, M. F. Toney, L. T. Schelhas, W. Tumas, J. Tate, A. Zakutayev, S. Lany, A. M. Holder and G. Ceder, Nat. Mater., 2019, 18, 732–739 CrossRef CAS PubMed.
- A. Belsky, M. Hellenbrandt, V. L. Karen and P. Luksch, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 364–369 CrossRef PubMed.
- R. Allmann and R. Hinek, Acta Crystallogr., Sect. A: Found. Crystallogr., 2007, 63, 412–417 CrossRef CAS PubMed.
- I. Tanaka, Nanoinformatics, Springer, 2018 Search PubMed.
- J. Schmidt, M. R. Marques, S. Botti and M. A. Marques, npj Comput. Mater., 2019, 5, 1–36 CrossRef.
- F. A. Faber, A. Lindmaa, O. A. Von Lilienfeld and R. Armiento, Phys. Rev. Lett., 2016, 117, 135502 CrossRef PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- B. Meredig, A. Agrawal, S. Kirklin, J. E. Saal, J. Doak, A. Thompson, K. Zhang, A. Choudhary and C. Wolverton, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094104 CrossRef.
- A. Seko, H. Hayashi, K. Nakayama, A. Takahashi and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 144110 CrossRef.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- C. W. Park and C. Wolverton, 2019, arXiv preprint arXiv:1906.05267.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- J. Lym, G. H. Gu, Y. Jung and D. G. Vlachos, J. Phys. Chem. C, 2019, 123, 18951–18959 CrossRef CAS.
- E. D. Cubuk, A. D. Sendek and E. J. Reed, J. Chem. Phys., 2019, 150, 214701 CrossRef PubMed.
- M. H. Segler, T. Kogej, C. Tyrchan and M. P. Waller, ACS Cent. Sci., 2018, 4, 120–131 CrossRef CAS PubMed.
- H. Altae-Tran, B. Ramsundar, A. S. Pappu and V. Pande, ACS Cent. Sci., 2017, 3, 283–293 CrossRef CAS PubMed.
- B. Sánchez-Lengeling and A. Aspuru-Guzik, ACS Cent. Sci., 2017, 3, 275–277 CrossRef PubMed.
- T. Mueller, A. Hernandez and C. Wang, J. Chem. Phys., 2020, 152, 050902 CrossRef PubMed.
- V. L. Deringer, M. A. Caro and G. Csányi, Adv. Mater., 2019, 31, 1902765 CrossRef CAS PubMed.
- Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. r. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson and M. A. Wood, J. Phys. Chem. A, 2020, 124, 731–745 CrossRef CAS PubMed.
- J. Noh, G. H. Gu, S. Kim and Y. Jung, J. Chem. Inf. Model., 2020 DOI:10.1021/acs.jcim.0c00003.
- S. Kim, J. Noh, G. H. Gu, A. Aspuru-Guzik and Y. Jung, 2020, arXiv:2004.01396.
- A. R. Oganov, C. J. Pickard, Q. Zhu and R. J. Needs, Nat. Rev. Mater., 2019, 4, 331–348 CrossRef.
- A. Franceschetti and A. Zunger, Nature, 1999, 402, 60 CrossRef CAS.
- K. Doll, J. Schön and M. Jansen, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 144110 CrossRef.
- M. Amsler and S. Goedecker, J. Chem. Phys., 2010, 133, 224104 CrossRef PubMed.
- F.-L. José, J. Phys.: Condens. Matter, 2020 DOI:10.1088/1361-648X/ab7e54.
- C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720 CrossRef CAS.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- I. A. Kruglov, A. G. Kvashnin, A. F. Goncharov, A. R. Oganov, S. S. Lobanov, N. Holtgrewe, S. Jiang, V. B. Prakapenka, E. Greenberg and A. V. Yanilkin, Sci. Adv., 2018, 4, eaat9776 CrossRef CAS PubMed.
- H. Zhu, J. Mao, Y. Li, J. Sun, Y. Wang, Q. Zhu, G. Li, Q. Song, J. Zhou and Y. Fu, Nat. Commun., 2019, 10, 270 CrossRef PubMed.
- Y. Zhang, H. Wang, Y. Wang, L. Zhang and Y. Ma, Phys. Rev. X, 2017, 7, 011017 Search PubMed.
- H. Xiang, B. Huang, E. Kan, S.-H. Wei and X. Gong, Phys. Rev. Lett., 2013, 110, 118702 CrossRef CAS PubMed.
- D. Bedghiou, F. H. Reguig and A. Boumaza, Comput. Mater. Sci., 2019, 166, 303–310 CrossRef CAS.
- E. V. Podryabinkin, E. V. Tikhonov, A. V. Shapeev and A. R. Oganov, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 99, 064114 CrossRef CAS.
- P. C. Jennings, S. Lysgaard, J. S. Hummelshøj, T. Vegge and T. Bligaard, npj Comput. Mater., 2019, 5, 1–6 CrossRef.
- P. Avery, X. Wang, C. Oses, E. Gossett, D. M. Proserpio, C. Toher, S. Curtarolo and E. Zurek, npj Comput. Mater., 2019, 5, 1–11 CrossRef.
- S. Curtarolo, W. Setyawan, G. L. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang and O. Levy, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- A. Seko, H. Hayashi and I. Tanaka, J. Chem. Phys., 2018, 148, 241719 CrossRef PubMed.
- A. Seko, H. Hayashi, H. Kashima and I. Tanaka, Phys. Rev. Mater., 2018, 2, 013805 CrossRef CAS.
- A. Halder, A. Ghosh and T. S. Dasgupta, Phys. Rev. Mater., 2019, 3, 084418 CrossRef CAS.
- A. Seko, T. Maekawa, K. Tsuda and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 054303 CrossRef.
- A. Mansouri Tehrani, A. O. Oliynyk, M. Parry, Z. Rizvi, S. Couper, F. Lin, L. Miyagi, T. D. Sparks and J. Brgoch, J. Am. Chem. Soc., 2018, 140, 9844–9853 CrossRef CAS PubMed.
- K. Kim, L. Ward, J. He, A. Krishna, A. Agrawal and C. Wolverton, Phys. Rev. Mater., 2018, 2, 123801 CrossRef CAS.
- J. Noh, J. Kim, H. S. Stein, B. Sanchez-Lengeling, J. M. Gregoire, A. Aspuru-Guzik and Y. Jung, Matter, 2019, 1, 1370–1384 CrossRef.
- B. Kim, S. Lee and J. Kim, Sci. Adv., 2020, 6, eaax9324 CrossRef PubMed.
- Y. Dong, D. Li, C. Zhang, C. Wu, H. Wang, M. Xin, J. Cheng and J. Lin, 2019, arXiv preprint arXiv:1908.07959.
- A. Nouira, N. Sokolovska and J.-C. Crivello, 2018, arXiv preprint arXiv:1810.11203.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- M. Krenn, F. Häse, A. Nigam, P. Friederich and A. Aspuru-Guzik, 2019, arXiv preprint arXiv:1905.13741.
- Y. Bengio, P. Simard and P. Frasconi, IEEE Trans. Neural Netw., 1994, 5, 157–166 CAS.
- I. Sutskever, O. Vinyals and Q. V. Le, presented in part at the Advances in neural information processing systems, 2014 Search PubMed.
- A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, presented in part at the Advances in neural information processing systems, 2017 Search PubMed.
- Y. Li, L. Zhang and Z. Liu, J. Cheminf., 2018, 10, 33 Search PubMed.
- N. De Cao and T. Kipf, 2018, arXiv preprint arXiv:1805.11973.
- D. Flam-Shepherd, T. Wu and A. Aspuru-Guzik, 2020, arXiv preprint arXiv:2002.07087.
- F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner and G. Monfardini, IEEE Trans. Neural Netw., 2008, 20, 61–80 Search PubMed.
- J. J. Irwin and B. K. Shoichet, J. Chem. Inf. Model., 2005, 45, 177–182 CrossRef CAS PubMed.
- D. P. Kingma and M. Welling, 2013, arXiv preprint arXiv:1312.6114.
- I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. Bengio, presented in part at the Advances in neural information processing systems, 2014 Search PubMed.
- K. Sohn, H. Lee and X. Yan, presented in part at the Advances in neural information processing systems, 2015 Search PubMed.
- M. Mirza and S. Osindero, 2014, arXiv preprint arXiv:1411.1784.
- A. Makhzani, J. Shlens, N. Jaitly, I. Goodfellow and B. Frey, 2015, arXiv preprint arXiv:1511.05644.
- A. B. L. Larsen, S. K. Sønderby, H. Larochelle and O. Winther, 2015, arXiv preprint arXiv:1512.09300.
- J. Hoffmann, L. Maestrati, Y. Sawada, J. Tang, J. M. Sellier and Y. Bengio, 2019, arXiv preprint arXiv:1909.00949.
- Ö. Çiçek, A. Abdulkadir, S. S. Lienkamp, T. Brox and O. Ronneberger, presented in part at the Medical Image Computing and Computer-Assisted Intervention, Cham, 2016 Search PubMed.
- S. Kajita, N. Ohba, R. Jinnouchi and R. Asahi, Sci. Rep., 2017, 7, 16991 CrossRef PubMed.
- C. R. Qi, H. Su, K. Mo and L. J. Guibas, presented in part at the Proceedings of the IEEE conference on computer vision and pattern recognition, 2017 Search PubMed.
- Y. Sawada, K. Morikawa and M. Fujii, 2019, arXiv preprint arXiv:1910.11499.
- Y. Dan, Y. Zhao, X. Li, S. Li, M. Hu and J. Hu, 2019, arXiv preprint arXiv:1911.05020.
- S. Kang and K. Cho, J. Chem. Inf. Model., 2018, 59, 43–52 CrossRef PubMed.
- A. Bhowmik, I. E. Castelli, J. M. Garcia-Lastra, P. B. Jørgensen, O. Winther and T. Vegge, Energy Storage Mater., 2019, 21, 446–456 CrossRef.
- G. H. Gu, J. Noh, I. Kim and Y. Jung, J. Mater. Chem. A, 2019, 7, 17096–17117 RSC.
- P. S. Gromski, J. M. Granda and L. Cronin, Trends Chem., 2019, 2, 4–12 CrossRef.
- F. Häse, L. M. Roch and A. Aspuru-Guzik, Trends Chem., 2019, 1, 282–291 CrossRef.
- L. M. Roch, F. Häse, C. Kreisbeck, T. Tamayo-Mendoza, L. P. Yunker, J. E. Hein and A. Aspuru-Guzik, Sci. Robot., 2018, 3, eaat5559 CrossRef.
- P. Nikolaev, D. Hooper, F. Webber, R. Rao, K. Decker, M. Krein, J. Poleski, R. Barto and B. Maruyama, npj Comput. Mater., 2016, 2, 16031 CrossRef.
- B. P. MacLeod, F. G. Parlane, T. D. Morrissey, F. Häse, L. M. Roch, K. E. Dettelbach, R. Moreira, L. P. Yunker, M. B. Rooney and J. R. Deeth, 2019, arXiv preprint arXiv:1906.05398.
- W. Sun, S. T. Dacek, S. P. Ong, G. Hautier, A. Jain, W. D. Richards, A. C. Gamst, K. A. Persson and G. Ceder, Sci. Adv., 2016, 2, e1600225 CrossRef PubMed.
- N. Thomas, T. Smidt, S. Kearnes, L. Yang, L. Li, K. Kohlhoff and P. Riley, 2018, arXiv preprint arXiv:1802.08219.
- D. Worrall and G. Brostow, presented in part at the Proceedings of the European Conference on Computer Vision (ECCV), 2018 Search PubMed.
- A. W. Senior, R. Evans, J. Jumper, J. Kirkpatrick, L. Sifre, T. Green, C. Qin, A. Žídek, A. W. Nelson and A. Bridgland, Nature, 2020, 1–5 Search PubMed.
- C. J. Pickard and R. J. Needs, Phys. Rev. Lett., 2006, 97, 045504 CrossRef PubMed.
- D. Grechishnikova, bioRxiv 863415, DOI:10.1101/863415.
| This journal is © The Royal Society of Chemistry 2020 |