Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evaluation of bismuth-based dispersion energy donors – synthesis, structure and theoretical study of 2-biphenylbismuth(III) derivatives†
Ana-Maria
Fritzsche
ab,
Sebastian
Scholz
a,
Małgorzata
Krasowska
c,
Kalishankar
Bhattacharyya
 c,
Ana Maria
Toma
ad,
Cristian
Silvestru
d,
Marcus
Korb
c,
Ana Maria
Toma
ad,
Cristian
Silvestru
d,
Marcus
Korb
 ef,
Tobias
Rüffer
ef,
Tobias
Rüffer
 e,
Heinrich
Lang
e,
Heinrich
Lang
 be,
Alexander A.
Auer
be,
Alexander A.
Auer
 *c and
Michael
Mehring
*c and
Michael
Mehring
 *ab
*ab
aTechnische Universität Chemnitz, Fakultät für Naturwissenschaften, Institut für Chemie, Professur Koordinationschemie, 09107 Chemnitz, Germany. E-mail: michael.mehring@chemie.tu-chemnitz.de
bCenter for Materials, Architectures and Integration of Nanomembranes (MAIN), Rosenbergstr. 6, 09126 Chemnitz, Germany
cMax-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Ruhr, Germany. E-mail: alexander.auer@kofo.mpg.de
dBabeş-Bolyai University, Faculty of Chemistry and Chemical Engineering, Department of Chemistry, Supramolecular Organic and Organometallic Chemistry Centre (SOOMCC), 11 Arany Janos, 400028 Cluj-Napoca, Romania
eTechnische Universität Chemnitz, Fakultät für Naturwissenschaften, Institut für Chemie, Professur Anorganische Chemie, 09107 Chemnitz, Germany
fThe University of Western Australia, Faculty of Science, School of Molecular Sciences, Crawley, Perth, WA 6009, Australia
First published on 20th April 2020
Abstract
A series of 2-biphenyl bismuth(III) compounds of the type (2-PhC6H4)3−nBiXn [n = 0 (1); n = 1, X = Cl (2), Br (3), I (4), Me (5); n = 2, X = Cl (6), Br (7), I (8)] has been synthesized and analyzed with focus on intramolecular London dispersion interactions. The library of the compounds was set up in order to investigate the Bi⋯π arene interaction by systematic variation of X. The structural analysis in the solid state revealed that the triarylbismuth(III) compound 1 shows an encapsulation of the metal atom but the distances between the bismuth atom and the phenyl centroids amount to values close to or larger than 4.0 Å, which is considered to be a rather week dispersion interaction. In the case of monomeric diorganobismuth(III) compounds 2–5 the moderate crowding effectively hinders the formation of intermolecular donor–acceptor interactions, but allows for intramolecular dispersion-type interactions with the 2-biphenyl ligand. In contrast, the structures of the monoorganobismuth compounds 6–8 show the formation of Bi–X⋯Bi donor–acceptor bonds leading to the formation of 1D ribbons in the solid state. These coordination bonds are accompanied by intermolecular dispersion interactions with Bi⋯Phcentroid distances <![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4.0 Å. In solution the diorganobismuth(III) halides 2–4 show a broadening of their NMR signals (H-8, H-8′ and H-9, H-9′ protons of the 2-biphenyl ligand), which is a result of dynamic processes including ligand rotation. For further elucidation of these processes compounds 2, 4 and 7 were studied by temperature-dependent NMR spectroscopy. Electronic structure calculations at the density functional theory and DLPNO-coupled cluster level of theory were applied to investigate and quantify the intramolecular London dispersion interactions, in an attempt to distinguish between basic intramolecular interactions and packing effects and to shed light on the dynamic behavior in solution.
4.0 Å. In solution the diorganobismuth(III) halides 2–4 show a broadening of their NMR signals (H-8, H-8′ and H-9, H-9′ protons of the 2-biphenyl ligand), which is a result of dynamic processes including ligand rotation. For further elucidation of these processes compounds 2, 4 and 7 were studied by temperature-dependent NMR spectroscopy. Electronic structure calculations at the density functional theory and DLPNO-coupled cluster level of theory were applied to investigate and quantify the intramolecular London dispersion interactions, in an attempt to distinguish between basic intramolecular interactions and packing effects and to shed light on the dynamic behavior in solution.
Introduction
Over the past several years, London dispersion interaction of main group elements has witnessed increasing interest both experimentally1–9 and theoretically,10–16 and was demonstrated to be relevant in the field of organometallic chemistry with regard to structure and properties even of small molecules. In recent reports it is discussed that weak dispersion interactions of the type metal⋯π arene contribute significantly to the assembling processes of molecular units in supramolecular structures, which might open up new directions of dynamic structural evolution of supramolecular architectures.6–8 With regard to this and to build up a better understanding of the basic principles intermolecular, London dispersion interactions for diverse arylbismuth compounds have been studied in our research groups,16–22 and the effect on polymorphism and phase transition in compounds of the type Ar3Bi (Ar = C4H3NMe, C4H3O, C4H3S, C4H3Se) was demonstrated.18,21 In the last years, the importance of intramolecular Bi⋯π arene interactions for the stabilisation of unusual organobismuth compounds, mainly bearing ligands of the terphenyl type, has been demonstrated by several other research groups (Scheme 1).23–32 Although it is now well accepted that dispersion interaction plays an important role in structure formation, there is still need for systematic investigations in order to determine the influence of e.g. the ligands X in organobismuth(III) compounds of the type Ar3−nBiXn (n = 0, 1, 2). A future aim is to make use of this type of interaction in supramolecular design strategies controlled by the strength and nature of the interaction of aryl ligands with bismuth and other heavy metals.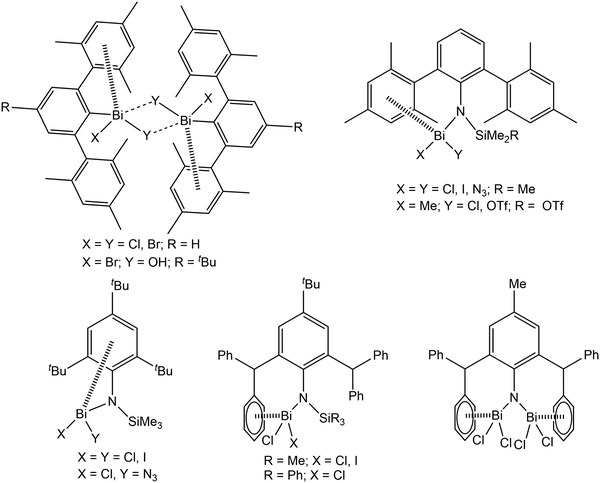 | ||
| Scheme 1 Selected molecules showing intramolecular Bi⋯π arene interactions with significant impact on structure and reactivity.24,27–32 | ||
To reach this goal theoretical work is necessary in addition to experimental studies. So far, computational studies on pnictogen⋯π arene interactions address mainly intermolecular interactions,13,16,20,21,33 whereas only a limited number of studies on intramolecular interactions of this type is reported.25,29,32 For example, intermolecular pnictogen⋯π arene interaction were investigated earlier using computational methods (BP86-D3/def2-TZVPD level of theory) by Frontera and coworkers on a series of systems involving different types of benzene derivatives and the heavier pnictogenes ECl3 (E = As, Sb, Bi).14,15 In a more recent paper we have investigated the intermolecular interaction between various compounds of the type BiX3 (X = H, Me, Ph, OH, OMe, F, Cl, Br) and C6H6 (Scheme 2, A). These studies have shown that the nature and strength of the dispersion interaction is strongly influenced by the ligand X.16,20 The higher the bismuth is polarized by X, the stronger is the interaction and the shorter is the Bi⋯Phcentroid distance. The calculations revealed a pure dispersive interaction for the methyl group, while the chlorine induces a significant donor–acceptor behaviour. This interplay between dispersion and donor–acceptor properties results from the (π → σ*) charge transfer. Another study was focused on the As, Sb and Bi adducts EX3⋯C6H6 (X = Me, OMe, Cl) (Scheme 2, B) and it was analysed how the dispersion interaction strength is altered by exchanging the pnictogen E. The interaction energies calculated at the DLPNO-CCSD(T) level increase from As < Sb < Bi and range from −10 kJ mol−1 to −40 kJ mol−1 for ECl3⋯C6H6 (E = As, Sb, Bi).34 In a recent paper we have also discussed the interaction between BiCl3 and benzene derivatives with either one or three substituents being R = CF3, NO2, NH2, OH, OCH(O) (Scheme 2, C). The results show that the substituents of the arene have a significant influence on the interaction strength and structure of the formed adducts (e.g. BiCl3⋯C6H5R) and especially substituents that increase the electron density in the aromatic ring increase the strength of the donor–acceptor interaction and vice versa.35 The overall interaction energy might transcend −70 kJ mol−1 in compounds of the type BiCl3⋯C6H3R3.
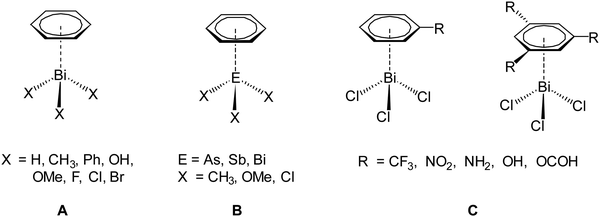 | ||
| Scheme 2 Different dispersion adducts of aromatic systems with trivalent heavy pnictogen compounds (EX3).16,20,34,35 | ||
On the basis of our previous studies here the synthesis, characterization and the crystal structures of the arylbismuth(III) compounds (2-PhC6H4)3−nBiXn [n = 0 (1); n = 1, X = Cl (2), Br (3), I (4), Me (5); n = 2, X = Cl (6), Br (7), I (8)] are reported (Scheme 3). They are composed of bismuth acting as DED (Dispersion Energy Donor) and 2-biphenyl as a rigid intramolecular ligand. The influence of the ligand X on the strength of the intramolecular bismuth⋯π arene interaction was analysed experimentally and by using electronic structure calculations.
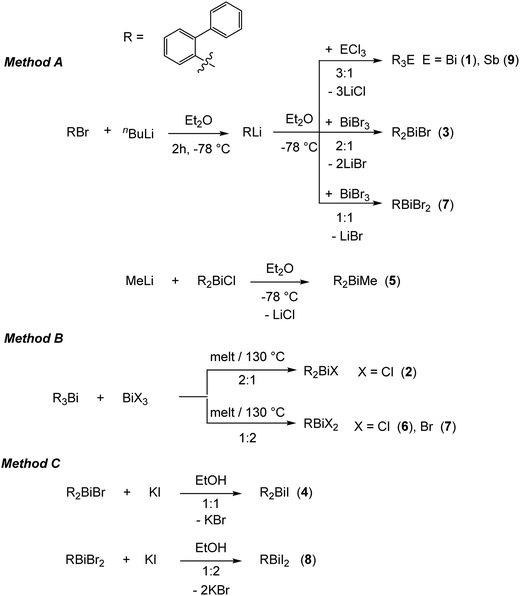 | ||
| Scheme 3 Synthetic routes for the preparation of the organobismuth(III) compounds (2-PhC6H4)3−nBiXn (1–8) and (2-PhC6H4)3Sb (9). | ||
Results and discussion
Synthesis
The first report on the synthesis of (2-PhC6H4)3Bi dates back to 1936, based on the reaction of the Grignard reagent 2-PhC6H4MgBr and BiCl3.36 Later on, the synthesis of the related derivatives of the lighter pnictogens, i.e. (2-PhC6H4)3E (E = P, As and Sb) using the Wurtz–Fittig method, employing sodium was reported.37 However, neither the determination of the crystal structures of these compounds nor of their halogen derivatives was published so far.The compounds reported herein of the type (2-PhC6H4)3−nBiXn [n = 0; (1); n = 1, X = Cl (2), Br (3), Me (5); n = 2, X = Cl (6), Br (7)] were prepared either via (i) salt elimination reactions between 2-biphenyllithium and BiX3 (X = Cl, Br), (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 2
1, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio), or methyllithium and (2-PhC6H4)2BiCl in Et2O solution, at −78 °C (Method A, Scheme 3), or (ii) solvent-free redistribution reactions between (2-PhC6H4)3Bi and BiX3 (1
1 molar ratio), or methyllithium and (2-PhC6H4)2BiCl in Et2O solution, at −78 °C (Method A, Scheme 3), or (ii) solvent-free redistribution reactions between (2-PhC6H4)3Bi and BiX3 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio) carried out at 130 °C (Method B, Scheme 3). The compounds were isolated as colorless crystalline solids in moderate to good yields. Treatment of the organobismuth(III) bromides in EtOH with KI gave, via halogen exchange reactions (Method C, Scheme 3), the iodides (2-PhC6H4)2BiI (4) and (2-PhC6H4)BiI2 (8) as yellow and orange solids in good yields. The compound (2-PhC6H4)3Sb (9) was prepared using the same synthetic procedure as described for 1 and was obtained as a colorless solid (Scheme 3). The compounds 1–9 are soluble in common organic solvents, but the bismuth compounds are air and heat sensitive. In solution and in the solid state the compounds slowly decompose and hence must be stored under inert conditions. The stability of the organobismuth(III) halides was analysed by time dependent 1H NMR spectroscopy (see ESI,† Fig. S1 and S2). The compounds decompose in the course of five to six days via redistribution reactions finally leading to the formation of biphenyl.
2 molar ratio) carried out at 130 °C (Method B, Scheme 3). The compounds were isolated as colorless crystalline solids in moderate to good yields. Treatment of the organobismuth(III) bromides in EtOH with KI gave, via halogen exchange reactions (Method C, Scheme 3), the iodides (2-PhC6H4)2BiI (4) and (2-PhC6H4)BiI2 (8) as yellow and orange solids in good yields. The compound (2-PhC6H4)3Sb (9) was prepared using the same synthetic procedure as described for 1 and was obtained as a colorless solid (Scheme 3). The compounds 1–9 are soluble in common organic solvents, but the bismuth compounds are air and heat sensitive. In solution and in the solid state the compounds slowly decompose and hence must be stored under inert conditions. The stability of the organobismuth(III) halides was analysed by time dependent 1H NMR spectroscopy (see ESI,† Fig. S1 and S2). The compounds decompose in the course of five to six days via redistribution reactions finally leading to the formation of biphenyl.
Molecular structures of the triarylpnictogen(III) compounds 1 and 9
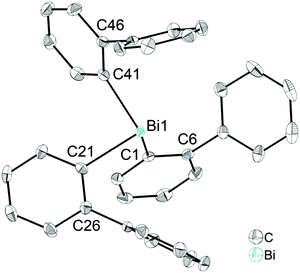
Single crystals suitable for X-ray diffraction analysis of 1 were grown from a n-hexane solution and the molecular structure is illustrated in Fig. 1. Selected bond lengths and angles are listed in the figure caption and the crystallographic data are given in Table S1 (ESI†). Compound 1 crystallizes in the monoclinic space group P21/n and is isomorphous with (2-PhC6H4)3Sb (9) (see the ESI,† Fig. S3). A detailed discussion of the crystal structure of 9 is presented in the ESI.† The molecular structure of 1 shows a trigonal pyramidal geometry at the metal atom with average C–E–C bond angles of 94.6° for 1. The average values of the Bi–C bond lengths of 2.261 Å are within the ranges reported for other arylbismuthine derivatives, i.e. Ph3Bi,20,38,39 Mes3Bi40 and (p-tolyl)3Bi.41Compound 1 shows an encapsulation of the bismuth atom by the 2-biphenyl ligands (Bi⋯Phcentroid: 3.99 Å, 4.04 Å and 4.06 Å), however, the Bi⋯Phcentroid distances are found close to 4.0 Å, which can be considered as the limit of significant London dispersion interaction for these systems based on previous theoretical work.35 However, the structure of 1 revealed 1D ribbon-like structures (Fig. S4(i), ESI†) which are formed via C–H⋯Phcentroid intermolecular contacts with a distance of C24–H24⋯Phcentroid 2.55 Å and an angle γ = 5.6° between the ring normal and the vector between the ring centroid and the hydrogen atom. The 1D ribbons are further connected via the C–H⋯Ph intermolecular contacts C43–H43⋯Phcentroid 3.06 Å (γ = 10.3°) to give a 2D network in the solid state (see the ESI,† Fig. S4(ii)).
Molecular structures of the diarylbismuth halides 2–4 and the diarylmethylbismuthine 5
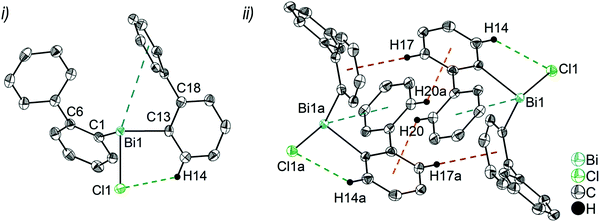
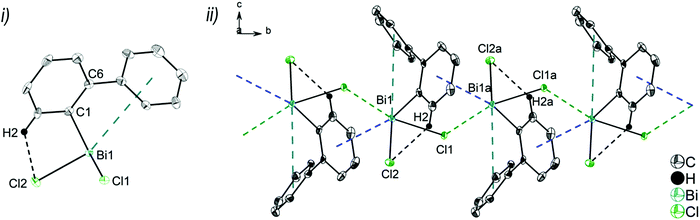
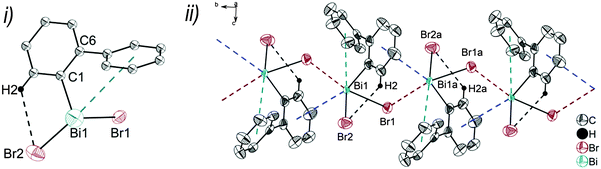
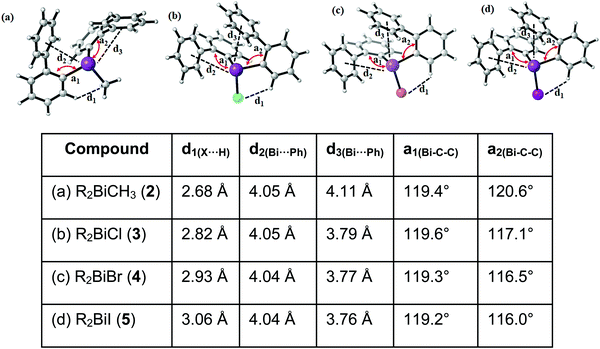
Single crystals suitable for X-ray crystallography were isolated upon crystallization at ambient temperature from a n-hexane solution (for 2, 3), from a CHCl3 solution (for 4) and by slow diffusion of Et2O into n-pentane solution at −28 °C (for 5). The molecular structures of the diarylbismuth(III) halides are depicted in figures 2–5, the selected bond lengths and angles are listed in the figure captions, and their crystallographic data are given in Table S1 (ESI†). The compounds crystallize in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (2 and 4) and the monoclinic space groups P21/n (3) and P21 (5). The asymmetric unit of 2 comprises two crystallographically independent molecules, denoted as 2a (Bi1) and 2b (Bi2). Related bond lengths and angles of 2a and 2b differ by up to 2%, however, in the following we focus on data of 2a. All the compounds show monomeric structures in the solid state with intramolecular dispersion interactions of the type Bi⋯π arene. The corresponding Bi⋯Phcentroid distances are Bi1⋯Phcentroid(I) 3.92 Å (2a, Fig. 2(i)), Bi1⋯Phcentroid(I) 3.82 Å (3, Fig. 3(i)) and for 4 Bi1⋯Phcentroid(I) 3.89 Å and Bi1⋯Phcentroid(II) 3.98 Å (Fig. 4(i)). The angle γ′, which is defined as the angle between the ring normal and the vector between the ring centroid and the bismuth atom, amounts to 46.5°. At least one of the Bi–C–C angles for 2a (Bi1–C13–C18 116.3(2)°), 3 (Bi1–C13–C18 114.6(3)°) and 4 (Bi1–C1–C6 116.2(8)°, Bi1–C13–C18 117.4(8)°) is slightly compressed in comparison to the triorganobismuthine 1. This is indicative for a dispersion interaction between bismuth and one phenyl moiety in 2–4.
(2 and 4) and the monoclinic space groups P21/n (3) and P21 (5). The asymmetric unit of 2 comprises two crystallographically independent molecules, denoted as 2a (Bi1) and 2b (Bi2). Related bond lengths and angles of 2a and 2b differ by up to 2%, however, in the following we focus on data of 2a. All the compounds show monomeric structures in the solid state with intramolecular dispersion interactions of the type Bi⋯π arene. The corresponding Bi⋯Phcentroid distances are Bi1⋯Phcentroid(I) 3.92 Å (2a, Fig. 2(i)), Bi1⋯Phcentroid(I) 3.82 Å (3, Fig. 3(i)) and for 4 Bi1⋯Phcentroid(I) 3.89 Å and Bi1⋯Phcentroid(II) 3.98 Å (Fig. 4(i)). The angle γ′, which is defined as the angle between the ring normal and the vector between the ring centroid and the bismuth atom, amounts to 46.5°. At least one of the Bi–C–C angles for 2a (Bi1–C13–C18 116.3(2)°), 3 (Bi1–C13–C18 114.6(3)°) and 4 (Bi1–C1–C6 116.2(8)°, Bi1–C13–C18 117.4(8)°) is slightly compressed in comparison to the triorganobismuthine 1. This is indicative for a dispersion interaction between bismuth and one phenyl moiety in 2–4.
Due to the Bi⋯π arene interactions the geometry at the bismuth atoms is best described as distorted pseudo-trigonal bipyramidal with the Phcentroidtrans to the halogen atom [Phcentroid–Bi1–Cl1 161.9° (for 2), Phcentroid–Bi1–Br1 161.5° (for 3)] and the carbon atoms placed in the equatorial positions [C1–Bi1–C13 93.30(12)°, C1–Bi1–Cl1 89.64(8)°, C13–Bi1–Cl1 92.89(9)° (for 2a), C1–Bi1–C13 96.09(17)°, C1–Bi1–Br1 92.33(14)°, C13–Bi1–Br1 93.63(14)° (for 3)].
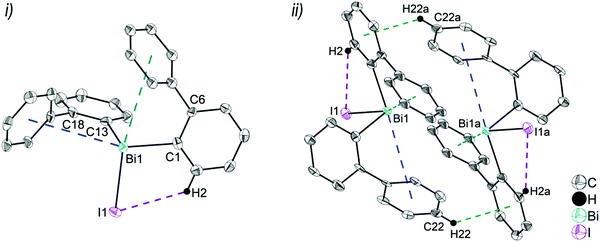
Intramolecular Bi⋯Ph contacts in 4 lead to a distorted square pyramidal coordination geometry at the bismuth atom, with the carbon atom C13 of one 2-biphenyl ligand placed in the axial positions. The basal plane of the square pyramid is described by the two Phcentroid ligands, the iodide atom and the carbon atom C1 of the second aryl ligand. This is supported by the bond angles C1–Bi1–C13 of 94.9(4)°, C13–Bi1–I1 of 93.9(3)°, C13–Bi1–Phcentroid(I) of 72.9°, C13–Bi1–Phcentroid(II) of 69.2°, Phcentroid(I)–Bi1–I1 of 158.8° and Phcentroid(II)–Bi1–C1 of 158.6°. Compounds 2a and 4 both form centrosymmetric dimers via two different C–H⋯Ph intermolecular contacts for 2a (C17b–H17barene⋯Phcentroid 2.73 Å (γ = 2.9°), C20b–H20barene⋯Phcentroid 2.93 Å, γ = 6.8°, Fig. 2(ii)) and for 4 (C22–H22arene⋯Phcentroid 2.77 Å, γ = 6.7°, see Fig. 4(ii)). Moreover, the dimers in 2a are connected via two additional intermolecular Cl⋯H contacts, Cl2a⋯H5c 2.75 Å and Cl1b⋯H21e 2.86 Å, which results in the formation of a 2D network in the solid state (Fig. S5, ESI†). In 4 the dimeric associates are connected via C–H⋯Phcentroid intermolecular contacts with C10–H10arene⋯Phcentroid distances of 2.81 Å (γ = 10.7°) leading to the formation of 1D ribbon-like structures (view along the a-axis, Fig. S6, ESI†). Noteworthy, compound 3 also forms a 1D ribbon (view along the c-axis) in the solid state via two different C–H⋯Phcentroid intermolecular contacts with C20–H20⋯Phcentroid 2.94 Å (γ = 12.6°), C5a–H5a⋯Phcentroid 3.07 Å (γ = 14.5°) (Fig. 3(ii)).
In addition the molecules of the monohalides 2a–4 reveal the presence of intramolecular C–H⋯halogen contacts, with distances of C14–H14⋯Cl1 2.81 Å (for 2a, Fig. 2(ii)), C14–H14⋯Br1 2.94 Å (for 3, Fig. 3(i)) and C2–H2⋯I1 3.05 Å (for 4, Fig. 4(i)), which are shorter than the sum of the van der Waals radii of the corresponding atoms (∑rvdW(H,Cl) = 3.02 Å, ∑rvdW(H,Br) = 3.06 Å and ∑rvdW(H,I) = 3.24 Å).42 Due to these intramolecular C–X⋯H interactions, the molecules are arranged in such a way that the halogen atom is placed closer to a 2-biphenyl ligand of the same molecular unit than to the bismuth atom of the neighbouring molecule.
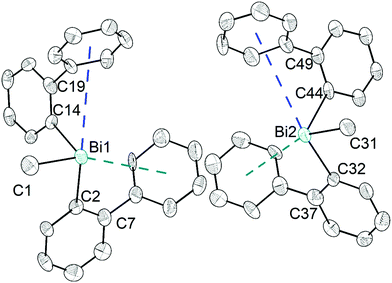
The heteroleptic triorganobismuth(III) compound 5 crystallises in the space group P21 with two crystallographically independent molecules. Both molecules adopt a distorted trigonal pyramidal geometry at the bismuth atom with average C–Bi–C bond angles of 93.0° (5a and 5b) (Fig. 5). In 5a the Bi⋯Phcentroid distances are 4.11 Å and 4.19 Å, and 4.10 Å and 4.24 Å in 5b. The Bi–C–C angles are close to 120° [5a: Bi1–C14–C19 120.8(12)° and Bi1–C2–C7 121.0(12)°; 5a: Bi2–C44–C49 122.5(12)° and Bi1–C32–C37 120.1(13)°], and thus not indicative for a significant intramolecular interaction between bismuth and the phenyl groups. Intermolecular Bi⋯Phcentroid contacts are neither found (Fig. S7, ESI†).
Analysis of the crystal structures of 2–5 reveals that the moderate crowding at the bismuth atom hinders strong intermolecular donor–acceptor interactions and that weak C–H⋯π arene interactions determine the crystal packing. Intramolecular Bi⋯Ph contacts are observed in the range 3.82–4.31 Å for the monomers, with the Bi⋯Phcentroid distances following the order 3 < 4 < 2 < 5 (Fig. 6). It might be concluded, that these interactions hinder free rotation of the biphenyl ligands, but the H⋯X contacts might also contribute to the stabilization of rotational isomers. For the diorganobismuth halides 2–4, the Bi–C–C bond angles are significantly compressed (deviation from ideal angle of 120°), while for 5 the Bi–C–C bond angles are close to 120°. This implies that in the organobismuth(III) halides the bismuth⋯π arene interaction is significantly more attractive in comparison to the triorganobismuth(III) compound 5. However, the trend for the Bi⋯Phcentroid distance does not follow the trend predicted for the interaction between bismuth halides and a π arene ligand. This suggests that packing effects in the crystal interfere with the weak intramolecular interaction. In order to assess, quantify and rationalize these results, an electronic structure calculations on the isolated molecular species was carried out, which will be discussed in a following section.
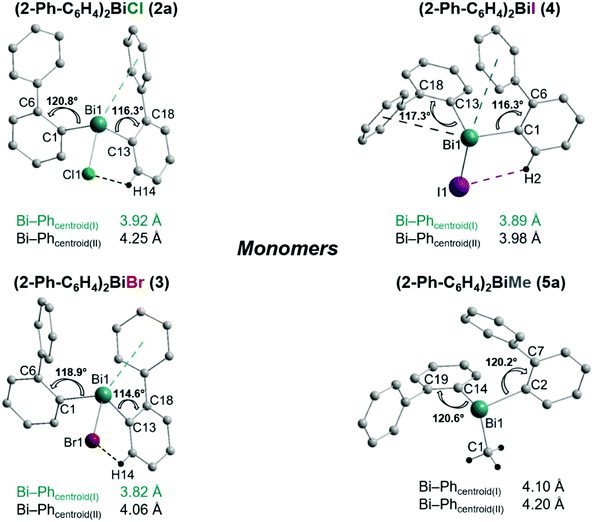 | ||
| Fig. 6 Comparison of the intramolecular Bi⋯Phcentroid distances and the Bi–C–C bond angles in the monomers of 2a, 3, 4 and 5a as observed in the solid state. | ||
Crystal structures of the arylbismuth(III) dihalides 6–8
Colorless, light yellow and orange single crystals suitable for X-ray crystallography were isolated upon crystallization by slow diffusion of n-pentane into Et2O solution at −28 °C (for 6), at ambient temperature by slow diffusion of n-hexane into CHCl3 solution (for 7) and from a CH2Cl2 solution at ambient temperature (for 8), respectively. The molecular structures of the arylbismuth(III) dihalides 6–8 are depicted in figures 7–9, the selected bond lengths and angles are listed in the figure captions and their crystallographic data are given in Tables S1 and S2 (ESI†). The compounds crystallize in the orthorhombic space group P212121 (for 6), the monoclinic space group P21/c (for 7) and triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (for 8) respectively. Compound 7 shows a disorder of the 2-biphenyl group with an occupancy ratio of 0.59
(for 8) respectively. Compound 7 shows a disorder of the 2-biphenyl group with an occupancy ratio of 0.59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
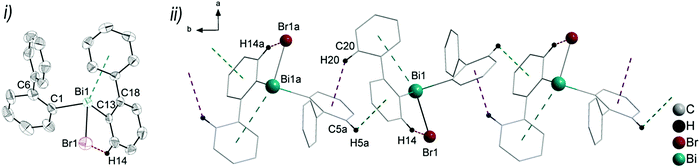
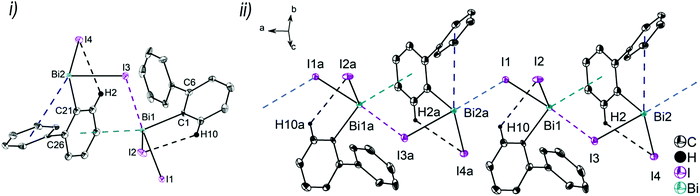
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.41. Thus, the supramolecular structures are shown and discussed only for the molecule that shows the higher occupancy for the aryl ring. The asymmetric units of 6 and 7 comprise one molecule of (2-PhC6H4)BiX2, with Bi1–C1, Bi–X1 and Bi–X2 bond lengths of: 2.230(7) Å, 2.684(2) Å and 2.476(2) Å (for 6); 2.234(11) Å, 3.124(1) Å and 2.610(1) Å (for 7). Compound 8 shows two crystallographically independent molecules in the asymmetric unit with Bi1–C1, Bi1–I1 and Bi1–I2 bond lengths of 2.247(5) Å, 3.0274(5) Å, 2.8353(5) Å and Bi2–C21, Bi2–I3 and Bi2–I4 bond lengths of 2.257(6) Å, 3.0191(5) Å and 2.8183(5) Å, respectively. The Bi–X bond lengths are in accordance with those observed for primary and secondary Bi–X bonds in other arylbismuth dihalides such as [PhBiX2(thf)] (X = Cl, Br, I).43,44 The crystal structure analyses of 6 and 7 reveal long Bi⋯Phcentroid distances (Bi1⋯Phcentroid 3.94 Å for 6, Fig. 7(i) and Bi1⋯Phcentroid 3.86 Å for 7, Fig. 8(i)). For the independent molecules of compound 8 the intramolecular Bi⋯Phcentroid distances amount to 4.044 Å for molecule 8a and 3.911 Å for molecule 8b (Fig. 9(i)). An indication for the intramolecular dispersion type Bi⋯π arene interaction are the Bi1–C1–C6 bond angles (6: 117.2(5)°, 7: 117.1(8)°, 8 116.7(4) and Bi2–C21–C26 118.3(4)°), which deviate from the ideal angle of 120°. Significant differences were not observed for the intramolecular Bi⋯Phcentroid distances in 6–8; they are slightly larger than those observed for compounds 2–4. However, a clear trend on the intramolecular Bi⋯Phcentroid distances related to the nature of X is not obvious.
0.41. Thus, the supramolecular structures are shown and discussed only for the molecule that shows the higher occupancy for the aryl ring. The asymmetric units of 6 and 7 comprise one molecule of (2-PhC6H4)BiX2, with Bi1–C1, Bi–X1 and Bi–X2 bond lengths of: 2.230(7) Å, 2.684(2) Å and 2.476(2) Å (for 6); 2.234(11) Å, 3.124(1) Å and 2.610(1) Å (for 7). Compound 8 shows two crystallographically independent molecules in the asymmetric unit with Bi1–C1, Bi1–I1 and Bi1–I2 bond lengths of 2.247(5) Å, 3.0274(5) Å, 2.8353(5) Å and Bi2–C21, Bi2–I3 and Bi2–I4 bond lengths of 2.257(6) Å, 3.0191(5) Å and 2.8183(5) Å, respectively. The Bi–X bond lengths are in accordance with those observed for primary and secondary Bi–X bonds in other arylbismuth dihalides such as [PhBiX2(thf)] (X = Cl, Br, I).43,44 The crystal structure analyses of 6 and 7 reveal long Bi⋯Phcentroid distances (Bi1⋯Phcentroid 3.94 Å for 6, Fig. 7(i) and Bi1⋯Phcentroid 3.86 Å for 7, Fig. 8(i)). For the independent molecules of compound 8 the intramolecular Bi⋯Phcentroid distances amount to 4.044 Å for molecule 8a and 3.911 Å for molecule 8b (Fig. 9(i)). An indication for the intramolecular dispersion type Bi⋯π arene interaction are the Bi1–C1–C6 bond angles (6: 117.2(5)°, 7: 117.1(8)°, 8 116.7(4) and Bi2–C21–C26 118.3(4)°), which deviate from the ideal angle of 120°. Significant differences were not observed for the intramolecular Bi⋯Phcentroid distances in 6–8; they are slightly larger than those observed for compounds 2–4. However, a clear trend on the intramolecular Bi⋯Phcentroid distances related to the nature of X is not obvious.
The structures of the arylbismuth(III) dihalides show the formation of 1D ribbons which occurs through short intermolecular Bi⋯X interactions approximately trans to the opposite halogen atom from the neighbouring molecule (6: Cl1a–Bi1a⋯Cl1 165.6(4)°; 7: Br1a–Bi1a⋯Br1 167.59(2)°; 8: I1–Bi1⋯I3 176.3(14)°; I3a–Bi2a⋯I1 177.7(14)°). The secondary bridging Bi⋯X distances are as follows; 6: Bi1a⋯Cl1 2.909(2) Å, (cf. ∑rvdW(Bi,Cl) 3.82–4.36 Å42,45); Bi1a⋯Br1 2.790(1) Å, (cf. ∑rvdW(Bi,Br) 3.90–4.40 Å42,45); 8: Bi1⋯I3 3.221(5) Å, Bi2a⋯I1 3.209(2) Å; (∑rvdW(Bi,I) 4.05–4.58 Å42,45). The primary Bi–X distances in the X–Bi⋯X bridges are, as expected, shorter (6: Bi1–Cl1 2.684(2) Å; 7: Bi1–Br1 3.1240(10) Å; 8: Bi1–I1 3.027(5) Å, Bi2a–I3a 3.019(5) Å). In addition to these donor–acceptor Bi⋯X bonds for the dihalides 6–8, intermolecular Bi⋯π arene interactions between the bismuth atom and the phenyl ring of the neighbouring molecule are present. In combination they lead to the formation of zig-zag chains along one crystallographic axis (1D ribbons in Fig. 7(ii)–9(ii)). The Bi⋯Phcentroid distances amount to 3.42 Å (for 6), 3.70 Å (for 7), 3.56 Å (for 8) and are comparable to those observed in [PhBiX2(thf)], (X = Cl, Br, I; Bi⋯Phcentroid distances in the range between 3.43 Å and 3.54 Å).43,44 The competition between donor–acceptor and dispersion interaction is commonly observed for this type of ArBiX2 compounds. The crystal structures 6 and 7 show very similar features, even though they are not isostructural. The environment at the bismuth atom for 6 and 7 becomes distorted octahedral based on the core [(2-PhC6H4)BiX3(Phcentroid)2], with the C1 atom of the biphenyl ligand, the Xbridging atoms and the intermolecular Phcentroid occupying the equatorial positions. The Phcentroid involved in intramolecular interaction and the terminal halogen atom are placed in the axial positions with Phcentroid–Bi1–Cl2 159.2° (for 6) and Phcentroid–Bi1–Br2 162.3° (for 7). In 8 the Bi2 atom adopts a distorted square pyramidal geometry with the carbon atom of the biphenyl ligand in apical position and the vector of the intramolecular Bi⋯Phcentroid contact placed trans to the terminal iodide atom I4. This is reflected in the bond angles of Phcentroid–Bi2–I4 150.0°, Phcentroid–Bi2–C21 69.6°, Phcentroid–Bi2–I3 112.4° and C21–Bi2–I3 90.34(17)°. A distorted square pyramidal environment was observed for the Bi1 atom, with the basal plane formed by the carbon atom C1 of the biphenyl ligand, two Ibridging atoms and Phcentroid, while the axial position is occupied by I2 (cf. corresponding bond angles Phcentroid–Bi1–C1 150.2°, I1–Bi1–I3 176.3°, I2–Bi1–C1 96.3°, I2–Bi1–I1 95.1°, I2–Bi3–I1 88.4°, I2–Bi1–Phcentroid 112.4°).
Furthermore, a 2D network is formed based on short intermolecular C–H⋯Cl bonds (for 6) and C–Harene⋯Ph contacts (for 7 and 8) between parallel 1D layers connected through C8–H8b⋯Cl2a 2.80 Å (for 6, Fig. S8, ESI†), C11–H11⋯Phcentroid 2.84 Å (γ = 13.1°, for 7, Fig. S9, ESI†) and C10–H1A⋯Phcentroid 2.87 Å (γ = 17.1°, for 8, Fig. S10, ESI†).
Computational study of diarylbismuth halides 2–4 and the diarylmethlybismuthine 5
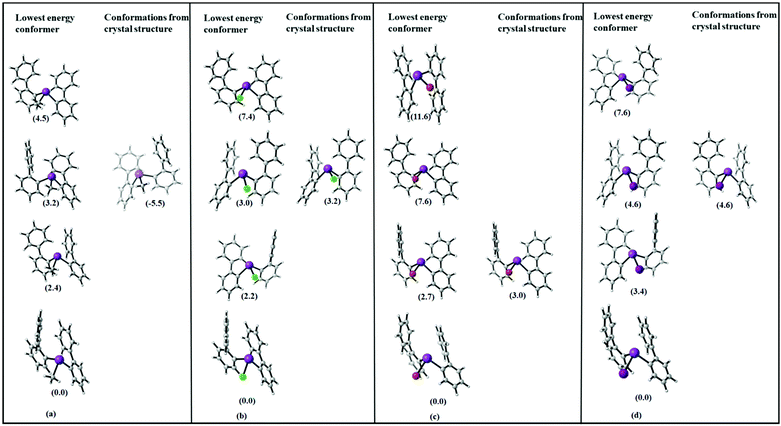
As one of the aims of this study is to rationalize intramolecular Bi⋯π arene interactions using a library of flexible ligands, the crystallographic analyses are supplemented by computational studies. While in most of the presented compounds intermolecular interactions are dominating in the crystal structure, in compounds 2–5 intramolecular Bi⋯π arene interactions seem to dominate. Hence, we start by discussing whether the trends observed in the crystal structures are purely due to intramolecular interactions, or whether crystal packing effects play a major role.In order to assess the molecular structures of compounds 2–5, one has to take into account that this particular system has several “soft” degrees of freedom leading to a rich variety of possible conformers. In order to compare and assess the structures found by the crystallographic analysis, first of all, an overview over the most important low energy conformers has to be obtained. For this purpose, a conformational sampling approach recently published by Grimme et al. was carried out.46 In this scheme, a multistep multilevel procedure is used to screen a large part of the conformational space, select the lowest energy conformers and refine them at a higher level of theory.
The relative energies of the lowest energy conformations of 2–5 after a final optimization at the PBE-D3/def2-TZVP level of theory are shown in Fig. 10. Note that previous studies have shown that this level of theory provides a good balance between computational effort and accuracy in comparison to high-level methods.34,35 The structural parameters, i.e. the computed Bi⋯Phcentroid distances and the Bi–C–C angle, are displayed in Fig. 11. For all compounds the same structural motif with one close Bi⋯Ph contact is found as the lowest energy structure. Given the crystal structures discussed in the previous sections, the results for the fully relaxed structures are quite remarkable. From methyl to iodide, the bismuth-to-phenyl centroid distance and the two Bi–C–C angles with the organic substituents monotonously decrease from 4.11 to 3.76 Å and from 120.6° to 116.0°, respectively, as might be expected for an increasing strength of the intramolecular Bi⋯π arene interaction.
 | ||
| Fig. 10 Schematic representation of the four lowest energy conformers In for each compound (a) R2BiCH3 (2), (b) R2BiCl (3), (c) R2BiBr (4), and (d) R2BiI (5) (R = 2-PhC6H4). The lowest energy geometries of each compound are set to zero (energy in kJ mol−1, structures see Fig. 11 and 12). | ||
The question is why the structures observed in the crystal do not show the expected trends. Fig. 12 includes the structures found in the conformational search and in addition the minimum geometries obtained by optimising the molecular structures as obtained from the single crystal X-ray structure analysis.
Obviously, none of the conformers found in the crystal structure represents the most stable conformer but the molecular structures derived from 5, the chloride 3 and iodide 5 resemble each other.
In Table 1, the energy differences between molecules as present in the crystal (with optimized hydrogen positions) and the fully optimized geometries along with the energy difference to the lowest conformer are given. This energy difference arises at least partially from packing effects but also includes the error of DFT in computing equilibrium geometries. While these two effects might be difficult to disentangle, the size of the observed effect with around 10–70 kJ mol−1 already allows to estimate that packing effects – especially due to CH⋯π and π⋯π interactions in the crystal play a significant role for these structures. This has also been observed in previous work on the crystal structures of arylbismuth(III) compounds in which computational methods have been applied to quantify the effects of intermolecular interactions in crystal structures. Here, it was found that typical Bi⋯π arene interactions for BiPh3 range in the order of 30–40 kJ mol−1 while intermolecular CH⋯π and π⋯π interactions yield interaction energies of similar strength, which results in a rich polymorphism observed in single crystal X-ray structure analysis.20
| Structure | Energy difference of H-optimized crystal structure and fully relaxed molecular structure | Energy difference of fully relaxed structure to the lowest energy conformer |
|---|---|---|
| R2BiCH3 (2) | −60.3 | −5.5 |
| R2BiCl (3) | −11.0 | −3.2 |
| R2BiBr (4) | −28.1 | −3.0 |
| R2BiI (5) | −56.1 | −4.6 |
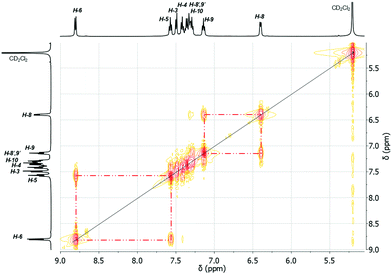
Solution NMR studies of compounds 1–9
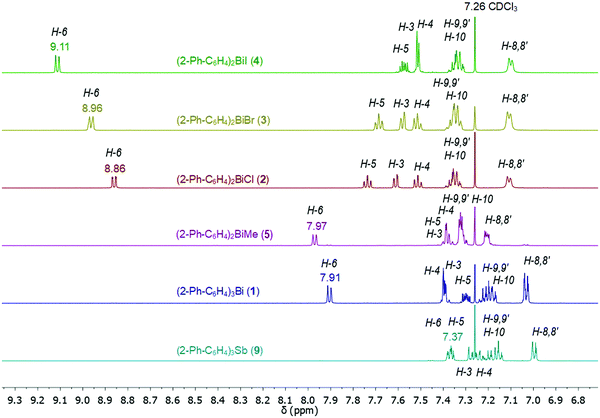
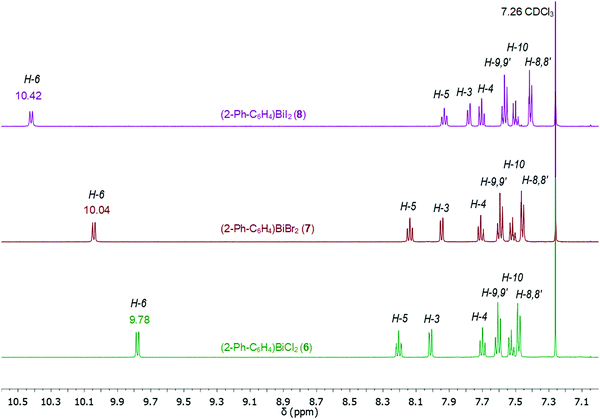
Compounds 1–9 were investigated by solution 1H and 13C{1H} NMR spectroscopy at ambient temperature in CDCl3 solution. The assignment of resonance signals is based on 2D NMR (COSY, Fig. S14–S22, ESI;† HSQC and HMBC) correlation spectra, according to the numbering shown in Scheme 4.The 1H NMR spectra of compounds 1–9 show the expected resonance signals corresponding to the aromatic protons of the 2-biphenyl ligand (Fig. 15 and 16). For the diarylbismuth(III) halides 2–4 and the heteroleptic diaryl(methyl)bismuth(III) compound 5 the 1H NMR spectra show only one set of signals indicating the equivalence of the organic ligands. A very large downfield shift is observed for the resonance signals that belong to the H-6 proton placed in the ortho position to the bismuth atom. The shift depends on the nature of X and increases following the order 2-PhC6H4 < Me < Cl < Br < I (Fig. 13). Characteristic shifts to δ = 8.86 ppm for 2 (X = Cl), 8.96 ppm for 3 (X = Br) and 9.11 ppm for 4 (X = I) are observed, while the triorganobismuth(III) compounds 1 and 5 show resonance signals at δ = 7.91 ppm and δ = 7.97 ppm, respectively. For comparison the corresponding triarylantimony(III) compound 9 was prepared, which shows a resonance signal for the H-6 proton at δ = 7.37 ppm. Even more pronounced downfield shifts were observed in the case of the monoarylbismuth(III) dihalides 6–8 showing a similar dependence (vide infra) on the nature of the substituent X attached to the bismuth atom (Cl < Br < I, Fig. 14). The corresponding resonance signals for H-6 are observed at δ = 9.78 ppm for 6 (X = Cl), 10.04 ppm for 7 (X = Br) and 10.42 ppm for 8 (X = I). In the literature, a similar trend of the chemical shifts with regard to the halide was described for arylbismuth(III) and arylantimony(III) halides for the signal belonging to the H-6 proton placed in the ortho position to the metal atom. For example, in the series of compounds Ar2EX and ArEX2 (E = Sb, Ar = 2-(Me2NCH2)C6H4, X = Ar, Cl, Br, I),47,48 (E = Bi, Ar = 2-(Et2NCH2)C6H4, X = Ar, Cl, Br, I)49 the chemical shift depends on both the metal atom and on the nature of X, but similar trends with regard to the nature of X are observed (Table 2). There is a small difference between the chemical shifts in compounds of the type ArBiX2 (Δ = 0.10 ppm for Cl < Br and Br < I each, Ar = 2-(Et2NCH2)C6H4),49 which is in good agreement with the corresponding values for 2–4 (Δ = 0.10 ppm for Cl < Br and Δ = 0.15 ppm for Br < I). In the case of the reported dihalides ((Et2NCH2)C6H4)BiX249 the differences of the chemical shifts of Δ = 0.14 ppm for Cl < Br and Δ = 0.28 ppm for Br < I are significantly smaller than those found in the compounds 6–8 (Δ = 0.26 ppm for Cl < Br and Δ = 0.38 ppm for Br < I). To the best of knowledge the chemical shift of δ = 10.42 ppm for H-6 in (2-PhC6H4)BiI2 is exceptional for arylbismuth(III) halides.
| Compounds | Substituent X | Chemical shift δ (ppm) | H⋯X distance (Å) | C⋯X distance (Å) | C–H⋯X angle (°) | Lit. |
|---|---|---|---|---|---|---|
| Ar2BiX Ar = 2-PhC6H4 | Ar (1) | 7.91 | — | — | This work | |
| Cl (2) | 8.86 | 2.808 | 3.458 | 126.4 | This work | |
| Br (3) | 8.96 | 2.943 | 3.560 | 125.1 | This work | |
| I (4) | 9.11 | 3.034 | 3.727 | 130.9 | This work | |
| Me (5) | 7.97 | — | — | — | This work | |
| Ar2BiX Ar = Ph | Cl | 8.30 | — | — | — | 44 |
| Br | 8.36 | 2.820 | 3.505 | 129.0 | ||
| I | 8.41 | — | — | — | ||
| Ar2BiX Ar = 2-(Et2NCH2)C6H4 | Ar | 7.70 | — | — | 49 | |
| Cl | 8.55 | 2.815 | 3.436 | 125.1 | 49 | |
| Br | 8.65 | 2.925 | 3.547 | 125.5 | 49 | |
| I | 8.75 | 3.128 | 3.814 | 132.1 | 49 | |
| Ar2SbX Ar = 2-(Me2NCH2)C6H4 | Ar | 7.53 | — | — | 47 | |
| Cl | 7.86 | 2.724 | 3.360 | 126.3 | 48 | |
| Br | 7.90 | 2.838 | 3.481 | 125.8 | 48 | |
| I | 7.96 | 3.104 | 3.769 | 129.9 | 48 | |
| ArBiX2 Ar = 2-PhC6H4 | Cl (6) | 9.78 | 2.739 | 3.727 | 130.9 | This work |
| Br (7) | 10.04 | 2.991 | 3.392 | 126.5 | This work | |
| I (8) | 10.42 | 3.054 | 3.682 | 125.1 | This work | |
| ArBiX2 Ar = Ph | Cl | 8.97 | 2.732 | 3.400 | 129.5 | 44 |
| Br | 9.12 | 2.774 | 3.496 | 132.6 | 43 | |
| I | 9.22 | 2.948, 2955 | 3.677, 3.694 | 133.0, 135.6 | 43 | |
| ArBiX2 Ar = 2-(Et2NCH2)C6H4 | Cl | 9.17 | — | — | — | 49 |
| Br | 9.31 | — | — | — | 49 | |
| I | 9.59 | 3.077 | 3.757 | 129.9 | 49 | |
| ArSbX2 Ar = 2-(Me2NCH2)C6H4 | Cl | 8.28 | 2.764 | 3.346 | 120.4 | 48 |
| Br | 8.58 | 2.818 | 3.473 | 126.9 | 48 | |
| I | 8.68 | 3.073 | 3.738 | 129.9 | 48 | |
An explanation for the large downfield shift of the hydrogen atom in ortho position to the bismuth atom was given by Suzuki and coworkers. Firstly, they point at the participation of H-6 in hydrogen bonds, i.e. the presence of a weak H⋯halogen interaction, and secondly to the anisotropic deshielding effect due to the proximity of the hydrogen atom to the Bi–X bond as discussed for the chiral bismuthines [2-(Me2NCH2)C6H4][4-MeC6H4]BiX (X = para-tolyl, F, Cl, Br, I)50 and [2-(tBuSO2)C6H4][4-MeC6H4]BiX (X = Cl, Br).51 Note that our preliminary calculations of the 1H NMR chemical shifts indicate that the downfield shift is not reproduced using a nonrelativistic approach. It seems likely that the increasing downfield shift is mainly due to the so-called Inverse Halogen Dependence (IHD) which is caused by spin orbit coupling on the heavy halogen atom and its effect on the 1H NMR shift. Similar effects for through space interactions and an IHD have been reported for iodo alkyl and aryl compounds by Kaupp et al. and for ion pairs by Ariai et al.52,53
The 13C{1H} NMR spectra of the di- and monoarylbismuth(III) halides also exhibit a downfield shift for the C-6 carbon resonance signals, which follows the order Cl < Br < I (2: δ = 138.24 ppm, 3: δ = 139.77 ppm, 4: δ = 142.75 ppm, Fig. S11, ESI,†6: δ = 138.02 ppm, 8: δ = 140.70 ppm, 9: δ = 146.35 ppm, Fig. S12, ESI†).
In the 1H NMR spectra of compounds 2–4 significant broadening of the NMR signals at ambient temperature is observed, which is indicative for a dynamic process in solution. In order to study the dynamic behavior, variable temperature 1H NMR spectra were recorded in CD2Cl2 for compounds 3 (Fig. 15) and 4 (Fig. S13, ESI†), in the temperature range of 293 K to 178 K. At ambient temperature the 1H NMR spectra of 3 and 4 show characteristic resonance signals at δ = 7.11 ppm and δ = 7.10 ppm, respectively, which belong to the H-8 and H-8′ protons of the biphenyl ligand. This might be interpreted as a result of a dynamic interaction of dispersion type between bismuth and the aryl ligand.
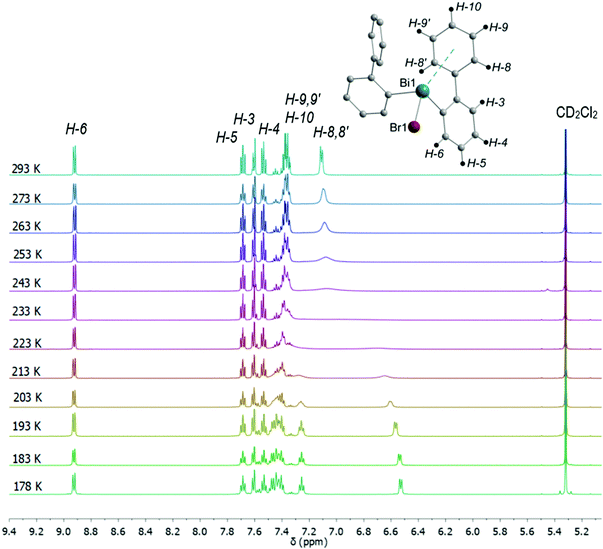 | ||
| Fig. 15 Temperature dependent 1H NMR spectra of (2-PhC6H4)2BiBr (3) measured in CD2Cl2 showing the region for aromatic protons including the numbering scheme. | ||
As the temperature was lowered, the resonances belonging to the H-8 and H-8′ protons further coalesced, with a coalescence temperature (Tc) of 233 K. The corresponding free energies of activation ΔG‡ are 42.8 kJ mol−1 for 3 and 43.3 kJ mol−1 for 4. For the signal assigned to the H-9 and H-9′ protons a broadening is observed above 243 K. By subsequent cooling of the solution to 178 K, the 1H NMR spectra show two sets of doublet resonances (integral ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), i.e. at δ = 6.51 for H-8 and at δ = 7.47 for H-8′ in 3, at δ = 6.66 for H-8 and δ = 7.44 for H-8′ in 4 and two sets of triplet resonances (integral ratio of 1
1), i.e. at δ = 6.51 for H-8 and at δ = 7.47 for H-8′ in 3, at δ = 6.66 for H-8 and δ = 7.44 for H-8′ in 4 and two sets of triplet resonances (integral ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), i.e. at δ = 7.25 for H-9 and δ = 7.41 for H-9′ in 3, and at δ = 7.26 for H-9 and at δ = 7.39 for H-9′ in 4. This assignment is supported by a COSY NMR spectrum of compound 3 at 178 K (Fig. 16). For the aryl protons (H-3–H-6) belonging to the aromatic ring C6H4 changes are not observed, being indicative for a fast flip of the aryl ligand. These results indicate that at 293 K the aryl groups attached to the bismuth atom are equivalent and free rotation of the phenyl rings around the C–C bond is allowed, while at low temperature the dynamic process becomes slower, being consistent with the nonequivalence of H-8 and H-8′ as well as H-9 and H-9′ protons. Thus, in solution the rotation of the phenyl group is frozen, but the Bi⋯π arene interaction does not freeze. The 2-biphenylbismuth dibromide 7 shows a small upfield shift of its 1H NMR signals (CD2Cl2) at 178 K, but no significant changes in comparison to the spectrum measured at 293 K are observed, which indicates the equivalence of H-8 and H-8′ as well as H-9 and H-9′ in the 2-biphenyl ligand even at low temperature.
1), i.e. at δ = 7.25 for H-9 and δ = 7.41 for H-9′ in 3, and at δ = 7.26 for H-9 and at δ = 7.39 for H-9′ in 4. This assignment is supported by a COSY NMR spectrum of compound 3 at 178 K (Fig. 16). For the aryl protons (H-3–H-6) belonging to the aromatic ring C6H4 changes are not observed, being indicative for a fast flip of the aryl ligand. These results indicate that at 293 K the aryl groups attached to the bismuth atom are equivalent and free rotation of the phenyl rings around the C–C bond is allowed, while at low temperature the dynamic process becomes slower, being consistent with the nonequivalence of H-8 and H-8′ as well as H-9 and H-9′ protons. Thus, in solution the rotation of the phenyl group is frozen, but the Bi⋯π arene interaction does not freeze. The 2-biphenylbismuth dibromide 7 shows a small upfield shift of its 1H NMR signals (CD2Cl2) at 178 K, but no significant changes in comparison to the spectrum measured at 293 K are observed, which indicates the equivalence of H-8 and H-8′ as well as H-9 and H-9′ in the 2-biphenyl ligand even at low temperature.
Computational study of the structural dynamics
In order to study the internal degrees of freedom that contribute to the structural dynamics in these systems we have first computed potential energy surfaces for the structurally simplest compounds 6–8, by varying the dihedral angle alpha (see Fig. 17 and Table 3) and beta (see Fig. 18 and Table 4) separately and relaxing all other degrees of freedom at the PBE-D3/def2-TZVP level of theory. The resulting curves are displayed in Fig. 17 and 18 and show that already for only one substituent there are several minima connected by transition states with barriers ranging between a few and 40 kJ mol−1.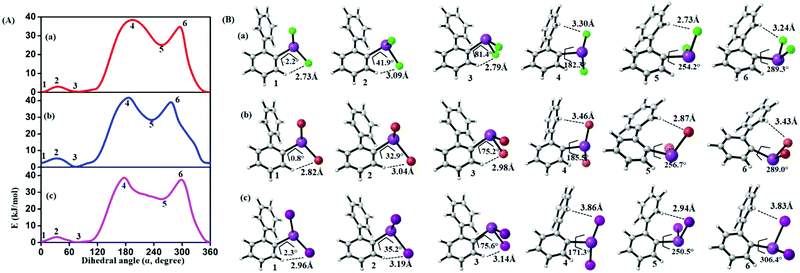 | ||
| Fig. 17 (A) Computed potential energy surfaces (2-PhC6H4)BiX2; (a) X = Cl, (b) X = Br, (c) X = I, along with relaxed C–C–Bi–X dihedral (α) scan at PBE-D3/def2-TZVPP level of theory. (B) Selected conformers of (2-PhC6H4)BiX2 taken from PES; (a) X = Cl, (b) X = Br, (c) X = I. The respective dihedral angle and the shortest hydrogen bond between the nearest hydrogen atom and halogen are shown in each geometry (1, 3, and 5 (2, 4, and 6)) denotes the local minima (maxima) of the respective compound). For details on the dihedral definition see ESI.† | ||
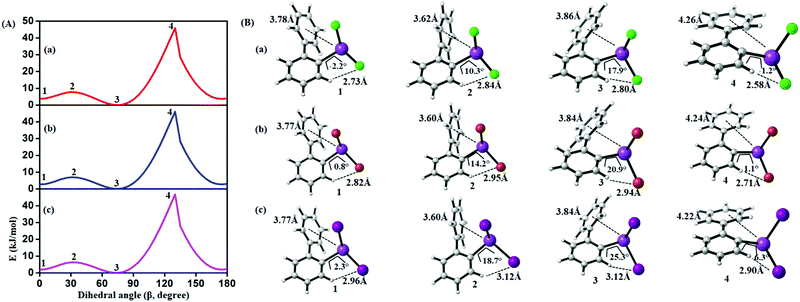 | ||
| Fig. 18 (A) Computed potential energy surface of halogen (X) substituted (2-PhC6H4)BiX2 along with C–C–C–C dihedral (β) rotation at PBE-D3/def2-TZVPP level of theory (1 and 3 (2 and 4)) denotes the local minima (maxima) of the respective compound). (B) Selected conformers of (2-PhC6H4)BiX2 taken from PES; (a) X = Cl, (b) X = Br, (c) X = I. Respective dihedral angle, shortest hydrogen bond distance between the nearest hydrogen (H) atom and halogen (X), center-to-center distance between bismuth atoms and phenyl moieties are shown in each geometry. For details on the dihedral definition see ESI.† | ||
From the results given in Fig. 17 it is concluded that the BiX2 moieties are able to undergo a pseudo rotation with very low barrier, switching between two hydrogen bonded motifs. A full rotation is hindered by the organic substituent (barrier height of more than 30 kJ mol−1) and the halide⋯π interaction leads to a local minimum high in energy (see Table 3). Note that the barrier for rotation around the central C–C bond in biphenyl itself has been reported as 8–10 kJ mol−1.54
| Compound | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| (2-PhC6H4)BiCl2 (6) | 0.0 | 3.1 | 0.2 | 38.4 | 24.8 | 36.4 |
| (2-PhC6H4)BiBr2 (7) | 2.4 | 5.4 | 0.0 | 42.3 | 28.3 | 40.7 |
| (2-PhC6H4)BiI2 (8) | 0.4 | 3.3 | 0.0 | 39.9 | 25.7 | 39.03 |
Fig. 18 depicts the corresponding potential energy surfaces from the rotation of the phenyl moiety which exhibit a low barrier for a 90° tilt connecting two minima with short Bi1⋯Phcentroid distances. The full rotation, however, is hindered by repulsion of the phenyl ring and the halide substituents as can be concluded from the bond distances and angles as given in Fig. 18 resulting in a barrier of more than 40 kJ mol−1 (Table 4).
| Compound | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| (2-PhC6H4)BiCl2 (6) | 3.6 | 7.5 | 0.0 | 45.9 |
| (2-PhC6H4)BiBr2 (7) | 2.9 | 6.9 | 0.0 | 46.0 |
| (2-PhC6H4)BiI2 (8) | 2.1 | 6.3 | 0.0 | 46.7 |
In order to study and rationalize the effects that we observe for compound 3 in the temperature dependent NMR measurement (see Fig. 15), we have extended the study of the conformational degrees of freedom to include transition states between different conformers. While this system is considerably more complex than that of compounds 6–8, the minimum structures obtained from the conformational search already indicate which degrees of freedom are decisive for the observed temperature dependence of the NMR in solution.
Starting from the minimum energy conformer (Fig. 12), it can be seen that the protons H-6 and H-6′ (see Fig. 15), for example, are not equivalent. However, if compared to its mirror image, the protons H-6 and H-6′ are exchanged, while protons H-8 and H-8′ are still distinguishable. The barrier that we compute for this process is 22.5 kJ mol−1 (see Fig. 19), which is well above the estimated conversion barrier for the process observed above 178 K. Hence, we conclude that a pseudo-rotation in which the phenyl rings slide across each other converting the structure to its mirror image and averaging the corresponding protons is the process present at low temperatures. This also allows us to assess that the strength of the Bi⋯π arene interactions rather falls within this range (below 20 kJ mol−1), as the interaction is disrupted and re-established in this process.
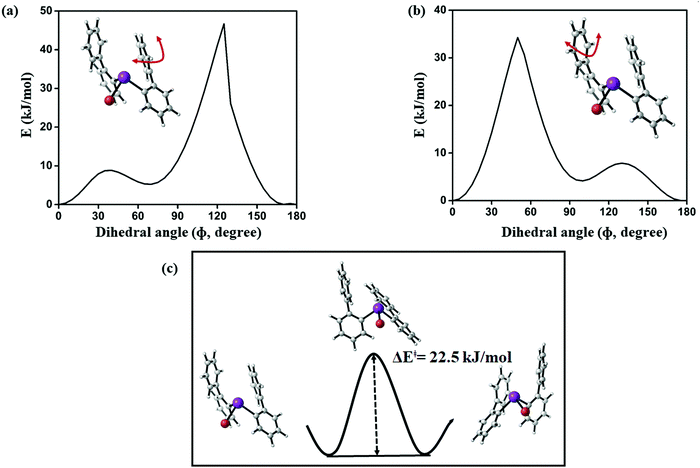 | ||
| Fig. 19 (a and b) Computed potential energy surface of aryl ring rotation for (2-PhC6H4)2BiBr (3) and (c) calculated barrier between equivalent conformations of 3 (PBE-D3/def2-TZVP) level of theory. | ||
Corresponding transition state searches between the different conformers (Fig. 19) exhibit barriers of more than 40 kJ mol−1 as soon as a full rotation of a phenyl moiety is considered, which is in agreement with the results obtained for the monosubstituted species discussed above. Hence, the averaging of protons H-8 and H-8′, for example, which is observed above 230 K is likely to result from rotation around the central C–C bond in the 2-biphenyl ligand occurring at higher temperatures, for which the major contribution likely comes from steric hindrance during the rotation.
Thus, we conclude that steric hindrance of the biphenyl ligands rather than a significantly strong dispersion interaction with bismuth is responsible for the trapped rotation of the biphenyl ligand observed in the temperature dependent NMR experiment between 180 K and 220 K.
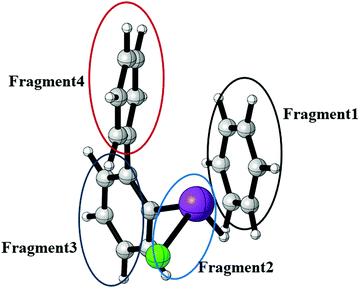
In order to quantify the Bi⋯π arene interaction in these compounds in more detail, we have carried out further electronic structure calculations at the DLPNO-CCSD(T) level of theory applying the local energy decomposition (LED) for a molecular model system that allows to express the intermolecular interaction in terms of interactions between molecular fragments (see Fig. 20).
In previous studies it was found that for Bi⋯π arene interactions a broad range of interaction energies can be observed due to the unique property of heavy main group elements to act as dispersion energy donors and as electron acceptors. For mostly dispersive Bi⋯π arene interactions as observed in organobismuth compounds, interaction energies around 20 kJ mol−1 are found, while an additional donor/acceptor component increases the interaction strength to above 40 kJ mol−1. In conjunction with aromatic substituents that optimises the donor properties of the arene interaction energies of up to 70 kJ mol−1 can be obtained.35 In order to quantify and rationalize the Bi⋯π arene interaction studied here, we focus on compound 3. For this purpose, a model structure was constructed that allows to interpret the intermolecular interaction at the DLPNO-CCSD(T) level of theory applying the local energy decomposition (LED). Fig. 20 displays the structure and the decomposition of the Bi⋯π arene interaction strength computed for this model (Table 5).
| Total interaction energy decomposition (ΔEtotalint) | |||
|---|---|---|---|
| ΔEHFint | ΔEC-CCSDint | ΔEC-C(T)int | ΔEtotalint |
| 43.0 | −55.2 | −9.2 | −21.4 |
| Correlation energy decomposition (ΔEC-CCSDint) | ||
|---|---|---|
| ΔEC-CCSDdisp | ΔEC-CCSDno-disp | ΔEC-CCSDint |
| −54.0 | −1.2 | −55.2 |
| Inter-fragment dispersion contribution (ΔEC-CCSDdisp) | |||
|---|---|---|---|
| 1 ↔ 2 | 1 ↔ 3 | 1 ↔ 4 | ΔEC-CCSDdisp |
| −22.9 | −21.3 | −9.8 | −54.0 |
The results clearly indicate that the interaction of the moiety with the shortest Bi⋯π arene contact is almost exclusively bound by dispersion. A repulsive Hartree–Fock contribution of +43 kJ mol−1 and a very small attractive non-dispersive correlation contribution (−1 kJ mol−1) in the LED which are compensated by the dispersion contribution (−54 kJ mol−1) to yield an overall interaction of −21 kJ mol−1 are typical features of purely dispersive interactions. The Bi⋯π interaction contributes roughly −23 kJ mol−1 to the total dispersion interaction in comparison to −21 and −10 kJ mol−1 for the interaction of this moiety with the biphenyl fragment (see Table 5).
At first glance it appears surprising that the nature of the interactions is almost purely dispersive, given the fact that one of the substituents on the bismuth is chlorine, which is known to increase the donor/acceptor character of Bi⋯π arene interaction. However, the DLPNO-CCSD(T) quantification shows that the interaction strength is in line with what is computed for organobismuth compounds and also falls within the range of the weaker examples for these interactions.
Coming back to the results of the computational study of the barriers associated with the internal degrees of freedom discussed above, the energies in Table 5 also allow to assess how much of these are caused by the specific Bi⋯π arene interaction. With an estimate of intramolecular π–π interactions of 20–30 kJ mol−1 and a Bi⋯π arene interaction of about 20 kJ mol−1 it can be argued that while processes which disrupt several of these interactions – like for a rotation of a phenyl moiety (Fig. 19a and b) – necessarily exhibit barriers in the order of 40 kJ mol−1 while degrees of freedom in which only the Bi⋯π interaction is disrupted will exhibit barriers around 20 kJ mol−1. Crystal packing effects, on the other hand, which we estimate to be quite a bit larger than that (around 40 kJ mol−1) will in sum dominate structure formation in this case. The analysis of the specific Bi⋯π arene interaction in these systems is not only in line with the observations from the conformational study and the NMR experiments above, but also explains why crystal packing effects dominate the solid state structures, as CH–π and π–π interactions of the same strength compete with this binding motif.
Discussion and conclusion
In this work we report on the synthesis and characterisation of a library of compounds of the type (2-PhC6H4)3−nBiXn [n = 0 (1); n = 1, X = Cl (2), Br (3), I (4), Me (5); n = 2, X = Cl (6), Br (7), I (8)] and (2-PhC6H4)3Sb (9), and study intra- and intermolecular London dispersion interactions. The focus of this work lies on the variation of the intramolecular Bi⋯π arene interaction strength between the outer phenyl ring of the 2-biphenyl ligand and the bismuth atom upon variation of the ligand X. The triorganobismuth(III) compound 1 shows an encapsulation of the metal atom due to the crowded ligands, but a pronounced dispersion interaction is not observed (bismuth⋯Phcentroid ∼4.0 Å). In the less crowded monoarylbismuth compounds (2-PhC6H4)BiX2 (6–8), intramolecular Bi⋯π arene interactions are present, but the structures are dominated by intermolecular donor–acceptor bonds between the bismuth and halide atoms. Thus, 1D ribbon-like structures are formed. Short intermolecular Bi⋯Phcentroid distances are also observed in these structures, which are shorter than the intramolecular Bi⋯Phcentroid distances and accompany the donor acceptor bonds. The diarylbismuth(III) compounds (2-PhC6H4)2BiX (2, X = Cl (2), X = Br (3), X = I (4), X = Me (5)) do not show intermolecular donor–acceptor bonds but only intramolecular bismuth⋯Ph contacts with one of the phenyl groups belonging to the 2-biphenyl ligand. It seems that in this case the moderate crowding leads to the monomeric structures even in the solid state. The single crystal X-ray diffraction analyses of these diorganobismuth(III) compounds revealed that the expectations of shorter Bi⋯Phcentroid distances related to the nature of the halogen substituents and thus to a higher polarizability of the Bi–X moiety are not fulfilled. The shortest distance of 3.82 Å is found for (2-PhC6H4)2BiBr (3) which is slightly shorter than the longest distance of 3.92 Å as observed for (2-PhC6H4)2BiCl (2), and the corresponding distance of 3.89 Å for (2-PhC6H4)2BiI (4) is found in between. Thus, packing effects, e.g. resulting from C–H⋯Ph contacts have to be considered and make it impossible to draw a meaningful conclusion only from the single crystal X-ray data. A conformational analysis exhibits that the structures found in the experimental crystallographic analysis actually do not correspond to the lowest energy conformers for the isolated molecules. Our results confirm that rather the intermolecular interactions than the intramolecular interactions determine the molecular structure in the solid state. An analysis of the lowest energy structures obtained by conformational search and geometry optimization, on the other hand, show the expected trends for the intramolecular Bi⋯Phcentroid distances related to the nature of the ligand X in (2-PhC6H4)2BiX. While the acceptor character on the bismuth atom increases (as a result of the interaction with X), the Bi⋯Phcentroid distance decreases, inducing strain on the substituents which is also reflected in the corresponding Bi–C–C bond angles. In addition to the structural analysis in the solid state NMR spectra in solution were recorded, which reveal information about structural dynamics in solution. A pronounced downfield shift in the 1H NMR spectra for the resonance signal assigned to the H derived from the experimental observations of the temperature dependence of the NMR chemical shifts and transition state calculations for the different conformers indicate that at high temperatures the phenyl moieties freely rotate. At temperatures below 200 K a process with a barrier of 40 kJ mol−1 is frozen, lifting the equivalence of several protons, while other pairs of hydrogen atoms, such as the ortho protons, still yield averaged signals. Based on the electronic structure calculations it can be suggested that the low temperature species is the lowest energy conformer, which converts with its mirror image via a process in which the Bi⋯π arene interaction is broken and re-established and which has a barrier in the order of 20 kJ mol−1. Hence, the Bi⋯π arene interaction can be estimated to be in the order of 20 kJ mol−1 or less. This is confirmed by a study of a model compound at the DLPNO-CCSD(T) level of theory applying the local energy decomposition. Thus for the (2-PhC6H4)2BiCl system, the specific interaction is suggested to be 23 kJ mol−1 and the analysis indicates that it is almost purely a dispersion interaction.Experimental
General procedure
All procedures were carried out under anhydrous nitrogen or argon using standard Schlenk techniques. Solvents were freshly distilled over appropriate drying reagents immediately prior to use. Reagents such as 2-bromobiphenyl were purchased from commercial suppliers and used as received. ATR-FTIR spectra were recorded with a Bio Rad FTS-165 spectrometer (Bio-Rad) with a Golden Gate (SpectroMat) sample adapter. 1H and 13C{1H} NMR spectra were recorded at ambient temperature in CDCl3 (dried over 4 Å molecular sieve) with an Avance III 500 spectrometer (Bruker) at 500.30 MHz and 125.81 MHz, respectively, and are referenced internally to the deuterated solvent relative to Si(CH3)4 (δ = 0.00 ppm). NMR signals are given in ppm. The NMR spectra were processed using the software MestReNova (version 11.0.4-1899855). The temperature dependent 1H NMR spectra were recorded in CD2Cl2 at different temperatures from 268 K to 178 K. Calculations of the rate constant k were performed by full line shape analysis with the DNMR program, which is implemented in the TopSpin 2.1 program package. The activation parameters were calculated by use of the Eyring equation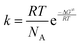 , where R is the general gas constant, T is the absolute temperature, NA is the Avogadro constant, h is the Planck constant and ΔG≠ is the activation Gibbs free energy. The CHN-analyses were performed with a FlashEA 1112 analyzer (Thermo Fisher Scientific). The melting points of compounds were determined with a Melting Point B-540 apparatus (Büchi) and are uncorrected. Powder X-ray diffractograms were measured at ambient temperature with a Stadi P diffractometer (STOE) using Ge(111)-monochromatized Cu-Kα radiation (40 kV, 40 mA). Figures and schemes were created with ChemDraw Prime® (version 17.1)56 and Origin® Pro 2017.57
, where R is the general gas constant, T is the absolute temperature, NA is the Avogadro constant, h is the Planck constant and ΔG≠ is the activation Gibbs free energy. The CHN-analyses were performed with a FlashEA 1112 analyzer (Thermo Fisher Scientific). The melting points of compounds were determined with a Melting Point B-540 apparatus (Büchi) and are uncorrected. Powder X-ray diffractograms were measured at ambient temperature with a Stadi P diffractometer (STOE) using Ge(111)-monochromatized Cu-Kα radiation (40 kV, 40 mA). Figures and schemes were created with ChemDraw Prime® (version 17.1)56 and Origin® Pro 2017.57
Crystallographic studies
Crystal data, data collection and refinement parameters for compounds 1–5 and 6–9 are given in Tables S1 and S2 (ESI†), respectively. Data were collected with either a Rigaku-Oxford Gemini S diffractometer (CrysAlisPro, Version 1.171.38.41l, Rigaku OD, 2015) at 120 K (1), 115.7 K (3), 100 K (5) and 293 K (7) or a Bruker Venture D8 diffractometer (APEX3 v2017.3-0, Bruker AXS) at 100 K (2, 4, 6, 8 and 9) using graphite-monochromatized Cu-Kα radiation (λ = 1.54184 Å for 1, 2, 5) and Mo-Kα radiation (λ = 0.71073 Å for 3, 4, 6–9). Crystals of the compounds were embedded in an inert oil (Krytox®, GPL107) and a suitable crystal was selected under an optical microscope and mounted on a CryoLoop (Hampton Research, type: 20 micron and 0.2–0.3 mm diameter), with the CryoLoop fixed on a tiny glass needle. The structures were solved by direct methods using SHELXS-201358,59 and refined by full matrix least-squares procedures on F2 using SHELXL-2013.60,61 All non-hydrogen atoms were refined anisotropically, while all hydrogen atoms were geometrically placed and refined isotropically in riding modes using default parameters. The crystallographic data for 1–9 have been deposited at the Cambridge Crystallographic Data Centre as supplementary publications CCDC 1948644 (1), 1948645 (2), 1950689 (3), 1948646 (4), 1948647 (5), 1948648 (6), 1950690 (7), 1948649 (8), 1948650 (9).† Visualization of the crystal structures was performed with Diamond (version 4.562).PXRD analyses were performed for compounds 1–9 and the diffraction patterns of the measured diffractograms are in good agreement with those simulated from the single crystal X-ray crystallographic data for 1–5, 7, 9 (see ESI,† Fig. S23–S27, S29 and S31). Only in the case of 6 and 8 a different pattern was observed when comparing to the ones simulated from the single crystal X-ray analyses, most probably due to the formation of polymorphs (see ESI,† Fig. S28 and S30). In case of 5 the crystals made available were all observed to be twinned into several different domains, with the major domains comprising about 50% of all reflections. Comparatively high R factor for this kind of structure are assumed to be partial overlap of reflections, while measurements at higher detector distances did not help to get better data.
Computational details
All calculations were performed using the development version of the Orca 4.1 program. Initially, we have carried out conformational sampling using the GFN2-XTB program to get insight into the thermally accessible minimum energy structure of 2–5. Then, all conformers generated by GFN2-XTB63,64 are fully optimized using the PBE65,66 density functional in conjunction with the def2-TZVP67 basis set and the def2/J auxiliary basis set.68 The default effective core potentials69,70 (def2-ECP) were used for iodine and bismuth. Fine integration grids (grid 4) were used for DFT optimizations. Stationary points were confirmed by analytical harmonic vibrational frequency calculations. Dispersion correction71,72 (D3) with Becke–Johnson (BJ) damping73 was used for DFT calculations. Based on the relative energy ordering, we have identified the four lowest energy structures for each compound (2–5). Transition structure calculation are analysed by frequency calculations to identify only one imaginary frequency at same level of theory. The energies were refined at the DLPNO-CCSD(T)74–80 level of theory employing the cc-pVQZ81 basis set for lighter elements (H, C, Cl, and Br). Additionally, the cc-pVQZ-PP70,82 and cc-pwCVQZ-PP83 basis sets combined with the SK-MCDHF-RSC effective core potential were used for iodine and bismuth, accordingly. Additionally, def2/JK,84 def2/C85 and cc-pwCVQZ-PP/C86 (for bismuth) auxiliary basis sets were used in DLPNO-CCSD(T) calculations. TightPNO87,88 settings were utilized in all DLPNO-CCSD(T) calculations. Additionally, local energy decomposition10,12 (LED) analysis was performed on different conformers of biphenyl compounds in order to analyse dispersion energy contributions in a particular molecule.Nuclear magnetic shieldings were computed using M06L,89 TPSS,90 and double hybrid PBEP86 and utilized pcSseg-391 basis set for lighter elements and all-electron Sapporo-DKH3-TZP-201292 basis set for bismuth. AutoAux93 was used to generate auxiliary basis sets for bismuth. Fine integration grids were used (grid 6 for M06L and TPSS, and grid 4 for PBEP86). Resolution of the identity (RI) approximation94–102 with corresponding auxiliary basis sets were employed in all calculations.
Method A. A solution of nBuLi in n-hexane (1.72 mL, 2.5 M, 4.29 mmol) was added dropwise at −78 °C via a syringe, to a stirred solution of 2-bromobiphenyl (1.000 g, 4.29 mmol) in anhydrous Et2O (50 mL). The reaction mixture was stirred for 1 h at −78 °C. After that a solution of BiBr3 (1.925 g, 4.29 mmol) in Et2O (90 mL) was added, the reaction mixture was kept at −78 °C for 2 h and then stirred for four days at room temperature. The solvent was evacuated in vacuo and the oily residue was extracted with toluene and CHCl3, followed by filtration of the extract and removal of the solvent in vacuo to give an oily light brownish precipitate which was washed with n-hexane (5 × 10 mL). Yield: 0.799 g (36%) yellow single crystals suitable for X-ray analysis were grown from diffusion of n-hexane into CHCl3 solution (v/v 1
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3).
3).
Method B. A mixture of (2-PhC6H4)3Bi (0.796 g, 1.19 mmol) and BiBr3 (1.068 g, 2.38 mmol) was melted and stirred for 15 minutes at 130 °C in the absence of any solvent. After cooling to ambient temperature the solid product was extracted with Et2O (20 mL), the solution filtered and the solvent was evacuated in vacuo to give 0.280 g (45%) of the title compound as light yellow powder. M.p. = 189–192 °C. Elemental analysis calcd (%) for C12H9BiBr2 (521.99 g mol−1): C, 27.61; H, 1.74. Found: C, 27.39; H, 1.55. ATR FTIR (cm−1): 3058 (w), 3037 (w), 2346 (w), 2136 (w), 1594 (w), 1573 (m), 1548 (w), 1494 (m), 1481 (w), 1452 (s), 1444 (s), 1415 (s), 1344 (w), 1311 (m), 1285 (m), 1269 (m), 1239 (m), 1178 (m), 1157 (s), 1112 (m), 1074 (s), 1053 (s), 1003 (w), 974 (s), 953 (m), 920 (s), 878 (m), 849 (s), 778 (s), 750 (vs), 743 (vs), 719 (s), 706 (vs), 646 (m), 612 (m), 544 (s), 517 (s), 428 (s), 412 (m). 1H NMR (500.30 MHz, CDCl3): δ 7.46 (m, 2H, H-8,8′, C6H5), 7.53 (t, 1H, H-10, 3JH–H = 7.5 Hz, C6H5), 7.59 (t, 2H, H-9,9′, 3JH–H = 7.4 Hz, C6H5), 7.71 (ddd, 1H, H-4, 3JH–H = 7.5 Hz, 4JH–H = 1.2 Hz, C6H4), 7.95 (dd, 1H, H-3, 3JH–H = 7.6 Hz, 4JH–H = 1.3 Hz, C6H4), 8.14 (ddd, 1H, H-5, 3JH–H = 7.5 Hz, 4JH–H = 1.3 Hz, C6H4), 10.04 (dd, 1H, H-6, 3JH–H = 7.7 Hz, 4JH–H = 1.3 Hz, C6H4). 13C{1H} NMR (125.81 MHz, CDCl3): δ 128.27 (s, C-8,8′), 129.47 (s, C-10), 129.92 (s, C-4), 130.55 (s, C-9,9′), 132.95 (s, C-3), 135.37 (s, C-5), 140.70 (s, C-6), 142.13 (s, C-7), 147.84 (s, C-2), C-1 could not be detected.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge financial support from the DFG SPP1807 “Control of London Dispersion Interactions in Molecular Chemistry”. We thank Prof. S. Spange for access to the IR instrument. We are grateful to Anja Veit and Lutz Mertens for measuring the IR spectra and PXRD, respectively. We also thank Ute Stöβ and Janine Freytag for performing the CHN analyses. We thank Sebastian Scharf und Sebastian Notz for measuring the temperature dependent NMR spectra. M. Korb thanks the Fonds der Chemischen Industrie for a PhD Chemiefonds fellowship. Ana Toma is grateful for financial support from the DAAD within the frame of the Eastern Europe Partnership program. Cristian Silvestru is grateful for financial support by TU Chemnitz of a short term scientific guest exchange. Anca Silvestru is thanked for ongoing fruitful cooperation in the field of organometallic synthesis. A. A. Auer, M. Krasowska and K. Bhattacharyya would like to acknowledge funding the Max Planck Society and the Max-Planck-Institut für Kohlenforschung. Open Access funding provided by the Max Planck Society.References
- C. Silvestru, H. J. Breunig and H. Althaus, Chem. Rev., 1999, 99, 3277–3328 CrossRef CAS PubMed.
- H. Schmidbaur and A. Schier, Organometallics, 2008, 27, 2361–2395 CrossRef CAS.
- V. M. Cangelosi, M. A. Pitt, W. J. Vickaryous, C. A. Allen, L. N. Zakharov and D. W. Johnson, Cryst. Growth Des., 2010, 10, 3531–3536 CrossRef CAS.
- J. Zukerman-Schpector and E. R. T. Tiekink, The Importance of Pi-Interactions in Crystal Engineering, John Wiley & Sons, Ltd, 2012, pp. 275–299 Search PubMed.
- M. M. Watt, M. S. Collins and D. W. Johnson, Acc. Chem. Res., 2013, 46, 955–966 CrossRef CAS PubMed.
- I. Caracelli, I. Haiduc, J. Zukerman-Schpector and E. R. T. Tiekink, Coord. Chem. Rev., 2013, 257, 2863–2879 CrossRef CAS.
- I. Caracelli, J. Zukerman-Schpector, I. Haiduc and E. R. T. Tiekink, CrystEngComm, 2016, 18, 6960–6978 RSC.
- E. R. T. Tiekink, Coord. Chem. Rev., 2017, 345, 209–228 CrossRef CAS.
- D. J. Liptrot and P. P. Power, Nat. Rev. Chem., 2017, 1, 0004 CrossRef.
- W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2016, 12, 4778–4792 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- G. Bistoni, A. A. Auer and F. Neese, Chem. – Eur. J., 2017, 23, 865–873 CrossRef CAS PubMed.
- R. Lo, P. Švec, Z. Růžičková, A. Růžička and P. Hobza, Chem. Commun., 2016, 52, 3500–3503 RSC.
- A. Bauzá, D. Quiñonero, P. M. Deyà and A. Frontera, CrystEngComm, 2013, 15, 3137–3144 RSC.
- A. Bauzá, D. Quiñonero, P. M. Deyà and A. Frontera, Phys. Chem. Chem. Phys., 2012, 14, 14061–14066 RSC.
- A. A. Auer, D. Mansfeld, C. Nolde, W. Schneider, M. Schürmann and M. Mehring, Organometallics, 2009, 28, 5405–5411 CrossRef CAS.
- D. Mansfeld, M. Mehring and M. Schürmann, Z. Anorg. Allg. Chem., 2004, 630, 1795–1797 CrossRef CAS.
- A. M. Preda, W. B. Schneider, M. Rainer, T. Rüffer, D. Schaarschmidt, H. Lang and M. Mehring, Dalton Trans., 2017, 46, 8269–8278 RSC.
- A. M. Toma, A. Pop, A. Silvestru, T. Rüffer, H. Lang and M. Mehring, Dalton Trans., 2017, 46, 3953–3962 RSC.
- A. M. Preda, M. Krasowska, L. Wrobel, P. Kitschke, P. C. Andrews, J. G. MacLellan, L. Mertens, M. Korb, T. Rüffer, H. Lang, A. A. Auer and M. Mehring, Beilstein J. Org. Chem., 2018, 14, 2125–2145 CrossRef CAS PubMed.
- A. M. Preda, W. B. Schneider, D. Schaarschmidt, H. Lang, L. Mertens, A. A. Auer and M. Mehring, Dalton Trans., 2017, 46, 13492–13501 RSC.
- L. Wrobel, T. Rüffer, M. Korb, H. Krautscheid, J. Meyer, P. C. Andrews, H. Lang and M. Mehring, Chem. – Eur. J., 2018, 24, 16630–16644 CrossRef CAS PubMed.
- K. Srinivas, P. Suresh, C. N. Babu, A. Sathyanarayana and G. Prabusankar, RSC Adv., 2015, 5, 15579–15590 RSC.
- H. J. Breunig, N. Haddad, E. Lork, M. Mehring, C. Mügge, C. Nolde, C. I. Raţ and M. Schürmann, Organometallics, 2009, 28, 1202–1211 CrossRef CAS.
- C. Hering-Junghans, M. Thomas, A. Villinger and A. Schulz, Chem. – Eur. J., 2015, 21, 6713–6717 CrossRef CAS PubMed.
- C. Hering-Junghans, A. Schulz and A. Villinger, Chem. Commun., 2015, 51, 13834–13837 RSC.
- C. Hering-Junghans, A. Schulz, M. Thomas and A. Villinger, Dalton Trans., 2016, 45, 6053–6059 RSC.
- B. Twamley, C. D. Sofield, M. M. Olmstead and P. P. Power, J. Am. Chem. Soc., 1999, 121, 3357–3367 CrossRef CAS.
- J. Bresien, C. Hering-Junghans, A. Schulz, M. Thomas and A. Villinger, Organometallics, 2018, 37, 2571–2580 CrossRef CAS.
- R. J. Schwamm, C. M. Fitchett and M. P. Coles, Chem. – Asian J., 2019, 14, 1204–1211 CrossRef CAS PubMed.
- A. Schulz, M. Thomas and A. Villinger, Z. Anorg. Allg. Chem., 2017, 643, 1406–1414 CrossRef CAS.
- J. Bresien, A. Schulz, M. Thomas and A. Villinger, Eur. J. Inorg. Chem., 2019, 1279–1287 CrossRef CAS.
- J. Fanfrlik, R. Sedlak, A. Pecina, L. Rulisek, L. Dostal, J. Moncol, A. Ruzicka and P. Hobza, Dalton Trans., 2016, 45, 462–465 RSC.
- M. Krasowska, W. B. Schneider, M. Mehring and A. A. Auer, Chem. – Eur. J., 2018, 24, 10238–10245 CrossRef CAS PubMed.
- M. Krasowska, A.-M. Fritzsche, M. Mehring and A. A. Auer, ChemPhysChem, 2019, 20, 2539–2552 CrossRef CAS PubMed.
- D. E. Worrall, J. Am. Chem. Soc., 1936, 58, 1820–1821 CrossRef CAS.
- D. E. Worrall, J. Am. Chem. Soc., 1940, 62, 2514–2515 CrossRef CAS.
- D. M. Hawley and G. Ferguson, J. Chem. Soc. A, 1968, 2059–2063 RSC.
- P. G. Jones, A. Blaschette, D. Henschel and A. Weitze, Z. Kristallogr., 1995, 210, 377–378 CrossRef CAS.
- T. Ogawa, T. Ikegami, T. Hikasa, N. Ono and H. Suzuki, J. Chem. Soc., Perkin Trans. 1, 1994, 3479–3483 RSC.
- V. Stavila, J. H. Thurston, D. Prieto-Centurión and K. H. Whitmire, Organometallics, 2007, 26, 6864–6866 CrossRef CAS.
- S. Alvarez, Dalton Trans., 2013, 42, 8617–8636 RSC.
- W. Clegg, R. J. Errington, G. A. Fisher, D. C. R. Hockless, N. C. Norman, A. G. Orpen and S. E. Stratford, J. Chem. Soc., Dalton Trans., 1992, 1967–1974 RSC.
- W. Clegg, R. J. Errington, G. A. Fisher, R. J. Flynn and N. C. Norman, J. Chem. Soc., Dalton Trans., 1993, 637–641 RSC.
- M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812 CrossRef CAS PubMed.
- S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862 CrossRef CAS PubMed.
- S. Kamepalli, C. J. Carmalt, R. D. Culp, A. H. Cowley, R. A. Jones and N. C. Norman, Inorg. Chem., 1996, 35, 6179–6183 CrossRef CAS.
- L. M. Opris, A. Silvestru, C. Silvestru, H. J. Breunig and E. Lork, Dalton Trans., 2003, 4367–4374 RSC.
- A. Soran, H. J. Breunig, V. Lippolis, M. Arca and C. Silvestru, J. Organomet. Chem., 2010, 695, 850–862 CrossRef CAS.
- H. Suzuki, T. Murafuji, Y. Matano and N. Azuma, J. Chem. Soc., Perkin Trans. 1, 1993, 2969–2973 RSC.
- H. Suzuki, T. Murafuji and N. Azuma, J. Chem. Soc., Perkin Trans. 1, 1993, 1169–1175 RSC.
- M. Kaupp, O. L. Malkina, V. G. Malkin and P. Pyykkö, Chem. – Eur. J., 1998, 4, 118–126 CrossRef CAS.
- J. Ariai and G. Saielli, ChemPhysChem, 2019, 20, 108–115 CrossRef CAS PubMed.
- M. Rubio, M. Merchan and E. Orti, Theor. Chim. Acta, 1995, 91, 17–29 CrossRef CAS.
- MestReNova, (version 11.0.4-18998), Mestrelab Research S. L., Santiago de Compostela, 2017 Search PubMed.
- ChemDraw® Prime (version 17.1), PerkinElmer Informatics, Waltham, MA, 2018 Search PubMed.
- Origin® Pro 2017, OriginLab, Northampton, MA, 2017 Search PubMed.
- G. M. Sheldrick, SHELXS-2013, Program for Crystal Structures Solution, University of Göttingen, 2013 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- G. M. Sheldrick, SHELXL-2013, Program for Crystal Structures Refinement, University of Göttingen, 2013 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- K. Brandenburg and H. Putz, Diamond – Crystal and Molecular Structure Visualization (version 4.5), Bonn, 2018 Search PubMed.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563–2569 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101 CrossRef PubMed.
- F. Neese, A. Hansen and D. G. Liakos, J. Chem. Phys., 2009, 131, 064103 CrossRef PubMed.
- F. Neese, A. Hansen, F. Wennmohs and S. Grimme, Acc. Chem. Res., 2009, 42, 641–648 CrossRef CAS PubMed.
- A. Hansen, D. G. Liakos and F. Neese, J. Chem. Phys., 2011, 135, 214102 CrossRef PubMed.
- D. G. Liakos, A. Hansen and F. Neese, J. Chem. Theory Comput., 2011, 7, 76–87 CrossRef CAS PubMed.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- C. Riplinger, P. Pinski, U. Becker, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- K. A. Peterson, J. Chem. Phys., 2003, 119, 11099–11112 CrossRef CAS.
- K. A. Peterson and K. E. Yousaf, J. Chem. Phys., 2010, 133, 174116 CrossRef PubMed.
- F. Weigend, J. Comput. Chem., 2008, 29, 167–175 CrossRef CAS PubMed.
- F. Weigend, A. Kohn and C. Hattig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- C. Hättig, G. Schmitz and J. Koßmann, Phys. Chem. Chem. Phys., 2012, 14, 6549–6555 RSC.
- D. G. Liakos and F. Neese, J. Chem. Theory Comput., 2015, 11, 4054–4063 CrossRef CAS PubMed.
- D. G. Liakos, M. Sparta, M. K. Kesharwani, J. M. L. Martin and F. Neese, J. Chem. Theory Comput., 2015, 11, 1525–1539 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- F. Jensen, J. Chem. Theory Comput., 2015, 11, 132–138 CrossRef CAS PubMed.
- T. Noro, M. Sekiya and T. Koga, Theor. Chem. Acc., 2013, 132, 1363 Search PubMed.
- G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2017, 13, 554–562 CrossRef CAS PubMed.
- E. J. Baerends, D. E. Ellis and P. Ros, Chem. Phys., 1973, 2, 41–51 CrossRef CAS.
- J. L. Whitten, J. Chem. Phys., 1973, 58, 4496–4501 CrossRef CAS.
- B. I. Dunlap, J. W. D. Connolly and J. R. Sabin, J. Chem. Phys., 1979, 71, 3396–3402 CrossRef CAS.
- M. Feyereisen, G. Fitzgerald and A. Komornicki, Chem. Phys. Lett., 1993, 208, 359–363 CrossRef CAS.
- O. Vahtras, J. Almlöf and M. W. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518 CrossRef CAS.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- R. A. Kendall and H. A. Fruchtl, Theor. Chem. Acc., 1997, 97, 158–163 Search PubMed.
- F. Weigend and M. Haser, Theor. Chem. Acc., 1997, 97, 331–340 Search PubMed.
- F. Weigend, M. Häser, H. Patzelt and R. Ahlrichs, Chem. Phys. Lett., 1998, 294, 143–152 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Crystallographic data and structure refinement details for 1–6 (Table S1) and 7–9 (Table S2); 1H NMR spectra of 2 and 7 (Fig. S1 and S2); single crystal X-ray structures of 9 (Fig. S3) and 1 (Fig. S4); wire and stick models of supramolecular assemblies of 2 (Fig. S5), 4 (Fig. S6), 5 (Fig. S7) and 6–8 (Fig. S8–S10); 13C{1H} NMR spectra of compounds 1–5, 9 (Fig. S11) and 6–8 (Fig. S12); temperature dependent 1H NMR spectra of 4 (Fig. S13); 1H–1H COSY NMR spectra of 1–9 (Fig. S14–S22); PXRD pattern of compounds 1–9 (Fig. S23–S31). CCDC 1948644 (1), 1948645 (2), 1950689 (3), 1948646 (4), 1948647 (5), 1948648 (6), 1950690 (7), 1948649 (8), 1948650 (9). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9cp06924k |
| This journal is © the Owner Societies 2020 |