DOI:
10.1039/C9RA05159G
(Paper)
RSC Adv., 2019,
9, 29440-29447
Electron delocalization in single-layer phthalocyanine-based covalent organic frameworks: a first principle study†
Received
8th July 2019
, Accepted 12th September 2019
First published on 18th September 2019
Abstract
In this work, we first investigate the localized electronic states in the band structures of three single-layer COFs based on typical building units of COFs chemistry. Our results confirm that the polar nature of strong bonds in these building units is a hindrance to a fully delocalized structure and disfavors the band-like mechanism of transport. We then show that a rational design of the building units can lead to dispersive band states in the electronic structure and results in conducting single-layer COFs. We demonstrate this strategy by investigating the charge carrier transport in a series of single-layer Ni-phthalocyanine (NiPc) covalent organic frameworks (COFs), namely, NiPc-P, NiPc-2P, and NiPc-3P. Three proposed COFs exhibit semiconducting band gaps ranging from 0.55 to 0.91 eV. Their room-temperature intrinsic mobility is predicted to be in range of 200–600 cm2 V−1 s−1 and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–60
000–60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm2 V−1 s−1 for electrons and holes, respectively, which are comparable to those of phosphorene and higher than those of the trigonal prismatic molybdenum disulfide. NiPc are dynamically and mechanically stable and can be synthesized via the co-evaporation between Ni and corresponding tetracyano linkers. Importantly, we demonstrate that the properties of the single-layer COFs can be tuned by engineering the organic building blocks. Our theoretical study not only provides insight into the design principles for semiconducting single-layer COFs but also highlights the significance of reticular chemistry in the development of a new generation of two-dimensional materials for optoelectronic applications.
000 cm2 V−1 s−1 for electrons and holes, respectively, which are comparable to those of phosphorene and higher than those of the trigonal prismatic molybdenum disulfide. NiPc are dynamically and mechanically stable and can be synthesized via the co-evaporation between Ni and corresponding tetracyano linkers. Importantly, we demonstrate that the properties of the single-layer COFs can be tuned by engineering the organic building blocks. Our theoretical study not only provides insight into the design principles for semiconducting single-layer COFs but also highlights the significance of reticular chemistry in the development of a new generation of two-dimensional materials for optoelectronic applications.
1. Introduction
The experimental realization of atom-thick graphene1 has stimulated the field of two-dimensional materials, one of the most exciting topics in condensed matter physics and materials science. Lacking a band gap, however, prohibits the application of graphene in electronic devices despite its exceptional conducting and mechanical properties.2 Loosely speaking, there are currently two approaches to overcome this problem; one can either chemically modify graphene to open a band gap3 or seek an alternative with comparable electronic structure. Single-layer molybdenum disulfide (MoS2) is an excellent example with a direct band gap of 1.8 eV,4 yet its low charge mobility of ca. 200 cm2 V−1 s−1 at room-temperature5 is a hindrance to semiconducting applications. Recently, a single-layer structure of phosphorus atoms, i.e., phosphorene, has received much attention due to its tunable band gap and high intrinsic charge mobility.6–9 Nonetheless, phosphorene is chemically unstable owing to its degradation in air.10 The quest for a superior material beyond graphene remains an ongoing topic.11,12
Moving beyond inorganic materials, two-dimensional (but not necessarily a single layer) covalent organic frameworks (2D-COFs)13,14 have emerged as a promising class of materials due to their chemical and structural diversity. In COFs chemistry, one can precisely design a new COF structure with a desired network or crystal topology by carefully choosing building units with appropriate geometries and functional groups; this design principle is closely related to a subfield of crystal design called reticular chemistry pioneered by Yaghi and workers.15–17 This approach has been further extended to the woven structures where different building blocks are connected via both mechanical and covalent bonds.18 Similar to the interlocked molecules,19 the weaving COFs' components cannot be separated without breaking the strong covalent bonds in the building units, making them exciting materials for mechanical and dynamic application. Besides carrying a rich chemistry, COFs can have a wide range of applications from gas storage to catalysis.14,15,20 Furthermore, 2D-COFs have shown promising in semiconducting applications and their atom-thick form which we referred here as single-layer COFs can be experimentally realized.21–24 However, to the best of our knowledge, none of the reported COFs so far has exhibited the charge mobility of 10 cm2 V−1 s−1. Furthermore, the charge transport mechanism is mainly due to the band-like interlayer transport between the π–π stacking layers.25 The intralayer transport, however, is what makes two-dimensional materials like graphene attractive. Indeed, single-layer COFs do not host delocalized electrons as graphene or other conjugated polymers.26 Realizing single-layer COFs as the next generation of two-dimensional semiconducting materials is still a remaining challenge.
In this work, we first examine the electron localization in single-layer COFs constructed from several typical linkages. We then discuss the use of a π-conjugated building unit, e.g., phthalocyanine (Pc), as the building unit to form a full electron delocalized COF layer. We further confirm the electron delocalization in phthalocyanine-based single-layer COFs (single-layer NiPc) by investigating the electronic structure and charge carrier mobility for a series of hypothetical COFs structures, namely, NiPc-P, NiPc-2P, and NiPc-3P (Fig. 1) corresponding to one, two, and three benzene unit(s) between the phthalocyanine units, respectively. As shown later, Ni plays an insignificant role in Pc-COFs' electronic structure and should not change our discussion on the electron delocalized nature of the organic backbone. Rather, the metal centers here link the organic building units together to form the extended structure of NiPc via the metal-directed reaction.27 We choose Ni, amongst other possible metals,28 mainly because of the computational convenience. In particular, NiPc compounds are closed shell structures, and the magnetic ordering can be ignored.29 Our results show that NiPc present high charge carrier mobilities and good mechanical stability in comparison to MoS2 and graphene (we choose to compare our compounds against MoS2 and graphene throughout the paper because they are well-studied materials whose experimental measurements are available). Moreover, NiPc can be synthesized via the co-evaporation reaction, as shown in our calculation below. Importantly, their band gap and charge mobility can be engineered by changing the length of the building units. We anticipate NiPc are promising 2D materials for semiconducting and optoelectronic applications.
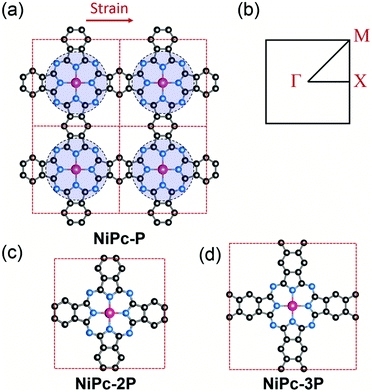 |
| | Fig. 1 Crystal structure of a 2 × 2 supercell of the single-layer NiPc-P (a) and its first Brillouin zone with Γ = [0, 0], X = [0, 1/2], and M = [1/2, 1/2] (b). NiPc-P structure can be constructed by connecting benzene with the NiC8N8 units (the blue circles). The unit cell of NiPc-2P (c) and NiPc-3P (d). The arrow indicates the direction of applied strain in the charge mobility calculation. Atom code: Ni, magenta; N, blue; C, grey. Hydrogen atoms are omitted for clarity. | |
2. Computational details
2.1 Kohn–Sham DFT calculations
Kohn–Sham density functional theory calculations (KS-DFT)30,31 with B3LYP32–34 exchange–correlation functional are performed to optimize the structures as well as compute one-electron properties by means of CRYSTAL09.35,36 We employ the triple-zeta valence with polarization (pob-TZVP)37 basis sets for Ni, S, O, N, C, and H. To avoid the basis dependency, for molybdenum (Mo) we reoptimize the Mo's basis functions taken from TCM CRYSTAL basis set library. We first remove the diffuse sp functions (exponents less than 0.1), and then variationally optimize the inner sp functions. The basis set optimization is performed on a Mo atom and can be found in section S1 of the ESI.† Our calculated band gap for MoS2 using this basis set (see section S6 of the ESI†) is in an excellent agreement with the band gap predicted by the plane wave calculation from the previous work.38 The Monkhorst–Pack grid39 with a density of 2π × 0.02 Å−1 is used to sample the reciprocal space. The convergent criterion for energy is set to 10−10 Hartree. The thresholds for the evaluation of Coulomb and exchange integrals are 10−7, 10−7, 10−7, 10−7, 10−16, corresponding with the parameters 7 7 7 7 16 under TOLONTEG keyword in the CRYSTAL input. For the geometry optimization, the convergent criteria for RMS energy gradient and RMS displacement are set to 3 × 10−5 and 1.2 × 10−4 Hartree, respectively. The fact that the optimized NiPc structures are at the stationary points on potential energy surface is confirmed by the vibrational frequency at Γ point and the phonon calculation using a 2 × 2 super cell. For single-layer MoS2 and graphene, the phonon calculation is performed using a 3 × 3 super cell. For one-dimensional structures and other COFs structures (boroxine-COF, boronate-COF, triazine-COF, and CS-COF), only the vibrational frequency at Γ point is calculated. The absence of the imaginary frequency confirms the dynamical stability of all the structures.
2.2 Absolute band edges
The band edges are aligned to the vacuum by computing the work function. The single-layer models for 2D-COFs are constructed by setting a distance of 50 Å between two adjacent layers. As a result, the interaction between periodic images is negligible, and this allows us to calculate the work function bywhere Φ is the work function, W is the electrostatic potential of the vacuum, and EF is the Fermi level. For one dimensional structure (1D), the distance between two adjacent ribbons is set to 500 Å.
2.3 Intrinsic charge carrier mobility
Boltzmann Transport Equation (BTE)40 combined with the deformation potential (DP) theory41 are applied to calculate the electron/hole mobility at the low carrier concentration. For two-dimensional systems, the carrier mobility μ2Dβ along a longitudinal strain β is given by| |
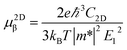 | (2) |
where C2D, m*, E1 are the in-plane stiffness, the effective mass, the DP constant, respectively. e, ℏ, kB, T are the elementary charge, reduce Planck constant, Boltzmann constant, and temperature, respectively. Similarly, for one-dimensional systems the mobility equation is| |
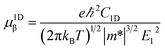 | (3) |
where C1D is the 1D stiffness. In this approach, the relaxation-time τ is primarily due to the acoustic phonon. Other scattering mechanisms, such as optical phonon, defect, impurity, are ignored. This approximation is sufficient to describe the coherent transfer of charge carriers since the lattice constants for all the structures are much larger than the wavelength of electrons or holes at room temperature ca. 70 Å. More details about the mobility calculations can be found in the ESI.†
3. Results and discussions
3.1 Electron localization in typical building units
In COFs chemistry, the framework structures are formed via linking the organic building units together using strong covalent bonds, such as B–O, C–N, B–N, etc.16 However, the difference in the electronegativities of the constituent atoms makes these bonds polar and the assembling building units are often not fully π-conjugated. This localization of electron is very similar to the case of hexagonal boron nitride (hBN) when compared to graphene.42 As a result, the charge carriers are more likely to hop between these localized building units rather than band-like transport through the material.43 In order to provide some insight into this electron localization, we study band structure for single-layer COFs constructed from three typical secondary building units (SBU), i.e., boroxine (B–O), boronate (B–O), and triazine (C–N).15 These SBU share the same three points of extension, which can be seen as a three-coordinated (3-c) vertex in the language of reticular chemistry.44,45 Connecting the 3-c vertices with the benzene units or links (edges) results in three COF structures with an underlying two-dimensional hca network or a kagome lattice (Fig. 2a). We name them as boroxine-COF, boronate-COF, and triazine-COF based on the corresponding SBU that they are built from. Three COFs have the same space group of P6/mmm (no. 191) and this symmetry are preserved in the geometry optimization (Fig. 2b). Amongst them, boroxine-COF and triazine-COF are in facto COF-1 and CTF-1, respectively, which have been synthesized in the bulk phase.46,47 Boronate-COF can be seen as a simplified model of COF-5.46 Fig. 3 shows the band structures for these single-layer COFs. Our result shows that these are large band gap materials (4.11–5.11 eV). Importantly, there exist the flat band edges for all of them, indicating the electron localized states. Our argument is consistent with the study by Wang et al.48 where they find the flat band edges in the boroxine-based COFs due to the poor aromaticity of boroxine unit. Our calculated band gap for boroxine-COF is 5.11 eV which is larger than their predicted value of 3.5 eV. The discrepancy here can be attributed to their use of a local exchange–correlation functional PBE instead of B3LYP, a hybrid functional, as in this work. However, this difference does not affect our present discussion on the electron localization. To further confirm the nondispersive character, we compute the effective mass at the band edges and find that the calculated values using the parabolic assumption for the bands are in range of 3.73–125me which are too large for conducting applications and for the validity of the parabolic assumption for the band edges in the first place (Table 1). Thus, a low in-plane mobility is expected for these single-layer COFs. In fact, the charge transport mechanism in 2D-COFs is predominated by the intralayer transfer mechanism, which has been proved to have band-like nature with an estimated optimal mobility of ca. 10 cm2 V−1 s−1.25 This is further supported by the fact that almost all reported mobility for 2D-COFs have not exceeded the optimal value thus far.49,50
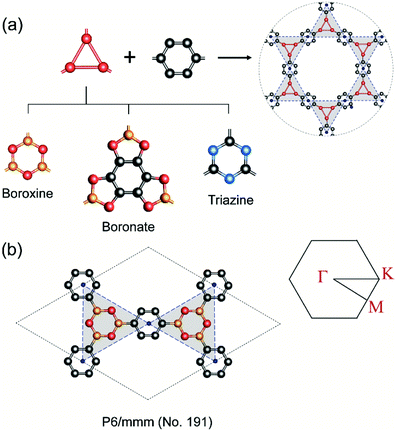 |
| | Fig. 2 (a) Assembling benzene (a link or edge) with the three-coordinated secondary building unit (i.e., boroxine, boronate, triazine) results in three COFs boronate-COF, boroxine-COF, triazine-COF which share the underlying kagome lattice. (b) Boroxine-COF's unit cell and its first Brillouin zone with Γ = [0, 0], M = [0, 1/2], and K = [−1/3, 2/3]. Atom code: C, grey; O, red; B, orange; N, blue. Hydrogen atoms are omitted for clarity. | |
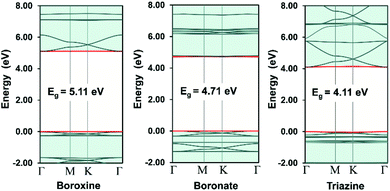 |
| | Fig. 3 Electronic band structures for the single-layer 2D-COFs. The red curves are the band edges, i.e., valence band maximum (VBM, lower) and conduction band minimum (CBM, upper). The Fermi level is set to zero. | |
Table 1 Effective mass (in unit me) along Γ–M for single-layer for 2D-COFs
| Boroxine-COF |
Electron |
26.32 |
| Hole |
61.80 |
| Boronate-COF |
Electron |
125.10 |
| Hole |
42.56 |
| Triazine-COF |
Electron |
4.50 |
| Hole |
3.73 |
| CS-COF |
Electron |
0.32 |
| Hole |
2.86 |
Recently, Guo et al.50 has reported the realization of a 2D-COF structure, namely, CS-COF (CS stands for conjugated and stable) with a delocalized electronic structure. Indeed, the bulk phase of CS-COF exhibits a high hole mobility of 4.2 cm2 V−1 s−1, which is one of the most conductive materials among reported semiconducting COFs. In order to re-examine the electron delocalization in CS-COF, we compute the band structure for a simplified model of CS-COF in which the pyrene units are substituted by benzene (Fig. 4). CS-COF also has P6/mmm (no. 191) space group as well as the underlying hca topology. Our result shows that CS-COF has a lightly dispersive CBM and VBM together with a band gap of 2.20 eV. Interestingly, relatively small effective masses of 0.32 and 2.86me are found for electron and hole, respectively, indicating delocalized states. It is worth noting that the benzene units are linked directly to the C6N6 units (indicated by the blue circles in Fig. 4) via two C–N bonds instead of a single bond as in the other COFs structures discussed above. This assembly results in a partially π-conjugated planar system. However, the hole mobility of CS-COF is still a bit large for practical applications. This non dispersive nature of valence band is in fact due to the underlying kagome lattice. Indeed, Thomas et al.51 have rationalized the origin of the flat bands in single-layer 2D-COFs using KS-DFT calculations and tight-binding model. Hence, the extension of the bandwidth in CS-COFs can also be interpreted as the result of the increase in the nearest-neighbor interactions in the kagome lattice.
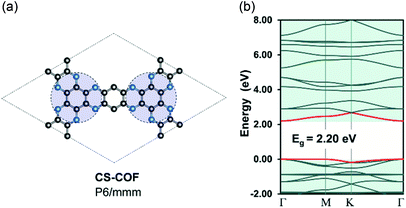 |
| | Fig. 4 Single-layer structure (a) and electronic band structure (b) for CS-COF. The red curves are the band edges, i.e. VBM (lower) and CBM (upper). Hydrogen atoms are omitted for clarity. Atom code: C, grey; N, blue; H, pink. The Fermi level is set to zero. | |
A similar example of highly delocalized COFs is the single-layer Fe-phthalocyanine (FePc) reported by Abel et al.27 FePc exhibits a fully delocalized electronic structure which has been confirmed later by a theoretical study on a series of two-dimensional metal-phthalocyanine (MPc with M = Fe, Co, Ni, Cu, Zn, Mg).29 In MPc, the benzene molecules are assembled with the metal-phthalocyanine units to form an extended two-dimensional system or a square lattice which has been shown to have dispersive band states.51 As in the case of CS-COF, there is no single bond to separate the system into the electron localized building units. This differs from the electron localized states in boroxine-COF, boronate-COF, or triazine-COF. Hence, one can expect that MPc are potentially conducting materials. To the best of our knowledge, there has not been any extensive study on the electron delocalization in Pc-COFs, especially in the context of COFs chemistry. This inspires us to conduct a systematic study on the electronic structure as well as the in-plane charge transport for Pc-COFs. In particular, we study the transport properties for NiPc with a different number of benzene rings between the phthalocyanine units (Fig. 1). Although other phthalocyanine-based COFs have been reported before, however, most of these structures are composed of the localized building units linked together by polar single bonds. Hence, we do not consider them in our study. For other properties like magnetism which have been studied considerably, we refer the reader to existing literatures.29,52–58
3.2 Structural and electronic structures
All NiPc structures are fully relaxed under P4/mmm space group. The vibrational frequency calculations at the high symmetric points in the first Brillouin zone, i.e., Γ, X, and M, show no imaginary mode, affirming their dynamic stability. The calculated Ni–N bond length of 1.923 Å for NiPc-P is in excellent agreement with the PBE+U bond length of 1.922 Å from the previous calculation.29 Our calculated band gap at B3LYP level for NiPc-P is 0.55 eV which is slightly higher than the PBE+U band gap of 0.34 eV by Zhou and Sun.29 However, it has been shown that for the extended organic frameworks B3LYP gives a more consistent result in comparison with the experiment.59,60 The band gap for NiPc-2P and NiPc-3P are 0.73 and 0.82 eV, respectively (Fig. 5). Hence, expanding the link, i.e., increasing the number of the benzene units, gradually widens the gap between the band edges. Interestingly, the trend in single-layer NiPc is opposite to what have previously observed in the boroxine-based COFs in which increasing the number of benzene ring reduces the band gap. Moreover, the band edges of NiPc-2P are at Γ instead of M as those of NiPc-P and NiPc-3P even though they share the same space group symmetry. Three NiPc structures exhibit highly dispersive VBM and CBM with a width of 0.94–1.77 eV and 0.62–1.3 eV, respectively. Not surprisingly, the bands are less dispersive as the unit cell becomes larger by expanding the linkers. This implies the highly electron delocalized states, thereby favoring a band-like transport mechanism of charge carrier. From the density of states plot (Fig. 5), we can see that both C and N contribute to the CBM, whereas VBM is dominated by the C atoms. Loosely speaking, this suggests that the phthalocyanine mainly contribute to the conduction band, in contrast, the benzene units are dominant in the valence band. Furthermore, Ni plays a negligible role in the band edges, suggesting that electron and hole primarily transport along the organic backbone. Since the band-like transport is most likely the primary mechanism, we further compute the charge carrier mobility along the organic backbone to quantify the transport property of NiPc in the next section.
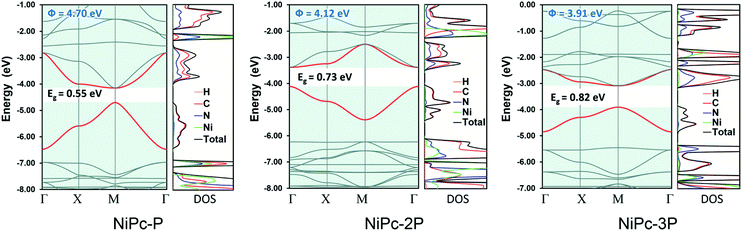 |
| | Fig. 5 Electronic band structure and density of states (DOS) for NiPc-P, NiPc-2P, and NiPc-3P. The work functions (Φ) are also presented. The VBM and CBM are highlighted in red. | |
3.3 Intrinsic charge carrier mobility
We compute the intrinsic electron and hole mobility NiPc along the organic backbone. The effective masses are obtained by fitting the band edges along the appropriate k-point path, i.e., Γ–X for NiPc-2P, X–M for NiPc-P and NiPc-3P. The deformation potential (DP) constant E1 and the in-plane stiffness C2D are calculated by means of the constant strain rate approach. Owing to the uncertainty of the method as well as the lack of the experimental value, we also perform the calculation on the trigonal prismatic molybdenum disulphide (1H MoS2) sheet sing the same procedure for the sake of comparison (Table 2). The calculated mobility for MoS2 are 117 and 422 cm2 V−1 s−1 for electron and hole, respectively, which are in excellent agreement with the previous work.5,38,61 The charge mobility calculation for MoS2 can be found in section S6 of the ESI.† For NiPc-P, the hole mobility of 61.7 × 103 cm2 V−1 s−1 is two order of magnitude larger than that of electron, i.e., 252 cm2 V−1 s−1. A similar trend is observed for NiPc-2P or NiPc-3P, suggesting that the NiPc structures are hole conducting materials with exceptionally high mobility. NiPc's electron and hole mobility are in the same order of magnitude with the theoretical mobility of phosphorene9 and that of graphdiyne ribbons.62 As more benzene are added between the phthalocyanine units, the electron-acoustic phonon scattering becomes stronger as indicated by the smaller in-plane stiffness (Table 2). As a result, it is expected that the electron and hole mobility should become smaller. Surprisingly, the electron mobility is increasing, whereas an opposite trend is observed for the hole mobility. This can be explained by the substantial reduction in the electron mass as the conjugated bridge is extended. On the contrary, the hole mass is slightly increasing. This large change in the electron mass is in line with the fact that the linker expansion separates the phthalocyanine units which is the main constituent of the conduction band as shown in the DOS. Therefore, the hole mobility is determined by the scattering process with phonon, meanwhile the electronic velocity (≡ℏk/m*) controls the electron mobility of the NiPc compounds.
Table 2 DP constant E1, in-plane stiffness C2D, effective mass, and intrinsic charge carrier mobility for the single-layer NiPc and MoS2
| |
E1 (eV) |
C2D (J m−2) |
m* (me) |
μ2Dβ (cm2 V−1 s−1) |
| Electron |
| NiPc-P |
−3.39 |
237 |
1.08 |
252 |
| NiPc-2P |
−3.25 |
206 |
0.82 |
409 |
| NiPc-3P |
−3.29 |
179 |
0.60 |
657 |
| MoS2 |
−9.21 |
160 |
0.48 |
117 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Hole |
| NiPc-P |
−2.36 |
237 |
0.10 |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
| NiPc-2P |
−2.62 |
206 |
0.13 |
25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| NiPc-3P |
−2.15 |
179 |
0.16 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
| MoS2 |
−3.85 |
160 |
0.60 |
422 |
To further confirm the band-like charge transport along the organic backbone, we also compute the charge mobility for the one-dimensional forms of NiPc, namely 1D-NiPc (Fig. 6). Unlike their two-dimensional counterparts, the band gaps are decreasing as the link is expanded. However, the same argument can be applied, specifically the electron mobility is determined by the electronic velocity. The band edges of 1D-NiPc-2P are at Γ instead of X as for 1D-NiPc-P and 1D-NiPc-3P; this swapping of band edge positions is in line with the similar observation for the single-layer NiPc discussed above. In comparison with the single-layer NiPc, the one-dimensional forms show much lower charge carrier mobilities (Table 3). However, they are also hole conducting materials due to large hole mobility compared to that of electron. Both single-layer and one-dimensional NiPc structures possess high charge carrier mobilities, confirming the band-link transport mechanism of charge carriers along the organic frameworks.
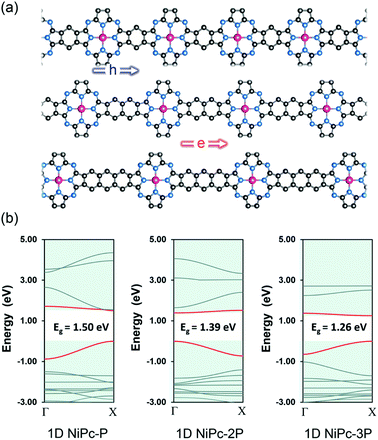 |
| | Fig. 6 One dimensional structure (ribbon) of NiPc (a) and their electronic band structures (b). The Fermi level is set to zero. The VBM and CBM are highlighted in red. | |
Table 3 DP constant E1, stretching modulus C1D, effective mass, and intrinsic charge carrier mobility for 1D-NiPc
| |
E1 (eV) |
C1D (10−7 J m−1) |
m* (me) |
μ1Dβ (cm2 V−1 s−1) |
| Electron |
| NiPc-P |
−6.70 |
2.40 |
0.28 |
181 |
| NiPc-2P |
−10.32 |
2.30 |
0.85 |
14 |
| NiPc-3P |
−10.17 |
2.22 |
0.73 |
17 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Hole |
| NiPc-P |
−5.82 |
2.40 |
0.15 |
619 |
| NiPc-2P |
−6.58 |
2.30 |
0.15 |
465 |
| NiPc-3P |
−5.43 |
2.22 |
0.14 |
684 |
3.4 Mechanical and thermodynamical stability
In addition to the intriguing electronic and electric properties, NiPc are mechanically stable. Indeed, the computed in-plane stiffness (C2D) implies that the NiPc-3P is as stiff as MoS2. Remarkably, the in-plane stiffness for NiPc-P and NiPc-2P is 1.50 and 1.29 times higher than that of MoS2, respectively. Expanding the link induces a reduction in the NiPc's stiffness. Our calculated in-plane stiffness for NiPc-P is about three times higher than the previous prediction on Pc-P.58 To explain this discrepancy, we compute the stiffness for Pc-P and compare it to that of NiPc-P using the same approach. Our result shows that our calculated C2D for Pc-P and NiPc-P are very similar (see section S9 of the ESI†). Hence, Ni plays a minor role in the mechanical property of single-layer NiPc-P and the disparity with previous work is because of the difference in the level of theory employed. In order to validate the accuracy of the current approach, we compute mechanical properties for single-layer MoS2 and graphene whose experimental values are accessible. In fact, our estimated Young's modulus for MoS2 using a thickness of 0.65 nm, however, is 246 GPa, which is very consistent with the experimental value of 270 ± 100 GPa.63 For graphene (see section S9 of the ESI†), its calculated stiffness of 390 J m−2 agrees very well with the reported values of ca. 350–370 J m−2 from the literatures.64–66 The agreement with the experimental measurements confirms the accuracy of our calculations and the predicted mechanical properties for NiPc COFs are reliable.
Last but not least, NiPc are thermodynamically stable and can be formed via co-evaporation between Ni and tetracyano linkers (Scheme 1). In fact, our proposed reaction is inspired by a similar approach used to synthesize Fe-phthalocyanine structure by Abel and co-worker.27 The Gibbs free energy at 400 K and 1 atm are significantly negative, suggesting that the formation reactions are thermodynamically favored (Table 4). Furthermore, the same observation is preserved at higher temperatures as show in the section S4 of the ESI.† Hence, our result demonstrates a possible way to realize these fascinating materials in the laboratory.
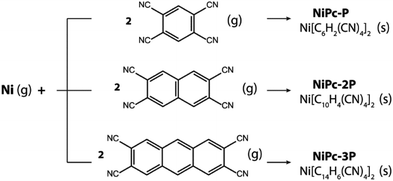 |
| | Scheme 1 Co-evaporation of Ni and the corresponding tetracyano linkers resulting in single-layer NiPc-P, NiPc-2P, and NiPc-3P. | |
Table 4 Thermodynamic quantities at 400 K and 1 atm for the formation reactions in Scheme 1
| |
ΔS (cal mol−1 K−1) |
ΔH (kcal mol−1) |
ΔG (kcal mol−1) |
| NiPc-P |
−182 |
−304 |
−231 |
| NiPc-2P |
−188 |
−289 |
−213 |
| NiPc-3P |
−195 |
−281 |
−203 |
4. Conclusions
In summary, we have studied the electronically localized character of some typical building units in COFs chemistry. Next, we have investigated the electronic structure and charge transporting property for three single-layer phthalocyanine-based COFs in which the electrons are fully delocalized over the entire material. We have shown that these organic structures are promising two-dimensional materials with exceptional high carrier mobility and good mechanical stability in comparison with the renowned inorganic atom-thick materials such as MoS2 and phosphorene. Most importantly, their properties can be tuned by systematically expanding the building unit via adding benzene to the organic linker. Our delocalization argument highlights the importance of a good understanding of the electronic structure of the building linkages in designing new conducting COFs. One can straightforwardly inspect the electronic delocalization of the potential linker, for example, using a KS-DFT calculation or a conjugation argument on the chemical structure. Also, a systematic screening on a large set of organic linkages from the computational perspectives can offer outstanding candidates to construct new frameworks with desired properties, and this is under investigation. Another interesting direction would be modifying the organic backbones with different functional groups to tune the electronic structure as well as the transporting properties of this class of materials. We believe that our work has provided a theoretical insight into the design principle of conducing single-layer COFs for optoelectronic applications.
Conflicts of interest
The authors declare no competing financial interests.
Acknowledgements
The authors are grateful for the supercomputing support from the Institute for Material Research, Tohoku University, Japan. Nguyen-Nguyen's research group acknowledges the financial support by the Institute for Computational Science and Technology (ICST), Ho Chi Minh City. H. Q. Pham thanks Dr Hiroyasu Furukawa and Mr Kyle E. Cordova from UC Berkeley for their valuable discussions.
References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- M. J. Allen, V. C. Tung and R. B. Kaner, Chem. Rev., 2010, 110, 132 CrossRef CAS PubMed.
- V. Georgakilas, M. Otyepka, A. B. Bourlinos, V. Chandra, N. Kim, K. C. Kemp, P. Hobza, R. Zboril and K. S. Kim, Chem. Rev., 2012, 112, 6156 CrossRef CAS PubMed.
- K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805 CrossRef PubMed.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147 CrossRef CAS PubMed.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tománek and P. D. Ye, ACS Nano, 2014, 8, 4033 CrossRef CAS PubMed.
- Y. Cai, G. Zhang and Y. W. Zhang, Sci. Rep., 2014, 4, 6677 CrossRef CAS PubMed.
- A. Castellanos-Gomez, J. Phys. Chem. Lett., 2015, 6, 4280 CrossRef CAS PubMed.
- J. Qiao, X. Kong, Z.-X. Hu, F. Yang and W. Ji, Nat. Commun., 2014, 5, 4475 CrossRef CAS PubMed.
- J. S. Kim, Y. Liu, W. Zhu, S. Kim, D. Wu, L. Tao, A. Dodabalapur, K. Lai and D. Akinwande, Sci. Rep., 2015, 5, 8989 CrossRef CAS PubMed.
- R. F. Service, Science, 2015, 348, 490 CrossRef CAS PubMed.
- R. Roldán, L. Chirolli, E. Prada, J. A. Silva-Guillén, P. San-Jose and F. Guinea, Chem. Soc. Rev., 2017, 46, 4387 RSC.
- A. P. Cote, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166 CrossRef CAS PubMed.
- S. J. Lyle, P. J. Waller and O. M. Yaghi, Trends in Chemistry, 2019, 1, 172 CrossRef.
- X. Feng, X. Ding and D. Jiang, Chem. Soc. Rev., 2012, 41, 6010 RSC.
- P. J. Waller, F. Gandara and O. M. Yaghi, Acc. Chem. Res., 2015, 48, 3053 CrossRef CAS PubMed.
- O. M. Yaghi, Molecular Frontiers Journal, 2019, 03, 66 CrossRef.
- Y. Liu, Y. Ma, Y. Zhao, X. Sun, F. Gándara, H. Furukawa, Z. Liu, H. Zhu, C. Zhu, K. Suenaga, P. Oleynikov, A. S. Alshammari, X. Zhang, O. Terasaki and O. M. Yaghi, Science, 2016, 351, 365 CrossRef CAS PubMed.
- J. F. Stoddart, Chem. Soc. Rev., 2009, 38, 1802 RSC.
- S. Y. Ding and W. Wang, Chem. Soc. Rev., 2013, 42, 548 RSC.
- J. W. Colson, A. R. Woll, A. Mukherjee, M. P. Levendorf, E. L. Spitler, V. B. Shields, M. G. Spencer, J. Park and W. R. Dichtel, Science, 2011, 332, 228 CrossRef CAS PubMed.
- X.-H. Liu, C.-Z. Guan, S.-Y. Ding, W. Wang, H.-J. Yan, D. Wang and L.-J. Wan, J. Am. Chem. Soc., 2013, 135, 10470 CrossRef CAS PubMed.
- L. Xu, X. Zhou, W. Q. Tian, T. Gao, Y. F. Zhang, S. Lei and Z. F. Liu, Angew. Chem., 2014, 126, 9718 CrossRef.
- X.-H. Liu, C.-Z. Guan, D. Wang and L.-J. Wan, Adv. Mater., 2014, 26, 6912 CrossRef CAS PubMed.
- S. Patwardhan, A. A. Kocherzhenko, F. C. Grozema and L. D. A. Siebbeles, J. Phys. Chem. C, 2011, 115, 11768 CrossRef CAS.
- M. Kertesz, C. H. Choi and S. Yang, Chem. Rev., 2005, 105, 3448 CrossRef CAS PubMed.
- M. Abel, S. Clair, O. Ourdjini, M. Mossoyan and L. Porte, J. Am. Chem. Soc., 2011, 133, 1203 CrossRef CAS PubMed.
- A. B. Sorokin, Chem. Rev., 2013, 113, 8152 CrossRef CAS PubMed.
- J. Zhou and Q. Sun, J. Am. Chem. Soc., 2011, 133, 15113 CrossRef CAS PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- R. Dovesi, V. R. Saunders, R. O. C. Roetti, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco and M. Llunell, CRYSTAL09, 2009 Search PubMed.
- R. Dovesi, R. Orlando, B. Civalleri, C. Roetti, V. R. Saunders and C. M. Zicovich-Wilson, Z. Kristallogr., 2005, 220, 571 CAS.
- M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2013, 34, 451 CrossRef CAS PubMed.
- Y. Cai, G. Zhang and Y.-W. Zhang, J. Am. Chem. Soc., 2014, 136, 6269 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- P. Allen, Boltzmann Theory, and Resistivity of Metals, Kluwer Academic Publishers, Norwell, Massachusetts, USA, 1st edn, 1996 Search PubMed.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72 CrossRef CAS.
- M. Topsakal, E. Aktürk and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115442 CrossRef.
- S. Jin, M. Supur, M. Addicoat, K. Furukawa, L. Chen, T. Nakamura, S. Fukuzumi, S. Irle and D. Jiang, J. Am. Chem. Soc., 2015, 137, 7817 CrossRef CAS PubMed.
- D. J. Tranchemontagne, J. L. Mendoza-Cortés, M. O'Keeffe and O. M. Yaghi, Chem. Soc. Rev., 2009, 38, 1257 RSC.
- M. J. Kalmutzki, N. Hanikel and O. M. Yaghi, Sci. Adv., 2018, 4, eaat9180 CrossRef CAS PubMed.
- A. P. Côté, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166 CrossRef PubMed.
- P. Kuhn, M. Antonietti and A. Thomas, Angew. Chem., Int. Ed., 2008, 47, 3450 CrossRef CAS PubMed.
- R.-N. Wang, X.-R. Zhang, S.-F. Wang, G.-S. Fu and J.-L. Wang, Phys. Chem. Chem. Phys., 2016, 18, 1258 RSC.
- S. Wan, F. Gándara, A. Asano, H. Furukawa, A. Saeki, S. K. Dey, L. Liao, M. W. Ambrogio, Y. Y. Botros, X. Duan, S. Seki, J. F. Stoddart and O. M. Yaghi, Chem. Mater., 2011, 23, 4094 CrossRef CAS.
- J. Guo, Y. Xu, S. Jin, L. Chen, T. Kaji, Y. Honsho, M. A. Addicoat, J. Kim, A. Saeki, H. Ihee, S. Seki, S. Irle, M. Hiramoto, J. Gao and D. Jiang, Nat. Commun., 2013, 4, 2736 CrossRef PubMed.
- S. Thomas, H. Li, C. Zhong, M. Matsumoto, W. R. Dichtel and J.-L. Bredas, Chem. Mater., 2019, 31, 3051 CrossRef CAS.
- Y. Ma, Y. Dai, Z. Zhang, L. Yu and B. Huang, Appl. Phys. Lett., 2012, 101, 062405 CrossRef.
- P. Wang, X. Jiang, J. Hu, X. Huang and J. Zhao, J. Mater. Chem. C, 2016, 4, 2147 RSC.
- L.-H. Li, J.-Q. Li and L.-M. Wu, J. Phys. Chem. C, 2012, 116, 9235 CrossRef CAS.
- D. M. Sedlovets, M. V. Shuvalov, Y. V. Vishnevskiy, V. T. Volkov, I. I. Khodos, O. V. Trofimov and V. I. Korepanov, Mater. Res. Bull., 2013, 48, 3955 CrossRef CAS.
- Y. Wang, H. Yuan, Y. Li and Z. Chen, Nanoscale, 2015, 7, 11633 RSC.
- J. Zhou and Q. Sun, Nanoscale, 2014, 6, 328 RSC.
- Y. Wang, H. Zhang, G. Zhang and Y. Guo, RSC Adv., 2015, 5, 94645 RSC.
- T. L. Doan, H. L. Nguyen, H. Q. Pham, N. N. Pham-Tran, T. N. Le and K. E. Cordova, Chem.–Asian J., 2015, 10, 2660 CrossRef CAS PubMed.
- L. Valenzano, B. Civalleri, S. Chavan, S. Bordiga, M. H. Nilsen, S. Jakobsen, K. P. Lillerud and C. Lamberti, Chem. Mater., 2011, 23, 1700 CrossRef CAS.
- R. Fivaz and E. Mooser, Phys. Rev., 1967, 163, 743 CrossRef CAS.
- M. Long, L. Tang, D. Wang, Y. Li and Z. Shuai, ACS Nano, 2011, 5, 2593 CrossRef CAS PubMed.
- S. Bertolazzi, J. Brivio and A. Kis, ACS Nano, 2011, 5, 9703 CrossRef CAS PubMed.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- X. Wei, B. Fragneaud, C. A. Marianetti and J. W. Kysar, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205407 CrossRef.
- A. Bosak, M. Krisch, M. Mohr, J. Maultzsch and C. Thomsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 153408 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Basis set for Mo, crystal structures, all details on the mobility calculation. See DOI: 10.1039/c9ra05159g |
| ‡ Current address: Department of Chemistry, Chemical Theory Centre, and Supercomputing Institute, University of Minnesota, 207 Pleasant Street SE, Minneapolis, Minnesota 55455, United States. |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Dong Q. Lea,
Nguyen-Nguyen Pham-Tran*ab,
Yoshiyuki Kawazoecd and
Duc Nguyen-Manh
*a,
Dong Q. Lea,
Nguyen-Nguyen Pham-Tran*ab,
Yoshiyuki Kawazoecd and
Duc Nguyen-Manh e
e
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–60
000–60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm2 V−1 s−1 for electrons and holes, respectively, which are comparable to those of phosphorene and higher than those of the trigonal prismatic molybdenum disulfide. NiPc are dynamically and mechanically stable and can be synthesized via the co-evaporation between Ni and corresponding tetracyano linkers. Importantly, we demonstrate that the properties of the single-layer COFs can be tuned by engineering the organic building blocks. Our theoretical study not only provides insight into the design principles for semiconducting single-layer COFs but also highlights the significance of reticular chemistry in the development of a new generation of two-dimensional materials for optoelectronic applications.
000 cm2 V−1 s−1 for electrons and holes, respectively, which are comparable to those of phosphorene and higher than those of the trigonal prismatic molybdenum disulfide. NiPc are dynamically and mechanically stable and can be synthesized via the co-evaporation between Ni and corresponding tetracyano linkers. Importantly, we demonstrate that the properties of the single-layer COFs can be tuned by engineering the organic building blocks. Our theoretical study not only provides insight into the design principles for semiconducting single-layer COFs but also highlights the significance of reticular chemistry in the development of a new generation of two-dimensional materials for optoelectronic applications.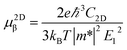
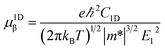

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700
700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700
700
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)





