Transformation of the coordination complex [Co(C₃S₅)₂]²⁻ from a molecular magnet to a potential qubit

Abstract

Mononuclear transition metal complexes demonstrate significant potential in the divergent applications of spintronics and quantum information processing. The facile tunability of these complexes enables structure function correlations for a plethora of relevant magnetic quantities. We present a series of pseudotetrahedral [Co(C₃S₅)₂]²⁻ complexes with varying deviations from D_2d symmetry to investigate the influence of structural distortions on spin relaxation dynamics and qubit viability, as tuned by the variable transverse magnetic anisotropy, E. To overcome the traditional challenge of measuring E in species where D ≫ E, we employed a different approach of harnessing ac magnetic susceptibility to probe the emergence of quantum tunneling of magnetization as a proxy for E. Across the range of values for E in the series, we observe magnetic hysteresis for the smallest value of E. The hysteresis disappears with increasing E, concomitant with the appearance of an observable, low frequency (L-band) electron paramagnetic resonance (EPR) signal, indicating the potential to controllably shift the molecule's utilization from classical to quantum information processing applications. The development of design principles for molecular magnet information processing requires separate design principles for classical versus quantum regimes. Here we show for the first time how subtle structural changes can switch the utility of a complex between these two types of applications.

---

Introduction

A bottom-up approach to synthesizing functional components of information storage devices is vital for molecular spintronics. Within this area, paramagnetic high-spin coordination complexes are attractive candidates for spin-based data storage and information processing applications owing to their readily tunable M_S states. The field of molecular magnetic information processing can be bisected into two distinct areas: classical high-density information storage and quantum information processing (QIP).^1,2 Each of the two applications requires fundamentally distinct design principles. Classical data storage necessitates molecules that display magnetic hysteresis, in an analogous fashion to bulk magnets, while QIP requires spectroscopically addressable transitions for manipulation. The key quantity differentiating the suitability of high-spin molecules to the aforementioned applications is the presence of transverse zero-field splitting (E), which mixes the M_S states of a spin, S. In classical data storage applications, the mixing induces quantum tunnelling of magnetization (QTM) and destabilizes information stored in the orientation of the magnetic moment. Thus, the minimization of E is an overarching design principle.³ In contrast, high-spin coordination complexes with non-negligible E are attractive candidates as molecular hosts for QIP. Here, the M_S mixing promoted by E induces relaxation of spectroscopic selection rules and enables otherwise forbidden transitions to function as candidate qubits. This latter property is highly advantageous for the design of multi-qubit molecular processors.^4,5 Thus, E is a crucial parameter that gates the respective application of coordination complexes in either classical or quantum information processing.

Commanding the delicate interplay of parameters required to tune E requires careful consideration of coordination geometry and electronic structure for a metal ion. Yet, explicit studies illustrating the influence of specific structural changes on magnitude and sign of E are relatively rare, in contrast to the axial zero-field splitting (D), which is reasonably well understood. Tuning and measuring changes in D is well established from the field of single-molecule magnets (SMMs).^6,7 These species are a class of paramagnetic molecules that feature an energy barrier for spin reversal,⁸ that promotes their utility for classical data storage. While there is ample literature concerning maximizing D, and thus the spin reversal barrier (U = DS²), considerably fewer reports are devoted to understanding the rational tuning of E through ligand field variations.^9,10 A large body of literature in particular exists on magneto-structural correlations in systems with large, negative D values. Yet, in such systems it is very difficult to probe E spectroscopically or magnetically. This extremely challenging, and occasionally prohibitive, nature of direct measurement of E generates an absence of direct correlations of changes in E to the observation of magnetic hysteresis or qubit viability. To ameliorate the spectroscopic elusiveness of E we employed ac magnetic susceptibility as a probe of the emergence of QTM, which is a bulk proxy for E, as it enables QTM through admixture of M_S levels.

Electron paramagnetic resonance (EPR) spectroscopy is an invaluable technique to measure the zero-field splitting (ZFS) parameters of magnetic molecules. Yet, owing to the limited operational microwave frequencies and magnetic fields currently available, it is often difficult to use the technique to study complexes with highly axial anisotropy (D ≫ E). Fortunately, ac susceptibility is a powerful probe of slow magnetic relaxation in which QTM, facilitated by a number of factors including E, is often a prominent relaxation pathway at low temperatures. Ac susceptibility is an indispensable technique for the investigation of magnetic properties such as magnetic ordering and spin glass behaviour in solid state materials,¹¹ yet, it is rarely the key technique employed to inspect E in coordination complexes. Herein, we report tuning the coordination geometry in a series of S = 3/2 pseudo-tetrahedral Co²⁺ complexes, A₂[Co(C₃S₅)₂] (A = Bu₄N⁺ (1), Ph₄P⁺ (2), PPN⁺ (3), [K(18c6)]⁺ (4)). Across 1–4, we observe a diminishing value of E by monitoring the low temperature QTM. Importantly, concomitant with a decrease in E, a transition of the utility of the molecule from quantum to classical information application occurs, as evidenced by the observation of an L-band (1.36 GHz) EPR signal for 1 and magnetic hysteresis for 4.

Results and discussion

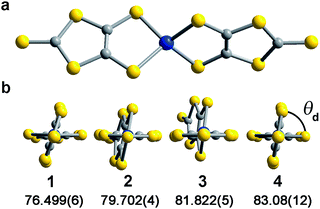
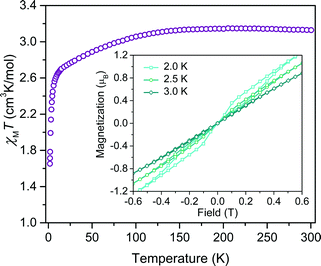
Investigation of whether small structural changes can induce a transition in viability from the quantum to classical regime of information processing poses an appreciable challenge due to the synthetic requirement of varying one zero-field splitting parameter while maintaining the same electronic structure. To approach this challenge, we focused on the C₃S₅²⁻ ligand motivated by its denticity and planarity, which guides late transition metal ions toward four-coordinate geometries with subtle deviations away from D_2d idealized symmetry. Here, the majority of such deviations amount to variation in the interligand dihedral angle (θ_d) between the planes defined by the C₃S₅²⁻ planar ligands (Fig. 1). Each member of the series of [Co(C₃S₅)₂]²⁻ complexes was synthesized via ligation of the bidentate, nuclear-spin free ligand, 4,5-dimercapto-1,3-dithiole-2-thionate (C₃S₅²⁻), to CoCl₂ in MeOH followed by the addition of the appropriate cation (Bu₄N⁺ (1), Ph₄P⁺ (2), PPN⁺ (3) and [K(18-c-6)]⁺ (4)) to affect precipitation of the desired salt. Single-crystal X-ray diffraction studies of all complexes reveal an elongated pseudo-tetrahedral coordination environment surrounding the Co²⁺ center, as illustrated in Fig. 1a. Several metrical parameters are remarkably consistent across the series. First, the average Co–S bond distances in all complexes are comparable (2.305(8) Å) and are consistent with the average Co–S distances reported for tetrahedrally coordinated high-spin Co²⁺S₄ complexes in the literature.¹² Further, individual S–Co–S bite angles in 1–4 do not deviate significantly from the average value of the series (93.9(3)°). Yet, despite this consistency, a distortion away from D_2d symmetry is observed as a function of counterion in 1–4 (Fig. 1). Indeed, a twist of the planar C₃S₅²⁻ ligands relative to one another distorts the dihedral angles away from the ideal angle of 90°, as illustrated in Fig. 1b. Across the series of compounds, the dihedral angle ranges from 76.499(6)° to 83.08(12)° in 1 and 4, respectively. The low-coordinate nature of the Co²⁺ complexes imparts flexibility, allowing the dihedral angle to remain flexible while maintaining the ∼94° bite angle. Importantly, the invariant bite angle across the series imposes a near degeneracy of the d_x²−y² and d_xy orbitals resulting in the large axial anisotropy previously observed in [Co(C₃S₅)₂]²⁻.^10,13 This specific structural variation observed across the series presents a unique opportunity to study the influence of a specific subtle distortion in the ligand field on the slow magnetic relaxation by inducing non-negligible rhombicity (E/D ≠ 0) with minimal influence on D (i.e. the height of the spin reversal barrier). Importantly, the nearest intermolecular Co⋯Co distances are nearly constant in the series, ranging from 8.66(8) to 10.14(7) Å. This consistency is an effective control for dipolar interactions between the paramagnetic centers, thereby highlighting the dominance of changes in the ligand field as the most important influence on relaxation processes (see Fig. S14†).

Fig. 1 (a) Molecular structure of [Co(C₃S₅)₂]²⁻ as determined by X-ray crystallography for 2. The blue, yellow, and grey spheres represent Co, S, and C atoms respectively. (b) Depiction of the variation in dihedral angle across compounds 1–4.

To probe the magnetic structure of compounds 1–4, variable-temperature dc magnetic susceptibility measurements were performed under an applied dc field of 0.1 T between 1.8 and 300 K. The relatively uniform 300 K χ_MT values of 3.0–3.3 cm³ K mol⁻¹ supports assignment of a S = 3/2 ground state with large g_iso values in the range of 2.53–2.65, consistent with other highly axial cobalt thiolate complexes.^7d,g As an illustrative example, the 300 K χ_MT value of 4 persists with decreasing temperature until ∼175 K, whereupon the value gradually decreases to 2.6 cm³ K mol⁻¹ at 10 K (Fig. 2). At temperatures lower than 10 K, the χ_MT value rapidly declines with decreasing temperature. For complexes 1–4, the gradual decline in χ_MT below 150 K is indicative of a large axial ZFS, as expected owing to the structural similarity with other previously reported pseudo-tetrahedral Co²⁺ complexes.^7d,g Determination of the magnitude and sign of the zero-field splitting parameters proceeded through collection and fitting the variable-temperature, variable-field magnetization data (see ESI Fig. S3†). The program DAVE 2.0 (ref. 14) was employed to fit the data with the spin Hamiltonian Ĥ = DŜ_z² + E(Ŝ_x² − Ŝ_y²) + g_isoβSH. The parameter D is the axial zero-field splitting parameter, E is the transverse zero-field splitting parameter, Ŝ_i (i = x, y, z) are the spin operators, g_iso is the isotropic g value, β is the Bohr magneton, S is the spin, and H is the magnetic field. Our fits consistently estimate D to range from −161 to −187 cm⁻¹ for 1–4. We note the difficulty in accurately determining the magnitude of D, and more significantly E, from magnetization data of microcrystalline sample of highly magnetically anisotropic complexes, especially considering the difficulty in ensuring a randomly oriented microcrystalline sample. However, simulations of the magnetization curves with E values up to 3 cm⁻¹ do not change the appearance of the magnetization curves due to the low rhombicity of the complex, thus precluding accurate determination of this parameter by dc magnetometry. Indeed, it is particularly challenging to assess low energy differences via magnetometry data alone, particularly when the value of D is significantly larger than E, thus masking the impact of altering this parameter. Nevertheless, the validity of these fits is supported by theoretical calculations as illustrated below.

Fig. 2 Temperature dependent magnetic susceptibility (χ_MT) of a polycrystalline powder of 4 collected under an applied field of 0.1 T. Inset: overlay of hysteresis curves collected on 4 at 2 K, 2.5 K, and 3 K at a scan rate of 8 mT s⁻¹.

Investigation of the influence of θ_d on the dynamic magnetic properties first proceeded via acquisition of variable field magnetization data below 5 K to search for magnetic hysteresis, a property suggestive of classical data storage. Of this series, the least distorted compound, 4, is the only species to display magnetic hysteresis (Fig. 2 inset). Variable-temperature hysteresis curves reveal that the behaviour persists until 3 K, when the open loop collapses completely. Compound 4 is only one of very few mononuclear transition metal complexes exhibiting hysteresis at temperatures accessible above 1.5 K measured at relatively low magnetic field scanning rates.¹⁵ The observation of hysteresis in only one member of 1–4 immediately illustrates the significant influence of subtle distortions of the immediate ligand sphere on the magnetic properties of [Co(C₃S₅)₂]²⁻.

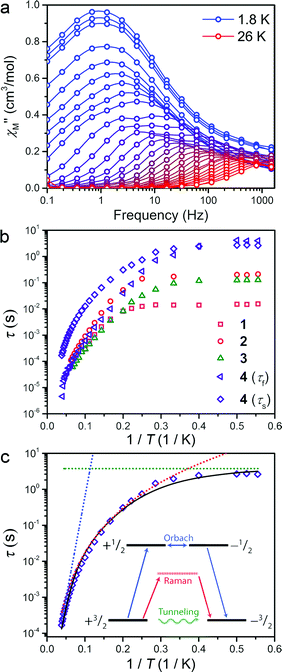
The presence of magnetic hysteresis in a single species of the series is surprising given the nearly identical zero-field splitting parameters determined from the dc susceptibility and magnetization data. Thus, ac magnetic susceptibility experiments, which yield information on the exact relaxation processes responsible for spin reversal, were pursued to search for the impact of subtle differences in the ZFS values. Specifically, we searched to correlate E with data obtained from dynamic magnetic measurements. One feature, which enables us to probe the ZFS parameters, is the presence of slow magnetic relaxation, which manifests by the observation of a peak in the out-of-phase component of ac susceptibility (χ′′_M). When this slow relaxation is induced by negative axial anisotropy, it is the hallmark of single-molecule magnet behaviour. Investigation of compounds 1–4 by variable temperature ac-susceptibility under zero applied dc field revealed a signal in the χ′′_M component of the ac susceptibility indicating a slowly relaxing magnetic moment. At 1.8 K, 1–4 all exhibit a peak in χ′′_M with maxima occurring at 0.7 to 10 Hz, respectively. The data sets for each complex exhibit two distinguishable or slightly overlapping peaks, a consequence of changing ac field frequencies enabling access to different pathways for reversal. Several examples of this behaviour are documented in the literature.¹⁶ For 1–3, the fast relaxation peak, which occurs at higher frequencies, exhibits little discernible temperature dependence, whereas 4 possesses two readily distinguishable peaks in χ′′_M, both of which can be tracked throughout the temperature range of study (see Fig. 3a). Close inspection of the temperature dependence of the χ′′_M peak in 1–4 reveals a temperature independent regime below 3 K, where QTM is the operative relaxation pathway. Above 3 K, the peak in χ′′_M shifts to higher frequencies with increasing temperature until it disappears from the accessible frequency window at 15 K. However, 4 is notable in that its χ′′_M peaks can be monitored at temperatures up to 26 K, thus permitting a more thorough analysis of the temperature dependence of its relaxation times (τ). Akin to the dc susceptibility data, 1–3 display similar behaviour to each other, while 4 is again an outlier, corroborating the observation of magnetic hysteresis in 4, and further suggesting a minimum value for E in 4.

Fig. 3 (a) Variable temperature out-of-phase ac susceptibility of 4 between 0.1 and 1500 Hz collected under zero dc field from 1.8 to 26 K. (b) Overlay of the temperature dependent relaxation times of compounds 1–4. (c) Fit to the slow relaxation process (τ_s) of 4 in the temperature range of 1.8 to 26 K. The fit, and the inset, highlight contributions from Orbach (blue), Raman (red) and QTM (green) relaxation processes and their origins.

The temperature dependence of the magnetic relaxation time yields mechanistic information regarding spin reversal, information that is highly sensitive to structural changes in magnetic systems. Thus, the variable frequency and temperature ac susceptibility data were fit to a general Debye model¹⁷ to extract the spin relaxation times (τ) for each compound. Compound 4 is a slight exception here, requiring a modified two-site Debye model.¹⁸ The extracted relaxation times for 1–4, presented in Fig. 3b, highlight the temperature independent regime below 3 K at zero dc field, owing to QTM³ or possibly avalanche processes.¹⁹ Above 3 K however, all compounds exhibit thermally activated relaxation, often attributed to two-phonon mediated Raman and Orbach spin relaxation processes, which impart a Tⁿ and exponential dependence on T for τ, respectively.²⁰ In order to understand the relative contributions of each pathway in 1–4, we fit the temperature profiles of τ to account for QTM, Raman, and Orbach relaxation according to the equation, τ⁻¹ = ν_QTM + BTⁿ + τ₀⁻¹e^U_eff/kT. ν_QTM is the tunnelling frequency, T is the temperature, k is Boltzmann's constant, U_eff is the effective spin-reversal barrier, B is the Raman coefficient, and τ₀⁻¹ is the attempt frequency. The fit to the slow relaxation process (τ_s) in 4, presented as an illustrative example in Fig. 3c, highlights the relative contributions of the various relaxation processes across the temperature range of measurement. Below 3 K, QTM is the dominant relaxation pathway as indicated by the temperature independence of the relaxation time. With increasing temperature, Raman relaxation begins to take effect, inducing the observed curvature in the temperature profile of τ, up to 22 K where Orbach relaxation dominates as indicated by the linear temperature dependence on the logarithm of τ.

Fitting the high temperature data to an Orbach relaxation process yields effective relaxation barriers (U_eff) in the range of 31–35 cm⁻¹ for 1–3, while the slow relaxation time in 4 exhibits a barrier of 91 cm⁻¹, one of the largest reported barriers for mononuclear transition metal complexes (see Fig. 3c).²¹ The glaring disagreement between our theoretically expected barrier (U_eff = 2D = 320 cm⁻¹) and the observed ones suggests the potential overestimation of D, or more likely the inappropriate assignment of an Orbach process at the higher temperatures of analysis.²² Regardless, the low temperature relaxation times draw attention toward the stark differences in the QTM frequency (ν_QTM) between compounds 1–4, which spans two orders of magnitude, ranging from 61 Hz to 0.26 Hz for 1 and 4, respectively.

The chelating coordination mode of the planar ligand in compounds 1–4 provides a unique opportunity to investigate a select magneto-structural correlation in [Co(C₃S₅)₂]²⁻. To exclude the influence of counterion nuclear spins on QTM,²³ and to focus our study on the variable dihedral angle, we synthesized the deuterated analogue of 2 for comparison. We probed this compound by ac susceptibility and determined there was no statistically significant difference between its properties and those of its protiated counterpart (see ESI for further discussion†). There is, however, a striking correlation between the dihedral angle of the dithiolate ligands in 1–4 with ν_QTM extracted from ac susceptibility measurements. Compound 1, possessing a dihedral angle of 76.5(1)°, exhibits the highest ν_QTM (61 Hz), whereas 4, bearing the least distorted angle of 83.1(1)°, exhibits the lowest frequency for QTM (0.26 Hz). We note that 2 and 3 do not rigorously follow the proposed trend, which we attribute to the canted binding mode of the C₃S₅²⁻ ligand that induces a slight deviation from the ligand field trend.

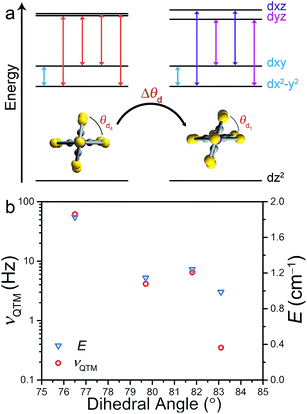
Correlation between ν_QTM and θ_d is credited to deviation from D_2d symmetry (i.e. θ_d < 90°). Inspection of the qualitative d-orbital splitting diagram in Fig. 4 highlights the extent to which the near degeneracy of the d_xy and d_x²−y² orbitals is removed, imposed by the invariant bite angle of the C₃S₅²⁻ ligand across the series, thus distorting the pseudo-tetrahedral complex from T_d to D_2d symmetry. Our analysis is further supported by computational studies that reveal the lowest lying electronic excited state is relatively constant across the series, indicating relatively minor changes to the energies of the d_xy and d_x²−y² orbitals (see ESI Table S7†). The low-coordinate nature of these complexes, as well as the rigidity of the binding mode of the planar ligand, imposes selective distortion of the dihedral angle due to crystal packing forces. Twisting of the dihedral angle away from 90° breaks the degeneracy of the d_xz and d_yz orbitals in the d-orbital energy diagram depicted in Fig. 4a. The incomplete cancellation of the contributions from transitions to d_xz and d_yz orbitals results in a nonzero E component of zero-field splitting. As depicted in the d-orbital splitting diagram in Fig. 4a, the energy separation between the d_xz and d_yz orbitals widens as the dihedral twist increases, thus resulting in a larger E component of ZFS. The values of E for compounds 1–4 were determined through a wave function based approach. State-averaged CASSCF/CASPT2 calculations of 1–4 were performed as implemented in the Molcas 8.0 software package.^24,25 The lowest 40 doublet and 10 quartet states (the full d-manifold) were included and used in subsequent state-interaction calculations in order to determine the effects of spin orbit coupling and ultimately the D and E parameters (see ESI for details†).

Fig. 4 (a) Illustration of the d-orbital splitting for [Co(C₃S₅)₂]²⁻ as a function of deviation from ideal D_2d symmetry. The arrows highlight the various transitions contributing to D (blue) and E (purple and pink). (b) E (blue triangles) and ν_QTM (red circles) as a function of the variable dihedral angle. The error on ν_QTM is smaller than the size of the data points.

With increasing deviation of θ_d from 90°, ν_QTM increases as a result of an increasing E that facilitates mixing of the M_S levels and magnetization tunneling through the spin-reversal barrier. Compounds 1–4 enable us to utilize ac susceptibility as an indirect probe of E, a value inherently difficult to measure in highly axially anisotropic complexes, through measurement of the QTM frequency. The results summarized in Fig. 4b clearly support our magneto-structural and d-orbital splitting analysis and illustrate the utility of employing ac susceptibility as an indirect probe of E in 1–4.

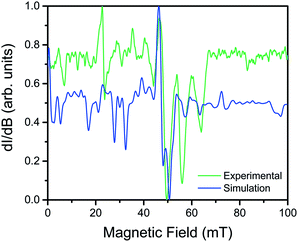
Utility of a coordination complex for quantum computing is predicated on the ability to manipulate its spin. Practically, this necessitates the observation of an EPR transition for pulsed manipulation. Yet, prior investigations of 2 revealed EPR silence and the unfeasibility of addressing any transitions as a consequence of a large, negative D and small E.⁴ However, the surprising correlation between the dihedral angle and QTM frequency provided the motivation to investigate the possibility of addressing intra-Kramers transitions within the M_S = ±3/2 doublet at very low magnetic fields. Previously, we demonstrated that the extremely small value of E in 2 prevented observation of this transition; by increasing E with increasing distortion from D_2d symmetry across this series we created the potential for an EPR accessible transition. Yet, in order to access said transitions, low frequency EPR is necessary to bring the resonance to a field accessible by commercial spectrometers (<1.4 T). Thus, we investigated the two extremes in the series, 1 and 4, by the rare application of L-band (1.368 GHz) EPR spectroscopy to high-spin cobalt ions. Remarkably, while 4, which possesses the smallest E, elicited no signal, the cw-EPR spectrum of 1 reveals a rich signal, displaying a multitude of resonances between 10 and 70 mT (see Fig. 5). The energetically well-isolated M_S = ±3/2 Kramers doublet permitted treatment of the spectrum as an effective S′ = 1/2, with highly anisotropic effective g′-values. Simulation of the spectrum in EasySpin²⁶ allowed assignment of the observed features, which are attributed to very weak transitions within the hyperfine structure of the ±3/2 Kramers doublet due to electronuclear interactions with the I = 7/2 nuclear spin of the ⁵⁹Co nucleus (see ESI S16†). The observation of resonances in the cw-EPR spectrum of the species with the largest value of E (1), concomitant with observation of hysteresis in the species with the smallest value of E (4), clearly demonstrates the impact of θ_d on the potential utility of the system. For 4, the θ_d leads to a low E, inducing magnetic hysteresis and potential for classical information storage. In 1, however, the θ_d leads to a larger E, which negates the hysteresis but enables access to EPR transitions at low frequency, and thus potential application for QIP. The actual potential of the system for QIP will be evaluated via pulsed L-band EPR spectroscopy in a future study.

Fig. 5 Overlay of the experimental cw-EPR spectrum (green) and simulation (blue). The experimental spectrum was collected on 1 at L-band (ν = 1.368 GHz) at 110 K. The simulation was performed in EasySpin using an effective spin Hamiltonian (S′ = 1/2) with rhombic g-values and a rhombic hyperfine interaction (g_i, A_i, i = x, y, z). The blue spectrum was simulated using the following parameters: g′_x = 0.79(5), g′_y = 0.84(3), g′_z = 6.8(2), A′_x = 142(1) MHz, A′_y = 149(1) MHz, A′_z = 2026(1) MHz.

Outlook

Deriving magneto-structural correlations in high-spin molecular species is vital for creating design principles to develop components for classical information storage, spintronics, and quantum information processing. Specifically, the foregoing results further develop the impact of specific structural and electronic changes on application for classical versus quantum computing schemes. Our analysis of highly uniaxially anisotropic complexes reveals an unequivocal trend between increased QTM frequencies with increased deviation from D_2d symmetry owing to the concurrent increase in the magnitude of E. This drastic influence of a single structural distortion of [Co(C₃S₅)₂]²⁻ permitted the application of ac susceptibility as an indirect probe of E throughout the series. Consequently, the subtle distortion of θ_d away from D_2d symmetry led to the observation of both magnetic hysteresis and addressable EPR transitions in the two extremes of θ_d, respectively. The discovery that [Co(C₃S₅)₂]²⁻ bridges the fields of SMMs and QIP through subtle structural distortions opens new avenues to investigate the suitability of transition metal complexes for applications in quantum and classical information processing.

Acknowledgements

We are grateful to Drs James P. S. Walsh and William E. Antholine for productive discussions and experimental assistance. We all thank Prof. Toru Shiozaki for invaluable discussions, and B. V. thanks him for encouraging this research. We also thank Ms Charlotte Stern. We thank the NSF for funding the qubit studies through CHE-1455017 and the AFOSR for funding the magnetic anisotropy studies through FA9550-14-1-0358. The L-band spectrometer is supported by J. S. Hyde, T. G. Camenisch, and J. J. Ratke through the National Biomedical EPR Center NIH P41 Award EB001980 to J. S. H. BV was supported by the National Science Foundation (CHE-1351598). We are also thankful to the MCW for travel support of J. Z. for the low frequency EPR experiments. We acknowledge support from Northwestern University, the International Institute for Nanotechnology.

References

1. L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186.
2. M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197.
3. D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268–297.
4. M. S. Fataftah, J. M. Zadrozny, D. M. Rogers and D. E. Freedman, Inorg. Chem., 2014, 53, 10716.
5. M. S. Fataftah, J. M. Zadrozny, S. C. Coste, M. J. Graham, D. M. Rogers and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 1344.
6. (a) G. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135; (b) M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Maganas and F. Neese, Coord. Chem. Rev., 2015, 15, 177–214.
7. (a) D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224; (b) W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2010, 132, 18115; (c) D. Weismann, Y. Sun, Y. Lan, G. Wolmershauser, A. K. Powell and H. Sitzmann, Chem.–Eur. J., 2011, 17, 4700; (d) J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732; (e) S. Mossin, B. L. Tran, D. Adhikari, M. Pink, F. W. Heinemann, J. Sutter, R. K. Szilagyi, K. Meyer and D. J. Mindiola, J. Am. Chem. Soc., 2012, 134, 13651; (f) J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125; (g) J. M. Zadrozny, J. Telser and J. R. Long, Polyhedron, 2013, 64, 209; (h) Y.-Y. Zhu, C. Cui, Y.-Q. Zhang, J.-H. Jia, X. Guo, C. Gao, K. Qian, S.-D. Jiang, B.-W. Wang, Z.-M. Wang and S. Gao, Chem. Sci., 2013, 4, 1802; (i) J. Martínez-Lillo, T. F. Mastropietro, E. Lhotel, C. Paulsen, J. Cano, G. De Munno, J. Faus, F. Lloret, M. Julve, S. Nellutla and J. Kryzystek, J. Am. Chem. Soc., 2013, 135, 13737; (j) K. E. R. Marriott, L. Bhaskaran, C. Wilson, M. Medarde, S. T. Ochsenbein, S. Hill and M. Murrie, Chem. Sci., 2015, 6, 6823–6828; (k) A. K. Bar, C. Pichon and J.-P. Sutter, Coord. Chem. Rev., 2016, 308, 346–380; (l) S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289, 379–392.
8. D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, Oxford, 2006.
9. J. M. Zadrozny, S. M. Greer, S. Hill and D. E. Freedman, Chem. Sci., 2016, 7, 416.
10. (a) J. M. Zadrozny, J. Telser and J. R. Long, Polyhedron, 2013, 64, 209–217; (b) K. Fukui, H. Ohya-Nishiguchi and N. Hirota, Bull. Chem. Soc. Jpn., 1991, 64, 1205; (c) E. A. Suturina, D. Maganas, E. Bill, M. Atanasov and F. Neese, Inorg. Chem., 2015, 54, 9948–9961; (d) M. Idešicova, J. Titiš, J. Krzystek and R. Boča, Inorg. Chem., 2013, 52, 9409–9417.
11. (a) J. A. Mydosh, Spin Glasses, Taylor and Francis, London/Washington DC, 1993; (b) J. Hertz, K. A. Fischer, Spin Glasses, Cambridge University Press, New York, 1989.
12. (a) J. R. Dorfman, C. P. Rao and R. H. Holm, Inorg. Chem., 1985, 24, 453; (b) W. P. Chung, J. C. Dewan, M. Tuckerman and M. A. Walters, Inorg. Chim. Acta, 1999, 291, 388–394; (c) P. C. Tellinghuisen, W. T. Robinson and C. J. Wilkins, J. Chem. Soc., Dalton Trans., 1985, 7, 1289–1293; (d) T.-A. Okamura, S. Takamizawa, N. Ueyama and A. Akamura, Inorg. Chem., 1998, 37, 18–28.
13. (a) D. Dai, H. Xiang and M.-H. Whangbo, J. Comput. Chem., 2008, 29, 2187; (b) M.-H. Whangbo, E. E. Gordon, H. Xiang, H.-J. Koo and C. Lee, Acc. Chem. Res., 2015, 48, 3080.
14. R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggot, C. M. Brown, J. R. D. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341–358.
15. (a) S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 4300; (b) J. Vallejo, A. Pasual-Álvarez, J. Cano, I. Castro, M. Julve, F. Lloret, J. Krzystek, G. De Munno, D. Armentano, W. Wernsdorfer, R. Ruiz-García and E. Pardo, Angew. Chem., Int. Ed., 2013, 52, 14075–14079; (c) I. Banerjee, A. Jana, S. Singh, J. Marek, E. del Barco and M. Ali, Polyhedron, 2013, 66, 162–166.
16. (a) R. Boča, J. Miklovic and J. Titiš, Inorg. Chem., 2014, 53, 2367; (b) J. Miklovic, D. Valigura, R. Boča and J. Titiš, Dalton Trans., 2015, 44, 12484; (c) M. Dolai, M. Ali, J. Titiš and R. Boča, Dalton Trans., 2015, 44, 13242.
17. (a) K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341; (b) C. J. F. Bottcher, Theory of Electric Polarization, Elsevier, New York, 1952; (c) S. M. J. Aubin, Z. M. Sun, L. Pardi, J. Kryzystek, K. Folting, L. C. Brunel, A. L. Rheingold, G. Christou and D. N. Hendrickson, Inorg. Chem., 1999, 38, 5329.
18. J. Miklovic, D. Valigura, R. Boča and J. Titiš, Dalton Trans., 2015, 44, 12484.
19. (a) K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2013, 135, 17952; (b) S. McHugh and M. P. Sarachik, Mod. Phys. Lett. B, 2011, 25, 1795; (c) M. Sarachik, Magnetic Avalanches in Molecular Magnets, in Molecular Magnets: Physics and Applications, ed. J. Batolome, F. Luis, J. F. Fernandez, Springer, New York, 2014.
20. A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Metals, Dover Publications, Inc., New York, 1986.
21. (a) J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577; (b) V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M.-E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, J. Am. Chem. Soc., 2015, 137, 9792–9795; (c) Y. Rechkemmer, F. D. Breitgoff, M. van der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. van Slageren, Nat. Commun., 2016, 7, 10467; (d) Y.-Y. Zhu, C. Cui, Y.-Q. Zhang, J.-H. Jia, X. Gao, C. Gao, K. Qian, S.-D. Jiang, B.-W. Wang, Z.-M. Wang and S. Gao, Chem. Sci., 2013, 4, 1802.
22. (a) J. M. Zadrozny, D. J. Xiao, M. Atanasov, J. R. Long, M. Atanasov, F. Neese, F. Grandjean and G. J. Long, Inorg. Chem., 2013, 52, 13123–13131; (b) M. Atanasov, J. M. Zadrozny, J. R. Long and F. Neese, Chem. Sci., 2013, 4, 139–156.
23. (a) T. Fukuda, K. Matsumura and N. Ishikawa, J. Phys. Chem. A, 2013, 117, 10447–10454; (b) N. Ishikawa, M. Sugita and W. Wernsdorfer, J. Am. Chem. Soc., 2005, 127, 3650–3651.
24. (a) B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157; (b) K. Andersson, P.-A. Malmqvist, B. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483; (c) K. Andersson, P.-A. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218.
25. F. Aquilante, L. De Vico, N. Ferre, G. Ghigo, P.-A. Malmqvist, P. Neogrady, T. B. Pedersen, M. Pitonak, M. Reiher, B. O. Roos, L. Serrano-Andres, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224.
26. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.

---

Footnote

† Electronic supplementary information (ESI) available: Methods and additional characterization and discussion. CCDC 1479868, 1480094 and 1480095 crystallographic information of 1–4 can be obtained from the Cambridge Structural Database. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6sc02170k

---