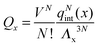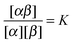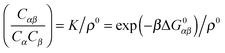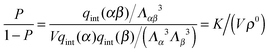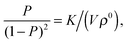Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theory and simulation of DNA-coated colloids: a guide for rational design
Stefano
Angioletti-Uberti†
a,
Bortolo M.
Mognetti†
b and
Daan
Frenkel
*c
aInternational Research Centre for Soft Matter, Beijing University of Chemical Technology, 100029 Beijing, P. R. China
bCenter for Nonlinear Phenomena and Complex Systems, Université Libre de Bruxelles, Code Postal 231, Campus Plaine, B-1050 Brussels, Belgium
cDepartment of Chemistry, University of Cambridge, Lensfield Road, CB2 1EW Cambridge, UK. E-mail: df246@cam.ac.uk
First published on 14th January 2016
Abstract
By exploiting the exquisite selectivity of DNA hybridization, DNA-coated colloids (DNACCs) can be made to self-assemble in a wide variety of structures. The beauty of this system stems largely from its exceptional versatility and from the fact that a proper choice of the grafted DNA sequences yields fine control over the colloidal interactions. Theory and simulations have an important role to play in the optimal design of self assembling DNACCs. At present, the powerful model-based design tools are not widely used, because the theoretical literature is fragmented and the connection between different theories is often not evident. In this Perspective, we aim to discuss the similarities and differences between the different models that have been described in the literature, their underlying assumptions, their strengths and their weaknesses. Using the tools described in the present Review, it should be possible to move towards a more rational design of novel self-assembling structures of DNACCs and, more generally, of systems where ligand–receptor are used to control interactions.
I. Introduction
Colloidal suspensions are well described by the same statistical mechanical equations as systems of atoms or small molecules. As a consequence, colloids behave in many respects as ‘scaled-up’ models of atoms, and like atoms, colloidal suspensions can be found in phases that resemble gases, liquids or crystals. There are, however, important differences. One is that colloids move in a solvent, rather than in vacuum. The other is that, through modification of the colloid or the solvent, we can tune the interactions between colloids in a way that is not possible for atoms or small molecules. Due to our ability to control colloidal interactions, colloids exhibit a much richer phase behaviour than atomic systems. Over the past two decades, our ability to design colloidal interactions has undergone a quantum jump with the development of so-called DNA-coated colloids (DNACCs), colloidal particles functionalised with short sequences of single-stranded DNA (ssDNA). DNA allows the colloids to bind selectively, either directly or through single-stranded linkers, to other particles or surfaces coated with complementary ssDNA sequences.DNA-coated colloids were developed by the groups of Mirkin and Alivisatos1,2 in the 1990s. Over the past decades, DNACCs (sometimes referred to as “spherical nucleic acid”3) have been studied intensively because of their promise for the development of new classes of ordered colloidal materials (see e.g.ref. 4–7). Furthermore, this system has interesting biomedical applications as ultra-sensitive biomarkers, detectors or efficient drug- and gene-delivery carriers.8–10 In all cases, applications exploit the selectivity of DNA–DNA hybridization between a complementary pair, as well as specific features of the physics of multivalent interactions.
Several reviews on DNACCs have appeared in the literature, both from an experimental11,12 and from a theoretical13,14 perspective. Very recently, Jones have provided a general overview describing the use of DNA-mediated interactions for the programmable self-assembly of nanomaterials,15 highlighting the connections, and the differences, between DNACCs and DNA-based nanotechnology.
The focus of the present Perspective is different. It is not our aim to provide a comprehensive overview of all simulation and modelling results in the field, but rather, to present a critical assessment of the various theoretical and computational approaches that have been proposed to describe DNACCs. However, this Perspective is not just a Review: to illustrate the points that we make, we also include new results. We aim to highlight the connections between different theoretical models, and explain the differences between various coarse-graining strategies used to describe DNACCs. We believe that the present perspective is timely, as the rational design of novel DNACC-based materials will require a complete integration of theory and experiment.
At present, theory and computational work are mostly used to explain experimental observations a posteriori. Yet these experiments are still largely driven by empirical or semi-empirical rules.16 Even when model predictions preceded experiments, the link between theory and experiments is often less than clear.
At present, there is a bewildering variety of DNACC models in the literature, and this very fact makes it difficult for the non-expert to decide what approach to use. The net result is that most models are never used by experimentalists. More worrying is the fact that theoretical models that have been shown to be based on questionable premises continue to be used in the literature, thus carrying the risk that analysis of the experimental data is flawed. For these reasons, the aim of this review is to discuss the various models in terms of their underlying assumptions, their range of applicability and their relative strengths and weaknesses, so that experimentalists can use them in an informed way.
The remainder of the paper will be structured as follows. In Section II, we describe the general principles common to the various analytical theoretical models, and then proceed to discuss the connections between them. In particular, we aim to establish a ‘hierarchy of accuracy’ in terms of the effects included. These analytical models contain input parameters that depend on the molecular structure of the system, e.g. the specific DNA-sequence grafted on the colloids, or details of the spacer used for grafting. When a systematic study of the effect of these parameters is required, and in order to relax some simplifying assumptions necessarily included in the analytical models, one should resort to computer experiments, i.e. simulations. We will deal with these “experiments” in Section III, where we will focus on the various coarse-graining strategies that have been proposed in the literature. In particular, we discuss which microscopic features are retained in the various models, and which are ignored. In particular, we will focus on the question if the model can yield meaningful predictions of the relevant experiments. In the Concluding section (Section IV), we will identify possible new directions where the existing theoretical and computational framework could be profitably integrated with experiments to yield a more rational design of DNACC-based systems.
II. Theory
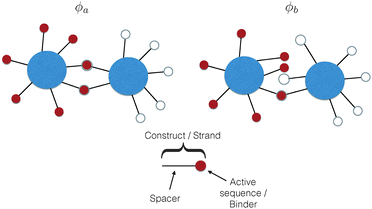
The common idea behind basically all theoretical models to describe DNA-mediated interactions in DNACCs17–27 is to account correctly for the interactions induced by the DNA strands that coat the colloids (a schematic of the system is depicted in Fig. 1). On the one hand, as in general for all colloidal systems stabilised by (non-absorbing) grafted polymers, a non-specific repulsion arises from compression of the DNA strands trapped between the colloidal cores. On the other hand, a highly specific inter-particle attraction occurs because of the decrease in free-energy due to bond formation1,2 (Fig. 2 provides a schematic illustration). That bond-mediated interactions are the driving force leading to aggregation is also evident from experimental studies that show no aggregation between DNACCs grafted with non-complementary strands.1,2,25 In fact, other (non-specific) attractive interactions, in particular those arising from the van der Waals forces between the colloidal cores, are typically much weaker than those arising from bond formation on the length-scales at which bond-mediated binding occurs. This is mainly due to the fact that the non-specific steric repulsive forces due to DNA compression prevent the colloids to approach at short distances where dispersion forces are strong.26 For similar reasons, the length-scale for binding, i.e. the typical distance between colloidal cores between bound particles, is dictated by the length of the spacer used to graft DNA on the surface of the colloids, which is typically in the range of nanometers to tens of nanometers.17 In various practical realisations of DNACCs, other polymer chains than DNA are grafted to the colloidal surface. Using an additional different polymer for steric stabilisation makes it possible to tune repulsion and attraction separately. Both theory and experiments have shown that tuning the relative strength of attraction and repulsion can lead to self-assembly of aggregates of different types.28–30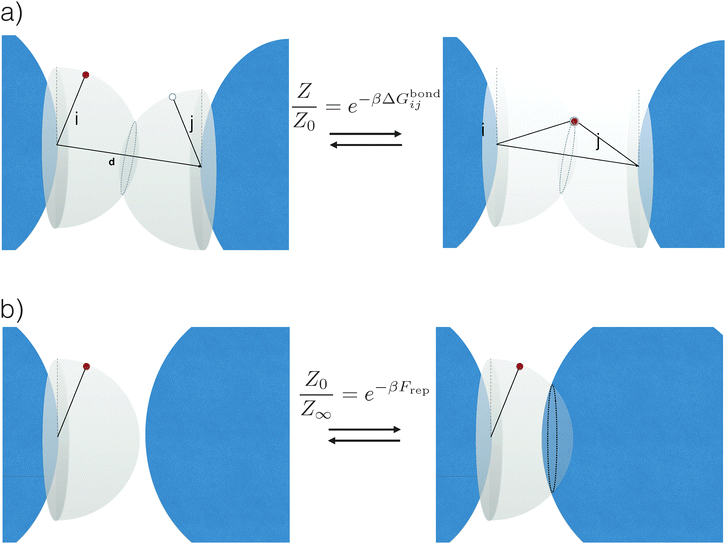 | ||
| Fig. 2 Schematic representation of the origin of attractive and repulsive forces, here shown for a simple system of strands considered as rigid rods and in the case where only a single bond can be formed. (a) Upon binding, the system acquires an additional energy ΔGbondij, which depends on both the chemical identity of the active strands (white and red circles) as well as on details of the spacer (black sticks) and position of the tethering points (see eqn (3)). In particular, note that whereas in the unbound state (left) the active strands can freely move on a hemisphere, upon binding (right) they are forced to stay on a circle: this reduction in configurational space is at the origin of ΔGcnf, (see eqn (4)). (b) When all colloids are far apart from each other, the active strands can span a whole hemisphere. However, this space is again reduced once colloids start to get closer. This reduction is at the origin of the dominant repulsive forces Frep between DNACCs. | ||
It is crucial to note that the interaction between two grafted colloid is due to both energy and entropy, the latter accounting for the fact that often not just one but several binding configurations are possible (see Fig. 1). Hence, to compute the interaction strength, we need to evaluate a free energy, rather than an energy, as would be the case for atoms in vacuum. To compute the free energy of interaction of DNACCs, we start from the statistical mechanical relation between the free energy F of a system and its partition function Z. We consider an arbitrary number of colloids, each of which has an arbitrary number of strands grafted on its surface. We choose a reference state where all colloids are at infinite distance from each other, and calculate the free-energy with respect to this state:
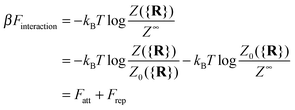 | (1) |
Since Z = Z0 + Zbound, Fatt is always negative (and, hence, attractive). Instead Frep is the ratio between two partition functions where bonds are never allowed, although in one case (Z0) strands can feel the excluded volume due to all colloids, including the one on which they are grafted, whereas in the other (Z∞) strands can only feel the latter. If we assume that only repulsive interactions between the colloidal cores and the strands occur, i.e. we consider non-adsorbing polymers, a good approximation for most type of polymers used in DNACCs, then Z0/Z∞ < 1, and Frep is always positive (i.e. repulsive).
Use of eqn (1) would allow one to calculate the interaction between DNACCs including all type of many-body interactions arising from bond formations, and for arbitrary position of the colloids. This expression does not assume that DNA-mediated interactions are pairwise additive – and, in fact, often they are not.28,31,32 For this reason, the general expression is needed to compute the interaction free energy of dense phases of DNACCs.
Let us next consider how Fatt and Frep can be calculated. One route is both obvious and pointless: ‘brute-force’ atomistic simulations. Simulations that would describe the colloids, the DNA and the solvent in atomistic detail are simply much too expensive to be used to predict, say, phase diagrams. Fully atomistic simulations can certainly be used to study certain aspects of DNACCs, but not to study a suspension containing hundreds or thousands of such particles. In what follows, some degree of coarse-graining is therefore essential. Typically, this means that we will use an implicit solvent model and that we will assume that the binding free energy between complementary DNA strands is known. In other words: models to describe systems consisting of many DNACCs are always coarse-grained.
To arrive at an analytically tractable coarse-grained model, the following assumptions are commonly made: (1) we usually ignore the spatial extent of the nucleotide sequences that can hybridise to bind two strands together. The hybridising strand is then represented as a point-like attractive site, also called ‘active site’ or ‘sticky end’, tethered to the colloidal surface by a long chain – the spacer or linker17,19–27 (see also Fig. 1). Representing the ‘sticky’ binding sequence as a point is a reasonable approximation as long as the spacer is much longer than the sticky end, a situation typically encountered in experimental systems.1,2,5,17,21 Considering extended sticky ends results in slightly different binding affinities between constructs.23,33 Accounting for the finite spatial extent for sticky end does not qualitatively change the theoretical treatment of DNACCs, and hence we limit our discussion to point-like sticky ends. (2) We ignore steric interactions between different strands and, more generally, any non-selective strand–strand interaction. This approximation is very common, but it is likely to break down for dense DNA ‘brushes’.
With the above assumptions, Frep can be expressed as:
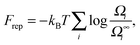 | (2) |
The calculation of Fatt is more challenging, since here we need to account for all possible binding configurations with an arbitrary number of bonds (see Fig. 1). In order to do that, it is useful to split the problem of calculating Fatt into two parts. The first stage involves calculating the bond formation energy for all individual pairs of (i, j) strands, and the second stage accounts for the fact that there may be many ways in which the DNA strands on adjacent colloids may be connected (as illustrated in Fig. 1). If the spacer does not influence the structure of the sticky end, one can split the bond formation free energy into two terms:21,23,26,28
| ΔGbondij = ΔG0ij + ΔGcnf(ri, rj, {Ri}). | (3) |
The first term on the r.h.s. of eqn (3) is the free-energy of binding for untethered, complementary DNA strands i and j in solution: exp[−βΔG0ij] = Keqijρ0, where Keqij denotes the equilibrium binding constant, and ρ0 the standard concentration of 1 M. The second term represents the configurational entropic cost associated with linking two tethered strands i and j: the number of configurations of a linked ij strand is less than that of the unlinked i and j strands35 (see Fig. 2a). ΔGcnf(ri, rj, {Ri}) depends on the exact positions of the grafting points, and on the position of all nearby colloids in the system, since these exclude all strand configurations that would intersect them. Ref. 22 and 23 give an explicit expression that can be used to calculate this quantity for arbitrary linkers and colloids positions, which in its most general case reads:
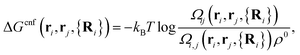 | (4) |
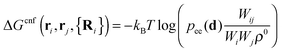 | (5) |
ΔGcnf(ri, rj, {Ri}) can be either calculated analytically for simple polymer models, or computed via Monte Carlo simulations, as we discuss in Section III. In a small number of (important) cases, it can be approximated analytically.17,21,23 The different theories that have been proposed to estimate Fatt make different approximations to calculate this quantity. However, all models20–22,25 assume that strands are non-interacting (although the interaction can still be included in calculating the bond energy23). This approximation is reasonable when different chains are not close to each other. At higher grafting densities (see e.g.ref. 31 and 32), the simple analytical approaches break down, but the simple theories can still be used to gain insight in the effect of the structure of the spacer (e.g. rigid rods or freely jointed chains) on the interactions between DNACCs. For example, “theory accounts” quite well for the experimentally observed trends in the melting properties of DNACCs.21,22
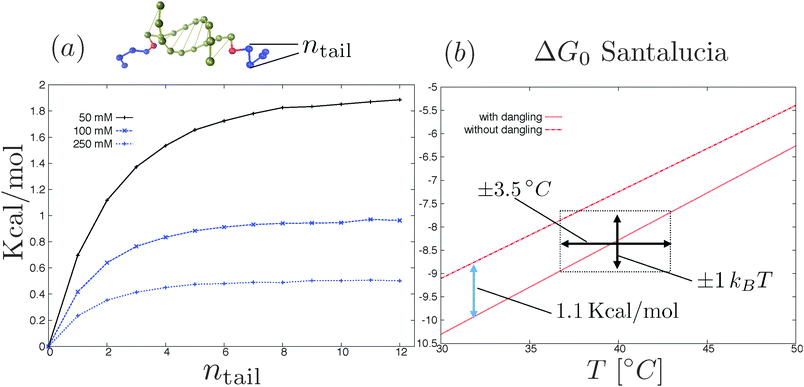
Under the assumption that the binding free energy ΔGbondij between i and j does not depend on the presence of other strands (i.e. the non interaction assumption), knowledge of ΔGbondij for all possible pairs of constructs (i, j) is sufficient to write down an exact expression for the partition function Z:
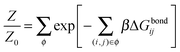 | (6) |
An exact enumeration of the terms in eqn (6) becomes rapidly intractable since the number of binding configurations increases very rapidly with the number of strands in the system. Hence eqn (6) is typically simplified under some assumptions. It is at this level of approximation that differences between the various analytical theories show up.17,19,21,23,25,27 Short of exact enumeration, Z/Z0, and hence Fatt, can be calculated to any given accuracy via Monte Carlo simulations using thermodynamic integration,36 providing a route to fully include all possible competitive effects between formation of different binding configurations, as well as about the spatial distribution of the strands. The exact solution reads:23,24,26
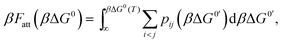 | (7) |
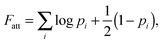 | (8) |
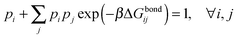 | (9) |
In our derivation of eqn (8) and (9) we used an approximate yet very accurate formula for counting the degeneracy of each binding configuration, accounting for the fact that no two linkers can bind to the same target.27 From a combinatorial point of view, it turns out that our procedure can be mapped onto Wertheim's theory for the equilibrium properties of fluids with highly directional inter-molecular forces.37–39 Wertheim's solution is a basic ingredient of the widely used SAFT theory.40 In practice, each reactive DNA strand (or, more generally, each binder) must be considered in the Wertheim picture as a spatially and orientationally fixed particle with a single binding site, but each having a unique bond energy, which in our case must also be defined as in eqn (3). In our system, we also have the additional benefit that some of the approximations Wertheim used are always exactly satisfied conditions, in particular the fact that if two strands are bound a third one cannot bind at the same time. Once the problem is cast in these terms, it becomes mathematically equivalent to that of Wertheim.
The approximations underlying eqn (8) and (9) become exact in the case of mobile constructs, see ref. 28 and Section III for more details. Finally, we stress that although these equations provide the Fatt induced by the interaction between grafted strands. It is easy to show that they remain the same when binding between these strands is not direct, but is mediated by (or compete with), free complementary strands in solution, another widely used bonding scheme in DNACCs. In practice, eqn (8) and (9) remain valid, as well as the configurational part of the bond free-energy ΔGcnf, whereas the solution hybridisation free-energy ΔG0ij between strands must be shifted with a density dependent factor.
Since eqn (8) and (9) agree extremely well with the corresponding MC simulations, they also properly reproduce all the (important) correlations introduced by the competition between strands for the same binding partner. Moreover, they are completely general in that they can be used to treat an arbitrary number of different binding pairs, with any spatial distribution. Hence, they can be used to calculate colloid–colloid interactions also when highly non-homogeneous DNA coatings are present, as in the experimental system reported by Pine and coworkers mimicking patchy particles.41
Earlier expressions that have been proposed in the literature17,19,21,22 can be derived as approximations of eqn (8) and (9) under different assumptions.27 In particular, the aforementioned models all shared a mean-field approximation for binding, i.e. unlike eqn (8) and (9) they do neglect correlations that are due to the fact that two strands cannot bind simultaneously to the same binding partner (the ‘valence constraint’23). Furthermore, strands were not only treated as if they were completely independent from each other, but also as if they were all statistically equivalent. The first approximation becomes progressively worse as the binding strength of bonds increases (relative to kBT). This drawback can be heuristically corrected by a self-consistent mean field treatment,42 which yields the mean-field version of eqn (9). The assumption that all bonds are statistically equivalent gets worse as the grafting of chains becomes more heterogeneous, since in this case each strand will experience a different environment. However, if we assume that both approximations are justified, then the expression for Fatt simplifies:17,19,21,22
| Fatt ≈ −kBT〈n〉 | (10) |
A possible way to estimate Fatt for an arbitrary number of types of strands was proposed by Rogers and Crocker.25 Heuristically keeping eqn (10) as the expression for the attractive contribution, they proposed to use mass balance equations valid for chemical reactions in solution to describe binding between grafted strands, an approach dubbed “Local Chemical Equilibrium” (LCE). In ref. 25 it is assumed that the binding for grafted strands can be treated as an equilibrium binding reaction in solution with a non-homogeneous distribution of active sites. This distribution is obtained by Monte Carlo sampling the position of the end-point of polymer chains. Fatt is then approximated as:
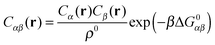 | (11) |
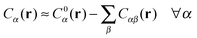 | (12) |
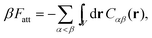 | (13) |
A. Equilibrium in bulk binary reactions
In order to derive the (LCE) expression for DNA binding, it is important to realise that tethered DNA strands are distinguishable. The derivation of the condition for local chemical equilibrium is therefore different from the case where the reactants and products comprise molecules that are indistinguishable. As an illustration, we will assume that the tethering of DNA strands results in a confinement of the ‘reactive’ ends, but that the free-energy cost of tethering can be ignored (this assumption can subsequently be refined). We consider the hybridisation reaction α + β ⇌ αβ. As we can ignore the tethering free energy, we can treat the mixture of α, β and αβ strands as an ideal gas of distinguishable particles. We assume that, α, β and αβ are confined to a volume V that is small, but large enough to contain many molecules. The partition function of a system with Nα (Nβ) monomers of type α (β) and Nαβ complexes is then: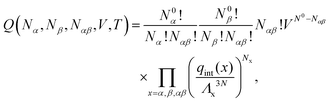 | (14) |
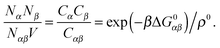 | (15) |
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1) or less. This is typically the case when the average distance between grating points is not small compared with the length of the tether.
(1) or less. This is typically the case when the average distance between grating points is not small compared with the length of the tether.
It may seem surprising that the approach of ref. 25 yields results that were compatible with the experimental data, given the fact that eqn (12) is based on an approximation, and that the mean-field assumption is not expected to be particularly good in the case studied in ref. 25. It is probably more likely that the accuracy of the experiments reported in ref. 25 was insufficient to discriminate between different models.23,43
For this reason, the best way to discriminate between various approximate models is to use computer ‘experiments’ in which ‘exact’ Monte Carlo simulations of a specific model are used to compare between different approximations. In particular, if a model cannot reproduce the behaviour of a well-characterised model system, its agreement with experiments must be fortuitous. In ref. 24, we compared the different analytical theories with MC calculations to test the validity of mass balance equations and found that LCE can give results that differ substantially from the ‘exact’ simulation results, especially at high binding strengths (see also Fig. 3). It should come as no surprise that the agreement worsens at high binding energies as eqn (10) is only recovered from our analytical theory eqn (8) in the weak-binding limit pi → 1.27
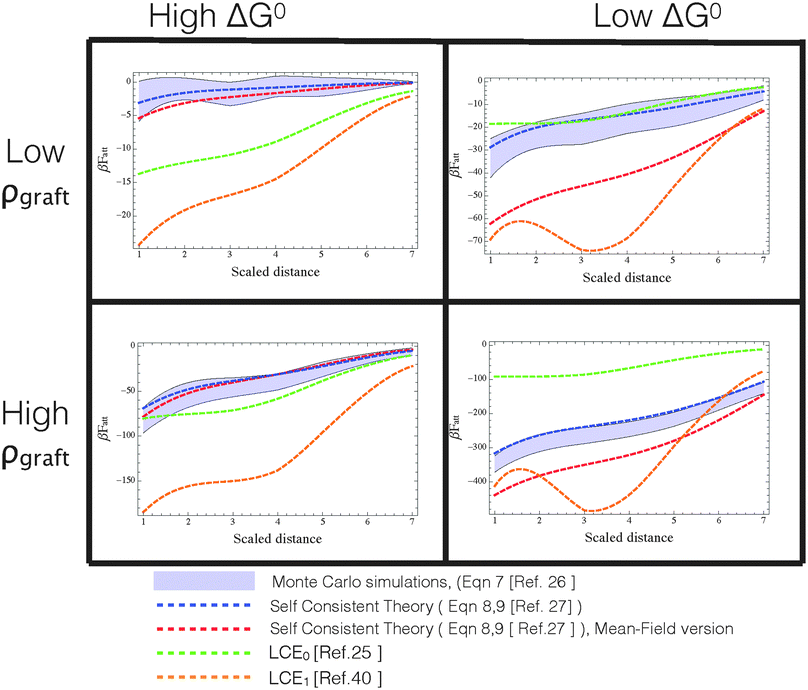 | ||
Fig. 3
F
att as a function of distance between DNA-functionalized planes at various temperatures and coating densities, calculated via different approximate analytical theories (dashed lines) and Monte Carlo data (shaded region representing the uncertainty determined in the simulations). Different panels represent different combinations of βΔG0 = [−10,−15] from left to right (roughly proportional to temperature), and strands grafting densities ρgraft ≈ [0.006,0.03] strands per nm2 from top to bottom. For reproducibility of these results, we mention that planes have a surface area of 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 884 nm2 and either 93 or 19 (randomly grafted) strands in the high and low density regime, respectively. Color code: red = self-consistent theory with added spatial averaging of receptors,23 blue = self-consistent theory, green = LCE0 as in the original version,25 orange = LCE1, as modified by Rogers and Manoharan.44 Note that only the self-consistent theory properly describe the Monte Carlo data in all ranges of densities and βΔG0. Both forms of LCE provide a decent comparison at high ΔG0 (=high temperatures) and high grafting densities, but fail outside this regime. 884 nm2 and either 93 or 19 (randomly grafted) strands in the high and low density regime, respectively. Color code: red = self-consistent theory with added spatial averaging of receptors,23 blue = self-consistent theory, green = LCE0 as in the original version,25 orange = LCE1, as modified by Rogers and Manoharan.44 Note that only the self-consistent theory properly describe the Monte Carlo data in all ranges of densities and βΔG0. Both forms of LCE provide a decent comparison at high ΔG0 (=high temperatures) and high grafting densities, but fail outside this regime. | ||
A more positive finding is that, in the weak-binding limit eqn (10) remains still valid for an otherwise arbitrary distribution of binding strengths. No such good news is in store for the LCE: it fails, even in the weak-binding limit because mass-balance equations can only be used to calculate the bond densities when considering the binding between free-strands in solution, not for grafted strands, where the local mass-conservation implicit in eqn (12) does not hold. However, starting from our self-consistent equations, eqn (8) and (9) we can show that a better LCE approximation for the binding densities is given by:
| C0α(r) = Cα(r)/pα | (16) |
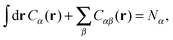 | (17) |
The theoretical work presented thus far is based on various assumptions, as summarised in Table 1. The validity of the approximations involved in the theory should be tested against numerical simulations for the same model system, whereas the quality of the underlying molecular model (flexibility, binding strength, inter-molecular interactions) should be checked against experiments. The most stringent experimental test to date is the ability to reproduce the inter-colloidal potentials as measured in optical-tweezer experiments. Probably even more importantly than reproducing quantitative data, the presented theoretical framework also provides important qualitative insight: it allows one to rationalize various important properties of DNACCs, such as the fact the DNA-mediated binding of DNACCs has a much sharper temperature response than free DNA in solution. As a consequence, DNACCs show higher selectivity in discriminating between slightly different target DNA strands as used in biosensing applications.8 Moreover, the theory explains why DNACCs have a higher dissociation (‘melting’) temperature than free DNA in solution21 and it accounts for the dependence of the melting temperature of DNACCs on the type of spacer used for grafting DNA.21,45 Within the model, all these effects follow from either multivalent effects due to the large number of binding configurations, or from the entropic penalty ΔGcnf arising due to grafting constrains upon bond formation.
| Main approximations implicit in analytical theories |
| 1. No strand–strand interaction besides those contained within ΔGbondij |
| 2. No interactions besides excluded volume between colloids and strand |
| Features included in analytical theories |
| 1. Effects induced by changes in binding strength in solution via ΔG0ij |
| 2. Effects of spacer configurational entropy, i.e. spacer structure |
| 3. Presence of multiple bond formation |
| 4. Competition for bonds between different strands – but only in general treatment of eqn (8) and (9) and equivalent LCE, i.e. effects due to competing binding configurations |
The availability of an accurate and predictive theory (eqn (8) and (9)) made it possible to explore how the competition between different strands for binding would affect the phase behaviour of DNACCs. Examples are the prediction of the design rules for mixed-strand DNACCs that can undergo re-entrant melting, and the possibility to achieve temperature independent interactions due to purely entropy-driven binding.29 Although the subsequent experiments that reported both effects44 used a slightly different system than the example discussed in ref. 29, the physical basis of the observed effects was the same. The easiest way to see this is by considering the predicted temperature dependence of the inter-colloidal potential of the systems of ref. 29 and 44. The underlying cause of the reentrant melting is simply that the effective attraction first increases with decreasing temperature, and then drops again, whereas the reason for a widened solid–fluid coexistence stems from purely entropy-driven (and hence temperature independent, considering Fatt/kBT) interactions, see Fig. 4. The first behaviour is due to a thermal control of the dominant type of bond in systems featuring competing linkages,29,42 while the second arises from purely combinatorial factors between configurations featuring the same number of hybridised strands, but a different number of bonds between colloids (since some of the hybridise strands do not contribute to inter-particle binding).29,44
 | ||
| Fig. 4 Schematic representation of the variation of the strength of the effective pair-attraction between DNA-coated colloids. Panel a shows the case of a non-monotonic temperature dependence of the interaction strength. Such behaviour can be realised in DNA coated colloids and results in a re-entrant phase diagram in which the solid phase melts upon both heating and cooling (see text and ref. 29 and 46). DNA-mediated reentrant melting has been observed in subsequent experiments.44 In ref. 29, the DNA-mediated potentials were induced via inter- and intra-particle hybridisation between grafted strands, whereas in ref. 44 an indirect hybridisation via free-strands in solution was used. Panel b shows the case where attraction at low temperatures is entropy-dominated. In that case, the attraction strength is approximately ΔFatt ≈ −TΔS, which, when multiplied by βΔFatt, becomes temperature independent. A temperature-independent (scaled) interaction results in a temperature-density phase diagram with a constant width of the gas-aggregate coexistence region. | ||
The fact that seemingly different systems can be described by the same theory and exhibit the same behaviour, allows us to make an important general point: as long as we have quantitative information about the strength of the ligand–receptor interactions, the nature of the linkers is immaterial. ssDNA is a very convenient molecule to link different colloids together, but there are many other candidates (for example, the cucurbit[8] uril system,47 or sialic acid/hemagglutinin complexes when nanocolloids/virus interactions are concerned48,49): the underlying physics remains exactly the same. We stress this fact because the development of applications non-DNA-based multivalent binding is expanding rapidly,50 and such applications can be rationalized, and designed, using the presented framework.
In the context of DNA-mediated interaction, cooperativity is often mentioned as a crucial aspect. In the theoretical description above, cooperativity plays no role; we assume explicitly that the formation of one bond does not change the binding strength of others, and yet our theoretical predictions agree very well with experiment. To avoid all confusion, we stress that, of course, the fact that one bond between two colloids has formed, makes it easier for subsequent bonds to form, simply because the loss of translational entropy of the binding partner is incurred in the first binding event only. However, that phenomenon has nothing to do with a phenomenon where, at a microscopic level, the strength of subsequent bonds is enhanced by a change in the local environment. In fact, the latter type of cooperativity is very hard to demonstrate,51–54 and it would seem that all experiments where special, cooperative effects were invoked (in the context of an overly simplistic theory)51–54 can, in fact, be explained within the theoretical framework that we discuss here, without cooperativity. This does not mean that there cannot be cooperative effects but simply that the evidence is lacking, if agreement with a simpler theory can be viewed as Occam's razor.
Having said this, there are definitely cases where cooperativity – but, in this case almost certainly negative cooperativity – could play a role: in nano-sized colloids, and possibly for the recently developed micron-size colloids,55 grafted strands can be close enough to each other to feel the local change in the environment upon binding, be it entropic or electrostatic in origin.18,56,57 Our key message is that the sharper melting behaviour of DNACCs, the key experimental finding that is often cited as evidence in support of the cooperativity model,18 is perfectly well explained by our simple model that ignores cooperativity (and, in fact, by even much simpler, non-cooperative models12). On the experimental front, a sharper melting is also clearly observed for systems of micron-sized DNACCs where grafting densities were too low for any cooperativity to occur.19,20 It is appealing that a simple theory that needs not invoke specific, system-dependent cooperative effects can provide a unified explanation of DNACC melting for a wide range of systems.
III. Simulations
Any numerical model of DNACC systems must account for the multi-scale nature of the problem. The reason is that the physical properties of DNACCs depend on both microscopic and mesoscopic features, such as the sticky-end sequences, the structure of the spacers, and the grafting density of the DNA units, that enter into the design of the system at different length scales. In fact, the differences between various types of DNACCs are substantial. For instance, whilst nano-sized DNACCs may be coated with only a few dozen DNA strands, micron-sized DNACCs may be coated with tens of thousands of DNA strands,55,58 although typically the coating density in this case is much lower than for nanocolloids.Not surprisingly, particles that are that different require different coarse-grained modelling and simulation strategies. The modelling approaches for micron and nano-sized colloids will be reviewed in Sections IIIA and IIIC respectively. In Section IIIB we extend the discussion to micron-sized particles with mobile rather than grafted strands, e.g. suspensions of functionalised lipid-bilayers and emulsions. Although, in principle, fully atomistic modelling of DNACCs is conceivable, the cost of such an approach would be prohibitive and, as in other areas of colloid science, there is no need for such a brute-force approach. However, it should also be clear that microscopic details matter as the interaction between ssDNA strands depends sensitively on their nucleotide sequence. Any model, no matter how coarse-grained, must take this specificity into account.
Roughly speaking, there are three classes of coarse-grained models that account for the DNA specificity in different ways. The most detailed approaches explicitly account for the pairing of the individually-resolved nucleotides (see part 1 of Fig. 5).59–61 Recently, more portable but expensive models, also capturing the double stranded structure of DNA, have been introduced.62–64
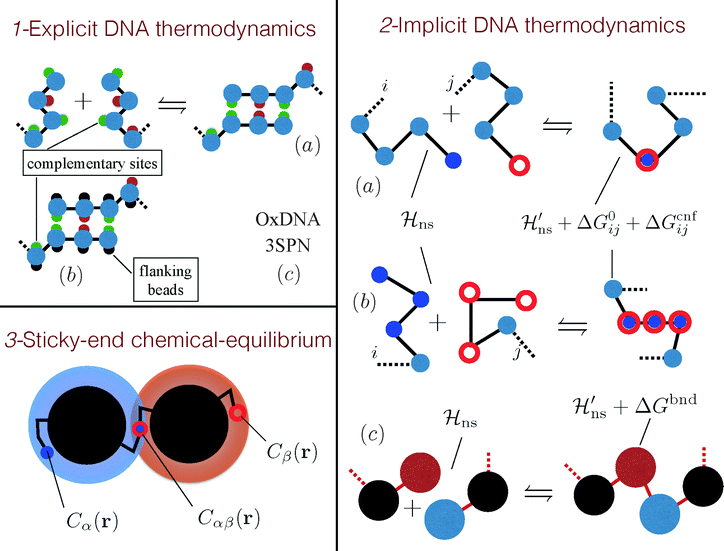 | ||
| Fig. 5 Modelling DNA hybridisation in DNACC systems. (1) Models that feature explicit DNA thermodynamics attempt to recover DNA hybridisation with an explicit modelling of the dimerisation process. (a) Ref. 59 and 60 used a bead-and-spring ssDNA representation decorated by sites that selectively attract. (b) This model was ameliorated by ref. 61 that introduced flanking beads to avoid binding between more than two bases. Although the molecular mechanism for binding is retained in these models, none of them tries to match the real thermodynamics of DNA hybridisation but simply use an effective nucleotide–nucleotide interaction which should be considered as a tunable model parameter. (c) Nucleotide level models, such as SNP364 or OxDNA,62,63 have been parametrised using thermodynamic experiments. (2) Models that feature an implicit DNA hybridisation rely on empirical estimates of the hybridisation free energy of the sticky ends (ΔG0ij).69,70 (a) Chains, interacting by non selective Hamiltonians (Hns), hybridise by coalescing the two reactive end-elements according to ΔG0ij and to a configurational cost (ΔGcnfij), that depends on the algorithm that generates the hybridised chain.23,24,31,72 Notice that the non selective Hamiltonians of the free and bound states are not the same.23,31,72 (b) A similar scheme was previously proposed by Mladek et al. that also considered the case in which more reactive sites bind resulting in a rigid dsDNA segment.31,32 (c) For long λ-DNA ref. 74–76 used a blob representation in which reactive blobs are chained according to an hybridisation free energy ΔGbnd. (3) For ideal spacers23 a local chemical equilibrium balance can be used to calculate the fraction of hybridised strands (αβ).23,25,28 The concentrations of the sticky ends around the colloids C(r) are calculated by the end-to-end distribution functions of the tethered spacers,25 while the equilibrium constant between sticky ends is ΔG0ij. | ||
A more coarse-grained approach uses empirical rules for the binding free-energy of DNA sequences. In this description, the binding sequences are represented as structureless points (see part 2 of Fig. 5), and the binding free-energy is given by eqn (3), as discussed in Section II. Finally, a less well-founded, but nevertheless frequently used approach is based on the ‘chemical equilibrium’ approximation (see part 3 of Fig. 5). The chemical equilibrium theory treats binding reaction as a dimerisation reaction in a confined gas of sticky end groups. The advantage of this approach is that it is simple and, when the balance between free and bound ideal constructs is properly implemented (see Appendix B in ref. 23), it becomes equivalent to rigorous treatments. However these methods are practical only in the ‘mean field limit’, where the spatial distributions of sticky ends are not strongly dependent on the exact position of the grafting points.
A. Micron-sized particles
Micron-sized colloids may be coated with several thousands of constructs per particle.17,20–22,25,55,58,65,66 A detailed representation of such a large number of constructs is usually not computationally feasible even when the aim is only to study the effective interaction between two colloids. The problem is, however, not as serious as it seems, because large particles tend to have a radius of curvature that is much larger than the length of the binding strands. Under these conditions, one can use the Derjaguin approximation (see e.g.ref. 67) to calculate effective pair potentials between colloids26,29,68 from knowledge of the distance-dependence of the interaction between two flat, parallel surfaces. If this approximation is not used, a local chemical equilibrium approach (or a “spatially averaged” version of the self-consistent equations, see ref. 23 and 27, and Fig. 3) is still tractable, but for all approaches based on the explicit calculation of interaction between complementary strands, use of the Derjaguin approximation becomes imperative. With the Derjaguin approximation, the fact that micron-sized colloids can be coated with very large numbers of DNA strands does not create a technical challenge. As discussed Section II, most theoretical approaches developed to study DNACCs are based on the assumption that non-binding strand–strand interactions can be ignored. We stress that this assumption is not essential (and questionable for nano-sized colloids: see ref. 31 and 32 and Section IIIC), but in many cases, the neglect of non-binding strand–strand interactions is justified, in which case an accurate estimate of ΔGcnf is all that is required to obtain quantitatively accurate potentials from computer simulations. In practice, we calculate the partition function of unbound strands and the configurational part of the binding free energy of two strands, ΔGcnf, by simulation. The strand–strand binding free energy ΔG0 is not obtained from simulation but from the empirical SantaLucia rules.69,70 Again, more sophisticated rules could be used where necessary. Once these two ingredients are known, and if strand–strand interactions can be neglected, the theoretical approaches described in Section II can be used to calculate accurate inter-particle potentials. As was demonstrated in experiments of Bracha for DNA-chips et al.71 strand conformations are weakly affected by DNA–DNA interaction up to thousand strands per μm2. Moreover, a rough estimate26 suggests that the contribution of non-bonded spacer interactions to the free energy of the system is of the order of one kBT unit per strand, which is much smaller in absolute terms than the typical values of the configurational and combinatorial free-energy that are around ≈10kBT for typical spacers.21A notable exception of a micron-size system where non-bonded strand interactions may be significant is provided by the densely grafted micron-sized colloids studied by Pine and co-workers.55,58 The reason why higher grafting densities could be reached in ref. 55 and 58 is that in these experiments, grafting was achieved by using click chemistry, rather than via the use of rather bulky streptavidin constructs that anchor the biotinylated spacers.
Having sketched the various theoretical approaches to predict the binding strength of DNACCs, we next consider how to estimate the change in the configurational free energy ΔGcnf of the grafted strands as the distance between colloids is varied. In general, ΔGcnf can be computed using Monte Carlo simulations.23,24,72 Practical aspects of these calculations for ssDNA constructs are discussed in Appendix B. In this modelling, it is important to account for intra-chain Coulomb interactions. For instance, ssDNA constructs have been modelled as uniformly charged, freely-jointed chains (FJC)34 with screened Debye–Hückel interaction (see, e.g.ref. 73). Such an approach has been used to model micron-sized23,24,72 and, as we will discuss later, nano-sized31,32 DNACCs. When accounting for electrostatic interactions in this way, the electrostatic contribution has to be removed from the phenomenological DNA hybridisation free energies, to avoid double counting.
The numerical approach to compute the configurational contribution to the DNACC interaction described in Appendix B is efficient for short to medium length linkers that can be coarse-grained into at most a few dozen Kuhn segments. However, the same methods would be computationally unfeasible when applied to very long chains. Numerical studies of colloids functionalised by very long DNA strands such as λ-DNA77,78 require a further simplification of the description of the DNA degrees of freedom. Bozorgui and Martinez74–76 employed a numerical approach based on the ‘blob’ representation of long polymer chains79,80 in which entire DNA constructs are lumped into sites interacting via gaussian potentials.79–81 Multi-blob models have been used by Mladek et al.,31,32 but the approach, whilst fairly accurate, quickly becomes cumbersome. The potentials between the blob and the colloids have been parametrised by using explicit ‘all-monomer’ simulations, while the hybridisation reactions between complementary strands is simulated using a dedicated MC move that attempts to join two complementary blobs with a cost equal to ΔGbondij, where ΔGcnf is given by the energy of an harmonic spring connecting the centres of the two blobs of the form βΔGcnf = 0.534(r/Rg − 0.730)2, where Rg is the gyration radius of the strand and the numerical values have also been parametrised using all monomer simulations (see part 2c of Fig. 5).
The ultimate aim of coarse-grained modelling of DNACCs is to predict their phase behaviour. Once the tools are in place to compute the DNACC interactions, standard free-energy calculations36 can be used to compute phase diagrams. Examples of such studies can be found in ref. 74–76. These simulations showed that DNACCs exhibit very interesting phase behaviour. For example, the simulations showed that the liquid–crystal–vapour triple point disappears as the number of grafted chains drops below a threshold of around 12. In that case, the ‘ground-state’ at zero pressure but high densities is a liquid, not a crystal.76 Recent simulations on ‘patchy’ colloids,82 showed similar behaviour in such systems.
B. Mobile tethers
Recent experiments have studied DNACCs where the DNA strands are mobile, rather than grafted in fixed positions. Examples include emulsions83–85 and lipid bilayers33,86,87 functionalised by hydrophobised DNA constructs terminated by reactive sticky end sequences.It is straightforward to extend the theoretical tools to model DNACCs with grafted DNA strands to the case where these strands are mobile: due to the translational degrees of freedom of the binders, the hybridisation free-energy needs to include an extra configurational term (ΔGtrn) that accounts for the constraint on the relative position of two tethering points when bound
| ΔGbondij = ΔG0ij + ΔGcnfij + ΔGtrnij. | (18) |
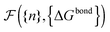 calculated as a function of the number of bridges between bound colloids ({n}) and the matrix of the hybridisation free energies ΔGbondij (where i and j now represents a strand type, not a single specific strand). Taking the large number of binder per particle limit, a saddle-point approximation provided the most probable number of bridges between colloids (
calculated as a function of the number of bridges between bound colloids ({n}) and the matrix of the hybridisation free energies ΔGbondij (where i and j now represents a strand type, not a single specific strand). Taking the large number of binder per particle limit, a saddle-point approximation provided the most probable number of bridges between colloids (![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) )
)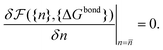 | (19) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) } one can calculate the attractive potential between colloids
} one can calculate the attractive potential between colloids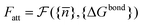 | (20) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) are expressed in term of probability of making bridges between colloids). It is possible to generalise this discussion to systems featuring different types of bonds including not only bridges but also loops.33 Slightly different expressions are obtained in presence of infinite reservoirs of binders as shown in the study of a vesicle interacting with a large supported lipid bilayer.87
are expressed in term of probability of making bridges between colloids). It is possible to generalise this discussion to systems featuring different types of bonds including not only bridges but also loops.33 Slightly different expressions are obtained in presence of infinite reservoirs of binders as shown in the study of a vesicle interacting with a large supported lipid bilayer.87
Eqn (19) and (20) were used to simulate rigid colloids functionalised by mobile strands (a possible experimental realisation being that of ref. 86) in which colloidal suspensions are sampled using an effective interaction free energy Fatt({Ri(t)}) + Frep({Ri(t)}) that only depends on the positions of the colloids {Ri(t)}.
We note that the behaviour of DNACCs with mobile linkers can be qualitatively different from that of DNACCs with grafted linkers, in other words: mobile linkers introduces new physics in the system. For example, ref. 28 showed that the inter-colloidal potential induced by DNA-hybridisation of mobile linkers is intrinsically a multi-body interaction. This is due to the fact that each construct on a given particle can bridge all the neighbouring particles. Hence, different neighbouring colloids may compete for the same linkers. As the number of bonds with different neighbours are now correlated, the free-energy cannot be decomposed into the sum of pair-interactions. The fact that DNACCs with mobile linkers have intrinsically multi-body interactions can be exploited used to control the ‘valency’ (preferred number of complementary neighbours) of a particle.28 This is interesting because conventional approaches to tune the valency of colloids are based on the use of different number of interacting ‘patches’. However, the preparation of well-controlled patchy colloids is non-trivial. In contrast, DNACCs with mobile linkers can have a preferred valency without the need of physically creating real patches on the surface of the colloid.41
Even more complex effects should be expected for systems of mobile strands where the colloid to which they are attached is deformable, as in the case of DNA-functionalised vesicles,33 where the flexibility of the lipid membrane plays a non-negligible role87 in determining the bond-mediated interaction. For instance, Hu and collaborators88 considered the interaction between two membranes that were coated with complementary proteins (rather than DNA). They found that the equilibrium constant for protein–protein binding (i.e. ΔGbond in our nomenclature) decreases by a factor that is controlled by the roughness of the membranes.88 This effect, when translated to DNA-mediated interaction, can be expected to have important consequences for the self-assembly.
C. Nano-sized particles
Modelling the interaction between nano-size DNACCs is more demanding than modelling their micron-sized counterparts. The underlying reason is simple: the length-scale separation that justifies the factorisation between the different driving forces and facilitates modelling of micron-sized particles is less pronounced for nano-sized particles.There are other differences as well: many of the earlier experiments on DNACCs (although not the most recent ones55,58) used a bulky streptadivin–biotin construct to tether DNA strands to the surface of micron-sized colloids. In contrast, DNA anchoring to gold nano-particles is usually achieved by bonding the (much smaller) thiol group to the gold surface. As a consequence, the density of the DNA strands on nano-sized colloids is sufficiently high that the interaction between different DNA-strands cannot be neglected for a quantitative modelling. Constructing a coarse-grained model of nano-sized DNACCs is therefore much more system-specific than for micron-sized colloids. A case in point is the coarse-grained model developed by Mladek et al. in an attempt to reproduce a typical experimental system.5 Construction of the model required three coarse-graining steps. In the first step, simulations were performed on nano-colloids (12 nm diameter) functionalised by 60 homogeneously charged freely-jointed chains representing the 665 base-pair constructs used in experiments.5 At this level of description, no DNA hybridisation was taken into account. Hence, the particles were simply treated as nano-colloids sterically stabilised with densely grafted chains. The simulations probed the repulsive interaction between two such colloids. Subsequently, a multi-blob model was constructed to reproduce the computed repulsive interaction between the nano-colloids. The ends of the coarse-grained chains were then functionalised with units that could hybridise. However, for the nano-sized colloids, the spatial extent of the ‘sticky’ end group could not be ignored, nor the fact that, upon hybridisation, two such groups combine to form a double helix that is more rigid than the unbound sticky ends. Hence, although in this model too the hybridisation free energy is calculated using the SantaLucia nearest neighbour rules,69,70 the conformational changes upon hybridisation are accounted for in the model (see part 2b of Fig. 5).
Using this fairly complex model, the authors computed the crystallization behaviour of the nano-sized DNACCs and they computed the structural properties of the crystalline solid. Encouragingly, the simulations predicted the correct stable crystal structure and gave very good estimates for the temperature at which the solid melts. However, the estimated crystal lattice spacing was off by some 10% (presumably because the experimental estimates of the persistence length of ssDNA show a considerable spread). The other important finding was that three-body interactions play an important role and must be correctly included in order to predict the structure and melting of the crystalline phase. As the above discussion shows, coarse-grained modelling of nano-sized DNACCs is not simple. However, with the use of a coarse-grained polymer model and the empirical SantaLucia nearest neighbour rules, it is still much more efficient than a brute force simulation of nano-size DNACCs. Indeed, both the system sizes (hundreds to thousands of colloids) and the timescale for hybridisation are such that atomistic simulations of the phase behaviour of DNACCs is out of the question for the foreseeable future, whilst calculation of the pair interaction between nano-sized DNACCs is, at lest at present, not an attractive proposition.
There are, however, good reasons to use models for DNA that, whilst not atomistic, do reproduce the structure and dynamics at the nucleotide level. In fact, much effort has been devoted to the development of coarse-grained models that are capable of reproducing the hybridisation free energy, the binding kinetics and the mechanical properties of DNA complexes.62–64 As the interactions that drive DNA hybridisation are primarily the hydrophobic forces between neighbouring bases, such models require a nucleotide-level description of the biopolymer.
Although there have been extensive and very successful simulations of systems with few DNA strands, the models used are still not an attractive proposition to simulate the collective behaviour of DNACCs, as such simulations would require the study of systems of hundreds (or thousands) of colloids each coated with dozens of strands. Moreover, computing the thermodynamic properties from equilibrium simulations requires sampling times that are much longer than the time for a typical hybridisation/de-hybridisation events. Hence, at present, this is not yet possible with the models of ref. 62–64.
For this reason, even more coarse-grained – but still nucleotide-based – descriptions have been developed starting with the work of Starr and Sciortino.59,60 In the approach of ref. 59 and 60, the nucleotides are described as (repulsive) spheres functionalised with a binding site. Neighbouring monomers are bound together by a so-called FENE potential.89 A bending rigidity term between each three consecutive monomers is also used. A binding site, specifying the type of base, is connected to each monomer via a FENE potential. These binding sites selectively interact with complementary sites via Lennard Jones potentials. This model has been used to study the assembly of dendrimer-like structures functionalised by four DNA arms,59,60 self-assembly mediated by linkers90 and crystallisation of nanoparticles.91 A model that is closely related to that of Starr and Sciortino59 was deployed by Knorowski and collaborators92 (see part 1b of Fig. 5). As in ref. 59 and 60, DNA constructs were modelled by mean of beads carrying selective binding sites. However, two flanking repulsive sites were added to every bead belonging to the sticky end part of the construct. The function of the flanking beads is to provide directionality to the interaction between complementary bases and to prevent (unphysical) multi-base interaction. This model has been used to probe the stability of different crystals92,93 and to investigate the dynamics of crystallisation.61 Recently the model of Starr and Sciortino59 has been used by Theodorakis and collaborators to study the pair interactions between nanoparticles functionalised by up to eight constructs.94 This study highlighted the need for a potential further refinement of the model, as the simulations showed the presence of spurious bound states in which the ssDNA strands that form a duplex were oriented parallel, rather than anti-parallel. Parallel hybridisation is not found in real DNA, as the strongly polarity-dependent Watson–Crick pairing between complementary nucleotides uniquely favours anti-parallel hybridised sequences.
The model of Knorowski has been further developed by Li et al.95,96 In particular the size of the beads in the sticky part and in the spacer part of the construct have been differentiated to qualitatively account for the different mechanical properties of the ssDNA and of the dsDNA spacers. This model is parametrised in such a way that each bead corresponds to ≈2–3 bases. This relatively detailed model was subsequently used to parametrise an effective pair-potential that is composed of a short range repulsion due to the electrostatics of the system, and an attractive interaction provided by the hybridisation of the sticky-ends.97,98 Using the effective model the authors rationalised experimental finding on the dynamics of crystallisation,97,99 while the detailed model has been used to probe the stability of the crystals95,96 and to investigate the microscopic structure of the facets of DNACCs-made crystal.99 Detailed molecular models have also been used to investigate interaction between DNA constructs and the nanoparticle substrate (e.g.ref. 100 and 101), and to study the changes in the structure of dsDNA when used to assemble crystalline structures.102 However, these studies go beyond the scope of the present review, where we focus on the physical properties of DNACCs that are related to the reversible biding of multiple DNA complementary pairs, rather than the formation of a single pair formation.
D. Modelling perspectives
There are, in principle, two ways to construct a proper coarse-grained model for DNACCs. One (the top-down) approach is to derive a coarse-grained model from a fully atomistic model for DNA,62–64,104 and use it to simulate DNACCs. This type of approach thus starts with a system at the top of the “complexity scale”, and uses systematic coarse-graining techniques to move towards the bottom of the same scale. Such an approach still retains a molecular based description, and should be able to describe the hybridisation thermodynamics of DNA. The second approach is instead to start with the choice of the ingredients of the coarse-grained model (e.g. ideal chains, rods, monomers, blobs, hybridisation sites etc.) and then to use comparison with the available experimental information to tune its parameters. At present, the top-down approach is not yet as extensively used as that comparing coarse-grained models directly with experiment. An encouraging example in this direction is the work of Lequieu et al.105 and Ding et al.,106 who recently reported studies of pair potentials between nanoparticles functionalised by few constructs of reactive DNA, using the 3SPN model previously used to study the dimerisation of DNA in solution (ref. 64 and 104). The OxDNA model of Ouldridge and coworkers62,63 is another valuable CG model that has been tested in multiple DNA nanotechnology systems. To our knowledge, OxDNA has not yet been used to improve the modelling of DNACCs.There are other aspects of the modelling that need to be improved. One is related to the naive use of nearest-neighbour rules to compute DNA binding free energies in constructs. Recent experimental/theoretical investigation by Di Michele et al.103 showed that the SantaLucia nearest-neighbour rules69,70 overestimate the hybridisation free energy ΔG0 in the case of DNA oligomers that are extended to include strings of non-complementary bases.103 Considering for instance two complementary sequences of ssDNA decorated by two inert strings at their 5′ terminals (snapshot of Fig. 6a), ref. 103 reported that ΔG0 increases with the length of the inert tails until reaching a plateau for a number of inert bases equal to ≈5–7 (plot in Fig. 6a). In particular the presence of the inert tails destabilises double helix formation and hence decreases the melting temperature of the oligomers. Such an effect is due to the electrostatic interactions between the charged backbones of the DNA that is not included in the nearest neighbour rules.107 Quite surprisingly ref. 103 showed that the shift in the hybridisation free energy due to the tails (at salt concentration that are typical of DNA coated colloids experiments25) can be as large as the stacking contribution of the nearest-neighbour rules due to the first dangling (i.e. non-hybridised) base in the nucleotide sequence, a standard term entering the nearest-neighbour rules (see Fig. 6b). The relevance of the inert tails to the calculation of the hybridisation free energy ΔG0 seems to limit the degree of ‘responsible’ coarse graining of DNA mediated interactions (also in other DNA nanotechnology systems108). In particular if we consider models with explicit hybridisation thermodynamics, the importance of the electrostatic interactions between the inert tails and the DNA duplex requires an explicit description of the charged backbones in the tails and in the duplex at the atomistic level. Interestingly the latest version of OxDNA introduced Debye–Hückel interactions73 between the backbone sites.63
 | ||
| Fig. 6 (a) Shift in the hybridisation free energy as due to the electrostatic interactions between the inert tails (blue beads in the top rendering of the two oligomers) and the paired bases as a function of the number of inert bases.103 Electrostatic interactions are modelled using the linearised Debye–Hückel73 theory at three different salt concentrations. Further details of the simulation method are reported in ref. 103. (b) SantaLucia hybridisation free energy of two oligomers (3′-AACCGACAG-5′ and complementary strand) with and without two (G) dangling bases attached to the 5′ terminals of the reactive sequences for 100 mM NaCl concentration.69,70 The stacking contribution of the Santalucia rules (blue arrow in the figure) is comparable with the tail contribution (see part a). Notice that an error of ±1kBT in the nearest-neighbour rules69,70 results in a bigger incertitude of the melting temperature (black arrows). | ||
The problem is that the binding free energy computed for a typical configurations of the dangling segments of the free oligomers,103 may not be transferable. This is the case, for instance, if the tails are more stretched when bridging two colloids than when they are free in solution. Hence, estimates of ΔG0 obtained from experiments for free strands might not be reliable once the same strands have been grafted. These ‘minor’ effects are not so minor when one realises that a bias of one kBT in ΔG0 results in a shift in the melting temperatures of about ≈±3.5 K (see Fig. 6b). Hence, when analysing accurate experiments,25 neglect of the dangling tail effects can affect the interpretation of the results, once the experimental resolution gets better than a few Kelvin.17
There is also the ‘no-free-lunch’ theorem of coarse graining. As was pointed out in a different context many years ago by Louis, the design of an optimal model that carefully reproduces the structural properties of a system may result in a model that is not representative of the thermodynamics of that system (and vice versa).109
Finally we stress something that has been stressed many times: structures may be mechanically stable, but thermodynamically unstable. Demonstrating that one structure is more stable than another typically requires the calculation of the free energy (or, more precisely, the chemical potential) of both systems. Using MC or molecular dynamics to see what kind of structure forms by annealing from a disordered state92,93,95–97 is interesting, but it does not demonstrate that the structure that forms is stable (in fact, Ostwald's rule110 suggests the opposite). The problem is that the first stages of the self-assembly process are those with a smaller barrier from the starting disordered state. These states can simply represent mechanically stable metastable states, which would transform to the true thermodynamically stable state at much longer times (if at all). These longer times may not be accessible with experiments, and are certainly many orders of magnitude larger than the time-scales accessible by computer simulations. We also notice that, in order to correctly reproduce the stable phases observed in experiments, studies using this simulated annealing approach typically start with simulations boxes compatible with the shape and number of particle experimentally observed, which must thus be known a priori. Since maximal packing appears to be, at least for conventional binary DNACCs system, one of the major driving force behind formation of specific lattices,16 starting with experimentally available conditions necessarily biases the simulation toward the expected structure. In short: constructing a phase diagram requires the calculation of the free energy of each possible phase,36 unless a direct, hysteresis-free transition between the two phases can be observed. One of the main challenges in the simulation of the phase diagram of DNACCs was precisely the need to carry out free-energy calculations31,32,75,76 that properly account for the hybridisation between the binders. Fortunately, efficient MC algorithms have been developed to calculate the density of states of an aggregate as a function of the number of bridges between particles, whose integration can then be used to calculate the free energy of the crystal.72,75,76 These algorithms have been successfully combined with various techniques to select among the many possible candidate phases. For example, in view of the rich polymorphism offered by DNACCs, genetic algorithms111,112 have been used to identify possible crystal structures, whose relative thermodynamic stability was then probed by free-energy calculations, providing phase diagrams in quantitative agreement with experiments without an a priori knowledge of crystals parameters.31,32
IV. Conclusions
Theoretical and computational modelling have proven to be powerful tools to rationalise the observed behaviour of DNACCs,17,21–23,25,92,95–97,113 and, in some cases, to predict novel phenomena,29,44 with some theoretical predictions for unconventional yet experimentally accessible systems still waiting to be tested.28,76Understanding DNACCs behaviour means understanding their mutual interactions as a function of the system's parameters. In this regard, we have shown how the presently available theoretical framework can be used to design interactions of almost arbitrary complexity: how these could lead to interesting effects (see for instance ref. 114 and 115 for some applications) is yet to be systematically investigated. An important factor to highlight in this regard is that the analytical framework we described assumes thermodynamic equilibrium for bond formation, i.e. it implicitly considers the bonding network to be equilibrated on the timescale of colloidal diffusion. Hence, in order to connect the effective inter-particle potential predicted by theory with experimental observations (that are of finite duration) one requires both the bond-formation and bond-breaking rates to be fast compared to the timescale for colloidal diffusion. Until now, this was a strong assumption. However, although this was not true for general bonding schemes previously typically employed, Rogers and Manoharan44 have recently shown a very powerful and general scheme exploiting toe-holding mechanisms that can make such assumption essentially correct. Proof of this point is already observable in their experimental results, whose trends could be rationalised using a local chemical equilibrium approach that implicitly makes such an assumption. Hence, we would expect such scheme to lead to a more reliable comparison between theory and experiments, opening new and truly exciting perspectives for this field.
Most of the focus in the DNACCs has probably been on their self-assembly property, and much remains to be done to exploit this system to its full potential, in particular in the design of functional materials for applications. In our view, however, other DNACCs based technologies will benefit from interpreting experiments in view of the presented framework, selective drug delivery and biosensing being two likely candidates. It should be stressed that, besides describing DNACCs – systems that have important nanomedicine applications in their own regard8–10 – the theoretical and computational methods outlined here apply more generally to all systems whose interactions are dominated by the formation of non-covalent, multiple and reversible ligand–receptor bonds, i.e. supramolecular, multivalent based systems. A wide variety of such systems are already under intense investigation for nanomedical applications,48,49,116,117 and we envisage important cross-fertilization of ideas between these fields and DNACC research. In particular, understanding how to embed binding selectivity in multivalent-based systems, and not just increase their binding strength, seems to be a crucial point where theoretical work118 might prove useful to rationalise observed effects,116 and speed up the rational design of applications.
Finally, we stress that there is much need for further theoretical and computational developments. For applications that will require quantitative predictions, more accurate experiments are needed to inform the parametrisation of existing, or the development of, novel models. An illustration is the tail effect discussed in Section III. Understanding the role of non-specific attractive interactions, and also of strand–strand interactions, are further challenges that have still not been properly investigated. The need for such improved modelling has become urgent with the arrival of recent experiments of the Pine group, who was able to reach coating densities that are much higher than what was previously achievable.55,58 Interestingly these experiments reported enhanced crystallisation rates; it would be interesting to understand these results using properly extended models. Finally, other challenges clearly arise when considering systems where the colloid itself can be deformed upon binding (hence effectively coupling ΔGcnf with the shape of the colloidal core), such as the case of functionalised vesicles.
After the long gestation period that followed the early work by Mirkin and Alivisatos, the field is moving rapidly. Exciting times lie ahead of the DNACCs field. We hope that this review will have clarified some of the key unifying concepts that need to be understood in the move towards the rational design of DNACC-based structures. In this regard, we make freely available a python-based set of routines that we developed to calculate ligand–receptor mediated interaction free energies using our self-consistent equations at the following address http://https://github.com/sangiole/DNACC.
Appendix A: Breakdown of local chemical equilibrium and mean-field approximations
To illustrate the breakdown of LCE and mean-field like approaches in the limit of small numbers of binding strands, first consider the normal dimerisation reaction between two “molecules” α and β.| α + β ⇌ αβ. |
| μα + μβ = μαβ | (A1) |
where qint(x) is the contribution to the partition of x due to all internal degrees of freedom. The equilibrium condition A1 can be written as
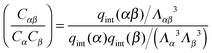 | (A2) |
In order to convert to number densities, we note that [x] = Cx/ρ0 where ρ0 is the “standard” number density (1 molar = 6.022 × 1026 molecules per m3). Then
Next consider the case where we still have an ideal gas mixture, but now with only very few molecules in the ‘reaction volume’ (in the case of tethers, this translates into: ‘a tether of a given type (say α) can only bind with a small number of nearby complementary tethers. In that case, LCE breaks down. To see this, consider the extreme (but not unrealistic) case of a volume V containing a single molecule of type α and a single copy of β. As before, α and β can react to form αβ. Let us denote by P the probability that molecule α (or β) is part of a dimer, then P/(1 − P) is simply given by the ratio of the corresponding single-particle partition functions:
Now compare this with the LCE expression. The number density of α(β) equals P/V and the number density of αβ is (1 − P)/V. Hence, LCE predicts:
which is clearly not correct. Hence, we should not expect LCE and in general mean field theories not accounting for the exact position of the tethering points) to work if only small numbers of monomers can interact. However, this is precisely the situation if the grafting distance between strands is not small compared to the effective length of the strands. On the other hand Fig. 3 shows that the self-consistent approach performs very well also at low grafting density.
Appendix B: Numerical estimate of configuration contribution to binding free energy
In this appendix, we describe how the hybridisation free energy between two ssDNA constructs can be calculated numerically. The method was employed in ref. 23 and 24.Two independent Monte Carlo runs are used to generate two interacting FJCs with free and bound end points, respectively, using the Rosenbluth algorithm.36 In the bound case one grows a single longer chain using a bias to constraint the two end-points to the tethering points119,120 (see the top inset of Fig. 7). In ref. 23 and 24, while growing a hybridised chain, we biased the choice of the new segments using the end-to-end distribution function of an ideal FJC of length equal to the number of missing segments119 (notice that this is not the unique choice possible120). By sampling the corresponding Rosenbluth weights36 (see the right y-axis of Fig. 7 for the bound case) it is possible to calculate Wi,j and Wij
| Wi,j = 〈W(f)〉 Wij = 〈W(b)〉 | (B1) |
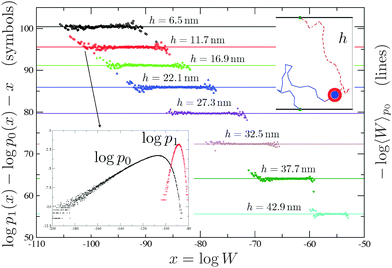 | ||
| Fig. 7 Inset bottom: The algorithm used in ref. 23 and 24 generates chains with Rosenbluth weights that are distributed according to a distribution function (p0) which is different from the distribution obtained using equilibrium runs (p1). The average of the Rosenbluth weight using p0 (right y-axis), together with the corresponding result for free constructs, is used in eqn (5) to calculate ΔGcnf. Using the overlapping between p1 and p0 and the results of ref. 121 we can calculate, in an independent way, −log〈W〉p0 (left y-axis and symbols). The agreement between symbols and the straight line is perfect. The algorithm of ref. 72 samples between free and bound states in a way that the Rosenbluth weights are distributed with p1. In this case ΔGcnf can be measured comparing the time spent by the system in the free and in the bound state.72 | ||
The accuracy of the aforementioned calculations depends on the quality of the sampling, which can be probed using the overlapping method developed in ref. 121, a typical output being shown in Fig. 7 (see the caption for further details). Moreover ref. 72 developed a dynamic scheme based on the configurational bias method122 that allows to sample between hybridised and free chains on the fly, hence without the need of precomputing ΔGcnf, for every couple of constructs that could potentially bind.
Acknowledgements
This work was supported by ERC AdG grant 227758 (COLSTRUCTION) and EPSRC Programme Grant EP/I001352/1. S. A-U. acknowledges financial support from the Beijing Municipal Government Innovation Center for Soft Matter Science and Engineering. BMM is supported by the Université Libre de Bruxelles. We acknowledge the present and the past members of the group of Daan Frenkel (P. Varilly, B. Mladeck, M. E. Leunissen, F. J. Martinez-Veracoechea, J. Dobnikar) and of the group of Erika Eiser (L. Di Michele, T. Yanagishima, Z. Ruff) for collaborating with us on the subjects reported by this Perspective.References
- C. A. Mirkin, R. C. Letsinger, R. C. Mucic and J. J. Storhoff, A DNA-based method for rationally assembling nanoparticles into macroscopic materials, Nature, 1996, 382, 607 CrossRef CAS PubMed.
- A. P. Alivisatos, K. P. Johnsson, X. Peng, T. E. Wilson, C. J. Loweth, M. P. Bruchez and P. G. Schultz, Organization of ‘nanocrystal molecules’ using DNA, Nature, 1996, 382, 609 CrossRef CAS PubMed.
- J. I. Cutler, E. Auyeung and C. A. Mirkin, Spherical nucleic acids, J. Am. Chem. Soc., 2012, 134(3), 1376–1391 CrossRef CAS PubMed.
- S. Y. Park, A. K. R. Lytton-Jean, B. Lee, S. Weigand, G. C. Schatz and C. A. Mirkin, DNA-programmable nanoparticle crystallization, Nat. Mater., 2008, 451, 553–556 CrossRef CAS PubMed.
- D. Nykypanchuk, M. M. Maye, D. van der Lelie and O. Gang, DNA-guided crystallization of colloidal nanoparticles, Nat. Mater., 2008, 451, 549–552 CrossRef CAS PubMed.
- M. M. Maye, M. Thilak Kumara, D. Nykypanchuk, W. B. Sherman and O. Gang, Switching binary states of nanoparticle superlattices and dimer clusters by DNA strands, Nat. Nanotechnol., 2010, 5(2), 116–120 CrossRef CAS PubMed.
- Y. Zhang, F. Lu, K. G. Yager, D. van der Lelie and O. Gang, A general strategy for the DNA-mediated self-assembly of functional nanoparticles into heterogeneous systems, Nat. Nanotechnol., 2013, 8(11), 865–872 CrossRef CAS PubMed.
- T. Andrew Taton, C. A. Mirkin and R. L. Letsinger, Scanometric DNA array detection with nanoparticle probes, Science, 2000, 289(5485), 1757–1760 CrossRef.
- N. L. Rosi, D. A. Giljohann, C. Shad Thaxton, A. K. R. Lytton-Jean, M. S. Han and C. A. Mirkin, Oligonucleotide-modified gold nanoparticles for intracellular gene regulation, Science, 2006, 312(5776), 1027–1030 CrossRef CAS PubMed.
- D. Zheng, D. A. Giljohann, D. L. Chen, M. D. Massich, X.-Q. Wang, H. Iordanov, C. A. Mirkin and A. S. Paller, Topical delivery of siRNA-based spherical nucleic acid nanoparticle conjugates for gene regulation, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(30), 11975–11980 CrossRef CAS PubMed.
- L. Di Michele and E. Eiser, Developments in understanding and controlling self assembly of DNA-functionalized colloids, Phys. Chem. Chem. Phys., 2013, 15(9), 3115–3129 RSC.
- N. Geerts and E. Eiser, DNA-functionalized colloids: physical properties and applications, Soft Matter, 2010, 6(19), 4647–4660 RSC.
- P. E. Theodorakis, N. G. Fytas, G. Kahl and C. Dellago, Self-assembly of DNA-functionalized colloids, 2015, arXiv preprint, arXiv:1503.05384.
- C. Knorowski and A. Travesset, Materials design by DNA programmed self-assembly, Curr. Opin. Solid State Mater. Sci., 2011, 15(6), 262–270 CrossRef CAS.
- M. R. Jones, N. C. Seeman and C. A. Mirkin, Programmable materials and the nature of the DNA bond, Science, 2015, 347(6224), 1260901 CrossRef PubMed.
- R. Macfarlane, B. Lee, M. Jones, N. Harris, G. Schatz and C. A. Mirkin, Nanoparticle superlattice engineering with DNA, Science, 2011, 334, 204–208 CrossRef CAS PubMed.
- P. L. Biancaniello, A. J. Kim and J. C. Crocker, Colloidal interactions and self-assembly using DNA hybridization, Phys. Rev. Lett., 2005, 94, 058302 CrossRef PubMed.
- R. Jin, G. Wu, Z. Li, C. A. Mirkin and G. C. Schatz, What controls the melting properties of DNA-linked gold nanoparticle assemblies?, J. Am. Chem. Soc., 2003, 125(6), 1643–1654 CrossRef CAS PubMed.
- N. A. Licata and A. V. Tkachenko, Statistical mechanics of DNA-mediated colloidal aggregation, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74(4), 041408 CrossRef PubMed.
- A. J. Kim, P. L. Biancaniello and J. C. Crocker, Engineering DNA-mediated colloidal crystallization, Langmuir, 2006, 22(5), 1991–2001 CrossRef CAS PubMed.
- R. Dreyfus, M. E. Leunissen, R. Sha, A. V. Tkachenko, N. C. Seeman, D. J. Pine and P. M. Chaikin, Simple quantitative model for the reversible association of DNA coated colloids, Phys. Rev. Lett., 2009, 102, 048301 CrossRef PubMed.
- R. Dreyfus, M. E. Leunissen, R. Sha, A. Tkachenko, N. C. Seeman, D. J. Pine and P. M. Chaikin, Aggregation-disaggregation transition of DNA-coated colloids: experiments and theory, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041404 CrossRef PubMed.
- P. Varilly, S. Angioletti-Uberti, B. M. Mognetti and D. Frenkel, A general theory of DNA-mediated and other valence-limited colloidal interactions, J. Chem. Phys., 2012, 137, 094108 CrossRef PubMed.
- B. M. Mognetti, P. Varilly, S. Angioletti-Uberti, F. J. Martinez-Veracoechea, J. Dobnikar, M. E. Leunissen and D. Frenkel, Predicting DNA-mediated colloidal pair interactions, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, E378 CrossRef CAS PubMed.
- W. B. Rogers and J. C. Crocker, Direct measurements of DNA-mediated colloidal interactions and their quantitative modeling, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(38), 15687–15692 CrossRef CAS PubMed.
- M. E. Leunissen and D. Frenkel, Numerical study of DNA-functionalized microparticles and nanoparticles: explicit pair potentials and their implications for phase behavior, J. Chem. Phys., 2011, 134(8), 084702 CrossRef PubMed.
- S. Angioletti-Uberti, P. Varilly, B. M. Mognetti, A. V. Tkachenko and D. Frenkel, Communication: a simple analytical formula for the free energy of ligand–receptor-mediated interactions, J. Chem. Phys., 2013, 138, 021102 CrossRef PubMed.
- S. Angioletti-Uberti, P. Varilly, B. M. Mognetti and D. Frenkel, Mobile linkers on DNA-coated colloids: valency without patches, Phys. Rev. Lett., 2014, 113, 128303 CrossRef PubMed.
- S. Angioletti-Uberti, B. M. Mognetti and D. Frenkel, Reentrant melting as a design principle for DNA-coated colloids, Nat. Mater., 2012, 11, 518–522 CrossRef CAS PubMed.
- D. Nykypanchuk, M. M. Maye, D. van der Lelie and O. Gang, DNA-based approach for interparticle interaction control, Langmuir, 2007, 23(11), 6305–6314 CrossRef CAS PubMed.
- B. M. Mladek, J. Fornleitner, F. J. Martinez-Veracoechea, A. Dawid and D. Frenkel, Quantitative prediction of the phase diagram of DNA-functionalized nanosized colloids, Phys. Rev. Lett., 2012, 108(26), 268301 CrossRef PubMed.
- B. M. Mladek, J. Fornleitner, F. J. Martinez-Veracoechea, A. Dawid and D. Frenkel, Procedure to construct a multi-scale coarse-grained model of DNA-coated colloids from experimental data, Soft Matter, 2013, 9, 7342–7355 RSC.
- L. Parolini, B. M. Mognetti, J. Kotar, E. Eiser, P. Cicuta and L. Di Michele, Volume and porosity thermal regulation in lipid mesophases by coupling mobile ligands to soft membranes, Nat. Commun., 2015, 6, 5948 CrossRef CAS PubMed.
- Y. Zhang, H. Zhou and Z.-C. Ou-Yang, Stretching single-stranded DNA: interplay of electrostatic, base-pairing and base-pair stacking interactions, Biophys. J., 2001, 81(2), 1133–1143 CrossRef CAS PubMed.
- A more precise definition takes into account the Boltzmann weighted phase space volume of the bound vs. unbound states for the linker. As long as one consider non interacting strands, the two are actually the same.
- D. Frenkel and B. Smit, Understanding molecular simulation: from algorithms to applications, Academic Press, 2001, vol. 1 Search PubMed.
- M. S. Wertheim, Fluids with highly directional attractive forces. i. Statistical thermodynamics, J. Stat. Phys., 1984, 35, 19–34 CrossRef.
- M. S. Wertheim, Fluids with highly directional attractive forces. ii. Thermodynamic perturbation theory and integral equations, J. Stat. Phys., 1984, 35, 35–47 CrossRef.
- M. S. Wertheim, Fluids with highly directional attractive forces. iii. Multiple attraction sites, J. Stat. Phys., 1986, 42, 459–476 CrossRef.
- W. G. Chapman, K. E. Gubbins, C. G. Joslin and C. G. Gray, Theory and simulation of associating liquid mixtures, Fluid Phase Equilib., 1986, 29, 337–346 CrossRef CAS.
- Y. Wang, Y. Wang, R. Dana, V. N. Manoharan, L. Feng, A. D. Hollingsworth, M. Weck and D. J. Pine, Colloids with valence and specific directional bonding, Nature, 2012, 491, 51–55 CrossRef CAS PubMed.
- B. Mognetti, M. E. Leunissen and D. Frenkel, Controlling the temperature sensitivity of DNA-mediated colloidal interactions through competing linkages, Soft Matter, 2012, 8, 2213 RSC.
- W. B. Rogers and J. C. Crocker, Reply to mognetti et al.: DNA handshaking interaction data are well described by mean-field and molecular models, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(7), E380 CrossRef CAS.
- W. B. Rogers and V. N. Manoharan, Programming colloidal phase transitions with DNA strand displacement, Science, 2015, 347(6222), 639–642 CrossRef CAS PubMed.
- M. E. Leunissen, R. Dreyfus, R. Sha, N. C. Seeman and P. M. Chaikin, Quantitative study of the association thermodynamics and kinetics of DNA-coated particles for different functionalization schemes, J. Am. Chem. Soc., 2010, 132(6), 1903–1913 CrossRef CAS PubMed . PMID: 20095643.
- O. Gang, Colloidal self-assembly: melting also on cooling, Nat. Mater., 2012, 11(6), 487–488 CrossRef CAS PubMed.
- U. Rauwald and O. A. Scherman, Supramolecular block copolymers with cucurbit [8] uril in water, Angew. Chem., Int. Ed., 2008, 47(21), 3950–3953 CrossRef CAS PubMed.
- I. Papp, C. Sieben, K. Ludwig, M. Roskamp, C. Böttcher, S. Schlecht A. Herrmann and R. Haag, Inhibition of influenza virus infection by multivalent sialic-acid-functionalized gold nanoparticles, Small, 2010, 6(24), 2900–2906 CrossRef CAS PubMed.
- J. Vonnemann, C. Sieben, C. Wolff, K. Ludwig, C. Böttcher, A. Herrmann and R. Haag, Virus inhibition induced by polyvalent nanoparticles of different sizes, Nanoscale, 2014, 6(4), 2353–2360 RSC.
- C. Fasting, C. A. Schalley, M. Weber, O. Seitz, S. Hecht, B. Koksch, J. Dernedde, C. Graf, E.-W. Knapp and R. Haag, Multivalency as a chemical organization and action principle, Angew. Chem., Int. Ed., 2012, 51(42), 10472–10498 CrossRef CAS PubMed.
- G. Ercolani, Assessment of cooperativity in self-assembly, J. Am. Chem. Soc., 2003, 125(51), 16097–16103 CrossRef CAS PubMed.
- A. Mulder, J. Huskens and D. N. Reinhoudt, Multivalency in supramolecular chemistry and nanofabrication, Org. Biomol. Chem., 2004, 2(23), 3409–3424 CAS.
- J. Huskens, A. Mulder, T. Auletta, C. A. Nijhuis, M. J. W. Ludden and D. N. Reinhoudt, A model for describing the thermodynamics of multivalent host–guest interactions at interfaces, J. Am. Chem. Soc., 2004, 126(21), 6784–6797 CrossRef CAS PubMed.
- F. J. Martinez-Veracoechea and M. E. Leunissen, The entropic impact of tethering, multivalency and dynamic recruitment in systems with specific binding groups, Soft Matter, 2013, 9(12), 3213–3219 RSC.
- Y. Wang, Y. Wang, X. Zheng, T. Ducrot, M.-G. Lee, G.-R. Yi, M. Weck and D. J. Pine, Synthetic strategies toward DNA-coated colloids that crystallize, J. Am. Chem. Soc., 2015, 137(33), 10760–10766 CrossRef CAS PubMed.
- P. S. Randeria, M. R. Jones, K. L. Kohlstedt, R. J. Banga, M. Olvera de la Cruz, G. C. Schatz and C. A. Mirkin, What controls the hybridization thermodynamics of spherical nucleic acids?, J. Am. Chem. Soc., 2015, 137(10), 3486–3489 CrossRef CAS PubMed.
- M. Doyen, K. Bartik and G. Bruylants, DNA-promoted auto-assembly of gold nanoparticles: effect of the DNA sequence on the stability of the assemblies, Polymers, 2013, 5(3), 1041–1055 CrossRef.
- Y. Wang, Y. Wang, X. Zheng, É. Ducrot, J. S. Yodh, M. Weck and D. J. Pine, Crystallization of DNA-coated colloids, Nat. Commun., 2015, 6, 7253 CrossRef CAS PubMed.
- F. W. Starr and F. Sciortino, Model for assembly and gelation of four-armed DNA dendrimers, J. Phys.: Condens. Matter, 2006, 18(26), L347 CrossRef CAS PubMed.
- J. Largo, F. W. Starr and F. Sciortino, Self-assembling DNA dendrimers: a numerical study, Langmuir, 2007, 23(11), 5896–5905 CrossRef CAS PubMed.
- C. Knorowski and A. Travesset, Dynamics of DNA-programmable nanoparticle crystallization: gelation, nucleation and topological defects, Soft Matter, 2012, 8(48), 12053–12059 RSC.
- T. E. Ouldridge, A. A. Louis and J. P. K. Doye, Structural, mechanical and thermodynamic properties of a coarse-grained DNA model, J. Chem. Phys., 2011, 134(8), 085101 CrossRef PubMed.
- B. E. K. Snodin, F. Randisi, M. Mosayebi, P. Sulc, J. S. Schreck, F. Romano, T. E. Ouldridge, R. Tsukanov, E. Nir, A. A. Louis, et al., Introducing improved structural properties and salt dependence into a coarse-grained model of DNA, 2015, arXiv preprint, arXiv:1504.00821.
- D. M. Hinckley, G. S. Freeman, J. K. Whitmer and J. J. de Pablo, An experimentally-informed coarse-grained 3-site-per-nucleotide model of DNA: structure, thermodynamics and dynamics of hybridization, J. Chem. Phys., 2013, 139(14), 144903 CrossRef PubMed.
- P. L. Biancaniello, J. C. Crocker, D. A. Hammer and V. T. Milam, DNA-mediated phase behavior of microsphere suspensions, Langmuir, 2007, 23(5), 2688–2693 CrossRef CAS PubMed.
- Q. Xu, L. Feng, R. Sha, N. C. Seeman and P. M. Chaikin, Subdiffusion of a sticky particle on a surface, Phys. Rev. Lett., 2011, 106, 228102 CrossRef CAS PubMed.
- R. J. Hunter, Foundations of colloid science, 2001 Search PubMed.
- F. J. Martinez Veracoechea, B. M. Mognetti, S. Angioletti-Uberti, P. Varilly, D. Frenkel and J. Dobnikar, Designing stimulus-sensitive colloidal walkers, Soft Matter, 2014, 10, 3463–3470 RSC.
- J. SantaLucia, A unified view of polymer, dumbbell and oligonucleotide DNA nearest-neighbor thermodynamics, Proc. Natl. Acad. Sci. U. S. A., 1998, 95(4), 1460–1465 CrossRef CAS.
- J. SantaLucia Jr and D. Hicks, The thermodynamics of DNA structural motifs, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 415–440 CrossRef PubMed.
- D. Bracha, E. Karzbrun, G. Shemer, P. A. Pincus and R. H. Bar-Ziv, Entropy-driven collective interactions in DNA brushes on a biochip, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(12), 4534–4538 CrossRef CAS PubMed.
- R. De Gernier, T. Curk, G. V. Dubacheva, R. P. Richter and B. M. Mognetti, A new configurational bias scheme for sampling supramolecular structures, J. Chem. Phys., 2014, 141(24), 244909 CrossRef PubMed.
- J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, 2006 Search PubMed.
- B. Bozorgui and D. Frenkel, Liquid–vapor transition driven by bond disorder, Phys. Rev. Lett., 2008, 101(4), 045701 CrossRef PubMed.
- F. J. Martinez-Veracoechea, B. Bozorgui and D. Frenkel, Anomalous phase behavior of liquid–vapor phase transition in binary mixtures of DNA-coated particles, Soft Matter, 2010, 6(24), 6136–6145 RSC.
- F. J. Martinez-Veracoechea, B. M. Mladek, A. V. Tkachenko and D. Frenkel, Design rule for colloidal crystals of DNA-functionalized particles, Phys. Rev. Lett., 2011, 107, 045902 CrossRef PubMed.
- T. Schmatko, B. Bozorgui, N. Geerts, D. Frenkel, E. Eiser and W. C. K. Poon, A finite-cluster phase in λ-DNA-coated colloids, Soft Matter, 2007, 3(6), 703–706 RSC.
- N. Geerts, T. Schmatko and E. Eiser, Clustering versus percolation in the assembly of colloids coated with long DNA, Langmuir, 2008, 24(9), 5118–5123 CrossRef CAS PubMed.
- P. G. Bolhuis, A. A. Louis, J. P. Hansen and E. J. Meijer, Accurate effective pair potentials for polymer solutions, J. Chem. Phys., 2001, 114(9), 4296–4311 CrossRef CAS.
- C. Pierleoni, B. Capone and J.-P. Hansen, A soft effective segment representation of semidilute polymer solutions, J. Chem. Phys., 2007, 127(17), 171102 CrossRef PubMed.
- G. D'Adamo, A. Pelissetto and C. Pierleoni, Coarse-graining strategies in polymer solutions, Soft Matter, 2012, 8(19), 5151–5167 RSC.
- F. Smallenburg and F. Sciortino, Liquids more stable than crystals in particles with limited valence and flexible bonds, Nat. Phys., 2013, 9(9), 554–558 CrossRef CAS.
- M. Hadorn, E. Boenzli, K. T. Sørensen, H. Fellermann, P. Eggenberger Hotz and M. M. Hanczyc, Specific and reversible DNA-directed self-assembly of oil-in-water emulsion droplets, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(50), 20320–20325 CrossRef CAS PubMed.
- L.-L. Pontani, I. Jorjadze, V. Viasnoff and J. Brujic, Biomimetic emulsions reveal the effect of mechanical forces on cell–cell adhesion, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(25), 9839–9844 CrossRef CAS PubMed.
- L. Feng, L.-L. Pontani, R. Dreyfus, P. Chaikin and J. Brujic, Specificity, flexibility and valence of DNA bonds guide emulsion architecture, Soft Matter, 2013, 9(41), 9816–9823 RSC.
- S. A. J. van der Meulen and M. E. Leunissen, Solid colloids with surface–mobile DNA linkers, J. Am. Chem. Soc., 2013, 135(40), 15129–15134 CrossRef CAS PubMed.
- S. F. Shimobayashi, B. Matteo Mognetti, L. Parolini, D. Orsi, P. Cicuta and L. Di Michele, Direct measurement of DNA-mediated adhesion between lipid bilayers, Phys. Chem. Chem. Phys., 2015, 17(24), 15615–15628 RSC.
- J. Hu, R. Lipowsky and T. R. Weikl, Binding constants of membrane-anchored receptors and ligands depend strongly on the nanoscale roughness of membranes, Proc. Natl. Acad. Sci. U. S. A., 2013, 110(38), 15283–15288 CrossRef CAS PubMed.
- G. S. Grest and K. Kremer, Molecular dynamics simulation for polymers in the presence of a heat bath, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33(5), 3628 CrossRef CAS.
- C. Wei Hsu, F. Sciortino and F. W. Starr, Theoretical description of a DNA-linked nanoparticle self-assembly, Phys. Rev. Lett., 2010, 105(5), 055502 CrossRef PubMed.
- W. Dai, S. K. Kumar and F. W. Starr, Universal two-step crystallization of DNA-functionalized nanoparticles, Soft Matter, 2010, 6(24), 6130–6135 RSC.
- C. Knorowski, S. Burleigh and A. Travesset, Dynamics and statics of DNA-programmable nanoparticle self-assembly and crystallization, Phys. Rev. Lett., 2011, 106, 215501 CrossRef CAS PubMed.
- C. Knorowski and A. Travesset, Self-assembly and crystallization of hairy (f-star) and DNA-grafted nanocubes, J. Am. Chem. Soc., 2014, 136(2), 653–659 CrossRef CAS PubMed.
- P. E. Theodorakis, C. Dellago and G. Kahl, A coarse-grained model for DNA-functionalized spherical colloids, revisited: effective pair potential from parallel replica simulations, J. Chem. Phys., 2013, 138(2), 02510 CrossRef PubMed.
- T. I. Li, R. Sknepnek, R. J. Macfarlane, C. A Mirkin and M. Olvera de la Cruz, Modeling the crystallization of spherical nucleic acid nanoparticle conjugates with molecular dynamics simulations, Nano Lett., 2012, 12(5), 2509–2514 CrossRef CAS PubMed.
- T. I. Li, R. Sknepnek and M. Olvera de la Cruz, Thermally active hybridization drives the crystallization of DNA-functionalized nanoparticles, J. Am. Chem. Soc., 2013, 135(23), 8535–8541 CrossRef CAS PubMed.
- S. Dhakal, K. L. Kohlstedt, G. C. Schatz, C. A. Mirkin and M. Olvera de la Cruz, Growth dynamics for DNA-guided nanoparticle crystallization, ACS Nano, 2013, 7(12), 10948–10959 CrossRef CAS PubMed.
- J. W. Zwanikken, P. Guo, C. A. Mirkin and M. Olvera de la Cruz, Local ionic environment around polyvalent nucleic acid-functionalized nanoparticles, J. Phys. Chem. C, 2011, 115(33), 16368–16373 CAS.
- E. Auyeung, T. I. Li, A. J. Senesi, A. L. Schmucker, B. C. Pals, M. Olvera de La Cruz and C. A. Mirkin, DNA-mediated nanoparticle crystallization into wulff polyhedra, Nature, 2014, 505(7481), 73–77 CrossRef PubMed.
- O. Lee and G. C. Schatz, Molecular dynamics simulation of DNA-functionalized gold nanoparticles, J. Phys. Chem. C, 2009, 113, 2316–2321 CAS.
- O.-S. Lee and G. C. Schatz, Interaction between DNAs on a gold surface, J. Phys. Chem. C, 2009, 113(36), 15941–15947 CAS.
- V. A. Ngo, R. K. Kalia, A. Nakano and P. Vashishta, Supercrystals of DNA-functionalized gold nanoparticles: a million-atom molecular dynamics simulation study, J. Phys. Chem. C, 2012, 116(36), 19579–19585 CAS.
- L. Di Michele, B. M. Mognetti, T. Yanagishima, P. Varilly, Z. Ruff, D. Frenkel and E. Eiser, Effect of inert tails on the thermodynamics of DNA hybridization, J. Am. Chem. Soc., 2014, 136(18), 6538–6541 CrossRef CAS PubMed.
- M. Kenward and K. D. Dorfman, Brownian dynamics simulations of single-stranded DNA hairpins, J. Chem. Phys., 2009, 130(9), 095101 CrossRef PubMed.
- J. P. Lequieu, D. M. Hinckley and J. J. de Pablo, A molecular view of DNA-conjugated nanoparticle association energies, Soft Matter, 2015, 11, 1919 RSC.
- Y. Ding and J. Mittal, Insights into DNA-mediated interparticle interactions from a coarse-grained model, J. Chem. Phys., 2014, 141(18), 184901 CrossRef PubMed.
- It has been reported that dangling sequences can stabilise RNA–RNA duplexes.123,124 This result may look puzzling in view of the conclusions of ref. 103. It is likely that tails stabilise RNA duplexes by selective interactions as suggested by the fact that, contrarily to ref. 103, the effect is sequence-dependent123,124.
- N. Srinivas, T. E. Ouldridge, P. Šulc, J. M. Schaeffer, B. Yurke, A. A. Louis, J. P. K. Doye and E. Winfree, On the biophysics and kinetics of toehold-mediated DNA strand displacement, Nucleic Acids Res., 2013, 41(22), 10641–10658 CrossRef CAS PubMed.
- A. A. Louis, Beware of density dependent pair potentials, J. Phys.: Condens. Matter, 2002, 14(40), 9187 CrossRef CAS.
- W. Ostwald, Studien über die bildung und umwandlung fester körper, Z. Phys. Chem., 1897, 22, 289–330 CAS.
- D. Gottwald, G. Kahl and C. N. Likos, Predicting equilibrium structures in freezing processes, J. Chem. Phys., 2005, 122(20), 204503 CrossRef PubMed.
- J. Fornleitner, F. Lo Verso, G. Kahl and C. N. Likos, Genetic algorithms predict formation of exotic ordered configurations for two-component dipolar monolayers, Soft Matter, 2008, 4(3), 480–484 RSC.
- A. Travesset, Binary nanoparticle superlattices of soft-particle systems, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(31), 9563–9567 CrossRef CAS PubMed.
- F. Varrato, L. Di Michele, M. Belushkin, N. Dorsaz, S. H. Nathan, E. Eiser and G. Foffi, Arrested demixing opens route to bigels, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(47), 19155–19160 CrossRef CAS PubMed.
- L. Di Michele, F. Varrato, J. Kotar, S. H. Nathan, G. Foffi and E. Eiser, Multistep kinetic self-assembly of DNA-coated colloids, Nat. Commun., 2013, 4, 2007 Search PubMed.
- C. B. Carlson, P. Mowery, R. M. Owen, E. C. Dykhuizen and L. L. Kiessling, Selective tumor cell targeting using low-affinity, multivalent interactions, ACS Chem. Biol., 2007, 2(2), 119–127 CrossRef CAS PubMed.
- C. W. Cairo, J. E. Gestwicki, M. Kanai and L. L. Kiessling, Control of multivalent interactions by binding epitope density, J. Am. Chem. Soc., 2002, 124(8), 1615–1619 CrossRef CAS PubMed.
- F. J. Martinez-Veracoechea and D. Frenkel, Designing super selectivity in multivalent nano-particle binding, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(27), 10963–10968 CrossRef CAS PubMed.
- L. Ronald and G. Treloar, The statistical length of long-chain molecules, Rubber Chem. Technol., 1946, 19(4), 1002–1008 CrossRef.
- C. D. Wick and J. I. Siepmann, Self-adapting fixed-end-point configurational-bias monte carlo method for the regrowth of interior segments of chain molecules with strong intramolecular interactions, Macromolecules, 2000, 33(19), 7207–7218 CrossRef CAS.
- G. C. A. M. Mooij and D. Frenkel, The overlapping distribution method to compute chemical potentials of chain molecules, J. Phys.: Condens. Matter, 1994, 6(21), 3879 CrossRef CAS.
- J. I. Siepmann and D. Frenkel, Configurational bias monte carlo: a new sampling scheme for flexible chains, Mol. Phys., 1992, 75(1), 59–70 CrossRef CAS.
- T. Ohmichi, S.-I. Nakano, D. Miyoshi and N. Sugimoto, Long RNA dangling end has large energetic contribution to duplex stability, J. Am. Chem. Soc., 2002, 124(35), 10367–10372 CrossRef CAS PubMed.
- S. Limmer, H.-P. Hofmann, G. Ott and M. Sprinzl, The 3′-terminal end (ncca) of tRNA determines the structure and stability of the aminoacyl acceptor stem, Proc. Natl. Acad. Sci. U. S. A., 1993, 90(13), 6199–6202 CrossRef CAS.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © the Owner Societies 2016 |