 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Nanoparticle induced miscibility in LCST polymer blends: critically assessing the enthalpic and entropic effects
Priti
Xavier
,
Praveen
Rao
and
Suryasarathi
Bose
 *
*
Department of Materials Engineering, Indian Institute of Science, Bangalore-560012, India. E-mail: sbose@materials.iisc.ernet.in
First published on 9th November 2015
Abstract
The use of copolymer and polymer blends widened the possibility of creating materials with multilayered architectures. Hierarchical polymer systems with a wide array of micro and nanostructures are generated by thermally induced phase separation (TIPS) in partially miscible polymer blends. Various parameters like the interaction between the polymers, concentration, solvent/non-solvent ratio, and quenching temperature have to be optimized to obtain these micro/nanophase structures. Alternatively, the addition of nanoparticles is another strategy to design materials with desired hetero-phase structures. The dynamics of the polymer nanocomposite depends on the statistical ordering of polymers around the nanoparticle, which is dependent on the shape of the nanoparticle. The entropic loss due to deformation of polymer chains, like the repulsive interactions due to coiling and the attractive interactions in the case of swelling has been highlighted in this perspective article. The dissipative particle dynamics has been discussed and is correlated with the molecular dynamics simulation in the case of polymer blends. The Cahn–Hillard–Cook model on variedly shaped immobile fillers has shown difference in the propagation of the composition wave. The nanoparticle shape has a contributing effect on the polymer particle interaction, which can change the miscibility window in the case of these phase separating polymer blends. Quantitative information on the effect of spherical particles on the demixing temperature is well established and further modified to explain the percolation of rod shaped particles in the polymer blends. These models correlate well with the experimental observations in context to the dynamics induced by the nanoparticle in the demixing behavior of the polymer blend. The miscibility of the LCST polymer blend depends on the enthalpic factors like the specific interaction between the components, and the solubility product and the entropic losses occurring due to the formation of any favorable interactions. Hence, it is essential to assess the entropic and enthalpic interactions induced by the nanoparticles independently. The addition of nanoparticles creates heterogeneity in the polymer phase it is localized. This can be observed as an alteration in the relaxation behavior of the polymer. This changes the demixing behavior and the interaction parameter between the polymers. The compositional changes induced due to the incorporation of nanoparticles are also attributed as a reason for the altered demixing temperature. The particle shape anisotropy causes a direction dependent depletion, which changes the phase behavior of the blend. The polymer-grafted nanoparticles with varying grafting density show tremendous variation in the miscibility of the blend. The stretching of the polymer chains grafted on the nanoparticles causes an entropy penalty in the polymer blend. A comparative study on the different shaped particles is not available up to date for understanding these aspects. Hence, we have juxtaposed the various computational studies on nanoparticle dynamics, the shape effect of NPs on homopolymers and also the cases of various polymer blends without nanoparticles to sketch a complete picture on the effect of various particles on the miscibility of LCST blends.
1. Introduction
The dynamics behind the pattern evolution in various types of condensed matter plays a significant role in their morphological control, which in turn determines the mechanical, electrical and transport properties in these materials. Hence, understanding the driving force behind the hierarchical patterning of these materials has emerged as an interesting area of soft matter research and development, including polymeric materials.1,2 Various methods have been adopted to develop micro- and nanodimensional architectures in polymers, copolymers and polymer blends for the fabrication of high performance functional materials. In this context, designing multiphasic polymeric materials with nanoscale structural co-continuity is of great significance. They offer myriad opportunities in electrical, electronic, automotive, packaging industries. Polymer blending has been used as a convenient and cost effective method in developing materials of preferred properties.3 In addition, the polymer blending is applied in the recycling technology as well as it can form cheaper feedstock for the production of high performance blends.4The properties of a polymer blend are very much dependent on the composition of the components in the blend and blending of the preexisting polymers is a means of engineering the properties of both the individual homopolymers into one material.3 The phase separation kinetics in the binary polymer blend depends on various factors like the dynamic asymmetry among the blend components, the interaction between the polymers, concentration, solvent/non-solvent ratio and so on.5 Thermally induced phase separation (TIPS) in a miscible polymer blends is an alternate route to design these types of materials with heterogeneous morphology. A miscible polymer blend is characterised by heterogeneities of the order of the statistical segments of the homopolymers.2,6
The concept of blending two polymers and also the synthesis of polymer composites trace back to the late 19th century, as reported in this literature.2,4 But it is not more than three decade ago that the usage of these particles as compatibilizers in polymer blends was well recognized. The effect on the demixing kinetics of polymer blends by the incorporation of NPs is relatively newer areas of research. Due to this reason, the volumes of studies done on understanding the wetting and phase separation in polymer blends in the presence of nanoparticles are comparatively lesser than the ones on polymer composites. Extensive studies were done to understand the distribution of particles in the polymer and it was observed that it is both size and shape dependent. The theoretical model developed for these observations is in trend with the experimental studies. The properties of polymer nanocomposites are highly dependent on the dispersion of these particles in the matrix. The localisation of nanoparticles in different phases in the polymer blend is of great significance and it is determined by surface energy parameters and also depends on the viscosity of phases. The Reference Interaction Site Model (RISM) in the case of neat polymer blends showed that the attractive interaction can induce correlations in the blend which in turn cause an increase in the entropic term of the free energy of mixing.7,8 Also, the statistical ordering of the polymer around a NP is shape dependent, which in turn changes the stretching free energy of the polymer. This suggests that particle–polymer interaction with the free energy should be dependent on the shape of the particle. However, the interaction between the NPs and the macromolecules playing a huge role in the miscibility, the interaction of polymers on the NP surface causing a change in the configuration and conformational entropic changes have to be assessed and understood carefully. In order to generate and study this hybrid structure, simulation techniques are often incorporated with information at molecular to microscopic levels. A combination of Self Consistent Field Theory (SCFT) or mean field theory and molecular dynamics is developed to gain insights into the polymer blend demixing.9,10 SCFT or mean field theory is significant in these cases, where the demixing is associated with thermorheological complexities due to the large chain length.11,12
This perspective is focused on understanding the effect of various nanoparticles, their shape, and surface chemistry (polymer grafting) on the demixing temperature of Lower Critical Solution Temperature (LCST) polymer blends. In addition, this perspective highlights the enthalpic and entropic factors behind the induced changes brought about by these nanoscopic particles. In order to obtain a thorough comprehension and given the brevity of this perspective, studies related to PS/PVME13 and PMMA/SAN14,15 blends have been discussed in more detail as these two blends represent two extremities in the chain dynamics as the former being dynamically asymmetric and the latter being symmetric and the crystallization induced phase separation in the case of PMMA/PVDF16,17 in the presence of NPs is also not dealt. The NPs have a particular effect in the case of PS/PVME blends, where the phase separation is dependent on the difference in the relaxation time of the individual components as compared to PMMA/SAN where there is a negligible difference in the relaxation time of individual components. We briefly also highlight the effect of NP on other LCST systems18 like PMMA/PαMSAN,19 PC/PαMSAN.20
2. Polymer blends
2.1 Miscibility from a thermodynamics perspective
An in-depth knowledge on the thermodynamics of polymer blends is a prerequisite for a profound understanding of the effect of various nanoparticles on demixing. Hence, the basic concepts of polymer demixing have been revisited in this section.The formation of a homogeneous polymer blend is associated with negative free energy of mixing and is expressed as,
| ΔGmix = ΔHmix − TΔSmix | (1) |
The large chain length causes the polymer solutions to deviate from ideal conditions explained in the solution theory for small molecules. The miscibility in the case of polymer blends cannot be attained at a molecular level, except for certain cases like in the case of PS/PPO, where a nanometer level miscibility is attained.24 But in the other cases there is a level of heterogeneity associated with the thermodynamically miscible systems. Hence, these blends can be considered as partially miscible, rather than completely miscible. The partially miscible polymer blend systems is unlike the immiscible blend, where, the former (partially miscible blend) is characterized by a wide interface with good interfacial adhesion and the latter (immiscible blend) is characterized by a coarse morphology and a sharp interface. According to Patterson25 there are three major contributions to binary interaction parameters – the dispersive, free volume and specific interactions.
2.2 Partially miscible polymer blends (LCST and UCST)
The phase diagram of a partially miscible binary polymer blend is given in Fig. 1. As observed, there are three distinct regions; (i) the single miscible region between the two binodal regions; (ii) there are four fragmented regions between the binodal and spinodal; (iii) two phase separated spinodal regions of immiscibility. The region between S1 and S2 is unstable, as the curve appears concave downwards. At S1 and S2, the second derivative of the free energy is zero. There are two types of partially miscible blends depending on the border line of miscibility/critical solution temperatures. The lower critical solution temperature (LCST) polymer blends are miscible at lower temperatures and phase separated at higher temperature and the upper critical solution temperature (UCST)blends phase separate at the lower temperature.26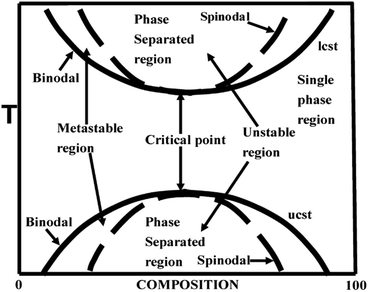 | ||
| Fig. 1 Phase diagram of LCST and UCST blends, adapted from ref. 94. | ||
2.3 Mechanism of phase separation – Spinodal Decomposition (SD) and Nucleation and Growth (NG)
The phase separation occur when either a compositional, temperature or pressure change forces it to enter (i) the metastable or (ii) the unstable region. The phase separation that occurs through the metastable region is characterized by the nucleation and growth (NG) mechanism. This is in general characterized by the matrix-droplet morphology. The phase separation mechanism in which there is occurrence of a delocalized spontaneous concentration fluctuation is called spinodal decomposition (SD). The spontaneous change in concentration fluctuation is the reason for the bicontinuous morphology in the case of SD.26 The demixing in a partially miscible blend is a thermo-rheologically complex process due to the large chain length and slow diffusion rate. This suggests the possibility of applying mean field theory in finding the demixing temperature in the case of these blends.11,122.4 Theory of miscibility
The miscibility is expressed by the Flory–Huggins interaction parameter (χ) which has been derived from the solubility parameter (δ). The interaction parameter is dependent on the temperature. The Flory–Huggins (FH)27 theory demonstrates the basic reason for the diminished miscibility on blending two polymers which is due to the minor contribution to the combinatorial entropy of mixing. The lattice theory and a parameter called the Hildebrand solubility parameter have been introduced in this theory which explains the miscibility conditions.28,29 In the case of polymer–polymer systems, miscibility is achieved if the individual components have comparable solubility parameters. The Flory–Huggins interaction parameter (χ) has been related to the solubility parameter (δ) as,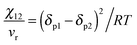 | (2) |
The FH theory has been extended by the Paul and Barlow30,32 heat of mixing approach, where the homopolymer is considered as a copolymer with sub-units of the same chain. The FH theory was later modified by Coleman and Painter33 where all the thermodynamic effects are divided into three groups as configurational entropy, van der Waals interactions and certain specific interactions. The concepts like non-randomness, orientation, free volume, etc. are explained in this theory.
2.5 Chain dynamics in the presence of nanoparticles
The perplexity of the dynamics of a polymer being influenced by another polymer becomes more complicated in the presence of NPs. It was found that NPs are capable of acting as compatibilizers in the case of immiscible polymer blends.34 For instance, carbon black acts as a potential compatibilizer in various elastomeric blends.35 Silica particles have also shown to compatibilize various elastomeric rubber blends36 and techno-commercially important blends like PP/PA-6.37 TiO2 has also seen to act as a compatibilizer in PET/PP blends.38Apart from the compatibilization effect brought about by these particles in the immiscible blend, it was observed that the NPs are capable of slowing down the phase separation in the case of miscible blends. Lipatov39 proposed a theory with limited predictive ability on the effect of nanoparticles on miscibility. For instance, the addition of silica particles induced miscibility and a cloud point shift in the case of PVA/PMMA blends. The effect of particle size and geometry was not taken into account in this case. We now highlight the existing theories that predict/propose NP induced miscibility in partially miscible polymer blends.
3. Effect of particles on the demixing temperature: revisiting the existing models/theories
3.1 Effect of various particles on the demixing of polymer blends
The Cahn Hilliard Cook model40,41 was generalized for the development of a model that predicts the influence of immobile filler particles of different shapes like spheres, fibres and platelets on phase separation. Target patterns are created in the early stages of phase separation in the polymer phase where the particle is selectively localized. The off-critical compositions are characterised by an encapsulation layer at the surface of fillers instead of a target pattern. The filler shape was found to have a large effect on the propagation of the composition waves as the particles can act as planar interfaces. The development of the film structure is hence a sum of the effect of the development of the composition wave, which causes changes in the filler–filler interaction. It was also observed in this simulation study that the dimensionality of the filler particles has an effect on the composition wave only at intermediate timescales. It was also found to be stable only in the blends where the particle size is large compared to the spinodal wave. The composition waves close to the fillers are more stable for particle with dimensions in more directions.42An isolated spherical particle in an ultra-thin blend film of a critical composition can affect phase separation by developing a spherical composition wave disturbance at the early stage of phase separation. The phase separation pattern propagates as a ring into the medium where the filler particle is located. The target rings have a wavelength, λ0 and it forms a target pattern that gets disconnected and it gets absorbed into the background spinodal pattern. This phenomenon occurs when the characteristic scale of the bulk demixing pattern gets coarsened to the size of the filler particle. The later stage of phase separation is characterized by the weakened perturbing influence of the particle as the background phase-separation pattern scale surpasses the filler particle size. In this case of an ultrathin phase separating blend, the thickness of the film surpass the formation of the surface directed wave normal to the solid surface.43
3.2 Correlation of the amplitude of concentration fluctuation with the filler size
Target patterns are the composition waves propagating into the bulk, until they are weighed down by the background spinodal decomposition pattern. The spinodal decomposition occurs by controlled thermal fluctuations and hence these parameters greatly determine the radial extent of the composition waves. There is a direct correlation of the amplitude of the local composition fluctuations with the filler size.42Fig. 2 shows the angular-averaged composition profile ψ(z), with z = r − R (radial distance from the surface of the filler particle). The amplitude of the local composition fluctuations becomes more sharply defined with an increased filler size in comparison to a planar particle where, R → ∞. The impact of surface interactions are expressed by the introduction of the terms g and h which corresponds to the interaction parameter. A filler particle with a ‘neutral’ and ‘non selective interaction has a tendency to align the pattern perpendicular to the interface. The compositional alignment can be more pronounced in the case of a planar surface. The filler induced phase separation is also affected by the blend composition. The compositions which are far off critical are capable of suppressing the spinodal instability by forming a layer of composition enrichment called the ‘‘encapsulation layer’’. This type of phase separation is not characterised by the formation of a target pattern.44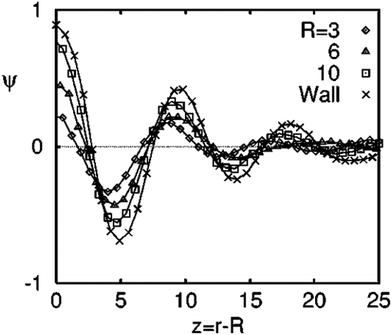 | ||
| Fig. 2 The angular-averaged composition profile ψ(z), with z = r − R (radial distance from the surface of the filler particle), adapted from ref. 42http://dx.doi.org/10.1103/PhysRevE.60.5812. | ||
According to the studies done by Hall et al.,45 a monotonic variation is observed with the filler dimensionality in a homopolymer in the presence of different shapes of fillers like rods, disks and cubes. The depletion, stabilization, and bridging behaviour of these particles are shape dependent. Shape dependent low angle features of nanoparticles are predicted for the collective polymer structure factor associated with competing macrophase fluctuations and microphase-like ordering. The statistical ordering of the polymer around a NP is shape dependent, which in turn affects the particle–polymer interaction. The cube shaped particles are least miscible on depletion and bridging and disks are least susceptible to phase separation. Rods require higher interfacial attraction due to the low surface area shared between any of the two close and non-aligned rods. This observation is in contrast with the large surface area and the higher number of configurations observed in polymer bridging two disks or cubes. It can hence be concluded that miscibility window monotonically broadens with a decrease in NP dimensionality (as seen in Fig. 3).
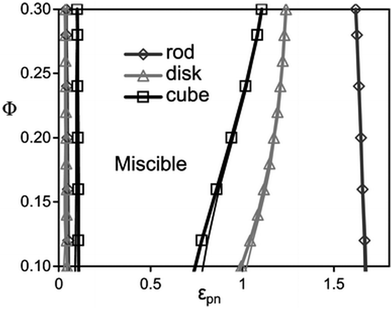 | ||
| Fig. 3 The spinodal boundaries are obtained based on non-convergence (thick curves) and linear extrapolation of disks, rods and cubes, respectively (Hall et al.,45 Reproduced with permission from The Royal Society of Chemistry). | ||
3.3 Spherical particles/isotropic particles
In order to predict the demixing behavior in a polymer blend in the presence of spherical nanoparticles, Ginzburg has proposed a theory46 based on self-consistent field/ density function theory (SCF-DFT). It was proposed that the shifting of phase separation temperature by the addition of fillers is greatly affected by the interaction of the particle with the polymer and also by the geometrical structure. In this theory, a model homopolymer binary mixture (A/B) with the degree of polymerization NA = NB = N has been chosen and the monomer radius was assumed to be r0 ∼ 0.2 to 0.5 nm. The added particles have an affinity towards phase A. The Flory interaction parameter is given by, χAP = 0, χBP = χAB = χ. If the volume fraction of the nanoparticle is ψ, then the volume fraction of polymers A and B is given as (1 − ψ)φ and (1 − ψ)(1 − φ), respectively. The free energy per unit volume is given as the sum of the polymer–polymer, particle–particle and polymer–particle interaction,| F = Fpol + Fpart + Fint | (3) |
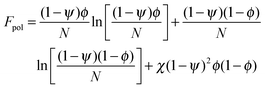 | (3a) |
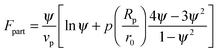 | (3b) |
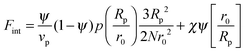 | (3c) |
In the first term of eqn (3) (as shown in eqn (3a)), the free energy of mixing has been calculated by using the Flory–Huggins theory by adding the corrections for the volume occupied by the nanoparticle. The second term in eqn (3) (given by eqn (3b)), shows the contribution of the particle as such and it consists of the ideal and non-ideal “entropic free energy” of the hard spheres. The non-ideal contribution was approximated using the Carnahan–Starling approximation.47 This equation of state gives a better approximation of free energy with a fair accuracy. The NPs can be approximated as A monomer when the interpolating factor, p (Rp/r0) with the non-ideal term has been approximated as Rp/r0 → 1, as x → 1, p(x) → 0 and as x ≫1, p(x) → 1. It has to be noted that any interpolating function will give a result similar to what was obtained in this case. The interpolating function used in this case is, p(x) = max(tanh (x − 1), 0). The third term as seen in eqn (3c) gives the interaction between the particle and the polymer, which constitutes both enthalpic and entropic contribution. The entropic term (the first term in the RHS of eqn (3c)) is due to the stretching of the polymer in the vicinity of the NPs. The stretching free energy (h) is given as
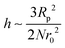 | (3d) |
3.4 Rod shaped particles
The interactions in binary fluid–rod mixtures have been explained using simulations by Peng et al.48 This model explains about the evolution of phase-separating fluids which irreversibly drives the self-assembly of nanoscopic rods into supramolecular networks which leads to the formation of continuous reinforcing structures. The binary system is described by a continuous order parameter, which is given as the sum of the volume fraction of A and B. The function ψ(r) is given as ψ(r) = φA(r) + φB(r). The flux of ψ is proportional to the derivative of the free energy (F), with respect to the order parameter,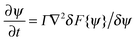 | (4a) |
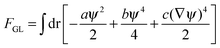 | (4b) |
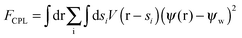 | (4c) |
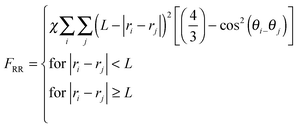 | (4d) |
4. An assessment of the effect of various nanoparticles on the demixing temperature: examining various experimental studies
It has been theoretically proved that the introduction of nanoparticles can facilitate thermodynamic miscibility in a polymer blend system. It is applicable to both miscible and immiscible blends, even though the influence is more prominent in the case of immiscible blends. The study of Nesterov et al.49 showed that these kinds of systems can be at equilibrium due to the improved thermodynamic stability due to the introduction of fillers and also at non equilibrium, as the molecular mobility of the macromolecules has been diminished, preventing the phase separation of the system. An increased or decreased phase separation temperature is observed in the case of the LCST blend, PVA/PMMA, by the introduction of fillers. It has been observed that the addition of fillers in a large concentration, where both the components transit into the boundary has shown an improved phase separation temperature. The lower concentration of fillers can diminish the phase separation temperature as the effect is the redistribution of the blend components according to the molar mass between the filler surfaces. The fillers are capable of changing the phase separation temperature by altering the interactions in the boundary layer or by changing the molecular mass distribution of the molar mass distribution in the blend matrix.50Contradicting results compared to the study of Karim et al.51 was observed in the case of addition of fumed silica particles in the PS/PB UCST blend. The phase boundary in this case has been shifted vertically on the addition of fillers (see Fig. 4). This suggests that the shift of the critical temperature does not depend on the relative polymer composition. This observation is very significant as it led to developing a different dimension in the research on understanding the demixing mechanism of polymer blends in the presence of nanoparticles (see Fig. 4).
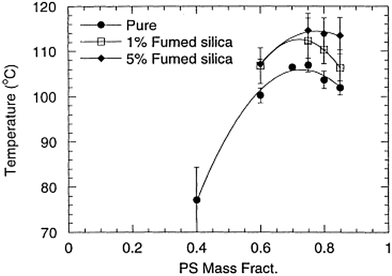 | ||
| Fig. 4 Phase diagram of addition of UCST blend PS/PB in the presence of fumed silica particles (A Karim et al.51 reproduced by permission from Elsevier, Copyright © 2000 Elsevier Science Ltd, All rights reserved). | ||
The phase separation kinetics depends on various factors like the dynamic asymmetry among the blend components, molecular weight of the polymer, processing conditions, solvent used, etc. These factors control the demixing apart from the shape of the particle in the blend. Due to these reasons, our perspective has been restricted mostly to understand the change in the chain dynamics in two LCST, polymer blends; PS/PVME and PMMA/SAN, the first being a dynamically asymmetric blend and the second being a dynamically symmetric blend.
PS/PVME is a dynamically asymmetric blend and this dynamic asymmetry is induced by large differences in the molecular weight or Tg (glass transition temperature) of the components. The main feature of VPS is the buildup of self-generated stresses in the more elastic phase during phase separation. This leads to the formation of a percolating network of the more elastic phase even if it is the minor phase. This percolated network structure coarsens with time via a volume shrinking process and eventually breaks into disconnected domains that can be considered as a kind of disintegration or phase inversion, as mentioned by Tanaka.52–56 The induction of the network structure, volume shrinking process and disintegration behavior are characteristic features of VPS that cannot be observed in normal phase separation mechanisms (NPS), i.e. spinodal decomposition (SD) and nucleation and growth (NG). Various phase separation mechanisms apart from NG and SD mechanisms like transient gel induced viscoelastic phase separation (T-VPS), nucleation of aggregate-like PS-rich in the stable disperse-matrix morphology (ANG) and also aggregate-like PS-rich phase nucleates in the early stages of phase separation, and forms a percolating network of the minor PS-rich phase through coalescence at later stages (C-VPS) observed by Yeganeh et al.57 Various phase separation mechanisms like fracture phase separation (FPS)54 and viscoelastic phase separation (VPS) at various quench depths, showing transitions like brittle to ductile fracture in PS/PVME.58
4.1 Isotropic/spherical particles
As mentioned previously, the PS/PVME blend is a dynamic asymmetric blend and the phase separation and the morphology development were explained by a dynamic asymmetric parameter. As explained by a model proposed by Tanaka,55 the dynamic asymmetry parameter (ξ) in the case of the polymer mixture has been calculated as the ratio of relaxation time (which is the reciprocal of the crossover frequency of the storage and loss modulus) of the slow component to the relaxation time of the fast component (τ1 and τ2, respectively).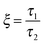 | (5a) |
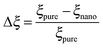 | (5b) |
A similar phenomenon was observed in the case of a critical composition 60/40 PS/PVME, in the presence of silver nanoparticles (nAg). Similar to the previous case, nAg particles are preferentially located in the PVME phase. The strong concentration fluctuation in these cases is affected by the presence of these particles causing a changed pattern in the domain growth. The continuity in the PS phase has been retained for higher temperatures also. The demixing temperature has also increased by the addition of 0.5 wt% nAg. This enhanced miscibility is contingent to the enhanced intermolecular interaction between the components of the blend. This is due to the local confinement brought about by nAg particles in the PVME environment, affecting the overall dynamics of the blend. The addition of various shaped particles has affected the concentration fluctuation, interfacial driven elasticity, phase morphology and the local segmental dynamics of the chain PS/PVME blends differently in different regions of the phase diagram. PS/PVME is a blend exhibiting nonlocal entropy of mixing resulting in the formation of an equilibrium nanoheterogeneous structure, as seen in Fig. 5.60
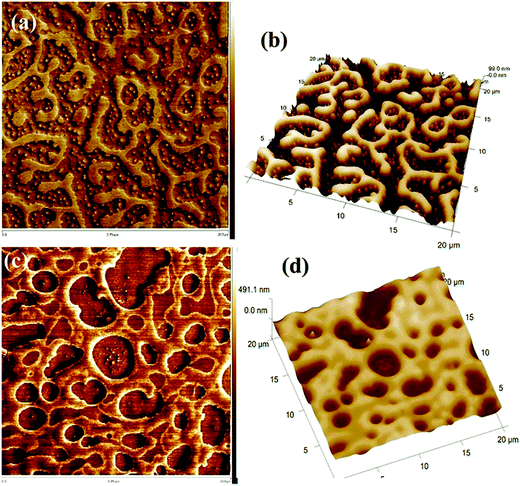 | ||
| Fig. 5 AFM image showing the localization of silver nanoparticles (Bharati et al.,60 reproduced by permission of American Chemical Society, Copyright © 2014, American Chemical Society). | ||
Studies by Gharachorlou et al.61 shows that the addition of silica particles (4 vol%) has increased the demixing temperature to a significant amount ca. 10 °C. The reason for phase separation has been explained as the high entropy of the particles and the replacement of the PVME chains with the PVME covered silica particles which reduced the enthalpic portion of the free energy by reducing the number of PS/PVME interactions. Addition of 4% silica has changed the morphology from network to droplet type. They suggested that if the concentration of NPs is around 2–5 vol%, it can cause network formation in the system. This causes drastic enhancement in the rheological properties, see Fig. 6.
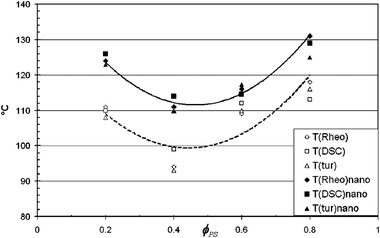 | ||
| Fig. 6 Phase separation temperature of the PS/PVME blend in the presence of silica by various experimental methods (Garachorlou et al.,61 adapted from American Chemical Society, Copyright © 2008, American Chemical Society). | ||
In all of the three cases, the NPs were hydrophilic and were localized in the PVME phase, decreasing the dynamic asymmetry of the blend and changing the mechanism of phase separation. The work by Xia et al.62 has been extended to understand the effect of the surface phenomenon of the silica particles on the localization and thereby the phase separation mechanism. The hydrophilic silica particles have an affinity towards the PVME phase and hydrophobic silica has affinity towards the PS phase. Hence, by the particles being localized in the PS phase will increase the dynamic asymmetry of the blend. The temperature of demixing has been evidently increased on the addition of hydrophilic PVME, i.e., ca. 5 °C increase by the addition of 8 wt% of the particles. A distinct alteration in the morphological transition has been seen in the case of both the hydrophilic and the hydrophobic particles due to the difference in the dynamic asymmetry brought about by these particles in each case. This can also be attributed to the difference in alignment of both hydrophilic and hydrophobic particles in their respective cases. This is clearly visible in the TEM images in Fig. 7a.
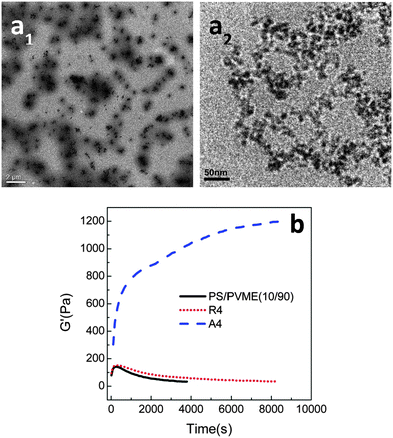 | ||
| Fig. 7 (a) TEM mages of PS/PVME blend with hydrophobic silica (a1) and hydrophilic silica (a2) (b) time sweep plots from rheology experiment, Xia et al.62 reprinted with permission from American Chemical Society, Copyright © 2013, American Chemical Society. | ||
Fig. 7b shows the dependence of G′ with respect to time for both the hydrophilic and hydrophobic particles, thereby suggesting that the demixing temperature had different effects in the presence of both of these particles.63 The differently modified silica particles have different effects on the interaction parameter and also on the surface energy. The hydrophilic silica in the PVME phase decreases the dynamic asymmetry and makes compositional asymmetry a predominant factor in the morphology development. The addition of hydrophobic silica increased the dynamic asymmetry and decreased the compositional asymmetry. Regardless of the localization, the addition of both of the particles has stabilized the morphology. The spinodal temperature has increased from 90.7 °C for the neat blend to 94.2 °C, 95.9 °C, 103.3 °C and 110.8 °C for 1, 2, 4 and 8 wt% of hydrophilic silica. It can be concluded that by the addition of a threshold amount of particles, i.e., 2–4 wt%, a transition from network to droplet morphological transition was observed.
All the aforementioned cases showed that the addition of nanoparticles has altered the phase separation temperature of the blends. Also, it was observed that the presence of NPs in polymer nanocomposites can alter the dynamics of polymer chain segments. Dynamics of two different timescales is observed in such cases due to the different compositional environments. This is a dominant factor in changing the surface and bulk viscoelastic behaviour.10 It was proved that the dimensionality of the filler particles has an effect on the composition wave at the intermediate stages of phase separation. It was also found to be stable only in those blends where the particle size is large compared to the spinodal wave. The composition waves about the filler are dependent on the particle dimensions. Hence, in order to investigate the effect of NP shape on the development of compositional waves, NPs of varied shapes and surface modifications were discussed here.
The simulation studies done by Karim et al.65 on model PS/PVME blends suggest that the presence of fillers helps in the development of concentration waves and is observed to be dependent on the filler shape. The simulation work highlighted the effect of concentration of silica particles of 100 nm on a comparable thickness of film. The spin coated films of near-critical composition of PS and PVME with filler particles as silica beads with an average size of ∼100 nm were analysed. Phase separation was achieved by annealing to a shallow quench depth. The AFM topography images obtained matches with the simulation showing the circular filler induced composition fluctuation. The pattern located far from the filler particles bear a resemblance to the typical spinodal decomposition pattern observed in the case of the blends without fillers. A near critical composition of the blend was chosen so that the polymer blend shows spinodal decomposition in the absence of any filler. Fig. 8 shows as an intermediate stage of phase separation. The line profile image in the AFM image shows the magnitude of perturbation around the silica particles which appear as bright spheres. The films have been washed to remove the PVME phase to obtain a better contrast. PS rich ring patters are observed in the washed films.
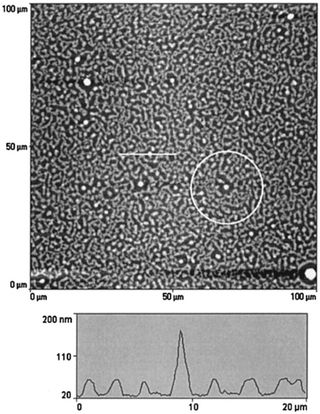 | ||
| Fig. 8 A circular filler induced composition fluctuation in PS and PVME with silica beads, Karim et al.,65 adapted with permission from American Chemical Society, Copyright © 1999, American Chemical Society. | ||
Transient waves generated in these films in the presence of silica resulted in the formation of compositional waves on the surface, which has become a determining feature in breaking the symmetry pattern in the phase separation process within the surface forming compositional waves.65 We have observed that the development of target composition patterns about the filler particles has characteristics in common with the idealized 2D Cahn–Hilliard–Cook simulations of blend films with fillers. In the presence of fillers these phase separating blends show the development of composition waves which have the symmetry of the filler particles.
It was observed that the addition of nanoparticles contributed a compatibilizing effect in the LCST blends. The effect of spherical nanoparticles has been compared with the block copolymer. The nanosilica used in this case was modified with dimethyl dichlorosilane, which made the particles hydrophobic. This caused the particles to be localized in the PS phase. This confined the dynamics of PS chains enhancing the dynamic asymmetry of the system. The self-generated stresses are strengthened and inhibit the reduction of system free energy by network break up in such cases. The SEBS-g-MA block copolymer used here was localized at the interface and acted as an obstacle for polymer chains to diffuse through the interface. This is the contributing factor for the stabilized network at the interface and the controlled phase separation. On comparing both the cases, it was observed that the addition of NPs has pinned the phase separation by kinetically trapping nanoparticles in controlling the kinetics of phase separation which was found to be superior compared to the block copolymer-based compatibilizers (see Fig. 9).66
 | ||
| Fig. 9 Comparison of the compatibilizer and the filler in the case of PS/PVME blends (a) neat blend (b) in the presence of the SEBS-g-MA block copolymer (c) in the presence of nanosilica, Reproduced from Yeganeh et al.,66 with permission of The Royal Society of Chemistry. | ||
The effect of spherical particles has also been extended on systems like PMMA/SAN which is a dynamically symmetrical blend. Due to the preferential adsorption of nanoparticles on one of the polymer phase, a surface layer is formed with composition that differs from the initial composition of the blend in the bulk. In the case of the PMMA/SAN blend with silica particles, there is a formation of the hydrogen bond between the carbonyl groups in PMMA and silanol groups at the surface of silica particles. These cause a decrease in the average molecular weight of PMMA in the bulk increasing the critical interaction parameter causing an increase in the phase separation temperature (see Fig. 10). The compositional change brought about by the selective adsorption of one of the phases on the polymer on the NP was explained by Cohen-Addad67 by calculating the weight of the bound polymer. It can hence be concluded that the smaller the particles, more polymer will be adsorbed on to the surface of the polymer and significantly affect the effective composition.68
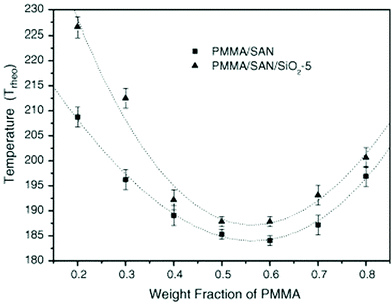 | ||
| Fig. 10 Phase diagram of PMMA/SAN in the presence of silica, Huang et al.,68 reprinted with permission from Elsevier, Copyright © 2005, Elsevier Science Ltd, All rights reserved. | ||
It was found that in the case of a homogeneous PMMA/SAN blend, the silica NPs are uniformly dispersed in the blend film. During demixing, the NPs were observed to be partitioned into PMMA wetting layers and also PMMA domains. A slowed domain growth was observed and the kinetics of demixing followed a coalescence model. The correlation length ξ was found to increase a function ξ ∼ t1/3 for the neat blends and also the blends containing 2 and 5 wt% NPs. Even though there is a decrease in the kinetics of demixing, the correlation length was observed to be unaltered.69
The addition of hydrophilic silica nanoparticles has stabilized the morphology, and improved the thermal and mechanical properties in polycarbonate/poly(methyl methacrylate) (PMMA/PC) blends. The compatibilization studies with NPs was compared with a tin(II) 2-ethylhexanoate catalyst in this case. The addition of nanoparticles has kinetically arrested the morphology of PMMA/PC blends, but the thermal and mechanical properties of blends were improved significantly upon the addition of nanoparticles. Hence the addition was considered superior to the catalyst addition in this case.70
The addition of C60 fullerenes in poly(tetramethyl bisphenol A polycarbonate) and deuterated polystyrene (TMPC/PSD) manifested a reduced spinodal temperature (7–10 °C) at a loading of 1–2 mass%. These observations were based on neutron scattering experiments. However, the loading of 0.2–0.5 mass% imparted a small increase in Ts. The observed non-monotonic variation in demixing with the addition of NPs is due to the competitive interplay of the asymmetric component interactions and also the NP dispersion.71
The addition of three different surface functionalized NPs were studied in the case of dPMMA/SAN 50/50 blend. NPAs are colloidal silica particles with a diameter of 22 nm and a surface with methyl and hydroxyl groups. NPw and NPs are silica particles (diameter 15 nm) which are weakly and strongly segregated by grafting with PMMA brushes having Mws of 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 and 2100 g mol−1. The difference in the functionality of the particles causes a difference in their segregation behavior. NPA distribute throughout the PMMA phase, NPw in the PMMA phase and at the PMMA/SAN interface and NPs locate only at the PMMA/SAN interface. In this paper, it has been provided experimental evidence that the process of roughening in polymer blend films is driven by the underlying phase-separated morphology, which in turn is dependent on the surface functionalities of the NPs. The polymer film contains 2 wt% NP was annealed for 24 h. The RMS roughness (Rq) is obtained from Fig. 11a and a watershed segmentation was used to distinguish the boundaries between peaks as seen in Fig. 12b. By omitting the patches around the edge of Fig. 11b and c has been obtained. The fluctuation in the spinodal wavelength (λs) is determined from the mean diameter of the colored patch. The midlayer morphology (40 μm) consists of the continuous B phase (light) and domains of A (dark circles) as seen in Fig. 11c. The roughening and rupture is caused by the Laplace pressure induced by a phase-separated structure. The major focus of the paper was to understand the dewetting of the polymer blend layer of long wavelength fluctuation which was developed by short wave-length spinodal waves. Still, interesting insights were obtained on the effect of localization on the development of spinodal waves by analyzing the roughness factor. As observed from the previous figure, it was observed that the localization of particles in the PMMA/SAN interface has caused a jamming of the morphology.86 This was understood by the low roughness values. This study provides a proof on understanding the effect of particles, irrespective of their shape, arresting the phase morphology.72
700 and 2100 g mol−1. The difference in the functionality of the particles causes a difference in their segregation behavior. NPA distribute throughout the PMMA phase, NPw in the PMMA phase and at the PMMA/SAN interface and NPs locate only at the PMMA/SAN interface. In this paper, it has been provided experimental evidence that the process of roughening in polymer blend films is driven by the underlying phase-separated morphology, which in turn is dependent on the surface functionalities of the NPs. The polymer film contains 2 wt% NP was annealed for 24 h. The RMS roughness (Rq) is obtained from Fig. 11a and a watershed segmentation was used to distinguish the boundaries between peaks as seen in Fig. 12b. By omitting the patches around the edge of Fig. 11b and c has been obtained. The fluctuation in the spinodal wavelength (λs) is determined from the mean diameter of the colored patch. The midlayer morphology (40 μm) consists of the continuous B phase (light) and domains of A (dark circles) as seen in Fig. 11c. The roughening and rupture is caused by the Laplace pressure induced by a phase-separated structure. The major focus of the paper was to understand the dewetting of the polymer blend layer of long wavelength fluctuation which was developed by short wave-length spinodal waves. Still, interesting insights were obtained on the effect of localization on the development of spinodal waves by analyzing the roughness factor. As observed from the previous figure, it was observed that the localization of particles in the PMMA/SAN interface has caused a jamming of the morphology.86 This was understood by the low roughness values. This study provides a proof on understanding the effect of particles, irrespective of their shape, arresting the phase morphology.72
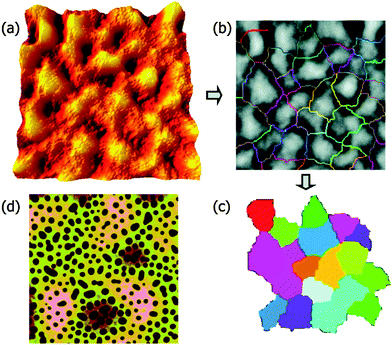 | ||
| Fig. 11 Quantification of the surface (a–c) and midlayer (d) features in SFM images, Chung et al.,86 adapted with permission from American Chemical Society, Copyright © 2007, American Chemical Society. | ||
 | ||
| Fig. 12 Phase diagram of PMMA/SAN in the presence of clay, Pang et al.,74 reprinted with permission from Elsevier, Copyright © 2005, Elsevier Science Ltd, All rights reserved. | ||
4.2 Anisotropic particles
The effect of anisotropic particles like clay on the phase separation temperature of various polymer blends has been analyzed. Unlike spherical particles, these particles have a high surface area exposed to the polymer surface. Therefore, the thermodynamics, kinetics and morphology of phase separation are altered on the addition of a very small amount of particles. The driving force for self-assembly is directly related to the anisotropy of the particle. So if the polymer blend phase separates due to the effect of the particle, the osmotic effect produced in the phase separation of the individual phases is directly related to the shape of the particles. The concept of directional depletion interaction of particles has to be analyzed to understand the entropic factors contributing to the phase behavior. A study on the depletion interaction on the polymer with colloidal particles showed that the range for interaction in the case of depletion attraction is 10% smaller than the radius of gyration Rg of the polymer chain. The phase separation can be compared to the case of the hard sphere colloids and it is devoid of any attractive and long-range interactions, which competes with entropic effects to produce ordered phases It has to be carefully assessed that whether the improved miscibility is due to the improved anisotropy.Very precise techniques like small-angle neutron scattering (SANS) and a two-dimensional combinatorial method based on light scattering were used to study the effect of dimethyl dioctadecylammonium substituted montmorillonite (2C18M) on the dPS/PVME blend and corroborated by single-point static cloud-point light scattering. It was found that the addition of layered silicates up to a volume fraction of 0.04 is found to leave the phase diagram unchanged. It was also observed that the Flory Huggins parameter at high temperature is independent of layered silicate upto a volume fraction of 0.008.73
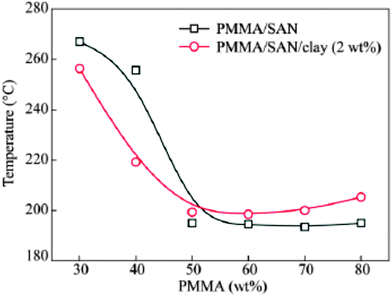
A compositional dependent behavior was observed in the case of a clay filled PMMA/SAN blend (see Fig. 12). The clay particles migrate from the PMMA-SAN boundary in the initial stage to the PMMA-rich region at the late stage of phase separation due to the affinity of clay towards the PMMA phase. Tb and Ts of PMMA/SAN and the metastable region have been observed to be expanded. The isothermal small angle light scattering (SALS) studies show the decrease of the domain coarsening rate for the blend matrix due to the retardation of macromolecular diffusion. The compositional difference in the surface layer and the polymer matrix has been attributed to this phenomenon. The surface layer of the polymer on the clay acts as nuclei for a new phase by inducing phase separation according to the nucleation or spinodal mechanism.74 The localization of NPs in one of the phases will increase the viscosity of the corresponding phase and thereby slowing down the domain growth. This can be either due to the attraction of the NPs to the polymer matrix or due to the confinement of the polymer chains. NP is well dispersed in a polymer only when the radius of the NP is less than the radius of gyration of the polymer. Thermodynamic stability can be achieved in such cases due to enthalpic effects on account of increased contacts with the polymer chain.
Graphene oxide (GO) or reduced graphene oxide (rGO) improved the intermolecular coupling in PS/PVME blends by imparting a molecular level miscibility. This has increased the rheological demixing temperature in the case of this blend.75 A similar observation was seen in the case of PαSAN/PMMA blends with dynamic symmetry.76
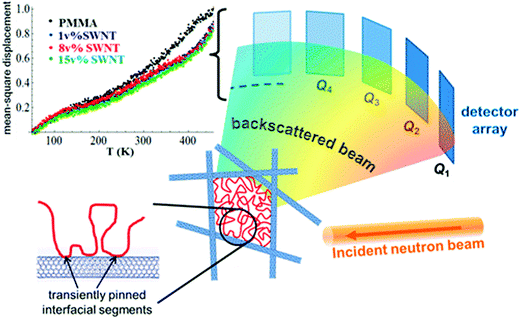 | ||
| Fig. 13 MSD amplitude in the pure polymer and in the SWNT composites showing shorter-range atomic motions in the composites and the schematic representation of the heterogeneity induced in the polymer composite in the presence of heterogeneous particle, Ashkar et al.,77 adapted with permission from American Chemical Society, Copyright © 2014, American Chemical Society. | ||
The addition of rod shaped CdSe-TOPO particles has been analyzed in the case of PS/PVME blends. The work mostly describes about how the particles are kinetically trapping the co-continuous morphology in the blend in the presence of 2 vol% of CdSe particles.78 It was observed that a network of nanoparticles percolates throughout the PVME domains at relatively lower volume fractions indicating that kinetic arrest occurs due to attractive interactions between particles. This is similar to the case of colloidal gels in the suspensions of attractive particles. The particle size also plays a role. In the case of these rod-shaped particles, aggregation-induced gelation of particles has aided in stabilizing the co-continuous morphologies.
The addition of MWNTs has increased the phase separation temperature of the PS/PVME blend by imparting a molecular level miscibility. The preferential wetting of PVME onto MWNTs has been observed from AFM and this has observed to reduce the interaction parameter χ in the blends. The addition of particles could retain the interconnected network of the PS/PVME blend.79 It was found in another study that the addition of MWNTs has affected the cooperativity of dynamically asymmetric blends of the PS/PVME blend, which was confirmed by the study on chain connectivity effects by dielectric spectroscopy. The high entropic losses in the case of blends with MWNTs are due to the lower number of conformations available for a polymer chain.80 The evolution of transient morphologies in PS/PVME blends, which varied from nucleation and growth, C-VPS, spinodal decomposition and T-VPS were assessed in the presence of MWNTs. The interaction of MWNTs in the blend alters the dynamic asymmetry of the system and creates a heterogeneous environment. This can be correlated with the chain connectivity effects by evaluating the effective glass transition of the PVME phase and the length of the cooperatively rearranging region (CRR) of various blends.81
The spinodal decomposition temperature demonstrates an increase in the miscibility in PMMA/SAN in the presence of various functionalized MWNTs. Thermally induced phase separation causes a selective localization of MWNTs in the PMMA phase. The miscibility of PMMA in SAN was enhanced in the presence of MWNTs. The bimodal and the slowed down segmental relaxation in the presence of MWNTs by dielectric spectroscopy supports the delayed phase separation as observed from rheology.82
In the case of the dynamically symmetrical, blend PαMSAN/PMMA as reported by Bose et al.83 It was observed that the rheological phase separation temperature (Trheo) decreased in the blends in the presence of MWNTs. The phase separation caused selective localization of MWNTs in the PαMSAN phase of the blends, which were initially randomly distributed in the mono-phasic materials as observed from the electron microscopic images. The significant changes in the viscosity ratios in the blends also resulted in a shift in the phase inversion concentration towards lower PαMSAN content. The MWCNTs lead to a significant slowdown of the segmental dynamics in the blends inducing phase separation in the PMMA/SAN blends. This is due to the selective localization of MWCNTs in the PMMA phase.
4.3 Polymer grafted nanoparticles
A controlled dispersion of nanoparticles in a polymer matrix is essential in achieving significant enhancement in the characteristic properties of the polymer composites. A tailored nanoparticle-polymer interface is essential for obtaining a homogeneous dispersion of NPs. The aggregation between the nanoparticles can be reduced by grafting the particles with polymer chains, which results in an increased density of polymers at the interface.The effect of PS (5 kg mol−1) functionalized Au nanorods in the miscible blends of PS (152 kg mol−1) and poly(2,6-dimethyl-p-phenylene oxide) (PPO) (42 kg mol−1) was monitored by both experimental and theoretical methods. The dispersion of PS grafted NPs in various blend compositions were studied in detail. When the volume fraction of PPO was varied from 0 to 0.50, the NPs appeared to be aggregated, due to the unfavorable brush-matrix interaction, where χ = 0. More favorable interactions are induced when the volume fraction of PPO is higher in the system, as PS/PPO forms a miscible blend with χ < 0. A complete dispersion is obtained in the case of homopolymer PPO, where favorable PS/PPO interactions are present. This is evident as observed in the TEM images and the schematic representation as given in Fig. 14. The effect of polymer brush density is studied by the SCFT calculations in the case of compositions where χ = 0. When the brush and the matrix are chemically similar, the nanoparticle dispersion depends on the values of N, P, and σ (brush grafting density). A dry brush condition is observed when P ≫ N, where the brush on the NPs rejects the relatively large matrix polymers. A wet brush condition is observed when the brush is located within the matrix polymer. From these experimental studies it can be concluded that the nanoparticle dispersion in polymer composites is a function of α = P/N and the particle aggregation is due to the depletion–attraction forces that result from dry brushes.84
 | ||
| Fig. 14 (a) Schematic showing the dispersion of polymer modified nanorods in various blends (b) TEM images of a similar case. (a1) ϕPPO = 0.00; (a2) shows a lower magnification image that captures the aggregate distribution. (b–e) Correspond to ϕPPO = 0.25, 0.50, 0.75, and 1.00, respectively (the scale bars corresponds to 200 nm), Hore et al.,84 adapted with permission from American Chemical Society, Copyright © 2012, American Chemical Society. | ||
The effect of PS grafted silver nanoparticles (PS-g-nAg) was compared with the neat silver nanoparticles (nAg) on the demixing of the PS-Br/PVME blend. Two molecular weights of matrix polystyrene were studied in this case, as seen in Table 1. The particles were localized in the PVME phase due to the favourable PS–PVME contacts in the case of both the molecular weights. It was observed that the demixing temperature was increased by ∼18 °C in the case where the Mw of the grafted polymer chain is comparable to that of the matrix polymer. The nAg particles with PS brushes prevent the core–core interaction between the nAg particles. The favorable interaction between PS chains in the nAg particles gives a homogeneous dispersion in the PVME phase. Thermodynamic miscibility is imparted to the system due to the reduced conformational fluctuation due to this.85
| PS/PVME blends | Isochronal temperature sweep (tan delta) Trheo ± 2 °C | Spinodal temperature Ts ± 2 °C |
|---|---|---|
| 60 (9 kDa)/40 | 85 | 89 |
| 60 (35 kDa)/40 | 104 | 112 |
| 60 (9 kDa)/40 with 0.5 wt% bare nAg | 95 | 96 |
| 60 (9 kDa)/40 with 0.5 wt% PS-g-nAg | 98 | 107 |
| 60 (35 kDa)/40 with 0.5 wt% bare nAg | 114 | 121 |
The selective localization of silica particles in the PMMA/SAN blend was tuned by varying the chain length of polystyrene grafted on it. The particles with short grafts (PS ∼ 500 g mol−1) was localized in the interface and the particle with long grafts (PS ∼ 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1) was localized in the PMMA-rich phase. This was determined by the interfacial tension factors as the interfacial tension of the PS–SAN pair is higher than that of the PS–PMMA pair. It was observed that SiO2–PS particles localized at the PMMA/SAN enhanced the stability. The significance of particle localization on the rheological transition temperature is one of the major inferences which could be drawn from this work (Fig. 15).87
000 g mol−1) was localized in the PMMA-rich phase. This was determined by the interfacial tension factors as the interfacial tension of the PS–SAN pair is higher than that of the PS–PMMA pair. It was observed that SiO2–PS particles localized at the PMMA/SAN enhanced the stability. The significance of particle localization on the rheological transition temperature is one of the major inferences which could be drawn from this work (Fig. 15).87
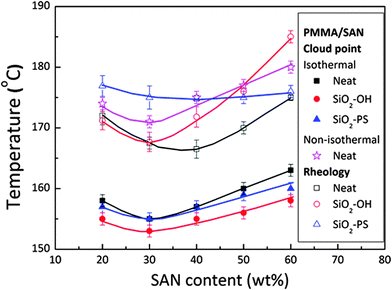 | ||
| Fig. 15 Phase diagram of variously modified silica in the PMMA/SAN blend, Huang et al.87 adapted with permission from American Chemical Society, Copyright © 2012, American Chemical Society. | ||
The demixing of the PS/PVME blend in the presence of polystyrene grafted MWNTs (PS-g-MWNT Mw ∼ 9000 g mol−1) was dramatically by ∼33 °C with respect to the control blend and these effects were due to the entropic and enthalpic factors. The length of the cooperative rearranging region was decreased by the addition of PS-g-MWNTs showing a confinement effect on the chain dynamics and it enhanced the inter-chain concentration fluctuation.88
The demixing the near critical composition of the LCST mixture of PS/PVME was studied in the presence of highly curved gold nanoparticles which were densely brushed with varying graft length of PS.89 The gold nanoparticles brushed with 3 kDa polystyrene (graft density ca. Σ = 1.7 chains per nm−2) and that for 53 kDa PS (Σ = 1.2 chains per nm2). The localization of PS (3 kDa)-g-nAu in the PVME phase can be expected to be of entropic origin due to expulsion from the PS phase as Rg,matrix chains > Rg,grafted chains (where Rg is the radius of gyration of the polymer chain), the localization of PS (53 kDa)-g-nAu in the PS phase is believed to be facilitated by favorable melt/brush interactions. The PS (53 kDa)-g-nAu nanoparticles delayed the demixing by 12 °C with respect to the neat mixture due to enthalpic interactions between the grafted PS and the free PS, the entropic losses (deformational entropic losses on blending, translational entropic loss of the free PS and the conformational entropic loss of the grafted PS) and the interface of the grafted and the free chains.95 The localisation has been represented using a cartoon as seen in Fig. 16.
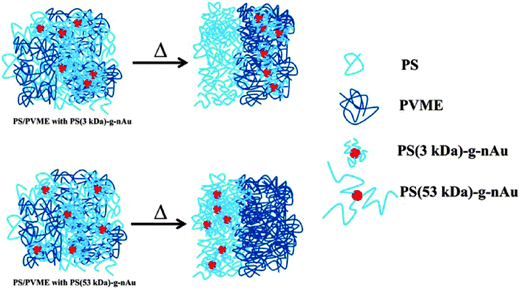 | ||
| Fig. 16 Schematic representation showing the change in localization by different graft density of PS on gold nanoparticles, Kar et al.,95 Reprinted with permission from American Chemical Society, Copyright © 2014, American Chemical Society. | ||
Various cases as discussed above lacks to provide an in-depth insight into the dynamical perturbations induced by the NPs on the polymer chains and thereby the miscibility criteria. It was observed in the study of polymer composites that the NPs with high anisotropy, like carbon nanotubes, exhibit very low percolation thresholds. A comparably higher surface to volume ratio is obtained in these particles. These types of particles are capable of creating two dynamic environments in the polymer. The polymer adsorbed on the surface of the nanotubes appears as a sequence of train segments and these interfacial train segments shows a transient immobilization. The loop and tail segments appear away from the interface and the end segments remain mobile in these cases. This is the reason for the appearance of two distinct polymer regions in the presence of the nanotube – the train segments having an effectively frozen dynamics around the nanotubes and the loop and trail regions with faster motions, which are away from the interface. These interactions can restrict the local and cooperative relaxations. These changes in the polymer dynamics can clearly affect the hierarchical polymer dynamics in the case of blends.77
Bimodal relaxations suggesting different ‘dynamical’ environments were noted in the case of PS/PVME blends in the presence of MWNTs.80 The dielectric loss modulus spectra showed a bimodal distribution in the presence of MWNTs. This is the characteristic of a heterogeneous environment. The presence of MWNTs has caused more entropic losses causing a lower number of conformations for the polymer chain. This results can be supported with the dielectric relaxation studies of the miscible polymer blend PVPh–PVEE (poly(4-vinylphenol)/poly(vinyl ethyl ether)). The miscibility in this polymer blend is imparted due to hydrogen bonds in the mixture. PVPh–PVEE segments with intermolecular hydrogen bonds showing a slow relaxation, whereas the free PVEE segments showed a fast relaxation. A second segmental relaxation was also observed in the blends with 60 and 80% PVPh due to the restricted relaxation of PVEE confined in a the rigid matrix PVPh.90 Hence the broad relaxation spectra gives an indication of different degrees of coupling, as proposed in the case of the PVPh–PVEE blend, which is also similar to the case of the PS/PVME blend with a heterogeneous environment in the presence of MWNTs.
4.4 Janus particles
Asymmetry is created onto these particles due to the difference in the chemical composition, polarity, color or any characteristic properties, unlike anisotropically shaped particles. Due to the amphiphilicity in the particles, they are generally localized at the interface. The adsorption energy is comparable to that of block copolymers with a sufficient contribution to the enthalpic contribution to the free energy of the system. The study of various amounts of Janus particles [polystyrene-block polybutadiene-block-poly(methyl methacrylate) (SBM) triblock terpolymer] in PS/PMMA blends with various weight ratios was carried out. The SEM and TEM images (as seen in Fig. 17) shows that at a given concentration, the addition of Janus particles leads to the formation of morphologies with a smaller domain size stabilizing the blend.91 | ||
| Fig. 17 SEM images of PS/PMMA 60/40 (top row); nonstained TEM images of the 80/20 blend (center and lower row) with various amounts of Janus particles [polystyrene-block polybutadiene-block-poly(methyl methacrylate) (SBM) triblock terpolymer] as indicated in each image, Walther et al.,91 Reprinted with permission from American Chemical Society, Copyright © 2014, American Chemical Society. | ||
5. Perspective and outlook
Taken together, it can be concluded that ordered structures of different length scales in a polymer blend can be created by the hydrodynamic factors and flow fields which determine the phase separation in the blend. In the case of a polymer blend with rod like particles, which has strong interaction to one of the phases, the synergistic effect of the wetting of the particle to the polymer phase and the rod–rod interactions create self-assembling rods. The non-spherical particles are capable of showing different types of self-assembly-oriented attachments similar to liquid crystalline polymers. Nanowires and nanotubes are characterised by bundle like structures, showing aggregation induced gelation. It is hence evident that the shape anisotropy is a determining factor for the development of self-assembled structures. This can be compared with the rods which “pushes and corrals”, as suggested by Peng and his co-workers.48,92 So it can be concluded that the self-assembling particles in the polymer blend affects the hydrodynamic and flow field factor creating a self-assembled polymer structure.93 These observations from the simulation studies corroborate with the experimental results. The nanoparticles are capable of affecting the demixing kinetics irrespective of their shape, but the critical concentration required for the network formation was found to be lower for nanorods than for nanospheres in similar blends.The addition of anisotropic particles has an enhanced effect on the compositional wave of concentration fluctuation compared to that of the isotropic particles. The concentration of anisotropic particles required to produce the compositional effect is comparatively smaller compared to that of the isotropic particles. It is well evident from the experimental studies that lower concentration of NPs (∼0.25 wt% or lesser) has affected the demixing temperature in the case of anisotropic particles like MWNTs, rGO, clay, etc. compared with the high loading percent of spherical particles (∼1 wt%). Even though it has been proved that anisotropic functionalized particles (Janus particles) are capable of stabilizing the blend, providing an enthalpic contribution to the free energy, the effect of demixing temperature by incorporating these particles requires more focused research.
It was also observed from the literature that the demixing temperature is conspicuously affected by the NP localization than the particle dimension, which is observed in the case of dynamically asymmetric blends. The localization of particles changes the statistical ordering of the polymer chain, changing the relaxation time and the asymmetry parameter (ξ). The localization of particles in the hydrophilic PVME phase has induced a change in the dynamic asymmetry of the blend, delaying the phase separation temperature. A highly anisotropic particle with surface functionalization, with the synergistic effect has enhanced the inter-chain concentration fluctuation. The localization in the hydrophilic phase contributed to the spinodal temperature has been delayed ca. 33 °C in the case of PS-g-MWNTs (PS ca. 9000 g mol−1) incorporated in the PS/PVME blend. Here PS-g-MWNTs were localized in the PVME phase, changing the dynamic asymmetry of the blend. It has to be noted that the molecular weight of the grafted chain was lower than that of the matrix PS. In another case, the addition of PS-g-Au particles (PS ca. 53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1; Mw of the grafted polymer is higher than that of the matrix) has delayed the demixing by ca. 12 °C. The PS matrix in which the particle is localized will experience a translational entropic loss, at the expense of conformational losses for the grafted chains. It is interesting to note that these changes are attributed by the free energy balance of the PS/PVME blend, due to the enthalpic interactions or entropic losses. In most of these reported cases, the role of a polymer brush and a chemically identical matrix has been dealt with.
000 g mol−1; Mw of the grafted polymer is higher than that of the matrix) has delayed the demixing by ca. 12 °C. The PS matrix in which the particle is localized will experience a translational entropic loss, at the expense of conformational losses for the grafted chains. It is interesting to note that these changes are attributed by the free energy balance of the PS/PVME blend, due to the enthalpic interactions or entropic losses. In most of these reported cases, the role of a polymer brush and a chemically identical matrix has been dealt with.
Future work in the direction on understanding the graft density of the grafted polymer having a similar molecular weight as that of the host is essential in differentiating the effect of enthalpic interactions and entropic losses. Still the question on the melt–brush interaction of chemically dissimilar grafts, compared to the matrix polymer has to be studied in more detail. Polymers of diverse properties can be fabricated by adding nanoparticles which show multifunctional properties like electrical, mechanical and optical with controlled morphology and particle orientation. These can be potential materials for various applications like sensing, microfluidic channels and so on.
References
- A. C. Balazs, T. Emrick and T. P. Russell, Science, 2006, 314, 1107–1110 CrossRef CAS PubMed.
- S. Chandran, N. Begam, V. Padmanabhan and J. Basu, Nat. Commun., 2014, 5, 3697–3706 Search PubMed.
- L. A. Utracki, Polymer Blends Handbook, Kluwer Academic Pub, 2002 Search PubMed.
- A. V. Shenoy, Rheology of filled polymer systems, Springer Science & Business Media, 1999 Search PubMed.
- C. C. Han, B. J. Bauer, J. C. Clark, Y. Muroga, Y. Matsushita, M. Okada, Q. Tran-cong, T. Chang and I. C. Sanchez, Polymer, 1988, 29, 2002–2014 CrossRef CAS.
- C. Roland and K. Ngai, Macromolecules, 1991, 24, 5315–5319 CrossRef CAS.
- K. S. Schweizer and J. G. Curro, Phys. Rev. Lett., 1988, 60, 809–812 CrossRef CAS PubMed.
- B. J. Kim, J. Bang, C. J. Hawker and E. J. Kramer, Macromolecules, 2006, 39, 4108–4114 CrossRef CAS.
- T. M. Madkour, S. A. Salem and S. A. Miller, Phys. Chem. Chem. Phys., 2013, 15, 5982–5991 RSC.
- B. Frieberg, J. Kim, S. Narayanan and P. F. Green, ACS Nano, 2014, 8, 607–613 CrossRef CAS PubMed.
- A. Ajji and L. Choplin, Macromolecules, 1991, 24, 5221–5223 CrossRef CAS.
- G. H. Fredrickson and R. G. Larson, J. Chem. Phys., 1987, 86, 1553–1560 CrossRef CAS.
- J. Halary, J. Ubrich, J. Nunzi, L. Monnerie and R. Stein, Polymer, 1984, 25, 956–962 CrossRef CAS.
- M. Suess, J. Kressler and H. W. Kammer, Polymer, 1987, 28, 957–960 CrossRef CAS.
- M. E. Fowler, J. W. Barlow and D. R. Paul, Polymer, 1987, 28, 2145–2150 CrossRef CAS.
- M. Sharma, K. Sharma and S. Bose, J. Phys. Chem. B, 2013, 117, 8589–8602 CrossRef CAS PubMed.
- M. M. Coleman, D. F. Varnell and J. P. Runt, in Polymer Alloys III, ed. D. Klempner and K. Frisch, Springer US, 1983, vol. 20, ch. 7, pp. 59–70 Search PubMed.
- R. E. Bernstein, C. A. Cruz, D. R. Paul and J. W. Barlow, Macromolecules, 1977, 10, 681–686 CrossRef CAS.
- J. Chen, S. H. Goh, S. Y. Lee and K. S. Siow, J. Appl. Polym. Sci., 1995, 56, 761–767 CrossRef CAS.
- S. H. Goh, Eur. Polym. J., 1990, 26, 1149–1151 CrossRef CAS.
- M. F. Y Gnanou, Organic and Physical Chemistry of Polymers, Wiley-Interscience, 2008 Search PubMed.
- M. L. Huggins, J. Phys. Chem., 1942, 46, 151–158 CrossRef CAS.
- P. J. Flory, J. Chem. Phys., 1942, 10, 51–61 CrossRef CAS.
- S. Li, L. C. Dickinson and J. C. Chien, J. Appl. Polym. Sci., 1991, 43, 1111–1116 CrossRef CAS.
- D. Patterson, Polym. Eng. Sci., 1982, 22, 64–73 Search PubMed.
- P. C. Painter and M. M. Coleman, Essentials of polymer science and engineering, DEStech Publications, Inc., 2008 Search PubMed.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, 1953 Search PubMed.
- C. M. Hansen, Ind. Eng. Chem. Prod. Res. Dev., 1969, 8, 2–11 CAS.
- A. F. Barton, Chem. Rev., 1975, 75, 731–753 CrossRef CAS.
- D. Paul and J. Barlow, Polymer, 1984, 25, 487–494 CrossRef CAS.
- M. M. Coleman, C. J. Serman, D. E. Bhagwagar and P. C. Painter, Polymer, 1990, 31, 1187–1203 CrossRef CAS.
- K. R. Thomas, N. Clarke, R. Poetes, M. Morariu and U. Steiner, Soft Matter, 2010, 6, 3517–3523 RSC.
- M. M. Coleman and P. C. Painter, Prog. Polym. Sci., 1995, 20, 1–59 CrossRef CAS.
- F. Fenouillot, P. Cassagnau and J. C. Majesté, Polymer, 2009, 50, 1333–1350 CrossRef CAS.
- W. Hess, C. Scott and J. Callan, Rubber Chem. Technol., 1967, 40, 371–384 CrossRef CAS.
- Y. Zhang, S. Ge, B. Tang, T. Koga, M. Rafailovich, J. Sokolov, D. Peiffer, Z. Li, A. Dias and K. McElrath, Macromolecules, 2001, 34, 7056–7065 CrossRef CAS.
- F. Zoukrami, N. Haddaoui, C. Vanzeveren, M. Sclavons and J. Devaux, Polym. Int., 2008, 57, 756–763 CrossRef CAS.
- W. Li, J. Karger-Kocsis and R. Thomann, J. Polym. Sci., Part B: Polym. Phys., 2009, 47, 1616–1624 CrossRef CAS.
- Y. S. Lipatov, Prog. Polym. Sci., 2002, 27, 1721–1801 CrossRef CAS.
- J. W. Cahn, Acta Metall., 1961, 9, 795–801 CrossRef CAS.
- W.-S. Tung, V. Bird, R. J. Composto, N. Clarke and K. I. Winey, Macromolecules, 2013, 46, 5345–5354 CrossRef CAS.
- B. P. Lee, J. F. Douglas and S. C. Glotzer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 5812 CrossRef CAS.
- L. Sung, A. Karim, J. Douglas and C. Han, Phys. Rev. Lett., 1996, 76, 4368 CrossRef CAS PubMed.
- D. Benderly, A. Siegmann and M. Narkis, J. Polym. Eng., 1997, 17, 461–490 CAS.
- L. M. Hall and K. S. Schweizer, Soft Matter, 2010, 6, 1015–1025 RSC.
- V. V. Ginzburg, Macromolecules, 2005, 38, 2362–2367 CrossRef CAS.
- N. F. Carnahan and K. E. Starling, J. Chem. Phys., 1969, 51, 635–636 CrossRef CAS.
- G. Peng, F. Qiu, V. V. Ginzburg, D. Jasnow and A. C. Balazs, Science, 2000, 288, 1802–1804 CrossRef CAS PubMed.
- A. Nesterov and Y. Lipatov, Polymer, 1999, 40, 1347–1349 CrossRef CAS.
- A. Nesterov, Y. S. Lipatov, V. Horichko and O. Gritsenko, Polymer, 1992, 33, 619–622 CrossRef CAS.
- A. Karim, D. W. Liu, J. F. Douglas, A. I. Nakatani and E. J. Amis, Polymer, 2000, 41, 8455–8458 CrossRef CAS.
- H. Tanaka, Phys. Rev. Lett., 1993, 71, 3158–3161 CrossRef CAS PubMed.
- H. Tanaka, J. Phys.: Condens. Matter, 2000, 12, R207 CrossRef CAS.
- H. Tanaka, Phys. Rev. Lett., 1996, 76, 787–790 CrossRef CAS PubMed.
- H. Tanaka, arXiv preprint arXiv, 1307.1518, 2013.
- H. Tanaka and T. Araki, Chem. Eng. Sci., 2006, 61, 2108–2141 CrossRef CAS.
- J. K. Yeganeh, F. Goharpey and R. Foudazi, RSC Adv., 2014, 4, 12809–12825 RSC.
- T. Xia, Y. Huang, X. Jiang, Y. Li, X. Wang and G. Li, RSC Adv., 2014, 4, 33431–33434 RSC.
- T. Xia, Y. Huang, X. Peng and G. Li, Macromol. Chem. Phys., 2010, 211, 2240–2247 CrossRef CAS.
- A. Bharati, P. Xavier, G. P. Kar, G. Madras and S. Bose, J. Phys. Chem. B, 2014, 118, 2214–2225 CAS.
- A. Gharachorlou and F. Goharpey, Macromolecules, 2008, 41, 3276–3283 CrossRef CAS.
- T. Xia, Y. Huang, X. Jiang, Y. Lv, Q. Yang and G. Li, Macromolecules, 2013, 46, 8323–8333 CrossRef CAS.
- T. Xia, H. Ogawa, R. Inoue, K. Nishida, N. L. Yamada, G. Li and T. Kanaya, Macromolecules, 2013, 46, 4540–4547 CrossRef CAS.
- K. Yurekli, A. Karim, E. J. Amis and R. Krishnamoorti, Macromolecules, 2004, 37, 507–515 CrossRef CAS.
- A. Karim, J. F. Douglas, G. Nisato, D.-W. Liu and E. J. Amis, Macromolecules, 1999, 32, 5917–5924 CrossRef CAS.
- J. K. Yeganeh, F. Goharpey, E. Moghimi, G. Petekidis and R. Foudazi, Soft Matter, 2014, 10, 9270–9280 RSC.
- J. Cohen-Addad, Polymer, 1989, 30, 1820–1823 CrossRef CAS.
- Y. Huang, S. Jiang, G. Li and D. Chen, Acta Mater., 2005, 53, 5117–5124 CrossRef CAS.
- H.-J. Chung, A. Taubert, R. Deshmukh and R. J. Composto, EPL, 2004, 68, 219 CrossRef CAS.
- S. Xi, Y. Huang, Q. Yang and G. Li, Ind. Eng. Chem. Res., 2014, 53, 5916–5924 CrossRef CAS.
- Y.-C. Chua, A. Chan, H.-C. Wong, J. S. Higgins and J. T. Cabral, Macromolecules, 2010, 43, 9578–9582 CrossRef CAS.
- W. Li, Y. Zhang, J. Yang, J. Zhang, Y. Niu and Z. Wang, ACS Appl. Mater. Interfaces, 2012, 4, 6468–6478 CAS.
- K. Yurekli, A. Karim, E. J. Amis and R. Krishnamoorti, Macromolecules, 2003, 36, 7256–7267 CrossRef CAS.
- D.-z. Pang, M. Zuo, J.-s. Zhao and Q. Zheng, Chin. J. Polym. Sci., 2013, 31, 1470–1483 CrossRef CAS.
- P. Xavier, K. Sharma, K. Elayaraja, K. Vasu, A. Sood and S. Bose, RSC Adv., 2014, 4, 12376–12387 RSC.
- C. Özdilek, S. Bose, J. Leys, J. W. Seo, M. Wübbenhorst and P. Moldenaers, Polymer, 2010, 52, 4480–4489 CrossRef.
- R. Ashkar, M. Abdul Baki, M. Tyagi, A. Faraone, P. Butler and R. Krishnamoorti, ACS Macro Lett., 2014, 3, 1262–1265 CrossRef CAS.
- L. Li, C. Miesch, P. Sudeep, A. C. Balazs, T. Emrick, T. P. Russell and R. C. Hayward, Nano Lett., 2011, 11, 1997–2003 CrossRef CAS PubMed.
- P. Xavier and S. Bose, J. Phys. Chem. B, 2013, 117, 8633–8646 CrossRef CAS PubMed.
- P. Xavier and S. Bose, Phys. Chem. Chem. Phys., 2014, 16, 9309–9316 RSC.
- P. Xavier and S. Bose, Phys. Chem. Chem. Phys., 2015, 17, 14972–14985 RSC.
- K. Sharma, M. Sharma, A. Chandra and S. Bose, Macromol. Chem. Phys., 2013, 214, 2651–2669 CrossRef CAS.
- S. Bose, R. Cardinaels, C. Özdilek, J. Leys, J. W. Seo, M. Wübbenhorst and P. Moldenaers, Eur. Polym. J., 2014, 53, 253–269 CrossRef CAS.
- M. J. A. Hore and R. J. Composto, Macromolecules, 2012, 45, 6078–6086 CrossRef CAS.
- G. P. Kar, A. Bharati, P. Xavier, G. Madras and S. Bose, Phys. Chem. Chem. Phys., 2015, 17, 868–877 RSC.
- H.-j. Chung, K. Ohno, T. Fukuda and R. J. Composto, Nano Lett., 2005, 5, 1878–1882 CrossRef CAS PubMed.
- C. Huang, J. Gao, W. Yu and C. Zhou, Macromolecules, 2012, 45, 8420–8429 CrossRef CAS.
- G. P. Kar, P. Xavier and S. Bose, Phys. Chem. Chem. Phys., 2014, 16, 17811–17821 RSC.
- J. Chiefari, Y. Chong, F. Ercole, J. Krstina, J. Jeffery, T. P. Le, R. T. Mayadunne, G. F. Meijs, C. L. Moad and G. Moad, Macromolecules, 1998, 31, 5559–5562 CrossRef CAS.
- S. Zhang, P. C. Painter and J. Runt, Macromolecules, 2002, 35, 9403–9413 CrossRef CAS.
- A. Walther, K. Matussek and A. H. E. Müller, ACS Nano, 2008, 2, 1167–1178 CrossRef CAS PubMed.
- V. V. Ginzburg, G. Peng, F. Qiu, D. Jasnow and A. C. Balazs, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 4352–4359 CrossRef CAS.
- Q. H. Zeng, A. B. Yu and G. Q. Lu, Prog. Polym. Sci., 2008, 33, 191–269 CrossRef CAS.
- L. Robeson, Polymers, 2014, 6, 1251–1265 CrossRef.
- G. P. Kar, N. Begam, J. Basu and S. Bose, Macromolecules, 2014, 47, 7525–7532 CrossRef CAS.
| This journal is © the Owner Societies 2016 |
