Understanding the origin of the asynchronicity in bond-formation in polar cycloaddition reactions. A DFT study of the 1,3-dipolar cycloaddition reaction of carbonyl ylides with 1,2-benzoquinones

Abstract

The origin of the asynchronicity in bond-formation in polar cycloadditions has been studied by an ELF analysis of the electron reorganisation along the 1,3-dipolar cycloaddition of Padwa's carbonyl ylide 4 with the 1,2-benzoquinone 8. This reaction presents an unexpected asynchronous bond-formation, which is initialised through the nucleophilic attack of Padwa's carbonyl ylide on the carbonyl oxygen atom of the strongly electrophilically activated 1,2-benzoquinone. The present study allows for the establishment that along an asynchronous bond-formation, the more favourable two-center interaction begins at the most electrophilic center, which is the center with the highest spin density achieved through the charge transfer process, and not, as expected, at the center that presents the larger positive charge.

---

Introduction

Ever since the pioneering work of Huisgen,¹1,3-dipolar cycloaddition (13DC) reactions for the construction of 5-membered heterocycles have received a great deal of attention.² Most 13DC reactions involve additions to C–C multiple bonds. In contrast, much less attention has been attracted by the carbonyl C–O group as a dipolarophile. The interaction between unsymmetrical dipoles and dipolarophiles can give two isomeric adducts, depending upon the relative position of the substituent Z in the cycloadducts: head to head (5-regioisomer) or head-to-tail (4-regioisomer) (see Scheme 1). The selectivity for the formation of one adduct over the other is called regioselectivity, and this kind of isomer is called a regioisomer. Unlike Diels–Alder reactions, in which the degree of regioselectivity is often high, 13DC reactions present poor regioselectivity.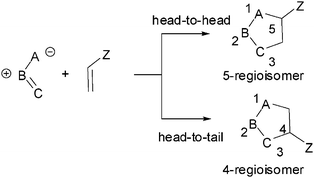

Scheme 1

An earlier study on the application of density functional theory (DFT) reactivity indices on the regioselectivity of 13DC reactions consistently suggested that the most favourable two-center interaction takes place between the strongest nucleophilic and electrophilic sites of the reagents.³ These nucleophilic/electrophilic interactions, which are responsible for the regioselectivity, originate asynchronous bond-formation processes. Analysis of the local electrophilicity,⁴ω_k, and local nucleophilicity,⁵N_k, indices allows for the characterisation of these relevant centres in a molecule. This study also evidenced the general observation that the most electrophilic reagent controls the asynchronicity in bond-formation process, that is, the bond-formation is initialised at the most electrophilic site of the molecule.³

13DC reactions have been widely studied from the theoretical point of view. For instance, the 13DC reaction between the electrophilically activated carbonyl ylide (CY) 1 and isatin 2 presents a complete regio- and chemoselectivity to yield spirocycloadduct 3 (see Scheme 2).⁶ Interestingly, the most favourable reactive channels were associated with the nucleophilic attack of the carbonyl oxygen atom of isatin 2 on the most electrophilic center of CY 1, the phenyl substituted carbon atom. This pattern of reactivity was attributed to the larger electrophilic character of CY 1, ω = 4.29 eV, compared with that of isatin 2, ω = 2.71 eV, which controls the direction of the electron flux along the polar cycloaddition.^6,7 The asynchronicity found along the bond-formation in the most favourable TS, where the length of the O–C forming bond, 1.96 Å, was shorter than that for the C–C forming bond (2.43 Å), was in agreement with the nucleophilic character of isatin 2.

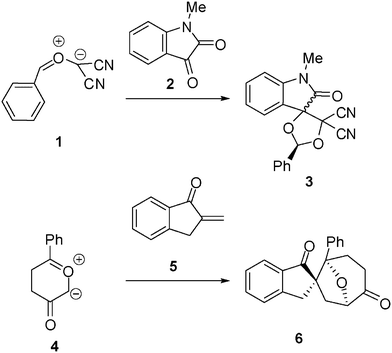Scheme 2

Recently, the regio- and chemoselective 13DC reaction of Padwa's CY 4 with α-methylene ketone 5 has been theoretically studied (see Scheme 2).⁸ In this 13DC reaction, the most favourable reactive channel was characterized by the nucleophilic attack of Padwa's CY 4 on the β-conjugated position of α,β-unsaturated ketone 5. At the most favourable TS, the C–C forming-bond distance at the β-conjugated position of 5, 2.53 Å, was shorter than that at the α position (2.90 Å). In both 1 + 2 and 4 + 5 13DC reactions, the bond-formation began at the most electrophilic center of CY 1 and α,β-unsaturated ketone 5.

The 13DC reactions of CYs with benzoquinones received scant attention⁹ until Nair's studies,¹⁰ which constituted a systematic attempt to disclose the stereoselectivity and synthetic usefulness of these reactions to obtain novel heterocycles. In this sense, the Rh(II) catalyzed cycloaddition of 1-diazo-5-phenyl-2,5-pentanedione 7 with the hindered 1,2-benzoquinone (12BQ) 8 proceeds smoothly, with complete stereo-, regio- and chemoselectivity, to afford cycloadduct (CA) 9 only^11,12 (see Scheme 3). Nair indicated that Padwa's CY 4 preferentially attacks the most electron-deficient carbonyl of 12BQ 8.¹²

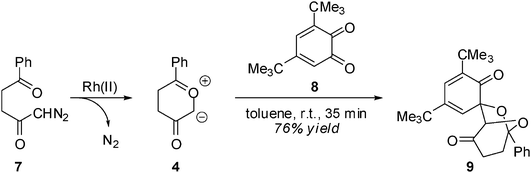Scheme 3

With the aim of establishing the origin of asynchronicity in bond-formation in polar cycloadditions, we present here a DFT study of the 13DC reaction between Padwa's CY 4 and 12BQ 8, (see Scheme 4).¹² With this aim, the electron-reorganisation along the most favourable reaction channel of this 13DC reaction is analyzed by a topological analysis of the electron localisation function (ELF) along the reaction coordinate.¹³

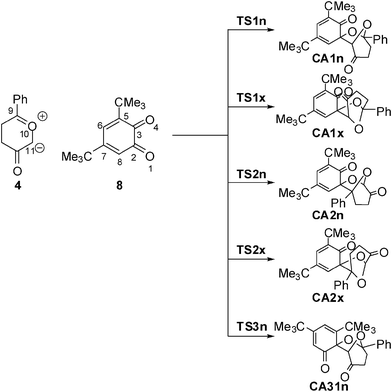Scheme 4

Computational methods

DFT calculations were carried out using the B3LYP¹⁴ exchange–correlation functionals, together with the standard 6-31G* basis set.¹⁵ The optimisations were carried out using the Berny analytical gradient optimisation method.¹⁶ The stationary points were characterized by frequency calculations in order to verify that TSs have one and only one imaginary frequency. The intrinsic reaction coordinate (IRC)¹⁷ paths were traced in order to check the energy profiles connecting each TS to the two associated minima of the proposed mechanism using the second order González-Schlegel integration method.¹⁸ The electronic structures of stationary points were analyzed by the natural bond orbital (NBO) method¹⁹ and by the topological analysis of the ELF, η(r).¹³ The ELF study was performed with the TopMod program²⁰ using the corresponding monodeterminantal wavefunctions of the selected structures of the IRC. Solvent effects of toluene (ε = 2.37) have been considered at the same level of theory using a self-consistent reaction field (SCRF)²¹ based on the polarizable continuum model (PCM) of the Tomasi's group.²² All calculations were carried out with the Gaussian 03 suite of programs.²³

The global electrophilicity index,²⁴ω, is given by the following simple expression,²⁴ω = (μ²/2η), in terms of the electronic chemical potential μ and the chemical hardness η. Both quantities may be approached in terms of the one electron energies of the frontier molecular orbital HOMO and LUMO, ε_H and ε_L, as μ ≈ (ε_H + ε_L)/2 and η ≈ (ε_L − ε_H), respectively.²⁵ Recently, we have introduced an empirical (relative) nucleophilicity index, N,²⁶ based on the HOMO energies obtained within the Kohn–Sham scheme,²⁷ and defined as N = E_HOMO(Nu) − E_HOMO(TCE). The nucleophilicity is referred to tetracyanoethylene (TCE), because it presents the lowest HOMO energy in a large series of molecules already investigated in the context of polar cycloadditions. This choice allows us conveniently to handle a nucleophilicity scale of positive values.²⁶ Local electrophilicity⁴ and nucleophilicity⁵ indices, ω_k and N_k, were evaluated using the following expressions: 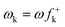and 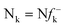where 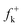and are the Fukui functions for a nucleophilic and electrophilic attacks, respectively.²⁸

Results and discussion

In order to understand the origin of the asynchronicity in bond-formation in polar cycloaddition reactions, this theoretical study has been divided into four different parts: i) mechanistic study of the 13DC reaction of Padwa's CY 4 with 12BQ 8; ii) analysis of the 13DC reaction based on DFT reactivity indices; iii) ELF analysis of the bond-formation at the most favourable reactive channel of the 13DC reaction of Padwa's CY 4 with 12BQ8′, and iv) analysis of factors controlling the asynchronicity in bond-formation in polar 13DC reactions.

1) Mechanistic study of the 13DC reaction of Padwa's CY 4 with 12BQ 8

Eight reactive channels are feasible for the 13DC reaction between the two asymmetrical reagents, Padwa's CY 4 and 12BQ 8. They are related to the endo and exo stereoisomeric approach modes, named n and x, the two regioisomeric approach modes of CY 4 towards the two carbonyl groups of 12BQ 8, and the two chemoselective attack modes of CY 4 on the C2=O1 and C3=O4 carbonyl groups of 12BQ 8 (see Scheme 4). The two regioisomeric channels associated with the attacks on the C2=O1 carbonyl group are named 1 and 2, and those associated with the attacks on the C3=O4 carbonyl group are named 3 and 4.

An analysis of the stationary points found along the potential energy surface (PES) associated with these competitive eight reactive channels indicates that these 13DC reactions take place through an asynchronous bond-formation mechanism. Four TSs, TS1n, TS1x, TS2n and TS2x, associated with the participation of the C2=O1 carbonyl group of 12BQ 8, and their corresponding cycloadducts CA1n, CA1x, CA2n and CA2x, were located and characterized (see Scheme 4). For the chemoisomeric channels associated with the participation of the C3=O4 carbonyl group of 12BQ 8, only the most favourable reactive channelviaTS3n, will be discussed. Note that for the 13DC reaction involving 12BQ 8, the CAs associated with the participation of the carbonyl C3=O4 group are not experimentally observed.¹²

Analysis of the IRCs from the TSs to the reagents allows for the attainment of a series of molecular complexes (MCs), which open the corresponding reactive channels. These MCs are minima on the PES. As reference for activation energies, we consider here only MC1n, associated with the most favourable reactive channel. From Padwa's CY 4 and 12BQ 8, formation of MC1n is exothermic by −9.1 kcal mol⁻¹. This stabilisation energy is higher than that associated with the formation of MCs, typically 5 kcal mol⁻¹ below the reagents, indicating a strong electronic interaction between both fragments (see later).

The activation energies associated with the reactive channels involving the C2=O1 carbonyl group of 12BQ 8 are 2.0 (TS1n), 4.3 (TS1x), 12.9 (TS2n) and 7.4 (TS2x) kcal mol⁻¹ (activation energies are relative to MC1n, see Table 1). The most favourable reactive channelvia the endoTS1n presents a very low activation energy; in fact, TS1n is 7.1 kcal mol⁻¹ below Padwa's CY 4 plus 12BQ 8. These energy results show that exoTS1x is located 2.3 kcal mol⁻¹ above endoTS1n, in reasonable agreement with the endo selectivity experimentally observed. In addition, the most favourable regioisomeric channelvia exoTS2x is 5.4 kcal mol⁻¹ more energetic than that viaTS1n. Therefore, this 13DC reaction is completely regioselective. Finally, the most favourable reactive channel associated with the participation of the C3=O4 carbonyl group of 12BQ 8 is 5.2 kcal mol⁻¹ (TS3n) higher in energy than that associated with TS1n (see Table 1). Therefore, this 13DC reaction is also completely chemoselective. Formation of the corresponding CAs is strongly exothermic; ca. −40 kcal mol⁻¹ for regioisomeric channels 1, and ca. −35 kcal mol⁻¹ for regioisomeric channels 2. This high energy stabilisation makes these processes thermodynamically irreversible.

Table 1 Total (E, in au) and relative (ΔE, in kcal mol⁻¹) energies, in gas-phase and toluene, of the stationary points involved in the 13DC between Padwa's CY 4 and 12BQ 8

	Gas-phase		Toluene
	E	ΔE	E	ΔE
4	−575.569905		−575.577605
8	−695.956646		−695.954760
MC1n	−1271.541118	−9.1	−1271.548142	−9.9
TS1n	−1271.537794	−7.1	−1271.544569	−7.7
TS1x	−1271.534227	−4.8	−1271.541862	−6.0
TS2n	−1271.520522	3.8	−1271.529231	2.0
TS2x	−1271.529277	−1.7	−1271.538269	−3.7
TS3n	−1271.529622	−1.9	−1271.537586	−3.3
TS3x	−1271.525770	0.5	−1271.533005	−0.4
TS4n	−1271.522993	2.2	−1271.532099	0.2
TS4x	−1271.516967	6.0	−1271.526058	4.0
CA1n	−1271.588606	−38.9	−1271.594331	−38.9
CA1x	−1271.590764	−40.3	−1271.596498	−40.2
CA2n	−1271.581569	−34.5	−1271.588275	−35.1
CA2x	−1271.582921	−35.4	−1271.588848	−35.4
CA3n	−1271.580419	−33.8	−1271.586510	−34.0
CA3x	−1271.575992	−31.0	−1271.582397	−31.4
CA4n	−1271.566788	−25.2	−1271.573520	−25.8
CA4x	−1271.561727	−22.1	−1271.569042	−23.0

---

As these 13DC reactions were performed in toluene, solvent effects on energies and geometries were considered by full optimisation of the gas-phase stationary points using a SCRF based on the PCM of Tomasi's group. When the solvent effects of toluene are included, all stationary points are stabilized between 4 and 6 kcal mol⁻¹. As the stabilisation of MC1n, TSs and CAs is similar, solvent effects have unappreciable effects on the kinetics and thermodynamics of these 13DC reactions. Analysis of the relative energies of the TSs associated with the stereo-, regio- and chemoselective channels indicates that there is no appreciable variation in selectivities when solvent effects are included. In spite of the large zwitterionic character of the TSs (see later), the low polar character of toluene is responsible for these poor results.

The geometries of TSs associated with the five analysed channels are displayed in Fig. 1. A comparative analysis of the geometries of TSs obtained in gas-phase and in toluene indicates that inclusion of solvent effects on the geometry optimisation produces minor changes related to gas-phase calculations.²⁹ At the TSs associated with the participation of the C2=O1 carbonyl group, the lengths of the O1–C9 and C2–C11 forming bonds are: 2.129 and 2.578 Å at TS1n, 2.140 and 2.387 Å at TS1x, while at the regioisomeric TSs, the lengths of the O1–C11 and C2–C9 forming bonds are 2.049 and 2.749 Å at TS2n, and 2.083 and 3.040 Å at TS2x, respectively. At TS3n, associated with the participation of the C3=O4 carbonyl group, the lengths of the O4–C9 and C3–C11 forming bonds are 2.153 and 2.286 Å, respectively. The regioisomeric TSs associated with channels 2 are more asynchronous than those associated with the more favourable channels 1. The less favourable TS3n presents the lower asynchronicity. It is noteworthy that the lengths of the C–O forming bonds in all TSs are shorter than the C–C forming bonds.

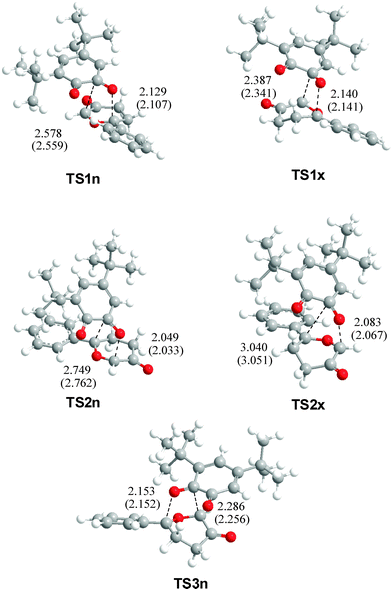Fig. 1 B3LYP/6-31G* in vacuo geometries of selected TSs of the reaction between CY 4 and 12BQ 8. Forming bond distances are in angstroms (values of the geometries optimized in toluene are in parenthesis).

The extension in bond-formation at the TSs is provided by the bond order (BO).³⁰ At the TSs associated with the participation of the C2=O1 carbonyl group, the BO values of the O1–C9 and C2–C11 forming bonds are 0.25 and 0.16 at TS1n, and 0.24 and 0.26 at TS1x, respectively. At the regioisomeric TSs, the BO values for O1–C11 and C2–C9 forming bonds are 0.30 and 0.14 at TS2n, and 0.29 and 0.08 at TS2x, respectively. The regioisomeric TS2n and TS2x are more asynchronous and more advanced than TS1n and TS1x. It is noteworthy that at the most favourable TS1n, and at the regioisomeric TS2n and TS2x, the bond-formation at the carbonyl O1 oxygen is more advanced than that at the carbonyl C2 carbon. At TS3n, associated with the participation of the C3=O4 carbonyl group, the BO values of the O4–C9 and C3–C11 forming bonds are 0.25 and 0.33, respectively.

The non-polar or polar character of these cycloadditions was analysed evaluating the charge transfer (CT) at the corresponding TSs. The natural charges at the TSs appear shared between Padwa's CY 4 framework and that of 12BQ 8. At the TSs associated with the participation of the C2=O1 carbonyl group, the charge transferred from CY 4 to 12BQ 8 is 0.31e (TS1n), 0.32e (TS1x), 0.38e (TS2n) and 0.36e (TS2x). These high values point to a large polar character of these 13DC reactions, in which Padwa's CY 4 acts as nucleophile⁸ and 12BQ 8 acts as electrophile. It is interesting to note that the most asynchronous TS2n and TS2x present the larger CT. This behaviour is in agreement with the larger dipole moment of TS2n and TS2x, μ = 6.76 and 7.43 Debyes, than that of TS1n and TS1x, μ = 2.68 and 5.04 Debyes, respectively. TS2n and TS2x may be associated with the more favourable nucleophilic/electrophilic interaction along the eight competitive reactive channels (see later). However, the steric hindrance that appears between the bulky tert-butyl substituents present at 12BQ 8 and the phenyl group of CY 4 and/or intramolecular dipolar interactions may be responsible for the larger energy of TS2n and TS2x than the less energetic TS1n.

Finally, analysis of the natural charges at MC1n indicates that at this early stage of the reaction, there is already an appreciable CT from Padwa's CY 4 to 12BQ 8, 0.11e. This CT may be responsible for the large stabilisation of MCn related to separate reagents, namely 9.1 kcal mol⁻¹.

2) Analysis of 13DC reactions of Padwa's CY 4 with 12BQs based on DFT reactivity indices

Studies carried out on cycloaddition reactions have shown that the reactivity indices defined within the conceptual DFT are powerful tools for establishing the polar character of such reactions.^7,8,31 The static global properties of Padwa's CY 4, 12BQs 8 and 8′ (see Scheme 5), and the non-substituted 12BQ 10, namely electronic chemical potential (μ), chemical hardness (η), global electrophilicity (ω), and global nucleophilicity (N), are shown in Table 2.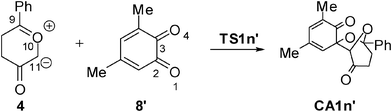

Scheme 5

Table 2 Electronic chemical potential (μ), chemical hardness (η), global electrophilicity (ω), and global nucleophilicity (N), in eV, of Padwa's CY 4, 12BQs 8, 8′ and 10, 1,2-cyclohexanedione 11 and cyclohexanone 12

Compound	μ	η	ω	N
1,2-Benzoquinone 10	−5.19	3.20	4.21	2.33
12BQ 8′	−4.93	3.29	3.68	2.55
12BQ 8	−4.83	3.25	3.59	2.67
CY 4	−3.75	2.49	2.82	4.13
1,2-Cyclohexanedione 11	−4.24	4.38	2.05	2.70
Cyclohexanone 12	−3.35	6.05	0.93	2.74

---

The electronic chemical potential of 12BQs, μ = −4.83 eV (8), −4.93 eV (8′) and μ = −5.19 eV (10), is lower than that of Padwa's CY 4, μ = −3.75 eV. Therefore, it is expected that along a polar 13DC reaction, the CT will take place from CY 4 to these 12BQs, in clear agreement with the CT analysis performed at the TSs.

The electrophilicity of Padwa's CY 4, ω = 2.82 eV,⁸ allows for the classification of this species as a strong electrophile within the electrophilicity scale.³² On the other hand, it presents a high nucleophilicity value, N = 4.13 eV, being classified also as a strong nucleophile within the nucleophilicity scale.³³ Therefore, Padwa CY 4 can behave as a strong electrophile and as a strong nucleophile in polar processes.⁸

The electrophilicity of 12BQs is ω = 3.59 eV (8), 3.68 eV (8′) and 4.21 eV (10) eV, and classifies them as strong electrophiles within the electrophilicity scale. The non-substituted 12BQ 10 is more electrophilic than 12BQs 8 and 8′. On the other hand, the nucleophilicity of these species, N = 2.67 eV (8), 2.55 eV (8′) and 2.33 eV (10), indicates that they are moderate nucleophiles. As expected, alkyl substitution decreases the electrophilicity and increases the nucleophilicity of 12BQs. Therefore, 12BQs can behave as strong electrophiles and moderate nucleophiles in polar processes.

The electrophilicity of 1,2-cyclohexanedione 11 and cyclohexanone 12 were also computed (see Table 2). 1,2-Cyclohexanedione 11 is a strong electrophile, ω = 2.05 eV, while cyclohexanone 12, ω = 0.93 eV, is a marginal electrophile. Therefore, conjugation of two carbonyl groups increases considerably the electrophilicity of 1,2-dicarbonyl compounds, explaining the high electrophilicity of 12BQs 8, 8′ and 10.

An analysis of the global reactivity indices indicates that in a polar 13DC reaction, 12BQ 8 will act as a strong electrophile, while Padwa's CY 4 will act as a strong nucleophile. This behaviour allows for the explanation of the large CT found at the TSs. These values also explain the strong stabilisation of MC1n, which undergoes some CT from CY 4 to 12BQ 8, namely 0.11e.

In a polar cycloaddition between asymmetrical reagents, the most favourable two-center interaction will take place between the more electrophilic center, characterized by the highest value of the local electrophilicity index⁴ω_k at the electrophile, and the more nucleophilic center, characterized by the highest value of the local nucleophilicity index⁵N_k at the nucleophile.³ The local electrophilicity indices, ω_k, of 12BQ 8 and the local nucleophilicity indices, N_k, of Padwa's CY 4 are presented in Table 3. For CY 4, the most nucleophilic center corresponds to the carbonyl substituted C11 carbon, N_C11 = 1.67 eV.⁸ For 12BQ 8, the most electrophilic centres correspond to the O1 and O4 oxygen atoms, ω_O1 and ω_O4 = 0.61 eV. It is noteworthy that at 12BQ 8, the carbonyl O1 and O4 oxygen atoms are more electrophilically activated than the carbonyl C2 and C3 carbons; ω_C2 = 0.43 eV and ω_C3 = 0.50 eV. As a consequence, the more polar processes should be those associated with the attack of the most nucleophilic center of Padwa's CY 4, the C11 carbon, on the most electrophilic center of 12BQ 8, the carbonyl O1 or O4 oxygen atoms. This analysis makes it possible to explain the larger asynchronicity and larger CT found at the regioisomeric TS2n and TS2x. On the other hand, the electrophilic activation at the carbonyl O1 oxygen is higher than that found at the carbonyl C2 carbon, allowing for the explanation of the more advanced character of the O–C forming bond than the C–C one at the most favourable TS1n, and the regioisomeric TS2n and TS2x.

Table 3 Local electrophilicity (ω_k, in eV) of 12BQ 8, 1,2-cyclohexanedione 11 and cyclohexanone 12, and local nucleophilicity (N_k, in eV) of Padwa's CY 4

ω k	8	11	12
O1	0.61	0.48	0.27
C2	0.43	0.51	0.46
C3	0.50	0.51
O4	0.61	0.48
C5	0.30
C6	0.40
C7	0.38
C8	0.25
Nk	4
C9	0.73
C11	1.67
O13	0.69

---

Finally, the carbonyl carbons of 1,2-cyclohexanedione 11 and cyclohexanone 12 are more electrophilically activated, ω_C = 0.51eV (11) and 0.46 eV (12), than the carbonyl oxygens, ω_O = 0.48 eV (11) and 0.27 eV (12). Therefore, as expected in an asynchronous bond-formation process involving carbonyl compounds, the bond-formation at the carbon atom of these carbonyl derivatives will be more advanced than at the oxygen atom.³⁴

3) ELF topological analysis of the bond-formation at the 13DC reaction of Padwa's CY 4 with 12BQ 8′

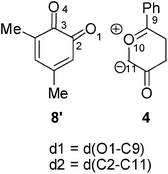
Recent theoretical studies have shown that the topological analysis of the ELF along the reaction path associated with a cycloaddition is a valuable tool for understanding the changes of bonding along the reaction.^7,8,35 Consequently, the topology of ELF of some relevant points chosen from the IRC from TS1n′ to CA1n′, as a simplified model (see Scheme 5), was analyzed in order to understand the unexpected asynchronicity in bond-formation at the 13DC reaction between Padwa's CY 4 and 12BQ 8. In this 13DC reaction, the two bulky t-butyl groups present in 12BQ 8 are replaced by two methyl groups in order to simplify the ELF analysis. Note that this substitution does not produce any appreciable change in the bond-formation process along the 13DC reaction. The lengths of the O1–C9 and C2–C11 forming bonds at the TS1n′ model, 2.127 and 2.580 Å, are close to those found at TS1n, 2.129 and 2.578 Å. At TS1n′, CT is the same to that computed at TS1n (0.31 e). The N populations of the more relevant valence basins³⁶ of the selected structures along the IRC are listed in Table 4, while the attractor positions and atom numbering for these relevant points are shown in Fig. 2, where d1 stands for O1–C9 forming bond distance and d2 represents C2–C11 forming bond distance.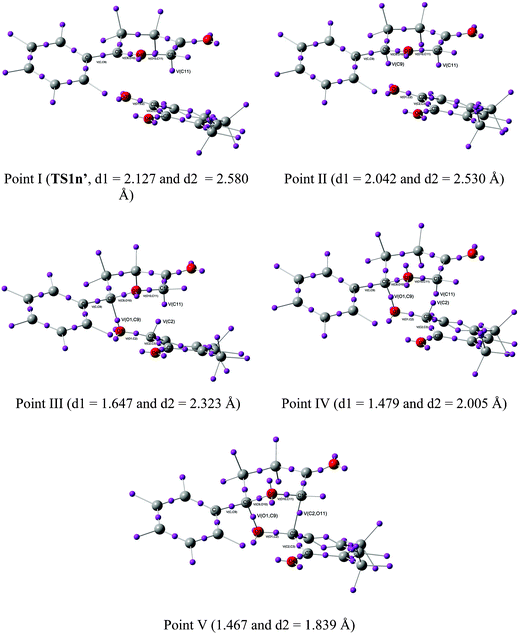

Fig. 2 ELF attractors at selected points of the IRC from TS1n′ to CA1′.

Table 4 Valence basin populations N calculated from the ELF of TS1n′ and some selected points associated with the asynchronous formation of the O1–C9 and C2–C11 σ bonds along the 13DC reaction between Padwa's CY 4 and 12BQ 8′

Points	I (TS1n′)	II	III	IV	V
d1(O1–C9)	2.127	2.042	1.647	1.479	1.467
d2(C2–C11)	2.580	2.530	2.323	2.005	1.839
V(O1)	2.77	2.80	2.54	2.52	2.52
V'(O1)	2.73	2.75	2.71	2.60	2.52
V(O1,C2)	1.95	1.87	1.50	1.38	1.37
V(C2,C3)	2.41	2.45	2.45	2.33	2.26
V(C9,O10)	1.93	1.86	1.51	1.36	1.24
V(O10,C11)	1.63	1.63	1.53	1.43	1.32
V(O10)	3.95	4.04	4.48	2.70	2.57
V'(O10)	—	—	—	2.09	2.27
V(C9)	—	0.04	—	—	—
V(O1,C9)	—	—	0.82	1.18	1.24
V(C11)	0.64	0.64	0.58	0.71	—
V(C2)	—	—	0.25	0.61	—
V(C2,C11)		—	—	—	1.55

---

The ELF picture of attractors at TS1n′ (point I, d1 = 2.127 Å, d2 = 2.580 Å) shows the expected monosynaptic attractors associated with the two lone pairs of the O1 oxygen atom (V(O1) and V'(O1)) of 12BQ 8′ and those corresponding to the O10 oxygen atom of CY 4 (i.e.V(O10)). Monosynaptic attractors associated with bond-formation are neither observed at C9 and O1 nor in the C9–O1 bond region. A monosynaptic attractor is found at the nucleophilic C11 center of the CY 4 framework, V(C11), with an electronic population of 0.64e. It is noteworthy that the monosynaptic basin V(C11) is already present in the ELF of Padwa's isolated CY 4.⁸ Therefore, TS1n′ does not present any relevant electronic change associated with the σ bond-formation in these 13DC reactions.

As both fragments approach each other at d1 = 2.042 Å and d2 = 2.530 Å, point II, the picture of the attractors changes slightly. Besides the monosynaptic attractor, V(C11), whose electronic density is the same as that shown in TS1n′, a second monosynaptic basin appears at the C9 carbon of the Padwa's CY 4 moiety, V(C9), which shows a scarce electronic population of 0.04e. Note that the electronic population of this monosynaptic basin increases in the region of 2.042 Å > d1 > 1.647 Å, prior to the formation of the first C9–O1 bond. At point III, d1 = 1.647 Å and d2 = 2.323 Å, it can clearly be seen that while V(C9) disappears, one new disynaptic attractor, V(O1,C9), associated with the formation of the first σ C9–O1 bond, appears, displaying an electronic population of 0.82e. At this point, another monosynaptic attractor also appears simultaneously at the C2 atom, V(C2), displaying an electronic population of 0.25e. The V(C11) attractor shows a slight decrease of the electronic population to 0.58e. A strong decrease of the electronic populations of neighbouring attractors of the O1–C9 bond compared with the electronic population analyzed at the TS is observed: almost 0.4 e are reduced from point II to III in both attractors V(C9,O10) and V(O1,C2) whereas slight changes in the electronic population of basin V(O10,C11) are displayed. The population associated with V(O10) increases smoothly from point I to III. These changes can be understood as the electronic reorganisation required to form the first σ bond between the carbon C9 atom of the CY 4 fragment and the oxygen O1 atom of the 12BQ 8′ moiety. From d1 = 2.042 Å (point II) to d1 = 1.479 Å (point IV), this electronic reorganisation pattern remains unchanged, completing the formation of the O1–C9 bond.

At point IV, d1 = 1.479 Å and d2 = 2.005 Å, the electronic population of the attractor V(O1,C9) is increased to 1.18e, as well as those associated with the monosynaptic attractors V(C11) and V(C2), with 0.71 and 0.61e, respectively. The electronic populations of V(C9,O10), V(O1,C2) and V(O10,C11) attractors decrease slightly as the reaction proceeds. At this point, a second monosynaptic attractor associated with O10, V'(O10), which reaches together with V(O10) a total electronic population of 4.79e, can be observed. At point IV takes place the maximum of CT along this polar 13DC reaction, 0.38e.

Finally, at point V, d1 = 1.467 Å and d2 = 1.839 Å, when the reaction is very advanced, the two V(C11) and V(C2) monosynaptic attractors merge into only one attractor, V(C2,C11), displaying an electronic population of 1.55e, which is associated with formation of the second σC2−C11 bond. The V(O1,C9) attractor shows a population of 1.24e. Consequently, the picture of these attractors is the expected for cycloadduct CA1n′ of the reaction developing between Padwa's CY 4 and 12BQ 8′.

It is noteworthy to remark that the IRC region that comprises point IV separates the two stages of the one-step mechanism of this 13DC reaction.³⁸ While during the first stage of the reaction, which involves a large region of the IRC between separated reagents and point IV (d1 > 1.479 Å and d2 > 2.005 Å), the electron reorganisation is mainly associated with the formation of the first σ O–C bond, at the second stage of the reaction, which involves a short region at the end of the IRC, the second σ C–C bond is formed.

From this ELF analysis it can be concluded that along this 13DC reaction, the more significant changes on the asynchronous bond-formation take place at three well characterized points of the IRC, all them after passing the TS. At point II, d1 = 2.042 Å and d2 = 2.530 Å, a V(C9) monosynaptic attractor emerges at the C9 carbon atom of Padwa's CY 4. This monosynaptic attractor appears before the formation of the first σ O–C bond. At point III, d1 = 1.647 Å and d2 = 2.323 Å, two significant changes are observed: i) while the V(C9) monosynaptic attractor disappears, a new V(O1,C9) disynaptic attractor associated with the formation of the first O–C bond appears; and ii) a new V(C2) monosynaptic attractor emerges at the C2 carbon atom of 12BQ 8′. This V(C2) monosynaptic attractor together with the V(C11) one, which is already present at Padwa's CY 4, are responsible for the formation of the second C–C bond at the end of the cycloaddition, which takes place at point V, d1 = 1.467 Å and d2 = 1.839 Å.

The present ELF analysis corroborates the early observation obtained from the geometrical and electronic analysis at TS1n: along the nucleophilic attack of Padwa's CY 4 on the strongly electrophilically activated 12BQ 8, the bond-formation begins at the carbonyl O1 oxygen of 12BQ 8, instead of, as expected, at the carbonyl C2 carbon.

4) Factors controlling the asynchronicity in bond-formation in polar 13DC reactions

What is the origin for the unexpected initial C–O bond-formation in the carbonyl C=O group of benzoquinones? Analysis of natural charges at 12BQ 8′ indicates that while the carbonyl O1 oxygen is negatively charged, −0.48e, the carbonyl C2 carbon is positively charged, +0.45e, as expected for a polarized carbonyl C=O double bond. Note that this charge distribution is similar to that found in cyclohexanone 12 (see Fig. 3). Therefore, it is likely that the nucleophilic attack will take place at the electron-deficient carbonyl carbons. However, analysis of local electrophilicity indicates that the most electrophilic centres of 12BQ 8 are the carbonyl O1 and the O4 oxygen atoms (see Table 3).

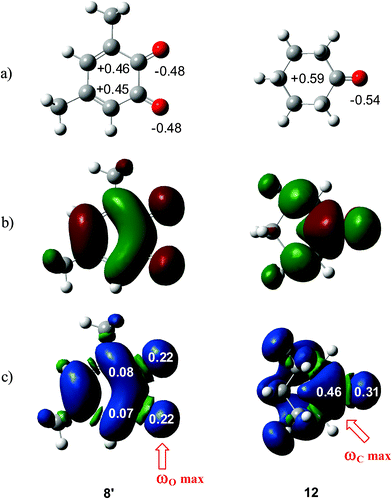Fig. 3 (a) Natural charges and (b) LUMO of 12BQ 8′ and cyclohexanone12, and (c) natural atomic spin densities (ASDs) of the anion radicals of 8′ and 12.

Along the approach of nucleophilic CY 4 towards the strongly electrophilically activated 12BQ 8′, a large amount of electron density is transferred to the electrophile. Note that at TS1n′ the CT is very large, 0.31e, reaching a value of 0.38e at point IV of the IRC, at which the second C1–C9 bond is being formed. The transferred electron density delocalizes in the electrophilic 12BQ 8′. In the extreme case of transferring an amount of electron density equivalent to one electron, 12BQ 8′ becomes a radical anion. An analysis of the natural atomic spin density (ASD) at the radical anion of 12BQ 8′ indicates that the ASD is mainly located at the two carbonyl oxygen atoms, 0.22 at O1 and 0.22 at O4, rather than at the carbonyl carbon atoms, where ASD is 0.07 at C2 and 0.08 at C3 (see Fig. 3). Similar results are obtained using the Mulliken ASD. Note that these values are closer to those of the Fukui functions 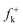for nucleophilic attacks obtained from the LUMO of 12BQ 8′.

Previous ELF studies on the electron-reorganisation along asynchronous cycloadditions have highlighted the formation of two monosynaptic attractors before the formation of a new σ bond,^8,35d which, in the case of non-polar cycloadditions, is associated with some pseudo-radical character.^35g,h Consequently, it appears that along a polar cycloaddition, the CT that takes place from the nucleophile towards the electrophile favours the electron reorganisation needed to reach the formation of these monosynaptic attractors in both the nucleophile and the electrophile. Thus, in the case of 12BQs, the large ASD concentration at the carbonyl oxygen atoms may favour the formation of the O–C bond along the first stage of the reaction, where most of the CT has been completed. This fact allows for finding an explanation of the unexpected asynchronous bond-formations found at the corresponding TSs. Note that at the radical anion of cyclohexanone 12, the largest ASD concentration takes place at the carbonyl carbon, 0.46, instead of at the carbonyl oxygen, 0.31 (see Fig. 3). Therefore, in a polar cycloaddition involving ketones, the bond-formation at the more favourable reactive channels will begin at the carbonyl carbon.³⁴

Consequently, the asynchronicity in bond-formation in polar cycloadditions involving asymmetrical electrophilic reagents is not controlled by charge separation, but by spin reorganisation resulting from the CT that takes place from nucleophiles to electrophiles through electronic interactions. Unlike aldehydes and ketones, in which the ASD is concentrated at the positively charged carbonyl carbons, in the case of 12BQs, the ASD is mainly located at the negatively charged oxygens.

Although these electrophilic centres are well predicted by analysis of Fukui functions 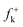for nucleophilic attacks, which can be obtained from the LUMO coefficients, this molecular orbital does not participate in the bond-formation in polar processes as stated by the FMO theory.³⁹ Note that the energy gap between the HOMO of Padwa's CY 4 and the LUMO of 12BQ 8, 41.3 kcal mol⁻¹, is very large when it is compared with the energy barrier involved in the 13DC reaction (the most favourable TS1n is placed −7.1 kcal mol⁻¹ below reagents: Padwa's CY 4 plus 12BQ 8). Consequently, at this reaction energy level, HOMO electrons of Padwa's CYs 4 can not reach the LUMO of 12BQ 8.

Conclusions

The mechanism of the 13DC reaction of Padwa's CY 4 with the hindered 12BQ 8 has been theoretically studied using DFT methods at the B3LYP/6-31G* level. Due to the asymmetry of both reagents, eight competitive reactive channels are feasible. B3LYP/6-31G* energies indicate that this 13DC reaction presents a large endo selectivity, and a total regio- and chemoselectivity, in clear agreement with the experimental outcome, in which only an isomeric CA is observed.

Geometrical and electronic analyses of the most favourable TS1n indicate that this cycloaddition, which has a very low activation energy of 2.0 kcal mol⁻¹, takes place via an asynchronous bond-formation mechanism with a large polar character. Analysis of the CT at TS1n shows that the electron-density flows from Padwa's CY towards 12BQ, a behaviour predicted by analysis of DFT reactivity indices at the ground state of the reagents.

Interestingly, this 13DC reaction presents an unexpected asynchronous bond-formation, i.e., the bond-formation at the carbonyl O1 oxygen of the electrophilic 12BQ is advanced rather than that at the C2 carbon. ELF analysis puts in evidence the two-stage nature of this 13DC reaction.³⁸ First, the C–O bond is formed by the nucleophilic attack of Padwa's CY on the carbonyl oxygen atom of 12BQ , and once this bond has been completely formed, the C–C bond-formation begins at the second stage of the cycloaddition. Analysis of the natural ASD at the radical anion of 12BQ shows that the ASD is mainly located at the oxygen atoms, allowing for an explanation for the initial bond-formation at the oxygen atom of these strong electrophilic 12BQs.

The present study allows for the establishment of the origin of the asynchronicity in polar cycloadditions involving asymmetrically substituted reagents. Along the most favourable two-center interaction, the bond-formation begins at the most electrophilic center, which is the center with the highest ASD, achieved through the charge transfer process, and not, as expected, at the most positively charged center. In most of the carbonyl compounds, this electrophilic center corresponds with the most positively charged carbon atom, but does not in 12BQs, presenting an unexpected asynchronous bond-formation.

Acknowledgements

We are grateful to the Spanish Government (project CTQ2009-11027/BQU), and Fondecyt project under contract 1100278. P. P. thanks the Vicerrectoría de Investigación y Doctorados of the Universidad Andrés Bello (UNAB) for continuous support and to the project DI-UNAB 35-10/R. Professor Domingo also thanks Fondecyt by support through the Cooperación Internacional.

References

1. R. Huisgen, Angew. Chem., Int. Ed. Engl., 1963, 2, 565–598.
2. A. Padwa, in 1,3-Dipolar Cycloaddition Chemistry, Wiley-Interscience, New York, 1984, pp. 1–2.
3. M. J. Aurell, L. R. Domingo, P. Perez and R. Contreras, Tetrahedron, 2004, 60, 11503–11509.
4. L. R. Domingo, M. J. Aurell, P. Perez and R. Contreras, J. Phys. Chem. A, 2002, 106, 6871–6875.
5. P. Pérez, L. R. Domingo, M. Duque-Noreña and E. Chamorro, THEOCHEM, 2009, 895, 86–91.
6. G. Bentabed-Ababsa, A. Derdour, T. Roisnel, J. A. Sáez, L. R. Domingo and F. Mongin, Org. Biomol. Chem., 2008, 6, 3144–3157.
7. G. Bentabed-Ababsa, A. Derdour, T. Roisnel, J. A. Sáez, P. Pérez, E. Chamorro, L. R. Domingo and F. Mongin, J. Org. Chem., 2009, 74, 2120–2133.
8. W. Benchouk, S. M. Mekelleche, M. J. Aurell and L. R. Domingo, Tetrahedron, 2009, 65, 4644–4651.
9. V. Nair and S. Kumar, Synlett, 1996, 1143–1147.
10. V. Nair, K. C. Sheela, K. V. Radhakrishman, C. Rajesh and P. M. Treesa, J. Heterocycl. Chem., 2000, 37, 659–668.
11. (a) A. Padwa, G. E. Fryxell and L. Zhi, J. Am. Chem. Soc., 1990, 112, 3100–3109; (b) A. Padwa and M. D. Weingarten, Chem. Rev., 1996, 96, 223–270; (c) V. Nair, K. V. Radhakrishman, K. C. Sheela and N. P. Rath, Tetrahedron, 1999, 55, 14199–14210.
12. V. Nair, K. C. Sheela, D. Sethumadhavan, R. Dhanya and N. P. Rath, Tetrahedron, 2002, 58, 4171–4177.
13. (a) A. Savin, A. D. Becke, J. Flad, R. Nesper, H. Preuss and H. G. Vonschnering, Angew. Chem., Int. Ed. Engl., 1991, 30, 409–412; (b) A. Savin, B. Silvi and F. Colonna, Can. J. Chem., 1996, 74, 1088–1096; (c) A. Savin, R. Nesper, S. Wengert and T. F. Fassler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1809–1832; (d) B. Silvi, J. Mol. Struct., 2002, 614, 3–10.
14. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
15. W. J. Hehre, L. Radom, P. v. R. Schleyer, and J. A. Pople, in Ab initio Molecular Orbital Theory, Wiley, New York, 1986.
16. (a) H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218; (b) H. B. Schlegel, Geometry Optimization on Potential Energy Surface, in Modern Electronic Structure Theory, ed. D. R. Yarkony, World Scientific Publishing, Singapore, 1994.
17. K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163.
18. (a) C. González and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527; (b) C. González and H. B. S.chlegel, J. Chem. Phys., 1991, 95, 5853–5860.
19. (a) A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746; (b) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
20. S. Noury, X. Krokidis, F. Fuster and B. Silvi, Comput. Chem., 1999, 23, 597–604.
21. (a) J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027–2094; (b) B. Y. Simkin and I. Sheikhet, Quantum Chemical and Statistical Theory of Solutions-A Computational Approach, Ellis Horwood, London, 1995, pp. 78–101.
22. (a) E. Cances, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041; (b) M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327–335; (c) V. Barone, M. Cossi and J. Tomasi, J. Comput. Chem., 1998, 19, 404–417.
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian03, 2004.
24. R. G. Parr, L. von Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924.
25. (a) R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516; (b) R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989.
26. (a) L. R. Domingo, E. Chamorro and P. Pérez, J. Org. Chem., 2008, 73, 4615–4624; (b) L. R. Domingo and P. Pérez, Org. Biomol. Chem., 2011, 9, 7168–7175.
27. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133–1138.
28. R. Contreras, P. Fuentealba, M. Galván and P. Pérez, Chem. Phys. Lett., 1999, 304, 405–413.
29. W. Benchouk, S. M. Mekelleche, B. Silvi, M. J. Aurell and L. R. Domingo, J. Phys. Org. Chem., 2011, 24, 611–618.
30. K. B. Wiberg, Tetrahedron, 1968, 24, 1083–1096.
31. L. R. Domingo and J. A. Sáez, Org. Biomol. Chem., 2009, 7, 3576–3583.
32. L. R. Domingo, M. J. Aurell, P. Perez and R. Contreras, Tetrahedron, 2002, 58, 4417–4423.
33. P. Jaramillo, L. R. Domingo, E. Chamorro and P. Perez, THEOCHEM, 2008, 865, 68–72.
34. L. R. Domingo and J. Andres, J. Org. Chem., 2003, 68, 8662–8668.
35. (a) S. Berski, J. Andres, B. Silvi and L. R. Domingo, J. Phys. Chem. A, 2003, 107, 6014–6024; (b) V. Polo, J. Andrés, R. Castillo, S. Berski and B. Silvi, Chem.–Eur. J., 2004, 10, 5165–5172; (c) L. R. Domingo, M. T. Picher, P. Arroyo and J. A.Saez, J. Org. Chem., 2006, 71, 9319–9330; (d) S. Berski, J. Andres, B. Silvi and L. R. Domingo, J. Phys. Chem. A, 2006, 110, 13939–13947; (e) V. Polo, J. Andres, S. Berski, L. R. Domingo and B. Silvi, J. Phys. Chem. A, 2008, 112, 7128–7136; (f) L. R. Domingo, E. Chamorro and P. Pérez, Lett. Org. Chem., 2010, 7, 432–439; (g) L. R. Domingo and J. A. Saez, J. Org. Chem., 2011, 76, 373–379.
36. The ELF yields basins of attractors, which are classified as core basins and valence basins. The latter are characterized by the synaptic order that is the number of atomic valence shells to which they participate.³⁷ Thus, there are monosynaptic, disynaptic, trisynaptic basins and so on. Monosynaptic basins, labeled V(A), correspond to the lone pairs or non-bonding regions, while disynaptic basins connect the core of two nuclei A and B and, thus, corresponds to a bonding region between A and B and labeled V(A,B). This description recovers Lewis's picture of the bonding and provide very suggestive graphical representations of molecular systems.
37. B. Silvi and A. Savin, Nature, 1994, 371, 683–686.
38. L. R. Domingo, J. A. Sáez, R. J. Zaragozá and M. Arno, J. Org. Chem., 2008, 73, 8791–8799.
39. K. Fukui, in Molecular Orbitals in Chemistry, Physics, and Biology, New York, 1964.

---

Footnote

† This paper is dedicated to Professor A. Padwa on his 75th birthday.

---