 Open Access Article
Open Access ArticleExploring aromatic rings with planar tetracoordinate group 13–15 atoms†
Dumer S.
Sacanamboy
 ab,
Pamela L.
Gamero-Begazo
ab,
Pamela L.
Gamero-Begazo
 b,
Kevin E.
Parco-Valencia
b,
Kevin E.
Parco-Valencia
 b,
Diego
Inostroza
b,
Diego
Inostroza
 c,
Lina
Ruiz
c,
Lina
Ruiz
 d,
Luis
Leyva-Parra
d,
Luis
Leyva-Parra
 *e,
Gabriel
Merino
*e,
Gabriel
Merino
 *f and
William
Tiznado
*f and
William
Tiznado
 *a
*a
aUniversidad Andres Bello, Facultad de Ciencias Exactas, Departamento de Ciencias Químicas, Centro de Química Teórica & Computacional (CQT&C), Avenida República 275, 8370146 Santiago de Chile, Chile. E-mail: wtiznado@unab.cl
bDoctorado en Fisicoquímica Molecular, Facultad de Ciencias Exactas, Universidad Andres Bello, Avenida República 275, Santiago de Chile, Chile
cLaboratoire de Chimie Théorique, LCT, Sorbonne Université, CNRS, F-75005 Paris, France
dInstituto de Ciencias Biomédicas, Facultad de Ciencias de la Salud, Universidad Autónoma de Chile, Santiago de Chile, Chile
eFacultad de Ingeniería y Arquitectura, Universidad Central de Chile (UCEN), Santa Isabel 1186, 8370146, Santiago, Chile. E-mail: luis.leyva@ucentral.cl
fDepartamento de Física Aplicada, Centro de Investigación y de Estudios Avanzados Mérida Km. 6 Antigua carretera a Progreso Apdo. Postal 73, Cordemex, Yuc., 97310, Mérida, Mexico. E-mail: gmerino@cinvestav.mx
First published on 18th September 2024
Abstract
This study examines systems containing planar tetracoordinate group 13–15 atoms (E) within pentagonal C4H2E rings bridged by Si or Ge atoms. A detailed chemical bonding analysis of eleven candidates shows that true tetracoordination is achieved only in the C4H2NGe2+ system.
For the past five decades, the study of planar hypercoordinate carbon1–21 has revealed fascinating architectures, although they remain scarce compared to the abundance of van’t Hoff–LeBel-type molecules. Why pursue such unusual systems? As Hoffmann stated, “the purpose of studying nonclassical molecules is to learn from the abnormal the making of molecules that are untypical or abnormal test our understanding of that fundamental yet fussy entity – the chemical bond”.22 This challenge motivates the exploration of other entities with planar hypercoordinate atoms.
The study of planar tetracoordinate carbons (ptCs) began with Monkhorst's work on planar transition states in the stereomutation of methane. Hoffmann and co-workers later explored the electronic factors stabilizing these structures,23,24 showing that replacing the hydrogen atoms of methane with σ-electron donors strengthens the electron-deficient σ-bonds, while introducing π-acceptors delocalizes the central carbon's lone pair. These concepts have guided the design of ptC structures, many of which have been successfully realized in both the gas phase and laboratory settings. The field has since expanded to include systems with higher coordination numbers, such as planar penta- and hexacoordinate carbon atoms.10,12,25–32
Building on Hoffmann's proposal to stabilize a ptC within an aromatic framework, some of us extended this idea by replacing three consecutive protons in an aromatic hydrocarbon with a tetracationic tetrel fragment, Tr24+, fragment (Tr = C–Pb). The Tr atoms form a 3c–2e σ-bond (Tr-ptC-Tr) and participate in π-delocalization via their vacant pz orbitals, stabilizing various planar hypercoordinate atom systems.15,17,19–21 When Tr is carbon, the structure is a local minimum, while heavier atoms yield global minima.
In this work, we apply our approach to achieve a ptE, where E is an element from group 13–15. We replace a single carbon atom in the cyclopentadienyl anion (C5H5−) with an E element and adjust the electron count accordingly. We screened 56 combinations with the formula C4H2ETr2n, where Tr = Si−Pb and n denotes the charge (−1 for group 13, 0 for group 14, and +1 for group 15 systems). All these structures were identified as minima on their potential energy surfaces (PESs) at the PBE033-D334/def2-TZVP35 level (see Scheme 1 for details). Eleven were found to be global minima. Born–Oppenheimer molecular dynamics (BO–MD) simulations confirm the kinetic stability of these systems. However, despite being global minima and appearing tetracoordinate initially, bond analysis shows that only C4H2NGe2+ has a truly planar tetracoordinate atom.
To efficiently evaluate numerous candidates, we used a targeted search on the PES with ptE structures as starting points within the AUTOMATON software.36 This approach reduced the search space and identified 18 promising structures (E = B–Tl with Tr = Si; E = Si with Tr = Ge; E = As, Sb, Bi with Tr = Si; E = N, P with Tr = Ge; E = N with Tr = Pb). A subsequent random initial population search of these 18 combinations in AUTOMATON identified 11 global minima with a potential ptE atom.
Let us focus on the eleven global minima. Fig. S1–S18 (ESI†) show these global minima and other low-lying configurations for all 56 candidates. For E = group 13, five anions (C4H2ESi2−, E = B–Tl) adopt a prospective ptE arrangement. Among neutral systems (E = group 14), only one, C4H2SiGe2, achieves a potential ptE global minimum. The remaining five global minima are cations, involving group 15 atoms: three (As, Sb, Bi) bonded to Si (C4H2ESi2+), and two (N, P) bonded to Ge (C4H2EGe2+).
To evaluate kinetic stability, we performed Born–Oppenheimer molecular dynamics (BO–MD) simulations at 450 K. These simulations confirmed that the eleven global minima retained their integrity and planarity, with no evidence of isomerization. This is further supported by the minimal root mean square deviation (RMSD) values (Fig. S19, ESI†), with primary fluctuations being out-of-plane movements of the Tr ligands, which consistently returned to a planar configuration.
All eleven global minima are singlets with C2v symmetry. Energy differences between the global minima and their lowest triplet state (ΔES–T) show trends (see Table S1, ESI†). For anions, ΔES–T increases with heavier E atoms (22.9 to 27.6 kcal mol−1). The neutral system exhibits a higher ΔES–T of 46.3 kcal mol−1. In contrast, cations show a decreasing ΔES–T trend from 63.3 (As) to 34.7 kcal mol−1 (Bi) with Tr = Si, and from 72.1 (N) to 63.9 kcal mol−1 (P) with Tr = Ge, indicating that lighter atoms enhance stability in cationic systems. Furthermore, the T1-diagnostics from the converged CCSD wave functions are below the standard multireference threshold of 0.02, ranging from 0.012 to 0.017 (Table S1, ESI†), validating the reliability of our single-reference computations.
The adaptive natural density partitioning (AdNDP) method was used to understand the bonding interactions. AdNDP extends natural bond orbitals (NBO) to describe both localized and delocalized bonding by partitioning electron density into n-center two-electron (nc–2e) bonds.37,38Fig. 1 shows the AdNDP results for these systems (excluding group 13 ones). The analysis reveals 2c–2e σ-bonds connecting the pentagonal C4E moiety, with Tr atoms connected to this pentagon by 2c–2e σ-bonds with C1 and a 3c–2e Tr–E–Tr σ-bond. The σ-bonding picture is completed by two C2–H 2c–2e σ-bonds and one lone pair on each Tr atom. AdNDP also identifies three fully delocalized π-bonds, suggesting aromaticity according to Hückel's 4n + 2 rule. These results are consistent with the Wiberg bond indices (WBI) reported in Table S2 (ESI†).
 | ||
| Fig. 1 AdNDP analysis of C4H2SiGe2, C4H2ESi2+ (E = As, Sb, Bi) and C4H2EGe2+ (E = N and P) at the PBE0-D3/def2-TZVP level. ON stands for occupation number. | ||
In the group 13 systems, ptB, ptAl, and ptGa exhibit a similar bonding pattern (Fig. S20, ESI†). However, ptIn and ptTl deviate from this one. Fig. S21 (ESI†) shows that their bonding is better described by delocalized σ-bonds connecting the In or Tl atoms, neighboring carbons, and Si ligands. The larger atomic sizes of In and Tl disrupt the localized σ-bonding pattern, resulting in bond lengths exceeding typical single bonds, as predicted by Pyykkö.39 This suggests weaker covalent interactions in the In and Tl systems, consistent with WBI values near 0.5 (Table S2, ESI†).
So, both AdNDP and WBI indicate covalent interactions between E and its four neighboring atoms across all eleven global minima. However, ionic interactions are also significant due to the electronegativity differences between C, E, and Tr. NPA charge analysis shows that only B and N systems carry negative charges (−0.39 and −0.77 |e|, respectively, Table S2, ESI†). The negative charge on B is unexpected given the higher electronegativity of C (2.55) compared to B (2.04) and Si (1.90). Bader analysis40 confirms that only N in ptN bears a negative charge (−1.29 |e|), consistent with N's higher electronegativity, while C atoms bonded to N carry slight negative charges of −0.16 |e| (Table S3, ESI†)
These findings raise questions about the role of the electrostatic interactions. The interacting quantum atoms (IQA) method41–44 provides additional insight (Table S4, ESI†). IQA results indicate that the E–Tr interactions are repulsive (27.9–175.2 kcal mol−1) except for N–Tr (−343.0 kcal mol−1). This raises the question: why are these molecular architectures favored? IQA shows that the strongly attractive E-C1 and Tr-C1 interactions counterbalance the repulsive E–Tr forces, maintaining E and Tr at bond distances and favoring the covalent E–Tr interaction. This is reflected in the consistently attractive E–Tr exchange–correlation component (−34.8 to −60.1 kcal mol−1) across all systems, aligning with the AdNDP and WBI analyses. However, true planar tetracoordination requires net attractive interactions with all four ligands. Among the systems studied, only ptN features a genuinely planar tetracoordinate atom.
To further investigate the aromatic character of these systems, we analyzed the magnetically induced current density in response to an external magnetic field. Aromatic compounds typically exhibit a net diatropic ring current.45–48 For example, the cyclopentadienyl anion, a well-known aromatic molecule, has a net ring current strength (RCS) of 11.0 nA T−1, comparable to benzene net RCS of 12.2 nA T−1.
Focusing on C4H2NGe2+, Fig. 2 shows planes (0.5 Å above the molecular plane) with vector plots of the total and dissected (σ- and π-components) current density. These reveal a global diatropic ring current involving the entire periphery of the molecule (π), a local diatropic cyclic circuit around the Ge2ptN region (σ), and a paratropic ring current within the pentagonal C4E ring (σ). The net RCS of 11.2 nA T−1 indicates significant aromatic character, primarily attributed to the π-component (9.8 nA T−1). In the remaining ten systems, despite the net interatomic interaction energies suggesting the E atom is not truly tetracoordinate, particularly due to a lack of a net attractive interaction with the Tr atoms, they still exhibit aromatic character based on the magnetic criterion (Fig. S22–S25, ESI†). Net RCS values range from 8.0 to 4.2 nA T−1 in the group 13 series, decreasing from Al to Tl, consistent with all non-negligible covalent interactions suggested by the bonding analysis (AdNDP, WBI, and the delocalization index from IQA).
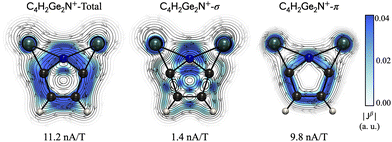 | ||
| Fig. 2 Vector plots on the molecular plane 0.5 Å above the plane for C4H2NGe2+, and RCSs (total, σ and π, in nA T−1) computed at the PBE0/def2-TZVP level. | ||
In summary, this study extends our established approach for stabilizing planar tetracoordinate carbon atoms to explore planar tetracoordinate elements from groups 13–15. We identified eleven new global minima by replacing three consecutive protons in five-membered heterocyclic rings with a Tr24+ fragment (Tr = Si to Pb). Each system features a 3c–2e Tr-E-Tr σ-bond and three globally delocalized π-bonds, where the E atom appears structurally tetracoordinated. The stability of these systems was confirmed through exhaustive potential energy surface scans and Born–Oppenheimer molecular dynamics simulations. However, detailed interacting quantum atoms (IQA) analysis reveals that only C4H2NGe2+ contains a truly planar tetracoordinate nitrogen (ptN), with N forming net attractive interactions with its four neighboring atoms. In the other systems, Coulombic repulsion leads to a net E–Tr repulsive interaction, despite covalent bonding indicated by the attractive exchange–correlation component. All systems exhibit a net diatropic ring current, mainly of π-character, which decreases from Al to Tl in group 13. These findings highlight the importance of using refined methods to accurately assess chemical bonding and coordination in these exotic structures.
This work was supported by the financial support of the National Agency for Research and Development (ANID) through FONDECYT project 1211128 (W. T.) and Scholarship Program/BECAS DOCTORADO UNAB (D. S, P. G.-B, K. P.-V). Powered@NLHPC: This research was partially supported by the supercomputing infrastructure of the NLHPC (CCSS210001). Cinvestav supported the work in Mexico. LL-P, GM, and WT designed the work and concepts, analyzed the data, drafted the manuscript, and finalized it. DS, PG-B, DI, and KP-V conducted the global minima search, structural data analysis, and energy refinements. DI and LR carried out BOMD simulations, NBO, and AdNDP analyses. LL-P, DI, and LR conducted the aromaticity analysis. All authors participated in discussions and approved the final manuscript.
Data availability
The data underlying this study is available in the manuscript and its ESI.†Conflicts of interest
There are no conflicts to declare.Notes and references
- J. B. Collins, J. D. Dill, E. D. Jemmis, Y. Apeloig, P. V. Schleyer, R. Seeger and J. A. Pople, J. Am. Chem. Soc., 1976, 98, 5419–5427 CrossRef CAS.
- G. Erker, Commun. Inorg. Chem., 1992, 13, 111–131 CrossRef CAS.
- D. Röttger and G. Erker, Angew. Chem., Int. Ed. Engl., 1997, 36, 813–827 CrossRef.
- W. Siebert and A. Gunale, Chem. Soc. Rev., 1999, 28, 367–371 RSC.
- G. Merino, M. A. Méndez-Rojas, H. I. Beltrán, C. Corminboeuf, T. Heine and A. Vela, J. Am. Chem. Soc., 2004, 126, 16160–16169 CrossRef CAS PubMed.
- N. Perez, T. Heine, R. Barthel, G. Seifert, A. Vela, M. A. Mendez-Rojas and G. Merino, Org. Lett., 2005, 7, 1509–1512 CrossRef CAS PubMed.
- R. Keese, Chem. Rev., 2006, 106, 4787–4808 CrossRef CAS PubMed.
- G. Merino, M. A. Mendez-Rojas, A. Vela and T. Heine, J. Comput. Chem., 2007, 28, 362–372 CrossRef CAS PubMed.
- N. Perez-Peralta, M. Sanchez, J. Martin-Polo, R. Islas, A. Vela and G. Merino, J. Org. Chem., 2008, 73, 7037–7044 CrossRef CAS PubMed.
- L. M. Yang, E. Ganz, Z. Chen, Z. X. Wang and P. V. R. Schleyer, Angew. Chem., Int. Ed., 2015,(54), 9468–9501 CrossRef CAS PubMed.
- Z.-H. Cui, V. Vassilev-Galindo, J. L. Cabellos, E. Osorio, M. Orozco, S. Pan, Y.-H. Ding and G. Merino, Chem. Commun., 2017, 53, 138–141 RSC.
- V. Vassilev-Galindo, S. Pan, K. J. Donald and G. Merino, Nat. Rev. Chem., 2018, 2, 0114 CrossRef CAS.
- M.-h Wang, M. Orozco-Ic, L. Leyva-Parra, W. Tiznado, J. Barroso, Y.-H. Ding, Z.-H. Cui and G. Merino, J. Phys. Chem. A, 2021, 125, 3009–3014 CrossRef CAS PubMed.
- L. Leyva-Parra, L. Diego, D. Inostroza, O. Yañez, R. Pumachagua-Huertas, J. Barroso, A. Vásquez-Espinal, G. Merino and W. Tiznado, Chem. – Eur. J., 2021, 27, 16701–16706 CrossRef CAS PubMed.
- D. Inostroza, L. Leyva-Parra, A. Vásquez-Espinal, J. Contreras-García, Z.-H. Cui, S. Pan, V. S. Thimmakondu and W. Tiznado, Chem. Commun., 2022, 58, 13075–13078 RSC.
- L. Leyva-Parra, D. Inostroza, O. Yañez, J. C. Cruz, J. Garza, V. García and W. Tiznado, Atoms, 2022, 10, 27 CrossRef CAS.
- D. Inostroza, L. Leyva-Parra, O. Yañez, J. C. Cruz, J. Garza, V. García, V. S. Thimmakondu, M. L. Ceron and W. Tiznado, Int. J. Quantum Chem., 2023, 123, e27008 CrossRef CAS.
- D. Inostroza, L. Leyva-Parra, O. Yañez, A. L. Cooksy, V. S. Thimmakondu and W. Tiznado, Chemistry, 2023, 5, 1535–1545 CrossRef CAS.
- O. Yañez, A. Vásquez-Espinal, R. Pino-Rios, F. Ferraro, S. Pan, E. Osorio, G. Merino and W. Tiznado, Chem. Commun., 2017, 53, 12112–12115 RSC.
- O. Yañez, A. Vásquez-Espinal, R. Báez-Grez, W. A. Rabanal-León, E. Osorio, L. Ruiz and W. Tiznado, New J. Chem., 2019, 43, 6781–6785 RSC.
- O. Yañez, R. Báez-Grez, J. Garza, S. Pan, J. Barroso, A. Vásquez-Espinal, G. Merino and W. Tiznado, Chem. Phys. Chem., 2020, 21, 145–148 CrossRef PubMed.
- R. Hoffmann and H. Hopf, Angew. Chem., Int. Ed., 2008, 47, 4474–4481 CrossRef CAS PubMed.
- H. Monkhorst, Chem. Commun., 1968, 1111–1112 RSC.
- R. Hoffmann, R. W. Alder and C. F. Wilcox, J. Am. Chem. Soc., 1970, 92, 4992 CrossRef CAS.
- K. Exner and P. V. R. Schleyer, Science, 2000, 290, 1937–1940 CrossRef CAS PubMed.
- Y. Pei, W. An, K. Ito, P. V. R. Schleyer and X. C. Zeng, J. Am. Chem. Soc., 2008, 130, 10394–10400 CrossRef CAS PubMed.
- Y. Wang, F. Li, Y. Li and Z. Chen, Nat. Commun., 2016, 7, 11488 CrossRef CAS PubMed.
- S. Pan, J. L. Cabellos, M. Orozco-Ic, P. K. Chattaraj, L. Zhao and G. Merino, Phys. Chem. Chem. Phys., 2018, 20, 12350–12355 RSC.
- L. Leyva-Parra, L. Diego, O. Yañez, D. Inostroza, J. Barroso, A. Vásquez-Espinal, G. Merino and W. Tiznado, Angew. Chem., Int. Ed., 2021, 60, 8700–8704 CrossRef CAS PubMed.
- L.-M. Yang, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, Phys. Chem. Chem. Phys., 2015, 17, 17545–17551 RSC.
- L.-M. Yang, V. Bačić, I. A. Popov, A. I. Boldyrev, T. Heine, T. Frauenheim and E. Ganz, J. Am. Chem. Soc., 2015, 137, 2757–2762 CrossRef CAS PubMed.
- L.-M. Yang, I. A. Popov, T. Frauenheim, A. I. Boldyrev, T. Heine, V. Bačić and E. Ganz, Phys. Chem. Chem. Phys., 2015, 17, 26043–26048 RSC.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- O. Yanez, R. Baez-Grez, D. Inostroza, W. A. Rabanal-Leon, R. Pino-Rios, J. Garza and W. Tiznado, J. Chem. Theory Comput., 2019, 15, 1463–1475 CrossRef CAS PubMed.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217 RSC.
- D. Y. Zubarev and A. I. Boldyrev, J. Org. Chem., 2008, 73, 9251–9258 CrossRef CAS PubMed.
- P. Pyykkö, J. Phys. Chem. A, 2015, 119, 2326–2337 CrossRef PubMed.
- R. F. W. Bader and R. F. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, 1990 Search PubMed.
- A. M. Pendás, M. A. Blanco and E. Francisco, J. Chem. Phys., 2004, 120, 4581–4592 CrossRef PubMed.
- A. M. Pendás, E. Francisco and M. A. Blanco, J. Comput. Chem., 2005, 26, 344–351 CrossRef PubMed.
- M. A. Blanco, A. Martín Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096–1109 CrossRef CAS PubMed.
- A. M. Pendás, M. A. Blanco and E. Francisco, J. Comput. Chem., 2007, 28, 161–184 CrossRef PubMed.
- J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- D. Sundholm, H. Fliegl and R. J. Berger, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678 CAS.
- L. Leyva-Parra, R. Pino-Rios, D. Inostroza, M. Solà, M. Alonso and W. Tiznado, Chem. – Eur. J., 2024, 30, e202302415 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cc02780a |
| This journal is © The Royal Society of Chemistry 2024 |

