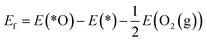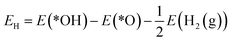Shifting the scaling relations of single-atom catalysts for facile methane activation by tuning the coordination number

Abstract

We investigate oxidative methane activation on a wide range of single transition metal atom catalysts embedded on N-doped graphene derivatives using density functional theory calculations. An inverse scaling relationship between *O formation and its hydrogen affinity is observed, consistent with a previous report. However, we find that the latter scaling line can be shifted towards a more reactive region by tuning the coordination number (CN) of the active metal sites. Specifically, we find that lowering the CN plays an important role in increasing the reactivity for methane activation via a radical-like transition state by moving the scaling lines. Thus, in the new design strategy suggested here, different from the conventional efforts focusing mainly on breaking the scaling relations, one maintains the scaling relations but moves them towards more reactive regions by controlling the coordination number of the active sites. With this design principle, we suggest several single atom catalysts with lower C–H activation barriers than some of the most active methane activation catalysts in the literature such as Cu-based zeolites.

---

1. Introduction

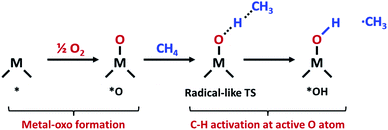
The increasing availability of natural gas and shale gas drives the demand for efficient catalysts for methane conversion.¹ Methane, the most abundant component of natural gas (>70%), is an attractive feedstock due to its large reserves and various uses. In the chemical industry, methane is converted into various high value-added products such as alcohols, C₂₊ alkanes and olefins through multistep indirect processes involving methane steam reforming.² However, the direct conversion of methane is still challenging due to high dissociation energy in the first C–H bonds. The non-polar and inert nature of methane thus hampers greatly the methane activation and leads to energy-intensive processes for conversion.³

In nature, methane is oxidized to methanol by an enzymatic system called a methane monooxygenase (MMO) under ambient conditions. The active sites of particulate MMO (pMMO) have been suggested as di-copper clusters coordinated by N atoms.^4,5 At the active site of pMMO, methane is oxidatively activated via a radical-like transition state (TS).⁶ In this mechanism, the C–H bond is dissociated by the surface O atom in the metal-oxo group which forms the CH₃ radical (Fig. 1).

Fig. 1 Schematic of oxidative methane activation via a radical-like TS.

Many heterogeneous methane activation catalysts such as cation-exchange zeolites^7–9 and metal–organic frameworks (MOFs)^10,11 also follow a similar radical-like TS. The net reaction of methane activation can be written as *O + CH₄ → *OH + ·CH₃ (* = adsorption site). In this radical-like TS, the active site (*O) formation energy (E_f) and the hydrogen affinity (E_H) of this active *O species have been proposed as a suitable descriptor of reactivity for methane activation.^12–15 The universal linear scaling relationship between E_H and the TS energy of methane activation was identified for various catalysts such as cation-exchanged zeolites, MOFs, decorated graphene nanosheets, metal oxides, and transition metal surfaces.¹² Furthermore, the E_H has an inverse linear scaling relationship with active site (*O) formation energy (E_f) due to the trade-off between the stability and reactivity of *O.^12–14 Interestingly, two, rather than one, universal, distinct linear scaling lines between E_f and E_H were observed.¹² For example, catalysts lying on the higher-reactivity linear scaling line include cation-exchange zeolites and metal oxides, and those on the lower-reactivity line include MOFs, decorated graphene nanosheets, and transition metal surfaces, but the origin of such distinct scaling lines was not clearly understood. One possibility for the origin of the two scaling lines offered by the authors includes the ability of the substrate to delocalize the changes in charge during the *O formation.¹² That is, substrates which poorly delocalize charges (insulating substrates) tend to follow the higher-reactivity linear scaling line, while substrates exhibiting higher conductivity follow the lower-reactivity line. However, in a more recent study that considered various types of MOF for methane activation, a full range of charge delocalization was observed but it resulted in only one scaling line, suggesting that the charge delocalization may not be responsible for the existence of two distinct scaling lines.¹³ The origin of different scaling lines which can serve as an important design principle to discover more efficient catalysts thus remains unexplained, and the latter understanding is the subject of this paper we intend to address here.

One key factor that differentiates these two linear scaling lines, which we focus on, is the coordination number (CN) of active sites. The CN is an important descriptor that often determines adsorption energies, and indeed linear scaling relations between CN and binding energies were identified,¹⁶ and CN-based descriptors have been suggested for predicting adsorption energies on transition metals,^17–19 graphene-based single atom catalysts²⁰ and C–H activation at the O atom in metal oxides.^21,22 Specifically, our initial analysis of Latimer et al.¹² for methane activation catalysts indicated that the CNs of active cations in cation-exchange zeolites or coordinatively unsaturated sites (CUS) in metal oxides located in the high-reactivity scaling line were generally lower than those of catalysts in the low-reactivity line.¹² Thus, we conjectured that decreasing the CN may lead to the shifting of the linear scaling relationship towards more reactive methane activation regions.

In this study, we investigated the effect of active site CN on the scaling relationships between E_f and E_H for methane activation reactions. To systematically study the effect of coordination environments, we considered single metal atoms anchored at the N-doped graphene with various coordination numbers (denoted as M@N_xC_y), which also mimics the active sites of pMMO. Recently, Cui et al. experimentally showed that graphene-confined single Fe sites could oxidize methane into C1 oxygenates at room temperature.²³ By combinatorially combining various transition metals and anchoring sites with different N contents, we have considered 182 M@N_xC_y catalysts in total in the present study. We note that, in a previous study,¹² 94 catalysts including a wide range of structural motifs (e.g. zeolites, graphene, MOFs, metal oxides, nanoparticles and metal surfaces) were considered, but due to various structural motifs a systematic understanding of the effect of CN on the scaling relation was difficult to obtain. With M@N_xC_y as model systems, we herein demonstrate the concept of shifting the linear scaling lines towards more reactive regions by controlling (decreasing) the CN of active metal species. This finding agrees with previous experiments that the superior catalysts reported so far mainly consist of low CN sites. Therefore, we suggest that tuning the CN as well as E_f (or E_H) plays a key role in increasing the reactivity for methane activation, and as a result, several promising catalysts such as Cu@C₃, Zn@C₃, Zn@N₂C and Zn@N₃ are identified here that can be tested experimentally.

2. Computational details

Structure relaxation and total electronic energy calculations were performed with spin-polarized density-functional theory (DFT) methods implemented in the Vienna Ab initio Simulation Package (VASP) with the projector-augmented wave pseudopotential (PAW).^24–26 The Perdew–Burke–Ernzerhof (PBE)²⁷ functional combined with Grimme's D3-dispersion correction²⁸ with the Becke–Johnson (BJ) damping²⁹ was employed. The cutoff energy was set to 400 eV and k-points were sampled using the (2 × 2 × 1) and (1 × 2 × 1) Monkhorst–Pack mesh³⁰ for the basal plane and edge site of graphene, respectively. Geometry optimizations were performed until energy differences and forces on each atom are converged to 10⁻⁵ eV and −0.05 eV Å⁻¹, respectively. The climbing-image nudged elastic band (CI-NEB)³¹ calculations were performed to calculate activation energy with eight intermediate images. Atomic charge analysis was performed by using the Bader partitioning scheme.³² Due to the limitations in description of triplet O₂ by plane wave DFT calculations, we corrected the electronic energy of O₂(g) by ensuring the experimental standard enthalpy of reaction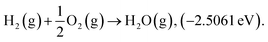 ³³

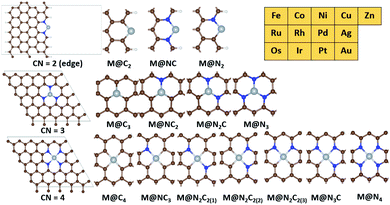
A graphene basal plane is modelled by using the (5 × 5) supercell of hexagonal graphene while a graphene edge site is modelled by using the (5 × 5) supercell of zigzag edge graphene (Fig. 2). All slab models contain at least 15 Å of vacuum in the c-axis. 15 Å of vacuum is added in the a-axis in the edge site of graphene. The calculation details for zeolites and IrO₂(110) are given in the ESI (Fig. S1 and S2†).^34,35

Fig. 2 Calculation models for M@N_xC_y catalysts. Grey, brown, blue and white balls represent transition metal, carbon, nitrogen and hydrogen atoms, respectively. The 13 late transition metals considered in this study are shown as a table.

3. Results and discussion

3.1. Structures of single-atom catalysts

Based on the active sites of MMO, we construct the transition metal (M)–N coordination moiety denoted as M@N_x which is embedded on graphene (Fig. 2). M@N_x catalysts having CN = 2,^36,37 3 (ref. 38–40) and 4 (ref. 41) have been experimentally identified and utilized for various catalytic reactions. To investigate more systematically the effect of CN on various SACs for methane activation, we additionally consider M@N_xC_y and M@C_x moieties, which incorporate the M–C coordination environments. Since the M@N_xC_y catalysts have a common structural motif (graphene) but different CNs, we expect that the M@N_xC_y moieties are suitable for investigating the isolated effects of CN. For SACs with CN = 2, we consider metal atoms anchored by two atoms in the graphene edge, while we consider the basal plane of graphene for constructing SACs with CN = 3 and CN = 4. The metal atoms are located at the vacancy site of graphene and anchored by N or C atoms, as in experiments.^23,36–43 Most of the M@N_xC_y catalysts have been synthesized for late transition metals such as Fe,^23,38,43 Co,^36,41 Ni,⁴⁰ Cu,³⁹ Zn⁴⁴ and Ru.^45,46 Thus, we focus on 13 late transition metals for M@N_xC_y catalysts, and hence, a total of 182 catalysts are considered in this study as summarized in Fig. 2.

3.2. Several scaling lines of reactivity by G_f and G_H

The reaction mechanism of oxidative methane activation via a radical-like TS is divided into two parts (Fig. 1): active site (*O) formation and C–H bond dissociation, which are estimated by the formation energy of *O (E_f) and hydrogen affinity at *O (E_H), respectively, following Nørskov and coworkers.¹² The E_f and E_H determine the coverage of *O atoms and ability for C–H bond dissociation at an *O atom, respectively, and hence, these two descriptors are suitable for estimating the reactivity for methane activation via the radical-like TS.¹² The E_f and E_H are defined as follows.

A 2D-volcano plot is obtained for the rate of methane activation at 150 °C as a function of two descriptors (G_f and G_H) (details are given in the ESI†). In this 2D-volcano plot, the reactivity increases with more negative G_f and G_H, which facilitate *O formation and C–H bond dissociation simultaneously. However, an inverse scaling relationship between G_f and G_H, which originates from the trade-off between the stability and reactivity of *O, hinders the simultaneous decrease of both G_f and G_H.¹³ A more stabilized *O (more negative G_f) leads to the less reactive *O (more positive G_H). A destabilized *O would activate methane with a lower activation energy, while it would result in a decreased population of active *O atoms. Consequently, the optimal reactivity for methane activation is observed at a balanced combination of G_f and G_H.

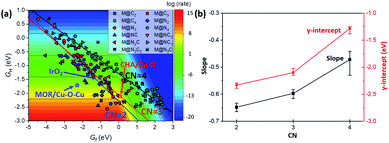
In the 2D-volcano plot of M@N_xC_y catalysts, we verify that an inverse scaling relationship between G_f and G_H still holds for the M@N_xC_y model catalysts considered here (Fig. 3a). However, different linear scaling lines are observed rather than one universal line, consistent with a previous report.¹² We find that the most distinctive feature in different linear scaling lines is the coordination number of the active sties of M@N_xC_y catalysts. Interestingly, M@N_xC_y catalysts with lower CNs (CN = 2 and CN = 3) are located at more reactive regions (lower left-side of the 2D volcano plot), than those with CN = 4. Notably, most of the M@N_xC_y catalysts near the optimal region (red zone in the volcano plot) are catalysts with CN = 2.

Fig. 3 (a) 2D-volcano plot for methane activation at 150 °C as a function of G_f and G_H. Blue, red and black lines represent linear scaling lines of CN = 2, 3 and 4, respectively. (b) Changes in the slope and y-intercept of the linear scaling line with CN. Each data point represents an average value, while the error bar represents the range of slopes (or y-intercepts) at each CN.

Since the catalytic performance for alkane activation changes with the oxidant,⁴⁷ we compared the 2D-volcano plot for methane activation using O₂ with that using N₂O (Fig. S3†). We found that *O formation becomes more facilitated when using N₂O than when using O₂, and thus, G_f obtained by using N₂O is more negative than G_f using O₂. Consequently, the overall rate for methane activation increases with the help of facilitated *O formation and weakly oxygen binding SACs move towards the top of the volcano. However, the results are not significantly changed and the trend in the shift of the scaling relationship towards a more reactive region with decreasing CN is unchanged by the oxidant.

3.3. Origin of shifted scaling relationships

To understand the origin of different scaling lines, we first briefly comment on the effect of charge delocalization since the ability of the substrate to delocalize changes in charge following *O formation was suggested as a possible origin of different scaling lines.¹² Materials that exhibit higher conductivity (graphene, metal and perovskites) tended to yield a lower-reactivity scaling line, while insulating substrates (zeolites and insulating oxides) tended to yield a higher-reactivity scaling line. However, unlike the latter speculation, we obtained different linear scaling lines for M@N_xC_y catalysts even though the substrates of M@N_xC_y catalysts considered in this study are all from the same graphene moiety. This difference is due to the fact that in the prior work only M@N₄ moiety embedded graphene was considered and other M@N_xC_y moieties with different CNs were not studied.¹² To examine the charge delocalization effect further, we calculated the fractional degree of charge delocalization (χ_ox) following Rosen et al. (Fig. S4†).¹³ A wide range of χ_ox values are obtained at each moiety; however, no relationship between χ_ox and different scaling lines was observed. Thus, the ability for charge delocalization would not be a main origin for different scaling lines, consistent with the earlier conclusion based on MOFs.¹³ We note in passing that most MOFs considered in the latter previous work¹³ mainly consisted of open metal sites with CN = 5 or 6 and accordingly the effect of CN has not been exhibited, but with additional consideration of MOFs with low CN, higher-reactivity scaling lines might be found.

The CN as well as ligand atoms affect the scaling relations, which we systematically investigate below. To quantify the change in the linear scaling line, we compare the slopes and y-intercepts of each linear scaling line. We first examine the effect of ligand atoms by comparing the slopes and y-intercepts of the scaling lines of M@N_xC_y catalysts with the same CN (Fig. S5†). We find that the slopes and y-intercepts differ by only ∼0.05 and ∼0.1 eV, respectively, when the ligand atoms change (–N vs. –C). However, when CN changes (Fig. S6†), slopes and y-intercepts change noticeably by ∼0.2 and ∼1 eV, respectively. The average y-intercept of the linear scaling line increases in the order of −2.31 (CN = 2) < −2.07 (CN = 3) < −1.29 (CN = 4) (Fig. 3b). This result clearly indicates that decreasing CN indeed shifts the linear scaling line towards a more reactive region for methane activation (lower left-side of the 2D volcano).

We further consider Cu-based zeolites (CHA/Cu–O and MOR/Cu–O–Cu), which have been previously reported as superior catalysts in experiments.^7–9 All of the latter catalysts are indeed located near the top of the theoretical volcano-plot for methane activation¹² in which the reaction proceeds via a radical-like TS. We note in passing that IrO₂(110), in which the C–H activation occurs via the surface-stabilized CH₃, is also one of the more active methane activation catalysts operating at relatively low temperatures,^48–50 and is thus included here. However, we assume the radical-like TS for IrO₂(110) for consistency following ref. 12 since IrO₂(110) still lies near the top of the volcano with the radical-like TS.¹² These experimentally verified catalysts have low CN (Fig. S1 and S2†). For example, CNs of Cu before *O formation are 2 and 3 in CHA/Cu–O and MOR/Cu–O–Cu, respectively. Interestingly, these catalysts do lie on the linear scaling line of low CN (CN = 2 and CN = 3), suggesting a generality of the trend that the decreased CN results in a shifted linear scaling line towards a desired region.

3.4. Effect of CN on BEP relationship

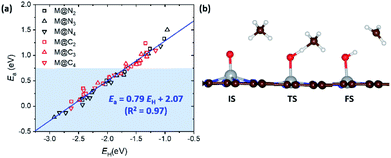
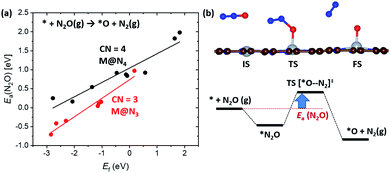
In the previous section, we demonstrated the shifted thermodynamic scaling relationships determined by CN. Here, we investigate the effect of CN on the scaling relationship in activation energy (the BEP relationship). First, we focus on the effect of CN on activation energy for C–H bond dissociation (E_a(CH₄)) by comparing E_H and E_a(CH₄). E_a(CH₄) represents the transition state (TS) energy of methane activation referenced to *O + CH₄(g). A universal BEP relation is obtained between E_H and E_a(CH₄) as E_a(CH₄) = 0.79E_H + 2.07 (eV) with R² = 0.97 (Fig. 4 and Table S1†), which is similar to that reported in the literature (E_a(CH₄) = 0.75E_H + 1.96 (eV)).^12,13 The slope and y-intercept of linear scaling lines are almost unchanged by the CN (Fig. S7†), indicating that the effect of CN on the BEP relationship in E_Hvs. E_a(CH₄) is minor.

Fig. 4 (a) Linear scaling relationship between E_H and E_a. The area shaded in blue is E_a < 0.75 eV. (b) The optimized geometries for the initial state (IS), transition state (TS) and final state (FS) in methane activation.

Next, we focus on the BEP relation in the active site formation by considering, for example, N₂O as an oxidant. We compare E_f and E_a(N₂O), which represents TS energy in the reaction of * + N₂O → *O + N₂ referenced to the * + N₂O(g) (Fig. 5). In contrast to the universal BEP relation in C–H bond dissociation, the linear BEP relation line of E_a(N₂O) changes with the CN. The linear BEP line shifts downwards (more negative E_a(N₂O)) with decreasing CN. Thus, if the E_f is the same for two different catalysts, *O formation is kinetically more favorable for catalysts with a lower CN compared to that with a higher CN.

Fig. 5 (a) Shifted linear scaling relationships between E_f and E_a(N₂O) determined by CN. Black and red data points represent M@N₃ and M@N₄, respectively. (b) The optimized geometries of the IS, TS and FS for *O formation when using N₂O and associated energy diagram for E_a(N₂O). E_a(N₂O) < 0 eV indicates that *O formation proceeds via exothermic N₂O adsorption and low activation energy.

These results indicate that the E_a(CH₄) is mainly determined by the E_H (or chemical properties of *O), while the kinetics for *O formation is determined by E_f as well as CN (structural motif). Thus, the shift of the linear scaling relationship originates mainly from the effect of CN on the *O formation.

To understand the physical origin of the shifted scaling relationship with CN in *O formation, we focused on the changes of electronic structures of the metal atom. The charge, d-band center and spin of the metal atom are considered (Fig. S8 and S9†). Among them, we found a correlation between metal charge and CN. The net charge of the metal atom becomes more positive with increasing CN for almost all SACs. Thus, we conclude that the shifted net charge of the metal atom with increasing CN leads to the shifted linear scaling relationship.

3.5. Thermodynamic stability of potential catalysts

In the previous section, we found several promising catalysts which may be superior to Cu-based zeolites (Fig. 3a), which are some of the best methane activation catalysts via the radical-like TS in the literature.^7–9 Also, various catalysts show E_a(CH₄) < 0.75 eV, corresponding to TOF = 1 s⁻¹ at room temperature (Fig. 4a).⁵¹ Before suggesting potentially promising materials for practical applications, the synthetic possibility is important to consider.⁵² Since the synthesizability is a result of many factors, including precursors, reaction conditions, thermodynamics, kinetics, etc., here we only consider the thermodynamic stability of the SACs due to their simplicity. The stability of a SAC is estimated by comparing the binding energy of the single metal atom at a defective site relative to the bulk states as follows.

E_b = E(M@N_xC_y) − E(@N_xC_y) − E(M(bulk))

E(M@N_xC_y), E(@N_xC_y), and E(M(bulk)) represent the electronic energy of M@N_xC_y, the defective @N_xC_y site without the metal, and a unit cell of bulk metal divided by the number of atoms in the cell. The calculated E_b values are listed in Tables S2 and S3.† Here, we chose the electronic energy of one metal atom in the unit cell as E(M). If E_b < 0, binding of a single metal atom at a defective site is thermodynamically more favorable than aggregation. We chose E_b < 0.1 eV as a criterion for stable SACs which could prevent diffusion and aggregation of single TM atoms.

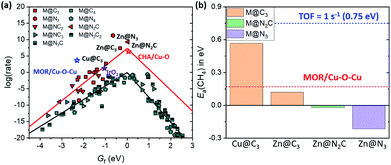
For SACs satisfying this stability condition (E_b < 0.1 eV), we plotted the 1D-volcano for methane activation by using G_f (Fig. 6a). Although SACs having CN = 2 show superior catalytic activity than SACs having CN = 3, these catalysts often show E_b > 0.1 eV. Thus, among the stable SACs, several SACs such as Cu@C₃, Zn@C₃, Zn@N₂C and Zn@N₃ are expected to show promising catalytic activity compared to IrO₂(110) and Cu-based zeolites. The calculated E_a(CH₄) values on these catalysts are comparable or somewhat lower than those of IrO₂(110) and MOR/Cu–O–Cu (Fig. 6b, S10 and S11†). Thus, Cu and Zn-based M@N_xC_y catalysts with CN = 3 are identified as promising candidates for low temperature methane activation.

Fig. 6 (a) 1D-volcano plot for methane activation on stable M@N_xC_y catalysts. Red and black lines represent scaling lines in CN = 3 and CN = 4, respectively. (b) Calculated E_a(CH₄) on Cu@C₃, Zn@C₃, Zn@N₂C and Zn@N₃. Blue and red lines represent E_a(CH₄) corresponding to TOF = 1 s⁻¹ (0.75 eV) and that on MOR/Cu–O–Cu, respectively. The E_a(CH₄) of Zn@N₂C and Zn@N₃ is less than 0 eV, since the adsorption of CH₄ is exothermic and C–H bond dissociation proceeds with almost zero activation energy (<0.1 eV).

To further consider the thermodynamic stability of the proposed Cu@C₃, Zn@C₃, Zn@N₂C and Zn@N₃, we calculated their formation energies (E_form). Unlike E_b, E_form includes the energy for forming the @N_xC_y defective site (details are given in the ESI†). We compared the E_form of Cu@C₃, Zn@C₃, Zn@N₂C and Zn@N₃ with that of experimentally reported M@N_xC_y catalysts (e.g. Ag@N₄, Ru@N₄, Co@N₄ and Cu@N₄).^53–60 Among the proposed candidates, we found that E_form of Zn@N₂C and Zn@N₃ is comparable to or more negative (i.e. more stable) than that of Ag@N₄ and Ru@N₄ (Table S4†).

Since the methane activation generally proceeds under harsh conditions, the stability of M@N_xC_y moieties (in particular Zn@N₂C and Zn@N₃ that are identified here as promising) under experimental conditions should be considered. For example, partial oxidation of methane into methanol with Cu-based zeolites has been experimentally reported at temperatures of 100–200 °C.^7,8,61 Recently, room temperature methane conversion into various C1 oxygenates was experimentally achieved at Fe@N₄ sites.²³ Based on our current finding that Zn@N₂C and Zn@N₃ are more reactive (lower activation barriers) for the methane activation than Cu-zeolites and Fe@N₄, we expect that these M@N_xC_y catalysts will facilitate methane activation under milder conditions (e.g. T < 100 °C). Various M@N_xC_y catalysts have also been reported to be stable during the catalytic reaction at ∼100 °C. The alcohol oxidation at Co@N_x and Cu@N_x sites has been reported at 70–130 °C.^53–56 The Ru@N₄ (ref. 57) and Co@N_x (ref. 58 and 59) sites catalyzed selective hydrogenation at 100–110 °C. Thus, we expect that the suggested catalysts such as Zn@N₂C and Zn@N₃ will be durable under the experimental conditions.

3.6. Applying a new design strategy

Since our calculations verified that the slopes and intercepts of the linear scaling lines (i.e., activity) are determined by the CN of active sites, it is desirable to consider tuning the CN as well as E_f (or E_H). Based on the scaling relationship between E_f and E_H, the 2D-volcano plot can be reduced to a 1D-volcano plot by using one descriptor (G_f) (Fig. 6a). In the 1D-volcano plot, the scaling line of CN = 3 is in a higher reactivity region than that of CN = 4. For example, the log(rate) of the volcano top in the scaling line with CN = 3 is higher than that of CN = 4 by approximately 10. This result clearly indicates that lowering the CN which determines the kind of volcano is the primary factor before tuning the G_f. Such a suggestion correlates with the observation that all active sites identified in this study as well as prior work¹² in the higher-reactivity line have low CN. After choosing the suitable active site CN, the E_f of active sites can be tuned. For both scaling lines, the top of the 1D-volcano plot is then observed at G_f = 0 eV which is the optimal energetics. In the 1D-volcano plot using N₂O as an oxidant, we also found the same trend (Fig. S12†), indicating that the design strategy is applied oxidant-independently. Consequently, active sites with low CN and G_f = 0 eV are suggested to be optimal catalysts for methane activation.

In terms of the expansion of the porphyrin system having a dianionic N4 ligand motif, the synthesis and application of subphthalocyanine, subporphyrin, and triphyrin with planar triangular mono-anionic N3 ligands have recently been published.^62–64 Due to the fact that these N3 motifs are located in the delocalized π phyrin system, all of them can be expected to capably synthesize homogeneous M@N₃ counterpart catalysts, which can exhibit the same effects as the graphene-doped M@N₃ presented in this work. However, due to the formation of compounds with low CN, it possibly generates complexes with high CN as a result of dimerization or oligomerization. In addition, the generated M–O species can also react with C–H bond(s) present in a homogeneous catalyst rather than C–H bonds of methane. To overcome such limitations, one can consider heterogenization through grafting the homogeneous M@N₃ to the carriers or supports.

4. Conclusions

In this study, we suggest a rational design strategy of single atomic sites for methane activation based on the effect of coordination number (CN) on the scaling relationships. We considered 182 M@N_xC_y catalysts for C–H bond cleavage reactions of methane based on the *O formation energy (E_f) and its hydrogen binding affinity (E_H). The linear scaling relationship between E_f and E_H is not broken; however, we found that the linear scaling lines can be shifted by the CN so that the volcano plot can be moved up towards more reactive regions. Specifically, decreasing the CN moves the linear scaling lines towards a desired region for methane activation. The active sites of some superior catalysts found in this study and those previously reported in the experimental literature (e.g. Cu-zeolites) indeed have low coordination numbers. The BEP relationship between E_H and E_a(CH₄) is not significantly changed by the CN, while the BEP relationship between E_f and E_a(N₂O) is shifted by the CN. With the help of moved scaling lines, catalysts with lower CN could facilitate both *O formation and C–H dissociation. Based on this design guideline, several relatively stable catalysts are found promising for experimental verification. We expect that the shifted scaling relationships in undercoordinated active sites for higher reactivity could prove useful for further designing improved catalysts for methane activation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge generous support from the Korean Government through the National Research Foundation of Korea (NRF-2019M3D3A1A01069099) and supercomputing time from Korea Institute of Science and Technology Information (KISTI).

Notes and references

1. B. P. Center, Annual Energy Outlook, 2020.
2. B. Wang, S. Albarracín-Suazo, Y. Pagán-Torres and E. Nikolla, Catal. Today, 2017, 285, 147–158.
3. X. Meng, X. Cui, N. P. Rajan, L. Yu, D. Deng and X. Bao, Chem, 2019, 5, 2296–2325.
4. R. Balasubramanian, S. M. Smith, S. Rawat, L. A. Yatsunyk, T. L. Stemmler and A. C. Rosenzweig, Nature, 2010, 465, 115–119.
5. S. M. Smith, S. Rawat, J. Telser, B. M. Hoffman, T. L. Stemmler and A. C. Rosenzweig, Biochemistry, 2011, 50, 10231–10240.
6. J. C. Da Silva, R. C. Pennifold, J. N. Harvey and W. R. Rocha, Dalton Trans., 2016, 45, 2492–2504.
7. M. H. Groothaert, P. J. Smeets, B. F. Sels, P. A. Jacobs and R. A. Schoonheydt, J. Am. Chem. Soc., 2005, 127, 1394–1395.
8. V. L. Sushkevich, D. Palagin, M. Ranocchiari and J. A. van Bokhoven, Science, 2017, 356, 523–527.
9. J. S. Woertink, P. J. Smeets, M. H. Groothaert, M. A. Vance, B. F. Sels, R. A. Schoonheydt and E. I. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18908–18913.
10. P. Verma, K. D. Vogiatzis, N. Planas, J. Borycz, D. J. Xiao, J. R. Long, L. Gagliardi and D. G. Truhlar, J. Am. Chem. Soc., 2015, 137, 5770–5781.
11. D. J. Xiao, E. D. Bloch, J. A. Mason, W. L. Queen, M. R. Hudson, N. Planas, J. Borycz, A. L. Dzubak, P. Verma and K. Lee, Nat. Chem., 2014, 6, 590–595.
12. A. A. Latimer, A. R. Kulkarni, H. Aljama, J. H. Montoya, J. S. Yoo, C. Tsai, F. Abild-Pedersen, F. Studt and J. K. Nørskov, Nat. Mater., 2017, 16, 225–229.
13. A. S. Rosen, J. M. Notestein and R. Q. Snurr, ACS Catal., 2019, 9, 3576–3587.
14. T. Z. Gani and H. J. Kulik, ACS Catal., 2018, 8, 975–986.
15. G. Kumar, S. L. J. Lau, M. D. Krcha and M. J. Janik, ACS Catal., 2016, 6, 1812–1821.
16. F. Calle-Vallejo, D. Loffreda, M. T. Koper and P. Sautet, Nat. Chem., 2015, 7, 403–410.
17. X. Ma and H. Xin, Phys. Rev. Lett., 2017, 118, 036101.
18. F. Calle-Vallejo, J. Tymoczko, V. Colic, Q. H. Vu, M. D. Pohl, K. Morgenstern, D. Loffreda, P. Sautet, W. Schuhmann and A. S. Bandarenka, Science, 2015, 350, 185–189.
19. F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, P. Sautet and D. Loffreda, Angew. Chem., Int. Ed., 2014, 53, 8316–8319.
20. H. Xu, D. Cheng, D. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348.
21. C. Zhou, B. Zhang, P. Hu and H. Wang, Phys. Chem. Chem. Phys., 2020, 22, 1721–1726.
22. V. Fung, F. F. Tao and D.-e. Jiang, J. Phys. Chem. Lett., 2017, 8, 2206–2211.
23. X. Cui, H. Li, Y. Wang, Y. Hu, L. Hua, H. Li, X. Han, Q. Liu, F. Yang and L. He, Chem, 2018, 4, 1902–1910.
24. P. E. Blöchl, Physical Review B: Condensed Matter and Materials Physics, 1994, 50, 17953–17979.
25. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
26. G. Kresse and D. Joubert, Physical Review B: Condensed Matter and Materials Physics, 1999, 59, 1758–1775.
27. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
28. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104–154119.
29. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
30. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
31. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
32. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
33. M. W. Chase Jr, J. Phys. Chem. Ref. Data, Monogr., 1998, 9, 1–1951.
34. A. R. Kulkarni, Z.-J. Zhao, S. Siahrostami, J. K. Nørskov and F. Studt, ACS Catal., 2016, 6, 6531–6536.
35. M. H. Mahyuddin, T. Tanaka, Y. Shiota, A. Staykov and K. Yoshizawa, ACS Catal., 2018, 8, 1500–1509.
36. W. Zheng, J. Yang, H. Chen, Y. Hou, Q. Wang, M. Gu, F. He, Y. Xia, Z. Xia and Z. Li, Adv. Funct. Mater., 2020, 30, 1907658.
37. F. Li, G.-F. Han, H.-J. Noh, S.-J. Kim, Y. Lu, H. Y. Jeong, Z. Fu and J.-B. Baek, Energy Environ. Sci., 2018, 11, 2263–2269.
38. Y. Wang, X. Cui, J. Zhao, G. Jia, L. Gu, Q. Zhang, L. Meng, Z. Shi, L. Zheng and C. Wang, ACS Catal., 2018, 9, 336–344.
39. Z. Yang, B. Chen, W. Chen, Y. Qu, F. Zhou, C. Zhao, Q. Xu, Q. Zhang, X. Duan and Y. Wu, Nat. Commun., 2019, 10, 1–7.
40. Q. Fan, P. Hou, C. Choi, T. S. Wu, S. Hong, F. Li, Y. L. Soo, P. Kang, Y. Jung and Z. Sun, Adv. Energy Mater., 2020, 10, 1903068.
41. E. Jung, H. Shin, B.-H. Lee, V. Efremov, S. Lee, H. S. Lee, J. Kim, W. H. Antink, S. Park and K.-S. Lee, Nat. Mater., 2020, 19, 436–442.
42. J. Zhao, Q. Deng, S. M. Avdoshenko, L. Fu, J. Eckert and M. H. Rümmeli, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 15641–15646.
43. D. H. Lee, W. J. Lee, W. J. Lee, S. O. Kim and Y.-H. Kim, Phys. Rev. Lett., 2011, 106, 175502.
44. L. Han, S. Song, M. Liu, S. Yao, Z. Liang, H. Cheng, Z. Ren, W. Liu, R. Lin and G. Qi, J. Am. Chem. Soc., 2020, 142, 12563–12567.
45. C. Zhang, J. Sha, H. Fei, M. Liu, S. Yazdi, J. Zhang, Q. Zhong, X. Zou, N. Zhao and H. Yu, ACS Nano, 2017, 11, 6930–6941.
46. H. Tao, C. Choi, L.-X. Ding, Z. Jiang, Z. Han, M. Jia, Q. Fan, Y. Gao, H. Wang and A. W. Robertson, Chem, 2019, 5, 204–214.
47. X. Rozanska, E. V. Kondratenko and J. Sauer, J. Catal., 2008, 256, 84–94.
48. Z. Liang, T. Li, M. Kim, A. Asthagiri and J. F. Weaver, Science, 2017, 356, 299–303.
49. C.-C. Wang, S. S. Siao and J.-C. Jiang, J. Phys. Chem. C, 2012, 116, 6367–6370.
50. M. Kim, A. Franklin, R. Martin, F. Feng, T. Li, Z. Liang, A. Asthagiri and J. F. Weaver, J. Phys. Chem. C, 2019, 123, 27603–27614.
51. J. K. Nørskov, F. Studt, F. Abild-Pedersen and T. Bligaard, Fundamental concepts in heterogeneous catalysis, John Wiley & Sons, 2014.
52. J. Jang, G. H. Gu, J. Noh, J. Kim and Y. Jung, J. Am. Chem. Soc., 2020, 142, 18836–18843.
53. M. Li, S. Wu, X. Yang, J. Hu, L. Peng, L. Bai, Q. Huo and J. Guan, Appl. Catal., A, 2017, 543, 61–66.
54. X. Zhao, Y. Zhou, A.-L. Jin, K. Huang, F. Liu and D.-J. Tao, New J. Chem., 2018, 42, 15871–15878.
55. J. Xie, K. Yin, A. Serov, K. Artyushkova, H. N. Pham, X. Sang, R. R. Unocic, P. Atanassov, A. K. Datye and R. J. Davis, ChemSusChem, 2016, 10, 359–362.
56. L. Zhang, A. Wang, W. Wang, Y. Huang, X. Liu, S. Miao, J. Liu and T. Zhang, ACS Catal., 2015, 5, 6563–6572.
57. X. Wang, W. Chen, L. Zhang, T. Yao, W. Liu, Y. Lin, H. Ju, J. Dong, L. Zheng and W. Yan, J. Am. Chem. Soc., 2017, 139, 9419–9422.
58. P. Zhou, L. Jiang, F. Wang, K. Deng, K. Lv and Z. Zhang, Sci. Adv., 2017, 3, e1601945.
59. X. Sun, A. I. Olivos-Suarez, D. Osadchii, M. J. V. Romero, F. Kapteijn and J. Gascon, J. Catal., 2018, 357, 20–28.
60. Y. Chen, R. Guo, X. Peng, X. Wang, X. Liu, J. Ren, J. He, L. Zhuo, J. Sun, Y. Liu, Y. Wu and J. Luo, ACS Nano, 2020, 14, 6938–6946.
61. S. Grundner, M. A. Markovits, G. Li, M. Tromp, E. A. Pidko, E. J. Hensen, A. Jentys, M. Sanchez-Sanchez and J. A. Lercher, Nat. Commun., 2015, 6, 1–9.
62. A. Meller and A. Ossko, Monatsh. Chem., 1972, 103, 150–155.
63. Y. Inokuma, J. H. Kwon, T. K. Ahn, M. C. Yoo, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2006, 45, 961–964.
64. S. Shimizu, Chem. Rev., 2017, 117, 2730–2784.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc05632d

---