Defected vanadium bronzes as superb cathodes in aqueous zinc-ion batteries

Abstract

There is a growing need for fast, efficient, safe, and low-cost energy storage. Aqueous zinc-ion batteries (AZIBs) may be able to address this need, but suffer from fast capacity fade and poor ion diffusion kinetics due to unstable structures and non-optimised interspacing of layered cathode materials. Herein, we propose a structural engineering strategy by synergistically inducing anionic defects and cationic groups within vanadium bronze structures to improve kinetics and boost capacity. The materials discovered and used as the cathodes in AZIBs showed a high capacity of 435 mA h g⁻¹ at a current density of 0.2 A g⁻¹ and excellent stability with 95% capacity retention after 1500 cycles at 10 A g⁻¹. This combined experimental and computational study systemically indicated that rapid Zn²⁺ storage was achieved from both a highly porous structure and enlarged d-spacing combined with improved electron conductivity as determined by density of states calculations. The modification of vanadium bronze-type cathodes achieved by controlled pre-intercalated species and tailored oxygen deficiency opens up an avenue for the realization of superior material design, whose feasibility is proved in this work.

---

1. Introduction

The extensive concerns of limited resources, safety and the environmental issues of current energy storage techniques have fueled new research on sustainable battery revolution to satisfy the burgeoning global market.¹ Alkali metal batteries have achieved dramatic progress in improving safety through introducing all-solid-state^2,3 or water-in-salt electrolyte^4,5 concepts; however, their specific capacity still remains inadequate (<200 mA h g⁻¹) and technical issues such as poor ionic conductivity and high cost of concentrated metal salts limit their practical applications.^6–9 Aqueous zinc-ion batteries (AZIBs), a promising candidate for the next generation of energy storage devices, possess a high theoretical capacity of 820 mA h g⁻¹ based on zinc anodes and a suitable redox potential of −0.76 V vs. a standard hydrogen electrode (SHE), and have shown a competitive performance when utilizing mild aqueous electrolytes.^10,11 However, the challenge of designing suitable cathodes still remains because of the relatively large radius of intercalated hydrated Zn²⁺ and a strong electrostatic force between divalent Zn²⁺ and host structures.^12,13 To date, various types of cathodes have been developed for AZIBs such as Prussian blue analogs, manganese and vanadium oxide-based cathodes.¹⁴ Among them, vanadium-based cathodes exhibit a high theoretical capacity (>300 mA h g⁻¹) because of the active valence states of V (III to V) during the zinc (de)intercalation process.¹⁵ Additionally, the layered crystal structures of cathodes can offer two-dimensional open channels for fast ion diffusion,^16–18 which can be modified by the pre-intercalation of foreign cations, forming expanded interlayer spacing materials such as metal dichalcogenides,¹⁹ birnessite manganese oxides²⁰ and vanadium bronzes,²¹ thereby improving electrochemical properties.^22–24 Various attempts based on vanadium-based cathodes have been reported; the developed materials suffer from inadequate reversibility and rate performance due to the strong electrostatic-induced collapse and low electron conductivity of vanadium bronzes.²⁵ Meanwhile, notwithstanding the well-proven optimization of battery performance via cathode–electrolyte interfacial modification, widely observed in lithium-ion batteries,^26,27 similar investigations in AZIBs are still rather limited. In addition, introducing lattice water into vanadium-based cathodes for AZIBs has been intensively investigated to significantly reduce the effective charge of Zn²⁺ by forming a shield of hydroxyl groups or/and water molecules coordinated with the aqueous media. Thus, a lower activation energy is required for the interfacial transfer and less electrostatic interaction.^28–32 Likewise, there are few reported works on vanadium oxides, which suggested tailored electronic structures for facilitating mass transfer properties via the introduction of oxygen deficiencies.^33,34 Therefore, it is necessary to explore a general route for further boosting the energy storage properties of vanadium bronze structures by overcoming their inherent deficiencies and unravel their mechanism for unlocking their potential for practical applications.

Herein, we deliberately introduced rich defects, including oxygen deficiencies, foreign cations and lattice water, into the fluoride-etched porous vanadium pentoxide framework to form a distinct ammonium vanadium bronze associated with the NH₄V₄O₁₀ (NVO) structure and used this as a cathode for AZIBs. The tailored oxygen-deficient hydrated NH₄V₄O₁₀ (O_d-NVO·nH₂O) with a large specific surface area showed remarkable improvement in the Zn²⁺ diffusion kinetics and enlarged accessible sites for the inserted Zn²⁺. This benefits not only from a highly porous microstructure and a further expanded interlayer space for optimized interfacial properties compared with NVO, but also from enriched defects within the host framework for tuning the electronic structures and lowering the ionic diffusion energy barrier. Thus, the corresponding AZIBs show a specific capacity of 435 mA h g⁻¹ at a current density of 0.2 A g⁻¹ and 106.5% capacity retention after 1500 cycles under a current density of 10 A g⁻¹ (244 mA h g⁻¹ was attained compared to 229 mA h g⁻¹ at the 2^nd cycle). More impressively, the as-developed O_d-NVO·nH₂O improved the rate performance from 19% to 43% of capacity retention as the current density was increased 28 fold compared with the original NVO. A two-pronged mechanism of zinc (de)intercalation facilitated by both oxygen defects and interplanar engineering was carefully clarified by both experimental and computational approaches, which suggest a universal strategy for designing high-performance vanadium-based oxides. This also provides a deep insight for understanding the synergistic effect of both oxygen vacancies and NH₄⁺/H₂O “pillar” functionalities.

2. Results and discussion

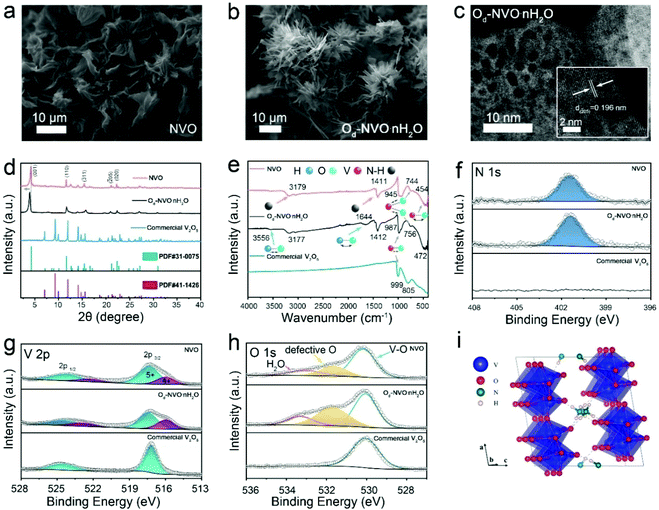
The synthesis of both NVO and O_d-NVO·nH₂O was achieved by a facile hydrothermal reaction (Experimental section). The increased amounts of oxalic acid and NH₄F were employed in the preparation of O_d-NVO·nH₂O, which generated distinct morphological changes from flower-like architectures to urchin-like nanoribbons compared with the as-obtained NVO, as shown by scanning electron microscopy (SEM) in Fig. 1a and b. Furthermore, in contrast to the observation by transmission electron microscopy (TEM) of NVO (Fig. S1†), the characterization showed a relatively porous microstructure with a clear lattice plane indexed to the (205) facet in the O_d-NVO·nH₂O material, as shown in Fig. 1c. The porosity is likely the result of enriched defects and etching of the microstructure through the synergy of reducing reagents and NH₄F as precursors.^35,36 For further evaluation of porosity in the as-prepared samples, BET measurement was carried out, which strongly verified a relatively larger specific surface area of 57.1 m² g⁻¹ in O_d-NVO·nH₂O compared with 20.6 m² g⁻¹ in NVO. In addition, the pore size distribution indicates that the majority of pore diameters were 2 nm, which corresponds well with the observations from the HRTEM image (Fig. S2†). As shown by X-ray diffraction (XRD) in Fig. 1d, the XRD pattern of NVO was indexed to the monoclinic crystalline phase of NH₄V₄O₁₀ (JCPDS: 31-0075) in the C₂/m space group, which was composed of the bilayers of V–O polyhedral stacking along the c-axis and pre-intercalated NH₄⁺ accommodated within the interplanar sites.³⁷ Similarly, O_d-NVO·nH₂O possesses the corresponding features of diffraction peaks but with a slight shift to lower 2θ values, as observed in the (001) facet (2θ = 3.905°), which suggests an expanded interlayer spacing along the c-axis of 10.4 Å compared with the as-prepared NVO (9.6 Å), according to Bragg's equation. Moreover, commercial V₂O₅ (JCPDS: 41-1426) was also adopted as a comparable material to explore the effects of pre-intercalated NH₄⁺ in V₂O₅ frameworks on the performance of AZIBs. Fig. 1e shows the Fourier-transform infrared spectra (FITR) of NVO, O_d-NVO·nH₂O and commercial V₂O₅, respectively. It can be clearly seen that the absorption bands of the materials have a series of similar vibrational modes, which can be assigned to the V–O bending, V–O–V stretching and V=O stretching at the wavenumbers of 472 cm⁻¹ (454 cm⁻¹), 756 cm⁻¹ (744 cm⁻¹) and 987 cm⁻¹ (945 cm⁻¹) for O_d-NVO·nH₂O (and NVO), respectively.^38,39 A slight red shift of the characteristic FTIR bands at the V=O stretching mode in the as-prepared samples compared with commercial V₂O₅ could be attributed to the pre-intercalated species bonded with apical oxygen in VO_x polymorphs. The result corresponds to the observation of the linear expansion of (001) d-spacing in the XRD results, and agrees with the previously reported work on Li⁺ pre-intercalated V₂O₅.⁴⁰ In particular, the bands at around 1412 and 3177 cm⁻¹ conform to the symmetric bending and asymmetric stretching modes of N–H, respectively,³⁷ which confirms that NH₄⁺ exists in both NVO and O_d-NVO·nH₂O materials. Moreover, it is seen that there are two distinct bands at 1644 and 3556 cm⁻¹ corresponding to the bending and stretching modes of H–O, respectively,⁴¹ which indicates the presence of H₂O in O_d-NVO·nH₂O. Thermogravimetric analysis (TGA) was carried out to evaluate the mass loss during the elevation of temperature. It needs to be emphasized that the partial NH₄⁺ species could also escape from the framework accompanied with the water. Therefore, it is difficult to determine the actual amount of water content from the TGA measurement. However, the plot in Fig. S3† shows a greater weight loss in the O_d-NVO·nH₂O sample compared with NVO. Further confirmation of NH₄⁺ is provided by the presence of N via X-ray photoelectron spectroscopy (XPS), which is shown in Fig. 1f, wherein a clear N 1s core-level spectrum for both NVO and O_d-NVO·nH₂O materials is observed. For a quantitative analysis of N elemental concentration in the as-prepared materials, relative sensitivity factors were used to calculate the varying amounts of NH₄⁺ species, interpreted as a ratio of N : V, which was 1 : 3.94 for NVO and 1 : 3.9 for O_d-NVO·nH₂O, suggesting a negligible change in N concentration through the specific modification. In addition, the V 2p core-level spectrum next to the N 1s spectrum shows mixed oxidation states of V compared with that in commercial V₂O₅ (Fig. 1g), which indicates that a partial reduction of V⁵⁺ species has occurred when extraneous cations were introduced into the V₂O₅ frameworks. More specifically, the peaks with a binding energy of 517.3 ± 0.2 eV in all three materials refer to V⁵⁺ 2p_3/2, while a lower binding energy of 516.1 eV was assigned to V⁴⁺ 2p_3/2 and only observed in NVO and O_d-NVO·nH₂O. The same results of mixed valence states can also be found in other reported works on pre-intercalated vanadium oxides.^42–44 Furthermore, proportion calculations of varied V species peak areas indicate that the average oxidation states were V^4.65+ and V^4.74+ for O_d-NVO·nH₂O and NVO, respectively. The relatively lower valence state of V species in O_d-NVO·nH₂O was anticipated since more reducing reagents were used in the preparation process, resulting in oxygen deficiency-induced reduction of V oxidation states, which is discussed in the DFT analysis (vide infra). Fig. 1h shows the O 1s core-level spectrum of all materials. It is noteworthy that important defective oxygen species peak in both O_d-NVO·nH₂O and NVO with a binding energy of 531.6 eV, which is in good agreement with previous reports of oxygen defects in vanadium oxide-based materials.^45–48 Moreover, the proportion of defective oxygen concentration in O_d-NVO·nH₂O was much higher than that in NVO, which can be simplified by comparing the ratio between two oxygen species peak areas within the O 1s spectrum (O_d : O_V is 27 : 73 for NVO and 43 : 57 for O_d-NVO, respectively). Further evidence of existing oxygen deficiency was verified by electron paramagnetic resonance (EPR; Fig. S4a†), which showed a signal at g ≈1.98 assigned to the unsaturated oxygen species (oxygen vacancies) in the spectrum. It should be noted that there was no trace of F⁻ species observed from both XPS survey and core level of F 1s spectra in O_d-NVO·nH₂O (Fig. S4b and c†). However, the addition of NH₄F is crucial not only for producing a highly porous microstructure, but also for adjusting an appropriate pH value and concentration of vanadyl species in aqueous solution during the preparation process (Fig. S5†). As a consequence, it can be seen that some impurity phases can be evidently distinguished from the XRD of a control sample of O_d-NVO·nH₂O without the addition of NH₄F in the preparation process (Fig. S6†). At this stage note that the partial occupancy of N sites results in many potential geometry structures of NVO. Subsequently, a 1 × 3 × 1 supercell of NVO was built to eliminate interactions between images for DFT calculations. We calculated the total energies of the different configurations of NH₄V₄O₁₀, and the structure with the lowest total energy is shown in Fig. 1i. Three NH₄⁺ form the N–H⋯O hydrogen bonds with the adjacent O atom. Among them, two NH₄⁺ are close to each other, while the third one is far away from them. All three NH₄⁺ locate on different sites, but they are close to each other along the (010) orientation (more discussion is provided in the DFT section).

Fig. 1 SEM images of (a) NVO and (b) O_d-NVO·nH₂O; (c) HRTEM of the as-obtained O_d-NVO·nH₂O; (d) XRD patterns and (e) FTIR spectra of NVO, O_d-NVO·nH₂O and commercial V₂O₅; XPS spectra of the (f) N 1s region, (g) V 2p region and (h) O 1s region in NVO, O_d-NVO·nH₂O and commercial V₂O₅, respectively; (i) the most stable geometry of the NH₄V₄O₁₀ supercell calculated by the GGA+U functional.

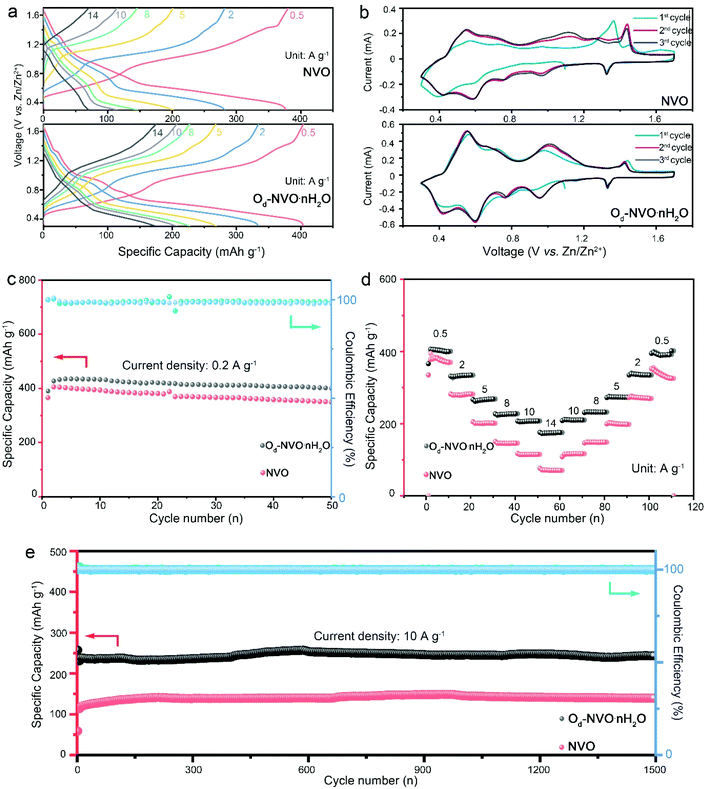
The as-obtained NVO, O_d-NVO·nH₂O and commercial V₂O₅ were assembled for the battery performance evaluation in coin cell configurations. Fig. 2a shows the galvanostatic charge/discharge (GCD) profiles of NVO and O_d-NVO·nH₂O under varying applied current densities from 0.5 to 14 A g⁻¹. It is clear that the distinct plateaus in the charge/discharge process can be distinguished in accordance with multiple redox couples of cyclic voltammetry (CV) curves for different anionic/cathodic reactions (Fig. 2b). Additionally, a distinct electrochemical reaction behavior can be discerned through comparing the GCD profiles and steady changes of CV profiles in the first three cycles of the batteries, which indicates a relatively larger specific capacity and higher reversibility of Zn²⁺ intercalation/extraction achieved in O_d-NVO·nH₂O compared to NVO. In contrast, the CV profile of commercial V₂O₅ shows a dominant anodic peak at around 1.3 V, indicating a different electrochemical process during Zn²⁺ insertion/extraction (Fig. S7†). A further investigation of long cycle measurements under a low current density of 0.2 mA g⁻¹ also exhibited a better performance of O_d-NVO·nH₂O with a maximum specific capacity of 435 mA h g⁻¹ compared with 405 mA h g⁻¹ of NVO. Moreover, the cycling stability of O_d-NVO·nH₂O shows a 92% capacity retention after 50 cycles of the charge/discharge process with a corresponding coulombic efficiency (CE) over 99%. In contrast, there was 14% decay of capacity in NVO under identical conditions. Comparatively, the battery using commercial V₂O₅ as the cathode material underwent a long activation process with a gradual increase of specific capacity from an initial capacity of 109 mA h g⁻¹ to 256 mA h g⁻¹ after 25 cycles (Fig. S7a†). This can be explained via sluggish zinc intercalation kinetics in the commercial V₂O₅ electrode existing due to the inadequate interlayer space and shortage of “lubricants” (lattice water/NH₄⁺).^23,49 The rate performance was evaluated by a stepwise increase in current densities from 0.5 to 14 A g⁻¹ and returning to 0.5 A g⁻¹ with 10 cycles at each current density, respectively. Impressively, O_d-NVO·nH₂O exhibited superior rate capability in Fig. 2d and reversibility with a capacity of 406 mA h g⁻¹ at 0.5 A g⁻¹ in the initial first 10 cycles and 175 mA h g⁻¹ at 14 A g⁻¹, which can be calculated as 43% capacity retention after 28-fold increase of current densities. Additionally, upon returning to 0.5 A g⁻¹, the capacity remains 401 mA h g⁻¹, suggesting a much more robust reversibility compared with many reported vanadium-based cathodes which showed a significant decay after rate cycling tests.^50–54 In contrast, NVO shows inferior rate performance with a capacity of 382 mA h g⁻¹ at 0.5 A g⁻¹ and 71 mA h g⁻¹ at 14 A g⁻¹. Thus, there is only 19% capacity retention, revealing a relatively larger energy barrier, thus inhibiting fast Zn²⁺ diffusion. Similarly, an unfavorable rate performance of commercial V₂O₅ can be observed in Fig. S7b,† showing that the cell suffers from both low capacity and long activation process. In addition, after 1500 cycling measurements for both NVO and O_d-NVO·nH₂O cells under a current density of 10 A g⁻¹, the high reversibility with outstanding capacity retention, as shown in Fig. 2e, was verified. Both NVO and O_d-NVO·nH₂O showed negligible capacity fading with a clear determination of a specific capacity of 244 mA h g⁻¹ at the 1500^th cycle compared with 229 mA h g⁻¹ at the 2^nd cycle for O_d-NVO·nH₂O cells. Comparatively, 138 mA h g⁻¹ and 100 mA h g⁻¹ was observed for the 1500^th cycle and 2^nd cycle, respectively, for NVO cells. Moreover, a much longer period of activation cycling behavior and low capacity performance were observed for the commercial V₂O₅ cell under 5 A g⁻¹ for 1500 cycles (Fig. S7c†). The above results imply that the O_d-NVO·nH₂O electrode possesses improved reversibility and superior specific capacity, which was observed under high current densities during the charge/discharge process. This can be interpreted as facilitating Zn²⁺ diffusion kinetics due to the tailored porous structure and lattice defects. Meanwhile, the introduction of lattice water and NH₄⁺ not only offers a charge shielding screen to smoothen the electrostatic interaction between V₂O₅ sheets and guest Zn²⁺, but also contributes to the enlargement of the bilayer and inhibition of “lattice breathing”.^23,55 The Ragone plot (Fig. S8†) shows a high energy density of 288 W h kg⁻¹ and an outstanding power density of 358 W kg⁻¹ for the O_d-NVO·nH₂O electrode, which is superior to previously studied cathodes such as Ca_0.25V₂O₅·nH₂O (267 W h kg⁻¹),⁵⁶ Zn_0.25V₂O₅·nH₂O (250 W h kg⁻¹),⁴³ Zn₂V₂O₇ (166 W h kg⁻¹),⁵⁷ Zn₃V₂O₇(OH)₂·2H₂O (214 W h kg⁻¹),⁵⁸ Na₃V₂(PO4)₂F₃@C (97.5 W h kg⁻¹)⁵⁹ and K₂V₈O₂₁ (222.3 W h kg⁻¹).⁶⁰

Fig. 2 (a) Galvanostatic charge/discharge profiles of NVO and O_d-NVO·nH₂O cathodes at different current densities; (b) cyclic voltammetry plots of NVO and O_d-NVO·nH₂O at a scan rate of 0.2 mV s⁻¹ for the first three cycles; (c) long-cycle charge/discharge measurements of NVO and O_d-NVO·nH₂O cells under a current density of 0.2 A g⁻¹; (d) rate performance evaluations of NVO and O_d-NVO·nH₂O cells; (e) long cycling stability of NVO and O_d-NVO·nH₂O cells under a current density of 10 A g⁻¹.

To investigate the inherent cycle-dependent ion transport properties within the as-developed electrodes, electrochemical impedance spectroscopy (EIS) was carried out to determine the purely Ohmic resistance (R_s) and charge transfer resistance (R_ct) for both initial and after cycling states. The analysis of EIS is plotted in Fig. S9† and the summarized results revealed that both NVO and O_d-NVO·nH₂O possessed relatively lower R_s (0.64 Ω and 0.68 Ω for NVO and O_d-NVO·nH₂O, respectively, Table S1†) compared with that of commercial V₂O₅ (R_s = 1.93 Ω). Meanwhile, the R_ct of O_d-NVO·nH₂O (R_ct = 33.4 Ω) at the initial state demonstrated a much improved charge transport behavior between the electrode and electrolyte compared with assembled NVO (R_ct = 128.8 Ω) and V₂O₅ cells (R_ct = 186.2 Ω) measured under identical conditions, which verifies a dramatically enhanced interfacial engineering of the O_d-NVO·nH₂O materials. Moreover, the R_ct of O_d-NVO·nH₂O (22.5 Ω) was still much smaller than those of both NVO and commercial V₂O₅ (NVO: R_ct = 52.6 Ω, commercial V₂O₅: R_ct = 128.8 Ω) after cycling, which confirms the excellent ionic diffusion kinetics and electrochemical properties resulting from the different types of defects and pre-intercalated guest species. Additionally, evaluation of capacity contributions derived from capacitive and diffusion behaviors was investigated for NVO and O_d-NVO·nH₂O materials, respectively, as shown in Fig. S10.† The quantified CV profile (Fig. S10a and b†) clearly indicated that there is 74% capacitive contribution among all the current responses at a scan rate of 0.5 mV s⁻¹ in O_d-NVO·nH₂O, which is much higher than that in NVO (43%) under the same sweep rate (Fig. S10c and d†). Similarly, a growing fraction of capacitive contribution can be observed as the sweep rates are increased from 0.1 to 1 mV s⁻¹ in both electrodes. Therefore, the predominantly capacitive controlled behaviors of O_d-NVO·nH₂O are responsible for its high-rate capability. Further analysis of CV profiles was carried out using the following equation:⁶¹

i = aν^b

The above equation can be rewritten as log(i) = b log(ν) + log(a), and is used to describe the relationship between the measured peak current (i) and the sweep rate (v) from CV plots. In particular, the coefficient b shows capacitive response if the value = 1, whereas an absolute diffusion-controlled kinetics is verified when the b value is equal to 0.5, corresponding to the faradaic (de)intercalation.⁶² Therefore, for both materials, three pairs of redox peaks were calculated, as shown in Fig. S11;† the b values of 0.71, 1.01, 1.04, 0.88, 0.76 and 0.75 were found in O_d-NVO·nH₂O implying that a surface-controlled capacitive behavior prevailed, whereas relatively lower b values of 0.33, 0.98, 0.92, 0.62, 0.77 and 0.71 correspond mainly to diffusion-controlled redox reactions in NVO electrodes. Moreover, the overpotential gaps of O_d-NVO·nH₂O between A1(2) and C1(2) redox pairs at each scan rate were smaller than those in NVO, which was attributed to a relatively weaker polarization along with a boosted Zn²⁺ insertion/extraction process in O_d-NVO·nH₂O. In addition to the CV analysis of the as-fabricated batteries, the galvanostatic intermittent titration technique (GITT) measurement was utilized to acquire Zn²⁺ diffusion coefficients to strengthen the proof of improved kinetics from the multiscale optimizations in O_d-NVO·nH₂O. The calculated Dzn²⁺ during the charge/discharge process at each state of zinc extraction/insertion states are shown in Fig. S12,† which clearly indicate that the Dzn²⁺ of O_d-NVO·nH₂O (10⁻⁸–10⁻⁹ cm² s⁻¹) are higher than those observed in NVO (10⁻⁹–10⁻¹⁰ cm² s⁻¹). Thus, by determining the kinetic behaviors from the CV analysis, the large proportion of pseudocapacitive behaviors of O_d-NVO·nH₂O effectively demonstrates the feasibility of a promising strategy for improving the rate performance and reversibility of cathodes in AZIBs.

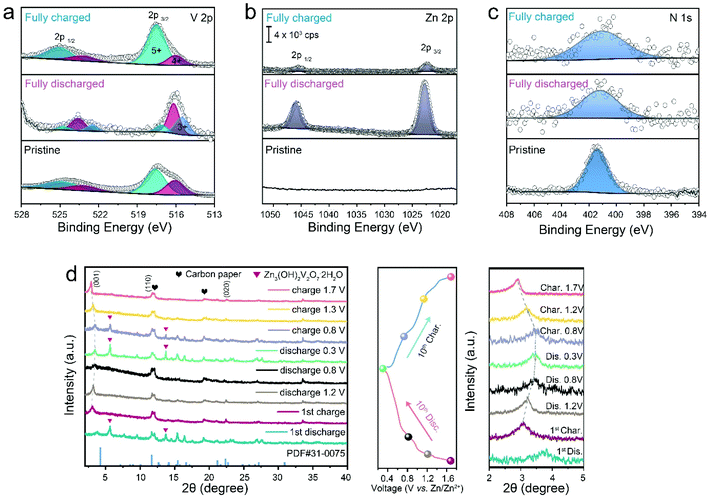
The highly reversible zinc (de)intercalation process in terms of crystal structures and chemical states of O_d-NVO·nH₂O materials was evaluated at varying charge/discharge states via ex situ XPS and XRD. Fig. 3a shows an obvious reduction of valence states in fully discharged O_d-NVO·nH₂O electrodes through an observation of newly emerging V³⁺ (2p_3/2: 515.5 eV) and intensified V⁴⁺ (2p_3/2: 516.2 eV) components. However, the hybrid V species recovered to their original states and were slightly more oxidative for fully charged O_d-NVO·nH₂O electrodes. The related phenomena are in good accordance with previously reported vanadium-based cathode materials.^42,43 In addition, the core-level spectrum of Zn 2p in Fig. 3b clearly shows that no zinc signal was observed in the pristine cathode, while a substantive peak (2p _3/2: 1022.8 eV) in the Zn 2p spectrum was found in the fully discharged electrode, indicating the intercalation of Zn²⁺ into the cathodes. After the charge process, the majority of Zn 2p species were deintercalated from O_d-NVO·nH₂O, which presents a pair of subtle peaks related to the Zn 2p sites, consistent with previous studies.⁶³Fig. 3c confirms that the NH⁴⁺ species always exist in the cathodes at the same peak position (1s: 401.5 eV) regardless of different states of charge/discharge, which illustrates a stable structural support within the bilayers of the VO_x polyhedral network. As a result, the reversible chemical states and anchored NH₄⁺ “pillar” of O_d-NVO·nH₂O materials under different conditions validated by ex situ XPS suggest robust electrochemical properties during the Zn²⁺ insertion/extraction process.

Fig. 3 Ex situ XPS spectra of (a) V 2p, (b) Zn 2p and (c) N 1s at initial, charge/discharge states of the O_d-NVO·nH₂O electrode, respectively; (d) XRD patterns of the O_d-NVO·nH₂O electrode measured under different charge/discharge states in both 1^st and 10^th cycles.

After clarifying various chemical states during the Zn²⁺ insertion/extraction processes, ex situ XRD was employed to investigate the crystal phase evolution of O_d-NVO·nH₂O under different charge/discharge states. Fig. 3d shows the ex situ characterized XRD pattern of the O_d-NVO·nH₂O cathode at both 1^st and 10^th cycles at 0.5 A g⁻¹ with various charge/discharge states according to the plateaus in the GCD curves. It is noteworthy that there is a second reversible phase of Zn₃V₂O₇(OH)₂·2H₂O (JCPDS no. 87-0417, space group: P3̄m1) appearing only in the 1^st and 10^th discharged states, and likewise observed as weakened diffraction peaks in subsequently multi-cycled electrodes charged at 0.8 V, which has also been widely identified in previous studies of K₂V₈O₂₁,⁶⁰ V₆O₁₃·nH₂O³⁰ and Cu_0.1V₂O₅·0.08H₂O.⁴² Additionally, it is seen that the (001) reflection sites (shown in a magnified 2θ region from 2° to 5°) showed an evidently steady shift to a higher 2θ value referring to a contraction of d-spacing from 13.1 to 10.7 Å from an initial charged state to a fully discharged state at the 10^th cycle. In contrast, the interlayer space expands back to lower 2θ and hence suggests a reduced electrostatic interaction within the bilayers because of the extraction of Zn²⁺.⁴³ Hence, the reversible phase changes in the O_d-NVO·nH₂O cathode further validate a robust cycling performance and bring an insight into the zinc storage mechanism from the perspective of its phase evolution.

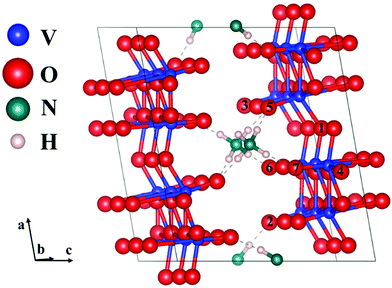
To understand the structural difference between O_d-NVO·nH₂O and NVO, DFT simulations were adopted to elucidate the formation and relevant properties of oxygen point vacancies in NVO, and the electrostatic interactions of Zn²⁺ with oxygen ions. For NH₄V₄O₁₀, one oxygen was removed from the 1 × 3 × 1 supercell ((NH₄)₃V₂₄O₆₀) to model oxygen point vacancies.

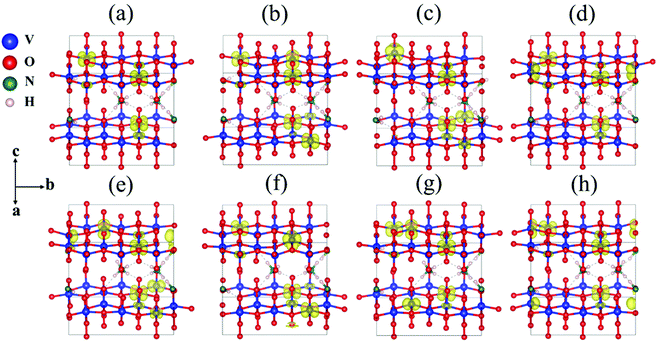
As the interaction (hydrogen bonds) between NH₄⁺ and oxygen is weak compared to chemical bonds, we chose different oxygens with different coordination numbers and these form hydrogen bonds with NH₄⁺ for defect calculations. These oxygens are shown in Fig. 4. The formation energy of oxygen point vacancies was calculated and is listed in Table 1, according to the equation:

E_f = E_{(NVO (VO))} + 1/2E_(O2) − E_(NVO) (1)

where E_f is the formation energy of oxygen vacancy defects in the NVO supercell, E_(O2) is the energy of oxygen molecules, and E_{(NVO (VO))} and E_(NVO) are the energies of NVO with or without oxygen vacancies.

Fig. 4 The most stable geometry structure of the 1 × 3 × 1 NH₄V₄O₁₀ supercell with labelling of different oxygens. O1 is the two-coordinated oxygen and O3 only bonds with one vanadium. O4 is the three-coordinated oxygen. O2, O5, O6, and O7 have additional hydrogen bonds with NH₄⁺.

Table 1 The formation energies of different oxygen point vacancies calculated by the GGA+U functional

Label	Formation energy (eV)
O1	1.89
O2	2.37
O3	2.49
O4	2.03
O5	2.53
O6	1.81
O7	1.83

---

The formation energies range from 1.81 to 2.53 eV, which indicates that the formation process of oxygen point vacancies was endothermic. The lowest formation energy corresponding to the removal of O6 is 1.81 eV. For O7, O1, and O4 sites, the values are 1.83, 1.89, and 2.03 eV, respectively. These values are close to that of the O6 site. The O6 site has one-coordinated vanadium and one hydrogen bond. The coordination environment of O7 is similar to that of O6, but it is close to another NH₄⁺. The O1 site is coordinated with two vanadium ions. As the similarity of coordination number and local environments is low for each structure, we calculated the projected density of states (PDOS) and the total density of states (TDOS) of perfect NVO and NVO with different oxygen point vacancies to identify the fundamentals of the low defect formation energy.

As electrons are liberated when an oxygen vacancy is formed, NVO presents n-type characteristics with oxygen point vacancies. As shown in Fig. 5b, the defect states (gap states) of NVO with O6 site vacancies are closer to the Fermi level than perfect NVO (Fig. 5a). The defect states (donor) of the defective NVO located nearer the conduction band minimum (CBM) compared to the perfect NVO make it easier for electrons to be excited into the conduction band from the donor level, which increases the electronic conductivity of NVO with oxygen vacancies. Fig. S13† shows that the remaining TDOS of O1, O4, and O7 sites also have two peaks (defect states) at around −1 to 0 eV below the Fermi level. The average defect formation energy for those with more peaks below the Fermi level is 1.89 eV, while the average defect formation energy for the remaining oxygen point vacancies (only show one peak at around 0.5 eV) is 2.46 eV. The gap in value is 0.57 eV. When O1, O4, O6, and O7 are extracted, the TDOS indicates that more vanadium ions are reduced. We also calculated the corresponding spin densities for perfect NVO and reduced NVO with an oxygen vacancy at the O1, O2, O3, O4, O5, O6, and O7 sites to verify our explanation, as shown in Fig. 6. When the spin density of perfect NVO is used as a reference, it is clear that the oxygen point vacancies of O1, O4, O6, and O7 sites could produce more localized electrons than the O2, O3 and O5 sites. These oxygen point vacancies yield localized electrons on the additional two vanadium sites neighboring the vacancy than perfect NVO, while there is only one vanadium with localized electrons for O2, O3, and O5 sites compared with perfect NVO. In summary, when oxygen point vacancies are formed, these localized electrons stabilize the system and make the total energy decrease. The O6 vacancy is the most stable oxygen point vacancy because it produces more localized electrons around it and hence the most likely to take part in the reduction of NVO. The formation of oxygen point vacancy in NVO decreases the potential electrostatic attraction with Zn²⁺. On the other hand, due to the strong electrostatic interaction of Zn²⁺, the accumulation of localized electrons also forcefully facilitates the reversible Zn²⁺ de-intercalation with thermoneutral Gibbs free energy.³³ Eventually, these two factors effectively increase the reversibility of the Zn²⁺ insertion/extraction processes and thus enhance the capacity and rate performance. Therefore, the corresponding DFT results convincingly confirmed the observations that oxygen vacancies in NVO are beneficial for Zn-ion storage.

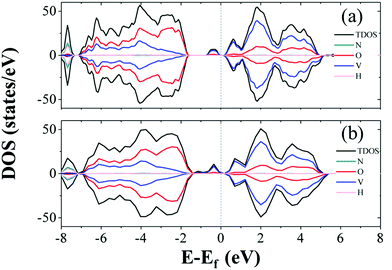Fig. 5 The projected density of states (PDOS) and the total density of states (TDOS) of (a) perfect NVO and NVO with oxygen point vacancy of (b) O6. The dotted lines denote the Fermi levels.

Fig. 6 Spin densities for (a) perfect NVO and reduced NVO with an oxygen vacancy at (b) O1, (c) O2, (d) O3, (e) O4, (f) O5, (g) O6 and (h) O7 sites. The isosurface shown is set at 0.01 electrons per ų.

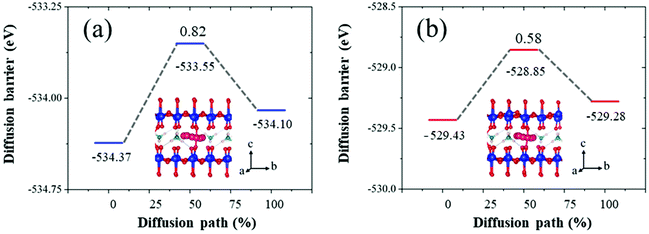
Additionally, to investigate the effect of an oxygen vacancy in NVO on ion transport performance, the minimum energy migration pathways and barriers for Zn ions with both perfect and defective NVO were investigated using the CI-NEB method.⁶⁴ A previous study of NVO found that the diffusion process along the 001 orientation has an extremely high energy barrier of 2.89 eV.⁶⁵ Therefore, here the most stable and the metastable insertion sites of Zn ions were chosen for the diffusion pathway along the 010 orientation, and the specific structures are shown in Fig. S14.† The insertion energy of Zn ions in perfect and defective NVO was calculated and used to determine the most and metastable insertion sites as follows:

E_in = E_NVO-Zn − E_NVO − E_Zn (2)

where E_in is the insertion energy of Zn ions, E_NVO-Zn is the total energy of perfect and defective NVO with the insertion of Zn ions, E_NVO is the total energy of perfect and defective NVO and E_Zn is the energy of bulk Zn.

In Table 2, the defect site in defective NVO means that the insertion site is close to the oxygen vacancy, and the insertion site of 4 in perfect NVO is similar to the defect site. Upon comparing the insertion energies of Zn ions of these insertion sites in perfect and defective NVO, we found that the oxygen vacancy is favorable for the insertion of Zn ions with a lower insertion energy during the intercalation process and the highest value of reduction reaches up to 0.13 eV. This is in agreement with a previous study that it is beneficial for the diffusion process for a more smooth potential energy surface.³³ Subsequently, the corresponding minimum energy migration pathways prove this in Fig. 7. The diffusion barrier in perfect NVO is 0.82 eV, while the diffusion barrier in defective NVO is 0.58 eV. The introduction of an oxygen vacancy significantly decreases the diffusion barrier of Zn ions in defective NVO.

Fig. 7 The diffusion barrier and minimum energy migration pathway of Zn ions in (a) perfect NVO and (b) defective NVO. The blue, red, green, fuchsia and light pink spheres represent V, O, N, Zn, and H, respectively.

Table 2 The insertion energy (E_in) of Zn ions of the most stable, metastable, and those near defect sites in perfect and defective NVO

Label	E in (eV)	Label	E in (eV)
Perfect NVO		Defective NVO
4	1.17	Defect site	1.10
5	0.71	5	0.70
6	0.98	6	0.85

---

3. Conclusion

Through defect engineering by inducing cations, interlayer water and anionic vacancies within vanadium bronze materials, we successfully delivered a proof-of-concept demonstration on designing high-performance cathode materials for AZIBs. The tailored O_d-NVO·nH₂O cathode achieved a high specific capacity of 435 mA h g⁻¹ at 0.2 A g⁻¹, and 244 mA h g⁻¹ at 10 A g⁻¹ after 1500 cycles with a negligible capacity decay. In particular, an extraordinary rate capability of 43% capacity retention after a 28-fold increase of current densities from 0.5 A g⁻¹ to 14 A g⁻¹ was attained. Additionally, the corresponding electrochemical properties were comprehensively evaluated by ex situ characterization and DFT simulations, which revealed encouraging Zn²⁺ kinetics and superior reversibility embodied with a transformation of capacitive-dominated energy storage behavior compared with pristine NVO cathodes. Indeed, the DFT results adequately elaborated different possibilities for oxygen-deficient sites and their contributions to facilitate Zn²⁺ diffusion properties. Meanwhile, the calculated density of states also suggested improved conductivity for O_d-NVO·nH₂O. Hence, inducing multitype defects offers a feasible avenue to regulate the electronic structures and microstructures of vanadium-based cathodes towards advanced energy storage applications.

Authors contribution

G.C., G.H., I.P.P. and J.L. designed the project; J.L. and F.W. performed the materials synthesis; J.L. tested the battery performance; N.L. carried out DFT calculations; S.Z. and J.G. performed materials characterization; J.L., Z.L., W.L., P.R.S., D.J.L.B. and C.J.C. conducted the data analysis; G.C., G.H. and I.P.P. directed the project; J.L., G.C., and G.H. co-wrote the paper and all authors contributed to the revision of the draft.

Conflicts of interest

There is no conflicts of interest.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 21703248 and 51602193), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB20000000), the Engineering and Physical Sciences Research Council (EPSRC, EP/L015862/1, EP/R023581/1), the STFC Batteries Network (ST/R006873/1) and the Shanghai “Chen Guang” Project (16CG63).

References

1. N. Günter and A. Marinopoulos, J. Energy Storage, 2016, 8, 226–234.
2. F. Zheng, M. Kotobuki, S. Song, M. O. Lai and L. Lu, J. Power Sources, 2018, 389, 198–213.
3. Y. Gong, K. Fu, S. Xu, J. Dai, T. R. Hamann, L. Zhang, G. T. Hitz, Z. Fu, Z. Ma, D. W. Mcowen, X. Han, L. Hu and E. D. Wachsman, Mater. Today, 2018, 21, 594–601.
4. B. Safe, L. Suo, O. Borodin, Y. Wang, X. Rong, W. Sun, X. Fan, S. Xu, M. A. Schroeder, A. V. Cresce, F. Wang, C. Yang, Y. Hu, K. Xu and C. Wang, Adv. Energy Mater., 2017, 7, 1701189.
5. M. R. Lukatskaya, J. I. Feldblyum and D. G. Mackanic, Energy Environ. Sci., 2018, 11, 2876–2883.
6. J. Gon, B. Son, S. Mukherjee, N. Schuppert, A. Bates, O. Kwon, M. Jong, H. Yeol and S. Park, J. Power Sources, 2015, 282, 299–322.
7. C. Sun, J. Liu, Y. Gong, D. P. Wilkinson and J. Zhang, Nano Energy, 2017, 33, 363–386.
8. L. Suo, O. Borodin, W. Sun, X. Fan, C. Yang, F. Wang, T. Gao, Z. Ma, M. Schroeder, A. Von Cresce, S. M. Russell, M. Armand, A. Angell, K. Xu and C. Wang, Angew. Chem., 2016, 85287, 7136–7141.
9. H. Chen, Z. Zhang, Z. Wei, G. Chen, X. Yang, C. Wang and F. Du, Sustainable Energy Fuels, 2020, 4, 128–131.
10. F. Wang, O. Borodin, T. Gao, X. Fan, W. Sun, F. Han, A. Faraone, J. A. Dura, K. Xu and C. Wang, Nat. Mater., 2018, 17, 543–549.
11. M. Song, H. Tan, D. Chao and H. J. Fan, Adv. Funct. Mater., 2018, 28, 1–27.
12. J. Ming, J. Guo, C. Xia, W. Wang and H. N. Alshareef, Mater. Sci. Eng., R, 2019, 135, 58–84.
13. C. Li, X. Zhang, W. He, G. Xu and R. Sun, J. Power Sources, 2020, 449, 227596.
14. W. Xu and Y. Wang, Nano-Micro Lett., 2019, 11, 90.
15. B. Tang, L. Shan, S. Liang and J. Zhou, Energy Environ. Sci., 2019, 12, 3288–3304.
16. D. Xiong, X. Li, Z. Bai and S. Lu, Small, 2018, 14, 1703419.
17. L. Peng, Y. Zhu, D. Chen, R. S. Ruoff and G. Yu, Adv. Energy Mater., 2016, 6, 1600025.
18. J. Zhao, H. Ren, Q. Liang, D. Yuan, S. Xi, C. Wu, W. Manalastas, J. Ma, W. Fang, Y. Zheng, C. Du, M. Srinivasan and Q. Yan, Nano Energy, 2019, 62, 94–102.
19. K. D. Rasamani, F. Alimohammadi and Y. Sun, Mater. Today, 2017, 20, 83–91.
20. X. Sun, V. Du, B. L. Mehdi, N. D. Browning and L. F. Nazar, Chem. Mater., 2016, 28, 534–542.
21. J. L. Andrews, S. Singh, C. Kilcoyne, P. J. Shamberger, G. Sambandamurthy and S. Banerjee, MRS Commun., 2017, 7, 634–641.
22. D. Selvakumaran, A. Pan, S. Liang and G. Cao, J. Mater. Chem. A, 2019, 7, 18209–18236.
23. X. Yao, Y. Zhao, F. A. Castro and L. Mai, ACS Energy Lett., 2019, 4, 771–778.
24. J. Li, K. McColl, X. Lu, S. Sathasivam, H. Dong, L. Kang, Z. Li, S. Zhao, A. G. Kafizas, R. Wang, D. J. L. Brett, P. R. Shearing, F. Corà, G. He, C. J. Carmalt and I. P. Parkin, Adv. Energy Mater., 2020, 10, 2000058.
25. J. Zhou, L. Shan, Z. Wu, X. Guo, G. Fang and S. Liang, Chem. Commun., 2018, 54, 4457–4460.
26. H. Maleki, K. Sari and X. Li, Adv. Energy Mater., 2019, 9, 1901597.
27. D. Li, S. Lu, A. Koo, K. Adair and X. Sun, Nano Energy, 2018, 44, 111–120.
28. F. Wang, W. Sun, Z. Shadike, E. Hu, X. Ji, T. Gao, X. Yang, K. Xu and C. Wang, Angew. Chem., Int. Ed., 2018, 57, 11978–11981.
29. D. Kundu, S. H. Vajargah, L. Wan, B. Adams, D. Prendergast and L. F. Nazar, Energy Environ. Sci., 2018, 11, 881–892.
30. J. Lai, H. Zhu, X. Zhu, H. Koritala and Y. Wang, ACS Appl. Energy Mater., 2019, 2, 1988–1996.
31. M. Yan, P. He, Y. Chen, S. Wang, Q. Wei, K. Zhao, X. Xu, Q. An, Y. Shuang, Y. Shao, K. T. Mueller, L. Mai, J. Liu and J. Yang, Adv. Mater., 2018, 30, 1703725.
32. F. Wan and Z. Niu, Angew. Chem., Int. Ed., 2019, 58, 16358–16367.
33. Z. Batteries, M. Liao, J. Wang, L. Ye, H. Sun, Y. Wen, C. Wang, X. Sun, B. Wang and H. Peng, Angew. Chem., 2020, 132, 2293–2298.
34. Z. Li, Y. Ren, L. Mo, C. Liu, K. Hsu, Y. Ding, X. Zhang, X. Li, L. Hu, D. Ji and G. Cao, ACS Nano, 2020, 14, 5581–5589.
35. L. Cheng, M. Xu, Q. Zhang, G. Li, J. Chen and Y. Lou, J. Alloys Compd., 2019, 781, 245–254.
36. Y. Zhang, J. Zheng, Y. Zhao, T. Hu, Z. Gao and C. Meng, Appl. Surf. Sci., 2016, 377, 385–393.
37. E. A. Esparcia, M. S. Chae, J. D. Ocon and S. Hong, Chem. Mater., 2018, 30, 3690–3696.
38. Y. Liu, B. Shen, X. Liu, Y. Wu, X. He and Q. Li, Int. J. Electrochem. Sci., 2017, 12, 5483–5491.
39. Y. Xu, H. Dong, M. Zhou, C. Zhang, Y. Wu, W. Li, Y. Dong and Y. Lei, Small Methods, 2018, 1800349, 1800349.
40. A. M. El-sayed, S. Mohamed and A. Mousa, J. Chin. Chem. Soc., 2006, 5, 559–565.
41. A. Qian, K. Zhuo, M. S. Shin, W. W. Chun, B. N. Choi and C. Chung, ChemSusChem, 2015, 8, 2399–2406.
42. Y. Yang, Y. Tang, S. Liang, Z. Wu, G. Fang, X. Cao, C. Wang, T. Lin, A. Pan and J. Zhou, Nano Energy, 2019, 61, 617–625.
43. D. Kundu, B. D. Adams, V. Duffort, S. H. Vajargah and L. F. Nazar, Nat. Energy, 2016, 1, 1–8.
44. V. Bondarenka, H. Tvardauskas, M. Senulis, A. Pašiškevičius and S. Grebinskij, Acta Phys. Pol., A, 2011, 119, 135–136.
45. W. Li, D. Kong, T. Yan, M. Shi, D. Kong and Y. Feng, J. Solid State Chem., 2020, 286, 121296.
46. C. Lv, C. Yan, G. Chen, Y. Ding, J. Sun and Y. Zhou, Angew. Chem., Int. Ed., 2018, 57, 6073–6076.
47. M. Huang, J. Bian, W. Xiong and R. Zhang, J. Mater. Chem. A, 2018, 6, 3602–3609.
48. B. Guo, L. Chen, S. Shi, A. Ishaq, D. Wan, Z. Chen, L. Zhang, H. Luo and Y. Gao, RSC Adv., 2017, 7, 10798–10805.
49. M. Yan, P. He, Y. Chen, S. Wang, Q. Wei, K. Zhao, X. Xu, Q. An, Y. Shuang, Y. Shao, K. T. Mueller, L. Mai, J. Liu and J. Yang, Adv. Mater., 2018, 30, 1–6.
50. Y. Yang, Y. Tang, G. Fang, L. Shan, J. Guo, W. Zhang, C. Wang, L. Wang, J. Zhou and S. Liang, Energy Environ. Sci., 2018, 11, 3157–3162.
51. B. Tang, J. Zhou, G. Fang, F. Liu, C. Zhu, C. Wang, A. Pan and S. Liang, J. Mater. Chem. A, 2019, 7, 940–945.
52. P. He, G. Zhang, X. Liao, M. Yan, X. Xu, Q. An, J. Liu and L. Mai, Adv. Energy Mater., 2018, 8, 1–6.
53. L. Shan, Y. Yang, W. Zhang, H. Chen, G. Fang, J. Zhou and S. Liang, Energy Storage Mater., 2019, 18, 10–14.
54. S. Islam, M. H. Alfaruqi, B. Sambandam, D. Y. Putro, S. Kim, J. Jo, S. Kim, V. Mathew and J. Kim, Chem. Commun., 2019, 55, 3793–3796.
55. T. Wu, K. Zhu, C. Qin and K. Huang, J. Mater. Chem. A, 2019, 7, 5612–5620.
56. C. Xia, J. Guo, P. Li, X. Zhang and H. N. Alshareef, Angew. Chem., Int. Ed., 2018, 57, 3943–3948.
57. B. Sambandam, V. Soundharrajan, S. Kim, M. H. Alfaruqi, J. Jo, S. Kim, V. Mathew, Y. K. Sun and J. Kim, J. Mater. Chem. A, 2018, 6, 3850–3856.
58. C. Xia, J. Guo, Y. Lei, H. Liang, C. Zhao and H. N. Alshareef, Adv. Mater., 2018, 30, 1–7.
59. W. Li, K. Wang, S. Cheng and K. Jiang, Energy Storage Mater., 2018, 15, 14–21.
60. B. Tang, G. Fang, J. Zhou, L. Wang, Y. Lei, C. Wang, T. Lin, Y. Tang and S. Liang, Nano Energy, 2018, 51, 579–587.
61. G. He, M. Qiao, W. Li, Y. Lu, T. Zhao, R. Zou, B. Li, J. A. Darr, J. Hu, M.-M. Titirici and I. P. Parkin, Adv. Sci., 2017, 4, 1600214.
62. F. Ming, H. Liang, Y. Lei, S. Kandambeth, M. Eddaoudi and H. N. Alshareef, ACS Energy Lett., 2018, 3, 2602–2609.
63. B. Sambandam, V. Soundharrajan, S. Kim, M. H. Alfaruqi, J. Jo, S. Kim, V. Mathew, Y. Sun and J. Kim, J. Mater. Chem. A, 2018, 6, 15530–15539.
64. G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901.
65. Q. Li, X. Rui, D. Chen, Y. Feng, N. Xiao, L. Gan, Q. Zhang, Y. Yu and S. Huang, Nano-Micro Lett., 2020, 12, 1–12.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nr03394d

‡ These authors contributed equally to this work.

---