 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular physics of jumping nanodroplets†‡
Sreehari
Perumanath
 a,
Matthew K.
Borg
a,
Matthew K.
Borg
 a,
James E.
Sprittles
a,
James E.
Sprittles
 b and
Ryan
Enright
b and
Ryan
Enright
 *c
*c
aSchool of Engineering, University of Edinburgh, Edinburgh EH9 3FB, UK
bMathematics Institute, University of Warwick, Coventry CV4 7AL, UK
cThermal Management Research Group, ηET Dept., Nokia Bell Labs, Dublin D15 Y6NT, Ireland. E-mail: ryan.enright@nokia-bell-labs.com
First published on 22nd July 2020
Abstract
Next-generation processor-chip cooling devices and self-cleaning surfaces can be enhanced by a passive process that requires little to no electrical input, through coalescence-induced nanodroplet jumping. Here, we describe the crucial impact thermal capillary waves and ambient gas rarefaction have on enhancing/limiting the jumping speeds of nanodroplets on low adhesion surfaces. By using high-fidelity non-equilibrium molecular dynamics simulations in conjunction with well-resolved volume-of-fluid continuum calculations, we are able to quantify the different dissipation mechanisms that govern nanodroplet jumping at length scales that are currently difficult to access experimentally. We find that interfacial thermal capillary waves contribute to a large statistical spread of nanodroplet jumping speeds that range from 0–30 m s−1, where the typical jumping speeds of micro/millimeter sized droplets are only up to a few m s−1. As the gas surrounding these liquid droplets is no longer in thermodynamic equilibrium, we also show how the reduced external drag leads to increased jumping speeds. This work demonstrates that, in the viscous-dominated regime, the Ohnesorge number and viscosity ratio between the two phases alone are not sufficient, but that the thermal fluctuation number (Th) and the Knudsen number (Kn) are both needed to recover the relevant molecular physics at nanoscales. Our results and analysis suggest that these dimensionless parameters would be relevant for many other free-surface flow processes and applications that operate at the nanoscale.
1. Introduction
Excess surface energy conversion processes, such as coalescence-induced droplet jumping, can be harnessed to augment the operational performance of many industrial processes: heat transfer applications,1–4 droplet transport,5–8 anti-icing surfaces,9 self-cleaning surfaces,10 thermal diodes,11 metal nanoparticle formation12 and energy harvesting.13 For example, in condensation heat transfer, drop-wise condensation has high phase-change heat transfer performance compared to film-wise condensation,14 provided the condensate droplets are rapidly removed from the surface to limit liquid conduction resistance and expose the condensing surface for re-nucleation. Traditionally, in passive systems, gravity is required to remove droplets from an inclined/vertical plate,15,16 but the droplet radius (R) has to be of the order of the capillary length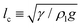 , where γ is the liquid–vapor interfacial tension, ρl is the liquid density and g is the acceleration due to gravity; such that sub-millimetre sized water droplets cannot be dislodged. However, by harnessing coalescence-induced droplet jumping, it has been recently demonstrated that micrometric water droplets can be spontaneously shed from a carefully-designed condensing surface resulting in further enhancements of this heat transfer process.17
, where γ is the liquid–vapor interfacial tension, ρl is the liquid density and g is the acceleration due to gravity; such that sub-millimetre sized water droplets cannot be dislodged. However, by harnessing coalescence-induced droplet jumping, it has been recently demonstrated that micrometric water droplets can be spontaneously shed from a carefully-designed condensing surface resulting in further enhancements of this heat transfer process.17
Experimental studies of this phenomenon on engineered surfaces have shown that droplets much smaller than lc are removed from superlyophobic surfaces (with contact angle θc ≥ 150° and small contact angle hysteresis) by a self-induced jumping mechanism caused by coalescence with neighbor droplets.18,19 Indeed, it transpires that nature has already been harnessing this phenomenon for self-cleaning of cicada wings10 and plant leaves,20 and in dew droplet removal from gecko skin.21
Previous studies have shown that while the jumping process is limited by gravity for droplets with R ∼ lc,22 it is suppressed by internal viscous dissipation for smaller ones.23,24 Therefore, the jumping speed Vg (subscript ‘g’ indicates ‘in the presence of a gas’) is expected to be a non-monotonic function of R, and its maximum is observed to be ≈0.25U![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19,24–26 for water droplets near room temperature with R ≈ 100 μm,19 where
19,24–26 for water droplets near room temperature with R ≈ 100 μm,19 where 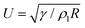 is the inertial-capillary velocity scale. Notably, U is only a good predictor of Vg when viscous effects are negligible, which occurs when the Ohnesorge number
is the inertial-capillary velocity scale. Notably, U is only a good predictor of Vg when viscous effects are negligible, which occurs when the Ohnesorge number 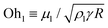 is sufficiently small, where μl is the liquid dynamic viscosity. Experimentally, jumping has been observed for water droplets down to R ≈ 500 nm (i.e. as high as Ohl ≈ 0.17).27
is sufficiently small, where μl is the liquid dynamic viscosity. Experimentally, jumping has been observed for water droplets down to R ≈ 500 nm (i.e. as high as Ohl ≈ 0.17).27
The precise mechanism of coalescence-induced droplet jumping9,17,30–32 and how to enhance the jumping speed33–35 have been studied across length scales. It is now generally understood that coalescence-induced jumping results from the excess surface energy released after coalescence being partially converted into translational kinetic energy of the resulting droplet. During droplet coalescence, after the rupture of the intervening fluid film, a liquid bridge will form, grows and impacts the underlying surface (see Fig. 1(a)–(c)), providing a reaction force for the final droplet to jump.24,28,36 Despite the significant efforts exploring the mechanism and application of coalescence-induced droplet jumping, little is known about the process at the smallest of length scales. Continuum physics predicts a monotonic decrease and eventual suppression of droplet jumping due to viscous dissipation, but this physical picture is far from certain, if one considers nanophysical effects that become important with decreasing system size.
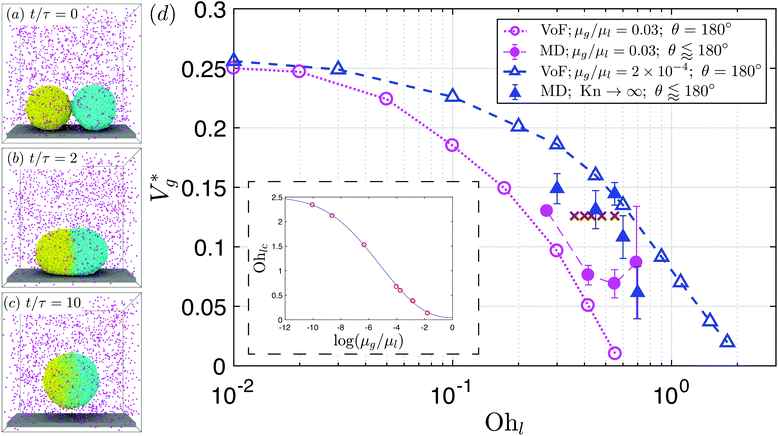 | ||
Fig. 1 (a–c) MD simulation snapshots of two water nanodroplets (R = 7.2 nm; Ohl = 0.45) coalescing and jumping in nitrogen (Kn ≈ 10.2). Molecules from different droplets are colored differently for illustration purposes. Nitrogen molecules are colored in pink. Here, 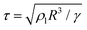 is the inertial-capillary time scale. (d) Scaled jumping speed is the inertial-capillary time scale. (d) Scaled jumping speed 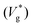 as a function of Ohl comparing different computational methods. Subscript ‘g’ denotes coalescence in finite Kn and the superscript ‘*’ indicates that the jumping speed is normalized using the corresponding inertial-capillary velocity scale. Brown ‘×’ symbols represent results from Liang and Keblinski (2015).28 For systems where the dynamics is predominantly controlled by liquid properties (i.e. the gas is passive), the scaled jumping speed decreases monotonically with Ohl due to increased viscous dissipation. This is exhibited by both MD in vacuum (Kn → ∞) and VoF simulations with small μg/μl. For large enough droplets (i.e. small Ohl) coalescing in an outer fluid, MD and corresponding VoF predictions agree well (μg/μl = 0.03 case). Deviations are observed as the size is decreased (Ohl increased), due to non-classical effects, which are not incorporated in continuum simulations. Inset shows the dependence of the cut-off Ohnesorge number (Ohlc) on the viscosity ratio. As shown previously,29 when the viscosities of both fluids are matched, jumping is still expected (i.e. Ohlc > 0 when μg/μl = 1). As the gas viscosity is reduced considerably below that of the coalescing liquid, it will become increasingly ‘passive’ and the dynamics is solely governed by the properties of the coalescing liquid. Consequently, the jumping speeds should asymptote to those in vacuum as μg/μl is decreased. This feature is qualitatively captured by current VoF simulations. The solid blue line is a fit to the VoF data (see section 2 of the ESI‡). as a function of Ohl comparing different computational methods. Subscript ‘g’ denotes coalescence in finite Kn and the superscript ‘*’ indicates that the jumping speed is normalized using the corresponding inertial-capillary velocity scale. Brown ‘×’ symbols represent results from Liang and Keblinski (2015).28 For systems where the dynamics is predominantly controlled by liquid properties (i.e. the gas is passive), the scaled jumping speed decreases monotonically with Ohl due to increased viscous dissipation. This is exhibited by both MD in vacuum (Kn → ∞) and VoF simulations with small μg/μl. For large enough droplets (i.e. small Ohl) coalescing in an outer fluid, MD and corresponding VoF predictions agree well (μg/μl = 0.03 case). Deviations are observed as the size is decreased (Ohl increased), due to non-classical effects, which are not incorporated in continuum simulations. Inset shows the dependence of the cut-off Ohnesorge number (Ohlc) on the viscosity ratio. As shown previously,29 when the viscosities of both fluids are matched, jumping is still expected (i.e. Ohlc > 0 when μg/μl = 1). As the gas viscosity is reduced considerably below that of the coalescing liquid, it will become increasingly ‘passive’ and the dynamics is solely governed by the properties of the coalescing liquid. Consequently, the jumping speeds should asymptote to those in vacuum as μg/μl is decreased. This feature is qualitatively captured by current VoF simulations. The solid blue line is a fit to the VoF data (see section 2 of the ESI‡). | ||
Understanding the collective jumping behaviour of coalescing nanodroplets can aid us in the design of highly efficient passive thermal management systems that exploit dominant nanoscale physics3 and to enable efficient electrostatic energy harvesting,37 where they can act as charge carriers. Furthermore, jumping nanodroplets can potentially be used in vacuum distillation technology for purifying and separating metals.38–40 This motivated Liang and Keblinski28 to perform molecular dynamics (MD) simulations of coalescing argon nanodroplets. They observed droplet jumping for Ohl as large as 0.55 (i.e. even larger than that observed experimentally) and a surprising Ohl independent scaled jumping speed 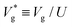 , which has so far evaded any explanation.
, which has so far evaded any explanation.
Our recent study41 has shown that thermal capillary waves42–46 on a droplet's surface make the onset of coalescence a stochastic process and that the thermal motion of molecules crucially affects its initial stages. Furthermore, a factor that is usually overlooked is the involvement of ambient gas in the overall dynamics. For nanodroplets, the natural length scale of the process is ∼R and the mean free path of the gas molecules is typically λ ∼ 10–100 nm, so the gas flow near the droplet interface will deviate from thermodynamic equilibrium and rarefied gas dynamics become important.
Clearly, modelling nanodroplet coalescence requires a method which can incorporate such non-classical effects. By using MD, we can naturally capture the spatio-temporal scales associated with thermal fluctuations and rarefied gas flow, which are currently beyond experimental capabilities, and understand their influence on nanodroplet jumping.47
2. Simulation details
In this work, we investigate coalescence-induced jumping of water and argon nanodroplets. The former is important for industrial applications and the latter is for comparing our results with previous findings, where the physics was unresolved. Another advantage of using water is that it has negligible vapor pressure at the operating temperature (300 K) and so the effect of rarefaction on jumping speed can be isolated by adding a non-condensing gas outside, such as nitrogen. Simulations are initiated with two nanodroplets equilibrated on a superlyophobic surface. After equilibration, the droplets are brought together at a small speed. This procedure is repeated under various ambient conditions for different droplet sizes. A large number of independent realisations are performed for each case in order to provide reliable statistical information. To connect to continuum-level modelling, where molecular physics is not currently accounted for, we compare our results with predictions of 3D volume-of-fluid (VoF) simulations in order to develop a more comprehensive picture of the size dependence of Vg. Further details of the MD and VoF simulations are provided in the ESI.‡3. Results and discussion
Fig. 1(d) compares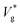 as a function of Ohl between MD and VoF simulations. For Ohl > 0.1, which is of interest to nanodroplets technologies, VoF simulations predict a monotonic decrease of
as a function of Ohl between MD and VoF simulations. For Ohl > 0.1, which is of interest to nanodroplets technologies, VoF simulations predict a monotonic decrease of 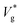 . A part of this is verified in our experiments,24 and a cut-off Ohnesorge number (Ohlc) is identified that depends on the viscosity ratio between the two phases (μg/μl; see inset of Fig. 1(d)). Here, Ohlc is defined as the minimum Ohl at which the VoF simulations predict no jumping occurs. MD results in the vacuum limit follow a similar trend exhibited by VoF simulations when μg/μl is made deliberately small, but become increasingly stochastic. We define the Knudsen number, Kn ≡ λ/R, to characterise the gas rarefaction. In the vacuum limit, the vapor pressure of water within MD simulations is so low that for all cases simulated, Kn > 10. Consequently, if thermal fluctuations were absent, MD simulations with Kn → ∞ are considered equivalent to VoF simulations in the limit μg/μl → 0. In such cases, where the dynamics is governed by the coalescing liquid, the decrease of
. A part of this is verified in our experiments,24 and a cut-off Ohnesorge number (Ohlc) is identified that depends on the viscosity ratio between the two phases (μg/μl; see inset of Fig. 1(d)). Here, Ohlc is defined as the minimum Ohl at which the VoF simulations predict no jumping occurs. MD results in the vacuum limit follow a similar trend exhibited by VoF simulations when μg/μl is made deliberately small, but become increasingly stochastic. We define the Knudsen number, Kn ≡ λ/R, to characterise the gas rarefaction. In the vacuum limit, the vapor pressure of water within MD simulations is so low that for all cases simulated, Kn > 10. Consequently, if thermal fluctuations were absent, MD simulations with Kn → ∞ are considered equivalent to VoF simulations in the limit μg/μl → 0. In such cases, where the dynamics is governed by the coalescing liquid, the decrease of 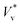 with Ohl is in accordance with the classical notion (subscript ‘v’ denotes ‘coalescence in vacuum’). Comparing these simulations with coalescence of water droplets in nitrogen allows us to isolate the influence of the ambient gas on the overall dynamics.
with Ohl is in accordance with the classical notion (subscript ‘v’ denotes ‘coalescence in vacuum’). Comparing these simulations with coalescence of water droplets in nitrogen allows us to isolate the influence of the ambient gas on the overall dynamics.
When a surrounding gas is present, the agreement between VoF and MD simulations worsens as Ohl is increased (i.e. as R is reduced; μg/μl = 0.03 case in Fig. 1(d)). For water nanodroplets coalescing in nitrogen (μg/μl = 0.0589; not shown in figure), although our VoF simulations predict Ohlc = 0.38, we observe jumping for at least until Ohl = 0.7. We will show that these deviations occur as a result of the increased non-continuum effects at small length scales, which are not incorporated into VoF simulations. Limited by computational expenses, presently we are unable to study systems with smaller Ohl in MD simulations than what is shown in Fig. 1(d). The figure also shows results from a previous research on argon nanodroplets28 that did not explicitly consider the effect of the ambient gas. We observe that: (a) their jumping speeds are bounded by our VoF results in the limit of vanishing outer phase viscosity and (b) the jumping speeds are remarkably constant over a range of Ohl, where we expect it to decrease due to the growing importance of viscous effects in the liquid. Evidently, such systems require analysis that considers the dynamics of the coalescing liquid (through Ohl), the ambient gas (both through μg/μl and Kn) and the thermal fluctuations at the interface (through Th, the thermal fluctuation number defined later on). In what follows, we isolate these molecular effects in order to determine their influence on nanodroplet jumping.
3.1 Effect of outer gas and rarefaction
Here, we simulate water nanodroplets coalescing in nitrogen at different pressures (p∞) and therefore Knudsen numbers (as Kn ∝ p∞−1). Given the small scale of the droplets, λ ∼ R and is much larger than the characteristic height of the gas lubrication film underneath the coalescing droplets. Therefore, we expect the gas underneath the coalescing droplets to be in thermodynamic non-equilibrium. Fig. 2(a) and (b) show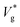 as a function of Kn for Ohl = 0.45 and Ohl = 0.55, respectively. The clear transition in the jumping characteristics around Kn ≈ 1 strongly indicates the role of gas kinetic effects, which we quantify below.
as a function of Kn for Ohl = 0.45 and Ohl = 0.55, respectively. The clear transition in the jumping characteristics around Kn ≈ 1 strongly indicates the role of gas kinetic effects, which we quantify below.
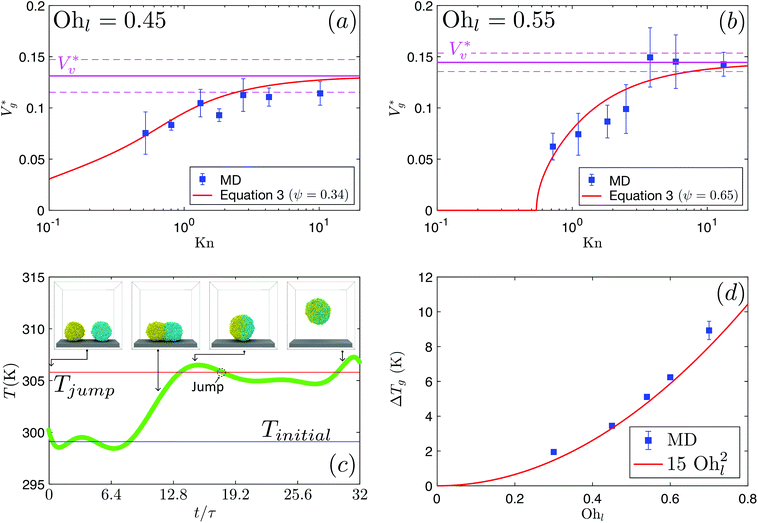 | ||
Fig. 2 (a) Scaled jumping speeds of water nanodroplets in nitrogen as a function of Kn for Ohl = 0.45 and (b) for Ohl = 0.55 droplets obtained from MD simulations. In (a), although a characteristic change in 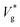 is observed near Kn ≈ 1, an extrapolation of the fit to our eqn (3) predicts non-zero jumping speed for a wider range of Kn (down to Kn = 0.035) as compared to (b). At 300 K, nitrogen approaches super-critical behaviour near 30 atm, and this restricts us from simulating lower Kn, while keeping μg/μl constant. The decrease in is observed near Kn ≈ 1, an extrapolation of the fit to our eqn (3) predicts non-zero jumping speed for a wider range of Kn (down to Kn = 0.035) as compared to (b). At 300 K, nitrogen approaches super-critical behaviour near 30 atm, and this restricts us from simulating lower Kn, while keeping μg/μl constant. The decrease in 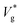 at low Kn is due to the increased drag from the surrounding gas. (c) Temperature rise due to viscous dissipation during coalescence of two water nanodroplets with R = 4.1 nm (Ohl = 0.6) in vacuum and corresponding simulation snapshots. (d) Comparison of the temperature rise (ΔT = Tjump − Tinitial) in the droplets obtained from MD simulations with our eqn (2). at low Kn is due to the increased drag from the surrounding gas. (c) Temperature rise due to viscous dissipation during coalescence of two water nanodroplets with R = 4.1 nm (Ohl = 0.6) in vacuum and corresponding simulation snapshots. (d) Comparison of the temperature rise (ΔT = Tjump − Tinitial) in the droplets obtained from MD simulations with our eqn (2). | ||
As the total gas/liquid interfacial area decreases by ΔA when two spherical droplets coalesce, a finite amount of energy is released: γΔA. Portions of this released energy are: (a) dissipated due to internal viscous losses (Eμ), (b) used to overcome adhesion from the surface (Wadh), (c) used to maintain a circulatory flow field inside the droplet after coalescence (Ecirculation) and (d) used to overcome drag from the surrounding gas during coalescence (Wdrag). The remainder will appear as the translational kinetic energy of the final droplet, if it jumps off the symmetry-breaking surface.
By assuming Ecirculation ≈ 0 for relatively large Ohl droplets studied here, where viscosity quickly dampens internal motion, a generalized energy-balance gives
| γΔA = Wadh + Eμ + Wdrag + mdVg2, | (1) |
We evaluate Eμ, which is related to the rise in the overall temperature of the droplets ΔTg, by studying coalescence in vacuum. Notably, temperature is far easier to measure in MD than directly computing Eμ from gradients of flow fields. Fig. 2(c) shows a typical temperature rise during coalescence of two R = 4.1 nm droplets. In section 3 of the ESI,‡ we derive an expression for ΔTg:
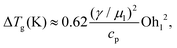 | (2) |
The ideal way of estimating Wdrag is by explicitly determining the viscous stress over the entire surface and summing the work done against it over the time scale of coalescence. However, evaluating local stress tensors on the droplet surface in nanoscale systems is highly challenging as there are strong thermal fluctuations and rarefied gas effects (such as velocity slip) across interfaces, and the process happens rapidly making it difficult to obtain sufficient statistics to resolve a gradient. Compared to Stokes drag on a spherical particle moving in an infinite viscous medium with small Kn, we identify three reasons by which the drag on coalescing droplets is different: (a) the surrounding gas is rarefied, resulting in finite Kn, (b) there is no ‘far field’ due to the presence of the wall underneath both droplets and (c) the dynamically coalescing droplets generate a complex flow geometry. We separately analyse each of these factors and establish a rough estimate of Wdrag, which captures the underlying physics. In section 4 of the ESI,‡ we demonstrate the significance of reduction factors in modifying Stokes drag and derive an expression for 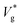 :
:
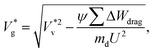 | (3) |
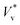 to obtain
to obtain 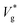 . We use ensemble average values of our vacuum-limit MD data to estimate
. We use ensemble average values of our vacuum-limit MD data to estimate 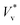 , since thermal fluctuations are important at this scale (see below). In Fig. 2(a) and (b), we fit the data to eqn (3) with only ψ as the fitting parameter (see section 4.1 of the ESI‡ for fitting statistics). Our results show that the additional dissipation mechanism introduced by the ambient gas results in a lower jumping speed compared to its vacuum limit and this is quantified by Kn.
, since thermal fluctuations are important at this scale (see below). In Fig. 2(a) and (b), we fit the data to eqn (3) with only ψ as the fitting parameter (see section 4.1 of the ESI‡ for fitting statistics). Our results show that the additional dissipation mechanism introduced by the ambient gas results in a lower jumping speed compared to its vacuum limit and this is quantified by Kn.
3.2 Stochastic nature of the jumping speed
Our MD simulations reveal that, under similar but independent realisations of the same two nanodroplets, the jumping speed does not have a unique value. In stark contrast to the classical notion, where similar initial conditions for a particular droplet size predict relatively similar jumping speed, the presence of thermal fluctuations brings in a statistical nature to the jumping speed, especially for nanodroplets, for which a thermal fluctuation number: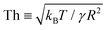 ,49 defined as the ratio of the characteristic amplitude of surface thermal fluctuations
,49 defined as the ratio of the characteristic amplitude of surface thermal fluctuations 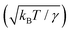 41 to R, is large. Fig. 3(a) and (b) show the distribution of
41 to R, is large. Fig. 3(a) and (b) show the distribution of 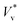 for droplets with R = 3.1 nm (Th ≈ 0.1) and R = 5.1 nm (Th ≈ 0.05), respectively.
for droplets with R = 3.1 nm (Th ≈ 0.1) and R = 5.1 nm (Th ≈ 0.05), respectively.
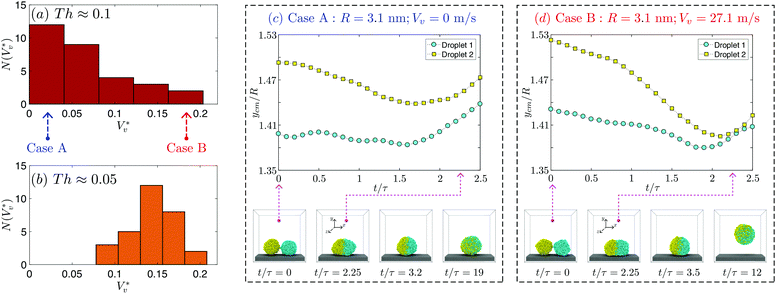 | ||
Fig. 3 Distribution of normalised coalescence-induced jumping speeds in vacuum 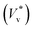 for (a) R = 3.1 nm (Ohl = 0.7; U = 147.6 m s−1) and (b) R = 5.1 nm (Ohl = 0.55; U = 114.3 m s−1) droplets, showing how the contribution of thermal motion of the liquid molecules to the jumping speed differs with for (a) R = 3.1 nm (Ohl = 0.7; U = 147.6 m s−1) and (b) R = 5.1 nm (Ohl = 0.55; U = 114.3 m s−1) droplets, showing how the contribution of thermal motion of the liquid molecules to the jumping speed differs with 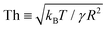 . Simulations are performed in vacuum to isolate the effects of thermal fluctuations. Vv is obtained from MD simulations by measuring the instantaneous speed of the coalesced nanodroplet in the direction normal to the wall at the moment it loses contact with it. For each case, 30 realisations are performed to obtain the distribution; the initial conditions of all realisations are different. Here, . Simulations are performed in vacuum to isolate the effects of thermal fluctuations. Vv is obtained from MD simulations by measuring the instantaneous speed of the coalesced nanodroplet in the direction normal to the wall at the moment it loses contact with it. For each case, 30 realisations are performed to obtain the distribution; the initial conditions of all realisations are different. Here, 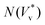 denotes the number of realisations (out of total 30) in which the scaled jumping speed in vacuum came between a specified range. For droplets with larger Th, the pronounced influence of thermal fluctuations renders the distribution to be significantly skewed and wider. (c and d) Time-varying position of y coordinate (normal to the wall) of the centre-of-mass (ycm) normalised with R of each droplet on the superlyophobic surface right after they establish the first contact until the bridge hits the underlying surface. Corresponding simulation snapshots show (case A) Vv = 0 m s−1 when the bridge does not grow parallel to y, and (case B) Vv = 27.1 m s−1, when the bridge does grow in the direction normal to the wall. Here, R is estimated from the equi-molar line from a time-averaged density profile of a droplet.41 The value of ycm/R > 1 is due to the finite thickness of the water-vapor interface and the way R is defined. Oscillation in ycm/R value is caused by thermal fluctuations. denotes the number of realisations (out of total 30) in which the scaled jumping speed in vacuum came between a specified range. For droplets with larger Th, the pronounced influence of thermal fluctuations renders the distribution to be significantly skewed and wider. (c and d) Time-varying position of y coordinate (normal to the wall) of the centre-of-mass (ycm) normalised with R of each droplet on the superlyophobic surface right after they establish the first contact until the bridge hits the underlying surface. Corresponding simulation snapshots show (case A) Vv = 0 m s−1 when the bridge does not grow parallel to y, and (case B) Vv = 27.1 m s−1, when the bridge does grow in the direction normal to the wall. Here, R is estimated from the equi-molar line from a time-averaged density profile of a droplet.41 The value of ycm/R > 1 is due to the finite thickness of the water-vapor interface and the way R is defined. Oscillation in ycm/R value is caused by thermal fluctuations. | ||
A single nanodroplet's centre-of-mass naturally fluctuates up and down on a superlyophobic surface, because of interfacial thermal fluctuations (see section 5 of the ESI‡). When two such droplets approach each other, their centers-of-mass can be at different heights, as seen in two independent cases of the same droplet size (case A and case B) in Fig. 3(c) and (d). In case A, by the time the bridge hits the surface, one of the droplets (yellow squares) has its centre-of-mass above that of the other. Such an asymmetry can slow down the jumping speed, because (a) the impact of the bridge is non-normal to the wall resulting in only a component of the reaction force on the droplet being directed normal to the wall and (b) the flow momentum vectors in the upper half of the droplets that are directed parallel to the plane of the wall are now not effectively redirected into the out-of-plane direction from the wall. The jumping speed will be maximal when the impact is normal to the surface and there is effective redirection of the flow momentum vectors24 – as in case B. Since at most times, the bouncing results in an asymmetric coalescence, the skewness of the distribution shown in Fig. 3(a) is expected. We do not observe such significant skewness for larger droplets where Th is relatively small (Fig. 3(b)), and there is a diminishing significance of thermal fluctuations on large droplets. As shown in Fig. 3(c) and (d), the jumping speeds in two realisations of the same system can differ by as much as 27 m s−1.
3.3 Discussion
Our results show that the nanodroplet jumping is governed not just by Ohl (which quantifies the viscous dissipation within the droplet) and μg/μl (which quantifies the viscous dissipation on the surface of the droplet in the continuum limit), but also by two other dimensionless numbers that represent the molecular physics: Kn and Th. Kn has an effect on reducing the drag below that imposed by μg/μl due to the rarefaction, while Th depends only on droplet size and can exist at any Kn; its influence is on making the jumping speed have a wide statistical spread about the nominal jumping speed in the absence of thermal fluctuations.In the presence of an outer fluid, the final droplet jumps at a lower speed compared to its vacuum limit, because in addition to the internal viscous losses there will be dissipation in the gas phase. In such cases, 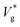 decreases monotonically with decreasing Kn, which is quantified by our eqn (3). Our results and that of ref. 26 show a clear deviation from predictions of VoF simulations with identical viscosity ratio as Ohl is increased (see Fig. 1). Based on the results presented above, our interpretation of this phenomena is that
decreases monotonically with decreasing Kn, which is quantified by our eqn (3). Our results and that of ref. 26 show a clear deviation from predictions of VoF simulations with identical viscosity ratio as Ohl is increased (see Fig. 1). Based on the results presented above, our interpretation of this phenomena is that 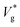 is larger than expected because the drag on the droplets is not as severe as what is predicted by VoF simulations, which do not account for interfacial slip and other complex rarefaction effects. This reduction in drag is relatively higher for smaller droplets as their Kn is larger by definition, while keeping λ constant (coalescence of argon droplets in vapour at a certain condition, for example). The difference between our MD results and that of ref. 26 is mainly due to a higher droplet-surface adhesion we imposed. We verify convergence of our
is larger than expected because the drag on the droplets is not as severe as what is predicted by VoF simulations, which do not account for interfacial slip and other complex rarefaction effects. This reduction in drag is relatively higher for smaller droplets as their Kn is larger by definition, while keeping λ constant (coalescence of argon droplets in vapour at a certain condition, for example). The difference between our MD results and that of ref. 26 is mainly due to a higher droplet-surface adhesion we imposed. We verify convergence of our 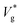 with that of ref. 26 as wettability is reduced in section 4 of the ESI.‡
with that of ref. 26 as wettability is reduced in section 4 of the ESI.‡
The rarefied gas effects quantified here can be used to study jumping of liquid metal nanodroplets for application in latest vacuum distillation technology,38–40 where rarefied gas effects are expected to be pronounced (Kn ∼ 1–10). Here we expect a significant enhancement of the jumping speed.
The influence of interfacial thermal fluctuations has often been overlooked in the literature, even in molecular simulations,33,36 where, as revealed here, its impact is non-negligible. For instance, the extreme normalised jumping speed shown in Fig. 3(d) correspond to 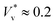 , which is nearly as high as its maximum limit that is only expected for microscale droplets24,25 (i.e. where Ohl is small and there are negligible gravitational effects).
, which is nearly as high as its maximum limit that is only expected for microscale droplets24,25 (i.e. where Ohl is small and there are negligible gravitational effects).
Although MD simulations capture the full picture of droplet coalescence, its extreme computational expense puts a cap on the maximum droplet size that can be simulated. A generalized continuum framework, which incorporates slip at various interfaces and can model thermal fluctuations, can be expected to reproduce the MD results. Such multiscale simulation tools are promising candidates to model interfacial fluid flows in many micro/nanoscale devices. Thermal fluctuations have already been incorporated into continuum models for the breakup of liquid jets49 and thin films50 using fluctuating hydrodynamic theory;51 modelling nanodroplet jumping using a similar method seems like a promising way forward. Moreover, it would be interesting to incorporate electric charge effects to understand the role of double layers and applied fields in the context of the molecular effects on droplet jumping identified here.
4. Conclusion
In summary, we performed molecular dynamics simulations of coalescence-induced jumping of nanodroplets on atomically smooth superlyophobic surfaces and studied the effect of gas rarefaction and interfacial thermal fluctuations on the jumping speed. Our results suggest that, for a fixed viscosity ratio, nanodroplet jumping involves an interplay of three dimensionless parameters: Ohl, Kn and Th. While Ohl characterises the viscous losses inside the droplets, Kn characterises the thermodynamic non equilibrium effects in the surrounding gas – thereby explaining a reduction in drag compared to predictions of continuum simulations, and Th characterises the effect of interfacial thermal fluctuations – describing the statistical nature of jumping speed in nanodroplets. Insights from our theoretical analysis and the results can be used to bound performance characteristics of future micro/nano-fluidic devices, which employ coalescence-induced manipulation of nanodroplets for heat-transfer and various biological and materials processing at the nanoscale. For designing such engineering systems, robust modelling procedures need to be developed that account for various nanoscale aspects of the jumping process identified here.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors would like to dedicate this article to Prof. Jason Reese, our mentor, colleague and friend, who passed away in March 2019. The authors thank Dr Livio Gibelli for valuable discussions. The MD simulation results were obtained using ARCHER, the UK's national supercomputer. This research is supported by EPSRC Grants No. EP/N016602/1, EP/P020887/1, EP/P031684/1, EP/S029966/1 and EP/R007438/1.References
- J. Rose, Int. J. Heat Mass Transfer, 1967, 10, 755–762 CrossRef CAS.
- G. A. O′neill and J. Westwater, Int. J. Heat Mass Transfer, 1984, 27, 1539–1549 CrossRef.
- K. F. Wiedenheft, H. A. Guo, X. Qu, J. B. Boreyko, F. Liu, K. Zhang, F. Eid, A. Choudhury, Z. Li and C.-H. Chen, Appl. Phys. Lett., 2017, 110, 141601 CrossRef.
- S. Gao, W. Liu and Z. Liu, Nanoscale, 2019, 11, 459–466 RSC.
- U. Zimmerli, P. G. Gonnet, J. H. Walther and P. Koumoutsakos, Nano Lett., 2005, 5, 1017–1022 CrossRef CAS.
- X. Qin, Q. Yuan, Y. Zhao, S. Xie and Z. Liu, Nano Lett., 2011, 11, 2173–2177 CrossRef CAS.
- C. Bakli, S. Perumanath and S. Chakraborty, Nanoscale, 2017, 9, 12509–12515 RSC.
- C. Zhu, Y. Gao, Y. Huang, H. Li, S. Meng, J. S. Francisco and X. C. Zeng, Nanoscale, 2017, 9, 18240–18245 RSC.
- J. B. Boreyko and C. P. Collier, ACS Nano, 2013, 7, 1618–1627 CrossRef CAS.
- K. M. Wisdom, J. A. Watson, X. Qu, F. Liu, G. S. Watson and C.-H. Chen, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 7992–7997 CrossRef CAS.
- J. B. Boreyko, Y. Zhao and C.-H. Chen, Appl. Phys. Lett., 2011, 99, 234105 CrossRef.
- J. Boneberg, A. Habenicht, D. Benner, P. Leiderer, M. Trautvetter, C. Pfahler, A. Plettl and P. Ziemann, Appl. Phys. A, 2008, 93, 415–419 CrossRef CAS.
- N. Miljkovic, D. J. Preston, R. Enright and E. N. Wang, Appl. Phys. Lett., 2014, 105, 013111 CrossRef.
- J. W. Rose, Proc. Inst. Mech. Eng., Part A, 2002, 216, 115–128 CrossRef CAS.
- H.-Y. Kim, H. J. Lee and B. H. Kang, J. Colloid Interface Sci., 2002, 247, 372–380 CrossRef CAS.
- P. Dimitrakopoulos and J. J. L. Higdon, J. Fluid Mech., 1999, 395, 181–209 CrossRef CAS.
- N. Miljkovic, R. Enright, Y. Nam, K. Lopez, N. Dou, J. Sack and E. N. Wang, Nano Lett., 2013, 13, 179–187 CrossRef CAS.
- M. Kollera and U. Grigull, Heat Mass Transfer, 1969, 2, 31–35 Search PubMed.
- J. B. Boreyko and C. H. Chen, Phys. Rev. Lett., 2009, 103, 2–5 Search PubMed.
- B. Mockenhaupt, H.-J. Ensikat, M. Spaeth and W. Barthlott, Langmuir, 2008, 24, 13591–13597 CrossRef CAS.
- J. A. Watson, B. W. Cribb, H. M. Hu and G. S. Watson, Biophys. J., 2011, 100, 1149–1155 CrossRef CAS.
- B. Peng, S. Wang, Z. Lan, W. Xu, R. Wen and X. Ma, Appl. Phys. Lett., 2013, 102, 151601 CrossRef.
- F.-C. Wang, F. Yang and Y.-P. Zhao, Appl. Phys. Lett., 2011, 98, 053112 CrossRef.
- R. Enright, N. Miljkovic, J. Sprittles, K. Nolan, R. Mitchell and E. N. Wang, ACS Nano, 2014, 8, 10352–10362 CrossRef CAS.
- T. Mouterde, T.-V. Nguyen, H. Takahashi, C. Clanet, I. Shimoyama and D. Quéré, Phys. Rev. Fluids, 2017, 2, 112001 CrossRef.
- F. Liu, G. Ghigliotti, J. J. Feng and C.-H. Chen, J. Fluid Mech., 2014, 752, 39–65 CrossRef CAS.
- H. Cha, C. Xu, J. Sotelo, J. M. Chun, Y. Yokoyama, R. Enright and N. Miljkovic, Phys. Rev. Fluids, 2016, 1, 064102 CrossRef.
- Z. Liang and P. Keblinski, Appl. Phys. Lett., 2015, 107, 0–5 CAS.
- S. Lei, N. Wang, H. Liu, K. Nolan and R. Enright, ASME 2015 13th International Conference on Nanochannels, Microchannels, and Minichannels, 2015, pp. 1–8.
- R. Enright, N. Miljkovic, A. Al-Obeidi, C. V. Thompson and E. N. Wang, Langmuir, 2012, 28, 14424–14432 CrossRef CAS.
- R. Enright, N. Miljkovic, N. Dou, Y. Nam and E. N. Wang, J. Heat Transfer, 2013, 135, 091304 CrossRef.
- Y. Nam, H. Kim and S. Shin, Appl. Phys. Lett., 2013, 103, 161601 CrossRef.
- S. Gao, Q. Liao, W. Liu and Z. Liu, J. Phys. Chem. Lett., 2018, 9, 13–18 CrossRef CAS.
- H. Vahabi, W. Wang, J. M. Mabry and A. K. Kota, Sci. Adv., 2018, 4, eaau3488 CrossRef CAS.
- K. Wang, Q. Liang, R. Jiang, Y. Zheng, Z. Lan and X. Ma, RSC Adv., 2016, 6, 99314–99321 RSC.
- Q. Sheng, J. Sun, W. Wang, H. S. Wang and C. G. Bailey, J. Appl. Phys., 2017, 122, 245301 CrossRef.
- N. Miljkovic, D. J. Preston, R. Enright and E. N. Wang, Nat. Commun., 2013, 4, 2517 CrossRef.
- S. Ali, K. Srinivas Rao, C. Laxman, N. Munirathnam and T. Prakash, Sep. Purif. Technol., 2012, 85, 178–182 CrossRef CAS.
- W. Zhang, Y. Tian, D.-C. Liu, F. Wang, B. Yang and B.-Q. Xu, J. Mater. Res. Technol., 2020, 9, 3590–3597 CrossRef CAS.
- G. Zha, C. Yang, Y. Wang, X. Guo, W. Jiang and B. Yang, Sep. Purif. Technol., 2019, 209, 863–869 CrossRef CAS.
- S. Perumanath, M. K. Borg, M. V. Chubynsky, J. E. Sprittles and J. M. Reese, Phys. Rev. Lett., 2019, 122, 104501 CrossRef CAS.
- J. S. Rowlinson and B. Widom, Molecular Theory of Capillarity, Clarendon Press, Oxford, 1982 Search PubMed.
- A. Werner, F. Schmid, M. Müller and K. Binder, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 728–738 CrossRef CAS.
- S. W. Sides, G. S. Grest and M.-D. Lacasse, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 60, 6708–6713 CrossRef CAS.
- J. Eggers and E. Villermaux, Rep. Prog. Phys., 2008, 71, 036601 CrossRef.
- J. Lucassen, M. van den Tempel, A. Vrij and F. T. Hesselink, Proc. K. Ned. Akad. Wet., Ser. B: Phys. Sci., 1970, 73, 109–123 CAS.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, New York, 2nd edn, 2017 Search PubMed.
- W. F. Phillips, Phys. Fluids, 1975, 18, 1089–1093 CrossRef.
- C. Zhao, J. E. Sprittles and D. A. Lockerby, J. Fluid Mech., 2019, 861, R3 CrossRef CAS.
- Y. Zhang, J. E. Sprittles and D. A. Lockerby, Phys. Rev. E, 2019, 100, 023108 CrossRef CAS.
- L. D. Landau and E. M. Lifshitz, Statistical Physics Part 2, Course of Theoretical Physics, Pergamon Press, Oxford, 1980, vol. 9, pp. 86–91 Search PubMed.
Footnotes |
| † All simulation data within the publication can be freely accessed from: DOI: 10.7488/ds/2851 |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nr03766d |
| This journal is © The Royal Society of Chemistry 2020 |
