The strongest dative bond in main-group compounds. Theoretical study of OAeF⁻ (Ae = Be–Ba)

Abstract

Quantum chemical calculations of the anions OAeF⁻ (Ae = Be–Ba) have been carried out using ab initio methods at the CCSD(T)/def2-TZVPP level and density functional theory employing BP86 with various basis sets. The equilibrium structures have linear geometries for Ae = Be and Mg but they are strongly bent for Ae = Sr and Ba while the calcium species has a quasi-linear structure with a very low bending potential. The calculated bond dissociation energies suggest a record-high BDE of D_e = 144.08 kcal mol⁻¹ for OBeF⁻ at the CCSD(T)/def2-TZVPP level, which is the strongest BDE for a dative bond that has been found so far. The BDE of the heavier homologues have a continuously decreasing order for Ae with Be > Mg (113.01 kcal mol⁻¹) > Ca (84.06 kcal mol⁻¹) > Sr (72.06 kcal mol⁻¹) > Ba (60.00 kcal mol⁻¹). The calculation of the charge distribution reveals a significant charge donation OAe ← F⁻ with a declining sequence for the heavier atoms Ae. The oxygen atom in OAeF⁻ carries always a higher partial charge than the fluorine atom, which contradicts the standard electronegativities of the atoms. The surprising partial charges are explained with the bonding situation of the atoms in the actual electronic structure. The bonding analysis of the OAe–F⁻ bonds using the EDA-NOCV method shows that the bonds have much more electrostatic character than the Ae–F⁻ bonds in the diatomic anions. This finding is supported by the results of the LED partitioning approach. The dative interactions have three major and one minor component. The assignment of a quadruple bond for the heavier species with Ae = Ca, Sr, Ba is not reasonable. The driving force for the bent geometries is the accumulation of electronic charge in the lone-pair region at the Ae atoms, which enhances the electrostatic attraction with the other atoms. An adequate description of the bonding situation is given by the formula O⁻–Ae⁺ ← F⁻.

---

Introduction

Recently we reported theoretical work on the diatomic anions AeF⁻ (Ae = Be–Ba), which possess surprisingly strong dative bonds between the closed-shell species Ae and F⁻.^1,2 The calculated bond dissociation energies are between 87.5 kcal mol⁻¹ for BeF⁻ and 68.8 kcal mol⁻¹ for MgF⁻ and they show an unusual increasing trend MgF⁻ < CaF⁻ < SrF⁻ < BaF⁻. The strong bonds were explained by the inductive force of F⁻, which heavily polarizes the (n)s² valence electrons of the Ae atoms, inducing in turn four dative covalent interactions^3–5 of the heavier species involving the (n − 1)d AOs of Ca–Ba.^1,2 The fluorine anion F⁻ being isoelectronic to Ne is a weak electron donor due to the high electronegativity of fluorine and the alkaline earth atoms are weak electron acceptors. We speculated that replacing the weak electron acceptors Ae with the stronger electron acceptors AeO could lead to even higher bond dissociation energies (BDEs). Earlier studies by one of us showed that diatomic BeO is likely the strongest neutral Lewis acid, which even binds the extremely weak Lewis base He with a BDE of D_e ∼ 3 kcal mol⁻¹.^6–9

The objective of this work is to search for compounds that possess even stronger dative bonds than diatomic AeF⁻. A logical step is the replacement of the weak Lewis acceptor atom Ae by the strong Lewis acid AeO.

Here we present quantum chemical calculations using ab initio methods and density functional theory of the anions OAeF⁻ (Ae = Be–Ba) and an analysis of the OAe–F⁻ bonds. None of the triatomic anions has yet been observed experimentally. The calculated results show that the compounds are very stable species with record-breaking strong dative bonds and unusual properties that can be observed in the gas phase. The theoretically predicted vibrational spectra are a helpful guide for identifying the molecules in experiments.

Methods

The bond lengths, vibrational frequencies and BDEs of OAeF⁻ (Ae = Be–Ba) and in the electronic singlet ground state were calculated at the CCSD(T)¹⁰ and BP86^11,12 level in conjunction with the basis sets def2-TZVPP.¹³ The CCSD(T) calculations were carried out to give quantitatively accurate numerical values and the DFT calculation were performed to provide a basis for the EDA-NOCV calculations and for investigating the performance of the BP86 functional, which was found to be very good. The calculations were carried out with the program Gaussian 16.¹⁴ The NBO calculations were performed using the program NBO 7.0.¹⁵ We also calculated atomic partial charges using the Hirshfeld¹⁶ and CM5¹⁷ methods with the program Gaussian 16, and calculated Voronoi¹⁸ charges and Mayer¹⁹ bond order with the program Multiwfn.²⁰

The bonding situation in the molecules was further analyzed by means of an energy decomposition analysis (EDA) which was introduced by Morokuma1²¹ and by Ziegler and Rauk²² in conjunction with the natural orbitals for chemical valence (NOCV)^23,24 method. The EDA-NOCV^25,26 calculations were carried out with the ADF 2018.105 program package^27,28 at the BP86-D3(BJ)²⁹ level with Slater-type basis function of DZP quality³⁰ using the BP86/def2-TZVPP optimized geometries. DZP is a double-ζ quality basis set augmented by a set of polarization functions. The use of larger basis sets does not lead to significantly different energy values, but can lead to unphysically large numerical contributions from atomic orbitals of higher quantum number such as (n + 1)s AOs of Ae atom, which represent numerical artifacts. In this analysis, the intrinsic interaction energy (ΔE_int) between two fragments can be divided into three energy components as follows:

ΔE_int = ΔE_elstat + ΔE_Pauli + ΔE_orb (1)

The electrostatic ΔE_elstat term represents the quasiclassical electrostatic interaction between the unperturbed charge distributions of the prepared fragments, the Pauli repulsion ΔE_Pauli corresponds to the energy change associated with the transformation from the superposition of the unperturbed electron densities of the isolated fragments to the wavefunction, which properly obeys the Pauli principle through explicit antisymmetrization and renormalization of the production wavefunction. The orbital term ΔE_orb comprises the mixing of orbitals, charge transfer and polarization between the isolated fragments. The energy change involved in the latter step, which is the main difference between the Morokuma²¹ and Ziegler/Rauk²² approaches, is calculated with an extension of Slater's transition state method³¹ for energy differences. It is often referred as ETS method. The orbital term ΔE_orb can be further decomposed into contributions from each irreducible representation of the point group of the interacting system as follows:

The combination of the EDA with NOCV enables the partition of the total orbital interactions into pairwise contributions of the orbital interactions which is very vital to get a complete picture of the bonding. The charge deformation Δρ_k(r), resulting from the mixing of the orbital pairs ψ_k(r) and ψ_−k(r) of the interacting fragments presents the amount and the shape of the charge flow due to the orbital interactions (eqn (3)), and the associated energy term ΔE_orb provides the size of stabilizing orbital energy originated from such interaction (eqn (4)) where F^TS_−k,−k and F^TS_k,k are the Fock matrix elements defined for the transition state electron density (the mid density between a molecule and fragments).^25,26

The EDA-NOCV approach was previously criticized because its results are allegedly path-dependent.^32–34 This was rebutted in a detailed discussion of the method.³⁵ More details about the EDA-NOCV method and its application are given in recent review articles.^36–42

Upon request of one referee we carried out additional calculations for the analysis of the chemical bonds. We employed the local energy decomposition^43–45 (LED) method in conjunction with ab initio calculations at the DLPNO-CCSD(T)^46–50 level. DLPNO-CCSD(T) recovers >95% of triples contribution and 99.8% of correlation energy.⁴⁹ The LED approach decomposes the interaction energy between the frozen fragments into the Hartree–Fock and correlation interaction energies:

ΔE_int = ΔE^HF_int + ΔE^C_int + ΔE_el-prep (5)

Hartree–Fock part of interaction energy consists of the electrostatic and exchange terms.

ΔE^HF_int = ΔE_elstat + ΔE_exch (6)

Correlation interaction energy on the other hand is decomposed into:

ΔE^C_int = ΔE^C-SP_CT(A→B) + ΔE^C-SP_CT(B→A) + ΔE^C_disp + ΔE^C-WP + ΔE^C-T (7)

where ΔE^C-SP_CT terms are the instantaneous strong-pair charge transfer terms, ΔE^C_disp = ΔE^C-SP_disp + ΔE^C-WP_disp is a dispersion term, consisting of strong-pair and weak-pair interaction, ΔE^C-WP is the rest of weak-pair interactions, while ΔE^C-T is the triples correction.

Geometries, energies and vibrational frequencies

Fig. 1 shows the calculated geometries of diatomic AeO and the triatomic anions OAeF⁻ at the CCSD(T)/def2-TZVPP and BP86/def2-TZVPP levels of theory. The calculated bond lengths for AeO are slightly longer than the experimental values,⁵¹ especially for BP86/def2-TZVPP for the heavier species, but the differences are not a concern as we are mainly interested in the changes resulting from the binding of F⁻. The lighter OAeF⁻ species with Ae = Be, Mg are predicted to have linear structures whereas the heavier anions with Ae = Sr, Ba possess a bent equilibrium geometry. The calcium species OCaF⁻ has a linear structure at the CCSD(T)/def2-TZVPP level. It has a bending angle of 144.7° at BP86/def2-TZVPP, but this is only 0.5 kcal mol⁻¹ higher than for the linear form. The bent equilibrium structures of OSrF⁻ and OBaF⁻ are 2.7 kcal mol⁻¹ and 3.6 kcal mol⁻¹ lower in energy than the linear forms, which are transition states (number of imaginary modes 1) at the CCSD(T)/def2-TZVPP. The energy differences at BP86/def2-TZVPP are a bit higher, i.e. 5.2 kcal mol⁻¹ for OSrF⁻ and 8.6 kcal mol⁻¹ for OBaF⁻. The anions OAeF⁻ are isoelectronic with the difluorides AeF₂, which have been studied before. Experimental and theoretical work suggest that the lighter molecules BeF₂ and MgF₂ have linear geometries but the heavier homologues CaF₂, SrF₂, BaF₂ are strongly bent but with a soft bending potential between ∼0.2 kcal mol⁻¹ (CaF₂) and ∼5 kcal mol⁻¹ (BaF₂) which is similar to the calculated values for OAeF⁻ (Fig. 1).^52,53 A theoretical study suggested that d-orbital participation of the heavier Ae atoms Ca–Ba and core-polarization make major contributions to the bending.⁵²

Fig. 1 Optimized geometries of OAe and OAeF⁻ (Ae = Be–Ba) at the CCSD(T)/def2-TZVPP [BP86/def2-TZVPP] level. Bond lengths in Å and angles in degree. The experimental value for the Ae–O bond lengths given in italics are taken from ref. 51. Number of imaginary frequencies i. The linear structures of OSrF⁻ and OBaF⁻ are transition states at both levels of theory, the linear structure of OCaF⁻ is a transition state at BP86/def2-TZVPP. ΔE gives the energy differences between the linear and bent geometries in kcal mol⁻¹.

Fig. 1 shows that the Ae–O distances of the anions OAeF⁻ are longer than in diatomic AeO. The Ae–F bonds in OAeF⁻ are also longer than in AeF⁻ except for the magnesium species, where the calculated Mg–F distance in OMgF⁻ at both levels of theory is shorter than in MgF⁻ (1.840 Å at CCSD(T)/def2-TZVPP and 1.847 Å at BP86/def2-TZVPP).⁵⁴ It is interesting that the Ae–O and Ae–F bonds in the bent structures of the heavier anions are shorter than in the linear form. This does not agree with the commonly assumed trend with respect to spⁿ hybridization.

Table 1 gives the theoretically predicted vibrational frequencies and IR intensities of the molecules OAeF⁻ and for diatomic AeO and AeF⁻, which will be useful to identify the anions. The frequency shift Δ of the stretching modes between the diatomic and triatomic species shows some unexpected trends. The Ae–O stretching frequencies of OBeF⁻ and OMgF⁻ are predicted to possess a blue shift toward higher wave numbers compared with free BeO and MgO although the bond distances are clearly longer in the anions. In contrast, the heavier anions OAeF⁻ (Ae = Ca, Sr, Ba) exhibit a red shift to lower wavenumbers. The red shift at CCSD(T)/def2-TZVPP is much smaller for the calcium and strontium species than at BP86/def2-TZVPP. This does not seem to be related to the structures (curved or linear) of the anions. The linear form of OCaF⁻ at CCSD(T)/def2-TZVPP possess also a small red shift of the Ca–O stretching mode. The Ae–F stretching frequencies of all triatomic species OAeF⁻ are red-shifted toward lower wave numbers relative to diatomic AeF⁻. The red shift is particularly large for OBeF⁻.

Table 1 Calculated vibrational frequencies υ and frequency shifts Δ with respect to AeO (cm⁻¹) and IR intensities I (km mol⁻¹) of OAeF⁻ and AeO (Ae = Be–Ba)

Molecule	CCSD(T)/def2-TZVPP [BP86/def2-TZVPP]
	Ae–O stretch			Ae–F stretch			O–Ae–F bent
	υ	Δ	I.^b	υ	Δ	I	υ.	I.^b
a Degenerate. b Intensitites are not available at CCSD(T).
BeO	1434.0 [1454.5]	—	[4.2]	—	—	—	—	—
BeF^−	—	—	—	1028.0 [1007.2]	—	[14.3]	—	—
OBe–F^−	1519.3 [1481.2]	+85.3 [+26.7]	[204.9]	683.8 [665.0]	−344.2 [−354.7]	[4.6]	396.0^a [385.3]^a	[34.0]
MgO	783.7 [801.8]	—	[13.8]	—	—	—	—	—
MgF^−	—	—	—	577.7 [540.8]	—	[37.7]	—	—
OMg–F^−	847.2 [827.4]	+33.9 [+25.6]	[73.3]	524.4 [502.8]	−53.3 [−45.5]	[10.9]	171.4^a [170.1]^a	[48.6]
CaO	589.3 [751.8]	—	[68.5]	—	—	—	—	—
CaF^−	—	—	—	485.6 [511.6]	—	[44.5]	—	—
OCa–F^−	584.8 [601.6]	−4.5 [−150.2]	[93.9]	401.0 [406.2]	−84.6 [−111.1]	[91.8]	54.3^a [74.5]	[51.8]
SrO	407.8 [657.3]	—	[74.5]	—	—	—	—	—
SrF^−	—	—	—	410.6 [428.5]	—	[48.6]	—	—
OSr–F^−	402.1 [526.5]	−5.7 [−130.8]	[87.9]	306.0 [356.4]	−104.6 [−76.4]	[133.0]	43.4 [112.3]	[26.9]
BaO	618.9 [641.9]	—	[129.6]	—	—	—	—	—
BaF^−	—	—	—	408.3 [409.1]	—	[56.9]	—	—
OBa–F^−	485.6 [517.3]	−133.3 [−124.6]	[50.4]	319.7 [317.8]	−88.6 [−93.9]	[134.5]	88.8 [116.3]	[13.2]

---

Table 2 shows the calculated BDEs of the anions for breaking the bonds. The calculated BDE for the reaction OBeF⁻ → BeO + F⁻ is very high at both theory levels and is D_e = 144.8 kcal mol⁻¹ at CCSD(T)/def2-TZVPP and D_e = 142.6 kcal mol⁻¹ at BP86/def2-TZVPP. To our knowledge, this is the highest value for the BDE of a donor–acceptor bond between two closed-shell species for main group compounds and transition metal complexes that has been reported so far. The alternative electron-sharing rupture of the OBeF⁻ bond toward BeO⁻ + F has an even higher BDE, because the calculated electron affinity of BeO (1.99 eV) is clearly lower than the electron affinity of fluorine (3.33 eV).⁵⁵ The BDEs for the reaction of the heavier homologues OAeF⁻ → AeO + F⁻ (Ae = Mg–Ba) are significantly smaller than for the beryllium anion. Unlike the diatomic anions AeF⁻,^1,2 the triatomic anions OAeF⁻ exhibit a continuously decreasing trend Be > Mg > Ca > Sr > Ba, which concurs with the common trend of electron-sharing bonds of main-group compounds, typically becoming weaker for heavier-row atoms.

Table 2 Calculated bond dissociation energies D_e of the [OAeF]⁻ (Ae = Be–Ba) species

	[OAeF]^− (S) → OAe (S) + F^− (S)		[OAeF]^− (S) → OAe^− (D) + F (D)		[OAeF]^− (S) → [AeF]^− (S) + O (T) [O (S)]^a		[OAeF]^− (S) → AeF (D) + O^−(D)
	CCSD(T)/def2-TZVPP	BP86/def2-TZVPP	CCSD(T)/def2-TZVPP	BP86/def2-TZVPP	CCSD(T)/def2-TZVPP	BP86/def2-TZVPP	CCSD(T)/def2-TZVPP	BP86/def2-TZVPP
a Using the experimental value for the ^3P → ^1D excitation energy of oxygen atom 45.3 kcal mol^−1: Kramida, A., Ralchenko, Yu., Reader, J., and NIST ASD Team (2022). NIST Atomic Spectra Database (ver. 5.10), [Online]. Available: https://physics.nist.gov/asd [2023, August 21]. National Institute of Standards and Technology, Gaithersburg, MD. DOI: https://doi.org/10.18434/T4W30F.
[OBeF]^−	144.8	142.6	158.2	163.1	150.1 [201.3]	164.7 [229.8]	157.8	161.0
[OMgF]^−	113.1	114.9	142.9	143.2	97.5 [148.7]	113.3 [178.3]	111.4	116.5
[OCaF]^−	84.6	78.4	125.8	129.9	83.5 [134.7]	108.3 [173.4]	95.0	102.4
[OSrF]^−	72.6	72.1	118.6	125.1	75.7 [127.0]	101.5 [166.5]	94.4	95.7
[OBaF]^−	60.0	62.5	111.9	120.9	70.3 [121.5]	108.7 [173.8]	74.5	100.3

---

Table 2 gives also the BDEs for breaking the O–AeF⁻ bonds. The bond rupture yielding the electronic ground state of the fragments O (³P) and AeF⁻ (¹Σ⁺) at CCSD(T)/def2-TZVPP has slightly higher D_e values for the bonds O–BeF⁻ (150.1 kcal mol⁻¹), O–SrF⁻ (75.7 kcal mol⁻¹) and O–BaF⁻ (70.3 kcal mol⁻¹), smaller D_e values for O–MgF⁻ (97.5 kcal mol⁻¹) and a comparable D_e value for O–CaF⁻ (83.5 kcal mol⁻¹) than for the respective OAe–F⁻ bonds. Both sets of O–AeF⁻ and OAe–F⁻ bonds have the same regular trend of the BDEs Be ≫ Mg > Ca > Sr > Ba, which underlines the peculiar feature of the diatomic anions AeF⁻.^1,2 But the bond dissociation reaction OAeF⁻ (singlet) → O (³P) + AeF⁻ (¹Σ⁺) is spin-symmetry forbidden. The spin-symmetry allowed formation of O (¹D) + AeF⁻ (¹Σ⁺) is thermodynamically 45.3 kcal mol⁻¹ higher in energy. The BDE for the dissociation reaction OAeF⁻ (singlet) → AeF (²Σ⁺) + O⁻ (²P) is higher at CCSD(T)/def2-TZVPP than for the reaction yielding O (³P) and AeF⁻ (¹Σ⁺), whereas BP86/def2-TZVPP gives slightly lower values for Ae = Ca–Ba. Thus, the strong OAe–F⁻ bonds are the lowest energy symmetrically allowed reaction channels for fragmentation. All triatomic anions are thermodynamically very stable species.

Bonding analysis

We analyzed the electronic structure and bonding situation in the triatomic anions OAeF⁻ with a variety of methods. Table 3 shows the atomic partial charges calculated with four different methods. It was previously found in our study of AeF⁻ that the charge distribution suggested by the popular NBO method is not reasonable, because the (n)p valence AOs of Ae are not treated as genuine valence orbitals, which leads to a negligible charge donation Ae ← F⁻.^1,2 The data in Table 3 show that the same problematic results occur for OAeF⁻. The NBO method gives a miniscule charge donation OAe ← F⁻ between 0.01–0.12e, whereas the other three methods suggest a much larger charge donation between 0.28–0.62e. Since a significant charge donation is supported by further analysis of the electronic structure, we think that the NBO charges are not a reliable indicator of the charge distribution in these molecules.

Table 3 Calculated partial charges (q) and bond orders P of the OAe–F⁻ (Ae = Be–Ba) species at the respective equilibrium geometries

CCSD/def2-TZVPP [BP86/def2-TZVPP]
q					P(Ae–F^−)
Atoms	NBO^a	Hirshfeld^a	Voronoi^b	CM5^a	Bond	Wiberg^a	Mayer^b
a Obtained at the CCSD/def2-TZVPP (density = current) level with Gaussian program. b Obtained at the CCSD/def2-TZVPP (density = current) level with Multiwfn program.
O	−1.66 [−1.67]	−0.75 [−0.69]	−0.81 [−0.75]	−0.96 [−0.90]	OBe–F^−	0.18 [0.22]	0.74 [0.87]
Be	1.54 [1.55]	0.14 [0.05]	0.19 [0.11]	0.48 [0.40]
OBe	−0.12 [−0.12]	−0.61 [−0.64]	−0.62 [−0.64]	−0.48 [−0.51]	O–BeF^−	0.50 [0.60]	1.84 [2.08]
F	−0.88 [−0.88]	−0.39 [−0.36]	−0.39 [−0.36]	−0.52 [−0.49]
O	−1.62 [−1.58]	−0.82 [−0.74]	−0.99 [−0.90]	−0.97 [−0.89]	OMg–F^−	0.10 [0.15]	0.53 [0.68]
Mg	1.55 [1.50]	0.34 [0.21]	0.49 [0.38]	0.58 [0.47]
OMg	−0.07 [−0.08]	−0.48 [−0.53]	−0.50 [−0.52]	−0.39 [−0.43]	O–MgF^−	0.53 [0.74]	1.64 [1.93]
F	−0.93 [−0.92]	−0.51 [−0.47]	−0.50 [−0.48]	−0.61 [−0.57]
O	−1.62 [−1.56]	−0.88 [−0.76]	−1.05 [−0.90]	−1.05 [−0.99]	OCa–F^−	0.08 [0.13]	0.36 [0.54]
Ca	1.61 [1.49]	0.50 [0.29]	0.59 [0.39]	0.76 [0.62]
OCa	−0.01 [−0.07]	−0.38 [−0.47]	−0.46 [−0.51]	−0.29 [−0.37]	O–CaF	0.50 [0.82]	1.41 [1.82]
F	−0.99 [−0.93]	−0.62 [−0.53]	−0.55 [−0.48]	−0.71 [−0.63]
O	−1.58 [−1.49]	−0.85 [−0.73]	−1.00 [−0.85]	−1.09 [−1.00]	OSr–F^−	0.07 [0.15]	0.31 [0.52]
Sr	1.53 [1.41]	0.46 [0.26]	0.50 [0.33]	0.81 [0.66]
OSr	−0.05 [−0.08]	−0.39 [−0.47]	−0.50 [−0.52]	−0.28 [−0.34]	O–SrF^−	0.59 [0.91]	1.40 [1.77]
F	−0.95 [−0.92]	−0.60 [−0.53]	−0.50 [−0.48]	−0.72 [−0.66]
O	−1.64 [−1.50]	−0.87 [−0.72]	−1.00 [−0.79]	−1.13 [−1.04]	OBa–F^−	0.06 [0.16]	0.24 [0.49]
Ba	1.58 [1.42]	0.50 [0.26]	0.50 [0.24]	0.85 [0.70]
OBa	−0.06 [−0.08]	−0.37 [−0.46]	−0.50 [−0.55]	−0.28 [−0.34]	O–BaF^−	0.64 [0.90]	1.42 [1.74]
F	−0.94 [−0.92]	−0.64 [−0.54]	−0.51 [−0.45]	−0.71 [−0.66]

---

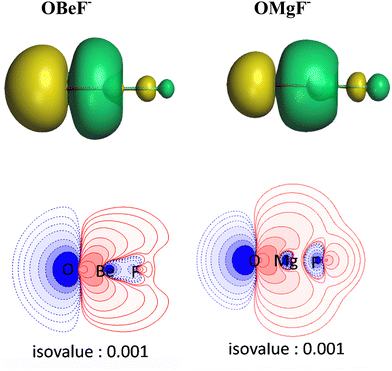
There is another interesting result concerning the charge distribution in the anions OAeF⁻. All four methods suggest that the oxygen atom carries a higher negative partial charge than fluorine, which does not agree with the electronegativity of the atoms. The difference between the negative charges at the terminal atoms towards oxygen is very large. The result is not an artefact of the partitioning procedures for calculating partial charges. Fig. 2 shows the molecular electrostatic potential (MEP) of the molecules, which shows clearly that the oxygen atom carries a larger negative charge than fluorine. It has been shown before that the MEP results are the physically most reliable data for giving the charge distribution in a molecule.⁵⁶ The MEP result does not depend on the chosen value for the contour line. Fig. 2 is obtained with a value of 0.02 a.u. Fig. S2 of ESI,‡ shows the MEP with a much smaller value of 0.001 a.u. for the contour line. It also shows that oxygen carries a higher negative charge than fluorine.

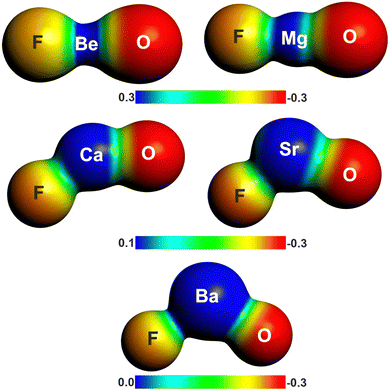Fig. 2 Plot of the electrostatic potentials of OAeF⁻ at the BP86/def2-TZVPP level. Computed with value of 0.001 a.u. for the contour of the electronic density.

The seemingly paradoxical result can be understood when one realizes that the common scales for atomic electronegativities are average values derived from compounds in standard electronic states. The electronegativity of an atom is the power to attract electronic charge from another atom in a chemical bond, but it is affected by the actual bonding situation. A recent example concerns the carbon atom in the compound class of carbones CL₂ where the C atom has a ¹D (2s²2p²) reference state. There are dative bonds L → C ← L where the ligands L donate electronic charge into the vacant 2p AOs of carbon. The bonding situation makes the carbon atom in carbones to have a much higher electronegativity than in standard organic molecules.^{41,42,57–61} There have been early studies where different values for the electronegativity of the valence orbitals in an atom were proposed, but they are hardly ever used and it seems that this approach is forgotten.^62,63 The present results suggest that the charge distribution in OAeF⁻ is affected by the different nature of the two bonds, i.e. electron-sharing interactions between oxygen and Ae versus dative interactions between fluorine and Ae.

Table 3 gives also the bond order of the molecules using the frequently chosen Wiberg method⁶⁴ as well as the Mayer bond orders.^19,65 The Wiberg bond orders (WBOs) are originally derives from semiempirical CNDO/2 calculations, which neglect the orbital overlap. It has been shown that his can lead to misleading values particularly for polar bonds^66–68 The data in Table 3 show that the WBO values are much smaller than the bond orders suggested by the Mayer partitioning method, which explicitly considers the interatomic overlap. The Mayer bond orders (MBOs) are significantly higher than the WBO data for the very polar OAe–F⁻ and particularly for the O–AeF⁻ bonds. The MBO values indicate for the latter bonds a substantial multiple bond character whereas the WBO values are always <1. But we want to point out that the bond order values of polar bonds may not be directly taken as measure for the bond multiplicity. Polar bonds have lower bond orders <1 for an electron-pair single bond due to the smaller overlap than non-polar bonds.⁶⁸ A polar triple bond can have an MBO value significantly smaller than 3 and yet it may possess three bonding electron pairs. This holds in particular for very polar bonds which were found in AeF⁻ (ref. 1 and 2) and which are present in OAeF⁻. More sophisticated methods are needed to provide a meaningful answer to the question of bond multiplicity.

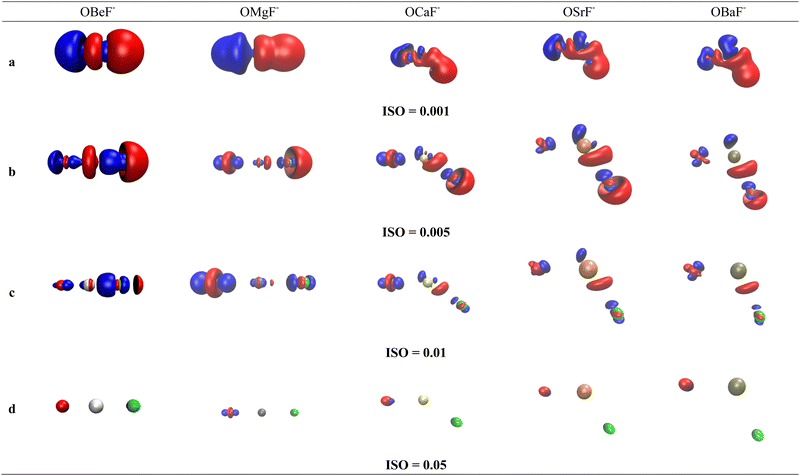
Much insight is gained by examination of the difference density maps where the charge distribution of free OAe and F⁻ is subtracted from the charge in OAe–F⁻. This is shown in Fig. 3 for OBeF⁻ using four different values for the isosurface, which gives interesting information about the charge flow. The difference density map of the rather diffuse charge with the isosurface value of 0.001e a.u.⁻³ in Fig. 3 shows charge depletion from F⁻ and Be and charge enhancement in the F⁻–BeO bonding region and at oxygen atom. More interesting information comes from Fig. 3b and c which displays the charge flow in the areas of higher charge density, which are directly associated with the formation of the F⁻–BeO bond and the change in the O–Be bond. There is clearly an increase in the electronic charge between F⁻ and BeO as well as between O and BeF⁻. The red and blue areas of decrease and increase of charge at Be nicely illustrate the 2s → 2p_σ hybridization at Be. Note that the difference density maps do not distinguish between charge in the σ and π bonding regions, because the degenerate π bonds are rotationally symmetric. The variation in information revealed by using different values for the isosurface is a warning against the indiscriminate use of isodensity plots at a given value.

Fig. 3 Charge density difference maps at the BP86/def2-TZVPP level. OAeF⁻ and the fragments OAe + F⁻ (Ae = Be–Ba) with different values for the isodensity surfaces Iso given in e a.u.⁻³. The direction of the charge flow is red → blue.

The difference density maps of OMgF⁻ show similar features as for OBeF⁻ but there are interesting changes in the AO shell alterations of the atoms. There is a 2s → 2p_σ hybridization at oxygen which is still visible at the iso value 0.05e a.u.⁻³ for OMgF⁻ but not for OBeF⁻. The density difference maps of the heavier homologues with bent geometries show nicely the appearance of charge concentration in the region with lone-pair character at Ae = Ca, Sr, Ba, which comes from the polarization of the rather soft valence electrons of the metal. This mechanism has already been pointed out by Kaupp et al. in their theoretical study of AeX₂ (X = halogen).⁵² There is charge accumulation in the lone-pair region of the three heavy Ae atoms in the diffuse areas with isovalues 0.001e a.u.⁻³ and 0.005e a.u.⁻³ shown in Fig. 3b and c. It disappears for Ba in the area with an isovalue of 0.01e a.u.⁻³ shown in Fig. 3d, because of the more dispersed valence charge.

A very detailed information about the nature of the bonding interaction and the associated charge flow is available from EDA-NOCV calculations. The EDA provides a quantitative estimate of the attractive (covalent and electrostatic) and repulsive (Pauli repulsion) contributions to the interatomic interactions. The NOCV component partitions the covalent (orbital) interactions into pairwise contributions, relating the results to the frontier orbital model of Fukui⁶⁹ and the orbital symmetry rules of Woodward and Hoffman.⁷⁰ A nice feature of the EDA-NOCV approach is that the individual orbital interactions can be graphically represented by the associated deformation densities and the connected orbitals. The aim of the EDA-NOCV calculations is a detailed and quantitative analysis of the electronic interactions that lead to the unusual chemical bonds in the molecules described in this work.

Table 4 shows the numerical results for the anions OAeF⁻ using AeO (S) and F⁻ (S) in the electronic singlet states as interacting fragments at the BP86/def2-TZVPP optimized equilibrium geometries. The intrinsic interaction energies ΔE_int have very similar values and the same trend Be > Mg > Ca > Sr > Ba as the BDE values shown in Table 2, because the only relaxation of the fragments comes from the change in the AeO bond lengths. Inspection of the various energy terms suggest that the OAe–F⁻ binding comes mainly from the electrostatic attraction ΔE_elstat which provides between 74.3% (Ae=Be) and 59.3% (Ae=Ba) to the total attraction. The EDA-NOCV analysis shows that the covalent character of the OAe–F⁻ bonds given by the percentage contribution of the orbital term ΔE_orb increases steadily from Be to Ba.

Table 4 EDA-NOCV results of OAeF⁻ using OAe (S) and F⁻ (S) in the electronic singlet states as interacting fragments. All molecules are calculated at the equilibrium geometries except for the linear structure of OBaF⁻. The calculations were carried out at the BP86/DZP level using BP86/def2-TZVPP optimized geometries. Energy values are given in kcal mol⁻¹

Fragments	OBe (S) + F^− (S)	OMg (S) + F^− (S)	OCa (S) + F^− (S)	OSr (S) + F^− (S)	OBa (S) + F^− (S)	OBa (S) + F^− (S)
Structure	Linear	Linear	Bent	Bent	Bent	Linear
a The values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb. b The values in parentheses give the percentage contribution to the total orbital interactions ΔEorb.
ΔEint	−147.5	−113.5	−79.5	−73.7	−69.8	−62.3
ΔEPauli	57.3	64.4	53.8	47.8	48.6	41.9
ΔEelstat^a	−152.2 (74.3%)	−129.9 (73.0%)	−89.7 (67.3%)	−79.5 (65.4%)	−70.2 (59.3%)	−57.4 (55.1%)
ΔEorb^a	−52.7 (25.7%)	−48.0 (27.0%)	−43.6 (32.7%)	−42.0 (34.6%)	−48.2 (40.7%)	−46.8 (44.9%)
ΔEorb1^b	−24.4 (46.3%)	−29.1 (60.6%)	−19.3 (44.3%)	−12.7 (30.2%)	−21.0 (43.6%)	−18.3 (39.1%)
ΔEorb2^b	−10.1 (19.2%)	−6.8 (14.2%)	−8.5 (19.5%)	−12.4 (29.5%)	−10.8 (22.4%)	−10.1 (21.6%)
ΔEorb3^b	−10.1 (19.2%)	−6.8 (14.2%)	−6.3 (14.4%)	−9.0 (21.4%)	−10.8 (22.4%)	−10.1 (21.6%)
ΔEorb4^b	−4.9 (9.3%)	−3.0 (6.3%)	−4.5 (10.3%)	−3.6 (8.6%)	−1.5 (3.1%)	−5.1 (10.9%)
ΔErest^b	−3.2 (6.0%)	−2.0 (4.7%)	−5.0 (11.5%)	−4.3 (10.3%)	−4.1 (8.5%)	−3.1 (6.7%)

---

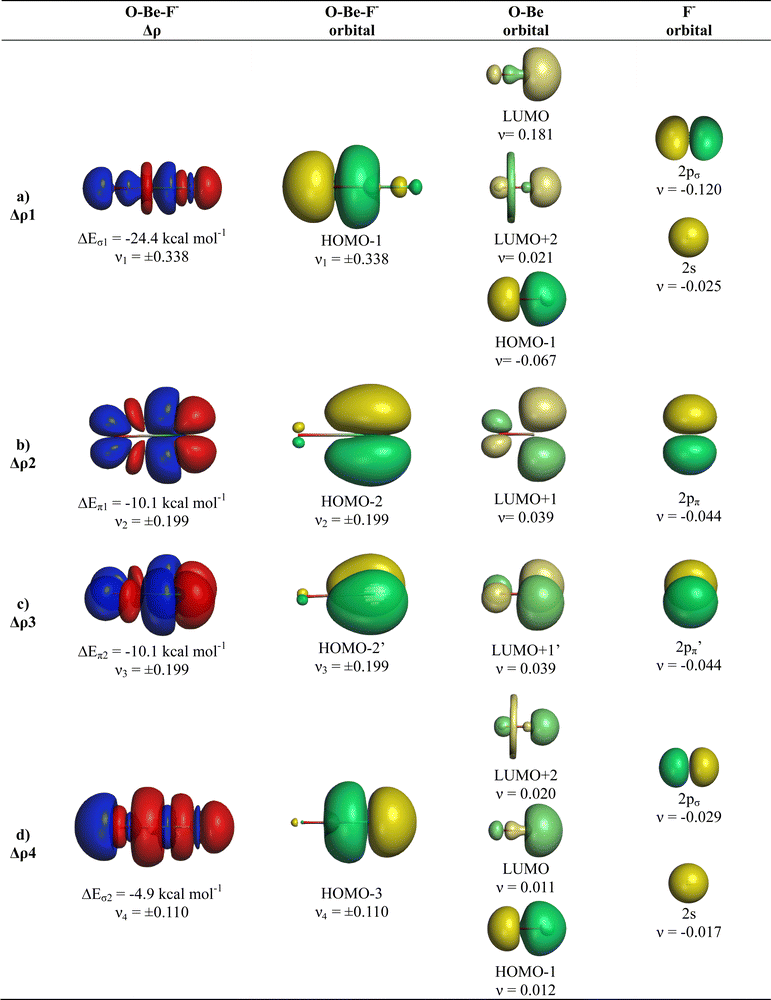
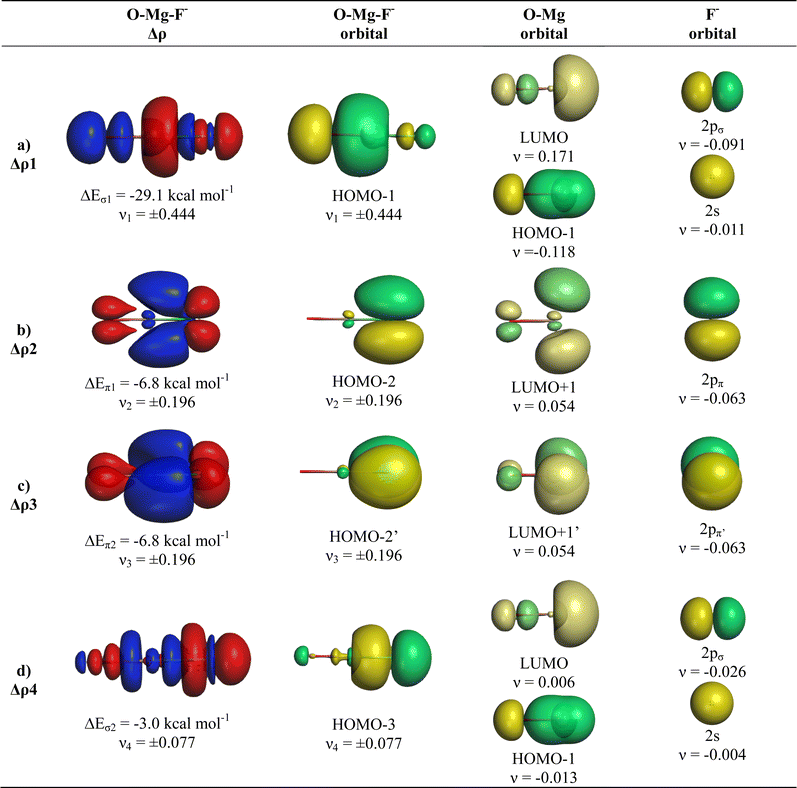
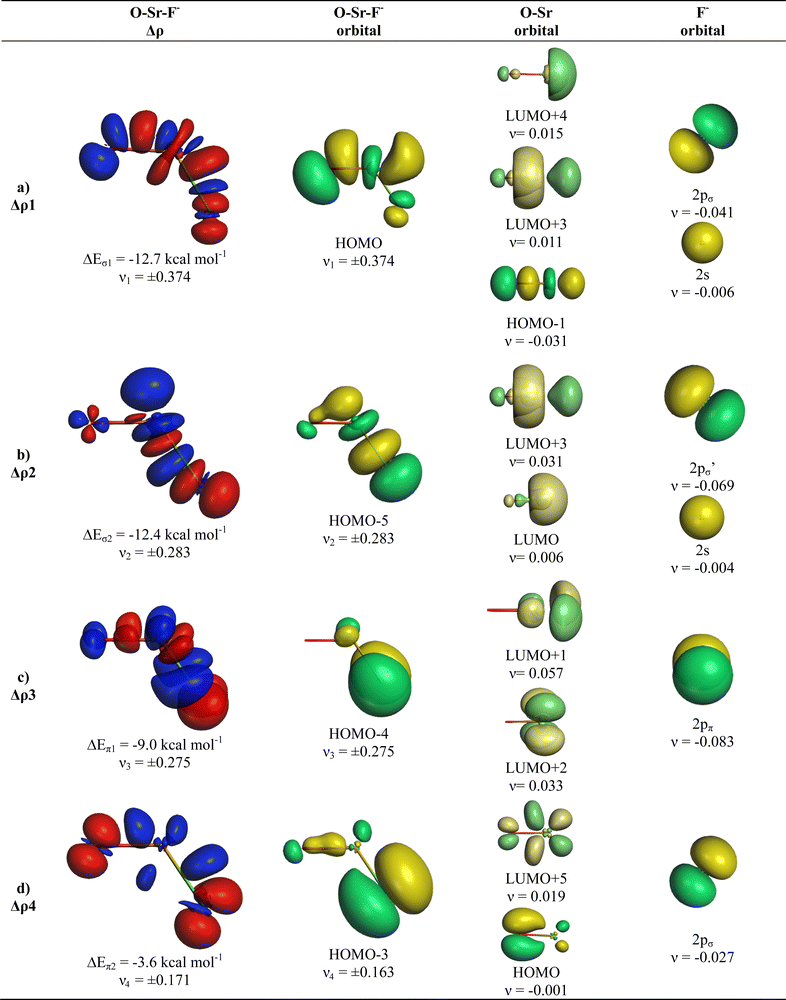
The breakdown of the total orbital term ΔE_orb into pairwise contributions gives deep insight into the formation of the covalent bonds. There are four occupied AOs of F⁻ which can serve as donor orbitals into the four vacant acceptor orbitals of AeO. For the lighter systems we found that there are indeed four pairwise contributions ΔE_orb1 − ΔE_orb4 which provide >90% to ΔE_orb in the linear equilibrium structures of OAeF⁻ (Ae = Be, Mg). Fig. 4 shows the deformation densities Δρ and the associated most important interacting MOs of OBeF⁻. The strongest orbital term ΔE_orb1 comes from the σ donation OBe (LUMO) ← F⁻ (2p_σ,2s) with some further small mixing of OBe orbitals where the contribution of the fluorine 2s AO is small but important, because it allows a second albeit weak σ donation ΔE_orb4 OBe (LUMO+2) ← F⁻ (2p_σ,2s). The stabilization due to the formation of the σ-bonding HOMO−1 of OBeF⁻ comes from the bonding overlap of the 2p_σ AO of F⁻ with the small inside green area at Be atom of OBe, which is hidden by the diffuse shaped green area. It becomes visible by inspection of the HOMO−1 of OBeF⁻ with different isodensity values, which are displayed in Fig. 5 along with the HOMO−1 of OMgF⁻. The figure shows on top the 3D surfaces of the orbital with an isovalue of 0.05e a.u.⁻³. Below are the contour line diagrams with different isovalues in the plane that contains the bond axis. The latter figure nicely shows the attractive interference of the fragment orbitals which lead to a stabilization of ΔE_σ1 = 24.4 kcal mol⁻¹ (OBeF⁻) and ΔE_σ1 = 29.1 kcal mol⁻¹ (OMgF⁻). A peculiar feature of the orbital mixing between the OAe and F⁻ fragments is the sign reversal in the Ae–F region. There is a diffuse bonding region (red lines) away from the Be–F axis and a blue bonding region close to the axis. The latter blue region is even interrupted by the red region, which does not affect the overall positive interference (bonding interaction) of the orbitals.

Fig. 4 Plot of deformation densities Δρ of OBeF⁻. The pairwise orbital interactions and the associated interaction energies (ΔE_orb) between fragments OBe (S) and F⁻ (S) in OBeF⁻ at the equilibrium structure as well as the shape of the most important interacting MOs. The direction of the charge flow is red → blue. (Isovalue 0.03e a.u.⁻³).

Fig. 5 (Top) Plot of the 3D shape of the HOMO−1 orbitals with an isovalue of 0.03e a.u.⁻³ of OBeF⁻ and OMgF⁻ and (bottom) contour line plot of the same orbital HOMO−1 in the plane containing the bond axis with different isovalues at the BP86/def2-TZVPP level. The isovalue below each plot represents the value of the outermost contour in the graph, and the values for the contour settings are in the order of 0.001, 0.002, 0.004, 0.008, 0.02, 0.04, 0.08, 2.0, 4.0e a.u.⁻³.

The orbital interactions ΔE_orb2 and ΔE_orb3 are due to the degenerate π donation OBe (LUMO+1) ← F⁻ (2p_π). Although the stabilization of ΔE_orb4 in OBeF⁻ is rather small, it contributes 9.3% to the covalent bonding and it builds up a different orbital (HOMO−3) than the σ interaction ΔE_orb1 which leads to HOMO−1. The remaining orbital interactions ΔE_rest come from atomic polarization and O–Be interactions and they not relevant for the OBe–F⁻ bond. The HOMO of OBeF⁻ is a degenerate π orbital located mainly at oxygen atom which is only spuriously affected by the bonding interaction with F⁻. The five energetically highest lying orbitals of OBeF⁻ along with those of the other OAeF⁻ anions are shown in Fig. S1 of ESI.‡

It is amazing that four bonding orbitals between two main-group atoms of the first octal row elements can be formed. It was previously suggested that C₂ has a quadruple bond,^71–73 but this claim was disputed by several workers.^74–78 As mentioned in the introduction, a quadruple bond was suggested for AeF⁻ (Ae = Ca, Sr, Ba) because the heavier alkaline atoms use valence d-orbitals for covalent bonding. Although there are four bonding orbitals between OBe and F⁻ we do not think that OBeF⁻ has a genuine quadruple bond. One reason is that the OBe–F⁻ bond comes mainly from electrostatic attraction. According to the EDA-NOCV results, only 25.7% of the bond comes from covalent (orbital) interaction. Another reason is the fact that the chemical bonds in OAeF⁻ are delocalized over three atoms and that a localized description is not appropriate for depicting the bonding situation. We refer to the chemical bonds in OCBBCO, which has a linear structure where all atoms are bonded by triple bonds.⁷⁹ The representation with a Lewis structure that has only triple bonds not only violates the octet rule, it also disregards the appearance of delocalized bonds. Bond delocalization over more than two atoms was not recognized by Gilbert Lewis and it limits the use of Lewis-type structures for describing chemical bonds.⁸⁰

The deformation densities Δρ and the interacting MOs of OMgF⁻ are very similar to those of OBeF⁻ and they are displayed in Fig. 6. The shape of the HOMO−1 hides like the HOMO−1 of OBeF⁻ the bonding character of the orbital. The bonding nature of the HOMO−1 becomes visible by the contour line diagrams shown in Fig. 5 where the isovalues of OMg–F⁻ appear blue in the high-density areas. A close examination of the deformation density reveals the accumulation of electronic charge in the bonding region between Mg and F⁻ with concomitant polarization at fluorine. The numerical results in Table 4 show that the energy contribution of the fourth bond ΔE_orb4 provides only 6.3% of the total covalent bond, but the associated deformation density illustrates the accumulation of electronic charge in the OMg–F⁻ bonding region, which is characteristic for a covalent interaction that comes from the interference of the wave functions.

Fig. 6 Plot of deformation densities Δρ of OMgF⁻. The pairwise orbital interactions and the associated interaction energies (ΔE_orb) between fragments OMg (S) and F⁻ (S) in OMgF⁻ at the equilibrium structure, as well as the shape of the most important interacting MOs. The direction of the charge flow is red → blue. (Isovalue 0.03e a.u.⁻³).

The analysis of the bent equilibrium structures of OAeF⁻ (Ae = Ca, Sr, Ba) is very interesting, because the heavier alkaline earth atoms use their (n)d functions as valence orbitals besides the (n)s orbitals in contrast to the lighter homologues which have (n)p valence orbitals. All three complexes have four pairwise orbital interactions ΔE_orb1 − ΔE_orb4 to the covalent OAe–F⁻ bonding due to OAe ← F⁻ charge donation like the linear structures of the lighter complexes, but the contribution of ΔE_orb4 to the orbital interactions decreases from the calcium adduct (10.3%) to the barium complex where it is only 3.1% of ΔE_orb (Table 4). Fig. 7 shows that the orbital interactions ΔE_orb1, ΔE_orb2 and ΔE_orb4 in OCaF⁻ come from donation of F⁻ into vacant orbitals of CaO which involve mainly valence d AOs of Ca as acceptor orbitals. The LUMO+2 of CaO is mainly a Ca sd_σ hybridized orbital whereas the degenerate LUMO+1/LUMO+1′ are sd_π hybridized orbitals. Since the molecule has a bent geometry there is only one genuine occupied π orbital (HOMO−4) whereas the other occupied valence orbitals that are formed by the interaction between CaO and F⁻ (HOMO, HOMO−1, HOMO−3) are by definition σ orbitals. The shape of the HOMO−3 indicates that it can be considered as in-plane π interaction, although this is not a structurally correct assignment. The mixing of the HOMO of CaO in ΔE_orb3 and ΔE_orb4 indicates the concomitant polarization along with the bond formation due to the interference of the fragment wave functions. The five highest lying MOs of OCaF⁻ are shown in Fig. S1 of ESI.‡

Fig. 7 Plot of deformation densities Δρ of OCaF⁻. The pairwise orbital interactions and the associated interaction energies (ΔE_orb) between fragments OCa (S) and F⁻ (S) in OCaF⁻ at the equilibrium structure, as well as the shape of the most important interacting MOs. The direction of the charge flow is red → blue. (Isovalue 0.03e a.u.⁻³).

The deformation densities Δρ and the interacting MOs of OSrF⁻ show interesting differences to those of OCaF⁻ and are shown in Fig. 8. The π-orbital interaction ΔE_orb2 and the in-plane pseudo-π interaction ΔE_orb3 of OCaF⁻ become ΔE_orb3 and ΔE_orb4 in OSrF⁻. The significantly stronger bending in OSrF⁻ (123.0°) than in OCaF⁻ (144.7°) enhances the second σ interaction in the former anion, which is ΔE_orb4 in OCaF⁻ and becomes the second strongest orbital term ΔE_orb2 in OSrF⁻, which is only slightly weaker (−12.4 kcal mol⁻¹) than ΔE_orb1 (−12.7 kcal mol⁻¹). Examination of the shape of the valence orbitals clearly shows that the d-AOs of Sr are the dominant acceptor orbitals of the metal.

Fig. 8 Plot of deformation densities Δρ of OSrF⁻. The pairwise orbital interactions and the associated interaction energies (ΔE_orb) between fragments OSr (S) and F⁻ (S) in OSrF⁻ at the equilibrium structure, as well as the shape of the most important interacting MOs. The direction of the charge flow is red → blue. (Isovalue 0.03e a.u.⁻³).

We analysed in OBaF⁻ both using the linear structure and with the bent equilibrium geometry in order to identify the driving force for bending. Table 4 shows the numerical EDA-NOCV results for both structures. The bent equilibrium structure encounters stronger Pauli repulsion ΔE_Pauli than the linear form, but the total interaction energy ΔE_int is clearly more attractive in the energy minimum form. This is mainly due to the larger Coulomb attraction ΔE_elstat in the latter structure, which has a significantly shorter OBa–F⁻ bond than the former. But the orbital (covalent) interactions in the bent form are also slightly stronger than in the linear form. Stronger orbital interactions in the bent structure are found for ΔE_orb1 − ΔE_orb3 but not for ΔE_orb4, which has a negligible contribution in the equilibrium geometry. This makes the assignment of a quadruple bond between F⁻ and BaO inappropriate. The same conclusion holds for the bent structures of the Ca and Sr homologues.

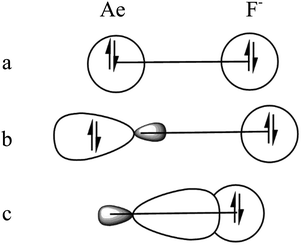
Fig. 9 and 10 show the deformation densities Δρ and the interacting MOs for ΔE_orb1 − ΔE_orb4 of the two structures. The orbitals of the acceptor fragment BaO suggest that the d-AOs are the most important acceptor orbitals of the metal. The strongest orbital interaction ΔE_orb1 comes now from the donation of F⁻ into the 5d_π AO and (with smaller contribution) 6p_π AOs of Ba, which underline the strong contribution of the (n − 1)d AOs for covalent bond particularly for Ba. Close examination of the deformation densities in the liner and bent structures reveals the appearance of local charge accumulation at barium in the region of lone-pair, which comes from the charge donation into vacant d-AOs of the metal. This is clearly visible in the strong orbital interactions ΔE_orb1 − ΔE_orb3. The results nicely agree with the finding of Kaupp et al. about the relevance of d-orbitals for the heavy alkaline earth atoms.⁵² The accumulation negative charge toward the lone-pair area but away from the bonding region explains why the bent structure is mainly stabilized by electrostatic (Coulomb) interaction than by stronger covalent bonding. The detailed bonding analysis suggests that the OAe–F⁻ bonds have a higher electrostatic character than the Ae–F⁻ bonds in the diatomic anions.^1,2 The covalent contributions to the OAe–F⁻ bonds come from dative interactions which have multiple-bond character, but the assignment of a quadruple bond like in the heavier AeF⁻ anion with Ae = Ca, Sr, Ba is not reasonable. We suggest that the bonding situation is best described with a bond line O–AeF⁻ for the electron-sharing bond and an arrow OAe ← F⁻ for the dative bond where the line above Ae in the bent structures signals the accumulation of local charge in the lone-pair region, although the overall charge of Ae is positive (Fig. 11). The situation may be compared with CO, where the carbon atoms carries a positive partial charge but the chemical reactivity and the dipole moment are dominated by the local charge accumulation in the lone-pair region.

Fig. 9 Plot of deformation densities Δρ of OBaF⁻. The pairwise orbital interactions and the associated interaction energies (ΔE_orb) between fragments Oba (S) and F⁻ (S) in OBaF⁻ of the bent equilibrium structure, as well as the shape of the most important interacting MOs. The direction of the charge flow is red → blue. (Isovalue 0.03e a.u.⁻³).

Fig. 10 Plot of deformation densities Δρ of OBaF⁻. The pairwise orbital interactions and the associated interaction energies (ΔE_orb) between fragments OBa (S) and F⁻ (S) in OBaF⁻ of the linear structure, as well as the shape of the most important interacting MOs. The direction of the charge flow is red → blue. (Isovalue 0.03e a.u.⁻³).

Fig. 11 Schematic representation of the bonding situation in the linear and bent structures of OAeF⁻. The bonding line O⁻–Ae⁺F⁻ indicates electron-sharing bonding and the arrow O⁻Ae⁺ ← F⁻ indicates dative bonding both having multiple bond character. The line above Ae signals the accumulation of electronic charge in the lone-pair region in spite of the overall positive charge of Ae atom.

There is a common feature in the deformation densities associated with the orbital interactions ΔE_orb1 and ΔE_orb4 and the MOs of the AeO fragments. Fig. 4 and 6–10 show that an occupied orbital of AeO is involved in the dative interactions OAe ← F⁻ which suggests that there is concomitant polarization in the diatomic moiety. The mode of action between OAe and F⁻ involves a charge induced interaction of the F⁻ ion on the OAe moiety, which in turn yields a favorable hybridization of the vacant orbitals of Ae overlapping with the occupied AOs of F⁻ and leading to a stabilizing interference of the wave functions. This was already found in the diatomic anions AeF⁻, where the charge induction of F⁻ leads to a polarization of the (n)s valence electrons of Ae and the formation of a vacant (n)sp(σ) AO. This is schematically shown in Fig. 12. A related mechanism is operative in OAeF⁻.

Fig. 12 Schematic representation of the σ bond formation in AeF⁻ in three steps. (a) Initial charge distribution in Ae atom and F⁻ where the arrows indicate the total electronic charge; (b) polarization of the valence electrons in Ae and (n)s² → (n)s/p(σ) hybridization; (c) concomitant formation of the vacant orthogonal (n)s/p(σ) orbital at Ae atom which overlaps with the occupied σ orbitals of F⁻ which leads to a polar covalent Ae–F⁻ bond.

Are the OAe–F⁻ bonds really dative bonds? The anion dissociates into the closed-shell species OAe and F⁻, but this does not necessarily indicate that the finally formed bond has dative character. For example, rupture of the carbon–carbon bond of many olefins like F₂C=CF₂ gives carbenes CF₂ in the ¹A₁ singlet state but the double bond comes from the interaction between CF₂ in the ³B₁ triplet state.⁸¹ Likewise dissociate the NaBH₃⁻ Cluster into the closed-shell fragments Na⁻ and BH₃ but the Na–B bond is better described as electron-sharing interactions between Na and BH₃⁻ both in their doublet state.⁸² There is a curve crossing of the ΔE_orb values along the fragmentation pathway when the two sets of fragments are used in the EDA-NOCV calculations, which indicates that the fragments that provide the best description for the chemical bond in the molecule have a different electronic state than the fully separated fragments after dissociation. It could be envisaged that the charge donation OAe ← F⁻ at the equilibrium geometry leads to an electron-sharing interaction between OAe⁻ anion and neutral F in the doublet states. We analysed the anions OAe–F⁻ with the EDA-NOCV method using OAe⁻ and neutral F as interacting fragments. The numerical results are shown in Table S1 of ESI.‡ The calculated values for the orbital interactions ΔE_orb are for all species at the equilibrium geometry significantly larger than using closed-shell fragments OAe and F⁻. Since the final dissociation products are also OAe and F⁻ it becomes obvious that there is no curve crossing of the ΔE_orb, which clearly indicates that the OAe–F⁻ bonds are really dative bonds. It has been shown in numerous previous studies using the EDA-NOCV method that the relative amount of ΔE_orb is a useful indicator for the nature of the nature of the chemical bonds and for the best description of the interacting fragments.

We have further investigated the nature of OAe–F⁻ bonds with a completely different approach which is based on the electronic structures that come from the ab initio calculations at the DLPNO-CCSD(T)/def2-TZVP level using geometries optimized at CCSD(T)/TZVP. The numerical result of the local energy decomposition (LED) method^43–45 are given in Table 5. The LED scheme breaks down the interaction energy between the fragments into different energy terms than the EDA-NOCV approach, but the main conclusion is the same. The electrostatic attraction ΔE^HF_elst is the dominant term of the attraction. The correlation interaction energy ΔE^C_int mostly covers here the charge-transfer term, which can be interpreted as the instantaneous ion pair formation. The most important information comes from the direction of the charge transfer terms ΔE_CT which show that the dynamic charge transfer OAe ← F⁻ completely dominates while the opposite stabilization is negligible. For the interpretation of the remaining terms we refer to the literature.^43–45 They are not important for this study.

Table 5 Local energy decomposition (LED) calculations of OAeF⁻ anions fragmented into OAe (1) and F⁻ (2) singlet fragments. The calculations were carried out at the DLPNO-CCSD(T)/def2-TZVPP level using geometries optimized at CCSD(T)/TZVPP. Energy values are given in kcal mol⁻¹

	[OBe]|[F^−]	[OMg]|[F^−]	[OCa]|[F^−]	[OSr]|[F^−]	[OBa]|[F^−]
ΔE^Cint = ΔE^C-SPCT(1→2) + ΔE^C-SPCT(2→1) + ΔE^Cdisp + ΔE^C-WP + ΔE^C-T
ΔEint	−146.1	−113.3	−90.2	−77.4	−66.1
ΔEel-prep	176.0	173.0	130.7	122.9	96.7
ΔE^HFelst	−273.1	−248.0	−189.5	−162.9	−132.1
ΔE^HFexch	−10.5	−9.9	−11.1	−13.7	−11.3
ΔE^Cint	−38.6	−28.5	−20.2	−23.7	−19.3
ΔE^C-SPCT(1→2)	−0.3	−0.2	−0.8	−1.6	−1.4
ΔE^C-SPCT(2→1)	−38.3	−30.3	−22.1	−21.3	−16.9
ΔE^Cdisp	−1.5	−0.9	−1.4	−2.0	−1.7
ΔE^C-WP	−0.04	−0.06	−0.07	−0.07	−0.08
ΔE^C-T	1.7	3.0	4.2	1.1	0.8

---

We want to comment on the finding of the EDA-NOCV approach and the LED method that the stabilizing interactions of the OAe–F⁻ bonds comes mainly from electrostatic attraction, particularly in the lighter species where Ae = Be, Mg. This is sometimes referred as ionic contribution, which is misleading. Polar covalent bonds have a higher electrostatic character than nonpolar covalent bonds, because the accumulated charge in the bonding region is shifted towards the more electronegative atom where it encounters stronger nuclear attraction. It is a widespread misconception that the charge accumulation at the center of a bond is caused by the electrostatic attraction by two nuclei, which would be stronger than the attraction by only one nucleus. This is not correct, because the electrostatic attraction increases when the electronic charge moves closer to one nucleus and therefore, the contribution of the Coulomb attraction increases at polar bonds. It is the interference of the wave function which leads to a charge accumulation in the bonding region. This has been shown before in several theoretical studies^83,84 and it was nicely demonstrated with a qualitative model by Rioux.⁸⁵ The frequently used naming of ionic rather than electrostatic contribution comes from valence-bond (VB) calculation, which does not have a term for polar bonds. VB calculations give the electronic structure of a molecule with a mixture of two-center terms A–B which comprise the electron-sharing covalent term (λ_A − λ_B) (“Heitler–London (HL)” term) and the two ionic terms (λ_A|⁻λ_B⁺) and (λ⁺_Aλ_B|⁻) as well as the mixing of the terms.⁸⁶ This is a mathematically valid approach, but the appearance of the ionic terms in the calculations must not be identified with ionic bonding. Ionic bonding is found in ionic solids and in solvents where the overlaps of the wave functions are negligible. Polar bonds in molecules are covalent bonds with higher electrostatic character but they are not ionic bonds. The widespread use of the VB model, which was strongly advocated by Pauling,⁸⁷ led to the still frequent use of the term “ionic contribution” although quantum chemical calculations employ in most cases MO or DFT methods. For a more detailed discussion we refer to recent publications of the topic.^68,80,88,89

The final question concerns the different trends of the BDE for Ae–F⁻ and OAe–F⁻. We explained the increase of the bond strength in the diatomic anions AeF⁻ from Ae=Mg to Ae=Ba with the availability of the (n − 1)d AOs of the heavier alkaline earth atoms as acceptor orbitals, which leads to a strengthening of the covalent interactions. It remains to explain why the diatomic oxides AeO show a decreasing order for the BDE when the Ae atoms become larger. Table 6 shows the electron affinities of Ae atoms and diatomic AeO. The experimentally known values for the atoms show that the heavier atoms have a slightly increasing trend for the heavier elements, whereas the trend of the oxides AeO has the opposite order. There is a clear decline of the electron affinity of AeO for the heavier Ae Atoms, which exhibits the same order as the BDE values of OAe–F⁻. Experimental values for the electron affinity of diatomic AeO are not available except for MgO.⁹⁰ The measured value of 37.6 kcal mol⁻¹ is in reasonable agreement with the calculated value of 30.0 kcal mol⁻¹. We think that the trend of the calculated electron affinities in Table 6 is reliable. The data suggest that the Lewis acidity of AeO continuously decreases for the heavier atoms Ae whereas the acceptor ability of the atom Ae increases from Mg to Ba.

Table 6 Electron affinities of atoms Ae and diatomic AeO (in kcal mol⁻¹)

Ae	Ae atom^a	AeO^b
a Experimental value taken from ref. 91.^91 b Calculated at CCSD(T)/def2-TZVPP.
Be	<0	46.4
Mg	<0	30.0
Ca	0.46	18.6
Sr	1.15	10.0
Ba	3.23	7.9

---

Summary and conclusion

The results of this work are summarized as follows:

• The equilibrium structures of the anions OAeF⁻ have linear geometries for Ae = Be and Mg but they are strongly bent for Ae = Sr and Ba. The calcium species is calculated at the CCSD(T)/def2-TZVPP level to have a linear geometry but at BP86/def2-TZVPP is has bending angle of 144.7° which is 0.5 kcal mol⁻¹ below the linear form. The bending potential of the strontium and barium anions is rather low (<10 kcal mol⁻¹).

• The calculated bond dissociation energies of the OAe–F⁻ bonds suggest a record-high BDE of D_e = 144.8 kcal mol⁻¹ for OBeF⁻ at the CCSD(T)/def2-TZVPP level, which is the strongest BDE for a dative bond that has been found so far. The BDE of the heavier homologues have a continuously decreasing order for Ae with Be > Mg (113.1 kcal mol⁻¹) > Ca (84.6 kcal mol⁻¹) > Sr (72.6 kcal mol⁻¹) > Ba (60.0 kcal mol⁻¹).

• The calculations suggest that the Ae–O distances in the anions OAeF⁻ become a bit longer than in diatomic AeO. However, the Ae–O stretching mode of OBeF⁻ and OMgF⁻ is predicted at both levels of theory to have a blue shift towards higher wave numbers whereas the heavier homologues OCaF⁻, OSrF⁻ and OBaF⁻ have a red shift for the Ae–O mode. The calculated Ae–O frequency shifts and the Ae–F stretching vibration are a guideline for the hitherto unknown anions OAeF⁻.

• The calculation of the charge distribution reveals a significant charge donation OAe ← F⁻ with decreasing order for the heavier atoms Ae using the Hirshfeld, Voronoi and CM5 methods. In contrast, the NBO method suggests only negligible charge donation, which comes from the fact that only the (n)s but not the (n)p AOs of atoms Ae are treated as valence orbitals.

• The oxygen atom in OAeF⁻ carries always a higher partial charge than the fluorine atom. This is suggested by all charge partitioning methods and by the molecular electrostatic map. The charge distribution contradicts the standard electronegativities of the atoms which assign fluorine to be more electronegative than oxygen. The surprising partial charges are explained with the bonding situation of the atoms in the actual electronic structure, which may lead to uncommon partial charges.

• The bonding analysis of the OAe–F⁻ bonds using the EDA-NOCV method shows that the bonds have a much higher electrostatic character than the Ae–F⁻ bonds in the diatomic anions. The dative interactions have three major and one minor component. The assignment of a quadruple bond for the heavier species with Ae = Ca, Sr, Ba is not reasonable. The driving force for the bent geometries is the accumulation of electronic charge in the lone-pair region at the Ae atoms, which enhances the electrostatic attraction with the other atoms. A reasonable description of the bonding situation is given by the formula O⁻−Ae⁺ ← F⁻.

Note added in proof

The statement about the strongest dative bond refers to atoms heavier than hydrogen and helium. Proton affinities are dative bonds which can be much stronger than calculated in this work.⁹²

Data availability

The data supporting this article have been included as part of the ESI.‡

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

L. Z. and G. F. acknowledge the financial support from Nanjing Tech University (no. 39837123, 39837132 and the International Cooperation fund), the National Natural Science Foundation of China (no. 22373050), Natural Science Foundation of the Jiangsu province (no. BK20211587), and the State Key Laboratory of Materials-Oriented Chemical Engineering (no. SKL-MCE-23A06), and the Postgraduate Research & Practice Innovation Program of Jiangsu Province (KYCX23_1404). L. Q. and L. Z appreciate the Supported by Cultivation Program for The Excellent Doctoral Dissertation of Nanjing Tech University (2024-10). We appreciate the high performance center of Nanjing Tech University for supporting the computational resources. We also thank the PL-Grid Infrastructure and the Academic Computational Centre Cyfronet of the University of Science and Technology in Krakow for providing computational resources. GF is grateful to Holger Bettinger for pointing out the strength of proton affinities.

References

1. R. Liu, L. Qin, Z. Zhang, L. Zhao, F. Sagan, M. Mitoraj and G. Frenking, Genuine quadruple bonds between two main-group atoms. Chemical bonding in AeF⁻ (Ae = Be–Ba) and isoelectronic EF (E = B–Tl) and the particular role of d orbitals in covalent interactions of heavier alkaline-earth atoms, Chem. Sci., 2023, 14, 4872–4887.
2. L. Qin, Y.-Q. Liu, R. Liu, X. Yang, Z.-H. Cui, L. Zhao, S. Pan, S. Fau and G. Frenking, Analysis of the Unusual Chemical Bonds and Dipole Moments of AeF⁻ (Ae = Be−Ba): A Lesson in Covalent Bonding, Chem. – Eur. J., 2024, e202304136.
3. The term “covalent” was suggested by Irving Langmuir in 1921 (Ref. 4) as expression for the two-electron bond introduced in 1921 by Gilbert Lewis (Ref. 5). There are two types of two-electron covalent bonds. One type is the electron-sharing bond A-B where both atoms contribute one electron each to the bond. The other type of covalent electron-pair bond is the dative bond A → B where both electrons are provided by one atom A. The two types of electron pair bonds were already distinguished by Lewis and the donor and acceptor fragments of a dative bond A → B are often referred to as Lewis aced and Lewis base. The symbol of an arrow → for a dative bond was introduced by Sidgwick: N. V. Sidgwick, Structure of Divalent Carbon Compounds, Chem. Rev., 1931, 9, 77–88.
4. I. Langmuir, Types of Valence, Science, 1921, 54, 59–67.
5. G. N. Lewis, The Atom and the Molecule, J. Am. Chem. Soc., 1916, 38, 762–785.
6. W. Koch, J. R. Collins and G. Frenking, Are there neutral helium compounds which are stable in their ground state? a theoretical investigation of HeBCH and HeBeO, Chem. Phys. Lett., 1986, 132, 330–333.
7. W. Koch, G. Frenking, J. Gauss, D. Cremer and J. R. Collins, Helium chemistry: theoretical predictions and experimental challenge, J. Am. Chem. Soc., 1987, 109, 5917–5934.
8. G. Frenking, W. Koch, J. Gauss and D. Cremer, Stabilities and nature of the attractive interactions in HeBeO, NeBeO, and ArBeO and a comparison with analogs NGLiF, NGBN, and NGLiH (NG = He, Ar). A theoretical investigation, J. Am. Chem. Soc., 1988, 110, 8007–8016.
9. G. Frenking, W. Koch and J. R. Collins, Fixation of nitrogen and carbon monoxide by beryllium oxide: theoretical investigation of the structures and stabilities of NNBeO, OCBeO, and COBeO, J. Chem. Soc., Chem. Commun., 1988, 1147–1148.
10. G. D. Purvis, III and R. J. Bartlett, A full coupled-cluster singles and doubles model: the inclusion of disconnected triples, J. Chem. Phys., 1982, 76, 1910–1918.
11. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
12. J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
13. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
14. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, 2016.
15. E. D. Glendening, C. R. Landis and F. Weinhold, NBO 7.0: new vistas in localized and delocalized chemical bonding theory, J. Comput. Chem., 2019, 40, 2234–2241.
16. F. L. Hirshfeld, Bonded-atom fragments for describing molecular charge densities, Theor. Chim. Acta, 1977, 44, 129–138.
17. A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, Charge Model 5: An Extension of Hirshfeld Population Analysis for the Accurate Description of Molecular Interactions in Gaseous and Condensed Phases, J. Chem. Theory Comput., 2012, 8, 527–541.
18. C. Fonseca Guerra, J.-W. Handgraaf, E. J. Baerends and F. M. Bickelhaupt, Voronoi deformation density (VDD) charges: assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD methods for charge analysis, J. Comput. Chem., 2004, 25, 189–210.
19. I. Mayer, Charge, bond order and valence in the AB initio SCF theory, Chem. Phys. Lett., 1983, 97, 270–274.
20. T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
21. K. Morokuma, Molecular Orbital Studies of Hydrogen Bonds. III. C=O⋯H–O Hydrogen Bond in H₂CO⋯H₂O and H₂CO⋯2H₂O, J. Chem. Phys., 2003, 55, 1236–1244.
22. T. Ziegler and A. Rauk, On the calculation of bonding energies by the Hartree Fock Slater method, Theor. Chim. Acta, 1977, 46, 1–10.
23. M. Mitoraj and A. Michalak, Donor–Acceptor Properties of Ligands from the Natural Orbitals for Chemical Valence, Organometallics, 2007, 26, 6576–6580.
24. M. Mitoraj and A. Michalak, Applications of natural orbitals for chemical valence in a description of bonding in conjugated molecules, J. Mol. Model., 2008, 14, 681–687.
25. A. Michalak, M. Mitoraj and T. Ziegler, Bond Orbitals from Chemical Valence Theory, J. Phys. Chem. A, 2008, 112, 1933–1939.
26. M. P. Mitoraj, A. Michalak and T. Ziegler, A Combined Charge and Energy Decomposition Scheme for Bond Analysis, J. Chem. Theory Comput., 2009, 5, 962–975.
27. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967.
28. E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, O. Baseggio, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, C. Cappelli, L. Cavallo, C. Daul, D. P. Chong, D. V. Chulhai, L. Deng, R. M. Dickson, J. M. Dieterich, F. Egidi, D. E. Ellis, M. van Faassen, L. Fan, T. H. Fischer, A. Förster, C. Fonseca Guerra, M. Franchini, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. Goez, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, S. Gusarov, F. E. Harris, P. van den Hoek, Z. Hu, C. R. Jacob, H. Jacobsen, L. Jensen, L. Joubert, J. W. Kaminski, G. van Kessel, C. König, F. Kootstra, A. Kovalenko, M. V. Krykunov, P. Lafiosca, E. van Lenthe, D. A. McCormack, M. Medves, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, C. A. Peeples, P. H. T. Philipsen, D. Post, C. C. Pye, H. Ramanantoanina, P. Ramos, W. Ravenek, M. Reimann, J. I. Rodríguez, P. Ros, R. Rüger, P. R. T. Schipper, D. Schlüns, H. van Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solá, M. Stener, M. Swart, D. Swerhone, V. Tognetti, G. te Velde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, ADF, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2019, https://www.scm.com.
29. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
30. E. Van Lenthe and E. J. Baerends, Optimized Slater-type basis sets for the elements 1–118, J. Comput. Chem., 2003, 24, 1142–1156.
31. J. C. Slater, in Adv. Quantum Chem., ed. P.-O. Löwdin, Academic Press, 1972, vol. 6, pp. 1–92.
32. D. M. Andrada and C. Foroutan-Nejad, Energy components in energy decomposition analysis (EDA) are path functions; why does it matter?, Phys. Chem. Chem. Phys., 2020, 22, 22459–22464.
33. M. Solà, M. Duran and J. Poater, The energy components of the extended transition state energy decomposition analysis are path functions: the case of water tetramer, Theor. Chem. Acc., 2021, 140, 33.
34. J. Poater, D. M. Andrada, M. Solà and C. Foroutan-Nejad, Path-dependency of energy decomposition analysis & the elusive nature of bonding, Phys. Chem. Chem. Phys., 2022, 24, 2344–2348.
35. F. M. Bickelhaupt, C. Fonseca Guerra, M. Mitoraj, F. Sagan, A. Michalak, S. Pan and G. Frenking, Clarifying notes on the bonding analysis adopted by the energy decomposition analysis, Phys. Chem. Chem. Phys., 2022, 24, 15726–15735.
36. L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Energy decomposition analysis, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1345.
37. G. Frenking and F. Matthias Bickelhaupt, The Chemical Bond, 2014, pp. 121–157.
38. L. Zhao, M. Hermann, N. Holzmann and G. Frenking, Dative bonding in main group compounds, Coord. Chem. Rev., 2017, 344, 163–204.
39. L. Zhao, M. Hermann, W. H. E. Schwarz and G. Frenking, The Lewis electron-pair bonding model: modern energy decomposition analysis, Nat. Rev. Chem., 2019, 3, 48–63.
40. L. Zhao, S. Pan and G. Frenking, in Comprehensive Computational Chemistry, ed. M. Yáñez and R. J. Boyd, Elsevier, Oxford, 1st edn, 2024, pp. 322–361.
41. G. Frenking, R. Tonner, S. Klein, N. Takagi, T. Shimizu, A. Krapp, K. K. Pandey and P. Parameswaran, New bonding modes of carbon and heavier group 14 atoms Si–Pb, Chem. Soc. Rev., 2014, 43, 5106–5139.
42. G. Frenking, M. Hermann, D. M. Andrada and N. Holzmann, Donor–acceptor bonding in novel low-coordinated compounds of boron and group-14 atoms C–Sn, Chem. Soc. Rev., 2016, 45, 1129–1144.
43. A. Altun, M. Saitow, F. Neese and G. Bistoni, Local Energy Decomposition of Open-Shell Molecular Systems in the Domain-Based Local Pair Natural Orbital Coupled Cluster Framework, J. Chem. Theory Comput., 2019, 15, 1616–1632.
44. A. Altun, R. Izsák and G. Bistoni, Local energy decomposition of coupled-cluster interaction energies: interpretation, benchmarks, and comparison with symmetry-adapted perturbation theory, Int. J. Quantum Chem., 2021, 121, e26339.
45. W. B. Schneider, G. Bistoni, M. Sparta, M. Saitow, C. Riplinger, A. A. Auer and F. Neese, Decomposition of Intermolecular Interaction Energies within the Local Pair Natural Orbital Coupled Cluster Framework, J. Chem. Theory Comput., 2016, 12, 4778–4792.
46. S. Saebo and P. Pulay, Local Treatment of Electron Correlation, Annu. Rev. Phys. Chem., 1993, 44, 213–236.
47. F. Neese, F. Wennmohs and A. Hansen, Efficient and accurate local approximations to coupled-electron pair approaches: an attempt to revive the pair natural orbital method, J. Chem. Phys., 2009, 130, 114108.
48. F. Neese, A. Hansen and D. G. Liakos, Efficient and accurate approximations to the local coupled cluster singles doubles method using a truncated pair natural orbital basis, J. Chem. Phys., 2009, 131, 064103.
49. Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, Communication: an improved linear scaling perturbative triples correction for the domain based local pair-natural orbital based singles and doubles coupled cluster method [DLPNO-CCSD(T)], J. Chem. Phys., 2018, 148, 011101.
50. C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, Natural triple excitations in local coupled cluster calculations with pair natural orbitals, J. Chem. Phys., 2013, 139, 134101.
51. G. H. K. P. Huber, Molecular Spectra and Molecular Structure, Media, New York, 1979.
52. M. Kaupp, P. V. R. Schleyer, H. Stoll and H. Preuss, The question of bending of the alkaline earth dihalides MX2 (M = beryllium, magnesium, calcium, strontium, barium; X = fluorine, chlorine, bromine, iodine). An ab initio pseudopotential study, J. Am. Chem. Soc., 1991,(113), 6012–6020.
53. M. Hargittai, The molecular geometry of gas-phase metal halides, Coord. Chem. Rev., 1988, 91, 35–88.
54. The calculated Ae–F bond lengths [Å] in AeF⁻ at CCSD(T)/def2-TZVPP [BP86/def2-TZVPP] reported in ref. 1 are 1.429 [1.428] for BeF⁻, 1.840 [1.847) for MgF⁻, 2.104 [1.992] for CaF⁻, 2.237 [2.134] for SrF, 2.339 [2.234] for BaF⁻.
55. Computational Chemistry Comparison and Benchmark Data Base Release 22. Standard Reference Database 101, National Institute of Standards and Technology, 2022.
56. J. S. Murray and P. Politzer, Molecular electrostatic potentials and noncovalent interactions, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1326.
57. R. Tonner, F. Öxler, B. Neumüller, W. Petz and G. Frenking, Carbodiphosphoranes: The Chemistry of Divalent Carbon(0), Angew. Chem., Int. Ed., 2006, 45, 8038–8042.
58. R. Tonner and G. Frenking, C(NHC)₂: Divalent Carbon(0) Compounds with N-Heterocyclic Carbene Ligands—Theoretical Evidence for a Class of Molecules with Promising Chemical Properties, Angew. Chem., Int. Ed., 2007, 46, 8695–8698.
59. R. Tonner and G. Frenking, Divalent Carbon(0) Chemistry, Part 1: Parent Compounds, Chem. – Eur. J., 2008, 14, 3260–3272.
60. R. Tonner and G. Frenking, Divalent Carbon(0) Chemistry, Part 2: Protonation and Complexes with Main Group and Transition Metal Lewis Acids, Chem. – Eur. J., 2008, 14, 3273–3289.
61. S. Klein, R. Tonner and G. Frenking, Carbodicarbenes and Related Divalent Carbon(0) Compounds, Chem. – Eur. J., 2010, 16, 10160–10170.
62. J. Hinze, The concept of electronegativity of atoms in molecules, Theor. Comput. Chem., 1999, 6, 189–212.
63. D. Bergmann and J. Hinze, Electronegativity and Molecular Properties, Angew. Chem., Int. Ed. Engl., 1996, 35, 150–163.
64. K. B. Wiberg, Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane, Tetrahedron, 1968, 24, 1083–1096.
65. I. Mayer, Bond order and valence: Relations to Mulliken's population analysis, Int. J. Quantum Chem., 1984, 26, 151–154.
66. A. J. Bridgeman, G. Cavigliasso, L. R. Ireland and J. Rothery, The Mayer bond order as a tool in inorganic chemistry, J. Chem. Soc., Dalton Trans., 2001, 2095–2108.
67. I. Mayer, Bond order and valence indices: a personal account, J. Comput. Chem., 2007, 28, 204–221.
68. L. Zhao, S. Pan and G. Frenking, The nature of the polar covalent bond, J. Chem. Phys., 2022, 157, 034105.
69. K. Fukui, Theory of Orientation and Stereoselection, Springer Verlag, Berlin, 1975.
70. R. B. Woodward and R. Hoffmann, The Conservation of Orbital Symmetry, Verlag Chemie, Weinheim, 1970.
71. S. Shaik, D. Danovich, W. Wu, P. Su, H. S. Rzepa and P. C. Hiberty, Quadruple bonding in C2 and analogous eight-valence electron species, Nat. Chem., 2012, 4, 195–200.
72. D. Danovich, P. C. Hiberty, W. Wu, H. S. Rzepa and S. Shaik, The Nature of the Fourth Bond in the Ground State of C₂: The Quadruple Bond Conundrum, Chem. – Eur. J., 2014, 20, 6220–6232.
73. S. Shaik, D. Danovich, B. Braida and P. C. Hiberty, The Quadruple Bonding in C₂ Reproduces the Properties of the Molecule, Chem. – Eur. J., 2016, 22, 4116–4128.
74. W. Zou and D. Cremer, C₂ in a Box: Determining Its Intrinsic Bond Strength for the X¹Σ⁺_g Ground State, Chem. – Eur. J., 2016, 22, 4087–4099.
75. M. Hermann and G. Frenking, The Chemical Bond in C₂, Chem. – Eur. J., 2016, 22, 4100–4108.
76. M. Piris, X. Lopez and J. M. Ugalde, The Bond Order of C₂ from a Strictly N-Representable Natural Orbital Energy Functional Perspective, Chem. – Eur. J., 2016, 22, 4109–4115.
77. D. L. Cooper, R. Ponec and M. Kohout, New insights from domain-averaged Fermi holes and bond order analysis into the bonding conundrum in C₂, Mol. Phys., 2016, 114, 1270–1284.
78. D. W. O. de Sousa and M. A. C. Nascimento, Is There a Quadruple Bond in C₂?, J. Chem. Theory Comput., 2016, 12, 2234–2241.
79. L. C. Ducati, N. Takagi and G. Frenking, Molecules with All Triple Bonds: OCBBCO, N₂BBN₂, and [OBBBBO]²⁻, J. Phys. Chem. A, 2009, 113, 11693–11698.
80. L. Zhao, W. H. E. Schwarz and G. Frenking, The Lewis electron-pair bonding model: the physical background, one century later, Nat. Rev. Chem., 2019, 3, 35–47.
81. D. M. Andrada, J. L. Casals-Sainz, Á. Martín Pendás and G. Frenking, Dative and Electron-Sharing Bonding in C₂F₄, Chem. – Eur. J., 2018, 24, 9083–9089.
82. S. Pan and G. Frenking, Comment on “Realization of Lewis Basic Sodium Anion in the NaBH₃⁻ Cluster”, Angew. Chem., Int. Ed., 2020, 59, 8756–8759.
83. K. Ruedenberg, The Physical Nature of the Chemical Bond, Rev. Mod. Phys., 1962, 34, 326–376.
84. W. Kutzelnigg, The Physical Mechanism of the Chemical Bond, Angew. Chem., Int. Ed. Engl., 1973, 12, 546–562.
85. F. Rioux, The Covalent Bond Examined Using the Virial Theorem, Chem. Educ., 2003, 8, 101.
86. S. Shaik and P. C. Hiberty, A Chemist's Guide to Valence Bond Theory, 2007, pp. 40–80.
87. L. Pauling, The Nature of the Chemical Bond, Cornell University Press, 1960.
88. S. Pan and G. Frenking, A Critical Look at Linus Pauling's Influence on the Understanding of Chemical Bonding, Molecules, 2021, 26, 4695.
89. G. Frenking, Heretical thoughts about the present understanding and description of the chemical bond*, Mol. Phys., 2022, 121, e2110168.
90. J. H. Kim, X. Li, L.-S. Wang, H. L. de Clercq, C. A. Fancher, O. C. Thomas and K. H. Bowen, Vibrationally Resolved Photoelectron Spectroscopy of MgO- and ZnO- and the Low-Lying Electronic States of MgO, MgO-, and ZnO, J. Phys. Chem. A, 2001, 105, 5709–5718.
91. J. C. Wheeler, Electron Affinities of the Alkaline Earth Metals and the Sign Convention for Electron Affinity, J. Chem. Educ., 1997, 74, 123.
92. R. Tonner, G. Heydenrych and G. Frenking, First and Second Proton Affinities of Carbon Bases, Chem. Phys. Chem., 2008, 9, 1474.

---

Footnotes

† This paper is dedicated to Prof. Manfred Reetz on the occasion of his 80th birthday.

‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01909a

§ L. Q., R. L. and F. S. contributed equally.

---