Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Controlling and predicting alkyl-onium electronic structure†
Frances K. Towers
Tompkins
a,
Lewis G.
Parker
 a,
Richard M.
Fogarty
a,
Richard M.
Fogarty
 b,
Jake M.
Seymour
b,
Jake M.
Seymour
 a,
Ekaterina
Gousseva
a,
David C.
Grinter
a,
Ekaterina
Gousseva
a,
David C.
Grinter
 c,
Robert G.
Palgrave
c,
Robert G.
Palgrave
 d,
Christopher D.
Smith
a,
Roger A.
Bennett
d,
Christopher D.
Smith
a,
Roger A.
Bennett
 a,
Richard P.
Matthews
a,
Richard P.
Matthews
 *e and
Kevin R. J.
Lovelock
*e and
Kevin R. J.
Lovelock
 *a
*a
aDepartment of Chemistry, University of Reading, UK. E-mail: k.r.j.lovelock@reading.ac.uk
bDepartment of Chemistry, Imperial College London, UK
cDiamond Light Source, UK
dDepartment of Chemistry, University College London, UK
eDepartment of Biosciences, University of East London, UK. E-mail: RMatthews3@uel.ac.uk
First published on 16th August 2024
Abstract
X-ray photoelectron spectroscopy (XPS) and ab initio calculations show that fully alkylated onium cation electronic structure can be tuned using both the alkyl chains and the central onium atom. The key for tuning the central onium atom is methyl versus longer alkyl chains, allowing selection of the optimum cation for a wide range of applications, including catalysis and biocides.
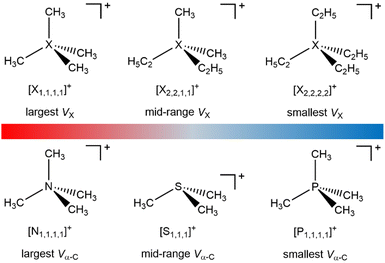
Fully alkylated onium cations feature in a wide range of applications,1 including organic synthesis,2–4 biocides,5,6 electrochemical energy storage materials,7,8 friction/corrosion additives,9,10 and solar energy capture/storage materials.11 Two key structural variations of alkylated oniums are: (i) alkyl substituents, CnH2n+1, e.g. from four CH3 in tetramethylammonium ([N1,1,1,1]+), to much longer alkyls; (ii) central X atom e.g. tetraalkylammonium ([Nn,n,n,n]+), trialkylsulfonium ([Sn,n,n]+) or tetraalkylphosphonium ([Pn,n,n,n]+) (Fig. 1). This structural variation gives the potential to finely tune properties and performance,8 although the focus has been on using the cation alkyl chain to control hydrophobicity or steric interactions.
 | ||
| Fig. 1 Fully alkylated onium cation structures (see ESI,† Section S3 for cations studied). | ||
Electrostatic interactions are key for onium–anion and onium–neutral molecule interactions, as there are no π-bonds and only σ-bonds on fully alkylated onium cations. In synthesis, hydrogen bonding catalysis is based on electrostatic interactions between onium cations and substrates,2,3 and phase-transfer catalysis relies on anion–onium cation electrostatic interactions.4 For biocides the first stage of [Nn,n,n,n]+ interaction with a cell membrane is via an electrostatic interaction between the positively charged [Nn,n,n,n]+ headgroup and anionic parts of the membrane.5,6,12–15 Moreover, a single calculable electronic descriptor that can capture through-bond effects has been used to understand the impact of substituents on [Nn,n,n,n]+,16,17 and a range of calculated electronic structure properties (e.g. orbital energies) have been used to predict the impact of [Nn,n,n,n]+ supporting electrolytes on electrochemical performance.8 Despite these extensive examples, there is still a large knowledge gap in the electronic structure of fully alkylated onium cations that underpins electrostatic interactions in the wide variety of applications. Using a combination of experimental X-ray photoelectron spectroscopy (XPS) and lone-ion-SMD (solvation model based on density) density functional theory (DFT) calculations we provide both experimental and computational evidence on liquid-phase onium cations.
Element-specific XPS core-level binding energies, EB(core), are capable of capturing multiple electronic structure descriptors for each onium cation, e.g. EB(N 1s) and EB(C 1s). Moreover, EB(core) and the electrostatic potential at a nucleus, Vn, have been found to be linearly correlated for ionic liquids (ILs),18,19 meaning that EB(core) can be readily interpreted unlike e.g. chemical shifts in NMR. Furthermore, Vn is an excellent localised non-covalent bonding/reactivity strength descriptor;20 atoms with large EB(core) and large Vn will attract electrons relative to atoms with small EB(core) and small Vn.
ILs with relatively weakly interacting anions, e.g. [NTf2]− (bis[(trifluoromethane)sulfonyl]imide) or [FSI]− (bis(fluorosulfonyl)imide), can be used to probe intrinsic cation properties, as cations are effectively in a sea of anions that give non-specific interactions.18,19 Additionally, lone-cation-SMD calculations (i.e. with no counteranions) capture the inherent cation properties.
The range of onium cations studied in the liquid-phase using XPS to date is limited, with the main focus on onium cations in ILs21–25 (ILs have sufficiently low vapour pressure to be used with standard XPS apparatus26). A key finding for XPS of [Nn,n,n,n]+-based ILs was the impact of cations with linear (e.g. [N6,6,6,14]+ ammonium cation) versus ring (e.g. [C8C1Pyrr]+ pyrrolidinium cation) alkyl on the IL electronic structure; cation–anion interactions were linked to the conformational flexibility of the cation.22,23 However, the number of different onium cations studied was relatively limited, leaving open questions, e.g. what is the influence of the alkyl substituent on onium electronic structure? Herein, we measured EB(core) for 12 [onium cation][NTf2] and two [onium cation][FSI] ILs using XPS and performed lone-ion-SMD DFT calculations (ESI† Section S3) for 31 onium cations to address these questions.
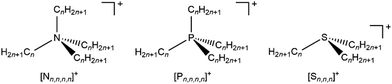
Varying the alkyl chain length of [Nn,n,n,n]+ from methyl to longer has a significant and predictable impact on EB(Ncation 1s). N 1s XPS for the two ILs [N4,1,1,1][NTf2] and [N4,2,2,2][NTf2] gave a relatively large ΔEB(Ncation 1s) of −0.36 eV (Fig. 2a and 3a and ESI,† Table S8), representing ΔEB(Ncation 1s) going from three CH3 to three longer alkyl chains. Each successive change of one CH3 to one longer alkyl gives ΔEB(Ncation 1s) of ∼−0.12 eV (Fig. 2a), as demonstrated by ΔEB(Ncation 1s) from [N4,1,1,1][NTf2] to [N3,2,1,1][NTf2] to [N4,4,4,1][NTf2] to [N4,2,2,2][NTf2] (Fig. 2a and 3a and ESI,† Table S8). This effect of the alkyl chain lengths on cation electronic structure is independent of the anion identity, as the same ΔEB(Ncation 1s) effect is observed when the [FSI]− anion was used, e.g. [N4,4,4,1][FSI] versus [N4,1,1,1][FSI] (ESI,† Fig. S17 and Table S8).
 | ||
| Fig. 2 Experimental and calculated core XP spectra: (a) N 1s,exp. for [cation][NTf2] where cation = [N3,1,1,1]+, [N4,1,1,1]+, [N6,1,1,1]+, [N3,2,1,1]+, [N4,4,4,1]+, [N8,8,8,1]+, [C4C1Pip]+, [C8C1Pyrr]+, [N4,2,2,2]+ and [N8,2,2,2]+; (b) N 1s,calc. for [N1,1,1,1]+, [N2,1,1,1]+, [N2,2,1,1]+, [N2,2,2,1]+ and [N2,2,2,2]+; (c) S 2p,exp. for [S2,2,1][NTf2] and [S2,2,2][NTf2]; (d) S 2p,calc. for [S1,1,1]+, [S2,1,1]+, [S2,2,1]+ and [S2,2,2]+. Experimental XP spectra are area normalised and charge referenced using methods given in ESI,† Section S5. Traces are vertically offset for clarity. | ||
 | ||
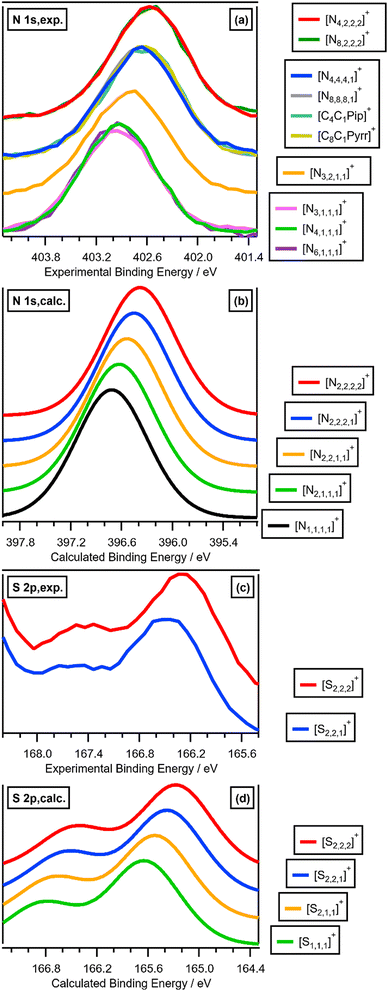
| Fig. 3 (a) Experimental and calculated EB(Ncation 1s). (b) Experimental and calculated EB(Scation 2p3/2). (c) Calculated EB(Pcation 2p3/2). Where n is used as a label in this figure, n ≥ 2. | ||
Changing the alkyl substituent from ethyl to longer had no discernible impact on EB(Ncation 1s), with clear evidence from three cases: (i) [Nn,1,1,1]+ (where n = 3, 4 and 6) gave the same EB(Ncation 1s); (ii) [Nn,2,2,2]+ (where n = 4 and 8) gave the same EB(Ncation 1s); (iii) [N4,4,4,1]+ and [N8,8,8,1]+ gave the same EB(Ncation 1s) (Fig. 2a and ESI,† Table S8).
Linear versus large ring alkyl chains, e.g. ammonium versus pyrrolidinium, had no discernible impact on experimental EB(Ncation 1s). Cations with one CH3 substituent and either all linear longer alkyl chains ([N4,4,4,1][NTf2], [N8,8,8,1][NTf2]) or large ring alkyl chains ([C4C1Pip][NTf2], [C8C1Pyrr][NTf2]) gave the same EB(Ncation 1s) within experimental uncertainty (Fig. 2a and ESI,† Table S8).
Calculated EB(Ncation 1s) match experimental EB(Ncation 1s) very well, both visually (Fig. 2a and b and ESI,† Fig. S18) and an excellent linear correlation (ESI,† Fig. S20). Going from [N1,1,1,1]+ to [N2,2,2,2]+, each time a CH3 is changed to a longer alkyl chain gives ΔEB(Ncation 1s) ∼−0.08 eV (Fig. 2b and 3a), which is slightly smaller than the experimental ΔEB(Ncation 1s) of ∼−0.12 eV. This difference may arise from the choice of functional/basis set combinations; the wB97XD functional was selected as it has minimal self-interaction error and correctly describes long-range electron–electron interactions (important in determining ionisation energies). An alternative explanation is the failure of the SMD model to capture local interactions (switching from IL SMD to water SMD had a small impact on ΔEB(Ncation 1s), Fig. S19c, S19d and Table S9, ESI†).
The effect of varying alkyl chain lengths for all key fully alkylated oniums is the same. For [Sn,n,n]+ and [Pn,n,n,n]+ cations the effect of changing from methyl to longer alkyl substituents on EB(Scation 2p) and EB(Pcation 2p) respectively match those of EB(Ncation 1s) for [Nn,n,n,n]+. Comparing experimental S 2p XPS for the two ILs [S2,2,1][NTf2] and [S2,2,2][NTf2] gave ΔEB(S 2p3/2) = −0.16 eV (Fig. 2c and 3b). Furthermore, going from [S2,2,1]+ to [S2,2,2]+, gives a calculated ΔEB(S 2p3/2) = −0.10 eV (Fig. 2c and 3b and ESI,† Table S8), demonstrating that the calculations match the experiments very well. Moreover, for [Pn,n,n,n]+ each time a methyl is changed to a longer alkyl gives ΔEB(Pcation 2p3/2) ∼−0.07 eV (Fig. 3c and ESI,† Fig. S21).
The excellent matches for the experimental and calculated EB(Xcation core) (where X = N, S or P) demonstrate that the changes in the experimental EB(Xcation core) are due to ground state effects and can be related directly to the molecular electrostatic potential at the central onium atom nucleus, VX (Fig. 5). The differences in EB(Xcation core) for fully alkylated onium cations are explained by the alkyl group inductive effect, where the additive strength is –CH2CH2CH3 ≈ –C2H5 < –CH3.27 Four CH3 substituents gives the largest EB(Xcation core) = largest VX = strongest X atom electrostatic interaction. Conversely, four longer alkyl substituents gives the smallest EB(Ncation 1s) = smallest VX = weakest X atom electrostatic interaction.
Changing the alkyl groups from linear to branched (i.e. going from each α-C atom having one C and two H to each α-C atom having two C and one H) gives a small impact on EB(Ncation 1s) and VN. Changing the cation from [N2,2,2,2]+ to [Ni3,i3,i3,i3]+ (i3 = isopropyl, ESI,† Table S3) gave ΔEB(Ncation 1s) = −0.09 eV (ESI,† Fig. S22 and Table S9). [Ni3,i3,i3,i3]+ is unlikely to be stable in solution, but adding one branched alkyl group to give e.g. [Ni3,2,2,2]+ will give stable cations and will allow fine tuning of EB(Ncation 1s) and VN.
The electronic environment of the carbon atoms in onium cations can be finely controlled by changing Xcation (Fig. 4 and ESI,† Section S14), as demonstrated by using our second spectroscopic handle, EB(C 1s). EB(Cα-C 1s) and therefore VC can be tuned using the central X atom identity. The experimental order for EB(Cα-C 1s) is N > S > P (Fig. 4), which matches literature EB for N versus P (S was not included in ref. 22), partial charge calculations,28 and also matches the order of the central atom electronegativity, i.e. N > S > P, so nitrogen withdraws the most electron density from α-C to Xcation (Fig. 5).
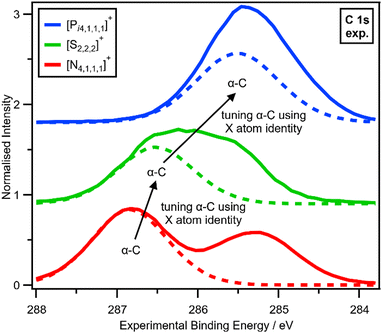 | ||
| Fig. 4 Tuning α-C using X atom identity. Experimental C 1s XP spectra for [Pi4,1,1,1][NTf2], [S2,2,2][NTf2] and [N4,1,1,1][NTf2] ionic liquids. Experimental XP spectra are area normalised and charge referenced using methods given in ESI,† Section S5. Traces are vertically offset for clarity. | ||
V X for Xcation can be inferred from EB(Cα-C 1s), given that all onium cations will have approximately the same overall charge of +1, so any change in Vα-C will have the opposite effect on VX. EB(Cα-C 1s) and Vα-C trend N > S > P, so VX (relative to a neutral X atom) trends P > S > N.
Both EB(Xcation core) and EB(Cα-C 1s) can be tuned using the counteranion identity.19,21,22 Changing from Cl− to [NTf2]− had the same effect (within experimental uncertainty) of +0.4 eV on EB(Cα-C 1s), ΔEB(Ncation 1s) and ΔEB(Pcation 2p).19,21,22 This effect of the anion is similar in magnitude to changing from four alkyl substituents to four longer alkyl substituents (Fig. 3).
Given that the onium cation headgroup will dominate any electrostatic interaction with a substrate, both VX and Vα-C are clearly vital descriptors. We have demonstrated that both VX and Vα-C can be predictably controlled for onium cations by the choice of alkyl chain length and central X atom identity. Furthermore, for certain applications where cation–anion are likely to be bound together (e.g. ion pairing in solvents with low relative permittivity, in ionic liquids), the counteranion identity can also contribute strongly to both VX and Vα-C.
We envisage this information being useful in two areas. Firstly, VX and Vα-C are expected to be very useful descriptors for developing models using both quantitative structure–property relationships (QSPR) and machine learning. Such descriptors could be calculated using the same DFT methods demonstrated here, or a cheaper but cruder method would be to use the linear relationships developed here to make predictions of VX and Vα-C. Secondly, a semi-quantitative judgement of the optimum onium cation to be used in any application can be made using our results. The largest VX (i.e. strongest X atom electrostatic interaction) would be [X1,1,1,1][FAP] (the very weakly electrostatically interacting anion [FAP]− = tris(pentafluoroethyl)trifluorophosphate19), and the smallest VX (i.e. weakest X atom electrostatic interaction) would be e.g. [X2,2,2,2]Cl. For biocides for example, a strong electrostatic interaction is expected to be desirable. Therefore, focusing on electronic effects (and ignoring steric effects) [X1,1,1,1]+ would be better than [X2,2,2,2]+. However, such a selection is challenging as both VX and Vα-C are affected in opposite directions by the central X atom identity, and a single site interaction model cannot be assumed.
We have presented new experimental and calculated electronic descriptors for judging electrostatic interaction strengths in fully-alkylated onium cations (Fig. 5). Xcation, α-C and Calkyl can be predictably tuned using a combination of the alkyl chain lengths, the central X atom identity and the counteranion.
We acknowledge support from the Royal Society for a University Research Fellowship for K. R. J. L. (URF\R\150353 and URF\R\211005) and further awards (RGF\EA\180089, RGF\R1\180053, RF\ERE\210061 and RF\ERE\231015). R. P. M. acknowledges support from the Royal Society of Chemistry through the RSC Research Fund grant (R21-4762139998). We acknowledge Diamond Light Source for time on Beamline B07-B under Proposals SI29413, SI30367, SI31939, SI33378 and SI35207.
Data availability
The data underlying this study are openly available in the University of Reading Research Data Archive at https://doi.org/10.17864/1947.001349. Analysed data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Notes and references
- F. Bures, Top. Curr. Chem., 2019, 377, 14 CrossRef.
- S. Shirakawa, et al. , Angew. Chem., Int. Ed., 2015, 54, 15767–15770 CrossRef CAS PubMed.
- T. Nakamura, et al. , Chem. – Asian J., 2020, 15, 463–472 CrossRef CAS PubMed.
- O. G. Mancheño and M. Waser, Eur. J. Org. Chem., 2023, 8 Search PubMed.
- S. Mohapatra, et al. , J. Hazard. Mater., 2023, 445, 130393 CrossRef CAS.
- M. C. Jennings, et al. , ACS Infect. Dis., 2015, 1, 288–303 CrossRef CAS PubMed.
- D. R. MacFarlane, et al. , J. Phys. Chem. B, 1999, 103, 4164–4170 CrossRef CAS.
- F. Mast, et al. , J. Am. Chem. Soc., 2024, 146, 15119–15129 CrossRef CAS.
- A. E. Somers, et al. , ACS Appl. Mater. Interfaces, 2013, 5, 11544–11553 CrossRef CAS PubMed.
- C. Verma, et al. , Adv. Colloid Interface Sci., 2022, 306, 102723 CrossRef CAS.
- N. M. Mustafa, et al. , Heliyon, 2024, 10, e27381 CrossRef CAS.
- P. Gilbert and L. E. Moore, J. Appl. Microbiol., 2005, 99, 703–715 CrossRef CAS PubMed.
- D. Kwasniewska, et al. , Pathogens, 2020, 9, 459 CrossRef CAS.
- C. C. Zhou and Y. L. Wang, Curr. Opin. Colloid Interface Sci., 2020, 45, 28–43 CrossRef CAS.
- S. P. Denyer, Int. Biodeterior. Biodegrad., 1995, 36, 227–245 CrossRef CAS.
- A. F. Zahrt, et al. , Science, 2019, 363, eaau5631 CrossRef CAS PubMed.
- J. J. Henle, et al. , J. Am. Chem. Soc., 2020, 142, 11578–11592 CrossRef CAS.
- E. Gousseva, et al. , J. Phys. Chem. B, 2022, 126, 10500–10509 CrossRef CAS PubMed.
- E. Gousseva, et al. , J. Phys. Chem. B, 2024, 128, 5030–5043 CrossRef CAS.
- C. H. Suresh and S. Anila, Acc. Chem. Res., 2023, 56, 1884–1895 CrossRef CAS.
- S. Men, et al. , Phys. Chem. Chem. Phys., 2011, 13, 15244–15255 RSC.
- R. K. Blundell and P. Licence, Phys. Chem. Chem. Phys., 2014, 16, 15278–15288 RSC.
- R. K. Blundell and P. Licence, Chem. Commun., 2014, 50, 12080–12083 RSC.
- R. M. Fogarty, et al. , Phys. Chem. Chem. Phys., 2019, 21, 18893–18910 RSC.
- J. M. Seymour, et al. , Phys. Chem. Chem. Phys., 2021, 23, 20957–20973 RSC.
- K. R. J. Lovelock, et al. , Chem. Rev., 2010, 110, 5158–5190 CrossRef CAS PubMed.
- R. W. Taft, et al. , J. Am. Chem. Soc., 1978, 100, 7765–7767 CrossRef CAS.
- L. K. Scarbath-Evers, et al. , Phys. Chem. Chem. Phys., 2015, 17, 20205–20216 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cc03388d |
| This journal is © The Royal Society of Chemistry 2024 |