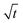Open Access Article
Open Access ArticleCharacterizing the hygroscopicity and volatility of single levitated aerosol droplets via optical tweezers-Raman spectroscopy†
Yu-Kai
Tong
 a,
Teng
Fang
a,
Zhijun
Wu
b,
Min
Hu
*b and
Anpei
Ye
a,
Teng
Fang
a,
Zhijun
Wu
b,
Min
Hu
*b and
Anpei
Ye
 *a
*a
aKey Laboratory for the Physics and Chemistry of Nanodevices, School of Electronics, Peking University, Beijing 100871, China. E-mail: yap@pku.edu.cn
bState Key Joint Laboratory of Environmental Simulation and Pollution Control, College of Environmental Sciences and Engineering, Peking University, Beijing 100871, China. E-mail: minhu@pku.edu.cn
First published on 8th September 2022
Abstract
The hygroscopicity and volatility of airborne particles depict the thermodynamic process of the gas-particle partition of semivolatile organic components, which then have substantial impacts on the atmospheric chemistry and lifetime of aerosols. Characterizing relevant physical and chemical parameters is the base for understanding the aerosol evolution process, analyzing evolution motivation and predicting the evolution path. In this work, we captured single levitated aerosol droplets without any contact using a self-developed aerosol optical tweezers (AOT) system, simulated the hygroscopic-volatilization thermodynamic evolution process of ambient aerosols by changing the relative humidity around the trapped droplet, and measured key thermodynamic parameters via Raman spectroscopy including the particle size, refractive index, diffusion coefficient, volatile flux, and vapor pressure. Moreover, possible phase transitions in the aerosol droplets such as glassy and gel transitions were discussed, which provided an important reference for understanding the behaviors of actual atmospheric aerosols.
Environmental significanceThe mass transfer process is inextricable from the atmospheric evolution of aerosol droplets. The hygroscopicity and volatility are two chief mass transfer processes that influence the lifetime, gas-particle partition and heterogeneous chemistry of aerosols. However, characterizing the mass transfer process is quite challenging because of the nonlinear boundary problem of the convection–diffusion equation, especially for the diffusion coefficient. Herein, we in situ measured some key mass transfer coefficients via a self-constructed aerosol optical tweezers system, which has possible implications on mass transfer in actual atmospheric particles. |
1 Introduction
Aerosols comprising various inorganic/organic components are ubiquitous in the ambient atmosphere, especially in the troposphere. Due to the complex chemical compositions and diverse morphologies, the physicochemical evolution of aerosol droplets is strikingly different from that of bulk solutions.1–5 To effectively analyze the driving forces of air pollution and predict climate changes, it is crucial to investigate the response behaviors of aerosols to environmental changes, such as mass transfer, volatility, phase separation, and cloud nucleation.Conventional studies on physicochemical properties of aerosols usually utilize particle ensembles and bulk phase samples as research targets. For example, Ovadnevaite et al.6 analyzed the impact of surface tension on cloud droplet activation by observing the size distribution of nascent ultrafine mode particles in North Atlantic marine air masses; Estillore et al.7 investigated the hygroscopic growth of organosulfate aerosol ensembles using a Multi-Analysis Aerosol Reactor System. Although these studies investigated the properties of aerosols by analyzing statistical indicators (e.g. size distribution and number concentration) of copious bulk phase aerosol particles, they cannot provide indisputable evidence of the evolving process of aerosols on an individual particle basis.
Of note, some other techniques have been developed to study the properties of single aerosol particles such as aerosol time-of-flight mass spectrometry (A-ToF),8,9 single-particle soot photometry (SP2),10,11 electrodynamic balance-Raman spectroscopy (EDB-Raman),12,13 and Bessel beam traps (BBTs).10,14–16 A-ToF uses two laser beams to respectively desorb and ionize the particle. The particle transit time – which is a function of the particle aerodynamic diameter – between these two laser beams is then measured by PMTs and used for particle sizing. The particle composition is characterized by mass analyzing the ions using a time-of-flight mass spectrometer. One advantage of this technique is that the target aerosol samples are introduced into the instrument under atmospheric conditions, which is similar to the airborne state of real aerosols. However, A-ToF is a destructive method for target particles and is only capable of determining the particle size and composition, unavailable for observing the evolution of single aerosols. The SP2 is exclusive for detecting the mass concentration of black carbon (BC) in individual soot particles. The BC mass is achieved through the use of laser-induced incandescence for strongly absorbing black carbon. However, it is also a destructive technique in that the particle is vaporized in the process of incandescence. EDB-Raman and BBT are two in situ observation techniques which can trap single levitated particles for static detection. Nonetheless, EDB-Raman employs electrodes to construct a trap to capture a levitated particle which demands the particle to be charged in advance. The actually detected particles are distinct from the natural aerosol particles which are electroneutral. Electrostatic effects should not be neglected especially for the micro-scaled aerosols with various electrolyte salts.17,18 Moreover, EDB-Raman uses two different systems to respectively trap and detect the particles that also increases the operation complexity. The BBT utilizes Bessel beams which can maintain tight focus over relatively long distances to trap single levitated particles. One prominent advantage of this method is that it is available to trap and study airborne submicron particles down to ∼600 nm at which the size of chief ambient aerosols, particularly in the accumulation mode, locates. A caveat, however, is that the BBT needs a gas phase flow to maintain an axial z position (height) balance, rendering its z position stability weaker than that of optical tweezing. Besides, considering that the trapped particle in BBT is submicron, the Ohnesorge number of which will be close to 1 so that the aerodynamic disturbance from the gas flow to the evolution of the particle, especially to the heterogeneous chemical process occurred at the surface of the particle, cannot be overlooked.
Recently, two novel single particle techniques have been widely used to characterize ambient aerosols which are atomic force microscopy (AFM)19–21 and confocal microscopy.22–24 One key step of these techniques is generating super-micrometer droplets via a pneumatic micro-dispenser and depositing a single droplet on a hydrophobic substrate. These methods can acquire the information of a single particle; however, the contact with nanoneedle tips or substrate limits their utility of simulating the thermodynamic process of ambient aerosols.
The optical tweezers system, which can capture a single particle without contact in a three-dimensional laser trap, has been extensively used in the manipulation of micron sized particles such as cells and bacteria.25–30 The timescale of the consecutive stable trapping is up to hours which provides an excellent approach to mimic the airborne state and explicitly investigate the evolution process of natural aerosols.31 A fair amount of studies on the mass transfer of single aerosol particles have been conducted using aerosol optical tweezers. Leng et al.32 imposed rapid pulsed relative humidity (RH) processes on substrate-deposited microdroplets and observed the dynamic hygroscopicity via a rapid scan vacuum FTIR spectrometer. Preston et al.33 put an optically-trapped aerosol droplet in a sinusoidal RH oscillation and found that the radius of the droplet would sinusoidally change following the RH with the same frequency, and the amplitude and frequency of the size fluctuation were dictated by the RH frequency and the diffusion coefficient of water molecules. Cai et al.34,35 used the time-resolved Raman spectra of optically-trapped droplets over the course of humidity steps and measured the vapor pressures of copious organic aerosols, including maleic acid, citric acid, glycerol etc. Moridnejad et al.36 researched the hygroscopicity of a high-viscosity aerosol and found that the morphology-dependent resonances in its Raman spectra underwent abrupt changes which indicated that the phase of the aerosol might transform into a glassy state. Notably, the isotopic tracer method is another ingenious approach which can directly unveil the hygroscopic process of aerosol droplets.12,37–39 In this method, the moisture (H2O) used to maintain the ambient RH is changed into D2O vapor after the droplet reaches an equilibrium with the environment; thus the process of mass transfer can be observed according to the time evolution of the H2O peak and D2O peak in the Raman spectra of the droplet.
In this work, we constructed an aerosol optical tweezers system and investigated the hygroscopicity and volatility of various inorganic/organic aerosol droplets. We first researched and presented the time evolution of the radius and refractive index (RI) in aqueous NaCl droplets under RH steps. Afterwards, we discussed the obstruction of mass transfer under arid conditions in aqueous sucrose droplets and measured the diffusion coefficient of moisture. Finally, the volatility of aqueous citric acid droplets under constant RH was investigated; the volatile flux and vapor pressure of citric acid droplets were also measured.
2 Experimental
2.1 Reagents and sample preparation
Three types of mother aqueous solution were used in this work to generate aerosol droplets, including sodium chloride (NaCl), sucrose (C12H22O11), and citric acid (CA, C6H8O7). Solute NaCl was purchased from Tong Guang Fine Chemical Co. (Beijing, China). Solute sucrose was purchased from Beijing Chemical Works (Beijing, China), and CA was purchased from Beijing Modern Oriental Fine Chemical Co., Ltd. (Beijing, China). The molarities of NaCl, sucrose and CA were 1 mol L−1, 0.5 mol L−1, and 0.5 mol L−1, respectively. The solutions were prepared with double-distilled water (18.2 MΩ cm; Milli-Q; MilliporeSigma, Burlington, MA, USA).2.2 Aerosol optical tweezers system
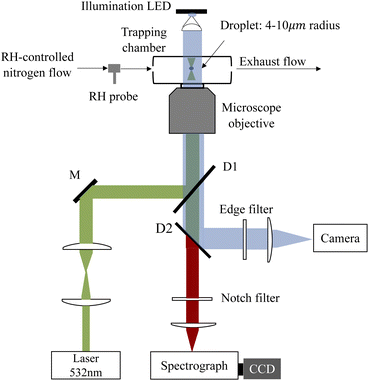
A schematic of the AOT system is shown in Fig. 1. A 532 nm laser beam (Excelsior-532-200, Spectra Physics) was used to both trap the aerosol droplet and excite its Raman signal. The power of the laser beams used was ∼20 mW. The laser beam is first expanded by a pair of confocal lenses to make it slightly wider than the rear aperture of the microscope objective lens. Then the beam is reflected by a dichroic mirror and coupled into the objective lens of an inverted microscope (Axiovert 200, Zeiss), forming an optical trap in a tailored chamber mounted above the objective. The objective is responsible for both focusing the beam and collecting the Raman backscattering signals. The Raman spectra were dispersed by using a 1200 grooves per nm grating and recorded with a spectrograph (SpectaPro 2300i, Acton) equipped with a liquid nitrogen cooled CCD (Spec-10, Princeton Instruments) working at a temperature of −120 °C. The resolution of the spectrograph is 1.5 cm−1.The droplet was trapped in a tailored chamber. A schematic of the aerosol chamber is shown in Fig. S1 in the ESI.† The chamber is made up of two coaxial cylinders which are connected by a ring baffle mounted in the middle position of the cylinders, dividing the chamber into top and bottom compartments. The top compartment was used for mixing the dry/wet nitrogen and the aerosol flow. The incoming mixing flow was first obstructed by the inner cylinder baffle which can slow the flow rate. Then the flow entered the hollow inner cylinder through the gap between the upper rim of the cylindrical inwall and the top coverslip and reached the optical trap in the bottom compartment. The exhaust flow was discharged through the bottom port. The design of such a flow path can considerably prevent the destabilization on the trapped particle caused by the gas flow. The chamber was placed on the inverted microscope with the bottom coverslip contacting with a 100× oil-immersed objective. The top coverslip was used for illumination and bright-field imaging of the trapped droplets via a 470 nm illumination LED.
The RH in the chamber was controlled with dry and humidified nitrogen, the ratio of the dry/wet nitrogen was modulated in real time with two mass flow meters (MC series, Alicat Scientific) controlled by using a custom developed LabVIEW software and PID algorithm. The total mixed gas flow rate introduced into the chamber was kept constant at 60 sccm. The RH could be regulated at a maximum rate of 5% RH min−1; the value of RH was monitored with a RH probe (HC2A-S, ROTRONIC). To retrieve the actual RH value in the chamber, the RH probe was placed first at the entrance and then at the exit of the chamber; the readouts of the probe in two positions were examined and are shown in the ESI (see Fig. S2 in the ESI†). It can be seen that the position of the RH probe has no pronounced influences on RH monitoring. Thus, the RH values reported hereafter were measured with the RH probe placed at the entrance of the chamber.
A medical ultrasonic nebulizer (Mint PN100) was used to generate the aerosols in this work. Once a droplet was captured from an incoming aerosol train, the flow admission was stopped, and the inlet was sealed immediately to maintain a constant RH in the chamber. The atomization rate of the nebulizer is 0.5 mL min−1; the radii of the generated droplets are 1–10 μm with a median of 5 μm.
2.3 Determination of the radius and refractive index
Microdroplets can work as an optical resonant cavity such that when the incident laser enters the droplet, total internal reflection will occur at the interface between the droplet and ambient medium. Upon the wavelength of the light (including the incident light and the resultant inelastic scattering light) commensurating with the size of the droplet, a standing wave will form, which will superimpose a series of extremely sharp peaks on the spontaneous Raman scattering spectrum.40–44 These are the so-called whispering gallery modes (WGMs) or morphology dependent resonances (MDRs).The wavelength of the WGMs is determined from the morphology (particularly radius) and RI of the microdroplet. The WGMs are equispaced in the Raman spectra; an estimate of the droplet size and RI can be determined from the spacing between the resonances in a droplet Raman spectrum, which can be approximated by using45
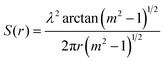 | (1) |
2.4 Characterizing the hygroscopicity
The hygroscopicity depicts the mass transfer process of ambient moisture from the interface into the interior of the aerosol droplets. Analyzing this process with the convection–diffusion equation needs to solve an intricate non-linear boundary value problem, which makes the measurements of the diffusion coefficient quite challenging. The differential step isothermal method developed by Aristov et al.48–51 circumvents this obstacle and works well to simulate the hygroscopic process of high viscosity droplets. The mass transfer of a spherical droplet can be modeled as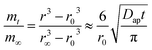 | (2) |
Based on the droplet radii retrieved from the WGM signals in the measured Raman spectra, the water diffusion coefficient Dap can then be calculated by linear-fitting r3 − r03 and the square root of time, 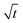 .
.
2.5 Characterizing the volatility
The volatility depicts the mass transfer process that semivolatile species escape from the particulate phase to the gaseous phase and can be assessed from the volatile flux and vapor pressure of the semivolatile species. The volatile flux F is defined as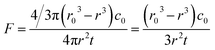 | (3) |
Moreover, assuming that the vapor pressure of the semivolatile component, i, at infinite distance is zero, the vapor pressure above the droplet surface, pi,r, can be estimated according to the specific Maxwell equation34,52,53
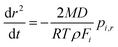 | (4) |
3 Results and discussion
Here, we first investigated the hygroscopicity of aerosols of aqueous NaCl and sucrose at room temperature. Then, we measured the volatile flux and vapor pressure of CA microdroplets.3.1 Quantitative analysis of hygroscopicity
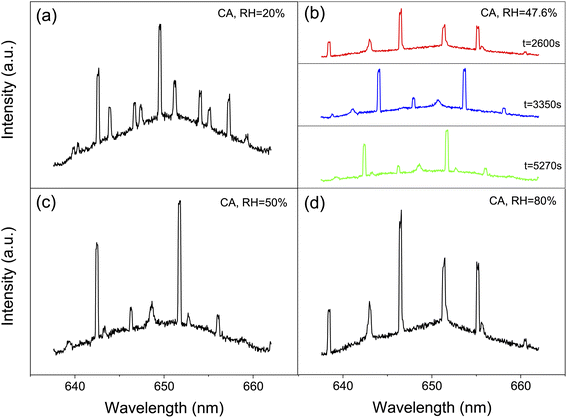
We captured single aerosol droplets in the AOT system, modulated the RH in the trapping chamber, and investigated the size response of the droplets when undergoing RH steps. After reaching the preset RH value, the fluctuation of RH is less than ±0.5%. Fig. 2 shows a series of representative stills of the Raman spectra of CA droplets. It can be seen that the spectra recorded under different RHs has appreciable differences. Fig. 2(b) shows three snapshots of the Raman spectra at a constant RH value. It can be seen that although the RH is constant, the spectra at different times are still different due to the thermodynamic evolution. For example, new WGM peaks sprouted in the spectrum, and the existing peaks also shifted, which reflected the potential volatilization dynamics of CA droplets. This will be discussed in detail in Section 3.2.| Solute | RH (%) | D ap (m2 s−1) | Ref. |
|---|---|---|---|
| Sucrose | 10 | 2.92 × 10−16 | Preston et al.33 |
| 26 | 4.52 × 10−16 | Nadler et al.12 | |
| 30 | 2.39 × 10−15 | Preston et al.33 | |
| 32 | 1.60 × 10−15 | Davies et al.38 | |
| 40 | 1.00 × 10−13 | Bastelberger et al.57 | |
| 27 → 30 | 4.74 × 10−16 | This work | |
| 30 → 27 | 5.03 × 10−16 | ||
| 37 → 40 | 5.73 × 10−15 | ||
| 40 → 37 | 7.25 × 10−15 | ||
| 10 → 27 | 4.62 × 10−16 |
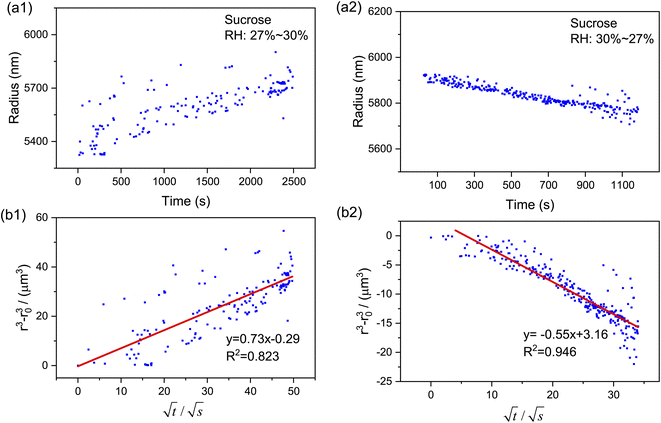
Moreover, as can be seen from Fig. 4(b1) and (b2), the calculated r3 − r03 is linear with 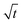 perfectly. The measured water diffusion coefficients are shown in Table 1. Our results are in line with previous studies where the Dap was measured using different methods. To acquire high-quality cavity-enhanced Raman spectra, a high-power laser beam was used, which may accelerate the transfer of water and lead to measured diffusion coefficients higher than the true values. In spite of this, the deviation caused by the laser heating effect is lower than one order of magnitude. Considering the relatively wide discrepancy of the literature values listed in Table 1, the measured values herein are still meaningful. More discussion on this problem can be seen in Section S4 in the ESI.† The mixing time, τmixing, by diffusion of volatile molecules within an aerosol can be estimated from the diffusion coefficient,23,37,58
perfectly. The measured water diffusion coefficients are shown in Table 1. Our results are in line with previous studies where the Dap was measured using different methods. To acquire high-quality cavity-enhanced Raman spectra, a high-power laser beam was used, which may accelerate the transfer of water and lead to measured diffusion coefficients higher than the true values. In spite of this, the deviation caused by the laser heating effect is lower than one order of magnitude. Considering the relatively wide discrepancy of the literature values listed in Table 1, the measured values herein are still meaningful. More discussion on this problem can be seen in Section S4 in the ESI.† The mixing time, τmixing, by diffusion of volatile molecules within an aerosol can be estimated from the diffusion coefficient,23,37,58
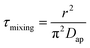 | (5) |
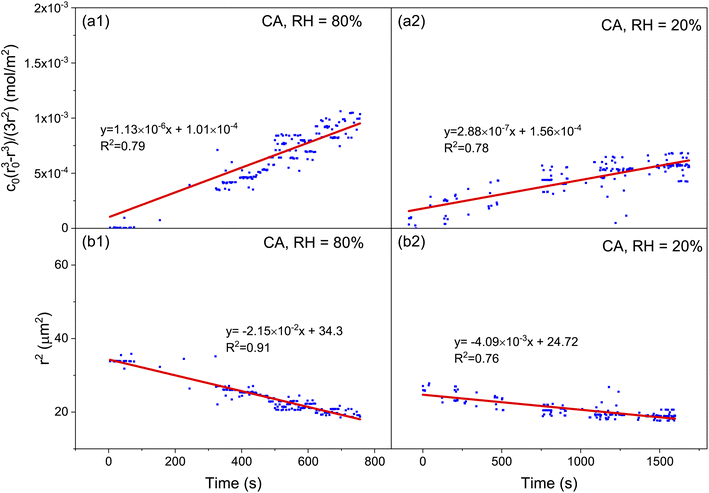
3.2 Volatility of citric acid
The pervasive secondary organic aerosols (SOAs) are confirmed to have diverse semivolatile components (SVOCs), which are influential in the atmospheric lifetime, long-range transport and optical properties of aerosols.59 Most of the SVOCs are humic-like substances, including dicarboxylic acids, polyols, esters, and ethers. Herein, we used citric acid as the surrogate SVOCs and measured its volatile flux and vapor pressure.Fig. 5 shows the time evolution of the radius of single levitated CA droplets at constant RH values. It can be seen that although RH is constant, the radius of CA keeps decreasing in the thermodynamic process of volatility. Besides, the rate of radius reduction at higher RH (80%) is higher than that at lower RH (50%). Fig. 6(a1) and (a2) show the relationship of (r03 − r3)c0/3r2 and t under moist and arid conditions, respectively. It can be seen that at RH = 80%, the slope of (r03 − r3)c0/3r2versus t is one order of magnitude higher compared with RH = 20%, which indicates that more volatile molecules transfer from the particulate phase to the gaseous phase at equal time intervals. Moreover, a similar discrepancy in the slope of r2 and t can also be seen in Fig. 6(b1) and (b2), which means the vapor pressure of the volatile components (i.e., CA) at RH = 80% is higher than that at RH = 20%. The measured values of volatile flux and vapor pressure are summarized in Tables 2 and 3. Previous studies measured the vapor pressures of CA under diverse conditions which led to high deviations among the results. The values of our measurements lay between those of Cai et al.34 and Booth et al.60
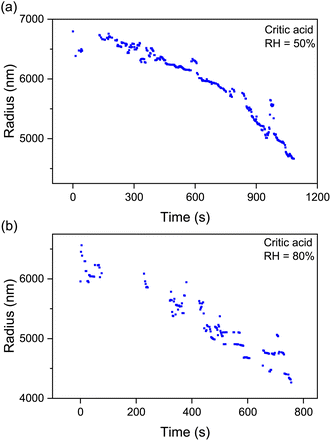 | ||
| Fig. 5 Time evolution of the radius of droplets of citric acid at constant RH values: (a) RH = 50%; (b) RH = 80%. The sustained decrease of the radius indicates the volatility of CA. | ||
| Solute | RH (%) | Volatile flux mol (m−2 s−1) | Error coefficient |
|---|---|---|---|
| Citric acid | 20 | 2.88 × 10−7 | 0.1 |
| 50 | 7.3 × 10−7 | 0.1 | |
| 80 | 1.13 × 10−6 | 0.1 |
Shi et al.63 found that at low RH (RH < 40%), CA would transit to a gel state whose viscosity largely increased. It is plausible to speculate that the CA droplet trapped at RH = 20% in this work underwent phase transition after reaching an equilibrium moisture content with the gas phase, which impeded the gas-particle partition of CA and led to an inhibition in volatility.
4 Conclusions
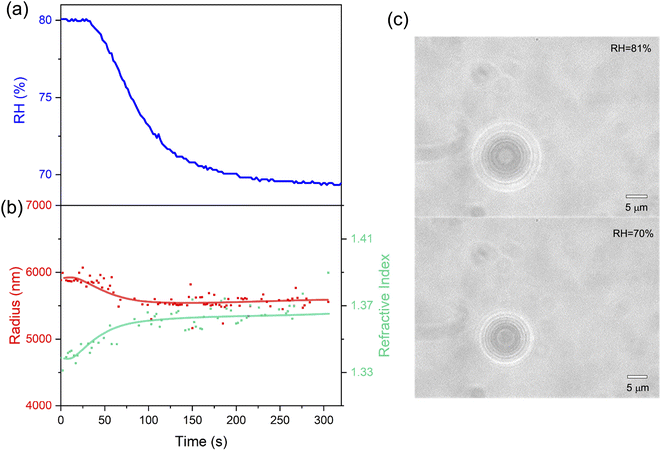
In this work, we constructed an optical tweezers system and investigated the hygroscopicity-volatility properties of various levitated inorganic/organic droplets. The system was simple and highly efficient compared with EDB-Raman and BBT. The results show that the RH has no obvious effect on the hygroscopicity of inorganic aerosol droplets such as those of sodium chloride, and its droplet radius can promptly respond to the change of ambient RH. When RH decreases, the droplet of NaCl loses water leading to a reduction of the radius and an increase of the refractive index. The hygroscopicity of organic aerosol droplets (e.g., sucrose) changes significantly at low RH, and its radial response lags far behind the change of RH, indicating that the water transfer in sucrose droplets under low RH is blocked (glass phase transition may occur). Besides, volatility of semivolatile aerosols (e.g., citric acid) was detected by measuring the volatile flux and vapor pressure. The results indicate that the volatilization flux at low RH (20%) is one order of magnitude lower than that at high RH (80%). This may be attributed to the fact that citric acid droplets undergo gel phase transition at low RH, which leads to the blockage of mass transfer.The optical tweezing technique is subject to several caveats. One is that real aerosols have appreciable amounts of photosensitive substances which not only deteriorate the trapping efficiency but also mask the Raman signals. Moreover, the optical tweezers can only capture primary supermicron particles which limit their utilization in secondary submicron aerosols. Considerable work remains to be done to overcome these disadvantages.
Besides, the composition of natural aerosols is incredibly complex, and the hygroscopicity and volatility of multi-component aerosols need to be researched in the future. The lucubration of the molecular driving factors related to these properties is also imperative.
Author contributions
Yu-Kai Tong proposed the idea of the project, performed the measurements, conducted the data analysis, and led in writing the manuscript. Anpei Ye contributed to funding the research, constructed the optical tweezers system, provided instructions for the experiments and revised the manuscript. Teng Fang co-conducted the data analysis. Zhijun Wu and Min Hu were responsible for the conceptualization of aerosol droplets and discussion of methodology.Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (U19A2007, 32150026 and 92043302) and the National Key Research & Development Program of China (2017YFC0209504).References
- P. C. Arroyo, G. David, P. A. Alpert, E. A. Parmentier, M. Ammann and R. Signorell, Science, 2022, 376, 293–296 CrossRef CAS PubMed
.
- B. R. Bzdek, J. P. Reid and M. I. Cotterell, Commun. Chem., 2020, 3, 105 CrossRef CAS
.
- Z. Chen, P. Liu, Y. Liu and Y.-H. Zhang, Acc. Chem. Res., 2021, 54, 3667–3678 CrossRef CAS PubMed
.
- Z. Chen, P. Liu, W. Wang, X. Cao, Y.-X. Liu, Y.-H. Zhang and M. Ge, Environ. Sci. Technol., 2022, 56, 7637–7646 CrossRef CAS
.
- H. Wei, E. P. Vejerano, W. Leng, Q. Huang, M. R. Willner, L. C. Marr and P. J. Vikesland, Proc. Natl. Acad. Sci. U.S.A., 2018, 115, 7272–7277 CrossRef CAS PubMed
.
- J. Ovadnevaite, A. Zuend, A. Laaksonen, K. J. Sanchez, G. Roberts, D. Ceburnis, S. Decesari, M. Rinaldi, N. Hodas, M. C. Facchini, J. H. Seinfeld and C. O. Dowd, Nature, 2017, 546, 637–641 CrossRef CAS PubMed
.
- A. Du, Y. Li, J. Sun, Z. Zhang, B. You, Z. Li, C. Chen, J. Li, Y. Qiu, X. Liu, D. Ji, W. Zhang, W. Xu, P. Fu and Y. Sun, Sci. Total Environ., 2022, 829, 154661 CrossRef CAS
.
- C. A. Noble and K. A. Prather, Mass Spectrom. Rev., 2000, 19, 248–274 CrossRef CAS
.
- W. Li, L. Shao, D. Zhang, C.-U. Ro, M. Hu, X. Bi, H. Geng, A. Matsuki, H. Niu and J. Chen, J. Clean. Prod., 2016, 112, 1330–1349 CrossRef CAS
.
- A. P. Ault and J. L. Axson, Anal. Chem., 2017, 89, 430–452 CrossRef CAS PubMed
.
- A. Yoshida, N. Moteki, S. Ohata, T. Mori, R. Tada, P. Dagsson-Waldhauserová and Y. Kondo, Aerosol Sci. Technol., 2016, 50, 1–4 CrossRef CAS
.
- K. A. Nadler, P. Kim, D.-L. Huang, W. Xiong and R. E. Continetti, Phys. Chem. Chem. Phys., 2019, 21, 15062–15071 RSC
.
- Z. Liang, Y. Chu, M. Gen and C. K. Chan, Atmos. Chem. Phys., 2022, 22, 3017–3044 CrossRef CAS
.
- J. S. Walker, A. E. Carruthers, A. J. Orr-Ewing and J. P. Reid, J. Phys. Chem. Lett., 2013, 4, 1748–1752 CrossRef CAS PubMed
.
- J. W. Lu, A. M. J. Rickards, J. S. Walker, K. J. Knox, R. E. H. Miles, J. P. Reid and R. Signorell, Phys. Chem. Chem. Phys., 2014, 16, 9819–9830 RSC
.
- J. W. Lu, M. Isenor, E. Chasovskikh, D. Stapfer and R. Signorell, Rev. Sci. Instrum., 2014, 85, 095107 CrossRef
.
- A. A. Fedorets, L. A. Dombrovsky, E. Bormashenko and M. Nosonovsky, Int. J. Heat Mass Transfer, 2019, 133, 712–717 CrossRef
.
- E. A. Parmentier, P. Corral Arroyo, R. Gruseck, L. Ban, G. David and R. Signorell, J. Phys. Chem., 2022, 126, 4456–4464 CrossRef CAS PubMed
.
- A. D. Hritz, T. M. Raymond and D. D. Dutcher, Atmos. Chem. Phys., 2016, 16, 9761–9769 CrossRef CAS
.
- H. D. Lee, A. D. Estillore, H. S. Morris, K. K. Ray, A. Alejandro, V. H. Grassian and A. V. Tivanski, J. Phys. Chem., 2017, 121, 8296–8305 CrossRef CAS PubMed
.
- H. D. Lee and A. V. Tivanski, Annu. Rev. Phys. Chem., 2021, 72, 235–252 CrossRef CAS PubMed
.
- Q. Zhou, S.-F. Pang, Y. Wang, J.-B. Ma and Y.-H. Zhang, J. Phys. Chem. B, 2014, 118, 6198–6205 CrossRef CAS PubMed
.
- Y. Zhang, C. Cai, S.-F. Pang, J. P. Reid and Y.-H. Zhang, Phys. Chem. Chem. Phys., 2017, 19, 29177–29186 RSC
.
- T. Lu and E. Spruijt, J. Am. Chem. Soc., 2020, 142, 2905–2914 CrossRef CAS PubMed
.
- T. Fang, P. Yuan, C. Gong, Y. Jiang, Y. Yu, W. Shang, C. Tian and A. Ye, Analyst, 2022, 147, 1961–1967 RSC
.
- Y. Liu, J. Xu, Y. Tao, T. Fang, W. Du and A. Ye, Analyst, 2020, 145, 3297–3305 RSC
.
- B. Zhou, L. Sun, T. Fang, H. Li, R. Zhang and A. Ye, J. Biophot., 2022, 15, e202100312 CAS
.
- T. Fang, W. Shang, C. Liu, Y. Liu and A. Ye, Anal. Chem., 2020, 92, 10433–10441 CrossRef CAS
.
- T. Fang, W. Shang, C. Liu, J. Xu, D. Zhao, Y. Liu and A. Ye, Anal. Chem., 2019, 91, 9932–9939 CrossRef CAS
.
- H. Ma, Y. Zhang and A. Ye, Chin. Sci. Bull., 2013, 58, 2594–2600 CrossRef CAS
.
- U. K. Krieger, C. Marcolli and J. P. Reid, Chem. Soc. Rev., 2012, 41, 6631–6662 RSC
.
- C.-B. Leng, S.-F. Pang, Y. Zhang, C. Cai, Y. Liu and Y.-H. Zhang, Environ. Sci. Technol., 2015, 49, 9107–9115 CrossRef CAS PubMed
.
- T. C. Preston, J. F. Davies and K. R. Wilson, Phys. Chem. Chem. Phys., 2017, 19, 3922–3931 RSC
.
- C. Cai, D. J. Stewart, J. P. Reid, Y.-h. Zhang, P. Ohm, C. S. Dutcher and S. L. Clegg, J. Phys. Chem., 2015, 119, 704–718 CrossRef CAS
.
- C. Cai, D. J. Stewart, T. C. Preston, J. S. Walker, Y.-H. Zhang and J. P. Reid, Phys. Chem. Chem. Phys., 2014, 16, 3162–3172 RSC
.
- A. Moridnejad, T. C. Preston and U. K. Krieger, J. Phys. Chem., 2017, 121, 8176–8184 CrossRef CAS PubMed
.
- H. C. Price, B. J. Murray, J. Mattsson, D. O'Sullivan, T. W. Wilson, K. J. Baustian and L. G. Benning, Atmos. Chem. Phys., 2014, 14, 3817–3830 CrossRef
.
- J. F. Davies and K. R. Wilson, Anal. Chem., 2016, 88, 2361–2366 CrossRef CAS PubMed
.
- A. Moridnejad and T. C. Preston, J. Phys. Chem., 2016, 120, 9759–9766 CrossRef CAS PubMed
.
- R. Thurn and W. Kiefer, Appl. Opt., 1985, 24, 1515–1519 CrossRef CAS PubMed
.
- R. Thurn and W. Kiefer, J. Raman Spectrosc., 1984, 15, 411–413 CrossRef CAS
.
- L. Mitchem and J. P. Reid, Chem. Soc. Rev., 2008, 37, 756–769 RSC
.
- R. J. Hopkins, L. Mitchem, A. D. Ward and J. P. Reid, Phys. Chem. Chem. Phys., 2004, 6, 4924–4927 RSC
.
- B. Vennes, A. Rafferty and T. C. Preston, J. Opt. Soc. Am. B, 2021, 38, 893–906 CrossRef
.
- J. P. Reid, H. Meresman, L. Mitchem and R. Symes, Int. Rev. Phys. Chem., 2007, 26, 139–192 Search PubMed
.
- R. D. Gatherer, R. M. Sayer and J. P. Reid, Chem. Phys. Lett., 2002, 366, 34–41 CrossRef CAS
.
- T. C. Preston and J. P. Reid, J. Opt. Soc. Am. A, 2015, 32, 2210–2217 CrossRef PubMed
.
- Y.-K. Tong, Y. Liu, X. Meng, J. Wang, D. Zhao, Z. Wu and A. Ye, Phys. Chem. Chem. Phys., 2022, 24, 10514–10523 RSC
.
- Y. Aristov, I. Glaznev, A. Freni and G. Restuccia, Chem. Eng. Sci., 2006, 61, 1453–1458 CrossRef CAS
.
- C. Cai, S. Tan, H. Chen, J. Ma, Y. Wang, J. P. Reid and Y. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 29753–29763 RSC
.
- X.-J. Lv, Z. Chen, J.-B. Ma and Y.-H. Zhang, Spectrochim. Acta Mol. Biomol. Spectrosc., 2020, 226, 117552 CrossRef CAS
.
- X.-J. Lv, Z. Chen, J.-B. Ma and Y.-H. Zhang, J. Aerosol Sci., 2019, 138, 105449 CrossRef CAS
.
- A. Logozzo and T. C. Preston, J. Phys. Chem., 2022, 126, 109–118 CrossRef CAS PubMed
.
- D. L. Bones, J. P. Reid, D. M. Lienhard and U. K. Krieger, Proc. Natl. Acad. Sci. U.S.A., 2012, 109, 11613–11618 CrossRef CAS PubMed
.
- B. Zobrist, V. Soonsin, B. P. Luo, U. K. Krieger, C. Marcolli, T. Peter and T. Koop, Phys. Chem. Chem. Phys., 2011, 13, 3514–3526 RSC
.
- B. Zobrist, C. Marcolli, D. A. Pedernera and T. Koop, Atmos. Chem. Phys., 2008, 8, 5221–5244 CrossRef CAS
.
- S. Bastelberger, U. K. Krieger, B. Luo and T. Peter, Atmos. Chem. Phys., 2017, 17, 8453–8471 CrossRef CAS
.
- L. Renbaum-Wolff, J. W. Grayson, A. P. Bateman, M. Kuwata, M. Sellier, B. J. Murray, J. E. Shilling, S. T. Martin and A. K. Bertram, Proc. Natl. Acad. Sci. U.S.A., 2013, 110, 8014–8019 CrossRef CAS PubMed
.
- A. Mellouki, T. J. Wallington and J. Chen, Chem. Rev., 2015, 115, 3984–4014 CrossRef CAS PubMed
.
- A. M. Booth, M. H. Barley, D. O. Topping, G. McFiggans, A. Garforth and C. J. Percival, Atmos. Chem. Phys., 2010, 10, 4879–4892 CrossRef CAS
.
-
C. L. Yaws, P. K. Narasimhan and C. Gabbula, Handbook of Antoine Coefficients for Vapor Pressure, Knovel, New York, 2nd edn, 2009 Search PubMed
.
- A. J. Huisman, U. K. Krieger, A. Zuend, C. Marcolli and T. Peter, Atmos. Chem. Phys., 2013, 13, 6647–6662 CrossRef
.
- X.-M. Shi, F.-M. Wu, B. Jing, N. Wang, L.-L. Xu, S.-F. Pang and Y.-H. Zhang, Chemosphere, 2017, 188, 532–540 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2va00175f |
| This journal is © The Royal Society of Chemistry 2022 |