Thiol–maleimide “click” chemistry: evaluating the influence of solvent, initiator, and thiol on the reaction mechanism, kinetics, and selectivity

Abstract

The mechanism and kinetics of thiol–maleimide “click” reactions carried out under a variety of conditions have been investigated computationally and using experimental competition reactions. The influence of three different solvents (chloroform, ethane thiol, and N,N-dimethylformamide), five different initiators (ethylamine, diethylamine, triethylamine, diazabicyclo[2.2.2]octane, and dimethylphenyl-phosphine), and seven different thiols (methyl mercaptan, β-mercaptoethanol, thioacetic acid, methyl thioglycolate, methyl 3-mercaptopropionate, cysteine methyl ester, and thiophenol) on the energetics and kinetics of thiol–maleimide reactions have been examined using density functional methods. Computational and kinetic modeling indicate that the choice of solvent, initiator, and thiol directly influences whether product formation follows a base-, nucleophile-, or ion pair-initiated mechanism (or some combination thereof). The type of mechanism followed determines the overall thiol–maleimide reaction kinetics. Insights from computational studies are then used to understand the selectivity of ternary thiol–maleimide reactions between N-methyl maleimide, thiophenol, and 1-hexanethiol in different combinations of solvents and initiators. The results provide considerable insight into the interplay between reaction conditions, kinetics, and selectivity in thiol–maleimide reactions in particular and thiol-Michael reactions in general, with implications ranging from small molecule synthesis to bioconjugation chemistry and multifunctional materials.

---

Introduction

Reactions between thiols and maleimides have long been recognized as some of the most efficient Michael-type additions.^1–3 The withdrawing effects of two activating carbonyls coupled with the release of ring strain upon product formation provide a significant driving force for thiol–maleimide reactions. Given their reliability, efficiency, and selectivity, thiol–maleimide reactions have been a primary means of bioconjugation⁴ for several decades. More recently there has been increasing interest in utilizing thiol–maleimide reactions in polymer and materials synthesis.^3,5 Much of this interest has grown with the emergence of click chemistry,^6,7 especially as applied to the synthesis of macromolecules and new materials.^7–9

The mechanism of thiol–maleimide reactions is most often written as a typical Michael-type addition. Entrance into the catalytic cycle (Scheme 1a) requires the initial formation of some quantity of nucleophilic thiolate anion. There are two prominent means of forming these initial quantities of thiolate anions: one that utilizes base and another that utilizes nucleophiles.¹⁰ Along the base-initiated mechanism, a catalytic amount of weak base (e.g. triethylamine, Et₃N) is used to deprotonate some quantity of available thiol (Scheme 1b). The resulting thiolate anion, a strong nucleophile, attacks the π-bond of maleimide, resulting in a strongly basic enolate intermediate. This intermediate deprotonates an additional equivalent of thiol, giving the desired addition product as well as another equivalent of thiolate that can perpetuate the catalytic cycle.

Scheme 1 (a) Mechanism for the thiolate-catalyzed addition of a thiol to an N-substituted maleimide. (b) Formation of a thiolate anion from an acid–base equilibrium reaction. (c) Formation of a thiolate anion following a nucleophile-initiated mechanistic pathway.

Various nucleophiles can also be used to initiate thiol-Michael reactions.^3,10,11 The nucleophile-initiated mechanism (Scheme 1c) differs from the base-initiated mechanism in the manner in which a thiolate anion is formed. Along the nucleophile-initiated mechanism the nucleophile (typically a nitrogen or phosphorus-centered nucleophile) first attacks the π-bond of maleimide to give a zwitterionic enolate intermediate. This enolate deprotonates a thiol to give a thiolate anion, which then progresses along the same catalytic pathway as when initiated by a base. It is important to note that the nucleophilic pathway results in the formation of some amount of nucleophile addition byproduct. This byproduct formation is typically inconsequential, however, as most nucleophile-initiated thiol-Michael reactions proceed rapidly even in the presence of trace amounts (<1%) of initiator.

Thiol–maleimide reactions can also be carried out using radical initiators.¹² In comparison to base-initiated thiol–maleimide reactions, however, radical-initiated thiol–maleimide reactions proceed less rapidly given that the radical-initiated pathway typically favors more electron rich alkenes.^13,14 Base- and nucleophile-initiated thiol–maleimide reactions are also advantageous as they avoid the formation of radical–radical termination products and are not sensitive to O₂.

Interestingly, recent studies by Lowe, Haddleton, and Bowman have found that the kinetics and mechanism (base-initiated or nucleophile-initiated) that a given thiol-Michael reaction follows depends on the specific combination of base/nucleophile, Michael acceptor, and thiol.^11,15 This discovery is very useful for the design of selective thiol-Michael reactions^15–19 wherein several different thiols or Michael acceptors are present in a single reaction mixture (e.g. ternary or quaternary systems). While research in the area of selective thiol-Michael reactions has increased significantly over the past few years, several mechanistic questions remain. More generally, a comprehensive understanding of the structural, energetic, and kinetic factors that influence whether a given combination of thiol, Michael acceptor, and base/nucleophile follows a base-initiated pathway, nucleophile-initiated pathway, or some combination of both has yet to be developed. There have also been few investigations²⁰ aimed at elucidating the influence that experimental conditions (solvent, equivalents of initiator, etc.) have on thiol-Michael energetics and kinetics. Mechanistic details are particularly lacking in the case of thiol–maleimide reactions as a result of their very rapid kinetics.

Herein we present a thorough, fundamental investigation of the mechanism of thiol additions to maleimide derivatives. The energetics of both base-initiated and nucleophile-initiated mechanisms have been studied computationally at the MO6-2X/6-311G(2D,P)//B3LYP/6-31+G(D) level of theory.^21,22 Initial computational studies focus on mapping out the various mechanistic pathways available for the Et₃N promoted addition of methyl mercaptan (1) to N-methyl maleimide (NMM) in chloroform (CHCl₃). With mechanistic insights gained from these initial investigations, computational studies are then extended to include four additional bases/nucleophiles (ethylamine, diethylamine, 1,4-diazabicyclo[2.2.2]octane, and dimethylphenyl-phosphine), two additional solvents (ethyl mercaptan and N,N-dimethylformamide), and six additional thiols (β-mercaptoethanol, thioacetic acid, methyl thioglycolate, methyl 3-mercaptopropionate, cysteine methyl ester, and thiophenol), all shown in Fig. 1. Computational investigations suggest that, under most conditions, the first step along the base-initiated mechanism does not involve the direct deprotonation of a thiol by base as is commonly shown and discussed in the literature. Nucleophile-initiated pathways, often believed to be inoperative for thiol–maleimide additions, are computationally predicted to contribute to product formation in the presence of primary and secondary amines, a result that is supported experimentally. Rates of thiol–maleimide additions are found to increase substantially in highly polar solvents (e.g. DMF), and these rate increases can be attributed to differences in the reaction mechanism under different solvent conditions. The reactivity of different thiols is predicted to vary in accordance with thiol pK_a's, and to be generally independent of their nucleophilicity. Computational results are supported by experimental investigations of reactions between NMM and two different thiols that demonstrate the influence of different experimental conditions on thiol–maleimide selectivity in ternary reactions. The results provide not only a significantly more detailed understanding of thiol–maleimide reactions but also provide a path toward a greater understanding of thiol-Michael reactions in general and the design of selective thiol–maleimide reactions in particular.

Fig. 1 Chemical structures of the maleimide, bases/nucleophiles, thiols, and solvents investigated in the current study, as well as the dielectric constant of each solvent.

Computational details

All calculations were performed within the Gaussian09 suite of programs.²³ Initial conformational searches of all species were performed by scanning all freely rotating dihedral angles at the HF/6-31G(D) level of theory to locate their approximate global energy minimum structures prior to full geometry optimization. Approximate locations of transition states were determined by performing relaxed potential energy surface scans (B3LYP/6-31G(D))²² along the internal coordinates corresponding to bond breaking and/or bond formation. Potential transition state structures were then refined by performing a Berney optimization at a higher level of theory (discussed below). Transition states were confirmed by IRC calculations and were distinguished as having a single imaginary vibrational frequency. All potential energy surface scans, geometry optimizations, and single-point calculations were performed at 298.15 K, 1.0 atm pressure, and in a PCM solvent model²⁴ for chloroform, ethyl mercaptan, or N,N-dimethylformamide.

Theoretical investigations of methane thiolate additions to N-allyl and N-propargyl maleimide have been carried out previously²⁵ using the compound CBS-QB3 method developed by Petersson and co workers,²⁶ and results were found to agree well with experimental observations. Similarly, computational investigations of radical-initiated thiol–ene reactions have been carried out¹⁴ at the CBS-QB3 level and were found to predict reaction enthalpies within ±0.5 kcal mol⁻¹ mean absolute deviation (MAD) of experimental data. The number of heavy atoms present in large initiators (e.g. DBU, PMe₂Ph) and thiols (e.g. thiophenol) investigated in the current study render these systems unsuitable for study at the CBS-QB3 level. Recent computational investigations by Houk²⁷ and Qi²⁸ have found that a combination of geometry optimizations at the B3LYP/6-31+G(D) level²² followed by single-point energy calculations using Truhlar's MO6-2X functional²¹ with a large basis set provide thiol-Michael reaction energetics that are in good agreement with CBS-QB3 benchmarks. All reaction and transition state enthalpies and free energies reported herein were obtained at the MO6-2X/6-311G(2D,P)//B3LYP/6-31+G(D) level of theory.

Results and discussion

Et₃N-initiated mechanism in chloroform

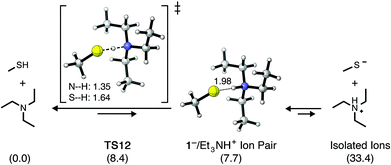
The Et₃N-initiated addition of methyl mercaptan (1) to NMM in CHCl₃ was chosen as a starting point for investigating the energetics, kinetics, and mechanism of thiol–maleimide reactions. As discussed above thiol–maleimide reactions are ideally suited to display rapid reaction kinetics given (i) the nucleophilicity of thiolate anions, (ii) the highly activated π-bond of maleimide derivatives, (iii) the strong basicity of the enolate intermediate, and (iv) the general acidity of most thiols. Indeed, the computed energetics of the catalytic addition of methane thiolate (1⁻) to NMM in CHCl₃ (Fig. 2) indicate a propagation step free energy barrier of ΔG^‡ = 8.1 kcal mol⁻¹ (TS8) leading to the slightly endergonic (ΔG° = 3.7 kcal mol⁻¹) formation of resonance-stabilized enolate intermediate 9. Deprotonation of another equivalent of thiol by this enolate intermediate, i.e. the chain-transfer step, requires an additional free energy barrier of ΔG^‡ = 4.8 kcal mol⁻¹ (TS10). The reaction generates thiol–maleimide addition product 11 along with another equivalent of thiolate anion, and is predicted to be exergonic overall by −11.7 kcal mol⁻¹. This catalytic cycle assumes that sufficient quantities of thiolate anion have been formed, either from the acid–base equilibrium established between 1 and Et₃N or from deprotonation of 1 by the enolate anion formed upon nucleophilic addition of Et₃N to NMM (Scheme 1b and c). Given that one or both of these processes is believed to occur in order to enter into the catalytic cycle shown in Scheme 1a it is important to compare their relative energetics.

Fig. 2 Calculated relative free energies of stationary points along the thiolate-catalyzed mechanism of methane thiolate (1⁻) addition to NMM. Free energies are expressed in kcal mol⁻¹ and were calculated at 298 K in a solvent model for CHCl₃. Distances of bonds breaking or forming in TS8 and TS10 are given in angstroms (Å).

It is often assumed that the equilibrium between methyl mercaptan (1) and Et₃N will provide initial quantities of methyl thiolate (1⁻) and Et₃NH⁺ in solution, noting that the pK_a of methyl mercaptan (∼10.5) is slightly lower than the pK_a of Et₃N (10.65). These values refer, of course, to their acid dissociation constants in water. When thiol–maleimide additions are used to prepare organic materials, however, the reactions are most commonly carried out as neat solutions or in organic solvents such as CHCl₃, which are considerably less able to stabilize the formation of 1⁻ and Et₃NH⁺ as compared to water. Lowe et al. have suggested^11a that attack on the π-bond of a Michael acceptor may initially occur by a thiolate/Et₃NH⁺ ion pair, such as 1⁻/Et₃NH⁺. Scheme 2 shows the calculated structures and relative energetics corresponding to proton transfer from 1 to Et₃N in CHCl₃, resulting in the formation of an ion pair as well as isolated ions. The free energy barrier for proton transfer from 1 to Et₃N is relatively low (ΔG^‡ = 8.4 kcal mol⁻¹, TS12), however, the formation of a 1⁻/Et₃NH⁺ ion pair is calculated to be endergonic by 7.7 kcal mol⁻¹ (K_eq = 2.3 × 10⁻⁶). The formation of isolated thiolate and ammonium ions 1⁻ and Et₃NH⁺ is significantly less favored at ΔG° = 33.4 kcal mol⁻¹. Qi et al. computationally studied the energetics of the trimethylamine (Me₃N)-mediated addition of 1 to divinylsulfone and noted similar energetics for proton transfer from 1 to Me₃N.²⁸ Computational results therefore suggest that (i) the equilibrium between 1 and Et₃N in CHCl₃ strongly favors the neutral reactants, (ii) very little of the 1⁻/Et₃NH⁺ ion pair will be present in solution, and (iii) essentially no free thiolate anion will be formed by direct deprotonation of 1 by Et₃N.

Scheme 2 Energetics of the acid–base equilibrium between methyl mercaptan (1) and triethylamine (Et₃N) calculated in CHCl₃. The relative free energy (ΔG° and ΔG^‡, kcal mol⁻¹) of each species or pair of species is given in parentheses. Dashed lines indicate bonds being broken/formed while dotted lines indicate noncovalent interactions. Distances are given in Å.

While very little of the 1⁻/Et₃NH⁺ ion pair is predicted to be present in CHCl₃, only a small amount of nucleophilic thiolate is necessary to initiate the self-sustaining catalytic cycle shown in Scheme 1a. The lowest energy transition state²⁹ found for the reaction between a 1⁻/Et₃NH⁺ ion pair and NMM, TS13, is shown in Fig. 3 and has a free energy barrier of ΔG^‡ = 22.8 kcal mol⁻¹. The resulting enolate intermediate 14 can abstract a proton from either Et₃NH⁺ or from another equivalent of 1 (both pathways are shown in Fig. 3). Interestingly, the highest free energy barrier along the pathway for proton transfer from Et₃NH⁺ corresponds to the energy required to disrupt the noncovalent interaction between the ammonium center and its carbonyl hydrogen bond acceptor (TS15). Once this noncovalent interaction is broken the transfer of a proton from Et₃NH⁺ to the enolate proceeds energetically downhill through transition state TS16 to give thiol addition product 11 and Et₃N. The free energy of transition state TS15 is found to be 5.3 kcal mol⁻¹ above enolate intermediate 14, indicating an overall free energy barrier of ΔG^‡ = 24.7 kcal mol⁻¹ for Et₃N-mediated addition of 1 to NMM along this pathway.

Fig. 3 Relative free energies (kcal mol⁻¹) of stationary points for the addition of a 1⁻/Et₃NH⁺ ion pair to NMM. Two mechanistic possibilities follow the initial propagation transition state (TS13): one involving proton transfer from Et₃NH⁺ (TS15–TS16) and another involving proton transfer from methyl mercaptan (TS17). Only the latter results in formation of thiolate anion 1⁻. Dashed lines indicate bonds being broken/formed. Dotted lines indicate noncovalent interactions. Distances are given in Å.

Alternatively, enolate intermediate 14 can abstract a proton from 1 as shown in chain transfer transition state TS17. Proton transfer from 1 is found to require ΔG^‡ = 7.6 kcal mol⁻¹ relative to enolate intermediate 14, indicating that proton transfer from Et₃NH⁺ (TS15–16) is energetically more favorable by 2.3 kcal mol⁻¹. However, only catalytic amounts of Et₃N are used to promote thiol–maleimide reactions and therefore the concentration of 1 will almost always exceed the concentration of Et₃NH⁺ in the reaction mixture. This is especially true in the early stages of thiol–maleimide reactions when the concentration of thiol is at its greatest. Therefore, while proton transfer from Et₃NH⁺ to enolate intermediate 14 is favored energetically, the transfer of a proton from 1 may still be favored kinetically depending on the relative concentrations of Et₃NH⁺ and 1 in solution. This difference is important because proton transfer from Et₃NH⁺does not produce any of the strongly nucleophilic thiolate anion 1⁻ whereas proton transfer from 1 does. Because no thiolate anion is formed in the first scenario, subsequent thiol–maleimide reactions must proceed along the same mechanistic pathway starting from the formation of a 1⁻/Et₃NH⁺ ion pair and proceeding through TS15, with an overall free energy barrier of ΔG^‡ = 24.7 kcal mol⁻¹. The alternative pathway involving proton transfer from 1 to enolate 14 through TS17does result in the formation of nucleophilic 1⁻, which can react directly with NMM along the catalytic cycle shown in Scheme 1a with a free energy barrier of ΔG^‡ = 8.5 kcal mol⁻¹. This second scenario is more consistent with the experimentally observed rapid kinetics of Et₃N-mediated thiol–maleimide reactions. Which mechanistic pathway(s) is taken will depend on the relative concentrations of starting materials and intermediates as a function of time and, therefore, benefits significantly from kinetic analysis, as will be discussed in subsequent sections.

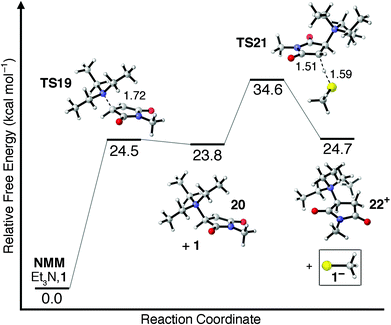
One other potential means of forming the thiolate anion 1⁻ involves the nucleophilic addition of Et₃N to NMM. Et₃N is generally considered a poor nucleophile as a result of steric crowding around its central nitrogen atom. The transition state for nucleophilic addition of Et₃N to NMM in CHCl₃ is shown as TS19 in Fig. 4, and is found to have a barrier of ΔG^‡ = 24.5 kcal mol⁻¹. Surprisingly, this free energy barrier is only 1.7 kcal mol⁻¹ less favored than the free energy barrier for attack of NMM by a 1⁻/Et₃NH⁺ ion pair (TS13, Fig. 3). The zwitterionic intermediate 20 formed following nucleophilic attack is found to be only 0.7 kcal mol⁻¹ more stable than TS19. Deprotonation of 1 by zwitterionic enolate intermediate 20 requires an additional 10.8 kcal mol⁻¹ (TS21), indicating that unimolecular β-scission of the N–C bond is energetically and kinetically more favored than the bimolecular chain-transfer pathway. The overall free energy barrier of ΔG^‡ = 34.6 kcal mol⁻¹ required to form 1⁻ along a nucleophile-initiated mechanism is 7.6 kcal mol⁻¹ greater than the free energy barrier to its formation along a base-initiated mechanism (TS17, Fig. 3) and is therefore unlikely to contribute significantly to the overall reaction mechanism. It should be reiterated, however, that all potential mechanistic pathways leading to the formation of a nucleophilic thiolate anion should be considered because once even small quantities of thiolate are available to react with NMM the rapid, catalytic thiolate addition mechanism shown in Scheme 1a becomes viable.

Fig. 4 Relative free energies (kcal mol⁻¹) of stationary points located along the nucleophile-initiated mechanism leading to methane thiolate formation (1⁻). Dashed lines indicate bonds being broken/formed, and distances are given in Å.

Kinetic modeling

Reaction energetics presented in Fig. 2–4 and Scheme 2 were used to calculate reaction rates using activated complex theory. Rate constants for individual mechanistic steps are provided in the ESI (Table S1†). Both forward and reverse rate constants were calculated for each individual step and modeled for all reactions. Kinetic modeling of thiol–maleimide addition reactions was performed with the initial concentrations of both thiol 1 and NMM taken to be 3.0 M and the concentration of Et₃N taken to be 0.3 M (10 mol%). With these initial conditions and the rate constants calculated for each possible mechanistic step, the concentrations of all starting materials, intermediates, and products were modeled as a function of time using the program Kintecus.³⁰ Including and simultaneously modeling all mechanistic pathways that can potentially lead to the formation of addition product 11, however favorable or unfavorable they may be, should result in the most accurate model of the thiol–maleimide reaction mechanism and kinetics. Furthermore, significant insights can be gained by selectively including or excluding individual reaction pathways from the overall kinetic model. For example, the influence of chain transfer from thiol 1 to intermediate 14 through TS17 (Fig. 3) on overall reaction kinetics can be assessed by including or excluding that specific mechanistic pathway in the kinetic model. This creates an artificial yet informative means of evaluating the relative contributions of different mechanistic pathways to overall reaction kinetics and product formation.

Results from computational and kinetic modeling of the Et₃N-promoted additon of 1 to NMM in CHCl₃ are shown in Fig. 5. Four different mechanistic scenarios are overlaid on the same plot. For each mechanistic scenario the formation of addition product 11 is plotted as a function of time. All four mechanistic scenarios include the catalytic thiolate addition pathway shown in Fig. 2. Where the pathways differ is in the process by which thiolate anion 1⁻ is formed. The green trace, labeled “Acid–Base Pathway,” plots product formation when the only mechanism available for thiolate formation is by deprotonation by Et₃N (Scheme 2). Each of the other three scenarios include attack of NMM by a 1⁻/Et₃NH⁺ ion pair through TS13 and lead to intermediate 14 (Fig. 3). The red trace plots product formation when chain-transfer occurs only from Et₃NH⁺ through TS15, while the black trace plots product formation when chain-transfer occurs only from 1 through TS17. Lastly, the blue trace is a “fully inclusive” mechanism wherein all possible reaction paths are included in the kinetic model.

Fig. 5 Results of kinetic modeling of the Et₃N-mediated addition of methyl mercaptan (1) to NMM in CHCl₃. The blue trace plots alkene conversion when all potential mechanistic pathways discussed in Fig. 2–4 and Scheme 2 are included in the model. The black, red, and green traces selectively exclude specific pathways as a means of evaluating their influence on the overall reaction kinetics.

With all mechanistic pathways included in the kinetic model (Fig. 5, blue trace) the Et₃N-promoted addition of 1 to NMM is predicted to reach 50% within 93 seconds. Interestingly, only 2% of 11 is predicted to form by 30 minutes when the only pathway available for thiolate formation is the direct deprotonation of 1 by Et₃N (green trace). Increasing the molar equivalents of Et₃N by a factor of 100 does not substantially change this observation, as the predicted yield of 11 after 30 minutes only increases to 7% when 10 molar equivalents of Et₃N are included in the model. This prediction indicates that even a 10-fold excess of Et₃N cannot shift the acid–base equilibrium in CHCl₃ toward the formation of sufficient 1⁻ to drive the reaction forward. Overall, these results strongly suggest that, in nonpolar solvents, the mechanism of Et₃N-promoted thiol–maleimide reactions begins with the attack of the maleimide π-bond by a thiolate/Et₃NH⁺ ion pair rather than direct deprotonation of the thiol by Et₃N.

As noted earlier, two different pathways are possible following the attack of NMM by a 1⁻/Et₃NH⁺ ion pair and the subsequent formation of enolate intermediate 14. Chain-transfer can occur by deprotonation of Et₃NH⁺ or by deprotonation of thiol 1. The influence of chain-transfer from Et₃NH⁺ can be examined by removing the thiol chain-transfer pathway from the kinetic model. The results of this scenario are shown as the red trace in Fig. 5. When chain-transfer from Et₃NH⁺ (TS15) is the only chain-transfer pathway available the formation of 11 is predicted to be quite slow, reaching less than 20% conversion within 30 minutes. By contrast, the black trace plots product formation when the only chain-transfer pathway included in the kinetic model is through TS17, i.e. chain-transfer from thiol 1. Under this hypothetical scenario the rate of product formation increases significantly, reaching 50% conversion in only 18 seconds. These results suggest that chain-transfer from 1 to 14 plays a more significant role in the formation of thiol–maleimide addition product 11 than chain-transfer from Et₃NH⁺, despite the fact that chain-transfer from Et₃NH⁺ is predicted to have a lower free energy barrier (TS15vs.TS17, Fig. 3). The key difference between the two pathways being that chain-transfer from 1 to 14does produce nucleophilic thiolate 1⁻ whereas chain-transfer between Et₃NH⁺ and 14 produces Et₃N and addition product 11 but no thiolate. It should be reiterated that the formation of thiolate 1⁻ is necessary for the characteristically rapid kinetics of thiol–maleimide click additions to be observed, as the rate-determining step in the thiol–maleimide catalytic cycle is predicted to have a free energy of only ΔG^‡ = 8.5 kcal mol⁻¹ (Fig. 2). Once initial quantities of thiolate are formed the catalytic cycle can become self-sustaining. Calculations and kinetic analysis presented herein suggest that neither the acid–base equilibrium between 1 and Et₃N nor the chain-transfer from Et₃NH⁺ to enolate 14 are able to form sufficient free thiolate 1⁻ and therefore do not contribute significantly to the formation of thiol–maleimide addition product 11. It is also predicted that the nucleophilic pathway does not contribute to thiolate formation. This prediction is not surprising given that the rate-determining step along the nucleophilic pathway (Fig. 4) is 7.6 kcal mol⁻¹ less favorable than the rate-determining step to thiolate formation along the ion pair pathway (Fig. 3).

Collectively the kinetic results presented in Fig. 5 provide significant insights into the role that Et₃N plays in promoting thiol–maleimide click reactions. The insights and conclusions drawn from the above discussion, however, refer specifically to computational and kinetic modeling of the Et₃N-mediated addition of methane thiolate (1) to NMM in CHCl₃. Several reseaerchers have noted that the kinetics of thiol-Michael reactions can vary significantly with different combinations of solvent, initiator, and thiol.^3,11,20 Even greater insights into thiol–maleimide click chemistry can be obtained by extending the above analysis to include a wider variety of solvents, bases/nucleophiles, and thiols. The next few sections will summarize results of modeling thiol–maleimide reactions under these different reaction conditions.

Influence of different solvents

Two additional solvent models were investigated to examine their role in the Et₃N-mediated addition of 1 to NMM: ethyl mercaptan (EtSH) and N,N-dimethylformamide (DMF). The use of the PCM solvent model for EtSH is expected to provide a reasonable representation of the energetics and kinetics of thiol–maleimide reactions run under neat conditions, while the solvent model for DMF was chosen to better understand the effects of running thiol–maleimide reactions in a polar solvent. Stationary points found along the reaction paths shown in Scheme 2 and Fig. 2–4 were each conformationally searched and re-optimized in EtSH and DMF. The resulting energetics calculated for the acid–base reaction between 1 and Et₃N are shown in Table 1 while the energetics of the catalytic addition of 1⁻ to NMM, the addition of an 1⁻/Et₃NH⁺ ion pair to NMM, and the nucleophilic addition of Et₃N to NMM are all summarized in Table 2.

Table 1 Comparison of the calculated free energies (ΔG°)^a and equilibrium constants for the formation of a 1⁻/Et₃NH⁺ ion pair and free ions 1⁻ and E₃NH⁺ in solvent models for CHCl₃, EtSH, and DMF. Also included are the free energies of proton transfer from 1 to DMF in the absence of Et₃N (DMF-catalysis)

Solvent	Ion pair	Free ions	K eq ion pair	K eq free ions
a Free energies are given in kcal mol^−1 at 298.15 K and 1.0 atm pressure.
CHCl3	7.7	33.4	2.3 × 10^−6	3.3 × 10^−25
EtSH	7.0	27.4	7.9 × 10^−6	9.0 × 10^−21
DMF	5.7	13.1	6.6 × 10^−5	2.6 × 10^−10
DMF catalysis	14.4	19.4	2.7 × 10^−11	6.6 × 10^−15

---

Table 2 Relative free energies (ΔG°)^a of stationary points along catalytic cycle,^b ion pair,^c and nucleophile-initiated^d reaction pathways involved in the Et₃N-mediated addition of 1 to NMM as a function of solvent (CHCl₃, EtSH, and DMF)

Solvent	Propagation T.S.	Intermediate	Chain transfer T.S.
a Energies are reported in kcal mol^−1. b See Fig. 2. c See Fig. 3. d See Fig. 4.
Thiolate addition to NMM (catalytic cycle)
CHCl3	8.1	3.7	8.5
EtSH	8.7	4.3	9.2
DMF	11.2	6.6	12.3
Ion pair pathway to thiolate formation
CHCl3	22.8	19.4	27.0
EtSH	22.0	17.9	26.6
DMF	19.9	16.6	23.8
Nucleophile initiated pathway to thiolate formation
CHCl3	24.5	23.8	34.6
EtSH	24.2	23.1	33.8
DMF	23.5	21.7	32.0

---

As shown in Table 1, more polar solvents are better able to stabilize the formation of methane thiolate (1⁻) and Et₃NH⁺ from the acid–base reaction between 1 and Et₃N. In all three solvents the formation of the 1⁻/Et₃NH⁺ ion pair is predicted to be endergonic, however the relative free energy of the ion pair decreases from 7.7 kcal mol⁻¹ in CHCl₃ to 7.0 kcal mol⁻¹ in EtSH and ultimately 5.7 kcal mol⁻¹ in DMF. A greater difference in calculated free energies is observed for the formation of free ions 1⁻ and Et₃NH⁺, where the acid–base reaction is notably more favored in DMF (ΔG° = 13.1 kcal mol⁻¹) than in EtSH or CHCl₃ (ΔG° = 27.4 and 33.4 kcal mol⁻¹, respectively). Such a large difference is significant because any solvent that sufficiently stabilizes the formation of 1⁻ provides a direct pathway to the rapid catalytic cycle of thiolate addition to NMM (Scheme 1a), bypassing the less energetically favorable ion pair mechanism. It is known²⁰ that high-dielectric constant solvents such as DMF can promote thiol–maleimide reactions in the absence of a catalyst. In such cases it is the solvent itself that promotes deprotonation of a thiol to give a nucleophilic thiolate anion. The free energy of proton transfer from 1 to DMF is also included in Table 1 so that the kinetics of DMF-catalyzed thiol–maleimide reactions can be modeled as well.³¹

Table 2 summarizes the influence of solvent on the free energies of stationary points along the catalytic thiolate addition, ion pair addition, and nucleophile-initiated mechanistic pathways shown in Fig. 2–4, respectively. For each solvent modeled the overall free energy barrier along the nucleophile-initiated pathway is at least 7.2 kcal mol⁻¹ higher than the overall free energy barrier along the ion pair pathway to thiolate formation. The nucleophile-initiated mechanism is therefore not predicted to contribute significantly to thiolate formation in any of the three solvents investigated. For all stationary points along each of the three pathways summarized in Table 2 the free energies of stationary points in EtSH are predicted to be within 0.8 kcal mol⁻¹ of those modeled in CHCl₃. This observation suggests that the kinetics of thiol–maleimide reactions run as neat mixtures are likely to be similar to the same reactions run in CHCl₃, though the reaction concentration and the dielectric constant of a given neat reaction solution will influence experimental results. The relative energetics of stationary points along both the ion pair and nucleophile-initiated pathways are predicted to decrease with increasing solvent dielectric, i.e. progressing from CHCl₃ to DMF. For the catalytic addition of thiolate to NMM, however, the opposite is true. The predicted free energy barrier to chain-transfer, which is rate-determining in each solvent, increases from ΔG^‡ = 8.5 kcal mol⁻¹ in CHCl₃ to 9.2 kcal mol⁻¹ in EtSH and finally 12.3 kcal mol⁻¹ in DMF. This trend results primarily from differences in the free energy of solvation of methane thiolate 1⁻. Nonpolar solvents such as CHCl₃ are less able to solvate small, highly charged species such as 1⁻, whereas DMF solvates such species quite well. A free thiolate anion is therefore predicted to be more reactive in CHCl₃ than in DMF. Upon addition of 1⁻ to NMM the negative charge once localized on 1⁻ becomes a resonance stabilized enolate intermediate with its net negative charge distributed across several atoms. The solvation free energies of these more delocalized anions (e.g. the propagation transition state, enolate intermediate, and chain-transfer transition state) were each found to be more similar across the three different solvents investigated.

The kinetics of Et₃N-mediated addition of 1 to NMM in EtSH and DMF were modeled using the same procedure as described in the previous section, and the results are plotted in Fig. 6. The predicted rate of alkene conversion in CHCl₃ and the DMF-catalyzed addition of 1 to NMM are also included in Fig. 6 for comparisson. Two mechanistic scenarios were modeled for each solvent: solid lines in Fig. 6 correspond to the rate of product formation when all possible mechanistic pathways were included in the kinetic model while dashed lines plot product formation when the only pathway available for thiolate formation is by the acid–base reaction between 1 and Et₃N. Only one plot is presented for the DMF-catalyzed addition of 1 to NMM formation because no Et₃N is included in the model.

Fig. 6 Results of kinetic modeling of the Et₃N-mediated addition of methyl mercaptan (1) to NMM in DMF (purple traces), CHCl₃ (blue traces), and EtSH (red traces). Solid lines indicate that all potential pathways to methane thiolate formation (acid–base, ion pair, and nucleophilic) are included in the model. Dashed lines indicate that the only pathway to thiolate formation included in the model is from the direct deprotonation of 1 by Et₃N. The dotted purple trace corresponds to the DMF-catalyzed addition of 1 to NMM in the absence of Et₃N.

As can be seen in Fig. 6 the solid and dashed purple lines corresponding to Et₃N-mediated thiol–maleimide reactions in DMF, overlap with each other.³² This result indicates that the rates of thiol–maleimide reactions in DMF are predicted to be the same regardless of whether thiolate (1⁻) is formed through the acid–base reaction between 1 and Et₃N or along an ion pair addition pathway. DMF is therefore predicted to be sufficiently polar that the ion pair addition pathway to thiolate formation is completely bypassed in DMF and thiol–maleimide reactions do occur following direct deprotonation of a thiol by a base, as commonly described in the literature. As noted above, however, highly polar solvents such as DMF are able to promote thiol-Michael reactions in the absence of an initiator. Therefore the kinetics of DMF-catalyzed addition of 1 to NMM was also examined, and the results are shown as the dotted purple tract in Fig. 6. Results of kinetic modeling show that the DMF-catalyzed thiol–maleimide reaction requires 3 minutes to reach 50% conversion, as compared to only 6 seconds in the presence of 10 mol% Et₃N. This result is not surprising given that the formation of an ion pair between DMF and 1 requires ΔG° = 14.4 kcal mol⁻¹, and separation of that ion pair to give free thiolate 1⁻ requires ΔG° = 19.4 kcal mol⁻¹ (Table 1). The formation of free thiolate 1⁻ by proton transfer to DMF is therefore calculated to be 6.3 kcal mol⁻¹ less favored than proton transfer to Et₃N in DMF. Computational results differ somewhat from experimental investigations by Du Prez that demonstrated the catalyst-free addition of isooctyl-3-mercaptopropionate to NMM in DMF is complete within one minute.²⁰ This difference between computational and experimental results may be expected, however, because mercaptopropionates are known^18,19 to undergo thiol-Michael reactions faster than alkane thiols. Differences in thiol reactivity will be evaluated and discussed in a later section.

The kinetics of thiol–maleimide reactions in EtSH are predicted to be similar to their kinetics in CHCl₃. One significant difference between EtSH and CHCl₃ is apparent in Fig. 6, namely that the direct formation of thiolate 1⁻ through deprotonation by Et₃N is predicted to contribute somewhat to product formation in EtSH (dashed red line) whereas the acid–base pathway is not predicted to contribute to product formation when the reaction is carried out in CHCl₃ (dashed blue line). This observation results from the fact that the formation of free ions 1⁻ and Et₃NH⁺ in EtSH is predicted to be 6.0 kcal mol⁻¹ more favored than in CHCl₃ (ΔG° = 27.4 vs. 33.4 kcal mol⁻¹, Table 1). It is therefore possible that the acid–base reaction between 1 and Et₃N plays some role in thiol–maleimide additions in EtSH, however reaction kinetics based on thiolate formation along this acid–base reaction alone are not in agreement with experimental observations. Computational predictions only agree with experimental observations when the mechanistic pathway involving attack of NMM by a 1⁻/Et₃NH⁺ ion pair, followed by chain-transfer from another equivalent of thiol, is included in the model. These results further support the conclusion that thiol–maleimide reactions in less polar solvents, likely including those carried out as neat solutions, follow an ion pair mechanism for initial thiolate formation.

Influence of different initiators

It has been widely demonstrated^{3,10,11,15,20} that the choice of initiator can influence the kinetics and yields of thiol-Michael reactions. The current study was therefore expanded beyond Et₃N to examine the influence of four additional initiators: EtNH₂, Et₂NH, DBU, and DMPP. The energetics of proton transfer between each initiator and methyl mercaptan (1) were calculated in solvent models for both CHCl₃ and DMF, and the results are summarized in Table 3. As may be expected, proton transfer from 1 to phosphine-centered initiator DMPP is found to be highly endergonic with the free energy of forming a 1⁻/DMPPH⁺ ion pair calculated to be ΔG° = 27.6 kcal mol⁻¹ in CHCl₃. Across the series of amine bases, computational results in CHCl₃ predict the free energy of transferring a proton from 1 to base decrease with greater amine substitution from ΔG° = 11.2 kcal mol⁻¹ for the formation of a 1⁻/EtNH₃⁺ ion pair to ΔG° = 7.7 kcal mol⁻¹ for the formation of a 1⁻/Et₃NH⁺ ion pair. It's noteworthy that the calculated free energies of proton transfer between 1 and the series of amines do not correlate with the amine pK_a's. Lowe and Haddleton have observed¹¹ experimentally that the kinetics of amine-initiated thiol-acrylate reactions also do not correlate with the pK_a's of each amine, further highlighting that acid–base reactivity alone often cannot explain thiol-Michael reaction kinetics. Lastly, proton transfer from 1 to the amidine base DBU is predicted to be the most favorable of the series, with ΔG° = 6.0 kcal mol⁻¹ for the formation of 1⁻/DBUH⁺ in CHCl₃. Importantly, the formation of free ions 1⁻ and DBUH⁺ in CHCl₃ is predicted to require 22.4 kcal mol⁻¹. This value is lower than the rate-determining step of the ion pair mechanism involving Et₃N (ΔG^‡ = 27.0 kcal mol⁻¹, Table 2) suggesting that very strong bases such as DBU may be able to bypass the ion pair mechanism and contribute to thiol–maleimide reactions by the direct deprotonation of thiols, even in nonpolar solvents.

Table 3 Free energies (ΔG°)^a calculated for the formation of an ion pair between 1 and each initiator as well as for the formation of free ions 1⁻ and Initiator-H⁺. pK_a's of nitrogen-centered bases are provided for reference

Initiator	CHCl3		DMF		pKa ^b
	Ion pair	Free ions	Ion pair	Free ions
a Free energies are reported in kcal mol^−1. b pKa values taken from ref. 33.
EtNH2	11.2	39.1	9.9	15.7	10.63
Et2NH	10.2	36.4	7.8	13.6	10.98
Et3N	7.7	33.4	5.7	13.1	10.65
DBU	6.0	22.4	1.9	2.0	11.50
DMPP	27.6	42.5	28.8	30.3	—

---

As can be seen in Table 3, the transfer of a proton from 1 to each of the nitrogen-centered bases is more favorable in DMF than in CHCl₃. This observation is most pronounced when comparing the free energy required to form free ions in solution, where switching to DMF is predicted to stabilize the formation of free thiolate by 20–23 kcal mol⁻¹ relative to CHCl₃. Computational and kinetic³⁴ results predict that, in DMF, all four nitrogen-centered bases are able to directly deprotonate enough of thiol 1 to initiate the catalytic thiol–maleimide cycle shown in Scheme 1a. In short, the kinetics of thiol–maleimide reactions in highly polar solvents such as DMF are predicted to be largely independent of the base used because the polarity of the solvent is able to promote the formation of sufficient free thiolate to bypass the ion pair mechanism. Furthermore, as shown in the preceeding section, DMF is able to catalyze thiol–maleimide reactions itself, absent any base. In nonpolar solvents such as CHCl₃, however, the ion pair mechanism and/or nucleophile-initiated mechanism are predicted to be necessary for the formation of initial quantities of thiolate, except in the cases of highly basic species such as DBU.

Listed in Table 4 are the relative free energies calculated for the formation of methane thiolate (1⁻) along both the ion pair and nucleophile-initiated mechanisms for each of the five initiators investigated. The one exception is that no propagation transition state could not be located along the ion pair pathway involving DMPP.³⁵ Computations predict that the overall free energy barrier to forming thiolate 1⁻ along an ion pair mechanistic pathway is lowest for DBU (ΔG^‡ = 18.9 kcal mol⁻¹) and highest for EtNH₂ (ΔG^‡ = 29.7 kcal mol⁻¹). The overall free energy barriers for secondary and tertiary amine bases Et₂NH and Et₃N are predicted to be identical within error (ΔG^‡ = 26.7–27.0 kcal mol⁻¹). This predicted similarity in reaction energetics between Et₂NH and Et₃N comes despite the fact that the formation of an ion pair between 1 and Et₃N is calculated to be 2.5 kcal mol⁻¹ more favorable than the formation of an ion pair with Et₂NH. The discrepancy can be explained upon examination of the propagation transition states involving 1, each of the different nitrogen-centered bases, and NMM (Fig. 7). Primary and secondary amine bases EtNH₂ and Et₂NH, though less energetically favored to deprotonate methyl mercaptan 1, are able to simultaneously hydrogen bond with both the nucleophilic thiolate anion and the amide carbonyl of NMM as shown in propagation transition states TS23 and TS24 (Fig. 7a and b), respectively. Tertiary Et₃N, by contrast, can only form one hydrogen bond between the Et₃NH⁺ and the nucleophilic thiolate as shown in TS13. Similar differences in hydrogen bonding are observed in the enolate intermediates and chain transfer transition states involving each of the three amines. This balance between basisity and hydrogen-bonding ability helps explain the different reaction energetics summarized in Table 4.

Fig. 7 Propagation transition states EtNH₂-mediated (a), Et₂NH-mediated (b), Et₃N-mediated (c), and DBU-mediated (d) addition of 1 to NMM in CHCl₃. Dashed lines indicate bonds being broken/formed while dotted lines indicate hydrogen bonding interactions. Distances are given in Å.

Table 4 Calculated reaction and transition state free energies (ΔG°, ΔG^‡)^a for the ion pair and nucleophile-initiated pathways leading to thiolate formation for each of the five initiators investigated

Initiator	Propagation	Enolate	Chain transfer	Initiator	Zwitterion	Chain transfer
	TS	Int	TS (from 1)	Addition TS	Int	TS
a Free energies reported in kcal mol^−1 using a solvent model for CHCl3. b No propagation transition state could be found for attack of the π-bond of NMM by the 1^−/DMPPH^+ ion pair.
EtNH2	26.2	22.0	29.7	23.0	20.7	33.3
Et2NH	22.6	18.4	26.7	22.3	20.2	32.1
Et3N	22.8	19.4	27.0	24.5	23.8	34.6
DBU	17.1	12.1	18.9	21.5	16.4	24.2
DMPP		—	—	21.7	14.9	24.5

---

DBU is also only able to form one hydrogen bond in its propagation transition state (TS25, Fig. 7d). It's interesting to note that in TS25 the DBUH⁺ ion is found to hydrogen bond with the NMM carbonyl rather than thiolate anion 1⁻. This difference in hydrogen bonding interactions between Et₃NH⁺ in TS13 and DBUH⁺ in TS25 reflects the fact that DBU is the stronger base and separation of the 1⁻/DBUH⁺ ion pair is less energetically costly than separation of the 1⁻/Et₃NH⁺ ion pair (Table 3). The strength of DBU also results in the lowest calculated free energy barrier to thiolate formation along the DBU-mediated ion pair pathway (ΔG^‡ = 18.9 kcal mol⁻¹).

Also shown in Table 4 are the relative energetics of nucleophilic pathways involving each of the five initiators. The propagation transition state free energy barriers for addition of each initiator to NMM are all predicted to fall within the relatively small range of ΔG^‡ = 21.5–24.5 kcal mol⁻¹. Much greater differences are observed when comparing the stabilities of resulting zwitterionic intermediates and subsequent chain-transfer free energy barriers. Each of the amine bases form largely unstable zwitterionic intermediates that are only slightly more stable than their propagation transition states. Furthermore, chain-transfer transition states between 1 and each of the ammonium intermediates are predicted to be quite high, ranging from ΔG^‡ = 32.1–34.6 kcal mol⁻¹. DBU and DMPP are both predicted to form more stable zwitterion intermediates and have chain-transfer free energy barriers between ΔG^‡ = 24–25 kcal mol⁻¹. These computational results are consistent with observations by Lowe^11a and Mayr³⁶ that the high catalytic activity of DBU is best explained by a model wherein DBU is able to react both as a base and as a nucleophile.

While it's interesting to compare the nucleophile-initiated free energy barriers of different initiators it is more instructive to compare the relative free energy barriers of nucleophile-initiated versus ion pair mechanistic pathways for each individual initiator. For example, DMPP will only follow a nucleophile-initiated pathway because its ion pair pathway is so energetically unfavorable it could not be located. More subtle trends are observed for the nitrogen-centered initiators. The rate-determining steps along the ion pair and nucleophile-initiated pathways involving EtNH₂ are within 3.6 kcal mol⁻¹ of each other at ΔG^‡ = 29.7 kcal mol⁻¹ (ion pair) and ΔG^‡ = 33.3 kcal mol⁻¹ (nucleophile-initiated). It is therefore possible that the nucleophile-initiated EtNH₂ pathway may contribute to thiolate formation. For the more sterically bulky Et₃N the nucleophile pathway is 7.6 kcal mol⁻¹ less favored than the ion pair pathway, and earlier kinetic analysis (Fig. 5) indicated that the nucleophile-initiated pathway does not contribute to thiolate formation or overall thiol–maleimide reactivity. Et₂NH and DBU fall in between EtNH₂ and Et₃N with the free energy difference between their ion pair and nucleophile-initiated pathways to thiolate formation calculated to be ΔΔG^‡ = 5.4 and 5.3 kcal mol⁻¹, respectively. It is therefore possible that Et₂NH may also follow a hybrid mechanism involving some thiolate formation by both the ion pair and nucleophile-initiated pathways. DBU may also follow a hybrid mechanism, however DBU is the only initiator for which both the ion pair (ΔG^‡ = 18.9 kcal mol⁻¹) and direct deprotonation (ΔG° = 22.4 kcal mol⁻¹) pathways are predicted to be more favorable than its nucleophilic addition pathway. It is therefore less likely that the nucleophile-initiated pathway for DBU will contribute to the overall thiol–maleimide reaction mechanism.

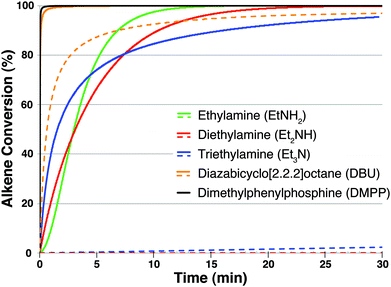
Fig. 8 shows a plot of alkene conversion versus time for each of the five initiators studied. For nitrogen-centered initiators the kinetic modeling conditions used in Fig. 8 were identical to those used previously in Fig. 5 and 6. For DMPP the only difference in modeling conditions was in the initial quantity of initiator, which was reduced to 1% as is more typical^3,10,11b for nucleophilic thiol-Michael initiators. As before, solid lines indicate that all possible mechanistic pathways were included in the kinetic model for each initiator. Dashed lines correspond to kinetic results when the only available pathway for thiolate formation is the direct deprotonation of 1, i.e. the acid–base pathway. Kinetic modeling of computational results suggest that DMPP exhibits the fastest overall reaction kinetics, a result that is in broad general agreement with experimental observations of DMPP-initiated thiol-Michael reactions.^{10,11b,16,17,20} One of the primary reasons DMPP-mediated thiol–maleimide reactions are predicted to be so rapid is because they follow a nucleophile-initiated mechanism exclusively. No protic species are formed along a nucleophile-initiated pathway and therefore the reaction proceeds along an anion chain-like mechanism. Protic species (e.g. Et₃NH⁺) have the effect of slowing down product formation at longer reaction times because they can undergo a rapid and exergonic acid–base reaction with any thiolate (e.g.1⁻) present, especially in nonpolar solvents. The consumption of 1⁻ by conjugate acid species causes the initially rapid kinetics of thiol–maleimide reactions to level off over time. Along a nucleophile-initiated reaction pathway, by contrast, all nucleophilc 1⁻ anions formed are available to react with NMM along the rapid catalytic cycle shown in Scheme 1a and alkene conversion does not slow dramatically as a function of time. This distinction can be applied broadly to thiol-Michael reactions that follow a nucleophile-initiated mechanism: because they do not produce protic species nucleophile-initiated thiol-Michael additions typically exhibit exceptionally rapid kinetics.

Fig. 8 Kinetic modeling of the addition of 1 to NMM in the presence of five different initiators: EtNH₂ (green traces), Et₂NH (red traces), Et₃N (blue traces), DBU (orange traces), and DMPP (black trace). Solid lines indicate that all potential pathways to methane thiolate formation (acid–base, ion pair, and nucleophilic) are included in the model. Dashed lines indicate that the only pathway to thiolate formation included in the model is the acid–base pathway involving direct deprotonation by a nitrogen-centered base. All results are modeled in CHCl₃.

The relative kinetics of product formation using nitrogen-centered initiators are more nuanced. DBU is predicted, by far, to exhibit the most rapid thiol–maleimide kinetics (Fig. 8, solid orange line). Additionally, as indicated by the dashed orange line in Fig. 8, DBU is the only nitrogen-centered base capable of initiating the thiol–maleimide reaction by its direct deprotonation of 1 in CHCl₃. Each of the other three amine bases must follow an ion pair mechanism, nucleophile-initiated mechanism, or some combination of both in order to produce initial quantities of thiolate 1⁻. When comparing the three amine bases, the initial rate of alkene conversion is most rapid with Et₃N followed by Et₂NH and finally EtNH₂. The initial rate therefore appears to follow the calculated trend in acid–base reactivity (Table 3). At longer reaction times, however, this ordering is switched as EtNH₂ is the first amine predicted to reach >90% alkene conversion, followed by Et₂NH and finally Et₃N. A closer examination of the kinetics of EtNH₂-mediated thiol–maleimide reactions can help explain this observation. The kinetic profile of the EtNH₂-mediated addition of 1 to NMM has a short induction period wherein less than 10% alkene conversion is observed within the first minute. This slow induction period is the result of the high free energy barriers to both the ion pair and nucleophile-initiated pathways for EtNH₂ (ΔG^‡ = 29.7 and 33.3 kcal mol⁻¹, respectively). After the first minute, however, the rate of EtNH₂-mediated alkene conversion increases rapidly and does not level off significantly. This rapid rate increase and lack of leveling suggests that the nucleophilic pathway is contributing to product formation in EtNH₂-mediated thiol–maleimide reactions. The kinetic profile of Et₂NH-mediated addition of 1 to NMM, while slightly slower by comparison, also does not level off significantly at longer reaction times. As noted earlier the nucleophile-initiated pathway for Et₂NH is calculated to be within 5.4 kcal mol⁻¹ of its ion pair mechanism, which is not as close as for EtNH₂ (ΔΔG^‡ = 3.6 kcal mol⁻¹) but closer than for Et₃N (ΔΔG^‡ = 7.6 kcal mol⁻¹). Alkene conversion as promoted by Et₃N does level off at longer reaction times likely because little, if any, thiolate is formed by the nucleophilic addition of Et₃N to NMM.

Computational results indicating that EtNH₂ and Et₂NH may nucleophilically add to NMM as a means of producing thiolate 1⁻ complement experimental studies of amine-mediated thiol-Michael reactions.^10,11 As noted earlier, Lowe and Haddleton have discussed the nucleophilic behavior of primary amines in thiol-acrylate reactions.¹¹ Several amines have also been shown to nucleophilically add to N-substituted maleimides. O'Dell et al. have synthesized³⁷ a variety of linear and crosslinked polymers by reacting bismaleimides with oligomeric bisamines. Schlup et al. have extensively studied³⁸ the addition of primary amines and aniline to maleimide derivatives using mid- and near-IR spectroscopy. More recently, Du Prez et al. have studied²⁰ the addition of both n-propyl and n-octyl amine to NMM in DMF by both ¹H NMR spectroscopy and LC-MS. Experimental studies have shown that secondary amines also undergo Michael addition to maleimides, though the addition of secondary amines is notably slower than the addition of primary amines.^37,38 To the best of our knowledge, tertiary amines (e.g. Et₃N) have not been shown to undergo nucleophilic addition to maleimide derivatives. To more directly compare computational studies presented herein and experimental investigations of amine additions to NMM, each amine initiator was stirred in a 1 : 1 molar ratio with NMM in CHCl₃ at ambient temperature (see ESI Scheme S1† and accompanying spectra). In the case of Et₃N, 1.0 equiv. of tert-butanol was added to the reaction mixture as a non-nucleophilic proton source. The nucleophilic Michael addition of hexylamine to NMM was obtained in >95% yield, in contrast to 79% addition of Et₂NH and 0% addition of Et₃N.³⁹ These experimental results support computational predictions that EtNH₂, and to a lesser extent Et₂NH, can nucleophilically add to NMM, even in a nonpolar solvent and at ambient temperature while the nucleophilic addition of Et₃N is not observed under these conditions.

Overall, computational modeling of the influence that initiators have on thiol–maleimide reactions helps explain the varying relationships between initiator pK_a, nucleophilicity, and reaction kinetics. DMPP exclusively follows a nucleophilic pathway, inducing the very rapid formation of thiol–maleimide addition product 11. DBU is strong enough to directly deprotonate 1, however the overall mechanism of DBU-mediated thiol–maleimide reactions is predicted to involve a combination of direct deprotonation and ion pair addition. A full understanding of the kinetics and mechanism of amine-mediated addition of 1 to NMM requires consideration of (i) the pK_a of the amine, (ii) hydrogen-bonding interactions observed along ion pair reaction pathways (Fig. 7), and (iii) the favorability of forming catalytic thiolate 1⁻ along a nucleophile-initiated pathway.

Influence of different thiols

Results so far have all used methyl mercaptan (1) as the representative thiol. To extend the current results beyond methyl mercaptan six additional thiols were investigated (2–7, Fig. 1). To reduce the overall computational burden of studying each mechanistic pathway for every combination of thiol, initiator, and solvent the seven different thiols were evaluated by comparing their acid–base reactivity with Et₃N in CHCl₃ along with the nucleophilicity of their resulting thiolate anions. Table 5 summarizes the relative free energies of hydrogen atom transfer transition states between thiols 1–7 and Et₃N, the formation of each thiolate/Et₃NH⁺ ion pair, the formation of isolated thiolate and Et₃NH⁺ ions, and calculated nucleophilicity N indicies⁴⁰ for each thiolate anion.

Table 5 Calculated reaction and transition state free energies (ΔG°, ΔG^‡)^a for hydrogen transfer between thiols 1–7 and Et₃N in CHCl₃ as well as the calculated nucleophilicity N index^b for each thiol

Thiol	1	2	3	4	5	6	7
a Free energies are reported in kcal mol^−1. b Nucleophilicity N indicies are given in eV, see ref. 40 and the ESI for full details.
TS	8.4	7.0	3.2	6.7	10.4	10.2	5.4
Ion pair	7.7	6.7	−2.0	4.6	8.8	9.3	3.8
Free ions	33.4	28.8	21.6	28.2	32.3	30.1	24.2
N	5.35	5.11	4.70	5.06	5.23	5.12	5.38

---

Calculations show that thiol functionality can significantly impact the favorability of Et₃N-mediated thiol–maleimide reactions. The free energy of forming an ion pair between thiols 1–7 and Et₃N in CHCl₃ is predicted to span a range of over 11 kcal mol⁻¹, from ΔG° = −2.0 kcal mol⁻¹ (thioacetic acid, 3) to ΔG° = 9.3 kcal mol⁻¹ (cysteine methyl ester, 6). Thioacetic acid 3 is the only thiol for which the formation of an ion pair, i.e.3⁻/Et₃NH⁺, is predicted to be exergonic. Relative energies of ion pair formation are also found to correlate relatively well with their S⋯H hydrogen-bond distances (see Fig. S17 of the ESI†): more stable ion pairs are observed to have longer S⋯H hydrogen-bond distances and vice versa. Overall the favorability of forming an ion pair with Et₃N follows the following trend from lowest to highest relative free energy: thioacetic acid (3), thiophenol (7), methyl thioglycolate (4), β-mercaptoethanol (2), methyl mercaptan (1), methyl 3-mercaptopropionate (5), and cysteine methyl ester (6). The trend in the relative free energy of forming free ions upon deprotonation of thiols 1–7 by Et₃N in CHCl₃ is quite similar, with only the order of the last three thiols being switched.

Recently Bowman and coworkers have taken advantage of differences in reactivity between two or more thiols and Michael acceptors to achieve selective thiol-Michael reactions in ternary^16,17 and even quaternary^18,19 mixtures. One study in particular¹⁹ evaluated the relative reactivities of 4, 5, 7, and 1-hexanethiol (a longer chain analogue of 1) by setting up competition reactions between pairs of thiols and methyl acrylate in CDCl₃ using 10 mol% Et₃N as a catalyst. These experiments revealed the following order of Et₃N-mediated thiol-Michael reactivity toward methyl acrylate: 7 > 4 > 5 > 1-hexanethiol (most rapid to least rapid). This trend observed experimentally by Bowman agrees well with the trend in calculated free energies of ion pair formation (Table 5), supporting the theory that differences in thiol reactivity in thiol-Michael reactions are primarily related to the pK_a of the thiol. The one discrepancy between experimental and computational results is found in the ordering of 5 and 1-hexanethiol (modeled computationally as methyl mercaptan 1). Experiments suggest 5 is more reactive than 1-hexanethiol in thiol-acrylate reactions while computations predict the formation of an ion pair between 1 and Et₃N is more favorable than between 5 and Et₃N. This discrepancy suggests that 1 may not be a perfect model for 1-hexanethiol. The difference may also reveal differences in the reactivity of methyl acrylate relative to NMM. It is also noteworthy that the experimental and computational trends match exactly when comparing experimental selectivities to the calculated free energies of forming free thiolate ions.

No correlation is observed between the experimental trend in thiol reactivity and calculated nucleophilicity N indicies. This is likely because all seven thiolate anions are considered strong nucleophiles given that each has an N index between 4.7–5.4, where any organic molecule with an N index greater than 3.0 is considered a strong nucleophile. Any of the strongly nucleophilic thiolate anions, once formed, will react readily and rapidly with the highly electrophilic NMM. The key to differences in thiol reactivity therefore appears to be the ease (or difficulty) of formining initial quantities of thiolate anions rather than the nucleophilicity of the thiolate itself. This observation again highlights the importance that the pK_a of a thiol will play in the overall kinetics of thiol–maleimide reactions, though previous insights regarding the influences of solvent and initiator will also need to be taken into account (e.g. all thiols are predicted to react rapidly with NMM when DMF is the solvent or when DBU is the base, etc.).

Experimental investigations of ternary thiol–maleimide reactions

A primary aim of this manuscript, in addition to providing a deeper understanding of thiol–maleimide reactions, is to elucidate how different reaction conditions can be used to promote selectivity in thiol-Michael, and particularly thiol–maleimide, reactions. To date we are unaware of any examples of selective thiol–maleimide reactions involving ternary mixtures of a maleimide derivative with two different thiols.⁴¹ The high reactivity of maleimide toward a wide range of thiols can make the selective addition of one thiol in the presence of another particularly challenging. Insight from computational investigations of the influence of solvent, initiator, and thiol on thiol–maleimide reactions can aid significantly in developing and understanding selective thiol–maleimide reactions in ternary mixtures. The results of ternary reactions run under different reaction conditions also provide a means of experimentally evaluating computational results discussed in this manuscript.

Thiophenol (7) and 1-hexanethiol (HT, a model for methyl mercaptan 1) were chosen for model ternary reactions with NMM. The two thiols were mixed in equimolar ratios with NMM in either CDCl₃ or DMF in the presence or absence of different initiators (Table 6). Each mixture was stirred at ambient temperature until complete consumption of NMM was observed by ¹H NMR spectroscopy (see the ESI† for complete spectral results). Percent yields of thiophenol addition product A and 1-hexanethiol addition product B were calculated by ¹H NMR spectroscopy and are provided in Table 6.

Table 6 Ternary reactions^a between NMM, 7, and HT given different ratios^b of thiol–maleimide addition products depending on the choice of solvent and initiator^c

Entry	Solvent	Initiator	Product A	Product B	A/B
a All reactions were run at room temperature with equimolar amounts of NMM, 7, and HT. b Product ratios determined by ^1H NMR spectroscopy. c Full experimental details and representative ^1H NMR spectroscopic results can be found in the ESI.
1	CDCl3	0.1 Et3N	94	6	16
2	CDCl3	0.1 DBU	77	23	3
3	CDCl3	0.01 DBU	83	17	5
4	CDCl3	0.01 DMPP	96	4	24
5	DMF	None	97	3	32
6	DMF	0.1 Et3N	85	15	6
7	DMF	0.1 DBU	36	64	0.6

---

When NMM, 7, and HT are mixed in CHCl₃ in the presence of 0.1 equiv. Et₃N the thiophenol addition product A is produced in 94% yield along with 6% of HT addition product B (entry 1). Computational and kinetic modeling have shown that methyl mercaptan 1 must initially follow an ion pair mechanism with an overall barrier of ΔG^‡ = 27.0 kcal mol⁻¹ in order to form thiolate 1⁻ because the direct deprotonation by Et₃N in CHCl₃ requires ΔG° = 33.4 kcal mol⁻¹. Deprotonation of the more acidic thiophenol 7 by Et₃N in CHCl₃, by contrast, requires only ΔG° = 24.2 kcal mol⁻¹, with an ion pair mechanism involving 7 and Et₃N likely to have an even lower free energy barrier. Experimental results are therefore in line with the conclusion that thiols react in order of their acidity. The use of a stronger base in the same solvent should increase the relative favorability of deprotonating HT, leading to an increase in the formation of product B. Indeed, when 0.1 equiv. of DBU is used as the base the percent of product B formed increases almost four-fold from 6% to 23% (entry 2). Computational results suggest the use of DBU drops the overall free energy barrier required to form thiolate 1⁻ considerably (ΔG^‡ = 18.9 kcal mol⁻¹, Table 4) and similarly increases the favorability of directly deprotonating the alkane thiol (ΔG° = 22.4, Table 3). Therefore a greater quantity of hexanethiolate is present when DBU is used rather than the same quantity of Et₃N, which enables the formation of product B to be more competitive with the formation of product A. This effect can be mitigated, however, by reducing the equivalents of DBU as shown in entry 3. When 0.01 equiv. of DBU is used to initiate the reaction a small but reproducable increase in selectivity is observed, with the yield of product A increasing to 83%.⁴²

Switching to a non-basic initiator, DMPP (entry 4), results in an increase of selectivity above that of Et₃N: 96% A and 4% B. This result is further supportive of the conclusion that the difference in selectivity between Et₃N and DBU in CHCl₃ is a result of the higher pK_a of DBU. The trace amounts of product B formed when DMPP is used as the initiator must result from deprotonation of HT by the zwitterionic enolate formed upon nucleophilic addition of DMPP to NMM. This enolate intermediate is more basic (pK_a ≈ 25) than Et₃N and DBU and can readily deprotonate both thiols 7 and HT. The observation that product A is dominant when DMPP is used as the initiator further corroborates the conclusion that the concentration of strong base (in this case enolate) influences selectivity in ternary reactions involving two different thiols. Decreasing the concentration of strong base, whether DBU as in entries 2 and 3 or enolate (via DMPP in entry 4), will result in greater observed selectivity.

Lastly, the role of solvent was investigated. Mixing NMM, 7, and HT in DMF in the absence of an initiator resulted in higher selectivity than any of the results in CHCl₃: 97% A and 3% B (entry 5). This result is an interesting case where the solvent itself is able to act as a selective initiator for ternary thiol–maleimide reactions. Selectivity is explained by the difference in the ability of DMF to deprotonate 1versus its ability to deprotonate 7. As seen in Table 1, proton transfer from 1 to DMF to give free thiolate 1⁻ requires ΔG° = 19.4 kcal mol⁻¹. Kinetic modeling predicts that DMF can catalyze the addition of 1 to NMM in the absence of an iniator, however the reaction is relatively slow (3 minutes to reach 50% conversion, Fig. 6). Proton transfer from 7 to DMF is calculated to be notably more favorable, requiring only ΔG° = 10.6 kcal mol⁻¹ to form free thiolate 7⁻. Kinetic analysis of the DMF-catalyzed addition of 7 to NMM is predicted to be rapid (90% conversion within 100 seconds), results that agree well with the experimental observations of DMF-catalyzed thiol–maleimide reactions by Du Prez²⁰ noted earlier. The difference in thiol pK_a is again found to be the primary factor determining selectivity.

Adding 10 mol% Et₃N to the DMF mixture of NMM, 7, and HT results in a reduction of selectivity, giving 85% product A and 15% product B (entry 6). The free energy required for Et₃N to deprotonate 1 in DMF is predicted to be ΔG° = 13.1 kcal mol⁻¹ (Table 1), which is 6.3 kcal mol⁻¹ lower than the free energy necessary for DMF itself to deprotonate 1. Again, the greater ease of forming hexanethiolate makes formation of product B more competitive with product A, though product A is still favored under these conditions. To further investigate the influence of initiator pK_a in polar solvents, 0.1 equiv. of DBU was used to initiate the ternary reaction in DMF. With DBU present as the initiator (entry 7) a reversal of selectivity is observed, with 36% formation of product A and 64% formation of product B. The combined influences of high solvent polarity and 10% of a strong base result in facile formation of significant quantities of both phenylthiolate and hexanethiolate. With significant quantities of both thiolates present the observed yields of products A and B no longer reflect differences in thiol pK_a. The observation that products A and B are formed in nearly equal amounts in DMF with 10% DBU implies that the thermodynamic and kinetic differences giving rise to the product yields in entry 6 are subtle and may be outside the scope and error limits of the computational methods used herein. These results highlight the importance of understanding and optimizing reaction conditions when selective thiol addition is desired. Simply choosing a polar solvent and strong base with the intention of increasing reaction kinetics can, as demonstrated in Table 6, significantly disfavor selectivity.

The experimental results summarized in Table 6 corroborate many of the computational and kinetic results discussed throughout this study. Furthermore, they highlight several of the means by which the selective addition of one thiol to maleimide can be achieved in the presence of another thiol. Of primary importance is a sufficient difference in the pK_a of the two thiols. Second, weakly basic or strictly nucleophilic initiators promote greater selectivity. If a strong base is necessary then it should be used at very low catalyst loading to promote greater selectivity. Lastly, nonpolar solvents can help accentuate differences in thiol pK_a, promoting greater selectivity. If a highly polar solvent capable of catalyzing the thiol–maleimide reaction itself is necessary (e.g. DMF, H₂O, or DMSO) then greater selectivity can be expected in the absence of any catalyst.

Conclusions

The energetics and mechanism of base- and nucleophile-initiated thiol additions to maleimide has been fully explored using computational methods. While the catalytic cycle of thiolate addition to maleimide is straightforward, the mechanism leading to initial formation of catalytic thiolate can follow a combination of several potential mechanistic pathways: direct deprotonation of the thiol by an initiator, attack of the maleimide π-bond by a thiol-initiator ion pair, and/or nucleophilic attack of maleimide by the initiator. Which mechanism(s) is dominant depends on the specific combination of solvent, initiator, and thiol. Understanding how each of these reaction parameters influences the mechanism and, therefore, kinetics of thiol–maleimide addition enables the design and tuning of selective thiol–maleimide reactions. The results are important for understanding and developing optimal means of using thiol–maleimide additions in the synthesis of organic materials and macromolecules, and can also enable the design of selective thiol–maleimide reactions. Conclusions from this study are expected to have broader implications in thiol-Michael in general. Investigations of the influence of different Michael acceptors in thiol-Michael reactions are currently underway.

Acknowledgements

The authors gratefully acknowledge financial support from Wesleyan University and the National Science Foundation CAREER program (award CHE-1352239). We thank Wesleyan University for computer time supported by the NSF under grant number CNS-0619508.

Notes and references

1. A. Michael, Am. Chem. J., 1887, 9, 115.
2. B. D. Mather, K. Viswanathan, K. M. Miller and T. E. Long, Prog. Polym. Sci., 2006, 31, 487–531.
3. For a recent review of thiol-Michael reactions and their applications see: D. P. Nair, M. Podgórski, S. Chatani, T. Gong, W. Xi, C. R. Fenoli and C. N. Bowman, Chem. Mater., 2014, 26, 724–744.
4. See, for example: (a) T. Miyadera and E. M. Kosower, J. Med. Chem., 1972, 15, 534–537; (b) S. S. Ghosh, P. M. Koa, A. W. McCue and H. L. Chappelle, Bioconjugate Chem., 1990, 1, 71–76; (c) M. Brinkley, Bioconjugate Chem., 1992, 3, 2–13, and references therein; (d) M. E. Gindy, S. Ji, T. R. Hoye, A. Z. Panagiotopoulos and R. K. Prud'homme, Biomacromolecules, 2008, 9, 2705–2711; (e) H.-Y. Yeh, M. V. Yates, A. Mulchandani and W. Chen, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 16522–17525; (f) L. C. Radu, J. Yang and J. Kopecek, Macromol. Biosci., 2009, 9, 36–44.
5. For recent representative examples of thiol–maleimide reactions used in the synthesis of macromolecular and other materials, see: (a) M. Li, P. De, S. R. Gondi and B. S. Sumerlin, J. Polym. Sci., Part A: Polym. Chem., 2008, 46, 5093–5100; (b) R. J. Pounder, M. J. Stanford, P. Brooks, S. P. Richards and A. P. Dove, Chem. Commun., 2008, 5158–5160; (c) L. A. Connal, C. R. Kinnane, A. N. Zelikin and F. Caruso, Chem. Mater., 2009, 21, 576–578; (d) M. J. Stanford and A. P. Dove, Macromolecules, 2009, 42, 141–147; (e) K. Peng, I. Tomatsu, A. V. Korobko and A. Kros, Soft Matter, 2009, 6, 85–87; (f) M. J. Stanford, R. L. Pflughaupt and A. P. Dove, Macromolecules, 2010, 43, 6538–6541; (g) L. Billiet, O. Gok, A. P. Dove, A. Sanyal, L.-T. T. Nguyen and F. E. Du Prez, Macromolecules, 2011, 44, 7874–7878; (h) T. Pauloehrl, G. Delaittre, M. Bastmeyer and C. Barner-Kowollik, Polym. Chem., 2012, 3, 1740–1749; (i) J. Zhu, C. Waengler, R. B. Lennox and R. Schirrmacher, Langmuir, 2012, 28, 5508–5512; (j) E. A. Phelps, N. O. Enemchukwu, V. F. Fiore, J. C. Sy, N. Murthy, T. A. Sulchek, T. H. Barker and A. J. Garcia, Adv. Mater., 2012, 24, 64–70; (k) K. C. Koehler, K. S. Anseth and C. N. Bowman, Biomacromolecules, 2013, 14, 538–547; (l) P. Gobbo, M. C. Biesinger and M. S. Workentin, Chem. Commun., 2013, 49, 2831–2833; (m) A. D. Baldwin and K. L. Kiick, Polym. Chem., 2013, 4, 133–143.
6. H. C. Klob, M. G. Finn and K. B. Sharpless, Angew. Chem., Int. Ed., 2001, 40, 2004–2021.
7. J. E. Mose and A. D. Moorhouse, Chem. Soc. Rev., 2007, 36, 12491262.
8. The growing applications of click chemistry in macromolecular and materials synthesis has lead to a recommendation that the criteria for classifying reactions as “click” in such applications be updated to better reflect the challenges specific to materials synthesis, see: C. Barker-Kowollik, F. E. Du Prez, P. Espeel, C. J. Hawker, T. Junkers, H. Schlaad and W. Van Camp, Angew. Chem., Int. Ed., 2011, 50, 60–62.
9. (a) C. J. Hawker and K. L. Wooley, Science, 2005, 309, 1200–1205; (b) R. K. Iha, K. L. Wooley, A. M. Nyström, D. J. Burke, M. J. Kade and C. J. Hawker, Chem. Rev., 2009, 109, 5620–5686.
10. For recent reviews of thiol–ene reactions, focusing on both thiol-Michael and radical initiated thiol–ene reactions, see: (a) A. B. Lowe, Polym. Chem., 2010, 1, 17–36; (b) C. E. Hoyle, A. B. Lowe and C. N. Bowman, Chem. Soc. Rev., 2010, 39, 1355–1387; (c) A. B. Lowe, Polym. Chem., 2014, 5, 4820–4870.
11. (a) J. W. Chan, C. E. Hoyle, A. B. Lowe and M. Bowman, Macromolecules, 2010, 43, 6381–6388; (b) G.-Z. Li, R. K. Randev, A. H. Soeriyadi, G. Rees, C. Boyer, Z. Tong, T. P. Davis, C. R. Becer and D. M. Haddleton, Polym. Chem., 2010, 1, 1196–1204.
12. For recent reviews focusing on radical-initiated thiol–ene reactions, see: (a) C. E. Hoyle, T. Y. Lee and T. Roper, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 5301–5338; (b) C. E. Hoyle and C. N. Bowman, Angew. Chem., Int. Ed., 2010, 49, 1540–1573; (c) M. J. Kade and C. J. Hawker, J. Polym. Sci., Part A: Polym. Chem., 2010, 48, 743–750.
13. N. B. Cramer, S. K. Reddy, A. K. O'Brien and C. N. Bowman, Macromolecules, 2003, 36, 7964–7969.
14. For a computational study of radical-initiated thiol–ene reactions, see: B. H. Northrop and R. N. Coffey, J. Am. Chem. Soc., 2012, 134, 13804–13817.
15. W. Xi, C. Wang, C. J. Kloxin and C. N. Bowman, ACS Macro, 2012, 1, 811–814.
16. H. Matsushima, J. Shin, C. N. Bowman and C. E. Hoyle, J. Polym. Sci., Part A: Polym. Chem., 2010, 48, 3255–3264.
17. S. Chatani, D. P. Nair and C. N. Bowman, Polym. Chem., 2013, 4, 1048–1055.
18. S. Chatani, C. Wang, M. Podgórski and C. N. Bowman, Macromolecules, 2014, 47, 4949–4954.
19. S. Chantani, M. Podgórski, C. Wang and C. N. Bowman, Macromolecules, 2014, 47, 4894–4900.
20. L.-T. T. Nguyen, M. T. Gokmen and F. E. Du Prez, Polym. Chem., 2013, 4, 5527–5536.
21. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
22. (a) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789; (b) A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377; (c) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
23. M. J. Frisch, et al., Gaussian 09, Revision A.1 (see ESI† for the full reference).
24. (a) S. Miertus, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129; (b) M. Cossi, V. Barone, R. Cammi and J. Tomasi, Chem. Phys. Lett., 1996, 255, 327–335.
25. R. M. Stolz and B. H. Northrop, J. Org. Chem., 2013, 78, 8105–8116.
26. (a) M. R. Nyden and G. A. Petersson, J. Chem. Phys., 1981, 75, 1843–1862; (b) G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090; (c) G. A. Petersson, T. Tensfeldt and J. A. Montgomery, J. Chem. Phys., 1991, 94, 6091–6101; (d) J. A. Montgomery, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1994, 101, 5900–5909.
27. E. H. Krenske, R. C. Petter, Z. Zhu and K. N. Houk, J. Org. Chem., 2011, 76, 5074–5081.
28. C. Wang and C. Qi, Tetrahedron, 2013, 69, 5348–5354.
29. Three unique propagation transition states for the attack of the NMM π-bond by a 1⁻/Et₃NH⁺ ion pair were found, with TS13 being the most energetically favorable. The next most energetically favorable propagation transition state found has a relative free energy of ΔG^‡ = 26.1 kcal mol⁻¹.
30. J. C. Ianni, Kintecus, version 5.20, 2014. http://www.kinteus.com (accessed May 3, 2014).
31. A combination of explicit and implicit solvation was used to calculate the free energy of proton transfer from 1 to DMF, see Fig. S14 of the ESI† for structures and a complete explanation of the modeling details.
32. In the case of DMF, the solid and dashed lines also include the pathway wherein DMF itself deprotonates 1 to give free thiolate 1⁻. The concentration of DMF used in the kinetic model was taken to be 12.9 M, corresponding to the concentration of pure DMF at room temperature.
33. Amine pK_a values from: H. K. Hall Jr., J. Am. Chem. Soc., 1957, 79, 5441–5444 . Aqueous pK_a of DBU from: F. Ravalico, S. L. James and J. S. Vyle, Green Chem., 2011, 13, 1778–1783.
34. See Fig. S19 of the ESI† for a plot of alkene conversion versus time for the four nitrogen-centered bases as modeled in DMF.
35. All attempts to locate the propagation transition state for addition of a 1⁻/DMPPH⁺ ion pair to NMM optimized to give starting materials 1, DMPP, and NMM. It was therefore concluded that DMPP is not able to act as a base along an ion pair reaction pathway such as the one shown in Fig. 3.
36. M. Baidya and H. Mayr, Chem. Commun., 2008, 1792–1794.
37. L. R. Dix, J. R. Ebdon, N. J. Flint, P. Hodge and R. O'Dell, Eur. Polym. J., 1995, 31, 647–652.
38. Z. Shen and J. R. Schlup, J. Appl. Polym. Sci., 1998, 67, 267–276.
39. Yields of nucleophilic Michael-addition products were calculated from relative integration ratios of ¹H NMR spectroscopic signals corresponding to starting materials (NMM and amines) and the product.
40. L. R. Domingo and P. Pérez, Org. Biomol. Chem., 2011, 9, 7168–7175.
41. Thiol-Michael selectivity within ternary mixtures of N-propyl maleimide, thiol 5, and an additional Michael acceptor (phenyl vinyl sulfonate, metyl acrylate, or methyl methacrylate) have been carried out and thiol addition to N-propyl maleimide is preferred, see ref. 19.
42. Increasing the equivalents of DBU decreases the selectivity in the ternary mixture; however high loading (e.g. 0.5 equiv.) of DBU also promotes side reactions such as the Michael addition of DBU to NMM.

---

Footnote

† Electronic supplementary information (ESI) available: Full experimental details and ¹H NMR spectroscopic results of amine additions to NMM and of competition reactions between NMM, 7, and HT; full computational details regarding the calculation of nucleophilicity N indices and energetics of proton transfer from thiols 1 and 7 to DMF; plot of thiolate/Et₃NH⁺ ion pair energies versus S⋯H distances; complete tables of all calculated rate constants; a kinetic plot of alkene conversion versus time for N-centered initiators in DMF; Cartesian coordinates of all stationary points reported in this manuscript; and the full author list for ref. 23. See DOI: 10.1039/c5py00168d

---