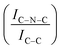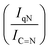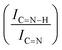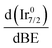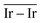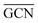Open Access Article
Open Access ArticleEnhanced stability of sub-nanometric iridium decorated graphitic carbon nitride for H2 production upon hydrous hydrazine decomposition†
Silvio
Bellomi
 a,
Ilaria
Barlocco
a,
Xiaowei
Chen
a,
Ilaria
Barlocco
a,
Xiaowei
Chen
 b,
Juan J.
Delgado
b,
Rosa
Arrigo
b,
Juan J.
Delgado
b,
Rosa
Arrigo
 c,
Nikolaos
Dimitratos
c,
Nikolaos
Dimitratos
 de,
Alberto
Roldan
de,
Alberto
Roldan
 *f and
Alberto
Villa
*f and
Alberto
Villa
 *a
*a
aDipartimento di Chimica, Università degli Studi di Milano, via Golgi 19, I-20133 Milano, Italy. E-mail: alberto.villa@unimi.it
bDepartamento de Ciencia de los Materiales, Ingeniería Metalúrgica y Química Inorgánica, Facultad de Ciencias, Universidad de Cádiz, Campus Río San Pedro, Puerto Real (Cádiz) E-11510, Spain
cSchool of Science, Engineering and Environment, University of Salford, M5 4WT, Manchester, UK
dDipartimento di Chimica Industriale “Toso Montanari”, Alma Mater Studiorum Università di Bologna, Viale Risorgimento 4, Bologna 40126, Italy
eCenter for Chemical Catalysis-C3, Alma Mater Studiorum Università di Bologna, Viale Risorgimento 4, Bologna 40136, Italy
fCardiff Catalysis Institute, School of Chemistry, Cardiff University, Main Building, Park Place, CF10 3AT, Cardiff, UK. E-mail: RoldanMartinezA@cardiff.ac.uk
First published on 30th November 2022
Abstract
Stabilizing metal nanoparticles is vital for large scale implementations of supported metal catalysts, particularly for a sustainable transition to clean energy, e.g., H2 production. In this work, iridium sub-nanometric particles were deposited on commercial graphite and on graphitic carbon nitride by a wet impregnation method to investigate the metal–support interaction during the hydrous hydrazine decomposition reaction. To establish a structure–activity relationship, samples were characterized by transmission electron microscopy and X-ray photoelectron spectroscopy. The catalytic performance of the synthesized materials was evaluated under mild reaction conditions, i.e. 323 K and ambient pressure. The results showed that graphitic carbon nitride (GCN) enhances the stability of Ir nanoparticles compared to graphite, while maintaining remarkable activity and selectivity. Simulation techniques including Genetic Algorithm geometry screening and electronic structure analyses were employed to provide a valuable atomic level understanding of the metal–support interactions. N anchoring sites of GCN were found to minimise the thermodynamic driving force of coalescence, thus improving the catalyst stability, as well as to lead charge redistributions in the cluster improving the resistance to poisoning by decomposition intermediates.
Introduction
Metal nanoparticles (NPs) dispersed on carbonaceous supports are of high interest in catalysis. In particular, platinum-group-metals, i.e. Ru, Rh, Pd, Os, Ir and Pt, remain essential for many sustainable chemical processes, including biomass valorisation and hydrogen production, due to their excellent catalytic performances and durability.1,2Establishing a structure–activity and stability relationship in heterogeneous catalysis is challenging.3 The dependency of the catalytic activity upon particle size, structure of the active phase and support effects has been demonstrated for several catalytic processes4 thanks to recent advances in characterization techniques.5,6 Indeed, the number and composition of accessible conformations at operative conditions are strongly dependent upon the NP diameter, leading to dimension-specific catalytic activities where “every atom counts”. Usually, the smaller the particle size, the higher is the catalyst performance due to an enhanced number of superficial atoms able to react with the substrates.7,8
Among the many reports available in the literature regarding supported metal particles as catalysts,4,9 remarkable results were obtained using NPs with sizes below 2 nm. For example, the activity of Rh NPs in the hydrogenation of cyclohexene10 and phenols11 is greatly enhanced when particle sizes are 0.4 nm and 1.3 nm, respectively. However, Rogers and co-workers12 found that Pd nanoclusters of about 20 atoms have lower durability than larger NPs for the furfural hydrogenation reaction. Indeed, despite the intriguing properties related to sub-nanometric metal clusters, one of the biggest challenges is still finding practical ways to stabilise them against migration and ripening phenomena.
The support plays a fundamental role in stabilizing metal clusters, avoiding undesired sintering processes.13,14 Carbon materials are highly attractive as catalyst supports, because of their relatively low costs and high tunability of the physicochemical properties. Indeed, chemical modification of a carbon surface can improve the stabilization of few-atom clusters and single atoms,15–20 and strongly influence the nature of the metal species, in a way which resembles organic ligands in organometallic catalysis, thus opening up the opportunity to realize high site specificity.20–23 The presence of heteroatoms (e.g. N, O, B, and P) and surface defects provide three main advantages: (i) to act as nucleation/growth sites for metal clusters,24,25 (ii) to stabilize metal clusters through coordinative bonds suppressing undesired sintering processes,21,22 and (iii) to alter the cluster electronic configuration to facilitate adsorption/desorption of substrates, thus enhancing reaction rates. In a recent study Liu and co-workers, it was demonstrated that Ir nanodots embedded in a carbon skeleton with an average size of 1.19 nm were remarkably stable in the electrocatalytic nitrogen reduction reaction (NRR), exhibiting excellent electrocatalytic NRR performances under both acidic and alkaline conditions.26 Concerning heteroatom stabilization, Kim and co-workers observed that sub-2 nm Pt NPs deposited on O-doped carbon enhanced the catalytic activity in the oxygen reduction reaction (ORR) with respect to the pristine support.27 In formic acid decomposition (FAD), the effect of dopants (i.e. O, P and N) was unveiled, highlighting a great improvement in the catalytic performances and stability of Pt NPs.28 Xu and co-workers reported an exceptionally high catalytic activity for FAD (14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 h−1) performed over Pd NPs immobilized in N-doped hierarchically porous carbons at 333 K. In addition, the N functionalities enabled them to stabilize ultra-fine nanoparticles (1.1 ± 0.2 nm), enhancing the catalyst activity with respect to the pristine counterparts.29 Different electrocatalysis reports also confirmed the possibility of stabilizing nanoparticles below 2 nm by employing N-functionalised carbon materials.30–35 Recent studies indicated graphitic carbon nitride as an ideal support for stabilizing small NPs,36,37 nanoclusters,38,39 and single atom species39–45 due to its unique properties.46 The peculiar electronic structure and the N-rich framework composed of amine-bridged tri/heptazine moieties in these systems provide many adsorption sites for grafting metal clusters on their surface.47
400 h−1) performed over Pd NPs immobilized in N-doped hierarchically porous carbons at 333 K. In addition, the N functionalities enabled them to stabilize ultra-fine nanoparticles (1.1 ± 0.2 nm), enhancing the catalyst activity with respect to the pristine counterparts.29 Different electrocatalysis reports also confirmed the possibility of stabilizing nanoparticles below 2 nm by employing N-functionalised carbon materials.30–35 Recent studies indicated graphitic carbon nitride as an ideal support for stabilizing small NPs,36,37 nanoclusters,38,39 and single atom species39–45 due to its unique properties.46 The peculiar electronic structure and the N-rich framework composed of amine-bridged tri/heptazine moieties in these systems provide many adsorption sites for grafting metal clusters on their surface.47
Hydrazine (N2H4) is one of most promising hydrogen carriers.48,49 It is a carbon-free fuel, and has a hydrogen content of 12.5 wt%.50 However, hydrazine possesses an intrinsic hypergolic nature, namely, the risk of explosion is one of the most serious problems related to its handling, especially in the presence of active metals that may catalyze its decomposition.51 One solution to this challenge is N2H4 dilution in water, forming hydrous hydrazine (N2H4⋯H2O), which contains an 8 wt% intrinsic stoichiometric content of hydrogen.52,53 N2H4⋯H2O is reported to decompose catalytically through two different pathways:54
| N2N4 → N2(g) + 2H2(g) ΔH0 = −95.4 kJ mol−1 | (1) |
| 3N2N4 → N2(g) + 4NH3(g) ΔH0 = −157.0 kJ mol−1 | (2) |
The first reaction (eqn (1)) represents the complete reforming pathway, where molecular hydrogen and nitrogen are produced. The second path (eqn (2)) produces nitrogen and ammonia and is the thermodynamically favored process. The selectivity of the process depends upon several reaction conditions, such as pressure, temperature and nature of the catalyst.55–57 Previous studies have shown that iridium is effective in the catalytic decomposition of hydrous hydrazine. Singh and co-workers reported the activity of a series of monometallic nanoparticles (Rh, Co, Ir, Cu, Ni, Fe, Pt and Pd) for the hydrous hydrazine decomposition and, at 298 K, although very active, Ir was only able to achieve 7% of H2 selectivity, and no information on the stability of the catalysts was reported.58 The low Ir selectivity was confirmed by computational Density Functional Theory (DFT) studies of hydrazine decomposition over an Ir(111) slab, underlining the ability of the surface to decompose the substrate preferentially through the incomplete decomposition pathways (eqn (2)).59 Jang and co-workers prepared honeycomb Ir NPs immobilized on γ-Al2O3 through a soak-dry procedure, with a nominal metal loading of 2 wt% (2 wt% Ir/γ-Al2O3). The authors demonstrated the ability of such catalysts to decompose hydrous hydrazine at ambient temperature, but no detailed information on catalytic activity, stability and H2 selectivity was reported.60 Furthermore, Motta and co-workers synthesized by a decomposition–precipitation method sub-nanometric (>2 nm) Ir NPs supported on CeO2 (1 wt% Ir/CeO2) and tested it in the hydrous hydrazine decomposition, varying the reaction temperature. They demonstrated that increasing the reaction temperature resulted in a higher activity but a lower selectivity toward H2.57
In this work, Ir sub-nanometric clusters supported on graphitic carbon materials (graphite and GCN) were studied in the hydrous hydrazine decomposition reaction. Graphite and GCN present comparable electronic and morphological properties, but a remarkably different N intrinsic content, which allowed us to rationalise the enhanced stability of supported sub-nanometric Ir particles on carbonaceous supports and unveil the effect of N-functionalities. To disclose structure–activity correlations and metal–support interactions, fresh and used catalysts were characterized by HR-TEM and XPS in combination with computational techniques. The combined experimental and computational approach presented herein provided an in depth understanding of the enhanced stability observed over GCN at the atomistic scale and of the role of metal–support interactions.
Experimental method
Materials and chemicals
Graphite was obtained from Johnson Matthey. IrCl3xH2O (99.9%), N2H4⋯H2O (98%), sodium hydroxide (NaOH, ≥98%), molten cyanamide, Ludox HS40 SiO2 particles, NH4HF2, NaBH4 and ethanol were acquired from Sigma-Aldrich.Catalyst synthesis
Iridium wet impregnation procedure
In a typical wet impregnation procedure, slightly varied from the work of Shao and co-workers,36 a final MeOH volume of 100 mL was employed. In a 250 mL round bottom flask, 0.5 g of the desired support was introduced and left under stirring (1250 rpm) for 15 min. After the specified time, the temperature was slowly increased up to 323 K, the desired amount of precursor (IrCl3xH2O, 99.9%) was introduced, and the mixture was slowly heated up to 343 K and left under reflux conditions for 8 h. The amount of support and precursor were calculated to have a nominal metal loading of 1 wt%. After the specified time, a 20-fold molar excess of aqueous NaBH4 was quickly added, and the reaction mixture was left under stirring for 1 h to ensure complete reduction of the impregnated precursor. The solid was filtered, washed several times with EtOH (1 L g−1) and water (1 L g−1), and dried overnight at RT in air.Catalytic tests
Liquid phase N2H4⋯H2O decomposition was performed at a constant reaction temperature of 323 K, under kinetic conditions,57 using a 35 mL two-necked round bottom flask, with one of the flask's necks connected to the pressure detection sensor. Gaseous products evolution was monitored through the Man On the Moon X102 kit measuring the partial pressures of the released product, as reported in several reports concerning H2 production.62–64 In a typical procedure, the required amount of catalyst (N2H4⋯H2O/metal molar ratio 1000/1) was added to the reactor, where 5.0 mL of a 0.5 M NaOH aqueous solution was placed and heated at the desired temperature, until the registered pressure exhibited a plateau, indicating that equilibrium has been achieved. Once equilibrated, the pressure was released to avoid over-pressures within the reactor. Finally, 300 µL of a 3.3 M hydrous hydrazine aqueous solution was injected into the reactor through a vacuum septum, using a syringe, with the final mixture stirring at 1400 rpm. Once the substrate was injected, the data collection started with a sampling time of 0.3 s until the end of the decomposition reaction, indicated by a pressure plateau. To ensure experimental reproducibility and assess measuring uncertainty, all the catalytic tests were performed three times. Selectivity towards H2 generation (x) was evaluated based on eqn (3):| 3N2H4 → 4(1 − x)NH3 + 6xH2 + (1 + 2x)N2 | (3) |
The released gaseous products were allowed to pass into a trap containing a 0.05 M HCl aqueous solution to ensure the removal of NH3,65 if any, hence the gas pressure measured during the reaction contained only N2 and H2, enabling us to obtain the molar ratio (λ) as 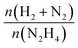 by means of the perfect gas law (pV = nRT). Therefore, H2 selectivity was calculated through eqn (4):
by means of the perfect gas law (pV = nRT). Therefore, H2 selectivity was calculated through eqn (4):
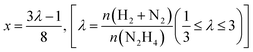 | (4) |
Catalytic activity was calculated as the ratio between moles of converted substrate and metal moles, normalized with respect to the reaction time (t). All the metal species were considered active in the hydrous hydrazine decomposition. Considering the high number of sampling data, it was possible to calculate the initial activity for time approaching zero (t → 0) through numerical data treatment. Data analysis and elaboration were performed with in-house developed Python scripts based on Numpy66 and Scipy,67 well-established libraries for numerical analysis.
Catalysts characterization
TEM experiments were performed on a double Cs aberration-corrected FEI Titan3 Themis 60–300 microscope equipped with a monochromator, a X-FEG gun and a high efficiency XEDS ChemiSTEM, which consists of 4-windowless SDD detectors. HR-STEM imaging was performed at 200 kV and using a high-angle annular dark-field (HAADF) detector with a camera length of 11.5 cm. The HAADF-STEM technique is sensitive to the atomic number of the elements, whose intensity is roughly proportional to the square of the atomic number (Z2) and makes it possible to distinguish small nanoparticles supported on light supports. XEDS mappings were performed using a beam current of 200 pA and a dwell time per pixel of 128 µs. To improve the visual quality of the elemental maps obtained, these were filtered using a Gaussian blur of 0.8 using Velox software. Based on the STEM-HAADF images of the catalysts, the diameters of more than 200 metal particles randomly selected were measured and the corresponding metal particle size distributions (PSD) were determined. Based on these PSDs, mean particle diameter (d) was calculated according to the following expression: d = nidi/ni, where ni ≥ 200. For average particle size calculation ImageJ software was used.X-ray photoelectron spectroscopy (XPS) analyses were performed on a Kratos Axis Ultra DLD instrument. Spectra were recorded using monochromatized Al Kα radiation (1486.6 eV), with an X-ray power of 150 W. The spectrometer was operated in the Constant Analyser Energy mode, with a pass energy of 20 eV. Powder samples were pressed into pellets, which were stuck on double-sided adhesive conducting polymer tape. Surface charging effects were compensated by making use of the Kratos coaxial neutralization system. XPS data analysis was performed with CasaXPS Software, version 2319PR1-0, developed by Neal Fairley (Casa Software Ltd, 2013). The N1s XPS peaks were fitted using the model reported in ref. 68 for the GCN and ref. 69 the graphite systems. The C1s XPS peaks were fitted using the model reported in ref. 68 for the GCN and ref. 70 for the graphite systems. The Ir 4f was fitted using the model reported in ref. 71. The O1s XPS peaks were fitted according to the model reported in ref. 70. Table S1 (ESI†) summarizes the fitting models employed.
Inductively coupled plasma optical emission spectroscopy (ICP-OES) analyses, using a PerkinElmer Optima 8000 emission spectrometer, were performed to confirm the Ir metal loading and to detect metal leaching in the reaction solution.
Computational details
Periodic plane-wave density functional theory (pw-DFT) calculations were carried out using the Vienna Ab-initio Simulation Package (VASP).72,73 In order to take into account the correlation–exchange electronic contributions, the Perdew–Burke–Ernzerhof (PBE) functional was employed, based on previous reports on metal–support interaction,31,74 with a kinetic energy of 520 eV chosen as the cutoff value for the expansion of the plane-waves basis set. All calculations employed long-range dispersion correction as proposed by the Grimme – DFT-D3 method,75,76 which shows an improvement on pure DFT to evaluate molecular interactions.77–80 The optimization thresholds for electronic energies and ionic forces relaxation were respectively 10−6 eV and 0.02 eV Å−1. Accurate electronic structures were obtained by means of the tetrahedron method as implemented in VASP. The Brillouin zone was sampled using a 5 × 5 × 1 Γ-centred k-point mesh generated through the Monkhorst–Pack method, minimising any Pulay stress.81 We calculated the Bader charges difference (BCD) and charge density difference (CDD) using eqn (5) and (6) respectively.| q(BCD) = q(Combined) − q(Surf) − q(Ir15) | (5) |
| ρ(CCD) = ρ(Combined) − ρ(Surf) − ρ(Ir15) | (6) |
| Eads = ESystem − ESurf − ECluster | (7) |
| Eads = ESystem − ESurf* − ECluster | (8) |
| Edef = Eads − Eadh | (9) |
Simulation models
To evaluate the key features of the catalysts, different simulation models were employed. Represented in Fig. S1 (ESI†), we modelled pristine (PG) and single vacancy (SV) graphene representing graphite, and graphitic N (gN) and triple pyridinic N (3pN) to model GCN. All surfaces were generated with the Atomic Simulation Environment (ASE)85 and modelled on a p(8 × 8) graphene slab supercell with 27 Å vacuum along the c-axis to avoid any interaction between adjacent images.A metal–cluster model simulating the true size of the supported nanoparticles experimentally observed is prohibitively expensive to compute using electronic structure methods. For this reason, a simplified model cluster containing 15 Ir atoms was modelled on the graphitic support. Indeed, cluster–support interfaces have been shown to participate in many reactions74,86–90 and, therefore, it is essential to consider them on realistic catalytic models.
The most stable conformations of the Ir15 clusters on the different surfaces, i.e., PG, SV, gN and 3pN, were found from ∼800 cluster structures generated by an in-house modified version of the unbiased Birmingham Parallel Genetic Algorithm (BPGA),91 and evaluated at the DFT level following a three-step process. The first step in the global optimisation protocol is the generation of ∼200 supported clusters for each surface, considering a pool size of 10 members with crossover and mutation operation procedures performed by means of randomization and displacement operators, respectively. The initial pool members were randomly generated with a cluster to surface height of 2.0 Å. A mutation rate of 10% was employed to guarantee the generational variety among the structures.90 It is worth noting that, for each surface, the same number of generated structures was considered, unbiases leading to a final pool of 10 fittest NP structures, i.e., the most stable. The energy of all these structures was determined by VASP using a soft optimization protocol, i.e., thresholds for electronic and ionic relaxation energies respectively of 10−4 eV and 10−3 eV, Γ-point only and a frozen support geometry. An increased number of initial non-self-consistent steps and linear-mixing involving the metal d-orbitals were found to improve the wavefunction convergence. The Brillouin-zone evaluation was eased using the second order Methfessel–Paxton method with a smearing width of 0.1 eV. In the second step, the final pool of 10 elements was re-optimised with an enhanced k-space sampling (5 × 5 × 1, Γ-centred Monkhorst–Pack k-point mesh) and thresholds for electronic energies and ionic forces of 10−6 eV and 0.02 eV Å−1, while maintaining the support frozen. Finally, the fittest candidate was fully relaxed, i.e., NP and support, and the electronic structure was investigated with the accurate computational settings explained in the computational details section.
Results and discussion
Commercial graphite and synthesized GCN were employed as supports for Ir nanoparticles (1 wt%) prepared by a wet impregnation (WI) procedure. Firstly, the catalysts were evaluated in the hydrous hydrazine decomposition reaction at 323 K with a N2H4⋯H2O: catalyst molar ratio of 1000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Stability tests up to 5 repeated reaction runs were performed. Then, fresh catalysts and used catalysts were thoroughly characterized using XPS and TEM to elucidate the structure–activity and stability relationships rationalizing the kinetic results. Finally, a detailed computational investigation was combined with the characterization and kinetic results to obtain unique atomic scale insights on the metal support interactions explaining the different catalytic trends observed in the stability tests.
1. Stability tests up to 5 repeated reaction runs were performed. Then, fresh catalysts and used catalysts were thoroughly characterized using XPS and TEM to elucidate the structure–activity and stability relationships rationalizing the kinetic results. Finally, a detailed computational investigation was combined with the characterization and kinetic results to obtain unique atomic scale insights on the metal support interactions explaining the different catalytic trends observed in the stability tests.
Catalytic activity
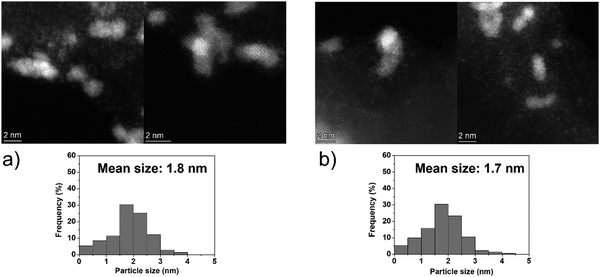
The catalytic performances of Ir NPs deposited on graphite (Ir/graphite) and GCN (Ir/GCN) were evaluated in liquid-phase hydrous hydrazine decomposition. The pressure of evolved gaseous products (H2 and N2) was recorded and elaborated, resulting in a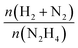 versus time profile, where n(H2 + N2) and n(N2H4) are respectively the moles of gaseous products and initial substrate. Higher
versus time profile, where n(H2 + N2) and n(N2H4) are respectively the moles of gaseous products and initial substrate. Higher 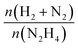 ratio, higher activity and higher selectivity toward H2.
ratio, higher activity and higher selectivity toward H2.
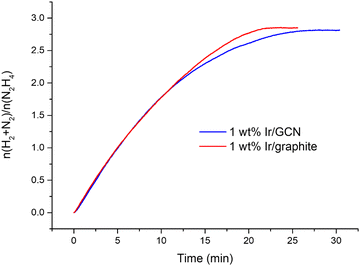
The kinetic profiles for the two catalysts were examined for 30 minutes of reaction (Fig. 1), where a pressure plateau indicates the end of the hydrous hydrazine decomposition reaction, which means that hydrous hydrazine conversion reaches the maximum. The two catalysts resulted in comparable profiles, exhibiting excellent initial activities of 4024 h−1 and 3654 h−1, calculated for t → 0, and remarkable high H2 selectivity of 95% and 94% respectively for Ir/graphite and Ir/GCN, calculated at the pressure plateau.
A crucial feature of a catalyst for commercial applications is the durability over repeated reaction runs, especially when precious metals such as Ir are involved. For this reason, stability tests were performed on both Ir/graphite and Ir/GCN, by filtering and reusing the catalyst without any further treatment.
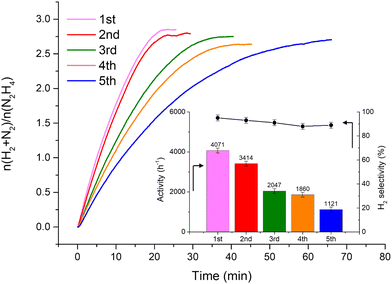
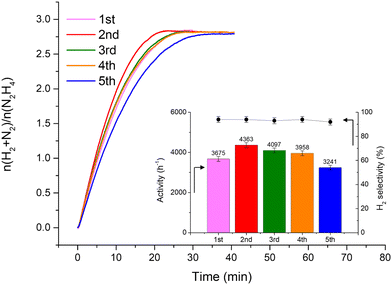
Fig. 2 shows that the Ir/graphite rapidly deactivates decreasing up to 70% from its initial activity (from 4071 h−1 to 1121 h−1) after five repeated cycles, with a slight decrease of the H2 selectivity (from 95 to 89%). In contrast, the Ir/GCN exhibited remarkable stability (3675 h−1 to 3241 h−1) and almost constant H2 selectivity (from 94 to 92%) after five cycles of the reaction (Fig. 3). In both cases, the H2 selectivity is still very high after 5 runs of catalytic tests.
Catalyst characterization
Fresh and used materials were thoroughly characterized to disclose the structure–stability relationship. Information on the catalyst morphology, e.g., distribution on the support, particle size and structural changes after stability tests, were obtained through TEM analysis. XPS was employed to investigate the surface composition, e.g., superficial composition, oxidation state and exposed iridium atoms (fresh and after 5 repeated reaction cycles).Fig. 4 shows representative STEM-HAADF images of the fresh Ir/graphite catalysts and those used for 5 runs. In the fresh catalyst, small Ir particles in the range from 0.5 to 4.0 nm can be observed, presenting a mean size of 1.9 ± 0.4 nm. The mean size changes only slightly in the sample used for 5 runs, 2.1 ± 0.5 nm (Fig. 4). Ir particles preferentially located at the graphite planes boundaries and agglomerated to form a net were observed (Fig. S2 and S3, ESI†).
 | ||
| Fig. 4 Representative HAADF-STEM images and Ir particle size distribution of 1 wt% Ir/graphite, (a) fresh and (b) after 5 runs. Inset histograms show the particle size distribution. | ||
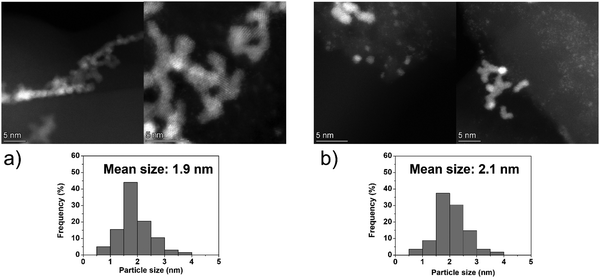
On the other hand, the Ir clusters were homogeneously distributed and well-dispersed on GCN (Ir/GCN), in agreement with the N anchoring sites observed from HAADF-STEM (Fig. S4, ESI†). The Ir clusters presented a narrow particle size distribution, from 0 to 3.5 nm with a mean size of 1.8 ± 0.4 nm, which remained constant, 1.7 ± 0.4 nm, after their use in the N2H4 decomposition reaction for 5 repeated runs (Fig. 5). Noticeably, in Ir/GCN, many small clusters and single atoms (SAs) were observed either on fresh or 5 runs used catalysts (Fig. 5 and Fig. S5, ESI†). Nonetheless, the particle size distributions of the catalysts were obtained without considering the SAs due to the increased complexity of the related statistic. Overall, the TEM results indicate that both catalysts exhibit exceptionally good structural stability after 5 reaction runs.
 | ||
| Fig. 5 Representative HAADF-STEM images and Ir particle size distribution of 1 wt% Ir/GCN, (a) fresh and (b) after 5 runs. Inset histograms show the particle size distribution. | ||
Table 1 summarizes the chemical species observed on the surface and their atomic concentration as obtained from the survey analysis of the XPS spectra. The results show that Ir/GCN, either fresh or used, presents a higher extent of exposed metal (1.3 and 1.0% respectively for fresh and 5 runs used) than graphite supported particles (0.8 and 0.3% respectively for fresh and 5 runs used). This indicates a better dispersion of sub-nanometric particles over GCN, as well as an enhanced stability under reaction conditions. Moreover, Ir/graphite, after 5 runs, exhibited an increase of 1.2 At% of N 1s components, suggesting a deactivation due to poisoning of the catalysts from residual hydrous hydrazine decomposition intermediates.
| Samples | C1s/atomic% | N1s/atomic% | Ir4f/atomic% |
|---|---|---|---|
| Ir/graphite fresh | 99.2 | 0.0 | 0.8 |
| Ir/graphite 5 runs | 98.5 | 1.2 | 0.3 |
| Ir/GCN fresh | 64.0 | 34.7 | 1.3 |
| Ir/GCN 5 runs | 65.2 | 33.8 | 1.0 |
For all the catalysts, high-resolution (HR) C 1s, N 1s, and Ir 4f XPS spectra were fitted (Fig. 6 and Fig. S6–S9, ESI†) using a fitting model as described in the experimental section. For the C 1s region of all the graphite samples, four main peaks were considered: the most intense peak at a binding energy (BE) of 284.3–284.4 eV is assigned to C in sp2 bonding configuration; the peaks at BEs of 285.1–285.2, 285.6–285.7 and 286.2–286.3 eV are assigned to C in sp3 configuration, C–O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O respectively.92 C 1s XPS spectra for GCN samples show an asymmetric peak of BE 285.4–285.5 eV, assigned to the C–N
O respectively.92 C 1s XPS spectra for GCN samples show an asymmetric peak of BE 285.4–285.5 eV, assigned to the C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C moieties.68 A more intense symmetric peak of BE 288.7–288.8 eV, related to C
C moieties.68 A more intense symmetric peak of BE 288.7–288.8 eV, related to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C components was also observed.93 It is worth noting that after Ir deposition on graphite, the C 1s spectra (Fig. S6, ESI†) remain largely unchanged, indicating the presence of similar C species with a similar relative distribution. Differently, for GCN a net decrease in the intensity ratio between C–N
C components was also observed.93 It is worth noting that after Ir deposition on graphite, the C 1s spectra (Fig. S6, ESI†) remain largely unchanged, indicating the presence of similar C species with a similar relative distribution. Differently, for GCN a net decrease in the intensity ratio between C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C peaks was observed after the sub-nanometric particles immobilization (Fig. S7, ESI†) indicating a smaller amount of superficial C–N
C peaks was observed after the sub-nanometric particles immobilization (Fig. S7, ESI†) indicating a smaller amount of superficial C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C moieties. We postulate that this is an electronic effect due to the interaction of the Ir clusters with the C–N
C moieties. We postulate that this is an electronic effect due to the interaction of the Ir clusters with the C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C sites. Furthermore, an additional decrease in the intensity ratio is observed after the first reaction run of stability tests (
C sites. Furthermore, an additional decrease in the intensity ratio is observed after the first reaction run of stability tests (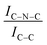 from 1.67 to 1.44, Table 2), indicating that, upon reaction, Ir clusters are mobilised and redeposited as smaller clusters, covering more C–N
from 1.67 to 1.44, Table 2), indicating that, upon reaction, Ir clusters are mobilised and redeposited as smaller clusters, covering more C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C sites. The increase of the catalytic activity of Ir/GCN between the first and the second run (from 3675 to 4363 h−1, Fig. 3) could be a consequence of this structural transformation.
C sites. The increase of the catalytic activity of Ir/GCN between the first and the second run (from 3675 to 4363 h−1, Fig. 3) could be a consequence of this structural transformation.
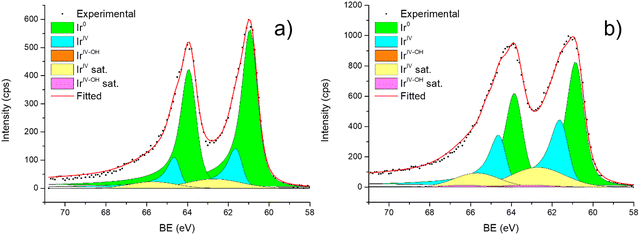 | ||
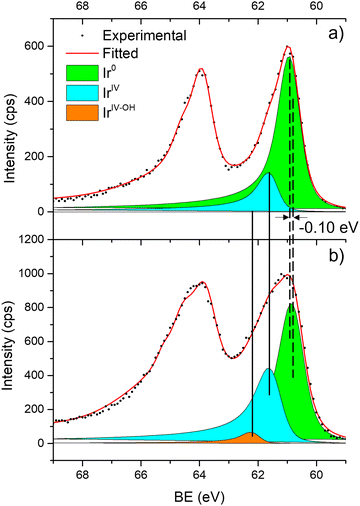
| Fig. 6 Fitting of high-resolution spectra of Ir 4f in (a) Ir/graphite and (b) Ir/GCN fresh catalysts. | ||
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (285.5 eV) and C
C (285.5 eV) and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (288.8) and the increase between qN and C
C (288.8) and the increase between qN and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–H ratios with C
N–H ratios with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N after the immobilization of sub-nanometric Ir particles and used catalyst
N after the immobilization of sub-nanometric Ir particles and used catalyst
For GCN, the N 1s region (Fig. S8, ESI†) was fitted with four components, consistent with the literature on heptazine-based carbon nitride. Namely, pyridine-like (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N, 398.5–398.6 eV), conjugated amines (C
N, 398.5–398.6 eV), conjugated amines (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–H, 399.9–400.0 eV), quaternary N (400.9–401.0 eV) and NOx species (404.1–404.2 eV).94,95 Upon sub-nanometric particles immobilization, the N 1s spectra exhibited an increase in the intensity ratios between qN and C
N–H, 399.9–400.0 eV), quaternary N (400.9–401.0 eV) and NOx species (404.1–404.2 eV).94,95 Upon sub-nanometric particles immobilization, the N 1s spectra exhibited an increase in the intensity ratios between qN and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–H peaks with respect to the C
N–H peaks with respect to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N one, indicating a higher coverage of pyridinic sites, thus highlighting a more favourable interaction. Table 2 summarizes the intensity ratio trend of C–N
N one, indicating a higher coverage of pyridinic sites, thus highlighting a more favourable interaction. Table 2 summarizes the intensity ratio trend of C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C with C
C with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C 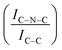 , qN with C
, qN with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N 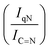 and C
and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–H with C
N–H with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N 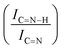 for the nitride samples.
for the nitride samples.
Fig. 6 shows the Ir 4f regions of Ir/graphite and Ir/GCN. Three main contributions were included in the fitting: metallic (Ir0), rutile-type (IrIV) and an Ir(IV)–OH component found in amorphous Ir oxyhydroxides, whose oxidation state is still unclear.96,97 This species was found forming on a carbon support by electrodeposition from an IrCl3 solution.71 We consider this a Ir(IV)–OH specie at the surface of the nanoparticle, for simplicity referred to in the text as IrIV-OH. Ir0, IrIV and IrIV-OH 4f7/2 components were assigned respectively to BE of 60.75, 61.70 and 62.30 eV. In addition, IrIV and IrIV-OH presented an asymmetric line shape and appeared in combination with satellite peaks at 1 eV higher BEs.
The Ir/graphite presented a lower IrIV-OH/IV/Ir0 ratio than the Ir/GCN sample, indicating a higher number of metallic Ir fraction with respect to the nitride sample, which can be related to slightly larger particles. Previous studies attributed the higher ratio between the oxidized and metallic fractions to an enhanced reactivity of the particles leading to surface oxidation in air (IrIV-OH/IrIV) and to a stronger electronic interaction of the precursor with the support, making it more difficult to reduce to the metallic state.98
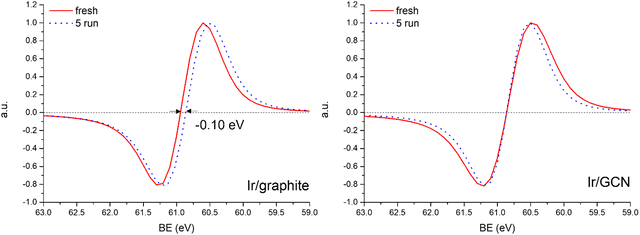
A detailed comparison of the HR Ir 4f of fresh Ir/graphite and Ir/GCN highlighted a negative shift in the Ir0 peak (core level shift, CLS = −0.10 eV, Fig. 7) when GCN is employed as the support. This shift indicates an increased electron density at the Ir sub-nanometric particles surface due to the N moieties of the support,32,99 strengthening the Ir–support interaction. Indeed, the CLS agrees with the observed intensity ratio decrease between C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C peaks (Table 2 and Fig. S3, ESI†) and the comparison of IrIV-OH/IV/Ir0 ratio (Fig. 1), highlighting an Ir–N interaction.
C peaks (Table 2 and Fig. S3, ESI†) and the comparison of IrIV-OH/IV/Ir0 ratio (Fig. 1), highlighting an Ir–N interaction.
The analysis of the HR Ir 4f spectra for fresh and used samples included the Na 2s contribution, which overlaps with the Ir 4f of the used sample (Fig. S5, ESI†). The presence of adsorbed Na species on used samples is attributed to the solvent employed in the reaction, 0.5 M NaOH, which after 5 reaction runs significantly increased as shown by the magenta peak in Fig. S5 (ESI†). Nonetheless, a comparison of fresh and used samples for both the catalysts demonstrated a negative core level shift (CLS) of −0.10 eV in the Ir07/2 BE of Ir/graphite after stability tests (Fig. 8), whereas no shift was observed for the other contributions (IrIV-OH, IrIV). These results support the deactivation of Ir/graphite due to residual adsorbates of the hydrous hydrazine decomposition reaction on the Ir active sites. In particular, it has been previously demonstrated that residual adsorbates lead to deactivation of the Ir catalyst.100,101 Differently, no CLS was detected for the GCN supported catalysts (Fig. 8), suggesting improved resistance toward residual adsorbates of the hydrous hydrazine decomposition reaction.
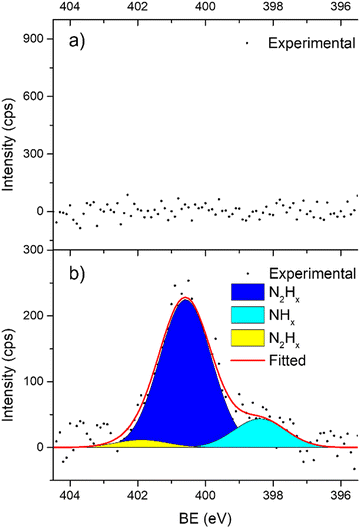
In support of our assumption on catalyst poisoning, previous literature69,102 demonstrated that residual NHx (x = 1–2) and N2Hx species can be detected in HR-XPS of the N 1s signal; in detail the N2Hx nitrogen atom strongly bound to the metal surface and the one far away can be observed at BE of 400.2 and 401.5 eV respectively, while the NHx (x = 1–2) signal is observable at BE of 398.6 eV. Thus, employing these models in an analysis of the N 1s region of the Ir/graphite samples, fresh and 5 runs used, was performed to confirm the preliminary results on catalyst poisoning, highlighting in the 5 runs used catalysts all the above-mentioned signals. Fig. 9 summarizes these results.
As expected, the fresh catalysts did not present any signal in the N 1s region, but on the other hand after 5 runs all the above-mentioned components are observed, namely, N2Hx and NHx. As stated by the authors the presence of N2Hx and NHx moieties respectively suggests a complete and an incomplete decomposition of N2H4⋯H2O.69,102 Noticeably, the relative percentage area of the fitted contribution is in good agreement with the experimental selectivity observed for Ir/graphite used for 5 runs, where the catalysts resulted in 89% H2 selectivity and presented a relative percentage area of complete decomposition adsorbed intermediates (N2Hx) of 87%. Furthermore, this result agrees with the survey (Table 1) and the Ir 4f region (Fig. 8) analyses.
Thus, the higher initial catalytic activity of fresh Ir/graphite compared to Ir/GCN is attributed to a synergistic effect between the lower IrIV-OH/IV/Ir0 (Fig. 1) and the localization of numerous NPs on the graphitic planes boundaries (Fig. S2, ESI†), recently reported to increase the NPs’ reactivity with respect to the ones located on graphitic basal planes.103 For Ir/graphite, TEM images of the used sample showed slight coalescence (2.1 ± 0.5 nm, Fig. 4 and Fig. S3, ESI†). The XPS analysis suggested a deactivation of the catalyst due to residual adsorbates of the decomposition reaction, explained through survey data, supported by the detailed analysis of the Ir07/2 peak performed, where a core level shift of −0.10 eV was observed compared to the fresh catalyst, and confirmed by the N 1s region analysis of the used samples, where an increasing content of residual decomposition adsorbates, namely NHx and N2Hx species was observed, but also to Ir leaching during the reaction.
Differently, Ir/GCN exhibited a lower decrease in Ir exposed (from 1.3% to 1.0) due to the partial adsorption of the reaction products on the active sites and better stabilized particles, and furthermore no Ir leaching was observed from the ICP-AES analysis. Overall, there are two beneficial effects of the presence of N anchoring sites: stabilizing the nanoparticles, therefore avoiding leaching, and preventing the active sites from deactivation under reaction conditions.
DFT results
Atomistic simulations were conducted to rationalise the superior performance, i.e., resistance to poisoning and structural integrity, exhibited by the Ir particles supported on GCN compared to the graphite supported ones. PG and SV structures were chosen to model respectively an ideal basal plane and a structure with undercoordinated C, typical from boundaries and intrinsic defects. This choice is supported by previous reports where SV was identified as the most reactive intrinsic punctual defect for adsorption processes.65,104,105 With regard to GCN, the employed models (gN and 3pN) mimic its typical grafting sites, while maintaining a simplified representation of a realistic structure.106,107 Modelling isolated functionalities, namely SV, gN and 3pN, in the carbon lattice is beneficial for the properties rationalization, especially in combination with experiments. Indeed, simplified models allowed an accurate investigation of the supported Ir nanoclusters resulting in a reliable and accurate analysis of the most stable geometries and related electronic structure.Nanocluster adsorption
The geometries of modelled nanoclusters on the different surfaces were generated with the three-step Genetic Algorithm (GA) method described. Once the fittest candidates were obtained from the GA screening, different properties were computed and analysed to rationalize the experimental observations, i.e., enhanced stability under reaction conditions and poisoning resistance.Regarding the structural stability of the supported clusters, the presence of metal–support interactions influences the average bond length of the supported clusters, e.g., Ir–Ir bond length, which is related to the strain against sintering processes. Recently, it has been proved that stronger adsorption of clusters correlates with the average metal–metal bond lengths in the cluster.108,109 Thus, among the several descriptors available to analyse the structural stability of supported metal clusters, here, we have employed adsorption (Eads, eqn (7)), adhesion (Eadh, eqn (8)) and surface deformation (Edef, eqn (9)) energies, together with the average Ir–Ir bond distance (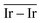 ), the support–cluster distance (d(C–S)), and the number of interfacial metal species (IrIF). Table 3 summarizes these results.
), the support–cluster distance (d(C–S)), and the number of interfacial metal species (IrIF). Table 3 summarizes these results.
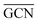 ) and average Ir–Ir bond distance (
) and average Ir–Ir bond distance (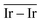 )
)
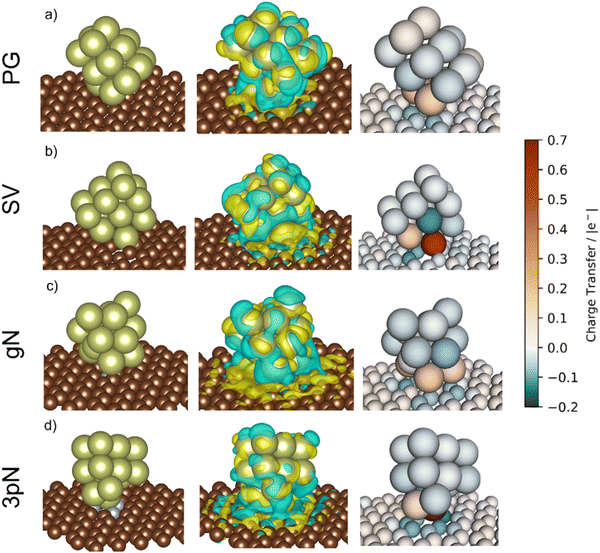
To obtain more precise information on the cluster support charge transfer, a detailed analysis of the charges flow after adsorption was performed together with a more qualitative representation, shown in Fig. 10. The evaluation of the Bader charges after adsorption (qclus), the summation, q+clus and q−clus, and number of positive and negative charges, nq+ and nq− localised in each Ir atom were evaluated. Table 4 summarizes the charge analysis.
| Support | Surface | q clus/|e| | q +clus/|e| | n q + /n° | q −clus/|e| | n q − /n° |
|---|---|---|---|---|---|---|
| Graphite | Ir15/PG | 0.22 | 0.41 | 5 | −0.19 | 8 |
| Ir15/SV | 0.47 | 0.73 | 3 | −0.25 | 12 | |
| GCN | Ir15/gN | 0.22 | 0.51 | 6 | −0.29 | 9 |
| Ir15/3pN | 0.47 | 0.79 | 2 | −0.31 | 13 |
To describe trends on the hydrazine decomposition process, Tafreshi and co-workers110 unveiled a relationship between Cu surface site coordination number (CN) and hydrazine binding strength. Despite the effectiveness of this approach, when dealing with sub-nanometric clusters, a CN based analysis does not lead to reliable results due to intrinsic limitations of a simplistic model. Differently, the generalized coordination number (GCN) represents a more structure sensitive model capturing the weight averaged coordination of the adsorption site in facets, edges, vertices and other low-coordinated sites.111 The GCN has been validated previously as an efficient catalytic activity descriptor due to its correlation with well-established descriptors such as the d-band center.112,113 Thus, we decided to employ the average generalized coordination number (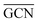 ) as a descriptor for the catalytic activity toward hydrazine adsorption.
) as a descriptor for the catalytic activity toward hydrazine adsorption.
Structural stability
The Ir deposited on PG (graphitic basal plane) and on SV (under-coordinated carbons) models demonstrated an exothermic and favourable adsorption of the cluster (negative adsorption and adhesion energies). Nonetheless, the presence of low-coordinated sites on the SV models favours the Ir cluster adsorption with respect to the basal planes by ΔESV–PGads = −8.502 and ΔESV–PGadh = −4.374 eV, which directly correlates to the surface deformation energies, ΔESV–PGdef = −4.128 eV. This agrees with the TEM images where Ir NPs were preferentially located at the low-coordinated graphitic boundaries (Fig. S3, ESI†). Measured features like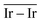 and charge transfer also indicate a stronger interaction with undercoordinated carbon atoms due to the shorter cluster support distance and higher charge transfer to the support in the SV than in the PG model. Indeed, although the Ir cluster morphology on the graphite models (PG and SV) is similar and both interact with the support with two Ir atoms, the charge transfer on SV is enhanced by the interaction of the cluster and the carbon dangling bonds compared to PG (Fig. 10). This enhanced charge transfer of the SV model directly correlates with the difference observed in the stability descriptors employed (Eads, Eadh, Edef, d(C–S), Table 4). The analysis performed allowed us to individuate low-coordinated carbons as mainly responsible for the cluster stabilization, i.e., coalescence prevention, due to an enhanced cluster to support charge transfer which resulted in improved adsorption, adhesion, and surface deformation energies, as well as closer cluster–support distance.
and charge transfer also indicate a stronger interaction with undercoordinated carbon atoms due to the shorter cluster support distance and higher charge transfer to the support in the SV than in the PG model. Indeed, although the Ir cluster morphology on the graphite models (PG and SV) is similar and both interact with the support with two Ir atoms, the charge transfer on SV is enhanced by the interaction of the cluster and the carbon dangling bonds compared to PG (Fig. 10). This enhanced charge transfer of the SV model directly correlates with the difference observed in the stability descriptors employed (Eads, Eadh, Edef, d(C–S), Table 4). The analysis performed allowed us to individuate low-coordinated carbons as mainly responsible for the cluster stabilization, i.e., coalescence prevention, due to an enhanced cluster to support charge transfer which resulted in improved adsorption, adhesion, and surface deformation energies, as well as closer cluster–support distance.
We can conclude that clusters immobilized on the PG model easily migrate to the SV sites, which in opposition are strongly anchored to the support. This is in good agreement with the TEM analysis performed on the Ir/graphite catalyst, where particles located at graphite plane boundaries were observed, exhibiting slight coalescence after 5 reaction runs.
The two N containing models (gN and 3pN) presented exothermic and favourable adsorption of the Ir clusters. The adsorption on the 3pN model resulted in more exothermic adsorption, ΔE3pN–gNads = −1.748 eV, and adhesion, ΔE3pN–gNadh = −2.080 eV, energies than the gN model. These results highlight an enhanced stabilization of clusters deposited on the heptazine rings (3pN) with respect to the graphitic N (gN), in agreement with the cluster–support distance analysed. The Ir cluster is closer to 3pN than to gN, despite the former presenting less interfacial Ir species (IrIF = 2) than the latter (IrIF = 3) due to, on gN, Ir interacting with C atoms vicinal to the graphitic N.114 Nonetheless, the Ir cluster on 3pN presents an enhanced cluster–support charge transfer compared to the gN one, although both models present a higher extent of negative charge distributed on the support compared to the graphite ones, well indicating an increased cluster–support interaction. This can be clearly seen on the charge density difference (CDD) analysis in Fig. 10. The structural and energetic analysis of the cluster immobilized on the gN and 3pN models allowed us to individuate the N moieties of GCN as the main one responsible for the cluster stabilization due to an enhanced cluster–support interaction. Indeed, the GCN models resulted in better stabilization of the clusters on both the studied surfaces, gN and 3pN, compared to the less-stabilizing of the graphite models, PG, which has also been individuated as the main one responsible for the Ir/graphite coalescence.
Overall, although in both systems best cluster stabilization was obtained on low-coordination sites (SV for graphite and 3pN for GCN), it is now clear that graphitic N (gN) supported clusters are better prevented from coalescence toward the 3pN deposed ones. Therefore, considering the supported cluster stability descriptors analysed and the charge-transfer studies performed, it was possible to rationalize the differences observed in TEM particle size distributions for Ir/graphite and Ir/GCN after stability tests.
Catalytic activity and poisoning resistance
According to previous studies in the literature,103 a low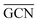 and a contraction of cluster interatomic distances leads to an increased catalytic activity. This expected behaviour is confirmed when comparing Ir15 clusters on SV and PG (Table 3) and considering the experimental values for the first run of Ir/graphite (4071 h−1).
and a contraction of cluster interatomic distances leads to an increased catalytic activity. This expected behaviour is confirmed when comparing Ir15 clusters on SV and PG (Table 3) and considering the experimental values for the first run of Ir/graphite (4071 h−1).
On the GCN models the analysis of 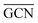 and
and 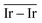 values (Table 3) suggest an enhanced reactivity of Ir clusters on 3pN compared to gN, which fully agrees with the catalytic activity of Ir/GCN (3675 h−1) when considering that the most stable clusters are the ones on the 3pN model. Thus, the simulation of graphite and GCN models were able to describe the experimental initial catalytic activity by employing
values (Table 3) suggest an enhanced reactivity of Ir clusters on 3pN compared to gN, which fully agrees with the catalytic activity of Ir/GCN (3675 h−1) when considering that the most stable clusters are the ones on the 3pN model. Thus, the simulation of graphite and GCN models were able to describe the experimental initial catalytic activity by employing 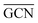 and
and 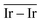 as reactivity descriptors, in agreement with recent computational studies on Pt clusters supported on carbonaceous materials.115 Furthermore, the comparison between Ir/graphite and Ir/GCN models in terms of
as reactivity descriptors, in agreement with recent computational studies on Pt clusters supported on carbonaceous materials.115 Furthermore, the comparison between Ir/graphite and Ir/GCN models in terms of 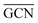 and
and 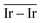 agrees with the higher catalytic activity observed (4024 h−1 and 3654 h−1, respectively) for the sub-nanometric Ir supported on graphite.
agrees with the higher catalytic activity observed (4024 h−1 and 3654 h−1, respectively) for the sub-nanometric Ir supported on graphite.
Previous studies on the hydrous hydrazine decomposition performed over supported Ir catalysts demonstrated that the metal clusters’ catalytic activity may decline due to the adsorption of residual decomposition intermediates, leading to poisoning of the active sites and catalyst deactivation. The authors were able to demonstrate that this can be substantially reduced when H2 is admixed to the reaction environment, namely, in the presence of a stronger reducing atmosphere favouring further decomposition of the residual adsorbates.100,102 Due to the experimental setup employed in this work, it was not possible to verify this hypothesis from the experiments. Nonetheless, quantitative analysis of the Bader charges performed (Table 4) provided detailed electronic information explaining the different catalytic performances of Ir/graphite and Ir/GCN.
The clusters on PG and SV models (graphite) both transferred electrons to the support after deposition, respectively 0.22 and 0.47 |e−| (Table 4). In the case of SV, the high electron transfer derives from the presence of carbon dangling bonds, i.e., unpaired electrons,109 which lead to more atoms with negative charges (nq− = 12, q−clus = −0.25 |e−|) distributed within the cluster (Fig. 10) compared to PG (nq− = 8, q−clus = −0.19 |e−|).
Thanks to a stronger cluster–support interaction of the SV model, the redistribution of negative charges on the cluster's surface, i.e., more reducing interfaces, can better disfavour the formation of the undesired bound intermediates compared to the PG model, which is more prone to undergoing poisoning of the active sites due to a weaker cluster–support interaction that resulted in less redistributed negative charges, as can be clearly seen in Fig. 10.
The presence of N on the GCN models led to a redistribution of the charges differently to the graphite models even though a similar charge transferred. The cluster supported on the gN model presented several atoms with a positive charge at the cluster–support interface (nq+ = 6, q+clus = 0.51 |e−|), which is clearly seen on the charge density difference (CDD) analysis in Fig. 10, and a high number of negative charges distributed on the cluster surface (nq− = 9, q−clus = −0.29 |e−|). In the 3pN model the support to cluster charge transfer is enhanced with respect to gN (Table 4). This charge transfer is due to the pyridinic N sites, leading to strongly localized positive charges at the cluster–support interface (nq+ = 2, q+clus = 0.79 |e−|), in agreement with recent computational studies,116,117 along with the highest number of negative charges distributed on the cluster surface (nq− = 13, q−clus = −0.31 |e−|), as shown in Fig. 10. Noticeably, both the GCN models exhibited a higher value of redistributed negative charges (q−clus = −0.29 and −0.31 |e−|, respectively for gN and 3pN) compared to the graphite models (q−clus = −0.19 and −0.25 |e−|, respectively for PG and SV). The presence of N moieties (gN and 3pN) leads to a stronger redistribution of charges within the clusters, with a higher extent of negative charges, i.e., electrons, on the cluster surfaces for both the gN and the 3pN models compared to the graphite models (PG and SV). These results agree with the XPS core level shift of −0.10 eV observed for the fresh catalysts and help to understand the enhanced poisoning resistance exhibited by Ir/GCN upon repeated reaction runs. Overall, the more electron-rich the clusters, the better is their resistance to poisoning by decomposition intermediates, e.g., N2Hx and NHx.
Conclusions
A combination of computational and experimental studies was employed to disclose the role of GCN functionalities in enhancing the stability of sub-nanometric iridium particles during the hydrous hydrazine decomposition reaction. Two different catalysts were synthesized using a modified wet impregnation method, 1 wt% Ir/graphite and 1 wt% Ir/GCN. Both the fresh catalysts exhibited remarkable initial catalytic activities (3654 h−1 and 4024 h−1 for Ir/GCN and Ir/graphite, respectively) and H2 selectivity (94 and 95%). The hydrous hydrazine decomposition kinetic profiles evidenced an enhanced stability of the Ir/GCN samples upon repeated reaction cycles with respect to Ir/graphite. TEM and XPS analyses showed that the deactivation of Ir/graphite can be attributed to partial irreversible adsorption of the reaction products (XPS core level shift in Ir0 of −0.10 eV after 5 runs and residual adsorbates detected in the N 1s region), Ir leaching and a partial aggregation of Ir particles, for those with a size <2 nm. On the other hand, Ir/GCN exhibited a higher stability, without significant modification of the structure of the catalyst. This result was rationalized at an atomic scale level through a combined TEM, XPS and DFT analysis and attributed to an enhanced metal–support interaction related to the N grafting sites of GCN. Low-coordinated carbons (SV) can efficiently adsorb and stabilize Ir clusters, better than the basal planes (PG) which drives the cluster agglomeration under reaction conditions. On the other hand, both the basal plane N (gN) and the heptazine rings (3pN) in GCN have a strong interaction with the clusters, minimising the thermodynamic driving force for their coalescence. In addition, a detailed analysis of the Bader charges of the supported Ir clusters revealed that the presence of N moieties on the support promotes a charge redistribution that enhances structural integrity and explains the poisoning resistance in terms of the electron enriched cluster surface. In conclusion, the combined experimental–computational approach allowed us to assign the GCN nitrogen anchoring sites as the main ones responsible for the sub-nanometric particle integrity and improved stability, and to rationalize the experimental reactivity and characterization results in terms of metal–support interactions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge computing time on the facilities of Supercomputing Wales and the Advanced Research Computing Cardiff (ARCCA) at Cardiff University. This work is partially supported by the project with the reference number PID2020-113809RB-C33 from the Ministry of Science, Innovation and Universities of Spain. S. B. thanks Dr S. Cattaneo for the fruitful discussions. This work is partially supported by the project with reference RV_PSR_SOE_2020_AVILL, Piano Sviluppo Unimi – Linea 3 – Bando SoE.References
- M. Besson, P. Gallezot and C. Pinel, Chem. Rev., 2014, 114, 1827–1870 CrossRef CAS PubMed.
- E. Gianotti, M. Taillades-Jacquin, J. Rozière and D. J. Jones, ACS Catal., 2018, 8, 4660–4680 CrossRef CAS.
- M. Che and C. O. Bennett, Advances in Catalysis, Elsevier, 1989, vol. 36, pp. 55–172 Search PubMed.
- T. S. Rodrigues, A. G. M. da Silva and P. H. C. Camargo, J. Mater. Chem. A, 2019, 7, 5857–5874 RSC.
- I. MacLaren and Q. M. Ramasse, Int. Mater. Rev., 2014, 59, 115–131 CrossRef CAS.
- S. J. Pennycook, M. F. Chisholm, A. R. Lupini, M. Varela, A. Y. Borisevich, M. P. Oxley, W. D. Luo, K. van Benthem, S.-H. Oh and D. L. Sales, Philos. Trans. R. Soc., A, 2009, 367, 3709–3733 CrossRef CAS PubMed.
- B. Zandkarimi and A. N. Alexandrova, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, 1–17 Search PubMed.
- Z. Zhang, B. Zandkarimi and A. N. Alexandrova, Acc. Chem. Res., 2020, 53, 447–458 CrossRef CAS PubMed.
- L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079 CrossRef CAS PubMed.
- J. D. Aiken and R. G. Finke, Chem. Mater., 1999, 11, 1035–1047 CrossRef CAS.
- A. L. Maksimov, S. N. Kuklin, Y. S. Kardasheva and E. A. Karakhanov, Pet. Chem., 2013, 53, 157–163 CrossRef CAS.
- S. M. Rogers, C. R. A. Catlow, C. E. Chan-Thaw, A. Chutia, N. Jian, R. E. Palmer, M. Perdjon, A. Thetford, N. Dimitratos and A. Villa, ACS Catal., 2017, 7, 2266–2274 CrossRef CAS.
- C. T. Campbell, Acc. Chem. Res., 2013, 46, 1712–1719 CrossRef CAS PubMed.
- C. T. Campbell, S. C. Parker and D. E. Starr, Science, 2002, 298, 811–814 CrossRef CAS PubMed.
- X. Wang, G. Sun, P. Routh, D.-H. Kim, W. Huang and P. Chen, Chem. Soc. Rev., 2014, 43, 7067–7098 RSC.
- M. S. Shafeeyan, W. M. A. W. Daud, A. Houshmand and A. Arami-Niya, Appl. Surf. Sci., 2011, 257, 3936–3942 CrossRef CAS.
- M. S. Shafeeyan, W. M. A. W. Daud, A. Houshmand and A. Shamiri, J. Anal. Appl. Pyrolysis, 2010, 89, 143–151 CrossRef CAS.
- C. Rivera-Cárcamo and P. Serp, ChemCatChem, 2018, 10, 5058–5091 CrossRef.
- S. Li, X. Lu, S. Zhao, M. Ceccato, X.-M. Hu, A. Roldan, M. Liu and K. Daasbjerg, ACS Catal., 2022, 12, 7386–7395 CrossRef CAS.
- Y. Hou, M. Qiu, M. G. Kim, P. Liu, G. Nam, T. Zhang, X. Zhuang, B. Yang, J. Cho and M. Chen, Nat. Commun., 2019, 10, 1–9 CrossRef CAS PubMed.
- X. Zhou, X. Liu, J. Zhang, C. Zhang, S. J. Yoo, J.-G. Kim, X. Chu, C. Song, P. Wang and Z. Zhao, Carbon N. Y., 2020, 166, 284–290 CrossRef CAS.
- X. Xing, R. Liu, M. Anjass, K. Cao, U. Kaiser, G. Zhang and C. Streb, Appl. Catal., B, 2020, 277, 119195 CrossRef CAS.
- J. Hao, W. Yang, Z. Peng, C. Zhang, Z. Huang and W. Shi, ACS Catal., 2017, 7, 4214–4220 CrossRef CAS.
- H. Li, L. Chen, P. Jin, Y. Li, J. Pang, J. Hou, S. Peng, G. Wang and Y. Shi, Nano Res., 2022, 15, 950–958 CrossRef CAS.
- S. K. Singh, K. Takeyasu and J. Nakamura, Adv. Mater., 2019, 31, 1804297 CrossRef PubMed.
- H. Liu, X. Wu, Y. Geng, X. Li and J. Xu, Green Energy Environ., 2022 DOI:10.1016/j.gee.2022.09.001.
- J. H. Kim, J. Y. Cheon, T. J. Shin, J. Y. Park and S. H. Joo, Carbon N. Y., 2016, 101, 449–457 CrossRef CAS.
- I. Barlocco, S. Bellomi, J. J. Delgado, X. Chen, L. Prati, N. Dimitratos, A. Roldan and A. Villa, Catal. Today, 2021, 382, 61–70 CrossRef CAS.
- Q. Wang, N. Tsumori, M. Kitta and Q. Xu, ACS Catal., 2018, 8, 12041–12045 CrossRef CAS.
- D. Liu, X. Chen, G. Xu, J. Guan, Q. Cao, B. Dong, Y. Qi, C. Li and X. Mu, Sci. Rep., 2016, 6, 1–13 CrossRef PubMed.
- X. Wu, B. Feng, W. Li, Y. Niu, Y. Yu, S. Lu, C. Zhong, P. Liu, Z. Tian and L. Chen, Nano Energy, 2019, 62, 117–126 CrossRef CAS.
- L. Yi, B. Feng, N. Chen, W. Li, J. Li, C. Fang, Y. Yao and W. Hu, Chem. Eng. J., 2021, 415, 129034 CrossRef CAS.
- D. Liu, X. Chen, G. Xu, J. Guan, Q. Cao, B. Dong, Y. Qi, C. Li, X. Mu, X. Wu, B. Feng, W. Li, Y. Niu, Y. Yu, S. Lu, C. Zhong, P. Liu, Z. Tian, L. Chen, A. Iemhoff, M. Vennewald, J. Artz, C. Mebrahtu, A. Meledin, T. E. Weirich, H. Hartmann, A. Besmehn, M. Aramini, F. Venturini, Z. Li, Y. Chen, S. Ji, Y. Tang, W. Chen, A. Li, J. Zhao, Y. Y. Xiong, Y. Wu, Y. Gong, J. Shen, H. Wu, W. Sun, J. Qiao, H. Cai, Z. Wang, K. Sun, L. Yi, B. Feng, N. Chen, W. Li, J. Li, C. Fang, Y. Yao, W. Hu, X. Xiao, H. Zhang, Y. Y. Xiong, F. Liang and Y. Yang, Chem. Eng. J., 2021, 6, 764–772 Search PubMed.
- J. Shen, H. Wu, W. Sun, J. Qiao, H. Cai, Z. Wang and K. Sun, Chem. Eng. J., 2019, 358, 340–350 CrossRef CAS.
- Q. Tian, Z. Zhou, R. Wang, J. Zhang and C. Wang, J. Alloys Compd., 2022, 918, 165523 CrossRef CAS.
- X. Shao, X. Yang, J. Xu, S. Liu, S. Miao, X. Liu, X. Su, H. Duan, Y. Huang and T. Zhang, Chem, 2019, 5, 693–705 CAS.
- D. Nandi, S. Siwal, M. Choudhary and K. Mallick, Appl. Catal., A, 2016, 523, 31–38 CrossRef CAS.
- W. Xue, W. Chang, X. Hu, J. Fan, X. Bai and E. Liu, J. Colloid Interface Sci., 2020, 576, 203–216 CrossRef CAS PubMed.
- H. Starukh, M. Koštejn, V. Matějka and P. Praus, Nanoscale Res. Lett., 2021, 16, 1–14 CrossRef PubMed.
- A. Iemhoff, M. Vennewald, J. Artz, C. Mebrahtu, A. Meledin, T. E. Weirich, H. Hartmann, A. Besmehn, M. Aramini, F. Venturini, F. W. Mosselmans, G. Held, R. Arrigo and R. Palkovits, ChemCatChem, 2022, 14(9) DOI:10.1002/cctc.202200179.
- Z. Chen, S. Mitchell, E. Vorobyeva, R. K. Leary, R. Hauert, T. Furnival, Q. M. Ramasse, J. M. Thomas, P. A. Midgley and D. Dontsova, Adv. Funct. Mater., 2017, 27, 1605785 CrossRef.
- X. Li, P. Cui, W. Zhong, J. Li, X. Wang, Z. Wang and J. Jiang, Chem. Commun., 2016, 52, 13233–13236 RSC.
- X. Jiang, L. Zhang, H. Liu, D. Wu, F. Wu, L. Tian, L. Liu, J. Zou, S. Luo and B. Chen, Angew. Chem., Int. Ed., 2020, 132, 23312–23316 CrossRef.
- Q. Bing and J. Liu, Appl. Surf. Sci., 2021, 562, 150186 CrossRef CAS.
- N. N. Zhang, J. Li and H. Xiao, ChemCatChem, 2022, 14(16) DOI:10.1002/cctc.202200275.
- Z. Zhao, Y. Sun and F. Dong, Nanoscale, 2015, 7, 15–37 RSC.
- T. Yuan, H. Gong, K. Kailasam, Y. Zhao, A. Thomas and J. Zhu, J. Catal., 2015, 326, 38–42 CrossRef CAS.
- S. K. Singh and Q. Xu, J. Am. Chem. Soc., 2009, 131, 18032–18033 CrossRef CAS PubMed.
- S. K. Singh, Z. H. Lu and Q. Xu, Eur. J. Inorg. Chem., 2011, 2232–2237 CrossRef CAS.
- J. K. Norskov and C. H. Christensen, Science, 2006, 312, 1322–1323 CrossRef CAS PubMed.
- Z. Zhang, S. Zhang, Q. Yao, X. Chen and Z.-H. Lu, Inorg. Chem., 2017, 56, 11938–11945 CrossRef CAS PubMed.
- S. J. Cho, J. Lee, Y. S. Lee and D. P. Kim, Catal. Lett., 2006, 109, 181–186 CrossRef CAS.
- A. K. Singh, M. Yadav, K. Aranishi and Q. Xu, Int. J. Hydrogen Energy, 2012, 37, 18915–18919 CrossRef CAS.
- P.-X. Zhang, Y.-G. Wang, Y.-Q. Huang, T. Zhang, G.-S. Wu and J. Li, Catal. Today, 2011, 165, 80–88 CrossRef CAS.
- L. Zhou, X. Luo, L. Xu, C. Wan and M. Ye, Catalysts, 2020, 10(8) DOI:10.3390/catal10080930.
- L. He, B. Liang, L. Li, X. Yang, Y. Huang, A. Wang, X. Wang and T. Zhang, ACS Catal., 2015, 5, 1623–1628 CrossRef CAS.
- D. Motta, I. Barlocco, S. Bellomi, A. Villa and N. Dimitratos, Nanomaterials, 2021, 11, 1340 CrossRef CAS PubMed.
- K. S. Sanjay, X. B. Zhang and Q. Xu, J. Am. Chem. Soc., 2009, 131, 9894–9895 CrossRef PubMed.
- X. Lu, S. Francis, D. Motta, N. Dimitratos and A. Roldan, Phys. Chem. Chem. Phys., 2020, 22, 3883–3896 RSC.
- Y. B. Jang, T. H. Kim, M. H. Sun, J. Lee and S. J. Cho, Catal. Today, 2009, 146, 196–201 CrossRef CAS.
- F. Goettmann, A. Fischer, M. Antonietti and A. Thomas, Chem. Commun., 2006, 4530–4532 RSC.
- M. Roselló-Merino, R. J. Rama, J. Díez and S. Conejero, Chem. Commun., 2016, 52, 8389–8392 RSC.
- L. Luconi, E. S. Osipova, G. Giambastiani, M. Peruzzini, A. Rossin, N. V. Belkova, O. A. Filippov, E. M. Titova, A. A. Pavlov and E. S. Shubina, Organometallics, 2018, 37, 3142–3153 CrossRef CAS.
- A. Telleria, P. W. N. M. van Leeuwen and Z. Freixa, Dalton Trans., 2017, 46, 3569–3578 RSC.
- I. Barlocco, S. Bellomi, S. Tumiati, P. Fumagalli, N. Dimitratos, A. Roldan and A. Villa, Phys. Chem. Chem. Phys., 2022, 24, 3017–3029 RSC.
- C. R. Harris, K. J. Millman, S. J. Van Der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg and N. J. Smith, Nature, 2020, 585, 357–362 CrossRef CAS PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser and J. Bright, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- A. I. Large, S. Wahl, S. Abate, I. da Silva, J. J. Delgado Jaen, N. Pinna, G. Held and R. Arrigo, Catalysts, 2020, 10 Search PubMed.
- D. J. Alberas, J. Kiss, Z. M. Liu and J. M. White, Surf. Sci., 1992, 278, 51–61 CrossRef CAS.
- R. Arrigo, R. Blume, V. Streibel, C. Genovese, A. Roldan, M. E. Schuster, C. Ampelli, S. Perathoner, J. J. Velasco Vélez and M. Hävecker, ACS Catal., 2021, 12, 411–430 CrossRef.
- V. Streibel, M. Hävecker, Y. Yi, J. J. Velasco Vélez, K. Skorupska, E. Stotz, A. Knop-Gericke, R. Schlögl and R. Arrigo, Top. Catal., 2018, 61, 2064–2084 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse, J. Non-Cryst. Solids, 1995, 192–193, 222–229 CrossRef.
- I. Fampiou and A. Ramasubramaniam, J. Phys. Chem. C, 2015, 119, 8703–8710 CrossRef CAS.
- R. Sure, J. Antony and S. Grimme, J. Phys. Chem. B, 2014, 118, 3431–3440 CrossRef CAS PubMed.
- S. Ehrlich, J. Moellmann, W. Reckien, T. Bredow and S. Grimme, ChemPhysChem, 2011, 12, 3414–3420 CrossRef CAS PubMed.
- H. Fang, A. Roldan, C. Tian, Y. Zheng, X. Duan, K. Chen, L. Ye, S. Leoni and Y. Yuan, J. Catal., 2019, 369, 283–295 CrossRef CAS.
- X. Lu, S. Francis, D. Motta, N. Dimitratos and A. Roldan, Phys. Chem. Chem. Phys., 2020, 22, 3883–3896 RSC.
- E. Nowicka, S. Althahban, T. D. Leah, G. Shaw, D. Morgan, C. J. Kiely, A. Roldan and G. J. Hutchings, Sci. Technol. Adv. Mater., 2019, 20, 367–378 CrossRef CAS PubMed.
- M. G. Quesne, A. Roldan, N. H. De Leeuw and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2019, 21, 10750–10760 RSC.
- J. D. Pack and H. J. Monkhorst, Phys. Rev. B: Solid State, 1977, 16, 1748–1749 CrossRef.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- P. Ramachandran and G. Varoquaux, Comput. Sci. Eng., 2011, 13, 40–51 Search PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- P. Raybaud, C. Chizallet, C. Mager-Maury, M. Digne, H. Toulhoat and P. Sautet, J. Catal., 2013, 308, 328–340 CrossRef CAS.
- C.-C. Chang, C.-Y. Liu and Y.-C. Sun, Phys. Chem. Chem. Phys., 2020, 22, 4967–4973 RSC.
- A. F. Yonezawa, G. R. Nagurniak, R. P. Orenha, E. H. da Silva, R. L. T. Parreira and M. J. Piotrowski, J. Phys. Chem. A, 2021, 125, 4805–4818 CrossRef CAS PubMed.
- I. Barlocco, S. Capelli, X. Lu, S. Bellomi, X. Huang, D. Wang, L. Prati, N. Dimitratos, A. Roldan and A. Villa, ChemCatChem, 2021, 13, 4210–4222 CrossRef CAS.
- J. Engel, S. Francis and A. Roldan, Phys. Chem. Chem. Phys., 2019, 21, 19011–19025 RSC.
- J. B. A. Davis, A. Shayeghi, S. L. Horswell and R. L. Johnston, Nanoscale, 2015, 7, 14032–14038 RSC.
- A. Villa, S. J. Freakley, M. Schiavoni, J. K. Edwards, C. Hammond, G. M. Veith, W. Wang, D. Wang, L. Prati and N. Dimitratos, Catal. Sci. Technol., 2016, 6, 694–697 RSC.
- B. Yue, Q. Li, H. Iwai, T. Kako and J. Ye, Sci. Technol. Adv. Mater., 2011, 12(3) DOI:10.1088/1468-6996/12/3/034401.
- T. S. Miller, A. B. Jorge, T. M. Suter, A. Sella, F. Corà and P. F. McMillan, Phys. Chem. Chem. Phys., 2017, 19, 15613–15638 RSC.
- J. Fu, B. Zhu, C. Jiang, B. Cheng, W. You and J. Yu, Small, 2017, 13, 1603938 CrossRef PubMed.
- V. Pfeifer, T. E. Jones, J. J. V. Vélez, R. Arrigo, S. Piccinin, M. Hävecker, A. Knop-Gericke and R. Schlögl, Chem. Sci., 2017, 8, 2143–2149 RSC.
- V. Pfeifer, T. E. Jones, J. J. Velasco Vélez, C. Massué, R. Arrigo, D. Teschner, F. Girgsdies, M. Scherzer, M. T. Greiner and J. Allan, Surf. Interface Anal., 2016, 48, 261–273 CrossRef CAS.
- Z. Li, X. Yang, N. Tsumori, Z. Liu, Y. Himeda, T. Autrey and Q. Xu, ACS Catal., 2017, 7, 2720–2724 CrossRef CAS.
- H. Wang, M. Ming, M. Hu, C. Xu, Y. Wang, Y. Zhang, D. Gao, J. Bi, G. Fan and J.-S. Hu, ACS Appl. Mater. Interfaces, 2018, 10, 22340–22347 CrossRef CAS PubMed.
- R. T. Rewick, B. J. Wood and H. Wise, J. Phys. Chem., 1979, 83, 2480–2485 CrossRef CAS.
- W. P. Krekelberg, J. Greeley and M. Mavrikakis, J. Phys. Chem. B, 2004, 108, 987–994 CrossRef CAS.
- A. C. M. Van Den Broek, J. Van Grondelle and R. A. Van Santen, J. Catal., 1999, 185, 297–306 CrossRef CAS.
- H. Zhong, T. Wang, Y. Mo, C. Zheng and Y. Chen, Electrochim. Acta, 2022, 404, 139602 CrossRef CAS.
- P. A. Denis and F. Iribarne, J. Phys. Chem. C, 2013, 117, 19048–19055 CrossRef CAS.
- I. Barlocco, S. Capelli, X. Lu, S. Tumiati, N. Dimitratos, A. Roldan and A. Villa, Nanoscale, 2020, 12, 22768–22777 RSC.
- N. Rono, J. K. Kibet, B. S. Martincigh and V. O. Nyamori, Crit. Rev. Solid State Mater. Sci., 2021, 46, 189–217 CrossRef CAS.
- F. Fina, S. K. Callear, G. M. Carins and J. T. S. Irvine, Chem. Mater., 2015, 27, 2612–2618 CrossRef CAS.
- H. Shi, S. M. Auerbach and A. Ramasubramaniam, J. Phys. Chem. C, 2016, 120, 11899–11909 CrossRef CAS.
- I. Fampiou and A. Ramasubramaniam, J. Phys. Chem. C, 2012, 116, 6543–6555 CrossRef CAS.
- S. S. Tafreshi, A. Roldan and N. H. De Leeuw, J. Phys. Chem. C, 2014, 118, 26103–26114 CrossRef CAS.
- A. S. Nair and B. Pathak, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1508 CAS.
- F. Calle-Vallejo, D. Loffreda, M. Koper and P. Sautet, Nat. Chem., 2015, 7, 403–410 CrossRef CAS PubMed.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, P. Sautet and D. Loffreda, Angew. Chem., Int. Ed., 2014, 53, 8316–8319 CrossRef CAS PubMed.
- S. Campisi, C. E. Chan-Thaw and A. Villa, Appl. Sci., 2018, 8, 1159 CrossRef.
- Z. Jia, M. Peng, X. Cai, Y. Chen, X. Chen, F. Huang, L. Zhao, J. Diao, N. Wang and D. Xiao, ACS Catal., 2022, 12, 9602–9610 CrossRef CAS.
- Z. Li, Y. Chen, S. Ji, Y. Tang, W. Chen, A. Li, J. Zhao, Y. Xiong, Y. Wu and Y. Gong, Nat. Chem., 2020, 12, 764–772 CrossRef CAS PubMed.
- C. Jin, L. Cheng, G. Feng, R. Ye, Z.-H. Lu, R. Zhang and X. Yu, Langmuir, 2022, 38, 3694–3710 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp04387d |
| This journal is © the Owner Societies 2023 |