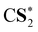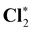Benchmark relativistic delta-coupled-cluster calculations of K-edge core-ionization energies of third-row elements†
Xuechen
Zheng
 a,
Chaoqun
Zhang
a,
Zheqi
Jin
b,
Stephen H.
Southworth
c and
Lan
Cheng
a,
Chaoqun
Zhang
a,
Zheqi
Jin
b,
Stephen H.
Southworth
c and
Lan
Cheng
 *a
*a
aDepartment of Chemistry, The Johns Hopkins University, Baltimore, MD 21218, USA. E-mail: lcheng24@jhu.edu
bDepartment of Chemistry, University College London, London, WC1E 6BT, UK
cChemical Sciences and Engineering Division, Argonne National Laboratory, Lemont, Illinois 60439, USA
First published on 5th May 2022
Abstract
A benchmark computational study of K-edge core-ionization energies of third-row elements using relativistic delta-coupled-cluster (ΔCC) methods and a revised core-valence separation (CVS) scheme is reported. High-level relativistic (HLR) corrections beyond the spin-free exact two-component theory in its one-electron variant (SFX2C-1e), including the contributions from two-electron picture-change effects, spin–orbit coupling, the Breit term, and quantum electrodynamics effects, have been taken into account and demonstrated to play an important role. Relativistic ΔCC calculations are shown to provide accurate results for core-ionization energies of third-row elements. The SFX2C-1e-CVS-ΔCC results augmented with HLR corrections show a maximum deviation of less than 0.5 eV with respect to experimental values.
I. Introduction
The recent rapid development of X-ray sources including a synchrotron,1–4 free-electron lasers,5–12 and high-harmonic generation13–17 enables the study of ultrafast nuclear and electronic dynamics.18–20 The accurate prediction of core-excited and ionized states plays an important role in studying these X-ray induced phenomena.21–24 Many computational methods used in calculations of core-level spectroscopy are based on response theories.25–54 These methods calculate the ground state and the difference between targeted core-excited or ionized states and the ground state. The response theory based methods can treat many core states on the same footing and can obtain transition properties conveniently. On the other hand, core-ionization and excitation energies obtained using response theories are often less accurate than valence ionization and excitation energies, because of the large relaxation of wave functions induced by the core hole. For example, core-ionization energies of second-row elements computed using the equation-of-motion ionization potential coupled-cluster singles and doubles (EOMIP-CCSD) method have errors of 1–3 eV.36 Triple or even quadruple excitations are often required to obtain quantitative results. Therefore, a “direct scheme” that separately optimizes wave functions or electron densities for the ground and core-excited or ionized states has emerged as a valuable alternative to response theories. The direct scheme can be combined with mean-field theories, including delta Hartree–Fock (ΔHF), delta DFT (ΔDFT) or orbital optimized DFT (OO-DFT), orthogonality-constrained DFT methods, an excited-state mean-field approach,55–67 the restricted-active-space self-consistent-field (ΔRASSCF) method and RAS second-order perturbation theory (ΔRASPT2),57,68–75 RAS-based higher-order electron-correlation methods,76–78 an excited-state-specific quantum Monte Carlo approach,79 and coupled-cluster (ΔCC) methods.37,80–82 Since the relaxation of wave functions has been explicitly taken into account, methods in this category have good performance in calculations of core-ionization and excitation energies. For example, the ΔCC singles and doubles with a noniterative inclusion of triple excitation [ΔCCSD(T)] method has been shown to provide accurate core-ionization energies of second-row elements with a maximum absolute deviation from experimental values of around 0.2 eV.80The direct approaches for calculations of core-ionized or excited states using wave function-based electron-correlation methods have a generic convergence difficulty. This arises from the coupling of targeted core-ionized or excited states with high-lying valence continuum states. The idea of core-valence separation (CVS),83 originally proposed for the response theory calculations of core-excited states, has been extended to the direct approaches to solve this divergence problem. Lee et al. have frozen core orbitals in the CC calculations of both the ground state and the core-ionized state in their ΔCC calculations.81 This avoids the convergence problem while in general overestimating core-ionization energies, since the ground state has more core electrons than the core-ionized state and hence more core-correlation energies. Our previous calculations80 have adopted a CVS variant that freezes the vacant core orbital in CC calculations. This tends to overestimate core-ionization energies by neglecting a part of correlation energies for the core-ionized states. Therefore, we have calculated a simple ad hoc correction to this approximation to obtain high accuracy for computed core-ionization energies. Matthews has developed a CVS variant that includes the excitations into the virtual core orbital when they involve at least one occupied orbital having a lower orbital energy.37 This CVS variant avoids the convergence problem and also performs well numerically. In this work, we study a revised version of the CVS condition to further understand the excellent performance of the Matthews variant.
In this paper, we aim to extend the applicability of CVS–ΔCC schemes for the accurate calculations of K-edge core-ionization energies of third-row elements. A new theoretical challenge lies in the accurate treatment of relativistic effects. The spin-free exact two-component theory in its one-electron variant (the SFX2C-1e scheme)84,85 has been shown to provide the accurate and efficient treatment of relativistic effects for the calculations of core-ionization energies of second-row elements.36,65,80 The SFX2C-1e scheme has also been recently used in OO-DFT calculations of third-row elements and has provided promising results.63 On the other hand, since high-level relativistic (HLR) corrections beyond the SFX2C-1e scheme have been shown to amount to −24 eV for the 1s ionization energy of Kr and −93 eV for that of Xe,86 it seems logical to expect the HLR corrections to play a role in the accurate calculations of third-row elements. Therefore, in the present study, we have included HLR corrections including two-electron picture change, spin–orbit coupling, the Breit interaction, and quantum electrodynamics (QED) effects. The SFX2C-1e-CVS-ΔCCSD(T) results augmented with HLR corrections are shown to provide the accurate Si, P, S, and Cl K-edge core-ionization energies for a benchmark set of molecules, with a maximum absolute error of below 0.5 eV compared with the experiment. In Section II, we discuss the computational methods used in this work, with an emphasis on the CVS conditions and the treatments of high-level relativistic corrections. We provide the computational details in Section III and discuss the computational results in Section IV. Finally, in Section V, we provide conclusions and perspectives for future work.
II. Theory
A ΔCC calculation of a core-ionization energy takes the difference between the CC energy of the neutral molecule and that of the core-ionized state. A CC wave function |ΨCC〉 is obtained by applying an exponential wave operator e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) to a Hartree–Fock (HF) wave function |ΨHF〉
to a Hartree–Fock (HF) wave function |ΨHF〉|ΨCC〉 = e![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) |ΨHF〉 |ΨHF〉 | (1) |
The cluster operator ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is a linear combination of elementary excitation operators weighted by cluster amplitudes. In the CC singles and doubles (CCSD) method, the cluster operator is composed of single and double excitations
is a linear combination of elementary excitation operators weighted by cluster amplitudes. In the CC singles and doubles (CCSD) method, the cluster operator is composed of single and double excitations
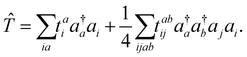 | (2) |
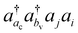 involving the unoccupied core orbital ac. Since ac has a lower orbital energy than valence occupied orbitals, the denominators |εj + εi − εac − εbv| may be very small. This leads to unphysical large cluster amplitudes and hence divergence of CCSD amplitude equations. A variety of CVS conditions have been proposed to solve this divergence problem for ΔCC calculations.37,80,81 In Section II.A, we discuss a revised version of the CVS condition for the ΔCC calculations of core-ionization energies used in the present study. Another computational challenge in accurate calculations of core-ionization energies is to treat relativistic effects accurately. In Section II.B, we present the methods for treating relativistic effects focusing on high-level relativistic corrections.
involving the unoccupied core orbital ac. Since ac has a lower orbital energy than valence occupied orbitals, the denominators |εj + εi − εac − εbv| may be very small. This leads to unphysical large cluster amplitudes and hence divergence of CCSD amplitude equations. A variety of CVS conditions have been proposed to solve this divergence problem for ΔCC calculations.37,80,81 In Section II.A, we discuss a revised version of the CVS condition for the ΔCC calculations of core-ionization energies used in the present study. Another computational challenge in accurate calculations of core-ionization energies is to treat relativistic effects accurately. In Section II.B, we present the methods for treating relativistic effects focusing on high-level relativistic corrections.
A. A revised CVS condition for ΔCC
The basic physical idea of core valence separation (CVS) is to exploit the locality of core holes to decouple targeted core-ionized states from high-lying valence continuum states without a significant loss of accuracy. A mathematical condition for CVS in ΔCC calculations involves excluding small denominators |εj + εi − εac − εbv| in solving CCSD amplitude equations for core-ionized states. In our previous work, we have adopted a simple CVS scheme that freezes the vacant core orbital in solution of CCSD amplitude equations.80 This scheme will be denoted as CVS0 in the following discussions. The CVS0 scheme avoids convergence difficulties and has been shown to provide accurate chemical shifts of core-ionization energies of second-row elements. Since the exclusion of the vacant core orbitals tends to underestimate the correlation energy of the core-ionized state, the CVS0 scheme tends to overestimate core-ionization energies. We have used a correction scheme to obtain accurate absolute core-ionization energies. Here, we have performed CCSD calculations for the core-ionized states excluding excitations having denominators below a given threshold. The differences between these calculations and the CVS0 calculations are obtained as the corrections to the CVS0 approximation. These corrections typically amount to 0.2–0.5 eV for second-row elements. CVS0–ΔCCSD(T) calculations augmented with these corrections have been shown to provide highly accurate absolute values for K-edge core-ionization energies of second-row elements.80 On the other hand, the computed results converge well with respect to the values of threshold only when using small basis sets. Although such calculations using triple-zeta basis sets provide good results, it is desirable to have an approach free from working with thresholds.Matthews has recently developed a CVS variant for ΔCC calculations,37 hereafter referred to as CVS(M). Instead of freezing all double excitations of the type 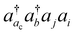 , the CVS(M) scheme only freezes
, the CVS(M) scheme only freezes 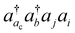 excitations with the orbital energies of the orbital i and j both higher than that of the orbital ac. Namely, the CVS(M) scheme retains
excitations with the orbital energies of the orbital i and j both higher than that of the orbital ac. Namely, the CVS(M) scheme retains 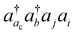 -type excitations, in which the orbital energy of the orbital i or j is lower than that of the vacant core orbital ac. Note that, when εj or εi is lower than εac, the corresponding excitation
-type excitations, in which the orbital energy of the orbital i or j is lower than that of the vacant core orbital ac. Note that, when εj or εi is lower than εac, the corresponding excitation 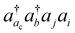 with a denominator |εj + εi − εac − εb| is free from the small denominator problem. The CVS(M) scheme has been demonstrated to be an excellent numerical solution to the divergence problem. In Table 1, we have summarized the CVS(M)-ΔCCSD(T) results for the benchmark set of core-ionization energies used in our previous study. The CVS(M)-ΔCCSD(T) results agree very well with the CVS0-ΔCCSD(T) results augmented with the corrections to the CVS0 approximation, with the latter denoted as CVS0-ΔCCSD(T) + ΔCVS in the table.
with a denominator |εj + εi − εac − εb| is free from the small denominator problem. The CVS(M) scheme has been demonstrated to be an excellent numerical solution to the divergence problem. In Table 1, we have summarized the CVS(M)-ΔCCSD(T) results for the benchmark set of core-ionization energies used in our previous study. The CVS(M)-ΔCCSD(T) results agree very well with the CVS0-ΔCCSD(T) results augmented with the corrections to the CVS0 approximation, with the latter denoted as CVS0-ΔCCSD(T) + ΔCVS in the table.
| CVS0-ΔCCSD(T) + ΔCVS80 | CVS(M)-ΔCCSD(T)37 | CVS-ΔCCSD(T) | Experiment107 | |
|---|---|---|---|---|
| C*O | 296.35 (0.14) | 296.35 (0.14) | 296.35 (0.14) | 296.21 |
| CO* | 542.64 (0.09) | 542.65 (0.10) | 542.65 (0.10) | 542.55 |
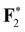
|
696.80 (0.11) | 696.83 (0.14) | 696.83 (0.14) | 696.69 |
| HF* | 694.45 (0.22) | 694.48 (0.25) | 694.48 (0.25) | 694.23 |
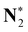
|
410.01 (0.03) | 410.02 (0.04) | 410.02 (0.04) | 409.98 |
| C*H4 | 290.79 (−0.12) | 290.77 (−0.14) | 290.77 (−0.14) | 290.91 |
| H2O* | 540.00 (0.10) | 540.01 (0.11) | 540.01 (0.11) | 539.90 |
| C*H2O | 294.54 (0.07) | 294.53 (0.06) | 294.53 (0.06) | 294.47 |
| CH2O* | 539.51 (0.03) | 539.52 (0.04) | 539.52 (0.04) | 539.48 |
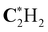
|
291.31 (0.17) | 291.31 (0.17) | 291.31 (0.17) | 291.14 |
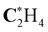
|
290.81 (−0.01) | 290.80 (−0.02) | 290.80 (−0.02) | 290.82 |
| C*O2 | 297.79 (0.10) | 297.78 (0.09) | 297.78 (0.09) | 297.69 |
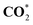
|
541.40 (0.06) | 541.41 (0.07) | 541.41 (0.07) | 541.34 |
| NNO* | 541.63 (0.21) | 541.65 (0.23) | 541.65 (0.23) | 541.42 |
| NN*O | 412.81 (0.22) | 412.81 (0.22) | 412.81 (0.22) | 412.59 |
| N*NO | 408.91 (0.20) | 408.92 (0.21) | 408.92 (0.21) | 408.71 |
| N*H3 | 405.67 (0.11) | 405.67 (0.11) | 405.67 (0.11) | 405.56 |
| HC*N | 293.48 (0.08) | 293.47 (0.07) | 293.47 (0.07) | 293.40 |
| HCN* | 406.86 (0.08) | 406.86 (0.08) | 406.86 (0.08) | 406.78 |
| C*H3OH | 292.46 (0.03) | 292.45 (0.02) | 292.45 (0.02) | 292.43 |
| CH3O*H | 539.18 (0.07) | 539.19 (0.08) | 539.19 (0.08) | 539.11 |
Interestingly, the excellent agreement between the CVS(M) and CVS0 + ΔCVS results indicates that, among double excitations involving the vacant core orbital, only those excitations correlating core orbitals lower than the vacant core orbital make significant contributions to computed core-ionization energies. An immediate question is about the physical origin of this numerical observation, e.g., whether all deeper core orbitals make equally important contributions. Since the vacant core orbital is highly localized, it is logical to assume that only the corresponding core orbital located at the same atom contributes significantly. Therefore, we propose a revised CVS condition aiming to improve our understanding. The revised scheme retains 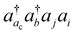 -type excitations only when the orbital i or j is in the same shell as ac. For example, for calculations of K-edge core-ionization energies presented here, we have included
-type excitations only when the orbital i or j is in the same shell as ac. For example, for calculations of K-edge core-ionization energies presented here, we have included 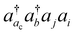 with ac being an ionized 1s α orbital and i or j the corresponding 1s β orbital. Computed core-ionization energies using the present revised CVS scheme are summarized in the third column of Table 1 and denoted as “CVS” in the table. They are nearly indistinguishable from the CVS(M) results. This verifies that the correlation contributions to ionization energies from correlating the vacant core orbital indeed arise mainly from the correlation of the corresponding core orbital in the same shell. We have used the revised CVS scheme in ΔCC calculations of third-row elements presented here.
with ac being an ionized 1s α orbital and i or j the corresponding 1s β orbital. Computed core-ionization energies using the present revised CVS scheme are summarized in the third column of Table 1 and denoted as “CVS” in the table. They are nearly indistinguishable from the CVS(M) results. This verifies that the correlation contributions to ionization energies from correlating the vacant core orbital indeed arise mainly from the correlation of the corresponding core orbital in the same shell. We have used the revised CVS scheme in ΔCC calculations of third-row elements presented here.
B. High-level relativistic corrections
Since core electrons are located near the nuclei and move faster than valence electrons, relativistic effects play an important role in the accurate calculations of core-ionization energies. The most rigorous treatment of relativistic effects in quantum chemistry is offered by the four-component Dirac–Coulomb–Breit (DCB) approach augmented with quantum electrodynamics (QED) effects (the DCB + QED approach).87 The DCB approach employs the one-electron Dirac Hamiltonian together with an electron–electron interaction![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ij written as a sum of the instantaneous Coulomb interaction
ij written as a sum of the instantaneous Coulomb interaction ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) Cij and the Breit term
Cij and the Breit term ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) Bij87
Bij87![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) ij = ij = ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) Cij + Cij + ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) Bij, Bij, | (3) |
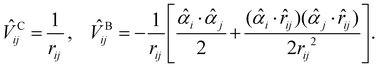 | (4) |
Our previous work has shown that the SFX2C-1e scheme provides sufficiently accurate treatment of relativistic effects for high accuracy calculations of core-ionization energies of second-row elements.80 The work by Southworth et al.86 has demonstrated that high-level relativistic corrections make significant contributions to 1s ionization energies of Kr and Xe; e.g., they contribute −24 eV and −93 eV to the Kr and Xe 1s ionization energies, respectively. It is thus important to investigate their contributions to the 1s core-ionization energies of third-row elements when aiming at high accuracy. We have obtained the 2e-pc, SO, and Gaunt-term contributions to core ionization energies as the corresponding corrections to 1s orbital energies and also from equation-of-motion coupled-cluster singles and doubles (EOM-CCSD)91,92 calculations. These two approaches have produced HLR corrections in close agreement with each other, indicating that the coupling of these HLR effects with an electron correlation and wave function relaxation plays a minor role in the calculations of core ionization energies. The work by Southworth et al. has shown that the 2e-pc correction for the 1s ionization energy of XeF2 is almost identical to that for the Xe atom. We have performed atomic and molecular calculations for 2e-pc, SO, and Breit-term contributions and have found that these corrections are also largely transferable from atoms to molecules. These results are documented in the ESI.† Therefore, in the present study, we have used the HLR corrections to the 1s orbital energies of the Si, P, S, and Cl atoms obtained from atomic calculations using spherically averaged occupation numbers as the corresponding HLR corrections to molecular 1s ionization energies.
We have also estimated the QED corrections to 1s core ionization energies using the corresponding corrections to atomic orbital energies. Kozioł and Aucar93 have calculated QED corrections to atomic 1s orbital energies including vacuum-polarization and self-energy contributions and fit the results (in Hartree) into a function of the nuclear charge Z
| ε(Z) = a × Zb, | (5) |
III. Computational details
All calculations presented here have been performed using the CFOUR program package.89,90,94–96 The benchmark set comprises 15 K-edge core-ionization energies of third-row elements including silicon 1s ionization energies in SiH4 and SiCl4, phosphorus 1s ionization energies in PH3, PCl3, POF3, PSF33, PF3, and PF5, sulfur 1s ionization energies in OCS, CS2, SF6, H2S, and SO2, and chlorine 1s ionization energies in HCl and Cl2. The structures of these molecules have been calculated at the SFX2C-1e-CCSD(T) level using correlation-consistent polarized core-valence triple-zeta (cc-pCVTZ) basis sets97,98 recontracted for the SFX2C-1e scheme (available on https://www.cfour.de). These structures in Cartesian coordinates are summarized in the ESI.†Basis-set effects on computed core-ionization energies are studied in Section IV.A. We have performed calculations of core-ionization energies using SFX2C-1e recontracted cc-pVXZ and cc-pCVXZ (X = T, Q, 5) basis sets and also the fully uncontracted versions cc-pVXZ-unc and cc-pCVXZ-unc (X = T, Q, 5). Inspired by the work in the literature,61,99,100 we have also studied a hybrid scheme using cc-pCVXZ-unc basis sets for the target atom and the cc-pVXZ basis sets for the other atoms. This hybrid approach is denoted as cc-pCVXZ-unc* (X = T, Q, 5). Contributions of the electron correlation are presented and discussed in Section IV.2. We have obtained electron-correlation contributions using the ΔCCSD101 and ΔCCSD(T)102 methods.
High-level relativistic corrections, i.e., those beyond the SFX2C-1e scheme, are studied in Section IV.2. In these calculations, the corrections to the targeted 1s ionization energies have been approximated using the corresponding corrections to the atomic 1s orbital energies, since these corrections are of atomic characteristic and the coupling between these relativistic corrections and correlations is small. In the ESI,† we show that their corrections to the molecular 1s orbital energies are essentially indistinguishable from the atomic ones. We have obtained the corrections to the atomic orbital energies using atomic Hartree–Fock (HF) calculations with spherically averaged occupation numbers using uncontracted ANO-RCC (ANO-RCC-unc)103,104 basis sets. 2e-pc Corrections have been obtained as the difference between the atomic SFDC and SFX2C-1e results, the spin–orbit correction as the difference between the atomic DC and SFDC results, and the contributions of the Breit terms as the difference between the atomic DCB and DC results. The atomic calculations have been performed using an efficient implementation of atomic HF calculations within the CFOUR program package for constructing atomic mean-field spin–orbit integrals. The details for this implementation will be published elsewhere. The QED corrections to the 1s orbital energies have been taken from the work by Kozioł and Aucar as given in eqn (5).93
IV. Results and discussion
In this section, we present the benchmark ΔCC calculations of K-edge core-ionization energies of third-row elements with a careful study of basis-set effects, electron-correlation contributions, and high-level relativistic (HLR) corrections. The best ΔCC results are shown to be essentially quantitative; the maximum deviation of the SFX2C-1e-CVS-ΔCCSD(T) results with HLR corrections with respect to experimental values is less than 0.5 eV. Thus, the computational protocol presented here is a promising candidate for the accurate prediction of core-ionization energies of third-row elements.A. Basis-set effects
The CVS-ΔCCSD(T) values for K-edge core-ionization energies computed using a variety of basis sets are summarized in Table 2. The standard correlation-consistent triple-ζ basis sets (cc-pVTZ) overestimate core-ionization energies by around 10 eV compared with calculations using the uncontracted basis sets. Note that the contraction coefficients of the cc-pVXZ sets have been obtained from the atomic calculations of the neutral atom with spherically averaged occupation numbers. Thus, they describe core orbitals in molecules without a core hole better than those in core-ionized states, in which the presence of the core hole induces significant relaxation of the wave function, especially core orbitals. For example, the difference between HF/cc-pVTZ and HF/cc-pVTZ-unc energies is only 0.002 eV for the neutral HCl molecule but amounts to as large as 10.2 eV for the core-ionized state of HCl. The inclusion of core-correlation functions can effectively improve the description of this relaxation. The cc-pCVTZ results improve significantly over the cc-pVTZ results. For second-row elements, we have found the cc-pCVXZ basis sets to be as accurate as the corresponding fully uncontracted cc-pCVXZ-unc basis sets. However, for third-row elements, the results obtained using cc-pCVXZ basis sets still differ from the cc-pCVXZ-unc results by 0.3–0.8 eV. Note that the uncontracted cc-pVXZ basis sets contain steep low angular momentum functions that can serve as the core-correlation functions. The difference between cc-pVXZ-unc and cc-pCVXZ-unc thus lies in the high angular momentum core-correlation functions. For example, the cc-pCVTZ-unc basis set for Cl has in addition two core-correlating d-type and one core-correlating f-type functions compared with the cc-pVTZ-unc set. This is a relatively minor effect and contributes around 0.1–0.3 eV to computed core-ionization energies.Since the core hole is highly localized and induces wave function relaxation for the targeted atom, it is only necessary to use uncontracted basis sets for the targeted atom. Therefore, we also use a hybrid scheme,61,99,100 in which we use uncontracted cc-pCVTZ basis sets on targeted atoms and standard cc-pVXZ basis sets on the other atoms. This hybrid approach is denoted as cc-pCVXZ-unc* and is significantly more efficient than using cc-pCVXZ-unc basis sets. For example, the cc-pCVTZ-unc* scheme has 186 basis functions for a calculation of PCl3, to be compared with 336 basis functions when using the cc-pCVTZ-unc basis sets for all atoms. As shown in Table 2, the cc-pCVTZ-unc* results agree very well with the results obtained using cc-pCVTZ-unc basis sets for all the atoms.
We have also studied basis-set effects by extending the cardinal number of the basis sets. Table 3 shows the computed core-ionization energies using cc-pCVXZ-unc* with X = T, Q, and 5. The ionization energies tend to decrease with the enlargement of basis sets. The difference between the cc-pCVTZ-unc* and cc-pCV5Z-unc* results is less than 0.2 eV. Therefore, the contributions of core-correlation functions using uncontracted basis sets on target atoms are more pronounced than the variation of the results with the increase of the cardinal number of basis sets. We will use the cc-pCVTZ-unc* scheme in the following calculations.
B. Electron-correlation and high-level relativistic contributions
As shown in Table 4, electron-correlation contributions are represented as the differences between the ΔHF and ΔCCSD(T) results. Our previous work on second-row elements has shown that the electron correlation contributes a small fraction of the total core-ionization energies, but makes significant contributions to chemical shifts of core-ionization energies, i.e., relative shifts of core ionization energies because of the chemical environment.80 We have seen similar electron-correlation effects for core-ionization energies of third-row elements. The electron correlation contributes up to 1 eV for absolute values, while it plays an important role in the accurate calculations of chemical shifts. For example, the relative shifts of sulfur 1s ionization energies in CS2 and SO2 are calculated to be 6.82 eV at the ΔHF level and 5.52 eV at the ΔCCSD(T) level. Triple corrections [the differences between ΔCCSD(T) and ΔCCSD results] contribute up to 0.3 eV. Therefore, it is logical to expect the contributions from higher-level excitations to be smaller. Thus, CVS-ΔCCSD(T) is expected to provide the accurate treatment of the electron correlation in the practical calculations of the core-ionization energies of third-row elements.An investigation of the electron-correlation and wave function relaxation contributions to HLR corrections including the 2e-pc, SO, and Gaunt-term corrections to core ionization energies are summarized in Table 5. The column “Koopmans” presents the corrections to orbital energies. They are in close agreement with the corresponding EOM-CCSD values with deviations below 0.015 eV. The coupling of these HLR corrections with the electron correlation and wave function relaxation thus does not play a significant role in present calculations. We use the corrections to 1s orbital energies in the rest of the present study. These results also support the use of the HLR corrections to orbital energies as corrections to core ionization energies being independently carried out in ref. 63. The high-level relativistic corrections to 1s ionization energies of Si, P, S and Cl atoms are summarized in Table 6. The two-electron picture change corrections and the differences between the SFDC and SFX2C-1e results increase these ionization energies by 0.4–0.8 eV. The spin–orbit corrections play a relatively minor role and amount to less than 0.01 eV. The contributions from the Breit interaction decrease these K-edge core-ionization energies by 1.0–1.8 eV. The QED corrections are smaller in magnitude and amount to −0.3 to −0.6 eV. The total high-level relativistic corrections to the 1s ionization energies of Si, P, S and Cl amount to −0.80, −1.02, −1.28 and −1.59 eV, respectively. Note that the high-level relativistic corrections increase rapidly with respect to the nuclear charge; the corrections to chlorine are around twice the values for silicon. It is important to consider high-level relativistic corrections to obtain the accurate absolute values of the core-ionization energies of third-row elements.
| Si | P | S | Cl | |
|---|---|---|---|---|
| Two-electron picture change | 0.451 | 0.563 | 0.692 | 0.839 |
| Spin–orbit coupling | −0.002 | −0.002 | −0.003 | −0.005 |
| Breit term | −0.950 | −1.198 | −1.488 | −1.823 |
| QED effects | −0.297 | −0.381 | −0.481 | −0.599 |
| Total ΔHLR | −0.798 | −1.019 | −1.280 | −1.588 |
C. Comparison with the experiment
Comparison with experimental values shows that the SFX2C-1e-ΔCCSD(T)/cc-pCVTZ-unc* results in Table 7 consistently overestimate the core-ionization energies of third-row elements by around 1 eV, because of the neglect of high-level relativistic corrections. Adding high-level relativistic corrections to SFX2C-1e-ΔCCSD(T)/cc-pCVTZ-unc* results provides computational results in excellent agreement with experimental values; the maximum deviation of the SFX2C-1e-ΔCCSD(T)/cc-pCVTZ-unc* + HLR results in Table 7 from the corresponding experimental values is 0.3 eV. This is consistent with the error estimate in the previous subsections that the errors in the treatment of basis-set effects and electron correlation contributions are both below 0.2 eV. SFX2C-1e-ΔCCSD(T) calculations augmented with HLR corrections thus have the potential of providing accurate predictions for the K-edge core-ionization energies of third-row elements.| SFX2C-1e-ΔCCSD(T) | SFX2C-1e-ΔCCSD(T) + ΔHLR | Experiment105,107–109 | |
|---|---|---|---|
| Si*H4 | 1848.0 (1.0) | 1847.2 (0.2) | 1847.0 |
| Si*Cl4 | 1851.5 (0.9) | 1850.7 (0.1) | 1850.6 |
| P*H3 | 2151.9 (1.0) | 2150.9 (0.0) | 2150.9 |
| P*Cl3 | 2155.0 (0.9) | 2154.0 (−0.1) | 2154.2 |
| P*OF3 | 2158.9 (1.1) | 2157.9 (0.1) | 2157.8 |
| P*SF3 | 2158.2 (1.1) | 2157.1 (0.1) | 2157.1 |
| P*F3 | 2157.3 (1.0) | 2156.3 (0.0) | 2156.4 |
| P*F5 | 2160.5 (1.1) | 2159.5 (0.1) | 2159.4 |
| OCS* | 2480.0 (1.3) | 2478.7 (0.0) | 2478.7 |
|
2479.2 (1.1) | 2478.0 (−0.1) | 2478.1 |
| S*F6 | 2491.3 (1.2) | 2490.0 (−0.1) | 2490.1 |
| H2S* | 2479.7 (1.2) | 2478.4 (−0.1) | 2478.5 |
| S*O2 | 2484.8 (1.1) | 2483.5 (−0.2) | 2483.7 |
| HCl* | 2831.6 (1.9) | 2830.1 (0.3) | 2829.8 |
|
2832.1 (1.8) | 2830.5 (0.3) | 2830.2 |
Let us take a close look at a discrepancy between two experimental results for the sulfur 1s ionization energies of the OCS molecule.105,106 As shown in Table 8, two measured values for the sulfur 1s ionization energies of OCS differ by 1.6 eV. Our computed result agrees well with the experimental result in ref. 105, while the difference between the computed value and the measured one in ref. 106 amounts to 1.6 eV and exceeds the estimated error of the computational approach. The measurement in ref. 105 derived core-ionization energies by analyzing the X-ray absorption spectrum. No error bar for the position of the derived ionization edge was given. The experimental study in ref. 106 directly measured the binding energy by photoelectron spectroscopy. The accuracy of binding energies depends on the accurate knowledge of the X-ray energy, kinetic energy offsets of the electron spectrometer, and the resolution of both the X-rays and electron spectrometer. This experimental measurement did not specify an error bar either. Therefore, it is suggested to revisit experimental measurements for this core-ionization energy. In addition, the computed result for the chlorine 1s ionization energy of SiCl4 differs from the experimental result in the measurement in ref. 106 by around 1 eV. This discrepancy also suggests a revisitation of experimental measurements for the Cl 1s ionization energy of SiCl4.
| Exp.106 | Exp.105,107–109 | ΔCCSD(T)/cc-pCVTZ-unc* + ΔHLR | |
|---|---|---|---|
| Si*H4 | 1847.1 | 1847.0 | 1847.2 |
| Si*Cl4 | 1850.9 | 1850.6 | 1850.7 |
| OCS* | 2480.3 | 2478.7 | 2478.7 |
|
2477.8 | 2478.1 | 2478.0 |
| S*F6 | 2490.3 | 2490.1 | 2490.0 |
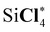
|
2830.4 | — | 2829.3 |
Accurate core-ionization energies computed here might also serve to benchmark more approximate treatments of the electron correlation and/or relativistic effects and to guide the improvement of more approximate treatments. For example, Cunha et al. have performed calculations for the 1s ionization energies of third-row elements by orbital optimized density functional theory (OO-DFT),63 in which relativistic effects have been treated using the SFX2C-1e scheme. The SFX2C-1e-OO-DFT calculations provide chemical shifts of K-edge core-ionization energies in excellent agreement with experimental values. Concerning absolute values, Cunha et al. have found that the use of the SCAN0 functional having a 25% Hartree–Fock exchange in SFX2C-1e calculations tends to overestimate these core-ionization energies. On the other hand, as we have shown in the present study, the high-level relativistic corrections amount to −1.0 to −1.8 eV for the core-ionization energies of these elements. Augmentation of the OO-DFT/SCAN0 results with high-level relativistic corrections shows that the SCAN0 functional actually tends to underestimate the core-ionization energies, while it represents the closest agreement with experimental results among the functionals used in ref. 63. This merely serves as an example of the usefulness of including HLR corrections in benchmark studies. A thorough OO-DFT study with the inclusion of HLR effects might be useful to identify the best functionals and understand the performance of various functionals.
V. Conclusions
Benchmark ΔCC calculations of K-edge core-ionization energies of third-row elements Si, P, S and Cl using a revised CVS condition with thorough analyses of the basis set, electron-correlation, and high-level relativistic effects are presented. A study of the revised CVS condition has shown that the contributions involving the vacant core orbital to the ionization energy mainly come from the correlation of the corresponding core orbital in the same shell. Basis-set effects have been demonstrated to be important; it is necessary to use uncontracted basis sets for targeted atoms in the accurate calculations of core-ionization energies of third-row elements. Furthermore, the use of uncontracted cc-pCVTZ basis sets for targeted atoms and cc-pVTZ sets for the other atoms appears to be an efficient and accurate alternative to the use of uncontracted basis sets for all atoms. The high-level relativistic corrections amount from −0.8 eV to −1.6 eV for Si, P, S, and Cl K-edge core-ionization energies. SFX2C-1e-CVS-ΔCCSD(T)/cc-pCVTZ-unc* calculations augmented with high-level relativistic corrections can provide highly accurate K-edge core-ionization energies of third-row elements with deviations from experimental values of lower than 0.5 eV.Data availability
The data that support the findings of this study are available within the article [and its ESI†].Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Diptarka Hait (Berkeley) for carefully reading the manuscript, providing helpful corrections and comments, and sharing ongoing research on high-level relativistic corrections in the course of the revision for the present manuscript. This material is based upon the work supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division, under the Contract Number DE-AC02-06CH11357. The computations at Johns Hopkins University have been carried out at the Advanced Research Computing at Hopkins (ARCH) core facility (rockfish.jhu.edu), which is supported by the National Science Foundation (NSF) under grant number OAC-1920103.References
- A. A. Zholents and M. S. Zolotorev, Phys. Rev. Lett., 1996, 76, 912–915 CrossRef CAS PubMed.
- J. W. Weigold, S. W. Pang, A. Madhukar, P. Chen, N. P. Kobayashi, D. Bimberg, D. G. Schlom, M. Urbanik, J. Luine, A. M. Hellwege, L. Holborn, A. L. Day, I. M. Lifschitz, V. V. Slyozov, B. R. Chalamala, Y. Wei, B. E. Gnade, J. H. Bernhard, E. D. Sosa, D. E. Golden, R. H. Reuss, S. Aggarwal and R. Ramesh, Science, 2000, 287, 2237–2240 CrossRef PubMed.
- A. Rousse, K. T. Phuoc, R. Shah, A. Pukhov, E. Lefebvre, V. Malka, S. Kiselev, F. Burgy, J.-P. Rousseau, D. Umstadter and D. Hulin, Phys. Rev. Lett., 2004, 93, 135005 CrossRef PubMed.
- S. Mobilio, F. Boscherini and C. Meneghini, Synchrotron radiation: basics, methods and applications, Springer-Verlag Berlin Heidelberg, 2015 Search PubMed.
- L. Young, E. P. Kanter, B. Krässig, Y. Li, A. M. March, S. T. Pratt, R. Santra, S. H. Southworth, N. Rohringer, L. F. DiMauro, G. Doumy, C. A. Roedig, N. Berrah, L. Fang, M. Hoener, P. H. Bucksbaum, J. P. Cryan, S. Ghimire, J. M. Glownia, D. A. Reis, J. D. Bozek, C. Bostedt and M. Messerschmidt, Nature, 2010, 466, 56 CrossRef CAS PubMed.
- B. W.-J. McNeil and N. R. Thompson, Nat. Photonics, 2010, 4, 814 CrossRef CAS.
- N. Rohringer, D. Ryan, R. A. London, M. Purvis, F. Albert, J. Dunn, J. D. Bozek, C. Bostedt, A. Graf, R. Hill, S. P. Hau-Riege and J. J. Rocca, Nature, 2012, 481, 488–491 CrossRef CAS PubMed.
- C. Pellegrini, A. Marinelli and S. Reiche, Rev. Mod. Phys., 2016, 88, 1–55 CrossRef.
- Z. Zhao, D. Wang, Q. Gu, L. Yin, M. Gu, Y. Leng and B. Liu, Appl. Sci., 2017, 7, 607 CrossRef.
- E. A. Seddon, J. A. Clarke, D. J. Dunning, C. Masciovecchio, C. J. Milne, F. Parmigiani, D. Rugg, J. C. Spence, N. R. Thompson, K. Ueda, S. M. Vinko, J. S. Wark and W. Wurth, Rep. Prog. Phys., 2017, 80, 1–73 CrossRef PubMed.
- A. Rudenko, L. Inhester, K. Hanasaki, X. Li, S. J. Robatjazi, B. Erk, R. Boll, K. Toyota, Y. Hao, O. Vendrell, C. Bomme, E. Savelyev, B. Rudek, L. Foucar, S. H. Southworth, C. S. Lehmann, B. Kraessig, T. Marchenko, M. Simon, K. Ueda, K. R. Ferguson, M. Bucher, T. Gorkhover, S. Carron, R. Alonso-Mori, J. E. Koglin, J. Correa, G. J. Williams, S. Boutet, L. Young, C. Bostedt, S.-K. Son, R. Santra and D. Rolles, Nature, 2017, 546, 129 CrossRef CAS PubMed.
- L. Young, K. Ueda, M. Gühr, P. H. Bucksbaum, M. Simon, S. Mukamel, N. Rohringer, K. C. Prince, C. Masciovecchio, M. Meyer, A. Rudenko, D. Rolles, C. Bostedt, M. Fuchs, D. A. Reis, R. Santra, H. Kapteyn, M. Murnane, H. Ibrahim, F. Legare, M. Vrakking, M. Isinger, D. Kroon, M. Gisselbrecht, A. L'Huillier, H. J. Wörner and S. R. Leone, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 032003 CrossRef.
- A. McPherson, G. Gibson, H. Jara, U. Johann, T. S. Luk, I. A. McIntyre, K. Boyer and C. K. Rhodes, J. Opt. Soc. Am. B, 1987, 4, 595–601 CrossRef CAS.
- C. Manus, G. Mainfray, A. L'Huillier, X. F. Li, L. A. Lompre and M. Ferray, J. Phys. B: At., Mol. Opt. Phys., 2002, 21, L31–L35 Search PubMed.
- T. Fan, P. Grychtol, R. Knut, C. Hernández-García, D. D. Hickstein, D. Zusin, C. Gentry, F. J. Dollar, C. A. Mancuso, C. W. Hogle, O. Kfir, D. Legut, K. Carva, J. L. Ellis, K. M. Dorney, C. Chen, O. G. Shpyrko, E. E. Fullerton, O. Cohen, P. M. Oppeneer, D. B. Milošević, A. Becker, A. A. Jaroń-Becker, T. Popmintchev, M. M. Murnane and H. C. Kapteyn, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 14206–14211 CrossRef CAS PubMed.
- F. Calegari, G. Sansone, S. Stagira, C. Vozzi and M. Nisoli, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 062001 CrossRef.
- Y. Pertot, C. Schmidt, M. Matthews, A. Chauvet, M. Huppert, V. Svoboda, A. von Conta, A. Tehlar, D. Baykusheva, J.-P. P. Wolf and H. J. Wörner, Science, 2017, 355, 264–267 CrossRef CAS PubMed.
- T. Pfeifer, C. Spielmann and G. Gerber, Rep. Prog. Phys., 2006, 69, 443–505 CrossRef.
- P. M. Kraus, M. Zürch, S. K. Cushing, D. M. Neumark and S. R. Leone, Nat. Rev. Chem., 2018, 2, 82–94 CrossRef CAS.
- R. Geneaux, H. J. Marroux, A. Guggenmos, D. M. Neumark and S. R. Leone, Philos. Trans. R. Soc., A, 2019, 377, 1–27 CrossRef PubMed.
- J. J. Rehr and R. C. Albers, Rev. Mod. Phys., 2000, 72, 621–654 CrossRef CAS.
- N. A. Besley and F. A. Asmuruf, Phys. Chem. Chem. Phys., 2010, 12, 12024–12039 RSC.
- P. Norman and A. Dreuw, Chem. Rev., 2018, 118, 7208–7248 CrossRef CAS PubMed.
- C. D. Rankine and T. J. Penfold, J. Phys. Chem. A, 2021, 125, 4276–4293 CrossRef CAS PubMed.
- S. DeBeer George, T. Petrenko and F. Neese, J. Phys. Chem. A, 2008, 112, 12936–12943 CrossRef CAS PubMed.
- T. Akama and H. Nakai, J. Chem. Phys., 2010, 132, 054104 CrossRef PubMed.
- K. Lopata, B. E. Van Kuiken, M. Khalil and N. Govind, J. Chem. Theory Comput., 2012, 8, 3284–3292 CrossRef CAS PubMed.
- I. Ljubić, A. Kivimäki and M. Coreno, Phys. Chem. Chem. Phys., 2016, 18, 10207–10217 RSC.
- A. A. Fouda and N. A. Besley, J. Comput. Chem., 2020, 41, 1081–1090 CrossRef CAS PubMed.
- M. Nooijen and R. J. Bartlett, J. Chem. Phys., 1995, 102, 6735–6756 CrossRef CAS.
- S. Coriani and H. Koch, J. Chem. Phys., 2015, 143, 181103 CrossRef PubMed.
- S. H. Southworth, R. Wehlitz, A. Picón, C. S. Lehmann, L. Cheng and J. F. Stanton, J. Chem. Phys., 2015, 142, 224302 CrossRef PubMed.
- B. Peng, P. J. Lestrange, J. J. Goings, M. Caricato and X. Li, J. Chem. Theory Comput., 2015, 11, 4146–4153 CrossRef CAS PubMed.
- D. R. Nascimento and A. E. DePrince, J. Chem. Phys. Lett., 2017, 8, 2951–2957 CrossRef CAS PubMed.
- M. L. Vidal, X. Feng, E. Epifanovsky, A. I. Krylov and S. Coriani, J. Chem. Theory Comput., 2019, 15, 3117–3133 CrossRef CAS PubMed.
- J. Liu, D. Matthews, S. Coriani and L. Cheng, J. Chem. Theory Comput., 2019, 15, 1642–1651 CrossRef CAS PubMed.
- D. A. Matthews, Mol. Phys., 2020, 118, e1771448 CrossRef.
- J. J. Rehr, F. D. Vila, J. J. Kas, N. Y. Hirshberg, K. Kowalski and B. Peng, J. Chem. Phys., 2020, 152, 174113 CrossRef CAS PubMed.
- M. L. Vidal, S. Coriani, P. Pokhilko and A. I. Krylov, J. Phys. Chem. Lett., 2020, 11, 8314–8321 CrossRef CAS PubMed.
- S. Ranga and A. K. Dutta, J. Chem. Theory Comput., 2021, 17, 7428–7446 CrossRef CAS PubMed.
- F. A. Asmuruf and N. A. Besley, Chem. Phys. Lett., 2008, 463, 267–271 CrossRef CAS.
- D. Maganas, S. DeBeer and F. Neese, Inorg. Chem., 2014, 53, 6374–6385 CrossRef CAS PubMed.
- D. Toffoli and P. Decleva, J. Chem. Theory Comput., 2016, 12, 4996–5008 CrossRef CAS PubMed.
- C. Ehlert and T. Klamroth, J. Comput. Chem., 2017, 38, 116–126 CrossRef CAS PubMed.
- K. J. Oosterbaan, A. F. White and M. Head-Gordon, J. Chem. Theory Comput., 2019, 15, 2966–2973 CrossRef CAS PubMed.
- M. W. Hanson-Heine, M. W. George and N. A. Besley, J. Chem. Phys., 2019, 151, 034104 CrossRef PubMed.
- K. Kuramoto, M. Ehara and H. Nakatsuji, J. Chem. Phys., 2005, 122, 014304 CrossRef PubMed.
- M. Ehara, K. Kuramoto and H. Nakatsuji, Chem. Phys., 2009, 356, 195–198 CrossRef CAS.
- D. Maganas, J. K. Kowalska, M. Nooijen, S. DeBeer and F. Neese, J. Chem. Phys., 2019, 150, 104106 CrossRef PubMed.
- A. B. Trofimov, T. Moskovskaya, E. V. Gromov, N. M. Vitkovskaya and J. Schirmer, J. Struct. Chem., 2000, 41, 483–494 CrossRef CAS.
- J. Wenzel, M. Wormit and A. Dreuw, J. Comput. Chem., 2014, 35, 1900–1915 CrossRef CAS PubMed.
- J. Wenzel and A. Dreuw, J. Chem. Theory Comput., 2016, 12, 1314–1330 CrossRef CAS PubMed.
- T. Fransson and A. Dreuw, J. Chem. Theory Comput., 2019, 15, 546–556 CrossRef CAS PubMed.
- T. S. Tan, J. J. Kas and J. J. Rehr, Phys. Rev. B, 2021, 104, 35144 CrossRef CAS.
- P. S. Bagus, Phys. Rev., 1965, 139, A619–A634 CrossRef.
- P. W. Deutsch and L. A. Curtiss, Chem. Phys. Lett., 1976, 39, 588–592 CrossRef CAS.
- A. Naves De Brito, N. Correia, S. Svensson and H. Ågren, J. Chem. Phys., 1991, 95, 2965–2974 CrossRef CAS.
- A. Schmitt and J. Schirmer, Chem. Phys., 1992, 164, 1–9 CrossRef CAS.
- N. A. Besley, A. T. Gilbert and P. M. Gill, J. Chem. Phys., 2009, 130, 124308 CrossRef PubMed.
- M. A. Ambroise and F. Jensen, J. Chem. Theory Comput., 2019, 15, 325–337 CrossRef CAS PubMed.
- D. Hait and M. Head-Gordon, J. Phys. Chem. Lett., 2020, 775–786 CrossRef CAS PubMed.
- D. Hait and M. Head-Gordon, J. Phys. Chem. Lett., 2021, 12, 4517–4529 CrossRef CAS PubMed.
- L. A. Cunha, D. Hait, R. Kang, Y. Mao and M. Head-Gordon, J. Phys. Chem. Lett., 2021, 1–36 Search PubMed , in revision, arXiv:2111.08405.
- W. D. Derricotte and F. A. Evangelista, Phys. Chem. Chem. Phys., 2015, 17, 14360–14374 RSC.
- P. Verma, W. D. Derricotte and F. A. Evangelista, J. Chem. Theory Comput., 2016, 12, 144–156 CrossRef CAS PubMed.
- S. M. Garner and E. Neuscamman, J. Chem. Phys., 2020, 153, 154102 CrossRef CAS PubMed.
- A. Grofe, J. Gao and X. Li, J. Chem. Phys., 2021, 155, 014103 CrossRef CAS PubMed.
- H. Ågren and H. J.-A. Jensen, Chem. Phys., 1993, 172, 45–57 CrossRef.
- A. B. Rocha, J. Chem. Phys., 2011, 134, 024107 CrossRef PubMed.
- I. Josefsson, K. Kunnus, S. Schreck, A. Föhlisch, F. de Groot, P. Wernet and M. Odelius, J. Phys. Chem. Lett., 2012, 3, 3565–3570 CrossRef CAS PubMed.
- R. V. Pinjari, M. G. Delcey, M. Guo, M. Odelius and M. Lundberg, J. Chem. Phys., 2014, 141, 124116 CrossRef PubMed.
- Y. Hao, L. Inhester, K. Hanasaki, S.-K. Son and R. Santra, Struct. Dyn., 2015, 2, 41707 CrossRef PubMed.
- M. Guo, E. Källman, L. K. Sørensen, M. G. Delcey, R. V. Pinjari and M. Lundberg, J. Chem. Phys. A, 2016, 120, 5848–5855 CrossRef CAS PubMed.
- L. H. Coutinho, F. de, A. Ribeiro, B. N. Tenorio, S. Coriani, A. C. dos Santos, C. Nicolas, A. R. Milosavljevic, J. D. Bozek and W. Wolff, Phys. Chem. Chem. Phys., 2021, 23, 27484–27497 RSC.
- A. E.-A. Fouda and P. J. Ho, J. Chem. Phys., 2021, 154, 224111 CrossRef CAS PubMed.
- J. Brabec, K. Bhaskaran-Nair, N. Govind, J. Pittner and K. Kowalski, J. Chem. Phys., 2012, 137, 171101 CrossRef PubMed.
- A. J. Jenkins, H. Hu, L. Lu, M. J. Frisch and X. Li, J. Chem. Theory Comput., 2022, 18, 141–150 CrossRef CAS PubMed.
- M. Huang, C. Li and F. A. Evangelista, J. Chem. Theory Comput., 2022, 18, 219–233 CrossRef CAS PubMed.
- S. M. Garner and E. Neuscamman, J. Chem. Phys., 2020, 153, 144108 CrossRef CAS PubMed.
- X. Zheng and L. Cheng, J. Chem. Theory Comput., 2019, 15, 4945–4955 CrossRef CAS PubMed.
- J. Lee, D. W. Small and M. Head-Gordon, J. Chem. Phys., 2019, 151, 214103 CrossRef PubMed.
- X. Zheng, J. Liu, G. Doumy, L. Young and L. Cheng, J. Phys. Chem. A, 2020, 124, 4413–4426 CrossRef CAS PubMed.
- L. S. Cederbaum, W. Domcke and J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1980, 22, 206–222 CrossRef CAS.
- K. G. Dyall, J. Chem. Phys., 2001, 115, 9136–9143 CrossRef CAS.
- W. Liu and D. Peng, J. Chem. Phys., 2009, 131, 1–5 Search PubMed.
- S. H. Southworth, R. W. Dunford, D. Ray, E. P. Kanter, G. Doumy, A. M. March, P. J. Ho, B. Krässig, Y. Gao, C. S. Lehmann, A. Picón, L. Young, D. A. Walko and L. Cheng, Phys. Rev. A, 2019, 100, 1–12 CrossRef.
- K. G. Dyall and K. Fægri Jr, Introduction to relativistic quantum chemistry, Oxford University Press, 2007 Search PubMed.
- K. G. Dyall, J. Chem. Phys., 1994, 100, 2118–2127 CrossRef CAS.
- L. Cheng and J. Gauss, J. Chem. Phys., 2011, 134, 244112 CrossRef PubMed.
- L. Cheng and J. Gauss, J. Chem. Phys., 2011, 135, 084114 CrossRef PubMed.
- J. F. Stanton and R. J. Bartlett, J. Chem. Phys., 1993, 98, 7029–7039 CrossRef CAS.
- A. I. Krylov, Annu. Rev. Phys. Chem., 2008, 59, 433–462 CrossRef CAS PubMed.
- K. Kozioł and G. A. Aucar, J. Chem. Phys., 2018, 148, 134101 CrossRef PubMed.
- CFOUR, Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package by J. F. Stanton, J. Gauss, L. Cheng, M. E. Harding, D. A. Matthews, P. G. Szalay with contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, O. Christiansen, F. Engel, R. Faber, M. Heckert, M. Hilgenberg, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, T. Kirsch, K. Klein, W. J. Lauderdale, F. Lipparini, T. Metzroth, L. A. Mück, D. P. O'Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the current version, see http://www.cfour.de.
- D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, J. Chem. Phys., 2020, 152, 214108 CrossRef CAS PubMed.
- J. F. Stanton, J. Gauss, J. D. Watts and R. J. Bartlett, J. Chem. Phys., 1991, 94, 4334–4345 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1995, 103, 4572–4585 CrossRef CAS.
- B. Kovač, I. Ljubić, A. Kivimäki, M. Coreno and I. Novak, Phys. Chem. Chem. Phys., 2014, 16, 10734–10742 RSC.
- R. Sarangi, M. L. Vidal, S. Coriani and A. I. Krylov, Mol. Phys., 2020, 118, e1769872 CrossRef.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- K. Faegri, Theor. Chem. Acc., 2001, 105, 252–258 Search PubMed.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- R. C. Perera and R. E. LaVilla, J. Chem. Phys., 1984, 81, 3375–3382 CrossRef CAS.
- A. W. Potts, H. F. Fhadil, J. M. Benson and I. H. Hillier, Chem. Phys. Lett., 1994, 230, 543–546 CrossRef CAS.
- W. L. Jolly, K. D. Bomden and C. J. Eyermann, At. Data Nucl. Data Tables, 1984, 31, 433–493 CrossRef CAS.
- S. Bodeur, P. Millié and I. Nenner, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 252–263 CrossRef CAS PubMed.
- O. Keski-Rahkonen and M. O. Krause, J. Electron Spectrosc. Relat. Phenom., 1976, 9, 371–380 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cp00993e |
| This journal is © the Owner Societies 2022 |