Selecting two-photon sequential ionization pathways in H₂ through harmonic filtering

Abstract

Recent experiments in gas-phase molecules have shown the versatility of using attosecond pulse trains combined with IR femtosecond pulses to track and control excitation and ionization yields on the attosecond timescale. The interplay between electron and nuclear motions drives the light-induced transitions favoring specific reaction paths, so that the time delay between the pulses can be used as the tracking parameter or as a control knob to manipulate the molecular dynamics. Here, we present ab initio simulations on the hydrogen molecule to demonstrate that by filtering the high harmonics in an attosecond pulse train one can quench or enhance specific quantum paths thus dictating the outcome of the reaction. It is then possible to discriminate the dominant sequential processes in two-photon ionization, as for example molecular excitation followed by ionization or the other way around. More interestingly, frequency filters can be employed to steer the one- and two-photon yields to favor electron emission in a specific direction.

---

1 Introduction

XUV-pump/IR-probe techniques are by far the most widely used to date to retrieve dynamical information in atoms and molecules with attosecond resolution.^1–5 The experimental feasibility of these setups in several laboratories over the world, with respect to the counterpart XUV/XUV schemes, is mostly associated with the low repetition rates within reach in the currently available XUV light sources. Moreover, applications using XUV attosecond pulse trains (APTs) dominate over the isolation of a single attosecond pulse,⁶ which unavoidably leads to a significant decrease of peak intensity and the difficulty of controlling the carrier envelope phase. Moreover, the characteristics of APTs make them suitable for specific applications such as the RABBITT (reconstruction of attosecond beating by interference of two-photon transitions) technique that exploits the high temporal resolution provided by each attosecond pulse within the train and the spectral definition given by the total duration of the train.^7–9 The increasing number of applications using APTs makes worth current investments to accomplish XUV conversion with high efficiency^10–13 and to design novel strategies for engineering the XUV frequency combs.^14–16 Forthcoming applications are expected to give access to still unexplored ultrafast processes and/or gain a certain degree of control of them, as we propose in the present work. A relatively straightforward approach for tailoring these pulses is the use of XUV harmonic filtering by means of monochromators,^2,17,18 thin metal filters^19,20 or multilayer mirrors.^21–23 Al or Sn filters are routinely used in high harmonic generation techniques.^19,24 For instance, a Sn filter applied to the harmonic spectra generated in medium gases such as Xe or Ar, allows transmission in the region below 20–25 eV with a reasonable efficiency, which enables applications for non-linear XUV optics or the so long awaited attosecond XUV-pump/XUV-probe experiments.²⁴

In the present manuscript, we investigate the use of a frequency filter as a mean to unravel the coupled electron-nuclear dynamics in an excited (ionized) molecule by suppressing/favoring specific multiphoton absorption paths. We first examine the outcome of realistic XUV APT-pump/IR-probe schemes employed in previous experimental studies^25–28 in the hydrogen molecule. In this kind of experiments, identification of the dominant electronic components in the wave packet and interpretation of the complex and tightly coupled electronic and nuclear motions induced by the XUV APT requires accurate theoretical simulations.^25–28 These previous works already showed that one can switch the electronic components in the pumped wave packet, coherently guiding the associated nuclear dynamics and, thus, altering the molecular vibrations triggered in the neutral. By introducing an IR pulse it is then possible to steer the ionization and dissociation channels by varying the delay between pulses, as well as by varying the laser parameters of the XUV APT.^26,27 Moreover, as it will be shown, the IR can further couple highly excited electronic states with energies lying above the ionization threshold, whose decay into the continuum proceeds as the nuclei move apart. These phenomena can only be accurately reproduced by coupling the electronic and nuclear degrees of freedom. New experimental efforts are now focused on identifying relevant few-photon photoexcitation and dissociation sequences in small gas-phase atoms and molecules by manipulating the light polarization^29–34 or by applying frequency filters.²⁴ Here, we demonstrate the versatility of the latter approach and how it allows one to unravel few-photon paths in pump–probe experiments.³⁴ We first examine the multiple excitation and ionization pathways, which can be disentangled in the simulations by analyzing different contributions for each symmetry of the ionized molecule. We then show how, by manipulating the spectral content of the comb, one could also experimentally select specific sequential ionization paths, and as a consequence, manipulate the photoelectron emission direction.

2 Methodology and computational details

The description of a coherently generated molecular wave packet by interaction of an attosecond pulse or an APT with the hydrogen molecule requires a theoretical method that goes beyond the Born–Oppenheimer approximation to describe both electronic and nuclear dynamics. A full quantum mechanical description of molecular dynamics including all degrees of freedom is only achievable nowadays for the simplest molecules: the hydrogen molecule, its isotopes and cations,³⁵ and even for these targets it remains a computational challenge. We compute the fully correlated two-electron molecular wave function for H₂ with our time-dependent Feshbach Close-Coupling (TDFCC) method, described in detail in ref. 35 and 36. For comprehensive purposes, we provide a brief review of the method and the specific parameters employed for the present simulations. Atomic units are used throughout the following, unless otherwise stated.

The method numerically solves the full dimensional (excluding rotation) time-dependent Schrödinger equation:

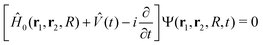where Ĥ₀(r₁,r₂,R) is the non-relativistic Hamiltonian of H₂ containing all electronic and nuclear (vibrational) degrees of freedom, and V̂(t) = (p̂₁ + p̂₂)·Â(t) is the laser-molecule interaction in the velocity gauge. The field-free molecular Hamiltonian Ĥ₀(r₁,r₂,R) can be formally written as:

Ĥ₀(r₁,r₂,R) = T̂(R) + Ĥ_el(r₁,r₂,R) (2)

where T̂(R) = −∇_R²/2μ is the nuclear kinetic energy, μ the reduced mass of the nuclei, and Ĥ_el(r₁,r₂,R) is the electronic Hamiltonian including the nucleus–nucleus repulsion potential term. We expand the time dependent wave function Ψ(r₁,r₂,R,t) in a basis of Born–Oppenheimer (BO) states built from products of electronic and nuclear wave functions. The neutral electronic states are obtained by direct diagonalization of the electronic Hamiltonian in a two-electron configurations basis set. We have employed the Feshbach formalism to calculate the continuum and autoionizing states, by projecting the same electronic Hamiltonian onto two orthogonal sub-spaces containing the resonant and direct components of the wave function. For the electronic continuum states, we use a multichannel [script L]₂ close-coupling procedure to impose the correct asymptotic behavior.³⁷

In order to reproduce common experimental conditions, the molecule is always assumed to be initially in its ground vibronic state, X¹Σ⁺_g(v = 0). The molecule is then irradiated with an attosecond pulse train and a few-femtosecond probe pulse with a central frequency corresponding to the 3rd harmonic of a 800 nm IR pulse. We assume collinear pulses with a polarization direction parallel to the molecular axis. Therefore, the dipole selection rules impose that one-photon absorption paths (more generally, an odd number of absorbed photons) will reach two-electron molecular states of ¹Σ⁺_u symmetry, while an even number of absorbed photons will populate ¹Σ⁺_g states.

For the pulse durations and frequencies here involved, we have checked that convergence is achieved including the six lowest bound sates of ¹Σ⁺_g symmetry and the six lowest ones of ¹Σ⁺_u symmetry. For the electronic continuum, the two lowest ionization thresholds, 1sσ_g and 2pσ_u states of the molecular ion, are included with an expansion in angular momenta for the electron in the continua up to l_max = 7 for both final symmetries ¹Σ⁺_g and ¹Σ⁺_u in the two-electron molecular wave function. For the specific simulations performed in this work, we find that the individual contributions of partial waves with l > 3 for the emitted electron are more than six orders of magnitude smaller than those with l < 3. Embedded in the electronic continuum we have also computed the first two series of autoionizing states, Q₁ (converging to the second ionization threshold) and Q₂ (converging to the third ionization threshold). The two-electron wave functions are built using a configuration interaction procedure using one-electron orbitals resulting from the diagonalization of the full dimensional one-electron molecular Hamiltonian. These one-electron eigenstates are in turn expanded in a basis set of coupled spherical harmonics including angular momenta up to l_max = 16 and 410 B-spline basis functions for the radial components defined in a finite range up to 60 a.u. We have checked that the same accuracy was already reached by including up to 300 B-splines in the radial expansion. Such basis set allows us to properly describe continuum states in the asymptotic region while avoiding unphysical reflections for the electron. The vibrational wave functions (bound and dissociative) result from diagonalizing the nuclear Hamiltonian using the previously computed electronic potential energy curves. We also use B-spline functions for the radial component of the nuclear wave functions, with 240 B-splines defined in a nuclear box of R_max = 12 a.u.

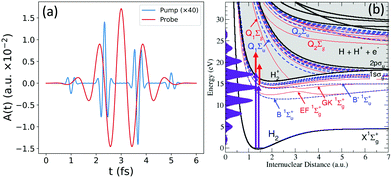
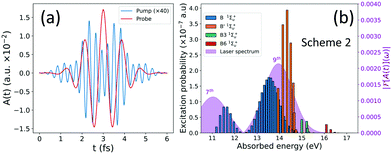
Fig. 1(b) shows the relevant excitation and ionization channels. It includes the ground state X¹Σ⁺_g of the neutral molecule, as well as the bound states (B, B′ and four more) and metastable autoionizing states (Q1 and Q2 series) of ¹Σ⁺_u symmetry in dashed blue lines; the equivalent bound states of ¹Σ⁺_g symmetry (EF, GK and three more bounds and the two lowest Q series) in dashed red; and the two ionization thresholds, 1sσ_g and 2pσ_u, in black full lines.

Fig. 1 (a) Vector potential, A(t), for the attosecond pulse train (APT, in blue) and the 3rd harmonic (red) of a 800 nm IR field. Both pulses are defined with a total duration of 6 fs and intensities of 1.14 × 10⁹ and 3.0 × 10¹¹ W cm⁻², respectively. (b) Energetics and relevant potential energy curves for the hydrogen molecule (see main text for details).

Fig. 1(a) shows the electromagnetic fields that describe our pump–probe scheme, with the attosecond pulse train (APT) in blue and the IR field in red. Fig. 1(b) also depicts the energy comb resulting from the APT in purple shadow, and the red arrows corresponding to the transitions induced by the probe pulse. The APT is generated from an 800 nm IR field and defined with a total duration of 6 fs, leading to an energy comb including up to the 17th harmonic, with a central frequency placed at the 9th harmonic of the train (at 13.95 eV) and an intensity of 1.14 × 10⁹ W cm⁻². We use as a probe pulse the 3rd harmonic (ω = 4.65 eV) of the same 800 nm IR field that generated the APT, with the same total duration of the train, 6 fs, and an intensity of 3 × 10¹¹ W cm⁻² (https://github.com/jfeist/laserfields). The intensity of the probe pulse is chosen to be two orders of magnitude larger than the APT to ensure that the processes that involve the transition with the frequency of the 3rd harmonic can be entirely associated with the action of the probe.

3 Pump–probe scheme

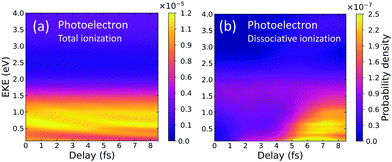
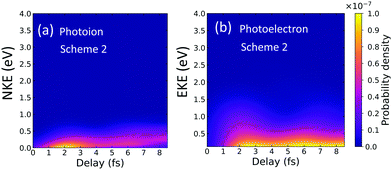
We calculate the energy-differential ionization yields that would be retrieved in the above described pump–probe experiment (depicted in Fig. 1). Several laboratories are nowadays capable of reproducing the spectra of the charged fragments as a function of time delay with attosecond resolution.³

In Fig. 2, we show the photoelectron spectra as a function of the time delay. The y-axis corresponds to the photoelectron kinetic energy and the x-axis to the time delay in femtoseconds (fs). In panel (a), electrons are measured, without distinguishing whether the molecular cation dissociates or remains bounded. In Fig. 2(b), we plot the contribution of the dissociative ionization channel. As can be seen, non-dissociative ionization dominates, being more than two orders of magnitude larger than dissociative ionization. With current coincident detection devices it is still possible to measure this minority channel.⁴ The time-delayed photoelectron spectrum for dissociative ionization, panel (b), shows a significant increase of the yields above 2–3 fs. For a deeper analysis on the origin of these features, we will disentangle the contributions from different final symmetries and cationic states, as well as the corresponding photoions distributions. These are shown in Fig. 3.

Fig. 2 Photoelectron spectra: ionization probabilities as a function of the electron kinetic energy (y-axis) and the time delay between pulses (x-axis). (a) Total ionization probabilities, including contributions from dissociative (H + H⁺ + e⁻) and non-dissociative (H₂⁺ + e⁻) ionization channels. (b) Dissociative ionization probability.

Fig. 3 Dissociative ionization yields (H + H⁺ + e⁻) as a function of the time-delay between pulses (x-axis) and of the kinetic energy of the charged fragments. Left panels: Photoion spectra. Right side panels: Photoelectron spectra. (a) and (b) Total dissociative ionization yields as a function of the kinetic energy of nuclei and electrons, respectively. (c) and (d) Two-photon dissociative ionization for the 1sσ_g state as a function of nuclear and electronic kinetic energies. (e) and (f) Two-photon dissociative ionization for the 2pσ_u state of the ion. (g) and (h) Dissociative ionization for an odd number of absorbed photons.

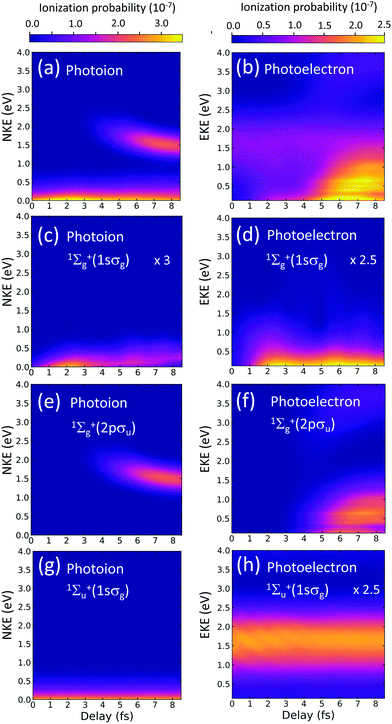
Left panels in Fig. 3 correspond to the photoion energy distributions as a function of the time delay. Right panels are the photoelectron counterpart. In our theoretical approach, the contributions from one- and two-photon absorption paths can be unambiguously unraveled. We separately plot the signal associated with each ionization threshold (1sσ_g and 2pσ_u) for the two optically allowed final symmetries (¹Σ⁺_u can be reached by a one-photon absorption from the ground state and ¹Σ⁺_g is only accessible after absorption of one photon of the harmonics of the comb and one photon from the probe pulse). Panel (a) [(b)] is the result of adding the yields in the three lowest panels in the left [right] column.

Panels (c) and (d) show the respective contributions to the photoion and photoelectron spectra for two-photon dissociative ionization (final symmetry ¹Σ⁺_g) through the 1sσ_g cationic state. Panels (e) and (f) show the two-photon yields associated with the 2pσ_u cationic state, where ionization is solely due to two-photon transitions. And panels (g) and (h) show the contribution for a final ¹Σ⁺_u symmetry, which is only significantly non-zero for the 1sσ_g cationic state.

In the left bottom panel, (g), we can see that the nuclear kinetic energy (NKE) distribution, integrated over all electron energies, is smooth and presents no modulation with the time delay. This time-independent signal would point us out to assume that this signal is mostly due to a one-photon absorption from the APT alone. Therefore, no dynamical information is encoded in these yields. Indeed, the signal corresponds, energetically, to one-photon direct ionization from the ground state after absorption of the 11th harmonic. Lower harmonics in the comb are not energetic enough to lead to dissociative ionization and larger ones are significantly less intense and also less favorable in a vertical transition. The fast decrease of the ionization probability shown in Fig. 3(g) as the NKE increases has been widely described in previous works on one-photon direct ionization.^38,39 In the photoelectron spectra, in panel (h), however, one can see a faint oscillating structure, appearing as stripes at different electron energies, that were totally washed out in the photoion spectra in (g). One could assign these features to interferences arising from one- and three-photon absorption paths, since these paths could optically reach a ¹Σ⁺_u final state. However, any possible three-photon transitions involving one of the harmonics of the comb and the probe pulse or the probe pulse by itself would release electrons at a different energy. These faint oscillations are however related to the population of doubly excited states. We have performed truncated simulations removing the doubly excited states (DES) and observed that these interference patterns completely disappear. We have further checked that they are only visible when both DES series of ¹Σ⁺_u and ¹Σ⁺_g symmetries are present, i.e. as long as any of the two series are absent in the expansion, a smooth photoelectron distribution appears. Consequently, these features are related to probe-induced transitions between the DES and the background continua.

The observable of interest is nevertheless the large signal induced by two-photon absorption paths, since the above-described faint oscillating features would be hardly visible in an eventual experiment. We now focus on analyzing the contributions associated with the second ionization threshold, the 2pσ_u, shown in Fig. 3(e) and (f). Ionization through the 2pσ_u cationic state may result from (i) ionization into the ground state of the cation followed by excitation of the remaining ion, or (ii) excitation into the higher states of ¹Σ⁺_u symmetry followed by ionization into the 2pσ_u electronic continuum. Both sequential paths are energetically possible and hard to distinguish looking at the energy of the fragments, given the relatively wide bandwidths of the pulses. In the first scenario, the 11th harmonic ionizes the molecule leaving behind a nuclear wave packet in the 1sσ_g cationic state, scenario which evolves in time moving towards larger internuclear distances. After approximately 4 fs, the nuclear wave packet reaches internuclear distances at which the energy difference between the 1sσ_g and the 2pσ_u becomes resonant or lower than the frequency of the probe pulse, which occurs for an internuclear distance larger than 3.5 a.u. (see Fig. 1(b)). For the second path, (ii), i.e. excitation following ionization, the 11th harmonic could excite high-lying states, whose potential energy curves are almost parallel to the 1sσ_g as shown in Fig. 1(b) and, after a given delay, the subsequent absorption of a photon from the probe pulse could eject an electron leaving the system into the 2pσ_u ionic state. Further analysis, shown in the next section, is required to unambiguously disentangle these quantum paths.

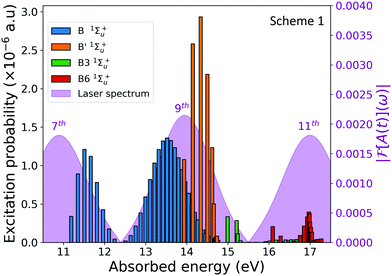
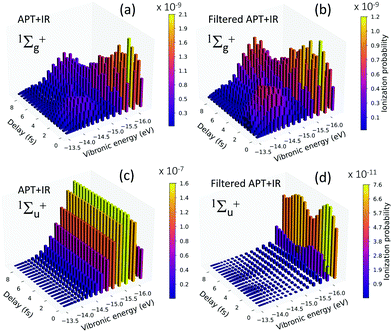
The observation of the two-photon signal associated with the ground state of the cation, plotted in Fig. 3(c) and (d), requires the combined absorption of the APT, more specifically the 7th and 9th harmonic, and the probe pulse. In the excitation process, a molecular wave packet with components from different electronic states is created, but also involves different manifolds of vibrational states within the same electronic state. Experimentally a direct measure of the excitation probabilities is hardly achievable, but the advantage of a full-dimensional theoretical method is that one can easily reproduce the pumped wave packet components that are later traced by the action of the probe. The excitation probabilities are shown in Fig. 4 as a function of the vibronic (vibrational + electronic) energies.

Fig. 4 Excitation probabilities for the ¹Σ⁺_u electronic states. We can distinguish the vibrational progression. Peaked structure results from the energy distribution of the APT comb. The energy distribution of the APT is shown as pink shadows.

The figure shows the vibrational progressions of the singly excited ¹Σ⁺_u states. Only those states with a non negligible population are plotted. As it is shown, the vibrational progression for the B' ¹Σ⁺_u state is solely given by the 9th harmonic, however the vibrational distribution of the B state presents a double peak structure resulting from the transitions induced by the 7th and the 9th harmonics of the APT. The pumped dynamics could be thus viewed as the build-up of two nuclear wave packets evolving in the same B state with different momenta. These complex electron-nuclear dynamics is imprinted in the ionization yields, as shown in the dissociative nuclear components of the 1sσ_g cationic state plotted in Fig. 3(c) and (d). Experimentally, it is not possible to distinguish these different channels in the measured signal, since only the total ionization signals shown in Fig. 3(a) and (b) would be retrieved. However, as already stated, it is possible to introduce frequency filters in order to quench specific quantum paths.

4 Filtering harmonics as a quantum path selective tool

We have simulated an experiment performed with a frequency filter, suppressing the generation of the higher harmonics of the APT. The resulting vector potential of the APT XUV field is shown in Fig. 5(a), together with the resulting excitation probabilities after the filter has been applied (Fig. 5(b)). Introducing an APT where the higher harmonics (>9th) have been filtered out will prevent the one-photon ionization process, while still leading to almost identical excitation probabilities.

Fig. 5 (a) Vector potential A(t) for an attosecond pulse train after applying a frequency filter (blue), and the probe pulse with a frequency of the 3rd harmonic of the generating 800 nm IR field (red). (b) Excitation probabilities for the ¹Σ⁺_u electronic states for the filtered pulse.

We then analyze the observable that would be measured in an eventual experiment with the filtered pulse. Fig. 6 shows the photoion and photoelectron spectra as a function of the time-delay between the pulses. We now show only the total yields, because we have checked that they are entirely dominated by the ¹Σ⁺_g(1sσ_g) states, the only ones significantly contributing to ionization. ¹Σ⁺_u(1sσ_g) and ¹Σ⁺_g(2pσ_u) channels are orders of magnitude smaller. The most striking feature that can be extracted from Fig. 6 is that these spectra match, almost exactly, the distributions shown in Fig. 3(c) and (d). From this comparison, we can first conclude that ionization into the 2pσ_u state in the scheme with the unfiltered pulse can only be due to the excitation of the cation after ionization. Furthermore, these results demonstrate that by filtering the high harmonics, we are effectively selecting ionization into a specific channel populated through a given quantum path, the two-photon sequential path with excitation by the pump followed by ionization into the cationic ground state by the probe.

Fig. 6 Photoion (a) and photoelectron (b) distributions for dissociative ionization as a function of the time-delay for a pump–probe scheme using a frequency filter.

As a solid numerical check to ensure that these distributions are solely due to excitation by the pump and subsequent ionization from the probe, we carried out simulations with the full APT but removing the continuum–continuum couplings, thus forcing ionization by the probe being only possible through transitions from the excited states. The resulting probabilities are almost identical to the ones shown in Fig. 6. The dominance of the sequential ionization–excitation versus excitation–ionization that was observed in the first scheme with the unfiltered pulse, in Fig. 3(a) and (b), can be understood in terms of the dominant configurations that define the molecular wave function. In brief, in the ground state of the molecule the 1sσ_g1sσ_g configuration dominates. In the ionization process ending into the ground state of the cation, the dominant configuration is [1sσ_g,l = 1], and exciting the remaining bound electron from the 1sσ_g to the 2pσ_u is a very probable transition that leads to a [2pσ_u,l = 1] configuration. However, the sequential excitation–ionization process would involve excitation into the bound electronic states with dominant configurations of the type 1sσ_gnpσ_u, with n ≥ 2, and the subsequent ionization event to reach the configuration [2pσ_u,l = 1]. For a transition through the first excited state, where the 1sσ_g2pσ_u configuration dominates, ionization into the [2pσ_u,l = 1] continuum would be still significant. However, this channel is not energetically open. It is only open for the higher states, with n > 2, but ionization would then imply a two-active electronic transition, i.e. would be associated to the electron correlation term, and consequently lead to much lower signal, almost negligible as shown in the present results.

The suppression of this specific one- and two-photon paths in the ionization process, allowing for a direct probe of the excited dynamics by filtering the high harmonics, is also measurable in the non-dissociative and total ionization yields (see appendix). Moreover, it can be also used to manipulate the photoelectron emission direction. As it is known and demonstrated in several previous experimental and theoretical works,^40,41 the light-induced ionization leading to final channels with different inversion symmetry allows for a certain degree of control on the photoelectron emission direction. The photoelectron angular distributions resulting from a coherent superposition of one- and two-photon absorption quantum paths can induce an asymmetry in the electron emission along the light polarization vector. This asymmetric photoelectron emission is shown in the left panels of Fig. 7 (for the pump–probe Scheme 1, with the unfiltered pulse). The resulting asymmetry depends on both the kinetic energy sharing between electrons and nuclei and on the time delay between the pulses. In Fig. 7, we pick a specific energy sharing for the electron (0.5 eV) and the nuclei (0.2 eV), and vary the time delay between the pump and the probe. Looking at Fig. 3, it can be seen that we are selecting a region where only the first ionization threshold contributes (1sσ_g), but the two-electron final wave packet has contributions from both ¹Σ⁺_g and ¹Σ⁺_u symmetries. In other words, different angular momenta are contributing to the same final state, which results in an asymmetric electron emission with respect to the plane perpendicular to the molecular axis. More interestingly, since the relative contribution of the states with different angular momentum varies with the time delay, the photoelectron angular distribution is also modified. The suppression of the higher harmonics signal will lead to a significant variation on the resulting photoelectron emission asymmetry, even reaching an almost totally symmetric electron distribution when the transmission of the high harmonics is fully turned off. The corresponding molecular frame angular distributions for the pump–probe Scheme 2, where the harmonics above the 9th has been filtered thus suppressing the one-photon ionization path, are symmetric as shown in the right panels in Fig. 7, for the same energy sharing and time delays.

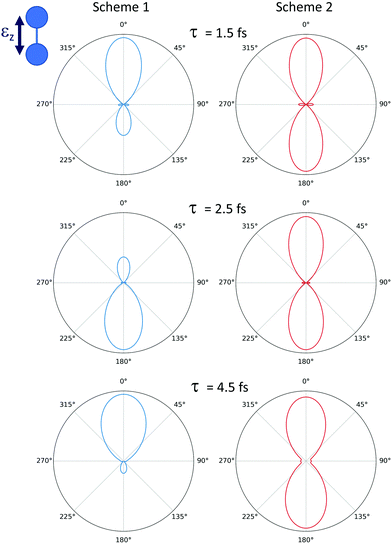Fig. 7 Photoelectron angular distribution for dissociative ionization of H₂, leading to a final electron energy of 0.5 eV and a nuclear kinetic energy of 0.2 eV. Left column: Pump–probe Scheme 1 (as depicted in Fig. 1). Right column: Pump–probe Scheme 2 using the XUV spectral filter for the APT. Each row corresponds to a different time delay indicated in the figure.

5 Conclusion

We have simulated a pump–probe scheme employing attosecond pulse train as a pump and a few-fs pulse built with the 3rd harmonic of the generating 800 nm IR field. Harmonic filtering of the APT has proven to be an efficient strategy to uncover the dominance of specific sequential paths in two-photon ionization, as well as a reliable tool to manipulate ionization yields and the photoelectron direction emission. We have shown that the use of a frequency filter makes it possible to experimentally unravel the dominance of ionization–excitation versus excitation–ionization. The later minority channel can be nevertheless enhanced by introducing an harmonic filter, allowing us to recover the time-delay dependencies of the ionization yields that capture the electron-nuclear dynamics induced in the excited wave packet. Harmonic filtering thus acts as a selective tool to enhance the time-delay varying yields that probe the system. It suppresses the ionization channels that would otherwise prevent the extraction of the dynamical information in an experimental setup.

Conflicts of interest

There are no conflicts to declare.

Appendix

Non-dissociative and total ionization yields

The dynamics of the wave packet created in the excited molecule is also captured in the total ionization yields and in the resulting vibrational progressions of the cation (H₂⁺) as a function of the time delay between the pump and the probe pulses. Fig. 8 shows the ionization probability of leaving the cation in each vibrational state as a function of the time-delay between the pulses. Panels (a) and (c) are the vibrationally-resolved non-dissociative ionization (NDI) probabilities for the pump–probe Scheme 1 (unfiltered train) for the final symmetries ¹Σ⁺_g (a) and ¹Σ⁺_u (c), respectively. As discussed in the main text, in our pump–probe scheme, the ionization yields are entirely dominated by the one-photon absorption (¹Σ⁺_u in panel c) being two orders of magnitude larger than the two-photon ionization yields (¹Σ⁺_g in panel a). Fig. 8(c) shows the expected distribution for one-photon direct ionization of H₂, with a maximum value for v = 2, i.e. the direct vertical transition from the ground state of the neutral molecule.

Fig. 8 Non-dissociative ionization (NDI) probability as a function of the absolute energies for the vibrational bound states of the cation and as a function of time-delay. Left panels: Results for the pump–probe scheme defined in the main text. (a) NDI for a final ¹Σ⁺_g symmetry, and (c) for a final ¹Σ⁺_u symmetry. Right panels: Results for the filtered pump–probe (Scheme 2 in the main text). (b) NDI for a final ¹Σ⁺_g symmetry, and (d) for a final ¹Σ⁺_u symmetry.

Fig. 8(b) and (d) are the results for Scheme 2, after filtering the higher harmonics (above the 9th harmonic). Consequently, the ¹Σ⁺_g is now two orders of magnitude larger than the ¹Σ⁺_u, since the one-photon ionization path is suppressed. Panels (a) and (b) are mostly identical, i.e. the dynamics that would be measured in an experiment with the filtered train in combination with the probe pulse is equivalent to retrieve the two-photon sequential path where ionization strictly follows the XUV-excitation.

More interestingly, these vibrational progressions vary in time. At short time delays, a double-peak distribution appears, because the absorption of the probe is transferring the nuclear momenta of the excited wave packet (see Fig. 4) into the cation. There is a wider distribution for the higher vibrational states, v = 10–15 (with absolute energies around −14.0 eV), which corresponds to transitions from the higher nuclear momentum components in the B state and the vibrational components in the B′ state. There is also a peak at lower vibrational states, populating v = 0–4, which corresponds to the probe absorption from the less energetic nuclear wave packet sitting in the B state and shown in Fig. 4. For larger time delays, however, there is a more complex modulation in the vibrational progression, since we have the faster motion of the nuclear wave packet components in the B state (resulting from the 9th harmonic) and the slower motion associated with the nuclear wave packet components in the B state (from the 7th harmonic) and in the B′ state (from the 7th harmonic).

The enhancement of excitation–ionization with respect to the ionization–excitation process in the pump–probe scheme using a frequency filter is also nicely reproduced in the total ionization yields shown in Fig. 9.

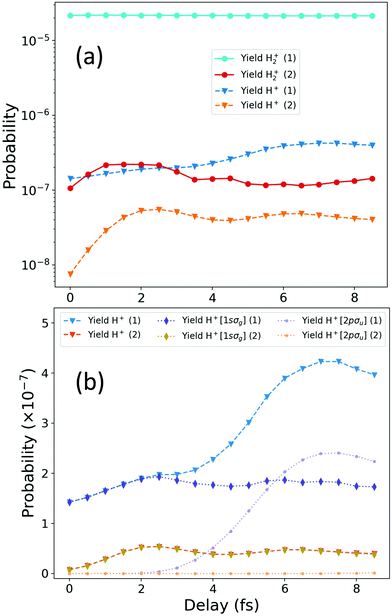Fig. 9 Total ionization yields as a function of the time delay between the APT and the probe pulse for the scheme with the unfiltered pulse (Scheme 1, blue lines labeled in the legends as ref. 1) and the scheme using the APT with the frequency filter (Scheme 2, warm-coloured lines labeled in the legends as ref. 2). (a) Total non-dissociative (H₂⁺) and dissociative (H + H⁺) ionization signal for each scheme. (b) Total dissociative ionization yields (H + H⁺) are plotted again for each scheme in linear scale, together with the contributions from each cationic state.

Fig. 9 shows the ionization yields as a function of the time delay between the APT and the probe pulse, for Scheme 1 (unfiltered APT) and Scheme 2 (filtered APT). In panel (a) of Fig. 9, we show in blue-coloured lines the non-dissociative [H₂⁺(1)] and dissociative [H⁺(1)] ionization yields for the unfiltered APT, Scheme 1. The warm-coloured lines, labeled as [[H₂⁺(2)] and [H⁺(2)]] correspond to the NDI and dissociative ionization for Scheme 2, i.e. using the XUV spectral filter. The most noticeable feature is the constant value of the NDI yield for the unfiltered pump–probe scheme, which necessarily implies that the signal dominated by the one-photon absorption from the ground state of the neutral molecule can only be due to the APT alone. Therefore, no dynamical information is encoded in the NDI channel, which is, indeed, two orders of magnitude larger than the dissociative one. This dominance could be partly predicted by simply looking at Fig. 1(a), where it is clear that the 11th harmonic of the APT ionizes the molecule, since its energy is almost perfectly resonant with the vertical transition from the neutral ground state. In high contrast, for Scheme 2, the 11th harmonic is fully filtered out, and as a result the one-photon absorption from the ground is energetically inaccessible for the APT and ionization is only possible through a two-photon absorption involving both the APT and the probe pulse. As a consequence, the ionization rates are two orders of magnitude lower than for Scheme 1, but we can now retrieve from the photoion yields, either H⁺ and H₂⁺, a direct probe of the excited states dynamics.

The dissociative ionization yields for both schemes show a modulation in time, although slightly different for each scheme, which already suggests that different quantum paths are contributing. In Fig. 9(b), we further disentangle the contribution of the different ionization thresholds to the dissociative ionization probabilities. Notice that for panel (a) a logarithmic time scale was employed, but a linear scale is used in panel (b), so the significant increase of the dissociative ionization yields for scheme 1, for time delays larger than 3 fs, is more visible. We again use cold-coloured lines for Scheme 1 and warm colours for Scheme 2. Triangle symbols correspond to the total dissociative ionization. Dotted lines with diamonds are the yields associated with the first ionization threshold and dotted lines with circles are the yields for ionization associated to the second ionization threshold, the purely dissociative 2pσ_u state of the cation. We first notice that the large increase after 3 fs only appears for Scheme 1, being entirely due to ionization through the 2pσ_u threshold, as discussed in the main manuscript from the analysis of the energy-differential yields plotted in Fig. 3. At short time delays, τ < 2fs, ionization through the 2pσ_u is strictly zero, but at larger delays it increases and even overcomes the ionization yield associated with the ground state of the cation, 1sσ_g (bluish diamonds) at around 6 fs, reaching a maximum value around 7 fs of delay. For Scheme 2, i.e. for the filtered APT, ionization entirely proceeds leaving the cation in its ground state, with zero probability of ionizing into excited states of the cation at any time delay. Since we already know that the excitation dynamics pumped by the train was unchanged with the presence of the filter, it is clear that the opening of the second ionization threshold after a given delay is given by a probe-induced transition between continuum states of the molecule, which are only possible after one-photon ionization only accessible by the APT in Scheme 1. The APT ionizes the molecule leaving the ion in its ground state of the cation. After a given delay (τ > 2 fs) the probe pulse can further excite the bound electron into the 2pσ_u state of the cation. This process is energetically accessible as long as the nuclear wave packet created upon ionization into the 1sσ_g cationic state has enough time to move towards larger internuclear distances, such that the second photon can be absorbed for a molecular geometry for which the energy gap between 1sσ_g and 2pσ_u is smaller. Fig. 9(b) already reveals that the modulation of the ionization probabilities with the time delay captured in the Scheme 2, which would be experimentally achievable, follow the same modulations as the dissociative ionization yield for the 1sσ_g cationic state for Scheme 1.

Acknowledgements

Calculations were performed at the Mare Nostrum Supercomputer of the Spanish Supercomputing Network (BSC-RES) and the Centro de Computación Científica de la Universidad Autónoma de Madrid (CCC-UAM). We thank P. Ranitovic for interesting discussions. Work supported by the European COST Action AttoChem CA18222, the French National Research Agency (ANR) in the frame of “the Investments for the futures” Programme IdEx Bordeaux – LAPHIA (ANR-10-IDEX-03-02), and the Spanish Ministry of Science and Innovation MICINN through the projects PDI2019-105458RB-I00, the “Severo Ochoa” Programme for Centres of Excellence in R&D (SEV-2016-0686) and the “María de Maeztu” Programme for Units of Excellence in R&D (CEX2018-000805-M).

Notes and references

1. F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. De Camillis, S. Anumula, F. Frassetto, L. Poletto, A. Palacios, P. Decleva, J. B. Greenwood, F. Martín and M. Nisoli, Science, 2014, 346, 336–339.
2. F. Calegari, G. Sansone, S. Stagira, C. Vozzi and M. Nisoli, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 062001.
3. M. Nisoli, P. Decleva, F. Calegari, A. Palacios and F. Martín, Chem. Rev., 2017, 117, 10760–10825.
4. L. Cattaneo, J. Vos, R. Y. Bello, A. Palacios, S. Heuser, L. Pedrelli, M. Lucchini, C. Cirelli, F. Martín and U. Keller, Nat. Phys., 2018, 14, 733–738.
5. A. Palacios and F. Martín, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1430.
6. E. Goulielmakis, M. Schultze, M. Hofstetter, V. S. Yakovlev, J. Gagnon, M. Uiberacker, A. L. Aquila, E. M. Gullikson, D. T. Attwood, R. Kienberger, F. Krausz and U. Kleineberg, Science, 2008, 320, 1614–1617.
7. P. M. Paul, E. S. Toma, P. Breger, G. Mullot, F. Augé, P. Balcou, H. G. Muller and P. Agostini, Science, 2001, 292, 1689–1692.
8. M. Isinger, R. J. Squibb, D. Busto, S. Zhong, A. Harth, D. Kroon, S. Nandi, C. L. Arnold, M. Miranda, J. M. Dahlström, E. Lindroth, R. Feifel, M. Gisselbrecht and A. L'Huillier, Science, 2017, 358, 893–896.
9. I. Pupeza, C. Zhang, M. Högner and J. Ye, Nat. Photonics, 2021, 15, 175–186.
10. S. Eich, A. Stange, A. Carr, J. Urbancic, T. Popmintchev, M. Wiesenmayer, K. Jansen, A. Ruffing, S. Jakobs, T. Rohwer, S. Hellmann, C. Chen, P. Matyba, L. Kipp, K. Rossnagel, M. Bauer, M. Murnane, H. Kapteyn, S. Mathias and M. Aeschlimann, J. Electron Spectrosc. Relat. Phenom., 2014, 195, 231–236.
11. H. Wang, Y. Xu, S. Ulonska, J. S. Robinson, P. Ranitovic and R. A. Kaindl, Nat. Commun., 2015, 6, 7459.
12. T. Fortier and E. Baumann, Commun. Phys., 2019, 2, 153.
13. L. Drescher, O. Kornilov, T. Witting, V. Shokeen, M. J. J. Vrakking and B. Schütte, Nat. Photonics, 2021, 15, 263–266.
14. E. Mansten, J. M. Dahlström, J. Mauritsson, T. Ruchon, A. L'Huillier, J. Tate, M. B. Gaarde, P. Eckle, A. Guandalini, M. Holler, F. Schapper, L. Gallmann and U. Keller, Phys. Rev. Lett., 2009, 102, 083002.
15. A. A. Eilanlou, Y. Nabekawa, K. L. Ishikawa, H. Takahashi, E. J. Takahashi and K. Midorikawa, Conference on Lasers and Electro-Optics 2010, Washington, DC, 2010, p. JThE121.
16. P. Raith, C. Ott, C. P. Anderson, A. Kaldun, K. Meyer, M. Laux, Y. Zhang and T. Pfeifer, Appl. Phys. Lett., 2012, 100, 121104.
17. J. Metje, M. Borgwardt, A. Moguilevski, A. Kothe, N. Engel, M. Wilke, R. Al-Obaidi, D. Tolksdorf, A. Firsov, M. Brzhezinskaya, A. Erko, I. Y. Kiyan and E. F. Aziz, Opt. Express, 2014, 22, 10747.
18. N. Fabris, P. Miotti, F. Frassetto and L. Poletto, Appl. Sci., 2019, 9, 2502.
19. E. Gustafsson, T. Ruchon, M. Swoboda, T. Remetter, E. Pourtal, R. López-Martens, P. Balcou and A. L'Huillier, Opt. Lett., 2007, 32, 1353.
20. M. Hartmann, V. Stooß, P. Birk, G. Borisova, C. Ott and T. Pfeifer, Opt. Lett., 2019, 44, 4749.
21. A. Guggenmos, Y. Cui, S. Heinrich and U. Kleineberg, Appl. Sci., 2018, 8, 2503.
22. M. Hofstetter, M. Schultze, M. Fieß, B. Dennhardt, A. Guggenmos, J. Gagnon, V. S. Yakovlev, E. Goulielmakis, R. Kienberger, E. M. Gullikson, F. Krausz and U. Kleineberg, Opt. Express, 2011, 19, 1767.
23. P. Siffalovic, M. Drescher, M. Spieweck, T. Wiesenthal, Y. C. Lim, R. Weidner, A. Elizarov and U. Heinzmann, Rev. Sci. Instrum., 2001, 72, 30–35.
24. I. Makos, I. Orfanos, A. Nayak, J. Peschel, B. Major, I. Liontos, E. Skantzakis, N. Papadakis, C. Kalpouzos, M. Dumergue, S. Kühn, K. Varju, P. Johnsson, A. L'Huillier, P. Tzallas and D. Charalambidis, Sci. Rep., 2020, 10, 3759.
25. X. Zhou, P. Ranitovic, C. W. Hogle, J. H. D. Eland, H. C. Kapteyn and M. M. Murnane, Nat. Phys., 2012, 8, 232–237.
26. P. Ranitovic, C. W. Hogle, P. Riviere, A. Palacios, X.-M. Tong, N. Toshima, A. Gonzalez-Castrillo, L. Martin, F. Martín, M. M. Murnane and H. Kapteyn, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 912–917.
27. F. P. Sturm, X. M. Tong, A. Palacios, T. W. Wright, I. Zalyubovskaya, D. Ray, N. Shivaram, F. Martín, A. Belkacem, P. Ranitovic and T. Weber, Phys. Rev. A, 2017, 95, 012501.
28. L. Martin, R. Y. Bello, C. W. Hogle, A. Palacios, X. M. Tong, J. L. Sanz-Vicario, T. Jahnke, M. Schöffler, R. Dörner, T. Weber, F. Martín, H. C. Kapteyn, M. M. Murnane and P. Ranitovic, Phys. Rev. A, 2018, 97, 062508.
29. M. Meyer, D. Cubaynes, D. Glijer, J. Dardis, P. Hayden, P. Hough, V. Richardson, E. T. Kennedy, J. T. Costello, P. Radcliffe, S. Düsterer, A. Azima, W. B. Li, H. Redlin, J. Feldhaus, R. Taïeb, A. Maquet, A. N. Grum-Grzhimailo, E. V. Gryzlova and S. I. Strakhova, Phys. Rev. Lett., 2008, 101, 193002.
30. A. Tóth, S. Borbély, G. Z. Kiss, G. J. Halász and A. Vibók, J. Phys. Chem. A, 2016, 120, 9411–9421.
31. A. Tóth, S. Borbély, G. J. Halász and A. Vibók, Chem. Phys. Lett., 2017, 683, 567–572.
32. A. A. Lutman, J. P. MacArthur, M. Ilchen, A. O. Lindahl, J. Buck, R. N. Coffee, G. L. Dakovski, L. Dammann, Y. Ding, H. A. Dürr, L. Glaser, J. Grünert, G. Hartmann, N. Hartmann, D. Higley, K. Hirsch, Y. I. Levashov, A. Marinelli, T. Maxwell, A. Mitra, S. Moeller, T. Osipov, F. Peters, M. Planas, I. Shevchuk, W. F. Schlotter, F. Scholz, J. Seltmann, J. Viefhaus, P. Walter, Z. R. Wolf, Z. Huang and H.-D. Nuhn, Nat. Photonics, 2016, 10, 468–472.
33. D. I. R. Boll, L. Martini, O. A. Fojón and A. Palacios, Phys. Rev. A, 2020, 101, 013428.
34. D. Slaughter, F. Sturm, R. Bello, K. Larsen, N. Shivaram, C. W. McCurdy, R. Lucchese, L. Martin, C. Hogle, M. Murnane, H. C. Kapteyn, P. Ranitovic and T. Weber, arXiv:2106.09014, 2021.
35. A. Palacios, J. L. Sanz-Vicario and F. Martín, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 242001.
36. A. Palacios, S. Barmaki, H. Bachau and F. Martín, Phys. Rev. A: At., Mol., Opt. Phys., 2005, 71, 063405.
37. M. Cortes and F. Martín, J. Phys. B: At., Mol. Opt. Phys., 1994, 27, 5741–5760.
38. F. Martín, J. Phys. B: At., Mol. Opt. Phys., 1999, 32, R197–R231.
39. A. Palacios, J. Feist, A. González-Castrillo, J. L. Sanz-Vicario and F. Martín, ChemPhysChem, 2013, 14, 1456–1463.
40. G. Sansone, F. Kelkensberg, J. F. Pérez-Torres, F. Morales, M. F. Kling, W. Siu, O. Ghafur, P. Johnsson, M. Swoboda, E. Benedetti, F. Ferrari, F. Lépine, J. L. Sanz-Vicario, S. Zherebtsov, I. Znakovskaya, A. L'Huillier, M. Y. Ivanov, M. Nisoli, F. Martín and M. J. J. Vrakking, Nature, 2010, 465, 763–766.
41. R. Y. Bello, F. Martín and A. Palacios, Faraday Discuss., 2021, 228, 378–393.

---