Two-dimensional self-assembly of benzotriazole on an inert substrate

Abstract

The ultra-high vacuum (UHV) room temperature adsorption of benzotriazole (BTAH), a well-known corrosion inhibitor for copper, has been investigated on the pristine Au(111) surface using a combination of surface sensitive techniques. The dimensionality of the molecule is reduced from the 3D crystal structure to a 2-dimensional surface confinement, which induces the formation of hydrogen bonded 1-dimensional molecular chains consisting of alternating pro-S and pro-R enantiomers mainly. The 0-dimensional system is characteristic of gas-phase BTAH, which undergoes a tautomeric equilibrium, with consequences for the resulting adsorbed species. The balance between hydrogen bonding, inter-chain van der Waals interactions and surface–molecule interactions, and the correlation with the dimensionality of the system, are discussed in light of the experimental results and a computational description of the observed features.

---

1. Introduction

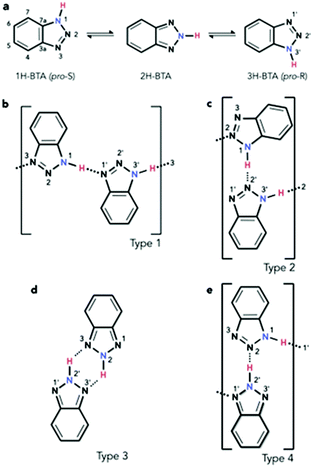
The investigation of molecules adsorbed on a surface allows the properties of systems of reduced dimensionality to be addressed, which can be rather different from those of a bulk material such as in the crystal phase.¹ Moreover, the use of unreactive substrates allows one to focus attention on lateral molecule–molecule interactions, whilst lessening the significance of molecule–surface interactions. The delicate balance of these can lead to self-assembly processes, for which a detailed understanding of both the intermolecular and the molecule–surface interactions is fundamental. Among the many interesting features of self-assembly,² one of particular interest is the potential formation of molecular chains to act as organic wires,³ especially over electronically decoupled substrates in the two-dimensional phase.⁴ An example of such chains in the bulk phase is obtained by imidazole moieties which can assemble into linear structures.⁵ In the case of benzotriazole (BTAH), a well-known corrosion inhibitor for copper and copper alloys in particular,⁶ the dimensionality of the system can be controlled by appropriately selecting the relevant experimental conditions. This may allow for a transition from a 3-dimensional crystal packing, 3D, as in the solid phase of pure BTAH, to a 2D confinement when adsorbed on an inert substrate. Gas phase BTAH, which occurs when the solid is sublimed, can be considered 0-dimensional.

In the condensed phase, BTAH exists mainly in the 1H-BTA (or the equivalent 3H-BTA) form (see Scheme 1 for numbering system of atoms), and 2D confinement of this species introduces chirality. Hence, in this respect, BTAH is considered a prochiral molecule. However, interchange of the two equivalent enantiomers is possible via the tautomeric equilibrium involving the 2H-BTA species (favoured in the gas phase), as shown in Scheme 1a.⁷ The equilibrium is defined as a balanced annular tautomerism, as both tautomers have similar energies.^7e Therefore, the determination of which is the prevalent species in 2D, and how the equilibrium might be shifted to one side or the other, is non-trivial. System dimensionality can be further reduced to 1-dimensional (1D) chains resulting from alternating enantiomers. Indeed, as illustrated in Scheme 1b, pro-S and pro-R enantiomers‡ can alternate by connecting through a N₁–H⋯N′₁ hydrogen bond (hereafter type 1 linkage), where in this case the N₁ atom belongs to the pro-S enantiomer, whereas the N′₁ belongs to the pro-R. This unit can propagate to form a 1D chain through an equivalent N′₃–H⋯N₃ linkage. Scheme 1c describes a N₁–H⋯N′₂ linkage; the resulting unit can propagate through an equivalent N′₃–H⋯N₂ linkage, forming a type 2 chain. A type 3 unit is characterised by two equivalent linkages, N₂–H⋯N′₃ and N′₂–H⋯N₃. In principle, the latter unit is better considered as a dimer which allows for propagation by succession of dimers forming a double row stabilised by weaker N′⋯H–C hydrogen bonding interactions, rather than a N–H⋯N′ hydrogen bonded chain. Moreover, the dimer is formed by two 2H-BTA molecules, and even though the tautomer is achiral, the dimer itself is not. A homochiral dimeric arrangement constituted by two pro-S(pro-R) molecules (not shown), connected by two equivalent N₁–H⋯N′₂ and N′₃–H⋯N₂ in the case of the pro-S enantiomer, will show similar characteristics to the type 3 dimer. A type 4 unit (Scheme 1e) is formed by a 1H-BTA and a 2H-BTA molecule connected through a N₂⋯H–N′₂ linkage. Although chain propagation through a N₁–H⋯N′₁ linkage and additional N′⋯H–C interactions is possible, this is very likely sterically hindered. Note that for type 1 chains, N₁–H⋯N′₁ links coupled by N′₃–H⋯N₃ links (reading from left to right) can become the equivalent N′₁–H⋯N₁ links coupled by N₃–H⋯N′₃ links (reading from right to left) by a simple proton transfer along the chain. With this change, the molecules have switched chirality so that the N′ atoms now belong to pro-S enantiomers and the N atoms to pro-R enantiomers. This is equivalent to a 180° rotation of the chain around the surface normal. In type 2 chains, a similar proton transfer leads to the inequivalent, achiral chain N₂–H⋯N′₃ links coupled by N′₂–H⋯N₁ links, in which case all molecules become the achiral 2H-BTA tautomer. In type 3, the proton transfer around the N₄H₂ six-membered ring leads to the equivalent description as N₃–H⋯N′₂ coupled by N′₂–H⋯N₂, which changes the type of tautomer, although the chirality of the dimer is not affected. In type 4, the proton transfer on the N′₂–H⋯N₂ linkage leads to a swap of the tautomers, whilst preserving the chirality. Although the Au(111) surface is often considered as an inert substrate, benzotriazole has been reported to act as a weak ligand in Au(I)-catalysed reactions,⁸ and 1,2,3-triazole has been reported to coordinate with colloidal gold nanoparticles.⁹ Therefore, some interaction with the azole moiety can be expected also for the Au(111) surface, especially at defective sites.

Scheme 1 Benzotriazole (C₆H₅N₃, BTAH) chemical structure and tautomeric equilibrium (a). Some of the possible basic dimeric structures based on hydrogen bonds: (b) the N₁–H⋯N′₁ linkage, (c) the N₁–H⋯N′₂ linkage, (d) the N₃⋯H–N′₂ + N₂–H⋯N′₃ double linkage, and (e) the N′₂–H⋯N₂ linkage. Atoms are labelled for ease of description and discussion.

Here, the adsorption behaviour of BTAH on the pristine Au(111) single crystal surface in a UHV (ultra-high vacuum) environment, using complementary surface sensitive techniques, is presented and discussed. Adsorption models are proposed based on the results obtained by Scanning Tunnelling Microscopy (STM), High Resolution Electron Energy Loss Spectroscopy (HREELS), X-ray Photoelectron Spectroscopy (XPS), Near Edge X-ray Absorption Fine Structure spectroscopy (NEXAFS), and theoretical investigations employing Density Functional Theory (DFT) calculations. This study highlights the subtle balance between intermolecular interactions (hydrogen bonding and van der Waals (vdW) interactions), and molecule–surface interactions responsible for the condensation and supramolecular organisation of benzotriazole on a non-reactive substrate. Specifically, weak molecule–surface interactions play an important role in stabilising the different tautomers. Hence, the rationalisation of the molecule–molecule and adsorbate–metal interactions and the characterisation of the arrangement of the different isomers become crucial for understanding the BTAH tautomeric equilibria and inferring dimensional controllability.

2. Results and discussion

2.1. Experimental

In Fig. 1, vibrational spectra recorded following BTAH deposition on Au(111) to saturation coverage and subsequent annealing are reported. A typical spectrum collected following BTAH adsorption at room temperature, Fig. 1 (black curve), shows only the vibrations generated by an out-of-plane buckling mode of the full molecule (ca. 275 cm⁻¹), 6- and 5-membered rings out-of-plane modes (ca. 415 cm⁻¹ and ca. 505 cm⁻¹ respectively), and an intense vibration at ca. 745 cm⁻¹ assigned to the C–H in phase out-of-plane bending mode (wagging), with a shoulder to the lower energy side due to a N₁–H out of plane vibration (ca. 690 cm⁻¹). A very weak C–N stretch is seen at ca. 1270 cm⁻¹. The observation of these modes, together with the absence of a N₁–H stretching mode (expected at ca. 3500 cm⁻¹ (ref. 7g)), and a very weak C–H stretching mode (ca. 3065 cm⁻¹), are an indication of parallel adsorption. Under the surface selection rule, the C–H and the N₁–H stretch would be largely dipole inactive, being parallel to the metal surface for a flat-lying molecule. Moreover, all other vibrations are expected to be very weak when compared to the out-of-plane modes. Spectral evolution upon annealing shows that after heating to 353 K, the 400–500 cm⁻¹ region changes in a way that the 6-membered ring torsion, 415 cm⁻¹, decreases in intensity faster than the out-of-plane mode (505 cm⁻¹). A new peak appears at ca. 980 cm⁻¹, attributed to stretches of the triazo group, coupled with an out of plane vibration of H-bonded N₁–H. The peak at ca. 1590 cm⁻¹ attributed to an in plane bending of a hydrogen bonded N₁H increases in intensity. The CH stretch at ca. 3075 cm⁻¹ also becomes more pronounced.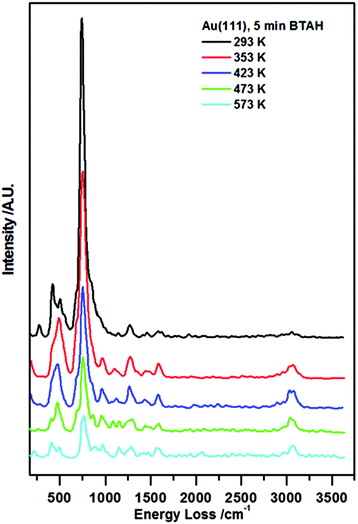

Fig. 1 Enhanced HREEL spectra of the as prepared BTAH on clean Au(111) and spectral evolution with annealing.

Following the other annealing steps, all signals decrease in intensity up to 573 K, and then disappear. The relative change of the ν(C–H)/ω(C–H) ratio with annealing temperatures may indicate reorganisation of the molecular layer at first, and then the tendency of the molecules to become more strongly adsorbed at step edges and aligned much more upright at extremely low coverage.^10,11

The molecular orientation and electronic structure of BTAH/Au(111) at saturation coverage, following adsorption at room temperature and without annealing, were also assessed via NEXAFS spectroscopy (Fig. 2). The fine structure of the π* resonance centred at ca. 400 eV photon energy (PE), with maxima at ca. 399.2, 399.9, 401.4 and 402.3 eV, differs from the one recorded for BTAH adsorbed on Cu(100),¹² and ZnO(101̄0),^1,3 which were ascribed to chemisorption of benzotriazolate species through one or two nitrogen atoms at the azole end. In the case of BTAH on Au(111), the position of the π* resonance states may be related to the formation of hydrogen bonded structures as discussed below. The features above ca. 405 eV are attributed to σ* resonances. The angular dependency of both π* and σ* resonances indicates that the molecular plane lies parallel or perhaps at a very small angle with the metal surface.^12,13

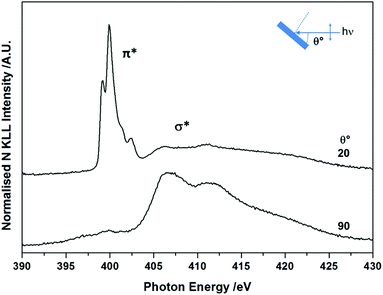Fig. 2 As prepared angular dependent NEXAFS N K-edge spectra at saturation coverage, collected at 298 K.

XPS measurements (see ESI2†) confirmed that BTAH adsorbs intact on the Au(111) surface upon dosing at room temperature. In fact, the N 1s region shows a signal which is best fitted with two Gaussian–Lorentzian (80/20) peaks with maxima at 400.4 eV and 399.4 eV (FWHM 0.85 eV) and an area ratio of 1.7 : 1 (expected 2 : 1). The two components represent C–N and N–H environments respectively.^14,15 Likewise, the C 1s region is characterised by a signal which is best fitted with two Gaussian–Lorentzian (80/20) peaks with maxima at 285.3 eV and 284.3 eV (FWHM 0.68 eV) and an area ratio of 1 : 2.2 (expected 1 : 2). The two components are attributed to C–N and C–C environments respectively.^14,15

Room temperature STM images of the saturated BTAH/Au(111) system show merely streaky features over the herringbone surface reconstruction due to the high mobility of the BTAH molecules. This implies that the overlayer is only weakly physisorbed. As a comparison, BTAH adsorbs on the Cu(111) surface as deprotonated and upright species, in the form of Cu(BTA)₂ and CuBTA.^10,11 In the case of the Cu(111) surface, temperature programmed desorption shows that a saturated monolayer is stable up to ca. 600 K when desorption occurs.¹¹ On Au(111), which exhibits the typical (22 × √3) reconstruction before dosing (Fig. S3.1†), ordered regions are observed by STM if a saturated layer prepared at 293 K is rapidly cooled to liquid nitrogen temperature (77 K) and subsequently imaged. The surface (Fig. 3a) is then characterised by areas of partial ordering and molecular features showing a tendency to organise in rows. Molecular features typically have rather elliptical shapes, perhaps pointed towards one end, with a size of ca. 0.7 × 0.5 nm. These measured dimensions compare well with the calculated ones for a gas-phase BTAH molecule.^10,11 However, there is no evident orientational relationship between the molecular axes and the crystallographic orientation of the surface. Molecules with a brighter appearance are considered to be adsorbed on the ridges of the herringbone reconstruction, which is not lifted (Fig. S3.2†).

Fig. 3 STM images obtained at 77 K of an as prepared (293 K) saturated surface: (a) 18.7 × 18.7 nm², 1.037 V, 0.1 nA. The inset highlights BTAH molecules with elongated shapes and a variety of orientations; 5 × 5 nm², 1.075 V, 0.09 nA; (b) annealed to 308 K, 37.5 × 37.5 nm², 1.033 V, 0.077 nA; (c) 318 K, 37.5 × 37.5 nm², 0.551 V, 0.01 nA.

As shown in the inset in Fig. 3a, only a few molecules are oriented parallel to each other. Line profiles taken along three different but equivalent [112̄] type directions suggest that some of the molecules in the adlayer may interact with each other to form double row structures (Fig. S3.3†). In particular, the periodicity along the double row propagation direction is ca. 0.68 nm. STM evidence indicates that the adsorbates are predominantly physisorbed flat-lying, and upon rapidly cooling the sample to LN₂ temperature, the molecular overlayer can be quenched into a (meta)stable state. Relatively mild annealing to 298 K promotes primarily desorption of the more weakly bound species, although some desorption of the monolayer is also seen. The availability of free space on the surface allows some molecular diffusion within the first layer, favouring molecular reorganisation and formation of ribbon-like structures (Fig. 3b). Ribbons appear as double rows with alternating features interlocked into a zip-like structure. At this temperature, the majority of the ribbons seem straight, of well-defined width and periodic along their length. On closer inspection, however, the ribbon's width is seen to vary between 0.63 and 0.73 nm, whereas the distance between neighbouring elements of the interlocked structure can vary from 0.5 nm, corresponding to the shorter dimension of a single BTAH molecule, to 0.78 nm. Some ribbons are seen to bend, as shown on the top right corner of Fig. 3b. In this case, the separation can be as large as 0.92 nm, whereas the width then typically varies between 0.78 and 0.85 nm.

With annealing to 308 K, the relative number of curved ribbons increases. In correspondence with the increased curvature, the elements of the chains seem more elongated and less defined. This is tentatively attributed to the increased availability of free space for each molecule, so that its orientation relative to the propagation direction of the chain becomes better defined, with the azole ends pointing in towards the middle of the chain, and therefore the long axis of the molecule becomes perpendicular to the chain direction.

The higher the annealing temperature, the longer the strands, but also the wider the empty areas, where atomic resolution of the gold substrate can be observed (see Fig. S3.4†).

After annealing to 318 K (Fig. 3c), the ribbons no longer run randomly across the surface, but assume a zig-zag pattern reminiscent of the herringbone reconstruction, which seems to influence the surface topography, exerting a confinement effect. In this configuration, the ribbon propagates along the ridges, so that the short molecular axis is parallel to the ridges, whereas the long molecular axis is almost normal to the ridges. Discrete four-fold features are often present at the elbows of the herringbone reconstruction. After annealing above 323 K, the quality of the STM images deteriorates and molecular features are seldom visible (Fig. S3.5†). However, HREELS in particular, and XPS, show evidence of molecular species up to 573 K. This implies that, while molecular coverage decreases with increasing temperature, more free space on the surface is available and molecules are able to diffuse freely. Hence they are no longer visible in the STM, although still present on the surface. A second type of feature seen up to 308 K corresponds to areas appearing as halos of characteristic doughnut shape, with the outer region brighter than the inner, several examples of which can be seen in Fig. 3b. Halo features are 5- or 6-fold structures, some of them being empty and some filled with an additional feature in the middle (Fig. S3.6†). These are bound even more weakly and may be easily displaced by the tip revealing atomic resolution of gold. Halos initially appear to increase in number, then also in surface area and in groups. They are thought to be the manifestation of trapped molecules within the pores created but the chains. These molecules can hop between surface sites and are also weakly bound to the molecules in the confining chains. This hopping motion gives rise to the halo appearance of diffuse hexagonal or pentagonal arrangements. Examples of these features are reported in Fig. S3.7.†

2.2. Modelling

Despite a large computational effort, azole adsorption has been considered on reactive substrates,^6,16–24 but not on inert materials such as herein described. As has been reported,¹⁶ it is challenging to describe the adsorption of BTAH on such reactive metal surfaces via DFT methods. In fact, both the contributions of the electronegative azole moiety preferentially interacting through chemisorption, and the benzene ring interacting via vdW forces, have to be taken into account. This scenario is only slightly modified when considering the adsorption on a less reactive surface such as Au(111). Another parameter to be considered is the BTAH tautomeric equilibrium⁷ (Scheme 1a) and its influence on the molecular configurations which can be produced upon adsorption. As already highlighted, although experimental evidence^7b,c suggests that benzotriazole exists mainly in the 1H-BTA (3H-BTA) form in the condensed phase, and 2H-BTA in the gas phase, DFT calculations show that in the gas phase the two tautomers have very similar energies. Their calculated relative stability depends on the method used (see ESI4†). The combination of 1H-BTA (3H-BTA) and 2H-BTA in the gas phase shows the possibility of favourable hydrogen bonding interactions. Dimers are described as shown in Scheme 1b–e and dimerization energies, E_dim, calculated using eqn (1), are summarised in Table 1:

E_dim = E_AB − (E_A + E_B) (1)

where E_AB is the energy the dimer, and E_A and E_B are the energies of the isolated molecules considered.

Table 1 Linkage, propagation properties and gas phase dimerization energies

Dimer type	Linkage	Propagation	E dim/eV vdW-DF	E dim/eV PBE-D3(BJ)
1	N1–H⋯N′1	N′3–H⋯N3	−0.400	−0.472
2	N1–H⋯N′2	N′3–H⋯N2	−0.254	−0.303
3	N2–H⋯N′3 + N′2–H⋯N1	“N′⋯H–C”	−0.451	−0.576
4	N′2–H⋯N2	N1–H⋯N′3 + “N′⋯H–C”	−0.331	−0.405

---

Gas phase calculations employing two different functionals (vdW-DF²⁵ and PBE-D3(BJ)²⁶) show that the most stable dimer is formed by two 2H-BTA molecules (type 3). This is likely a consequence of the double hydrogen bond between the molecules. Dimerization energies for the other dimers follow the same trend for both functionals, being somewhat lower for the vdW-DF functional. When adsorbed on the Au(111) surface, the most stable is the type 1 dimer, with the molecules’ longer axes essentially parallel to each other and oriented along closely packed directions (details are reported in ESI5†). Adsorption energies per molecule, E_ads, are calculated using eqn (2):

E_ads = (E_{dimer/Au(111)} − (2 × E_{BTAH, gas phase} + E_Au(111)))/2 (2)

where E_{dimer/Au(111)} is the energy for the dimer adsorbed on the Au(111) slab, E_{BTAH, gas phase} is the energy of the 1H-BTA tautomer, and E_Au(111) is the energy of the Au(111) slab. The results follow the same trend with the two functionals employed. The results are summarised in Table 2. The dependency of the dimers’ orientations with respect to surface crystallographic directions highlights that the interaction with the surface plays an important role in stabilising each dimer, especially types 1 and 3.

Table 2 Dimers’ adsorption energies (eV) per molecule on an Au(111) (6 × 6) slab with molecules’ longer axes orientated along [11̄0]-type and [112̄]-type directions

Dimer type	[11̄0]-type		[112̄]-type
	vdW-DF	PBE-D3(BJ)	vdW-DF	PBE-D3(BJ)
1	−0.905	−1.257	−0.896	−1.231
2	−0.827	−1.149	−0.826	−1.146
3	−0.885	−1.244	−0.871	−1.208
4	−0.835	−1.169	−0.839	−1.175

---

The repetition of dimers of types 1 and 2 is expected to form chains leading to propagation, whereas the repetition of the type 3 dimer can create a row-like feature. These, however, are very challenging to mimic by DFT, as the structures experimentally observed are incommensurate.

Therefore in order to obtain a deeper understanding of pseudo-periodic extended structures, isolated hexamers based on linkages 1, 2, and 3, and allowing for 1D propagation, were considered in the first instance. Adsorption energies per molecule within a hexamer, E_ads, are calculated using eqn (3):

E_ads = (E_{hexamer/Au(111)} − (6 × E_{BTAH, gas phase} + E_Au(111)))/6 (3)

where E_{hexamer/Au(111)} is the energy for each of the hexamers adsorbed on the Au(111) slab, E_{BTAH, gas phase} is the energy of the 1H-BTA tautomer (see ESI4†), and E_Au(111) is the energy of the Au(111) slab.

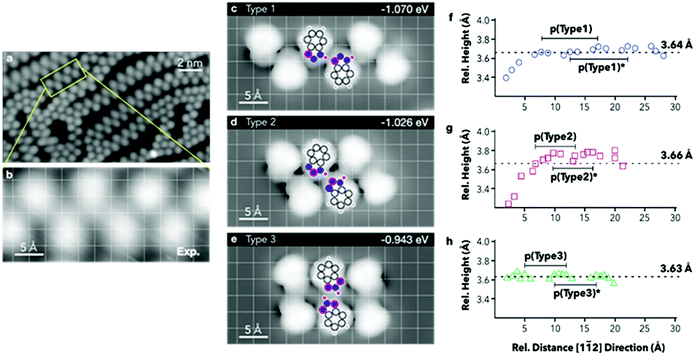
E _ads are then normalised by the surface area covered by the adsorbates. The computed energies per molecule (Table 3) show an increase in stability when forming chains where the tautomeric hydrogens are coordinated by a type 1 linkage, followed by type 2. However, when normalising to the footprint occupied by the hexamers, the adsorption energies show very small variations, with type 2 resulting to be the most stable. To achieve direct comparison with the extended chains experimentally observed (Fig. 4a and b), STM images for the three different hexamers were simulated (Fig. 4c–e). When comparing the portions of the chains highlighted in Fig. 4a and b with the STM simulation for the hexamers, the best agreement is found with a type 1 chain (Fig. 4c).

Fig. 4 (a) STM image after annealing to 308 K, 18.7 × 10.2 nm², 1.033 V, 0.077 nA; (b) magnification of the yellow rectangle in (a). (c–e) Simulated STM images for the hexameric chains, 1 V, constant current. A grid to guide the eye and a model representation are superposed to each simulated image. Top-right, adsorption energy per molecule. (f–h) Extrapolated N atom positions projected along the [112̄] direction.

Table 3 Hexamers’ E_ads normalised to a single molecule, and per single molecule and unit area

Hexamer type	Area/Å^2	E ads per molecule/eV		E ads per molecule per unit area/(eV Å^−2)
		vdW-DF	PBE-D3(BJ)	vdW-DF	PBE-D3(BJ)
Type 1	124.10	−1.070	−1.415	−0.0086	−0.0114
Type 2	108.37	−1.026	−1.349	−0.0094	−0.0095
Type 3	122.10	−0.943	−1.277	−0.0077	−0.0104

---

Extrapolated nitrogen atom positions, projected along the [112̄] direction (Fig. 4f–h), which may correspond to the expected line profiles, allowed emulation of the pseudo-periodicity of the chains formed by the hexamers. A pseudo-periodicity between 9.56 and 9.70 Å is calculated for a type 1 chain (Fig. 4c). However, STM images show much shorter periodicity, especially for straight segments, which could correspond to chains based on other types of interactions. In Fig. 4d and e chains based on type 2 and type 3 interactions, respectively, are shown. The extrapolated nitrogen atom positions for those arrangements have shorter pseudo-periodicities, 6.56–6.58 Å and 6.93–6.97 Å, respectively. The calculated pseudo-periodicities are in good agreement with those experimentally observed (Fig. S3.9†).

The presence of features exhibiting different types of interactions is further confirmed by the analysis of the HREEL spectra, when compared to the computed vibrations (details are reported in ESI6†).

As already highlighted, upon annealing to 318 K (Fig. 3c), a different molecular packing seems to occur. The observed topography suggests chains to be confined between the ridges of the herringbone reconstruction and BTAH molecules interacting with each other essentially through type 1 interaction.

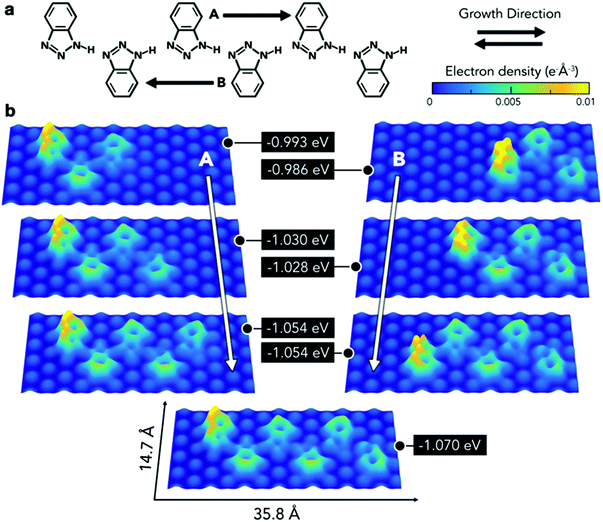
Therefore, further modelling was employed to obtain a deeper understanding of the interaction of this type of chain with the substrate (Fig. 5a). This consisted of calculating the adsorption energies per molecule for a series of chains composed of three to six BTAH molecules adsorbed on the Au(111) surface. A hexamer based on type 1 linkage was initially optimised on the surface. Then one molecule was removed from each end alternately, and the resulting configuration was re-optimised. The minimum number of molecules considered for this model corresponds to the shortest chain containing a BTAH molecule coordinated with two others (trimer), allowing therefore to consider both amino-[N] and imino-[NH] termini. Alternatively, this sequence can also be interpreted as growing the chain from the imino- to the amino-terminus and vice versa. In all cases, the growth from the amino- to imino-terminus was the most stable (growth direction B in Fig. 5). With increasing chain length, the different molecules lie on different adsorption sites; this represents a varying surface–molecule interaction along the chain. Because of the interaction with the substrate, the molecules are not able to link together via the optimal configuration for the N₁–H⋯N_3′ hydrogen bond, as seen in the gas phase, resulting in distorted angles.

Fig. 5 (a) Chemical representation of the type 1 chains modelled. A and B arrows indicate the growth direction. (b) Electron density of the different chains projected on a plane parallel to the surface at a distance of 2.0 Å. Adsorption energies are normalised to the number of BTAH molecules adsorbed.

This distortion appears more evident in the final stages of growth, where the last unit added to the pentameric chain to form the hexamer leads to higher electron density along these bonds.

The energetic implications of distortion of the H-bond, and change in adsorption sites in the growing chains, cannot be separated. The difference in energy can be explained by considering different contributions involving molecule–substrate and molecule–molecule interactions, where the difference between the set of n-mers decreases with increasing number of units (Fig. 5b, right). Remarkably, despite the fact that the molecules lie in different adsorption sites, the difference in energy for a given pair of adjacent n-mers is lower than 20 meV. The balance between these two phenomena, molecule–molecule and substrate–molecule interactions, can be used to explain the pseudo-periodicity of the extended chains recorded experimentally. Without the substrate these chains would not prefer to lie flat and form the structures observed here. The substrate represents an environment to propagate the chains in a pseudo-periodic arrangement, while allowing for distortion of the highly directional N₁–H⋯N_3′ hydrogen bond. Essentially, the longer the chain, the more significant is the hydrogen bonding, while the relative contribution from the interaction with the surface (which occurs mainly through the terminal molecule) decreases. This is demonstrated by the electron density plots. In addition, the peripheral region of the benzene rings exhibits a greater electron density than the inner area, implying that chains are expected to repel each other. Thus, the surface plays an important role, in that it acts as a template to create unidimensional arrangements on the substrate plane. Because the difference in adsorption sites does not lead to abrupt changes in adsorption energies, the growth of the extended linear chains can be ascribed to the fact that this particular type 1 configuration is driven by a comfortable assembly of the N₁–H⋯N₃ geometry between the 1H-BTAH building units.

2.3. Discussion

BTAH is a corrosion inhibitor for copper and its alloys well known since the 1950s.²⁷ However, the mechanisms, by which adsorption and passivation occur, remain thus far a matter of debate. Furthermore, there is no universal agreement on how BTAH adsorbs on such metallic substrates.^{6,10,11,16–20} Substantial efforts^{6,10,11,16–24,28,29} have addressed the identification of the structures that BTAH/BTA⁻ forms on low index copper surfaces, especially (111), through chemisorption at the azole moiety and/or physisorption through the delocalised π system. Previous investigations focused solely on reactive surfaces;^{6,10,11,16–24,28–30} in particular physisorbed H-bonded chains of BTAH on Cu(111) have been previously considered by DFT calculations,¹⁸ yet because copper deprotonation on the N₁–H bonds occurs,^10,11 polymerisation based on hydrogen bonding is not observed. When dosed on an inert substrate, which is ineffective in removing the N₁ hydrogen and unreactive toward the azole functionality, hydrogen bonding and vdW interactions are expected to prevail. Therefore a flat-lying adsorption is anticipated. Some aspects of BTAH chemistry and adsorption properties can be derived considering the dimensionality of the system.

2.3.1. The 3-dimensional and 0-dimensional systems. In the condensed phase, benzotriazole essentially exists in the 1H-BTAH (3H-BTA) form. To date, two polymorphs are known to exist: the α polymorph is reported as monoclinic and contains four molecules in the asymmetric unit cell.³¹ Of four symmetry-unrelated molecules, three form polymeric chains through N⋯H–N hydrogen bonds (as in the type 1 linkage), whilst the fourth molecule is linked to the chain through N⋯H–N and C–H⋯N hydrogen bonds. The β polymorph is characterised by a triclinic unit cell, containing ten molecules forming polymeric chains through N⋯H–N hydrogen bonds joining into a large and discrete supramolecular macrocycle.³² Therefore, BTAH essentially consists of the solid phase of the N⋯H–N hydrogen bonded 1H-BTAH tautomer. Moreover the 2H-BTA tautomer is not present in polymorphs α and β.^31,32 In the solid phase, the pro-S and pro-R enantiomers of Scheme 1 are indistinguishable, as chirality is introduced only by adsorption. Upon sublimation, the 2H-BTA tautomer readily forms because of the fast tautomerisation reaction.⁷

The 0-dimensional system is represented by gas-phase BTAH, for which the tautomerisation reaction occurs. The argument on the prevalence for one or the other tautomer is based on both DFT calculations and experimental evidence.⁷ In particular, the 1H-BTAH (3H-BTA) tautomer was concluded to be predominant in the condensed phases, in contrast to the 2H-BTA tautomer in the gas phase at low temperatures.^7b,c This was ascribed to a balance between lone pair repulsions favouring the 2H-BTA tautomer, and aromaticity favouring the 1H-BTAH one. Another factor considered was the tautomers’ dipole moment, much higher for 1H-BTAH, thus favouring interactions with itself and with a polar solvent.^7c However, gas phase stabilisation energy calculations show that the two tautomers in their ground states are essentially degenerate, and the different energy contents seem to be related to the different functionals used in the calculations [ref. 7f and ESI4†]. Therefore, the pseudo-degeneracy present in the gas phase can be lifted in the condensed phase, as in the solid or solution phases of BTAH, or upon a surface by substrate– and molecule–molecule interactions when adsorbed at different coverages. When considering the first excited state, BTAH seems to exist exclusively as the 2H-BTA tautomer, which unexpectedly, is also reported to be non-planar.^7d

2.3.2. The 2D surface confined system. When condensation on the surface occurs, it has to be assumed that the 2H-BTA tautomer arrives at the substrate and, because of the transition from the gas to the condensed phase, the tautomeric equilibrium shifts towards the formation of equal amounts of pro-S and pro-R species, which are now distinguishable. After condensation, self-organisation in double rows of flat lying molecules may occur. STM shows local ordering, but only a few molecules have their longer axes parallel to each other (Fig. 3a, inset). However, further identification of the molecular species on the saturated layer is very challenging, essentially because of the heterogeneity of the molecular orientations. On the basis of dimerization energies, some H-bonded pairs can reasonably be considered to form, but the relation between the pairs is not readily experimentally accessible. HREELS confirms the flat lying adsorption geometry, and strongly indicates that various molecular pairs may be present, albeit in different amounts.

2.3.3. The 1D surface confined system. The annealing treatments, following room temperature adsorption, allow the formation of racemic chains, which comprise alternating pro-S and pro-R enantiomers. The basic coordination between adjacent enantiomers occurs through a N₁–H⋯N′₁ hydrogen bond (Scheme 1b) corresponding to the more stable type 1 linkage. A chain based on such a linkage would be expected to be regular in its width and periodicity, and to propagate indefinitely on an electronically flat, jellium-type surface. However, several effects may influence the chain topology and propagation, such as pro-S/pro-S (pro-R/pro-R) defects, the inclusion of the 2H-BTA tautomer, the interaction of the molecular species with the substrate, and in particular the effect of the surface corrugation.

The 2H-BTA tautomer, other than terminating a chain, may in a broader sense play a role in the variation of the topology and periodicity of the chains. For example, the pro-S/pro-R alternation could change to pro-R/pro-S through a 2H-BTA tautomer, as in the pro-S/pro-R/2H-BTA/pro-R/pro-S sequence, and the 2H-BTA tautomer would appear as a kink in the chain. Shorter pseudo-periodicities of some chain sections point to some possible sequences of several 2H-BTA tautomers, which have to be regarded as a series of dimers one next to the other (as in type 3, Scheme 1d) stabilised by C–H⋯N intermolecular hydrogen bonds, weaker when compared to N–H⋯Ns′. Other possibilities for shorter pseudo-periodicities are sections of pro-S/pro-R chains based on interactions other than type 1. This agrees with the calculations on the adsorbed hexamers (Fig. 4), which show that when energies are normalised by the area covered by the hexamers, the type 2 (less stable than type 1 as a condensed dimer) becomes more favourable. Type 2 chains are therefore stabilised by the substrate.

The presence of both types of enantiomer, tautomers, and different types of interactions within a chain, is strongly suggested by both HREELS and STM, and supported by DFT modelling: (a) the HREEL experimental spectra can be best fitted with contributions derived from each of the chain linkages considered as shown in ESI6;† (b) the pseudo-periodicities and varying chain widths seen in STM (Fig. 3a–c and S3.9†) imply different coordination between the molecular species; and (c) DFT modelling shows that the variation in stabilisation energy is very small, rendering all the chain linkages feasible.

When the chain type based on the most favourable linkage 1 is considered, the interaction with the surface results in both variable molecule–molecule spacing and curvature of chain portions. This is accounted for by the model proposed in Fig. 5. In the absence of any surface potential, the two-dimensional chain growth would be independent of direction. However, when considering even a weakly modulated surface potential, anisotropy in the growth direction can arise. In the present case, the chains are effectively already ‘locked’ at one end. And the further added molecules will result in inequivalent positions when growing from one direction compared to the other. Presumably, the energy barriers to achieving optimal configurations (i.e. straight) by chain diffusion are too large on the surface, therefore different stabilisation energies arise, and those will determine the preferential growth direction. Surface corrugation effects are manifested most obviously at low coverage, when confinement of the chains between the herringbone ridges occurs.

These hydrogen bonded chains differ from those observed during the onset of adsorption of BTAH on Cu(111).¹⁰ In the latter case, chain-like features were considered to be constituted by a series of upright Cu(BTA)₂ species, likely anchored to the surface via the two N₂ atoms.^10,11 Propagation was ascribed to lateral interactions between the dimers, which remained as isolated units, with an average separation of 1.1–1.2 nm. Hence, a polymeric structure was not formed. Gattinoni and Michaelides have calculated that these stacked dimers are associated with hydrogen atoms adsorbed on the surface as impurities that favour surface reconstruction, and represent the lowest energy configuration.¹⁶ Indeed, atomic hydrogen is known to induce reconstruction of the Cu(111) surface.³³ The chains experimentally observed are also different from the so-called necklace polymer, which comprises upright BTA molecules intercalated by copper atoms.^16,18,20 Here, when adsorbed on Au(111), chains are formed by physisorbed, flat-lying BTAH molecules interacting through hydrogen bonds. The main difference between the two systems arises from the fact that deprotonation does not occur because a reactive metal is not involved, thus impeding the formation of metal–organic species. As the molecules are still intact and flat lying on Au(111), the possible intermolecular interactions are via hydrogen bonds to form the chains, and vdW inter-chain and chain–surface interactions.

Other than chain-like structures, centrosymmetric structures are observed via STM (see ESI3†). In order to form these kinds of structures, only molecules of the same chirality need to be considered. The structures mostly seen are hexamers, which correspond to the geometrical shape introducing least deformation on the N₁–H⋯N′₃ hydrogen bond. Occasionally, these 6-fold entities can trap an additional molecule. These are examples of 2-dimensional systems within an overall 1-dimensional framework.

The study of the adsorption of BTAH on an unreactive metal surface can now be described in more detail, shedding light on some crucial aspects of its behaviour on more reactive surfaces, such as whether or not deprotonation occurs during sublimation in a vacuum, or because of subsequent adsorption over a reactive surface,^10,11 and whether or not the 2H-BTA tautomer can be stabilised in the condensed phase. As discussed, there is substantial evidence pointing towards the condensation of an intact molecule. Therefore, any deprotonation thought to occur on reactive surfaces must be ascribed to the interaction with that substrate, especially with defective sites, or more likely with freely diffusing and very reactive adatoms. Those interactions may also be responsible for the stabilisation of the 2H-BTA tautomer, the presence of which is inferred by the comparison of computational and experimental evidence.

3. Experimental and computational details

The Au(111) single crystal was cleaned by Ar⁺ ion sputtering and annealing (ca. 830 K) cycles until a surface characterized by the typical (22 × √3) structure of the reconstructed clean substrate was observed by both LEED and STM. BTAH dosing was carried out by simply opening a gate valve separating a quartz crucible containing the compound from the main chambers containing the Au(111) crystal held at room temperature. BTAH has a vapour pressure high enough at room temperature to sublime under UHV conditions.³⁴ HREEL (VSW HIB 1001 double-pass spectrometer) measurements were carried out in a UHV system with a base pressure better than 1 × 10⁻¹⁰ mbar, in the specular direction (θ_i = θ_f = 45°), with a primary beam energy of 4 eV and a typical elastic peak resolution of ca. 50 cm⁻¹ (6.2 meV FWHM). A maximum likelihood based resolution enhancement method³⁵ was used to recover the spectra from the instrumental broadening, leading to an improved resolution of ca. 40 cm⁻¹ FWHM. STM experiments were performed in a separate UHV surface analysis system with a base pressure below 1 × 10⁻¹⁰ mbar consisting of a preparation chamber allowing for standard sample preparation and a microscope chamber housing a CreaTec low-temperature STM. STM data were collected at 77 K in constant-current mode using homemade PtIr tips. Images were processed using the WSxM software package.³⁶ NEXAFS studies were performed at the SuperESCA beamline^37,38 of the Elettra third generation synchrotron radiation source in Trieste, Italy. The experimental chamber was equipped with a Phoibos hemispherical energy analyzer (SPECS GmbH) with a homemade delay-line detector³⁹ and had a background pressure of about 2 × 10⁻¹⁰ mbar. NEXAFS data were collected by monitoring the yield of N KLL Auger electrons at 380 eV. Data were normalised following an established procedure that includes dividing the spectrum of the adsorbate covered surface by that of the clean surface,⁴⁰ having first divided each spectrum by the measured incident photon flux as recorded from a clean gold mesh located close to the main experimental chamber. Data were recorded for angles of incidence in the range 20° ≤ θ ≤ 90°; the angle between the X-ray beam and the electron energy analyser was 70° and the linear polarisation of ca. 100%.

Density Functional Theory (DFT)⁴¹ calculations were performed using a projector augmented wave (PAW⁴²) as implemented in the Vienna ab initio simulation package (VASP).⁴³ Structures were optimised by employing a non-semiempirical van der Waals density functional (vdW-DF²⁵) to describe the non-localised exchange–correlation. Valence electrons were described using plane-waves to an energy cut-off of 400 eV. The Grimme dispersion correction D3⁴⁴ scheme was applied to describe dispersion interactions when using the Perdew, Burke and Ernzerhof (PBE) functional.⁴⁵ In the latter case, Becke–Johnson (BJ) damping was used to modify the exchange potential of the PBE-D3 functional, which has been tested to produce better description of solids, as a consequence of avoiding repulsive interatomic forces at short distances.²⁶ The Au(111) surface was modelled by three layers of the metal where the top upper layer was allowed to relax. Adsorbed structures were simulated as isolated dimers and hexameric chains, which were optimised on (6 × 6) and (12 × 12) unit cells respectively. To avoid a spurious interaction between periodic images, a vacuum region >15 Å was included. The integration of the first Brillouin zone was sampled using 3 × 3 × 1 k-points for the dimers and the Γ-point for the larger unit cells containing the hexamers. All structures were relaxed using the conjugate gradient method with a restrictive convergence criterion for the self-consistent cycle of 10⁻⁶ eV, with residual forces smaller than 0.015 eV Å⁻¹. Born charges were calculated using density-functional perturbation theory (DFPT)⁴⁶ to obtain the simulated vibrational spectra. The procedure followed to calculate the intensities for the different vibrational modes is described in detail in ESI6.†

4. Conclusions

The room temperature adsorption of BTAH on Au(111) has been investigated using complementary surface sensitive techniques and theoretical calculations. Significant considerations regarding the dimensionality of the system were derived. BTAH is essentially present as the 1H-BTA tautomer in the 3D crystal structure, and is characterised by some degree of polymerisation through various N–H⋯N hydrogen bonds and weaker C–H⋯N intermolecular interactions. The 2D confined layer obtained upon saturated adsorption on an unreactive substrate is characterised by the presence of equal amounts of pro-S, pro-R enantiomers, and the 2H-BTA tautomer. Flat-lying 1D chains form mainly through the most favourable N⋯H–N interaction upon mild annealing, whilst pro-S, pro-R enantiomers and the 2H-BTA tautomer are still present. The subtle interplay between hydrogen bonding, surface–molecule and chain–chain van der Waals interactions has been highlighted. In the absence of surface corrugation, a chain would grow linearly and with a well-defined periodicity. The interaction with the substrate is responsible for irregular periodicity and widths of the chains. In a very low coverage regime, the surface reconstruction can exert some confinement effects on the chains, which are nevertheless free to diffuse to some extent. Centro-symmetric, probably homochiral, structures are seen as a minority feature; they represent 2D structures within an essentially 1D framework. Gas-phase BTAH, characterised by the tautomeric equilibrium reaction, represents the 0D system. Moreover, these results may contribute to understanding further the surface chemistry of benzotriazole, a well known corrosion inhibitor for copper and copper alloys.

Acknowledgements

FG has received funding from the European Community's Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 312284 for part of the research leading to these results (NEXAFS, XPS). The Engineering and Physical Sciences Research Council (EPSRC) is acknowledged for the funding of PhD studentships (JAGT and MJT – EP/J500549/1 and CRL – EP/M506631/1). JPG acknowledges funding from the EPSRC (EP/J018139/1). EaStCHEM is thanked for computational support via the EaStCHEM Research Computing Facility. Dr Christopher J. Baddeley (University of St Andrews) and Dr Silvano Lizzit (SuperESCA beam line, Elettra) are thanked for helpful discussions.

The research data supporting this publication can be accessed at http://dx.doi.org/10.17630/cd60b0e2-18bd-43e3-bacd-106d1050a19a.

Notes and references

1. N. Wintjes, J. Hornung, J. Lobo-Checa, T. Voigt, T. Samuely, C. Thilgen, M. Stöhr, F. Diederich and T. A. Jung, Chem. – Eur. J., 2008, 14, 5794.
2. J. V. Barth, G. Costantini and K. Kern, Nature, 2005, 437, 671.
3. P. Maksymovych, D. C. Sorescu, K. D. Jordan and J. T. Yates Jr., Science, 2008, 322, 1664.
4. C. Bombis, F. Ample, L. Lafferentz, H. Yu, S. Hecht, C. Joachim and L. Grill, Angew. Chem., Int. Ed., 2009, 48, 9966.
5. S. Horiuchi, F. Kagawa, K. Hatahara, K. Kobayashi, R. Kumai, Y. Murakami and Y. Tokura, Nat. Commun., 2012, 3, 1308.
6. (a) M. Finšgar and I. Milošev, Corros. Sci., 2010, 52, 2737; (b) M. B. Petrović Mihajlović and M. M. Antonijević, Int. J. Electrochem. Sci., 2015, 10, 1027.
7. (a) F. Tomás, J.-L. M. Abboud, J. Laynez, R. Notario, L. Santos, S. O. Nilsson, J. Catalán, R. Ma. Claramunt and J. Elguero, J. Am. Chem. Soc., 1989, 111, 7348; (b) C. Borin, L. Serrano-Andrés, V. Ludwig and S. Canuto, Phys. Chem. Chem. Phys., 2003, 5, 5001; (c) F. Tomás, J. Catalán, P. Pérez and J. Elguero, J. Org. Chem., 1994, 59, 2799; (d) J. Catalán and P. Pérez, Chem. Phys. Lett., 2005, 404, 304; (e) N. Jagerovic, M. L. Jimeno, I. Alkorta, J. Elguero and R. M. Claramunt, Tetrahedron, 2002, 58, 9089; (f) L. T. Ueno, R. O. Ribeiro, M. S. Rocha, M. E. V. Suarez-Iha, K. Iha and F. B. C. Machado, J. Mol. Struct. (THEOCHEM), 2003, 664–665, 207; (g) W. Roth, D. Spangenberg, Ch. Janzen, A. Westphal and M. Schmitt, Chem. Phys., 1999, 248, 17.
8. (a) H. Duan, S. Sengupta, J. L. Petersen, N. G. Akhmedov and X. Shi, J. Am. Chem. Soc., 2009, 131, 12100; (b) Y. Chen, W. Yan, N. G. Akhmedov and X. Shi, Synth. Org. Lett., 2010, 12, 344.
9. B. Pergolese, M. Muniz-Miranda and A. Bigotto, J. Phys. Chem. B, 2004, 108, 5698.
10. F. Grillo, D. W. Tee, S. M. Francis, H. Früchtl and N. V. Richardson, Nanoscale, 2013, 5, 5269.
11. F. Grillo, D. W. Tee, S. M. Francis, H. A. Früchtl and N. V. Richardson, J. Phys. Chem. C, 2014, 118, 8667.
12. J. F. Walsh, H. S. Dhariwal, A. Gutiérrez-Sosa, P. Finetti, C. A. Muryn, N. B. Brookes, R. J. Oldman and G. Thornton, Surf. Sci., 1998, 415, 423.
13. J. F. Walsh, H. S. Dhariwal, A. Gutiérrez-Sosa, R. Lindsey, G. Thornton and R. J. Oldman, Nucl. Instrum. Methods Phys. Res., Sect. B, 1995, 97, 392.
14. J. F. Moulder, W. F. Stickle, P. E. Sobol and K. D. Bomben, Handbook of X-ray Photoelectron Spectroscopy, Physical Electronics Inc., Eden Prairie (Minnesota), USA, 1995.
15. T. Kosec, D. K. Merl and I. Milošev, Corros. Sci., 2008, 50, 1987.
16. C. Gattinoni and A. Michaelides, Faraday Discuss., 2015, 180, 439.
17. A. Kokalj and S. Peljhan, Langmuir, 2010, 26, 14582.
18. A. Kokalj, S. Peljhan, M. Finšgar and I. Milošev, J. Am. Chem. Soc., 2010, 132, 16657.
19. S. Peljhan and A. Kokalj, Phys. Chem. Chem. Phys., 2011, 13, 20408.
20. X. Chen and H. Häkkinen, J. Phys. Chem. C, 2012, 116, 22346.
21. Y. Jiang and J. B. Adams, Surf. Sci., 2003, 529, 428.
22. A. Kokalj, Faraday Discuss., 2015, 180, 415.
23. N. Kovačević and A. Kokalj, Mater. Chem. Phys., 2012, 137, 331.
24. N. Kovačević and A. Kokalj, J. Phys. Chem. C, 2011, 115, 24189.
25. (a) M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401; (b) G. Román-Pérez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102.
26. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
27. Procter & Gamble, Ltd, British Patent, 625339, 1947.
28. S. Peljhan, J. Koller and A. Kokalj, J. Phys. Chem. C, 2014, 118, 933.
29. A. Kokalj, S. Peljhan and J. Koller, J. Phys. Chem. C, 2014, 118, 944.
30. S. Naumov, S. Kapoor, S. Thomas, S. Venkateswaran and T. Mukherjee, J. Mol. Struct. (THEOCHEM), 2004, 685, 127.
31. A. Escande, J. L. Galigné and J. Lapasset, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 1490.
32. S. Krawczyk and M. Gdaniec, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2005, 61, o2967.
33. (a) M. F. Luo, G. R. Hu and M. H. Lee, Surf. Sci., 2007, 601, 1461; (b) G. Lee and E. W. Plummer, Surf. Sci., 2002, 498, 229; (c) M. F. Luo, D. A. MacLaren, I. G. Shuttleworth and W. Allison, Chem. Phys. Lett., 2003, 381, 654; (d) K. Mudiyanselage, Y. Yang, F. M. Hoffmann, O. J. Furlong, J. Hrbek, M. G. White, P. Liu and D. J. Stacchiola, J. Chem. Phys., 2013, 139, 044712.
34. (a) Y. Park, S. H. Choi, H. Noh and Y. Kuk, Proc. SPIE, 2006, 6172, 617214–617211; (b) Y. Park, H. Noh, Y. Kuk, K. Cho and T. Sakurai, J. Korean Phys. Soc., 1996, 29, 745.
35. (a) B. G. Frederick, G. L. Nyberg and N. V. Richardson, J. Electron Spectrosc. Relat. Phenom., 1993, 64/65, 825; (b) B. G. Frederick and N. V. Richardson, Phys. Rev. Lett., 1994, 73, 772.
36. I. Horcas, R. Fernández, J. M. Gómez-Rodríguez, J. Colchero, J. Gómez-Herrero and A. M. Baro, Rev. Sci. Instrum., 2007, 78, 013705.
37. A. Baraldi, M. Barnaba, B. Brena, D. Cocco, G. Comelli, S. Lizzit, G. Paolucci and R. Rosei, J. Electron Spectrosc. Relat. Phenom., 1995, 76, 145.
38. A. Baraldi, G. Comelli, S. Lizzit, M. Kiskinova and G. Paolucci, Surf. Sci. Rep., 2003, 49, 169.
39. G. Cautero, R. Sergo, L. Stebel, P. Lacovig, P. Pittana, M. Predonzani and S. Carrato, Nucl. Instrum. Methods Phys. Res., Sect. A, 2008, 595, 447.
40. J. Stöhr, NEXAFS spectroscopy, in Springer Series in Surface Science, ed. R. Gomer, Springer, Berlin, 1992, vol. 25.
41. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
42. P. E. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953.
43. (a) G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1993, 47, 558; (b) G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169.
44. S. Grimme, J. Antony, S. Ehrlich and S. Krieg, J. Chem. Phys., 2010, 132, 154104.
45. (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396(E).
46. J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter, 2011, 83, 195131.

---

Footnotes

† Electronic supplementary information (ESI) available: NEXAFS N K-edge comparison with calculated N LDOS, C 1s and N 1s X-ray photoemission spectra, additional STM images, gas-phase and adsorbed dimer calculations, vibrational spectra calculation and comparison with HREELS. See DOI: 10.1039/c6nr00821f

‡ The assignment of the 1H-BTA and 3H-BTA enantiomers' absolute configurations after adsorption is done considering the Au(111) surface as a substituent at the N₁ and N′₃ atoms respectively.

---