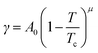Microfluidics of binary liquid mixtures with temperature-dependent miscibility

Abstract

Liquid–liquid microfluidic systems rely on the intricate control over the fluid properties of either miscible or immiscible mixtures. Herein, we report on the use of partially miscible binary liquid mixtures that lend their microfluidic properties from a highly temperature-sensitive mixing and phase separation behaviour. For a blend composed of the thermotropic liquid crystal 4-cyano-4′-pentylbiphenyl (5CB) and methanol, mixing at temperatures above the upper critical solution temperature (UCST; 24.4 °C) leads to a uniform single phase while partial mixing can be achieved at temperatures below the UCST. Thermally-driven phase separation inside the microfluidic channels results in the spontaneous formation of very regular phase arrangements, namely in droplets, plug, slug and annular flow. We map different flow regimes and relate findings to the role of interfacial tension and viscosity and their temperature dependence. Importantly, different flow regimes can be achieved at constant channel architecture and flow rate by varying the temperature of the blend. A consistent behaviour is observed for a binary liquid mixture with lower critical solution temperature, namely 2,6-lutidine and water. This temperature-responsive approach to microfluidics is an interesting candidate for multi-stage processes, selective extraction and sensing applications.

---

Stefan Guldin

Stefan Guldin is an Associate Professor in the Department of Chemical Engineering at University College London. Before joining UCL in 2014, he was a postdoctoral fellow of the German Academy of Science at EPFL, Switzerland. In 2012 he obtained a PhD from the University of Cambridge. Previously, he studied applied physics with an emphasis on soft matter at the TU Karlsruhe and TU Munich. At UCL, Stefan heads the Adaptive and Responsive Nanomaterials (AdReNa) group, which is devoted to the study material formation on the nanoscale by molecular self-assembly and implementation into functional nanoarchitectures for a variety of fields ranging from biomedical diagnostics and therapeutic drug monitoring to optical coatings and electrochemical devices.

---

Design, System, Application

Microfluidic processes generally rely on the handling of either miscible or immiscible liquid mixtures. In this work, we introduce a novel temperature-based microfluidic concept that is driven by and engineered through the underlying molecular characteristics rather than active or passive components on the microchannel architecture. We demonstrate how the temperature-dependent properties of regular solutions, namely miscibility, interfacial tension and viscosity, enable the detailed control over mixing and the formation of highly regular flow patterns. Such systems allow seamless switching between mixed and phase separated states in distinct flow regimes, thus offering novel routes for complex multi-stage processes, selective extraction and sensing applications.

Introduction

Microfluidics offers numerous advantages for fluid handling such as small sample volumes, the possibility to separate and detect substances with high sensitivity, as well as compatibility with low-cost and portable device architectures.¹ Consequently, microfluidic processes are used in a broad range of fields, including drug development,² point-of-care diagnostics,³ bioanalysis,⁴ systems biology,⁵ cell biology,⁶ chemical synthesis⁷ and production of foams and emulsions.⁸ These applications usually involve the use of either miscible or immiscible fluids. For processes that require liquid–liquid mass transfer, immiscible mixtures are typically chosen, and phase transfer then relies on the diffusion of target molecules across the liquid–liquid interface.^9–12 Different approaches have been developed to enhance transfer rates, either based on passive mixers, such as stream splitters¹³ or ridges,^14,15 or active mixers, including bubblers,¹⁶ magnetic bar micromixers^9,17 and magnetic fields to induce diffusion.¹⁸

In contrast, the use of temperature manipulation to achieve control over microfluidic properties has only been explored to a somewhat limited extend. Some examples include the variation of temperature to enhance convection for the mixing of miscible components¹⁹ as well as the (limited) temperature-induced tuning of interfacial tension and viscosity of immiscible water–oil mixtures.^20–23

Binary liquid systems that exhibit temperature-dependent miscibility are referred to as regular solutions and characterised by having an upper critical solution temperature (UCST), a lower critical solution temperature (LCST) or both. In liquid systems with an UCST, the solution is miscible above this temperature threshold. Cooling below the coexistence curve leads to phase separation. This behaviour is typically represented in a phase diagram, described by composition ϕ vs. temperature T. The temperature response is opposite for a liquid system with a LCST. A comprehensive overview of conventional binary liquid mixtures and their critical solution temperatures can be found in a monograph by Francis.²⁴ Despite the broad library of suitable liquid–liquid combinations with the above-described behaviour, to-date regular solutions have received little attention in microfluidic environments.

In this work, we introduce the use of a temperature-responsive binary molecular system for microfluidic applications. In recent years, 4-cyano-4′-pentylbiphenyl (5CB) in its native form has attracted significant interest in liquid crystal microfluidics due to unique thermofluidic properties, including a temperature-tunable flow profile and fluidic resistance, as well as temperature-induced molecular reorientation and controlled nucleation and growth of stable reconfigurable domains.^25–28 Herein, we investigate the fluidic behaviour in a 50/50 v/v blend of 5CB with methanol (MeOH), in particular the influence of temperature. We carefully mix and phase separate the liquid blend and relate the observed flow patterns to the role of temperature-modulated interfacial tension and viscosity. Finally, we compare findings to a binary liquid mixture with a LCST, namely water and 2,6-lutidine to probe the general applicability of our approach.

Experimental

Reagents

The liquid crystal 4-cyano-4′-pentylbiphenyl (5CB) (CAS 40817-08-1, 99.5%) was purchased from Synthon Chemicals. MeOH (CAS 67-56-1, HPLC grade) and 2,6-lutidine (CAS 108-48-5, 98%) were obtained from Sigma Aldrich. All chemicals were used as received.

Mixing characterisation

Mixing of MeOH and 5CB was studied in a glass microfluidic chip with a channel width of 300 μm and a channel depth of 120 μm containing static micromixer with staggered oriented ridges (Chemtrix BV, chip no. 3227). Pure MeOH and pure 5CB were infused into the chip with a syringe pump (Cronus, Sigma 1110) at a flow rate of 5 μl min⁻¹ for each stream. The temperature was controlled with a custom-built Peltier-based chip holder (see ESI,† Fig. S1). Another k-type thermocouple was attached with an adhesive tape (DuPont, Kapton) on top of the microfluidic chip to verify that the temperature gradient between the bottom and top surface was below 1 °C. The mixing was studied for a range of temperatures from 40 °C to 12 °C. Images of the micromixer were taken in reflection mode due to the nature of the Peltier-based chip holder, with a digital camera (FLIR, Chamaleon3) mounted on a stereo microscope (VWR).

Interfacial tension

The interfacial tension was measured via the pendant drop method. 2 ml of a 50/50 v/v mixture of MeOH and 5CB was prepared and mixed at 40 °C in a temperature controlled quartz cuvette (Quantum Northwest, qpod 2e). The mixture was cooled to the desired temperature (below the UCST) and left without stirring until the macroscopic phase separation was completed. Then, a syringe with a 22 gauge blunt tip needle was dipped into the solution to carefully withdraw an aliquot of the bottom 5CB-rich phase. The tip of the needle was subsequently lifted and immersed in the upper MeOH-rich phase before a droplet was dispensed. Images of the drops were acquired with a digital microscope (Visio-Tek, IWT) that was attached to one port of the temperature controlled quartz cuvette. Image analysis was carried out using the Krüss Advance software as well as the pendent drop plug-in for ImageJ.²⁹

Fabrication of microfluidics chips

Microfluidic chips for the study of different flow regimes were fabricated as shown in Fig. S2 in the ESI.† Two different techniques were used for the sandwich architecture, namely UV-curable adhesive bonding of cyclo-olefin polymer sheets (Zeonor) and thermal bonding of PVC. While the former resulted in higher optical quality chips, the latter enabled the realisation of more complex channel architectures, such as serpentines.

For thermally bonded chips, extruded sheets of PVC (Norva Plastics, 1.5 mm) were cut in a CNC engraving machine (Roland, EGX-400) according to the design. Both parts were then cleaned in water, dried in air, and subsequently aligned on top of each other to match the channel contours. The arrangement was fixed with two aluminium plates and then placed in an oven for 2 hours at 120 °C for thermal bonding, i.e., above the glass transition temperature of PVC but below its melting point. Then, the PVC sandwich was left to cool to room temperature. A leak test was subsequently carried out by injecting water into the channels.

The fabrication of UV-bonded chips involved the use of optically transparent cyclo-olefin polymer sheets (Zeonor, 1060R, 1.6 mm in thickness) and an UV curing adhesive (Norland, Optical Adhesive 61). In this case, the cut and cleaned sheets were oxygen plasma treated for 1 minute to enhance the wetting with the adhesive. Subsequently, both parts were aligned with the activated surface facing each other and held in position with an adhesive tape. A droplet of the optical adhesive was placed at the edge of the device to prime the contact area between both parts. The sandwich was then cured by UV light (320–400 nm, 3 Joules per cm²) for 10 minutes and subsequently left in an oven at 50 °C overnight to dry all residual adhesive and ensure maximum bonding strength.

Flow regimes characterisation

The formation of flow regimes was studied using the following experimental set-up (see ESI,† Fig. S3). Microfluidics chips were placed in a custom-built temperature-controlled chip holder that was connected with PTFE tubing. A binary 50/50 v/v liquid mixture of MeOH and 5CB (2 ml) was prepared and mixed at 40 °C in a temperature controlled quartz cuvette (Quantum Northwest, qpod 2e). Once the mixture was homogeneous and clear, the PTFE tubing was immersed in the solution. Flow rates were imposed with a 2.5 ml gas tight syringe connected to a syringe pump (Cronus, Sigma 1110) in withdrawal mode. The temperature of phase separation was controlled with a custom-built Peltier-based chip holder and the flow regimes were investigated with a digital microscope (Visio-Tek, IWT) that was placed on top of the microfluidic chips. Various rectangular channel architectures served in the course of this study, namely cross-sections of 500 × 500 μm²; 600 × 600 μm²; 700 × 700 μm²; 800 × 800 μm² and 900 × 900 μm². While thermally bonded PVC chips were used for the bulk of the study, high resolution images of the representative flow regimes of MeOH and 5CB were acquired using UV-cured Zeonor 1060R chips. In this case, a camera (Lumenera, Infinity 3–1) was connected to an optical microscope in transmission mode (Zeiss, Axio Scope A1) using differential interface contrast (PlasDIC) and recorded with the manufacturer's software (Lumenera, Infinity Analyze).

Experiments using binary liquid mixtures of water and 2,6-lutidine (70/30 v/v) were carried out in an analogous way, 2 ml of solution was prepared and mixed with a magnetic stir bar at room temperature. Once the mixture was homogeneous and clear, the PTFE tubing was immersed in the solution. The flow rate of the injected single-phase mixture was controlled with a 2.5 ml gas tight syringe in a syringe pump (Cronus, Sigma 1110). The flow regimes were observed at separation temperatures of 38 °C, 43 °C, 48 °C and 53 °C, respectively.

Results and discussion

This work is motivated by recent reports on the unique thermofluidic properties of 5CB in its native form^25–28 and our own findings related to the macroscopic phase behaviour of 5CB and MeOH.³⁰ When studied in the bulk, this mixture exhibits an UCST of 24.4 °C, a temperature range that can conveniently be accessed. Above the UCST, any composition is fully miscible and one single phase is observed. On the contrary, for a 50/50 v/v mixture below the UCST, two-phases coexist, one rich in MeOH and the other rich in 5CB. The phase composition after separation can be accurately predicted via the Lever rule. The deeper the temperature quench below the UCST, the purer the phases become in their principal component.

Temperature-dependent mixing

The mixing of pure 5CB and MeOH at temperatures above and below the UCST was investigated in a glass static micromixer with staggered oriented ridges that was mounted to a Peltier-controlled chip holder (Fig. 1a). At a chip temperature of 40 °C, 5CB and MeOH were transparent, indicating an isotropic state, and a length of mixing of around 60 mm was required to observe a single homogeneous phase (Fig. 1b). A similar behaviour was seen for a mixing temperature of 35 °C (Fig. 1c) and other temperatures above 24 °C.

Fig. 1 Temperature-dependent mixing of 5CB and MeOH, infused at the top (a1) and bottom (a2) inlet, respectively. Passive mixing was induced via a static micromixer with staggered oriented ridges (a3). (b–e) Snapshots of the microfluidic chip at various temperatures: 40 °C (b); 35 °C (c); 24 °C (d) and 12 °C (e).

These microfluidic observations are in close agreement with the T–φ phase diagram established in bulk experiments.³⁰ The interaction length needed to develop a fully mixed phase is related to the diffusivity of MeOH and 5CB in laminar regimes, as has previously been studied for other miscible liquids.³¹ The infused 5CB changed its appearance at the inlet, from transparent (Fig. 1b) to milky (Fig. 1c–e) for chip temperatures below 35 °C, indicating the expected phase transition of the liquid crystal from isotropic to nematic.³² However, once in contact with MeOH, the nematic infusion turned transparent before becoming a single phase with the MeOH infusion. This behaviour is related to the fact that 5CB exhibits a significant decrease in the isotropic-to-nematic phase transition temperature upon enrichment with MeOH, even for small volume fractions of MeOH.³⁰ When mixing at 24 °C (Fig. 1d), a temperature slightly below the previously reported UCST of 24.4 °C, we saw a biphasic annular-type flow pattern. For temperatures of more than 3 K below the UCST, slug flow was observed after the fluid streams passed through the micromixer (Fig. 1e). For a more detailed presentation of the mixing behaviour in the range of 40 °C to 12 °C, we refer to the ESI† (Fig. S4, ESI† video).

Microfluidic mixing of either miscible or immiscible blends can be achieved by elements to enhance diffusion, referred to as passive or active mixers depending on whether external energy is applied.³³ The setup used for this study introduces a combination of both to mix 5CB and MeOH, i.e. a passive static micromixer with an active control of temperature. While the use of passive mixers has been studied in detail using microfluidics, the control of temperature to enhance mixing in microfluidics remains relatively unexplored.³⁴ Some of the few examples include the use of two alternating heaters to enhance the natural convection of the miscible fluids¹⁹ and the use of a thermal bubble actuated nozzle-diffuse micro pump to create a wave interface that increases the contact area between immiscible liquids to accelerate the diffusion process.³⁵ From a thermodynamic point of view, the mixing obtained by those mixers rely on increasing the entropy of the system. In contrast, the strategy presented herein relates to the highly temperature-dependent enthalpy of mixing of the system, allowing to fine-tune the miscibility of the blend. The approach therefore leverages on the intrinsic molecular properties of the binary liquid mixture of 5CB and MeOH and offers unique opportunities for microfluidic applications. For example, a common limitation for mass transfer in liquid–liquid extraction with immiscible fluids is the need for the target compound to diffuse across the liquid–liquid interface.³⁶ The ability of this liquid mixture to form a single phase above the UCST allows for a temporary elimination of the liquid–liquid interface, thus simplifying the problem of mass transfer. We note that mixing was also achieved in other chip architectures, including split-ring micromixers as well as serpentine arrangements, where no passive mixing element was included to reduce the length of the mixing unit (see ESI,† Fig. S5).

Temperature driven phase separation in microchannels

The effect of quenching a single-phase 5CB/MeOH mixture (50/50 v/v) below the UCST was studied in a different experimental set-up by injecting the fluid at 30 °C into a homebuilt microfluidic chip made of PVC and investigating the phase separation behaviour upon cooling with an optical microscope. When the temperature of the solution reached the critical temperature, spontaneous emulsification was observed, as indicated by the appearance of small MeOH-rich droplets in a continuous 5CB-rich phase. The emulsification was discernible in the microscope as an opaque phase due to the large amount of small droplets that scattered the light isotropically. This opaqueness was transient and disappeared once the droplets grew by coalescence. After the initial microscopic phase separation took place, both phases spontaneously arranged inside the microfluidic channels to form highly regular flow patterns, without the need of passive or active flow elements.

To investigate the effect of the fluid velocity and temperature on the self-generated fluid patterns, we used microfluidic chips with different channel size (500 × 500 μm² to 900 × 900 μm²) and systematically varied the temperature (5 °C to 20 °C) and imposed flow rate (1 μl min⁻¹ to 100 μl min⁻¹). The velocity of each phase after phase separation, U, was estimated by dividing the flow rate by the channel cross-sectional area occupied by each phase after separation. Based on applying the Lever rule to the reported phase diagram, cooling of a 50/50 v/v 5CB/MeOH mixture results in two phases with equal volume, thus leading to equal velocities for the MeOH-rich and 5CB-rich phases (U_MeOH, U_5CB) inside the microchannels. It is important to note that in contrast to traditional systems with two independent inlets, our microfluidics configuration with mixed inlet phase does not provide an independent control over the respective flow velocities.

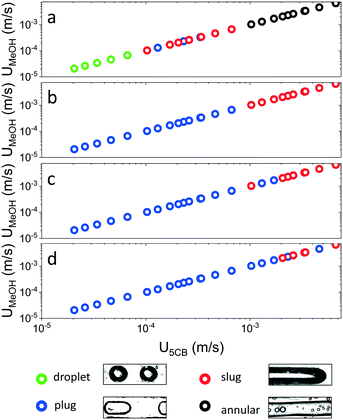
The phase-separated system attained four distinct self-arranged patterns, namely droplets, plugs, slugs, and annular flow, as shown in Fig. 2 as a function of the estimated fluid velocity U for four different temperatures. At 20 °C, droplets were perceived at velocities (U_MeOH, U_5CB) smaller than 0.0001 m s⁻¹. At higher velocities, the formed droplets extended in diameter beyond the width of the channel, resulting in so-called plugs, that were surrounded by a continuous 5CB phase. These plugs were observed for fluid velocities between 0.0001 m s⁻¹ and 0.0004 m s⁻¹. In close analogy to plug flow, we refer to slug flow when the characteristic length of the MeOH inclusion was at least 5 times the width of the channel.³⁷ Slug flow was found to occur for fluid velocities between 0.0001 m s⁻¹ and 0.001 m s⁻¹. At velocities above 0.001 m s⁻¹, annular flow was perceived. For a temperature of 15 °C and below, only plug flow was obtained for fluid velocities below 0.001 m s⁻¹. At higher velocities, we discerned slug flow, but the transition was temperature-dependent, with slug extending to higher velocities at lower temperatures. We note that a reminiscent dependence of flow patterns on flow velocities has been reported for an immiscible mixture of water and toluene,^38,39 which formed slug, slug-drop, a deformed interface, and parallel/annular flow, from low to high relative velocities respectively. However, the role of flow velocity alone is in our case not sufficient to describe our observed flow regimes.

Fig. 2 Estimated velocity of each phase after phase separation and corresponding two-phase regime. Four different regimes were observed, namely droplet, plug, slug and annular flow. a) 20 °C, b) 15 °C, c) 10 °C and d) 5 °C.

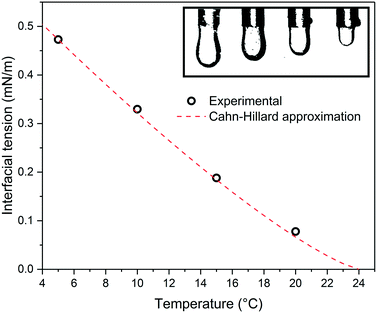
In order to relate the role of temperature to the fluid properties, we measured the temperature-dependent interfacial tension of the liquid mixture. The interfacial tension was determined via the pendant drop method, as shown in Fig. 3. In short, the binary liquid mixture was first heated above the UCST and then cooled to the target temperature. An aliquot of the 5CB rich bottom phase was then withdrawn from the bottom phase and immersed as droplet in the MeOH-rich top phase which then served for analysis. The measured interfacial tension was found to decrease as the temperature approached the UCST, from 0.47 mN m⁻¹ at 5 °C to 0.077mN m⁻¹ at 20 °C. The pronounced temperature effect on the interfacial tension is also visually evident, when observing the 5CB-rich droplet size in a MeOH-rich medium, shown in the upper right box of Fig. 3.

Fig. 3 Interfacial tension as a function of temperature. Values were determined via pendant drop experiments of 5CB-rich droplets immersed in a MeOH-rich phase. Representative droplets are shown in upper right box, from left to right at 5 °C, 10 °C, 15 °C and 20 °C.

The interfacial tension of a binary fluid below the UCST can be described by the Cahn–Hillard theory,⁴⁰

where A₀ is the critical amplitude of the interfacial tension near the critical point, T is a temperature below the UCST (or over the LCST), T_c is the UCST and μ is the characteristic universal exponent with an accepted empirical estimate of μ = 1.26.⁴¹A₀ is specific to the binary mixture. A value of A₀ = 15.92 ± 1.04 mN m⁻¹ was obtained herein for 5CB and MeOH by applying the experimental results for the interfacial tension at different temperatures to the Cahn–Hillard equation. When comparing the experimental data with the described approximation, it is evident that Cahn–Hillard model is appropriate to predict the interfacial tension below the UCST.

We relate this change in interfacial tension mainly to the compositional variation of the phases with temperature. At 20 °C, the mixture is very close to the UCST, and thus, both phases are more similar in composition, with around 30% of MeOH v/v dissolved in the 5CB-rich phase and a similar amount of 5CB mesogens dissolved in the MeOH-rich phase. As the temperature decreases, the composition of each phase becomes richer in its principal component, leading to an expected 16% of MeOH v/v dissolved in the 5CB rich phase at 5 °C. The change in composition also changes the density of each phase, making the 5CB-rich phase denser and MeOH-rich phase lighter as the temperature decreases (shown in the ESI,† Fig. S6). We refer to earlier studies on the role of composition-dependent density contrast for the interfacial tension of partially miscible liquids.^40,42,43

The results obtained herein are fundamentally different to previous reports on the interfacial tension of 5CB droplets immersed in immiscible matrices, i.e. water (with 1 mM CTAB) of or polydimethylsiloxane (PDMS).^44,45 In both cases, the obtained values were more than one order of magnitude higher as obtained herein and increased with temperature. The crucial effect of temperature on the interfacial tension is typical for solutions with an UCST and has been reported in a number of liquid–liquid systems, including cyclohexane/aniline,⁴⁶ MeOH/n-hexane,⁴⁷ and in polystyrene/cyclohexane.⁴⁸ According to our findings of molecular composition being the dominant factor for the interfacial tension, a solution with a LCST is expected to exhibit an inverse scaling with temperature. This is the case of the binary system 2,6-lutidine and water (LCST 34.1 °C), for which the reported interfacial tension increased from 0.007 mN m⁻¹ at 34.2 °C to 0.8 mN m⁻¹ at 60 °C.⁴⁹

The dynamic viscosity of the MeOH-rich and 5CB-rich phase after phase separation was measured with a rheometer (Discovery, HR-3) at 20 °C, 15 °C, 10 °C and 5 °C. The binary blend was heated to 40 °C in a temperature-controlled cuvette for uniform mixing and subsequently phase separated at a target temperature before aliquots of the upper and lower phase were separately extracted with a syringe. The obtained results are shown in the ESI† (Fig. S7). For the 5CB-rich phase, the measured dynamic viscosity was found to be inversely proportional to temperature, ranging from 26 mPa s at 5 °C to 7 mPa s at 20 °C. A less pronounced trend was observed for the MeOH-rich phase, where the dynamic viscosity was determined to be 0.76 mPa s at 5 °C and 0.33 mPa s at 20 °C, hence more than one order of magnitude lower than for the 5CB-rich phase. We note that for 2,6-lutidine/water, i.e. a binary liquid blend with a LCST, the dynamic viscosity was similarly reported to decrease with increasing temperature (while the interfacial tension increased with temperature as noted above).⁴⁹

An interplay of viscosity and interfacial tension with temperature has been previously reported in microfluidic studies of immiscible mixtures, such as water/mineral oil,²⁰ water doped with TiO2 nanoparticles/mineral oil,²¹ water/Dynalene SF and perfluoroperhydrophenanthrene,²² as well as gelatin emulsion/mineral oil.²³ In all cases, the dependence of the interfacial tension and viscosity on the temperature was found to be an important parameter for the control of droplet sizes and flow regimes. In contrast to previous studies, we investigate herein the behaviour of a binary liquid mixture with temperature-dependent phase composition, which consequently exhibits a more pronounced variability of fluid parameters with temperature. While in previous studies the interfacial tension of water and oil decreased from 52 mN m⁻¹ to 45 mN m⁻¹ for a temperature increase from 25 °C to 50 °C (i.e. by 10–15%),²¹ we were able to tune the interfacial tension from 0.47 mN m⁻¹ to 0.077 mN m⁻¹ through temperature variation from 5 °C to 20 °C, i.e. by a factor of 5.

Active flow pattern tuning

A direct application of using the 5CB/MeOH molecular system in microfluidics is the introduction of temperature as variable to control the self-arranged flow patterns. This is shown in Fig. 4, where an active tuning of the separated phases was achieved by exclusive variation of temperature at a constant flow rate and channel cross section. At the lower end of investigated temperature range (5 °C and below), where the interfacial tension of the mixture, density difference and dynamic viscosity of the phases were maximal, we found MeOH-rich plugs flowing in a 5CB-rich continuous phase. At a temperature of −1 °C (Fig. 4a), the continuous phase displayed a nematic arrangement, while at temperatures above, the 5CB-rich phase was in the isotropic state (Fig. 4b). As the temperature was increased to 10 °C, the pattern self-arranged to slug flow (Fig. 4b). Around 15 °C, a transitional behaviour was found towards the annular regime (Fig. 4c). At 20 °C, i.e. at minimal interfacial tension, density difference and dynamic viscosity of the phases, a fully developed annular flow was observed (Fig. 4d). Thus, this binary liquid mixture of 5CB and MeOH offers a new route to actively control flow regimes in microfluidics by its responsiveness to temperature. We note that the behaviour in this dynamic system was found to be completely reversible, i.e. identical flow patterns appeared when either heated or cooled towards the target temperature.

Fig. 4 Temperature-induced tuning of different flow patterns. Observed flow patterns at a fixed flow rate (70 μl min⁻¹) and channel cross section (700 × 700 μm²) with temperature as the only experimental variable: a) −1 °C, b) 5 °C, c) 10 °C, d) 15 °C and e) 20 °C. black arrow indicates flow direction.

To demonstrate the broad applicability of this approach, we studied the temperature-dependent flow patterns of a 30/70 v/v mixture of 2,6-lutidine/water with a LCST, where phase separation occurs upon heating. Please note that we chose an initial 30/70 v/v mixture, due to the phase separation of this blend ratio into equal relative volumes above the LCST. Three flow regimes were observed, namely plug, slug, and annular. Annular flow developed primarily at a temperature of 38 °C with fluid velocities between 0.003 and 0.006 m s⁻¹, while plug and slug flows were observed at temperatures above 38 °C and fluid velocities ranging from 0.00002 m s⁻¹ to 0.006 m s⁻¹. See the ESI,† with Fig. S8 for a schematic showing different flow regimes in dependence of temperature and fluid velocity and Fig. S9† for a flow regime diagram as a function of the phase velocity U at different temperatures.

We had recently reported the composition-dependent solvation of the two-phase 5CB/MeOH blend in macroscopic experiments towards target molecules, e.g. via π–π stacking.³⁰ The herein presented findings on the microfluidic mixing and separation behaviour makes this temperature-responsive approach an interesting candidate for selective extraction in multistage processes. Moreover, other blends composed of a liquid crystal with an alcohol such as 6CB/MeOH³⁰ and 5CB/ethanol⁵⁰ offer alternative temperature ranges where the phase separation can be tuned. The mixing and separation behaviour observed in 5CB/MeOH and 2,6-lutidine/water allows to anticipate the microfluidic properties of a wide variety of other liquid mixtures that exhibit a UCST or a LCST. Examples of such binary blends are cyclohexane/aniline,⁴⁶ methanol/n-hexane,⁴⁷ polystyrene/cyclohexane,⁴⁸ polyacrylamide/water, poly(acrylamide-co-acrylonitrile)/water,⁵¹ BMIMBF₄/water,⁵² OMIMBF₄/aliphatic and aromatic hydrocarbons,⁵³ ionic liquids/alcohols,⁵⁴n-propyl-tri-n-butylammonium iodide/water⁵⁵ as well as polymer ionic liquids with imidazolyl groups/water.⁵⁶

Conclusions

In conclusion, we report on the microfluidic behaviour of binary liquid mixtures with temperature-dependent miscibility. For a blend of the thermotropic liquid crystal 4-cyano-4′-pentylbiphenyl (5CB) and methanol (MeOH), mixing pure components (50/50 v/v) in microfluidic channels above the UCST (24.4 °C) led to a homogeneous single phase, while partial miscibility could be achieved below. Quenching the binary blend from a single phase inside the microchannel resulted in phase separation and spontaneous formation of very regular phase arrangements, namely in droplets, plug, slug and annular flow. The interfacial tension and the dynamic viscosity of the separated phases were found to be inversely proportional to the temperature, allowing active control over the flow regimes by temperature variation only, i.e. at constant channel architecture and flow rate. Our findings on tuning microfluidic flow by temperature-controlled manipulation of fluid properties are equally applicable to a binary mixture with LCST, here demonstrated for 2,6-lutidine and water, where an analogous but inverted behaviour was observed.

The use of binary liquid mixtures with temperature-dependent miscibility is in our view a promising approach for temperature-controlled microfluidics, in particular in applications involving multi-stage processes and mass transfer across interfaces. Applications of such molecular systems may be multi-fold and include drug delivery,⁵⁷ catalysis,⁵⁸ extraction and separation of bioactive compounds,⁵⁹ micelle-mediated pre-concentration protocols^60,61 and alternating current cloud point extraction.⁶²

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project received funding from the European Union's Q3 Horizon 2020 research and innovation programme under grant agreement No 633635 (DIACHEMO). The authors are grateful to Dr Nikolay Dimov for initial guidance on microfluidic design and fabrication methods and valuable support by Etienne Gianluca and Matej Janecek (EPFL) on pendant drop characterisation and analysis as well as Spyros Damilos (UCL) on the fabrication of microfluidics chips.

References

1. A. Manz, D. J. Harrison, E. M. J. Verpoorte, J. C. Fettinger, A. Paulus, H. Lüdi and H. M. Widmer, J. Chromatogr. A, 1992, 593, 253–258.
2. P. S. Dittrich and A. Manz, Nat. Rev. Drug Discovery, 2006, 5, 210–218.
3. C. D. Chin, V. Linder and S. K. Sia, Lab Chip, 2012, 12, 2118–2134.
4. S. K. Sia and G. M. Whitesides, Electrophoresis, 2003, 24, 3563–3576.
5. D. N. Breslauer, P. J. Lee and L. P. Lee, Mol. BioSyst., 2006, 2, 97–112.
6. S. Takayama, E. Ostuni, P. LeDuc, K. Naruse, D. E. Ingber and G. M. Whitesides, Chem. Biol., 2003, 10, 123–130.
7. G. M. Whitesides, Nature, 2006, 442, 368–373.
8. S. Xu, Z. Nie, M. Seo, P. Lewis, E. Kumacheva, H. A. Stone, P. Garstecki, D. B. Weibel, I. Gitlin and G. M. Whitesides, Angew. Chem., Int. Ed., 2005, 44, 724–728.
9. M. N. Kashid, A. Renken and L. Kiwi-Minsker, Chem. Eng. Sci., 2011, 66, 3876–3897.
10. K. K. Liu, R. G. Wu, Y. J. Chuang, H. S. Khoo, S. H. Huang and F. G. Tseng, Sensors, 2010, 10, 6623–6661.
11. H. Song, J. D. Tice and R. F. Ismagilov, Angew. Chem., Int. Ed., 2003, 42, 768–772.
12. M. S. G. Nandagopal, R. Antony and N. Selvaraju, Microsyst. Technol., 2016, 22, 349–356.
13. N. Schwesinger, T. Frank and H. Wurmus, J. Micromech. Microeng., 1996, 6, 99–102.
14. A. D. Stroock, S. K. W. Dertinger, A. Ajdari, I. Mezić, H. A. Stone and G. M. Whitesides, Science, 2002, 295, 647–651.
15. H. Song, M. R. Bringer, J. D. Tice, C. J. Gerdts and R. F. Ismagilov, Appl. Phys. Lett., 2003, 83, 4664–4666.
16. D. Ahmed, X. Mao, J. Shi, B. K. Juluri and T. J. Huang, Lab Chip, 2009, 9, 2738–2741.
17. L.-H. Lu, K. S. Ryu and C. Liu, in Micro Total Analysis Systems 2001, Springer, Netherlands, Dordrecht, 2001, pp. 28–30.
18. C. W. Yung, J. Fiering, A. J. Mueller and D. E. Ingber, Lab Chip, 2009, 9, 1171–1177.
19. S. J. Kim, F. Wang, M. A. Burns and K. Kurabayashi, Anal. Chem., 2009, 81, 4510–4516.
20. N. T. Nguyen, T. H. Ting, Y. F. Yap, T. N. Wong, J. C. K. Chai, W. L. Ong, J. Zhou, S. H. Tan and L. Yobas, Appl. Phys. Lett., 2007, 91, 084102.
21. S. M. S. Murshed, S. H. Tan and N. T. Nguyen, J. Phys. D: Appl. Phys., 2008, 41, 085502.
22. C. A. Stan, S. K. Y. Tang and G. M. Whitesides, Anal. Chem., 2009, 81, 2399–2402.
23. C. H. Yeh, K. R. Chen and Y. C. Lin, Microfluid. Nanofluid., 2013, 15, 775–784.
24. A. W. Francis, Critical solution temperatures, American Chemical Society, Washington, D. C., 1964, vol. 36.
25. A. Sengupta, U. Tkalec, M. Ravnik, J. M. Yeomans, C. Bahr and S. Herminghaus, Phys. Rev. Lett., 2013, 110, 048303.
26. A. Sengupta, Int. J. Mol. Sci., 2013, 14, 22826–22844.
27. Y.-K. Kim, B. Senyuk and O. D. Lavrentovich, Nat. Commun., 2012, 3, 1133.
28. T. Emeršič, R. Zhang, Ž. Kos, S. Čopar, N. Osterman, J. J. de Pablo and U. Tkalec, Sci. Adv., 2019, 5, eaav4283.
29. A. Daerr and A. Mogne, J. Open Res. Softw., 2016, 4, e3.
30. L. A. Serrano, M. J. Fornerod, Y. Yang, F. Stellacci and S. Guldin, Soft Matter, 2018, 14, 4615–4620.
31. J. Atencia and D. J. Beebe, Nature, 2005, 437, 648–655.
32. G. W. Gray, K. J. Harrison and J. A. Nash, Electron. Lett., 1973, 9, 130–131.
33. N. T. Nguyen and Z. Wu, J. Micromech. Microeng., 2005, 15, R1–R16.
34. K. Ward and Z. H. Fan, J. Micromech. Microeng., 2015, 25, 094001.
35. J. H. Tsai and L. Lin, J. Microelectromech. Syst., 2002, 11, 665–671.
36. A. L. Dessimoz, L. Cavin, A. Renken and L. Kiwi-Minsker, Chem. Eng. Sci., 2008, 63, 4035–4044.
37. H. Foroughi and M. Kawaji, Int. J. Multiphase Flow, 2011, 37, 1147–1155.
38. M. Kashid and L. Kiwi-Minsker, Chem. Eng. Process., 2011, 50, 972–978.
39. M. N. Kashid, A. Renken and L. Kiwi-Minsker, Ind. Eng. Chem. Res., 2011, 50, 6906–6914.
40. J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267.
41. J. S. Rowlinson and B. Widom, Molecular theory of capillarity, Dover Publications, 2002.
42. J. D. van der Waals, J. Stat. Phys., 1979, 20, 200–244.
43. M. E. Boudh-Hir and G. A. Mansoori, Phys. A, 1991, 179, 219–231.
44. P. K. Rai, M. M. Denn and C. Maldarelli, Langmuir, 2003, 19, 7370–7373.
45. J. W. Kim, H. Kim, L. Myoungbae and J. J. Magda, Langmuir, 2004, 20, 8110–8113.
46. D. Atack and O. K. Rice, Discuss. Faraday Soc., 1953, 15, 210–218.
47. S. Abbas, J. Satherley and R. Penfold, J. Chem. Soc., Faraday Trans., 1997, 93, 2083–2089.
48. J. S. Choi and Y. C. Bae, J. Chem. Eng. Data, 2016, 61, 4157–4163.
49. C. A. Grattoni, R. A. Dawe, C. Y. Seah and J. D. Gray, J. Chem. Eng. Data, 1993, 38, 516–519.
50. C. G. Reyes, J. Baller, T. Araki and J. P. F. Lagerwall, Soft Matter, 2019, 15, 6044–6054.
51. J. Seuring and S. Agarwal, Macromolecules, 2012, 45, 3910–3918.
52. J. E. L. Dullius, P. A. Z. Suarez, S. Einloft, R. F. De Souza, J. Dupont, J. Fischer and A. De Cian, Organometallics, 1998, 17, 815–819.
53. U. Domańska and A. Marciniak, J. Chem. Thermodyn., 2005, 37, 577–585.
54. J. M. Crosthwaite, M. J. Muldoon, S. N. V. K. Aki, E. J. Maginn and J. F. Brennecke, J. Phys. Chem. B, 2006, 110, 9354–9361.
55. M. Kleemeier, W. Schröer and H. Weingärtner, J. Mol. Liq., 1997, 73–74, 501–511.
56. H. Yoshimitsu, A. Kanazawa, S. Kanaoka and S. Aoshima, Macromolecules, 2012, 45, 9427–9434.
57. D. Schmaljohann, Adv. Drug Delivery Rev., 2006, 58, 1655–1670.
58. Y. Qiao, W. Ma, N. Theyssen, C. Chen and Z. Hou, Chem. Rev., 2017, 117, 6881–6928.
59. S. P. M. Ventura, F. A. E. Silva, M. V. Quental, D. Mondal, M. G. Freire and J. A. P. Coutinho, Chem. Rev., 2017, 117, 6984–7052.
60. C. D. Stalikas, TrAC, Trends Anal. Chem., 2002, 21, 343–355.
61. C. Bordier, J. Biol. Chem., 1981, 256, 1604–1607.
62. N. Sasaki, K. Hosokawa and M. Maeda, Lab Chip, 2009, 9, 1168–1170.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9me00127a

---