Oxazine: an anchoring group serving as functional kernels to construct single-molecule switches†
Shi
Li
a,
Yuxuan
Jiang
ab,
Yudi
Wang
 a,
Dongying
Lin
a,
Haoyang
Pan
ac,
Yongfeng
Wang
a,
Dongying
Lin
a,
Haoyang
Pan
ac,
Yongfeng
Wang
 a,
Stefano
Sanvito
d and
Shimin
Hou
a,
Stefano
Sanvito
d and
Shimin
Hou
 *ab
*ab
aKey Laboratory for the Physics and Chemistry of Nanodevices, School of Electronics, Peking University, Beijing 100871, China. E-mail: smhou@pku.edu.cn
bCentre for Nanoscale Science and Technology, Academy for Advanced Interdisciplinary Studies, Peking University, Beijing 100871, China
cInstitute of Spin Science and Technology, South China University of Technology, Guangzhou 511442, China
dSchool of Physics, AMBER and CRANN Institute, Trinity College, Dublin 2, Ireland
First published on 3rd January 2024
Abstract
As a central research target in molecular electronics, molecular switches have been extensively explored over the past decades. We theoretically demonstrate that when linking appropriate conjugated molecules to carbon electrodes, the de/rehydrogenation of 1,4-oxazine linkers efficiently switches single-molecule junctions between a low-conducting and a high-conducting state. This change is attributed to the modified energy gap of the central molecule as well as the charge rearrangement at the molecule–electrode interfaces. Based on the above findings, a single-molecule junction, employing an intramolecular proton transfer reaction as the switching mechanism, has been proposed. This realizes a maximum ON/OFF current ratio as high as 1.5 × 103. Furthermore, we show that an electrostatic gate field can control the proton transfer process and thus allow specific conductance states to be selected. Our findings provide a new perspective for the design of single-molecule switches relying on the anchoring groups rather than on the specific molecular backbones.
Introduction
Molecular electronics seeks to make full use of the characteristics of molecules to design and construct functional devices with the long-term goal of providing an alternative to traditional silicon-based technologies.1–4 As one of the key building blocks of electronic circuits, molecular switches interconverting between a high-conducting (“ON”) and a low-conducting (“OFF”) state have attracted much attention over the years.5–7 Two core issues in this field are how to construct single-molecule switches and how to efficiently control their electronic transport characteristics. To this end, various molecules with bistable and multistable states addressable via external stimuli, such as an electric field,8–15 light,16–24 pH,25–31 or mechanical forces,32–36 have been intensively investigated. For example, as typical photochromic molecules, azobenzene derivatives are able to isomerize reversibly between the cis and trans conformations under light irradiation and have been incorporated into single-molecule junctions as photoswitching units, realizing significant tuning of single-molecule conductance between the “ON” and “OFF” states.37–41 To the best of our knowledge, most of the studies to date have focused on the central molecule of a junction, while little research has been conducted to explore the potential of the anchoring groups. These link the central molecules to the electrodes and they may possibly work as switching kernels.The 1,4-oxazine molecule and its derivatives (Chart 1a), like phenoxazines and dioxazines, have sparked much interest owing to their numerous applications in the fields of pharmacology,42–45 photophysics46–50 and material science.51–55 Notably, the H atom bonded to the N atom in an oxazine ring can be controllably removed and re-added under certain conditions, introducing impressive flexibility to the molecule's chemical properties.56–59 Herein, we investigate the electronic transport properties of a set of oxazine-linked single-molecule junctions with carbon electrodes by employing the non-equilibrium Green's function formalism combined with density functional theory (that is, the so-called NEGF+DFT approach).60–64 This choice of carbon electrodes, graphene and single-walled carbon nanotubes (SWCNTs), is motivated by previous experimental and theoretical results demonstrating their advantageous applications in the construction of high-performance single-molecule devices operating at room and even higher temperatures.65–70 Our calculations show that, by connecting an anthracene molecule to graphene and SWCNT electrodes, the dehydrogenation of oxazine anchors triggers the switching of the investigated molecular junctions from an “OFF” to an “ON” state along with minor alterations of the junction geometry. This dramatic conductance switching effect is mainly attributed to the reduced energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the central molecule. Importantly, the conductance switching property of oxazine anchors is robust with respect to the curvature of SWCNT electrodes and moderate structural modifications of the molecular backbone.
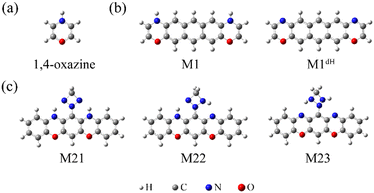 | ||
| Chart 1 The optimized atomic structures of the isolated 1,4-oxazine (a), M1/M1dH (b), and M21/M22/M23 (c). | ||
Furthermore, based on the above findings, we have considered a molecule with two oxazine rings as well as a triazetidine moiety (Chart 1c), which enables three stable tautomeric forms through intramolecular proton transfer. The molecular junctions incorporating these tautomers exhibit profoundly different low-bias conductance, realizing a maximum ON/OFF current ratio as high as 1.5 × 103. The intrinsic reaction coordinate (IRC) analysis suggests that the relative stability of the tautomers as well as the energy barrier for their interconversion can be controlled by means of an external electrostatic field, a feature that allows the specific conductance states to be selected.
Computational models and methods
Geometry optimization and electronic structure calculations have been performed by using SIESTA.71,72 SIESTA is an efficient DFT package, which implements improved Troullier–Martins pseudopotentials for describing the atomic cores and a finite-range numerical orbital basis set to expand the wave functions of the valence electrons.73 We construct a double zeta plus polarization (DZP) basis set for all the elements including H, C, N, and O. The exchange–correlation functional is treated at the level of the generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE) formulation.74 A conjugate gradient scheme is applied for geometry relaxation until the residual forces acting on the atoms are less than 0.02 eV Å−1. The vibrational and thermodynamic stabilities of the junctions constructed with SWCNT electrodes are verified by computing the phonon spectrum and performing molecular dynamics simulations (see Sections S1 and S2, ESI†).The electronic transport properties of single-molecule junctions have been investigated by using the SMEAGOL code, which is a practical implementation of the NEGF+DFT approach employing SIESTA as the DFT platform.75 The same pseudopotentials, basis set and GGA functional are used for both geometry relaxation and transport. The unit cell of the extended molecule consists of a central anthracene molecule, oxazine anchors, and two graphene or SWCNT electrodes with an armchair edge passivated with hydrogen atoms. Here, the transport is assumed to be along the z-axis and we always consider periodic boundary conditions in the plane transverse to transport. In order to model two-dimensional graphene electrodes, the distance between the neighboring graphene sheets is set to be 15 Å. The total transmission function T(E) of the junctions is evaluated as
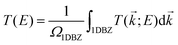 | (1) |
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) , E) is obtained as
, E) is obtained asT(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) , E) = Tr[ΓLGrMΓRGaM] , E) = Tr[ΓLGrMΓRGaM] | (2) |
Geometry optimization of the minima and transition states, vibrational frequency and intrinsic reaction coordinate (IRC) calculations have been carried out using the Gaussian16 DFT package.76–78 All DFT calculations are performed with the PBE density functional and the 6-311+G(d,p) basis set for H, C, N and O atoms. Harmonic frequency analysis confirms the stationary points as local minima (reactants and products) or first-order saddle points (transition states) and extracts zero-point vibrational energy (ZPE) corrections. IRC calculations are performed to verify that the reactant and the product are connected along the reaction pathway through the transition state.79,80
Results and discussion
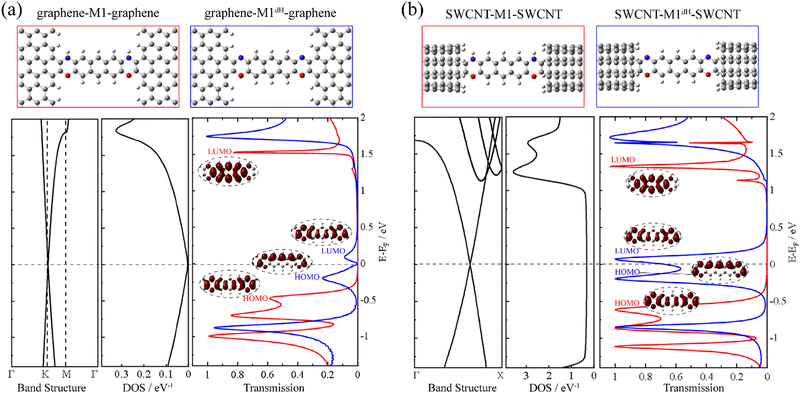
First, we construct a graphene-M1-graphene junction in which an anthracene molecule is sandwiched between two semi-infinite armchair-terminated graphene electrodes via oxazine anchoring groups. In order to find the equilibrium structure, we systematically vary the separation between the two graphene electrodes and optimize the positions of the anthracene molecule, the two oxazine groups and the atoms at the electrode edges until the total energy reaches a local minimum. The equilibrium transmission spectrum of graphene-M1-graphene (red line) is plotted in Fig. 1a, together with the conducting eigenchannels81,82 for selected transmission peaks around the Fermi level (EF). Clearly, these eigenchannels are not localized on the anthracene molecule but are delocalized along the entire central molecular backbone including the two oxazine anchors. Hence, here we consider M1 (Chart 1b) as the central molecule in the junction rather than anthracene. Combined with the inspection of the frontier molecular orbitals (FMOs) of M1 (see Fig. S6 in ESI†), it is confirmed that the transmission peaks centered at −0.50 eV and 1.51 eV originate from the M1 HOMO and LUMO, respectively. The HOMO-dominated peak decays rapidly toward EF and the LUMO-dominated peak lies far away from EF, both making minor contributions to the low-bias conductance of the graphene-M1-graphene junction. Then, we remove the two hydrogen atoms bonded to the nitrogen atoms and re-optimize the atomic structure of the junction, while keeping the electrode-to-electrode separation unchanged. Thus, we obtain a dehydrogenated junction labelled as graphene-M1dH-graphene. It is found that, upon dehydrogenation, the atomic structure of the junction undergoes minor changes; more specifically, all bond lengths vary by no more than 0.03 Å, even those at the molecule–electrode interfaces. A detailed comparison is shown in Fig. S7 (ESI†). The equilibrium transmission spectrum of the graphene-M1dH-graphene junction is also plotted in Fig. 1a with a blue line. The vertical axes of these transmission spectra are also set to a logarithmic scale in Fig. S8 (ESI†), highlighting their different transmission properties in the vicinity of the Fermi level. The M1dH HOMO- and LUMO-dominated transmission peaks now centered at −0.20 and 0.10 eV, respectively, both lie closer to EF and would definitely yield a considerable low-bias junction conductance. For example, the conductance of the graphene-M1dH-graphene junction is calculated to be 2.8 × 10−2 G0 at a bias voltage of 0.1 V, which is much greater than that (1.5 × 10−4 G0) of the graphene-M1-graphene junction at the same bias. Thus, dehydrogenation of oxazine anchoring groups results in a remarkable conductance enhancement.It is intriguing to observe that the closer to the Fermi level a state is, the lower the height of the transmission peak in Fig. 1a. This can be ascribed to the gradually decreasing density of states (DOS) of the pristine graphene electrode as the electron energy approaches the Fermi level.70,83 In order to decipher the effect of the electronic structure of graphene on the low transmission phenomena around EF, we replace the pristine graphene electrodes with (5,5) armchair SWCNT, which is a typical quasi-one-dimensional metal with a constant DOS around EF. The new molecular junctions are named SWCNT-M1-SWCNT and SWCNT-M1dH-SWCNT and the corresponding transmission spectra are displayed in Fig. 1b. As can be seen, when compared to those of the aforementioned junctions with graphene electrodes, the HOMO- and LUMO-dominated transmission peaks are enormously enhanced in SWCNT-M1-SWCNT and SWCNT-M1dH-SWCNT, while their energy locations undergo limited changes. Consequently, the transmission coefficient for SWCNT-M1-SWCNT is less than 0.01 from −0.3 to 1.0 eV, representing a steady “OFF” state of the switch at low bias voltages. In contrast, the transmission coefficient for SWCNT-M1dH-SWCNT is very high (>0.60) over a broad energy window around EF, roughly going from −0.4 to 0.2 eV. This can be used as an “ON” state of the switch.
Another possibility to enhance the low-bias conductance of graphene-M1dH-graphene is to replace the pristine graphene electrodes with nitrogen-doped (N-doped) ones, in which the Dirac point is shifted below EF and the DOS around EF increases markedly due to the additional π-electrons brought by the nitrogen dopants.70,83,84 Importantly, a remarkable conductance switching effect is also observed in this type of junction. In fact, after substituting one carbon atom with nitrogen in a rectangular unit cell of graphene containing 40 atoms, as shown in Fig. S9 (ESI†), the transmission spectrum of the junction after dehydrogenation towers over that of the junction before dehydrogenation in a broad energy range around EF. Overall, our calculations demonstrate that the dehydrogenation of oxazine anchoring groups triggers the molecular junctions with different types of carbon electrodes to switch from an “OFF” to an “ON” state along with minor alterations of the junction geometry.
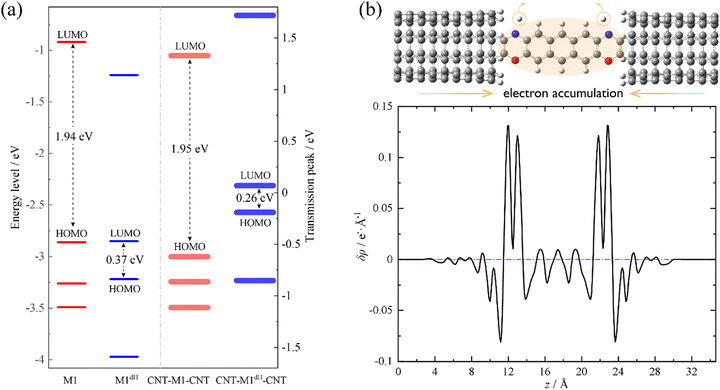
We now move to unveil the origin of this dramatic conductance switching effect. It is well known that the conductance of a single-molecule junction is determined by two fundamental factors: first, the alignment of the FMOs relative to the Fermi level of the electrodes and, second, the electronic coupling between the FMOs and the electrode continuum of states.85,86 Coarsely speaking, the former dictates the energy locations of transmission peaks relative to the electrode Fermi level and the latter influences the width and height of the transmission peaks. Evidently, the conductance switching effect along with the dehydrogenation of oxazine anchors is mainly dictated by the first factor. As shown in Fig. 2a, we compare the energy levels of the isolated molecules M1 (red thin lines) and M1dH (blue thin lines), together with the energy centers of the corresponding transmission peaks of the SWCNT-M1-SWCNT (red thick lines) and SWCNT-M1dH-SWCNT (blue thick lines) junctions. It should be noted that the vacuum level is taken as the energy origin for the molecular orbitals of the isolated molecules, whereas in the junctions the Fermi level is set to zero. The M1 HOMO−1, HOMO, and LUMO lie at −3.26, −2.86 and −0.92 eV, respectively, with a HOMO–LUMO gap of 1.94 eV. Upon dehydrogenation, the M1 HOMO becomes unoccupied and the new HOMO and LUMO of the dehydrogenated molecule M1dH (a singlet biradical) lie at −3.22 and −2.85 eV, respectively. That is to say, in the case of isolated molecules, the HOMO–LUMO gap is drastically reduced from 1.94 eV to 0.37 eV due to the dehydrogenation of the oxazine rings. Furthermore, when coupling to the state continuum of the carbon electrodes, the molecular levels further shift by the interaction between the central molecule and the two electrodes. This often occurs with charge transfer at the molecule–electrode interfaces, equalizing the chemical potential across the entire junction. Importantly, this charge-transfer process critically depends on the chemical identity of the anchoring groups. According to the Mulliken population analysis, we find that the central molecule (indicated by the shaded oval in Fig. 2b) is slightly positively charged (+0.03 e) in the SWCNT-M1-SWCNT junction but moderately negatively charged (−0.36 e) in the SWCNT-M1dH-SWCNT one. This suggests that the anchors are turned from electron donors to electron acceptors upon dehydrogenation, leading to a net electron transfer of about 0.4 e from the electrodes to the central molecule. In order to visually comprehend the charge rearrangement induced by dehydrogenation, we investigate the xy-plane averaged charge density difference δρ between SWCNT-M1-SWCNT (ρ0) and SWCNT-M1dH-SWCNT (ρdH), namely
| δρ(z) = ρdH(z) − ρ0(z) | (3) |
It should be noted that the conductance switching property of the oxazine anchoring groups is robust, to a certain extent, with respect to variations of both the electrodes and the central molecular backbone. Not only the curvature of the SWCNT electrodes (see Fig. S10a in the ESI†) but also the symmetry of the oxazine linkers on both sides of the junction (see Fig. S10b in the ESI†) have limited influence on the transport especially around EF. As shown in Fig. S11 (ESI†), the central benzene ring in M1 is substituted with an electron-donating group (oxhydryl) or an electron-withdrawing group (cyano), and the corresponding transport spectra suggest that the switching effect is immune to moderate structural modifications caused by chemical functionalization. Furthermore, when the molecular backbone is altered from an anthracene molecule to a benzene or hexacene (see Fig. S12 in the ESI†), the impressive promotion of the low-bias junction conductance upon dehydrogenation has always been observed although the transport spectra undergo great changes. Previous studies have shown that oxazine derivatives can convert between the two states with and without dehydrogenation under certain experimental conditions.56–59 Hence, we believe that 1,4-oxazine has the potential to function as a promising switch unit to construct single-molecule switches by linking suitable conjugated molecules to carbon electrodes.
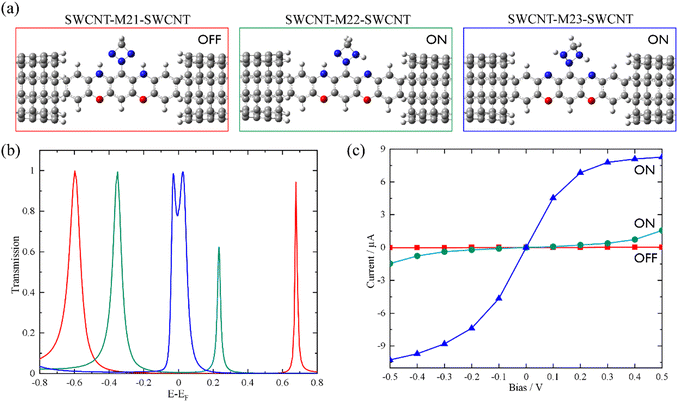
Based on the above findings, we next propose a molecular switch employing an intramolecular proton transfer reaction mechanism. As sketched in Chart 1c, we consider a molecule (denoted by M23) which has two dehydrogenated oxazine rings at both sides as well as a triazetidine moiety that substitutes on the central benzene. The molecule M23 with a singlet biradical character has two stable tautomeric forms M21 and M22, which can interconvert into each other through intramolecular proton transfer between the oxazine and triazetidine moieties. M21, M22 and M23 are sandwiched between two semi-infinite (5,5) SWCNT electrodes and the electronic transport properties of the corresponding junctions, namely, SWCNT-M21-SWCNT, SWCNT-M22-SWCNT and SWCNT-M23-SWCNT, have been investigated. From Fig. 3b, one can see clearly that the three tautomers deliver extremely different zero-bias transport properties and for each junction there are two prominent transmission peaks in the energy interval [−0.8 eV, +0.8 eV]. Combined with the inspection of the FMOs of the isolated molecules M21-M23 (see Fig. S13 in the ESI†), we confirm that the transmission peaks below and above EF can be respectively assigned to the HOMO and LUMO of the corresponding central molecule. Importantly, there is a clear trend, namely along with the dehydrogenation of oxazine anchoring groups (in other words, the intramolecular proton transfer from oxazine to triazetidine moieties), the HOMO- and LUMO-dominated transmission peaks gradually approach EF and result in an increasing transmission coefficient at EF. More in detail, the HOMO- and LUMO-dominated transmission peaks of SWCNT-M21-SWCNT are located at −0.60 and 0.68 eV, respectively, leading to a transmission coefficient at EF as small as 9.5 × 10−4. In contrast, the HOMO- and LUMO-dominated transmission peaks of SWCNT-M22-SWCNT (SWCNT-M23-SWCNT) are centered at −0.35 eV (−0.025 eV) and 0.23 eV (0.025 eV), respectively, leading to an enhanced transmission coefficient of 1.1 × 10−2 (8.2 × 10−1) at EF, which is roughly one (three) order(s) of magnitude larger than that of SWCNT-M21-SWCNT. Fig. 3c depicts the current–voltage (I–V) characteristics of these three junctions, which are calculated at finite bias voltages up to ±0.5 V with an interval of 0.1 V. These I–V curves show that SWCNT-M22-SWCNT and SWCNT-M23-SWCNT are more conducting than SWCNT-M21-SWCNT in the entire applied-voltage range. Note that the electrode-to-electrode separations are held unchanged during the proton transfer process and, in this sense, these three junctions can be regarded as three states of a switch: SWCNT-M21-SWCNT is the “OFF” state, while SWCNT-M22-SWCNT and SWCNT-M23-SWCNT realize two possible “ON” states. The maximum ON/OFF current ratio between SWCNT-M23-SWCNT (SWCNT-M22-SWCNT) and SWCNT-M21-SWCNT is ∼1.5 × 103 (∼40), found at a bias voltage of 0.1 V (0.4 V). The average values over the voltage range from −0.5 to 0.5 V are approximately 800 and 30 for the SWCNT-M23-SWCNT and SWCNT-M22-SWCNT junctions, respectively.
The HOMO–LUMO gaps of M21, M22, and M23 are respectively calculated to be 1.21, 0.54, and 0.07 eV, that is, the intramolecular proton transfer drastically reduces the HOMO–LUMO gap of the isolated molecules, analogous to the variation observed between M1 and M1dH (see Fig. S14 in the ESI†). According to Mulliken population analysis of these single-molecule junctions, intramolecular proton transfer induces remarkable electron reorganization inside the central molecule, mainly between the oxazine and triazetidine moieties. Specifically, the triazetidine moiety is negatively charged (−0.14 e) in SWCNT-M21-SWCNT but positively charged (+0.23 e) in SWCNT-M22 (M23)-SWCNT. However, the charge transfer between the central molecule and the two SWCNT electrodes is small: the central molecule is slightly positively charged (+0.07 e) in SWCNT-M21-SWCNT as well as in SWCNT-M22-SWCNT but slightly negatively charged (−0.06 e) in SWCNT-M23-SWCNT. Roughly speaking, although the dehydrogenation converts the oxazine anchoring groups from an electron donor to an electron acceptor, the ensuing charge rearrangement at the molecule–electrode interfaces is moderate, a fact that has a limited influence on the alignment of the FMOs relative to the Fermi level. As a result, the energy separations between the HOMO- and LUMO-dominated transmission peaks of the SWCNT-M21-SWCNT, SWCNT-M22-SWCNT, and SWCNT-M23-SWCNT junctions are 1.28, 0.58, and 0.05 eV, respectively, comparable to the HOMO–LUMO gap of the corresponding isolated molecules. Hence, the low-bias conductance enhancement here is mainly attributed to the decreased HOMO–LUMO gaps.
Having established that the designed molecular junction could support three stable conformational forms with robust differences in the low-bias conductance, a possible reversible mechanism among these ON and OFF states is outlined in what follows. This is achieved by controlling the intramolecular proton transfer process via an external electrostatic field as in a field-effect transistor configuration. To this end, we have performed the intrinsic reaction coordinate (IRC) calculations of the proton transfer process at the level of isolated molecules. The black lines in Fig. 4 and Fig. S15 (ESI†) depict the energy pathways for proton transfer without an external field. It is found that M21 is the most stable structure among these three tautomers, with M22 and M23 respectively lying 0.63 and 1.22 eV above M21. The calculated energy barriers from M21 to M22 and from M22 to M23 are 0.80 and 1.08 eV, respectively. Nevertheless, an external electrostatic field (marked with a black arrow in the inset of Fig. 4) applied in the plane of the molecule and perpendicular to its longitudinal axis could lower the energy barrier height for the proton transfer process. In particular, upon applying an electric field of about 1.1 V Å−1, the barrier for the M21-to-M22 transformation is reduced to 0.30 eV and now M22 is more stable than M21. An inversion of the relative stability under an external electric field is also obtained for M22 and M23 (see Fig. S15 in the ESI†). These calculations suggest that without an external gate field, the single-molecule switch tends to work in the SWCNT-M21-SWCNT form; in other words, at the “OFF” state. However, an external electrostatic gate field could trigger the switch to the “ON” state working in the SWCNT-M22 (M23)-SWCNT form. Although the calculated field strength needed for the stabilization of the “ON” states is rather high for direct experimental realization, appropriate chemical modifications of the central molecule may facilitate a more accessible interconversion at much reduced field strengths. Here, we simply provide a proof of concept that conductance control using an external electrostatic field is feasible for oxazine-anchored molecular junctions.
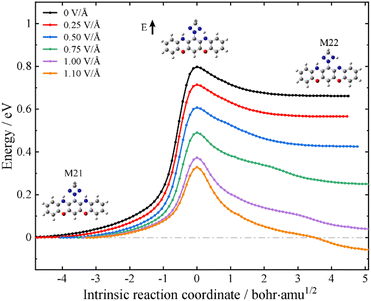 | ||
| Fig. 4 Energy along the intrinsic reaction path from M21 to M22 in the gas phase. The electric field vector is indicated by a black arrow in the inset. | ||
Conclusions
In summary, by employing the NEGF+DFT approach, we have investigated the electronic transport properties of molecular junctions in which an anthracene molecule is connected to graphene and SWCNT electrodes via oxazine anchors. Our calculations show that the dehydrogenation of oxazine anchors triggers the transition of the investigated molecular junctions from an “OFF” to an “ON” state along with minor alterations of the junction geometry. The dehydrogenation of oxazine rings not only reduces the HOMO–LUMO gap of the isolated molecule, but also introduces electron transfer from the electrodes to the central molecule in the junctions. This causes both the HOMO- and LUMO-dominated transmission peaks to approach the Fermi level. Furthermore, a molecule with two oxazine rings and a triazetidine moiety, which enables three stable tautomeric forms through intramolecular proton transfer, has been investigated. By sandwiching it between two (5,5) armchair SWCNT electrodes, these tautomers exhibit profoundly different low-bias conductances and the maximum ON/OFF current ratio is as high as 1.5 × 103. By applying an external electrostatic field, the relative stability of the tautomers, as well as the energy barrier for their interconversion, can be effectively controlled. Our findings demonstrate that 1,4-oxazine serves as a promising switch kernel when linking appropriate conjugated molecules to carbon electrodes. This provides a new perspective for the design and construction of single-molecule switches relying on the anchoring groups and not on the specific molecular backbones.Author contributions
Shi Li and Shimin Hou conceived the idea. Shi Li carried out the theoretical calculations, data analysis and wrote the initial draft. Yuxuan Jiang, Yudi Wang, Dongying Lin and Haoyang Pan carried out parts of theoretical calculations and helped to discuss and analyze the calculation results. Yongfeng Wang, Stefano Sanvito and Shimin Hou critically reviewed and helped to revise and polish the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was supported by the National Natural Science Foundation of China (Grant No. 21933002 and 22225202) and the High-performance Computing Platform of Peking University. SS thanks the Science Foundation Ireland (AMBER Center grant 12/RC/2278_P2) for financial support.Notes and references
- A. Nitzan and M. A. Ratner, Science, 2003, 300, 1384–1389 CrossRef CAS PubMed.
- M. L. Perrin, E. Burzuri and H. S. J. van der Zant, Chem. Soc. Rev., 2015, 44, 902–919 RSC.
- F. Evers, R. Korytar, S. Tewari and J. M. van Ruitenbeek, Rev. Mod. Phys., 2020, 92, 035001 CrossRef CAS.
- H. Fu, X. Zhu, P. Li, M. Li, L. Yang, C. Jia and X. Guo, J. Mater. Chem. C, 2022, 10, 2375–2389 RSC.
- L. Sun, Y. A. Diaz-Fernandez, T. A. Gschneidtner, F. Westerlund, S. Lara-Avila and K. Moth-Poulsen, Chem. Soc. Rev., 2014, 43, 7378–7411 RSC.
- J. L. Zhang, J. Q. Zhong, J. D. Lin, W. P. Hu, K. Wu, G. Q. Xu, A. T. S. Wee and W. Chen, Chem. Soc. Rev., 2015, 44, 2998–3022 RSC.
- G. Ke, C. Duan, F. Huang and X. Guo, InfoMat, 2020, 2, 92–112 CrossRef CAS.
- V. Meded, A. Bagrets, K. Fink, R. Chandrasekar, M. Ruben, F. Evers, A. Bernand-Mantel, J. S. Seldenthuis, A. Beukman and H. S. J. van der Zant, Phys. Rev. B, 2011, 83, 245415 CrossRef.
- I. Diez-Perez, Z. H. Li, S. Y. Guo, C. Madden, H. L. Huang, Y. K. Che, X. M. Yang, L. Zang and N. J. Tao, ACS Nano, 2012, 6, 7044–7052 CrossRef CAS PubMed.
- Y. Cao, S. H. Dong, S. Liu, Z. F. Liu and X. F. Guo, Angew. Chem., Int. Ed., 2013, 52, 3906–3910 CrossRef CAS PubMed.
- X. F. Guo, Adv. Mater., 2013, 25, 3397–3408 CrossRef CAS PubMed.
- M. L. Perrin, C. J. O. Verzijl, C. A. Martin, A. J. Shaikh, R. Eelkema, J. H. van Esch, J. M. van Ruitenbeek, J. M. Thijssen, H. S. J. van der Zant and D. Dulic, Nat. Nanotechnol., 2013, 8, 282–287 CrossRef CAS PubMed.
- V. Rabache, J. Chaste, P. Petit, M. L. Della Rocca, P. Martin, J. C. Lacroix, R. L. McCreery and P. Lafarge, J. Am. Chem. Soc., 2013, 135, 10218–10221 CrossRef CAS PubMed.
- B. Capozzi, Q. S. Chen, P. Darancet, M. Kotiuga, M. Buzzeo, J. B. Neaton, C. Nuckolls and L. Venkataraman, Nano Lett., 2014, 14, 1400–1404 CrossRef CAS PubMed.
- P. Zhou, J. T. Zheng, T. Y. Han, L. J. Chen, W. Q. Cao, Y. X. Zhu, D. H. Zhou, R. H. Li, Y. Y. Tian, Z. T. Liu, J. Y. Liu and W. J. Hong, Nanoscale, 2021, 13, 7600–7605 RSC.
- D. Gust, T. A. Moore and A. L. Moore, Chem. Commun., 2006, 1169–1178 RSC.
- C. Schaefer, R. Eckel, R. Ros, J. Mattay and D. Anselmetti, J. Am. Chem. Soc., 2007, 129, 1488–1489 CrossRef CAS PubMed.
- C.-J. Xia, K. Gao, D.-H. Zhang, M. Yang and F.-L. Feng, J. Appl. Phys., 2014, 116, 083704 CrossRef.
- T. Sendler, K. Luka-Guth, M. Wieser, J. Wolf, M. Helm, S. Gemming, J. Kerbusch, E. Scheer, T. Huhn and A. Erbe, Adv. Sci., 2015, 2, 1500017 CrossRef PubMed.
- A. Vezzoli, R. J. Brooke, S. J. Higgins, W. Schwarzacher and R. J. Nichols, Nano Lett., 2017, 17, 6702–6707 CrossRef CAS PubMed.
- J. F. Zhou, K. Wang, B. Q. Xu and Y. Dubi, J. Am. Chem. Soc., 2018, 140, 70–73 CrossRef CAS PubMed.
- A. S. Kozlenko, I. V. Ozhogin, A. D. Pugachev, M. B. Lukyanova, I. M. El-Sewify and B. S. Lukyanov, Top. Curr. Chem., 2023, 381, 8 CrossRef CAS PubMed.
- L. Ma, G. Tian and J.-T. Lu, Phys. Rev. B, 2022, 106, 165416 CrossRef CAS.
- P. Li, Y. Chen, B. Wang, M. Li, D. Xiang, C. Jia and X. Guo, Opto-Electron. Adv., 2022, 5, 210094 CAS.
- Z. H. Li, M. Smeu, M. A. Ratner and E. Borguet, J. Phys. Chem. C, 2013, 117, 14890–14898 CrossRef CAS.
- Z. H. Li, M. Smeu, S. Afsari, Y. J. Xing, M. A. Ratner and E. Borguet, Angew. Chem., Int. Ed., 2014, 53, 1098–1102 CrossRef CAS PubMed.
- M. Baghernejad, C. Van Dyck, J. Bergfield, D. R. Levine, A. Gubicza, J. D. Tovar, M. Calame, P. Broekmann and W. J. Hong, Chem. – Eur. J., 2019, 25, 15141–15146 CrossRef CAS PubMed.
- C. Zhan, G. Wang, X. G. Zhang, Z. H. Li, J. Y. Wei, Y. Si, Y. Yang, W. J. Hong and Z. Q. Tian, Angew. Chem., Int. Ed., 2019, 58, 14534–14538 CrossRef CAS PubMed.
- H. Audi, Y. Viero, N. Alwhaibi, Z. Chen, M. Iazykov, A. Heynderickx, F. Xiao, D. Guerin, C. Krzeminski, I. M. Grace, C. J. Lambert, O. Siri, D. Vuillaume, S. Lenfant and H. Klein, Nanoscale, 2020, 12, 10127–10139 RSC.
- C. L. Wu, A. Alqahtani, S. Sangtarash, A. Vezzoli, H. Sadeghi, C. M. Robertson, C. X. Cai, C. J. Lambert, S. J. Higgins and R. J. Nichols, Nanoscale, 2020, 12, 7914–7920 RSC.
- F. Yang, F. Chen, X. H. Wu, J. Luo, X. S. Zhou, J. R. Horsley, A. D. Abell, J. X. Yu, S. Jin and B. W. Mao, J. Phys. Chem. C, 2020, 124, 8496–8503 Search PubMed.
- J. J. Parks, A. R. Champagne, T. A. Costi, W. W. Shum, A. N. Pasupathy, E. Neuscamman, S. Flores-Torres, P. S. Cornaglia, A. A. Aligia, C. A. Balseiro, G. K. L. Chan, H. D. Abruna and D. C. Ralph, Science, 2010, 328, 1370–1373 CrossRef CAS PubMed.
- S. J. van der Molen and P. Liljeroth, J. Phys.: Condens. Matter, 2010, 22, 133001 CrossRef PubMed.
- F. Prins, M. Monrabal-Capilla, E. A. Osorio, E. Coronado and H. S. J. van der Zant, Adv. Mater., 2011, 23, 1545–1549 CrossRef CAS PubMed.
- S. Caneva, P. Gehring, V. M. Garcia-Suarez, A. Garcia-Fuente, D. Stefani, I. J. Olavarria-Contreras, J. Ferrer, C. Dekker and H. S. J. van der Zant, Nat. Nanotechnol., 2018, 13, 1126–1131 CrossRef CAS PubMed.
- M. C. Walkey, C. R. Peiris, S. Ciampi, A. C. Aragones, R. B. Dominguez-Espindola, D. Jago, T. Pulbrook, B. W. Skelton, A. N. Sobolev, I. D. Perez, M. J. Piggott, G. A. Koutsantonis and N. Darwish, ACS Appl. Mater. Interfaces, 2019, 11, 36886–36894 CrossRef CAS PubMed.
- S. Kurihara, D. Yoneyama and T. Nonaka, Chem. Mater., 2001, 13, 2807–2812 CrossRef CAS.
- A. S. Kumar, T. Ye, T. Takami, B.-C. Yu, A. K. Flatt, J. M. Tour and P. S. Weiss, Nano Lett., 2008, 8, 1644–1648 CrossRef CAS PubMed.
- C. C. Huang, S. J. Chen, K. B. Ornso, D. Reber, M. Baghernejad, Y. C. Fu, T. Wandlowski, S. Decurtins, W. J. Hong, K. S. Thygesen and S. X. Liu, Angew. Chem., Int. Ed., 2015, 54, 14304–14307 CrossRef CAS PubMed.
- M. J. Comstock, N. Levy, A. Kirakosian, J. Cho, F. Lauterwasser, J. H. Harvey, D. A. Strubbe, J. M. J. Frechet, D. Trauner, S. G. Louie and M. F. Crommie, Phys. Rev. Lett., 2007, 99, 038301 CrossRef PubMed.
- J. M. Mativetsky, G. Pace, M. Elbing, M. A. Rampi, M. Mayor and P. Samori, J. Am. Chem. Soc., 2008, 130, 9192–9193 CrossRef CAS PubMed.
- I. Kmentova, H. S. Sutherland, B. D. Palmer, A. Blaser, S. G. Franzblau, B. Wan, Y. Wang, Z. Ma, W. A. Denny and A. M. Thompson, J. Med. Chem., 2010, 53, 8421–8439 CrossRef CAS PubMed.
- M. M. Luebtow, L. Hahn, M. S. Haider and R. Luxenhofer, J. Am. Chem. Soc., 2017, 139, 10980–10983 CrossRef CAS PubMed.
- M. Sauer, K. H. Drexhage, U. Lieberwirth, R. Muller, S. Nord and C. Zander, Chem. Phys. Lett., 1998, 284, 153–163 CrossRef CAS.
- O. Sedlacek and R. Hoogenboom, Adv. Ther., 2020, 3, 1900168 CrossRef.
- P. Beaujean, F. Bondu, A. Plaquet, J. Garcia-Amoros, J. Cusido, F. M. Raymo, F. Castet, V. Rodriguez and B. Champagne, J. Am. Chem. Soc., 2016, 138, 5052–5062 CrossRef CAS PubMed.
- M. Tomasulo and F. M. Raymo, Org. Lett., 2005, 7, 4633–4636 CrossRef CAS PubMed.
- M. Tomasulo, S. Sortino and F. M. Raymo, Org. Lett., 2005, 7, 1109–1112 CrossRef CAS PubMed.
- M. Tomasulo, S. Sortino, A. J. P. White and F. M. Raymo, J. Org. Chem., 2005, 70, 8180–8189 CrossRef CAS PubMed.
- J. Vogelsang, T. Cordes, C. Forthmann, C. Steinhauer and P. Tinnefeld, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 8107–8112 CrossRef CAS PubMed.
- L. Han, D. Iguchi, P. Gil, T. R. Heyl, V. M. Sedwick, C. R. Arza, S. Ohashi, D. J. Lacks and H. Ishida, J. Phys. Chem. A, 2017, 121, 6269–6282 CrossRef CAS PubMed.
- M. Hintersteiner, A. Enz, P. Frey, A. L. Jaton, W. Kinzy, R. Kneuer, U. Neumann, M. Rudin, M. Staufenbiel, M. Stoeckli, K. H. Wiederhold and H. U. Gremlich, Nat. Biotechnol., 2005, 23, 577–583 CrossRef CAS PubMed.
- A. Laobuthee, S. Chirachanchai, H. Ishida and K. Tashiro, J. Am. Chem. Soc., 2001, 123, 9947–9955 CrossRef CAS PubMed.
- B. P. Mathew, A. Kumar, S. Sharma, P. K. Shukla and M. Nath, Eur. J. Med. Chem., 2010, 45, 1502–1507 CrossRef CAS PubMed.
- P. Panizzi, M. Nahrendorf, M. Wildgruber, P. Waterman, J.-L. Figueiredo, E. Aikawa, J. McCarthy, R. Weissleder and S. A. Hilderbrand, J. Am. Chem. Soc., 2009, 131, 15739–15744 CrossRef CAS PubMed.
- B. Zhao, K. Ranguelova, J. Jiang and R. P. Mason, Free Radic. Biol. Med., 2011, 51, 153–159 CrossRef CAS PubMed.
- Y. Zhang, P. Song, Q. Fu, M. Ruan and W. Xu, Nat. Commun., 2014, 5, 4238 CrossRef CAS PubMed.
- R. Usui, K. Yamamoto, H. Okajima, K. Mutoh, A. Sakamoto, J. Abe and Y. Kobayashi, J. Am. Chem. Soc., 2020, 142, 10132–10142 CrossRef CAS PubMed.
- Y. Wu, W. Liu, T. Liu, F. Li, T. Xiao, Q. Wu and Y. He, ChemElectroChem, 2018, 5, 2171–2175 CrossRef CAS.
- M. Brandbyge, J. L. Mozos, P. Ordejon, J. Taylor and K. Stokbro, Phys. Rev. B, 2002, 65, 165401 CrossRef.
- Y. Q. Xue, S. Datta and M. A. Ratner, Chem. Phys., 2002, 281, 151–170 CrossRef CAS.
- J. Zhang, S. Hou, R. Li, Z. Qian, R. Han, Z. Shen, X. Zhao and Z. Xue, Nanotechnology, 2005, 16, 3057–3063 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- Y. Cao, S. Dong, S. Liu, L. He, L. Gan, X. Yu, M. L. Steigerwald, X. Wu, Z. Liu and X. Guo, Angew. Chem., Int. Ed., 2012, 51, 12228–12232 CrossRef CAS PubMed.
- C. Jia, B. Ma, N. Xin and X. Guo, Acc. Chem. Res., 2015, 48, 2565–2575 CrossRef CAS PubMed.
- H. Sadeghi, S. Sangtarash and C. Lambert, Nano Lett., 2017, 17, 4611–4618 CrossRef CAS PubMed.
- X. F. Guo, J. P. Small, J. E. Klare, Y. L. Wang, M. S. Purewal, I. W. Tam, B. H. Hong, R. Caldwell, L. M. Huang, S. O'Brien, J. M. Yan, R. Breslow, S. J. Wind, J. Hone, P. Kim and C. Nuckolls, Science, 2006, 311, 356–359 CrossRef CAS PubMed.
- Z. Qian, S. Hou, J. Ning, R. Li, Z. Shen, X. Zhao and Z. Xue, J. Chem. Phys., 2007, 126, 084705 CrossRef PubMed.
- Y. Wang, H. Pan, D. Lin, S. Li, Y. Wang, S. Sanvito and S. Hou, Phys. Chem. Chem. Phys., 2022, 24, 21337–21347 RSC.
- A. Garcia, N. Papior, A. Akhtar, E. Artacho, V. Blum, E. Bosoni, P. Brandimarte, M. Brandbyge, J. I. Cerda, F. Corsetti, R. Cuadrado, V. Dikan, J. Ferrer, J. Gale, P. Garcia-Fernandez, V. M. Garcia-Suarez, S. Garcia, G. Huhs, S. Illera, R. Korytar, P. Koval, I. Lebedeva, L. Lin, P. Lopez-Tarifa, S. G. Mayo, S. Mohr, P. Ordejon, A. Postnikov, Y. Pouillon, M. Pruneda, R. Robles, D. Sanchez-Portal, J. M. Soler, R. Ullah, V. W. Z. Yu and J. Junquera, J. Chem. Phys., 2020, 152, 204108 CrossRef CAS PubMed.
- J. M. Soler, E. Artacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and D. Sanchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- N. Troullier and J. L. Martins, Phys. Rev. B, 1991, 43, 1993–2006 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. R. Rocha, V. M. Garcia-Suarez, S. Bailey, C. Lambert, J. Ferrer and S. Sanvito, Phys. Rev. B, 2006, 73, 085414 CrossRef.
- J. Andzelm and E. Wimmer, J. Chem. Phys., 1992, 96, 1280–1303 CrossRef CAS.
- J. A. Pople, P. M. W. Gill and B. G. Johnson, Chem. Phys. Lett., 1992, 199, 557–560 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS.
- R. Li, S. Hou, J. Zhang, Z. Qian, Z. Shen and X. Zhao, J. Chem. Phys., 2006, 125, 194113 CrossRef PubMed.
- M. Paulsson and M. Brandbyge, Phys. Rev. B, 2007, 76, 115117 CrossRef.
- Z. Jiang, H. Wang, Y. Wang, S. Sanvito and S. Hou, J. Phys. Chem. C, 2017, 121, 27344–27350 CrossRef CAS.
- Y. Li, X. Tu, H. Wang, S. Sanvito and S. Hou, J. Chem. Phys., 2015, 142, 164701 CrossRef PubMed.
- S. Braun, W. R. Salaneck and M. Fahlman, Adv. Mater., 2009, 21, 1450–1472 CrossRef CAS.
- X. Crispin, V. Geskin, A. Crispin, J. Cornil, R. Lazzaroni, W. R. Salaneck and J. L. Bredas, J. Am. Chem. Soc., 2002, 124, 8131–8141 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc03720g |
| This journal is © The Royal Society of Chemistry 2024 |