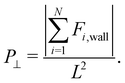Core-softened colloid under extreme geometrical confinement
Leandro B.
Krott†
a,
Thiago
Puccinelli
b and
José Rafael
Bordin†
 *b
*b
aCentro de Ciências, Tecnologias e Saúde, Campus Araranguá, Universidade Federal de Santa Catarina. Rua Pedro João Pereira, 150, CEP 88905120, Araranguá, SC, Brazil. E-mail: leandro.krott@ufsc.br
bDepartamento de Física, Instituto de Física e Matemática, Universidade Federal de Pelotas. Caixa Postal 354, CEP 96001-970, Pelotas, RS, Brazil. E-mail: thiagoponogueira@gmail.com; jrbordin@ufpel.edu.br
First published on 6th May 2024
Abstract
Geometrical constraints offer a promising strategy for assembling colloidal crystal structures that are not typically observed in bulk or under 2D conditions. Core-softened colloids, in particular, have emerged as versatile chemical building blocks with applications across various scientific and technological areas. In this study, we investigate the behavior of a core-softened model confined between two parallel walls. Employing molecular dynamics simulations, we analyze the system's response under extreme confinement, where only one or two layers of colloids are permitted. The system comprises particles modeled by a ramp-like potential confined within slit nanoslits created by two flat, purely repulsive walls with a lateral side L separated by a distance Lz. Through a systematic analysis of the phase behavior as Lz increases, or as the system undergoes decompression, for different values of L, we identified a mono-to-bilayer transition associated with changes in the colloidal structure. In the monolayer regime, we observed solid phases at lower densities than those observed in the 2D case. Importantly, we demonstrated that confinement at specific Lz values, allowing particle arrangement into two layers, can lead to the emergence of the square phase, which was not observed under monolayer or 2D conditions. By correlating thermodynamic, translational, and orientational ordering, as well as the dynamics of this confined colloidal system, our findings offer valuable insights into the utilization of geometrical constraints to induce and manipulate structural changes.
1 Introduction
Understanding the behavior of soft colloids is pivotal for various applications, including drug delivery, colloidal crystal formation, and nanoporous materials synthesis, as well as nanotechnology.1,2 Hard core-soft shell colloids consist of a rigid or hard core surrounded by a soft, deformable shell, finding utility in diverse fields such as self-assembly, encapsulation, and controlled release.3,4For example, polymeric core–shell particles typically comprise a solid, often inorganic core such as silica or polystyrene, enveloped by a soft polymer shell like polyethylene glycol (PEG) or poly(N-isopropylacrylamide) (PNIPAM). Similarly, microgel particles typically feature a soft, deformable shell encasing a crosslinked polymer hard core. The softness of these colloids imparts unique properties due to the simple interplay between the hard core and soft shell length scales in their interactions. Moreover, the straightforward control over the characteristic length scales makes them excellent chemical building blocks for obtaining a wide variety of bottom-up self-assembled morphologies in nanostructured materials.5–10
In this regard, it is noteworthy how confinement within narrow slits significantly alters the behavior of colloidal systems, introducing unique dynamics and properties.11–15 In these constrained spaces, colloidal and solute particles experience restricted motion and altered interactions,11,16,17 leading to distinctive phenomena compared to bulk systems.18 Confinement can induce structural changes, such as the formation of ordered and disordered layers of particles.14,19 Moreover, the presence of surfaces in close proximity can influence particle–surface interactions, resulting in adsorption or depletion effects. By adjusting the slit size, shape, and surface properties, it is possible to manipulate phase transitions and enhance colloidal stability,12,17,20–23 impacting the rheological and mechanical properties of the system.24–26 Therefore, by precisely tuning the dimensions and surface properties of the confining environment, researchers can exert control over colloidal assembly, manipulate nucleation kinetics, and control the formation of crystal polymorphs, enabling the design of novel materials with tailored functionalities for various applications.17,27–32
Many core-softened (CS) approaches have been proposed to model these complex fluids, including ramp-like, square and ramp shoulders, exponential, Hertzian, multi-Hertzian, and Gaussian potentials.33–42 For instance, in the work by Grillo and co-authors,5 a Hertzian potential was employed to reproduce the distinct patterns observed in soft colloids at liquid–liquid interfaces. Interestingly, they found that a key ingredient to observe a large variety of micropatterns is to first immobilize two layers of colloids onto a solid substrate one after the other. This approach allowed them to obtain structures that would not be observed if the particles were assembled in a single step at the water–oil interface. Another colloidal system with competitions between two conformations is composed of pure or grafted PEG colloids, polymer-grafted nanoparticles, and star polymers, and many studies have indicated that these systems are well described by ramp-like potentials.43–48 This approach assumes that the repulsive interactions between these macromolecules arise from a gradual increase in repulsion as these colloids approach each other, often mimicking the behavior of a ramp. This model accounts for the steric repulsion between polymer chains, which dominates the interactions at short distances, while also incorporating the effects of the particle's hard core.49 Originally proposed by Hemmer and Stell50 to study polyamorphism, many ramp-like potentials, continuous or discontinuous, have been employed to study systems with two characteristic length scales and their unique behavior, which includes solid and liquid polymorphism, polyamorphism, and water-like anomalies.33,51–65 Thus, ramp-like models are able to reproduce what is observed in experiments, such as colloidal clustering, formation of self-assembled mesophases, layering packing, and even synthesis of new structures.66–72
De Oliveira and colleagues have demonstrated that a continuous ramp-like shape can be constructed by combining a Lennard-Jones potential with a Gaussian well. This simple and purely repulsive model was initially used to reproduce and study water-like anomalies in bulk73,74 and under confinement.75,76 Recently, we revisited this 3D bulk model,77 uncovering the solid phases for this model and demonstrating that an order-disordered transition in the solid phase is related to the water-like anomalies. In the 2D limit, Cardoso et al.78 have shown that this model can reproduce complex tessellations observed in experiments. For instance, in the work by Rey et al.,79 it was observed that poly(N-isopropylacrylamide) nanogels can assemble into distinct patterns at liquid–liquid interfaces, including two triangular (or hexagonal) phases, one densely packed and one less dense, as well as stripe and square phases. The ramp-like model employed in this work also exhibits two distinct triangular phases, which we refer to as low and high-density triangular phases, respectively, and a stripe pattern phase,78 as observed in the aforementioned experimental investigation.79 Triangular and stripe patterns were also experimentally observed in the self-assembly of superparamagnetic spheres.66 Additionally, the polymer-like fluid, where colloids form linear aggregates, obtained in experiments of poly(ethylene glycol) chains grafted onto poly(styrene) particles, was reproduced by the potential. Also, this spherically symmetric approach led to a Kagome lattice phase, similar to the one reported experimentally for patchy colloids.80,81 Additionally, the ramp-like model led to reentrant melting phases between the distinct crystals, which are related to a second and a third region of water-like anomalies, and later shown that these extra anomalous regions vanish as the system transitions from a 2D-like, layered regime under confinement to the 3D limit.19 This, along with inspiration from experimental works,5,66,79 led to another question: if confinement can induce anomalous regions, can it induce new crystalline morphologies in the system?
To answer this question, we carried out molecular dynamics simulations of this CS fluid confinement in narrow slits – going from the limit where only one (2D limit) layer of colloids can fit and isothermically expanding to wider slits where two layers can fit. Our findings show how it is possible to obtain specific morphologies by tuning the wall separations, including a square crystal that was not observed in the 2D case. Combining thermodynamic, dynamic, and structural analysis, we demonstrate how the distinct structures can be obtained by simply controlling the nanoslits size. This paper is organized as follows: in Section 2, we present the model, the methods, and simulation details; in Section 3, we show and discuss the results; and in Section 4, we present the conclusions.
2 The model and simulation details
Molecular dynamics simulations involve solving Newton's equations for particle systems, calculating their positions and velocities while considering the interaction forces resulting from the potential energy U(r).82 The CS interaction in our system was constructed by combining a short-range attractive Lennard-Jones potential plus a repulsive Gaussian term centered at r0, with depth u0 and width c0.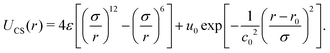 | (1) |
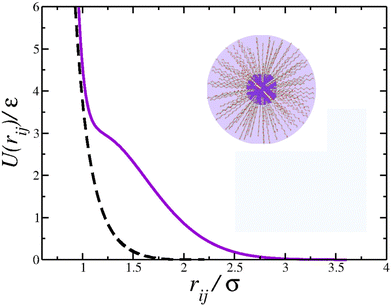
Using the parameters u0 = 5ε, c02 = 1.0, and r0/σ = 0.773,74,77,83 the potential 1 exhibits the ramp-like shape shown in Fig. 1 (solid purple line). As de Oliveira and co-authors have shown,84 both the real and the imaginary branch of the instantaneous normal mode (INM) spectra of this potential have a pronounced bimodality which must be connected with two different length scales – unlike simple liquids, as Lennard Jones fluids, who have only one scale. The first length-scale, correspondent to the hard-core, is located near r1 = 1.2σ, where the force has a local minimum,84 while the longer length scale, the soft corona, is located at r = 2.0σ, where the fraction of imaginary modes of the INM spectra has a local minimum and a maximum is expected in the radial distribution function84 – a schematic depiction of a polymer grafted nanoparticle as a CS particle can be seen in the inset of Fig. 1. Also, this specific set of parameters allowed us the observe distinct patterns in the 2D system, as open and close triangular lattices, stripes, kagome lattice,78 which are also obtained experimentally.5,66,80 The cutoff radius for the interaction is rc = 3.5σ.
In our system, N = 1000 particles were confined between parallel, smooth walls, whose interaction potential is purely repulsive, given by R6 potential, as follow19,23,85
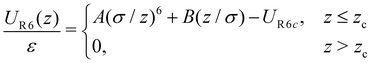 | (2) |
The simulations were conducted using a custom-made program in the canonical ensemble, which maintains a fixed number of particles N, volume V, and temperature T. A quasi-2D geometry was achieved by placing fixed confining walls with an area of L × L in the xy-plane separated by a distance Lz. Subsequently, systems with distinct separations, ranging between 2.0 and 4.4, were simulated. In these scenarios, the systems formed either one or two layers, referred to as monolayers or bilayers, respectively.
The particle density ρ is calculated as
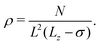 | (3) |
The temperature was held constant using the Nosé–Hoover thermostat with a coupling parameter Q = 2, and the equations of motion were integrated using the velocity Verlet algorithm. Simulations were conducted with 1 × 106 time steps for equilibration, followed by an additional 1 × 106 time steps to obtain averages and results. A time step of δt = 0.001 was considered. Equilibrium was monitored by analyzing pressure and energy as functions of time. Our simulations were performed along the isotherm T = 0.075, where both the 2D and 3D cases are in the solid phase.77,78
The structure was analyzed by means of the lateral radial distribution function (LRDF) g‖(r‖), defined as
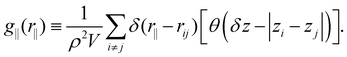 | (4) |
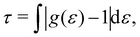 | (5) |
The cumulative two-body entropy also is a property obtained from the LRDF and a useful tool to analyze the particles longer-range structure. It is defined as90
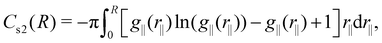 | (6) |
The orientational order for particles inside a slab of thickness δz = σ was characterized with the bond orientational order parameter Ψl,
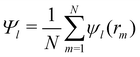 | (7) |
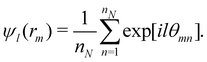 | (8) |
Once the strong confinement in the z-direction prevents diffusion along this axis, we proceeded to evaluate the dynamics within the xy-plane using the lateral diffusion coefficient,
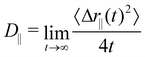 | (9) |
Furthermore, due to the slab geometry, it is important to compute the perpendicular pressure, P⊥, defined by
All quantities used in our simulations were given in LJ units.82 Some examples of reduced units are: reduced distance r* = r/σ, reduced temperature T* = kbT/ε, reduced pressure P* = σ2P/ε and reduced time 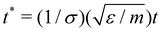 . For simplicity, the * will be omitted.
. For simplicity, the * will be omitted.
3 Results and discussion
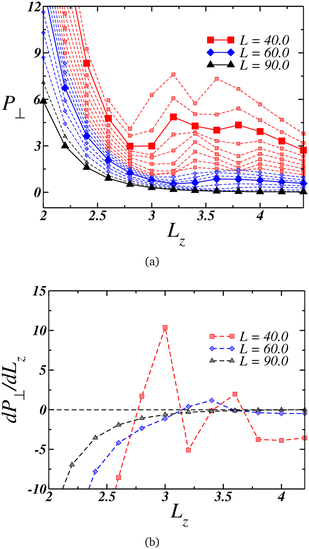
Under strong confinement, the pressure in the perpendicular direction to the nanoslit walls is strongly influenced by the slit size. It is relevant, then, to analyze the behavior of the perpendicular pressure, P⊥, as a function of the nanoslit width Lz. In that sense we illustrate in Fig. 2(a) the distinct behaviors of P⊥ for different wall sizes L.The larger plates exhibit a smooth behavior, as highlighted by the black triangles connected by the solid lines for L = 90.0, with the pressure decreasing as Lz increases. This behavior is reinforced by its derivative, shown in Fig. 2(b) depicted by the black triangles. On the other hand, at intermediate values of L, the perpendicular pressure initially decreases with Lz expansion down to a minimum, then increases to a maximum and decreases once again. This loop-like behavior is highlighted in Fig. 2(a) by the blue curves, with the curve for L = 60.0 being highlighted with blue diamonds connected by a solid line.
Although this behavior contradicts intuition since one would anticipate a decrease in P⊥ as the nanoslit size grows, it is striking how this pattern resembles a van der Waals loop observed in phase transitions. At lower L's, not only one but two loops were observed, as evidenced by the red square curves in Fig. 2(a), with the case L = 40.0 being highlighted with a solid line. The derivative of this curve is shown in Fig. 2(b). Similar van der Waals loops were observed in a previous work for the present model related to structural transitions between two and three layers.94 Therefore, we can expect that here it can be also related to it. For this reasons, a useful quantity to analyze at this point is the density profile along the confined direction.
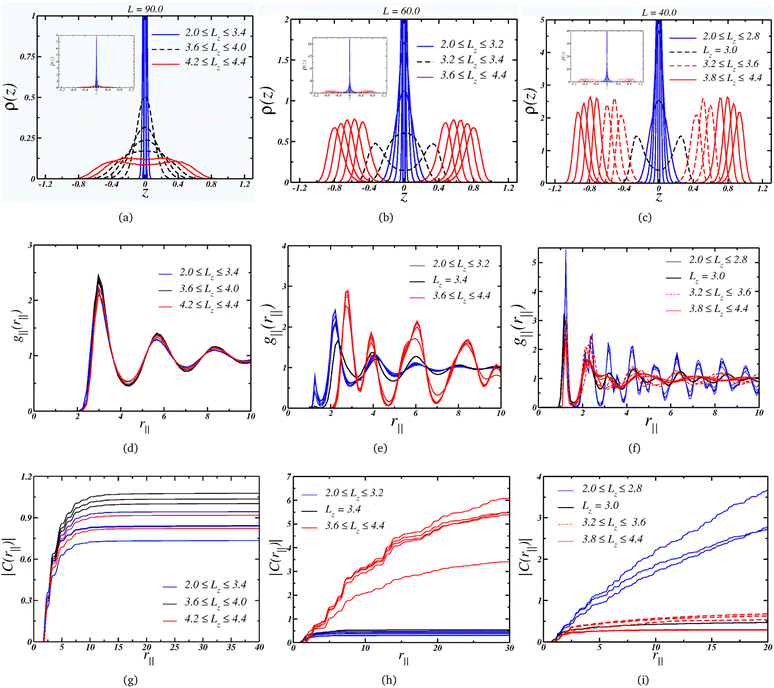
Starting with the case where L = 90.0, we can see from Fig. 3(a) that the system assumes a single-layer arrangement, or monolayer, when it is strongly compressed. This is indicated by the blue curves and the inset. As the separation, Lz, increases, the layer thickness also increases, as shown by the dashed black curves. For the wider nanoslits, the density profile assumes a bulk-like profile, represented by the red curves. Although for the larger separation, Lz = 4.4, there are two layers, the fact that ρ(z) ≠ 0 in the space between them indicates that the particles can change from one layer near a wall to another layer, exhibiting fluid-like behavior.
We can also check the colloidal particles arrangement by looking at the LRDF for this wall size, Fig. 3(d): essentially the same fluid-like g‖(r‖) is observed for all values of separation. The long-range translational ordering isn't affected, as indicated by the convergence of the cumulative two-body entropy in Fig. 3(g). Then, although there is a change from a 2D-like layering to a bulk-like layering, there is no change in the lateral structure, but as a consequence, the P⊥ × Lz curve is smooth. Also, the density range for this plate separation, L = 90, goes from ρ = 0.124 when Lz = 2.0 to ρ = 0.036 for the wider plate separation, Lz = 4.4. This means that the system is in a low density regime.
Moving on to the case, where the plate size L = 60.0 corresponds to a intermediate density regime, with 0.277 ≥ ρ ≥ 0.081 along the decompression curve. The Fig. 3(b) indicates that the arrangement goes from quasi-2D under high compression to a thicker monolayer as Lz increases – similar to the L = 90.0 case. However, the scenario changes when the separation is large enough to accommodate two layers. The black dashed curves show the separations where the layer splits into two well-defined layers – or the mono-to-bilayer transition. Interestingly, this transition from a monolayer to a bilayer coincides with the loop in P⊥ illustrated in Fig. 2(a).
Moreover, the LRDF indicates that the loop for L = 60.0 is also associated with a change in the colloids' structure. As depicted in Fig. 3(e), when the particles are arranged in a monolayer fashion, they display a fluid-like g‖(r‖) with short-range ordering, transitioning to a solid-like g‖(r‖) with longer-range ordering for wider nanoslits. This behavior might seem counter-intuitive, since one would expect a loss in ordering under decompression. However, this can be attributed to the properties of core-softened colloids.77,78 We illustrate in Fig. 3(e) that, as Lz expands, the occupancy in the first length scales diminishes while growing in the second length scale. The larger slit allows the particles to conform to a well-defined structure dominated by this greater length scale, while higher compression – or density – frustrates the system, leading to a less ordered structure dominated by the closer length scale. As indicated by the |C(r‖)| in Fig. 3(h), the solid-like phase exhibits long-range ordering, spanning to a distance R = L/2, whereas the fluid-like phase displays short-range ordering, converging at short distances.
Finally, the L = 40.0 case,where the system is in a higher density regime, 0.625≥ρ≥0.183, is depicted in Fig. 3(c), also exhibits a loop corresponding to the transition from a mono to a bi-layer arrangement. On the other hand, the second loop is associated with an increase in the peak in ρ(z) as Lz expands, as observed by comparing this case with the L = 60.0 case. Additionally, under the condition of small Lz, the colloids adopt a solid-like structure with long-range ordering, as shown in Fig. 3(f). Upon decompression, the structure transits to a fluid-like ordering, as indicated by the dashed red lines – this order–disorder transition corresponds to the first loop in Fig. 2(a). The second loop emerges when the fluid structure changes, as evident from the comparison of the dashed and solid curves in Fig. 3(f), resulting in a loss of longer-range ordering. This is supported by the cumulative two-body entropy. In the monolayer region, Fig. 3(i) suggests long-range ordering. Conversely, in the bilayer regime, two distinct behaviors are observed: both indicate short-range ordering, but one (the solid lines, corresponding to the wider slits) is shorter. This transition between two disordered phases corresponds to the second loop in Fig. 2.
To relate the fluid structure and mobility, we can juxtapose the behavior of the translational and orientational order parameters τ and Ψl with the self-diffusion coefficient D, illustrated in Fig. 4(a), (b), and (c), respectively. For instances with two loops, such as L = 40.0, we observe that τ diminishes with the plates' separation – as expected, given by the decreasing density. However, we can delineate three regimes: the ordered one, within the monolayer structure, and two exhibiting lower ordering in the bilayer region. Notably, the orientational pair ordering, Ψ2, also escalates. Evaluating the values of Ψl in the 2D-limit (Lz = 2.0), they resemble those observed in the Kagome phase for the 2D scenario,78,95 and, as depicted in Fig. 5(a), the system indeed adopts a Kagome monolayer crystal structure. Consequently, upon decompression, it transitions into two distinct clusterized fluids: at intermediate Lz values, worm-like clusters emerge (the initial fluid phase in the bilayer regime, Fig. 5(b)), and as Lz increases, these clusters break into smaller, dimer-like formations, as shown in Fig. 5(c) – for clarity, particles in different layers are color-coded (blue or red). Additionally, the diffusion coefficient, illustrated in Fig. 4(c), indicates that in the Kagome phase, particles are practically immobile – akin to a solid phase. Subsequently, they exhibit slow diffusion in the worm-like fluid phase and heightened mobility in the dimer-like fluid conformation. Consequently, we are able to illustrate the scenario along the P⊥ × Lz curve: the initial loop corresponds to a transition from a Kagome crystal to a worm-like fluid, coinciding with the colloids transitioning from a monolayer to bilayer arrangement. The subsequent loop denotes a transition between two clusterized fluids: worm-like and dimer-like.
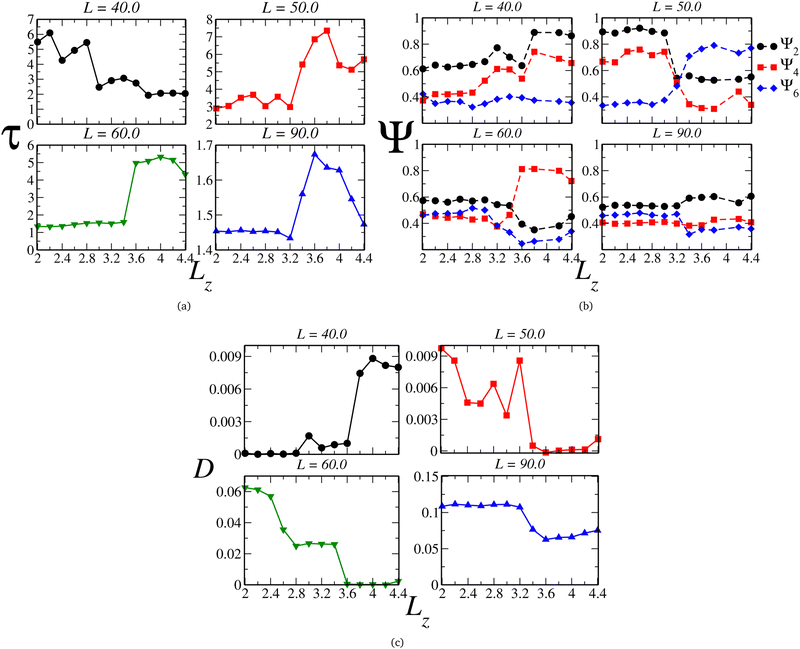 | ||
| Fig. 4 (a) Translational (τ) and (b) orientational (Ψ), respectively, ordering parameters and (c) lateral diffusion coefficient as function of Lz. | ||
Once the scenario for this curve was revealed, we applied this procedure to all the other curves in diagram 2(a). Along the curves with one loop, which are associated with the mono-to-bilayer transition, we observed distinct morphologies evolving in those transitions. For instance, let's compare the L = 50.0 and L = 60.0 cases. They correspond to densities ranges 0.400 ≥ ρ ≥ 0.118 and 0.277 ≥ ρ ≥ 0.081, respectively. The parameter τ, displayed in Fig. 4(a), indicates that along both curves, the system shifts from a less ordered to a more ordered morphology. Likewise, the diffusion coefficient D, illustrated in Fig. 4(c), signals a transition from higher to lower mobility. However, for L = 50.0, the less ordered phase indeed exhibits a value of τ that indicates high ordering, whereas for L = 60.0, τ aligns more closely with structured fluids.74,77,96 Additionally, we can observe in Fig. 4(b) that for L = 50.0, the system boasts a high value of Ψ2 in the monolayer regime, corresponding to a Stripe phase, as depicted in Fig. 5(d). As the slit expands allowing the formation of two layers, Ψ6 rises and dominates the particle orientation, as expected for a triangular phase. In our previous works,78,95 we referred to this as a Low-Density Triangular (LDT) phase, given that the particle separation equals the soft shell scale, as seen in Fig. 3(e). The snapshot in Fig. 5(d) showcases the LDT lattice in both layers – here, we connected the blue colloids separated by distances smaller than rb = 3.0 for better visualization of the LDT structure. Therefore, for L = 50.0, the loop in Fig. 2(a) constitutes a transition between two ordered phases: a Stripe phase in the monolayer regime to an LDT phase in the bilayer structure.
When it comes to the mono-to-bilayer transition for L = 60.0, the scenario is different. Here, there is a monolayer fluid for narrower slits, characterized by lower translational and orientational ordering and higher diffusion, and an ordered phase inside wider slits with D ≈ 0, as indicated by Fig. 4(a), (b), and (c) respectively. Even more surprisingly, the higher value of Ψ4 in the bilayer ordered phase indicates a square phase that was not observed in the 2D case.78 In fact, the snapshots in Fig. 5(f) and (g) support the fluid-to-square crystal transition associated with the mono-to-bilayer transition. Furthermore, it is worth noting that the square phase was only observed when the system was arranged in two layers – no single-layer case exhibited this crystalline structure. This observation, coupled with the absence of this phase in bulk 2D, reinforces that this morphology is induced by confinement in our model. These findings align with those obtained by Grillo and colleagues:5 the frustration induced by the confinement between two walls led to the square morphology that was not observed in the 2D case.78 Also, is relevant to remember that a square phase was not observed in the simulations for this model, but can be found in another CS models.97
Finally, even for the case where there is no loop in the P⊥ × Lz curve, we can observe effects of the mono-to-bilayer transition. For the case where L = 90.0, when the system is in the fluid phase, it is observed that the translational and orientational order parameters are smaller compared to the ordered phases, with respect to the value of Lz. Also, we would expect a decrease in fluid ordering and an increase in diffusion as the density decreases – or, in our case, as the slit widens. However, we can see in Fig. 4(a), (b), and (c) that for L = 90.0, this transition corresponds to an increase in τ and Ψ2 and a decrease in D. Although the model employed in this work, depicted by eqn (1), does exhibit water-like anomalies – indicating an increase in ordering and decrease in diffusion under expansion – we believe that confinement also plays a role, particularly in fluid dynamics. Fig. 4(c) displays a sharp decrease in D when there is enough space to start the formation of the second layer – as shown in Fig. 5(h) and (i), the snapshots for the system at Lz = 3.2 and Lz = 3.6, where the system transitions from higher to lower diffusion regimes – and where the density distribution width is changing from the 2D limit to the bilayer regime, as depicted in Fig. 3(a).
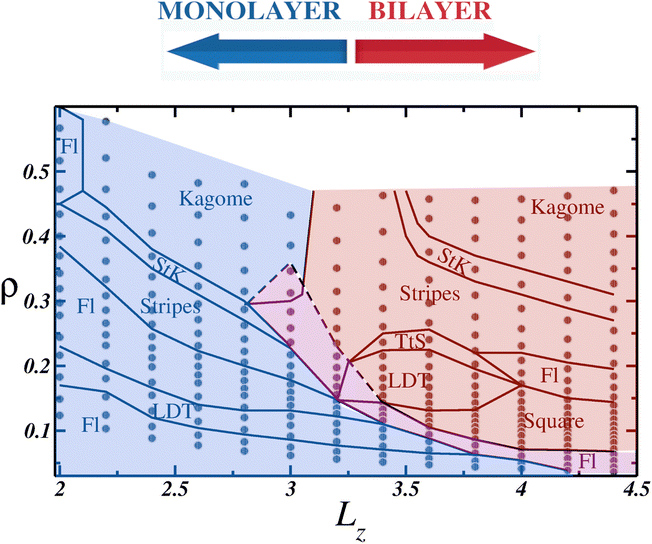
When using the entire procedure throughout this work, such as analyzing the density histogram, RDF, cumulative two-body entropy, orientational and translational order parameters, diffusion coefficient and snapshots applied to all values of L simulated, or all P⊥ × Lz, we were able to construct the ρ × LZ state diagram shown in Fig. 6.
While it serves as a qualitative state diagram, Fig. 6 illustrates how confinement in narrow spaces impacts the behavior of soft colloids. Within the monolayer region, depicted with a blue background, the system displays the same phases as those observed in the 2D case: initially a fluid (abbreviated to Fl in the diagram), followed by the LDT phase as the density increases. Subsequently, a clusterized fluid phase separates the ordered LDT and Stripes phases. In the high-density regime, a Stripes and Kagome coexistence region, denoted as StK in the phase diagram, emerges, and eventually, the Kagome structure is achieved. An intriguing observation within the monolayer region is that as Lz increases, the confined ordered phases can be observed at lower densities compared to the 2D case. For example, the Kagome crystal was observed at densities ρ ≈ 0.40 for Lz = 2.6, lower than in the 2D limit,78 and similar observations were made for the Stripes and LDT phases.
In between the monolayer and bilayer regimes lies the mono-to-bilayer fluid region, delineated by the magenta background. When arranged in two layers, represented by the red region in Fig. 6, we observe the LDT and square phases at low densities. Both structures transit to a Stripe pattern at higher densities, but while the square and Stripes phase is separated by a cluster phase, the LDT and Stripes coexist in the TtS region. Finally, akin to the monolayer regime, the Stripes phase transitions to the Kagome phase, with the StK coexistence region demarcating the phases.
4 Conclusions
In this study, we carried out molecular dynamics simulations to investigate the behavior of soft colloids under extreme confinement conditions. The colloidal particles were modeled using a core-softened potential with a ramp-like shape and confined within a slit slit characterized by lateral side L and width Lz. By systematically increasing the slit width, we constructed a state diagram illustrating the system's transition from the quasi-2D limit, or monolayer regime, to the bilayer regime.Our findings revealed distinct features in the P⊥ × Lz curves, particularly evident during the transition from one to two layers. We explored these transitions in detail for intermediate plate sizes, such as L = 50.0 and L = 60.0, where we observed transitions from stripes to low-density triangular (LDT) and from fluid to solid square phases, respectively. Additionally, for smaller plate sizes like L = 40.0, we observed a transition from Kagome to worm-like fluid. Some curves, such as L = 40.0, exhibited a second loop, indicating a transition from a worm-like fluid to one characterized by smaller, dimer-like clusters. Conversely, for larger plates such as L = 90.0, no evidence of a structural transition was observed. However, a notable decrease in the diffusion coefficient D was observed as the wall separation increased, corresponding to the emergence of the second layer and indicating a significant impact of the layering transition on the system's dynamics.
To demonstrate the utility of confinement in controlling the aggregation process for this model, we constructed the ρ × Lz diagram. In the monolayer regime, our findings indicated that open crystal phases, including LDT, Stripes, and Kagome, could be obtained at lower densities with increasing slit width. In the bilayer regime, a notable emergence of a square ordered phase, not observed in the 2D case, was detected. Those finding highlights how the extreme confinement inside narrow slits can be employed to stabilize quasi-2D structures and even obtain new arrangements.
Author contributions
LBK: conceptualization, data curation, formal analysis, methodology, software, investigation, validation, writing – review & editing. TP: software, validation, investigation, writing – review & editing. JRB: conceptualization, methodology, data curation, formal analysis, resources, funding acquisition, supervision, validation, visualization, writing – original draft, writing – review & editing.Data availability statement
The data that support the findings of this study and the computational codes are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Without public funding this research would be impossible. JRB thanks the National Council for Scientific and Technological Development – CNPq, grant numbers 405479/2023-9, 441728/2023-5 and 304958/2022-0, and the Rio Grande do Sul Research Foundation – FAPERGS, grant number 21/2551-0002024-5. TPON thanks the Coordination for the Improvement of Higher Education Personnel – CAPES, financing Code 001.Notes and references
- M. Karg, A. Pich, T. Hellweg, T. Hoare, L. A. Lyon, J. J. Crassous, D. Suzuki, R. A. Gumerov, S. Schneider, I. I. Potemkin and W. Richtering, Langmuir, 2019, 35, 6231–6255 CrossRef CAS PubMed.
- J. Liu, J. Huang, W. Niu, C. Tan and H. Zhang, Chem. Rev., 2021, 121, 5830–5888 CrossRef CAS PubMed.
- M. Siebenbürger, M. Fuchs and M. Ballauff, Soft Matter, 2012, 8, 4014–4024 RSC.
- N. J. Fernandes, H. Koerner, E. P. Giannelis and R. A. Vaia, MRS Commun., 2013, 3, 13–29 CrossRef CAS.
- F. Grillo, M. A. Fernandez-Rodriguez, M.-N. Antonopoulou, D. Gerber and L. Isa, Nature, 2020, 582, 219–224 CrossRef CAS PubMed.
- B. A. Humphreys, S. W. Prescott, T. J. Murdoch, A. Nelson, E. P. Gilbert, G. B. Webber and E. J. Wanless, Soft Matter, 2019, 15, 55–64 RSC.
- W. R. C. Somerville, A. D. Law, M. Rey, N. Vogel, A. J. Archer and D. M. A. Buzza, Soft Matter, 2020, 16, 3564–3573 RSC.
- J. Menath, J. Eatson, R. Brilmayer, A. Andrieu-Brunsen, D. M. A. Buzza and N. Vogel, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2113394118 CrossRef CAS PubMed.
- A. Scotti, M. F. Schulte, C. G. Lopez, J. J. Crassous, S. Bochenek and W. Richtering, Chem. Rev., 2022, 122, 11675–11700 CrossRef CAS PubMed.
- K. Kuk, L. Gregel, V. Abgarjan, C. Croonenbrock, S. Hänsch and M. Karg, Gels, 2022, 8, 516 CrossRef CAS PubMed.
- M. D. Carbajal-Tinoco, F. Castro-Román and J. L. Arauz-Lara, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 3745–3749 CrossRef CAS PubMed.
- T. Palberg, J. Phys.: Condens. Matter, 2014, 26, 333101 CrossRef PubMed.
- L. B. Krott, C. Gavazzoni and J. R. Bordin, J. Chem. Phys., 2016, 145, 244906 CrossRef PubMed.
- A. Villada-Balbuena, G. Jung, A. B. Zuccolotto-Bernez, T. Franosch and S. U. Egelhaaf, Soft Matter, 2022, 18, 4699–4714 RSC.
- Y. Zhang, B. Li, J. Liu, D. Han, S. Rohani, Z. Gao and J. Gong, Cryst. Growth Des., 2024, 24, 2645–2665 CrossRef CAS.
- O. A. Vasilyev, S. Dietrich and S. Kondrat, Soft Matter, 2018, 14, 586–596 RSC.
- X. Zhang, Q. Lyu, X. Chen, M. Li, L. Zhang and J. Zhu, ACS Appl. Mater. Interfaces, 2024, 16(12), 15308–15321 CrossRef CAS PubMed.
- J. Bordin, Phys. A, 2016, 459, 1–8 CrossRef CAS.
- L. B. Krott and J. R. Bordin, Colloids Interfaces, 2023, 7, 33 CrossRef.
- F. E. Mackay, K. Pastor, M. Karttunen and C. Denniston, Soft Matter, 2014, 10, 8724–8730 RSC.
- I. Travěnec and L. Šamaj, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 022306 CrossRef PubMed.
- M. Eshraghi and J. Horbach, Soft Matter, 2018, 14, 4141–4149 RSC.
- L. B. Krott, J. R. Bordin and M. C. Barbosa, J. Phys. Chem. B, 2015, 119, 291–300 CrossRef CAS PubMed.
- I. Williams, E. C. Oğuz, H. Löwen, W. C. K. Poon and C. P. Royall, J. Chem. Phys., 2022, 156, 184902 CrossRef CAS PubMed.
- A. Imperio, L. Reatto and S. Zapperi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 021402 CrossRef PubMed.
- L. Almenar and M. Rauscher, J. Phys.: Condens. Matter, 2011, 23, 184115 CrossRef CAS PubMed.
- M. H. Kim, S. H. Im and O. O. Park, Adv. Funct. Mater., 2005, 15, 1329–1335 CrossRef CAS.
- A. Fortini and M. Dijkstra, J. Phys.: Condens. Matter, 2006, 18, L371–L378 CrossRef CAS PubMed.
- Y. Peng, Z.-R. Wang, A. M. Alsayed, A. G. Yodh and Y. Han, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 011404 CrossRef CAS PubMed.
- S. Herrera-Velarde, E. C. Euán-Díaz and R. Castañeda-Priego, Colloids Interfaces, 2021, 5, 29 CrossRef CAS.
- Y.-T. Juan, Y.-F. Lai, X. Li, T.-C. Tai, C.-H. Lin, C.-F. Huang, B. Li, A.-C. Shi and H.-Y. Hsueh, Macromolecules, 2023, 56, 457–469 CrossRef CAS.
- P. J. M. Swinkels, Z. Gong, S. Sacanna, E. G. Noya and P. Schall, Soft Matter, 2023, 19, 3414–3422 RSC.
- P. Vilaseca and G. Franzese, J. Non-Cryst. Solids, 2011, 357, 419–426 CrossRef CAS.
- K. Schwenke, L. Isa and E. Del Gado, Langmuir, 2014, 30, 3069–3074 CrossRef CAS PubMed.
- M. J. Bergman, N. Gnan, M. Obiols-Rabasa, J.-M. Meijer, L. Rovigatti, E. Zaccarelli and P. Schurtenberger, Nat. Commun., 2018, 9, 5039 CrossRef PubMed.
- P. S. Mohanty, D. Paloli, J. J. Crassous, E. Zaccarelli and P. Schurtenberger, J. Chem. Phys., 2014, 140, 094901 CrossRef PubMed.
- G. Romeo and M. P. Ciamarra, Soft Matter, 2013, 9, 5401 RSC.
- F. Camerin, N. Gnan, J. Ruiz-Franco, A. Ninarello, L. Rovigatti and E. Zaccarelli, Phys. Rev. X, 2020, 10, 031012 CAS.
- J. Vialetto, F. Camerin, S. N. Ramakrishna, E. Zaccarelli and L. Isa, Adv. Sci., 2023, 10, 2303404 CrossRef CAS PubMed.
- S. Ciarella, M. Rey, J. Harrer, N. Holstein, M. Ickler, H. Löwen, N. Vogel and L. M. C. Janssen, Langmuir, 2021, 37, 5364–5375 CrossRef CAS PubMed.
- J.-M. Bomont, C. N. Likos and J.-P. Hansen, Phys. Rev. E, 2022, 105, 024607 CrossRef CAS PubMed.
- J. R. Bordin, Phys. A, 2018, 495, 215–224 CrossRef.
- M. Quesada-Perez, A. Moncho-Jorda, F. Martinez-Lopez and R. Hidalgo-Álvarez, J. Chem. Phys., 2001, 115, 10897 CrossRef CAS.
- C. Contreras-Aburto, J. M. Méndez-Alcaraz and R. Castañeda-Priego, J. Chem. Phys., 2010, 132, 174111 CrossRef CAS PubMed.
- S. Haddadi, M. Skepö, P. Jannasch, S. Manner and J. Forsman, J. Colloid Interface Sci., 2021, 581, 669–681 CrossRef CAS PubMed.
- M. S. Marques, T. P. O. Nogueira, R. F. Dillenburg, M. C. Barbosa and J. R. Bordin, J. Appl. Phys., 2020, 127, 054701 CrossRef CAS.
- T. Lafitte, S. K. Kumar and A. Z. Panagiotopoulos, Soft Matter, 2014, 10, 786–794 RSC.
- I. Bos, P. van der Scheer, W. G. Ellenbroek and J. Sprakel, Soft Matter, 2019, 15, 615–622 RSC.
- C. N. Likos, Phys. Rep., 2001, 348, 267–439 CrossRef CAS.
- P. C. Hemmer and G. Stell, Phys. Rev. Lett., 1970, 24, 1284–1287 CrossRef.
- E. A. Jagla, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 1478 CrossRef CAS.
- E. A. Jagla, J. Chem. Phys., 1999, 111, 8980–8986 CrossRef CAS.
- N. Xu, Chin. J. Polym. Sci., 2019, 37, 1065–1082 CrossRef CAS.
- Y. D. Fomin, Phys. Chem. Liq., 2020, 58, 290–301 CrossRef CAS.
- Z. Yan, S. V. Buldyrev, N. Giovambattista, P. G. Debenedetti and H. E. Stanley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 051204 CrossRef PubMed.
- H. M. Gibson and N. B. Wilding, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 061507 CrossRef CAS PubMed.
- L. Xu, N. Giovambattista, S. V. Buldyrev, P. G. Debenedetti and H. E. Stanley, J. Chem. Phys., 2011, 134, 064507 CrossRef PubMed.
- G. Das, N. Gnan, F. Sciortino and E. Zaccarelli, J. Chem. Phys., 2013, 138, 134501 CrossRef PubMed.
- J. Luo, L. Xu, C. A. Angell, H. E. Stanley and S. V. Buldyrev, J. Chem. Phys., 2015, 142, 224501 CrossRef PubMed.
- M. L. de Haro, A. Rodríguez-Rivas, S. B. Yuste and A. Santos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2018, 98, 012138 CrossRef CAS PubMed.
- S. Higuchi, D. Kato, D. Awaji and K. Kim, J. Chem. Phys., 2018, 148, 094507 CrossRef.
- V. N. Ryzhov, E. E. Tareyeva, Y. D. Fomin and E. N. Tsiok, Phys.-Usp., 2020, 63, 417 CrossRef.
- J. Martín-Roca, R. Martinez, F. Martínez-Pedrero, J. Ramírez and C. Valeriani, J. Chem. Phys., 2022, 156, 164502 CrossRef PubMed.
- J.-L. Bretonnet and J.-M. Bomont, Chem. Phys., 2022, 555, 111445 CrossRef CAS.
- T. Nogueira and J. R. Bordin, J. Mol. Liq., 2023, 390, 123127 CrossRef CAS.
- N. Osterman, D. Babič, I. Poberaj, J. Dobnikar and P. Ziherl, Phys. Rev. Lett., 2007, 99, 248301 CrossRef CAS PubMed.
- L. Isa, I. Buttinoni, M. A. Fernandez-Rodriguez and S. A. Vasudevan, Europhys. Lett., 2017, 119, 26001 CrossRef.
- J. Wang, C. F. Mbah, T. Przybilla, S. Englisch, E. Spiecker, M. Engel and N. Vogel, ACS Nano, 2019, 13, 9005–9015 CrossRef CAS PubMed.
- A. Villada-Balbuena, G. Jung, A. B. Zuccolotto-Bernez, T. Franosch and S. U. Egelhaaf, Soft Matter, 2022, 18, 4699–4714 RSC.
- C. Kang and A. Honciuc, J. Phys. Chem. Lett., 2018, 9, 1415–1421 CrossRef CAS PubMed.
- D. Wu and A. Honciuc, ACS Appl. Nano Mater., 2018, 1, 471–482 CrossRef CAS.
- J. R. Bordin, Soft Matter, 2023, 19, 7613–7624 RSC.
- A. Barros de Oliveira, P. A. Netz, T. Colla and M. C. Barbosa, J. Chem. Phys., 2006, 124, 084505 CrossRef PubMed.
- A. B. de Oliveira, P. A. Netz, T. Colla and M. C. Barbosa, J. Chem. Phys., 2006, 125, 124503 CrossRef PubMed.
- J. R. Bordin, A. B. de Oliveira, A. Diehl and M. C. Barbosa, J. Chem. Phys., 2012, 137, 084504 CrossRef CAS PubMed.
- L. B. Krott and M. C. Barbosa, J. Chem. Phys., 2013, 138, 084505 CrossRef PubMed.
- J. R. Bordin and L. B. Krott, J. Chem. Phys., 2023, 158, 134501 CrossRef CAS PubMed.
- D. S. Cardoso, V. F. Hernandes, T. Nogueira and J. R. Bordin, Phys. A, 2021, 566, 125628 CrossRef.
- M. Rey, M. A. Fernandez-Rodriguez, M. Karg, L. Isa and N. Vogel, Acc. Chem. Res., 2020, 53, 414–424 CrossRef CAS PubMed.
- Q. Chen, S. C. Bae and S. Granick, Nature, 2011, 469, 381–384 CrossRef CAS PubMed.
- X. Mao, Q. Chen and S. Granick, Nat. Mater., 2013, 12, 217–222 CrossRef CAS PubMed.
- P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, Oxford, 1987 Search PubMed.
- J. R. Bordin and M. C. Barbosa, Phys. Rev. E, 2018, 97, 022604 CrossRef CAS PubMed.
- A. Barros De Oliveira, E. Salcedo, C. Chakravarty and M. C. Barbosa, J. Chem. Phys., 2010, 132, 234509 CrossRef PubMed.
- L. B. Krott and M. C. Barbosa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 012110 CrossRef PubMed.
- M. S. Shell, P. G. Debenedetti and A. Z. Panagiotopoulos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 011202 CrossRef PubMed.
- J. R. Errington and P. D. Debenedetti, Nature, 2001, 409, 318 CrossRef CAS PubMed.
- J. E. Errington, P. G. Debenedetti and S. Torquato, J. Chem. Phys., 2003, 118, 2256 CrossRef CAS.
- J. R. Bordin and M. C. Barbosa, Phys. Rev. E, 2018, 97, 022604 CrossRef CAS PubMed.
- B. A. Klumov and S. A. Khrapak, Results Phys., 2020, 17, 103020 CrossRef.
- S. Prestipino, F. Saija and P. V. Giaquinta, J. Chem. Phys., 2012, 137, 104503 CrossRef PubMed.
- M. M. Hurley and S. J. Singer, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 5783–5786 CrossRef PubMed.
- V. Ramasubramani, B. D. Dice, E. S. Harper, M. P. Spellings, J. A. Anderson and S. C. Glotzer, Comput. Phys. Commun., 2020, 254, 107275 CrossRef CAS.
- J. R. Bordin, L. B. Krott and M. C. Barbosa, J. Phys. Chem. C, 2014, 118, 9497–9506 CrossRef CAS.
- T. Nogueira and J. R. Bordin, Phys. A, 2022, 605, 128048 CrossRef.
- J. R. Errington and P. D. Debenedetti, Nature, 2001, 409, 318 CrossRef CAS PubMed.
- M. Rey, A. D. Law, D. M. A. Buzza and N. Vogel, J. Am. Chem. Soc., 2017, 139, 17464–17473 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |