Open Access Article
Open Access ArticleIn situ polymer gelation in confined flow controls intermittent dynamics†
Barrett T.
Smith
 a and
Sara M.
Hashmi
a and
Sara M.
Hashmi
 *abc
*abc
aDepartment of Chemical Engineering, Northeastern University, USA. E-mail: s.hashmi@northeastern.edu
bDepartment of Mechanical & Industrial Engineering, Northeastern University, USA
cDepartment of Chemistry & Chemical Biology, Northeastern University, USA
First published on 31st January 2024
Abstract
Polymer flows through pores, nozzles and other small channels govern engineered and naturally occurring dynamics in many processes, from 3D printing to oil recovery in the earth's subsurface to a wide variety of biological flows. The crosslinking of polymers can change their material properties dramatically, and it is advantageous to know a priori whether or not crosslinking polymers will lead to clogged channels or cessation of flow. In this study, we investigate the flow of a common biopolymer, alginate, while it undergoes crosslinking by the addition of a crosslinker, calcium, driven through a microfluidic channel at constant flow rate. We map the boundaries defining complete clogging and flow as a function of flow rate, polymer concentration, and crosslinker concentration. Interestingly, the boundaries of the dynamic behavior qualitatively match the thermodynamic jamming phase diagram of attractive colloidal particles. That is, polymer clogging occurs in a region analogous to colloids in a jammed state, while the polymer flows in regions corresponding to colloids in a liquid phase. However, between the dynamic regimes of complete clogging and unrestricted flow, we observe a remarkable phenomenon in which the crosslinked polymer intermittently clogs the channel. This pattern of deposition and removal of a crosslinked gel is simultaneously highly reproducible, long-lasting, and controllable by system parameters. Higher concentrations of polymer and cross-linker result in more frequent ablation, while gels formed at lower component concentrations ablate less frequently. Upon ablation, the eluted gel maintains its shape, resulting in micro-rods several hundred microns long. Our results suggest both rich dynamics of intermittent flows in crosslinking polymers and the ability to control them.
1 Introduction
The flow behavior of crosslinking polymer solutions as they transition from liquid-like to solid-like material determines success or failure in several applications. Blood clots clog arteries and veins to initiate the repair of injured tissue or to cause injury themselves. Inks for 3D bioprinting need to balance viscosity, crosslinking degree and cell concentrations to avoid clogging the nozzle of ink-jet and extrusion equipment. Clogs in these applications may grow to block the channel, disrupting further flow. Flow disruption is typically undesirable, expect in the case of injury repair, in which further flow of blood would worsen the injury. However, in flow situations that involve polymer crosslinking in flow through small channels, no single a priori theoretical or empirical framework describes the conditions under which material flows or stops flowing.The development of a crosslinked hydrogel is well described in quiescence and in bulk rheology. However, shear forces are well known to affect the formation of gels, both in terms of gelation time scales and final gel properties. Shear forces change the dominant mechanisms of crosslinking and aggregation: in shear, intramolecular crosslinking is favored over intermolecular crosslinking, and diffusion-limited clustering gives way to shear-induced cluster–cluster interactions.1,2 Final cluster size is limited by shear, preventing the complete percolation of crosslinking networks.3,4 As such, bulk rheology experiments demonstrate that the growth of polymer gels is delayed by shear, since the ability of aggregates to form a percolated network is compromised by disruption of inter-aggregate bonds.5 At sufficiently high shear rates, gelation is completely inhibited.5,6 Further, gels formed in shear tend to be weaker than their counterparts formed in quiescence.5 These effects, while observed in bulk rheology, have not been studied in pressure-driven flow, nor within a microfluidic environment with shear gradients. However, understanding the behavior of gels in these environments is crucial in several applications, including 3D bioprinting.
3D bioprinting involves the extrusion of bio-inks through narrow nozzles to enable fabrication of intricate shapes. Bio-inks are complex fluids typically composed of a mixture of cells and crosslinked bio-polymers. Bulk rheology is used to characterize inks and optimize their design.7 For proper flowability and printability, inks should be viscous, shear thinning, and have a high yield stress.8–11 Polymers can be crosslinked before, during, or after the print to influence these properties and form the hydrogel structure. Failure to optimize the ink appropriately may result in print failure. An example of failure is nozzle clogging, where some obstruction prevents the flow of ink through the nozzle. Clogging causes interruption in flow and consequent unevenness in the print, and may require the replacement of the nozzle during a print.12,13
The parameter space involved in bioprinting is large and many factors contribute to preventing clogging and achieving a successful print. Leaving aside biological considerations, such as the presence and survival of cells, bioinks must have proper rheological properties to flow through small channels without clogging while also providing sufficient structural support to retain an appropriate shape upon leaving the channel. While high viscosity solutions are preferred for shape retention, they also require large forces to move through the nozzle, resulting in high shear stresses. If the viscosity is sufficiently high, 3D printers may not have sufficient driving pressure to maintain flow, resulting in a failed print. Highly viscous materials, particularly those which shear thin, may be too viscous to pump at low flow rates.14–18 Similarly, yield stresses above certain limits impede successful printing.17 Shear thinning can overcome these challenges and facilitate the pumping of viscous materials. Once flow is stopped however, any pump must overcome the increased viscosity caused by the low shear rate and the yield stress of the material.
Achieving a functional bioink print requires understanding the impact of component concentration and the degree of polymer crosslinking on rheology, and how rheology interacts with the speed and geometry of flow within the printer needle. However, most published works focus on a final printed product rather than fundamental in situ flow dynamics, and seek to avoid clogging rather than characterize conditions under which it occurs. A handful of studies synthesize control parameters into printability or process maps which show regions of parameter space suitable for printing and those which are not. Two examples use axes of polymer concentration and nozzle size to describe optimal printing conditions, albeit without crosslinking.14,19 Alternative representations in situations with crosslinking polymers include parameters such as flow rates,15 or measured characteristics like storage modulus.17
In contrast to polymer solutions, flows of malleable metals and colloidal flows have robust a priori frameworks for describing flow which include thermodynamics. In the more mature field of metal extrusion, for instance, thermodynamics and dynamic materials models determine both microstructure and macroscopic behavior at different processing conditions, with hundreds of different alloys well-described.20 In colloidal science, the jamming phase diagram characterizes thermodynamic phases, describing under which conditions suspensions are in a liquid or glassy state.21–23 The basic jamming diagram outlines the impact of colloid concentration, interparticle interaction, and forces applied to the system in determining the state of the material. Exploiting thermodynamics can control macroscopic flow behavior: applying and removing shear causes transitions from liquid to solid in colloidal hydrogels for use as bioinks or in support baths of 3D bioprinting applications.24,25 However, we have not seen any similar frameworks describing the transition between flowing and clogging in the confined flow of crosslinking polymer solutions.
To address this gap in our understanding, we comprehensively explore flow and clogging in a common biopolymer. We investigate a dilute polymer system with an added crosslinker: crosslinking drives a transition from a fluid to a gelled state. Simultaneously, we observe transitions in the dynamic behavior. The transition from flow to clogging includes a region where the dynamics are intermittent, due to deposition and ablation of the gel from the channel walls. While phase diagrams or processing maps refer to states of matter at thermodynamic equilibrium, we present our results in the form of a “dynamic” or “flow phase diagram” acknowledging that the material phase largely determines flow dynamics. Alginate is a biopolymer commonly used in food, cosmetics, and medicine, including about 1/4 of the published research in 3D bioprinting. We mix alginate and its crosslinking agent, calcium, in a microfluidic device in which two inlet streams meet at a Y-shaped junction. Upon examining a broad range of conditions, we find, for the first time, a surprising deposition/ablation pattern seen when alginate is crosslinked with calcium in flow through a microfluidic device. We have not seen descriptions or reproductions of any similar intermittent flow. When mixed with calcium, low concentrations of alginate quickly form a gel which deposits on the channel wall. As the gel grows and obstructs the flow, maintaining a constant flow rate in the channel requires an increase in driving pressure. This pressure increase, in turn, increases both the linear velocity of the fluid and the viscous shear stress felt at the wall. At a certain driving pressure however, the gel ablates from the wall and is washed out of the device, returning the driving pressure to baseline. Despite the simplicity of the chemical composition, the system exhibits rich dynamics. Remarkably, as long as flow is maintained, the gel continually grows and ablates at regular driving pressures and time intervals. Exploration of the flow phase diagram indicates that composition and flow rate control both the degree of deposition and the frequency of ablation.
2 Materials and methods
2.1 Materials
Sodium alginate and sodium chloride are obtained from Sigma-Aldrich. Calcium chloride is obtained from VWR. PDMS to make devices is purchased as the Sylgard 184 Silicone Elastomer Kit from DOW Silicones Corporation. All chemicals are used as received.Stock solutions of sodium alginate, calcium chloride, and sodium chloride are prepared in DI water (Milli-Q Advantage A10) above their target concentrations. Appropriate amounts of sodium chloride stock solution are added to the alginate and calcium solutions to achieve ratios of 25 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mg mL−1 and 2.5 mM
1 mg mL−1 and 2.5 mM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 mM, respectively, before dilution to the target concentrations.
100 mM, respectively, before dilution to the target concentrations.
The approximate molecular size of the alginate is estimated by the intrinsic viscosity measurement as described in literature.26 The zero-shear viscosity μ of alginate solutions is measured as a function of concentration using a Discovery HR-3 rheometer from TA Instruments, giving an approximate molecular weight ∼145 kDa. We explore flow behavior over a range of different chemical compositions and flow rates. We both independently vary the calcium and alginate concentrations, and also fix the crosslinking ratio to vary the total concentration of gel. Table 1 describes the experiments shown in Fig. 3 and which are examined more closely in Section 3.3. Table 1 lists the total flow rate (QT), alginate concentration (CAlg), and calcium concentration (CCa2+) for the experiments analyzed. In the experiments varying calcium concentration, CCa2+ ranges from 10 to 200 mM at fixed total flow rate QT = 1.2 μL min−1 and CAlg = 0.1 mg mL−1. In the experiments varying the gel concentration, CGel, QT is fixed at QT = 6 μL min−1. In these, CAlg ranges from 0.02 mg mL−1 to 0.2 mg mL−1, keeping the calcium crosslinking ratio fixed at CCa2+ = 1000 mM per CAlg = 1 mg mL−1. In varying QT, the same crosslinking ratio is used, with CAlg = 0.1 mg mL−1 and CCa2+ = 100 mM, while QT ranges from 1.2 to 12 μL min−1. For all conditions in Table 1, the concentration of sodium is proportional to the concentration of alginate or calcium, respectively. We find that sodium chloride is a necessary component in the gel deposition and ablation process, as described in ESI,† Fig. S1. Table 1 also indicates the total number of deposition/ablation events recorded and the total duration of each flow test. The exploration of the flow phase diagram, in Fig. 4a, represents many more experiments within the limits of alginate concentration between CAlg = 0.02 mg mL−1 and 10 mg mL−1 and calcium concentration between CCa2+ = 0.5 and 1000 mM, all obtained at QT = 1.2 μL min−1.
| Q T (μL min−1) | C Alg (mg mL−1) | C Ca2+ (mM) | Number of events | Total duration (s) |
|---|---|---|---|---|
| Varying CCa2+ | ||||
| 1.2 | 0.1 | 10 | 45 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 450 450 |
| 1.2 | 0.1 | 20 | 53 | 9900 |
| 1.2 | 0.1 | 100 | 118 | 7400 |
| 1.2 | 0.1 | 200 | 18 | 900 |
| Varying CGel | ||||
| 6.0 | 0.02 | 20 | 20 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
| 6.0 | 0.05 | 50 | 19 | 2250 |
| 6.0 | 0.1 | 100 | 17 | 700 |
| 6.0 | 0.2 | 200 | 54 | 1000 |
| Varying QT | ||||
| 1.2 | 0.1 | 100 | 38 | 875 |
| 2.4 | 0.1 | 100 | 34 | 1400 |
| 6.0 | 0.1 | 100 | 59 | 1200 |
| 12 | 0.1 | 100 | 149 | 3250 |
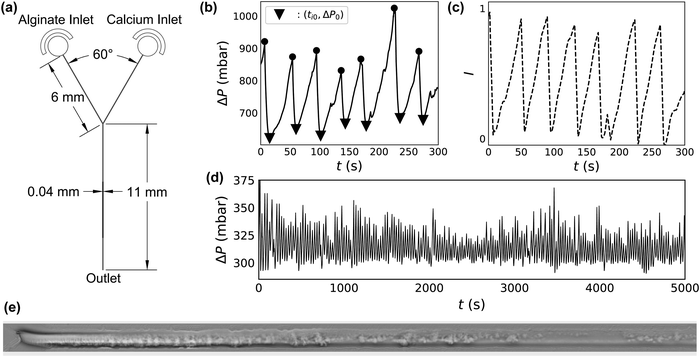
2.2 Microfluidic device
The microfluidic device design used in these experiments consists of two inlets meeting at a Y-shaped intersection (Fig. 1a). Inlet channels, 40 μm wide and 6 mm long meet at a 60° angle. The outlet channel is also 40 μm wide, but is longer, at 11 mm. All channels are 30 μm high. Soft lithography is used to manufacture these devices according to standard methods27 with one variation. Rather than core an opening in the PDMS to insert outlet tubing in an outlet well, the final millimeter of the outlet channel is cut to allow the effluent to discharge directly from the channel onto the glass slide. This is done to prevent the build-up of alginate gel in the outlet well.Experimental conditions are repeated in several different devices to ensure that the results are reproducible. Flow dynamics results obtained using different experimental conditions vary much more widely than the device-to-device variation at constant experimental conditions (ESI,† Fig. S2 and S3).
To test the dependence of alginate deposition on surface chemistry of the devices, we prepare several devices with varying surface chemistry. To verify that the same alginate deposition occurs on PDMS as well as glass, some devices are prepared with PDMS-coated glass slides. The same 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 PDMS
1 PDMS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) curing agent mixture is degassed and poured onto clean glass slides to a depth of 4 mm. These are then used in the same manner as uncoated glass slides. The difference in experimental results between PDMS coated and uncoated glass slides is within the variance seen from device-to-device (ESI,† Fig. S4). In other tests, PDMS devices are prepared, treated with plasma, and bonded to glass slides in the usual way before surface modification (ESI,† Fig. S5). Before beginning flow tests, these devices are flushed with chemical treatments to adjust the degree of hydrophobicity of the PDMS and glass surfaces. We use polyvinyl alcohol (PVA) to make the surfaces hydrophilic.28 Commercial glass treatment Aquapel makes the surfaces hydrophobic.29
curing agent mixture is degassed and poured onto clean glass slides to a depth of 4 mm. These are then used in the same manner as uncoated glass slides. The difference in experimental results between PDMS coated and uncoated glass slides is within the variance seen from device-to-device (ESI,† Fig. S4). In other tests, PDMS devices are prepared, treated with plasma, and bonded to glass slides in the usual way before surface modification (ESI,† Fig. S5). Before beginning flow tests, these devices are flushed with chemical treatments to adjust the degree of hydrophobicity of the PDMS and glass surfaces. We use polyvinyl alcohol (PVA) to make the surfaces hydrophilic.28 Commercial glass treatment Aquapel makes the surfaces hydrophobic.29
2.3 Characterizing devices
To ensure each device is working properly, and to characterize its hydraulic diameter before flow tests, we vary the driving pressure ΔP from 0 to 2000 mbar through each inlet simultaneously, using pure DI water. The measured flow rate increases linearly with driving pressure, indicating Poiseuille flow. The hydraulic radius of the devices is calculated accordingly using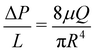 | (1) |
2.4 Flow tests
A pressure controller (Fluigent LU-FEZ) with an attached flow-rate meter is used control flow rates for the experiments. Each inlet tubing is flushed with the desired solution before the tubing is connected to the microfluidic device. Driving pressure ΔP is recorded every 100 ms for the duration of each experiment, which last typically at least 15 minutes but in some cases as long as nearly 6 hours (Table 1). ΔP can be measured to a maximum of 2000 mbar, with a resolution of 1 mbar. The response time of the pressure controller is 2 seconds.Flow rate is controlled independently for each of the two inlet streams. The flow rate ratio of alginate and calcium channels is held constant at 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The flow rates Q are typically 0.96 μL min−1 and 0.24 μL min−1 for alginate and calcium streams, respectively. However, the variable flow rate studies are obtained with Q varying from 0.96 μL min−1 to 9.6 μL min−1 for the alginate stream. We refer to the condition with Q = 0.96 μL min−1 for alginate and 0.24 μL min−1 for calcium in terms of the total flow rate, QT = 1.2 μL min−1.
1. The flow rates Q are typically 0.96 μL min−1 and 0.24 μL min−1 for alginate and calcium streams, respectively. However, the variable flow rate studies are obtained with Q varying from 0.96 μL min−1 to 9.6 μL min−1 for the alginate stream. We refer to the condition with Q = 0.96 μL min−1 for alginate and 0.24 μL min−1 for calcium in terms of the total flow rate, QT = 1.2 μL min−1.
Despite the variation in driving pressure due to the build-up of gel, QT remains constant. Although ΔP can increase by up to a factor of 3.5 over periods of several hundred seconds, QT increases only slightly due to hysteresis upon gel ablation (ESI,† Fig. S6). In these instances of ablation, QT increases by less than 50% for a period of a few seconds before returning to baseline.
2.5 Microscopy
We record gel deposition, clog formation and ablation using an inverted microscope (Leica DMi8) at 10× magnification in phase contrast mode. Images collected from several different devices and over different conditions show that the gelation looks approximately the same, even despite differences in the smoothness of the channel wall (ESI,† Fig. S7). Two videos of flow through the first 1.2 mm of the channel beyond the junction with simultaneous measurement of ΔP can be found in the ESI.† One video represents 5 minutes of footage, sped up by a factor of 5. The other shows the first minute of the same footage in real time, capturing a single deposition and ablation event, with annotations added to describe the process. The location of the sidewalls of the channel remains fixed during the duration of the flow test, despite deposition and ablation events, suggesting that the presence of alginate gel does not lead to deformation of the PDMS device.In phase contrast mode, gelation and deposition appear as darker regions in the raw microscopy images, allowing us to use intensity measurements as a proxy for the occurrence of gelation and deposition. To correlate video footage with ΔP(t), we first subtract the clean channel background from each frame. The numerical value of each pixel is summed to determine an overall brightness (I). Due to the background subtraction, bright regions correspond to gel deposits. We measure I in the first 500 μL of the channel for each frame of the video found in the ESI.† ΔP(t) and I(t) are shown in Fig. 1b and c.
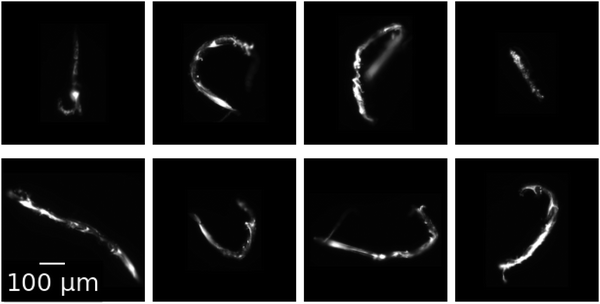
In a subset of flow test experiments, 200 nm diameter green fluorescent polystyrene particles (Molecular Probes F8888) are added to the alginate stream at 0.001% weight fraction. This assists visualization of the otherwise nearly transparent gels. At the end of these flow tests, ∼10 rods are carefully collected from the outlet of the device using a pipette, and then placed in a solution of 100 mM calcium chloride within a 96-well plate for imaging. Fluorescent images are then captured at 20× magnification and shown in Fig. 2.
3 Experimental results
3.1 Gel deposits and ablates intermittently
Mixing an alginate stream with a calcium stream at constant QT in a microfluidic Y-junction results in one of several phenomena. In the absence of calcium, alginate flows through the micro-channel without clogging, even at concentrations as high as CAlg = 10 mg mL−1. At high concentrations of alginate and calcium, the system clogs irreversibly. In between these two extremes of flow and clogging, an interesting intermittent flow behavior emerges. Fig. 1b shows ΔP(t) during this intermittent flow. The system demonstrates periodic behavior where, starting at ti0 and a baseline ΔP0 (triangles), the pressure begins to increase. ΔP then reaches a maximum (circles), followed by an abrupt drop in pressure back to ΔP0. The cycle then continues, with increases in ΔP(t) reaching a relatively constant maximum value before falling back to the baseline ΔP0.Video 1 (ESI†) shows the synchronized microscopy and pressure trace data of a deposition/ablation event in real time with descriptive annotations. A phase contrast microscopy video of the first 1.2 mm of the channel after the junction is shown on the top. Alginate flows in through the channel at the top of the image, at CAlg = 0.1 mg mL−1, while the calcium solution flows in from the channel at the bottom of the image, at CCa2+ = 100 mM. Fluid flows from left to right in the frame; QT = 12.0 μL min−1, and the linear velocity of the fluid is 20 mm s−1. The trace of the driving pressure is shown below the microscopy video, plotted as a dashed line and corresponding to the pressure trace seen in Fig. 1b.
Video 1 begins with a clean channel following an ablation event. Immediately, gel begins to deposit on the channel wall, starting at the junction where the streams meet. The gel deposit continues to grow for 39 s, as evidenced by the darkening of the channel. Concurrently, the driving pressure increases to maintain a constant flow rate. Ablation occurs at 0:39, and the driving pressure returns to baseline within 5 s. A slight transverse motion of the gel starts just before 10 s, in which the gel moves ∼10 μm in a few seconds. It is worth noting that this transverse displacement occurs at a rate much slower than the linear velocity of the fluid. The annotated video documents approximately the first minute of Fig. 1b in real time. A second video file, Video 2 (ESI†), is also one minute long: it shows the microscopy and corresponding pressure trace seen in Fig. 1b in its entirety, sped up by a factor of 5.
The microscopy reveals that alginate crosslinked by calcium forms a gel which occludes the channel simultaneously with an increase in driving pressure. Fig. 1(e) shows a phase contrast image of the first 1 mm of the channel downstream of the junction, obtained at t ∼ 168 s in Fig. 1b, inverted and with the background subtracted. In the inverted image, the gelled and deposited alginate appears as bright regions within the channel. Increases in the summed intensity of the inverted image, I(t), therefore suggest an increase in gel deposition. Fig. 1c shows I(t) of the first 500 μm of the image over the five minute portion of the flow test.
Analysis of Video 2 shows that the change in brightness in the 500 μm after the junction, I in Fig. 1c, correlates very well with ΔP (Fig. 1b). Thus, the required driving pressure increases to maintain a constant flow rate as the gel occludes the channel. Also due to constant flow rate, occlusion causes an increase in the fluid velocity and, therefore, the viscous shear stress on the wall. At a certain level of occlusion, shear stress pulls the clog from the wall and flushes it out of the device, returning the driving pressure to baseline. For this reason we refer to peaks in ΔP as ΔPAbl, the magnitude of which reflects the degree of occlusion. The gel then builds again, and, remarkably, the process repeats for up to hundreds of gel deposition/ablation events over several hours (Fig. 1d).
Close investigation of the microscopy imaging and simultaneous pressure traces reveals several interesting features of the deposition/ablation process. Comparison of the pressure measurements with microscopy suggests that the deposition occurs both at and immediately downstream of the junction between the alginate and calcium streams. During alginate deposition, the alginate gel deposits and grows on the channel wall in the first 500–1000 μm after the junction, as seen in Fig. 1e. While ΔP accounts for deposition anywhere in the channel, the close correlation between the microscopy and ΔP indicates that any deposition activity more than ∼1 mm downstream of the junction, beyond the field of view of the microscope image, has little effect on ΔP. Further microscopic investigation using z-stack microscopy suggests that the alginate gel deposits on all surfaces within the channel (ESI,† Fig. S8). Coating the glass slide with PDMS reveals that deposition occurs on the PDMS (ESI,† Fig. S4). Further, varying the device orientation with respect to gravity does not change the clogging pattern (ESI,† Fig. S9). This confirms that gel attachment on the wall of the device occurs independently of gravity and suggests that the build-up of gel happens by the diffusion of the crosslinked polymer to the surface of the growing gel layer on all sides.30
Within the deposition and ablation events, an additional phenomenon of partial ablation events sometimes occurs, with signatures in both ΔP(t) and microscopy video imaging. A partial ablation event occurs when material downstream from the junction is removed from the device separately from the main clog. One of these events occurs at t = 116 s in Fig. 1b, which corresponds to 0:22–0:23 in Video 2. A portion of deposited gel, downstream of the main deposit, breaks off of the channel wall and is eluted from the device. This partial removal results in a small dip in ΔP(t) for ∼1 s (∼5 s in real time). Then, the gel deposit continues to grow and obstruct the channel, requiring higher driving pressures. The magnitude of this dip is very small in comparison to the overall pressure increase, 5 mbar versus 200 mbar in Fig. 1b. Additionally, partial ablation events frequently occur at the same point within a particular channel, suggesting that variations in channel geometry and gel attachment may also play a role. At the same time, channel wall roughness is not required for gel deposition (ESI,† Fig. S7). This result is similar to deposition seen in other contexts, like colloidal deposition inside smooth metal pipes.30,31
3.2 Ablated gel maintains shape of formation
Upon ablation from the channel walls, the formed alginate gel maintains its shape as it leaves the device. Fig. 2 shows microscopic images of gels eluted during flow tests performed at chemical conditions of CAlg = 0.1 mg mL−1 and CCa2+ = 100 mM and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 flow rate ratio, QAlg = QCa2+ = 2 μL min−1. After elution and collection, which includes removal from the end of the channel by pipette, the gel rods maintain their shape as formed in the channel. The eight rods in Fig. 2 vary in length between 400 and 900 μm, with an average length of 650 μm. Their width is ∼30 μm, giving them an average aspect ratio of 22
1 flow rate ratio, QAlg = QCa2+ = 2 μL min−1. After elution and collection, which includes removal from the end of the channel by pipette, the gel rods maintain their shape as formed in the channel. The eight rods in Fig. 2 vary in length between 400 and 900 μm, with an average length of 650 μm. Their width is ∼30 μm, giving them an average aspect ratio of 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The rods are stable in a 100 mM calcium chloride solution for at least several weeks: they neither aggregate, disintegrate, nor change shape. They even maintain their shape upon pipetting to remove them from the channel exit. At this chemical composition, similar gels form at all other flow rate ratios investigated (see ESI,† Fig. S10). However, rods are formed most reliably during flow tests in which the intermittency behavior is slowest. As ablation frequency increases, the resulting rods become shorter and more globular.
1. The rods are stable in a 100 mM calcium chloride solution for at least several weeks: they neither aggregate, disintegrate, nor change shape. They even maintain their shape upon pipetting to remove them from the channel exit. At this chemical composition, similar gels form at all other flow rate ratios investigated (see ESI,† Fig. S10). However, rods are formed most reliably during flow tests in which the intermittency behavior is slowest. As ablation frequency increases, the resulting rods become shorter and more globular.
3.3 Calcium, alginate and flow rate control the intermittency
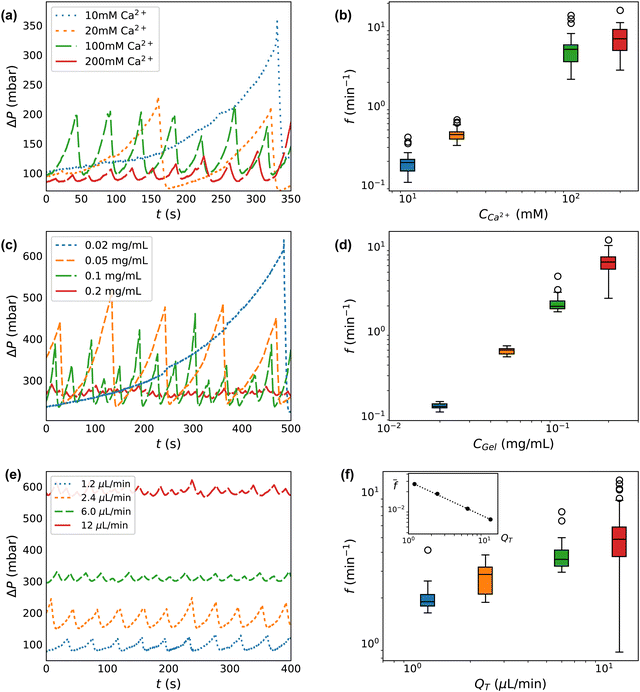
We next investigate our control over the deposition/ablation phenomena by adjusting the experimental parameters. We vary the concentration of calcium crosslinker, CCa2+, at fixed concentration of alginate CAlg. We next vary the total gel concentration, CGel, which is equal to CAlg at a fixed ratio of the calcium crosslinker. Then we vary the flow rates QT. These variations are captured in each of the three sections of Table 1.Increasing the concentration of the crosslinking agent (CCa2+) results in decreases to both the degree of clog occlusion and time of formation, as observed through ΔP(t). Fig. 3a shows ΔP(t) for calcium concentrations between 10 and 200 mM. The traces in Fig. 3a are truncated at 350 s to better display a comparison between the conditions. However, each flow test runs for between ∼1000–20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s total, with between ∼20–120 peaks in each pressure trace, as indicated in Table 1. Increasing CCa2+ only slightly decreases the size of features in ΔP. At CCa2+ = 10 mM, the average difference in driving pressure between baseline and clog ablation (ΔP0 − ΔPAbl) is 311 ± 108 mbar, while at CCa2+ = 200 mM, the average is 194 ± 183 mbar. These peak sizes represent a factor of ∼2–3 increase over the baseline driving pressure, ΔP0 ∼ 100 mbar. Much more dramatic is the change in ablation frequency, as measured by the inverse of the peak-to-peak time difference between ablation events. Within the 350 seconds shown in Fig. 3a, the CCa2+ = 200 mM condition exhibits 10 deposition/ablation events while the 10 mM condition has only 1 event. Consequently, the frequency of ablation (f) is much lower as CCa2+ decreases. At CCa2+ = 10 mM, f = 0.19 ± 0.06 min−1, while at 200 mM calcium, f = 7.62 ± 3.26 min−1, with error bars determined by the number of events given in Table 1. The increase of f with CCa2+ is seen in Fig. 3b. As CCa2+ increases by a factor of 20, f increases by a factor of ∼40.
000 s total, with between ∼20–120 peaks in each pressure trace, as indicated in Table 1. Increasing CCa2+ only slightly decreases the size of features in ΔP. At CCa2+ = 10 mM, the average difference in driving pressure between baseline and clog ablation (ΔP0 − ΔPAbl) is 311 ± 108 mbar, while at CCa2+ = 200 mM, the average is 194 ± 183 mbar. These peak sizes represent a factor of ∼2–3 increase over the baseline driving pressure, ΔP0 ∼ 100 mbar. Much more dramatic is the change in ablation frequency, as measured by the inverse of the peak-to-peak time difference between ablation events. Within the 350 seconds shown in Fig. 3a, the CCa2+ = 200 mM condition exhibits 10 deposition/ablation events while the 10 mM condition has only 1 event. Consequently, the frequency of ablation (f) is much lower as CCa2+ decreases. At CCa2+ = 10 mM, f = 0.19 ± 0.06 min−1, while at 200 mM calcium, f = 7.62 ± 3.26 min−1, with error bars determined by the number of events given in Table 1. The increase of f with CCa2+ is seen in Fig. 3b. As CCa2+ increases by a factor of 20, f increases by a factor of ∼40.
 | ||
| Fig. 3 Clog size and frequency of ablation is controllable with system parameters. (a), (c) and (e) Select raw pressure traces from experiments varying calcium CCa2+, total concentration CGel, and total flow rate QT respectively. (b), (d) and (f) Frequency histogram of peak pressures for experiments varying CCa2+, CGel, and QT, and respectively. The inset in (f) is the frequency normalized by the baseline shear rate which demonstrates that clogs form less frequently when accounting for flow rate. The box and whisker plots show the median value of a group as horizontal lines. The boxes encompass the first to the third quartile. The whiskers extend 1.5 times the interquartile range. The experimental conditions for each plot correspond to those shown in Table 1. | ||
By varying the concentration of all components proportionally, we isolate the effect of the total concentration of gel (CGel). Fig. 3c shows ΔP for each CGel, which corresponds to CAlg. The average difference in driving pressure between baseline and clog ablation varies dramatically over an order of magnitude of CGel. At CGel = 0.02 mg mL−1, this difference is ΔP0 − ΔPAbl = 310 ± 70 mbar, while at CGel = 0.2 mg mL−1, this difference is 10 ± 4 mbar. Compared to the baseline, ΔP0 ∼ 250 mbar, increasing CGel reduces the peak size from a 125% increase over ΔP0 to a 2% increase only. The difference in ablation frequency is similarly dramatic: within the 500 seconds displayed in Fig. 3c, the CGel = 0.2 mg mL−1 condition exhibits 23 deposition/ablation events compared to 1 at 0.02 mg mL−1. Fig. 3d shows f(Cgel), confirming that higher concentrations have a much higher frequency of ablation. At CGel = 0.02 mg mL−1, f = 0.13 ± 0.01 min−1, while at CGel = 0.2 mg mL−1, the frequency is 6.7 ± 1.6 min−1. An order of magnitude increase in CGel leads to a 50-fold increase in f.
Investigating CGel beyond CAlg = 0.2 mg mL−1 leads to difficulties in measurement due to the possibility of clogging. At high concentrations of gel, CAlg > 0.5 mg mL−1 and CCa2+ > 500 mM, the alginate channel clogs either at or directly upstream of the junction, preventing deposition of material in the channel downstream of the junction. As the amount of alginate is reduced from the clogging limit, starting at CAlg ≈ 0.3 mg mL−1 (with CCa2+ = 300 mM), the characteristic clog-ablation pattern is seen.
The total flow rate of the system also impacts clog formation and the degree of occlusion before ablation. Fig. 3e shows ΔP at each QT. The baseline driving pressure varies linearly according to QT, with 1.2 μL min−1 requiring about 60 mbar and 12 μL min−1 requiring about 600 mbar to maintain a constant QT in the absence of any gel occlusion. Interestingly, the difference between baseline driving pressure (ΔP0) and that at ablation (ΔPAbl) does not correlate with QT, ranging between ∼35–95 mbar only, despite the order of magnitude variation in QT. As seen in Fig. 3, the number of deposition/ablation events in 400 seconds increases slightly with increased QT, with 9 complete events at 1.2 μL min−1 and 19 at 12 μL min−1. This trend holds across all data gathered, as seen in Fig. 3f. At higher QT, clogs reach the point of ablation slightly faster in real-time, although there is more variance. At 1.2 μL min−1, clogs ablate at a frequency of 2.0 ± 0.4 min−1, while at 12 μL min−1, clogs ablate at a frequency of 5.0 ± 1.9 min−1.
While the absolute difference in driving pressure between baseline and clog ablation (ΔPAbl − ΔP0) and the frequency of ablation f do not vary significantly with QT, it is worth considering that QT controls both the baseline driving pressure and the baseline wall shear rate. Thus, the normalized pressure at ablation ΔPAbl/ΔP0 is lower at 12 μL min−1 than at 1.2 μL min−1: ΔPAbl/ΔP0 ∼ 162% at low flow rate, decreasing to 109% at high flow rate. Similarly, when the frequency of ablation is normalized by baseline wall shear rate, before ablation, this normalized frequency decreases with QT. The baseline wall shear rate is estimated using ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 4Q/πR03, where R0 is the measured hydraulic diameter for a clean device. The inset in Fig. 3f shows the decrease in
= 4Q/πR03, where R0 is the measured hydraulic diameter for a clean device. The inset in Fig. 3f shows the decrease in ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) = f/
= f/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . The dotted line indicates a power law dependence
. The dotted line indicates a power law dependence ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) ∼ QT−n, where the exponent n = 0.6.
∼ QT−n, where the exponent n = 0.6.
Other parameters also influence intermittent behavior, some in surprising ways. For instance, without sodium chloride present in the alginate stream, no deposition is seen (ESI,† Fig. S1). On the bulk scale, sodium chloride is not necessary to induce alginate gelation in the presence of calcium.32 However, not only is NaCl required for in-channel deposition, but its effect on deposition behavior is non-monotonic. As CNaCl increases relative to CAlg, the observed peaks in ΔP(t) decrease in magnitude, approaching the baseline condition which occurs in the absence of sodium. Deposition also depends on surface chemistry. Observed peaks in ΔP(t) are smaller when alginate and calcium mix in a channel with a hydrophilic coating than in a hydrophobically coated channel (ESI,† Fig. S5).
3.4 Boundaries of intermittent clogging
This remarkable behavior has limits that manifest as either flow or complete clogging. The boundaries of intermittent clogging depends on the concentrations of components and on flow rate. Fig. 4 shows the conditions at which flow (shaded blue), intermittent clogging (shaded yellow), and full channel clogging (shaded red) occur. The data shown in Fig. 4a indicate results obtained at QT = 1.2 μL min−1, representing the flow rate at which the largest number of flow tests are performed. The 31 data points in Fig. 4a each represent at least one flow test, and include the conditions in Table 1 where QT = 1.2 μL min−1. High concentrations of alginate and calcium lead to complete clogging of the channel. We consider the channel completely clogged when the pump reaches its maximum driving pressure of 2000 mbar and flow subsequently stops due to the obstruction of deposited gel. Most frequently, a complete clog manifests as the driving pressures of both calcium and alginate channels reach the maximum driving pressure (ESI,† Fig. S11). This behavior occurs in the large majority of all flow tests that fail at high concentrations, regardless of flow rate. In the remaining few instances however, the clog occurs in the alginate channel immediately upstream of the junction such that the calcium channel remains unobstructed and the calcium solution flow continues.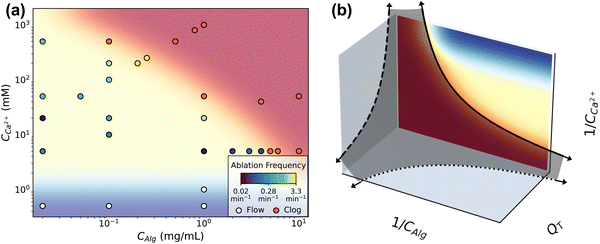 | ||
| Fig. 4 (a) The different dynamic regimes mapped on a CAlg/CCa2+ phase space. The background color corresponds to either the clogging regime (red), the flow regime with no deposition (blue), or intermittent deposition/ablation regime (yellow). The frequency of ablation at each point within the intermittent clogging regime is color coded on a log scale as per the legend. (b) By inverting the phase diagram from (a) the axes describe an analogy to the colloidal jamming phase diagram. The solid line shows the boundary between clogging and intermittency described in (a), in which data was obtained at constant flow rate QT. This boundary between clogging and intermittent flow qualitatively matches the boundary between the fluid and jammed phases of attractive colloids.23 The dark gray shaded surface separates the clogging phase, located close to the axes and origin, from the intermittent flow phase. The dotted and dashed lines complete the analogy. | ||
A critical minimum calcium concentration, CCa2+ ∼ 1 mM, is required to drive gelation and deposition, and consequently determines the region in which clogging and ablation occurs intermittently. At very low CCa2+ (<1 mM), we do not see significant deposition regardless of CAlg, and the flow is unperturbed. For instance, the driving pressure remains unchanged for the duration of an experiment lasting more than 600 s at conditions CCa2+ = 0.5 mM and CAlg = 1 mg mL−1 (ESI,† Fig. S11). As CCa2+ increases, intermittent dynamics appear. The location of the upper limit on CCa2+, i.e. where clogging occurs, depends on the alginate concentration. At high CAlg, a narrow range of CCa2+ gives rise to intermittent behavior. As CAlg decreases, the range of CCa2+ which gives rise to intermittent behavior increases in size. For example, at CAlg = 1 mg mL−1, the channel completely clogs at CCa2+ = 50 mM, while at CAlg = 0.02 mg mL−1, even CCa2+ = 5000 mM does not clog the channel but instead results in intermittent behavior.
Interestingly, higher QT than that shown in Fig. 4a may extend the range of intermittency. We observe intermittent behavior at CAlg = 10 mg mL−1, CCa2+ = 20 mM when QT is increased to QT = 6 μL min−1 (ESI,† Fig. S12). This same composition, CAlg = 10 mg mL−1 and CCa2+ = 20 mM, lies well within the red, clogging regime in Fig. 4a, obtained at QT = 1.2 μL min−1.
Exploration of the flow phase diagram more fully reveals the dependence of deposition/ablation frequency on system parameters. The color bar in Fig. 4a references the frequency of clog ablation at different conditions, with the color map shown on a log scale. As CCa2+ increases at a constant CAlg, moving vertically upward in the diagram, the frequency of ablation increases proportionally. Fig. 4a shows this increase at three different constant values of CAlg, while Fig. 3(b) provides the details for CAlg = 0.1 mg mL−1. Furthermore, increasing calcium at a fixed CAlg essentially increases the crosslink density. Thus we summarize this effect as f ∼ n, where n is crosslink density. Holding CCa2+ constant, however, and increasing CAlg, has little to no effect on f: Fig. 4a shows that color does not change significantly along horizontal lines until approaching the clogging boundary. Experimental conditions in Fig. 4a obtained along a line of slope 1, where CCa2+ ∼ CAlg, correspond to constant crosslink density n. Increasing both CCa2+ and CAlg simultaneously increases CGel, leading to an increase in f. Fig. 3d shows that this increase can be described by f ∼ CGel2. While all data shown in Fig. 4a occur at the same QT = 1.2 μL min−1, Fig. 3f and its inset indicate the behavior of f as a function of QT. While f does not depend strongly on QT, f normalized by the baseline shear rate, f/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , decreases with QT. This decrease is described by f/
, decreases with QT. This decrease is described by f/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ Q−0.6. Combining all of these observation results in an empirical relationship between f and system control parameters. We speculate that:
∼ Q−0.6. Combining all of these observation results in an empirical relationship between f and system control parameters. We speculate that:
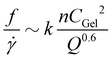 | (2) |
The production of eluted microgels is also controlled by the same system parameters that control the intermittent dynamics. Micro-rod formation happens throughout the region of intermittency. Rod shaped particles, such as the micro-rods found in Fig. 2, are most reliably formed in regions of the phase diagram where ablation frequency is slowest. As ablation frequency increases, the resulting rods become shorter and more globular.
3.5 Analogy to colloidal jamming
Intriguingly, the clogging behavior of this crosslinked polymer system may have analogies with colloidal jamming. In attractive colloidal systems, the transition between a liquid and jammed or glassy state is controlled by particle volume fraction ϕ, interparticle interaction strength U compared to thermal energy kBT, and the amount of stress applied to the system σ.21–23 The phase diagram describing the jamming transition is most often plotted in these three dimensions, on dimensionless axes kBT/U, 1/ϕ and σ/σ0, where σ0 is related to the yield stress of the material. Systems near the origin of this plot are “jammed” and behave as solids, while systems far from the origin are liquid. The details of the location and shape of the transitions between jammed, solid-like systems and un-jammed, liquid systems vary based on the materials involved.We observe that the dynamics of our crosslinking polymer system behave analogously to the thermodynamic phases of liquid and jammed colloids. That is, flow and intermittent flow represent dynamics of a fluid phase, while clogging is analogous to jamming. To demonstrate this, we invert the axes of Fig. 4a in Fig. 4b. Where the jamming phase diagram uses colloid concentration (1/ϕ), this system uses alginate concentration (1/CAlg). Where the jamming phase diagram uses energy of interparticle interaction (kBT/U), the corresponding variable in this system is the concentration of calcium (1/CCa2+), the means by which alginate molecules are attracted, or crosslinked, to one another. With the flow phase diagram in Fig. 4a inverted in this way, both flow and intermittent flow appear far from the origin. We note that the region in the plot where 1/CCa2+ → ∞ and 1/CAlg → 0 falls beyond the limits of Fig. 4a and represents highly concentrated, uncrosslinked polymer solutions, which may clog for reasons beyond gelation, including pump failure. The boundary between intermittency and clogging is represented by the solid line. Notably, the solid line matches qualitatively the boundary between jammed colloids, near the origin, and the fluid phase.23
The third axis in Fig. 4b, QT, is analogous to σ/σ0, but does not appear in Fig. 4a. However, measurements at different flow rates show that concentrations which lead to clogging at QT = 1.2 μL min−1, as shown in Fig. 4a, do not clog when the flow rate is increased. One example of this is shown in ESI,† Fig. S12, for CAlg = 10 mg mL−1 and CCa2+ = 20 mM flowing at QT = 6.0 μL min−1. Thus, higher flow rates expand the range of concentrations which do not clog. As such, data points within the red region at low QT move to the yellow region as QT increases. We indicate this by the dashed lines on the two planes defined by QT. Again, the shape of the boundary between flow and clogging qualitatively matches the thermodynamics defining colloidal liquids and jammed solids.
The jamming phase diagram provides a useful framework and set of parameters to map clogging, intermittency, and flow in crosslinking alginate. However, the analogy between flow dynamics and thermodynamics is not complete. In particular, the region of intermittent flow has no analog in the colloidal phases. Still, borrowing this conceptual framework may provide useful insights when examining other crosslinking polymers in flow. Alternate axes could incorporate channel geometry, to inform bioprinting applications, in which nozzles are usually symmetric and co-axial.33–35 Further nuance and complexity could be incorporated by investigating crosslinking reaction rates. Reaction rates become very important in biomedical contexts, as in the growth and ablation of blood clots in thromboembolism.36–38 Clot formation represents an enzyme catalyzed reaction in which thrombin both catalyzes fibrinogen polymerization and crosslinks the resulting fibrin polymers into a fibrin mat.39 Interestingly, a range of physiologically relevant wall shear rates and stresses overlap with the range observed in our experiments.40,41
4 Discussion and outlook
Our results demonstrate that simple polymeric solutions of alginate crosslinked by calcium give rise to various and rich dynamics when crosslinking occurs in microchannel flow: no clogging, complete clogging, and controllable persistently intermittent deposition/ablation. Our investigation suggests that both flow behavior and ablation frequency depend on chemical compositions and flow rates, and exhibit several interesting features that are worthy of additional discussion.Some surprising results occur when nearing the boundaries between the flow regimes. Most strikingly, within the intermittent clogging regime, the clogs grow to the largest extent near the boundary with unimpeded flow, as suggested by the largest values of ΔP − ΔP0, when the component concentrations are lowest. These conditions are farthest removed from the complete clogging regime. In contrast, the smallest intermittent clogs occur at higher component concentrations, closer to the boundaries of complete clogging. This seeming contradiction may be explained by the faster ablation frequency occurring at these higher concentrations.
The intermittent dynamics may also reveal material properties of the gel and its interaction with the channel walls. The frequency of ablation is presumably determined by a balance of adhesion forces and viscous shear forces, μ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . Increases in ΔP at constant QT suggest increasing local velocity and thus increasing shear forces. While alginate solution viscosity μ depends on alginate concentration, intermittent deposition/ablation behavior occurs at lower alginate concentrations in which the viscosity is similar to water. Therefore, the shear forces in the intermittent regime vary due to the shear rate rather than changes in viscosity, and accordingly with the velocity gradient within the cross-section of the channel. Using the measured peaks in ΔP, eqn (1) can be used to estimate the degree of radial occlusion of the channel and thus the increase in local shear rate
. Increases in ΔP at constant QT suggest increasing local velocity and thus increasing shear forces. While alginate solution viscosity μ depends on alginate concentration, intermittent deposition/ablation behavior occurs at lower alginate concentrations in which the viscosity is similar to water. Therefore, the shear forces in the intermittent regime vary due to the shear rate rather than changes in viscosity, and accordingly with the velocity gradient within the cross-section of the channel. Using the measured peaks in ΔP, eqn (1) can be used to estimate the degree of radial occlusion of the channel and thus the increase in local shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . In this way we estimate that the shear stresses at peak pressure, or the ablation stresses, are on the order of 1–10 Pa. Based on the relative increases in driving pressure, as seen in Fig. 3a and c, gels formed in lower concentration conditions experience more shear stress before ablation than those formed in the higher concentration conditions.30
. In this way we estimate that the shear stresses at peak pressure, or the ablation stresses, are on the order of 1–10 Pa. Based on the relative increases in driving pressure, as seen in Fig. 3a and c, gels formed in lower concentration conditions experience more shear stress before ablation than those formed in the higher concentration conditions.30
From the above, it stands to reason that gels formed in lower concentration solutions may adhere more strongly to the channel walls. Furthermore, bulk rheology suggests that gels at low polymer concentration or low crosslinking concentration are weaker than more concentrated gels.30,42 This may explain the larger increases in ΔP found at low CAlg and low CCa2+: the viscous shear forces of the fluid passing by the deposited gel can deform the gel easily without pulling it from the wall. This understanding may be further developed by measuring the rheological properties of the gels in situ. In situ rheological characterization of the gel would also reveal its mechanical response in flow, as bulk rheology methods are not sufficient to distinguish the dilute gel from water.
The shape of the pressure traces in Fig. 3 suggest that alginate deposition occurs faster with high concentration solutions than at low concentrations. That is, the slope of ΔP(t) during deposition is steeper for higher concentration conditions. Further, fitting ΔP(t) to a diffusively driven deposition model allows estimation of deposition efficiency as a function of system parameters.30 A larger percentage of the flowing alginate gel deposits at higher concentrations of components. However, deposition is less efficient at low concentrations. Because high component concentrations are associated with stiffer gels, it follows that stiffer gels deposit more efficiently.
Another intriguing feature of the intermittent flow regime is the production of micro-rods. Nearly all published methods of manufacturing or fabricating hydrogel micro-particles via microfluidics use two phases, typically a water-in-oil emulsion.43 In these, the oil phase serves as a suspending fluid to create monodisperse droplets or to control the location and rate of crosslinking. Premature crosslinking often causes clogging and device failure, and thus is avoided in these contexts.44 By contrast, we have identified a scheme where clogging is controllable without an oil phase, so that the resulting micro-rods are produced using only the aqueous phase. This single-phase procedure greatly simplifies the washing and separation of particles after production. The rods are stable in solution and sufficiently robust to maintain their shape upon pipetting. The diversity of chemical and physical conditions, represented in the intermittent region of the flow phase diagram, may allow for tuning both the size and stiffness of the gel rods, which are important features in many applications.45 The rods maintain their shape after ablation, with widths equal to the channel width. This suggests channel geometry dictates their width. Additionally, there is potential to tune the stiffness of the micro-rods by preparing them at different reaction conditions. Further characterization of gels in all areas of the flow phase diagram could describe this tunability.
5 Conclusion
We find an interesting pattern of deposition and ablation occurring when flowing alginate and calcium solutions at constant flow rates through microfluidic channels meeting in a Y-shaped junction. The alignment between pressure measurements and microscopy demonstrates that the gel deposit grows to occlude the channel and thus necessitates an increase in driving pressure to maintain the constant flow rate. This growth continues until shear stress pulls the gel off the wall, resulting in the ablation of the gel. The ablated gel maintains its shape to form stable rod structures several hundred microns long and 30 microns wide, the same width as the channel. Gel deposition and ablation happen with a regular frequency. We further find that we can control both the extent of the deposition and the frequency of ablation events by varying flow rate, the degree of crosslinking, and the concentration of gel.Interestingly, the conditions which give rise to faster ablation frequencies occur closer to the clogging regime, while slow frequency conditions occur closer to the flow regime. The novelty of the phenomenon we have discovered with such a simple system reveals that the behavior of crosslinking polymer solutions flowing through small channels exhibits rich and complicated dynamics. The boundaries between the dynamic regions of flow, clogging and intermittency find a useful and powerful analogy in the phase diagram describing colloidal jamming. Further exploration of these dynamics, along with investigations of the material properties of the deposited and eluted gel, can be used to exploit similarities to a variety of real-world situations in which polymeric clogging plays a vital role. Ultimately, these results open up numerous directions for future studies. Quantifying the limits on polymeric clogging behavior represents the first step toward designing tools to predict, diagnose, and even reverse such clogging.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is funded by the NSF CBET, CAREER Award 2239742.References
- A. Maleki, A.-L. Kjøniksen and B. Nyström, J. Phys. Chem. B, 2005, 109, 12329–12336 CrossRef CAS PubMed.
- Z. Liu, A. Maleki, K. Zhu, A.-L. Kjøniksen and B. Nyström, J. Phys. Chem. B, 2008, 112, 1082–1089 CrossRef CAS PubMed.
- W. de Carvalho and M. Djabourov, Rheol. Acta, 1997, 36, 591–609 CrossRef CAS.
- O. Ronsin, C. Caroli and T. Baumberger, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 1–7 CrossRef PubMed.
- A. Z. Nelson, Y. Wang, Y. Wang, A. S. Margotta, R. L. Sammler, A. Izmitli, J. S. Katz, J. Curtis-Fisk, Y. Li and R. H. Ewoldt, Soft Matter, 2022, 18, 1554–1565 RSC.
- S. M. Silva, F. V. Pinto, F. E. Antunes, M. G. Miguel, J. J. Sousa and A. A. Pais, J. Colloid Interface Sci., 2008, 327, 333–340 CrossRef CAS PubMed.
- Y. Liu, M. Hildner, O. Roy, W. A. Van Den Bogert, J. Lorenz, M. Desroches, K. Koppi, A. Shih, R. G. Larson, M. Science and E. Program, J. Rheol., 2023, 67, 791 CrossRef CAS.
- C. A. Verheyen, S. G. Uzel, A. Kurum, E. T. Roche and J. A. Lewis, Matter, 2023, 6, 1015–1036 CrossRef CAS.
- J. M. Townsend, E. C. Beck, S. H. Gehrke, C. J. Berkland and M. S. Detamore, Prog. Polym. Sci., 2019, 91, 126–140 CrossRef CAS PubMed.
- S. Ramesh, O. L. A. Harrysson, P. K. Rao, A. Tamayol, D. R. Cormier, Y. Zhang and I. V. Rivero, Bioprinting, 2021, 21, e00116 CrossRef.
- C. C. Piras and D. K. Smith, J. Mater. Chem. B, 2020, 8, 8171–8188 RSC.
- Z. Khan, K. Kahin and C. A. Hauser, Microfluidics, BioMEMS, and Medical Microsystems XIX, Proc. SPIE, 2021, 11637, 1163709 Search PubMed.
- A. Datar, D. W. Lee, S. Y. Jeon and M.-Y. Lee, Microarray Bioprinting Technology: Fundamentals and Practices, 2016, 19–51 Search PubMed.
- S. Aabith, R. Caulfield, O. Akhlaghi, A. Papadopoulou, S. Homer-Vanniasinkam and M. K. Tiwari, Addit. Manuf., 2022, 58, 103019 CAS.
- R. Attalla, E. Puersten, N. Jain and P. R. Selvaganapathy, Biofabrication, 2018, 11, 15012 CrossRef PubMed.
- S. E. El-Habashy, A. H. El-Kamel, M. M. Essawy, E.-Z. A. Abdelfattah and H. M. Eltaher, Biomater. Sci., 2021, 9, 4019–4039 RSC.
- J. Lee, S. J. Oh, S. H. An, W.-D. Kim and S.-H. Kim, Biofabrication, 2020, 12, 35018 CrossRef CAS PubMed.
- K. Takahashi, H. Takao, F. Shimokawa and K. Terao, Microfluid. Nanofluid., 2022, 26, 15 CrossRef CAS.
- Q. Wu, D. Therriault and M.-C. Heuzey, ACS Biomater. Sci. Eng., 2018, 4, 2643–2652 CrossRef CAS PubMed.
- Y. Prasad, K. Rao and S. Sasidhar, Hot working guide: a compendium of processing maps, ASM international, 2015 Search PubMed.
- A. J. Liu and S. R. Nagel, Nature, 1998, 396, 21–22 CrossRef CAS.
- A. J. Liu and S. R. Nagel, Nat. Rev. Phys., 2023, 1–2 Search PubMed.
- V. Prasad, L. Cipelletti and P. Segre, Nature, 2001, 411, 772–775 CrossRef PubMed.
- C. B. Highley, K. H. Song, A. C. Daly and J. A. Burdick, Adv. Sci., 2019, 6, 1801076 CrossRef PubMed.
- W. Cheng, J. Zhang, J. Liu and Z. Yu, View, 2020, 1, 20200060 CrossRef.
- A. Martinsen, G. Skjåk-Bræk, O. Smidsrød, F. Zanetti and S. Paoletti, Carbohydr. Polym., 1991, 15, 171–193 CrossRef CAS.
- J. C. McDonald, D. C. Duffy, J. R. Anderson, D. T. Chiu, H. Wu, O. J. Schueller and G. M. Whitesides, Electrophoresis, 2000, 21, 27–40 CrossRef CAS PubMed.
- T. Trantidou, Y. Elani, E. Parsons and O. Ces, Microsyst. Nanoeng., 2017, 3, 1–9 Search PubMed.
- A. R. Abate, D. Lee, T. Do, C. Holtze and D. A. Weitz, Lab Chip, 2008, 8, 516–518 RSC.
- B. T. Smith and S. M. Hashmi, arXiv, 2024, preprint, arXiv:2401.02530 DOI:10.48550/arXiv.2401.02530.
- S. M. Hashmi, M. Loewenberg and A. Firoozabadi, Phys. Fluids, 2015, 27, 083302 CrossRef.
- M. A. LeRoux, F. Guilak and L. A. Setton, J. Biomed. Mater. Res., 1999, 47, 46–53 CrossRef CAS PubMed.
- J. Gopinathan and I. Noh, Biomater. Res., 2018, 22, 11 CrossRef PubMed.
- O. Bonhomme, J. Leng and A. Colin, Soft Matter, 2012, 8, 10641–10649 RSC.
- E. Abelseth, L. Abelseth, L. De La Vega, S. T. Beyer, S. J. Wadsworth and S. M. Willerth, ACS Biomater. Sci. Eng., 2019, 5, 234–243 CrossRef CAS PubMed.
- S. Zhu, J. Chen and S. L. Diamond, Arterioscler., Thromb., Vasc. Biol., 2018, 38, 1528–1536 CrossRef CAS PubMed.
- J. Chen and S. L. Diamond, PLoS Comput. Biol., 2019, 15, e1007266 CrossRef CAS PubMed.
- M. S. Chatterjee, W. S. Denney, H. Jing and S. L. Diamond, PLoS Comput. Biol., 2010, 6, e1000950 CrossRef PubMed.
- A. L. Fogelson and K. B. Neeves, Annu. Rev. Fluid Mech., 2015, 47, 377–403 CrossRef PubMed.
- J. M. Dolan, J. Kolega and H. Meng, Ann. Biomed. Eng., 2013, 41, 1411–1427 CrossRef PubMed.
- K. S. Sakariassen, L. Orning and V. T. Turitto, Future Sci. OA, 2015, 1(4), FSO30 Search PubMed.
- C. Ouwerx, N. Velings, M. Mestdagh and M. A. Axelos, Polym. Gels Networks, 1998, 6, 393–408 CrossRef CAS.
- Y. Liu, Z. Chen and J. Xu, Green Chem. Eng., 2023, 16–30 CAS.
- A. G. Håti, D. C. Bassett, J. M. Ribe, P. Sikorski, D. A. Weitz and B. T. Stokke, Lab Chip, 2016, 16, 3718–3727 RSC.
- M. M. Villone and P. L. Maffettone, Rheol. Acta, 2019, 58, 109–130 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Two mp4 video files, Video 1 and Video 2, and supplementary figures in pdf. See DOI: https://doi.org/10.1039/d3sm01389h |
| This journal is © The Royal Society of Chemistry 2024 |