Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Selective lithium extraction from brine via chemical reduction of iron phosphate with aqueous iron compounds†
Jing
Wang
,
Alex W.
Hawkins
,
Amin T.
Saasi
,
Caroline G.
Morin
 ,
Geoffrey M.
Geise
,
Geoffrey M.
Geise
 and
Gary M.
Koenig
Jr
and
Gary M.
Koenig
Jr
 *
*
Department of Chemical Engineering, University of Virginia, 385 McCormick Road, Charlottesville, VA 22904-4741, USA. E-mail: jw9hq@virginia.edu; awh7fnb@virginia.edu; rdx3wp@virginia.edu; frm2zw@virginia.edu; geise@virginia.edu; gary.koenig@virginia.edu; Fax: +1-434-982-2658; Tel: +1-434-982-2714
First published on 17th July 2024
Abstract
Worldwide demand for lithium (Li) is surging due to increased production of Li-ion batteries to meet the needs for increasing numbers of electric vehicles and stationary energy storage systems. Conventional Li+ extraction from Li-bearing ores and brines has drawbacks of high chemical and energy inputs. In this work, chemical redox-driven processes were developed to selectively extract Li+ from brine meant to simulate a geothermal resource. Using additives that modify the redox potential of soluble iron compounds, ethylenediaminetetraacetic acid (EDTA) and citrate, the potential of the solution was shifted lower to drive reduction of a targeted solid electroactive material (FePO4, FP). Li+ from simulated brine sources (with molar ratio Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+ of 1
Na+ of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78) was extracted into the FP solid without additional energy inputs. The Li+ adsorption capacity for extraction with EDTA–Fe2+ solutions and citrate–Fe2+ solutions were 3.8 mmol Li+ g−1 FP and 2.5 mmol Li+ g−1 FP, respectively, and the selectivity factors for Li+ to Na+ for the two systems were 78 and 350, respectively. Similar extraction outcomes were achieved using a brine that more closely resembled the composition of geothermal fluids from the Salton Sea. This study more broadly provided insight into enhancing Li+ capture selectivity through modification of redox solution compositions.
78) was extracted into the FP solid without additional energy inputs. The Li+ adsorption capacity for extraction with EDTA–Fe2+ solutions and citrate–Fe2+ solutions were 3.8 mmol Li+ g−1 FP and 2.5 mmol Li+ g−1 FP, respectively, and the selectivity factors for Li+ to Na+ for the two systems were 78 and 350, respectively. Similar extraction outcomes were achieved using a brine that more closely resembled the composition of geothermal fluids from the Salton Sea. This study more broadly provided insight into enhancing Li+ capture selectivity through modification of redox solution compositions.
1. Introduction
The worldwide demand for lithium (Li) continues to increase due to the increased use of Li-ion batteries in stationary energy storage and electric vehicles, coupled with their already ubiquitous use for powering electronic devices.1 Li-ion batteries have a diversity of materials and compounds used for the cathode, anode, and electrolyte; however, in all combinations Li is required for these batteries.2 According to the United States Geological Survey, the worldwide production of Li increased from 82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 to 107
500 to 107![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 metric tons just between the years 2020 to 2021, and Li-ion batteries accounted for 80% of Li end use.3 New Li production sources and technologies are needed both to more sustainably support Li production and to prevent supply shortages. Supply limitations could cause Li prices to increase and impact the cost and adoption of energy storage technologies such as electric vehicles that are highly reliant on this resource and necessary for broader energy decarbonization.
000 metric tons just between the years 2020 to 2021, and Li-ion batteries accounted for 80% of Li end use.3 New Li production sources and technologies are needed both to more sustainably support Li production and to prevent supply shortages. Supply limitations could cause Li prices to increase and impact the cost and adoption of energy storage technologies such as electric vehicles that are highly reliant on this resource and necessary for broader energy decarbonization.
Li resources naturally exist in ores, brines and seawater, and major supplies of Li are extracted from Li-bearing ores and brines. Methods of calcination, chlorination, and acid/alkaline chemical treatment are used to digest ores and extract out Li+.4,5 Drawbacks of these methods include substantial consumption of chemical inputs, water resource consumption, and generation of waste. Conventional Li extraction resources and practices have also been associated with environmental conflicts related to the mining.6 Another continental source for Li exists in brine solution. More recently, there has been interest in extracting Li+ from brines which are less enriched in Li+ and/or have complications of many other cations present, in many cases with many-fold excess concentration of other cations relative to the Li+.7 The conventional method to extract Li+ from brine solution is solar evaporation followed by precipitation, where the water is driven out of the solution and the end products are selectively precipitated compounds.8 However, these methods require high energy inputs to drive out the water from the brine, which either needs to be provided by electricity/fuel input costs and extra processing, or more commonly evaporation in solar ponds. The solar evaporation drying process can take from months to years. Other efforts to extract Li+ from brines have included solvent extraction,9,10 ion exchange adsorption,11 electrochemical extraction,12 and membrane separation.13 Low cost, low environmental impact, and robust operation methods are needed for brine extraction.
Selective Li+ intercalation materials have indicated promise for extraction of Li+ due to their ion channels favorable for uptake of Li+.5,14 Commonly used materials include lithium titanium oxides (e.g., Li4Ti5O12 or Li2TiO3), lithium manganese oxides (e.g., LiMn2O4, Li1.6Mn1.6O4), and lithium iron phosphate (LiFePO4, LFP).8,15 These materials have generally been applied via methods of ion exchange adsorption, electrochemical driven separation, and redox mediated electrochemical separation.16 In the ion exchange adsorption method, the intercalation materials were pretreated with acid to exchange the Li+ with protons (H+). The H+ are then substituted by the Li+ when contacted with the Li+-containing brine, and the Li+ is subsequently released in the next acid solution treatment cycle.17,18 Ion exchange has required large amounts of acid as the proton sources. Additionally, the intercalation material needs to be stable in those acids. Manganese oxides in particular have known limitations with regards to dissolution of Mn when in contact with acid,19,20 thus processing must be controlled to minimize solid material dissolution and/or material modifications must be implemented to improve the structural stability.21–23 For electrochemical-driven Li+ separation, the cell contained a cathode, anode, and membrane separator, while the brine solution functioned as the electrolyte. During operation, Li+ from the brine intercalated into material within the anode or cathode depending on cell design, with the Li+ later released into a separate recovery solution. The driving force for extraction and release was electrochemical potential, with external electrical energy needed for operation.24,25 Additional considerations for the process have included side reactions such as water splitting, and the addition of organic solvents to facilitate the electrochemical reactions.26,27
Other processes have used intercalation materials for Li+ extraction and have included chemical redox as the driving force for Li+ insertion and extraction to the host material. For chemical redox, a potential difference is required between the solid intercalation materials and the soluble redox mediators. The most reported intercalation material for these chemical redox systems has been LFP. LFP is used as a commercial Li-ion battery cathode material with relatively low-cost constituent compounds, robust chemical stability, and reversible redox provided by the Fe. In prior work, the half-wave potential difference between LFP (0.186 V vs. Ag/AgCl) and potassium ferricyanide (K3Fe(CN)6) (0.247 V vs. Ag/AgCl) provided a thermodynamic driving force to oxidize the LFP.28 Similarly, a redox mediator with a half wave potential below FP would be desired to thermodynamically drive the reduction of FP (and uptake of Li+). Previously, studies have shown that ligands bonded with iron could shift soluble iron redox potentials lower.29 Even though LFP materials have ion channels well suited to Li+ uptake and transport, some prior work has reported relatively low selectivity for Li+ uptake in brine solutions with other cations when the relative Li+ concentration was low, for example in solutions with excess competing sodium and magnesium.14,30
In this work, we developed a chemical redox driven Li+ extraction system using dissolved iron redox mediators to extract Li+ from brine. The soluble iron was complexed separately with two different additives to the solution, ethylenediaminetetraacetic acid (EDTA) and citrate. The relevant redox couples will thus be referred to as EDTA–Fe2+ and citrate–Fe2+, respectively. The exact structures of the iron–ligand complexes were not investigated. The extraction brine was targeted to simulate solution conditions experienced for brine discharged after geothermal energy processing at the Salton Sea.31,32 In the simulated brine, we evaluated the Li+ extraction efficiency at high and low Li+ concentration. In brine with high Li+ concentration (1 M, molar ratio of Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M+/2+ of 1
M+/2+ of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, M+/2+ = Na, K, Mg), FP had high selectivity to Li+ in both EDTA–Fe2+ and citrate–Fe2+ redox systems. The FP reached 94% conversion/reduction, and the Li adsorption capacity was ∼6 mmol Li+ g−1 FP for EDTA–Fe2+. In brine with lower Li+ concentration (39 mM Li+, molar ratio of Li+
1, M+/2+ = Na, K, Mg), FP had high selectivity to Li+ in both EDTA–Fe2+ and citrate–Fe2+ redox systems. The FP reached 94% conversion/reduction, and the Li adsorption capacity was ∼6 mmol Li+ g−1 FP for EDTA–Fe2+. In brine with lower Li+ concentration (39 mM Li+, molar ratio of Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+, 1
Na+, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78), the extraction rate of the EDTA–Fe2+ was faster than of the citrate–Fe2+ system, with the Li+ adsorption capacity 3.8 mmol Li+ g−1 FP with redox EDTA–Fe2+ and 2.5 mmol Li+ g−1 FP with redox citrate–Fe2+. The selectivity factor αLiNa was 78 for EDTA–Fe2+ and 350 for redox citrate–Fe2+. These chemical redox-driven systems for Li+ extraction had high Li selectivity, high adsorption capacity, and no input energy consumption during the Li+ capture step. The Li+ selectivity difference between the two different redox couples facilitated by different soluble additives suggested control over relevant complexes and solution chemistry provided new routes improve Li+ uptake and selectivity during mediated Li+ capture with an intercalation material.
78), the extraction rate of the EDTA–Fe2+ was faster than of the citrate–Fe2+ system, with the Li+ adsorption capacity 3.8 mmol Li+ g−1 FP with redox EDTA–Fe2+ and 2.5 mmol Li+ g−1 FP with redox citrate–Fe2+. The selectivity factor αLiNa was 78 for EDTA–Fe2+ and 350 for redox citrate–Fe2+. These chemical redox-driven systems for Li+ extraction had high Li selectivity, high adsorption capacity, and no input energy consumption during the Li+ capture step. The Li+ selectivity difference between the two different redox couples facilitated by different soluble additives suggested control over relevant complexes and solution chemistry provided new routes improve Li+ uptake and selectivity during mediated Li+ capture with an intercalation material.
2. Materials and methods
2.1. Brine chemicals
All salts and chemicals were purchased from Sigma Aldrich and used as received. The chemicals used were: sodium chloride (NaCl), lithium chloride (LiCl), potassium chloride (KCl), sodium hydroxide (NaOH), potassium hydroxide (KOH), lithium hydroxide (LiOH), iron(II) chloride tetrahydrate (FeCl2·4H2O), iron(III) chloride (FeCl3), glacial acetic acid, magnesium chloride (MgCl2), potassium citrate, ethylenediaminetetraacetic acid (EDTA), N-methyl-2-pyrrolidone (NMP), boric acid, manganese chloride tetrahydrate (MnCl2·4H2O), and hydrogen peroxide solution (H2O2, 30%).2.2. Preparation of FP
FP powder was obtained via a chemical oxidation method from prior literature.33 In brief, 1 g of LFP (TOB, Xiamen) was mixed with a solution containing 5 mL of H2O2 (30% in water, Fisher), 5 mL of acetic acid, and 140 mL deionized water. The LFP was added to the solution and allowed to react for two hours at room temperature without stirring. At the conclusion of the reaction process, the FP powder was collected and rinsed with DI water via vacuum filtration and dried in an oven with air at 80 °C overnight. Full delithiation was assessed using powder X-ray diffraction (XRD).28 This LFP chemical oxidization method was also used to release the cations captured during the redox mediated extraction for analysis and will be referred to as the “chemical oxidation” method herein.2.3. Preparation of FP and LFP electrode for electrochemical measurements
LFP and FP electrochemical electrodes were fabricated by blending LFP or FP powder with Super P carbon black (CB, TIMCAL) and polymer binder polyvinylidene fluoride (PVDF, Alfa Aesar) at mass ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 LFP
1 LFP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CB
CB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PVDF. The powder mixture was blended using mortar and pestle by hand and wetted with NMP solvent. The resulting slurry was further mixed using an Ar-100 Thinky mixer. For LFP electrode used in cyclic voltammetry measurement, the slurry was pasted on the tip of a 5 × 1 cm nickel foam strip by hand. For LFP or FP electrodes used in electrochemical cells, the FP or LFP slurry was pasted on titanium rod with diameter of 0.046 mm (McMaster-Carr). For FP electrodes used in contact angle measurements, FP composites were fabricated by casting FP slurry onto an aluminum foil with a doctor blade with gap height of 100 μm. After pasting the FP or LFP slurry onto the metal current collectors, the electrodes were dried at 80 °C overnight in air in an oven to remove any residual NMP solvent.
PVDF. The powder mixture was blended using mortar and pestle by hand and wetted with NMP solvent. The resulting slurry was further mixed using an Ar-100 Thinky mixer. For LFP electrode used in cyclic voltammetry measurement, the slurry was pasted on the tip of a 5 × 1 cm nickel foam strip by hand. For LFP or FP electrodes used in electrochemical cells, the FP or LFP slurry was pasted on titanium rod with diameter of 0.046 mm (McMaster-Carr). For FP electrodes used in contact angle measurements, FP composites were fabricated by casting FP slurry onto an aluminum foil with a doctor blade with gap height of 100 μm. After pasting the FP or LFP slurry onto the metal current collectors, the electrodes were dried at 80 °C overnight in air in an oven to remove any residual NMP solvent.
2.4. Electrochemical characterization of FP and redox mediators
Cyclic voltammetry (CV) was used to determine the half-wave potential of redox mediators (EDTA–Fe2+ & citrate–Fe2+), LFP/FP, and Fe2+/Fe3+ solution. CV experiments were conducted with a Bio-Logic SP50. Separate platinum disc electrodes with diameters of 1.6 mm were used as the working and counter electrode. Ag/AgCl with saturated KCl was used as the reference electrode (Pine Research). Solutions were scanned at rates ranging from 10 mV s−1 to 200 mV s−1. In the testing solutions, in addition to the evaluated redox species, 3.04 M of NaCl and 39 mM of LiCl was also added which was a level intended to mimic the relevant concentrations in Salton Sea brine.32 Nitrogen gas was bubbled through the solutions during the entire preparation process to minimize air oxidation of Fe2+ species. For the half wave potential of EDTA–Fe2+, EDTA and FeCl2 with each 0.1 M were dissolved in 1 M acetic acid solution, and LiOH was added to dissolve the EDTA as well as to adjust the solution pH to 7. The scanned voltage range was from −0.5 V to 0.2 V vs. Ag/AgCl. For citrate–Fe2+, equimolar of potassium citrate and FeCl2 (0.1 M each) was dissolved in DI water, the scanned voltage range was from −0.5 V to 0.4 V vs. Ag/AgCl. For the half wave potential of Fe2+/Fe3+ (from chloride salts), equimolar of Fe2+/Fe3+ (0.05 M each) was prepared in DI water, and the scanned range was from 0 V to 1.2 V vs. Ag/AgCl. For using CV scans to calculate the diffusion coefficient of Fe solution redox species, the cathodic peak current was plotted against the square root of scan rate, and the slope of a linear least squares fit was extracted for the calculation.34For CV evaluation of LFP active material, the working electrode was prepared with procedures described in Section 2.3. The LFP electrode loaded within nickel foam was dipped in 1 M Li2SO4 solution and used as the working electrode and platinum wire (1 mm) was the counter electrode. The scanned voltage range was −0.25–0.75 V (vs. Ag/AgCl), and the scan rate was 0.2 mV s−1.
2.5. Simulated brine preparation and extraction procedures
Simulated brine with high Li+ concentration, but relatively low competing cations concentration (molar ratio Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M+/2+, 1
M+/2+, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), and low Li+ concentration, but high competing cations concentration (molar ratio Li+
1), and low Li+ concentration, but high competing cations concentration (molar ratio Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+, 1
Na+, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78), were both evaluated for Li+ extraction. In all the experiments with simulated brine solutions, the molar ratio of FeCl2 and ligands (EDTA, citrate) was kept at 1
78), were both evaluated for Li+ extraction. In all the experiments with simulated brine solutions, the molar ratio of FeCl2 and ligands (EDTA, citrate) was kept at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for all evaluated concentrations. To avoid Fe oxidation, FeCl2 was added to the brine solution last, and after all other chemicals had been dissolved. The brine solution was also at all times purged with nitrogen gas via bubbling through a sealed flask. All pH values reported were after the step of ligand addition/dissolution. The Li+ extracting FP solid (prepared from chemical oxidation of LFP), was contacted with brine solution in a porous pellet form. FP pellets were prepared by loading the FP powder into a 13 mm diameter pellet die and hydraulically pressing at 12
1 for all evaluated concentrations. To avoid Fe oxidation, FeCl2 was added to the brine solution last, and after all other chemicals had been dissolved. The brine solution was also at all times purged with nitrogen gas via bubbling through a sealed flask. All pH values reported were after the step of ligand addition/dissolution. The Li+ extracting FP solid (prepared from chemical oxidation of LFP), was contacted with brine solution in a porous pellet form. FP pellets were prepared by loading the FP powder into a 13 mm diameter pellet die and hydraulically pressing at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 psi for 2 min at room temperature. FP was in pellet form for convenience of collection after extraction.
000 psi for 2 min at room temperature. FP was in pellet form for convenience of collection after extraction.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) M+/2+, 1
M+/2+, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 1).
The detailed compositions of brine solutions with the two redox mediators can be found in Table S1 in ESI.† The total mass of the brine solution was 100 g, and the mass of each chemical was calculated based on assumed volume of 100 mL of brine solution. The procedure for preparing simulated brine solution with redox mediator, EDTA–Fe2+ is described in the following: (1) 1 M of acetic acid solution was prepared to mitigate dramatic solution pH swings. (2) 0.1 M of EDTA was added to the acetic acid solution. (3) Subsequently, LiOH was added to the solution mixture to facilitate EDTA dissolution and until the solution was clear. Additional LiOH was added, if needed, until the solution pH reached 7, and the corresponding concentration of Li+ was ∼1.3 M. (4) Target cation chloride salt (NaCl, KCl, MgCl2) with the same molar concentration as the Li+ were added and dissolved in the solution. (5) 0.1 M of FeCl2·4H2O was added last and the solution was stirred until all material dissolved. Nitrogen gas was bubbled in the solution throughout the process. (6) 0.5 g of FP pellet was directly added to the solution. For preparing brine solution with redox mediator citrate–Fe2+ solution, the experimental procedures were similar to the EDTA–Fe2+ solutions, except that (1) no acetic acid was added to the solution due to its chelation competition with citrate ligand, (2) there was no need for solution pH adjustment as the citrate ligand had high solubility in water without pH moderation, (3) LiCl was added as the Li source. Experiments with high concentration of Li+ were conducted for 24 hours at 23 °C and 75 °C. Duplicate experiments were completed for each brine solution, and average adsorption capacity were reported for each redox mediator.
1).
The detailed compositions of brine solutions with the two redox mediators can be found in Table S1 in ESI.† The total mass of the brine solution was 100 g, and the mass of each chemical was calculated based on assumed volume of 100 mL of brine solution. The procedure for preparing simulated brine solution with redox mediator, EDTA–Fe2+ is described in the following: (1) 1 M of acetic acid solution was prepared to mitigate dramatic solution pH swings. (2) 0.1 M of EDTA was added to the acetic acid solution. (3) Subsequently, LiOH was added to the solution mixture to facilitate EDTA dissolution and until the solution was clear. Additional LiOH was added, if needed, until the solution pH reached 7, and the corresponding concentration of Li+ was ∼1.3 M. (4) Target cation chloride salt (NaCl, KCl, MgCl2) with the same molar concentration as the Li+ were added and dissolved in the solution. (5) 0.1 M of FeCl2·4H2O was added last and the solution was stirred until all material dissolved. Nitrogen gas was bubbled in the solution throughout the process. (6) 0.5 g of FP pellet was directly added to the solution. For preparing brine solution with redox mediator citrate–Fe2+ solution, the experimental procedures were similar to the EDTA–Fe2+ solutions, except that (1) no acetic acid was added to the solution due to its chelation competition with citrate ligand, (2) there was no need for solution pH adjustment as the citrate ligand had high solubility in water without pH moderation, (3) LiCl was added as the Li source. Experiments with high concentration of Li+ were conducted for 24 hours at 23 °C and 75 °C. Duplicate experiments were completed for each brine solution, and average adsorption capacity were reported for each redox mediator.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) Na+, 1
Na+, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 78).
A simulated brine with a Li+
78).
A simulated brine with a Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+ molar ratio of 1
Na+ molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78 was studied to mimic the concentrations of those two cations in brine from Salton Sea.31,32 The procedures to prepare the brine solution were similar to those described above, except that the competing cation was specifically Na+, and the concentration of Li+ and Na+ were adjusted to 39 mM and 3.04 M. All salts appeared dissolved based on visual inspection, without residual solids present. The detailed composition of brine solutions with low Li+ concentration and high Na+ concentration (Li+
78 was studied to mimic the concentrations of those two cations in brine from Salton Sea.31,32 The procedures to prepare the brine solution were similar to those described above, except that the competing cation was specifically Na+, and the concentration of Li+ and Na+ were adjusted to 39 mM and 3.04 M. All salts appeared dissolved based on visual inspection, without residual solids present. The detailed composition of brine solutions with low Li+ concentration and high Na+ concentration (Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+ molar ratio of 1
Na+ molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78) can be found in ESI, Table S2.†
78) can be found in ESI, Table S2.†
Experiments were also conducted where the redox mediator concentrations were varied for solutions that were contacted with the FP. The concentrations of EDTA–Fe2+ were 15, 30, 50, 100, 200, and 300 mM. The same concentrations were also evaluated with citrate–Fe2+, except 100 mM was the highest concentration evaluated for citrate–Fe2+ due to solubility limitations. The Li+ extraction process for each redox concentration was also assessed at three different temperatures, 23 °C, 45 °C, and 75 °C. For experiments at elevated temperatures (45 °C and 75 °C), the FP was added after the brine solution reached the target temperature via heating in an oil bath. The extraction reactions all proceeded for 24 h.
Experiments were also conducted to assess the time progression of the Li+ extraction process. To compare the two mediators and because of citrate solubility limitations at higher concentrations, the condition chosen for comparison was 100 mM redox mediator (EDTA–Fe2+ or citrate–Fe2+) and 39 mM of Li+ and 3.04 M of Na+ (consistent the ratio of those cations at the Salton Sea). The temperature was 45 °C, and the reaction was allowed to proceed in independent experiments for intervals increasing in timescale of 2 h up to 24 h. Each of these experiments had nominally identical solution and FP preparation, where only the reaction timescale was varied. After the chemical reduction of FP by the solution had concluded, the FP powder was washed several times with deionized water and dried at 80 °C in an oven in air overnight.
Experiments were also conducted to evaluate multiple Li+ capture and release cycles for the FP/LFP solid. FP was reduced by simulated brine solution (39 mM of Li+ and 3.04 M of Na+) with 100 mM added redox mediator. The reaction proceeded at 45 °C for 24 h for each capture cycle. After the reduction and cation capture step, the cations were released via the chemical oxidation method (described earlier). The solution supernatant was collected for ion chromatography (IC) analysis, and the FP powder was collected and rinsed with DI water before the next round of reduction via contact with fresh brine solution. The capture and release process were repeated for 5 complete cycles. Both citrate–Fe2+ with EDTA–Fe2+ redox mediators were evaluated. Capture/release cycling experiments for each redox mediator were repeated twice and the average values were reported. The FP powder collected after 5 cycles of extraction/release of both redox mediators, and the initial FP prepared by chemical oxidation, imaged using scanning electron microscopy (SEM) imaging. The SEM was a FEI Quantum 650.
2.6. Brine solution with composition more representative of Salton Sea extraction
A brine solution with composition more representative of the Salton Sea brine was used for Li+ extraction using FP with redox mediators, EDTA–Fe2+ or citrate–Fe2+. The detailed brine compositions can be found in ESI, Table S3.† Due to solution stability limitations, Ca2+ was omitted from the original formulation during the brine preparation. Based on previous experimental optimizations of the reaction temperature and redox mediator concentration, the reduction reactions were continued for 24 h at 45 °C using 0.1 M of redox mediators. The captured cations were then released by chemical oxidation for IC analysis.2.7. Electrochemical Li+ uptake from brine
Electrochemical Li+ extraction from brine was achieved using a three-electrode system, where the working and counter electrode were FP and LFP, respectively, and Ag/AgCl with saturated KCl was the reference electrode. The preparation of LFP/FP electrodes were mentioned in Section 2.3, and the mass ratio of working (FP) to counter (LFP) electrode was at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 (e.g., there was excess capacity and Li+ in the LFP electrode). The three electrodes were submerged in a salt solution with a Li+
1.5 (e.g., there was excess capacity and Li+ in the LFP electrode). The three electrodes were submerged in a salt solution with a Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+ molar ratio of 1
Na+ molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78 dissolved in DI water. The voltage was kept constant throughout the lithiation process, with the potential below that necessary for intercalation of Li+ into the FP (0.242 V vs. Ag/AgCl). The constant voltage used for lithiation of the FP ranged from −0.3 V to 0 V (vs. Ag/AgCl), with increments of 0.1 V. For comparison with chemical lithiation, the electrochemical lithiation was stopped after achieving 50% extent of lithiation. The extent of lithiation was calculated based on the mass of active material (FP) and assumed theoretical capacity of 165 mA h g−1 FP. Upon completion of the extraction process, the working electrode (originally FP) was rinsed with 200 mL of DI water to remove residual salt solution. The captured cations from the solid electroactive material in the working electrode were released using the same chemical oxidizing method as for FP preparation.33 The supernatant of the solution after oxidation of the powder was collected for IC composition analysis. Duplicate experiments were conducted, and the average value was reported.
78 dissolved in DI water. The voltage was kept constant throughout the lithiation process, with the potential below that necessary for intercalation of Li+ into the FP (0.242 V vs. Ag/AgCl). The constant voltage used for lithiation of the FP ranged from −0.3 V to 0 V (vs. Ag/AgCl), with increments of 0.1 V. For comparison with chemical lithiation, the electrochemical lithiation was stopped after achieving 50% extent of lithiation. The extent of lithiation was calculated based on the mass of active material (FP) and assumed theoretical capacity of 165 mA h g−1 FP. Upon completion of the extraction process, the working electrode (originally FP) was rinsed with 200 mL of DI water to remove residual salt solution. The captured cations from the solid electroactive material in the working electrode were released using the same chemical oxidizing method as for FP preparation.33 The supernatant of the solution after oxidation of the powder was collected for IC composition analysis. Duplicate experiments were conducted, and the average value was reported.
2.8. Quantification of Li+ uptake
Progression of FP reduction was quantified using analysis of powder XRD patterns. XRD measurements were collected using Cu Kα radiation (wavelength = 1.5406 Å) with a PANalytical X'pert ProMPD. To quantify the compositions of cations intercalated into the FP during reduction, the powder sample was chemically oxidized to release the cations to the solution phase. The chemical oxidation method was the same used to prepare the initial FP powder from the purchased LFP, and followed methods published previously.33 After two hours of oxidation, the solution supernatant was collected and filtered to separate the solid powder from the suspension. Solution composition was then determined using IC. Samples for IC analysis were all 5 mL, and these solutions were used to flush and fill a 25 μL injection loop, which was used to inject the sample for analysis using a Thermo Scientific Dionex ICS-2100. IC calibration standards were prepared by using known concentrations of metal chloride salts ranging from 0.01 mM to 1 mM total cation concentration with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of Li+ and target cation M+/2+ (M: Na+, K+, Mg2+). Linear calibration curves of peak areas as a function of concentrations were obtained, which was later used to determine the Li+ and M+/2+ concentrations in evaluated samples. Cations in collected samples were diluted several folds using DI water to attain concentrations within the range of the calibration standards. Example calibration curves can be found in ESI, Fig. S1.†
1 molar ratio of Li+ and target cation M+/2+ (M: Na+, K+, Mg2+). Linear calibration curves of peak areas as a function of concentrations were obtained, which was later used to determine the Li+ and M+/2+ concentrations in evaluated samples. Cations in collected samples were diluted several folds using DI water to attain concentrations within the range of the calibration standards. Example calibration curves can be found in ESI, Fig. S1.†
2.9. Contact angle between FP composite electrode and brine solutions with redox mediator
The contact angle between FP composite electrode and brine solutions was measured with a Goniometer (Rame-Hart Instrument). The brine solution was 39 mM of Li+ and 3.04 M of Na+, with 100 mM added redox mediator. A 12 μl size brine droplet was dropped onto a FP composite electrode and the contact angle between the brine droplet and substrate was measured for 20 times consecutively with 0.5 s intervals, and the average angle of those measurements was calculated. The contact angle was extracted through image analysis provided with the equipment software. Fabrication of FP composite electrode was described in Section 2.3. Three different regions of the FP composite electrode were used as the substrate, and a total of 10 droplets of each brine solution were evaluated for their contact angles. The reported contact angle was the average of these 10 droplets, with the reported uncertainty the standard deviation of the ten droplet measurements for each brine solution.3. Results and discussion
3.1. Electrochemical characterization of iron redox mediators
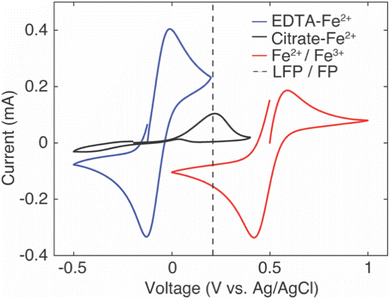
The intercalation material used to uptake Li+ in this study was FP, which has a half-wave potential of 0.242 V vs. Ag/AgCl, as measured from CV (CV scans can be found in ESI, Fig. S2†). The half-wave potential was obtained by taking the average of the cathodic peak potential and the anodic peak potential.35 This half wave potential was equivalent to 3.469 V vs. Li+/Li, and was consistent with the reported half-wave potential of FP.28 To drive Li+ from the brine solution into the FP, the Fe3+ in the FP must be reduced to Fe2+. To at minimum provide sufficient thermodynamic driving force towards FP reduction, the potential of the redox mediators in the surrounding electrolyte solution must be below the redox potential of FP. Without added ligands to the chloride brine solution, the half-wave potential of Fe2+/Fe3+ was 0.504 V vs. Ag/AgCl from CV scans (Fig. 1). This value was above that observed for FP/LFP, and thus would not drive FP reduction, at least within a reasonable range of relative state of oxidation/reduction of the soluble Fe. For example, when the solution was 99% Fe2+, the estimated Nernst potential was 0.385 V and still insufficient to reduce FP. Some prior studies have reported that when aqueous iron cations were complexed with specific ligands, the redox potential shifted much lower. For example, the redox potential of Fe was shifted to −1.04 V vs. Ag/AgCl,36 0.146 V vs. Ag/AgCl,37 and 0.865 V vs. Ag/AgCl38,39 when bonded to ligands from triethanolamine (TEA), sodium oxalate, and phenanthroline, respectively. Introduction of the ligands needs to also consider the chemical compatibility with the intercalation materials and other components in the brine solution. For example, the reported TEA–Fe solution was highly basic (pH > 10), and LFP/FP has previously been reported to have stability limitations when exposed to high pH solutions.5 Sodium oxalate has relatively low solubility in water, and even lower in relevant brine solutions – which makes achieving necessary redox mediator concentrations with the ligands to keep the reaction rate high a challenge. In this study, to shift redox potential of Fe2+/Fe3+ to be lower than FP, two additives were introduced into the brine solution, EDTA and citrate. The half-wave potentials of redox mediators (citrate/EDTA–Fe2+) were determined using CV (Fig. 1). From CV it was determined that the half wave potentials for the redox mediators EDTA–Fe2+ and citrate–Fe2+ were −0.07 V and −0.11 V vs. Ag/AgCl, respectively, in salt solution with 39 mM of Li+ and 3.04 M of Na+. The reversibility of EDTA–Fe2+ was higher than citrate–Fe2+ based on the more symmetric CV curves.37,40 The potential difference (ΔE) between the cathodic/anodic peak of the two redox mediators (EDTA–Fe2+, citrate–Fe2+) were 0.12 V and 0.67 V. The higher the (ΔE) suggested the redox reaction of citrate–Fe2+ was slower.373.2. Li+ extraction from simulated brine with high Li+ concentration
Before using redox mediators EDTA–Fe2+ and citrate–Fe2+ to extract Li, a control was conducted using Fe2+ to extract Li from solution. Assuming the Fe solution potential follows behavior consistent with the Nernst equation, at least a small amount of reduction of FP would be expected before there would be insufficient thermodynamic driving force to drive the redox forward. FP contacted a brine solution that had 1 M of LiCl, and was reduced by 0.1 M of Fe2+ at 75 °C. After 24 hours reduction, the lithium uptake by FP was about 0.4 mmol g−1 FP. This relatively low uptake was also reflected in the XRD measurements of the powder immediately after the control experiment. There was not a large peak at 17.4°, which would be expected if the powder had converted to LFP (Fig. S3†).EDTA–Fe2+ and citrate–Fe2+ had half-wave potentials below FP with magnitudes of 0.312 V and 0.352 V, respectively, which would thermodynamically drive FP reduction and Li+ insertion into the solid crystal structure. Chemical redox mediators were first evaluated to extract Li+ from simulated brine that contained only single monovalent cations (Li+ or Na+), and then Li+ with competing cations (Na+, K+, Mg2+) at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio. In the simulated brine, each ion concentration was ∼1 M, and each extraction continued for 24 h. Duplicate experiments were conducted with average values reported in Fig. 2.
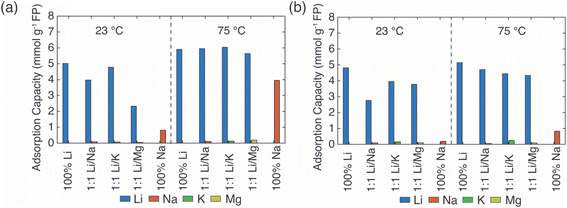
1 molar ratio. In the simulated brine, each ion concentration was ∼1 M, and each extraction continued for 24 h. Duplicate experiments were conducted with average values reported in Fig. 2.
In the EDTA–Fe2+ chemical redox extraction system, when the brine had Li+ only, the adsorption capacity of Li+ was 5 mmol Li+ g−1 FP at room temperature, and 6 mmol Li+ g−1 FP at 75 °C (Fig. 2a). The intercalation material achieved 94% conversion by Li+ uptake based on a theoretical full conversion of 6.4 mmol Li+ g−1 FP (assuming one Li+ per Fe in FP). In the brine with Na+ only, there was slight Na+ uptake at room temperature, which may have been due to the relatively higher activation energy barrier for intercalation of Na+.21 However, at elevated temperature, and without Li+ in the solution, about 4 mmol Na+ g−1 FP was inserted into FP. This suggested the higher temperature aided Na in overcoming the activation barrier for insertion into FP. Next, the redox mediator was evaluated in brine solutions that had equimolar of Li+ with competing cations, Li/M+/2+ (M+/2+ = Na+, K+, Mg2+). In the case of equimolar of Li+ to K+, at both room and elevated temperatures minimal K+ intercalated into the FP, and the K+ also did not interfere with Li+ adsorption as the Li+ adsorption capacity was similar to the adsorption capacity in brine only containing Li+ cations. Hence, K+ was considered as a spectator ion and was consistent with reported literature.41 For the brine solution containing Li+ and Na+, as Na+ competed with Li+, the Li+ adsorption capacity was slightly lower than the adsorption capacity in the brine only containing Li+ cations at 23 °C. There was low Na+ insertion at both 23 and 75 °C. This outcome may have been due to the high mobility of Li+ at high temperature as well as the high local Li+ near the FP interface due to the high bulk Li+ concentration. In addition, the activation energy barrier for Li+ was expected to be lower than Na+.21 In brine solution with equimolar of Li+/Mg2+, the Li+ adsorption capacity was significantly reduced to 2.3 mmol g−1 FP at room temperature. The reduced Li+ uptake might be caused by the formation of rigid network of Mg2+ at the FP particle surface that possibly negatively influenced Li+ transport and mobility to the storage sites in FP.41 At 75 °C, Li+ adsorption capacity was similar to the capacity achieved in brine only containing Li+ cations. This may have been due to the improved Li+ mobility at the elevated temperature coupled with the higher solid phase diffusion barriers for the higher charge density Mg2+.
In Li+ extraction with redox mediator, citrate–Fe2+, the Li+ adsorption capacity was ∼5 mmol g−1 FP at both 23 °C and 75 °C in brines only containing added Li+ cations, which was 78% conversion of the FP material based on the theoretical adsorption capacity by Li+ uptake (Fig. 2b). In the Na+ only brine solution, the Na+ insertion was less than 0.2 mmol Na+ g−1 FP at 23 °C but increased to ∼1 mmol Na+ g−1 FP at 75 °C. In brines with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of Li+ to competing ions (K+, Mg2+), the Li+ adsorption capacity was 4 mmol Li+ g−1 FP at 23 °C, and 0.5 mmol Li+ g−1 FP higher at 75 °C. The detected cations concentrations of K+, Mg2+ were both lower than 0.3 mmol g−1 FP and thus were not inserted into FP with high uptake. In brines with competing Na+, the Li+ adsorption capacity reduced to 2.8 mmol Li+ g−1 FP at room temperature, but achieved a similar adsorption capacity as it obtained in other examined brines at elevated temperature. The elevated temperature and high Li+ local concentration promoted Li+ adsorption.
1 molar ratio of Li+ to competing ions (K+, Mg2+), the Li+ adsorption capacity was 4 mmol Li+ g−1 FP at 23 °C, and 0.5 mmol Li+ g−1 FP higher at 75 °C. The detected cations concentrations of K+, Mg2+ were both lower than 0.3 mmol g−1 FP and thus were not inserted into FP with high uptake. In brines with competing Na+, the Li+ adsorption capacity reduced to 2.8 mmol Li+ g−1 FP at room temperature, but achieved a similar adsorption capacity as it obtained in other examined brines at elevated temperature. The elevated temperature and high Li+ local concentration promoted Li+ adsorption.
Overall, in the synthetic brine solution with high Li+ concentration (∼1 M) and with comparable concentration of competing cations (Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M+/2+, 1
M+/2+, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), both redox mediators had high uptake and selectivity to Li+ as opposed to the competing cations M+/2+ (M+/2+ = Na+, K+, Mg2+) at both room and elevated temperatures. The Li+ adsorption capacity for EDTA–Fe2+ mediator was slightly higher (∼1.5 mmol Li+ g−1 FP) than for citrate–Fe2+ at 75 °C. This might be due to the faster electron transfer rate of the EDTA–Fe2+ complex. A previous study reported that the electron transfer rate constant of Fe2+/Fe3+ with citrate ligand was 9.33 × 10−5 cm s−1 while it was 3.4 × 10−2 cm s−1 with EDTA ligands, although the surrounding solution was not equivalent to this work.29,42 The rate constant of EDTA–Fe2+/Fe3+ was three orders of magnitude higher than for citrate–Fe2+/Fe3+. K+ was consistent with a role of a spectator ion in both chemical redox brine systems because it neither competed with Li+ for storage sites nor interfered with the total Li+ intercalation at both 23 °C and 75 °C, and that was consistent with a previous report that used an electrochemical driving force to extract Li+ from brine.41 However, Mg2+ lowered the Li+ intercalation capacity significantly at room temperature for redox mediator EDTA–Fe2+, even though the amount of Mg2+ detected in FP was minimal. The lowered capacity may have resulted from slower charge transfer of Li+ induced by Mg2+. Mg2+ has been reported to form a rigid network in the electrical double layer at the surface of FP particles that can impede Li+ charge transfer.41 However, the reduction of Li+ uptake in the presence of Mg2+ was not observed for the same brine compositions with redox mediator citrate–Fe2+. We speculated that the slower diffusion of redox complex and electron transfer rate allowed sufficient time for Li+ concentration to replenish near the particle interface, which outweighed the impact of slower Li+ charge transfer caused by Mg2+. In addition, this higher Li adsorption capacity might be attributed to the chelation between Mg2+ and citrate that restricted the interference of Mg2+ to Li+ intercalation. Improvement of Li adsorption was not observed in redox mediator EDTA–Fe2+ system, which suggested the chelation of EDTA–Mg2+ was relatively low. In addition, the elevated temperature only resulted in slightly increasing Li+ adsorption for most of the brine solutions for citrate–Fe2+, which was in contrast with observations for redox mediator EDTA–Fe2+. Even though temperature increased the mobility of cations and would have been expected to facilitate mitigating mass transport limitations for cations near the surrounding particle surface, the relative impacts of the temperature on other factors such as the redox reaction kinetics would also be impacted by temperature. A more detailed assessment of temperature effects and the influence on relevant steps in the Li capture process will be the subject of future investigations.
1), both redox mediators had high uptake and selectivity to Li+ as opposed to the competing cations M+/2+ (M+/2+ = Na+, K+, Mg2+) at both room and elevated temperatures. The Li+ adsorption capacity for EDTA–Fe2+ mediator was slightly higher (∼1.5 mmol Li+ g−1 FP) than for citrate–Fe2+ at 75 °C. This might be due to the faster electron transfer rate of the EDTA–Fe2+ complex. A previous study reported that the electron transfer rate constant of Fe2+/Fe3+ with citrate ligand was 9.33 × 10−5 cm s−1 while it was 3.4 × 10−2 cm s−1 with EDTA ligands, although the surrounding solution was not equivalent to this work.29,42 The rate constant of EDTA–Fe2+/Fe3+ was three orders of magnitude higher than for citrate–Fe2+/Fe3+. K+ was consistent with a role of a spectator ion in both chemical redox brine systems because it neither competed with Li+ for storage sites nor interfered with the total Li+ intercalation at both 23 °C and 75 °C, and that was consistent with a previous report that used an electrochemical driving force to extract Li+ from brine.41 However, Mg2+ lowered the Li+ intercalation capacity significantly at room temperature for redox mediator EDTA–Fe2+, even though the amount of Mg2+ detected in FP was minimal. The lowered capacity may have resulted from slower charge transfer of Li+ induced by Mg2+. Mg2+ has been reported to form a rigid network in the electrical double layer at the surface of FP particles that can impede Li+ charge transfer.41 However, the reduction of Li+ uptake in the presence of Mg2+ was not observed for the same brine compositions with redox mediator citrate–Fe2+. We speculated that the slower diffusion of redox complex and electron transfer rate allowed sufficient time for Li+ concentration to replenish near the particle interface, which outweighed the impact of slower Li+ charge transfer caused by Mg2+. In addition, this higher Li adsorption capacity might be attributed to the chelation between Mg2+ and citrate that restricted the interference of Mg2+ to Li+ intercalation. Improvement of Li adsorption was not observed in redox mediator EDTA–Fe2+ system, which suggested the chelation of EDTA–Mg2+ was relatively low. In addition, the elevated temperature only resulted in slightly increasing Li+ adsorption for most of the brine solutions for citrate–Fe2+, which was in contrast with observations for redox mediator EDTA–Fe2+. Even though temperature increased the mobility of cations and would have been expected to facilitate mitigating mass transport limitations for cations near the surrounding particle surface, the relative impacts of the temperature on other factors such as the redox reaction kinetics would also be impacted by temperature. A more detailed assessment of temperature effects and the influence on relevant steps in the Li capture process will be the subject of future investigations.
Li+ intercalation and conversion of FP to LFP was also consistent with XRD patterns of the powders after contact with brine solutions containing the redox mediators (patterns can be found in ESI, Fig. S4 and S5†). The XRD peak associated with the [2 0 0] index at 17.4° indicated the formation of LFP. There was also no observed broadening of the peaks in the brine solution with mixed cations relative to the brines only containing Li+, which suggested no or minimal impurity cations insertion (i.e., other than Li+). These XRD results were consistent with the IC analysis of low amounts of competing cation insertion. The correlation of peak broadening and impure cations insertion were also corroborated with samples reduced in Na+ only solution, where the XRD peaks appeared broader and shifted.
3.3. Li+ extraction from simulated brine with low Li+ concentration and high Na+ concentration
After assessing the selectivity for Li+ uptake from brines with relatively high Li+ concentration, next the Li selectivity during chemical reduction of FP in the presence of solutions with low Li+ concentration (both absolute and relative) but high concentration of competing cations was evaluated. The Li+ concentration in the brine was 39 mM, while the Na+ concentration was 3.04 M, resulting in a molar ratio of Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+ of 1
Na+ of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78. These absolute and relative Li+ and Na+ concentrations were intended to match reports for discharged brine used to produce geothermal power at the Salton Sea.32,43 Since K+ was a spectator ion in brine solution, potassium-based salts were used to aid dissolution of EDTA in preparing redox mediator EDTA–Fe2+ and potassium citrate was used as the ligand source for redox mediator citrate–Fe2+. For both redox mediators, we evaluated the effect of mediator concentration and reaction temperature on Li+ uptake into the FP (adsorption capacity) and selectivity to Li+.
78. These absolute and relative Li+ and Na+ concentrations were intended to match reports for discharged brine used to produce geothermal power at the Salton Sea.32,43 Since K+ was a spectator ion in brine solution, potassium-based salts were used to aid dissolution of EDTA in preparing redox mediator EDTA–Fe2+ and potassium citrate was used as the ligand source for redox mediator citrate–Fe2+. For both redox mediators, we evaluated the effect of mediator concentration and reaction temperature on Li+ uptake into the FP (adsorption capacity) and selectivity to Li+.
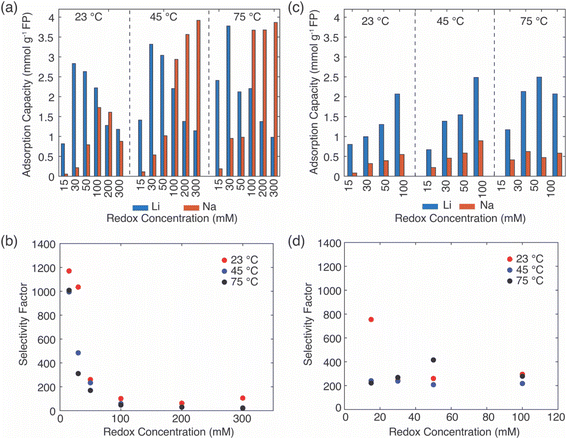
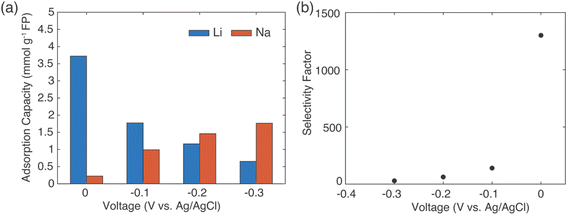
For the EDTA–Fe2+ system at 23 °C, the Li+ adsorption capacity increased with increasing redox EDTA–Fe2+ concentration from 15 mM to 30 mM (Fig. 3a). When the redox concentration was above 30 mM, more redox mediators were expected to provide more driving force that pushed more cations into the FP crystal structure. However, it resulted in more Na+ insertion rather than Li+ at concentration range from 50 mM to 300 mM. This outcome may have been due to the high concentration of Na+ surrounding the FP particle, such that more available Na+ was pushed into the FP crystal structure to accommodate the charge state change of EDTA–Fe2+. As more Na+ occupied the crystal lattice of FP, the amount of Li+ intercalation reduced, and the corresponding Li selectivity decreased. Selectivity factors αLiNa, were calculated to quantify the extent of selectivity for Li+ to Na+ extraction from the brine into the FP solid during the chemical redox. The equation to calculate αLiNa is shown in eqn (1).5,44
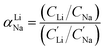 | (1) |
 are the concentration of Li+ and impurity cations (Na+) in the brine source. Higher values of αLiNa mean improved separation of Li+ and Na+ from brine. The αLiNa calculated for various concentrations of EDTA–Fe2+ can be found in Fig. 3b. The αLiNa decreased from 1200 to 19 at the corresponding concentrations from 15 mM to 300 mM. The lower redox concentration might result in slower transport of redox mediator near the particle surface, which allowed sufficient time for Li+ to distribute around the FP particle surface, thereby enhancing Li+ selectivity. Thus, increasing redox EDTA–Fe2+ concentration to above 50 mM was not necessary for improving both the Li extraction capacity and Li selectivity. Similar trends for Li+ and Na+ adsorption were also observed at higher reaction temperatures of 45 °C and 75 °C, and higher reaction temperatures resulted in more intercalation of both Li+ and Na+. At 75 °C, the maximum amount of Li+ intercalation was 1 mmol Li+ g−1 FP more than that at room temperature. The Na+ insertion was also increased, such that the highest amount of Na+ insertion was ∼2.3 times that observed at room temperature. The αLiNa at elevated temperatures were lower than at room temperature because higher temperature increased the mobility of both cations.
are the concentration of Li+ and impurity cations (Na+) in the brine source. Higher values of αLiNa mean improved separation of Li+ and Na+ from brine. The αLiNa calculated for various concentrations of EDTA–Fe2+ can be found in Fig. 3b. The αLiNa decreased from 1200 to 19 at the corresponding concentrations from 15 mM to 300 mM. The lower redox concentration might result in slower transport of redox mediator near the particle surface, which allowed sufficient time for Li+ to distribute around the FP particle surface, thereby enhancing Li+ selectivity. Thus, increasing redox EDTA–Fe2+ concentration to above 50 mM was not necessary for improving both the Li extraction capacity and Li selectivity. Similar trends for Li+ and Na+ adsorption were also observed at higher reaction temperatures of 45 °C and 75 °C, and higher reaction temperatures resulted in more intercalation of both Li+ and Na+. At 75 °C, the maximum amount of Li+ intercalation was 1 mmol Li+ g−1 FP more than that at room temperature. The Na+ insertion was also increased, such that the highest amount of Na+ insertion was ∼2.3 times that observed at room temperature. The αLiNa at elevated temperatures were lower than at room temperature because higher temperature increased the mobility of both cations.
In the extraction system with redox mediator citrate–Fe2+, the Li+ adsorption capacity increased as a function of mediator concentration for each of the temperatures evaluated (Fig. 3c). Due to solution stability/solubility limitations, the highest mediator concentration evaluated was 100 mM. The amount of Na+ insertion was less than 0.5 mmol g−1 FP across all conditions assessed. The αLiNa stabilized around 300 (Fig. 3d), except for the highest αLiNa at reduction with 15 mM citrate–Fe2+ at 23 °C. We speculated that this high Li+ selectivity was a combined outcome of the slow redox reaction, slow diffusion coefficient of the redox mediators, and low reaction temperature in the brine solution. The slow reaction enabled enough time for the cations around the intercalation material surface to be redistributed for Li+ to transport to the interface and then within the ion channels of the FP. Both low temperature and low redox concentration are beneficial for this slow redox reaction, and thus the αLiNa reached its highest value at 800. Although at high redox concentration the Li selectivity for citrate–Fe2+ was higher than for EDTA–Fe2+, the total Li+ uptake did not achieve the highest values observed for the EDTA–Fe2+, where the highest uptake achieved was still lower than EDTA–Fe2+ by ∼1 mmol Li+ g−1 FP. This outcome may have been due to the lower electron transfer rate constant of redox mediator citrate–Fe2+. Hence, when redox concentration was lower than 50 mM, reduction with mediator EDTA–Fe2+ had advantages of high Li adsorption capacity and Li selectivity, where for other solution conditions citrate–Fe2+ was more preferred.
For Li+ capture experiments with large amounts of competing Na+ insertion, the Na+ insertion into the FP influenced the resulting XRD patterns for the powders after contact with the brine (Fig. 4). From the IC results (Fig. 3), Na+ insertion into FP samples was greater for FP reduction conditions of high mediator concentration and high temperature. For comparison between the two mediators with identical temperature and mediator concentration during reaction, reacted FP powder after contact with brine at 45 °C and with mediator concentration of 0.1 M was evaluated using XRD. The XRD patterns were also evaluated in the context of the as-purchased LFP and the FP after chemical oxidation of the initial LFP powder. The [2 0 0] peak has previously been used to indicate the conversion between LFP/FP, as for LFP this peak is at 17.4° and for FP this peak is at 18.3°.28 A partial reduction of FP will result in the presence of both the LFP and FP [2 0 0] peaks, where the relative peak magnitude can be correlated to the relative amounts of each phase present.28 The XRD peaks suggested that both redox mediators EDTA–Fe2+ and citrate–Fe2+ drove nearly full conversion of FP, where the citrate–Fe2+ had a slight FP peak remaining and the EDTA–Fe2+ did not have a discernible FP peak remaining (Fig. 4). The two different mediators had noticeable differences in the peak broadening for the resulting powders. There was a greater extent of peak broadening for the powder reduced using EDTA–Fe2+. The EDTA–Fe2+ processed powder also had more Na+ intercalated into the material structure. Thus, the XRD was consistent with the lower selectivity when the EDTA–Fe2+ mediator was used, as the larger Na+ can introduce more strain and peak broadening in the crystal structure.14 Both the XRD and IC results were consistent with high conversion/reduction of the FP when in contact with both redox mediators, and higher selectivity for Li+ over Na+ for the citrate–Fe2+ mediator.
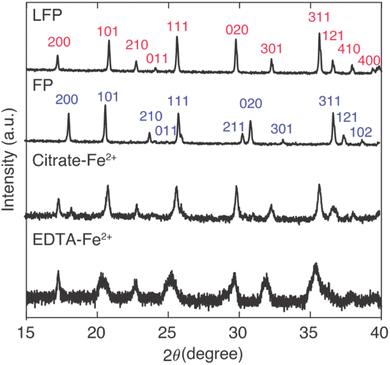 | ||
Fig. 4 XRD patterns for the as-received LFP powder, FP after chemical oxidation of the LFP, and chemically reduced FP after contact with brine containing citrate–Fe2+ mediator and EDTA–Fe2+ mediator, respectively. The mediator concentration was 0.1 M and the brine had 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78 Li+ 78 Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+ stoichiometry. The brine reaction was at 45 °C for a duration of 24 hours. Indexes were assigned based on PDF-01-078-7908 for LFP and PDF-04-017-0610 for FP.28 Na+ stoichiometry. The brine reaction was at 45 °C for a duration of 24 hours. Indexes were assigned based on PDF-01-078-7908 for LFP and PDF-04-017-0610 for FP.28 | ||
3.4. Li+ adsorption time evolution and uptake/release cycling
As discussed above, the Li+ uptake and selectivity were different depending on the redox mediator used to reduce the FP. However, the analysis above was only conducted on solid material after the conclusion of a chemical redox process, typically after 24 hours. As Li+ adsorption rate needed to be different to achieve the final uptake values, experiments were also conducted to assess the Li+ adsorption over time. Cation capture via chemical redox was conducted where the FP/LFP powder was collected after fixed times of reaction. Fresh synthetic brine solutions with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78 Li+
78 Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+ and both 0.1 M of EDTA–Fe2+ and citrate–Fe2+ mediators were prepared for each set of experiments to assess how uptake and selectivity varied with FP contact time with the brine at 45 °C. The contact intervals for the FP were in 2 hours increments up to a maximum of 24 hours. The resulting Li+ uptake as a function of reaction time for each redox mediator can be found in Fig. 5.
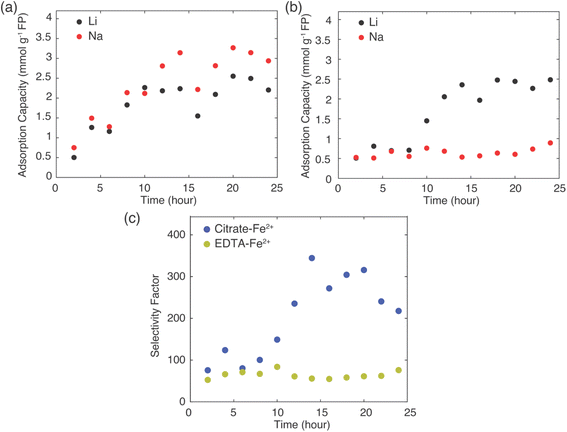
Na+ and both 0.1 M of EDTA–Fe2+ and citrate–Fe2+ mediators were prepared for each set of experiments to assess how uptake and selectivity varied with FP contact time with the brine at 45 °C. The contact intervals for the FP were in 2 hours increments up to a maximum of 24 hours. The resulting Li+ uptake as a function of reaction time for each redox mediator can be found in Fig. 5.
The total amount of Li+ extracted from brine was similar for both mediators at the conclusion of 24 hours reaction, at about 2.5 mmol Li+ g−1 FP. The Li+ adsorption into the FP plateaued at a shorter reaction time for the EDTA–Fe2+ system, after roughly 10 hours. However, the citrate–Fe2+ mediated reaction took about 15 hours of reaction time to plateau. Even though Li+ uptake rate was higher at the initiation of the chemical redox process for the EDTA–Fe2+ mediator, Li+ selectivity was relatively lower compared to citrate–Fe2+ mediator, with Li+ and Na+ inserted at nearly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio. For EDTA–Fe2+ mediator, at later times more Na+ was inserted compared to Li+ (Fig. 5a). For chemical redox using citrate–Fe2+ mediator, the total Na+ uptake was fairly constant with reaction time. After initial insertion of approximately 0.5 mmol Na+ g−1 FP, the intercalation of Na+ appeared to stop, and only Li+ uptake increased with reaction time until plateauing at about 15 hours (Fig. 5b).
1 molar ratio. For EDTA–Fe2+ mediator, at later times more Na+ was inserted compared to Li+ (Fig. 5a). For chemical redox using citrate–Fe2+ mediator, the total Na+ uptake was fairly constant with reaction time. After initial insertion of approximately 0.5 mmol Na+ g−1 FP, the intercalation of Na+ appeared to stop, and only Li+ uptake increased with reaction time until plateauing at about 15 hours (Fig. 5b).
Selectivity factors were calculated for these two extraction systems using eqn (1) to compare the separation of Li+ and Na+ from brine. As shown in Fig. 5c, over the initial 10 h of the Li+ extraction from the brine into the FP, the αLiNa using citrate–Fe2+ was slightly higher than for the EDTA–Fe2+. Beyond 10 hours extraction, the αLiNa for the citrate–Fe2+ greatly exceeded the EDTA–Fe2+, with the relative improvement being approximately a factor of 6. This outcome suggested that the choice of redox mediator provided a method to control and improve the selectivity for Li+ uptake into the FP. In previous reports, electrochemically-driven extraction of Li+ from brine into FP introduced a controlled pulsing mode to allow the cations to redistribute around the FP particle surface, which increased the relative local Li+ concentration near the FP interface.30 In another report, researchers showed that a polymer coating on FP can modify Li+ selectivity, and attributed the selectivity improvement to modifications in particle surface hydrophilicity.14 The surface hydrophilicity of intercalation material can be assessed in the context of contact angle measurements.14 A more hydrophilic surface tends to have lower contact angle with water droplets, and in prior reports more hydrophilic surfaces have resulted in more adsorption capacity,23 while a higher contact angle increased the selectivity of Li+ to Na+.14 In this work, 12 μl drops of brine solution (Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+, 1
Na+, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78) with either EDTA–Fe2+ or citrate–Fe2+ mediators were placed onto FP composite electrodes, and optical images of the brine drops were recorded (example contact angle images can be found in ESI, Fig. S6†). The contact angle of brine droplets with redox mediator citrate–Fe2+ and EDTA–Fe2+ was 119° ± 2° and 120° ± 2°, respectively, with the uncertainty being the standard deviation of the average contact angle for 10 replicate droplet measurements. The almost identical contact angles for brine solutions with both mediators and the FP electrode indicated the surface of FP had a similar hydrophilicity with both solutions, and this was not a factor which influenced Li+ selectivity differences for these two brine solutions.
78) with either EDTA–Fe2+ or citrate–Fe2+ mediators were placed onto FP composite electrodes, and optical images of the brine drops were recorded (example contact angle images can be found in ESI, Fig. S6†). The contact angle of brine droplets with redox mediator citrate–Fe2+ and EDTA–Fe2+ was 119° ± 2° and 120° ± 2°, respectively, with the uncertainty being the standard deviation of the average contact angle for 10 replicate droplet measurements. The almost identical contact angles for brine solutions with both mediators and the FP electrode indicated the surface of FP had a similar hydrophilicity with both solutions, and this was not a factor which influenced Li+ selectivity differences for these two brine solutions.
It is noted that relatively large fluctuations were observed with regards to uptake and selectivity in the results in Fig. 5. We speculate some of the fluctuations may have been dependent on relatively small differences in the initial Na uptake into the FP materials at the early stages of each experiment. The larger Na+ compared to Li+ would be expected to impact the total sites available within the FP material and the structural stability of the FP, even for relatively small differences in initial Na+ uptake. Future directions for investigating the instability could include investigating the influence of Na+ uptake on the FP structure and total cation uptake.
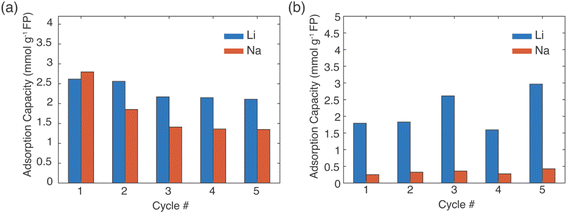
In a real Li+ extraction application, the FP solid material would run through multiple cycles of Li+ uptake/release, and maintaining selectivity over many cycles will reduce process downtime and/or cost for FP material replacement. The same FP material was used for five extraction and release cycles (Fig. 6). The FP was lithiated via chemical redox in brine of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78 Li+
78 Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+ with EDTA–Fe2+ or citrate–Fe2+ mediators. The extraction stage was always at 45 °C and allowed to proceed for 24 h. Delithiation/release was done using the chemical oxidation method described earlier. The FP material was able to uptake Li+ over the 5 cycles, although there was some variation in the specific amount of Li+ uptake. For chemical redox with EDTA–Fe2+, the Li+ adsorption capacity for the first two cycles was ∼2.5 mmol Li+ g−1 FP. Cycles 3–5 were lower at ∼2.2 mmol Li+ g−1 FP (Fig. 6a). The reduced uptake in the later cycles may have been caused by partial insertion of Na+, which could distort the crystal structure and block Li+ transport within the FP.14 For the citrate–Fe2+ mediated FP reduction, the Li+ adsorption was ∼2 mmol Li+ g−1 FP (Fig. 6b). For cycles 3 and 5, the adsorption capacity was slightly higher. This preliminary Li+ uptake/release demonstrated cycling of the FP material to extract Li+ from brine. Detailed assessment of changes in uptake and selectivity with extended cycling will be explored in future investigations of these materials.
Na+ with EDTA–Fe2+ or citrate–Fe2+ mediators. The extraction stage was always at 45 °C and allowed to proceed for 24 h. Delithiation/release was done using the chemical oxidation method described earlier. The FP material was able to uptake Li+ over the 5 cycles, although there was some variation in the specific amount of Li+ uptake. For chemical redox with EDTA–Fe2+, the Li+ adsorption capacity for the first two cycles was ∼2.5 mmol Li+ g−1 FP. Cycles 3–5 were lower at ∼2.2 mmol Li+ g−1 FP (Fig. 6a). The reduced uptake in the later cycles may have been caused by partial insertion of Na+, which could distort the crystal structure and block Li+ transport within the FP.14 For the citrate–Fe2+ mediated FP reduction, the Li+ adsorption was ∼2 mmol Li+ g−1 FP (Fig. 6b). For cycles 3 and 5, the adsorption capacity was slightly higher. This preliminary Li+ uptake/release demonstrated cycling of the FP material to extract Li+ from brine. Detailed assessment of changes in uptake and selectivity with extended cycling will be explored in future investigations of these materials.
The FP powder after 5 cycles of extraction and release were imaged by SEM, and for comparison the initial FP powder was also imaged (Fig. 7). The initial FP particles collected after chemical oxidation of LFP can be seen in Fig. 7a and b. The FP particles all had primary particles sizes less than 1 μm. Larger aggregate of the smaller particles of a few μm such as seen in Fig. 7a were also observed, but these larger aggregates did not have a consistent secondary particle morphology. FP powder after 5 cycles of extraction/release by redox mediator EDTA–Fe2+ can be found in Fig. 7c and d. The primary particles appeared slightly smaller, which may have resulted from particle fracture. It is noted that particles likely experienced increased stress depending on the amount of sodium insertion. A previous study reported that the volume expansion of first sodation was four times that of the first lithiation for FP materials.45 As for the FP after 5 cycles of extraction/release by redox mediator citrate–Fe2+, the morphology of the FP particles was more similar to the initial FP material, with relatively larger primary particles compared to the EDTA–Fe2+ cycling experiments. The SEM images suggested the primary particles and morphology of the FP was less impacted by extraction/release of Li+ citrate–Fe2+ as opposed to EDTA–Fe2+, suggesting the redox mediator with the relatively lower Na+ uptake may have greater structural resilience to cycling during Li+ extraction driven by redox mediators.
3.5. Diffusion coefficient of redox mediators in simulated brine with Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) Na+ molar ratio of 1
Na+ molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 78
78
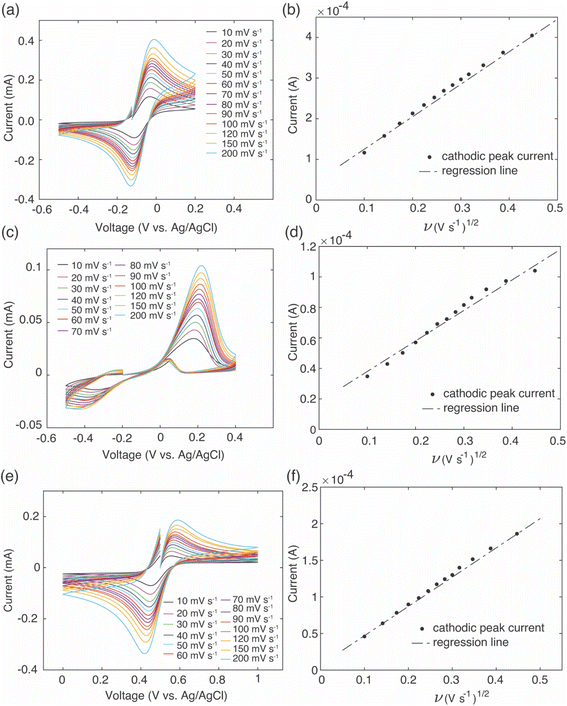
To provide insights into brine solution properties that may influence the Li+ uptake and selectivity, electrochemical analysis was conducted on the brine to determine effective diffusion coefficients for the redox mediators in the brine solution. To estimate the effective diffusion coefficient of the redox mediators, an equimolar solution of Fe2+ and Fe3+ was dissolved in simulated brine solution that had the same Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+ molar ratios along with the EDTA and citrate additives at room temperature. CV was performed at increasing scan rates using a three-electrode system of platinum disk counter and working electrodes and Ag/AgCl (in saturated KCl) as reference electrode. As the scan rate increased, the potential of the cathodic/anodic peaks gradually shifted to higher/lower potentials, and peak currents also increased with increasing scan rates (Fig. 8a, c and e). Cathodic peak currents were plotted against the square root of scan rate, and the linear relationship of these two variables indicated the reaction was diffusion limited (Fig. 8b, d and f). The slope of these plots was used to calculate the effective diffusion coefficient of the redox mediators using the Randles–Sevcik equation,34
Na+ molar ratios along with the EDTA and citrate additives at room temperature. CV was performed at increasing scan rates using a three-electrode system of platinum disk counter and working electrodes and Ag/AgCl (in saturated KCl) as reference electrode. As the scan rate increased, the potential of the cathodic/anodic peaks gradually shifted to higher/lower potentials, and peak currents also increased with increasing scan rates (Fig. 8a, c and e). Cathodic peak currents were plotted against the square root of scan rate, and the linear relationship of these two variables indicated the reaction was diffusion limited (Fig. 8b, d and f). The slope of these plots was used to calculate the effective diffusion coefficient of the redox mediators using the Randles–Sevcik equation,34| Ip = (2.687 × 105)n1.5SC(Dν)0.5 | (2) |
3.6. Comparison of electrochemical and chemical redox Li+ extraction processing
The results above demonstrated selective extraction of Li+ from brine using redox mediators to drive FP reduction and concurrent cation insertion. An alternative method for capture of Li+ from brine using intercalation materials that has been reported has involved application of electrochemical rather than chemical redox to drive reduction of the solid material.12 For comparison, selectivity for Li+ uptake was assessed using the same FP material used for the previous chemical redox Li+ extraction experiments. A salt solution containing LiCl and NaCl with a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78 that had the same target salts and concentration as the prior brine solution was prepared. FP and LFP were processed into composite electrodes coated on Ti wire for working and counter electrodes, respectively. The three-electrode system was completed with an Ag/AgCl (saturated KCl) reference electrode. The mass ratio of LFP
78 that had the same target salts and concentration as the prior brine solution was prepared. FP and LFP were processed into composite electrodes coated on Ti wire for working and counter electrodes, respectively. The three-electrode system was completed with an Ag/AgCl (saturated KCl) reference electrode. The mass ratio of LFP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) FP was kept at 1.5
FP was kept at 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to ensure the working electrode was capacity limiting. The two electrodes were kept separate from each other by multiple cm, and the amount of Li+ released from counter electrode LFP accounted for less than 0.5% of the total Li+ concentration in the brine solution. Hence, the influence of Li+ from the counter electrode was assumed negligible. Due to the low Li+ concentration, the polarization was large and the discharge plateau of FP in the brine solution shifted to a lower voltage.5,47 A constant voltage several hundred millivolts below the discharge plateau potential for FP in brine (0.242 V vs. Ag/AgCl) was applied to the three electrodes system to lithiate the working electrode (FP). Various voltages in the range of −0.3 V to 0.0 V (in intervals of 0.1 V vs. Ag/AgCl) were evaluated to determine the impact of voltage selected on the extent of Li+ extraction. The electrochemical lithiation was stopped after 50% of extent of discharge, determined based on the mass of the loaded FP with assumed theoretical capacity of 165 mA h g−1. The composition of cations intercalated into FP after 50% extent of discharge can be found in Fig. 9a. As the fixed potential applied during reduction of the FP increased, the amount of Li+ intercalated was reduced. The more negative applied potentials (greater driving for reduction of FP and cation insertion) resulted in increased Na+ insertion into the FP. The maximum Li adsorption capacity was achieved at 0.0 V and was 3.6 mmol Li+ g−1 FP, which was similar to the adsorption capacity achieved with both chemical redox mediators. As more Na+ inserted into FP with more negative fixed potential at the working electrode, the selectivity of the intercalation material to Li+ over Na+ decreased from 1300 to 28 (Fig. 9b). When the applied voltage was lower than 0.0 V, using redox mediators for extraction of Li+ had advantages over electrochemical extraction from the perspective of higher adsorption capacity and Li+ selectivity.
1 to ensure the working electrode was capacity limiting. The two electrodes were kept separate from each other by multiple cm, and the amount of Li+ released from counter electrode LFP accounted for less than 0.5% of the total Li+ concentration in the brine solution. Hence, the influence of Li+ from the counter electrode was assumed negligible. Due to the low Li+ concentration, the polarization was large and the discharge plateau of FP in the brine solution shifted to a lower voltage.5,47 A constant voltage several hundred millivolts below the discharge plateau potential for FP in brine (0.242 V vs. Ag/AgCl) was applied to the three electrodes system to lithiate the working electrode (FP). Various voltages in the range of −0.3 V to 0.0 V (in intervals of 0.1 V vs. Ag/AgCl) were evaluated to determine the impact of voltage selected on the extent of Li+ extraction. The electrochemical lithiation was stopped after 50% of extent of discharge, determined based on the mass of the loaded FP with assumed theoretical capacity of 165 mA h g−1. The composition of cations intercalated into FP after 50% extent of discharge can be found in Fig. 9a. As the fixed potential applied during reduction of the FP increased, the amount of Li+ intercalated was reduced. The more negative applied potentials (greater driving for reduction of FP and cation insertion) resulted in increased Na+ insertion into the FP. The maximum Li adsorption capacity was achieved at 0.0 V and was 3.6 mmol Li+ g−1 FP, which was similar to the adsorption capacity achieved with both chemical redox mediators. As more Na+ inserted into FP with more negative fixed potential at the working electrode, the selectivity of the intercalation material to Li+ over Na+ decreased from 1300 to 28 (Fig. 9b). When the applied voltage was lower than 0.0 V, using redox mediators for extraction of Li+ had advantages over electrochemical extraction from the perspective of higher adsorption capacity and Li+ selectivity.
3.7. Redox mediators to extract Li+ from more representative Salton Sea brine
As a final analysis, brine more representative of geothermal power discharge brine at the Salton Sea was used as the source brine for Li+ capture. The Li+ extraction conditions were kept the same as those used in the synthetic brine in that the redox mediator concentration was 0.1 M of EDTA–Fe2+ or citrate–Fe2+, and the reaction was allowed to proceed for 24 hours. The detailed composition of the brine can be found in ESI, Table S3.†32 Due to solution stability considerations, the Ca2+ was omitted. The Li+ extraction was carried out at three different temperatures, 23 °C, 45 °C, and 75 °C. The Li+ adsorption capacity for all experiments ranged from 1.52–2.02 mmol Li+ g−1 FP (Fig. 10a). Similar to the results discussed above with brine only containing Li+ and Na+ added cations, the EDTA–Fe2+ mediator was less selective for Li+ uptake compared to the citrate–Fe2+, and as the temperature increased the EDTA–Fe2+ was even less selective for Li+ uptake. For uptake driven by EDTA–Fe2+ mediator, the FP conversion attributed by the uptake of monovalent cations (Li+ and Na+) increased with increasing temperature at 58%, 70%, and 83% for 23 °C, 45 °C, and 75 °C, respectively (percentages based on assumption of complete conversion of FP requiring 6.4 mmol Li+ g−1 FP). The increased conversion coincided with increased uptake of Na+, thus suggesting increasing temperature drove greater conversion of FP but decreased selectivity. For citrate–Fe2+, the Li+ adsorption capacity did have an increase with increasing temperature from 23 °C to 45 °C, but did not increase again for the highest temperature of 75 °C (Fig. 10a). The uptake of Li+ and Na+ accounted for 30% and 38% conversion of FP from 23 °C to 45 °C, respectively, and increased Li+ adsorption accounted for the majority of FP conversion. In the brine solution with additional added cations, the Li+ selectivity was higher for citrate–Fe2+ relative to the EDTA–Fe2+ for all temperatures evaluated. The selectivity factor (αLiNa) was ∼400 for the reaction using citrate–Fe2+ and 60 for EDTA–Fe2+ (Fig. 10b).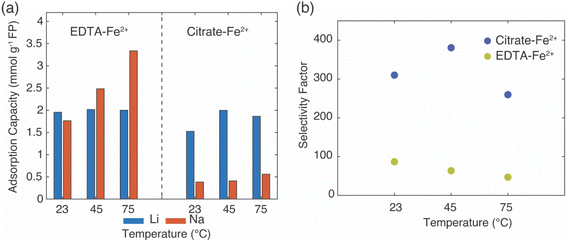 | ||
| Fig. 10 (a) Adsorption capacities for Li+ and Na+ and (b) selectivity factors αLiNa in FP from brine that more closely simulated Salton Sea brine (more specific composition in Table S3†). Cation uptake was driven by the redox mediator indicated on the figure. | ||
For reference, a comprison of the outcomes of this work with other Li+ extraction uptake and selectivity reported in the literature can be found in ESI Table S4.† It is noted that the prior reports were all electrochemical driven extraction. It is challenging to directly compare the reported works due to the variations of experimental conditions and feed brine compositions among the experiments. However, the reported Li+ uptake and selectivity factor could still be considered as benchmarks for future studies. The prior literature generally had Li+ uptake above 10 mg Li+ g−1 FP, and the Li+ adsorption capacity herein for reduction using both redox mediators was 14 mg Li+ g−1 FP. Note that the Na+ excess for the work herein was relatively high, being higher than all but one of the prior reported values aggregated (detailed data can be found in ESI, Fig. S7a†). Lower amounts of Li+ relative to Na+ in the brine increased the difficulty of selective Li+ separation. Some reported adsorption capacities were higher than our work. However, generally for those reports the brine solution was relatively less complex (containing only Li+ and Na+) and/or the molar excess for Na+ relative to Li+ was much lower. Both these factors make Li+ extraction easier. Meanwhile, maintaining high Li+ selectivity in brine solution with great molar excess of Na+ is challenging. For the reported αLiNa value above 350, Li+ extraction with redox mediator citrate–Fe 2+ shows a promising Li+ selectivity factor (Fig. S7b†). In addition, using redox molecules to facilite Li+ extraction has potential processing advantages with regards to not requiring input electrical energy to drive the cation insertion and avoiding contact between the brine and expensive membrane materials. Furthermore, redox mediated reduction may have scale up and operational advantages compared to electrochemical extraction methods.
4. Conclusion
Chemical mediator-driven Li+ extraction from brine into FP solid material using soluble complexes formed within the brine solution was investigated. Two redox mediators, EDTA–Fe2+ and citrate–Fe2+, were assessed, where each had a redox potential below that of the FP solid material to drive reduction of the FP and insertion of cations into the material structure. These two mediators drove chemical redox processes that selectively extracted Li+ from a variety of different brine solutions and processing conditions, including using brine with low and high Li+ concentration. For brines with low concentration of competing cations (Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+, 1
Na+, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), the FP had high Li selectivity using both mediators, and the dominantly competing cations in brine, Na+, K+, and Mg2+, were minimally intercalated. The FP material achieved 94% of conversion with one round of extraction compared to the theoretical adsorption capacity assuming one Li+ per FP. In the synthetic brine with higher concentration of competing cations (Li+
1), the FP had high Li selectivity using both mediators, and the dominantly competing cations in brine, Na+, K+, and Mg2+, were minimally intercalated. The FP material achieved 94% of conversion with one round of extraction compared to the theoretical adsorption capacity assuming one Li+ per FP. In the synthetic brine with higher concentration of competing cations (Li+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Na+, 1
Na+, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78), both redox mediators extracted 2.5 mmol Li+ g−1 FP. The redox mediator citrate–Fe2+ had higher Li+ selectivity than the redox mediator EDTA–Fe2+. This selectivity advantage still remained for brines with additional cations more representative of Salton Sea geothermal discharge brine. Applying redox mediators for Li+ extraction provided new insights to Li+ extraction from aqueous solutions, and a route to improve Li+ selectivity. The results suggested that at least for these two redox mediators evaluated that reducing the reaction rate favored increasing the selectivity for Li+ uptake from the brines. Redox mediated extraction was demonstrated to have encouraging results as a method to selectively extract Li+ from complex brine solutions. This scalable extraction setup provided a promising route towards Li extraction from complex brine solutions.
78), both redox mediators extracted 2.5 mmol Li+ g−1 FP. The redox mediator citrate–Fe2+ had higher Li+ selectivity than the redox mediator EDTA–Fe2+. This selectivity advantage still remained for brines with additional cations more representative of Salton Sea geothermal discharge brine. Applying redox mediators for Li+ extraction provided new insights to Li+ extraction from aqueous solutions, and a route to improve Li+ selectivity. The results suggested that at least for these two redox mediators evaluated that reducing the reaction rate favored increasing the selectivity for Li+ uptake from the brines. Redox mediated extraction was demonstrated to have encouraging results as a method to selectively extract Li+ from complex brine solutions. This scalable extraction setup provided a promising route towards Li extraction from complex brine solutions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by funds from the American-Made Geothermal Lithium Extraction Prize. Technical support was provided by the UVA Nanoscale Materials Characterization Facility (NMCF) on the XRD and SEM measurements. We thank Chen Cai for acquiring the SEM images.References
- S. Zavahir, T. Elmakki, M. Gulied, Z. Ahmad, L. Al-Sulaiti, H. K. Shon, Y. Chen, H. Park, B. Batchelor and D. S. Han, Desalination, 2021, 500, 114883 CrossRef CAS.
- J. Wang, Z. Nie and G. M. Koenig, Energy Technol., 2023, 11, 1–9 Search PubMed.
- B. W. Jaskula, Mineral Commodity Summaries: Lithium, U.S. Geological Survey, 2023, pp. 1–2 Search PubMed.
- T. Gao, N. Fan, W. Chen and T. Dai, China Geol., 2023, 6, 137–153 CAS.
- J. Wang and G. M. Koenig, Chem. - Eur. J., 2023, e202302776 Search PubMed.
- A. Scheidel, D. Del Bene, J. Liu, G. Navas, S. Mingorría, F. Demaria, S. Avila, B. Roy, I. Ertör, L. Temper and J. Martínez-Alier, Glob. Environ. Change, 2020, 63, 102104 CrossRef PubMed.
- A. Battistel, M. S. Palagonia, D. Brogioli, F. La Mantia and R. Trócoli, Adv. Mater., 2020, 32, 1905440 CrossRef CAS PubMed.
- Y. Xiong, J. Zhou, P. Lu, J. Yin, Y. Wang and Z. Fan, Matter, 2022, 5, 1760–1791 CrossRef CAS.
- Z. Zhou, W. Qin, Y. Liu and W. Fei, J. Chem. Eng. Data, 2012, 57, 82–86 CrossRef CAS.
- Y. Sun, Q. Wang, Y. Wang, R. Yun and X. Xiang, Sep. Purif. Technol., 2021, 256, 117807 CrossRef CAS.
- J. Sun, X. Li, Y. Huang, G. Luo, D. Tao, J. Yu, L. Chen, Y. Chao and W. Zhu, Chem. Eng. J., 2023, 453, 139485 CrossRef CAS.
- J. Xiong, L. He, D. Liu, W. Xu and Z. Zhao, Desalination, 2021, 520, 115326 CrossRef CAS.
- T. Hoshino, Desalination, 2015, 359, 59–63 CrossRef CAS.
- J. S. Kim, Y. H. Lee, S. Choi, J. Shin, H. C. Dinh and J. W. Choi, Environ. Sci. Technol., 2015, 49, 9415–9422 CrossRef CAS PubMed.
- Y. Orooji, Z. Nezafat, M. Nasrollahzadeh, N. Shafiei, M. Afsari, K. Pakzad and A. Razmjou, Desalination, 2022, 529, 115624 CrossRef CAS.
- J. Zhang, Z. Cheng, X. Qin, X. Gao, M. Wang and X. Xiang, Desalination, 2023, 547, 116225 CrossRef CAS.
- L. A. Limjuco, G. M. Nisola, C. P. Lawagon, S. Lee, J. G. Seo, H. Kim and W. Chung, Colloids Surf., A, 2016, 504, 267–279 CrossRef CAS.
- L. Tang, S. Huang, Y. Wang, D. Liang, Y. Li, J. Li, Y. Wang, Y. Xie and W. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 9775–9781 CrossRef CAS PubMed.
- L. R. Bao, J. Z. Zhang, W. P. Tang and S. Y. Sun, Desalination, 2023, 546, 116196 CrossRef CAS.
- K. Zhao, B. Tong, X. Yu, Y. Guo, Y. Xie and T. Deng, Chem. Eng. J., 2022, 430, 131423 CrossRef CAS.
- X. Zhao, L. Zheng, Y. Hou, Y. Wang and L. Zhu, Chem. Eng. J., 2022, 450, 138454 CrossRef CAS.
- Y. Wu, P. Shi, Y. Zhong and R. Cai, Energy Fuels, 2023, 37, 4083–4093 CrossRef CAS.
- Y. Wang, J. Zhang, Z. Cheng and X. Xiang, ACS Sustain. Chem. Eng., 2022, 10, 8970–8979 CrossRef CAS.
- W. Xu, D. Liu, X. Liu, D. Wang, L. He and Z. Zhao, Desalination, 2022, 546, 116188 CrossRef.
- Y. Mu, C. Zhang, W. Zhang and Y. Wang, Desalination, 2021, 511, 115112 CrossRef CAS.
- H. Kanoh, K. Ooi, Y. Miyai and S. Katoh, Langmuir, 1991, 7, 1841–1842 CrossRef CAS.
- S. Yang, F. Zhang, H. Ding, P. He and H. Zhou, Joule, 2018, 2, 1648–1651 CrossRef.
- D. Gupta, Y. Zhang, Z. Nie, J. Wang and G. M. Koenig, Chem. Eng. Sci., 2022, 251, 117443 CrossRef CAS.
- K. Gong, F. Xu, J. B. Grunewald, X. Ma, Y. Zhao, S. Gu and Y. Yan, ACS Energy Lett., 2016, 1, 89–93 CrossRef CAS.
- C. Liu, Y. Li, D. Lin, P. C. Hsu, B. Liu, G. Yan, T. Wu, Y. Cui and S. Chu, Joule, 2020, 4, 1459–1469 CrossRef CAS.
- A. E. Williams and M. A. McKibben, Geochim. Cosmochim. Acta, 1989, 53, 1905–1920 CrossRef CAS.
- S. Ventura, S. Bhamidi, M. Hornbostel and A. Nagar, Calif. Energy Comm., 2020, CEC-500-2020-020 Search PubMed.
- D. Lepage, F. Sobh, C. Kuss, G. Liang and S. B. Schougaard, J. Power Sources, 2014, 256, 61–65 CrossRef CAS.
- J. Wang and G. M. Koenig, J. Electrochem. Soc., 2023, 170, 050534 CrossRef CAS.
- N. Elgrishi, K. J. Rountree, B. D. McCarthy, E. S. Rountree, T. T. Eisenhart and J. L. Dempsey, J. Chem. Educ., 2018, 95, 197–206 CrossRef CAS.
- C. Noh, Y. Chung and Y. Kwon, J. Power Sources, 2020, 466, 228333 CrossRef CAS.
- Y. H. Wen, H. M. Zhang, P. Qian, H. T. Zhou, P. Zhao, B. L. Yi and Y. S. Yang, J. Electrochem. Soc., 2006, 153, A929 CrossRef CAS.
- H. Zhang and C. Sun, J. Power Sources, 2021, 493, 229445 CrossRef CAS.
- G. Wang, B. Huang, D. Liu, D. Zheng, J. Harris, J. Xue and D. Qu, J. Mater. Chem. A, 2018, 6, 13286–13293 RSC.
- N. Aristov and A. Habekost, World J. Chem. Educ., 2015, 3, 115–119 CAS.
- G. Yan, M. Wang, G. T. Hill, S. Zou and C. Liu, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, 1–9 Search PubMed.
- Y. H. Wen, H. M. Zhang, P. Qian, H. T. Zhou, P. Zhao, B. L. Yi and Y. S. Yang, J. Electrochem. Soc., 2006, 153, A929 CrossRef CAS.
- W. T. Stringfellow and P. F. Dobson, Energies, 2021, 14, 6805 CrossRef CAS.
- J. Xiong, Z. Zhao, D. Liu and L. He, Sep. Purif. Technol., 2022, 290, 120789 CrossRef CAS.
- B. Özdogru, H. Dykes, S. Padwal, S. Harimkar and Ö. Çapraz, Electrochim. Acta, 2020, 353, 136594 CrossRef.
- I. Persson, J. Solution Chem., 2018, 47, 797–805 CrossRef CAS PubMed.
- M. Pasta, A. Battistel and F. La Mantia, Energy Environ. Sci., 2012, 5, 9487–9491 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4se00703d |
| This journal is © The Royal Society of Chemistry 2024 |