Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Singlet fission is incoherent in pristine orthorhombic single crystals of rubrene: no evidence of triplet-pair emission†
David G.
Bossanyi
 *a,
Maik
Matthiesen
b,
Rahul
Jayaprakash
*a,
Maik
Matthiesen
b,
Rahul
Jayaprakash
 a,
Sayantan
Bhattacharya
c,
Jana
Zaumseil
a,
Sayantan
Bhattacharya
c,
Jana
Zaumseil
 b and
Jenny
Clark
b and
Jenny
Clark
 *a
*a
aDepartment of Physics and Astronomy, University of Sheffield, Hounsfield Road, Sheffield S3 7RH, UK. E-mail: jenny.clark@sheffield.ac.uk
bInstitute for Physical Chemistry, Heidelberg University, Heidelberg, Germany
cDepartment of Life Sciences, Imperial College, London SW15 4JD, UK
First published on 26th September 2023
Abstract
Singlet fission (SF) and its inverse, triplet–triplet annihilation (TTA), are promising strategies for enhancing photovoltaic efficiencies. However, detailed descriptions of the processes of SF/TTA are not fully understood, even in the most well-studied systems. Reports of the photophysics of crystalline rubrene, for example, are often inconsistent. Here we attempt to resolve these inconsistencies using time-resolved photoluminescence and transient absorption spectroscopy of ‘pristine’ rubrene orthorhombic single crystals. We find the reported time-resolved photoluminescence behaviour that hinted at triplet-pair emission is found only at specific sites on the crystals and likely arises from surface defects. Using transient absorption spectroscopy of the same crystals, we also observe no evidence of instantaneous generation of triplet-pair population with ∼100 fs excitation, independent of excitation wavelength (532 nm, 495 nm) or excitation angle. Our results suggest that SF occurs incoherently on a relatively slow (picosecond) timescale in rubrene single crystals, as expected from the original theoretical calculations. We conclude that the sub-100 fs formation of triplet pairs in crystalline rubrene films is likely to be due to static disorder.
1. Introduction
Photon up- and down-conversion are two promising strategies for pushing photovoltaic efficiencies beyond the Shockley–Queisser limit,1 but achieving efficient spectral conversion remains challenging. In molecular materials, singlet fission (SF), and its reverse, triplet–triplet annihilation (TTA), offer potential solutions.2 In SF, a high-energy singlet (spin-0) exciton (S1) converts to a pair of low-energy triplet (spin-1) excitons (T1 + T1).3,4 In TTA, the process is reversed.SF and TTA are generally accepted to proceed via intermediate triplet-pair states ((TT), (T⋯T))5,6 but the details of their formation and evolution are not yet fully described,7,8 even in archetypal SF/TTA materials such as crystalline pentacene and rubrene.7–27
1.1 Literature review: is singlet fission in single rubrene crystals fast (sub-picosecond) or slow?
Rubrene, whose structure is shown in Fig. 1a, is an example of a well-studied and archetypal SF/TTA material10–27 for which the SF process is still debated.13 In orthorhombic single crystals, for example, the peculiar symmetry of the C2h π-stacking, shown in Fig. 1b, means that electronic coupling between S1, charge-transfer (CT) and triplet-pair states should vanish. In this case, SF can only occur through coupling to symmetry-breaking vibrations and is predicted to proceed relatively slowly (incoherently) on picosecond timescales,18,28 presumably generating weakly-exchange-coupled or mixed-spin triplet-pair states (T⋯T)l.17,29 Recent spectroscopic studies on single rubrene crystals, however, are contradictory and many do not obviously support this theoretical hypothesis.10–16,18–24,27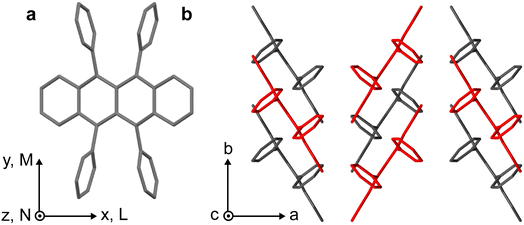 | ||
| Fig. 1 Crystal structure of rubrene. (a) Molecular structure of rubrene, indicating the molecular coordinate system. (b) Orthorhombic crystal structure of rubrene obtained from ref. 30. Molecules coloured red are displaced along the c-axis. | ||
For example, while some transient absorption15,20 and transient grating pump–probe experiments24 of rubrene crystals appear to support the calculations, showing triplet-pair population increasing approximately exponentially following photo-excitation (∼2 ps time-constant), other studies instead report near-instantaneous (instrument-limited, i.e. <25 fs) formation of triplet-pair signatures in rubrene single crystals.21–23,27 The latter signatures are not predicted by the calculations18,28 and current explanations for this surprising observation differ. The details of the proposed mechanisms and the discrepancies between them are nicely described in a recent review article.13 Broadly, it is suggested that at points on the potential energy surface, mixing between the diabatic S1 and triplet-pair states is allowed, due to vibronic coupling, and potentially via charge-transfer (CT) states. Depending on the strength of the coupling, this may enable direct, ‘coherent’ excitation of both S1 and triplet-pair states,21 supported by recent calculations.31 In this case, pure-spin exchange-coupled triplet-pair states, 1(TT), should be formed and we might therefore expect to observe 1(TT) emission.
1.2 Literature review: hunting for 1(TT) emission: time-resolved photoluminescence of rubrene single crystals
1(TT) emission has been observed in similar materials,7,32 where it was shown to occur via vibronic Herzberg–Teller mixing (intensity borrowing) between the triplet-pair state and the nearby bright S1 state.32,33 According to the Herzberg–Teller model, the first-order TT dipole moment is given by:34,35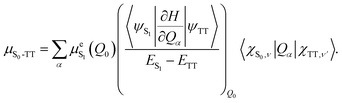 | (1) |
In crystalline rubrene, both of these criteria appear to be met: S1 and the triplet pairs (1(TT) or (T⋯T)) are almost isoenergetic32,36–38 and, as mentioned above, there is recent experimental evidence of significant vibronic coupling between S1 and the triplet pair in rubrene single crystals.21
Experimental hints of possible 1(TT) emission can be found in studies of the photoluminescence (PL) and absorption spectroscopy of rubrene single crystals in the literature.10,12 Ref. 10, for example, shows that the rubrene single-crystal PL spectrum at around 565 nm and around 607 nm exhibits different dynamic behaviour, suggesting that the PL may originate from more than one electronic state.10 In that study, only the redder part of the emission spectrum was quenched by an exciton splitter deposited at the surface of a rubrene crystal, while time-resolved PL spectroscopy measurements showed that the yellow-green part of the spectrum was short-lived, with a lifetime of approximately 15 ns compared with the delayed (∼1 μs) red emission.10 As a result of these observations, the authors of ref. 10 proposed a triplet exciton origin for the redder part of the spectrum.
Excellent work by Irkhin and co-workers offers further hints.12 They show that the strong S0–S1 transition dipole moment is polarised along the M-axis of the rubrene molecule and hence the c-axis of the rubrene crystal;12 see Fig. 1 for axes. The S0–S1 absorption (emission) spectrum of rubrene single crystals is therefore c-polarized, consisting of a vibronic progression, with the 0–0 transition at 2.32 eV (2.22 eV).12 Interestingly, rubrene crystals also possess pronounced ab-polarised absorption and emission. These ab-polarized absorption (emission) spectra appear as vibronic progressions with the same vibrational and 0–0 energy as the c-polarised spectra, yet with the 0–0 transition suppressed, giving the first apparent peak at 2.49 eV (2.04 eV).12 Suppressed 0–0 transitions such as this indicate Herzerg–Teller-type emission.
These results are suggestive. One interpretation of the spectral components might be that the S1 state is responsible for the c-polarised absorption/emission and the ∼isoenergetic triplet-pair state, which borrows intensity from S1 through Herzberg–Teller coupling, gives rise to the ab-polarised absorption/emission. This interpretation is consistent with the exciton quenching/time-resolved PL results from ref. 10, but it cannot explain the polarization dependence of the PL spectra.12 We would expect the 1(TT) dipole moment to retain the polarisation of the state from which it borrows intensity, in this case the M- and hence c-polarised S1.
An alternative explanation is that the ab-polarised absorption/emission arises from Herzberg–Teller coupling between S1 and a higher-lying singlet state that has its dipole moment along the L-axis, as originally suggested.12 A similar mechanism has been proposed to be active in other polyacenes39–41 and the effect would be especially pronounced in rubrene due to its unique crystal structure. However, this explanation cannot account for the different quenching and dynamical behaviour of the two components.10
1.3 Structure of this paper
In order to test the hypothesis that an emissive 1(TT) state is the source of ab-polarised absorption and emission in rubrene crystals, here we begin by attempting to reproduce the results of ref. 10, in which the emission at around 565 nm was initially found to decay much faster than that at 607 nm. We find that whilst we can indeed observe this effect, it occurs only at specific sites on the crystal surface and is therefore likely a result of morphological or surface inhomogeneities. We thus find no evidence of 1(TT) emission in orthorhombic single crystals.This result is interesting in the context of the transient absorption specroscopy studies mentioned above. If 1(TT) is non-emissive, the matrix element that couples S1 with the triplet-pair state through vibrational modes in eqn (1) would be expected to be small. However, as described above, recent ultrafast experiments21 have suggested that the vibronic coupling between S1 and the triplet-pair state is strong enough to enable ultrafast singlet fission (which is ordinarily forbidden due to the unique symmetry of the rubrene crystal18). Here we investigate this apparent discrepancy by studying the transient absorption spectroscopy of the same rubrene single crystals that were used for the photoluminescence study. We find no evidence in these crystals of ultrafast (sub-100 fs) singlet fission and triplet-pair formation.
2. Results
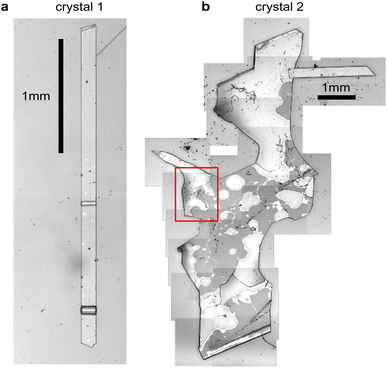
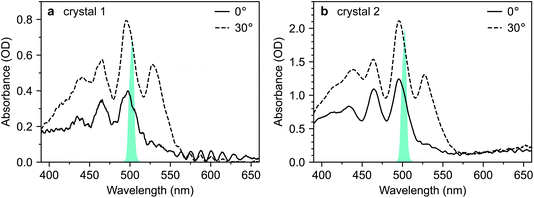
Fig. 2 shows microscope images of the two vapour-grown rubrene crystals (see Methods section, ESI†) used in this work. Crystal 1 (Fig. 2a) is a 0.7 μm thick platelet, 120 μm wide and several mm long, with few visible imperfections. Crystal 2 (Fig. 2b) is much larger, thicker, less uniform and more damaged. Optical experiments were confined to the region indicated by the red box in Fig. 2b. This region is approximately 2 μm thick.The absorption spectra of crystals 1 and 2 are shown in Fig. 3a and b, respectively, for incidence angles of 0° and 30°. The 0° spectra are consistent with the ab-polarised absorption of orthorhombic rubrene single crystals.12 The increased absorption and appearance of a peak at 532 nm upon rotation of the crystal to 30° incidence reflect the contribution of the c-polarised component. This demonstrates that the M-axes of the rubrene molecules, and hence the c-axis of the crystals, is normal to the substrate plane. Crystals 1 and 2 therefore have their largest dimensions in the ab-plane, as expected for vapour-grown rubrene crystals.12 Excitation at 532 nm therefore selectively excites the c-polarised transition, whilst excitation at around 500 nm excites both the c- and ab-polarised transitions, with the ratio of absorptions dependent on the incidence angle.
2.1 Site-dependent anomalous photoluminescence behaviour in single crystals
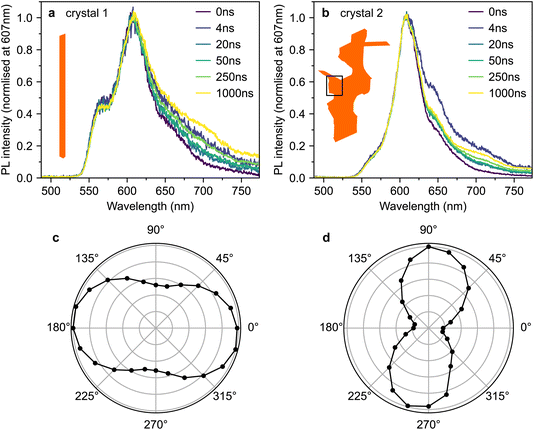
Fig. 4a and b show time-gated photoluminescence spectra, normalised at 607 nm, from crystals 1 and 2 following pulsed excitation at 500 nm. The pump was introduced at an incidence angle of 45° and therefore excites both the c- and ab-polarised absorption components. The pump spectra are shown in Fig. 3. PL (in all polarisations) was collected at normal incidence to the ab crystal plane (see Methods section, ESI†).Fig. 4c and d show the dependence of the PL intensity (integrated from 0–2 μs) on the rotation angle of a linear polariser placed before the detector. In both cases, the intensity exhibits the expected cos2(θ) pattern associated with dipole emission. The pattern is slightly less pronounced in crystal 1 (Fig. 4c), perhaps due to some PL ‘leakage’ from the edges of the crystal being picked up by the collection lens.
We observe slight changes with time to the shape of the PL tail beyond 620 nm in Fig. 4a and b, which suggests small contributions from lower-lying excited states.42 Similar low-energy bands of varying intensity are commonly observed in the PL tail of rubrene single crystals.12,15,16,21,23,42–46 The origins of such bands are debated; suggestions include oxygen-related mid-gap states45 or amorphous regions within the crystal.42 We note that the PL spectra from our crystals strongly resemble the spectra from ‘pristine’ rubrene single crystals in ref. 12 (see Fig. S3†).
Crucially, we do not find any significant differences in temporal behaviour between 565 nm and 607 nm and therefore between the c- and ab-polarised emission components, suggesting that at the positions measured, both components arise from the same excitonic species.
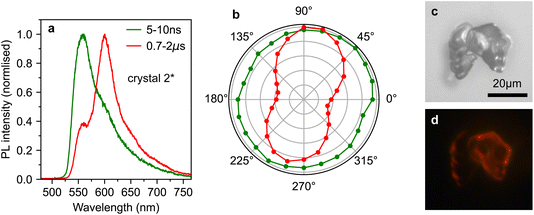
However, by scanning around the surface of crystal 2, we were able to find a spot that reproduced the behaviour observed in ref. 10, which we denote crystal 2*. The time-gated spectra from this spot (Fig. 5a) show a striking dependence on detection wavelength. A short-lived component that peaks at ∼565 nm (and is hence c-polarised only12) dominates during the first few nanoseconds, before giving way to a constant spectrum resembling the ab-polarised emission (plus the expected c-polarised ‘leakage’ due to experimental conditions12). These different dynamics are clearly evident when comparing the PL decay profiles in Fig. 5b. Beyond 50 ns, the PL dynamics of crystals 2 and 2* are identical. Initially however, the band at 565 nm appears as an extra component with a lifetime of a few nanoseconds.
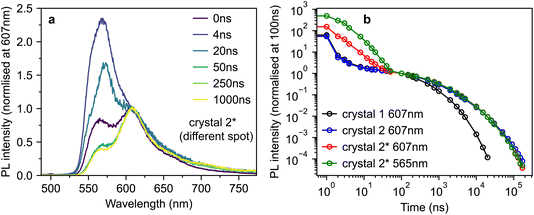 | ||
| Fig. 5 Anomalous photoluminescence behaviour of rubrene crystals. (a) Time-gated PL spectra, normalised at 607 nm, for crystal 2*, a different spot on the surface of crystal 2 that exhibited similar PL behaviour to that reported in ref. 10. (b) Time-dependence of the PL intensity from crystals 1, 2 and 2* at various detection wavelengths, normalised at 100 ns. | ||
To investigate the origins of the two emission components evident in crystal 2*, we measured the detection polarisation anisotropy of the PL intensity, shown in Fig. 6a and b. The long-lived, mainly ab-polarised component of crystal 2* (red, Fig. 6a and b) shows the same expected cos2(θ) dipole dependence as crystals 1 and 2 (Fig. 4c and d). In contrast, the short-lived, c-polarised component of crystal 2* (green, Fig. 6a and b) is almost completely isotropic.
If 1(TT) and S1, respectively, are the sources of the ab- and c-polarised emission components, we would not expect significant differences in their anisotropy, nor would we expect the c-polarised part to be observable only at specific sites on the crystal. Instead, the measurements in Fig. 4–6 indicate that the short-lived, c-like component arises from a sub-population of singlet excitons found only at certain points on the crystal due to morphological inhomogeneity.
This conclusion is in agreement with results in ref. 12, where they found that micrometer-sized defects on the crystal surface within the excitation/detection region resulted in a large enhancement in the PL shoulder at 565 nm. This was attributed to the scattering of c-polarised PL into the detector. Such scattering would explain why we measure this emission to be isotropic. Indeed, an examination of the surface of crystal 2 (Fig. 2b) reveals that several rough, micrometer-sized microcrystals are present on the surface. An example of such a surface microcrystal is shown in Fig. 6c, and it is clear from the PL image in Fig. 6d that these microcrystals can be significantly brighter than the bulk crystal. It therefore seems likely that such microcrystals or defects, rather than singlet and triplet origins, are the cause of the curious results in ref. 10.
We have demonstrated that there is no clear evidence of photoluminescence from the 1(TT) state in rubrene single crystals, despite the small S1–triplet-pair energy gap, suggesting that either 1(TT) behaves identically to the signature attributed to S1, which seems unlikely given the strong similarity to the S1 spectrum in solution,12 or the triplet pair is not emissive. Instead, our photoluminescence experiments show that previously observed differences in the behaviour of c-polarised and ab-polarised emission components are found only at particular sites on rubrene crystals. We have shown that these sites are likely to correspond to microcrystal surface defects.
This result introduces something of a conundrum. If 1(TT) is non-emissive in rubrene crystals, the matrix element that couples S1 with the triplet pair through vibrational modes in eqn (1) must be small. However, recent ultrafast experiments21 have suggested that the vibronic coupling between S1 and the triplet pair is strong, such that it enables ultrafast singlet fission (which is ordinarily forbidden due to the unique symmetry of the rubrene crystal18). We investigate this apparent discrepancy by studying the transient absorption spectroscopy of pristine rubrene crystals.
2.2 Transient absorption spectroscopy of pristine rubrene crystals demonstrates no evidence of coherent 1(TT) formation
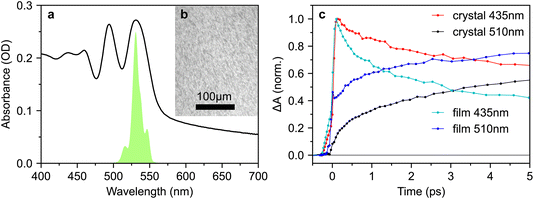
For this study, we use the same rubrene crystals shown in Fig. 2. We judged our crystals to be pristine, particularly crystal 1, by comparing their PL spectra against those reported in ref. 12, an extremely careful and comprehensive analysis of the absorption and emission properties of rubrene single crystals (see, for example, Fig. S3†). We note that the PL spectra reported by Miyata et al.21 and Bera et al.23 are both dominated by the 650 nm band, indicative of defective rubrene crystals.12,42,45 Furthermore, the PL spectrum (from platelet crystals very similar to ours) reported by Breen et al.22 is dominated by a band at 565 nm. We showed above, in accordance with ref. 12, that such emission can arise from microcrystal defects on the crystal surface and is associated with changes in PL dynamics. The lack of experimental details surrounding the acquisition of the PL spectrum make interpretation difficult; however, we note that such defects can be clearly seen in the microscope image presented by Breen et al.22 In fact, of the transient absorption literature reviewed above, only Ishibashi et al.20 report a PL spectrum consistent with pristine rubrene crystals.12 We will see below that potentially defective crystals may have a substantial impact on the measured transient absorption data.Fig. 7 reproduces the absorption spectra of crystals 1 and 2 from Fig. 3. Alongside, we plot the spectra of two different pump pulses used in our transient absorption experiments. The pulse centred at 495 nm selectively excites the 0–1 transition, which includes both ab- and c-polarised components.12 The pulse centred at 532 nm selectively excites the vibrationless 0–0 transition, which is exclusively c-polarised.12
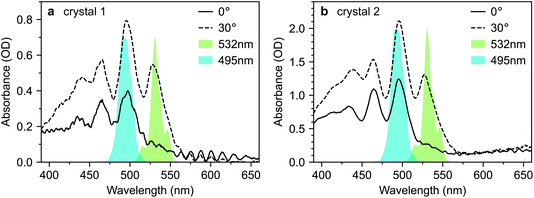 | ||
| Fig. 7 Selective excitation of rubrene single crystals. (a and b) Absorption spectra of rubrene single crystals 1 and 2 at incidence angles of 0° and 30°, reproduced from Fig. 3. The 495 nm and 532 nm pump spectra used in the transient absorption experiments presented in this paper are shown. The two pump wavelengths target the 0–1 and 0–0 vibronic transitions, respectively. | ||
According to the coherent mechanism proposed by Miyata et al.,21 excitation using either of these pump pulses should result in instrument-limited 1(TT) formation. In contrast, the incoherent pathway suggested by Breen et al.22 should only be activated when the initial photo-excited state is a vibrationally dressed S1 state. In that case, instrument-limited triplet-pair formation should be observed only when pumping at 495 nm. Comparing the dynamics of the triplet-pair population under these two excitation conditions should therefore enable us to distinguish between these two mechanisms. To obtain further confirmation of our conclusions above, that 1(TT) is not responsible for the ab-polarised absorption component, we also performed experiments at both 0° and 30° incidence.
2.3 No instantaneous triplet-pair formation in single crystals with ∼100 fs excitation
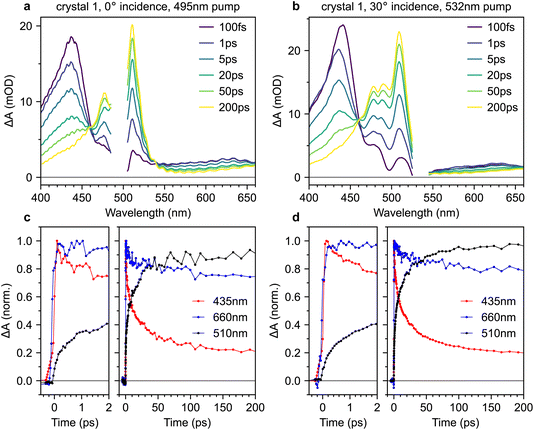
Fig. 8a and b show transient absorption spectra recorded in crystal 1 with 495 nm excitation at 0° incidence, and 532 nm excitation at 30° incidence, respectively (complete data sets for both crystals are shown in the ESI, Fig. S9–S12†). The band at 435 nm arises from the S1 → S3 excited-state absorption15,38 whilst the band at 510 nm is characteristic of T1 → T3.15,20–22,38 In the probe region beyond 550 nm, both singlet and triplet excited-state absorptions contribute.21,38,47 Absorptions from charge-separated states can also be present in the spectral region around 600–900 nm.14,48 We discount them here because they are usually observed only under ultraviolet excitation14,15,48 and are generally short-lived,48 unlike the persistent signal apparent at 660 nm in our measurements. We observe an isosbestic point between the singlet and triplet-pair absorption features, indicating that singlet fission is a one-to-one conversion between S1 and a triplet pair.15The transient absorption dynamics corresponding to Fig. 8a and b are plotted in Fig. 8c and d for probe wavelengths of 435 nm (mostly singlets), 660 nm (a mixture of singlets and triplet pairs) and 510 nm (almost entirely triplet pairs). The dynamics are normalised to the maximum signal at 435 nm. In Fig. S14,† we demonstrate that the dynamics at 510 nm are almost entirely uncontaminated by spectral overlap with nearby singlet bands and are thus a good measure of triplet-pair population.
We find no clear evidence of instrument-limited triplet-pair formation in Fig. 8c and d. The rise in the triplet-pair population at 510 nm starts after, and is less steep than, the rise of the photo-excited singlet population at 435 nm. This cannot be an artefact of the chirp correction procedure (see Methods section, ESI†) because it is also later, and less steep, than the rise of the signal at 660 nm. This behaviour is the same regardless of excitation wavelength.
In order to compare our measured triplet-pair dynamics with previous measurements, we attempted to extract time constants using multi-exponential fitting. We found that whilst a bi-exponential function gave a good fit, the extracted time constants varied significantly depending on the time window used for the fit. Moving to a tri-exponential function (Fig. 11a, below) provided a much more robust set of fitting parameters. However, as a result of the large number of fitting parameters (six) and clear non-exponential behaviour, it does not make sense to talk about time constants per se. Nevertheless, the fitting results are instructive, particularly when we come to compare the triplet-pair dynamics to those measured for a polycrystalline film below.
A tri-exponential fit to the triplet-pair dynamics of crystal 1 (532 nm excitation, 30° incidence), shown below in Fig. 11a, yielded time constants of 0.25(3) ps (23(2)%), 1.8(4) ps (26(3)%) and 14(3) ps (51(2)%). These three values are similar to those extracted by Breen et al.22 and the latter two time constants agree well with those reported by Ma et al.15 and Ishibashi et al.20 based on bi-exponential fitting. Our sub-picosecond component is slower than that of ref. 22 by a factor of 2–3. This might reflect differences in the instrument response time, though we reiterate that our initial triplet-pair rise is slower than the rise time of the singlet exciton signal.
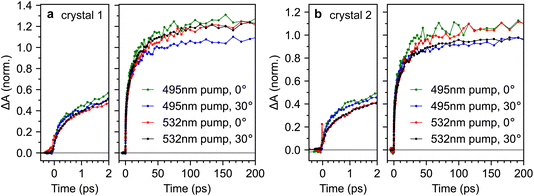
For completeness, Fig. 9 compares the triplet-pair dynamics probed at 510 nm for both crystals 1 and 2 under different excitation wavelengths and incidence angles (full datasets are also shown in ESI Fig. S9–S12†). We find that the dynamics are very similar across both crystals, incidence angles and excitation wavelengths. It appears that the triplet-pair dynamics exhibit a very slightly more pronounced sub-picosecond component when the excitation wavelength is 495 nm, resulting in a marginally larger population at 2 ps. At first glance, this appears to support the conclusions of Breen et al.22, that a vibrationally dressed photo-excited singlet state (only possible with 495 nm excitation in our experiment) is required to enable ultrafast triplet-pair formation. However, it is noticeable from Fig. 9 that the effect of excitation wavelength is more pronounced in crystal 2 than crystal 1. Crystal 2 is significantly more defective (see Fig. 2), suggesting that this may not be an intrinsic bulk effect.
2.4 Transient absorption spectroscopy of polycrystalline rubrene films shows instrument-limited formation of triplet pairs
Since many of the rubrene crystals reported in the literature exhibit PL spectra indicative of defects, and since we find that the effect of excitation wavelength on sub-picosecond triplet-pair formation is more pronounced in a more defective crystal, we repeated our measurements on a polycrystalline thin film. The absorption spectrum is shown in Fig. 10a and the microscope image in Fig. 10b reveals a polycrystalline texture on the micrometer length scale.Strikingly, when comparing the transient absorption dynamics of the film and crystal in Fig. 10c, we find very clear evidence of instantaneous triplet-pair formation in the polycrystalline sample. The initial rise of the triplet-pair signal at 510 nm exactly follows the rise of the photo-excited singlet at 435 nm, likely demonstrating 1(TT) formation within the instrument response. We demonstrate in Fig. S15† that this observation is not an artefact of spectral overlap. We note that the instantaneous triplet-pair formation in the polycrystalline film occurs even though the excitation wavelength is 532 nm. 532 nm is not sufficiently energetic to populate vibrationally dressed S1 states, thereby casting doubt on the mechanism proposed by Breen et al.22 to explain femtosecond singlet fission in rubrene.
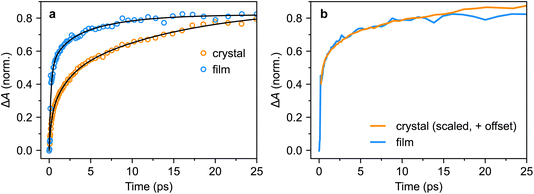
We repeated the tri-exponential fitting for the triplet-pair dynamics on the polycrystalline film. The fit is shown in Fig. 11a and we extracted time constants of 0.21(5) ps (59(12)%), 1(3) ps (16(23)%) and 6(6) ps (25(27)%). The large errors on the latter two components illustrate the limitations of such fitting, but it is clear that the sub-picosecond component is significantly greater, and slightly faster, than in the bulk crystal. More instructively, in Fig. 11b, we show that for the first few tens of picoseconds, the triplet-pair dynamics of the polycrystalline film can be explained as an instrument-limited initial offset of around 50% of the maximum population with subsequent dynamics that exactly match those of the bulk crystal.
For completeness, we also measured the time-resolved photoluminescence (TRPL) of our polycrystalline thin film under both 500 nm and 532 nm excitation (Fig. 12a and b respectively).
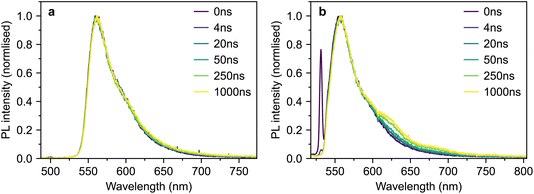 | ||
| Fig. 12 TRPL of polycrystalline rubrene. (a and b) Time-gated photoluminescence spectra of a polycrystalline rubrene film following excitation at 500 nm (a) and 532 nm (b). | ||
The spectra are similar in both cases and slightly blue-shifted compared with the single-crystal emission spectrum. Following 532 nm excitation (Fig. 12b), we observe a small shoulder growing in on a timescale of several nanoseconds at 630 nm. This is similar to a spectral feature previously assigned to 1(TT) in rubrene thin films.32 However, we observe no such behaviour following excitation at 500 nm (Fig. 12a). The slight changes in behaviour with excitation wavelength may be due rather to a different region of the film falling within the excitation spot across the two separate measurements. Furthermore, it is well known that defects in rubrene films can emit at around 630 nm (ref. 12). Further careful experiments are required before a concrete assignment of the polycrystalline thin-film photoluminescence spectrum can be made; these are beyond the scope of the current work.
3. Discussion
Our transient absorption results demonstrate that instantaneous, or instrument-limited, formation of triplet pairs following photo-excitation of crystalline rubrene occurs in polycrystalline thin films but not in bulk single crystals. Following this ultrafast rise for the film, the triplet-pair dynamics appear almost identical to those of the bulk crystal. The lack of femtosecond singlet fission in rubrene crystals is in line with expectations,18 raising the question of what factors enable it to occur in polycrystalline films.One possibility is that the triplet-pair state and S1 are mixed at certain sites within the film morphology where the C2h π-stacking symmetry breaks down due to static disorder, for example at grain boundaries or dislocations. At these sites, 1(TT) can be formed extremely rapidly, whilst elsewhere, triplet-pair formation dynamics mimic those of the bulk crystal, as shown in Fig. 11b. It is perhaps curious then that singlet fission is reported to be completely suppressed in truly amorphous solid rubrene,24 though this may simply be a result of weaker intermolecular couplings. Further experiments and calculations may be required to discover which intermolecular alignments are preferential for ultrafast singlet fission in rubrene.
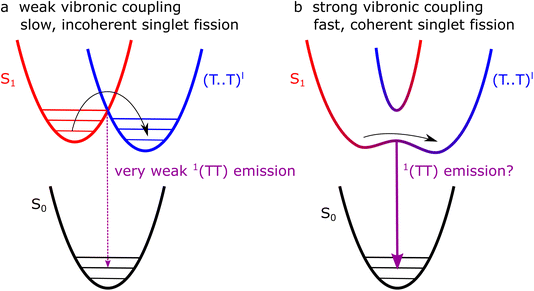
These two proposed types of singlet fission, bulk and defect, are shown schematically in Fig. 13a and b, respectively. In the bulk (a), low-energy librational modes provide weak vibronic coupling between S1 and triplet-pair states, enabling incoherent singlet fission to occur with a picosecond time constant. At sites where the symmetry constraint is broken (b), the triplet pair and S1 may become substantially mixed. Photo-excitation at such sites results in a coherent superposition of S1 and 1(TT).
The pathways proposed in Fig. 13 suggest that photoluminescence from 1(TT), enabled by vibronic coupling, or Herzberg–Teller intensity borrowing, might be present in polycrystalline thin films but, as we described above, not in single crystals. We have observed no clear 1(TT) emission in the polycrystalline films (Fig. 12), but note that the emission spectra are shifted compared with both solution and crystal spectra12 and more work is required to understand these spectra before fully ruling out 1(TT) emission.
We take our results to suggest that in pristine orthorhombic single crystals, only weakly bound triplet-pair states (T⋯T)l are formed. In samples with defect sites, on the other hand, it is likely that exchange-coupled triplet states 1(TT) are formed instantaneously at the defects due to the lack of symmetry constraints. The lack of direct spectroscopic evidence of 1(TT) states in defective films or crystals, however, remains to be resolved.
4. Conclusions
We have demonstrated that ultrafast instantaneous formation of triplet-pair states in crystalline rubrene occurs in polycrystalline films but not in single crystals, in contrast to recent reports. Our results are consistent with calculations showing that singlet fission in rubrene crystals is an incoherent process, occurring on the picosecond timescale, and driven by low-energy vibrational modes that weakly couple S1 to (T⋯T)l.We propose that the instantaneous triplet-pair formation that we readily observe in polycrystalline films arises from static disorder. At certain sites within the film morphology, molecules may be oriented in such a way as to break the symmetry and allow S1, charge-transfer states and triplet pairs to mix. At such sites, singlet fission can be a coherent process, producing 1(TT). Such mixing should result in site-dependent Herzberg–Teller emission from the 1(TT) state in polycrystalline rubrene, but we could not observe it.
Our results highlight the need for more detailed experiments to investigate the dependence of singlet fission on inter-molecular geometry in rubrene and to ensure that single-crystal studies are performed on pristine samples. Our results also suggest a strategy to avoid losses in singlet-fission systems from strongly exchanged coupled 1(TT) that rapidly decay radiatively and non-radiatively,33 by designing systems in which singlet fission is symmetry-constrained, as in rubrene.
Author contributions
DGB and JC conceived of the project; DGB and MM grew the crystals with supervision from JZ; DGB grew the polycrystalline films, and performed most of the experiments and all of the analysis with supervision from JC. RJ performed the optical microscopy measurements. SB built the non-collinear parametric amplifier for these experiments. The manuscript was written by DGB and JC with input from all authors.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
DGB thanks the EPSRC Centre for Doctoral Training in New and Sustainable Photovoltaics (EP/L01551X/1) for studentship support. JC and RJ thank the EPSRC for funding (EP/T012455/1, EP/M025330/1 and EP/S002766). We thank the EPSRC for a Capital Equipment award (EP/L022613/1 and EP/R042802/1), which provided the Lord Porter Laser Laboratory Facility used in this study. J. Z. and M. M. acknowledge funding by the Deutsche Forschungsgemeinschaft via SFB 1249 (C06).References
- J. Day, S. Senthilarasu and T. K. Mallick, Improving spectral modification for applications in solar cells: A review, Renewable Energy, 2019, 132, 186 CrossRef.
- M. J. Y. Tayebjee, D. R. McCamey and T. W. Schmidt, Beyond Shockley–Queisser: Molecular approaches to high-efficiency photovoltaics, J. Phys. Chem. Lett., 2015, 6, 2367 CrossRef CAS PubMed.
- A. Rao and R. H. Friend, Harnessing singlet exciton fission to break the Shockley–Queisser limit, Nat. Rev. Mater., 2017, 2, 17063 CrossRef CAS.
- L. Frazer, J. K. Gallaher and T. W. Schmidt, Optimizing the efficiency of solar photon upconversion, ACS Energy Lett., 2017, 2, 1346 CrossRef CAS.
- T. Yago, K. Ishikawa, R. Katoh and M. Wakasa, Magnetic field effects on triplet pair generated by singlet fission in an organic crystal: Application of radical pair model to triplet pair, J. Phys. Chem. C, 2016, 120, 27858 CrossRef CAS.
- M. I. Collins, D. R. McCamey and M. J. Y. Tayebjee, Fluctuating exchange interactions enable quintet multiexciton formation in singlet fission, J. Chem. Phys., 2019, 151, 164104 CrossRef.
- D. G. Bossanyi, M. Matthiesen, S. Wang, J. A. Smith, R. C. Kilbride, J. D. Shipp, D. Chekulaev, E. Holland, J. E. Anthony, J. Zaumseil, A. J. Musser and J. Clark, Emissive spin-0 triplet-pairs are a direct product of triplet–triplet annihilation in pentacene single crystals and anthradithiophene films, Nat. Chem., 2021, 13, 163 CrossRef CAS.
- A. Neef, S. Beaulieu, S. Hammer, S. Dong, J. Maklar, T. Pincelli, R. P. Xian, M. Wolf, L. Rettig and J. Pflaum, et al. , Orbital-resolved observation of singlet fission, Nature, 2023, 616, 275 CrossRef CAS.
- W.-L. Chan, M. Ligges, A. Jailaubekov, L. Kaake, L. Miaja-Avila and X.-Y. Zhu, Observing the multiexciton state in singlet fission and ensuing ultrafast multielectron transfer, Science, 2011, 334, 1541 CrossRef CAS.
- H. Najafov, B. Lee, Q. Zhou, L. C. Feldman and V. Podzorov, Observation of long-range exciton diffusion in highly ordered organic semiconductors, Nat. Mater., 2010, 9, 938 CrossRef CAS PubMed.
- P. Irkhin and I. Biaggio, Direct imaging of anisotropic exciton diffusion and triplet diffusion length in rubrene single crystals, Phys. Rev. Lett., 2011, 107, 017402 CrossRef PubMed.
- P. Irkhin, A. Ryasnyanskiy, M. Koehler and I. Biaggio, Absorption and photoluminescence spectroscopy of rubrene single crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 085143 CrossRef.
- W. Kim and A. J. Musser, Tracking ultrafast reactions in organic materials through vibrational coherence: vibronic coupling mechanisms in singlet fission, Adv. Phys.: X, 2021, 6, 1918022 Search PubMed.
- S. Tao, H. Matsuzaki, H. Uemura, H. Yada, T. Uemura, J. Takeya, T. Hasegawa and H. Okamoto, Optical pump-probe spectroscopy of photocarriers in rubrene single crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 75204 CrossRef.
- L. Ma, K. Zhang, C. Kloc, H. Sun, M. E. Michel-Beyerle and G. G. Gurzadyan, Singlet fission in rubrene single crystal: direct observation by femtosecond pump–probe spectroscopy, Phys. Chem. Chem. Phys., 2012, 14, 8307 RSC.
- L. Ma, G. Galstyan, K. Zhang, C. Kloc, H. Sun, C. Soci, M. E. Michel-Beyerle and G. G. Gurzadyan, Two-photon-induced singlet fission in rubrene single crystal, J. Chem. Phys., 2013, 138, 184508 CrossRef.
- G. B. Piland, J. J. Burdett, D. Kurunthu and C. J. Bardeen, Magnetic field effects on singlet fission and fluorescence decay dynamics in amorphous rubrene, J. Phys. Chem. C, 2013, 117, 1224 CrossRef CAS.
- H. Tamura, M. Huix-Rotllant, I. Burghardt, Y. Olivier and D. Beljonne, First-principles quantum dynamics of singlet fission: Coherent versus thermally activated mechanisms governed by molecular π-stacking, Phys. Rev. Lett., 2015, 115, 107401 CrossRef PubMed.
- K. A. Ward, B. R. Richman and I. Biaggio, Nanosecond pump and probe observation of bimolecular exciton effects in rubrene single crystals, Appl. Phys. Lett., 2015, 106, 223302 CrossRef.
- Y. Ishibashi, Y. Inoue and T. Asahi, The excitation intensity dependence of singlet fission dynamics of a rubrene microcrystal studied by femtosecond transient microspectroscopy, Photochem. Photobiol. Sci., 2016, 15, 1304 CrossRef CAS PubMed.
- K. Miyata, Y. Kurashige, K. Watanabe, T. Sugimoto, S. Takahashi, S. Tanaka, J. Takeya, T. Yanai and Y. Matsumoto, Coherent singlet fission activated by symmetry breaking, Nat. Chem., 2017, 9, 983 CrossRef CAS.
- I. Breen, R. Tempelaar, L. A. Bizimana, B. Kloss, D. R. Reichman and D. B. Turner, Triplet separation drives singlet fission after femtosecond correlated triplet pair production in rubrene, J. Am. Chem. Soc., 2017, 139, 11745 CrossRef CAS.
- K. Bera, C. J. Douglas and R. R. Frontiera, Femtosecond Raman microscopy reveals structural dynamics leading to triplet separation in rubrene singlet fission, J. Phys. Chem. Lett., 2017, 8, 5929 CrossRef CAS PubMed.
- D. M. Finton, E. A. Wolf, V. S. Zoutenbier, K. A. Ward and I. Biaggio, Routes to singlet exciton fission in rubrene crystals and amorphous films, AIP Adv., 2019, 9, 95027 CrossRef.
- D. G. Bossanyi, Y. Sasaki, S. Wang, D. Chekulaev, N. Kimizuka, N. Yanai and J. Clark, Spin statistics for triplet–triplet annihilation upconversion: Exchange coupling, intermolecular orientation, and reverse intersystem crossing, JACS Au, 2021, 1, 2188 CrossRef CAS PubMed.
- D. G. Bossanyi, Y. Sasaki, S. Wang, D. Chekulaev, N. Kimizuka, N. Yanai and J. Clark, optimized rubrene-based nanoparticle blends for photon upconversion, singlet energy collection outcompetes triplet-pair separation, not singlet fission, J. Mater. Chem. C, 2022, 10, 4684 RSC.
- Y. Liu, X. Yang, L. Ye, H. Ma and H. Zhu, Molecular stacking controlling coherent and incoherent singlet fission in polymorph rubrene single crystals, Aggregate, 2023, e347, DOI:10.1002/agt2.347.
- X. Xie, A. Santana-Bonilla, W. Fang, C. Liu, A. Troisi and H. Ma, Exciton–phonon interaction model for singlet fission in prototypical molecular crystals, J. Chem. Theory Comput., 2019, 15, 3721 CrossRef CAS.
- E. A. Wolf, D. M. Finton, V. Zoutenbier and I. Biaggio, Quantum beats of a multiexciton state in rubrene single crystals, Appl. Phys. Lett., 2018, 112, 83301 CrossRef.
- O. D. Jurchescu, A. Meetsma and T. T. M. Palstra, Low-temperature structure of rubrene single crystals grown by vapor transport, Acta Crystallogr., Sect. B: Struct. Sci., 2006, 62, 330 CrossRef PubMed.
- H.-G. Duan, A. Jha, X. Li, V. Tiwari, H. Ye, P. K. Nayak, X.-L. Zhu, Z. Li, T. J. Martinez, M. Thorwart and R. J. D. Miller, Intermolecular vibrations mediate ultrafast singlet fission, Sci. Adv., 2020, 6, eabb0052 CrossRef CAS PubMed.
- C. K. Yong, A. J. Musser, S. L. Bayliss, S. Lukman, H. Tamura, O. Bubnova, R. K. Hallani, A. Meneau, R. Resel, M. Maruyama, S. Hotta, L. M. Herz, D. Beljonne, J. E. Anthony, J. Clark and H. Sirringhaus, The entangled triplet pair state in acene and heteroacene materials, Nat. Commun., 2017, 8, 15953 CrossRef CAS PubMed.
- A. J. Musser and J. Clark, Triplet-pair states in organic semiconductors, Annu. Rev. Phys. Chem., 2019, 70, 323 CrossRef CAS PubMed.
- G. Orlandi and W. Siebrand, Theory of vibronic intensity borrowing. Comparison of Herzberg–Teller and Born-Oppenheimer coupling, J. Chem. Phys., 1973, 58, 4513 CrossRef CAS.
- A. C. Albrecht, On the theory of Raman intensities, J. Chem. Phys., 1961, 34, 1476 CrossRef CAS.
- W. G. Herkstroeter and P. B. Merkel, The triplet state energies of rubrene and diphenylisobenzofuran, J. Photochem., 1981, 16, 331 CrossRef CAS.
- F. Lewitzka and H.-G. Löhmannsröben, Investigation of triplet tetracene and triplet rubrene in solution, Z. fur Phys. Chem., 1986, 150, 69 CrossRef CAS.
- H. G. Löhmannsröben, Photophysical properties and laser performance of rubrene, Appl. Phys. B, 1988, 47, 195 CrossRef.
- S. R. Ellis, D. R. Dietze, T. Rangel, F. Brown-Altvater, J. B. Neaton and R. A. Mathies, Resonance Raman characterization of tetracene monomer and nanocrystals: Excited state lattice distortions with implications for efficient singlet fission, J. Phys. Chem. A, 2019, 123, 3863 CrossRef CAS PubMed.
- Y. Qian, X. Li, A. R. Harutyunyan, G. Chen, Y. Rao and H. Chen, Herzberg–Teller effect on the vibrationally resolved absorption spectra of single-crystalline pentacene at finite temperatures, J. Phys. Chem. A, 2020, 124, 9156 CrossRef CAS PubMed.
- Y. Qian, T. Zhang, J. Han, A. R. Harutyunyan, G. Chen, Y. Rao and H. Chen, Symmetry-breaking enhanced Herzberg–Teller effect with brominated polyacenes, J. Phys. Chem. A, 2021, 125, 3589 CrossRef CAS PubMed.
- Y. Chen, B. Lee, D. Fu and V. Podzorov, The origin of a 650 nm photoluminescence band in rubrene, Adv. Mater., 2011, 23, 5370 CrossRef CAS PubMed.
- S. Tavazzi, A. Borghesi, A. Papagni, P. Spearman, L. Silvestri, A. Yassar, A. Camposeo, M. Polo and D. Pisignano, Optical response and emission waveguiding in rubrene crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245416 CrossRef.
- X. Wen, P. Yu, C.-T. Yuan, X. Ma and J. Tang, Singlet and triplet carrier dynamics in rubrene single crystal, J. Phys. Chem. C, 2013, 117, 17741 CrossRef CAS.
- O. Mitrofanov, D. V. Lang, C. Kloc, J. M. Wikberg, T. Siegrist, W.-Y. So, M. A. Sergent and A. P. Ramirez, Oxygen-related band gap state in single crystal rubrene, Phys. Rev. Lett., 2006, 97, 166601 CrossRef PubMed.
- R. J. Stöhr, G. J. Beirne, P. Michler, R. Scholz, J. Wrachtrup and J. Pflaum, Enhanced photoluminescence from self-organized rubrene single crystal surface structures, Appl. Phys. Lett., 2010, 96, 231902 CrossRef.
- T. Zhu, Y. Wan, Z. Guo, J. Johnson and L. Huang, Two birds with one stone: Tailoring singlet fission for both triplet yield and exciton diffusion length, Adv. Mater., 2016, 28, 7539 CrossRef CAS PubMed.
- V. Jankus, E. W. Snedden, D. W. Bright, E. Arac, D. Dai and A. P. Monkman, Competition between polaron pair formation and singlet fission observed in amorphous rubrene films, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 224202 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3fd00150d |
| This journal is © The Royal Society of Chemistry 2024 |