Reactive collisions between electrons and BeH+ above dissociation threshold
Emerance
Djuissi
a,
Jeoffrey
Boffelli
 a,
Riyad
Hassaine
a,
Riyad
Hassaine
 a,
Nicolina
Pop
a,
Nicolina
Pop
 *b,
Vincenzo
Laporta
*b,
Vincenzo
Laporta
 c,
Kalyan
Chakrabarti
c,
Kalyan
Chakrabarti
 d,
Mehdi
Ayouz
d,
Mehdi
Ayouz
 e,
Arnaud
Bultel
e,
Arnaud
Bultel
 f,
János Zsolt
Mezei
f,
János Zsolt
Mezei
 ag and
Ioan F.
Schneider
ag and
Ioan F.
Schneider
 ah
ah
aLOMC-UMR6294, CNRS, Université Le Havre Normandie, 76600 Le Havre, France
bDept. of Phys.l Foundations of Engineering, Politehnica University of Timişoara, 300223 Timisoara, Romania. E-mail: nicolina.pop@upt.ro
cIstituto per la Scienza e Tecnologia dei Plasmi, CNR, 70126 Bari, Italy
dDept. of Mathematics, Scottish Church College, 700006 Kolkata, India
eLGPM, CentraleSupélec, Université Paris-Saclay, 8-10 Rue Joliot Curie, F-91190 Gifsur-Yvette, France
fCORIA-UMR6614, CNRS, Université de Rouen Normandie, 76800 Saint-Etienne du Rouvray, France
gHUN-REN Institute for Nuclear Research (ATOMKI), H-4001 Debrecen, Hungary
hLAC-UMR9188, Université Paris-Saclay, F-91405 Orsay, France
First published on 3rd June 2024
Abstract
Our previous studies of dissociative recombination and vibrational excitation/de-excitation of the BeH+ ion, based on the multichannel quantum defect theory, are extended to collision energies above the dissociation threshold, taking into account the vibrational continua of the BeH+ ion and, consequently, its dissociative excitation. We have also significantly increased the number of dissociative states of 2Π, 2Σ+ and 2Δ symmetry included in our cross section calculations, generating the most excited ones by using appropriate scaling laws. Our results are suitable for modeling the kinetics of BeH+ in edge fusion plasmas for collision energies up to 12 eV.
1 Introduction
Beryllium is considered as a plasma-facing material for the International Thermonuclear Experimental Reactor (ITER).1 Therefore, understanding its release and its transport is a crucial aspect of the project. The beryllium wall will be exposed to plasma heat radiation and particle bombardment at the edge of the reactor inducing chemical erosion.2,3 Consequently, the beryllium atoms will enter the plasma and can form, by reaction with the fuel atoms (H, D, and T), molecular species like BeH, BeD, and BeT, and their ions in the fusion device.2 Other molecular species will also be formed as beryllium interacts with impurities. The interaction of the edge and divertor hydrogen plasma with the beryllium walls results in the formation and release of beryllium hydrides. The lower temperatures in the edge and divertor plasma (∼0.5–100 eV) facilitate a large spectrum of collision processes and reactions between these species and the main plasma constituents of these regions.While the collision processes at incident electron energy below the ionic dissociation threshold – i.e. 2.7 eV – have been the subject of several previous studies,4–8 the extension of the collisional processes to higher energies is the main motivation of the present study. This is essential for the kinetic modeling of beryllium transport in the plasma and the determination of influxes of beryllium hydrides into the plasma.9
Moreover, BeH and its cation have been identified in stars including the Sun, in sunspots,10 and in several comets.11,12 Therefore, the accurate quantification of the relevant elementary processes involving these molecular species is of great importance for determining with the highest precision the physical and chemical conditions of these astrophysical media.
One of the most important reactive processes that can significantly change the character of the plasma is dissociative recombination (DR):
| BeH+ + e− → Be + H | (1) |
| BeH+(vi) + e− → BeH+(vf) + e− | (2) |
| BeH+ + e− → Be+ + H + e−. | (3) |
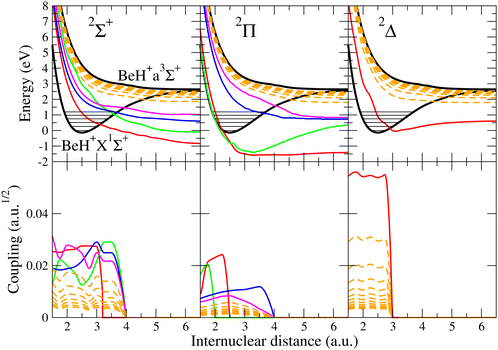
In our previous low-energy studies,4,5,7,8 we used the molecular structure data calculated by Brinne-Roos et al.13 – black, red, green, blue, and magenta curves presented in Fig. 1 – while the nuclear dynamics calculations were carried out in the framework of the stepwise multichannel quantum defect theory (MQDT).14–16 The incident electron energy range was chosen from 0.01 meV to 2.7 eV, just below the ionic dissociation threshold. In the present paper, we extend our earlier studies to higher collision energies, from 2.7 up to 12 eV. This requires the inclusion in the calculation of an increased number of dissociative states, and the consideration of the DE process, a major competitor to the DR and VT processes. Cross sections and rate coefficients for initial vibrational quantum numbers vi = 0–2 are provided for each elementary process.
Reactions (1)–(3) have been previously studied at high energy by some of us, using the complex potential method (CPM).6 Appropriate for the modelling of collisions between electrons and neutral molecules resulting in dissociative attachment, this method allowed an estimation of the cross sections for the case of positively charged targets, which had to be completed by a more detailed analysis, taking into account more mechanisms related to the involvement of Rydberg series of dissociative states, to the vibronic interactions and to multiple vibrational continua of the ion. All these mechanisms, important at high energy, are taken into account in the present work, using the MQDT. Moreover, the molecular structure data9,17 used as input for the dynamical calculations in this first attempt6 are different from those employed previously for low-energy calculations4,13 and subsequently,5,7,8 in the series of detailed MQDT studies on BeH+, BeD+ and BeT+, which are used in the present study too. More details and explanations are given later in the paper, where a critical comparison between the results coming from the two different studies is performed. All these facts make this work a different, novel approach of the DR, VT and DE of the beryllium hydride cations at high energy.
The paper is organized as follows: Section 2 is dedicated to our theoretical approach for both low- and high-energy collisions, including the building of the required molecular structure data sets. Section 3 is devoted to the results of DR, VT, and DE cross sections and rate coefficients for electron collision with the BeH+ ion at low, intermediate, and high energies/temperatures. The paper ends with conclusions.
2 Theoretical approach
The stepwise MQDT has been proved to be very suitable in many previous studies on different species, including BeH+ and its isotopologues,5,7,8 H2+ and its isotopologues,18,19 and BF+,20 for collisions with low as well as high energy of the incident electron in the case of HD+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 21 or for ArH+.22
21 or for ArH+.22
The elementary processes (1)–(3) involve ionization channels – describing the scattering of an electron by the target cation – and dissociation channels – accounting for atom–atom scattering. Below the ionic dissociative threshold, the mixing of these channels results in quantum interference of the direct mechanism – in which the capture takes place in a doubly excited dissociative state of the neutral system – and the indirect one – in which the capture occurs via a Rydberg bound state of the molecule belonging to a closed channel, this state being predissociated by a dissociative one. In both mechanisms, the autoionization – based on the existence of open ionization channels – is in competition with the predissociation and can lead to the excitation or to the de-excitation of the cation.
2.1 Molecular structure data
In order to describe the electron–molecular cation scattering, a full set of molecular data is required, which includes: (i) the potential energy curves (PECs) for the cation target BeH+ and the doubly excited dissociative states BeH** of the neutral, (ii) the electronic couplings between the dissociative states and the ionization continuum (e− + BeH+), and (iii) the quantum defects μ characterizing the mono-excited BeH* Rydberg states.For the neutral system, Roos et al.13 have characterized the molecular states for three different symmetries – four states for 2Σ+, four states for 2Π, and one state for 2Δ – by combining the multi-reference configuration interaction method with the complex Kohn variational method. In this way, they provided quasidiabatic PECs for the excited electronic states of BeH, including the autoionization widths.
Since the aim of the present paper is to extend the collisional calculations to high energies, we had to provide reasonably well-approximated data for further super-excited states situated above those characterizing the low energies, addressed in our previous studies. Therefore, we have used the scaling law based on the convergence of the quantum defects – with respect to the lowest excited state of the cation – with the increase of the principal quantum number of the resonant state.
For a given symmetry Λ (quantum number associated to the absolute value of the projection of the electronic orbital angular momentum on the molecular axis), labelling the principal quantum number of the most excited dissociative state computed ab initio as nΛh, and setting nΛmin = nΛh + 1, we generated the approximate PECs for the further excited dissociative (‘d’) states with principal quantum number n in the range [nΛmin, nΛmax] by applying the formula:
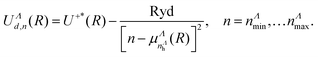 | (4) |
Here Ryd is the Rydberg constant, U+*(R) is the PEC of the lowest excited state of the ion, and UΛd,n(R) stands for the PECs of the states belonging to a Rydberg series of resonant dissociative states, characterized by the quantum defect function 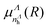 . After checking convergence, we set nΛmax = nΛmin + 11 for each symmetry and, consequently, we involve 42 resonant dissociative states in our model.
. After checking convergence, we set nΛmax = nΛmin + 11 for each symmetry and, consequently, we involve 42 resonant dissociative states in our model.
As for the resonance widths corresponding to these generated states, they are given by:
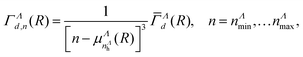 | (5) |
![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) Λd(R) is given by:
Λd(R) is given by: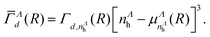 | (6) |
Once we have made the inventory of the whole set of relevant dissociative states of symmetry Λ – ab initio computed, or generated by the Rydberg scaling laws – we compute the electronic coupling between each dissociative continuum associated with the resonant state j (going from 1 to the maximum number of resonant states) and the ionization continuum, by the formula:
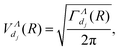 | (7) |
Fig. 1 presents all the molecular data necessary for the modeling of the quantum dynamics. On the first row, we show the potential energy curves for the 2Π, 2Σ+, and 2Δ electronic symmetries. The black curves are the PECs of the ground states (X1Σ+) and the lowest repulsive excited state (a3Σ+) of BeH+. The red, green, blue, and magenta colored curves are the PECs for the lowest resonant curves of BeH obtained by ab initio quantum chemistry calculations.13 Finally, the dashed orange curves are the new dissociative curves of BeH produced by the scaling law. On the second row, we present the couplings between the dissociative states of BeH and the ionization continuum for the 2Π, 2Σ+, and 2Δ symmetries. Following the same color code as that of the PECs we can distinguish the couplings 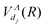 , either those obtained by ab initio methods or those produced by the scaling law. All dissociative states and couplings plotted in Fig. 1 have been included in the calculations.
, either those obtained by ab initio methods or those produced by the scaling law. All dissociative states and couplings plotted in Fig. 1 have been included in the calculations.
2.2 The MQDT method for low-energy collisions
The low energy region of the electron–molecular cation collisions was explored in our previous papers.4,5,7,8 There, we restricted ourselves to incident electron energies below the ionic dissociation threshold, and we considered the interference of the direct and indirect mechanisms. Here below are the major steps of the modeling of the collision dynamics.For each relevant symmetry Λ, we start by building the interaction matrix ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) Λ, whose non-vanishing matrix elements consist of the vibrationally integrated couplings:
Λ, whose non-vanishing matrix elements consist of the vibrationally integrated couplings:
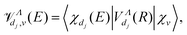 | (8) |
In the next stage, we solve the Lippmann–Schwinger matrix equation:
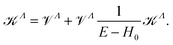 | (9) |
![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Λ by
Λ by ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) Λ in the right-hand side of the preceding equation, H0 being the zero-order Hamiltonian.
Λ in the right-hand side of the preceding equation, H0 being the zero-order Hamiltonian.
We then build the eigenchannels, using the diagonalized version of the reaction matrix ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Λ, and we perform eventually a frame transformation15 from the internal/reaction zone to the external/asymptotic region:
Λ, and we perform eventually a frame transformation15 from the internal/reaction zone to the external/asymptotic region:
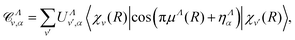 | (10) |
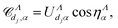 | (11) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) matrix elements obtained by replacing cosine with sine in eqn (10) and (11). Here α designates the eigenchannels defined through the diagonalization of the
matrix elements obtained by replacing cosine with sine in eqn (10) and (11). Here α designates the eigenchannels defined through the diagonalization of the ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Λ-matrix, UΛv,α and
Λ-matrix, UΛv,α and 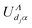 are elements of the corresponding eigenvectors, and
are elements of the corresponding eigenvectors, and 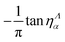 are the eigenvalues of
are the eigenvalues of ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) Λ.
Λ.
The projection matrices ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) Λ and
Λ and ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) Λ are used to build the generalized scattering matrix XΛ relying on both energetically open (o) and closed (c) channels:
Λ are used to build the generalized scattering matrix XΛ relying on both energetically open (o) and closed (c) channels:
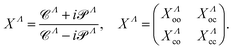 | (12) |
Applying Seaton's method on the elimination of the closed channels23 we finally obtain the scattering matrix:
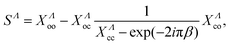 | (13) |
Once the scattering matrix is known, the DR and VT cross sections for a particular angular momentum quantum number Λ are given by:
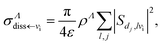 | (14) |
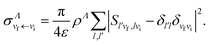 | (15) |
Summing over all possible molecular symmetries, the global DR and VT cross sections are obtained:
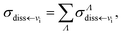 | (16) |
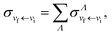 | (17) |
2.3 The MQDT method for high-energy collisions
At energies higher than the ionic dissociation threshold, we have to take into account the autoionization resulting into states from the continuum part of the vibrational spectrum of the cation ground state – which we will call from now on ‘core 1’ – leading to dissociative excitation (DE), eqn (3). When this process is included in our approach, the couplings between a given dissociation channel dj and an ionization channel v (eqn (8)) is extended to the continuum part of the vibrational spectrum. This is achieved by discretizing the continuum by using the Fourier-grid method,24 which relies on the grid-points that span the range of the internuclear distance relevant for the present work. The grid method gives at the same time, in one calculation, the full vibrational ladder. In order to achieve the convergence of the cross section for the high-energy region, we allowed for 180 quasi-continuum vibrational levels in the continuum.This procedure has been applied for the ground electronic state of BeH+ – the so-called ‘core 1’ – but also for the lowest excited electronic state, ‘core 2’, of 3Σ+ symmetry, having a repulsive PEC with the same dissociation limit as core 1, cf.Fig. 1. Every ionization channel v built on core 1, effective below or above the dissociation threshold, is coupled to further ionization channels built on core 2, labeled by w, situated entirely in the continuum:
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) Λwv = 〈χΛw|ṼΛ(R)|χΛv〉. Λwv = 〈χΛw|ṼΛ(R)|χΛv〉. | (18) |
Taking all the above into account, the extended ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) -matrix has the following form (the index Λ being omitted):
-matrix has the following form (the index Λ being omitted):
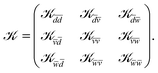 | (19) |
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ,
, ![[v with combining macron]](https://www.rsc.org/images/entities/i_char_0076_0304.gif) , and
, and ![[w with combining macron]](https://www.rsc.org/images/entities/i_char_0077_0304.gif) in eqn (19) span the ensembles of all available dissociation and ionization channels, with the latter ones built on cores 1 and 2, respectively. The first two rows and columns of the K-matrix are responsible for the DR at low energy, while the third row and the third column complete the
in eqn (19) span the ensembles of all available dissociation and ionization channels, with the latter ones built on cores 1 and 2, respectively. The first two rows and columns of the K-matrix are responsible for the DR at low energy, while the third row and the third column complete the ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) -matrix for the correct description of the DR at high energy, including the DE.
-matrix for the correct description of the DR at high energy, including the DE.
Similarly to the low-energy case, the Lippmann–Schwinger equation for the ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) -matrix can be solved exactly in second order assuming the interactions
-matrix can be solved exactly in second order assuming the interactions 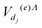 and Ṽ(e)Λ(R) to be independent on the energy of the incident electron. For a given Λ symmetry and for all v and w bound and continuum vibrational levels, all the interaction matrix elements except those given by eqn (8) and (18), i.e.
and Ṽ(e)Λ(R) to be independent on the energy of the incident electron. For a given Λ symmetry and for all v and w bound and continuum vibrational levels, all the interaction matrix elements except those given by eqn (8) and (18), i.e.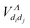 ,
, 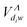 ,
, 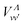 and
and 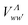 , vanish, since in the quasidiabatic representation chosen here, they concern pairs of channels associated with the same ionic core.25 Taking into account the non-vanishing matrix elements related to the available dissociation and ionization channels, the second order
, vanish, since in the quasidiabatic representation chosen here, they concern pairs of channels associated with the same ionic core.25 Taking into account the non-vanishing matrix elements related to the available dissociation and ionization channels, the second order ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) -matrix reads:16,21
-matrix reads:16,21
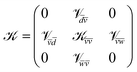 | (20) |
The inclusion of dissociative excitation induced by vibronic continuum levels of the two cores increases not only the dimensions of the interaction matrix ![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) (eqn (18) and the reaction
(eqn (18) and the reaction ![[scr K, script letter K]](https://www.rsc.org/images/entities/char_e148.gif) -matrix (19)), but also those of the frame transformation
-matrix (19)), but also those of the frame transformation ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) and
and ![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) matrices. Once we have the above-mentioned matrices, the scattering matrix is calculated following the steps presented in the previous subsection, according to eqn (12) and (13), respectively. The DE1 and DE2 processes are eventually treated as vibrational excitations from an initial vibrational state vi, to the discretized ionization continua of the two cores: the cross sections for these processes for each molecular symmetry are given by:
matrices. Once we have the above-mentioned matrices, the scattering matrix is calculated following the steps presented in the previous subsection, according to eqn (12) and (13), respectively. The DE1 and DE2 processes are eventually treated as vibrational excitations from an initial vibrational state vi, to the discretized ionization continua of the two cores: the cross sections for these processes for each molecular symmetry are given by:
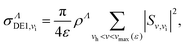 | (21) |
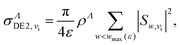 | (22) |
The total DE cross section is obtained by the sum of DE1 and DE2 for each symmetry, further summed up over all relevant molecular symmetries:
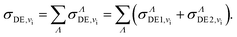 | (23) |
Finally, the cross sections for the DR and VT processes are those given in eqn (14)–(17), since they do not change with the inclusion of the discretised vibrational continua, in spite of the fact that the vibrational continua and the generated high-lying dissociative states are included in the structure of the scattering matrix.
3 Results and discussions
Applying the stepwise MQDT method outlined in the previous section we have calculated the dissociative recombination (eqn (1)), vibrational transition (excitation and de-excitation) (eqn (2)) and dissociative excitation (eqn (3)) cross sections of BeH+ for its lowest three (vi = 0–2) vibrational levels of its ground electronic state. The electron impact collision energies range between 0.01 meV and 12 eV, with a step of 0.02 meV for energies below the ionic dissociation limit and with a step of 1 meV for energies above the limit. These cross sections are then used to obtain thermal rate coefficients for electron temperatures ranging between 10 and 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. The calculated DR, DE, VE and VdE cross sections are given in Fig. 2–6, while the evaluated rate coefficients are given in Fig. 7–9.
000 K. The calculated DR, DE, VE and VdE cross sections are given in Fig. 2–6, while the evaluated rate coefficients are given in Fig. 7–9.
 | ||
| Fig. 3 Direct DR cross sections of BeH+ in its ground vibrational state: contribution of each symmetry. | ||
 | ||
| Fig. 4 Direct DR (continuous lines) and DE (dashed lines) cross sections of BeH+ in its electronic ground state for initial vibrational levels vi = 0–2. | ||
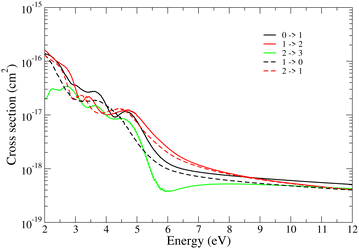 | ||
| Fig. 5 VE (continuous lines) and VdE (dashed lines) cross sections for BeH+ (vi = 0–2) for Δv = vf − vi = ±1 transitions. | ||
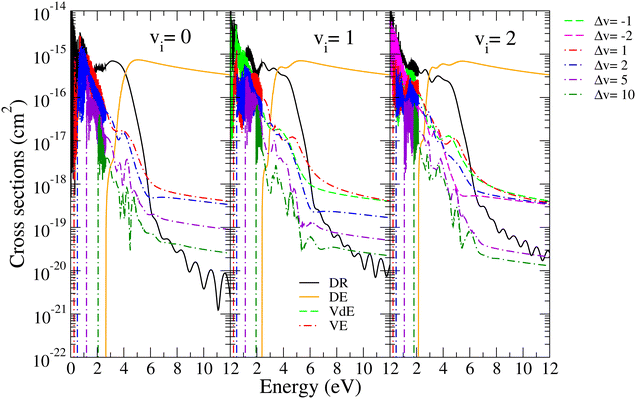 | ||
| Fig. 6 DR, DE, VdE, and VE cross sections for BeH+ in its ground electronic states for the lowest three vibrational levels of the target (vi = 0–2). Δv = vf − vi. | ||
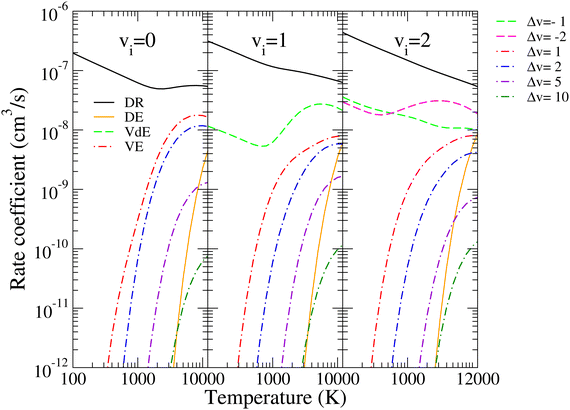 | ||
| Fig. 7 DR, DE, VdE, and VE rate coefficients of BeH+ in its ground electronic states for the lowest three vibrational levels of the target (vi = 0–2). Δv = vf − vi. | ||
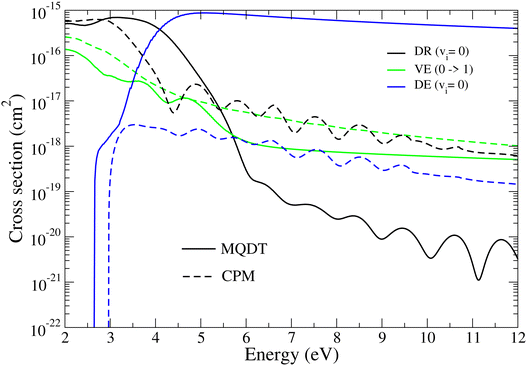 | ||
| Fig. 8 DR (black lines), VE (green lines), and DE (blue lines) cross sections for BeH+ (vi = 0) in its ground electronic states for the vibrational level vi = 0. The results are compared with those obtained by Laporta et al.6 (dashed lines). | ||
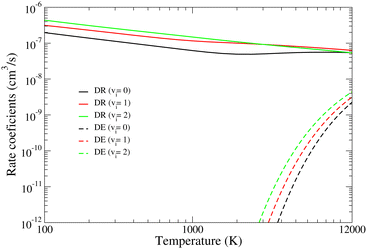 | ||
| Fig. 9 DR (continuous lines) and DE (dashed lines) rate coefficients of BeH+ for vi = 0–2. calculated using eqn (24) from the cross sections shown in Fig. 4. | ||
3.1 Cross sections
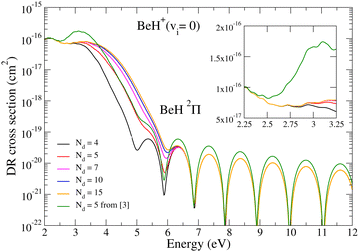
At energies below the dissociation threshold of the target, the cross sections for dissociative recombination and related processes are as a result of the quantum interference of the direct and indirect mechanisms. The direct mechanism is responsible for the smooth, bulk part of the cross section, while the indirect mechanism is responsible for the infinite number of resonances in the cross section. This behavior can be most easily understood according to eqn (13), where the first term is provided by the direct mechanism, while the second term containing closed ionisation channels is the indirect one. Moreover, the direct term is directly connected to the Franck–Condon overlap between the vibrational wave function of the dissociative state, the wave function of the target, and the vibronic interaction among the dissociation and ionization channels, according to eqn (8). The indirect mechanism loses its importance for higher collision energies due to the lack of bound vibrational levels of the mono-excited Rydberg states. Thus one can conclude that for collision energies higher than the ionic dissociation threshold, the total DR cross section reduces to the direct cross section only. This is visible for example in Fig. 6, where the Rydberg resonances disappear from the cross section as soon as we achieve the ionic dissociation threshold. In what follows we will discuss the dependence of our results on the number of dissociation states or different molecular symmetries included in the calculation for collisional energies ranging from 2 eV up to 12 eV.The convergence of the DR cross sections obtained for the vibrationally relaxed BeH+ target with the number of generated dissociative states is presented in Fig. 2. DR cross sections – direct mechanism only calculated for the most relevant 2Π molecular symmetry – are given as a function of the collision energy – ranging from 2 eV up to 12 eV – in a log-linear scale, for different numbers of dissociative states. The black curve stands for the DR cross section obtained with the original ab initio molecular states of Brinne-Roos et al.13 (Nd = 4). In contrast, the red, magenta, blue, and orange curves stand for the present cases having Nd = 5, 7, 10 and 15 generated dissociative states. These results are compared with the cross sections obtained in a previous study,4 where a global fifth dissociative state was generated starting from the ab initio states, labeled as Nd = 5 and shown in dark green in Fig. 2.
We obtained very good agreement with the previous low-energy cross sections up to 2.3 eV collision energies according to the inset of Fig. 2. In contrast, starting from the ionic dissociation threshold we find differences up to a factor of two. The explanation for this lies in the two different ways of generating the Nd = 5 and higher dissociative states. The shape of the cross sections is due to the Franck–Condon overlap among the dissociation, and target vibrational wave functions and vibronic interactions. The fall of the cross sections around 4 eV is due to the small vibronic interaction (see eqn (8)), while the dissociative wave function is responsible for the oscillations above 6 eV.
We have performed a convergence study by continuously increasing the number of generated dissociative states, by imposing an overall change in the DR cross section of less than 5%. This criterion led us to 11 generated states for each of the molecular symmetries (2Σ+, 2Π, and 2Δ) relevant in the present calculations.
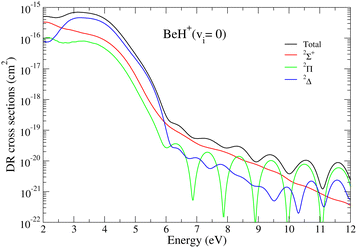
In Fig. 3 we present the direct DR cross sections of BeH+ in its ground vibrational level, illustrating the contribution of each molecular symmetry 2Σ+, 2Π, and 2Δ represented by solid red, green and blue curves, to the global – black curve in the same figure – cross section obtained as the sum over the three symmetries. Due to the more favorable crossing of the dissociative states with the ground state of the target, for collision energies below the ionic dissociation threshold, the 2Σ+ symmetry gives the largest contribution to the global DR cross section, followed by the 2Π and 2Δ symmetries. Between the ionic dissociation limit and 6 eV, the leading symmetry becomes the 2Δ. For still higher energies, the leading symmetry is either the 2Π or the 2Σ+ one.
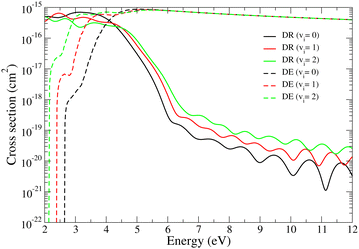
For energies above the ionic dissociation threshold, the vibrational continuum is discretized, allowing the consideration of the dissociative excitation (eqn (3)). Fig. 4 shows the total DR (black, red, and green continuous curves) and DE (dashed curves) cross sections obtained for the three lowest (vi = 0–2) vibrational levels of the target. One can notice that the behavior of the two dissociative processes is completely different. While the DR cross section following a plateau starts to decrease for collision energies approximately 1 eV above the ionic threshold and vanishes essentially above 6 eV, the DE cross section shows a strong threshold effect at the ionic dissociation energy and starts to increase, arriving at the magnitude of DR around 4 eV. Up to this energy point the total dissociation flux coming from the reaction zone is shared between the DR and DE processes, while starting from 6 eV that almost totally goes into DE. Moreover, starting from this energy, the DE cross sections show a smoothly decreasing behaviour.
Besides the dissociation channels given in eqn (1) and (3) we have studied their competitive vibrational transitions too (eqn (2)). Fig. 5 displays the Δv = ±1 vibrational transitions (excitations and de-excitations) cross sections from the lowest three vibrational levels of BeH+ for collision energies ranging from 2 eV to 12 eV. The black, red and green continuous curves stand for the 0 → 1, 1 → 2 and 2 → 3 vibrational excitations, and the dashed curves represent the 1 → 0 and 2 → 1 vibrational de-excitations, respectively. The cross sections show slight oscillations due to the Franck–Condon overlaps among the bound vibrational wave functions of the target, and tend towards zero at higher energy.
In Fig. 6, we illustrate the relative importance of all these processes for the lowest three initial vibrational levels of the target by representing their cross sections for collision energies ranging between 0.01 meV and 12 eV. The excitation and de-excitation cross sections have been calculated for all possible final states, in the figure we present only a few cases belonging to Δv = 1, 2, 5 and 10 excitations (dashed-dotted red, blue, violet, and dark green curves) and Δv = −1 and −2 de-excitations (dashed light green and magenta curves). One can see that for low collision energies, below the ionic dissociation threshold, the DR (black curves), VE and VdE cross sections are characterised by rich resonant structures due to the temporary capture into Rydberg states, but as we already discussed in our previous studies,4,5 overall they have a weak contribution to the total cross section. The oscillations in the VT cross sections observed at collision energies above the ionic dissociation threshold are due to the Franck–Condon overlap among bound vibrational wave functions. Similar to DE (orange curves), the vibrational excitation processes show strong thresholds at their respective excitation energies. The DR cross section shows a strong dependence on the initial vibrational level of the cation, due to the difference in vibrational wave functions of the initial state and due to the more favorable crossings of the dissociative state for 2Δ symmetry with the higher lying vibrational levels of the cation. In the low collision energy range, the DR is in competition with the VT processes, while at energies between the ionic dissociation threshold and around 4 eV, the two dissociation processes, DR and DE, compete, DR being dominant. DE is becoming more and more important and above 4 eV will take over the lead. Beyond 5 eV, DR and VT are strongly dominated by the DE, VT taking over the DR above 6 eV.
Finally, in Fig. 8, we compare our present results with those obtained previously6 for BeH+ on its ground level vi = 0. At low energies, between 0.5 eV and 3 eV, they display similar shapes and relatively close values, but they progressively disagree above 3 eV.
One of the reasons for disagreement, but certainly not the most important, is – as stated in the introduction – the use of different molecular structure data in the modeling of the fragmentation dynamics. Indeed, the PECs and couplings produced by R-matrix calculations9,17 used by Laporta et al.6 are different – although roughly in the same range – from those used in all our other studies, including this one, coming from quantum chemistry completed by the complex Kohn method.13 It is quite difficult to decide on the superiority of one of the approaches used to produce these input molecular data with respect to the other, especially in the absence of experimental results for the rate-coefficients, which could serve as an a posteriori criterion of choice.
More specifically, in ref. 9 and 17, CI calculations were performed using a reference space consisting of 1σ–6σ, 1π, and 2π orbitals, whereas a slightly smaller reference space consisting of 1σ–5σ and 1π orbitals has been employed in ref. 13, while using the more accurate MRCI technique.
Twelve resonant dissociative states have been obtained in ref. 9 and 17, initially in the adiabatic representation, and eleven ones in ref. 13, but in a quasidiabatic representation in this latter study, more appropriate, since ready to be used in an MQDT modeling of the dynamics.
While the number of the resonant dissociative states is roughly the same, the most physically relevant difference is that none of the dissociative states calculated in ref. 9 and 17 – unlike those produced in ref. 13 – are energetically open for dissociation at very low collision energies, below 0.5 eV. This leads to vanishing DR cross sections, which is in contradiction with the general trend observed for the lighter hydrogen-containing species – H2, HeH and LiH.
Moreover, in the present work, we completed substantially the input set relying on the data from ref. 13 by involving in the high-energy region the Rydberg series of dissociative states modeled by the scaling laws, as shown in Section 2.1.
On the other hand, the major differences between the two ensembles of results come from the methods used in exploring the quantum dynamics, intimately related to the mechanisms, taken into account or neglected. Here below we provide the most specific relevant details:
As shown in Section 2.3, eqn (21) and (22), DE competes with DR via two mechanisms, DE1 and DE2, relying on the two relevant vibrational continua, that of the ground and the lowest excited electronic state, respectively. We have shown previously21 that DE2 strongly dominates DE1 at high energy, and the account of this mechanism in the present approach explains the huge values of the DE with respect to that computed in the previous one, above 3 eV. This difference is coherent with that, in the converse sense, between the DR cross sections, manifesting itself above 5 eV, DR competing with DE.
As for the vibrational excitation, it displays significantly less differences, since they are related much more strongly than DR and DE to the discrete part of the vibrational structure of the electronic ground state – via the final level vf – almost identically involved in the two approaches.
Last but not least, applying the CPM method in the past, we neglected, unlike presently within the MQDT one, the vibronic couplings between ionization channels – the matrix elements related to the quantum defects in eqn (10). These couplings play an important role in the magnitude of the cross sections, as we have shown in our very first work devoted to the BeH system.4
3.2 Rate coefficients
By convoluting the cross sections with the Maxwell isotropic velocity distribution function of the free electrons26 we obtain the thermal or plasma rate coefficients: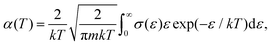 | (24) |
The rate coefficients corresponding to the cross sections presented in Fig. 6 are shown in Fig. 7, where the same color code is used. The rate coefficients are given for all (1)–(3) competitive processes having the BeH+ ion target in its lowest three vibrational levels. All DR, DE, and VdE rate coefficients, and only a few pertinent VE cases (Δv = 1, 2, 5 and 10) are shown. The electron temperature varies from 100 K to 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K.
000 K.
The thermal rate coefficients in contrast to the cross sections have smoother energy-/temperature-dependence, giving a more adequate description of the importance of each process. According to Fig. 7, the DR is the most important reactive process for the presented temperature range, followed by the vibrational de-excitations. The rates for the excitations (VE and DE processes) are reaching the magnitude of the DR/VdE rates only at higher temperatures, close to or above 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K. Their very sharp thresholds visible in the cross sections turn into monotonically increasing functions.
000 K. Their very sharp thresholds visible in the cross sections turn into monotonically increasing functions.
Moreover, Fig. 7 shows the dependence of the rate coefficients on the initial vibrational levels of the target, presented here for vi = 0–2. Depending on the vibrational quantum number of the initial and final states of the target, the rates show various temperature dependencies, from the smoothly decreasing behavior to more general functions showing at least one minimum/maximum. For DR, DE, and VdE, the magnitude of rate coefficients increases with the initial vibrational quantum numbers, while for VE one can observe the converse.
It is the very different dependence of the DR, DE, VE, and VdE processes on the initial and final channels that leads to very different energy/temperature dependence of the cross sections/rate coefficients. The most complex initial/final channel dependence can be observed for the DR and DE (see eqn (8)), while for VE/VdE we got a simpler Franck–Condon overlap according to eqn (18) between two bound vibrational levels of the target.
This can be once again seen in Fig. 9 and 10, where the DR, DE and the Δv = ±1 excitation (VE and VdE) rate coefficients of BeH+ for vi = 0–2 are plotted. By increasing the initial vibrational level of the target, we get larger rate coefficients for both dissociative processes. On the contrary, the VE and VdE rate coefficients are not showing this tendency since the cross section depends more strongly on the initial vibrational level of the target.
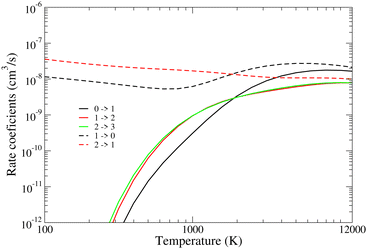 | ||
| Fig. 10 VE (continuous lines) and VdE (dashed lines) cross sections of BeH+ (vi = 0–2) calculated using eqn (24) from the cross sections shown in Fig. 5. | ||
4 Conclusions
The present paper extends our previous studies4,5,7,8 of the BeH+ and its isotopologues on the reactive collisions with electrons by considering higher collision energies facilitating the study of the dissociative excitation, occurring above the dissociation threshold of the molecular ion target. Starting from the original molecular data sets,4 and using simple scaling laws we have enlarged our set of molecular states participating in the fragmentation dynamics, resulting in a more realistic description of the dissociation and excitation of the molecular target. We produced cross sections and rate coefficients for DR, DE, VE, and VdE processes up to 12 eV collision energy, useful for the detailed kinetics modeling of the cold plasma close to the wall of the fusion devices.Data availability
The data underlying this article will be shared on reasonable request to the corresponding author.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the support from Fédération de Recherche Fusion par Confinement Magnétique (CNRS and CEA), La Région Normandie, FEDER, and LabEx EMC3 via the projects PTOLEMEE, the Normand Graduate School Materials and Energy Sciences (GS-MES), Bioengine COMUE Normandie Université, the Institute for Energy, Propulsion and Environment (FR-IEPE), from the Agence Universitaire de la Francophonie en Europe Centrale et Orientale (AUF ECO) via the project CE/MB/045/2021 “CiCaM – ITER”, International Atomic Energy Agency (IAEA) via de project CRP: “The Formation and Properties of Molecules in Edge Plasmas” and the European Union via COST (European Cooperation in Science and Technology) actions: TUMIEE (CA17126), MW-Gaia (CA18104), MD-GAS (CA18212), PROBONO (CA21128), PhoBioS (CA21159), COSY (CA21101), AttoChem (CA18222), PLANETS (CA22133) and DYNALIFE (CA21169). The authors are indebted to Agence Nationale de la Recherche (ANR) via the project MONA. This work was supported by the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES. J. Zs. M. acknowledges the financial support of the National Research, Development and Innovation Fund of Hungary, under the FK 19 funding scheme with project no. FK 132989. KC thanks SERB, India, for the financial support under grant no. CRG/2021/000357. V. L. thanks the European Union under NextGenerationEU via the project PLASMODD, PRIN 2022 Prot. n. 2022J5NBBN, and the “Consorzio RFX” via the Project n. DFM.AD007.018 NBTF-RFX-BFA-AWP2021_2023. M. A acknowledges the financial support of the Programme National PCMI, European project DigiQ and ANR QuanTEdu-France.Notes and references
- A. W. Kleyn, N. J. Lopes Cardozoa and U. Samm, Phys. Chem. Chem. Phys., 2006, 8, 1761–1774 RSC
.
- R. Celiberto, R. K. Janev and D. Reiter, Plasma Phys. Controlled Fusion, 2012, 54, 035012 CrossRef
.
- J. Paméla, G. F. Matthews, V. Philipps, R. Kamendje and JET-EFDA Contributors, J. Nucl. Mater., 2007, 1, 363–365 Search PubMed
.
- S. Niyonzima, F. Lique, K. Chakrabarti, Å. Larson, A. E. Orel and I. F. Schneider, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 87, 022713 CrossRef
.
- S. Niyonzima,
et al.
, At. Data Nucl. Data Tables, 2017, 115–116, 287–308 CrossRef CAS
.
- V. Laporta, K. Chakrabarti, R. Celiberto, R. K. Janev, J. Zs Mezei, S. Niyonzima, J. Tennyson and I. F. Schneider, Plasma Phys. Controlled Fusion, 2017, 59(4), 045008 CrossRef
.
- S. Niyonzima,
et al.
, Plasma Sources Sci. Technol., 2018, 27(2), 025015 CrossRef
.
- N. Pop, F. Iacob, S. Niyonzima, A. Abdoulanziz, V. Laporta, D. Reiter, I. F. Schneider and J. Zs Mezei, At. Data Nucl. Data Tables, 2021, 139, 101414 CrossRef CAS
.
- K. Chakrabarti and J. Tennyson, Eur. Phys. J. D, 2012, 66, 31 CrossRef
.
- V. P. Gaur, M. C. Pande and B. M. Tripathi, Bull. Astron. Inst. Czech., 1973, 24(2), 129 Search PubMed
.
- A. J. Sauval and J. B. Tatum, Astrophys. J., Suppl. Ser., 1984, 56, 193 CrossRef CAS
.
- R. Shanmugavel, S. P. Bagare and N. Rajamanickam, Serb. Astron. J., 2006, 173, 83–87 CrossRef CAS
.
- J. B. Roos, M. Larsson, Å. Larson and A. E. Orel, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 80, 012501 CrossRef
.
- A. Giusti, J. Phys. B: At. Mol. Phys., 1980, 13, 3867 CrossRef CAS
.
- I. F. Schneider, I. Rabadán, L. Carata, L. H. Andersen, A. Suzor-Weiner and J. Tennyson, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, 4849 CrossRef CAS
.
- J. Zs Mezei, K. Chakrabarti, M. D. Epée Epée, O. Motapon, C. H. Yuen, A. M. Ayouz, N. Douguet, S. F. dos Santos, V. Kokoouline and I. F. Schneider, ACS Earth Space Chem., 2019, 3, 2376 CrossRef
.
- K. Chakrabarti and J. Tennyson, J. Phys. B: At., Mol. Opt. Phys., 2015, 48(23), 235202 CrossRef
.
- M. D. Epée Epée, J. Zs Mezei, O. Motapon, N. Pop and I. F. Schneider, Mon. Not. R. Astron. Soc., 2016, 455, 276 CrossRef
.
- M. D. Epée Epée, O. Motapon, N. Pop, F. Iacob, E. Roueff, I. F. Schneider and J. Zs Mezei, Mon. Not. R. Astron. Soc., 2022, 512, 424 CrossRef
.
- J. Zs Mezei, F. Colboc, N. Pop, S. Ilie, K. Chakrabarti, S. Niyonzima, M. Lepers, A. Bultel, O. Dulieu, O. Motapon, J. Tennyson, K. Hassouni and I. F. Schneider, Plasma Sources Sci. Technol., 2016, 25(5), 055022 CrossRef
.
- K. Chakrabarti, D. Backodissa-Kiminou, N. Pop, Z. S. Mezei, O. Motapon, F. Lique, O. Dulieu, A. Wolf and I. F. Schneider, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 87, 022702 CrossRef
.
- E. Djuissi, A. Bultel, J. Tennyson, I. F. Schneider and V. Laporta, Plasma Sources Sci. Technol., 2022, 31, 114012 CrossRef CAS
.
- M. J. Seaton, Rep. Prog. Phys., 1983, 46, 16 CrossRef
.
-
G. Teschl, Graduate Studies in Mathematics, American Mathematical Society, Providence, RI, 2014, vol. 157 Search PubMed
.
- V. Sidis and H. Lefebvre-Brion, J. Phys. B: At. Mol. Phys., 1971, 8(4), 1040 CrossRef
.
- K. C. Mathur, A. N. Tripathi and S. K. Joshi, Astrophys. J., 1971, 165, 425 CrossRef CAS
.
| This journal is © the Owner Societies 2024 |