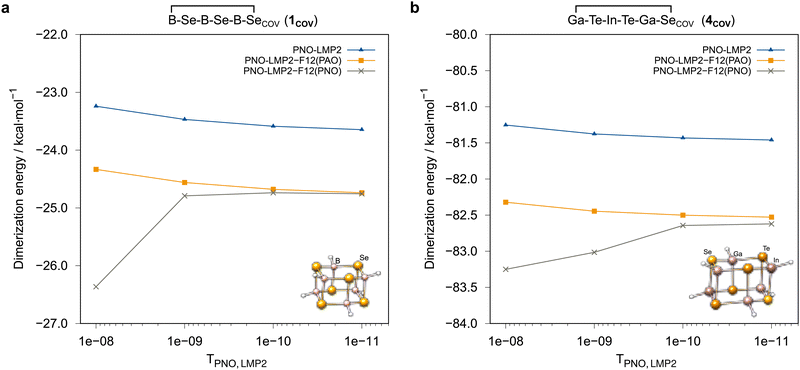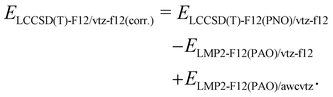Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The p-block challenge: assessing quantum chemistry methods for inorganic heterocycle dimerizations†
Thomas
Gasevic‡
 c,
Markus
Bursch‡
c,
Markus
Bursch‡
 *ad,
Qianli
Ma
*ad,
Qianli
Ma
 b,
Stefan
Grimme
b,
Stefan
Grimme
 c,
Hans-Joachim
Werner‡
c,
Hans-Joachim
Werner‡
 *b and
Andreas
Hansen‡
*b and
Andreas
Hansen‡
 *c
*c
aMax-Planck-Institut für Kohlenforschung, Kaiser-Wilhelm-Platz 1, 45470 Mülheim an der Ruhr, Germany. E-mail: bursch@kofo.mpg.de
bInstitut für Theoretische Chemie, Universität Stuttgart, Pfaffenwaldring 55, D-70569 Stuttgart, Germany. E-mail: werner@theochem.uni-stuttgart.de
cMulliken Center for Theoretical Chemistry, Rheinische Friedrich-Wilhelms-Universität Bonn, Beringstr. 4, 53115 Bonn, Germany. E-mail: hansen@thch.uni-bonn.de
dFACCTs GmbH, 50677, Koeln, Germany
First published on 17th April 2024
Abstract
The elements of the p-block of the periodic table are of high interest in various chemical and technical applications like frustrated Lewis-pairs (FLP) or opto-electronics. However, high-quality benchmark data to assess approximate density functional theory (DFT) for their theoretical description are sparse. In this work, we present a benchmark set of 604 dimerization energies of 302 “inorganic benzenes” composed of all non-carbon p-block elements of main groups III to VI up to polonium. This so-called IHD302 test set comprises two classes of structures formed by covalent bonding and by weaker donor–acceptor (WDA) interactions, respectively. Generating reliable reference data with ab initio methods is challenging due to large electron correlation contributions, core–valence correlation effects, and especially the slow basis set convergence. To compute reference values for these dimerization reactions, after thorough testing, we applied a computational protocol using state-of-the-art explicitly correlated local coupled cluster theory termed PNO-LCCSD(T)-F12/cc-VTZ-PP-F12(corr.). It includes a basis set correction at the PNO-LMP2-F12/aug-cc-pwCVTZ level. Based on these reference data, we assess 26 DFT methods in combination with three different dispersion corrections and the def2-QZVPP basis set, five composite DFT approaches, and five semi-empirical quantum mechanical methods. For the covalent dimerizations, the r2SCAN-D4 meta-GGA, the r2SCAN0-D4 and ωB97M-V hybrids, and the revDSD-PBEP86-D4 double-hybrid functional are found to be the best-performing methods among the evaluated functionals of the respective class. However, since def2 basis sets for the 4th period are not associated to relativistic pseudo-potentials, we obtained significant errors in the covalent dimerization energies (up to 6 kcal mol−1) for molecules containing p-block elements of the 4th period. Significant improvements were achieved for systems containing 4th row elements by using ECP10MDF pseudopotentials along with re-contracted aug-cc-pVQZ-PP-KS basis sets introduced in this work with the contraction coefficients taken from atomic DFT (PBE0) calculations. Overall, the IHD302 set represents a challenge to contemporary quantum chemical methods. This is due to a large number of spatially close p-element bonds which are underrepresented in other benchmark sets, and the partial covalent bonding character for the WDA interactions. The IHD302 set may be helpful to develop more robust and transferable approximate quantum chemical methods in the future.
1 Introduction
In the last decades, cutting-edge chemical synthesis involving inorganic main group compounds covering large parts of the periodic table experienced a renaissance.1 Compared to their organic counterparts, inorganic elements bring various challenges such as a plethora of possible bonding motifs and often more difficult electronic structures.2 A very prominent example of important and actively researched p-block chemistry is that of (frustrated) Lewis pairs (FLPs).3,4 Moreover, rings and clusters of p-block elements are of high interest in opto-electronics5–8 and as promising precursor materials for film composition.9–11 p-Block elements are further discussed to be incorporated into polymers for property optimization.12 In most of such compounds, the direct covalent bonds or the donor- and acceptor interactions of the p-elements are of key importance for their chemical properties and reactivity. Nevertheless, systems with heavier p-block elements are typically underrepresented in comprehensive thermochemistry databases like GMTKN5513 or LP14,14 even though more recent benchmark sets such as CHAL33615 or the supramolecular HS13L16 extend the evaluated chemical space in this respect. However, large organic substituents are often used in such sets to saturate the p-block elements, thus somewhat limiting the explicit insight into the respective interactions of the donor–acceptor pairs.Chemically diverse benchmark sets are extremely important for evaluation and cross-checking of contemporary theoretical (approximate first principle quantum mechanical or atomistic) models that have become a valuable tool for understanding a wide range of chemically diverse systems. However, suitable reference data for heavier p-elements are rare with consequences on the development and performance of these methods. For example, density functional theory (DFT) methods, the workhorse of modern quantum chemistry, are typically designed to be mostly accurate for (bio)organic chemistry with less focus on inorganic compounds. Further, most semi-empirical quantum mechanical (SQM) methods are limited in their parameterization space and accuracy regarding such elements.17–19 The problem of under-representation of chemical space becomes even more evident for the fast growing field of machine-learning (ML) techniques, which require huge amounts of carefully selected training data as well as thorough cross-validation.
To address this lack of reliable reference data for the interaction of (heavier) p-block elements, and inspired by the work of Frenking et al. on the dimerization of [BAlGaNPAs]H620 and comparable works,21,22 we compiled a new benchmark set of dimerization reactions termed IHD302, consisting of planar six-membered heterocyclic monomer structures composed purely of p-block elements from boron to polonium (excluding carbon). The so-called Inorganic Heterocycle Dimerizations 302 (IHD302) set is divided into two subsets, covalently bound and weaker donor–acceptor interacting dimers. The latter structures can be best characterized as strongly bound van der Waals complexes, i.e., non-equilibrium structures on a path to covalent bonding. This poses a particular challenge for mean-field electronic structure methods due to a strong interplay of covalent (short-range) electron correlation and London dispersion interactions, which are usually specially treated in DFT and SQM.
The generation of reliable reference data of high accuracy is indispensable, yet a challenge on its own due to the significant (core–valence) electron correlation effects in these molecules, which we discuss in detail in this work. This newly introduced benchmark set can be considered a particularly hard test for existing quantum chemical methods as well as a basis for their further development and improvement. Specifically, approximate SQM methods, such as PMx17,23,24 and GFNn-xTB19,25,26 or composite DFT schemes27 may be improved based on the data provided by the IHD302 benchmark set. In the course of this work, we assess the performance of 26 DFT functionals together with three different London dispersion corrections, five composite DFT approaches, and five SQM methods.
2 The IHD302 benchmark set
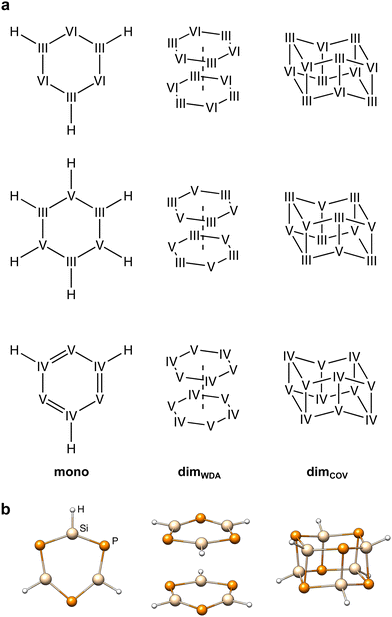
The IHD302 benchmark is composed of 302 neutral six-membered heterocycles and their respective non-covalently interacting and covalently bound dimers (cf.Fig. 1) in their singlet ground state. The monomers can be categorized into three main group element (E) combinations, [EIII3EVI3]H3, [EIII3EV3]H6, and [EIV3EV3]H3. These combinations were chosen inspired by experimentally accessible parent “inorganic benzenes”.8 Other combinations involving, e.g., V and VI would mainly result in non-planar environments and benchmark sets for non-covalent interactions of these element combinations such as the CHAL33615 by Goerigk and co-workers already exist. All main group III, IV, V, and VI elements from B (Z = 5) to Po (Z = 84) except carbon were taken into account with an average of 53 compounds per element. Carbon was excluded as a typically saturated organic element with less pronounced donor–acceptor chemistry. The element composition of the benchmark set is illustrated in Fig. 2. Some elements (e.g. lead) are less represented as the respective elements strongly tend to leave the planar monomer structure. To keep comparability throughout the benchmark set, these monomer structures were discarded. The nomenclature of the model compounds![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) A−B−C−D−E−F
A−B−C−D−E−F![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) gives the ring atoms in clockwise order, while hydrogen atoms are omitted for clarity as their positions are clearly defined according to Fig. 1 (examples:
gives the ring atoms in clockwise order, while hydrogen atoms are omitted for clarity as their positions are clearly defined according to Fig. 1 (examples: ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Ga(H)−Te−In(H)−Te−Ga(H)−Se
Ga(H)−Te−In(H)−Te−Ga(H)−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) ≙
≙ ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Ga−Te−In−Te−Ga−Se
Ga−Te−In−Te−Ga−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) ≙ [GaTeInTeGaSe]H3). Covalent and weak donor–acceptor dimers are further indicated by the subscripts “COV” and “WDA”, respectively. To maximize the interaction surface in the non-covalently interacting dimers, only planar local minima after optimization of the monomers were considered. If necessary, these rings were then saturated with three or six hydrogen atoms depending on the involved p-block elements to avoid open-shell or highly ionic systems.
≙ [GaTeInTeGaSe]H3). Covalent and weak donor–acceptor dimers are further indicated by the subscripts “COV” and “WDA”, respectively. To maximize the interaction surface in the non-covalently interacting dimers, only planar local minima after optimization of the monomers were considered. If necessary, these rings were then saturated with three or six hydrogen atoms depending on the involved p-block elements to avoid open-shell or highly ionic systems.
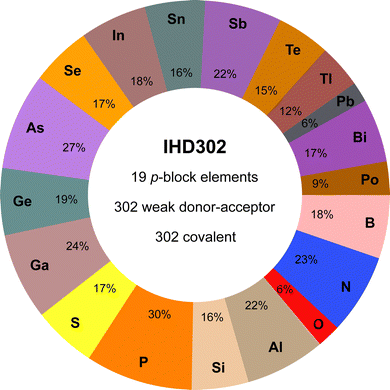 | ||
| Fig. 2 Percent contribution of elements to the systems of the IHD302 and key features of the data set (e.g., 23% of the IHD302 systems contain at least one nitrogen atom). | ||
The monomeric heterocycles consist of formal single- or double-bonded atoms, depending on their atomic properties. Especially, combinations of light p-block elements, yield partly aromatic monomers as in the borazine case (![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) B−N−B−N−B−N
B−N−B−N−B−N![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) ). These structures are also expected to yield positive dimerization energies due to the stabilization of the monomers. All other monomers are best described by combinations of single-bonds and lone-pairs, as specifically for the heavier elements, the tendency to form multiple bonds decreases quickly descending the periodic table. As the dimerization of most heterocyclic combinations involving heavier elements strongly favor covalent dimerization, weakly donor–acceptor interacting dimers were generated from the planar monomer structures without further optimization. Here, the dimers were generated by 180° rotation (simplest approach to obtain motifs that are as symmetrical as possible and therefore do not form homoatomic artificial bonds) and a displacement of the ring center by twice the van der Waals radii28,29 of the heaviest element involved. The covalent heterocyclic dimers were obtained by subsequent geometry optimization employing r2SCAN-3c30 as implemented in the ORCA program package.31,32r2SCAN-3c was previously found to produce excellent structures.30 Further, it yields very good energetic agreement with the high-level reference data as discussed in Section 4.1, supporting its suitability to reproduce the respective potential energy surface.
). These structures are also expected to yield positive dimerization energies due to the stabilization of the monomers. All other monomers are best described by combinations of single-bonds and lone-pairs, as specifically for the heavier elements, the tendency to form multiple bonds decreases quickly descending the periodic table. As the dimerization of most heterocyclic combinations involving heavier elements strongly favor covalent dimerization, weakly donor–acceptor interacting dimers were generated from the planar monomer structures without further optimization. Here, the dimers were generated by 180° rotation (simplest approach to obtain motifs that are as symmetrical as possible and therefore do not form homoatomic artificial bonds) and a displacement of the ring center by twice the van der Waals radii28,29 of the heaviest element involved. The covalent heterocyclic dimers were obtained by subsequent geometry optimization employing r2SCAN-3c30 as implemented in the ORCA program package.31,32r2SCAN-3c was previously found to produce excellent structures.30 Further, it yields very good energetic agreement with the high-level reference data as discussed in Section 4.1, supporting its suitability to reproduce the respective potential energy surface.
During optimization, most covalent dimers formed the archetypal crown-shaped dimer with six connecting bonds. Nevertheless, the three systems ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Tl−P−Tl−P−Tl−Bi
Tl−P−Tl−P−Tl−Bi![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV,
COV, ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Pb−N−Pb−N−Pb−Sb
Pb−N−Pb−N−Pb−Sb![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV, and
COV, and ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Sn−P−Pb−P−Sn−As
Sn−P−Pb−P−Sn−As![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV optimized into a minimum with only four formed connecting bonds (cf.Fig. 3). The correspondingly large number of formed bonds and close interatomic contacts results in challenging chemical situations and allows a clear focus on the p-block element interactions. Although large correlation contributions are expected in these systems, this is dynamic correlation, which can be treated correctly with single-reference methods. To exclude multi-reference cases, we looked for spin symmetry breaking for all structures of the IHD302 set following ref. 33 with unrestricted PBE0-D4, but found no hint for significant static correlation. In addition, we applied fractional occupation number weighted density (FOD)-based static correlation diagnostics34–38 for eight test systems (vide infra), which also showed no evidence for multi-reference cases (see the ESI,† for details).
COV optimized into a minimum with only four formed connecting bonds (cf.Fig. 3). The correspondingly large number of formed bonds and close interatomic contacts results in challenging chemical situations and allows a clear focus on the p-block element interactions. Although large correlation contributions are expected in these systems, this is dynamic correlation, which can be treated correctly with single-reference methods. To exclude multi-reference cases, we looked for spin symmetry breaking for all structures of the IHD302 set following ref. 33 with unrestricted PBE0-D4, but found no hint for significant static correlation. In addition, we applied fractional occupation number weighted density (FOD)-based static correlation diagnostics34–38 for eight test systems (vide infra), which also showed no evidence for multi-reference cases (see the ESI,† for details).
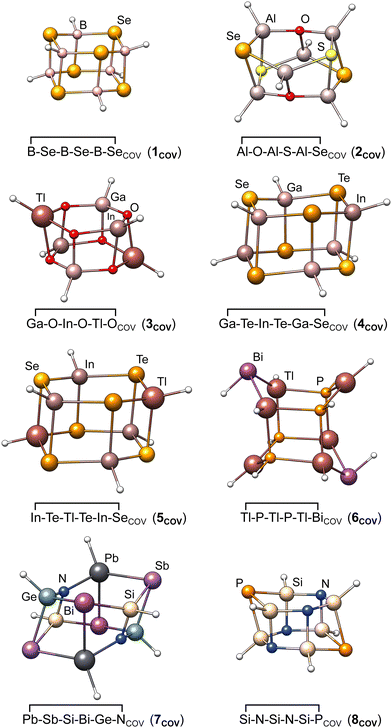 | ||
| Fig. 3 Molecular structures of the eight covalently bound heterocyclic dimers chosen as test systems for detailed method evaluation in Section 3.4. | ||
3 p-Block challenge 1: correlated wavefunction calculations
To provide reliable reference data, we used state-of-the-art explicitly correlated local coupled cluster theory, specifically PNO-LCCSD(T)-F1239–45 with special consideration of core–valence correlation. To this end, also new features were implemented (details are given in the following subsections). All correlated wavefunction theory calculations reported in this work were carried out with the Molpro package of ab initio programs (release 2023.2).46–48In principle, the wavefunction ansatz and the local approximations in the PNO-LCCSD(T)-F12 are rather similar as in the DLPNO-CCSD(T)![[F with combining macron]](https://www.rsc.org/images/entities/char_0046_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) method of the Neese group.49,50 A detailed comparison of both methods can be found in ref. 51. In particular, for F12 calculations, the PNO-LCCSD(T)-F12 program was found to be more efficient, robust, and accurate than the currently available DLPNO program, and therefore it has been used in the presented work. Alternative local correlation methods are, for example, the local natural orbital coupled cluster (LNO-CCSD(T)) methods of Nagy and Kallay,52–55 or geminal-based electronic structure methods of Tecmer and Boguslawski,56 but these methods have not been considered in the current work.
method of the Neese group.49,50 A detailed comparison of both methods can be found in ref. 51. In particular, for F12 calculations, the PNO-LCCSD(T)-F12 program was found to be more efficient, robust, and accurate than the currently available DLPNO program, and therefore it has been used in the presented work. Alternative local correlation methods are, for example, the local natural orbital coupled cluster (LNO-CCSD(T)) methods of Nagy and Kallay,52–55 or geminal-based electronic structure methods of Tecmer and Boguslawski,56 but these methods have not been considered in the current work.
3.1 Special localization schemes
Proper orbital localization is essential for reliable local correlation methods. In the following, we distinguish inner-core, outer-core, and valence molecular orbitals (MOs). The electrons in the outer-core and the valence orbitals are correlated in the post-Hartree–Fock calculations discussed in this section. In most calculations of the current work, the outer-core orbitals only comprise the (n − 1)d shells (with principle quantum number n) of p-block elements with Z ≥ 31. In some test calculations, the (n − 1)s,p orbitals were also correlated (cf. Section 3.4).Valence orbitals are localized using the intrinsic bond orbital (IBO) method.57 Core and outer core orbitals are localized using IBO(AO). This means that in the underlying Pipek–Mezey localization,58 contributions of individual intrinsic atomic orbitals (IAOs) rather than all those belonging to an atom are maximized. This minimizes mixing of nearly degenerate core orbitals (e.g., the different components of a p- or d-shell).
Before localization, the canonical orbitals are automatically resorted, so that inner-core orbitals come first, followed by the outer-core orbitals, and then the valence orbitals. This is achieved by computing the overlaps of the molecular orbitals with pure atomic core orbitals (stored in the basis set library) and ordering the orbitals such that the core part of the overlap matrix becomes closest to diagonal. This sort is necessary since the orbital energies of the outer-core orbitals are not always below those of all valence orbitals. The inner-core orbitals are then localized separately in order to avoid any mixing with correlated orbitals. In order to separate outer-core and valence orbitals as much as possible, we tested two different approaches, which are implemented in Molpro.
LOC_COREORB=SEP: in this case, outer-core and valence orbitals are localized separately, starting from the sorted canonical orbitals. The Fock matrix then has a block-diagonal structure, without couplings between the three groups. Thus, in LMP2-F12, the core–core, core–valence, and valence–valence pairs are uncoupled. This method works well if outer-core and valence orbitals are energetically well separated.
LOC_COREORB=MIX: first, outer-core and valence orbitals are localized together (using IBO localization). The intention of this step is to demix the outer-core and valence localized molecular orbitals (LMOs) as much as possible. Second, the LMOs are sorted such that the outer-core orbitals come first. Finally, the outer-core orbitals are re-localized among themselves using the IBO(AO) approach. This is necessary in order to demix (nearly) degenerate core orbitals and to obtain a unique set of LMOs.
The LOC_COREORB=MIX procedure is recommended for cases in which outer-core and valence orbitals mix significantly. This happened for some of the test systems (e.g. for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) In−Te−Tl−Te−In−Se
In−Te−Tl−Te−In−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) , vide infra). For consistency, it has been applied for all studied systems in this work. Using this approach, the partial charges of individual intrinsic atomic orbitals (IAOs) in the outer-core orbitals are very close to 2.0, i.e., they are almost perfectly separated from the valence orbitals.
, vide infra). For consistency, it has been applied for all studied systems in this work. Using this approach, the partial charges of individual intrinsic atomic orbitals (IAOs) in the outer-core orbitals are very close to 2.0, i.e., they are almost perfectly separated from the valence orbitals.
For calculations including also (n − 1)s,p correlation, we used exactly the same orbitals for the respective calculations with (n − 1)d outer-core orbitals, so that any effects originating from different orbital mixing can be excluded.
3.2 State-of-the-art explicitly correlated local MP2 and CCSD(T)
We applied the explicitly correlated pair natural orbital local second-order perturbation theory (PNO-LMP2-F12) and coupled cluster (PNO-LCCSD(T)-F12) methods as described in detail in previous work.39–45 Reviews of this method can be found in ref. 59 and 60. We employed tight domain options [DOMOPT=TIGHT] as summarized in ref. 45, 51 and 60. The PNO occupation number threshold for pairs involving outer-core orbitals is reduced by a factor of 100 (this happens by default, but was found to have a very small effect in the current calculations). Default values were used for all other options unless otherwise noted. The triples (T) amplitude equations were solved iteratively in a basis of triples natural orbitals (TNOs) as described in ref. 43.The explicitly correlated PNO-LMP2-F12 method uses F12 approximation 3*A61,62 along with the fixed amplitude approximation.63,64 This approach is simplest and most efficient but known to slightly overestimate the F12 correction compared to the formally more accurate 3C approximation,65 especially for small basis sets. However, experience has shown that approximation 3*A combined with local approximations yields very accurate results and converges to the complete basis set (CBS) limit at least as fast as approximation 3C.40,42,45 This is further corroborated by the tests carried out in the present work (cf. Section 3.4.4). For quadruple-ζ basis sets, the differences between results obtained with the two approximations usually become negligible.45,51,60 In the LCCSD-F12 part, the F12b approximation66,67 is used (shortly denoted F12 in the following), which was recently successfully applied to generate highly accurate reference isomerization and conformational energies.68
F12 methods are particularly well-suited for treating core and core–valence correlation effects in heavy main group elements,69 which are very slowly convergent with basis set size. However, since the core orbitals are spatially more compact than the valence orbitals, the optimum exponents γ of the F12 geminals F12(r12) = −1/γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−γr12) are larger than for valence orbitals. It has therefore been proposed to use pair-specific geminals with different exponents for valence–valence (vv), core–valence (cv), and core–core (cc) orbital pairs.70 This option has also been implemented into the PNO-LCCSD(T)-F12 program and is used here for the first time (cf. Section 3.4.1).
exp(−γr12) are larger than for valence orbitals. It has therefore been proposed to use pair-specific geminals with different exponents for valence–valence (vv), core–valence (cv), and core–core (cc) orbital pairs.70 This option has also been implemented into the PNO-LCCSD(T)-F12 program and is used here for the first time (cf. Section 3.4.1).
In the course of this work, we observed significant outliers of the LMP2-F12 energy contributions for some systems and basis sets. It turned out that these were due to the last term in the (F12 strong orthogonality projector)71–73
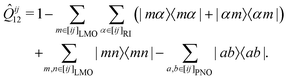 | (1) |
In the following, we will denote the methods with the PAO and PNO projectors as PNO-LMP2-F12(PAO) and PNO-LMP2-F12(PNO), respectively. The choice of the projector has hardly any effect on the LCCSD-F12 contribution beyond the additive LMP2-F12 one. Using the PAO projector in the LCCSD-F12 part is also possible in Molpro but leads to exceedingly large CPU and memory requirements. Using the PAO and PNO projectors in the PNO-LMP2-F12 and LCCSD-F12 parts, respectively, is possible with the program option PROJECTOR=MIXED.
3.3 Computational settings
In the PNO-LCCSD(T)-F12 calculations we employed the cc-pVnZ-PP-F12 (n = T or Q) basis sets of Hill and Peterson76 (cc-pVnZ-F1277 for atoms with Z ≤ 18) along with the associated OPTRI and MP2FIT auxiliary basis sets and the small-core effective core potentials (ECP10MDF, ECP28MDF, ECP60MDF)78–80 for elements with Z ≥ 31 (Ga) (simply denoted as vnz-f12 in the following). These basis sets include functions that are necessary for treating (outer) core–valence correlation effects, as well as diffuse functions as needed for non-covalent (long-range) interactions. For comparison, we also carried out a number of calculations using the larger aug-cc-pwCVnZ-PP81 (n = T, Q) basis sets (aug-cc-pVnZ for atoms with 2 ≤ Z ≤ 18 and cc-pVnZ for H). In the following, these sets are denoted shortly awcvnz. In the test calculations for which also the (n − 1)s,p orbitals were correlated, the aug-cc-pwCVnZ-PP (aug-cc-pwCVnZ for 2 ≤ Z ≤ 18) basis sets were exclusively used, since the vnZ-f12 basis sets do not contain tight polarization functions, which are essential in this case.Relativistic spin–orbit effects were estimated using the zeroth-order regular approximation (ZORA)82 and the exact two-component (X2C)83–90 approach. The spin–orbit (SO) contribution at the X2C-PBE0-D4/x2c-QZVPPall-2c91 level of theory for the dimerization energy of the heaviest system in the IHD302 set (![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Tl−Po−Tl−Po−Tl−Po
Tl−Po−Tl−Po−Tl−Po![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) ) is rather large (for a closed-shell molecule), 18.4 kcal mol−1 for the covalent and 5.9 kcal mol−1 for the WDA dimer, respectively (see ESI,† Table S7). Similarly large SOC contributions were calculated for heavy p-block dimers by Höfener et al.92 Nonetheless, X2C results without SO contribution agree well with the respective dimerization energies obtained with effective core potentials (ECPs). Hence, for all other calculations, we employed ECPs to account approximately for scalar relativistic effects, which become important for heavier elements. The same ECPs (vide supra) have also been used in the DFT and SQM calculations so that the comparison of wave function and approximate methods is on equal footing unless ECPs are missing for certain elements, as for Ga, Ge, As, and Se in the def2-QZVPP basis set (vide infa).
) is rather large (for a closed-shell molecule), 18.4 kcal mol−1 for the covalent and 5.9 kcal mol−1 for the WDA dimer, respectively (see ESI,† Table S7). Similarly large SOC contributions were calculated for heavy p-block dimers by Höfener et al.92 Nonetheless, X2C results without SO contribution agree well with the respective dimerization energies obtained with effective core potentials (ECPs). Hence, for all other calculations, we employed ECPs to account approximately for scalar relativistic effects, which become important for heavier elements. The same ECPs (vide supra) have also been used in the DFT and SQM calculations so that the comparison of wave function and approximate methods is on equal footing unless ECPs are missing for certain elements, as for Ga, Ge, As, and Se in the def2-QZVPP basis set (vide infa).
Density fitting for the Fock matrix employed the def2-QZVPP/JKFIT93 or aug-cc-pVnZ/JKFIT for light atoms, n = T or Q; the latter sets, which are available in the Molpro basis set library, have been derived from the cc-pVnZ/JKFIT basis sets of Weigend94 by adding for each angular momentum a shell of diffuse functions in an even-tempered manner. For the RI-approximations in the PNO-LMP2-F12 and PNO-LCCSD(T)-F12 calculations, the so-called CABS basis sets were employed, which comprise the union of the vnz-f12 orbital basis and the associated VnZ-PP-F12/OPTRI basis.95 For the CABS-singles corrections the complementing auxiliary (CA) orbital space was explicitly constructed by orthogonalizing the CABS basis set on the corresponding orbital basis.
The same CABS and DF basis sets were also employed in the PNO-LCCSD(T)-F12/awcvnz calculations, but in this case, the unions of the orbital and JKFIT basis sets were used to construct the CA space for the CABS-singles corrections (since there are no awcvnz/OPTRI basis sets available yet). In order to test the sensitivity of the results to the choice of the auxiliary basis sets, we also employed the quadruple-ζ DF and CABS basis sets (as well as few other choices for the RI basis, cf. Table S1 in the ESI†) in some PNO-LCCSD(T)-F12/awcvtz calculations. It should be noted that using the CABS basis, which corresponds to the respective orbital basis, is exactly equivalent to using the CABS approach96 in the F12 treatment. However, when the current orbital basis differs from the one used in the CABS basis this is no longer exactly the case. However, as long as all occupied orbitals can be well represented by the CABS basis this causes only minor errors. This is also corroborated by the tests carried out in the present work (cf. ESI,† Table S1).
The CABS singles correction is included in all results of this paper (also for LMP2 without F12). It was applied to all occupied orbitals (option CORE_SINGLES=1). Note that by default Molpro excludes uncorrelated core orbitals from the CABS correction, which can lead to significant errors for the systems under consideration (up to 0.4 kcal mol−1 for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Pb−Sb−Si−Bi−Ge−N
Pb−Sb−Si−Bi−Ge−N![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV (7COV), see ESI† (data correlation methods)), unless either the option CORE_SINGLES=1 or an appropriate CORE directive is given in the CABS singles calculation.
COV (7COV), see ESI† (data correlation methods)), unless either the option CORE_SINGLES=1 or an appropriate CORE directive is given in the CABS singles calculation.
Finally, we note that for an accurate description of the core–core correlation effects it was necessary to tighten the integral screening parameters in the PNO program (Molpro option BB_THRESH=10−8). Likely, this is due to near linear dependencies of the RI basis. When using tight screening thresholds, the different choices of the RI basis had only a negligible effect on the results and all results were numerically stable. However, with the default screening threshold (BB_THRESH=10−6), in some cases very large errors occurred with the CABS basis sets. These errors can be avoided by removing near linear dependencies of the RI basis using singular value decomposition (SVD). This yields results very close to those obtained with the tight screening threshold. However, SVD is rather expensive, since it requires diagonalizing the RI overlap matrix for each pair (because the RI domains are pair-dependent). SVD has therefore not been used in the final calculations.
3.4 Finding a suitable reference protocol
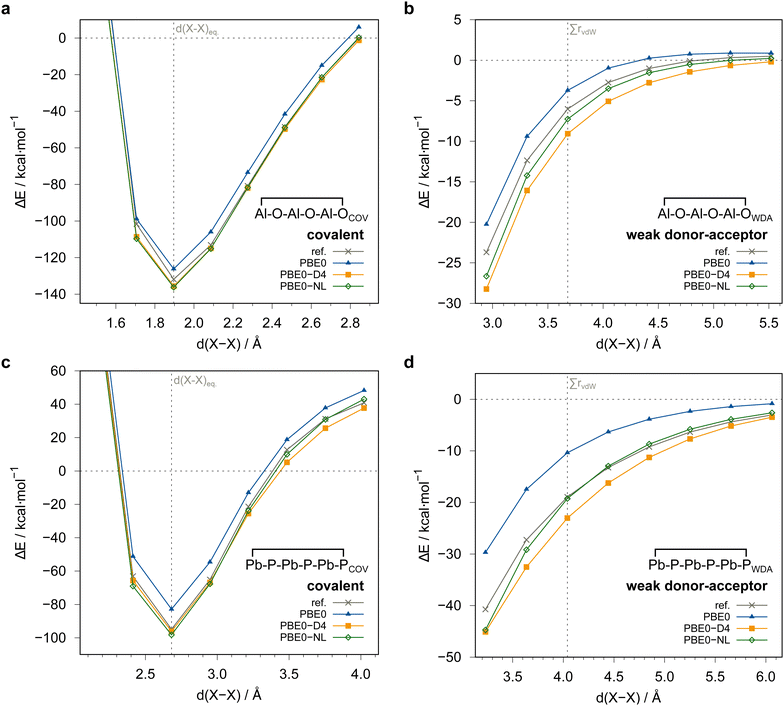
In order to check the dependence of the PNO-LCCSD(T)-F12 results on basis sets, thresholds, and further settings as well as to estimate the accuracy of the reference values, we carried out extensive test calculations for eight systems covering the majority of elements and all main group combinations (i.e., III–VI, III–V, IV–V in this order) included in the whole IHD302 benchmark set. The structures of the covalently bound dimers of these systems are shown in Fig. 3. Unless otherwise noted, the (n − 1)s,p orbitals were not correlated in these calculations.Initially, we tested whether the counter-poise (CP) correction should be applied to the dimerization energies to reduce basis set superposition effects (BSSE). Table S2 in the ESI,† shows that the CP corrections are significant for PNO–LMP2 (up to 7% of the respective dimerization energy), but negligibly small for PNO–LMP2–F12. We, therefore, decided not to apply CP corrections in further correlation calculations conducted in this work, which were mostly carried out with F12.
Fig. 4 summarizes the computed dimerization energies for different methods tested using the awcvqz basis (PROJECTOR=MIXED, THRPNO_LMP2=1d-10, cf. Section 3.2). The total electron correlation contributions to the respective binding energies are rather large. At the HF level, the weak donor–acceptor complexes are mostly unbound. For the covalently bound systems, most systems are bound at the HF level and the total correlation effect on the dimerization energies is huge (more than 70 kcal mol−1 for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) B−Se−B−Se−B−Se
B−Se−B−Se−B−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV (1COV)). This makes it extremely difficult to obtain results with sub-kcal mol−1 accuracy.
COV (1COV)). This makes it extremely difficult to obtain results with sub-kcal mol−1 accuracy.
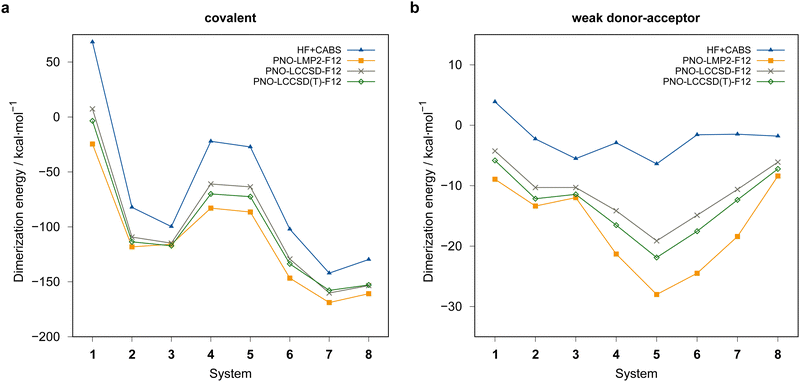 | ||
| Fig. 4 Comparison of computed dimerization energies using different methods and the awcvqz basis (see text) for the (a) covalent and (b) weak donor–acceptor bound systems depicted in Fig. 3. | ||
All dimerization energies are clearly overestimated at the LMP2-F12 level. In contrast, the LCCSD-F12 values are mostly too small, and the triples contributions to the binding energies are rather large and negative (−10.9 kcal mol−1 for 1COV with awcvqz). Only for the test systems 7 and 8, which belong to the IV–V class, they are positive. This may be related to the different electronic structures of these systems, where formal double bonds are converted to single bonds (cf.Fig. 1).
In the following sections, we investigate how explicit correlation, local approximations, core correlation, and the choice of the basis set affect the accuracy of the dimerization energies. Our goal is to obtain reference values with a relative accuracy of 1–2% for the covalently bound systems and <5% for the weak-donor acceptor structures, which means an absolute accuracy of 1–2 kcal mol−1 and 0.5 kcal mol−1, respectively. In exceptional cases, where the absolute values of the dimerization energies are very small relative to the total correlation contribution (e.g. for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) B−Se−B−Se−B−Se
B−Se−B−Se−B−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV (1COV)), slightly larger errors of our reference values protocol (vide infa) may occur.
COV (1COV)), slightly larger errors of our reference values protocol (vide infa) may occur.
Unfortunately, checking the intrinsic accuracy of the CCSD(T) method for these applications by including higher connected excitations in the coupled cluster expansion is computationally impossible due to the tremendous cost. Since neither the FOD plots34 for the eight test systems (see Fig. S9 in the ESI†) nor the rND static correlation diagnostic37 for the complete test set show signs of significant static correlation (see ESI,† for details), we are convinced that CCSD(T) is able to correctly describe the electronic structure of the systems in IHD302. Hence, based on previous experience and given that the electronic structures of systems in question are of single reference type, it can be assumed that it is in the same range as the above error bounds.
The exponents for cc and cv correlation decrease with increasing row number in the periodic table and increase from left to right in the periodic table. This is reflected in the optimized values, which represent compromises of the optimized values one would obtain for the individual atoms contained in the individual systems. Another possibility would be to optimize exponents for each of the 19 elements contained in the IHD302 set separately and then apply weighted averages of these values for the molecules. However, in view of the rather low sensitivity of the results to the choice of exponents, we did not attempt this. PNO-LCCSD(T)-F12 results for different choices of the geminal exponents and employing the vtz-f12 basis are summarized in Table S4 of the ESI.† Results for a subset of these test calculations are presented in Table 1. Given the rather small effect (compared to, e.g., the inclusion of cv and cc correlation, vide infra) of varying the geminal exponents and to avoid the geminal exponent optimization for all systems comprised in the IHD302 set, we decided to use just two fixed exponents for all systems, γvv = 1.0a0−1 for valence correlation, and γcc = γcv = 1.4a0−1 for cc+cv correlation. As shown in Table 1, this has only a small effect on the PNO-LCCSD(T)-F12 relative energies. In most cases, the dimerization energies are slightly larger than those obtained with the three optimized exponents thus bringing them closer to our best awcvqz results, especially for the covalent structures (see ESI†). For the 13 systems of the IHD302 set containing exclusively elements of the first three rows of the periodic table, only the valence electrons were correlated using the default value γ = 1.0a0−1.
| System | HF+CABS | vv | cc+cv+vv | |||
|---|---|---|---|---|---|---|
| γ (1.0) | γ (optv) | γ (1.0) | γ = (1.0, 1.4) | γ (opt3) | ||
| Covalent: | ||||||
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) B−Se−B−Se−B−Se B−Se−B−Se−B−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (1COV) (1COV) |
68.3 | −2.9 | −2.9 | −2.3 | −2.4 | −2.3 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Al−O−Al−S−Al−Se Al−O−Al−S−Al−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (2COV) (2COV) |
−82.2 | −112.2 | −112.9 | −113.3 | −113.2 | −112.9 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Ga−O−In−O−Tl−O Ga−O−In−O−Tl−O![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (3COV) (3COV) |
−99.8 | −111.7 | −111.7 | −115.0 | −115.5 | −115.4 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Ga−Te−In−Te−Ga−Se Ga−Te−In−Te−Ga−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (4COV) (4COV) |
−22.1 | −66.6 | −66.8 | −68.3 | −68.9 | −68.9 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) In−Te−Tl−Te−In−Se In−Te−Tl−Te−In−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (5COV) (5COV) |
−27.3 | −66.0 | −66.2 | −70.0 | −70.7 | −70.0 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Tl−P−Tl−P−Tl−Bi Tl−P−Tl−P−Tl−Bi![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (6COV) (6COV) |
−102.2 | −124.5 | −124.9 | −132.3 | −132.8 | −131.8 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Pb−Sb−Si−Bi−Ge−N Pb−Sb−Si−Bi−Ge−N![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (7COV) (7COV) |
−142.2 | −154.8 | −155.1 | −155.0 | −155.3 | −154.8 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Si−N−Si−N−Si−P Si−N−Si−N−Si−P![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (8COV) (8COV) |
−129.8 | −151.8 | −152.3 | |||
| Weak donor–acceptor: | ||||||
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) B−Se−B−Se−B−Se B−Se−B−Se−B−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (1WDA) (1WDA) |
3.9 | −5.6 | −5.7 | −5.4 | −5.5 | −5.6 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Al−O−Al−S−Al−Se Al−O−Al−S−Al−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (2WDA) (2WDA) |
−2.3 | −12.0 | −12.0 | −11.9 | −12.0 | −12.0 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Ga−O−In−O−Tl−O Ga−O−In−O−Tl−O![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (3WDA) (3WDA) |
−5.6 | −9.8 | −9.8 | −11.2 | −11.2 | −11.2 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Ga−Te−In−Te−Ga−Se Ga−Te−In−Te−Ga−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (4WDA) (4WDA) |
−2.9 | −15.5 | −15.5 | −16.0 | −16.1 | −16.2 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) In−Te−Tl−Te−In−Se In−Te−Tl−Te−In−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (5WDA) (5WDA) |
−6.4 | −19.8 | −19.8 | −21.0 | −21.3 | −21.1 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Tl−P−Tl−P−Tl−Bi Tl−P−Tl−P−Tl−Bi![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (6WDA) (6WDA) |
−1.6 | −14.9 | −14.9 | −16.9 | −17.1 | −16.8 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Pb−Sb−Si−Bi−Ge−N Pb−Sb−Si−Bi−Ge−N![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (7WDA) (7WDA) |
−1.5 | −11.4 | −11.3 | −11.7 | −11.8 | −11.8 |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Si−N−Si−N−Si−P Si−N−Si−N−Si−P![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (8WDA) (8WDA) |
−1.9 | −7.1 | −7.1 | |||
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) In−Te−Tl−Te−In−Se
In−Te−Tl−Te−In−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (5COV and 5WDA) calculated with the vtz-f12 basis, the observed behavior is as expected: approximation 3C underestimates the (positive) F12 contribution, yielding for both structures (covalent and weak donor–acceptor) results that are too negative as compared to the best awcvqz values. On the other hand, approximation 3*A overestimates the F12 contribution, thus somewhat underestimating the dimerization energy (too “positive” ΔE). For the covalently bound dimers, the differences relative to the awcvqz results amount to −1.4 and +1.0 kcal mol−1 for 3C and 3*A, respectively, while for the weak donor–acceptor ones, the corresponding differences are −1.0 and +0.4 kcal mol−1. A rather similar behavior is observed for
(5COV and 5WDA) calculated with the vtz-f12 basis, the observed behavior is as expected: approximation 3C underestimates the (positive) F12 contribution, yielding for both structures (covalent and weak donor–acceptor) results that are too negative as compared to the best awcvqz values. On the other hand, approximation 3*A overestimates the F12 contribution, thus somewhat underestimating the dimerization energy (too “positive” ΔE). For the covalently bound dimers, the differences relative to the awcvqz results amount to −1.4 and +1.0 kcal mol−1 for 3C and 3*A, respectively, while for the weak donor–acceptor ones, the corresponding differences are −1.0 and +0.4 kcal mol−1. A rather similar behavior is observed for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) B−Se−B−Se−B−Se
B−Se−B−Se−B−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV (1COV), although with the awcvtz basis, 3C seems to slightly overestimate the F12 corrections. Currently, we do not have an explanation for these subtle effects, but the results demonstrate that there is no disadvantage of using the simple and more efficient approximation 3*A.
COV (1COV), although with the awcvtz basis, 3C seems to slightly overestimate the F12 corrections. Currently, we do not have an explanation for these subtle effects, but the results demonstrate that there is no disadvantage of using the simple and more efficient approximation 3*A.
| Basis | Method | ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) B−Se−B−Se−B−Se B−Se−B−Se−B−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) In−Te−Tl−Te−In−Se In−Te−Tl−Te−In−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) |
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Ga−Te−In−Te−Ga−Se Ga−Te−In−Te−Ga−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) |
|||
|---|---|---|---|---|---|---|---|
| WDA | Covalent | WDA | Covalent | WDA | Covalent | ||
| a Projector=PAO,THRPNO_LMP2=1d-10. b Projector=PAO,THRPNO_LMP2=1d-8. | |||||||
| vtz-f12 | HF | 3.8 | 68.3 | −6.5 | −27.8 | −3.0 | −22.3 |
| HF+CABS | 3.9 | 68.3 | −6.4 | −27.3 | −2.9 | −22.1 | |
| MP2 | −9.4 | −25.0 | −33.0 | −92.9 | −24.8 | −88.8 | |
| MP2-F12/3C | −9.1 | −25.2 | −29.1 | −87.9 | −22.2 | −84.7 | |
| MP2-F12/3*A | −8.8 | −24.0 | −27.7 | −85.4 | −21.5 | −83.0 | |
| LMP2-F12/3*Aa | −8.8 | −24.1 | −27.7 | −85.3 | −21.2 | −82.6 | |
| LMP2-F12/3*Ab | −8.8 | −23.7 | −27.6 | −85.1 | −21.1 | −82.4 | |
| awcvtz | HF | 3.8 | 68.2 | −6.5 | −27.4 | −3.0 | −22.2 |
| HF+CABS | 3.9 | 68.3 | −6.4 | −27.3 | −2.9 | −22.1 | |
| MP2 | −9.8 | −24.1 | −29.0 | −85.3 | −22.2 | −81.5 | |
| MP2-F12/3C | −9.1 | −24.9 | −29.4 | −86.2 | −21.5 | −83.0 | |
| MP2-F12/3*A | −9.0 | −24.7 | −28.1 | −85.6 | −21.4 | −82.5 | |
| LMP2-F12/3*Aa | −8.9 | −24.8 | −27.9 | −86.0 | −21.3 | −82.5 | |
| LMP2-F12/3*Ab | −8.9 | −24.4 | −27.9 | −85.8 | −21.2 | −82.3 | |
| awcvqz | LMP2-F12/3*Aa | −8.9 | −24.6 | −28.0 | −86.5 | −21.3 | −82.9 |
The canonical and local results are in close agreement. The small differences seen with TLMP2PNO = 10−10 (program option THRPNO_LMP2) may originate from the PAO domain approximation and the RI and LMO domain approximations in the strong orthogonality projector (eqn (1)). If the default threshold THRPNO_LMP2=1d-8 is used, an additional error of up to 0.4 kcal mol−1 in case of ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) B−Se−B−Se−B−Se
B−Se−B−Se−B−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV (1COV) can arise. Given a total correlation contribution of over 90 kcal mol−1 (LMP2-F12, COV) this is certainly acceptable.
COV (1COV) can arise. Given a total correlation contribution of over 90 kcal mol−1 (LMP2-F12, COV) this is certainly acceptable.
For some test systems, we investigated the dependence of the results on the PAO and PNO thresholds (see ESI,† for details). The PAO domain sizes were varied by increasing the parameter REXT, which had a negligible effect. The PNO domains used in the PNO-LCCSD-F12 were enlarged by increasing the parameter THREN_CC from 0.90 to 0.997; this means that for each pair at least 99.7% of the semi-canonical PAO-LMP2 correlation energy is recovered with the PNO domains. Again, this affected the dimerization energies by less than 0.1 kcal mol−1. Also, the differences in the dimerization energies obtained with DEFAULT and TIGHT domain options, which affect PAO, PNO, and TNO domain sizes, are rather small. The same holds for the pair approximations. Therefore, the values generated with TIGHT domain options should be well converged with respect to the local approximations. This is also supported by comparisons of canonical and local MP2-F12 results (cf. Section 3.4.4).
However, as already mentioned in Section 3.2, some unexpected outliers were observed for the calculations with the awcvtz basis. It turned out that these were due to the choice of the local approximations in the F12 strong orthogonality projector (cf. Section 3.2). Fig. 5 shows the convergence of the PNO-LMP2-F12 dimerization energies as a function of the PNO threshold TLMP2PNO for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) B−Se−B−Se−B−Se
B−Se−B−Se−B−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV (1COV) and
COV (1COV) and ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Ga−Te−In−Te−Ga−Se
Ga−Te−In−Te−Ga−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV (4COV), where the effect of the projector is particularly strong. With the PAO projector, the convergence is smooth, but the domain correction underestimates the PNO domain error by about 0.2 kcal mol−1, if the default value TLMP2PNO = 10−8 is used. This error can be reduced to a completely negligible amount by using a tighter PNO threshold, e.g. TLMP2PNO = 10−10. In the current work, such problems were only observed for calculations with the awcvnz basis sets but not for vtz-f12. Hence, we applied TLMP2PNO = 10−10 for all further local calculations carried out with the awcvnz basis sets.
COV (4COV), where the effect of the projector is particularly strong. With the PAO projector, the convergence is smooth, but the domain correction underestimates the PNO domain error by about 0.2 kcal mol−1, if the default value TLMP2PNO = 10−8 is used. This error can be reduced to a completely negligible amount by using a tighter PNO threshold, e.g. TLMP2PNO = 10−10. In the current work, such problems were only observed for calculations with the awcvnz basis sets but not for vtz-f12. Hence, we applied TLMP2PNO = 10−10 for all further local calculations carried out with the awcvnz basis sets.
For all systems comprised in the IHD302 test set, the difference of the LMP2-F12(PAO)/vtz-f12 and respective LMP2-F12(PNO)/vtz-f12 dimerization energies of the covalent structures amounts on average to 0.21 kcal mol−1 (almost always >0) with a maximum deviation of only 0.33 kcal mol−1 (see ESI,† for details). For the weak donor–acceptor systems, the difference of the LMP2-F12 dimerization energies computed with PAO or PNO projector, respectively, is negligibly small (0.01 kcal mol−1 on average). Thus, with the vtz-f12 basis, the dependence of the results on the choice of the F12 projector is much less pronounced than for awcvnz basis sets.
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Tl−P−Tl−P−Tl−Bi
Tl−P−Tl−P−Tl−Bi![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) WDA (6WDA), the cc+cv correlation effect amounts to ≈2 kcal mol−1, and for the respective covalent structure structure (6COV) to about 7–8 kcal mol−1, depending on the choice of the geminal exponents. The corresponding values for
WDA (6WDA), the cc+cv correlation effect amounts to ≈2 kcal mol−1, and for the respective covalent structure structure (6COV) to about 7–8 kcal mol−1, depending on the choice of the geminal exponents. The corresponding values for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) In−Te−Tl−Te−In−Se
In−Te−Tl−Te−In−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (5WDA and 5COV) amount to ≈1 kcal mol−1 and about 4 kcal mol−1, respectively. These large effects demonstrate that including cc+cv correlation effects in these calculations is essential for obtaining accurate results.
(5WDA and 5COV) amount to ≈1 kcal mol−1 and about 4 kcal mol−1, respectively. These large effects demonstrate that including cc+cv correlation effects in these calculations is essential for obtaining accurate results.
In some calculations with the awcvtz basis, we tested also the effect of including the (n − 1)s and p orbitals in the correlation treatment. The effect on the weak donor–acceptor dimerization energies is rather small (see ESI,† for details). However, in some cases, the PNO-LMP2-F12 dimerization energies of the covalent structures containing several main group III elements were significantly reduced (up to 1.75 kcal mol−1 for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) In−Te−Tl−Te−In−Se
In−Te−Tl−Te−In−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV (5COV), i.e., here the correlation effect is positive). Note, however, that the cc+cv correlation is generally rather strongly over-estimated at the PNO-LMP2-F12 level. Core correlation effects are much smaller at the PNO-LCCSD(T)-F12 level (e.g., 1.15 kcal mol−1 for
COV (5COV), i.e., here the correlation effect is positive). Note, however, that the cc+cv correlation is generally rather strongly over-estimated at the PNO-LMP2-F12 level. Core correlation effects are much smaller at the PNO-LCCSD(T)-F12 level (e.g., 1.15 kcal mol−1 for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) In−Te−Tl−Te−In−Se
In−Te−Tl−Te−In−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV (5COV)).
COV (5COV)).
In all other tested cases, the effect of correlating the (n − 1)s,p orbitals was well below 1 kcal mol−1. Moreover, due to the employed pseudopotential approximation, estimating the accuracy of the (n − 1)s,p correlation effect is somewhat problematic. For the post-d elements, these orbitals are the lowest ones that are explicitly treated and have no radial nodes, which may lead to a significant overestimation of the respective correlation contributions. A more detailed study of these effects would require very expensive relativistic all-electron calculations, which is beyond the scope of this paper. We therefore decided not to include these orbitals in the final PNO–LCCSD(T)–F12 calculations for all molecules. Additionally, since the effects of correlating the (n − 1)d and (n − 1)s,p shells mostly have opposite signs, this may lead to some beneficial error compensations of remaining basis set deficiencies.
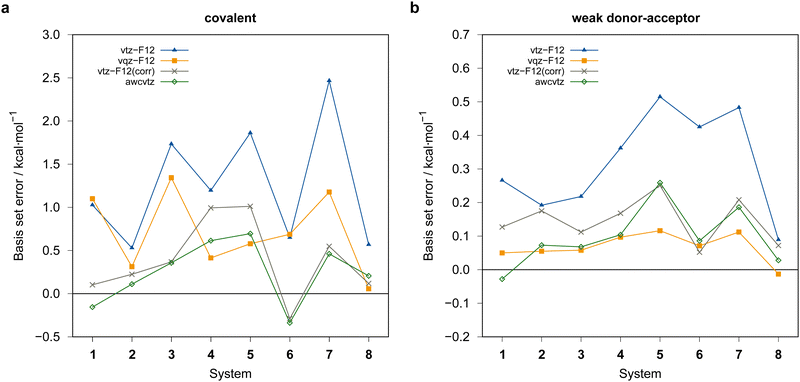
Generally, the vtz-f12 dimerization energies of the eight test systems (cf.Fig. 3) are significantly underestimated (i.e., the basis set errors are >0), up to about 0.5 kcal mol−1 for the weak-doner–acceptor structures and 2 kcal mol−1 for the covalently bound dimers, respectively. In view of the large and negative correlation contributions this is not unexpected, although the errors are much larger than those seen in previous PNO-LCCSD(T)-F12 benchmark calculations for reactions of organic molecules.68 Using the vqz-f12 basis, the deviation from the awcvqz dimerization energies for the tested weak donor–acceptor structures are all below 0.16 kcal mol−1. However, the errors for the covalently bound dimers are still rather large, up to 1.3 kcal mol−1 for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) B−Se−B−Se−B−Se
B−Se−B−Se−B−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV (1COV).
COV (1COV).
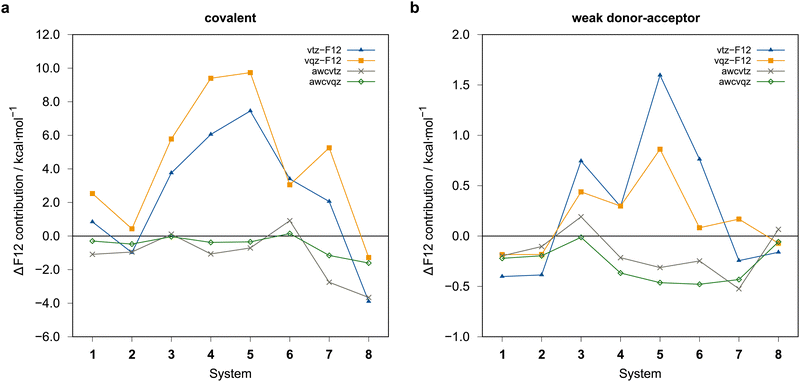
The rather large basis set errors obtained with the vtz-f12 and vqz-f12 basis sets are somewhat unexpected and unsual. They are related to the fact that in these sets only one set of additional d and f functions has been added to the underlying aug-cc-pV(n+1)Z-PP valence basis sets to describe the cc+cv effects,76 assuming that the F12 corrections would cover the rest. Without F12, this leads to strong intramolecular BSSE and much too large binding energies. The F12 contributions are therefore positive (up to almost 10 kcal mol−1) (cf.Fig. 7). Surprisingly, for the covalent structures, they are even larger with vqz-f12 than with vtz-f12. One positive aspect, however, is that F12 can reduce the errors in these cases from up to 10 kcal mol−1 to around 1 kcal mol−1 or even less.
These findings are exemplified in Table 3 for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) In−Te−Tl−Te−In−Se
In−Te−Tl−Te−In−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (5COV and 5WDA), one of our test systems with the largest remaining errors (with respect to the corresponding awcvqz dimerization energies). First, it can be seen that due to the intramolecular BSSE, the PNO-LMP2/vnz-f12 dimerization energies are much over-estimated (too negative). This also holds for the triples (T) contributions, which are not directly affected by the F12 terms. Except for the triples, this problem is largely cured by the F12 treatment.
(5COV and 5WDA), one of our test systems with the largest remaining errors (with respect to the corresponding awcvqz dimerization energies). First, it can be seen that due to the intramolecular BSSE, the PNO-LMP2/vnz-f12 dimerization energies are much over-estimated (too negative). This also holds for the triples (T) contributions, which are not directly affected by the F12 terms. Except for the triples, this problem is largely cured by the F12 treatment.
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) In−Te−Tl−Te−In−Se
In−Te−Tl−Te−In−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) (5WDA and 5COV) calculated with different PNO methods and basis sets
(5WDA and 5COV) calculated with different PNO methods and basis sets
| Basis | Projector | T LMP2PNO | γ [vv,cv,cc] | LMP2 | LMP2-F12 | LCCSD-F12 | LCCSD(T)-F12 | Δ(T) |
|---|---|---|---|---|---|---|---|---|
| Weak donor–acceptor: | ||||||||
| vtz-f12 | PNO | 1d-08 | [1.0,1.4,1.4] | −29.2 | −27.6 | −18.6 | −21.3 | −2.7 |
| vqz-f12 | PNO | 1d-08 | [0.8,1.3,1.4] | −28.7 | −27.9 | −18.9 | −21.7 | −2.9 |
| avcvtz | MIX | 1d-08 | [1.0,1.4,1.4] | −27.6 | −28.0 | −19.0 | −21.7 | −2.6 |
| awcvtz | MIX | 1d-10 | [1.0,1.4,1.4] | −27.6 | −27.9 | −19.1 | −21.7 | −2.6 |
| awcvqz | MIX | 1d-10 | [1.0,1.4,1.4] | −27.5 | −28.0 | −19.1 | −21.9 | −2.8 |
| Covalent: | ||||||||
| vtz-f12 | PNO | 1d-08 | [1.0,1.4,1.4] | −93.0 | −85.7 | −62.2 | −71.1 | −8.9 |
| vqz-f12 | PNO | 1d-08 | [0.8,1.3,1.4] | −96.1 | −86.6 | −62.7 | −72.2 | −9.5 |
| awcvtz | MIX | 1d-08 | [1.0,1.4,1.4] | −85.3 | −86.0 | −63.3 | −71.8 | −8.5 |
| awcvtz | MIX | 1d-10 | [1.0,1.4,1.4] | −85.4 | −86.1 | −63.4 | −71.9 | −8.5 |
| awcvqz | MIX | 1d-10 | [1.0,1.4,1.4] | −86.0 | −86.5 | −63.6 | −72.5 | −9.0 |
With the awcvtz and awcvqz basis sets, which have been specifically optimized to describe cc+cv correlation effects without F12, the F12 contributions to the binding energies are distinctively smaller than for the vnz-f12 basis, especially for the covalent structures. Moreover, they are mostly negative, indicating that the above-mentioned intramolecular BSSE effects (without F12) are strongly reduced. Employing the awcvtz basis, the errors for the covalent systems are all below 0.7 kcal mol−1 relative to the awcvqz results but about 4–5 times faster (somewhat system-dependent).
Unfortunately, the awcvtz basis is significantly larger than the vtz-f12 one, and due to the many additional high-angular momentum basis functions, the calculations with the awcvtz basis are at least twice as expensive compared to the respective vtz-f12 ones. Almost the same improvement as with the awcvtz basis can be obtained by adding a PNO-LMP2-F12(PAO) basis set correction to the respective PNO-LCCSD(T)-F12(PNO)/vtz-f12 energies
The amount of the basis set correction is mostly small (on average about −0.7 kcal mol−1 and −0.2 kcal mol−1 for the covalent and weak donor–acceptor complexes, respectively). Only for a few systems the correction is significantly larger (up to about −2.8 kcal mol−1 and −0.8 kcal mol−1, respectively; see ESI,† for details).
To further verify the effectiveness of the basis set correction, we also calculated the PNO-LCCSD(T)-F12/awcvnz (n = T, Q) dimerization energies for the eight systems with the largest correction values (see ESI,† for details). Even in these cases the agreement of the vtz-f12(corr) results with awcvqz ones is very satisfactory. The RMSD relative to the awcvqz results for all 16 test systems amounts to 0.17 kcal mol−1 and 0.52 kcal mol−1 (maximum errors: 0.29 and 1.01 kcal mol−1) for the WDA and COV systems, respectively. It appears that a significant part of the remaining errors is due to the basis set error of the relatively large triples contributions (up to −13.6 kcal mol−1 for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) B−Po−B−Po−B−Po
B−Po−B−Po−B−Po![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV with vtz-f12), which is often about 0.2–0.5 kcal mol−1 too small when computed with the vtz-f12 or awcvtz basis sets.
COV with vtz-f12), which is often about 0.2–0.5 kcal mol−1 too small when computed with the vtz-f12 or awcvtz basis sets.
3.5 Generation of reference dimerization energies
The conclusion from the tests in the previous sections is that likely the basis set problem will cause the largest uncertainties of the reference values for the IHD302 benchmark set. Therefore, it would in principle be desirable to use the awcvqz basis for the reference calculations. Unfortunately, the computational effort for PNO-LCCSD(T)-F12 calculations with this basis is clearly too large for the complete benchmark set. For example, a PNO-LCCSD(T)-F12/awcvqz calculation for![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) In−Te−Tl−Te−In−Se
In−Te−Tl−Te−In−Se![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV (5COV) (2202 basis functions, TIGHT domain settings) took about 66 hours on 4 (rather old) Intel® Xeon® CPU E5-2650 v4 @ 2.20 GHz nodes with a total of 74 processing cores.
COV (5COV) (2202 basis functions, TIGHT domain settings) took about 66 hours on 4 (rather old) Intel® Xeon® CPU E5-2650 v4 @ 2.20 GHz nodes with a total of 74 processing cores.
The large computational cost for these rather small molecules (up to 24 atoms) may be surprising at first sight. Partly, it is due to the large number of orbitals per atom that have to be correlated (7–8 LMOs per atom as compared to typically 2–3 LMOs for organic molecules); without pair or triples approximations, the computational effort scales cubic with the number of LMOs per atom. Furthermore, in these compact systems, there are no distant pairs, and screening as well as weak pair approximations have a much smaller impact than for extended organic molecules. And last but not least, the many high-angular momentum functions in the basis sets needed for post-d elements strongly increase the cost of the integral evaluations.
Due to its beneficial accuracy-cost ratio and because also awcvtz (PROJECTOR=MIXED,THRPNO_LMP2=1d-10) calculations for the whole IHD302 set would take several weeks of computation time, we decided to use the PNO-LCCSD(T)-F12/TIGHT/vtz-f12(corr.) (cf. (2) with γvv = 1.0a0−1 and γcc = γcv = 1.4a0−1; abbreviated as PNO-LCCSD(T)-F12/vtz-f12(corr.) in the following) for computing the dimerization energies for the whole benchmark set (see ESI,† for details).
According to all test calculations carried out in this work, most of the resulting values should be well within the target accuracy with a relative accuracy of 1–2% for the covalently bound systems and <5% for the weak-donor acceptor structures (i.e., an absolute accuracy of 1–2 kcal mol−1 and 0.5 kcal mol−1, respectively). Nonetheless, larger uncertainties for a few systems cannot be fully excluded, particularly for cases where the correlation contributions are much larger than the final absolute values. These residual errors are mainly basis errors. Compared to the awcvqz values, the triples contributions are typically too positive by about 0.5 kcal mol−1, i.e., the dimerization energies are slightly underestimated. Since most approximate methods tested (vide infra) give an MD < 0 with MD ≈ MAD (see ESI,† for details), these deviations would tend to be slightly smaller with real CBS reference values. Since the deviations of even the best DFT methods from the reference values are usually significantly larger, the residual uncertainty in the reference values should not lead to a significant increase in the scatter of methods evaluated on the IHD302. However, the statistic discriminability (i.e., the square root of the number of reference values times their estimated uncertainty and then divided by the number of systems) is about 0.1 kcal mol−1. This allows for a unambiguous ranking of even the best DFT methods.
3.6 Trends throughout the periodic table
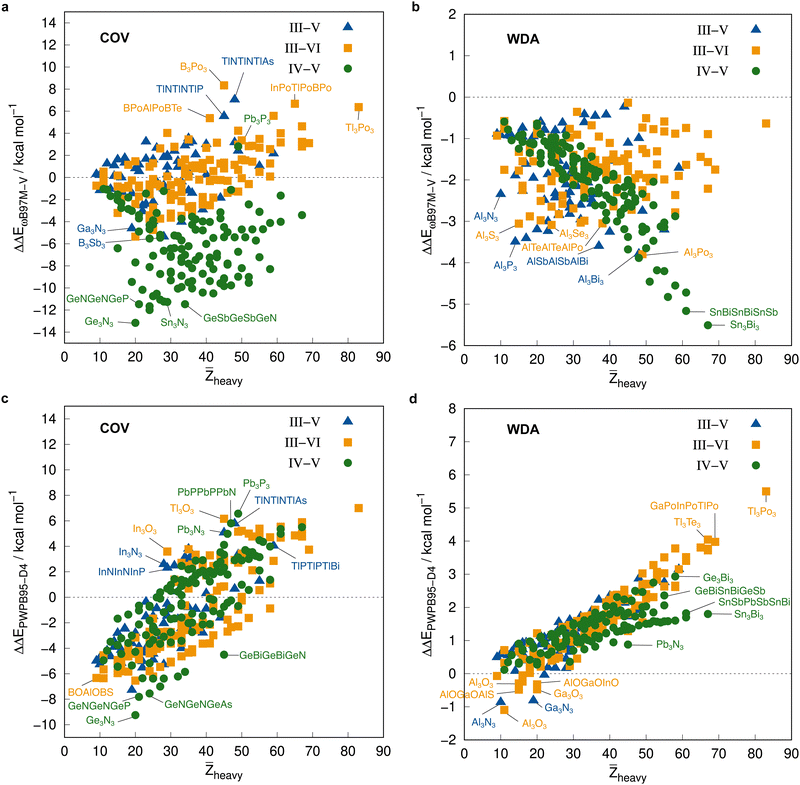
Before employing these reference values for the complete IHD302 in the next section to assess more approximate methods, we will use them to discuss trends in dimerization energies as a function of mean atomic number of the involved heavy atoms![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) heavy (see Fig. 8).
heavy (see Fig. 8).
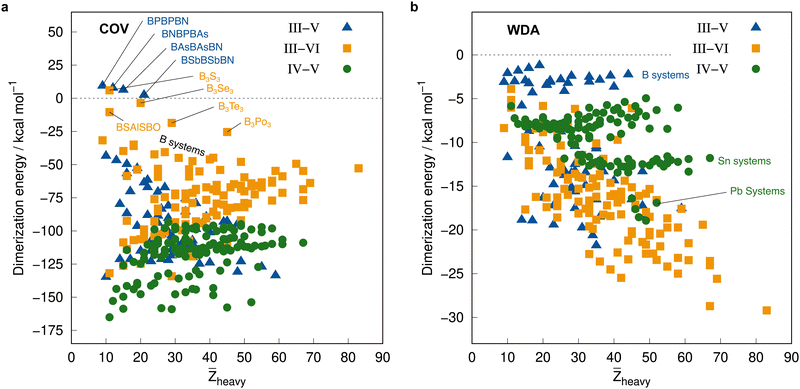 | ||
| Fig. 8 Correlation plot of the PNO-LCCSD(T)-F12/vtz-f12(corr.) reference dimerization energies in kcal mol−1 and the mean atomic number of the involved heavy atoms. | ||
The average ΔE = −95.5 kcal mol−1 of the covalent structures (Fig. 8a) is about four to five times larger than the respective value of the WDA structures (Fig. 8b) and also the range of the covalent dimerization energies is significantly larger (up to −165.1 kcal mol−1 for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Si−N−Si−N−Si−N
Si−N−Si−N−Si−N![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV). Nitrogen is the strongest Lewis base and especially in combination with lighter elements, this leads to large dimerization energies. In combination with heavier elements, which are less effective donors due to diffuse lone pairs, the ΔE becomes smaller. There are also a few systems with rather small negative or even positive ΔEs (up to 9.3 kcal mol−1 for
COV). Nitrogen is the strongest Lewis base and especially in combination with lighter elements, this leads to large dimerization energies. In combination with heavier elements, which are less effective donors due to diffuse lone pairs, the ΔE becomes smaller. There are also a few systems with rather small negative or even positive ΔEs (up to 9.3 kcal mol−1 for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) B−P−B−P−B−N
B−P−B−P−B−N![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV). These are exclusively systems with boron. Here, the planar monomers are presumably partially aromatic (comparable to borazine), resulting in little or no energetic benefit from dimerization. This effect becomes weaker in combination with heavier elements due to their lower hybridization degree, which leads to larger dimerization energies. There is, however, no clear trend of ΔE with increasing
COV). These are exclusively systems with boron. Here, the planar monomers are presumably partially aromatic (comparable to borazine), resulting in little or no energetic benefit from dimerization. This effect becomes weaker in combination with heavier elements due to their lower hybridization degree, which leads to larger dimerization energies. There is, however, no clear trend of ΔE with increasing ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) heavy. However, ΔEs of the IV–V systems are generally larger on average than those of the III–VI systems (the ΔEs of the III–V systems are typically in between).
heavy. However, ΔEs of the IV–V systems are generally larger on average than those of the III–VI systems (the ΔEs of the III–V systems are typically in between).
The mean ΔE for the WDA systems is −12.4 kcal mol−1, with all dimers bound (ΔE < 0), although especially the heavier III–VI systems show rather large dimerization energies for non-covalently bound neutral systems (up to −29.2 kcal mol−1 for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Tl−Po−Tl−Po−Tl−Po
Tl−Po−Tl−Po−Tl−Po![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) WDA). This indicates that the WDA structures represent bonding situations between non-covalent and covalent. Only the III–VI systems show a rough trend towards a linear increase of dimerization energy with
WDA). This indicates that the WDA structures represent bonding situations between non-covalent and covalent. Only the III–VI systems show a rough trend towards a linear increase of dimerization energy with ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) heavy, which is not recognizable for the III–V and IV–V systems.
heavy, which is not recognizable for the III–V and IV–V systems.
Additionally, the PNO-LCCSD(T)-F12/vtz-f12(corr.) correlation and triples contributions to the dimerization energies as well as the basis set correction, cv+cc correlation, and F12 contributions at the PNO-LMP2-F12 level of theory are analyzed for trends with respect to ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) heavy in the ESI† (Fig. S1–S4).
heavy in the ESI† (Fig. S1–S4).
4 p-Block challenge 2: DFT and SQM calculations
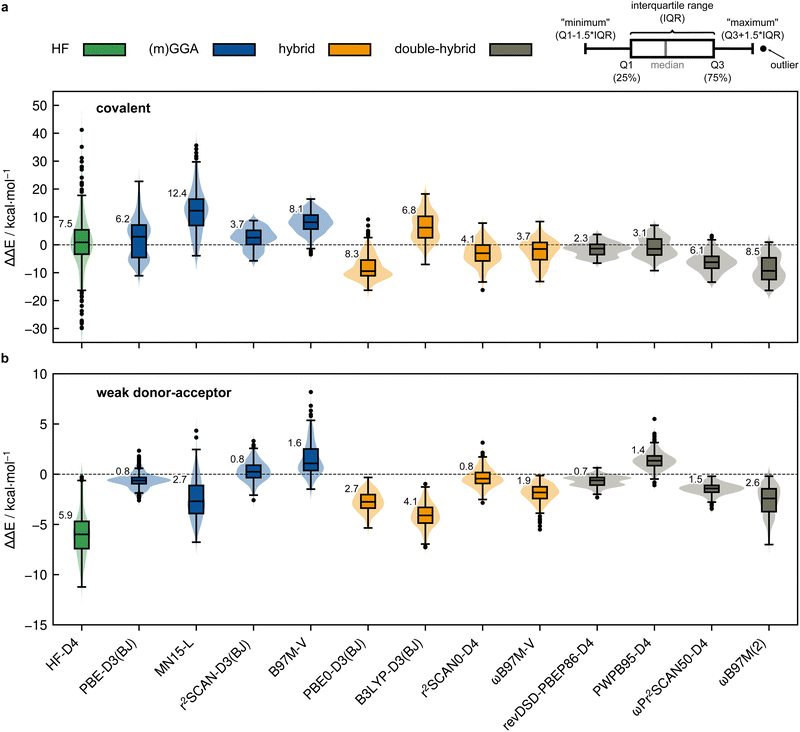
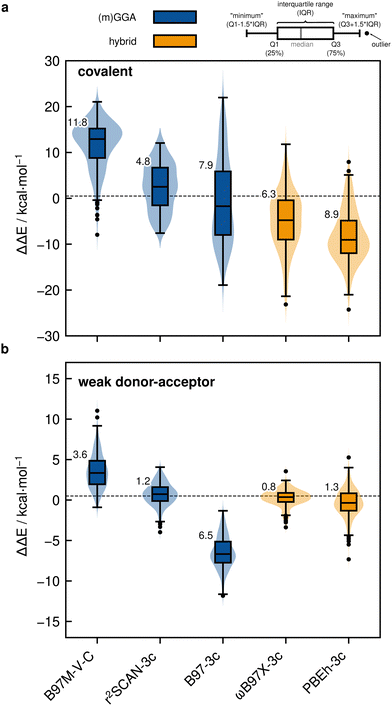
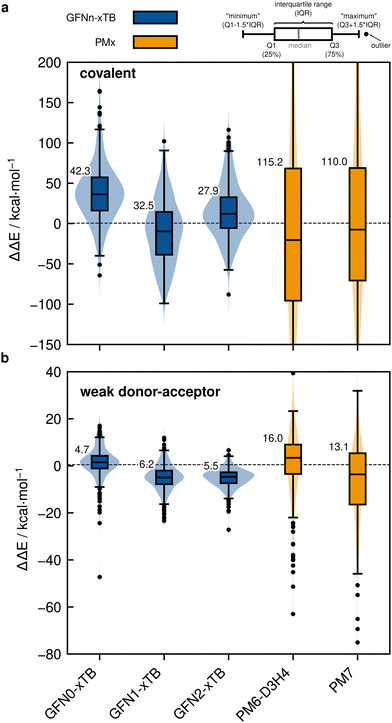
Based on the previously discussed PNO-LCCSD(T)/vtz-f12(corr.) reference dimerization energies, various contemporary and commonly used density functional theory (DFT) and semi-empirical quantum mechanical (SQM) methods have been assessed for their performance on the IHD302 benchmark set (Table 4). Seven (meta-)GGA, ten hybrid, and nine double-hybrid functionals (26 in total) were tested together with three different dispersion correction schemes (D3 with Becke–Johnson damping135,136 or zero-damping for the Minnesota functionals, D4,137–139 and the non-local DFT-NL140,141 variant of Vydrov and van Voorhis' VV10142 model). Furthermore, five composite DFT approaches and five SQM methods were covered. Because most force field methods are based on a separation of covalent and non-covalent interaction terms, their application for the here-considered situation in between both makes little sense although machine-learned potentials may be tested in the future if available for all considered elements.| Class | Method | RMSD/kcal mol−1 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Covalent | Weak donor–acceptor | ||||||||
| Plain | D3 | D4 | NL | Plain | D3 | D4 | NL | ||
| a As the PMx methods are not parameterized for Po, no data for Po-containing systems are included. | |||||||||
| FF | GFN-FF99 | 184.3 | 9.1 | ||||||
| UFF100 | 1416.3 | 1.0 | |||||||
| SQM | PM6-D3H423,101![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
158.8 | 33.2 | ||||||
PM724![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
162.7 | 17.9 | |||||||
| GFN0-xTB | 52.0 | 6.9 | |||||||
| GFN1-xTB25 | 46.7 | 7.6 | |||||||
| GFN2-xTB26 | 36.8 | 6.7 | |||||||
| Composite | B97M-V-C102 | 12.7 | 4.1 | ||||||
| B97-3c103 | 9.3 | 6.8 | |||||||
| r 2SCAN-3c30 | 5.7 | 1.5 | |||||||
| PBEh-3c104 | 10.0 | 1.8 | |||||||
| ωB97X-3c105 | 8.0 | 1.1 | |||||||
| HF-3c106 | 33.6 | 9.0 | |||||||
| (Meta-)GGA | PBE107 | 16.3 | 7.3 | 7.4 | 8.3 | 1.0 | 2.2 | ||
| BP86108,109 | 23.3 | 11.6 | 8.6 | 10.9 | 10.3 | 7.7 | |||
| B97M110 | 8.8 | 2.2 | |||||||
| TPSS111 | 14.9 | 7.0 | 9.6 | 9.5 | 3.9 | 4.7 | |||
| r 2SCAN112–115 | 8.1 | 4.3 | 4.8 | 4.7 | 1.0 | 1.5 | |||
| M06-L116 | 12.9 | 12.7 | 11.7 | 1.8 | 1.7 | 1.6 | |||
| MN15-L117 | 14.4 | 14.4 | 3.2 | 3.2 | |||||
| Hybrid | PBE0118 | 7.4 | 9.1 | 9.7 | 9.2 | 7.2 | 2.9 | 3.2 | 0.6 |
| B3LYP119,120 | 33.5 | 8.2 | 9.6 | 12.9 | 4.2 | 3.9 | |||
| TPSSh121 | 11.4 | 8.7 | 9.6 | 9.0 | 4.8 | 4.6 | |||
| r 2SCAN0122 | 5.0 | 5.6 | 5.1 | 6.2 | 4.5 | 1.3 | 1.0 | 1.0 | |
| M06123 | 7.7 | 6.8 | 5.8 | 1.2 | 1.6 | 2.2 | |||
| M06-2X123 | 6.9 | 6.7 | 1.7 | 2.0 | |||||
| MN15124 | 12.9 | 12.9 | 2.2 | 2.2 | |||||
| PW6B95125 | 9.8 | 5.8 | 8.0 | 6.1 | 3.4 | 3.6 | |||
| ωB97X126 | 8.7 | 1.1 | |||||||
| ωB97M127 | 4.8 | 2.1 | |||||||
| Double-hybrid | revDSD-PBEP86128 | 4.8 | 7.5 | 2.8 | 2.4 | 1.5 | 0.8 | ||
| PWPB95129 | 3.8 | 13.1 | 3.6 | 3.4 | 4.8 | 1.7 | |||
| ωB97M(2)130 | 9.7 | 3.0 | |||||||
| ωB97X-2131 | 7.0 | 2.1 | |||||||
| Pr2SCAN50 | 5.0 | 6.7 | 1.1 | 1.0 | |||||
| κPr2SCAN50 | 7.2 | 1.0 | |||||||
| ωPr2SCAN50 | 7.1 | 6.9 | 1.6 | 0.5 | |||||
| SOS0-PBE0-2132,133 | 7.6 | 11.2 | 1.8 | 1.7 | |||||
| B2NC-PLYP133,134 | 18.0 | 19.7 | 6.4 | 7.9 | |||||
All respective calculations were conducted with the ORCA 5.0.4,31 xTB 6.5.1,143 Molpro_2024.1,47,48 AMS 2023.104,144,145 DIRAC23,146,147 Turbomole 7.6,148 Q-Chem 5.4,149 and MOPAC 2016,150 program packages. Initially, all non-composite DFT functionals were evaluated in combination with Ahlrichs def2-QZVPP151 basis sets. To further analyze the DFT basis set errors, PBE0-D4 calculations were also carried out with the awcvtz and awcvqz basis sets (cf. Section 3.3), because PBE0-D4 showed a significant improvement in the MAD for the covalent subset. The different basis sets yield MADs of MADdef2-QZVPP = 8.8, MADawcvtz = 7.6, and MADawcvqz = 7.4 kcal mol−1. For the WDA subset, the basis sets perform equally and can be considered converged, making further counter-poise corrections obsolete. Nevertheless, no clear trend of general improvement is observed by using awcvtz for many other tested funtionals (see ESI†), which can in part be attributed to beneficial error compensation. Part of the different results obtained from both basis set families is because the calculations with awcvnz-pp basis sets use relativistic small-core pseudopotentials for all elements above Z = 19, and thus account implicitly for scalar relativistic effects. Unfortunately, for 4th row elements, this is not the case with the def2-QZVPP basis sets, which employ ECPs only for Z > 36 by default. This leads to rather large (up to 6.0 kcal mol−1) relativistic errors for some systems containing the elements Ga–Se. Detailed tests using the PBE0-D4 functional showed that safely-converged DFT results are obtained with the awcvqz-pp basis sets (see ESI†), but obviously these basis sets are not designed for DFT and much larger than necessary (and thus too expensive). Using the standard valence avtz-pp or avqz-pp basis sets, however, still lead for some systems to significant (up to 1.0 kcal mol−1) basis set errors relative to calculations with awcvqz. These errors are partly due to the basis set contractions, which are based on HF rather than DFT calculations. Recontracting the basis sets using atomic KS/PBE0 calculations significantly reduces the errors, in particular for systems containing group 13 and 14 elements. The contraction schemes were kept exactly as in the original avnz-pp basis sets. We denote the recontracted basis sets as aug-cc-pVnZ-PP-KS (short avnz-pp-ks, provided as additional ESI,† file). Calculations with the avqz-pp-ks sets (coefficients can be found in the ESI†) yielded excellent agreement with the awcvqz results. However, with the avtz-pp-ks sets errors of 0.5 kcal mol−1 remained for some systems. It turned out that these errors are mainly due to missing tighter f and g functions. We therefore recommend to use the avqz-pp-ks basis sets for all elements containing elements of the 4th period, and def2-QZVPP basis sets for all other atoms. For a subset, which contains all systems with elements of the 4th period (IHD201), this choice gave excellent agreement with corresponding awcvqz calculations (cf.Table 5). For the WDA dimers, the improvement of the avqz-pp-ks set is negligible. As these tests were only done during our revision process we will discuss mostly “pure” def2-QZVPP results in this work. We note that redesigned basis sets for DFT were very recently proposed by Determan and Wilson,152 but since their work appeared only after submission of our manuscript these were not tested in the current work.
![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Ga−N−Ga−N−Ga−N
Ga−N−Ga−N−Ga−N![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV dimer. The IHD201 subset consists of all fused systems that contain elements of the 4th period
COV dimer. The IHD201 subset consists of all fused systems that contain elements of the 4th period
| def2-QZVPP | avqz-pp-ks | awcvtz | awcvq | |
|---|---|---|---|---|
| MD | −9.4 | −7.6 | −7.8 | −7.5 |
| MAD | 9.5 | 7.7 | 8.0 | 7.7 |
| SD | 3.9 | 3.7 | 3.9 | 3.8 |
| AMAX | 15.8 | 16.5 | 16.8 | 16.9 |
| Relative wall time | 1.00 | 0.77 | 0.49 | 1.46 |
The semi-numerical chain-of-spheres integration for the Fock exchange integrals (RIJCOSX)153 has been applied with matching auxiliary basis sets (def2/J)154 which is the default in the ORCA program package. Nevertheless, tests on the def2/J basis showed that a auxiliary basis set error of up to 0.6 kcal mol−1 persists for the IHD302 benchmark set. These errors are due to the comparably small size of the def2/J auxiliary basis when used with very large, polarized basis sets like def2-QZVPP. Employing the larger def2/JK auxiliary basis set for both the Coulomb and exchange part eliminates this error and yields very similar results (neglibible RI error) as obtained with RIJK density fitting using def2/JK (see ESI,† for details). Therefore, it is recommended to use the def2/JK fitting basis sets for both J and K for functionals containing exact exchange. Root mean square deviations (RMSDs) for all tested methods are given in Table 4. A detailed statistical analysis of the results is presented in Section 4 (for the detailed data, see ESI†).
4.1 Assessment of DFT methods
Results for selected DFT methods evaluated in the extended def2-QZVPP basis set are depicted in Fig. 9. For the covalent subset of the IHD302, several trends were observed: (i) climbing Perdew's “Jacob's ladder” of DFT results in increased (more negative) dimerization energies within the same underlying exchange–correlation functional and (ii) the indispensable combination of already attractive functionals with D3, D4, and NL London dispersion corrections results in overestimation of the dimerization energies (Fig. 9a). We note that in comparison to D3, the newer D4 correction additionally includes charge-dependency and the three-body ATM term but both are not relevant for the investigated structures. Therefore, there is no general preference for D4 over D3 for this benchmark set, nor over VV10, but it depends largely on the fitted parameters and how well they perform in combination with the functional parameters. The overestimation of the dimerization energies is manifested in a switch of the sign of the MD upon dispersion correction for functionals such as PBE0 (MDplain = 5.9 kcal mol−1, MDD3(BJ) = −8.0 kcal mol−1) or TPSSh-D4 (MDplain = 10.9 kcal mol−1, MDD4 = −8.4 kcal mol−1). This results in mostly negative mean deviations for the dispersion-corrected functionals and is most pronounced for hybrid and double-hybrid functionals. This overbinding is also observed for NL (MDPBE0-NL = −8.3 kcal mol−1), thus largely excluding systematic issues of one of the dispersion corrections. An exception from this behavior is observed for very repulsive functionals like B3LYP. Some functionals that consider dispersion explicitly during the parameterization process such as Head-Gordon's ωB97M-V perform relatively well for the IHD302 dimerization energies but still tend to overbind. The Minnesota-type functionals that indirectly cover some medium-ranged dispersion effects via their parameterization consistently underestimate the dimerization energies in the range of MDM06-2X = 3.2 kcal mol−1 to MDMN15-L = 12.1 kcal mol−1. The D3(0) correction only slightly reduces this underestimation (MDM06-2X-D3(0) = 2.9 kcal mol−1).The observed overall overbinding trend of the explicitly dispersion-corrected functionals is mostly preserved for the weak donor–acceptor interacting dimers (cf.Fig. 9b) with the Minnesota functionals also adopting the behavior of the other functionals by yielding negative MDs. Nevertheless, the explicit treatment of London dispersion is highly recommended as it still significantly reduces the error for all tested (meta-)GGA functionals and most (double-)hybrid functionals. This is in line with the fact that DFT methods by construction do not cover London dispersion interactions (only potentially implicitly by parameterization), which is why corresponding corrections are indispensable for getting the right answer for the right reason which also holds true here. The D3, D4 and NL London dispersion corrections are also mostly in good agreement with each other. The most significant difference is found for PWPB95 which is an exception that can be traced back to its unsuited parameterization. It is hence recommended to check at least two different dispersion correction schemes for complicated systems. In the following, we only discuss dispersion-corrected approaches. Overall, both the covalent and also the weak donor–acceptor subset suffer from the over-attractive nature of many tested functionals with the latter being less affected. Here, the best-performing dispersion-corrected functionals regarding the covalent subset are r2SCAN-D3(BJ) (RMSDCOV = 4.3 kcal mol−1; RMSDWDA = 1.0 kcal mol−1) in the (m)GGA class, ωB97M-V (RMSDCOV = 4.8 kcal mol−1; RMSDWDA = 2.1 kcal mol−1) and r2SCAN0-D4 (RMSDCOV = 5.1 kcal mol−1; RMSDWDA = 1.0 kcal mol−1) in the hybrid class, and revDSD-PBEP86-D4 (RMSDCOV = 2.8 kcal mol−1; RMSDWDA = 0.8 kcal mol−1) in the double-hybrid class. Nevertheless, we note that the accuracy for the covalent subset is strongly functional dependent and even the best performing among the assessed functionals, which show reasonably small statistical errors, still yield significant outliers with several kcal mol−1 deviation from the reference dimerization energies thus limiting their scope if highly accurate predictions are required.
In summary, the introduction of physically motivated ingredients into the density functional upon climbing Jacob's ladder in combination with a well-established dispersion correction yields an untypically small benefit for the covalent subset. This indicates less effective residual error compensation between the various contributions to the total energy for functionals that yield accurate results for other benchmark studies. Although the dispersion corrections tested at shorter distances (attenuation region) are somewhat less accurate than in the long-range London regime, they are still qualitatively correct and physically needed. Hence, the general trend for the tested DFT methods to overestimate the dimerization energies hints at an over-attractive nature of many usually well-behaved functionals that manifests for this congested situation of many spatially close bonds and partially repulsive regimes covered by the IHD302 structures. In this case, only very repulsive functionals such as B3LYP still underestimate the covalent dimerization energies despite large dispersion corrections that cannot fully compensate for the functionals' comparably bad overall performance.
Fortuitous error compensation for less repulsive functionals applied without dispersion correction and thus misleading conclusions regarding their need and overall accuracy has been discussed previously.155 These results further underline that the IHD302 benchmark set challenges established and/or outdated design and parameterization strategies of density functionals. Specifically, fitting a robust dispersion correction directly in the process of the functional fit seems to be important to guarantee a well-balanced match of exchange–correlation functional and dispersion contributions, also for shorter distances than the usually evaluated London regime. This view is supported by the relatively good performance of Head-Gordon's ωB97M-V functional that is trained in the presence of the VV10 non-local dispersion correction. As ωB97M-V still systematically overbinds the investigated systems on average, incorporating more high-level benchmark sets that focus on the transition from non-covalent to covalent bonding as in the IHD302 set may further improve its performance. Inclusion of explicitly repulsive contacts into the parameterization process as provided in the R160x6,156 R739,157 or SH250158 test sets and the here introduced IHD302 benchmark set may therefore be beneficial to avoid over-attractiveness of the respective functional for comparable systems even though the element composition may differ. Moreover, residual errors of dispersion corrections in the medium- to short-ranged regime (assumed to be about 10–20% due to additional uncertainty of the damping function and the asymptotic errors of about 5% in the C6 coefficients)138 may be further reduced by inclusion of accurate fit data also covering repulsive p-block contacts.
To classify the DFT results, dispersion-corrected Hartree–Fock (HF-D4) dimerization energies close to the HF basis set limit (awcvtz with CABS singles correction, see Section 3.3) will be discussed here. HF is slightly less repulsive than, e.g., B3LYP, but cannot show over-attractiveness as it is parameter-free and medium to long-range correlation effects are only accounted for posteriorly by the D4 correction. Consistently, the dimerization energies for the WDA structures are overestimated more strongly than, e.g., with B3LYP, which is due to the less accurate description of the short- and medium-range correlation effects (i.e., in the damping range) with the D4 dispersion correction. The deviations from the reference values are negative in all cases up to −11.2 kcal mol−1 for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Pb−P−Pb−P−Pb−P
Pb−P−Pb−P−Pb−P![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) WDA (one of the test systems for the scans analyzed in the next section). In contrast to most of the tested DFT methods, HF-D4 does not produce a systematic error for the COV structures (MD ≈ 0), whereas the scatter of the deviations from the reference is significantly larger, because the D4 correction describes the formed σ bonds (to the H atoms or from the lone pairs) approximately well, but more difficult cases are not adequately taken into account. This is particularly the case for the IV–V systems with N (up to −39.8 kcal mol−1 deviation from the reference for
WDA (one of the test systems for the scans analyzed in the next section). In contrast to most of the tested DFT methods, HF-D4 does not produce a systematic error for the COV structures (MD ≈ 0), whereas the scatter of the deviations from the reference is significantly larger, because the D4 correction describes the formed σ bonds (to the H atoms or from the lone pairs) approximately well, but more difficult cases are not adequately taken into account. This is particularly the case for the IV–V systems with N (up to −39.8 kcal mol−1 deviation from the reference for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Sn−N−Sn−N−Sn−N
Sn−N−Sn−N−Sn−N![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV, which also has the most negative HF contribution to the dimerization energy of all IHD302 systems with −164.6 kcal mol−1) and for III–VI systems with boron (up to +41.2 kcal mol−1) deviation from the reference for
COV, which also has the most negative HF contribution to the dimerization energy of all IHD302 systems with −164.6 kcal mol−1) and for III–VI systems with boron (up to +41.2 kcal mol−1) deviation from the reference for ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) B−Po−B−Po−B−Po
B−Po−B−Po−B−Po![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) COV with a large positive HF contribution to the dimerization energy; this system also has the largest contribution of the correlation energy to ΔE (see ESI,† data_correlation_methods.xlsx).
COV with a large positive HF contribution to the dimerization energy; this system also has the largest contribution of the correlation energy to ΔE (see ESI,† data_correlation_methods.xlsx).
To analyze the observed errors of the dispersion-corrected DFT methods in greater detail, specifically in the more repulsive region of the PES, we conducted exemplary rigid potential energy surface scans of the inter-fragment distance for both dimer structures of ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Al−O−Al−O−Al−O
Al−O−Al−O−Al−O![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) and
and ![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Pb−P−Pb−P−Pb−P
Pb−P−Pb−P−Pb−P![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) , respectively (Fig. 10). All scans clearly show that the PBE0 functional, even though not considered a particularly repulsive functional, systematically underestimates the interaction energies for both the covalently and the weak donor–acceptor bound dimers. This underlines the need for adding a (London) dispersion correction to achieve agreement with the reference (PNO-LCCSD(T)-F12/awcvtz with PROJECTOR=MIXED and TRHPNO_LMP2=1d-10) PES curve. Despite a slight over-correction with the NL and D4 dispersion corrections is observed for both systems, their asymptotic behavior is fully correct. These results confirm also for such rather unusual systems that the residual error of properly dispersion-corrected DFT methods is mainly originating from the DFT exchange–correlation functional and less from uncertainties of the dispersion corrections at the short- and medium-range distances. Overall, the overestimation is most pronounced at short inter-fragment distances, while the error decreases in the asymptotic region. Further, the scans of the weak donor–acceptor dimers underline their non-equilibrium nature by not showing a minimum at the sum of van der Waals radii due to the donor–acceptor character of the interaction that is distinct from typically discussed non-covalent interactions at larger separation (London regime).
, respectively (Fig. 10). All scans clearly show that the PBE0 functional, even though not considered a particularly repulsive functional, systematically underestimates the interaction energies for both the covalently and the weak donor–acceptor bound dimers. This underlines the need for adding a (London) dispersion correction to achieve agreement with the reference (PNO-LCCSD(T)-F12/awcvtz with PROJECTOR=MIXED and TRHPNO_LMP2=1d-10) PES curve. Despite a slight over-correction with the NL and D4 dispersion corrections is observed for both systems, their asymptotic behavior is fully correct. These results confirm also for such rather unusual systems that the residual error of properly dispersion-corrected DFT methods is mainly originating from the DFT exchange–correlation functional and less from uncertainties of the dispersion corrections at the short- and medium-range distances. Overall, the overestimation is most pronounced at short inter-fragment distances, while the error decreases in the asymptotic region. Further, the scans of the weak donor–acceptor dimers underline their non-equilibrium nature by not showing a minimum at the sum of van der Waals radii due to the donor–acceptor character of the interaction that is distinct from typically discussed non-covalent interactions at larger separation (London regime).
Besides these systematic trends, it is observed that the functionals behave significantly differently with respect to the element composition of the system (Fig. 11). For example, the extent of the error of the dimerization energies obtained with PWPB95-D4, an overall well-performing DFA, does not follow the trends of the reference dimerization energies (cf.Fig. 8). Instead, the error becomes systematically more positive with increasing mean atomic number ![[Z with combining macron]](https://www.rsc.org/images/entities/i_char_005a_0304.gif) heavy for both dimer types and all main group combinations. For ωB97M-V, the error trends are much less systematic with the error distribution mostly following the trends of the reference dimerization energies for the covalent dimers, while mostly the IV–V element combination yields an inverted trend compared to PWPB95-D4.
heavy for both dimer types and all main group combinations. For ωB97M-V, the error trends are much less systematic with the error distribution mostly following the trends of the reference dimerization energies for the covalent dimers, while mostly the IV–V element combination yields an inverted trend compared to PWPB95-D4.
4.2 Composite methods
As DFT calculations with large basis sets can become computationally unfeasible for large molecules, composite approaches that employ smaller basis sets together with tailored corrections have proven to yield accurate results at a fraction of computation time for various chemical systems. The most prominent composite methods are the so-called “3c” methods including PBEh-3c,104 B97-3c,103r2SCAN-3c,30 and ωB97X-3c.105 The “3c” methods employ relatively small tailored basis sets and specifically adjusted corrections like D4 and a geometrical counter-poise correction to achieve good accuracy at much reduced computational cost. Another notable addition is Head-Gordon's B97M-V-C approach which combines the B97M-V functional with a def2-SVPD basis set and a tailored DFT-C counter-poise correction.102 For the covalent subset of the IHD302, comparable trends as for the non-composite functionals evaluated with the extended def2-QZVPP basis are observed. The inclusion of Fock-exchange in PBEh-3c and in the recent ωB97X-3c range-separated hybrid yields more negative covalent dimerization energies compared to the B97M-V-C, r2SCAN-3c, and B97-3c meta-GGA approaches. Comparable results are obtained for the weak donor–acceptor subset, even though B97-3c tends to overbind these systems (Fig. 12). Overall, specifically the more recent composite methods r2SCAN-3c and ωB97X-3c perform quite well with RMSDs of 5.7 kcal mol−1 and 8.0 kcal mol−1 for the covalent and 1.5 kcal mol−1 and 1.1 kcal mol−1 for the weak donor–acceptor subset, respectively. Impressively, they perform similarly or even slightly better than the parent functionals evaluated in a quadruple-zeta basis set thus underlining their high robustness. The very good performance of ωB97X-3c is specifically remarkable, as it employs large-core effective core potentials. The B97M-V-C approach is found to be less competitive, yielding significantly larger errors than its conventional DFT counterpart.4.3 Semi-empirical quantum mechanical methods
Due to their low computational cost, semi-empirical quantum mechanical methods have become a central part of automated conformational sampling and reaction screening workflows.159,160 Nevertheless, most of these methods are not or only sparsely parameterized for heavy p-block elements. Further, they typically yield limited accuracy for off-target elements and complicated electronic situations. Notable exceptions in terms of general applicability are the GFNn-xTB19 and PMx161 SQM families of methods. The corresponding error statistic is shown in Fig. 13. For the covalent subset of the IHD302, the GFNn-xTB methods yield RMSDs of 40.6 kcal mol−1 and 36.8 kcal mol−1, respectively for GNF1- and GFN2-xTB. The preliminary, non-self-consistent GFN0-xTB variant that is also used in the context of metallic clusters162 yields an RMSD of 52.0 kcal mol−1. These errors are one magnitude larger than those obtained with many well-performing DFT methods. This underlines the valuable focus of the IHD302 on direct p-block element interactions that manifests the weaknesses of the respective SQM methods. In conventional benchmark sets that often employ organic substituents for saturation of the p-block element, these are compensated by the respective substituent interactions. Accordingly, the difference between DFT and SQM methods is usually considerably smaller. The Hartree–Fock based PMx methods yield much higher RMSDs of 158.8 kcal mol−1 and 162.7 kcal mol−1 for PM6 and PM7, respectively, even exceeding the mean dimerization energy of −95.5 kcal mol−1 and therefore, these methods cannot be recommended. For the weak donor–acceptor subset, similar trends are observed for the GFNn-xTB and PMx methods. A comparison between the computational cost and the accuracy of different SQM and DFT methods can be found in the ESI† (Fig. S8). GFN2-xTB is, e.g., up to 2700 times faster than the efficient r2SCAN-3c composite DFT method in a single point calculation of![[upper bond 1 start]](https://www.rsc.org/images/entities/char_e010.gif) Tl−Po−Tl−Po−Tl−Po
Tl−Po−Tl−Po−Tl−Po![[upper bond 1 end]](https://www.rsc.org/images/entities/char_e011.gif) WDA. Overall, none of the semi-empirical methods yields satisfying results for the complete IHD302 benchmark. Nevertheless, GFN2-xTB may be considered a reasonable choice regarding the relatively large mean reference dimerization energies for the covalently bound dimers. Nevertheless, future improvements of SQM methods based on the presented benchmark data would be desirable, especially for modeling the metallic clusters of p-block elements.
WDA. Overall, none of the semi-empirical methods yields satisfying results for the complete IHD302 benchmark. Nevertheless, GFN2-xTB may be considered a reasonable choice regarding the relatively large mean reference dimerization energies for the covalently bound dimers. Nevertheless, future improvements of SQM methods based on the presented benchmark data would be desirable, especially for modeling the metallic clusters of p-block elements.
5 Summary and perspective
In this work, we compiled a novel benchmark set of dimerization energies of six-membered purely p-block inorganic heterocycles. The benchmark set termed Inorganic Heterocycle Dimerizations 302 (IHD302) includes 302 energies for two distinct dimerization motifs, covalent and non-equilibrium weak donor–acceptor dimers. Reference values for these 604 dimerization energies were computed at the PNO-LCCSD(T)-F12 level. Due to large electron correlation contributions, the importance of core–valence correlation effects, and slow basis set convergence, these calculations turned out to be extremely challenging. We therefore carried out extensive benchmarks for 16 selected systems (eight of these were initially more or less randomly selected and further eight, which showed particularly large basis set errors, were added later). It was found that the dominant part of the errors were due to the slow basis set convergence, while errors caused by the local approximations are negligible.At first, we employed the cc-pVTZ-PP-F12 basis sets of Hill and Peterson,76 which were specifically optimized for F12 calculations on heavy p-block elements, including correlation of the (n − 1)d shell. It turned out, however, that these basis sets are too small for reliably obtaining the required accuracy. Even with F12 methods, deviations of up to about 3 kcal mol−1 relative to more accurate calculations with the aug-cc-pwCVnZ (n = T, Q) basis sets were observed for the covalent binding energies. By employing a PNO-LMP2-F12 basis set correction denoted vtz-f12(corr.) and obtained with the aug-cc-pwCVTZ basis, the MADs and SDs of the 16 selected systems relative to the PNO-LCCSD(T)-F12/aug-cc-pwCVTZ and aug-cc-pwCVQZ results could be reduced to 0.26 ± 0.25 kcal mol−1 (max error 0.87 kcal mol−1) and 0.44 ± 0.28 kcal mol−1 (max error 1.01 kcal mol−1), respectively. For the weak donor–acceptor structures, the errors are even about three times smaller. The larger errors relative to the aug-cc-pwCVQZ basis mainly stem from the remaining basis set errors of the triples (T) contributions obtained with the TZ basis set. The errors of the vtz-f12(corr.) results are significantly smaller than the errors of the DFT methods. Therefore, we decided to compute the 602 reference values at the PNO-LCCSD(T)-F12/vtz-f12(corr.) level, which is computationally much cheaper than using the aug-cc-pwCVTZ or even the aug-cc-pwCVQZ basis sets.
Based on these reference data, the performance of 26 DFT functionals (evaluated with the def2-QZVPP basis set), five composite DFT approaches, and five semi-empirical quantum mechanical methods in combination with three different dispersion correction schemes (D3, D4, NL) were assessed. The best-performing dispersion-corrected functionals ordered by their rung on “Jacob's ladder” regarding the covalent subset are r2SCAN-D4 (meta-GGA, RMSDCOV = 4.8 kcal mol−1; RMSDWDA = 1.5 kcal mol−1), ωB97M-V (hybrid, RMSDCOV = 4.8 kcal mol−1; RMSDWDA = 2.1 kcal mol−1) and r2SCAN0-D4 (RMSDCOV = 5.1 kcal mol−1; RMSDWDA = 1.0 kcal mol−1), and revDSD-PBEP86-D4 (double-hybrid, RMSDCOV = 2.8 kcal mol−1; RMSDWDA = 0.8 kcal mol−1). Further, the r2SCAN-3c composite DFT method is found to yield good results regarding its reduced computational cost with RMSDCOV = 5.7 kcal mol−1 and RMSDWDA = 1.5 kcal mol−1, respectively.
Furthermore, we found significant errors (up to 6 kcal mol−1 in binding energies) due to missing scalar relativistic effects in calculations of molecules containing p-block elements of the 4th period, when using the def2-TZVPP or def2-QZVPP basis sets. This is because the def2 basis sets are associated to relativistic pseudo potentials only for elements with Z > 36. Further non-negligible errors (up to 1 kcal mol−1) can occur in DFT calculations when using standard correlation consistent basis sets, such as aug-cc-pVnZ-PP, since these are contracted with coefficients from Hartree–Fock calculations. We therefore generated for the elements Ga–Se recontracted aug-cc-pVQZ-PP-KS basis sets, in which the contraction coefficients are taken from DFT (PBE0) calculations. Using these basis sets for 4th row elements in combination with the ECP10MDF pseudo potentials leads to significant improvements of the overall accuracy and hence, we recommend this basis sets for accurate DFT calculations of systems including 4th row elements.
The application of a London dispersion correction is found to be mandatory, even though rather attractive functionals tend to be over-corrected due to a less effective error compensation (underestimation of repulsive interactions out-weighted by missing attractive long-range dispersion interactions). This behavior underlines that London dispersion should be considered during the construction process of the respective functional to guarantee a well-balanced match of functional and dispersion correction. In this regard, the IHD302 has proven to be a specifically indicative data set for the performance of dispersion-corrected functionals for p-block thermochemistry. The test set is also highly challenging for SQM methods as none of the tested (and currently available generally applicable) SQM methods is able to accurately reproduce the reference data, even though GFN2-xTB (RMSDCOV = 36.8 kcal mol−1; RMSDWDA = 6.7 kcal mol−1) clearly outperforms, e.g., PM7 (RMSDCOV = 162.7 kcal mol−1; RMSDWDA = 17.9 kcal mol−1). Overall, the clear focus on the p-block element interactions without organic substituent bias allows for a unique and systematic assessment of quantum chemical methods for these elements. Regarding the high importance of p-block compounds, e.g., in FLP chemistry or opto-electronics, the IHD302 seems to represent a valuable assessment which may significantly impact future method development in this field, allowing for the development of more robust and transferable approximate quantum chemical methods. This is made possible not least by efficient and sophisticated implementations of explicit local correlation methods such as PNO-LCCSD(T)-F12, which was successfully applied as reference in this work.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. G. and M. B. gratefully acknowledge financial support of the Max Planck Society through the Max Planck fellow program. T. G. is thankful for fruitful discussions and technical support from Thomas Froitzheim and Lukas Wittmann. Open Access funding provided by the Max Planck Society.Notes and references
- S. Aldridge and C. Jones, Chem. Soc. Rev., 2016, 45, 763–764 RSC.
- L. Zhao, S. Pan, N. Holzmann, P. Schwerdtfeger and G. Frenking, Chem. Rev., 2019, 119, 8781–8845 CrossRef CAS PubMed.
- D. W. Stephan and G. Erker, Angew. Chem., Int. Ed., 2015, 54, 6400–6441 CrossRef CAS PubMed.
- A. R. Jupp and D. W. Stephan, Trends Chem., 2019, 1, 35–48 CrossRef CAS.
- M. Veith, Chem. Rev., 1990, 90, 3–16 CrossRef CAS.
- S. Nakarnura, Semicond. Semimetals, 1997, 48, 391–443 Search PubMed.
- H. Asahi, Infrared Detect. Emit. Mater. Devices, Springer, Boston, MA, 2001, pp. 233–249 Search PubMed.
- K. Ota and R. Kinjo, Chem. – Asian J., 2020, 15, 2558–2574 CrossRef CAS PubMed.
- J. G. Ekerdt, Y. M. Sun, A. Szabo, G. J. Szulczewski and J. M. White, Chem. Rev., 1996, 96, 1499–1517 CrossRef CAS PubMed.
- F. C. Sauls and L. V. Interrante, Coord. Chem. Rev., 1993, 128, 193–207 CrossRef CAS.
- E. E. Foos, R. J. Jouet, R. L. Wells, A. L. Rheingold and L. M. Liable-Sands, J. Organomet. Chem., 1999, 582, 45–52 CrossRef CAS.
- A. M. Priegert, B. W. Rawe, S. C. Serin and D. P. Gates, Chem. Soc. Rev., 2016, 45, 922–953 RSC.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- G. Bistoni, A. A. Auer and F. Neese, Chem. – Eur. J., 2017, 23, 865–873 CrossRef CAS PubMed.
- N. Mehta, T. Fellowes, J. M. White and L. Goerigk, J. Chem. Theory Comput., 2021, 17, 2783–2806 CrossRef CAS PubMed.
- J. Gorges, S. Grimme and A. Hansen, Phys. Chem. Chem. Phys., 2022, 24, 28831–28843 RSC.
- T. Husch, A. C. Vaucher and M. Reiher, Int. J. Quantum Chem., 2018, 118, e25799 CrossRef.
- F. Spiegelman, N. Tarrat, J. Cuny, L. Dontot, E. Posenitskiy, C. Martí, A. Simon and M. Rapacioli, Adv. Phys. X, 2020, 5, 1710252 CAS.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- A. Y. Timoshkin and G. Frenking, Inorg. Chem., 2003, 42, 60–69 CrossRef CAS PubMed.
- A. Mohajeri and M. Ebadi, J. Phys. Chem. A, 2012, 116, 4678–4686 CrossRef CAS PubMed.
- H. Ni, D. M. York, L. Bartolotti, R. L. Wells and W. Yang, J. Am. Chem. Soc., 1996, 118, 5732–5736 CrossRef CAS.
- J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173 CrossRef CAS PubMed.
- J. J. P. Stewart, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS PubMed.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- E. Caldeweyher and J. G. Brandenburg, J. Phys.: Condens. Matter, 2018, 30, 213001 CrossRef PubMed.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2009, 113, 5806–5812 CrossRef CAS PubMed.
- S. Grimme, A. Hansen, S. Ehlert and J. M. Mewes, J. Chem. Phys., 2021, 154, 064103 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- H. Neugebauer, H. T. Vuong, J. L. Weber, R. A. Friesner, J. Shee and A. Hansen, J. Chem. Theory Comput., 2023, 19, 6208–6225 CrossRef CAS PubMed.
- S. Grimme and A. Hansen, Angew. Chem., Int. Ed., 2015, 54, 12308–12313 CrossRef CAS PubMed.
- C. A. Bauer, A. Hansen and S. Grimme, Chem. – Eur. J., 2017, 23, 6150–6164 CrossRef CAS PubMed.
- R. Nieman, J. R. Carvalho, B. Jayee, A. Hansen, A. J. A. Aquino, M. Kertesz and H. Lischka, Phys. Chem. Chem. Phys., 2023, 25, 27380–27393 RSC.
- M. K. Kesharwani, N. Sylvetsky, A. Köhn, D. P. Tew and J. M. L. Martin, J. Chem. Phys., 2018, 149, 154109 CrossRef PubMed.
- E. Ramos-Cordoba, P. Salvador and E. Matito, Phys. Chem. Chem. Phys., 2016, 18, 24015–24023 RSC.
- H.-J. Werner, G. Knizia, C. Krause, M. Schwilk and M. Dornbach, J. Chem. Theory Comput., 2015, 11, 484–507 CrossRef CAS PubMed.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2015, 11, 5291–5304 CrossRef CAS PubMed.
- M. Schwilk, Q. Ma, C. Köppl and H.-J. Werner, J. Chem. Theory Comput., 2017, 13, 3650–3675 CrossRef CAS PubMed.
- Q. Ma, M. Schwilk, C. Köppl and H.-J. Werner, J. Chem. Theory Comput., 2017, 13, 4871–4896 CrossRef CAS PubMed.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2017, 14, 198–215 CrossRef PubMed.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2020, 16, 3135–3151 CrossRef CAS PubMed.
- Q. Ma and H.-J. Werner, J. Chem. Theory Comput., 2021, 17, 902–926 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, I. Thomas, F. Miller, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, S. J. Bennie, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, S. J. R. Lee, Y. Liu, A. W. Lloyd, Q. Ma, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, T. F. Miller III, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and M. Welborn, MOLPRO, version 2023.1, a package of ab initio programs Search PubMed.
- F. Pavošević, P. Pinski, C. Riplinger, F. Neese and E. F. Valeev, J. Chem. Phys., 2016, 144, 144109 CrossRef PubMed.
- F. Pavošević, C. Peng, P. Pinski, C. Riplinger, F. Neese and E. F. Valeev, J. Chem. Phys., 2017, 146, 174108 CrossRef PubMed.
- H.-J. Werner and A. Hansen, J. Chem. Theory Comput., 2023, 19(20), 7007–7030 CrossRef CAS PubMed.
- M. Kallay, J. Chem. Phys., 2015, 142, 204105 CrossRef PubMed.
- P. R. Nagy, G. Samu and M. Kallay, J. Chem. Theory Comput., 2016, 12, 4897–4914 CrossRef CAS PubMed.
- P. R. Nagy and M. Kállay, J. Chem. Phys., 2017, 146, 214106 CrossRef PubMed.
- P. R. Nagy, G. Samu and M. Kállay, J. Chem. Theory Comput., 2018, 14, 4193–4215 CrossRef CAS PubMed.
- P. Tecmer and K. Boguslawski, Phys. Chem. Chem. Phys., 2022, 24, 23026–23048 RSC.
- G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843 CrossRef CAS PubMed.
- J. Pipek and P. G. Mezey, J. Chem. Phys., 1989, 90, 4916–4926 CrossRef CAS.
- H.-J. Werner, C. Köppl, Q. Ma and M. Schwilk, in Fragmentation: Towards Accurate Calculations on Complex Molecular Systems, ed. M. S. Gordon, Wiley, Chichester, UK, 2017, pp. 1–79 Search PubMed.
- Q. Ma and H.-J. Werner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, e1371 Search PubMed.
- W. Klopper and C. C. M. Samson, J. Chem. Phys., 2002, 116, 6397–6410 CrossRef CAS.
- H.-J. Werner, T. B. Adler and F. R. Manby, J. Chem. Phys., 2007, 126, 164102 CrossRef PubMed.
- S. Ten-no, Chem. Phys. Lett., 2004, 398, 56–61 CrossRef CAS.
- S. Ten-no, J. Chem. Phys., 2004, 121, 117–129 CrossRef CAS PubMed.
- S. Kedžuch, M. Milko and J. Noga, Int. J. Quantum Chem., 2005, 105, 929–936 CrossRef.
- T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- H.-J. Werner and A. Hansen, J. Chem. Theory Comput., 2023, 19, 7007–7030 CrossRef CAS PubMed.
- K. Peterson, C. Krause, H. Stoll, J. G. Hill and H.-J. Werner, Mol. Phys., 2011, 109, 2607–2623 CrossRef CAS.
- H.-J. Werner, G. Knizia and F. R. Manby, Mol. Phys., 2011, 109, 407–417 CrossRef CAS.
- H.-J. Werner, J. Chem. Phys., 2008, 129, 101103 CrossRef PubMed.
- T. B. Adler and H.-J. Werner, J. Chem. Phys., 2011, 135, 144117 CrossRef PubMed.
- T. B. Adler and H.-J. Werner, J. Chem. Phys., 2011, 135, 144117 CrossRef PubMed.
- C. Krause and H.-J. Werner, Phys. Chem. Chem. Phys., 2012, 14, 7591–7604 RSC.
- Q. Ma, M. Schwilk, C. Köppl and H.-J. Werner, J. Chem. Theory Comput., 2017, 13, 4871–4896 CrossRef CAS PubMed.
- J. G. Hill and K. A. Peterson, J. Chem. Phys., 2014, 141, 094106 CrossRef PubMed.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- B. Metz, M. Schweizer, H. Stoll, M. Dolg and W. Liu, Theor. Chem. Acc., 2000, 104, 22 Search PubMed.
- B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113 CrossRef CAS.
- K. A. Peterson and K. E. Yousaf, J. Chem. Phys., 2010, 133, 174116 CrossRef PubMed.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- W. Kutzelnigg and W. Liu, J. Chem. Phys., 2005, 123, 241102 CrossRef PubMed.
- W. Liu and D. Peng, J. Chem. Phys., 2006, 125, 044102 CrossRef PubMed.
- M. Iliaš and T. Saue, J. Chem. Phys., 2007, 126, 064102 CrossRef PubMed.
- D. Peng, W. Liu, Y. Xiao and L. Cheng, J. Chem. Phys., 2007, 127, 104106 CrossRef PubMed.
- M. K. Armbruster, F. Weigend, C. van Wüllen and W. Klopper, Phys. Chem. Chem. Phys., 2008, 10, 1748 RSC.
- A. Baldes and F. Weigend, Mol. Phys., 2013, 111, 2617–2624 CrossRef CAS.
- C. Holzer, Y. J. Franzke and A. Pausch, J. Chem. Phys., 2022, 157, 204102 CrossRef CAS PubMed.
- D. Peng, N. Middendorf, F. Weigend and M. Reiher, J. Chem. Phys., 2013, 138, 184105 CrossRef PubMed.
- Y. J. Franzke, L. Spiske, P. Pollak and F. Weigend, J. Chem. Theory Comput., 2020, 16, 5658–5674 CrossRef CAS PubMed.
- S. Höfener, R. Ahlrichs, S. Knecht and L. Visscher, ChemPhysChem, 2012, 13, 3952–3957 CrossRef PubMed.
- F. Weigend, J. Comput. Chem., 2008, 29, 167 CrossRef CAS PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291 RSC.
- K. E. Yousaf and K. A. Peterson, J. Chem. Phys., 2008, 129, 184108 CrossRef PubMed.
- E. F. Valeev, Chem. Phys. Lett., 2004, 395, 190–195 CrossRef CAS.
- M. S. Marshall, L. A. Burns and C. D. Sherrill, J. Chem. Phys., 2011, 135, 194102 CrossRef PubMed.
- J. M. L. Martin and S. Parthiban, W1 and W2 theories, and their variants: thermochemistry in the kJ mol−1 accuracy range, Springer, Basel, 2001, pp. 31–65 Search PubMed.
- S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 59, 15665–15673 CrossRef CAS PubMed.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- P. S. Brahmkshatriya, P. Dobeš, J. Fanfrlík, J. Řezáč, K. Paruch, A. Bronowska, M. Lepšík and P. Hobza, Curr. Comput.-Aid. Drug, 2013, 9, 118–129 CrossRef CAS PubMed.
- J. Witte, J. B. Neaton and M. Head-Gordon, J. Chem. Phys., 2017, 146, 234105 CrossRef PubMed.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104 CrossRef PubMed.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed.
- M. Müller, A. Hansen and S. Grimme, J. Chem. Phys., 2023, 158, 14103 CrossRef PubMed.
- R. Sure and S. Grimme, J. Comput. Chem., 2013, 34, 1672–1685 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2015, 142, 74111 CrossRef PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208–8215 CrossRef CAS PubMed.
- J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 9248 CrossRef CAS PubMed.
- S. Ehlert, U. Huniar, J. Ning, J. W. Furness, J. Sun, A. D. Kaplan, J. P. Perdew and J. G. Brandenburg, J. Chem. Phys., 2021, 154, 061101 CrossRef CAS PubMed.
- J. Ning, M. Kothakonda, J. W. Furness, A. D. Kaplan, S. Ehlert, J. G. Brandenburg, J. P. Perdew and J. Sun, Phys. Rev. B, 2022, 106, 075422 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- H. S. Yu, X. He and D. G. Truhlar, J. Chem. Theory Comput., 2016, 12, 1280–1293 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5656 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, J. Chem. Phys., 2003, 119, 12129–12137 CrossRef CAS.
- M. Bursch, H. Neugebauer, S. Ehlert and S. Grimme, J. Chem. Phys., 2022, 156, 10–12 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051 RSC.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924 RSC.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef PubMed.
- G. Santra, M. Cho and J. M. Martin, J. Phys. Chem. A, 2021, 125, 4614–4627 CrossRef CAS PubMed.
- L. Goerigk and S. Grimme, J. Chem. Theory Comput., 2011, 7, 291–309 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2018, 148, 241736 CrossRef PubMed.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2009, 131, 174105 CrossRef PubMed.
- M. Alipour, Chem. Phys. Lett., 2017, 684, 423–426 CrossRef CAS.
- N. Mehta, M. Casanova-Páez and L. Goerigk, Phys. Chem. Chem. Phys., 2018, 20, 23175–23194 RSC.
- F. Yu, J. Phys. Chem. A, 2014, 118, 3175–3182 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- E. Caldeweyher, J. M. Mewes, S. Ehlert and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 8499–8512 RSC.
- O. A. Vydrov and T. Van Voorhis, Phys. Rev. Lett., 2009, 103, 063004 CrossRef PubMed.
- W. Hujo and S. Grimme, J. Chem. Theory Comput., 2011, 7, 3866–3871 CrossRef CAS PubMed.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- AMS 2023.104, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2020, https://www.scm.com/ Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- DIRAC, a relativistic ab initio electronic structure program, Release DIRAC23 (2023), written by R. Bast, A. S. P. Gomes, T. Saue and L. Visscher and H. J. Aa. Jensen, with contributions from I. A. Aucar, V. Bakken, C. Chibueze, J. Creutzberg, K. G. Dyall, S. Dubillard, U. Ekström, E. Eliav, T. Enevoldsen, E. Faßhauer, T. Fleig, O. Fossgaard, L. Halbert, E. D. Hedegård, T. Helgaker, B. Helmich-Paris, J. Henriksson, M. van Horn, M. Iliaš, Ch. R. Jacob, S. Knecht, S. Komorovský, O. Kullie, J. K. Lærdahl, C. V. Larsen, Y. S. Lee, N. H. List, H. S. Nataraj, M. K. Nayak, P. Norman, A. Nyvang, G. Olejniczak, J. Olsen, J. M. H. Olsen, A. Papadopoulos, Y. C. Park, J. K. Pedersen, M. Pernpointner, J. V. Pototschnig, R. di Remigio, M. Repisky, K. Ruud, P. Sałek, B. Schimmelpfennig, B. Senjean, A. Shee, J. Sikkema, A. Sunaga, A. J. Thorvaldsen, J. Thyssen, J. van Stralen, M. L. Vidal, S. Villaume, O. Visser, T. Winther, S. Yamamoto and X. Yuan (available at DOI:10.5281/zenodo.7670749), see also (https://www.diracprogram.org).
- T. Saue, R. Bast, A. S. P. Gomes, H. J. A. Jensen, L. Visscher, I. A. Aucar, R. Di Remigio, K. G. Dyall, E. Eliav, E. Fasshauer, T. Fleig, L. Halbert, E. D. HedegÅrd, B. Helmich-Paris, M. Iliaš, C. R. Jacob, S. Knecht, J. K. Laerdahl, M. L. Vidal, M. K. Nayak, M. Olejniczak, J. M. H. Olsen, M. Pernpointner, B. Senjean, A. Shee, A. Sunaga and J. N. P. van Stralen, J. Chem. Phys., 2020, 152, 204104 CrossRef CAS PubMed.
- TURBOMOLE V7.6 2023, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.com.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, R. A. DiStasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801 CrossRef CAS PubMed.
- J. P. James, MOPAC2016, Stewart, Stewart Computational Chemistry, Colorado Springs, CO, USA, 2016, https://OpenMOPAC.net Search PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. J. Determan and A. K. Wilson, J. Chem. Phys., 2024, 160, 084105 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- V. M. Miriyala and J. Řezáč, J. Phys. Chem. A, 2018, 122, 2801–2808 CrossRef CAS PubMed.
- K. Kříž, M. Nováček and J. Řezáč, J. Chem. Theory Comput., 2021, 17, 1548–1561 CrossRef PubMed.
- K. Kříž and J. Řezáč, Phys. Chem. Chem. Phys., 2022, 24, 14794–14804 RSC.
- P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192 RSC.
- S. Dohm, M. Bursch, A. Hansen and S. Grimme, J. Chem. Theory Comput., 2020, 16, 2002–2012 CrossRef CAS PubMed.
- T. Husch, A. C. Vaucher and M. Reiher, Int. J. Quantum Chem., 2018, 118, e25799 CrossRef.
- A. Ricchebuono, E. Vottero, A. Piovano, E. Groppo, P. Raybaud and C. Chizallet, J. Phys. Chem. C, 2023, 127, 18454–18465 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Supplementary definitions of statistical measures, further computational details and supplementary figures and tables: esi.pdf; Cartesian coordinates of all compounds: IHD302.tar.xz; additional data for the correlated calculations: data_correlation_methods.xlsx; Detailed DFT and SQM results: data_dft_sqm.xlsx; The aug-cc-pVQZ-PP-KS basis sets: avqz-pp-ks.basis; Molpro example input files: pno_input_examples_molpro2024.1.zip. See DOI: https://doi.org/10.1039/d3cp06217a |
| ‡ These authors contributed equally. |
| This journal is © the Owner Societies 2024 |