Open Access Article
Open Access ArticleUnexpected and delayed fragmentation dynamics of the organometallic ferrocene induced by ion-collision†
F.
Aguilar-Galindo
 ab,
V. T. T.
Nguyen
c,
R.
Singh‡
c,
A.
Domaracka
ab,
V. T. T.
Nguyen
c,
R.
Singh‡
c,
A.
Domaracka
 c,
B. A.
Huber
c,
S.
Díaz-Tendero
c,
B. A.
Huber
c,
S.
Díaz-Tendero
 abd,
P.
Rousseau
abd,
P.
Rousseau
 c and
S.
Maclot
c and
S.
Maclot
 *e
*e
aDepartment of Chemistry, Universidad Autónoma de Madrid, 28049, Madrid, Spain
bInstitute for Advanced Research in Chemistry (IAdChem), Universidad Autónoma de Madrid, 28049 Madrid, Spain
cNormandie Univ., ENSICAEN, UNICAEN, CEA, CNRS, CIMAP, 14000, Caen, France
dCondensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, 28049 Madrid, Spain
eInstitut Lumière Matière UMR 5306, Université Claude Bernard Lyon 1, CNRS, Univ Lyon, 69100 Villeurbanne, France. E-mail: sylvain.maclot@univ-lyon1.fr
First published on 7th February 2024
Abstract
We have investigated the fragmentation dynamics of the organometallic ferrocene molecule after interaction with multiply charged ions using multicoincidence mass spectrometry and quantum chemistry calculations. We observed unexpected fragmentation dynamics of the two-body breakup channels from ferrocene dications revealing a charge screening effect from the iron atom and delayed fragmentation dynamics. These observations are rationalized through the population of a specific long-lived excited state, where one positive charge is located on each cyclopentadienyl ring.
1 Introduction
Metal–ligand bonds are central in coordination chemistry involving a metallic cation bound to several molecular anions. The p-electrons of the ligands interact with the d-electrons of the metal according to the 18-electrons rule.Ferrocene Fe(C5H5)2 is the prototype of organometallic complexes, and more specifically of metallocene compounds. Thus, it exhibits the typical stable sandwich structure with the Fe atom between the two C5H5 rings. In the ferrocene molecule, the iron atom which has an 18-electron configuration, exists in the +2 oxidation state. Both cyclopentadienyl rings satisfy Huckel's rule for aromatic compounds. Bonds are formed between a Fe2+ ion and two C5H5− rings. These bonds are remarkably stable, so they rarely break under normal reaction conditions. Serving as a model system for iron containing organic molecules of biological relevance, ferrocene is also an important molecule for studying fundamental multi-electron processes in complex quantum systems. For instance, organometallic compounds containing ferrocene can enhance conversion efficiency in organic photovoltaic cells.1 In general, metallocene in general and ferrocene derivatives in particular play a prominent role in synthetic chemistry, nano-medicine and material science thanks to their ubiquitous applications.2
Regarding astrochemistry, no ferrocene molecules or ions have been detected in space yet3 even though several organometallics are observed in the ISM, cosmic clouds and meteorites.4–7 Whereas the iron cation Fe+ (most abundant metal in space) and cyclopentadienyl rings C5H5− were detected8–11 and iron-aromatics compounds are suspected.12–14 Thus, one could easily imagine that signatures of the presence of ferrocene or larger related species will be evidenced in the future.
In the present study, we propose to investigate the dissociation dynamics of ferrocene cations induced by ion collisions, which relies on the transfer of charge and energy in the interaction. For this, we chose the combined experiment/theory approach using multicoincidence mass spectrometry and quantum chemistry calculations. We mainly focus on the fragmentation dynamics of doubly charged ferrocene and show that some fragmentation pathways involve a long-lived excited state leading to metastability of the dication and specific fragmentation dynamics.
2 Methods
2.1 Experiments
We performed the experiments with a crossed-beam device15,16 at the ARIBE facility, the low-energy ion beam facility of GANIL (Caen, France).17 A pulsed beam (500 ns) of multiply charged ions Xe20+ at an energy of 300 keV interacts with an effusive jet of neutral ferrocene molecules. This is produced by evaporation of a commercial high purity powder (Tokyo Chemical Industry Europe SA with >98% purity) in an external stainless steel container kept at 315 K. The gas injection line was gradiently heated up to 345 K to avoid condensation. The main process occurring in low-energy multiply charged ion collisions with neutral systems is electron capture, in which one or several electrons are transferred from the molecule to the incoming ion projectile. This leads to the formation of the singly (or multiply) ionized target molecule.18,19 After the interaction, the cationic products are orthogonally extracted into a linear time-of-flight mass spectrometer. We record the time-of-flight spectra in an event-by-event mode allowing to determine the initial charge state of the molecular system and to measure the correlation between the charged fragments produced in a single ion–molecule collision.202.2 Computational details
We computed the ground and excited electronic states of the doubly ionized ferrocene [Fe(C5H5)2]2+. We assume a sudden ionization and excitation in the collision. i.e. doubly ionized systems are formed in a Franck–Condon manner and, therefore, we fix the geometry at the (optimized) ground state geometry.Several electronic excited states of [Fe(C5H5)2]2+ were calculated using the CASPT2 method, which applies second order perturbation theory to the multireference CASSCF (Complete Active Space Self-Consistent Field) wavefunction. In particular, the chosen active space includes 12 electrons in 9 molecular orbitals (see Fig. 1), expanded used the ANO-S-VDZ basis set. In order to have accurate relative energies of the electronic excited states, we have used the extended multi-state CASPT2 (XMS-CASPT2) methodology.21,22 In addition to the default IPEA shift present in Open-MOLCAS (0.25 a.u.)23 we have used a real shift of 0.3, in order to treat the intruder states that appear due to the huge number of states included in the calculation (a total of 90 states). Multiconfigurational calculations were performed considering the C2v symmetry in order to reduce the computational effort. At least 10 states of each symmetry were considered, in order to describe all the states below the state of interest. These calculations were performed with the Open-MOLCAS (version 19.11) code.24,25
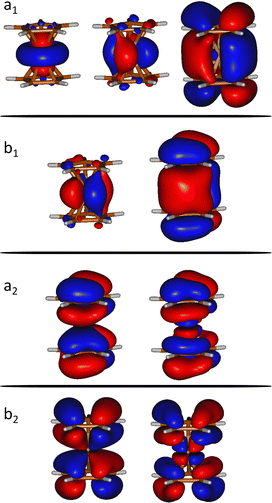 | ||
| Fig. 1 Orbitals included in the active space of the SA-CASSCF calculations (isovalue = 0.02 a.u.). a1, a2, b1 and b2 indicates the symmetry of the molecular orbitals within the C2v point group. | ||
We considered that all excitation energy is redistributed in the nuclear degrees of freedom. Then, the fragmentation mechanisms of the most relevant channels were computed by exploring the potential energy surface (PES) of the electronic ground state of the doubly ionized ferrocene. These calculations were carried out in the frame of the density functional theory (DFT), with the M06L functional.26 The electronic structure has been computed with effective core potentials (ECP), where a model potential substitutes the core electrons. In particular, we have employed the Stuttgart/Dresden ECPs (SDD) in combination with the compatible Dunning/Huzinaga full double zeta basis set (D95).27,28
We have also performed ab initio molecular dynamics simulations using the Atom Centered Density Matrix Propagation (ADMP).29–31 In these calculations, nuclei move in classical trajectories and the forces are computed on-the-fly at a quantum level; in this case in the frame of the density functional theory (DFT), using the same level of theory as for the PES exploration, M06L/SDD. In the performed dynamics, we used a time step of Δt = 0.1 fs and a fictitious mass of μ = 0.1 amu, with converged self-consistent field (SCF) results at each time step, thus ensuring adiabaticity of the trajectories, which were propagated up to tmax = 250 fs. The initial geometry in the trajectories is that of neutral ferrocene, doubly ionised in a Franck–Condon manner, [Fe(C5H5)2]2+. The excitation energy, Eexc is randomly distributed among the nuclear degrees of freedom in each trajectory. We performed 100 trajectories, 50 using Eexc = 10 eV and 50 more using Eexc = 20 eV; populated channels were analysed with statistics over the performed trajectories. Combining ab initio molecular dynamics and exploration of the potential energy surface, for the relevant fragmentation channels, constitutes a computational strategy which was first implemented in ref. 32 and, since then, it has been successfully employed to infer several ion–molecule collision experiments.18,33–35 The DFT calculations, PES exploration and the MD simulations, were performed using the Gaussian16 code.36
3 Results and discussion
3.1 Mass spectrometry
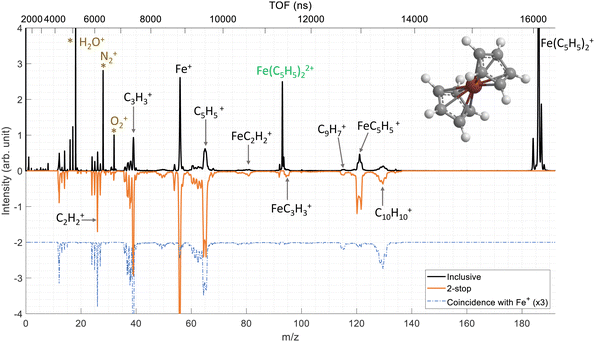
We have performed ion–molecule collision experiments with the ion projectile Xe20+ at 300 keV. The top part of the Fig. 2 presents the inclusive mass spectrum (black) of the cationic products of the interaction of Xe20+ ions with neutral ferrocene where the parent ion Fe(C5H5)2+ (m/z = 186) is the dominant species. The parent ion is also observed doubly charged Fe(C5H5)22+ (m/z = 93) showing that some ferrocene dications can be stable on the μs timescale.The other peaks correspond to fragments coming from the ionized ferrocene molecule. The main fragmentation channels involve the main components of the ferrocene molecule, meaning the iron atom and the cyclopentadienyl rings. Thus, we observe the fragments Fe+, C5H5+ and FeC5H5+ at m/z = 56, 65 and 121, respectively. It is important to note that throughout this manuscript, we only consider the main isotope of iron 56Fe. More unexpectedly, we observe peaks at m/z = 130, 129 and 115 associated with the two rings C10H10+, C10H9+ (H-loss) and C9H7+ (CH3-loss) which involve the bonding of the two rings with covalent bond(s) and the loss of an iron atom/ion.37
As a remark, we observe small fragments from the rings such as C2H2+ and C3H3+ at m/z = 26 and 39 but also fragments involving the iron atom bonded to a part of one ring such as FeC2H2+ and FeC3H3+ at m/z = 81 and 95, respectively.
3.2 Ion pair coincidences
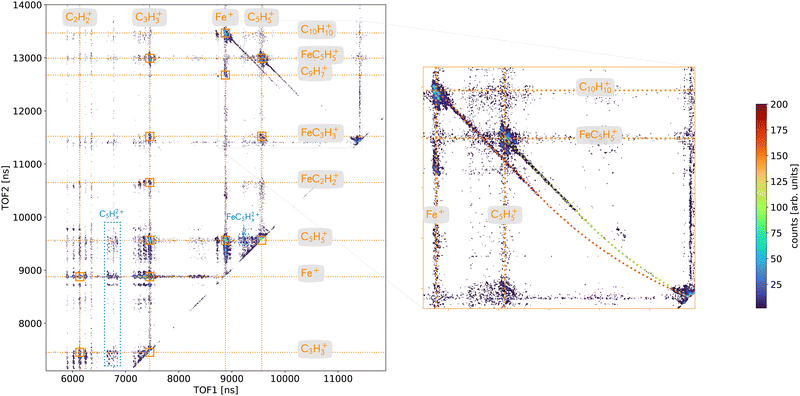
A deeper analysis of the fragmentation dynamics has been carried out by means of coincidence measurements of the emitted cationic fragments from a single collision (see details in ref. 20,32,33). In the case of the detection of two charged fragments (so-called 2-stop events) and if the fragments are singly charged, which is mostly the case, we can extract information about the fragmentation of the dication of ferrocene. The orange mass spectrum in the lower part of the Fig. 2 corresponds to the fragments measured for the 2-stop events. A more useful representation consists in plotting the time-of-flight of the slower cationic fragment (TOF2) as a function of the time-of-flight of the faster cationic fragment (TOF1) so called “correlation or coincidence map” (see Fig. 3).As mentioned earlier, if the two fragments are singly charged, the parent ion was a dication and the branching ratio of the most intense ion pairs associated with its dissociation (orange squares in the left part of the Fig. 3) are presented in Table 1. We observe that the main fragments previously listed are also present in the coincidence map. It is interesting to notice that more than 77% of the present channels contains an iron atom and more than 50% are involving bare iron cation Fe+. To illustrate this last point, the mass spectrum of the numerous ionic fragments in correlation with the ion Fe+ is shown as a blue dashed line in the lowest part of the Fig. 2.
| Channel | m 1 +/m2+ | BR (%) |
|---|---|---|
| C5H5+/FeC5H5+ | 65+/121+ | 9.6 |
| C5H5+/FeC3H3+ | 65+/95+ | 0.4 |
| C5H5+/C5H5+ | 65+/65+ | 3.8 |
| Fe+/C10H10+ | 56+/130+ | 1.6 |
| Fe+/C10H9+ | 56+/129+ | 1.7 |
| Fe+/C9H7+ | 56+/115+ | 0.7 |
| Fe+/C5H5+ | 56+/65+ | 7.6 |
| C3H3+/FeC5H5+ | 39+/65+ | 1.3 |
| C3H3+/FeC3H3+ | 39+/95+ | 0.5 |
| C3H3+/FeC2H2+ | 39+/81+ | 0.3 |
| C3H3+/C5H5+ | 39+/65+ | 3.0 |
| C3H3+/Fe+ | 39+/56+ | 8.6 |
| C3H3+/C3H3+ | 39+/39+ | 1.7 |
| C2H2+/Fe+ | 26+/56+ | 2.1 |
| C2H2+/C3H3+ | 26+/39+ | 1.0 |
The right part of the Fig. 3 is showing in details the two-body breakup channels C5H5+/FeC5H5+ and Fe+/C10H10+. Two-body fragmentation channels have been observed in the dissociation of doubly charged ferrocene produced by 70 eV electron impact37 while coincidence pairs involving further fragmentation were dominant in the dissociation of ferrocene dication following photoionization of inner shell electrons.38,39 We observe in Fig. 3 that the two islands show interesting features: long tails that correspond to delayed fragmentation processes, meaning dissociation occurring during the time-of-flight at the μs timescale, that transcribe metastable ionic states,40 which will be discussed in more details later on (see Section 3.2.2.2). The main intense part of the islands is due to prompt dissociations and discussed in the Section 3.2.2.1.
In addition, some islands are visible on the correlation map (Fig. 3 – left) which correspond to the dissociation of ferrocene trication into a singly and a doubly charged fragments (blue) and involve the fragments C5H52+ and FeC5H52+.
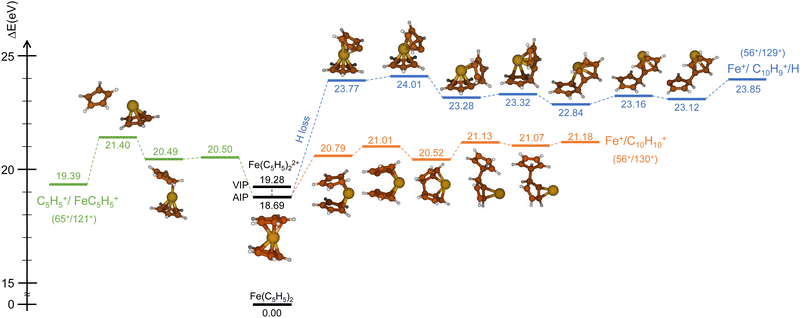
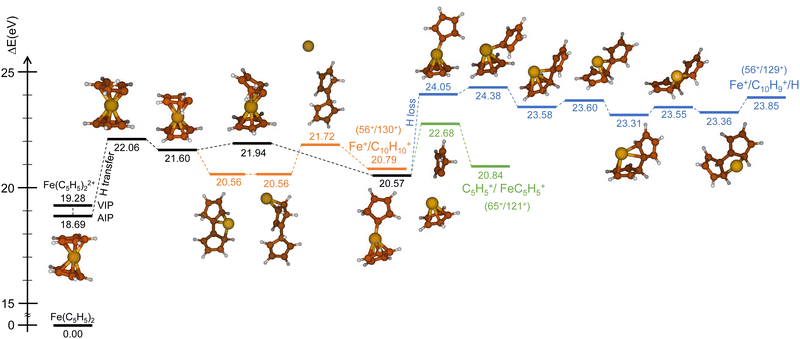
Similarly, we have explored the PES of the other channel C5H5+/FeC5H5+ (65+/121+) (green path in Fig. 4 and 5) but also the channel Fe+/C10H9+ (56+/129+) involving a neutral hydrogen loss (blue path in Fig. 4 and 5). This last channel, with a BR of 1.7% (so similar to the BR of Fe+/C10H10+), is interesting since the hydrogen transfer mechanism (Fig. 5) shows a common minimum with the channel C5H5+/FeC5H5+ at 20.57 eV. For the channel C5H5+/FeC5H5+ only ∼2 eV is necessary to pass the last barrier while for the channel Fe+/C10H9+ more than ∼3.5 eV is required. So depending on the internal energy available, the fragmentation dynamics can strongly vary.
Going back to the two-body breakup channels C5H5+/FeC5H5+ and Fe+/C10H10+, we will now discuss in detail the prompt and delayed fragmentation.
3.2.2.1 Prompt fragmentation dynamics. The slopes (s) of the islands are directly correlated to the ratio of momenta (p1,p2) and charges (q1,q2) of the 2 charged fragments involved (s = p1/p2·q2/q1). For a two-body breakup, the momenta are opposite (p1 = −p2) and thus for two singly charged fragments (q1 = q2 = 1) the slope is s = −1. The Fig. 3 shows that the slopes measured for each channels, C5H5+/FeC5H5+ and Fe+/C10H10+, are not equal to −1 like it should be (s ≃ −1.5). However, we have confidence in our measurements since the slope of the metastable tails are −1 and that other channels with expected slopes are correct (e.g. for C5H5+/FeC5H52+ with s = −2). The fact that the slopes are different from −1 could have two origins: (i) the final momenta are affected during the fragmentation process or (ii) the charges are not equal to one due to some shielding effect.
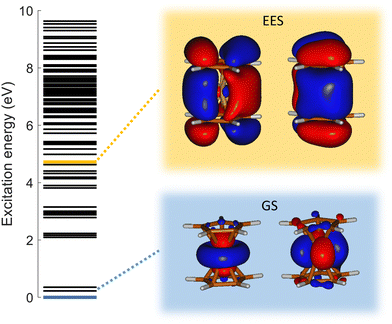
To answer this question, we performed exploration of the possible excited states that might be populated in the collision. Among the considered electronic excited states populated after double electron capture from the 9 molecular orbitals included in the active space (see computational details) we considered those below ∼10 eV. Among all these states (see scheme in Fig. 6), one in particular draws our attention: the electronic excited state of interest (EES from now on), which appears at E = 4.7 eV above the ground state (GS) of the dication. It corresponds to ionization from two π molecular orbitals; one electron from each is captured in the ionization (see orbitals with a single electron occupation in Fig. 6). Notice that their large and diffuse p-orbitals around the two cyclopentadienyl rings should lead to a high probability of single ionization from each ring. If the two charges remain on the rings during the dissociation, the neutral iron atom is located between them. The potential energy surface of the C5H5+/FeC5H5+ shows indeed that the iron atom is kept between two rings until dissociation, both for direct and for H transfer mechanisms (green path in Fig. 4 and 5). In that case, the iron atom is able to screen the charge of each fragment leading to reduced charges for the Coulomb repulsion and thus leading to a slope that differs from −1.
The same reasoning should also hold for channel Fe+/C10H10+. The different slope of −1 observed in the prompt fragmentation is again an indication of the charge screening during the fragmentation.
Analyzing the occupation of the molecular orbitals (see ESI†), one realizes that in the EES two holes are created in the cyclopentadienyl rings – occupation of ∼1 electron in each molecular orbital represented in Fig. 6. Therefore, charge screening by the Fe atom during the first steps in the fragmentation from the EES confirms why the slope differs from −1 in these channels.
In summary, in the ion collision the double capture comes from the extraction of electrons from π orbitals of the cyclopentadienyl rings populating excited states of the ferrocene dication. Relaxation into the ground state implies charge transfer, two electrons have to come from the Fe atom to the rings. The Fe atom generates a shielding effect avoiding the positive charge to get redistributed and keeping the system into an electronic excited state.
Finally, it is worth noting that the EES appears at 4.7 eV above the electronic ground state of the dication. Determined energy-transfer distributions in ionizing ion–molecule collisions show the peak with highest probability in this energy range.18,19
3.2.2.2 Delayed fragmentation dynamics. As aforementioned, the channels C5H5+/FeC5H5+ and Fe+/C10H10+ display tails associated to delayed fragmentation coming from a metastable ionic states (Fig. 3). It is interesting to notice that the slopes of the initial part of the tails are −1 and transcribed the fact that charge and nuclear dynamics had time to relax to a final state leaving fragmentation pathways through “classic” Coulomb repulsion. Simulated time-of-flight coincidences for the two ion pairs are shown with dashed lines in the right panel of Fig. 3. The observed tails corresponds to delayed dissociation of the ferrocene dication in the first acceleration region of the time-of-flight spectrometer. The time spent in the second acceleration region is so short that no significant dissociation signal is observed experimentally. Finally next the diagonal of the coincidence map, one can observe ion pairs associated with delayed dissociation of the dication in the field-free region of the spectrometer.
A time analysis of the tails can bring additional information about the metastable states such as lifetimes.40–43 Considering the signal along the structure of the tail, we can plot its intensity (I) as function of the time-of-flight difference (TOF2–TOF1) in Fig. 7 and deduce the decay constant (τ) of the metastable state of the dication of ferrocene for a given dissociation channel by fitting with an exponential formula given by T. A. Field and J. H. D. Eland in ref. 40:
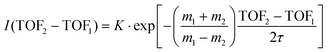 | (1) |
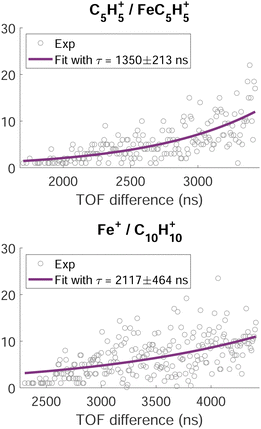 | ||
| Fig. 7 Intensity of the time-of-flight difference along the metastable tails (grey circles) of the channels C5H5+/FeC5H5+ (top) and Fe+/C10H10+ (bottom). The full purple lines correspond to the fit of the data points by eqn (1). | ||
For C5H5+/FeC5H5+ we found τ = 1350 ± 213 ns and for Fe+/C10H10+ we found τ = 2117 ± 464 ns.
As already discussed, the electronic GS of the dication corresponds to a double hole in d atomic orbitals of the iron atom. In the EES the double hole is created in π orbitals of the cyclopentadienyl ring. Thus, the decay from this state to the GS implies a charge migration from the ring towards the iron atom. However, EES is loosely coupled with the GS (oscillator strength f = 2.42 × 10−7), thus leading to a very long lifetime44 of 4273 μs, and explaining the metastability of the dication of ferrocene.
Due to the long lifetime of the EES, the direct radiative relaxation to the GS (or any other state below in energy) does not play a significant role on the deactivation mechanism. On the contrary, the system has enough time to evolve and to reach other point of the PES, where the ferrocene can populate other states through non-radiative paths such as conical intersections. In this way, the system, after reaching the electronic ground state, has enough internal energy to promote chemical reactivity. It is worth noting that the energy of the excited state in the Franck–Condon region (around 4.7 eV) is close to the highest barrier of the PES shown in Fig. 4 and 5. Thus, since the decay is expected to be non-radiative, this energy will make accessible all the proposed intermediate and products.
4 Conclusions
We have investigated the fragmentation dynamics of ferrocene cations adopting a joint experiment-theory approach. Experimentally, we used multiply charged Xe20+ ions at an energy of 300 keV to ionize ferrocene molecules and we measured the products of interaction by multicoincidence mass spectrometry. We observed that the parent ion can survive singly and doubly charged at the μs timescale after ion collision. We also measured many fragments that correspond to the main constituents of the molecule, namely the cyclopentadienyl rings C5H5 and the iron atom Fe and combinations between them. Interestingly we observed the fragments C10H10+, C10H9+ and C9H7+ implying a new intramolecular bound formation linking the two rings and a loss of the iron atom/ion.Concerning the dissociation of ferrocene dications, two peculiar fragmentation channels draw our attention: the two-body breakup channels C5H5+/FeC5H5+ and Fe+/C10H10+. These channels showed two contributions, a prompt and a delayed fragmentation. Thanks to theoretical computations, performed with the multi-reference wave-function method CASSCF, we have demonstrated that the latter can be explained by the existence of a long-lived excited state (>4000 μs) located 4.7 eV above the dication ground state and efficiently populated in the case of ion–molecule collisions. This excited state could explain why the prompt dissociation mechanisms of these channels displayed unexpected island slopes through charge screening from the iron atom. Potential energy surfaces of these channels corroborated our findings.
With this work we evidenced that the population of excited states above the ionization threshold is crucial to fully understand the fragmentation dynamics of ionized molecules after electron capture from specific molecular orbitals.
Author contributions
S. M. was the principal investigator of the experiment. P. R., V. T. T. N., R. S., A. D. and S. M. performed the experiment. P. R., V. T. T. N., B. A. H. and S. M. performed the experimental data analysis. S. D.-T. and F. A.-G. performed the theoretical calculations. All authors contributed to the writing of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This article is based upon work from COST action CA18212 – Molecular Dynamics in the GAS phase (MD-GAS), supported by COST (European Cooperation in Science and Technology) and from International Associated Laboratory (LIA) “Fragmentation DYNAmics of complex MOlecular systems – DYNAMO”. The experimental studies have been performed at the low-energy ion beam facility ARIBE at GANIL (Caen, France). The authors thank C. Feierstein-Plancq et J.-M. Ramillon for their technical support. The authors acknowledge the support of the French Agence Nationale de la Recherche (ANR), under grant ANR-18-CE30-0021 (project ANR FRAPA) and the Normandy Region and the European Union in the frame of operational program FEDER/FSE 2014-2020 (RIN MAGIC). The authors acknowledge the generous allocation of computer time at the Centro de Computación Científica at the Universidad Autónoma de Madrid (CCC-UAM). This work was partially supported by MICINN (Spanish Ministry of Science and Innovation) project PID2022-138470NB-I00 funded by MCIN/AEI/10.13039/501100011033, and the “María de Maeztu” (CEX2018-000805-M) Program for Centers of Excellence in RD. V. T. T. N. acknowledges NucPhys Master Degree and EACEA (project number: 610575-EPP-1-2019-1-ES-EPPKA1-JMD-MOB, contract: 2019-2130) for support.Notes and references
- L. Ye, Y. Cai, C. Li, L. Zhu, J. Xu, K. Weng, K. Zhang, M. Huang, M. Zeng, T. Li, E. Zhou, S. Tan, X. Hao, Y. Yi, F. Liu, Z. Wang, X. Zhan and Y. Sun, Energy Environ. Sci., 2020, 13, 5117–5125 RSC.
- D. Astruc, Eur. J. Inorg. Chem., 2017, 6–29 CrossRef CAS.
- A. Roy, S. V. Singh, J. K. Meka, R. Ramachandran, D. Sahu, A. Gautam, T. Vijay, J. Vishakantaiah, P. Janardhan, B. N. Rajasekhar, A. Bhardwaj, N. J. Mason and B. Sivaraman, Mon. Not. R. Astron. Soc., 2022, 517, 4845–4855 CrossRef CAS.
- S. Petrie, Aust. J. Chem., 2003, 56, 259–262 CrossRef CAS.
- M. Fioroni, Phys. Chem. Chem. Phys., 2014, 16, 24312–24322 RSC.
- M. Fioroni, Comput. Theor. Chem., 2016, 1084, 196–212 CrossRef CAS.
- M. Fioroni, in Transition Metal Organometallic/Metallorganic Chemistry: Its Role in Prebiotic Chemistry and Life's Origin, ed. A. Neubeck and S. McMahon, Springer International Publishing, Cham, 2021, pp. 1–41 Search PubMed.
- A. Garenne, P. Beck, G. Montes-Hernandez, L. Bonal, E. Quirico, O. Proux and J. Hazemann, Meteorit. Planet. Sci., 2019, 54, 2652–2665 CrossRef CAS.
- J. Cernicharo, M. Agúndez, C. Cabezas, B. Tercero, N. Marcelino, J. R. Pardo and P. de Vicente, Astron. Astrophys., 2021, 649, L15 CrossRef CAS PubMed.
- J. García de la Concepción, I. Jiménez-Serra, V. M. Rivilla, L. Colzi and J. Martín-Pintado, Astron. Astrophys., 2023, 673, A118 CrossRef.
- M. C. McCarthy, K. L. K. Lee, R. A. Loomis, A. M. Burkhardt, C. N. Shingledecker, S. B. Charnley, M. A. Cordiner, E. Herbst, S. Kalenskii and E. R. Willis, et al. , Nat. Astron., 2021, 5, 176–180 CrossRef.
- P. Marty, G. Serra, B. Chaudret and I. Ristorcelli, Astron. Astrophys., 1994, 282, 916–923 CAS.
- A. Klotz, P. Marty, P. Boissel, D. de Caro, G. Serra, J. Mascetti, P. de Parseval, J. Derouault, J.-P. Daudey and B. Chaudret, Planet. Space Sci., 1996, 44, 957–965 CrossRef CAS.
- A. Simon, C. Joblin, N. Polfer and J. Oomens, J. Phys. Chem. A, 2008, 112, 8551–8560 CrossRef CAS PubMed.
- T. Bergen, X. Biquard, A. Brenac, F. Chandezon, B. A. Huber, D. Jalabert, H. Lebius, M. Maurel, E. Monnand, J. Opitz, A. Pesnelle, B. Pras, C. Ristori and J. C. Rocco, Rev. Sci. Instrum., 1999, 70, 3244–3253 CrossRef CAS.
- F. Chandezon, B. Huber and C. Ristori, Rev. Sci. Instrum., 1994, 65, 3344–3353 CrossRef CAS.
- V. Bernigaud, O. Kamalou, A. Lawicki, M. Capron, R. Maisonny, B. Manil, L. Maunoury, J. Rangama, P. Rousseau, J. Y. Chesnel, L. Adoui and B. A. Huber, Publications de l'Observatoire Astronomique de Beograd, 2008, 84, 83–86 Search PubMed.
- S. Maclot, R. Delaunay, D. G. Piekarski, A. Domaracka, B. A. Huber, L. Adoui, F. Martín, M. Alcamí, L. Avaldi, P. Bolognesi, S. Díaz-Tendero and P. Rousseau, Phys. Rev. Lett., 2016, 117, 073201 CrossRef CAS PubMed.
- E. Erdmann, N. F. Aguirre, S. Indrajith, J. Chiarinelli, A. Domaracka, P. Rousseau, B. A. Huber, P. Bolognesi, R. Richter, L. Avaldi, S. Díaz-Tendero, M. Alcamí and M. Abuda, Phys. Chem. Chem. Phys., 2021, 23, 1859–1867 RSC.
- M. Capron, S. Díaz-Tendero, S. Maclot, A. Domaracka, E. Lattouf, A. awicki, R. Maisonny, J.-Y. Chesnel, A. Méry, J.-C. Poully, J. Rangama, L. Adoui, F. Martín, M. Alcamí, P. Rousseau and B. A. Huber, Chem. – Eur. J., 2012, 18, 9321–9332 CrossRef CAS PubMed.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef PubMed.
- T. Shiozaki, W. Gyorffy, P. Celani and H.-J. Werner, J. Chem. Phys., 2011, 135, 081106 CrossRef PubMed.
- G. Ghigo, B. O. Roos and P.-A. Malmqvist, Chem. Phys. Lett., 2004, 396, 142–149 CrossRef CAS.
- I. Fdez. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. A. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef PubMed.
- F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. Fdez. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. A. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- T. H. Dunning Jr. and P. J. Hay, Modern Theoretical Chemistry, Plenum, New York, 1977, vol. 3 Search PubMed.
- M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866–872 CrossRef CAS.
- H. B. Schlegel, J. M. Millam, S. S. Iyengar, G. A. Voth, A. D. Daniels, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 114, 9758–9763 CrossRef CAS.
- S. S. Iyengar, H. B. Schlegel, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2001, 115, 10291–10302 CrossRef CAS.
- H. B. Schlegel, S. S. Iyengar, X. Li, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2002, 117, 8694–8704 CrossRef CAS.
- S. Maclot, D. G. Piekarski, A. Domaracka, A. Méry, V. Vizcaino, L. Adoui, F. Martín, M. Alcamí, B. A. Huber, P. Rousseau and S. Díaz-Tendero, J. Phys. Chem. Lett., 2013, 4, 3903–3909 CrossRef CAS.
- D. G. Piekarski, R. Delaunay, S. Maclot, L. Adoui, F. Martín, M. Alcamí, B. A. Huber, P. Rousseau, A. Domaracka and S. Díaz-Tendero, Phys. Chem. Chem. Phys., 2015, 17, 16767–16778 RSC.
- E. Erdmann, M. abuda, N. F. Aguirre, S. Díaz-Tendero and M. Alcamí, J. Phys. Chem. A, 2018, 122, 4153–4166 CrossRef CAS PubMed.
- P. Rousseau, D. G. Piekarski, M. Capron, A. Domaracka, L. Adoui, F. Martín, M. Alcamí, S. Díaz-Tendero and B. A. Huber, Nat. Commun., 2020, 11, 3818 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian˜16 Revision C.01, Gaussian Inc. Wallingford CT, 2016 Search PubMed.
- T. Drewello, C. B. Lebrilla, H. Schwarz and T. Ast, J. Organomet. Chem., 1988, 339, 333–338 CrossRef CAS.
- E. Rühl, C. Heinzel, H. Baumgärtel and A. Hitchcock, Chem. Phys., 1993, 169, 243–257 CrossRef.
- Y. Tamenori, B. H. Boo and I. Koyano, J. Electron Spectrosc. Relat. Phenom., 1999, 101–103, 87–91 CrossRef.
- T. A. Field and J. H. Eland, Chem. Phys. Lett., 1993, 211, 436–442 CrossRef CAS.
- R. Delaunay, J.-P. Champeaux, S. Maclot, M. Capron, A. Domaracka, A. Méry, B. Manil, L. Adoui, P. Rousseau, P. Moretto-Capelle and B. A. Huber, Eur. Phys. J. D, 2014, 68, 162 CrossRef.
- H. Yuan, S. Xu, T. Li, Y. Liu, D. Qian, D. Guo, X. Zhu and X. Ma, Phys. Rev. A, 2020, 102, 062808 CrossRef CAS.
- L. Wei, B. Ren, Y. Zhang, J. Wang, B. Wang, J. Han, W. Yu, Y. Zou, L. Chen and B. Wei, Phys. Rev. A, 2021, 103, 012810 CrossRef CAS.
- K. Rohatgi-Mukherjee, Fundamentals of photochemistry, New Age International, 1978 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05430f |
| ‡ Present address: Physical Sciences, IUCTE, BHU, Varanasi-221005 India. |
| This journal is © the Owner Societies 2024 |