DOI:
10.1039/D2SM01540D
(Paper)
Soft Matter, 2023,
19, 1709-1719
The role of surface topography in the self-assembly of polymeric surfactants†
Received
24th November 2022
, Accepted 19th January 2023
First published on 20th January 2023
Abstract
We propose a classical density functional theory model to study the self-assembly of polymeric surfactants on curved surfaces. We use this model to investigate the thermodynamics of phase separation of a binary mixture of size asymmetric miscible surfactants on cylindrical and spherical surfaces, and observe that phase separation driven by size alone is thermodynamically unfavorable on both cylindrical and spherical surfaces. We use the theory, supplemented by dissipative particle dynamics (DPD) simulations, to predict pattern formation on a non-uniform surface with regions of positive and negative curvature. Our results suggest potential ways to couple surface topography and polymeric surfactants to design surfaces coated with non-uniform patterns.
1. Introduction
The spontaneous self-assembly of polymeric surfactants has long been exploited for the bottom-up fabrication of surfaces with complex patterns. It has long been known that simple chemical modifications of the surfactants allow tuning these patterns’ geometric features down to the nanoscale. More recently, it has also been appreciated that another way to control pattern formation is to modify the topography of the surface on which the surfactant is deposited, which can in some cases be advantageous.1–4 Notably, because changing the surface pattern modifies the interaction with the external environment, this route has been proven useful for a diverse range of applications, from drug-delivery and biosensing5,6 to nanolithography.7
Experimental observation of nanoscale patterns in binary mixtures of oligomeric surfactants of different lengths on a spherical nanoparticle4 triggered an active discussion and somewhat heated debate.8,9 Progress in understanding these experiments and rational design of nanoscale-pattern-forming systems relies on the ability to theoretically predict the features of the surface patterns formed by the surfactants as a function of surface topography. To this end, we combine well-established theories of polymer interactions and polymer brushes to build a free-energy density functional model describing a system of polymeric surfactants confined to move on a surface. Within the framework of classical density functional theory (DFT),10–12 we use our model to predict how surface topography, polymer size, and chemical identity determine the final self-assembly pattern. We show qualitatively that the same behaviour in terms of phase separation is observed on surfaces of uniform positive mean curvature, i.e., spheres and cylinders, and discuss a sinusoidally modulated surface as an archetypal system with non-uniform curvature. Dissipative particle dynamics (DPD) simulations are performed to confirm the validity of our results in regions of parameter space where the assumptions of the continuum-based thermodynamic model are difficult to justify.
The remaining paper is organised as follows. In Section 2, we present a detailed derivation of the theoretical model, highlighting its assumptions and thus its range of validity and accuracy. We also describe the details of the coarse-grained model used for the DPD simulations. In Section 3, we explore the thermodynamics of phase separation on surfaces of uniform, positive curvature, and on a sinusoidally modulated surface, taken as an archetypal example of the more general case of surfaces of non-uniform curvature. For the latter system, we also present results from DPD simulations to test the qualitative predictions of our DFT model. Finally, we use our new insights to address the controversy around micro-phase separation on nanoparticles, and discuss the practical application of our results in the wider context of materials science.
2. Methods
2.1. Theoretical model
Our aim is to provide a model for a binary mixture of polymeric surfactants that can account for (i) the chemical affinity between different polymers; (ii) differences in size between the two types of polymers; and (iii) effects due to the polymers being grafted on a surface of variable curvature. We consider one end of each polymer chain to be confined, but free to diffuse across the surface. This condition is satisfied by many types of surfactants where the end group is only physisorbed on the surface, for example, DNA coated colloids where DNA is chemically functionalised with a cholesteric group at one end, and then inserted into a lipid bilayer supported on the surface.13 In practice, we note that our model can be built by reformulating in continuous space the lattice model for a binary mixture of polymers of different lengths proposed by Van Lehn and Alexander-Katz in ref. 14, although in our case we additionally account for the effects of local curvature. A somewhat similar approach was adopted by Tung and Cacciuto as mentioned in ref. 15, although here we perform an additional step to recast the model in the framework of classical DFT, which allows us to consider a continuous, spatially-varying density field rather than homogeneous phases only.
As in the previous studies,10–12 we considered two types of polymeric surfactants with different chain lengths. In particular, we denote the number of Kuhn segments in the shorter and longer chains as NS and NL, respectively. Hereafter, unless stated otherwise, the subscripts S and L will be used to refer to quantities related to shorter (S) and longer (L) chains. Both types of chains are considered to be in the brush regime, allowing the use of DeGennes’ blob picture to derive the free energy density as a function of the local curvature. As we are interested in addressing potentially non-homogeneous densities of surfactants, we build a free energy functional whose associated density field is that of the grafting density of the two polymer chains, σS(x) and σL(x), x referring to a generic point on the grafting surface. We further simplify the problem by considering a fixed overall grafting density of chains, which we set equal to σ. In this case, we can recast our free-energy functional in terms of the local fraction of long chains ϕL(x), where clearly σi = ϕiσ, i = S, L, and σL + σS = σ. We then make an ansatz and take the free energy functional to be dependent only on the local density. We expect this approximation to improve as the gradients in the density field become smaller, the case in which one recovers the exact bulk density functional; in practice, this will occur if the surface curvature does not change appreciably on the length-scale of the surfactants. Another important aspect to highlight is that our theoretical model is an effective 2D theory: the local functional depends only on the 2D grafting density of the polymeric surfactants, not on the full 3D density field describing the whole polymer. On surfaces with spatially varying curvature, we should expect the theory to work only as long as the brush height is not much larger than the length-scale on which the surface curvature varies appreciably. This limitation will become clearer later, when discussing the form of the curvature contribution to the free-energy. It occurs because, in order to write down our simple analytical functional, we assume that the local environment felt by a given polymer is the same as that of a polymer grafted on a surface of constant mean curvature, regardless of the distance from the surface. However, as one moves away from the grafting point, the correlation with the underlying surface curvature close to this point becomes weaker. In other words, the top layer of the polymer will not know to which surface grafting point and surface curvature it belongs, and our assumption cannot hold anymore. With these premises, within this local density approximation, our free-energy functional can be written as:
| | 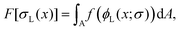 | (1) |
where
| | | f = fmix + fent + fcurv. | (2) |
The three terms appearing in
eqn (2) have the following form and physical interpretation. First,
| | | βfmix = 2σχϕL(1 − ϕL), | (3) |
represents the mixing enthalpy contribution to the free energy density, in a mean-field approximation. Here
β = 1/
kBT, where
kB and
T are Boltzmann's constant and the absolute temperature, respectively. The parameter
χ can be thought of as the Flory
χ parameter, where
χ > 0 for immiscible polymers, and
χ < 0 otherwise. In practice,
χ controls the tendency of the two surfactants to phase-separate. Unlike in Flory's classical model for polymer mixtures,
χ is not a per-monomer quantity, but rather measures the average interaction between two chains. In our model, we do not discuss the origin of the value of
χ, but treat it as a fully tunable parameter. The second term in
eqn (2),
| | βfent = σ[ϕL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(ϕL) + (1 − ϕL)log(1 − ϕL)], log(ϕL) + (1 − ϕL)log(1 − ϕL)], | (4) |
represents the mixing entropy contribution to the free-energy density in the mean-field approximation, and the third term,
fcurv, is the free-energy density of a mixed polymer brush, a contribution which depends on the underlying curvature of the surface. A recipe for calculating the brush free energy as a function of surface curvature for brushes of constant curvature was first provided for spheres by Daoud and Cotton,
16 and then discussed again by Bug
et al.
17 and Marques
et al.
18 also for more general cases. Using a similar approach, Hiergeist and Lipowsky
19 instead discussed the case of a single-component brush on cylinders. These models were later extended to a brush of mixed-length chains by Komura and Safran.
20 We refer the reader to the original publications for detailed derivations, presenting here a streamlined calculation to highlight the assumptions required to use these formulas for surfaces of non-constant curvature. The general idea is to use the Alexander–de Gennes blob model
16,21 to calculate the free energy of a brush. Within this picture, the height of a brush on a flat surface would be:
where
aK is the Kuhn length,
N is the number of Kuhn segments of the polymer,
ε0 is the blob size, linked to the grafting density of polymers
σ by
σ =
ε0−2,
‡ and
ν is the Flory exponent, related to the statistics of the polymer chain conformations. For a polymer in a good solvent, the case we will assume unless stated otherwise, we take
ν to be equal to an approximate (yet quite accurate) value of 3/5.
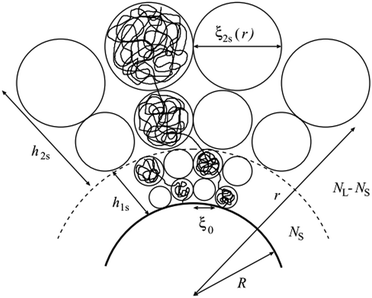 |
| | Fig. 1 The classic blob picture and scaling illustration applied to a bimodal polymer brush on a spherical or cylindrical surface. The blob size can be calculated from the observation that blobs form in such a way to be at touching distance from each other. Note that for spherical or cylindrical brushes this leads to a simple formula that only depends on the radial coordinate, although this is not generally the case (taken from the study by Komura and Safran).20 | |
The brush height on a spherical (hSph) or cylindrical (hCyl) surface with radius R is given by:
| | 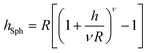 | (6) |
and
| | 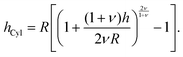 | (7) |
Within the blob model, the free energy density of a brush is given using the following expression:
| | 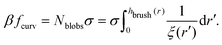 | (8) |
In
eqn (8),
Nblobs is the total number of blobs in a chain in the brush, and
ξ(
r′) is the size of the blob, which depends on the local curvature at a specific point on the surface. The blob size can be calculated by considering that the polymer chains separate into blobs that form a packed structure, see
Fig. 1 for reference.
Following this procedure, and considering the general case of a bicomponent brush, Komura and Safran20 derived the following formula for the blob size on spherical/cylindrical surfaces:
| | 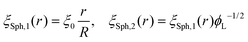 | (9) |
| | 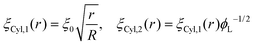 | (10) |
which, after some algebra, results in the curvature free-energy density for a two-component brush:
| | 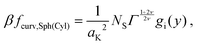 | (11) |
where
Γ = (
aK/
ξ0)
2 is the scaled grafting density, and the scaling function
gi, depends on the surface:
| | 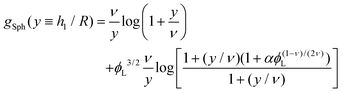 | (12) |
| | 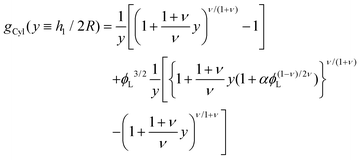 | (13) |
where
| | 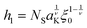 | (14) |
corresponds to the height of the short component on a flat surface, and
α = (
NL −
NS)/
NS is the asymmetry parameter.
In practice, the above procedure19,20 leads to a simple analytical form only if the mean curvature of the surface is constant, i.e., for cylindrical or spherical surfaces. The generalisation of this functional to surfaces with non-constant curvature is not trivial; it is not even clear if spherical blobs are a correct approximation, since the local grafting density (and so the corresponding blob size) does not vary in the same way in all directions on the grafting plane. Tung and Cacciuto15 attempted to resolve this by equating the local curvature free energy for surfaces of non-uniform curvature with that of a sphere with radius equal to the local mean radius of curvature. This approach is a generalization of the constant curvature case, and while it might work well for almost spherical surfaces, it is clearly only an approximation and it does not withstand the consistency test: it does not reproduce exact results (eqn (12) and (13)) on cylindrical surfaces. We later consider surfaces with non-uniform curvature that are locally indistinguishable from a cylinder and thus cannot be adequately described with the approach presented in ref. 15. Finally, we notice that generalisation of our approach to an arbitrary number of components would be trivial, albeit tedious. As for the two-component systems, the mixing entropy and enthalpy of many-component systems can be calculated in the mean-field, while the curvature-dependent repulsive contribution can be obtained by summing over the different layers that arise if polymers of different lengths are considered.
2.1.1. Calculating the equilibrium profile using DFT.
Once a free-energy functional has been established, calculating the spatially-dependent equilibrium value of the density ϕL(x) can be trivially performed using (classical) DFT.10,11 In practice, we need to minimise the free-energy functional via standard functional minimisation, under the constraint that the amounts of the two polymeric surfactants on the surface are fixed. Using the Euler–Lagrange procedure, we thus need to minimise the functional:| | 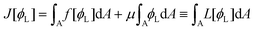 | (15) |
where μ is the Lagrange multiplier fixing the fraction of the long chains in the system, which, following the standard procedure, is equivalent to solving:| | 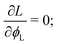 | (16) |
substituting eqn (1)–(4) and (10)–(13) yields the equation for ϕL(r). We will later study the case of a surface which is locally cylindrical, in the sense that its curvature only changes along one direction and is zero in the perpendicular direction. For such a surface, we obtain the equation:| | 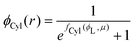 | (17) |
| | 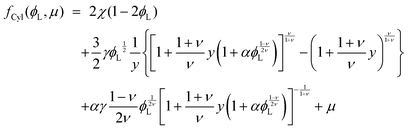 | (18) |
where 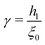 . The equivalent expression valid for a spherical surface (which could thus be used to define a spherical-surface approximation), is reported in the ESI.†
. The equivalent expression valid for a spherical surface (which could thus be used to define a spherical-surface approximation), is reported in the ESI.†
Notice that in eqn (18), ϕL depends on the position on the grafting surface r because of the spatially-dependent radius of curvature, R(r). Furthermore, notice that both equations provide an implicit expression for ϕL, of the form ϕL = p(ϕL), which must be solved self-consistently. A solution can be found in seconds on a standard laptop. We provide a Python implementation of the code used for this purpose.
2.2. Coarse-grained simulations
2.2.1. Interaction potentials and dynamical equations.
In the mean-field model, we rely on the local density approximation, and also on the validity of the blob picture implicit in calculating the curvature-dependent component of the brush free energy. To address potential pitfalls, especially for surfaces of non-uniform curvature, we performed additional particle-based simulations. Each polymeric surfactant is modelled as a string of connected spherical beads, where connected neighbours interact via the potential| | 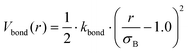 | (19) |
where r is the distance between two bonded beads, σB is the diameter of the bead, used as a unit of length, and kbond is the spring constant. Following previous works, we choose k = 40kBT.22 The head bead of a polymeric chain is constrained to move exclusively on the surface. This constraint is imposed via constrained dynamics as implemented in the widely used molecular dynamics code LAMMPS.23 The surface acts on all beads with a short-range, distance-dependent repulsive potential:| | 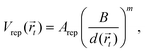 | (20) |
where 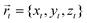 is the position of the tail bead, Arep = 1.0kBT is the energy parameter and B = 1.0σB sets the length-scale for the potential. In eqn (20), d(x,y,z) = z − f(x,y), where f(x,y) parametrises the surface. Finally, m = 6 is a positive parameter that controls the range of the repulsive potential. We model the non-bonded interactions between the beads via the soft and purely repulsive DPD potential:
is the position of the tail bead, Arep = 1.0kBT is the energy parameter and B = 1.0σB sets the length-scale for the potential. In eqn (20), d(x,y,z) = z − f(x,y), where f(x,y) parametrises the surface. Finally, m = 6 is a positive parameter that controls the range of the repulsive potential. We model the non-bonded interactions between the beads via the soft and purely repulsive DPD potential:| | 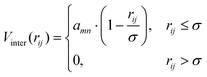 | (21) |
where rij is the distance between beads i and j, amn is the repulsion parameter between surfactants of types m and n: a11 = a22 = a12= 18.75kBT. In DPD simulations,24 the force on atom i due to atom j is subjected to conservative, dissipative, and random forces FCij, FDij, and FRij, respectively, and the total force| | 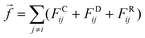 | (22) |
The dissipative force,| | FDij = −γwD(rij)(![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij·vij) ij·vij)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij, ij, | (23) |
and random force,| | FRij = σwR(rij)θij![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij, ij, | (24) |
are related to r-dependent weight functions and θij(t) is a randomly fluctuating variable, 〈θij(t) = 0〉 and 〈θij(t)θkl(t′)〉 = (δikδjl + δilδjk)δ(t − t′).
The simulation system is in the canonical (NVT) ensemble. We set the mass to unity, an irrelevant choice considering that we only evaluate the equilibrium properties of the system, which are independent of the mass. We fix the surface density of surfactants to σ = 4, following Glotzer et al.22 and study a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary mixture of long and short chains. The time step employed in integrating the equations of motion is set to dt = 10−4τ0, where
1 binary mixture of long and short chains. The time step employed in integrating the equations of motion is set to dt = 10−4τ0, where 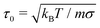 and each simulation is run for over 5 × 106 time steps. Periodic boundary conditions are implemented in x- and y-directions, but not in the z-direction.
and each simulation is run for over 5 × 106 time steps. Periodic boundary conditions are implemented in x- and y-directions, but not in the z-direction.
2.2.2. Geometry of the surface.
In order to study a simple yet non-trivial system, we chose a sinusoidally modulated surface described using the equation:| | 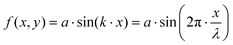 | (25) |
where a is the amplitude of the oscillating surface and k is the wave number.
Given eqn (25), it is trivial to calculate the mean and Gaussian curvatures in the Monge representation, which are given using the following equations, respectively:
| | 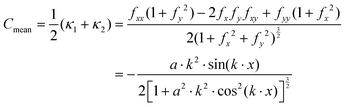 | (26) |
| | 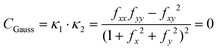 | (27) |
where
κ1 and
κ2 are the maximum and minimum of the normal curvature at a given point on a surface,
fi and
fij,
i,
j =
x,
y are a short-hand notation for the first and second derivatives, respectively, of
eqn (25). In order to connect to
eqn (12), (13) and (18), we recall that, on a cylinder, the mean curvature is related to the local radius of curvature with
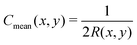
, whereas for a spherical surface we have
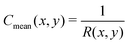
. For visual reference, the surface height profile and the corresponding curvature for our locally-cylindrical, sinusoidally-modulated surface are reported in the ESI.
†
We note that in eqn (25), locally, the surface has a curvature indistinguishable from that of a cylinder, since it is flat in y and only varies along the x direction. We also note that a sinusoidally modulated surface allows us to have both regions of positive curvature and regions of negative curvature, which is required for length-asymmetry-induced demixing of otherwise perfectly miscible surfactants.15
In our simulations, we employ combinations of a ∈ {0.25, 0.5, 1,2} and λ ∈ {10, 20, 40} to characterize different surface topographies. Fig. 2 presents a representative snapshot of a configuration from a simulation with (a, λ) = (2, 10) and chain lengths (NS, NL) = (2, 6) (i.e., α = 2).
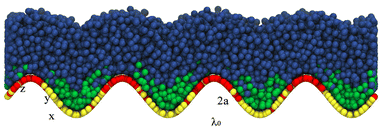 |
| | Fig. 2 Illustration of the model used in our simulations. Long surfactants (heads in red and tails in blue) locate in regions of positive curvature, while short surfactants (heads in yellow and tails in green) locate in regions of negative curvature. | |
3. Results and discussion
3.1. Curvature free energy and phase separation
First, let us discuss the form of free energy density contribution due to the curvature, eqn (11)–(14). Already a qualitative analysis of its shape is useful to infer a few important properties of the system. For this reason, we plot this quantity against the scaling parameter y = h1/R = h1Cmean, which is proportional to the local mean curvature of the underlying surface. For illustrative purposes, we make this plot for representative parameter choices characterising a bimodal brush, for both spherical (fSphcurv, solid lines) and cylindrical (fCylcurv, dashed lines) surfaces, in Fig. 3 and 4.
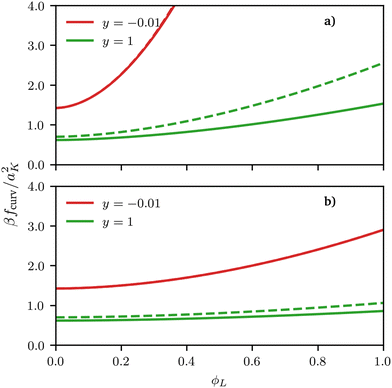 |
| | Fig. 3 Curvature free energy density fcurv, see eqn (2), for both spherical (solid lines) and cylindrical (dashed lines) surfaces as a function of ϕL for different values of the scaling variable y = h1/R. In both examples, σ = 0.5 and the size asymmetry between the two polymeric surfactants is (a) α = 10 (NL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NS = 11 NS = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and (b) α = 1 (NL 1) and (b) α = 1 (NL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NS = 2 NS = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Although the free energy curvature is almost indistinguishable for negative curvatures, it differs quantitatively for positive values, with the difference increasing for increasing values of the scaling variable, i.e., for increasing curvature. 1). Although the free energy curvature is almost indistinguishable for negative curvatures, it differs quantitatively for positive values, with the difference increasing for increasing values of the scaling variable, i.e., for increasing curvature. | |
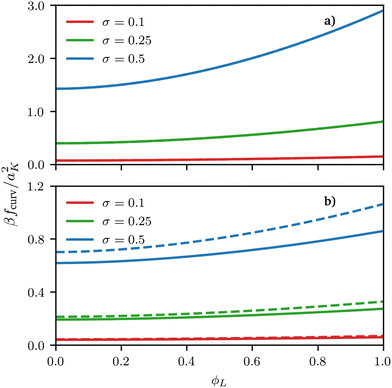 |
| | Fig. 4 Curvature free energy density fcurv, see eqn (12) and (13), for both spherical and cylindrical surface as a function of ϕL for different values of grafting density σ. In both examples, the size asymmetry is α = 1 but the surface curvature is negative in (a) y = h1/R = −0.01 and positive in (b) y = h1/R = 1. For negative curvature, at least at the grafting densities considered here, fcurv is basically indistinguishable between spheres and cylinders. | |
The most important thing to note is that for both spheres and cylinders, the curvature contribution to the local free energy is always a convex function 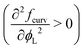 . This behaviour of the second derivative indicates that the curvature contribution thermodynamically stabilises a mixed homogeneous brush with respect to demixing into a linear combination of two phases of distinct composition.25 Whether or not de-mixing occurs in practice, depends on the total free energy density, including the entropy of mixing, eqn (4), which always favours mixing, and enthalpic contributions, eqn (3), which favours mixing or de-mixing depending on whether χ is negative or positive, respectively. Unlike the other two terms, the magnitude of the curvature term is controlled by both the curvature of the surface and the size asymmetry between the surfactants. The curvature term also increases super-linearly rather than linearly with respect to the grafting density σ (considering that σ = Γ/a2, see also eqn (11)). Thus, an appropriate choice of parameters can always be made to induce mixing by making the curvature term dominating.
. This behaviour of the second derivative indicates that the curvature contribution thermodynamically stabilises a mixed homogeneous brush with respect to demixing into a linear combination of two phases of distinct composition.25 Whether or not de-mixing occurs in practice, depends on the total free energy density, including the entropy of mixing, eqn (4), which always favours mixing, and enthalpic contributions, eqn (3), which favours mixing or de-mixing depending on whether χ is negative or positive, respectively. Unlike the other two terms, the magnitude of the curvature term is controlled by both the curvature of the surface and the size asymmetry between the surfactants. The curvature term also increases super-linearly rather than linearly with respect to the grafting density σ (considering that σ = Γ/a2, see also eqn (11)). Thus, an appropriate choice of parameters can always be made to induce mixing by making the curvature term dominating.
De-mixing of immiscible surfactants (χ > 0 in eqn (3)) on cylindrical surfaces was observed by Glotzer et al. using DPD simulations and experiments on nanowires and nanorods26 but in their case non-miscible polymeric surfactants χ > 0 were considered; here we show that de-mixing on cylinders can only be obtained for this type of enthalpic interaction and cannot be induced by size asymmetry alone. The similarity between our results for spherical and cylindrical surfaces shows that using a spherical surface approximation (for cylindrical surfaces) can be at least qualitatively accurate. In fact, for negative curvatures, the free-energy contributions calculated either using the exact formula for cylindrical surfaces or the locally-spherical approximation are basically indistinguishable, with differences smaller than 1% of the thermal energy. However, for positive curvatures, visible quantitative differences occur, which increase for increasing (scaled) curvature y and for increasing grafting densities, see Fig. 3 and 4.
Regarding the reasons behind these differences, we notice two things. On the one hand, the scaling of the blob size as a function of the distance from the centre is different between spheres and cylinders, and it is this difference that ultimately leads to a difference in the scaling functions y, see eqn (12) and (13). On the other hand, on a sphere or a flat plane, one can unambiguously define the blob size based on the local packing density, which is not true for any other surface, because the blob size on a general surface would need to depend on the direction considered (as it is clear by taking the case of a cylinder). Whereas a more precise treatment of this ambiguity in the form of a universal functional for the curvature free energy on an arbitrary surface might be a useful direction for future research; we notice that the locally-spherical approximation is rather good and, qualitatively, does not change the thermodynamics of the system. In fact, although a full validation of this approximation is outside the scope of this work, its prediction is consistent with the behaviour observed in particle-based simulations even on (generic) surfaces without cylindrical symmetry, see the ESI.†
3.2. Surfaces with non-uniform curvature
In the following, we want to use our density functional model to address the case when the curvature of the grafting surface varies in space. Although surfaces that are locally indistinguishable from a sphere do not exist (they are all spheres), we can create locally cylindrical surfaces, such as the one defined using eqn (25) and depicted in Fig. 2. For non-constant curvature, calculating the exact equilibrium profile can be carried out by solving eqn (18). Before we do that, let us analyse what we can expect based on the shape of the curvature free energy. To do this, we consider the free energy associated with swapping long and short surfactants between two regions of opposite curvatures. We consider a region of negative curvature centred around 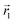 and the one with positive curvature centred around
and the one with positive curvature centred around 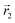 , initially with the same composition
, initially with the same composition 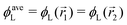 . If we swap long surfactants from the negative curvature region with short surfactants from the positive curvature region, the local densities at
. If we swap long surfactants from the negative curvature region with short surfactants from the positive curvature region, the local densities at 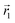 and
and 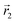 change
change 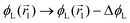 and because of mass conservation
and because of mass conservation 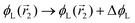 , with Δ > 0. For large enough size asymmetries, the curvature free energy is the one depicted in Fig. 3a. In this case, the contributions to the free energy coming from both the positive and negative curvature regions when de-mixing are negative, and the system spontaneously tends towards this state, resulting in regions of positive curvature having a larger ϕL compared to those of negative curvature. Because the curvature free energy can be made arbitrarily large compared to the entropic contribution to mixing, we expect de-mixing to occur even for otherwise perfectly miscible polymers (χ = 0). When the size asymmetry is not so large (for small parameters α, see Fig. 4), increasing ϕL in a large curvature region and decreasing it in a low curvature region incurs free energy changes of opposite sign, and thus whether or not de-mixing occurs depends on subtler details of the system.
, with Δ > 0. For large enough size asymmetries, the curvature free energy is the one depicted in Fig. 3a. In this case, the contributions to the free energy coming from both the positive and negative curvature regions when de-mixing are negative, and the system spontaneously tends towards this state, resulting in regions of positive curvature having a larger ϕL compared to those of negative curvature. Because the curvature free energy can be made arbitrarily large compared to the entropic contribution to mixing, we expect de-mixing to occur even for otherwise perfectly miscible polymers (χ = 0). When the size asymmetry is not so large (for small parameters α, see Fig. 4), increasing ϕL in a large curvature region and decreasing it in a low curvature region incurs free energy changes of opposite sign, and thus whether or not de-mixing occurs depends on subtler details of the system.
Having made this qualitative analysis, we now turn to a more quantitative approach, and use eqn (18) to calculate the equilibrium profile from local DFT theory. In the following calculations, we analyse the case of ideal perfectly miscible surfactants where the enthalpic interactions are zero (χ = 0). This is not an important restriction, because positive (negative) values of χ will merely strengthen (weaken) the de-mixing trend provided at χ = 0.
Fig. 5 presents representative density profiles for different asymmetries α and different values of the maximum curvature of the surface, which we obtained either by changing the maximum height of the sinusoidal surface or its wavelength, a and k in eqn (26), respectively. Continuous equilibrium profiles are obtained, with shorter/longer surfactants segregating to the regions of negative/positive curvature, as expected. Noticeably, the strength of segregation of the surfactants increases with increasing maximum curvature.
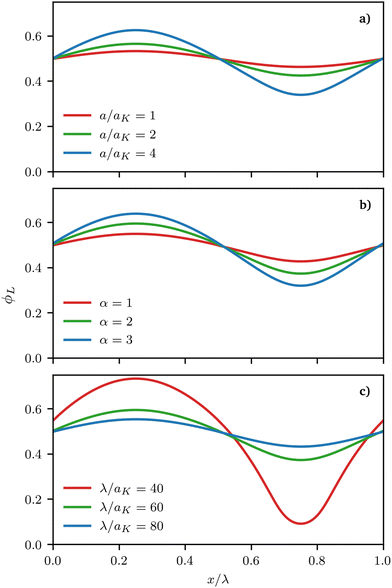 |
| | Fig. 5 Representative density profiles ϕL(x) for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary mixture of long and short surfactants obtained from the free energy minimisation procedure for different parameters. In all cases, surfactants are chemically perfectly miscible (χ = 0 in eqn (3)). Stronger deviations from a perfectly mixed mixture can be induced by (a) increasing the depth of the surface a (α = 4 and λ = 100aK) (b) increasing the size asymmetry between the surfactants (a = 2aK and λ = 60aK) and (c) increasing the wave-vector describing the underlying surface (a = 2aK, α = 2) (see eqn (25)). 1 binary mixture of long and short surfactants obtained from the free energy minimisation procedure for different parameters. In all cases, surfactants are chemically perfectly miscible (χ = 0 in eqn (3)). Stronger deviations from a perfectly mixed mixture can be induced by (a) increasing the depth of the surface a (α = 4 and λ = 100aK) (b) increasing the size asymmetry between the surfactants (a = 2aK and λ = 60aK) and (c) increasing the wave-vector describing the underlying surface (a = 2aK, α = 2) (see eqn (25)). | |
It should be noted that the analytical procedure we used to obtain these profiles is based on solving the Euler–Lagrange equations minimising the free energy of the system, under the constraint of a fixed composition and total number of surfactants. This procedure is only valid if the density profile ϕL minimising the free energy functional is continuous. We could not have observed a sharp phase boundary using the underlying functional minimisation procedure. Another potential problem of our approach is that the blob model used to describe the polymeric surfactant, invoked in the derivation of the formulas for fcurv by Komura and Safran, eqn (11)–(14), is only valid for sufficiently long polymers in the scaling regime. Thus, the theory is not applicable to large grafting densities (ξ0 < aK), nor to short polymers of a few Kuhn segments. The theory also clearly breaks down if a large negative curvature is present.§
In order to explore what happens for shorter surfactants, especially at the high grafting densities achieved in experiments,4 but out of the range of applicability of our formalism, we employ particle-based simulations. The overview of the observed configurations is given in Table 1. Without quantitative evaluation of the profiles, a rapid glance at the simulation results confirms the robustness of the behaviour predicted by the theory in its range of validity. The profiles are continuous without sharp boundary, i.e., no phase separation. Longer surfactants clearly concentrate in regions of positive curvature and shorter ones in regions of negative curvature. At least for the systems simulated, we observe a relatively high solubility of the short components in the longer ones and no pure phase (ϕL = 0 or ϕL = 1) is detected, however, in line with our theoretical predictions, the strength of segregation again increases by increasing A, k and α. We highlight that the aforementioned segregation behaviour is actually quite general and does not depend on having a locally cylindrical surface. In fact, the same behaviour is qualitatively observed also on surfaces where curvature varies concurrently in both x and y directions. Within our framework, surfaces of this kind could be studied by making the additional approximation that the polymeric surfactant behaved as if it was grafted on a sphere of the same mean curvature. In this case, one would have to solve the equivalent of eqn (18) for spheres, and substitute R with the local mean radius of curvature of the surface, see the ESI.†
Table 1 Representative snapshots of equilibrium patterns, viewed from the top perpendicular to the x–y plane, for different combinations of surface topographic parameters a and λ0, and different surfactant lengths ratio lS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lL for an otherwise perfectly miscible system where the repulsive potential between beads is the same independent of their type (here, a11 = a22 = a12= 18.75kBT). The head beads of short surfactants are depicted in yellow, whereas those for the long surfactants are shown in red (tails not shown for clarity). As the surface absolute mean curvature increases either due to an increase in a or λ0, and for increasing size asymmetry, microphase segregation becomes more prominent, with the long surfactants concentrating in regions of high (positive) curvature and short ones in regions of low (and negative) curvature. The corresponding surface densities are reported in the ESI
lL for an otherwise perfectly miscible system where the repulsive potential between beads is the same independent of their type (here, a11 = a22 = a12= 18.75kBT). The head beads of short surfactants are depicted in yellow, whereas those for the long surfactants are shown in red (tails not shown for clarity). As the surface absolute mean curvature increases either due to an increase in a or λ0, and for increasing size asymmetry, microphase segregation becomes more prominent, with the long surfactants concentrating in regions of high (positive) curvature and short ones in regions of low (and negative) curvature. The corresponding surface densities are reported in the ESI
l
S![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lL lL |
(a,λ0) |
| (1/2, 40) |
(1/2, 20) |
(1/2, 10) |
(1, 40) |
(1, 20) |
(1, 10) |
(2, 40) |
(2, 20) |
(2, 10) |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
|

|
|
|
|
|
|
|
|
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |

|
|
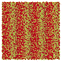
|
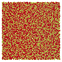
|
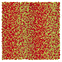
|
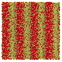
|

|
|

|
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |

|
|
|

|

|
|
|
|

|
As would be expected purely based on symmetry arguments and because of our local description, regions of the same mean curvature have the same ϕL value. However, this is the only real symmetry in our system, and other symmetries are only apparent from a quick look at the density profiles but fail to hold under proper quantitative scrutiny. For example, the deviation of the local composition from the average is larger for negative curvatures than for positive ones of the same value, or in other words, the deviation is not anti-symmetric with respect to the point of zero-curvature. This asymmetry can be measured by looking at different quantities related to δ(x) ≡ ϕL(x) − ϕ0L, the deviation of the local density field ϕL(x) from its average value ϕ0L. More precisely, if we define δmax(min) ≡ |max(min)x(δ(x))|, we can use these latter quantities to gauge the asymmetry in the segregation of the surfactants in high vs. low curvature regions via ΔΔ = δmax − δmin, plotted in Fig. 6 as a function of the wavelength of the sinusoidal surface λ = 2π/k and α. The maximum (minimum) value of density is always achieved in the region of maximum (minimum) curvature. Thus, ΔΔ helps measure the asymmetry in the strength of segregation of long surfactants between peaks and valleys on the grafting surface. When ΔΔ = 0, the maximum local deviation of ϕL is the same (but necessarily of an opposite sign, because of mass conservation) as the (negative) deviation observed in low-curvature regions, any deviation from zero indicating asymmetry. The sign of ΔΔ also allows to understand whether segregation is stronger in high (ΔΔ > 0) or low (ΔΔ < 0) curvature regions.
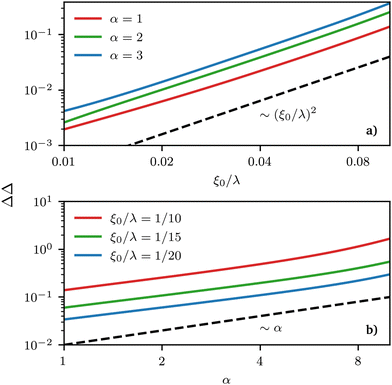 |
| | Fig. 6 Double logarithmic plot of the strength of segregation ΔΔ (see definition in text) as a function of (a) grafting surface wave-length λ (rescaled by ξ0 = σ−1/2) and (b) polymer asymmetry α. In this region, different power-law behaviours control the growth of these quantities. Note that by construction, ΔΔ cannot grow (shrink) indefinitely but can at the most reach a maximum(minimum) value of 1(0) and the power-law behaviour must thus be limited to a specific region of parameters’ values. | |
We observe that the segregation asymmetry is very sensitive to the underlying surface, growing super-linearly (almost perfectly quadratic) as a function of the wave vector 1/λ, and approximately linearly as a function of the size asymmetry α. In this regard, one question that we can ask is whether the strength and asymmetry of segregation depend separately on the height of the surface pattern and its wavelength, as measured using a and λ in eqn (25), or simply vary as a function of the maximum achievable surface curvature, Cmaxmean = a/2k2. To answer this question, we report the results of different computational experiments performed using different combinations of a and k and plot, δmin as a function of Cmaxmean, see Fig. 7 (the same situation occurs for δmax). As it can be easily observed, the data collapse on a set of master curves that indeed only depend on the asymmetry α and not on how the maximum curvature is achieved. This result is not trivial because the local curvature, and thus the individual density profiles, cannot be written as a function of Cmaxmean alone, but require at least two out of three variables between a, λ and Cmaxmean. In other words, profiles with the same maximum curvature but different values of a and k can be different and systems with different values of a and k but the same maximum curvature do not have to exhibit the same value of ϕL at a specific point in space. In fact, they generally do not, except at the points of maximum and minimum curvature, and hence the collapse of δmin (and δmax) on a master curve is observed.
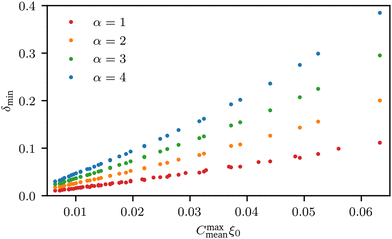 |
| | Fig. 7 Value of δmin as a function of the maximum curvature achieved in the system, for different values of polymer size asymmetry α. Different points with the same colours correspond to different combinations of a and k (see eqn (25)) at the same level of asymmetry. Clearly, all points collapse on the same master curve, indicating that it is not the particular value of (a, k) that controls segregation, but rather their combination into the maximum curvature obtained in the system, 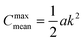 . . | |
3.3. Discussion
Our DFT approach is based on classical density functional theory reformulation of the lattice model developed by Van Lehn and Katz to study the self-assembly of mixtures of surfactants on a planar surface.14 We present a continuum version of their theory and additionally incorporate the effect of local curvature inspired by the work of Cacciuto and co-workers,15,27 while also combining analytical calculations with DPD simulations. An important difference between these latter works and ours is that in their model the chains were grafted to fixed points on the surface, while in our work, the polymers are mobile. The two studies thus represent similar but distinct systems with different physics. Our analytical formulation in terms of a local DFT model allows us to determine the equilibrium profile of the chains via functional optimisation and in this regard, it is closer in spirit to that of Egorov28 than that of Tung and Cacciuto.15,27 Egorov studied the phase separation on cylinders via a field-theoretical approach using self-consistent-field theory in a mean-field approximation. Our analysis of the brush free energy and its dependence on curvature predicts that on surfaces with constant mean curvature, that is, on spheres and cylinders, size asymmetry alone does not favour macro- or micro-phase separation; both require an enthalpic component favouring immiscibility. This result is consistent with those obtained by Tung and Cacciuto for spheres as well as spheroidal surfaces.15
Formation of stripe patterns, i.e., micro-phase separation, on nanoparticles was first reported in microscopy experiments by Stellacci and co-workers in 2004.4 Their observations triggered a lively discussion around the interpretation of the experiments,4,8,9 and the physical mechanism behind the observations, which was explored in various computational studies.14,15,22,26,27 We would like to point out that the observed stripe patterns in molecular dynamics or Monte Carlo simulations, both on spherical and cylindrical surfaces,22,26 and even on planar surfaces,14 might be due to long-lived metastable configurations, because the free-energy of different structures was not calculated and compared to prove their relative thermodynamic stability. In this regard, it is important to mention that free energy calculations were performed by Cacciuto and co-workers.15,27 However, in their simulations, the local concentration of surfactants was assumed to be that of a perfect phase-separated state (i.e., zero solubility of one component into another was assumed), while in their analytical calculations the free energy obtained, for spherical particles, was not sensitive to the number of stripes, meaning that they could not possibly distinguish between macro- and micro-phase separation. Thus, considering an additional positive interface contribution (not present in these analytical calculations, where only bulk terms were included), Cacciuto and co-workers’ results do not support the thermodynamic stability of microphase separation on spheres (as opposed to macro-phase separation), but only on surfaces of non-uniform curvature such as oblate or prolate spheroids.
Here we propose a different explanation for the occurrence of stripes, based on an analogy with other physical systems. The self-assembly of immiscible surfactants is a manifestation of a de-mixing transition and when de-mixing occurs via a nucleation and growth mechanism, macro-phase separation occurs. However, if de-mixing occurs within the spinodal region, where the mixed system is both globally and locally unstable with respect to de-mixing, phase separation leads to the formation of stripe-like domains with a characteristic wavelength.29 During spinodal decomposition, domains coarsen to their equilibrium macrophase separation with a slow power-law dynamics,30 which can lead to formation of kinetically arrested patterns similar to stripes. A spinodal decomposition mechanism would therefore explain not only the morphology of the observed patterns but also their appearance in experiments, and in molecular dynamics and Monte Carlo simulations: the patterns are the kinetically favourable state and, although not thermodynamically stable, their slow relaxation dynamics can make them appear stable on very long, even experimentally relevant, timescales. To the best of our knowledge, this connection between spinodal decomposition and self-assembly of surfactants on curved nano-surfaces has not been proposed before.
Besides exploring the fundamental mechanisms underlying pattern formation, our results can be implemented in practical applications. We have shown that size asymmetry can be exploited to obtain a non-homogeneous surfactant-density profile, with high-curvature regions populated with a higher density of longer surfactants, and vice versa. Using immiscible surfactants (χ > 0) would further enhance these segregation effects. As confirmed by DPD simulations, the surfactant density on surfaces with non-uniform curvature is coupled to the local curvature, which can be used to generate controllable and predictable chemical patterns with particular properties. For example, we predict that regions of higher curvature will contain more of the longer surfactants, and therefore be covered with a thicker surfactant layer. Thus, when surfactants are used as a selective barrier (e.g., in chemical etching), high-curvature regions end up being more protected. We note that exactly the opposite behaviour is expected for bare surfaces where regions of high and positive curvature are more exposed compared to regions of negative curvature, which can only be achieved with high incidence angles. Furthermore, such segregation induced by size asymmetry and curvature could be used to enforce a continuous chemical gradient that follows the underlying curvature profile even when chemically immiscible polymers are used.
In general, microphase separation can thermodynamically favour over macroscopic de-mixing, if an energy term exists that compensates the energy penalty due to the creation of an extra surface (a line energy in 2D). This situation can be realized on surfaces of uniform curvature by varying the splay energy of surfactants at the interface between domains with long vs short surfactant molecules. The splay term should be negative and larger in magnitude than the interface penalty, but not so large as to make the system unstable with respect to formation of ever smaller domains, which would eventually lead to mixing. The splay energy is itself non-local in nature, and for this reason controlling the pattern size by varying the splay energy is a non-trivial task, making this approach impractical in applications. In contrast, tuning the substrate curvature is relatively easy, since the stabilisation of a periodic stripe-like pattern with respect to macro-phase separation is due to a bulk energy term, which forces the pattern to follow the underlying surface. By increasing the maximum curvature of the substrate, or the size asymmetry between the surfactants, we can control the degree of segregation of the two surfactants (Fig. 3). Overall, due to the coupling between the local curvature and the density field of surfactants, we propose using substrates with controlled and spatially-inhomogeneous curvature as a general and facile strategy to direct the design of chemical patterns on nanoscopic surfaces.
4. Conclusions
We have built a continuum model for the density field of a mixture of polymeric surfactants on a curved substrate based on classical density functional theory. Using this model, we discussed the formation of nanoscale patterns in a binary mixture of surfactants of different lengths, showing that, although phase separation should not be expected on surfaces with constant mean curvature, continuous segregation driven purely by the underlying curvature of the substrate is possible, even when in the bulk the two surfactants are chemically perfectly miscible. More precisely, using a locally cylindrical surface as an archetypal example, we have shown by free energy minimisation that size asymmetry between the two polymeric surfactants can couple to non-homogeneities in the underlining local curvature of the surface, preferentially driving long surfactants to regions of high and positive curvature and shorter ones to regions of negative curvature. We also discuss the effect of changing the wavelength and height of the surface pattern, as well as surfactant size asymmetry, showing in particular that the strength of segregation in this system only depends on the maximum (or minimum) mean curvature of the system, and not on the exact way this curvature is achieved. To validate our findings, we performed DPD simulations. We observed that our qualitative analytical conclusions are robust and transferable to parameter regimes (high grafting densities and short surfactants) where some of the assumptions used in building the free energy functional are not a priori justified.
The form of our free energy is not compatible with phase separation of long-vs.-short surfactants due to size asymmetry alone, neither on cylindrical surfaces, nor on spherical surfaces. We discuss that previous results cannot unequivocally support the thermodynamic stability of stripe-like patterns on spherical surfaces compared to macrophase separation, even in the presence of chemical (enthalpic) immiscibility between surfactants. However, we speculate that such patterns could be the kinetic product of a spinodal-decomposition mechanism, which can lead to a slow and potentially kinetically arrested, long-lived state resembling stripes even on experimentally relevant timescales.
Finally, we discuss the potential value of our results for applications with polymeric surfactants as coatings. Our continuum model could be used for a fast qualitative screening of polymeric surfactants to design chemical patterns.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The work was supported by the Chinese National Science Foundation through the grants 11874398 and 12034019, by the Strategic Priority Research Program of the Chinese Academy of Sciences through the grant XDB33000000, and by an international collaboration grant from the K. C. Wong Educational Foundation. We also thank the Beijing University of Chemical Technology CHEMCLOUDCOMPUTING Platform for support with calculations.
Notes and references
- A. Kumar, H. A. Biebuyck and G. M. Whitesides, Langmuir, 1994, 10, 1498–1511 CrossRef CAS.
- D. Bethell, M. Brust, D. J. Schiffrin and C. Kiely, J. Electroanal. Chem., 1996, 409, 137–143 CrossRef.
- J. H. Fendler, Chem. Mater., 1996, 8, 1616–1624 CrossRef CAS.
- A. M. Jackson, J. W. Myerson and F. Stellacci, Nat. Mater., 2004, 3, 330–336 CrossRef CAS PubMed.
- G. Verma and P. A. Hassan, Phys. Chem. Chem. Phys., 2013, 15, 17016–17028 RSC.
- M. Yemini, M. Reches, J. Rishpon and E. Gazit, Nano Lett., 2005, 5, 183–186 CrossRef CAS PubMed.
- K. Keren, M. Krueger, R. Gilad, G. Ben-Yoseph, U. Sivan and E. Braun, Science, 2002, 297, 72–75 CrossRef CAS PubMed.
- J. Stirling, I. Lekkas, A. Sweetman, P. Djuranovic, Q. Guo, B. Pauw, J. Granwehr, R. Lévy and P. Moriarty, PLoS One, 2014, 9, e108482 CrossRef PubMed.
- Q. K. Ong and F. Stellacci, PLoS One, 2015, 10, e0135594 CrossRef PubMed.
- J. F. Lutsko, Adv. Chem. Phys., 2010, 144, 1 CAS.
- R. Evans, Adv. Phys., 1979, 28, 143–200 CrossRef CAS.
- M. te Vrugt, H. Löwen and R. Wittkowski, Adv. Phys., 2020, 69, 121–247 CrossRef.
- C. Linne, D. Visco, S. Angioletti-Uberti, L. Laan and D. J. Kraft, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2106036118 CrossRef CAS PubMed.
- R. C. Van Lehn and A. Alexander-Katz, J. Chem. Phys., 2011, 135, 141106 CrossRef PubMed.
- C. Tung and A. Cacciuto, J. Chem. Phys., 2013, 139, 194902 CrossRef PubMed.
- M. Daoud and J. P. Cotton, J. Phys., 1982, 43, 531–538 CrossRef CAS.
- A. Bug, M. Cates, S. Safran and T. Witten, J. Chem. Phys., 1987, 87, 1824–1833 CrossRef CAS.
- C. Marques, J. Joanny and L. Leibler, Macromolecules, 1988, 21, 1051–1059 CrossRef CAS.
- C. Hiergeist and R. Lipowsky, J. Phys. II, 1996, 6, 1465–1481 CrossRef CAS.
- S. Komura and S. A. Safran, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 5, 337–351 CrossRef CAS.
- Y. Zhulina, Polym. Sci. U.S.S.R., 1984, 26, 885–891 CrossRef.
- C. Singh, P. K. Ghorai, M. A. Horsch, A. M. Jackson, R. G. Larson, F. Stellacci and S. C. Glotzer, Phys. Rev. Lett., 2007, 99, 226106 CrossRef PubMed.
- S. Plimpton, J. Comput. Phys., 1997, 117, 1–42 CrossRef.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
-
H. B. Callen, Thermodynamics and an Introduction to Thermostatistics, 1998 Search PubMed.
- C. Singh, Y. Hu, B. P. Khanal, E. R. Zubarev, F. Stellacci and S. C. Glotzer, Nanoscale, 2011, 3, 3244 RSC.
- W. L. Miller, B. Bozorgui, K. Klymko and A. Cacciuto, J. Chem. Phys., 2011, 135, 244902 CrossRef PubMed.
- S. Egorov, Soft Matter, 2012, 8, 3971–3979 RSC.
- J. W. Cahn, Acta Metall., 1961, 9, 795–801 CrossRef CAS.
- R. V. Kohn and F. Otto, Commun. Math. Phys., 2002, 229, 375–395 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01540d |
‡ Note that if a bimodal brush is considered, i.e., for polymeric surfactants where the two polymers have different lengths like in the case we want to address, two layers will be formed. The first layer comprises both short and long polymers, whereas the second layer is made up of only the remainder of the longer polymers. For the second layer, the effective grafting density is reduced to 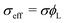 , see Fig. 1 for clarity and Ref. 20 for more details. , see Fig. 1 for clarity and Ref. 20 for more details. |
| § This is evident because for certain physically meaningful combinations of parameters, fcurv can assume non-physical imaginary values, a fact that can also lead to numerical problems during the self-consistent procedure and does not allow us to sample all potential parameter combinations. |
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article bcd,
Xianren
Zhang
bcd,
Xianren
Zhang
 a,
Jure
Dobnikar
a,
Jure
Dobnikar
 bcd and
Stefano
Angioletti-Uberti
*e
bcd and
Stefano
Angioletti-Uberti
*e
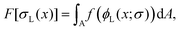
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(ϕL) + (1 − ϕL)log(1 − ϕL)],
log(ϕL) + (1 − ϕL)log(1 − ϕL)],
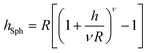
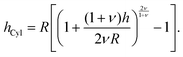
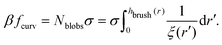
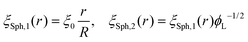
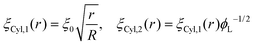
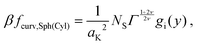
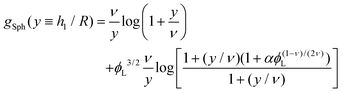
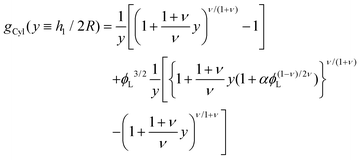
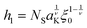
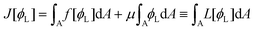
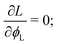
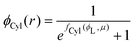
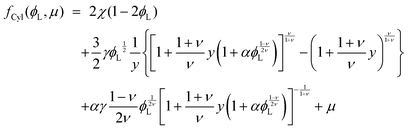
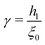 . The equivalent expression valid for a spherical surface (which could thus be used to define a spherical-surface approximation), is reported in the ESI.†
. The equivalent expression valid for a spherical surface (which could thus be used to define a spherical-surface approximation), is reported in the ESI.†
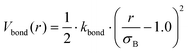
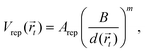
 is the position of the tail bead, Arep = 1.0kBT is the energy parameter and B = 1.0σB sets the length-scale for the potential. In eqn (20), d(x,y,z) = z − f(x,y), where f(x,y) parametrises the surface. Finally, m = 6 is a positive parameter that controls the range of the repulsive potential. We model the non-bonded interactions between the beads via the soft and purely repulsive DPD potential:
is the position of the tail bead, Arep = 1.0kBT is the energy parameter and B = 1.0σB sets the length-scale for the potential. In eqn (20), d(x,y,z) = z − f(x,y), where f(x,y) parametrises the surface. Finally, m = 6 is a positive parameter that controls the range of the repulsive potential. We model the non-bonded interactions between the beads via the soft and purely repulsive DPD potential: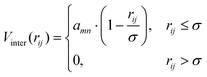
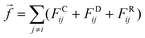
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij·vij)
ij·vij)![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij,
ij,![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ij,
ij,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary mixture of long and short chains. The time step employed in integrating the equations of motion is set to dt = 10−4τ0, where
1 binary mixture of long and short chains. The time step employed in integrating the equations of motion is set to dt = 10−4τ0, where 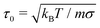 and each simulation is run for over 5 × 106 time steps. Periodic boundary conditions are implemented in x- and y-directions, but not in the z-direction.
and each simulation is run for over 5 × 106 time steps. Periodic boundary conditions are implemented in x- and y-directions, but not in the z-direction.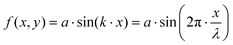
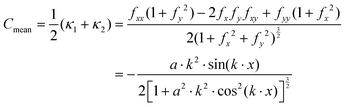
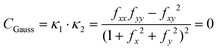
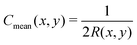 , whereas for a spherical surface we have
, whereas for a spherical surface we have 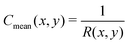 . For visual reference, the surface height profile and the corresponding curvature for our locally-cylindrical, sinusoidally-modulated surface are reported in the ESI.†
. For visual reference, the surface height profile and the corresponding curvature for our locally-cylindrical, sinusoidally-modulated surface are reported in the ESI.†

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NS = 11
NS = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and (b) α = 1 (NL
1) and (b) α = 1 (NL![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NS = 2
NS = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Although the free energy curvature is almost indistinguishable for negative curvatures, it differs quantitatively for positive values, with the difference increasing for increasing values of the scaling variable, i.e., for increasing curvature.
1). Although the free energy curvature is almost indistinguishable for negative curvatures, it differs quantitatively for positive values, with the difference increasing for increasing values of the scaling variable, i.e., for increasing curvature.
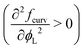 . This behaviour of the second derivative indicates that the curvature contribution thermodynamically stabilises a mixed homogeneous brush with respect to demixing into a linear combination of two phases of distinct composition.25 Whether or not de-mixing occurs in practice, depends on the total free energy density, including the entropy of mixing, eqn (4), which always favours mixing, and enthalpic contributions, eqn (3), which favours mixing or de-mixing depending on whether χ is negative or positive, respectively. Unlike the other two terms, the magnitude of the curvature term is controlled by both the curvature of the surface and the size asymmetry between the surfactants. The curvature term also increases super-linearly rather than linearly with respect to the grafting density σ (considering that σ = Γ/a2, see also eqn (11)). Thus, an appropriate choice of parameters can always be made to induce mixing by making the curvature term dominating.
. This behaviour of the second derivative indicates that the curvature contribution thermodynamically stabilises a mixed homogeneous brush with respect to demixing into a linear combination of two phases of distinct composition.25 Whether or not de-mixing occurs in practice, depends on the total free energy density, including the entropy of mixing, eqn (4), which always favours mixing, and enthalpic contributions, eqn (3), which favours mixing or de-mixing depending on whether χ is negative or positive, respectively. Unlike the other two terms, the magnitude of the curvature term is controlled by both the curvature of the surface and the size asymmetry between the surfactants. The curvature term also increases super-linearly rather than linearly with respect to the grafting density σ (considering that σ = Γ/a2, see also eqn (11)). Thus, an appropriate choice of parameters can always be made to induce mixing by making the curvature term dominating.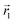 and the one with positive curvature centred around
and the one with positive curvature centred around 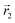 , initially with the same composition
, initially with the same composition 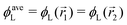 . If we swap long surfactants from the negative curvature region with short surfactants from the positive curvature region, the local densities at
. If we swap long surfactants from the negative curvature region with short surfactants from the positive curvature region, the local densities at 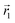 and
and 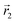 change
change 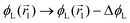 and because of mass conservation
and because of mass conservation 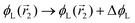 , with Δ > 0. For large enough size asymmetries, the curvature free energy is the one depicted in Fig. 3a. In this case, the contributions to the free energy coming from both the positive and negative curvature regions when de-mixing are negative, and the system spontaneously tends towards this state, resulting in regions of positive curvature having a larger ϕL compared to those of negative curvature. Because the curvature free energy can be made arbitrarily large compared to the entropic contribution to mixing, we expect de-mixing to occur even for otherwise perfectly miscible polymers (χ = 0). When the size asymmetry is not so large (for small parameters α, see Fig. 4), increasing ϕL in a large curvature region and decreasing it in a low curvature region incurs free energy changes of opposite sign, and thus whether or not de-mixing occurs depends on subtler details of the system.
, with Δ > 0. For large enough size asymmetries, the curvature free energy is the one depicted in Fig. 3a. In this case, the contributions to the free energy coming from both the positive and negative curvature regions when de-mixing are negative, and the system spontaneously tends towards this state, resulting in regions of positive curvature having a larger ϕL compared to those of negative curvature. Because the curvature free energy can be made arbitrarily large compared to the entropic contribution to mixing, we expect de-mixing to occur even for otherwise perfectly miscible polymers (χ = 0). When the size asymmetry is not so large (for small parameters α, see Fig. 4), increasing ϕL in a large curvature region and decreasing it in a low curvature region incurs free energy changes of opposite sign, and thus whether or not de-mixing occurs depends on subtler details of the system.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 binary mixture of long and short surfactants obtained from the free energy minimisation procedure for different parameters. In all cases, surfactants are chemically perfectly miscible (χ = 0 in eqn (3)). Stronger deviations from a perfectly mixed mixture can be induced by (a) increasing the depth of the surface a (α = 4 and λ = 100aK) (b) increasing the size asymmetry between the surfactants (a = 2aK and λ = 60aK) and (c) increasing the wave-vector describing the underlying surface (a = 2aK, α = 2) (see eqn (25)).
1 binary mixture of long and short surfactants obtained from the free energy minimisation procedure for different parameters. In all cases, surfactants are chemically perfectly miscible (χ = 0 in eqn (3)). Stronger deviations from a perfectly mixed mixture can be induced by (a) increasing the depth of the surface a (α = 4 and λ = 100aK) (b) increasing the size asymmetry between the surfactants (a = 2aK and λ = 60aK) and (c) increasing the wave-vector describing the underlying surface (a = 2aK, α = 2) (see eqn (25)).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) lL for an otherwise perfectly miscible system where the repulsive potential between beads is the same independent of their type (here, a11 = a22 = a12= 18.75kBT). The head beads of short surfactants are depicted in yellow, whereas those for the long surfactants are shown in red (tails not shown for clarity). As the surface absolute mean curvature increases either due to an increase in a or λ0, and for increasing size asymmetry, microphase segregation becomes more prominent, with the long surfactants concentrating in regions of high (positive) curvature and short ones in regions of low (and negative) curvature. The corresponding surface densities are reported in the ESI
lL for an otherwise perfectly miscible system where the repulsive potential between beads is the same independent of their type (here, a11 = a22 = a12= 18.75kBT). The head beads of short surfactants are depicted in yellow, whereas those for the long surfactants are shown in red (tails not shown for clarity). As the surface absolute mean curvature increases either due to an increase in a or λ0, and for increasing size asymmetry, microphase segregation becomes more prominent, with the long surfactants concentrating in regions of high (positive) curvature and short ones in regions of low (and negative) curvature. The corresponding surface densities are reported in the ESI

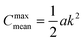 .
.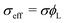 , see Fig. 1 for clarity and Ref. 20 for more details.
, see Fig. 1 for clarity and Ref. 20 for more details.




























