Q-switched and vector soliton pulses from an Er-doped fiber laser with high stability based on a γ-graphyne saturable absorber
Qingbo
Wang
 a,
Zhuo
Li
b,
Pan
Wang
a,
Zhuo
Li
b,
Pan
Wang
 *a,
Qiaoqiao
Xu
a,
Zhiwei
Zhang
b,
Zhi
Wang
a,
Yi
Huang
*a,
Qiaoqiao
Xu
a,
Zhiwei
Zhang
b,
Zhi
Wang
a,
Yi
Huang
 b and
Yan-ge
Liu
a
b and
Yan-ge
Liu
a
aInstitute of Modern Optics, Nankai University, Tianjin Key Laboratory of Micro-scale Optical Information Science and Technology, Tianjin 300350, China. E-mail: pan.wang@nankai.edu.cn
bSchool of Materials Science and Engineering, Nankai University, Tianjin 300350, China
First published on 11th April 2023
Abstract
As a Dirac material, an allotrope of graphene, namely γ-graphyne (γ-GY), is proved to have excellent nonlinear optical properties. Unfortunately, the saturable absorption properties and ultrafast photonics applications of γ-GY at the 1.5 μm band, which play vital roles in optical communication, have not been reported so far. Herein, γ-GY nanosheets (NSs) are prepared by an improved mechanochemical method, and a saturable absorber (SA) is fabricated by a laser-induced deposition method. The modulation depth (MD) and saturable fluence at 1.5 μm are found to be 5.40% and 23.46 μJ cm−2, respectively. Consequently, by inserting the as-prepared SA into an Er3+-doped fiber laser (EDFL), Q-switching and mode-locking operation with high stability are realized. Also, the mode-locking pulses are verified to be polarization-locked vector solitons (PLVSs) based on further study. With increasing pump power, the phase difference between the two orthogonal components increases, leading to the evolution of state of polarization (SOP). Additionally, the degrees of polarization (DOPs) are measured and all reach more than 97%, meaning high polarization stability. Therefore, this work not only broadens the application scope of γ-GY in ultrafast photonics, but also provides an important foundation for the study of soliton dynamics.
1. Introduction
Passive Q-switched/mode-locked fiber lasers (QSFLs/MLFLs) with high beam quality, excellent heat dissipation, high stability and flexible cavity structure, play an irreplaceable role in various crucial fields such as optical communication, precision metrology, ultrafine machining and biomedicine.1–6 Moreover, passive MLFLs have important research significance as an ideal platform for studying soliton nonlinear dynamics.7 Since the successful implementation of ultra-short pulse output based on graphene by Sun et al.,8 SAs based on two-dimensional (2D) materials have attracted great research interest because of their many similar photonic properties, such as broadband absorption, strong nonlinearity, ultrafast response time and saturable absorption properties.9,10 Unfortunately, there are still many shortcomings in the reported 2D materials used for SAs. As one of the most typical 2D materials for SAs, graphene has fast and ultra-wideband optical responses due to its zero-bandgap structure and high transparency, but the modulation ability is limited.11 Topological insulators have an innate giant MD (up to 95%) and broadband saturable absorption properties, but their development is hindered by the slow relaxation time and complex preparation process.12,13 The application of transition metal dichalcogenides, with advantages of layer-dependent bandgap and broadband operation, are limited in high-power lasers by their low laser damage threshold.14,15 In addition, the application of black phosphorus (BP) is seriously limited by its environmental instability.16,17 Therefore, the SA materials with excellent nonlinear optical properties and high stability are worth further exploration.GYs, as allotropes of graphene, are a new class of carbon nanomaterials, and similar to graphene, they also have a 2D structure and Dirac cone, so they have the characteristics of an ultrafast optical response and broadband optical absorption.18 GYs are formed by inserting ethynyl units between aromatic moiety rings in graphene. According to the number of inserted acetylene units, the GYs can be divided into GY, graphdiyne, graphtriyne, etc. Furthermore, GYs can be separated into α-, β- and γ-GY according to different sp–sp2 hybridization binding modes.19,20 It is worth mentioning that in addition to having one of the most stable structures of all GYs, γ-GY also has a natural band gap derived from the overlapping of carbon 2pz orbitals and the inhomogeneous π-bonding between sp- and sp2-hybridized carbon atoms.20,21 Meanwhile, the presence of sp-hybridized carbons with large conjugated structures enables γ-GY to have a stronger nonlinear response than that of graphene.22 Xi et al. demonstrated through a theoretical study that the electron mobility of γ-GY is ∼104 cm2 V−1 s−1 at room temperature due to strong longitudinal acoustic phonon scattering.23 In addition, the carrier relaxation time of γ-GY was accurately calculated by Jiang et al. in 2017, which was ∼170 fs at room temperature (300 K).24 Under the premise of homogeneous broadening, when the relaxation time of SA is much faster than other processes in the system, it can be regarded as an ideal fast SA.25 Under comprehensive considerations, γ-GY is expected to achieve fruitful results in the optoelectronic field.
Since the first demonstration by Baughman et al. in 1987,26 scientists have successively investigated γ-GY's applications in the fields of energy, environment and biomedicine.20,27–31 In addition, γ-GY also has a nonlinear transmittance, that is, high transmittance to a strong incident laser and low transmittance to a weak incident laser. Therefore, the γ-GY–SA can be used as a Q-switch to make the laser output Q-switching pulses, or as a mode-locker to make the laser output mode-locking pulses.31 However, although a few works have been reported on γ-GY as an SA for solid-state Q-switched lasers,22,32 related research studies on γ-GY are still scarce. There is no experimental report about a pulsed fiber laser based on a γ-GY–SA, especially in EDFL, which plays a vital role in the field of optical communication. As mentioned above, the MLFL, as an ideal platform to study the nonlinear dynamics of solitons, can generate a variety of soliton types by adjusting the cavity parameters, such as the vector soliton caused by nonlinear coupling between two polarization modes.7,33 Moreover, the study of vector solitons is not only beneficial for a deep understanding of the rich polarization dynamics of this soliton structure with more codability and diversity, but will also further expand their application potential in high-capacity optical communication.34–36 Therefore, it would be of great significance to explore the ultrafast photonics application of γ-GY at 1.5 μm, and further study the soliton dynamics based on it.
In this work, an improved mechanochemical method is used to synthesize γ-GY NSs, and based on these γ-GY NSs, a γ-GY–SA is prepared by the laser-induced deposition method. The MD and the saturation fluence of the γ-GY–SA at 1.5 μm are measured by the balanced twin-detector measurement method, verifying its saturable absorption characteristics. Subsequently, an EDFL based on a γ-GY–SA is constructed, and Q-switched and mode-locked pulses are obtained. Moreover, both QSFLs and MLFLs based on the γ-GY–SA in this work are found to have excellent stability. On this basis, the vector features of the conventional solitons (CSs) are systematically studied, and the polarization evolution trend of the vector soliton is explored during the increase of the pump power. To the best of our knowledge, this is the first report on the saturable absorption of γ-GY and its application at 1.5 μm, which is of great inspiration for the applications of γ-GY in ultrafast photonics, nonlinear optics and optical communications.
2. Materials and methods
2.1. Preparation and characterization of γ-GY NSs
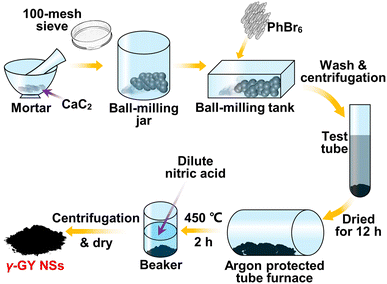
The currently known preparation methods of γ-GY NSs are mainly ultrasonic irradiation and mechanical ball milling.37,38 In this study, an improved mechanochemical method, shown in Fig. 1, is used to successfully synthesize γ-GY NSs. It is worth noting that compared with the preparation method used in ref. 38, a solvent-free dry grinding method is used in the preparation process in this work, which not only ensured the original advantages of the traditional mechanochemical method, such as simple operation and low cost, but also reduced the impurity content and further improved the quality of γ-GY NSs. Before the experiment, the block CaC2 (purity of 75%) is pulverized and sieved with a 100-mesh sieve to obtain CaC2 powder. Subsequently, CaC2 powder is added to a 200 mL ball-milling jar for ball milling. The purpose of this step is to reduce the particle size of CaC2 and increase the contact area of the reaction, which is more conducive to the progress of the reaction. After that, the ball-milled CaC2 powder and hexabromobenzene (PhBr6) are added into a ball-milling tank according to a molar ratio of 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and ball-milled for 12 h. The reaction product is washed with absolute ethanol and deionized water, and the solid powder is obtained by centrifugation, which is further dried in a vacuum drying oven at 80 °C for 12 h. Afterwards, the obtained solid powder is placed in an argon protected tube furnace and annealed at 450 °C for 2 h to volatilize the incompletely reacted PhBr6. Finally, the obtained powder is soaked in the dilute nitric acid and stirred for 24 h for impurity removal, followed by centrifugation and drying to obtain γ-GY NSs.
1 and ball-milled for 12 h. The reaction product is washed with absolute ethanol and deionized water, and the solid powder is obtained by centrifugation, which is further dried in a vacuum drying oven at 80 °C for 12 h. Afterwards, the obtained solid powder is placed in an argon protected tube furnace and annealed at 450 °C for 2 h to volatilize the incompletely reacted PhBr6. Finally, the obtained powder is soaked in the dilute nitric acid and stirred for 24 h for impurity removal, followed by centrifugation and drying to obtain γ-GY NSs.
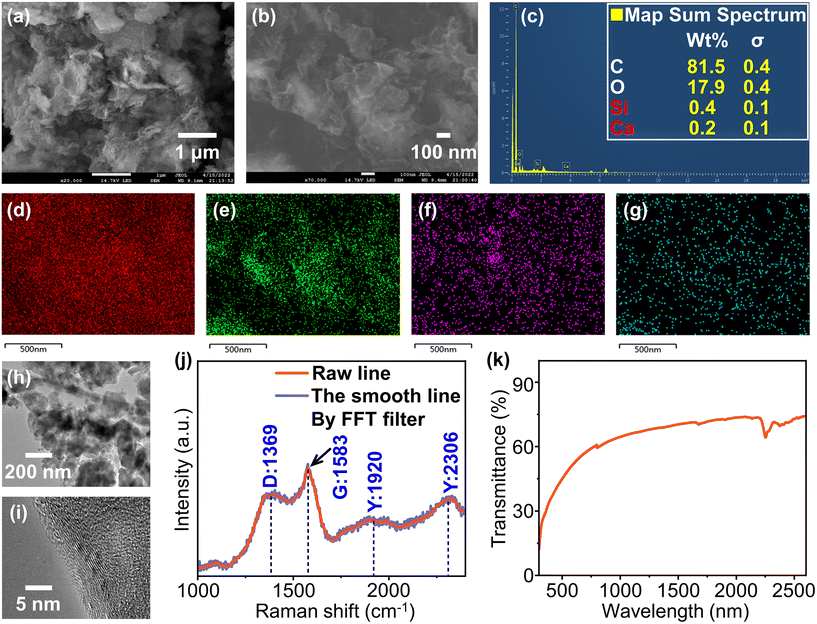
The scanning electron microscopy (SEM) images of γ-GY NSs are shown in Fig. 2a and b, indicating their distinct 2D curled sheet structure. The elemental composition of γ-GY NSs is analysed in detail by energy-dispersive X-ray spectroscopy (EDS), and the mappings are displayed in Fig. 2c–g. The elemental composition of γ-GY NSs includes mostly C and O elements, as well as a small amount of Si and Ca elements, where the impurities might be introduced during the ball-milling process. Fig. 2h and i show the characterization images of the microstructure of γ-GY NSs using transmission electron microscopy (TEM) and high-resolution transmission electron microscopy (HRTEM), respectively. It can be seen from these images that several large particles of irregular shape in the order of micrometers are agglomerated by nanoparticles. Fig. 2j shows the Raman spectrum of γ-GY NSs, and a smoothed line is obtained with an FFT filter. Four peaks appear at 1369 cm−1, 1583 cm−1, 1920 cm−1 and 2306 cm−1, corresponding to the D peak, G peak, the stretching vibration of sp-hybridized carbon, and the G′ bands ascribed to the double resonance inter-valley Raman scattering process, respectively. The positions of these four peaks are consistent with previous reports,38–40 which can also well prove that the sample prepared in this work and the γ-GY reported in those papers are the same substance. As shown in Fig. 2k, the transmission spectrum of γ-GY NSs ranging from 300 to 2600 nm is also measured. It is worth mentioning that the dip around 2250 nm in the VIS-IR transmission spectrum is caused by the strong absorption peak of γ-GY at 2250 nm, which is consistent with a previous report.32 It is demonstrated by this VIS-IR transmission spectrum that the γ-GY–SA has potential for broadband optical devices.
2.2. Fabrication and saturable absorption of the γ-GY–SA
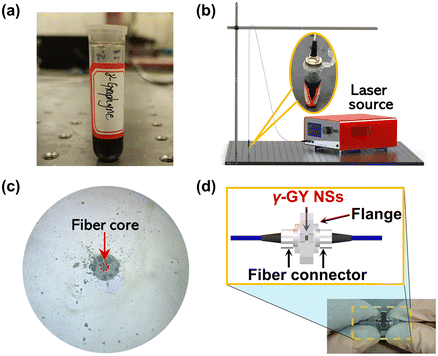
γ-GY NSs are deposited on a single-mode fiber patch cord facet by a laser-induced deposition method, which can flexibly control the sample thickness by changing the power and time, enabling the interaction with the light propagating within the fiber.41,42 A photograph of the γ-GY dispersion and the experimental setup of the laser-induced deposition method are shown in Fig. 3a and b. Firstly, the homogeneous dispersion with a concentration of 1 mg mL−1 is prepared with γ-GY NSs and isopropanol. Then, the fiber patch cord facet, which under the irradiation from a continuous wave (CW) laser with a power of 70 mW, is immersed in the dispersion for 20 min, and the micrograph of the fiber facet deposited with γ-GY NSs is shown in Fig. 3c. Finally, the γ-GY–SA is fabricated by connecting the two fiber patch cords using a flange, as shown in Fig. 3d.The laser-induced deposition method can avoid the additional nonlinear interference caused by the D-shaped and tapered fibers.43
Although the open-aperture Z-scan technology used in ref. 22 can accurately measure the nonlinear optical properties of materials, it cannot directly and efficiently measure the saturable absorption properties of the all-fiber SA prepared in this work. Therefore, the balanced twin-detector measurement method,44 as another efficient means of measuring the nonlinear optical properties of SA, is used to measure the nonlinear saturable absorption properties of the γ-GY–SA. The experimental setup used in the measurement is shown in Fig. 4a. The central wavelength and pulse duration of the pulsed fiber laser with a maximum average power of 21.5 mW, used in this experiment, are 1568.6 nm and 583 fs, respectively, while the coupling ratio of the used optical coupler is 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 90. By continuously adjusting the attenuator, the nonlinear variation trend of the transmittance of the γ-GY–SA is clearly presented. Considering the insertion loss of a self-assembled SA, it is impossible to accurately measure the SA transmittance when the average incident fluence is close to 0 μJ cm−2. In order to fill the data gap here, the following fitting formula is adopted to fit the experimental data:
90. By continuously adjusting the attenuator, the nonlinear variation trend of the transmittance of the γ-GY–SA is clearly presented. Considering the insertion loss of a self-assembled SA, it is impossible to accurately measure the SA transmittance when the average incident fluence is close to 0 μJ cm−2. In order to fill the data gap here, the following fitting formula is adopted to fit the experimental data:
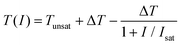 | (1) |
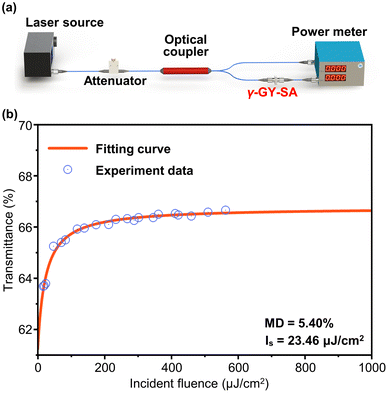 | ||
| Fig. 4 (a) Schematic of the balanced twin-detector measurement. (b) Relationship between transmittance of the γ-GY–SA and incident fluence. | ||
3. Experimental setup
The experimental setup of an EDFL ring cavity is shown in Fig. 5a. A piece of 0.5 m Er3+-doped fiber (EDF) (LIEKKI, Er110-4/125) is excited by the 980 nm pump light, which is injected into the cavity through a 980/1550 nm wavelength division multiplexer (WDM). A 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 optical coupler (OC) is used to output the laser, and a polarization-independent isolator (PI-ISO) is employed to force the unidirectional operation of the ring cavity. Meanwhile, the two polarization controllers (PCs) in the laser can be used to fine-tune the SOP of the circulating light in the ring cavity. The rest of the cavities are composed of a standard single-mode fiber (SMF).
80 optical coupler (OC) is used to output the laser, and a polarization-independent isolator (PI-ISO) is employed to force the unidirectional operation of the ring cavity. Meanwhile, the two polarization controllers (PCs) in the laser can be used to fine-tune the SOP of the circulating light in the ring cavity. The rest of the cavities are composed of a standard single-mode fiber (SMF).
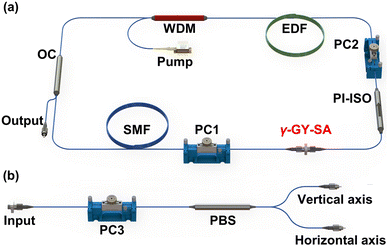 | ||
| Fig. 5 (a) Beam path of a pulsed fiber laser with a γ-GY–SA. (b) The setup of the polarization-resolved measurement. | ||
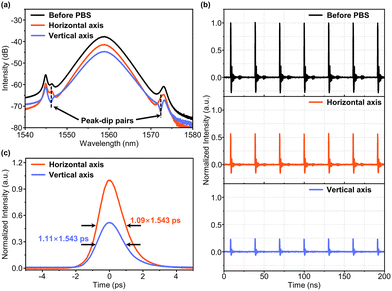
The polarization-resolved setup, shown in Fig. 5b, is used to investigate the vector natures of pulses from the MLFL based on the γ-GY–SA. After the vector soliton is incident on the polarization beam splitter (PBS), its two orthogonal components will be separated under the action of the PBS. In order to maintain the SOPs of the two orthogonal components, the output branch of the PBS is composed of polarization-maintaining fibers, while the role of PC3 is to regulate the phase difference between the two orthogonal components.
In addition, a 1.2 GHz photodetector (Thorlabs, DET01CFC/M) is used to detect the obtained laser signal, and a spectrometer (Yokogawa, AQ6370) is used to monitor the spectral information of the laser. An oscilloscope (Teledyne LeCroy, WaveRunner 620Zi) with a bandwidth of 2 GHz and a radio-frequency (RF) spectrum analyzer (Rigol, RSA3045) are used to record the time domain and RF information of the laser, respectively. The Stokes parameters and the DOP are measured using Agilent modules (Agilent, N7786B and 8184B).
4. Results and discussion
4.1. Q-switching operation of the EDFL
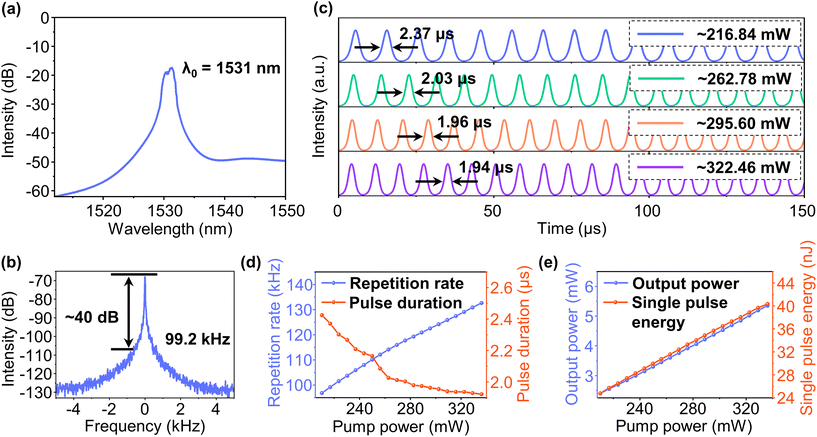
When the pump power is set to be 90.6 mW, a CW lasing can be obtained. After the pump power is further increased to 140.7 mW, a Q-switching operation can be realized by adjusting the PCs appropriately.Upon further increasing the pump power and adjusting PCs, stable Q-switched pulses can be achieved at a pump power of 216.84 mW. As can be seen from Fig. 6a and b, the central wavelength and repetition rate of the pulsed laser are 1531 nm and 99.2 kHz, respectively. Furthermore, as shown in the RF spectrum, the signal-to-noise ratio (SNR) at the fundamental frequency is 40 dB without any side peaks, indicating the stable operation of the QSFLs. To visually observe the output characteristics of the QSFLs at different pump powers, the temporal pulse trains under pump powers of 216.84 mW, 262.78 mW, 295.6 mW and 322.46 mW are displayed in Fig. 6c, respectively. It can be clearly observed that the pulse duration and the interval between pulses are gradually reduced with an increase in the pump power. In addition, no peak intensity modulation of the pulse trains is found under each pump power, and the symmetric Gaussian-like pulses are uniformly distributed in the time domain, indicating the high stability of the Q-switching operation.
The evolution of both repetition rate and pulse duration with increasing pump power in the range of 210.29 mW to 337.05 mW are illustrated in Fig. 6d, which are the typical features of Q-switched lasers.45 Different from the dependence of repetition rate on the cavity length in mode-locked lasers, the repetition rate of the QSFL is increased almost linearly from 96.84 kHz to 132.63 kHz with an increase in pump power. Under higher pump power, greater gain will be obtained and the saturation of the SA could be reached in a shorter time, resulting in a higher repetition rate of Q-switched pulse trains, while the pulse duration, in contrast, shows a continuously decreasing trend in the range from 2.43 μs to 1.92 μs, and its decreasing speed is reduced gradually. The reason for this phenomenon is that in the regime of high pump power, the accumulation speed of electrons in the upper energy level is slowed down by over-saturation.46
The output power and single-pulse energy as a function of pump power are recorded in Fig. 6e. It can be seen that during the experiment, the output power and single-pulse energy increase almost linearly in the range from 2.40 mW to 5.35 mW and 24.80 nJ to 40.35 nJ, respectively. The slope efficiency of the QSFL is determined to be 2.35% by linear fitting. Importantly, there is no reduction in the growth rate of the single-pulse energy and output power during the whole measurement. Thus, we believe that the maximum output power and maximum single-pulse energy of the pulse trains are both limited by the available pump power in our experiments, and the performance of the laser can be further improved by optimizing the laser cavity parameters.
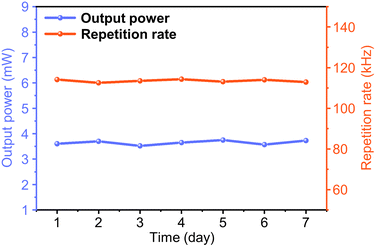
In order to test the long-term stability of the γ-GY–SA-based QSFLs, the variation of the output power and repetition rate over one week with a pump power of 262.78 mW is measured, as shown in Fig. 7. The output power and repetition rate fluctuate within a small range of 0.23 mW and 1.79 kHz, respectively, indicating a highly stable operation. For comparison, the reported temporal stability of several QSFLs based on different materials are listed in Table 1. It should be noted that the operating times of the lasers listed in Table 1, although they may not be the best performing for the same material, can qualitatively reflect the superior stability of the QSFL based on γ-GY in this work.
| Material | ΔT [%] | λ 0 [nm] | τ min [μs] | Reported work duration | Ref. |
|---|---|---|---|---|---|
| a τ min represents the minimum pulse duration. | |||||
| Graphene | — | 1539.6 | ∼2.3 | 0.5 h | 47 |
| Antimonene | 11.63 | 1558 | 1.42 | 2 h | 48 |
| BP | 8.3 | ∼1568 | 1.36 | 25 h | 49 |
| WS2 | 2 | ∼1561 | 2.396 | 14 days | 50 |
| Bi2Te3 | 25.7 | 1566.9 | 13 | 4 h | 51 |
| Ti3AlC2 | 16 | 1567.4 | 0.99 | 1 h | 52 |
| Ag | 5.8 | 1033 | 1.01 | 1.5 h | 53 |
| γ-GY | 4.09 | 1531 | 1.92 | 7 days | This work |
4.2. Mode-locking operation of the EDFL
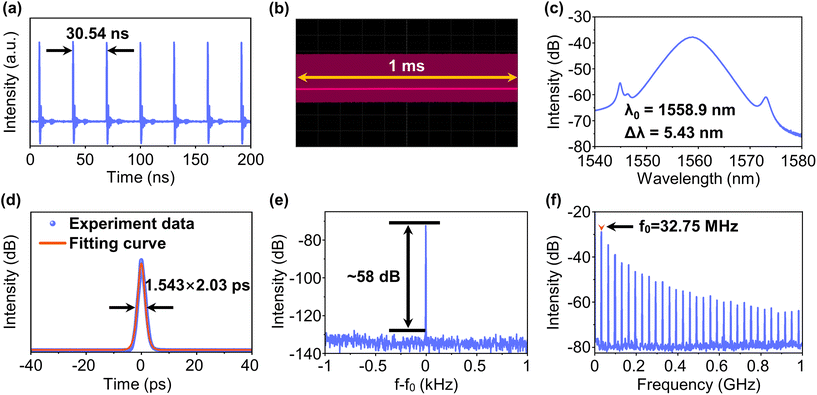
When the pump power reaches a threshold of 97.07 mW, the mode-locking operation is self-started by carefully adjusting the PCs. After further increasing the pump power to 134.82 mW, the stable CSs are obtained, and the characteristics are summarized in Fig. 8. The pulse interval of 30.54 ns shown in Fig. 8a corresponds to the total cavity length of the EDFL, indicating the mode-locking operation at a fundamental frequency of 32.75 MHz. Additionally, as shown in Fig. 8b, no intensity modulation of the oscilloscope trace is found within 1 ms, indicating the high stability of the mode-locking operation. The spectrum with a central wavelength of 1558.9 nm and the autocorrelation trace with sech2 pulse profile are shown in Fig. 8c and d, respectively. The 3 dB bandwidth of the spectrum and the pulse duration are 5.43 nm and 2.03 ps, respectively, while the calculated time–bandwidth product is 0.67, which is larger than the theoretical value (0.315) for the transform-limited sech2-shaped pulses, proving that the pulses are slightly chirped. The SNR at the fundamental frequency of 32.75 MHz, as shown in Fig. 8e, is about 58 dB, and there is no obvious signal of mode-locking instability in the wideband RF spectrum depicted in Fig. 8f, indicating an excellent stability.
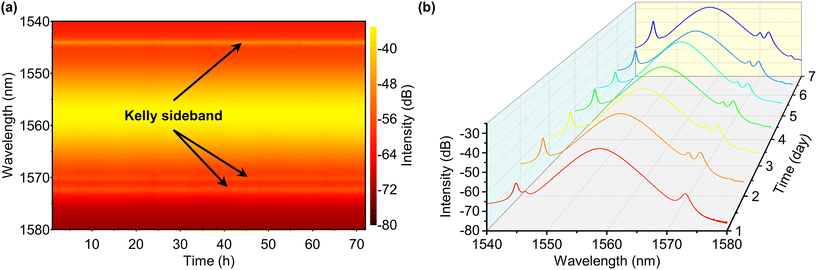
In order to better show the short-term stability of a γ-GY-based MLFL, optical spectra at a 1 hour interval and 72 hour span are measured, and plotted as shown in Fig. 9a. It can be seen that there is no obvious fluctuation in the spectral intensity during the whole measurement process, and the Kelly sideband positions have not changed. Furthermore, as shown in Fig. 9b, the long-term stability is fully demonstrated by the long-term optical spectrum measurement, in which the spectra of the MLFL remain relatively stable within 7 days.
For clarity, several MLFLs based on common 2D materials are listed in Table 2. It is also noteworthy that although the references listed in Table 2 may not demonstrate the best performance of the same materials, they can reflect the ideal properties of γ-GY with application potential in ultrafast photonics.
| Material | Stability | Characteristics of pulses | ||||
|---|---|---|---|---|---|---|
| Long term [day] | Short term [h] | λ 0 [nm] | Δλ [nm] | τ pulse [ps] | Ref. | |
| a CNT represents the carbon nanotube. | ||||||
| Graphene | 14 | 8 | 1559.12 | 6.16 | 0.433 | 56 |
| CNTa | — | 36 | 1960 | ∼3 | 4.3 | 57 |
| Antimonene | — | 8 | 1557.68 | 4.84 | 0.552 | 58 |
| Bismuthene | — | 55 | 1559.18 | 4.64 | 0.652 | 11 |
| MoS2 | — | 3 | ∼1042.15 | ∼6.55 | 656 | 59 |
| Bi2Te3 | 9 | — | 1560.8 | 9.15 | 0.286 | 60 |
| Bi4Br4 | — | 16 | 1559.23 | 23.26 | 0.172 | 61 |
| SnTe | — | 5 | 1562.05 | 4.23 | 0.691 | 62 |
| V2CTx | — | 24 | 1559.1 | 3.1 | 0.94 | 63 |
| Ti3C2Tx | — | 10 | 1891.82 | — | 2.18 | 64 |
| Ti2CTx | — | 3.5 | 1565.4 | 3.4 | 5.3 | 65 |
| γ-GY | 7 | 72 | 1558.9 | 5.43 | 2.03 | This work |
In order to analyze the SOPs of vector solitons, the normalized Stokes parameters S1, S2 and S3 and the DOP are measured. They are related to the output powers of the two orthogonal components, |u|2 and |v|2, and the phase difference between them Δφ as follows:73
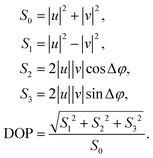 | (2) |
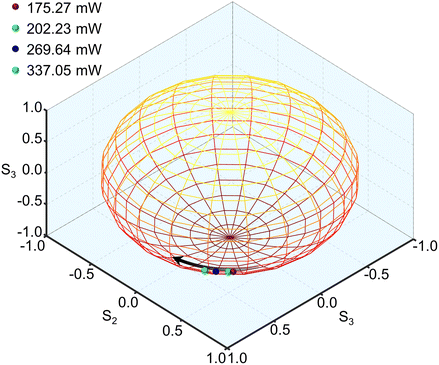
The average SOPs of vector solitons on the Poincare sphere within 1 ms under different pump powers are depicted in Fig. 11, respectively. The SOP is a fixed point on the Poincare sphere under each pump power, proving the stable polarization distribution of the PLVS. Moreover, with the increase of pump power, the position of the SOP changes monotonically along the arrow direction. In order to clearly show the changes in the SOP during the pump power increase, the parameters of each SOP are listed in Table 3. With the increase of pump power, the phase difference between the two orthogonal components of the PLVS increases significantly, which results in the position shift of SOP on the Poincare sphere. Additionally, under the four-pump power values, the DOPs are very high (>97%), which means the polarization distribution in the MLFL is close to the steady state.74
| Pump power [mW] | S 1 | S 2 | S 3 | DOP [%] | Δφ/π |
|---|---|---|---|---|---|
| 175.27 | 0.484 | 0.526 | −0.659 | 97.2 | −0.156 |
| 202.23 | 0.498 | 0.491 | −0.676 | 97.3 | −0.188 |
| 269.64 | 0.547 | 0.409 | −0.696 | 97.6 | −0.246 |
| 337.05 | 0.596 | 0.332 | −0.71 | 98.4 | −0.296 |
5. Conclusion
The saturable absorption properties of γ-GY and its ultrafast photonics application are investigated experimentally at the 1.5 μm optical communication band, for the first time as far as we know. The MD and saturable fluence of the γ-GY–SA at 1.5 μm are found to be 5.40% and 23.46 μJ cm−2, respectively. The stable Q-switched pulses centered at 1531 nm are obtained. When the maximum pump power of 337.05 mW is reached, the pulse duration drops to 1.92 μs, during which the repetition rate and output power are 132.63 kHz and 5.35 mW, respectively, corresponding to the maximum single pulse energy of 40.35 nJ. Subsequently, mode-locked pulses with a central wavelength of 1558.9 nm and 3 dB bandwidth of 5.43 nm are obtained in an EDFL based on the γ-GY–SA, and the pulse duration is found to be 2.03 ps. At the fundamental frequency of 32.75 MHz, the SNR is 58 dB. Meanwhile, the outstanding stability of QSFLs and MLFLs are fully verified in our experiment. Furthermore, it is demonstrated that the obtained soliton pulses are PLVSs, whose vector natures are characterized in detail. Also, the phase difference between the two orthogonal components of the vector soliton is increased with increasing pump power, resulting in the evolution of the polarization state. Our findings confirm the promising application of γ-GY in the field of ultrafast photonics and lay a solid foundation for its practical application.Author contributions
Q. W. and P. W. conceptualized the project and designed the experiments. Z. L. and Z. Z. prepared and characterized the γ-graphyne nanosheets. Q. W. and Q. X. fabricated the γ-graphyne saturable absorber and tested its nonlinear transmittance curve. Y. L. and P. W. put forward suggestions on comprehensive strategy and writing. Y. L., P. W., Z. W. and Y. H. provided guidance on the conduct of this work. Q. W. wrote the manuscript. All co-authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by the National Key Research and Development Program of China under Grant 2018YFB0504400, the National Natural Science Foundation of China under Grant 62205159, the National Key Natural Science Foundation of China under Grant 61835006, the Fundamental Research Funds for the Central University, Nankai University, under Grant 63221007, the National Key Research and Development Program of China under Grant 2020YFA0711500, and the National Natural Science Foundation of China under Grant 21875114.References
- N. G. Boetti, D. Pugliese, E. Ceci-Ginistrelli, J. Lousteau, D. Janner and D. Milanese, Appl. Sci., 2017, 7, 1295 CrossRef.
- A. M. R. Pinto and M. Lopez-Amo, Nanophotonics, 2013, 2, 355–368 CAS.
- H. A. Haus and W. S. Wong, Rev. Mod. Phys., 1996, 68, 423–444 CrossRef.
- G. G. Ycas, F. Quinlan, S. A. Diddams, S. Osterman, S. Mahadevan, S. Redman, R. Terrien, L. Ramsey, C. F. Bender, B. Botzer and S. Sigurdsson, Opt. Express, 2012, 20, 6631–6643 CrossRef CAS PubMed.
- R. R. Gattass and E. Mazur, Nat. Photonics, 2008, 2, 219–225 CrossRef CAS.
- V. S. Letokhov, Nature, 1985, 316, 325–330 CrossRef CAS PubMed.
- Z. Wang, K. Nithyanandan, A. Coillet, P. Tchofo-Dinda and P. Grelu, Nat. Commun., 2019, 10, 830 CrossRef CAS PubMed.
- Z. Sun, T. Hasan, F. Torrisi, D. Popa, G. Privitera, F. Wang, F. Bonaccorso, D. M. Basko and A. C. Ferrari, ACS Nano, 2010, 4, 803–810 CrossRef CAS PubMed.
- W. Liu, M. Liu, X. Liu, X. Wang, H. X. Deng, M. Lei, Z. Wei and Z. Wei, Adv. Opt. Mater., 2020, 8, 1901631 CrossRef CAS.
- M. Zhang, Q. Wu, F. Zhang, L. Chen, X. Jin, Y. Hu, Z. Zheng and H. Zhang, Adv. Opt. Mater., 2019, 7, 1800224 CrossRef.
- J. Du, Q. Wang, G. Jiang, C. Xu, C. Zhao, Y. Xiang, Y. Chen, S. Wen and H. Zhang, Sci. Rep., 2014, 4, 6346 CrossRef CAS PubMed.
- A. Zhang, Z. Wang, H. Ouyang, W. Lyu, J. Sun, Y. Cheng and B. Fu, Nanomaterials, 2021, 11, 1778 CrossRef CAS PubMed.
- S. Chen, C. Zhao, Y. Li, H. Huang, S. Lu, H. Zhang and S. Wen, Opt. Mater. Express, 2014, 4, 587–596 CrossRef.
- B. Fu, J. Sun, G. Wang, C. Shang, Y. Ma, J. Ma, L. Xu and V. Scardaci, Nanophotonics, 2020, 9, 2169–2189 CrossRef CAS.
- B. Chen, X. Zhang, K. Wu, H. Wang, J. Wang and J. Chen, Opt. Express, 2015, 23, 26723–26737 CrossRef CAS PubMed.
- J. O. Island, G. A. Steele, H. S. J. V. D. Zant and A. Castellanos-Gomez, 2D Mater., 2015, 2, 011002 CrossRef.
- X. Wang, A. M. Jones, K. L. Seyler, V. Tran, Y. Jia, H. Zhao, H. Wang, L. Yang, X. Xu and F. Xia, Nat. Nanotechnol., 2015, 10, 517–521 CrossRef CAS PubMed.
- C. Huang, Y. Li, N. Wang, Y. Xue, Z. Zuo, H. Liu and Y. Li, Chem. Rev., 2018, 118, 7744–7803 CrossRef CAS PubMed.
- S. W. Cranford, D. B. Brommer and M. J. Buehler, Nanoscale, 2012, 4, 7797 RSC.
- X. Li, B. Li, Y. He and F. Kang, New Carbon Mater., 2020, 35, 619–629 CrossRef CAS.
- H. Sevinçli and C. Sevik, Appl. Phys. Lett., 2014, 105, 223108 CrossRef.
- X. Zhang, H. Wang, K. Wu, Q. Li, Z. Shao, Q. Yang, C. Chen, X. Cui, J. Chen and J. Wang, Opt. Mater. Express, 2020, 10, 293–301 CrossRef.
- J. Xi, D. Wang, Y. Yi and Z. Shuai, J. Chem. Phys., 2014, 141, 034704 CrossRef PubMed.
- P. Jiang, H. Liu, L. Cheng, D. Fan, J. Zhang, J. Wei, J. Liang and J. Shi, Carbon, 2017, 113, 108–113 CrossRef CAS.
- E. Garmire, IEEE J. Sel. Top. Quantum Electron., 2000, 6, 1094–1110 CAS.
- R. H. Baughman, H. Eckhardt and M. Kertesz, J. Chem. Phys., 1987, 87, 6687–6699 CrossRef CAS.
- T. D. Daff, S. P. Collins, H. Dureckova, E. Perim, M. S. Skaf, D. S. Galvão and T. K. Woo, Carbon, 2016, 101, 218–225 CrossRef CAS.
- H. Qiu, M. Xue, C. Shen, Z. Zhang and W. Guo, Adv. Mater., 2019, 31, 1803772 CrossRef CAS PubMed.
- H. Zhang, M. Zhao, X. He, Z. Wang, X. Zhang and X. Liu, J. Phys. Chem. C, 2011, 115, 8845–8850 CrossRef CAS.
- Y. Zhang, G. Zhu, J. Lu, Z. Guo and J. Cao, RSC Adv., 2015, 5, 87841–87846 RSC.
- M. Feng, D. R. Bell, J. D. Luo and R. H. Zhou, Phys. Chem. Chem. Phys., 2017, 19, 10187–10195 RSC.
- Q. Yang, X. Zhang, Z. Yang, X. Ren, J. Wang, Q. Li, X. Cui and X. Zhu, Appl. Phys. Express, 2019, 12, 122006 CrossRef CAS.
- H. Zhang, D. Tang, L. Zhao and N. Xiang, Opt. Express, 2008, 16, 12618–12623 CrossRef CAS.
- Y. Jiang, T. Narushima and H. Okamoto, Nat. Phys., 2010, 6, 1005–1009 Search PubMed.
- Y. Luo, Y. Xiang, P. P. Shum, Y. Liu, R. Xia, W. J. Ni, H. Q. Lam, Q. Sun and X. Tang, Opt. Express, 2020, 28, 4216–4224 CrossRef PubMed.
- P. Serena, N. Rossi and A. Bononi, Opt. Express, 2012, 20, 7895–7900 CrossRef CAS.
- W. Ding, M. Sun, Z. Zhang, X. Lin and B. Gao, Ultrason. Sonochem., 2020, 61, 104850 CrossRef CAS.
- Q. Li, Y. Li, Y. Chen, L. Wu, C. Yang and X. Cui, Carbon, 2018, 136, 248–254 CrossRef CAS.
- Q. Li, C. Yang, L. Wu, H. Wang and X. Cui, J. Mater. Chem. A, 2019, 7, 5981–5990 RSC.
- C. Yang, Y. Li, Y. Chen, Q. Li, L. Wu and X. Cui, Small, 2019, 15, 1804710 CrossRef PubMed.
- J. W. Nicholson, R. S. Windeler and D. J. DiGiovanni, Opt. Express, 2007, 15, 9176–9183 CrossRef CAS PubMed.
- A. Martinez and Z. Sun, Nat. Photonics, 2013, 7, 842–845 CrossRef CAS.
- J. Guo, R. Shi, R. Wang, Y. Wang, F. Zhang, C. Wang, H. Chen, C. Ma, Z. Wang, Y. Ge, Y. Song, Z. Luo, D. Fan, X. Jiang, J. Xu and H. Zhang, Laser Photonics Rev., 2020, 14, 1900367 CrossRef CAS.
- P. Wang, D. Hu, K. Zhao, L. Jiao, X. Xiao and C. Yang, IEEE J. Sel. Top. Quantum Electron., 2018, 24, 1800207 Search PubMed.
- J. J. Degnan, IEEE J. Quantum Electron., 1995, 31, 1890–1901 CrossRef CAS.
- Y. Chen, G. Jiang, S. Chen, Z. Guo, X. Yu, C. Zhao, H. Zhang, Q. Bao, S. Wen, D. Tang and D. Fan, Opt. Express, 2015, 23, 12823–12833 CrossRef CAS PubMed.
- J. Wang, Z. Luo, M. Zhou, C. Ye, H. Fu, Z. Cai, H. Cheng, H. Xu and W. Qi, IEEE Photonics J., 2012, 4, 1295–1305 Search PubMed.
- J. Yuan, G. Liu, Y. Xin, F. Xing, K. Han, W. Zhang, F. Zhang and S. Fu, Opt. Mater., 2021, 118, 111256 CrossRef CAS.
- R. Zhao, J. He, X. Su, Y. Wang, X. Sun, H. Nie, B. Zhang and K. Yang, IEEE J. Quantum Electron., 2018, 24, 1–5 Search PubMed.
- L. Li, Y. Wang, Z. Wang, X. Wang and G. Yang, Opt. Commun., 2018, 406, 80–84 CrossRef CAS.
- Y. Chen, C. Zhao, S. Chen, J. Du, P. Tang, G. Jiang, H. Zhang, S. Wen and D. Tang, IEEE Photonics J., 2014, 20, 315–322 Search PubMed.
- H. Ahmad, H. S. M. Albaqawi, N. Yusoff, W. Y. Chong and M. Yasin, IEEE J. Quantum Electron., 2020, 56, 1–6 Search PubMed.
- B. Fu, P. Wang, Y. Li, M. Condorelli, E. Fazio, J. Sun, L. Xu, V. Scardaci and G. Compagnini, Nanophotonics, 2020, 9, 3873–3880 CrossRef CAS.
- C. Dou, W. Wen, J. Wang, M. Ma, L. Xie, C. Ho and Z. Wei, Photonics Res., 2019, 7, 283–288 CrossRef CAS.
- Q. Wang, J. Kang, P. Wang, J. He, Y. Liu, Z. Wang, H. Zhang and Y. Liu, Nanophotonics, 2022, 11, 3127–3137 CrossRef CAS.
- P. Huang, S. Lin, C. Y. Yeh, H. Kuo, S. Huang, G. Lin, L. Li, C. Su and W. Cheng, Opt. Express, 2012, 20, 2460–2465 CrossRef CAS.
- Y. Meng, Y. Li, Y. Xu and F. Wang, Sci. Rep., 2017, 7, 1–7 CrossRef PubMed.
- Y. Song, Z. Liang, X. Jiang, Y. Chen, Z. Li, L. Lu, Y. Ge, K. Wang, J. Zheng, S. Lu, J. Ji and H. Zhang, 2D Mater., 2017, 4, 045010 CrossRef.
- L. Lu, Z. Liang, L. Wu, Y. Chen, Y. Song, S. C. Dhanabalan, J. S. Ponraj, B. Dong, Y. Xiang, F. Xing, D. Fan and H. Zhang, Laser Photonics Rev., 2018, 12, 1700221 CrossRef.
- P. Yan, R. Lin, S. Ruan, A. Liu, H. Chen, Y. Zheng, S. Chen, C. Guo and J. Hu, Sci. Rep., 2015, 5, 8690 CrossRef CAS PubMed.
- W. Liu, X. Xiong, M. Liu, X. Xing, H. Chen, H. Ye, J. Han and Z. Wei, Appl. Phys. Lett., 2022, 120, 053108 CrossRef CAS.
- S. Ahmed, J. Qiao, P. K. Cheng, A. M. Saleque, M. I. Hossain, L. Zeng, J. Zhao, W. Qarony and Y. H. Tsang, Adv. Opt. Mater., 2021, 9, 2001821 CrossRef CAS.
- W. Huang, C. Ma, C. Li, Y. Zhang, L. Hu, T. Chen, Y. Tang, J. Ju and H. Zhang, Nanophotonics, 2020, 9, 2577–2585 CrossRef CAS.
- Z. Wang, H. Li, M. Luo, T. Chen and H. Zhang, ACS Appl. Nano Mater., 2020, 3, 3513–3522 CrossRef CAS.
- J. Yi, L. Du, J. Li, L. Yang, L. Hu, S. Huang, Y. Dong, L. Miao, S. Wen, V. N. Mochalin, C. Zhao and A. M. Rao, 2D Mater., 2019, 6, 045038 CrossRef.
- D. N. Christodoulides and R. I. Joseph, Opt. Lett., 1988, 13, 53–55 CrossRef CAS PubMed.
- Y. Song, H. Zhang, D. Tang and D. Shen, Opt. Express, 2012, 20, 27283–27289 CrossRef CAS PubMed.
- H. Zhang, D. Tang, L. Zhao and N. Xiang, Opt. Express, 2008, 16, 12618–12623 CrossRef CAS PubMed.
- C. R. Menyuk, Opt. Lett., 1987, 12, 614–616 CrossRef CAS PubMed.
- S. G. Evangelides, L. F. Mollenauer, J. P. Gordon and N. S. Bergano, J. Lightwave Technol., 1992, 10, 28–35 CrossRef.
- S. T. Cundiff, B. C. Collings, N. N. Akhmediev, J. M. Soto-Crespo, K. Bergman and W. H. Knox, Phys. Rev. Lett., 1999, 82, 3988–3991 CrossRef CAS.
- M. Han, S. Zhang, X. Li, H. Zhang, H. Yang and T. Yuan, Opt. Express, 2015, 23, 2424–2435 CrossRef CAS PubMed.
- V. Tsatourian, S. V. Sergeyev, C. Mou, A. Rozhin, V. Mikhailov, B. Rabin, P. S. Westbrook and S. K. Turitsyn, Sci. Rep., 2013, 3, 3154 CrossRef PubMed.
- C. Zhao, L. Dai, Q. Huang, Z. Huang, C. Mou, M. Al Araimi, A. Rozhin, S. Sergeyev and Z. Luo, Nanophotonics, 2020, 9, 2437–2443 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |