Open Access Article
Open Access ArticleRevealing the improved stability of amorphous boron-nitride upon carbon doping†
Onurcan
Kaya
 ab,
Luigi
Colombo
c,
Aleandro
Antidormi
a,
Mario
Lanza
ab,
Luigi
Colombo
c,
Aleandro
Antidormi
a,
Mario
Lanza
 d and
Stephan
Roche
*ae
d and
Stephan
Roche
*ae
aCatalan Institute of Nanoscience and Nanotechnology (ICN2), CSIC and BIST, Campus UAB, Bellaterra, 08193, Barcelona, Spain. E-mail: stephan.roche@icn2.cat
bSchool of Engineering, RMIT University, Melbourne, Victoria 3001, Australia
cDepartment of Materials Science and Engineering, The University of Texas at Dallas, Richardson, TX 75080, USA
dDepartment of Material Science and Engineering, King Abdullah University of Science and Technology, Thuwal, 23955, Saudi Arabia
eICREA Institucio Catalana de Recerca i Estudis Avancats, 08010 Barcelona, Spain
First published on 20th December 2022
Abstract
We report on a large improvement of the thermal stability and mechanical properties of amorphous boron-nitride upon carbon doping. By generating versatile force fields using first-principles and machine learning simulations, we investigate the structural properties of amorphous boron-nitride with varying contents of carbon (from a few percent to 40 at%). We found that for 20 at% of carbon, the sp3/sp2 ratio reaches a maximum with a negligible graphitisation effect, resulting in an improvement of the thermal stability by up to 20% while the bulk Young's modulus increases by about 30%. These results provide a guide to experimentalists and engineers to further tailor the growth conditions of BN-based compounds as non-conductive diffusion barriers and ultralow dielectric coefficient materials for a number of applications including interconnect technology.
New conceptsThe concept lies in the fact that novel amorphous structures combining boron, nitrogen and carbon stand as disruptive alternatives to silicon oxide in interconnect technologies of modern microelectronics. These structures display ultralow dielectric coefficients (below 2) and superior technology performances and stability. In the present work we find that a suitable combination of C, B, and N allows determination of the upper limit of such performances. Existing research in simulation in the study of materials for interconnect technology do not rely on accurate artificial intelligence algorithms that we have used in this study. As a result, our approach provides predictive modelling with results of strategic importance for the development of new materials technologies. Materials science suffers from the complexity of understanding the properties of highly disordered structures such as amorphous forms of boron-nitride. Experimental characterization is very difficult, and in the absence of accurate simulation techniques, it is almost impossible to progress in an efficient way. Our methodology and results demonstrate that machine learning techniques enable in-depth characterisation of amorphous materials properties, and provide predictions that will further guide engineers and experimentalists in the search of optimised growth conditions and integration. |
1. Introduction
For the past 20 years, the semiconductor industry has been searching for dielectric materials with low diffusivity to reduce the size of back-end-of-logic (BEOL) interconnects and to further promote the miniaturization of logic and memory devices in electronic circuits.1,2 However, most dielectric materials suffer from poor mechanical properties, insufficient chemical stability, and not-enough low metal diffusivity, which leads to reliability failures.3 Two-dimensional (2D) materials are being extensively studied as potential barrier materials for BEOL interconnects.4 However, 2D materials synthesized via scalable methods like chemical vapour deposition (CVD) and liquid-phase exfoliation (LPE) face significant integration challenges related to layer thickness control and to the presence of grain boundaries.5–7 In hexagonal boron nitride (h-BN), the preferred insulating 2D material due to its high band gap (∼6 eV), these native defects provoke prohibitive fluctuations of the electric field breakdown, which has led to the investigation of amorphous boron nitride (α-BN) films. In fact, dielectric materials used by the semiconductor industry are amorphous with silicon dioxide being the most used and important of them. The improved performance of amorphous materials is principally due to the lack of available dangling bonds and grain boundaries. Sputtered α-BN films with thickness ranging from 12 nm to 800 nm have shown a dielectric constant from 2.61 to 5.88.8,9 Atomically thin α-BN has been recently demonstrated to possess ultralow dielectric constant (k < 2), low metal diffusivity and high mechanical robustness.10,11 This recent breakthrough follows years of efforts in the pursuit of wafer-scale fabrication of atomically thin h-BN on various types of substrates, for potential use in the integration with graphene and/or transition metal dichalcogenides for nanoelectronic devices and circuits.12–16Importantly, α-BN can be prepared at much lower temperatures than h-BN, making its integration in a silicon device flow much easier while decreasing the energy and thus cost of production. The lower temperature and the lack of grain boundaries also make α-BN a desirable material for diffusion barriers and as a dielectric material adjacent to TMDs and graphene,10 with a variety of potential applications in spintronics,17 advanced data encryption technologies18 and neuromorphic computing devices.19–22 The excellent properties of atomically thin α-BN as a dielectric material highlight the potential for many applications, but before we can take advantage of this material, a deeper understanding of its microscopic structure and its relationship with the material performance (dielectric constant, thermal and chemical stability, electrical breakdown) is crucially needed. To that end, in-depth studies on the effect of the amorphous structure and alloying with carbon and hydrogen are of great interest. Indeed, carbon and hydrogen are typical contaminants in dielectrics grown at low temperature, e.g. SiO2 and Si3N4 synthesized with plasma enhanced CVD. In that respect, theoretical structural studies are advantageous over carrying out much more expensive and time consuming experimental approaches.
From the theoretical and computational perspective, atomistic calculations represent a suitable tool to describe complex structures of concern, giving access to details at the atomic and molecular level. However, the extremely disordered nature of amorphous materials requires a computational approach able to capture the interatomic potentials in arbitrary complex local environments, a challenge that can only be tackled with machine learning based methods.23,24 Specifically, classical molecular dynamics with the employment of force-fields derived using machine-learning and ab initio techniques constitute a powerful methodology to describe sufficiently large disordered material samples while keeping first-principles accuracy.
Here, using classical molecular dynamics, we report that C-doped α-BN undergoes a strong modification of its thermal stability and mechanical properties as a function of carbon concentration. Remarkably, for a C concentration of 20 at%, a large enhancement of thermal stability is observed together with a corresponding increase of Young's modulus. In order to properly describe the atomic interactions, we built a Gaussian Approximated Potential (GAP) trained on a suitably large dataset of atomistic structures obtained via ab initio calculations, which ensures the reliability and accuracy of the presented data. These results offer a practical strategy to tune the atomistic properties of α-BN through the addition of carbon atoms with a subsequent strong improvement of the observed performance of α-BN for electronic applications.
2. Machine learning-based approach for designing realistic disordered α-BN:C
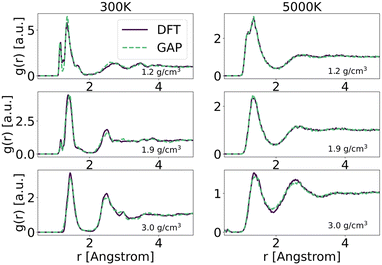
To explore in-depth the atomistic/molecular features of C-doped α-BN (α-BN:C), we employ atomistic calculations in the framework of classical molecular dynamics, carried out within the LAMMPS package.25 To properly describe the intrinsically complex nature of such disordered material, a new force-field has been generated based on machine-learning methods. Such methods have already shown a superior capability in the atomistic description of highly disordered materials, their main advantage relying on the possibility to fit a sufficiently complex potential without a predefined functional form. The resulting potential is capable of predicting the interatomic forces with accuracy comparable to first-principle calculations in a large number of configurations. In this work, we use the GAP framework, which is based on the Gaussian process regression methodology, typically using the Smooth Overlap of Atomic Positions (SOAP) kernel to describe the similarity between local environments in materials. One advantage of kernel regression is that the flexibility of the functional form naturally grows with the amount of training data. The general approach is to fit a potential to an initial training set of total energies, forces and stresses calculated using a given DFT electronic structure method (see for instance ref. 26 and 27).Here, we use a GAP model that we have specifically developed for α-BN:C. Most structures in the reference database are snapshots from DFT-MD or GAP-MD simulations of the disordered phases. The database used to train the potential is as large as 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 different structures, each consisting of a system of 2 to 200 atoms. The resulting potential has been validated by comparing the radial distribution functions of α-BN:C at 300 K and 5000 K using the DFT and GAP potential as shown in Fig. 1. GAP-MD simulations perfectly match with the DFT data at different temperatures and densities. The details of the generation and validation steps of the potential are given in the ESI.†
000 different structures, each consisting of a system of 2 to 200 atoms. The resulting potential has been validated by comparing the radial distribution functions of α-BN:C at 300 K and 5000 K using the DFT and GAP potential as shown in Fig. 1. GAP-MD simulations perfectly match with the DFT data at different temperatures and densities. The details of the generation and validation steps of the potential are given in the ESI.†
Finally, we employed the generated potential to explore a wide range of α-BN:C structures using classical molecular dynamics. Specifically, generation of amorphous samples of α-BN:C with varying C concentrations was simulated by the quenching “from-the-melt method” applied to randomly generated atomistic configurations (containing 1000 atoms) with a cubic shape (L = Lx = Ly = Lz ≈ 21 Å). The size of the systems was chosen to obtain a mass density close to the experimental value (2.1 g cm−3) as observed by Hong et al.10 and to be large enough to contain a reliable sampling of all the possible bonds and atomic structures as present in real fabricated samples. Furthermore, the dimension of the systems allows for a satisfactory analysis without resulting in prohibitive computational times. The details of the preparation of the samples as well as the size-dependence of the results are given in the Methods section in the ESI.†
3. Structural and morphological analysis
As a first result, we present the analysis of the structural properties of α-BN:C with different C concentrations. In this work we considered a carbon concentration ranging from 0 to 40 at%. A subset of the samples generated with VMD28 is shown schematically in Fig. 2a. In order to assess the degree of crystallinity vs. disorder of the samples we computed the radial distribution function g(r) (RDF) as a function of C concentration (Fig. 2b). All the systems are characterized by clear and recognizable peaks for interatomic distances smaller than 5 Å; no peak can be identified for larger distances, denoting the absence of long-range order in the samples independent of C concentration. In this respect, the amorphous character of α-BN is not affected by C concentration.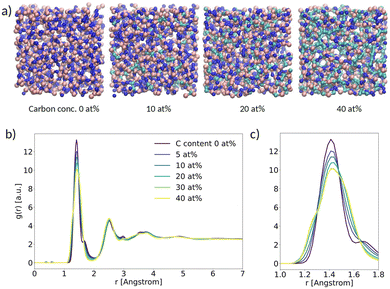 | ||
| Fig. 2 (a) Ball-and-stick picture of α-BN:C; (b) radial distribution function (RDF) versus spatial distance between atoms; (c) zoom-in of the main peak. | ||
The short-range order in α-BN:C is in turn dominated by the first nearest-neighbor distances contributing to the first peak located at an average distance of ∼1.42 Å (the average B–N chemical bond length). As can be seen from Fig. 2c, which shows a closer image of the first peak, a clear broadening is observed increasing with doping concentration, suggesting that it is induced by the presence of carbon atoms. Such modification is due to the formation of chemical bonds different from B–N (B–C, C–N, C–C), as can be verified from Fig. S3a and b in the ESI,† where the chemical decomposition of the first peak of the RDF in the two samples of α-BN:C with a C content of 0 and 40 at% is shown. The presence of carbon atoms in the compounded system determines the formation of new chemical bonds whose average length is slightly different from the B–N one. Specifically, the B–C, C–N and C–C bond average lengths are found to be ∼1.52 Å, ∼1.3 Å and ∼1.40 Å, respectively. The overall peak is consequently the convolution of peaks at different distances.
The local character of α-BN:C can also be understood by considering the average coordination number in the samples created as a function of doping concentration. The average coordination number is close to 3 as shown in Fig. S3c in the ESI,† denoting that most of the atoms are sp2-hybridized with some interesting feature induced by C incorporation. As can be observed, the average coordination number increases with C-content and reaches a maximum value for a C-content between 10 and 20 at%, whereas it decreases for larger concentrations. This finding highlights the role played by small concentration of carbon atoms in favoring a larger coordination number for all of the atoms in the sample. A more detailed insight can be obtained by looking at the actual number of atoms with a given coordination number. Fig. S3d in the ESI† shows the ratio of the number of sp2-hybridized atoms (having coordination number 3) to the number of sp3-hybridized atoms (having coordination number 4). Specifically, the sp2vs. sp3 ratios correspond to the data points with coordination number 3. As can be seen, the number of 3-coordinated atoms undergo a decrease by a factor of 2 with respect to the undoped sample when C is introduced. Differently stated, the presence of doping in the samples is responsible for a reduction of the sp2vs. sp3 ratio with a minimum observed around 20 at% C-content. The density of samples is also increased slightly from 2.18 g cm−3 to 2.21 g cm−3 with the increasing sp3 content.
A deeper understanding of the chemical composition of the samples can be obtained by looking at the number and the nature of chemical species involved in the bonds of the sample as a function of C-content. As shown in Fig. S3b in the ESI,† while the total number of B–N bonds monotonically decreases with increasing C content, the number of bonds involving C gradually increases. The most consistent chemical bonds involving C is B–C, whose quantity equals that of B–N bonds for a C-content of 30 at%. A generally smaller concentration is found for N–C and C–C bonds, increasing with doping.
4. Structural stability analysis
In order to assess the stability of α-BN:C, we employed the validated GAP potential to perform several MD calculations and extracted the atoms mean squared displacement (MSD) and diffusivity at different temperatures. The particle MSD and diffusivity, the latter being related to the behavior of MSD, namely D = limt→∞MSD(t)/6t, are generally very useful quantities and have been used to describe the “mobility” of the atoms in the solid and liquid phases of materials.29 In particular, in the low-temperature regime, the MSD tends to a non-zero constant whereas the diffusivity is zero; for higher temperatures the material undergoes structural rearrangements of the atomic positions and a non-zero slope of MSD is hence observed. From the comparison of diffusivity vs. temperature in our α-BN:C samples, an insight is obtained on the impact of C-content on the structural stability of α-BN:C. To this aim, we simulated a heating process of our samples consisting of a multi-step procedure. After equilibrating the samples at 300 K for 5 ps, the temperature was gradually modified by repeatedly performing the following steps: (1) the temperature is linearly increased with ΔT = 50 K in 10 ps; (2) the temperature is kept fixed in the following 50 ps. The above iterative scheme is repeated until a maximum temperature larger than 3000 K has been reached. The length of the different time intervals is chosen to be sufficiently large to allow for a statistically meaningful calculation of the MSD and diffusivity. The simulations were performed in a constant-temperature (NPT) ensemble with a Nosé-Hover thermostat for temperature control and a time step of 0.25 fs.The structural stability of α-BN:C can be obtained by looking at the time evolution of the potential energy of the samples during a heating phase of the system. To this aim, the samples are slowly heated at a constant rate from ambient temperature (300 K) up to 3500 K in 50 ps and the potential energy is consequently monitored. No qualitative change was observed when adopting different heating rates. Fig. 3 shows the curves of the potential energy for our systems, with the values rigidly shifted for the sake of visualization. In the plot the dashed curves represent the extrapolated lines at low temperature.
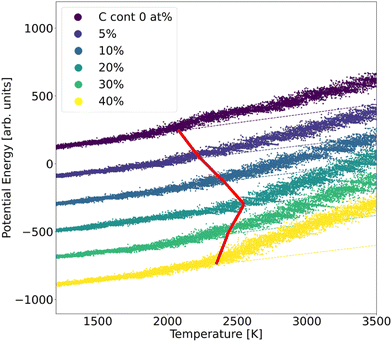 | ||
| Fig. 3 Potential energy curves of α-BN:C samples observed during a heating MD run. The dashed lines show the linear fit extracted from the low-temperature range. | ||
While the potential energy of the systems vs. temperature linearly increases in the low-temperature regime, a strong deviation of the former is observed for sufficiently high thermal energy. Eventually the potential energy takes on the values corresponding to the material liquid phase. The temperature at which the potential energy undergoes deviation from the linear trend observed in the low-temperature regime can be taken as a parameter of stability of the sample: the larger its value, the more structurally stable the system. As can be observed from Fig. 3, such a temperature strongly increases for a small amount of C-doping, reaching a maximum for a C-content between 10 and 20 at% in agreement with the sp2/sp3 increase discussed. A further increase of C-content leads to a reduction of the stability, so that a non-monotonic trend is found and identified to be driven by the ratio of sp2/sp3 defining the structural morphology of α-BN:C samples. The chemical composition of the sample also changes the thermal stability of the structure.
As an alternative way to calculate thermal stability, we show the computed diffusivity for the different α-BN:C samples as a function of temperature as shown in Fig. S4 in the ESI.† The curves have been averaged over 5 runs for each value of C-content and the vertical bars denote the corresponding errors. As can be observed, for low temperatures (up to ∼ 1500 K) the diffusivity is zero (within statistical accuracy) for all the samples, meaning that the atomic positions do not change over time and the material is structurally stable for all the C-doping values considered. For temperatures higher than 1500 K, thermal energy induces structural rearrangements in the system leading to atomic diffusion. The diffusivity consequently increases rapidly with temperature in a strongly non-linear fashion. In particular, we observe how the diffusivity in samples with a C-content of 10–20 at% is lower than that of samples with other doping levels up to T ∼ 2500 K. This points to stronger structural stability of the corresponding samples upon an increase in temperature. The samples with a C-content of 10–20 at% are indeed characterized by a considerably smaller diffusivity at generally high temperatures: a ratio of ∼3 is found when comparing the least and most stable systems at 2000 K.
Our MD simulations confirm previous results30,31 concerning the thermal stability of α-BN:C samples with increasing sp3 fraction. As shown in Fig. 3b, the increase of C-content up to 20 at% enhances the sp3 fraction in α-BN:C samples which leads to improved thermal stability. However, larger C-content in α-BN:C samples leads to graphitization of samples and a lower sp3 fraction. Since α-BN:C samples with 20 at% C content contain the largest sp3 content among all samples with negligible graphitisation content, a correlation between these structural features and the thermal stability becomes evident.
5. Mechanical properties
The mechanical properties of high-quality BN thin films have been studied experimentally recently and surprisingly have been found to be weakly dependent on the stack thickness. Monolayer BN was found to have a Young's modulus of 0.865 ± 0.073 TPa and a fracture strength of 70.5 ± 5.5 GPa, with negligible variation upon increasing the number of layers.32 The change of mechanical properties of amorphous BN is an important question to answer given its relevance in the context of integration in electronic devices.Here, we study Young's, bulk and shear moduli of α-BN:C, where we perform additional short MD quenches from 300 K to very low temperature, and finally a conjugate-gradient relaxation to minimize the forces on atoms; the cell vectors remained fixed to keep the density unchanged. For each optimized structure, we compute the full 6 × 6 matrix of elastic constants C without imposing symmetry operations, and invert this matrix to obtain the compliance matrix S. Using these elastic constants, we investigate the mechanical stability and properties of the α-BN:C structures at different C doping levels.
In order to validate the mechanical stability of α-BN:C, we check if the elastic constants satisfy these conditions: C11–C12 > 0, C11 > 0, C44 > 0 and C11 + 2C12 > 0. α-BN:C at all levels of C doping satisfies these conditions, hence it confirms the plausibility to form α-BN:C structures.33
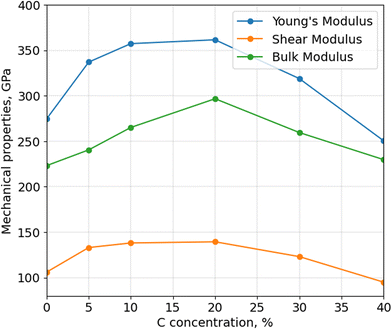
After calculating the thermal stability of α-BN:C, Young's, bulk and shear moduli are calculated using Voigt-Reuss-Hill approximation, as shown in Fig. 4. The mechanical properties of aBN:C samples are related to their sp2/sp3 ratios and density.34 All the moduli consistently show a non-monotonic trend, analogous to thermal stability and density, with a maximum in correspondence of doping between 10 and 20 at%. While the Young's modulus of undoped α-BN:C is 274.85 GPa, it increased to 361.54 GPa with 20 at% C. Similarly, bulk and shear moduli are increased from 223.13 GPa and 106.02 GPa to 296.70 GPa and 139.38 GPa. At 40 at% C doping, Young's and shear moduli become lower than that of undoped α-BN. Table 1 shows the comparison of our calculated Young's modulus values to the literature values. Interestingly, the maximum Young's modulus value obtained for the 20 at% C-doping level is only reduced by a factor of 3 compared to the nanoindentation measurement of pure crystalline hBN samples32 and by a factor of 2 compared to sheets with high concentration of vacancies,35 which shows a very strong resilience of mechanical strength for such highly disordered forms of structurally and chemically modified α-BN compounds. Meanwhile, Liu et al.34 obtained half of the value of Young's modulus. However, the density of the sample used is very low suggesting the origin of such difference. Poisson's ratio is also important to understand the mechanical behavior of materials. While Poisson's ratio for α-BN:C structures without any C content is calculated as 0.295, C-doped structures exhibit Poisson's ratio between 0.266 and 0.318 with no obvious trends with the level of C-content.
| Sample | E [GPa] |
|---|---|
| Nanoindentation measurement of monolayer h-BN | 865 ± 7332 |
| Monolayer hBN using Tersoff potentials | 627 − 64235–37 |
| Nanoindentation measurement of cubic BN | 600 ± 10038 |
| Amorphous BN w/C%20 – 2.21 g cm−3 (this work) | 362 |
| Amorphous BN – 2.18 g cm−3 (this work) | 275 |
| Amorphous BN – 1.45 g cm−3 | 106.234 |
Similar to what was observed for thermal stability, it has been reported that39,40 an increased sp3 fraction can improve Young's modulus. C-doping up to 20 at%, as shown earlier, increases the sp3 fraction in α-BN:C samples leading to better mechanical properties and higher material density. However, a larger C-content causes more sp2 content and C–C bonds which reduces the density and mechanical properties. Since they have the highest sp3 content, α-BN:C samples with 20 at% C-doping achieve the best mechanical properties and thermal robustness.
6. Conclusions
The recent growth of atomically thin amorphous boron nitride has provided a new opportunity for solving long standing challenges of stable low dielectric constant materials. However, despite the promising first results, it is crucial to fully understand the role of doping elements such as carbon and hydrogen on the stability of the material as well as their effects on sp2versus sp3 bonding in these highly disordered structures. In this paper, thanks to machine learning approaches, we show that it is possible to extend the exploration range of complexity of such amorphous materials, and that carbon doping enables further improvement of the sought after properties of α-BN. Future studies should consider the impact of other atomic entities such as hydrogen and combinations with carbon for instance. The results of this study opens a new pathway for improving the properties and stability of these amorphous compounds for their use in applications such as nanoelectronics, spintronics, photovoltaics and/or neuromorphic computing technologies.Author contributions
S. R. and L. C. conceived the research project. O. K. and A. A. performed the simulations. O. K., S. R., L. C. and M. L. discussed and analyzed the simulation data. O. K., L. C. and S. R. wrote the manuscript. All authors read and approved the manuscript.Data availability statement
The generated GAP potential can be found at Zenodo (https://zenodo.org) with DOI: 10.5281/zenodo.7500738.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has been supported by Samsung Advanced Institute of Technology and is conducted under the REDI Program, a project that has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 101034328. ICN2 acknowledges the Grant PCI2021-122092-2A funded by MCIN/AEI/10.13039/501100011033 and by the “European Union NextGenerationEU/PRTR”. Simulations were performed at the Center for Nanoscale Materials, a U.S. Department of Energy Office of Science User Facility, supported by the U.S. DOE, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. Additional computational support was received from the King Abdullah University of Science and Technology-KAUST (Supercomputer Shaheen II Cray XC40) and Texas Advanced Computing Center (TACC) at The University of Texas at Austin.References
- L. Zhao, M. Lofrano, K. Croes, E. Van Besien, Z. Tökei, C. J. Wilson, R. Degraeve, T. Kauerauf, G. P. Beyer and C. Claeys, Thin Solid Films, 2011, 520, 662–666 CrossRef.
- A. E. Kaloyeros and E. Eisenbraun, Annu. Rev. Mater. Sci., 2000, 30, 363–385 CrossRef.
- C. Wu, Y. Li, M. R. Baklanov and K. Croes, ECS J. Solid State Sci. Technol., 2014, 4, N3065–N3070 CrossRef.
- C.-L. Lo, M. Catalano, K. K. H. Smithe, L. Wang, S. Zhang, E. Pop, M. J. Kim and Z. Chen, npj 2D Mater. Appl., 2017, 1, 42 CrossRef.
- L. Jiang, Y. Shi, F. Hui, K. Tang, Q. Wu, C. Pan, X. Jing, H. Uppal, F. Palumbo, G. Lu, T. Wu, H. Wang, M. A. Villena, X. Xie, P. C. McIntyre and M. Lanza, ACS Appl. Mater. Interfaces, 2017, 9, 39758–39770 CrossRef CAS PubMed.
- A. Ranjan, N. Raghavan, M. Holwill, K. Watanabe, T. Taniguchi, K. S. Novoselov, K. L. Pey and S. J. O’Shea, ACS Appl. Electron. Mater., 2021, 3, 3547–3554 CrossRef CAS.
- C. Maestre, B. Toury, P. Steyer, V. Garnier and C. Journet, J. Phys.: Mater., 2021, 4, 044018 CAS.
- A. Prakash, V. Todi, K. B. Sundaram, L. Ross, G. Xu, M. French, P. Henry and S. W. King, ECS J. Solid State Sci. Technol., 2014, 4, N3122 CrossRef.
- Q. Abbas, H. Liang, J. Shi, Y. Chen, X. Xia, A. Ul Ahmad, J. Liu and G. Du, Mater. Lett., 2018, 227, 284–288 CrossRef CAS.
- S. Hong, C.-S. Lee, M.-H. Lee, Y. Lee, K. Y. Ma, G. Kim, S. I. Yoon, K. Ihm, K.-J. Kim, T. J. Shin, S. W. Kim, E.-C. Jeon, H. Jeon, J.-Y. Kim, H.-I. Lee, Z. Lee, A. Antidormi, S. Roche, M. Chhowalla, H.-J. Shin and H. S. Shin, Nature, 2020, 582, 511–514 CrossRef CAS PubMed.
- C.-M. Lin, C.-H. Hsu, W.-Y. Huang, V. Astié, P.-H. Cheng, Y.-M. Lin, W.-S. Hu, S.-H. Chen, H.-Y. Lin, M.-Y. Li, B. Magyari-Kope, C.-M. Yang, J.-M. Decams, T.-L. Lee, D. Gui, H. Wang, W.-Y. Woon, P. Lin, J. Wu, J.-J. Lee, S. S. Liao and M. Cao, Adv. Mater. Technol., 2022, 2200022 CrossRef CAS.
- S. Liu, R. He, L. Xue, J. Li, B. Liu and J. H. Edgar, Chem. Mater., 2018, 30, 6222–6225 CrossRef CAS.
- J. Lee, A. V. Ravichandran, J. Mohan, L. Cheng, A. T. Lucero, H. Zhu, Z. Che, M. Catalano, M. J. Kim, R. M. Wallace, A. Venugopal, W. Choi, L. Colombo and J. Kim, ACS Appl. Mater. Interfaces, 2020, 12, 36688–36694 CrossRef CAS.
- S. Sonde, A. Dolocan, N. Lu, C. Corbet, M. J. Kim, E. Tutuc, S. K. Banerjee and L. Colombo, 2D Mater., 2017, 4, 025052 CrossRef.
- A. F. Rigosi, H. M. Hill, N. R. Glavin, S. J. Pookpanratana, Y. Yang, A. G. Boosalis, J. Hu, A. Rice, A. A. Allerman, N. V. Nguyen, C. A. Hacker, R. E. Elmquist, A. R. H. Walker and D. B. Newell, 2D Mater., 2017, 5, 011011 CrossRef.
- B. J. Matsoso, C. Garcia-Martinez, T. H. Mongwe, B. Toury, J. P. M. Serbena and C. Journet, J. Phys.: Mater., 2021, 4, 044007 Search PubMed.
- M. V. Kamalakar, A. Dankert, J. Bergsten, T. Ive and S. P. Dash, Appl. Phys. Lett., 2014, 105, 212405 CrossRef.
- C. Wen, X. Li, T. Zanotti, F. M. Puglisi, Y. Shi, F. Saiz, A. Antidormi, S. Roche, W. Zheng, X. Liang, J. Hu, S. Duhm, J. B. Roldan, T. Wu, V. Chen, E. Pop, B. Garrido, K. Zhu, F. Hui and M. Lanza, Adv. Mater., 2021, 33, 2170205 CrossRef.
- Y. Shi, X. Liang, B. Yuan, V. Chen, H. Li, F. Hui, Z. Yu, F. Yuan, E. Pop, H.-S. P. Wong and M. Lanza, Nat. Electron., 2018, 1, 458–465 CrossRef.
- P. Kumar, K. Zhu, X. Gao, S.-D. Wang, M. Lanza and C. S. Thakur, npj 2D Mater. Appl., 2022, 6, 8 CrossRef.
- A. Krishnaprasad, D. Dev, S. S. Han, Y. Shen, H.-S. Chung, T.-S. Bae, C. Yoo, Y. Jung, M. Lanza and T. Roy, ACS Nano, 2022, 16, 2866–2876 CrossRef.
- A. C. Khot, T. D. Dongale, K. A. Nirmal, J. H. Sung, H. J. Lee, R. D. Nikam and T. G. Kim, ACS Appl. Mater. Interfaces, 2022, 14, 10546–10557 CrossRef.
- W. Yu, C. Ji, X. Wan, Z. Zhang, J. Robertson, S. Liu and Y. Guo, Int. J. Mech. Syst. Dyn., 2021, 1, 159–172 CrossRef.
- H. Babaei, R. Guo, A. Hashemi and S. Lee, Phys. Rev. Mater., 2019, 3, 074603 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef.
- B. Mortazavi, E. V. Podryabinkin, I. S. Novikov, S. Roche, T. Rabczuk, X. Zhuang and A. V. Shapeev, J. Phys.: Mater., 2020, 3, 02LT02 Search PubMed.
- B. Mortazavi, F. Shojaei, A. V. Shapeev and X. Zhuang, Carbon, 2022, 194, 230–239 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef.
- R. D. H. Rojas, G. Parisi and F. Ricci-Tersenghi, Soft Matter, 2021, 17, 1056–1083 RSC.
- M. Rouhani, F. Chau-Nan Hong and Y.-R. Jeng, Carbon, 2018, 130, 401–409 CrossRef.
- J. Hilbert, F. Mangolini, J. McClimon, J. Lukes and R. Carpick, Carbon, 2018, 131, 72–78 CrossRef.
- A. Falin, Q. Cai, E. J. Santos, D. Scullion, D. Qian, R. Zhang, Z. Yang, S. Huang, K. Watanabe, T. Taniguchi, M. R. Barnett, Y. Chen, R. S. Ruoff and L. H. Li, Nat. Commun., 2017, 8, 15815 CrossRef PubMed.
- J. Long, L. Yang and X. Wei, J. Alloys Compd., 2013, 549, 336–340 CrossRef.
- Y. Liu, Y. Pan, D. Yin, S. Song, L. Lin, X. Qi, M. Zhang and J. Yao, J. Non-Cryst. Solids, 2021, 558, 120664 CrossRef.
- Y. Liang, H. Qin, J. Huang, S. Huan and D. Hui, Nanotechnol. Rev., 2019, 8, 210–217 Search PubMed.
- M. Salavati, A. Mojahedin and A. H. Shirazi, Front. Struct. Civ. Eng., 2020, 14, 623–631 CrossRef.
- N. Li, N. Ding, S. Qu, L. Liu, W. Guo and C.-M. L. Wu, Comput. Mater. Sci., 2017, 140, 356–366 CrossRef.
- X. Jiang, J. Philip, W. J. Zhang, P. Hess and S. Matsumoto, J. Appl. Phys., 2003, 93, 1515–1519 CrossRef.
- N. Dwivedi, S. Kumar, H. Malik, G. Govind, C. Rauthan and O. Panwar, Appl. Surf. Sci., 2011, 257, 6804–6810 CrossRef.
- R. Jana, D. Savio, V. L. Deringer and L. Pastewka, Modell. Simul. Mater. Sci. Eng., 2019, 27, 085009 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Method section, supporting information and figures. Structural properties section, supporting figure. See DOI: https://doi.org/10.1039/d2nh00520d |
| This journal is © The Royal Society of Chemistry 2023 |