Electrocatalytic study of the hydrogen evolution reaction on MoS₂/BP and MoSSe/BP in acidic media

Abstract

Molecular hydrogen (H₂) production by the electrochemical hydrogen evolution reaction (HER) is being actively explored for non-precious metal-based electrocatalysts that are earth-abundant and low cost like MoS₂. Although it is acid-stable, its applicability is limited by catalytically inactive basal planes, poor electrical transport and inefficient charge transfer at the interface. Therefore, the present work examines its bilayer van der Waals heterostructure (vdW HTS). The second constituent monolayer boron phosphide (BP) is advantageous as an electrode material owing to its chemical stability in both oxygen and water environments. Here, we have performed first-principles based calculations under the framework of density functional theory (DFT) for the HER in an electrochemical double layer model with the BP monolayer, MoS₂/BP and MoSSe/BP vdW HTSs. The climbing image nudged elastic band method (CI-NEB) has been employed to determine the minimum energy pathways for Tafel and Heyrovsky reactions. The calculations reveal that the Tafel reaction shows no reaction barrier. Thereafter, for the Heyrovsky reaction, we obtained a low reaction barrier in the vdW HTSs as compared to that in the BP monolayer. Subsequently, we have observed no significant difference in the reaction profile of MoS₂/BP and MoSSe/BP vdW HTSs in the case of 2 × 2 supercell configuration. However, in the case of 3 × 3 and 4 × 4 configurations, MoSSe/BP shows a feasible Heyrovsky reaction with no reaction barrier. The coverages with 1/4H⁺ concentration (conc.) deduced high coverage with low conc. and low coverage with high conc. to be apt for the HER via the Heyrovsky reaction path. Finally, on observing the activation barrier of the Heyrovsky pathway along with that of second H adsorption at the surface, the Heyrovsky path is expected to be favoured.

---

1 Introduction

The availability of clean and renewable energy sources governs the tenable development. Innovation in systems like fuel cells, metal–air batteries and water electrolysis positively impacts the environment.¹ The cleanest alternative for the same is molecular hydrogen (H₂) and hence, in the present context, we consider materials that support its production.^2,3 The electrochemical reactions that are in sync with the clean environment aim involve the hydrogen oxidation reaction (HOR), oxygen reduction reaction (ORR), hydrogen evolution reaction (HER) and oxygen evolution reaction (OER).⁴ The former two are associated with fuel cells, while the latter two are associated with water splitting or water electrolysis. There exists a wide range of materials that can catalyze these electrochemical reactions by photocatalytic or electrocatalytic pathways.^5–10 The present paper focuses on the HER by electrocatalysts. The HER requires large overpotential to be initiated, and therefore catalysts are required to lower the overpotential.¹¹ In this respect, Pt has established itself to be an efficient catalyst.¹² However, its high cost and low abundance have urged the scientific community to find new materials for catalytic applications.¹³ In fact, any heterogeneous catalysis under periodic boundary conditions faces the challenge of possessing an apt catalytic material that decreases the reaction barrier.¹⁴

The HER can occur in both acidic and alkaline media. In either of the media, the reaction steps follow (i) adsorption of H, (ii) its reduction and (iii) desorption as H₂.¹⁵ Now, the HER has been reported to have sluggish kinetics in alkaline media with ambiguous active sites.^16,17 Since the electrolytic reactions at the electrode are acidic, we are focusing on acidic media in the present study. The adsorption step is very fast and is termed the Volmer step:¹⁸

Volmer reaction (fast): H⁺ + e⁻ → H_ad

The subsequent steps take place either through Tafel or Heyrovsky paths (Fig. 1).

Tafel reaction: 2H_ad → H₂

Heyrovsky reaction: H_ad + H⁺ + e⁻ → H₂

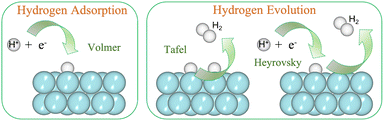Fig. 1 (Color online) HER steps: Volmer is the adsorption step, and Tafel/Heyrovsky is the evolution step.

As previously mentioned, the concept is to obtain material for the reaction that does not include precious metals like Pt. The literature has shown the transition metals (Fe, Ni, and Co), carbides, metal oxides (RuO₂ and IrO₂), graphene, non-layered 2D materials, metal–organic frameworks (MOFs) and transition metal dichalcogenides (TMDs) as effective HER catalysts.^{11,15,19–23} We restrict our study to the 2D materials that showcase quantum confinement effects with increased carrier mobility and large surface area.^24–26 This results in their increased catalytically active sites. The monolayer TMDs (in place of graphene) have established themselves as a potent material with optimal band gaps suitable for optoelectronics, photocatalysis and electrocatalysis.^27–33 In addition, due to their flexibility, these are widely studied for flexible electronic devices. The literature has reported their use as catalysts for the HER, especially on the surface of 1T′-MoS₂ and edge sites of 2H-MoS₂.^34–36 The former is metastable and coexists with other phases (1T′′ and 1T′′′).³⁷ Hence, we consider 2H-MoS₂ in our work. MoS₂ being acid-stable is an added advantage.³⁸ Furthermore, its heterojunctions have also shown promising HER catalytic behaviour.^16,39–41 It is pertinent to mention here that the tunability of 2D materials for specific applications is prevalent by defect engineering, strain engineering, stacking order, external field implementation, alloying and forming heterojunctions.^42–48 Amongst them, formation of heterojunctions with van der Waals forces in between the constituent monolayers are classified under van der Waals heterostructures (vdW HTSs). These have proved a real boon to the field of work because the constituent monolayers retain their properties simultaneously with their combined vdW HTS properties.⁴⁹ In addition, the electronegativity difference between the constituent monolayers actuates electron transfer, thereby affecting the HER.⁵⁰ Even if the constituent monolayers have inactive sites, the resulting vdW HTS can be obtained as an active electrocatalyst due to an inbuilt electric field at the interface.⁵¹

Presently, we explore the boron phosphide (BP) monolayer, MoS₂/BP and MoSSe/BP vdW HTSs for the HER. Recent studies have reported vdW HTSs with BP instead of graphene as it has a similar single atomic layered hexagonal structure, however, along with a band gap.⁵² The BP monolayer has been reported with low carrier effective mass, high carrier mobility, good mechanical strength, and stability in water environments.^53,54 Since the lattice parameter of MoS₂ and BP is similar, the MoS₂/BP vdW HTS becomes a plausible system with minimal lattice mismatch.⁵⁵ The BP monolayer has also been synthesized experimentally.⁵⁶ In addition, since Janus (MoSSe) has established itself with more catalytically active sites than MoS₂, we have also analyzed the MoSSe/BP vdW HTS. Any prior investigations for the HER on these systems are hitherto unknown; hence we have considered these systems for our work.

The aforementioned HER reaction path should account for the proton and electron free energies.⁵⁷ These are incorporated by the computational hydrogen electrode model as proposed by Nørskov et al.¹⁸ The model caters to the fundamental problem of large-scale calculation of a real system along with electrolyte by following the electrochemical double layer approach rather than external charge formation. The underlying approximation considers solvated protons up to the first bilayer. Until now, no study has been reported for the analysis of vdW HTSs using the computational hydrogen electrode model for the HER in acidic media to the best of our knowledge.⁵⁸ We have initially discussed the stacking configuration and electronic structure. Subsequently, the computational hydrogen electrode model is discussed. Thereafter, Tafel and Heyrovsky reaction paths are analyzed. Finally, we discuss the electrode potential and the reaction and activation energies.

2 Methodology

The first-principles based density functional theory (DFT) calculations have been employed in the present work.^59–64 The associated code chosen is the Vienna ab initio simulation package (VASP)^65–67 with projector augmented wave (PAW) pseudopotentials using plane wave basis. The generalized gradient approximation (GGA) that accounts for the exchange–correlation (xc) interaction amongst electrons is incorporated by the PBE xc functional (as proposed by Perdew–Burke–Ernzerhof (PBE)^68,69). The Brillouin zone (BZ) sampling of 2 × 2 K-mesh is used for conjugate gradient minimization with an energy tolerance of 0.001 meV and a force tolerance of 0.001 eV Å⁻¹. The intermediate, initial and final energetics are obtained by the BZ sampling of a 6 × 6 K-mesh. The plane wave cutoff energy is set to 500 eV. All the structures are built with 20 Å vacuum that avoids the electrostatic interactions among the periodic images. The two-body Tkatchenko–Scheffler vdW scheme has been employed for obtaining optimized structures.^70,71 This is an iterative scheme based on Hirshfeld partitioning of the electron density. We have employed the climbing-image nudged elastic band (CI-NEB) method to obtain the minimum energy path for the HER.^72,73 Note that we have not explicitly considered entropy calculations, as in approximation of solvated protons on the first layer, and 0.2–0.3 eV can be added all along the energetics.¹⁸ In reference to the previous literature, we have not included the spin–orbit coupling (SOC) in our calculations.^74–76

3 Results and discussion

3.1 Heterostructure

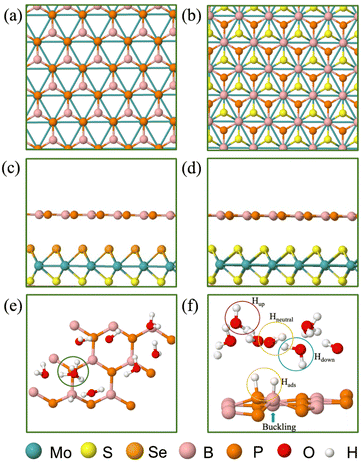
The present paper features the BP monolayer, MoS₂/BP and MoSSe/BP vdW HTSs for HER assessment. The lattice parameter of the BP monolayer is 3.20 Å and that of MoS₂ is 3.16 Å. Since the lattice mismatch between them is less (1.2% as obtained by (l(MoS₂) − l(BP))/l(BP), where l(MoS₂) and l(BP) is the lattice constant of MoS₂ and BP, respectively), the corresponding MoS₂/BP vdW HTS formed is commensurate.⁷⁷ Its corresponding structural and electronic properties are obtained from unit cell configuration (see Fig. S1–S3 in the ESI†), whereby, MoS₂/BP and MoSSe/BP form type 1 and type 2 alignment and it corroborates with the prior research.^55,78 Note that, initially, two stacking styles (see Fig. 2(a) and (b)) between the constituent monolayers were considered, wherein the stacking corresponding to Fig. 2(b) has minimum binding energy.³⁹ Therefore, we have proceeded with this stacking in our work.

Fig. 2 (Color online) (a) and (b) Top view of MoS₂/BP vdW HTS stacking configurations, (c) and (d) side view of minimum energy stacking configuration for MoSSe/BP and MoS₂/BP vdW HTSs, respectively, (e) 3 × 3 supercell of the BP monolayer schematic with 1/3H⁺ conc. i.e., 1H⁺/3H₂O, and (f) water molecule orientations of H_up, H_down and H_neutral. Buckling on BP can be observed at the H_ads site.

3.2 HER study

Now, we advance on HER study, for which we have constituted 2 × 2, 3 × 3 and 4 × 4 supercells. The former being smaller restricts the proton concentration (conc.) variability; therefore, we need larger supercells. In view of this, we are analyzing the 2 × 2 supercell along with 3 × 3 and 4 × 4, because, unlike the monolayer, the vdW HTS with further large supercell size becomes computationally demanding. The subsequent paragraphs discuss the concepts of coverage and proton conc. for clarity.

The first step is to obtain the coverage that gives ΔG_H ≃ 0 for our study. The number of adsorbed hydrogen (H_ads) per surface atom is defined as the coverage. ΔG_H is the free energy of atomic hydrogen adsorption and is expressed as:

ΔG_H = ΔE_H + ΔE_ZPE − TΔS_H

where

ΔE_H = E[nH] − E[(n − 1)H] − 1/2E[H₂]

In the aforementioned equations, ΔE_H is the hydrogen binding energy on the surface of the vdW HTS, E[nH] (or E[(n − 1)H]) is the energy of the configuration with n(or n − 1) number of H_ads, ΔE_ZPE is the zero-point energy of H_ads and ΔS_H is the entropy of H₂ in the gas phase. At 298 K, ΔE_ZPE − TΔS_H = 0.25 eV is well established in the literature.³⁸ We observe the 2 × 2 supercell with 25% H coverage (2H_ads per 8 surface atoms) and the 3 × 3 supercell with 11% H coverage (2H_ads per 18 surface atoms) with ΔG_H equal to −0.024 eV and 0.049 eV, respectively. We have deduced these coverages after trials up to 38%. The 4 × 4 supercell shares the same coverage and H⁺ conc. as in the case of the 2 × 2 supercell. We have chosen consecutive B and P atomic sites for H_ads as this configuration was found to be the most stable. Also, we observed buckling at the site of H_ads (see Fig. 2(f)).

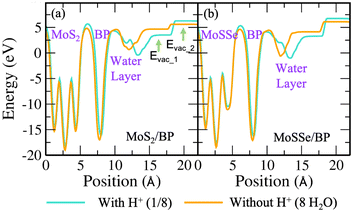
We now discuss the optimized systems consisting of a water layer (water–solid interface with a 3 Å thick water layer) without and with solvated protons (i.e., H⁺). Fig. 2(e) shows the BP monolayer (2H_ads) with H⁺ in the 3 × 3 supercell. Note that the H⁺ is in the form of hydronium (H₃O) in the water layer. The 2 × 2 supercell is a small supercell and therefore, only 1H⁺ is been considered. However, the corresponding H₂O molecules in the water layer are varied, thereby constituting 1/3 (i.e., 1H⁺/3H₂O) and 1/4 (i.e., 1H⁺/4H₂O) H⁺ conc. The configuration corresponding to the 3 × 3 supercell size has been studied for 1/8 (i.e., 1H⁺/8H₂O) H⁺ conc. The 4 × 4 supercell size with 12 and 16H₂O has been studied for 1/3 and 1/4H⁺ conc. The water orientation (see Fig. 2(f)) over the H_ads species is flat and H_up orientation is usually seen on the topmost layer. Further, all H₂O molecules are not H_down, rather, they are at some angular orientations other than strict H_up and H_down configurations. These orientations are essential because the electrostatic potential, as seen from the solid surface, also depends on the same. The stability of the vdW HTS along with water layer orientation is established by the similar profile of the radial distribution plot at 0 K and 300 K (see Fig. S8 in the ESI†).

3.3 Tafel reaction step

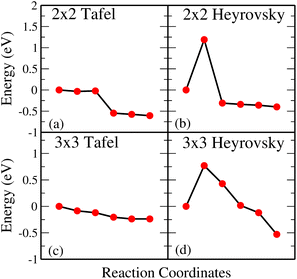
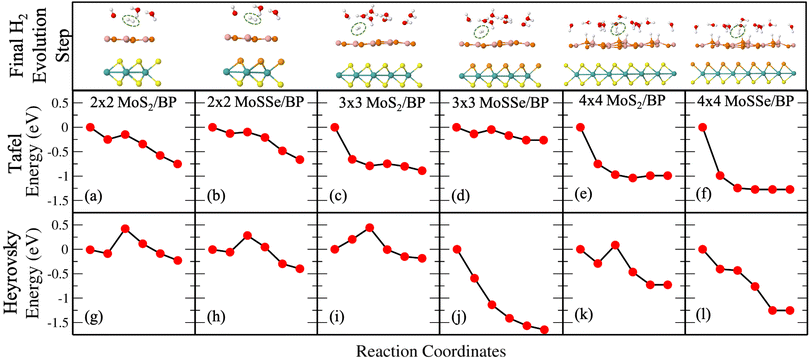
Fig. 3(a) and (b) give Tafel and Heyrovsky reaction steps, respectively on the BP monolayer. This corresponds to the 2 × 2 supercell with 3H₂O molecules and 1/3H⁺ conc., respectively. The BP monolayer acts as a reference to analyze the reactions for the MoS₂/BP and MoSSe/BP vdW HTSs. Here, we observe a reaction barrier in the Heyrovsky reaction step (1.19 eV) and not in the case of the Tafel reaction step. The reaction steps for the 3 × 3 supercell and 1/8H⁺ conc. are given in Fig. 3(c) and (d), whereby the Tafel reaction steps show no barrier and the Heyrovsky reaction steps show a reduced reaction barrier as compared to that in the 2 × 2 supercell. Further, we first discuss the Tafel reaction step analysis for the vdW HTSs. Fig. 4 highlights the Tafel reaction step on the MoS₂/BP ((a), (c) and (e)) and MoSSe/BP ((b), (d) and (f)) vdW HTSs. Firstly, no significant difference is observed between MoS₂/BP and MoSSe/BP vdW HTSs for the 2 × 2 supercell. The overview of the Tafel reaction analysis is consistent with Tafel being a surface reaction, thereby, lower or no observed reaction barrier. We observed that the minimum energy profile in the Tafel reaction is not continuously decreasing; instead, a slight hump is present. This corresponds to the buckling in the BP monolayer. As previously mentioned, the site of H_ads is buckled with respect to other sites, and during the H₂ evolution process, the corresponding BP site adjusts itself to the planar configuration (see Fig. 5). Note that the BP surface is considered for the reaction analysis as the basal plane of MoS₂ is not catalytically active.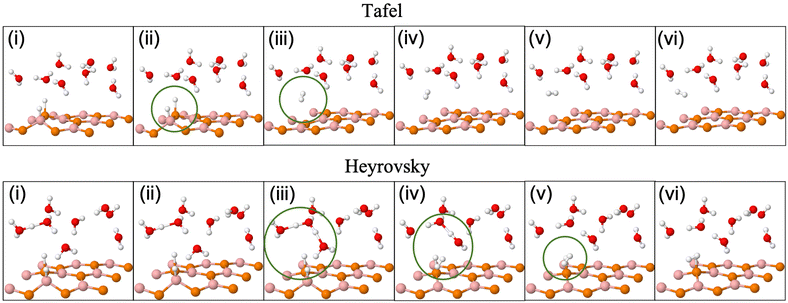

Fig. 3 (Color online) 2 × 2 supercell of the BP monolayer showing (a) Tafel reaction path and (b) Heyrovsky reaction path. The 3 × 3 supercell of the BP monolayer showing (c) Tafel reaction path and (d) Heyrovsky reaction path.

Fig. 4 (Color online) (a)–(f) Tafel reaction path (upper row) on MoS₂/BP and MoSSe/BP vdW HTSs for 2 × 2, 3 × 3 and 4 × 4 supercells. (g)–(l) Heyrovsky reaction path (lower row) on MoS₂/BP and MoSSe/BP vdW HTSs for 2 × 2, 3 × 3 and 4 × 4 supercells.

Fig. 5 (Color online) Tafel (upper row) and Heyrovsky (lower row) reaction profile snapshots on the 3 × 3 BP surface.

Now, the Tafel reaction path discussed in the manuscript is for two adjacent H-atom desorption as a molecular H₂. We have also performed the calculations on the 2 × 2 supercell to check the sites and the corresponding activation barrier (Volmer step). The first step consists of the transfer of H⁺ to H adsorbed at the P (H_adsP) or B (H_adsB) site, where the H_adsB shows lower barrier than H_adsP. The second step is the H adsorption when the surface already has H_ads at any other site. In the case of second H_adsB, with already existing H_adsP we obtain a barrier in the range of 0.05 eV – 0.08 eV. However, when the H_adsB precedes H_adsP, the final structure is at a higher ground energy state than the initial structure. Hence, this reaction path is not possible. The aforementioned observation is for both MoS₂/BP and MoSSe/BP vdW HTSs (see Fig. S9 in the ESI†).

3.4 Heyrovsky reaction step

Unlike Tafel, the Heyrovsky reaction step is not a pure surface reaction. It involves charge transfer, thereby affecting the reaction barrier and Fig. 4(g)–(l) substantiate the same. We have observed a reduction in the reaction barrier in the vdW HTSs as compared to that in the BP monolayer (refer to Fig. 3 and 4). The 4 × 4 supercell configuration puts forth the lowest reaction barrier amongst the three supercell configurations. MoS₂/BP and MoSSe/BP demonstrate this reduction from 0.43 eV (Fig. 4(g)) to 0.08 eV (Fig. 4(k)) and 0.28 eV (Fig. 4(h)) to 0 eV (Fig. 4(l)), respectively. Apart from previously discussed, we also considered the 4 × 4 supercell corresponding to the 15.6% H coverage (5H_ads per 32 surface atoms) with ΔG_H equal to 0.026 eV and 1/3H⁺ conc., for the Heyrovsky reaction step. In this case, a 0.09 eV reaction barrier is observed for MoS₂/BP, whereas MoSSe/BP showed 0 eV. Further, we observe a significant change in the case of MoSSe and this may be attributed to the combined effect of the coverage and the electronegativity difference within the MoSSe layer that affects the charge transfer at the interface.

Apart from the factors that are discussed above, there are structural parameters that affect the reaction steps. The H bonds in H₃O⁺ stretch before combining with the H_ads. At the transition state, H₂ is formed. After that, the atoms adjust themselves to low energy configuration. After the intermediate step, the B and P atoms adjust, corresponding to H_ads, along with the other H₂O molecules. As in the Tafel scenario, the steps post H₂ formation optimize the H₂ molecule in the water layer. The reaction barrier, therefore, depends on the buckling in the monolayer, the water molecule's orientation, and the coexisting water molecules with H⁺ (see Fig. 5).

Finally, we discuss the Heyrovsky reaction in MoS₂/BP for 1/4H⁺ conc. in the cases of 2 × 2 (i.e., 1H⁺/4H₂O), 3 × 3 (i.e., 2H⁺/8H₂O) and 4 × 4 (i.e., 4H⁺/16H₂O) supercells. We observed that the reaction barrier decreases from 0.43 eV (Fig. 4(g)) to 0.09 eV (Fig. 6(a)), 0.44 eV (Fig. 4(i)) to 0 eV (Fig. 6(b)) and 0.08 eV (Fig. 4(k)) to 0 eV (Fig. 6(c)) in 2 × 2, 3 × 3 and 4 × 4 supercells, respectively. This indicates that high coverage prefers low H⁺ conc. and vice versa for a reduction in the reaction barrier.

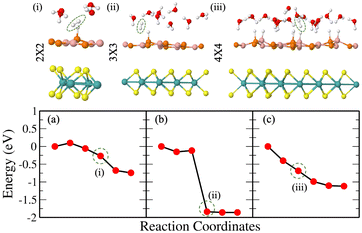Fig. 6 (Color online) Heyrovsky reaction path for the MoS₂/BP vdW HTS with 1/4H⁺ conc. in (a) 2 × 2 supercell, (b) 3 × 3 supercell and (c) 4 × 4 supercell.

Note that till now we discussed the H₂ evolution that includes H⁺ and H_adsB. The trend with supercell size is the same in the case of H_adsP as well (see Fig. S10 and S11 in the ESI†). However, for a particular supercell the reaction barrier for the latter is smaller than the former, indicating that H⁺ would initially prefer combining with H_adsP. We correlate this with the overpotential of the reaction, as discussed in the following section. Overpotential is the difference between the experimentally obtained reaction potential and the electrode potential. The electrode potential is analyzed only in the Heyrovsky reaction as it involves proton transfer. Therefore, this affects the work function and the potential at which the reaction takes place.

3.5 Electrode potential

The electrode potential (U) of the slab is reported relative to the normal hydrogen electrode (NHE):

U = ϕ − ϕ_NHE

Here, ϕ (E_vac – E_fermi) is the work function and ϕ_NHE is taken to be 4.44 eV.^18,38,79 The work function depends on the surface H coverage, the thickness or number of water bilayers, the water molecule orientation, and the system size. In small systems (here 2 × 2), the range of electrode potential analysis is limited to a few H⁺ conc. considerations. Fig. 7 presents the electrostatic potential plot where we have deduced the work function of 3 × 3 MoS₂/BP and MoSSe/BP. The same for 2 × 2 and 4 × 4 is shown in Fig. S14 and S15 of the ESI.† The potential drops are evident in Fig. 7, with a significant drop at the interface of BP and the water layer. The values of U corresponding to the water layer with and without H⁺ are reported in Table 1, which are in the range of −2.5 V to 1.3 V. We have incorporated dipole corrections as the vdW HTSs with two different surfaces maintain two potentials. Moreover, the H_ads and, therefore, the coverage affect the dipole–dipole interactions. As a result, we report the two values of U, i.e., U₁ and U₂, corresponding to two vacuum levels of E_{vac_1} and E_{vac_2}, respectively (Fig. 8).

Fig. 7 (Color online) Electrostatic potential plot of (a) MoS₂/BP and (b) MoSSe/BP vdW HTSs depicting the water layer with and without H⁺ in 3 × 3 supercell (i.e., 1/8H⁺ conc. and 8H₂O molecules, respectively).

Table 1 Electrode potential (U) of MoS₂/BP and MoSSe/BP with and without H⁺ in the water layer

vdW HTSs	With H^+		Without H^+
	U 1 (V)	U 2 (V)	U 1 (V)	U 2 (V)
MoS2/BP (2 × 2)	−2.31	0.48	1.04	0.70
MoSSe/BP (2 × 2)	−1.83	1.07	−0.68	1.31
MoS2/BP (3 × 3)	−2.09	−0.05	−0.09	0.84
MoSSe/BP (3 × 3)	−2.55	0.90	−0.79	1.19
MoS2/BP (4 × 4)	−2.12	0.39	−0.20	−0.75
MoSSe/BP (4 × 4)	−2.08	1.02	1.27	1.27

---

Fig. 8 (Color online) Variation of (a) reaction energy (ΔE_R = E_final − E_initial) and (b) activation energy (E_a), of configurations with respect to the change in electrode potential (ΔU = U_1initial − U_1final) from initial to final.

As the dependence of ϕ on water orientation has been previously discussed, we have explicitly optimized the H_down configuration for H₂O molecules. The Heyrovsky reaction path for the same in MoS₂/BP and MoSSe/BP 3 × 3 supercells can be seen in Fig. S16(a) and (b) of the ESI.† The obtained barrier is reduced as compared to the 2 × 2 supercells of MoS₂/BP and MoSSe/BP and the 3 × 3 supercell of MoS₂/BP. The corresponding electrode potential is also reported in Fig. S16(c) and (d) of the ESI.†

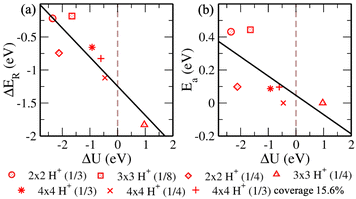
Now we progress towards the extrapolation approach to address the problem of potential change from initial to final in the case of the proton transfer Heyrovsky reaction. In this approach, we obtain reaction energies and activation energies of the system with different supercell sizes and H⁺ conc. The former represents the energy difference between the initial and final states, while the latter is the amount of energy required to overcome the reaction barrier. Thereafter, we obtain ΔE_R and E_avs. ΔU plot. ΔU signifies a change in electrode potential from initial to final. Moreover, the change in U₁ (corresponding to water layer potential) is significant as compared to the change in U₂ (corresponding to MoS₂ layer potential). The potential drop and charge transfer would accordingly affect the U₁ and U₂. Hence, the reaction taking place at the BP layer surface is crucial and we must consider U₁ for our analysis of electrode potential. Therefore, ΔU represented in the plot is corresponding to U₁. On extrapolating ΔE_R to ΔU = 0, we obtain −1.24 eV. The negative value indicates the spontaneity of the Heyrovsky reaction step. In the case of positive ΔE_R, the Heyrovsky reaction would have been the rate-determining step. The corresponding E_a is obtained as 0.05 eV. Hence, on comparing the vdW HTS with the monolayer, the synergistic effect of the two layers plays a role in affecting the overpotential and hence the reaction mechanism.

Now, we revisit the observations systematically. H_adsB shows lower ground state energy and reaction barrier than H_adsP. Also, we obtain a barrier in the range 0.05 eV – 0.08 eV when H_adsP precedes H_adsB at the surface. The vice versa observes higher ground state energy of the final structure state than the initial structure. Therefore, though the Tafel reaction path shows no reaction barrier, the above mentioned proton transfer (Volmer step) is restricted on sites. Subsequently, for the Heyrovsky reaction path, we observe the lower barrier for H₂ evolution that includes H⁺ and H_adsP. Hence, the extrapolated Heyrovsky E_a of 0.05 eV further indicates the Heyrovsky reaction path to be plausible.

Finally, it is pertinent to discuss the challenges for any further study. The present attempt to analyze the bilayer vdW HTSs with the explicit solvation approach (with few water layer molecules of 3 Å) would be computationally cumbersome if the monolayers or atomic layers increase. The large atomic size of the system also affects the proton concentration data and transition state search. Hence, the accountability of charge and potential should shift towards an approach that entails both explicit and implicit, and the employability of machine learning potentials. This would ensure the study of large systems with reduced computational time and cost.^80–82

4 Conclusion

In summary, we have modelled dynamically stable MoS₂/BP and MoSSe/BP vdW HTSs. They have been studied for the HER using the computational hydrogen electrode model. The optimized structure with the water layer showed a significant potential drop at the surface–water interface. The electrostatic potential is further affected by the proton solvated in the water layer and the H_ads constituting coverage over the surface. 2 × 2, 3 × 3 and 4 × 4 supercells with 25%, 11% and 25% H coverage have been deduced for the calculations. First, MoS₂/BP and MoSSe/BP vdW HTSs show reduced barrier height for both Tafel and Heyrovsky reactions in comparison to the BP monolayer. The Tafel reaction, being a surface reaction does not require charge transfer, herein corroborates with no or lower barrier observed in the MoS₂/BP and MoSSe/BP vdW HTSs. The analysis of H adsorption at B and P sites infers H_adsB with lower ground state energy. The second Volmer step restricts the path of H_adsB preceding the H_adsP. In the case of the Heyrovsky reaction, a reduced reaction barrier has been reported for H_adsP. Further, there is no significant difference between the MoSSe/BP and MoS₂/BP vdW HTS, as observed from the minimum energy reaction paths, except in the case of 11% coverage of MoSSe/BP with no reaction barrier. Hence, the MoSSe-based vdW HTS has shown that the Heyrovsky reaction favoured the HER for low coverage. On comparing the supercells (and hence different coverages) with respect to the same H⁺ conc., we observe high coverage to favour low H⁺ conc. and vice versa for a reduced reaction barrier. Finally, as per the extrapolation approach for ΔE_Rvs. ΔU, the Heyrovsky reaction mechanism is plausible.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

AS acknowledges IIT Delhi for the senior research fellowship. MJ acknowledges CSIR, India, for the senior research fellowship [grant no. 09/086(1344)/2018-EMR-I]. PB acknowledges UGC, India, for the senior research fellowship [1392/(CSIR-UGC NET JUNE 2018)]. S. B. acknowledges financial support from SERB under a core research grant (Grant No. CRG/2019/000647) to set up his high-performance computing (HPC) facility “Veena” at IIT Delhi for computational resources.

References

1. X. Zhang, A. Chen, L. Chen and Z. Zhou, Adv. Energy Mater., 2022, 12, 2003841.
2. S. Chu and A. Majumdar, Nature, 2012, 488, 294–303.
3. Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, 4998.
4. V. Vij, S. Sultan, A. M. Harzandi, A. Meena, J. N. Tiwari, W.-G. Lee, T. Yoon and K. S. Kim, ACS Catal., 2017, 7, 7196–7225.
5. Q. Lu, Y. Yu, Q. Ma, B. Chen and H. Zhang, Adv. Mater., 2016, 28, 1917–1933.
6. L. Cao and C. Wang, ACS Cent. Sci., 2020, 6, 2149–2158.
7. H. Jin, T. Song, U. Paik and S.-Z. Qiao, Acc. Mater. Res., 2021, 2, 559–573.
8. N. Abidi, K. R. G. Lim, Z. W. Seh and S. N. Steinmann, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1499.
9. N. Abidi, A. Bonduelle-Skrzypczak and S. N. Steinmann, ACS Appl. Mater. Interfaces, 2020, 12, 31401–31410.
10. M. Jain, D. Gill, S. Monga and S. Bhattacharya, J. Phys. Chem. C, 2023, 127, 15620–15629.
11. H. Zhang, X. Yang, H. Zhang, J. Ma, Z. Huang, J. Li and Y. Wang, Chem.–Eur. J., 2021, 27, 5074–5090.
12. J. N. Hansen, H. Prats, K. K. Toudahl, N. Mørch Secher, K. Chan, J. Kibsgaard and I. Chorkendorff, ACS Energy Lett., 2021, 6, 1175–1180.
13. G. Zhao, J. Chen, W. Sun and H. Pan, Adv. Funct. Mater., 2021, 31, 2010633.
14. Y. Shi, Z.-R. Ma, Y.-Y. Xiao, Y.-C. Yin, W.-M. Huang, Z.-C. Huang, Y.-Z. Zheng, F.-Y. Mu, R. Huang and G.-Y. Shi, et al. , Nat. Commun., 2021, 12, 1–11.
15. H. Jin, C. Guo, X. Liu, J. Liu, A. Vasileff, Y. Jiao, Y. Zheng and S.-Z. Qiao, Chem. Rev., 2018, 118, 6337–6408.
16. J. Wei, M. Zhou, A. Long, Y. Xue, H. Liao, C. Wei and Z. J. Xu, Nano-Micro Lett., 2018, 10, 1–15.
17. S. Li, S. Sirisomboonchai, X. An, X. Ma, P. Li, L. Ling, X. Hao, A. Abudula and G. Guan, Nanoscale, 2020, 12, 6810–6820.
18. E. Skúlason, G. S. Karlberg, J. Rossmeisl, T. Bligaard, J. Greeley, H. Jónsson and J. K. Nørskov, Phys. Chem. Chem. Phys., 2007, 9, 3241–3250.
19. Y. Wang, Z. Zhang, Y. Mao and X. Wang, Energy Environ. Sci., 2020, 13, 3993–4016.
20. Y. Wang, H. Zhang, X. Yang, J. Ma, Z. Huang and J. Li, Chemistry, 2020, 118, 5074–5090.
21. J. Du, F. Li and L. Sun, Chem. Soc. Rev., 2021, 50, 2663–2695.
22. D. V. Esposito, S. T. Hunt, Y. C. Kimmel and J. G. Chen, J. Am. Chem. Soc., 2012, 134, 3025–3033.
23. S. Trasatti, Electrochim. Acta, 1991, 36, 225–241.
24. S. H. Mir, V. K. Yadav and J. K. Singh, ACS Omega, 2020, 5, 14203–14211.
25. X. Zhang, B. Wang, X. Niu, Y. Li, Y. Chen and J. Wang, Mater. Horiz., 2018, 5, 1058–1064.
26. K. Khan, A. K. Tareen, M. Aslam, Y. Zhang, R. Wang, Z. Ouyang, Z. Gou and H. Zhang, Nanoscale, 2019, 11, 21622–21678.
27. A. Singh, P. Basera, S. Saini, M. Kumar and S. Bhattacharya, J. Phys. Chem. C, 2020, 124, 1390–1397.
28. Y. Chen, S. Huang, X. Ji, K. Adepalli, K. Yin, X. Ling, X. Wang, J. Xue, M. Dresselhaus and J. Kong, et al. , ACS Nano, 2018, 12, 2569–2579.
29. C. Rao, K. Gopalakrishnan and U. Maitra, ACS Appl. Mater. Interfaces, 2015, 7, 7809–7832.
30. E. Singh, P. Singh, K. S. Kim, G. Y. Yeom and H. S. Nalwa, ACS Appl. Mater. Interfaces, 2019, 11, 11061–11105.
31. H. Zeng, G.-B. Liu, J. Dai, Y. Yan, B. Zhu, R. He, L. Xie, S. Xu, X. Chen and W. Yao, et al. , Sci. Rep., 2013, 3, 1608.
32. C.-Y. Wang and G.-Y. Guo, J. Phys. Chem. C, 2015, 119, 13268–13276.
33. R. Kronberg, M. Hakala, N. Holmberg and K. Laasonen, Phys. Chem. Chem. Phys., 2017, 19, 16231–16241.
34. H. Wang, X. Xiao, S. Liu, C.-L. Chiang, X. Kuai, C.-K. Peng, Y.-C. Lin, X. Meng, J. Zhao and J. Choi, et al. , J. Am. Chem. Soc., 2019, 141, 18578–18584.
35. J. Chen, F. Li, Y. Tang and Q. Tang, J. Mater. Chem. C, 2020, 8, 15852–15859.
36. N. Abidi, A. Bonduelle-Skrzypczak and S. N. Steinmann, J. Phys. Chem. C, 2021, 125, 17058–17067.
37. C. Shang, Y. Fang, Q. Zhang, N. Wang, Y. Wang, Z. Liu, B. Lei, F. Meng, L. Ma and T. Wu, et al. , Phys. Rev. B, 2018, 98, 184513.
38. Q. Tang and D.-e. Jiang, ACS Catal., 2016, 6, 4953–4961.
39. A. Singh, M. Jain and S. Bhattacharya, Nanoscale Adv., 2021, 3, 2837–2845.
40. F. Ling, W. Kang, H. Jing, W. Zeng, Y. Chen, X. Liu, Y. Zhang, L. Qi, L. Fang and M. Zhou, npj Comput. Mater., 2019, 5, 20.
41. F. Keivanimehr, S. Habibzadeh, A. Baghban, A. Esmaeili, A. Mohaddespour, A. H. Mashhadzadeh, M. R. Ganjali, M. R. Saeb, V. Fierro and A. Celzard, Sci. Rep., 2021, 11, 1–9.
42. J. Wan, S. D. Lacey, J. Dai, W. Bao, M. S. Fuhrer and L. Hu, Chem. Soc. Rev., 2016, 45, 6742–6765.
43. J. Zhao, Q. Deng, A. Bachmatiuk, G. Sandeep, A. Popov, J. Eckert and M. H. Rümmeli, Science, 2014, 343, 1228–1232.
44. W. Bao, L. Jing, J. Velasco, Y. Lee, G. Liu, D. Tran, B. Standley, M. Aykol, S. Cronin and D. Smirnov, et al. , Nat. Phys., 2011, 7, 948–952.
45. J. Feng, X. Qian, C.-W. Huang and J. Li, Nat. Photonics, 2012, 6, 866–872.
46. F. Wang, Y. Zhang, C. Tian, C. Girit, A. Zettl, M. Crommie and Y. R. Shen, Science, 2008, 320, 206–209.
47. J. J. Humphrey, R. Kronberg, R. Cai, K. Laasonen, R. E. Palmer and A. J. Wain, Nanoscale, 2020, 12, 4459–4472.
48. J. Xie, X. Yang and Y. Xie, Nanoscale, 2020, 12, 4283–4294.
49. G. Swain, S. Sultana and K. Parida, Nanoscale, 2021, 13, 9908–9944.
50. G. Zhao, K. Rui, S. X. Dou and W. Sun, Adv. Funct. Mater., 2018, 28, 1803291.
51. S. Bawari, N. M. Kaley, S. Pal, T. V. Vineesh, S. Ghosh, J. Mondal and T. N. Narayanan, Phys. Chem. Chem. Phys., 2018, 20, 15007–15014.
52. H. Şahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453.
53. J. Wu, J.-H. Li and Y.-X. Yu, ACS Appl. Mater. Interfaces, 2021, 13, 10026–10036.
54. T. V. Vu, A. Kartamyshev, N. V. Hieu, T. D. Dang, S.-N. Nguyen, N. Poklonski, C. V. Nguyen, H. V. Phuc and N. N. Hieu, RSC Adv., 2021, 11, 8552–8558.
55. M. K. Mohanta, A. Rawat, N. Jena, Dimple, R. Ahammed and A. De Sarkar, ACS Appl. Mater. Interfaces, 2019, 12, 3114–3126.
56. B. Padavala, C. Frye, X. Wang, Z. Ding, R. Chen, M. Dudley, B. Raghothamachar, P. Lu, B. Flanders and J. Edgar, Cryst. Growth Des., 2016, 16, 981–987.
57. Y. Xiao and W. Zhang, Nanoscale, 2020, 12, 7660–7673.
58. J. D. Wiensch, J. John, J. M. Velazquez, D. A. Torelli, A. P. Pieterick, M. T. McDowell, K. Sun, X. Zhao, B. S. Brunschwig and N. S. Lewis, ACS Energy Lett., 2017, 2, 2234–2238.
59. R. M. Martin, Electronic Structure: Basic Theory and Practical Methods, Cambridge University Press, 2004.
60. R. M. Martin, L. Reining and D. M. Ceperley, Interacting Electrons, Cambridge University Press, 2016.
61. C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253.
62. L.-p. Feng, J. Su, S. Chen and Z.-T. Liu, Mater. Chem. Phys., 2014, 148, 5–9.
63. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
64. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
65. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
66. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
67. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
68. C. Stampfl and C. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 5521.
69. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
70. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
71. A. Tkatchenko, R. A. DiStasio Jr, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402.
72. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
73. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
74. C.-F. Fu, Q. Luo, X. Li and J. Yang, J. Mater. Chem. A, 2016, 4, 18892–18898.
75. J. Weng and S.-P. Gao, Phys. Chem. Chem. Phys., 2018, 20, 26453–26462.
76. K. Ren, W. Tang, M. Sun, Y. Cai, Y. Cheng and G. Zhang, Nanoscale, 2020, 12, 17281–17289.
77. A. U. Rahman, J. M. Morbec, G. Rahman and P. Kratzer, Phys. Rev. Mater., 2018, 2, 094002.
78. K. Ren, M. Sun, Y. Luo, S. Wang, J. Yu and W. Tang, Appl. Surf. Sci., 2019, 476, 70–75.
79. Q. He, X. Chen, S. Chen, L. Liu, F. Zhou, X.-B. Li and G. Wang, ACS Appl. Mater. Interfaces, 2018, 11, 2944–2949.
80. M. Liu, Y. Jin and J. Pan, Mater. Today Commun., 2022, 31, 103425.
81. S. Steinmann, Q. Wang and Z. W. Seh, Mater. Horiz., 2023, 10, 393–406.
82. C. Schran, F. L. Thiemann, P. Rowe, E. A. Müller, O. Marsalek and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2110077118.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00215b

---