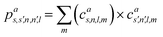Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Leveraging genetic algorithms to maximise the predictive capabilities of the SOAP descriptor†
Trent
Barnard
 a,
Steven
Tseng
a,
Steven
Tseng
 a,
James P.
Darby
a,
James P.
Darby
 b,
Albert P.
Bartók
b,
Albert P.
Bartók
 c,
Anders
Broo
c,
Anders
Broo
 d and
Gabriele C.
Sosso
d and
Gabriele C.
Sosso
 *a
*a
aDepartment of Chemistry, University of Warwick, Coventry, CV4 7AL, UK. E-mail: G.Sosso@warwick.ac.uk
bDepartment of Engineering, University of Cambridge, Trumpington St., Cambridge, CB2 1PZ, UK
cDepartment of Physics and Warwick Centre for Predictive Modelling, School of Engineering, University of Warwick, Coventry CV4 7AL, UK
dData Science and Modelling, Pharmaceutical Sciences, R&D, AstraZeneca Gothenburg, Pepparedsleden 1, Mölndal SE-431 83, Sweden
First published on 3rd November 2022
Abstract
The smooth overlap of atomic positions (SOAP) descriptor represents an increasingly common approach to encode local atomic environments in a form readily digestible to machine learning algorithms. The SOAP descriptor is obtained by using a local expansion of a Gaussian smeared atomic density with orthonormal functions based on spherical harmonics and radial basis functions. To construct this representation, one has to choose a number of parameters. Whilst the knowledge of the dataset of interest can and should guide this choice, more often than not some optimisation method is required to pinpoint the most effective combinations of SOAP parameters in terms of both accuracy and computational cost. In this work, we present SOAP_GAS, a simple, freely available computational tool that leverages genetic algorithms to optimise the relevant parameters for any given SOAP descriptor. To explore the capabilities of the algorithm, we have applied SOAP_GAS to a prototypical molecular dataset of relevance for drug design. In this process, we have realised that a diverse portfolio of different combinations of SOAP parameters can result in equally substantial improvements in terms of the accuracy of the SOAP-based model. This is especially true when dealing with the concurrent optimisation of the SOAP parameters for multiple SOAP descriptors, which we found often leads to further accuracy gains. Overall, we show that SOAP_GAS offers an often superior alternative to e.g. randomised grid search approaches to enhance the predictive capabilities of SOAP descriptors in a largely automatised fashion.
Design, System, ApplicationThe development of machine learning approaches for molecular design has now reached a stage where our ability to translate the molecular structure into one or more descriptors (or features, or fingerprints) is actually more important than the choice of the machine learning algorithm itself. The smooth overlap of atomic positions (SOAP) descriptor constitutes an increasingly popular approach to represent the local atomic environments of both molecules and solids. However, the (necessary) optimisation of the parameters intrinsic to this descriptor has traditionally been approached via either trial-and-error or via systematic, intrinsically inefficient approaches such as randomised grid searches. Here, we present SOAP_GAS, a computational framework that leverages genetic algorithms to optimise any given SOAP descriptor in a reliable and efficient way, surpassing the performance of grid search-based methods and providing a freely available tool for the community to improve on the performance of machine learning for applications such as drug design and discovery. To demonstrate the capabilities of SOAP_GAS, we apply it to the prototypical problem of predicting the solubility of a dataset of small drug-like molecules, thus showcasing the potential of this approach to boost the usefulness of machine learning methods in the context of machine learning for drug discovery. |
I. Introduction
The last few years have seen a rapidly growing interest in the application of machine learning (ML) techniques to understand, predict and determine the functional properties of a diverse array of molecules and materials.1–6 Properties ranging from the thermal conductivity of alloys7–11 to the solubility of pharmaceutical drugs12–18 have all been predicted with various levels of success using modern ML techniques. A large contributing factor to the meteoric rise of ML in the last two decades is the large amount of data that is becoming more easily accessible.19 There are a multitude of open access databases that anyone can use to train their own ML algorithms.20,21 This new insurgence of data, however, does not come without its own set of challenges. In the field of computational chemistry, a particularly arduous aspect of ML is determining how to translate structural or dynamical information about a system into a numerical array of descriptors (or features, or fingerprints) that can be fed into a ML algorithm. The resulting mathematical object needs to be complex enough to encapsulate all relevant information about the molecular structure. In order to avoid overfitting, the model should be of low dimensionality or it should not have any rapidly varying features. Alternatively, the model may be regularised, thereby preventing sharp features gaining dominance.As shown in previous work,22–25 the choice of descriptor has a large impact on the quality of predictions. There is a huge selection of descriptors available to use, and if some thought is not employed to understand which ones are appropriate, it may lead to poor results. A regularly used strategy is to utilise as many descriptors as possible to make predictions, however this is fallacious as it increases the likelihood of overfitting.22
One descriptor that has been proven to be sufficient in offering an accurate representation of any given molecular structure is the smooth overlap of atomic positions (SOAP) descriptor.26 Even though its most commonly used form only encodes up to three-body correlations,27 the SOAP descriptor has been gaining popularity given its impressive performance across a plethora of widely different classes of materials and problems ranging from hydrogen absorption of nano-clusters28 to the development of bespoke interatomic potentials.29,30 The premise of the SOAP descriptor is that it offers a convenient method to describe atomic environments that is invariant to any form of rotation, translation, reflection or permutation of equivalent atomic species.
The SOAP descriptor formalism26 is based on representing atomic environments by a scalar field centred on atom a, composed of Gaussian functions
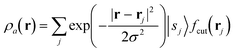 | (1) |
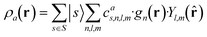 | (2) |
which can be shown to be invariant to rotations and reflections of the environment with respect to its central atom. Defined as such, each atomic environment is described by a single power spectrum. In addition, the formalism can be extended to describe molecules or condensed matter structures by averaging the representing density field across the constituent atoms. The basis set coefficients belonging to the same central atom species
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) are accumulated as:
are accumulated as: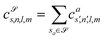 | (3) |
![[scr S, script letter S]](https://www.rsc.org/images/entities/char_e532.gif) for each distinct atom species within the structure. In order to reduce the complexity of the descriptors, it is also possible to sum all individual coefficients regardless of the central atom species information, although this leads to a loss of information.
for each distinct atom species within the structure. In order to reduce the complexity of the descriptors, it is also possible to sum all individual coefficients regardless of the central atom species information, although this leads to a loss of information.
SOAPs are not the only way to generate rotationally invariant molecular descriptors,32,33 however, some other rotationally invariant descriptors may be unsuitable to represent a heterogeneous dataset for ML purposes. For example, it is very challenging to perform ML with varying descriptor lengths without information being lost. When using SOAPs for ML it is possible to ensure the generated descriptor length does not scale with the number of atoms in the system leading to a uniform length descriptor vector for every element in the dataset. This is not the case for some other structural descriptors whereby they scale in length with the number of atoms in the molecule.22,34 The main drawback of SOAP descriptors is the potentially large computational cost, as the length ![[script L]](https://www.rsc.org/images/entities/i_char_e144.gif) of their power spectrum can be written as
of their power spectrum can be written as 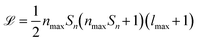 , where Sn is the number of neighbour species, nmax is the number of radial basis functions and lmax is the number of angular basis functions. In fitting ML models based on SOAP descriptors it is common to incur another factor proportional to Sn if a different model is defined for each centre species. This can lead, depending on the number of species used as centres and neighbors, to extremely large descriptor vectors which can be a challenge to compute due to the large amounts of computer memory required. As we show in sec. II however, it is possible to compress these vectors with a relatively small decrease in predictive performance.
, where Sn is the number of neighbour species, nmax is the number of radial basis functions and lmax is the number of angular basis functions. In fitting ML models based on SOAP descriptors it is common to incur another factor proportional to Sn if a different model is defined for each centre species. This can lead, depending on the number of species used as centres and neighbors, to extremely large descriptor vectors which can be a challenge to compute due to the large amounts of computer memory required. As we show in sec. II however, it is possible to compress these vectors with a relatively small decrease in predictive performance.
SOAPs work by using a series of orthonormal radial and angular basis functions to expand the local neighbourhood density around each atom. An individual expansion is used for each species of atom in the neighbourhood. In this paper we attempt to maximise the predictive capabilities of SOAPs by optimising the following parameters that are stipulated when generating SOAPs:
– nmax – the number of radial basis functions gn.
– lmax – the maximum degree of the spherical harmonics Ylm.
– cutoff – the cutoff distance for the basis function (Å).
– atom_sigma – the Gaussian smearing width of atom density σ (Å).
– centres – the atomic species used as centres for the basis functions.
– neighbours – the atomic species used as neighbours for the basis function.
The optimisation of these parameters is no easy feat, particularly when dealing with heterogeneous datasets. It is not obvious which sets of parameters will work when working with datasets that contain diverse molecular structures or models characterised by a variety of atomic species or environments. Initially, it may seem intuitive to simply use trial-and-error or even an exhaustive grid search strategy to optimise these parameters, however due to the large computational costs of generating SOAP descriptors, these methods are rather inefficient. A number of approaches have been proposed in the last few years to optimise the performance of the SOAP descriptor,35–38 including Bayesian optimisation,30 grid search,39,40 gradient descent41 and particle swarm optimizers.42
In this work, we have leveraged genetic algorithms (GAs)43,44 in order to optimise the above mentioned SOAP parameters for one or multiple SOAP descriptors – given a certain choice of centres and neighbours. At its core, a GA is a straightforward optimisation method where a set of different SOAP parameters is evaluated using a metric of choice. The best performing parameters are then combined by taking values randomly from pairs of parameters to create a new population. This is repeated for multiple generations until a sufficient level of accuracy is reached. The resulting framework, which we have named SOAP_GAS, is freely available on GitHub at https://github.com/gcsosso/SOAP_GAS.git.
SOAP_GAS allows to consistently and efficiently improve the accuracy of any given SOAP descriptor in a largely automatic fashion. It can be applied to heterogeneous datasets containing different molecular species in different forms (i.e. as isolated molecules as well as crystalline structures) thanks to the recent advances in terms of averaging described in ref. 45. It can also deal with large datasets, by leveraging the compression options recently introduced in ref. 46, and can optimise the parameters of multiple SOAP vectors at the same time.
Here, we have chosen to explore the capabilities of SOAP_GAS by applying it to a prototypical dataset for drug design and discovery, which includes ∼6000 small drug-like molecules and the values of their solubility in water as the target functional property. We stress that the aim of this work is not to advance the state-of-the-art with respect to this specific application of ML for drug design and discovery. Instead, we have picked this rather popular ML application so as to showcase the potential and general applicability of SOAP_GAS to any given molecular dataset.
We have found that, at least in the case of this particular “solubility” dataset, a number of significantly different combinations of SOAP parameters can result in similarly accurate models. Whilst some weak correlations exists between the different SOAP parameters, it may be concluded that pinpointing efficient combinations based on physical intuition alone is not an efficient strategy. Instead, SOAP_GAS offers a straightforward framework to identify these optimal combinations of SOAP parameters. It represents a solid alternative to the commonly used randomised grid search approach, which can prove rather inefficient/sub-optimal when dealing with the concurrent optimisation of the SOAP parameters of multiple SOAP vectors – which we have found to often result in more accurate descriptors when compared to concatenation of individually optimised SOAP vectors.
The paper is organised as follows: we start by presenting in sec. II the SOAP_GAS algorithm, its structure and its capabilities. We then apply the framework to a dataset of relevance for drug design and discovery. The results are discussed in sec. III and include some reflections on the accuracy of the algorithm, the correlations between the resulting SOAP parameters, a comparison in terms of accuracy and timing with respect to a randomised grid search approach as well as the concurrent optimisation of multiple SOAP descriptors.
II. Computational methods
A. Dataset utilized
We have chosen to apply the SOAP_GAS algorithm to a dataset containing the SMILES strings47 of 6119 drug-like molecules and their solubility. The solubility (S) i.e. the extent to which a chemical substance can dissolve in a solvent and form a homogeneous solution, is customarily represented using the base 10 logarithm as log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S, with S in moles per litre units.48,49 Based on the information contained in ref. 50 and 51, we believe that the solubility values in question refer to the thermodynamic solubility of these molecules. This dataset was curated by merging several sub-datasets containing solubility values characterised by an uncertainty inferior to 0.4log
S, with S in moles per litre units.48,49 Based on the information contained in ref. 50 and 51, we believe that the solubility values in question refer to the thermodynamic solubility of these molecules. This dataset was curated by merging several sub-datasets containing solubility values characterised by an uncertainty inferior to 0.4log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S so as to maximise the reliability of the experimental data (a notorious issue when dealing with solubility measures) quality. This particular threshold in terms of uncertainty corresponds to the standard deviation relative to the sets of experimental measurements of S obtained for the same compounds by different research groups.47 Prior to use, we discarded 35 compounds that were either inorganic (i.e. they contained no C atoms) or contained counter-ions.
S so as to maximise the reliability of the experimental data (a notorious issue when dealing with solubility measures) quality. This particular threshold in terms of uncertainty corresponds to the standard deviation relative to the sets of experimental measurements of S obtained for the same compounds by different research groups.47 Prior to use, we discarded 35 compounds that were either inorganic (i.e. they contained no C atoms) or contained counter-ions.
To generate three-dimensional molecular models from the SMILES strings, we employed the make3D method from Pybel, subsequently performing 50 steps of geometry optimisation via the MMFF94 force field.52 We note that this is not a sophisticated approach,53 particularly if compared to methods such ensemble descriptors,54 where several different conformations are generated, optimised and evaluated for any given molecular structure. However, as previously stated, this work does not seek to improve on the current performance of ML methods in the context of predictive models for solubility. Instead, we are aiming to illustrate the potential of SOAP_GAS – and to that end, any realistic three-dimensional rendition of the SMILES strings will serve to illustrate the differences between optimised and non-optimised SOAP descriptors.
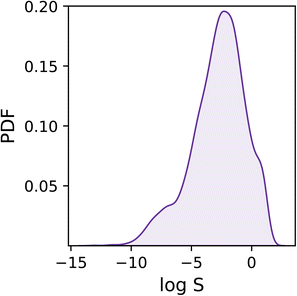
As shown in Fig. 1, the dataset is characterised by a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S range between −13.2 and 1.58, and a mean of −2.78. Overall, the target values are distributed rather homogeneously, albeit one can notice a tail in the distribution corresponding to low solubility values (i.e. log
S range between −13.2 and 1.58, and a mean of −2.78. Overall, the target values are distributed rather homogeneously, albeit one can notice a tail in the distribution corresponding to low solubility values (i.e. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S < −6) which we expect to prove difficult to deal with as they are under-represented within the dataset.
S < −6) which we expect to prove difficult to deal with as they are under-represented within the dataset.
Table 1 reports the frequency with which each atomic species occurs within the dataset. Unsurprisingly, given the nature of the dataset, C, N, O and H are the most numerous, with a significant population of Cl and S as well. We have chosen to consider only the atomic species that are present in at least 50 different molecules within the dataset, when constructing the SOAP vectors discussed in section III.
H 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 119 (6068) 119 (6068) |
Cl 3319 (1270) | P 269 (246) | K 8 (5) | As 3 (3) |
C 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 389 (6119) 389 (6119) |
S 1383 (990) | I 114 (78) | Sn 5 (5) | Ge 2 (1) |
O 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) 738 (4894) 738 (4894) |
F 699 (321) | Si 35 (16) | Hg 5 (5) | Ba 2 (2) |
| N 7302 (3289) | Br 373 (224) | Se 9 (6) | Zn 4 (4) | Ca 1 (1) |
| Mn 1 (1) | Cu 1 (1) | Sr 1 (1) | Ag 1 (1) |
B. The SOAP_GAS algorithm
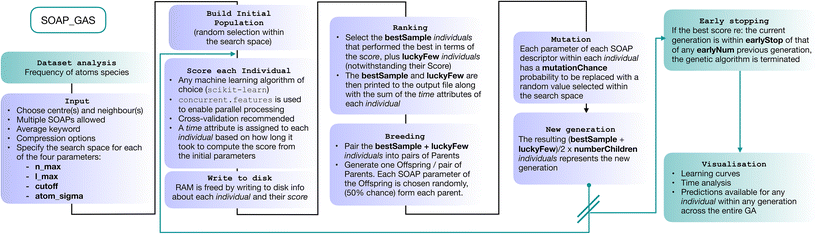
In this section we describe the SOAP_GAS algorithm (a schematics is provided in Fig. 2). We start by constructing a so-called initial population containing a certain number (popSize) of individuals. Each individual corresponds to a SOAP descriptor characterised by a fixed selection of atomic species as centres and neighbours as well as a randomly selected set of SOAP parameters (i.e., nmax, lmax, cutoff and atom_sigma, see sec. I). The user has the freedom to specify lower and upper boundaries (usually dictated by physical intuition and/or computational cost) for each of the four SOAP parameters.The choice of which atomic species are to be selected as centres and neighbours for the SOAP descriptor is left to the user. The average keyword within the SOAP descriptor (see next section) implements the structure-wise SOAP descriptor described in eqn (3), resulting in feature vectors of the same dimensionality across heterogeneous datasets containing different molecules or different number of molecules in a given structure. A simple script included in the SOAP_GAS package can be used to analyse a dataset of N molecular structures and gain information about the frequency by which a given atomic species is present within the dataset.
For each individual descriptor within the initial population we compute a score (or “fitness”, as customary in the GA literature), i.e. a metric that quantifies the accuracy of the individual in predicting the functional property of interest – in this case, the solubility of a given molecular species. In particular, in our case we have chosen to combine two popular metrics, the mean squared error (MSE) and the Pearson correlation coefficient (PCC), for both the training and test sets, as follows:
| Score = 2·MSEtr·(1 − PCCtr) + MSEte·(1 − PCCte), | (4) |
To obtain this score, we have employed a straightforward random forest (RF) model. RF is an ensemble learning technique that averages the predictions from a collection of decision trees and may be utilized for both classification and regression.55 Each decision tree is built on N data points that are bootstrapped, i.e., sampled with replacement, from the N-sized training data, with the results collected and averaged to obtain a single prediction, a procedure called bootstrap aggregation or “bagging”. The split at each node is selected only from a subset of the features, with the feature that minimizes the error being selected. This framework randomises the ensemble of decision trees, creating a set of independent predictions from weak learners that may not be as good individually but once aggregated and averaged, produces a better result. Furthermore, as bootstrapping creates multiple datasets that are distinct from the original to construct each decision tree, RFs are effective for modeling small datasets.56,57 In terms of the training/test split, we have used 33% of the dataset as the test set.
Once we have a score for each of the popSize individuals, we select a certain number (bestSample) of them according to their scores, plus a usually small number (luckyFew) of individuals regardless of their score. These selected individuals constitute the so-called “parents” of the next generation of SOAP parameters. At this point, we move onto the “breeding” procedure, where we randomly split the (even number of) parents into (bestSample + luckyFew)/2 pairs. Each pair of parents produces a “child”, i.e. a new SOAP descriptor characterised by a new set of SOAP parameters – randomly picked with a 50% chance from either of the parents. We then proceed to apply “mutations”: each SOAP parameter within each child has a certain probability (mutationChance) to be changed into a randomly picked value (within the boundaries specified for that SOAP parameter). Note that the resulting population size, popSize = [(bestSample + luckyFew)/2) × numberChildren)] is identical to the size of the initial population.
Once we have obtained the new generation, we repeat the process until we reach the desired level of accuracy. The idea at the heart of SOAP_GAS and GA algorithms in general is that they allow to progressively explore the search space in an efficient, targeted fashion, while introducing mutations and other degrees of freedom (such as the number of luckyFew) to avoid getting stuck in local minima of the parameter space. SOAP_GAS also features an early-stopping criterion: if the current generation is within a certain threshold (in terms of score, earlyStop), of a specific number (earlyNum) of any previous generations, the algorithm is considered to be converged.
It is worth mentioning that we have chosen not to introduce an elitism operator explicitly when generating new populations of parameters. In the context of GAs, elitism operators are used to select the best individuals for the next generation without applying any mutation. This implies that, once a particularly well-performing individual is found, it persists throughout the algorithm/generations until an even better-performing one comes along.
Whilst adopting an elitism operator is a perfectly valid strategy (albeit by no means a mandatory one), we have chosen not to because (a.) the SOAP_GAS algorithm selects the best performing individual that appears in any generation. Hence, there is no real need to keep the same individual in the population from generation to generation. In fact, it might be detrimental to do so, as a lesser extent of the feature space will be explored; (b.) an elitism operator can be constructed via suitable combinations of the input parameters. For instance, a large number of luckyFew individuals and a low number of bestSample as well as a low mutationChance would achieve a result almost identical to that of applying an actual elitism operator.
Note that, depending on the size of the dataset, the choice of centres and neighbours as well as the choice of nmax, lmax and cutoff, the dimensionality of the SOAP vector can grow to the point of causing issues in terms of memory requirements. Aside from the compression strategy discussed in the next sections, in order to free memory the SOAP_GAS algorithm writes to disk the information about each individual in a bespoke class that contains the SOAP vectors, the target values of the whole database as well as the score and each of the train/test splits used for the cross validation relative to that particular score.
It is worth noting, however, that grid search approaches can trivially and effectively leverage parallel computing in that each grid point can be evaluated independently from the others. Conversely, SOAP_GAS is by its very nature a sequential algorithm, as the construction of given i-th generation of individuals depends on the accuracy of the individuals within the (i − 1)-th generation. However, we can still take advantage of parallel computing for the evaluation of different individuals within a given generation. To this end, we have adopted the concurrent.futures Python module, which provides a simple platform to allocate different instances of the same task (in our case the evaluation of the different individuals using the very same RF model) to the available computing cores. A scaling test, demonstrating the quasi-linear scaling of SOAP_GAS with the number of CPU cores, can be found in the ESI.†
III. Results
A. Optimising individual SOAPs
As a first test of the SOAP_GAS framework, we have applied it to a number of different SOAP vectors characterised by different combinations of atomic species as centres and neighbours. In particular, we have built an “all–all” SOAP where the ten most abundant species (see Table 1) have been used as both centres and neighbours. We have also built ten different SOAP vectors where each of the ten most abundant species has been used as centre whilst all of the ten have been used as neighbours. Finally, we have also considered what we call a “double” SOAP, i.e. “all–all (double)”, which consists of two all–all SOAP's using different values for the cutoff and atom_sigma, allowing for short and long range structure to be described with different resolutions.In terms of the search space for the SOAP_GAS algorithm, we have chosen the following, rather wide range: 2 < nmax < 10, 2 < lmax < 10, 5 < cutoff < 20, and 0.1 < atom_sigma < 1.5. Note that these boundaries of the cutoff have been superseded by the following limits in the case of short/long SOAP in the context of the all–all (double) SOAP: 5 < cutoff < 12 and 12 < cutoff < 20 for short and long all–all SOAP, respectively.
The results are reported in Table 2 relative to the data set discussed in II A. The “vanilla” data refer to the results obtained via the following non-optimised set of SOAP parameters: cutoff = 5, lmax = 6, nmax = 12 and atom_sigma = 0.5 which have been taken off-the-shelf from the online documentation of the SOAP descriptor.58 The “GA” data refer to the results obtained via the SOAP_GAS algorithm. We report the score metric described in eqn (4) together with both the MSE and PCC (including the associated uncertainties as the standard deviation from a 5-fold cross validation). It is clear that applying the SOAP_GAS algorithm consistently results in SOAP vectors corresponding to more accurate models in all cases. The greatest improvements in terms of accuracy can be appreciated for those SOAP vectors whose centres correspond to frequently occurring atomic species in the data set, such as C, H, and O. Conversely, the gains are only marginals for SOAP vectors with e.g., P or I as centres. This is expected, as the predictive power of those descriptors is bound to be rather weak given the minimal occurrence of those species in the data set.
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) = 1, ν = 1 and
= 1, ν = 1 and ![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif) = 0 combination has been used in terms of compression (see text)
= 0 combination has been used in terms of compression (see text)
| Score | ||
|---|---|---|
| Vanilla | GA | |
| All–all | 0.483 | 0.309 |
| All–all (double) | 0.317 | 0.269 |
| C-ten | 0.573 | 0.341 |
| H-ten | 0.749 | 0.402 |
| O-ten | 2.66 | 1.963 |
| Cl-ten | 3.925 | 3.677 |
| N-ten | 6.047 | 5.428 |
| S-ten | 10.987 | 10.529 |
| F-ten | 11.688 | 11.369 |
| Br-ten | 12.412 | 12.114 |
| P-ten | 12.207 | 12.159 |
| I-ten | 14.361 | 14.267 |
| MSE | ||||
|---|---|---|---|---|
| Vanilla | GA | |||
| Test | Train | Test | Train | |
| All–all | 1.43 ± 0.108 | 1.152 ± 0.018 | 1.154 ± 0.065 | 0.929 ± 0.015 |
| All–all (double) | 1.186 ± 0.095 | 0.924 ± 0.015 | 1.106 ± 0.069 | 0.855 ± 0.015 |
| C-ten | 1.569 ± 0.107 | 1.252 ± 0.016 | 1.209 ± 0.067 | 0.973 ± 0.013 |
| H-ten | 1.748 ± 0.105 | 1.427 ± 0.037 | 1.293 ± 0.076 | 1.074 ± 0.02 |
| O-ten | 2.935 ± 0.235 | 2.683 ± 0.055 | 2.580 ± 0.202 | 2.325 ± 0.044 |
| Cl-ten | 3.394 ± 0.189 | 3.192 ± 0.037 | 3.265 ± 0.176 | 3.12 ± 0.38 |
| N-ten | 4.068 ± 0.178 | 3.83 ± 0.042 | 3.869 ± 0.17 | 3.676 ± 0.037 |
| S-ten | 4.891 ± 0.192 | 4.758 ± 0.044 | 4.812 ± 0.181 | 4.708 ± 0.04 |
| F-ten | 4.945 ± 0.229 | 4.841 ± 0.058 | 4.877 ± 0.238 | 4.823 ± 0.06 |
| Br-ten | 5.003 ± 0.176 | 4.915 ± 0.041 | 4.948 ± 0.176 | 4.902 ± 0.043 |
| P-ten | 4.968 ± 0.211 | 4.908 ± 0.05 | 4.955 ± 0.212 | 4.905 ± 0.05 |
| I-ten | 5.077 ± 0.208 | 5.057 ± 0.053 | 5.071 ± 0.208 | 5.057 ± 0.053 |
| PCC | ||||
|---|---|---|---|---|
| Vanilla | GA | |||
| Test | Train | Test | Train | |
| All–all | 0.85 ± 0.008 | 0.884 ± 0.001 | 0.881 ± 0.003 | 0.907 ± 0.001 |
| All–all (double) | 0.877 ± 0.005 | 0.908 ± 0.001 | 0.887 ± 0.002 | 0.916 ± 0.001 |
| C-ten | 0.835 ± 0.006 | 0.875 ± 0.001 | 0.875 ± 0.002 | 0.902 ± 0.001 |
| H-ten | 0.812 ± 0.006 | 0.853 ± 0.003 | 0.867 ± 0.002 | 0.893 ± 0.002 |
| O-ten | 0.654 ± 0.019 | 0.694 ± 0.005 | 0.705 ± 0.013 | 0.742 ± 0.004 |
| Cl-ten | 0.577 ± 0.016 | 0.61 ± 0.002 | 0.598 ± 0.014 | 0.621 ± 0.003 |
| N-ten | 0.45 ± 0.022 | 0.503 ± 0.005 | 0.49 ± 0.023 | 0.53 ± 0.005 |
| S-ten | 0.194 ± 0.019 | 0.259 ± 0.004 | 0.231 ± 0.011 | 0.275 ± 0.004 |
| F-ten | 0.166 ± 0.021 | 0.219 ± 0.006 | 0.202 ± 0.027 | 0.225 ± 0.006 |
| Br-ten | 0.124 ± 0.023 | 0.183 ± 0.005 | 0.161 ± 0.023 | 0.188 ± 0.005 |
| P-ten | 0.151 ± 0.021 | 0.186 ± 0.003 | 0.157 ± 0.018 | 0.186 ± 0.003 |
| I-ten | 0.03 ± 0.015 | 0.067 ± 0.004 | 0.047 ± 0.003 | 0.067 ± 0.053 |
Given the relatively small size of our dataset, it is important to make sure that the fact that the performance of the test set contributes to our score would not prevent us from making a reliable performance comparison between vanilla and SOAP_GAS result. To address this aspect, we have verified that using a validation set (which at no point is involved in either the training/test of the models) does not have an impact on our results. The details of this analysis can be found in the ESI.†
As in the case of specific SOAP vectors the performance improvements obtained via SOAP_GAS might appear rather small, it is worth to perform a simple statistical test to verify that these performance differences are in fact significant. To this end, we have performed a Z test59 (i.e., a statistical test to determine whether two population means are different when the variances are known) on our results in terms of the mean squared error (MSE).
The results are reported in the ESI,† and indicate that for the all–all (and double) SOAP as well as for the SOAP centred on C, H, O, N and S atoms, the performance differences we observe for SOAP_GAS compared to vanilla SOAP are significant with respect to a 95% confidence interval. However, the same cannot be said for the SOAP centred on the far less frequent atomic species, namely the halogen atoms. This is somewhat expected, in that our predictions are more accurate when using SOAP centred on the most frequent atomic species, which in turn is reflected in the extent of the accuracy improvement upon applying the SOAP_GAS framework to SOAP vectors centred on more or less frequent species.
We note that the computational cost of dealing with the all–all SOAP stretched the capabilities of “regular” computing nodes. Dedicated high-memory computing nodes are often needed when dealing with SOAP vectors. Rather than adopting that approach, here we instead chose to take advantage of the compression scheme described in ref. 46. Within this scheme the SOAP power spectrum is compressed through a combination of projecting the atomic neighbour density onto the surface of the unit sphere, which reduces the radially sensitive body order, and summing over the neighbour densities of different species, which reduces the element sensitive body order. Combining these operations in different ways leads to nine distinct options ranging from the full power spectrum, where the length scales as ![[scr O, script letter O]](https://www.rsc.org/images/entities/i_char_e52e.gif) (nmax2S2lmax) to the most extreme compression which scales as
(nmax2S2lmax) to the most extreme compression which scales as ![[scr O, script letter O]](https://www.rsc.org/images/entities/i_char_e52e.gif) (lmax).
(lmax).
In Table 3, we report the dimensionality as well as the accuracy of the all–all SOAP obtained with these different levels of compression and denote them using the same notation as in ref. 46; note that the μ = 0, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) = 0, ν = 2 and
= 0, ν = 2 and ![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif) = 0 option corresponds to the original uncompressed SOAP vector. In light of the results reported in Table 3, we chose to apply the μ = 0,
= 0 option corresponds to the original uncompressed SOAP vector. In light of the results reported in Table 3, we chose to apply the μ = 0, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) = 1, ν = 1 and
= 1, ν = 1 and ![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif) = 0 option as it provides an excellent compromise between accuracy and compression. In particular, this combination retains much of the accuracy of the non-compressed SOAP vector (with a score of 0.445 against a score of 0.368) whilst drastically reducing the dimensionality from 1471 to 141 elements. The loss of accuracy is to be expected, as this level of compression does not preserve information, although it is interesting that accuracy is no worse than with μ = 1,
= 0 option as it provides an excellent compromise between accuracy and compression. In particular, this combination retains much of the accuracy of the non-compressed SOAP vector (with a score of 0.445 against a score of 0.368) whilst drastically reducing the dimensionality from 1471 to 141 elements. The loss of accuracy is to be expected, as this level of compression does not preserve information, although it is interesting that accuracy is no worse than with μ = 1, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) = 0, ν = 1 and
= 0, ν = 1 and ![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif) = 0, which, subject to certain conditions, is known to preserve information. All the results presented in this section have been obtained using μ = 0,
= 0, which, subject to certain conditions, is known to preserve information. All the results presented in this section have been obtained using μ = 0, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) = 1, ν = 1 and
= 1, ν = 1 and ![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif) = 0.
= 0.
| μ |
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif)
|
ν |
![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif)
|
Dim. | Score |
|---|---|---|---|---|---|
| 0 | 2 | 0 | 0 | 8 | 3.756 |
| 2 | 0 | 0 | 0 | 22 | 2.845 |
| 1 | 1 | 0 | 0 | 15 | 2.587 |
| 0 | 1 | 0 | 1 | 71 | 0.739 |
| 0 | 0 | 0 | 2 | 386 | 0.584 |
| 0 | 1 | 1 | 0 | 141 | 0.445 |
| 1 | 0 | 1 | 0 | 281 | 0.442 |
| 0 | 0 | 2 | 0 | 1471 | 0.368 |
| 0 | 0 | 1 | 1 | 1401 | 0.366 |
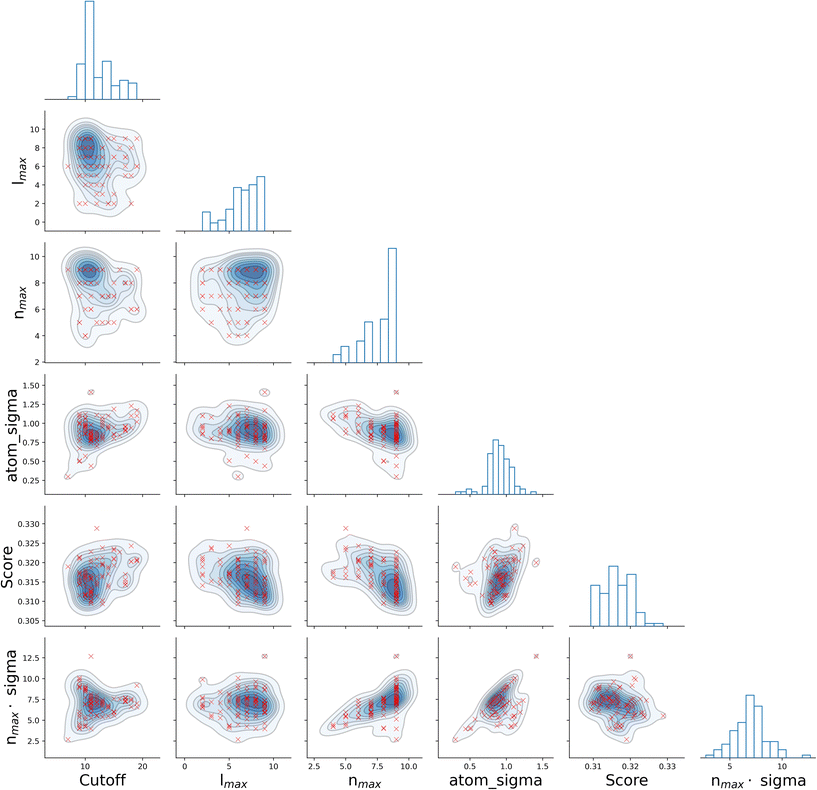
It is informative to look for correlations between the four SOAP parameters, as well as the resulting score. To this end, we have chosen the all–all SOAP, where every atomic species within the dataset is used as both centre and neighbour – with the exception of atomic species occurring in less than fifty molecules across the entire dataset (see Table 1) so that S = 10. We have run 96, independent instances of SOAP_GAS, where the initial values of each set of SOAP parameters for each individual within the initial population have been randomly selected. The SOAP parameters that resulted in the best score for each run are collected in Fig. 3. Overall, it is fair to say that there are no strong correlations between any of the SOAP parameters, albeit there is tendency for the accuracy (score) to improve when increasing the number or radial basis functions nmax. This is quite interesting, as one might think that an increase in e.g., cutoff should be accompanied by a larger nmax, as the greater spatial extent of the local atomic environment might need a greater number of radial basis functions. However, this is not the case. In fact, none of the SOAP parameters seem to be strongly correlated with the score. Again, this is somehow counter intuitive, as one might expect the SOAP vector to capture a greater deal of information about the molecular structure when increasing, e.g., the number of basis functions. As such, it appears that physical intuition alone might not suffice to guide the choice of the SOAP parameters – hence the need for an optimisation strategy such as the one offered by SOAP_GAS.
The results reported in Fig. 3 also allow us to draw some conclusions in terms of the reproducibility of the SOAP_GAS results. Namely, there are specific combinations of SOAP parameters that tend to feature much more prominently that others, as illustrated by the histograms in Fig. 3. Whilst it is perfectly possible for the SOAP_GAS to yield very different combinations of SOAP parameters that ultimately offer the same accuracy, the nmax = 9, lmax = 9, cutoff = 11 and atom_sigma = 0.8 scenario appears to be consistent in improving the score for the all–all SOAP vector.
In order to validate the robustness of the results obtained via the SOAP_GAS framework, we have applied the latter to an additional dataset, namely the QM7b dataset.60,61 This is a relatively low-noise dataset that contains 7211 molecules and features 13 target properties – we have chosen to focus on polarizability. The results, summarised in the ESI,† confirm the efficiency of the SOAP_GAS framework in improving the performance of the SOAP descriptor (notwithstanding the size of the dataset) and provide further evidence for a positive correlation between accuracy and nmax.
Given the results we have obtained for two different, entirely independent datasets, we argue that, at least for molecular datasets containing 102–103 data points, the existence of a Pareto front in terms of the SOAP parameters is a possibility – albeit of course we have no way to ensure that this result would hold for other datasets as well.
The performance of SOAP_GAS itself might depend to an extent upon the choice of specific GA parameters. This aspect is investigated in the next section.
B. SOAP_GAS: performance tuning
As opposed to brute-force optimisation approaches such as grid searches, GA are characterised by a number of parameters that allow for the fine tuning of the algorithm. In this section, we explore the impact of these parameters on both the accuracy of the resulting SOAP descriptors as well as the computational time needed, on average, to converge the GA to a satisfactory accuracy. In particular, we have:• The mutation chance, mutationChance.
• The population size, popSize.
• The early stopping criteria, earlyStop and earlyNum.
• The ratio between the number of children, numChildren, and the number of individuals, luckyFew, that are randomly selected as parents notwithstanding their score.
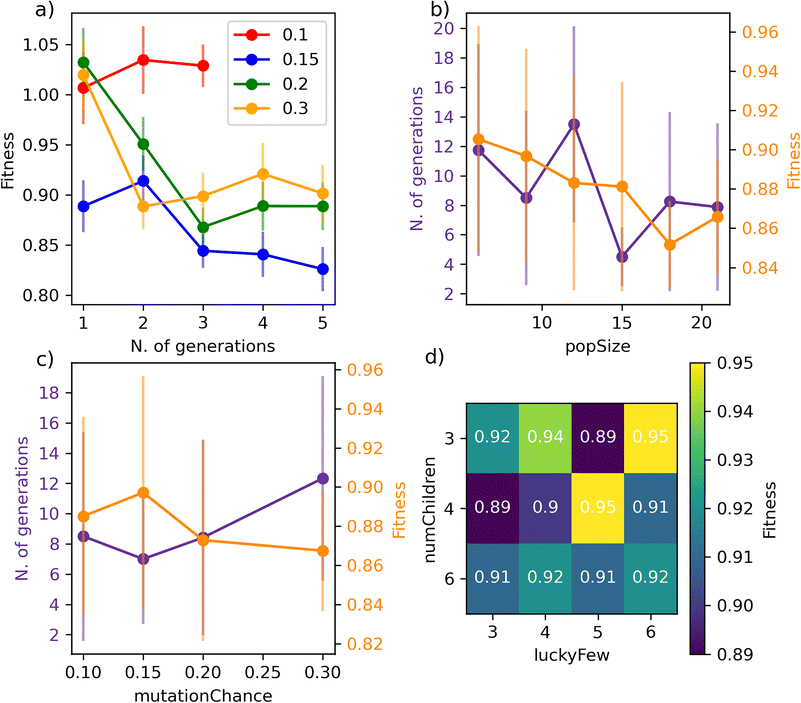
We begin with Fig. 4a), where we report the evolution of the score with the number of generations for a set of GA characterised by different mutationChance. It is clear that introducing a sufficient level of mutation is key for the GA to avoid getting stuck into a particular region of the search space (mutationChance = 0.1 in Fig. 4a)). Moving from a specific GA to the result reported in Fig. 4c), which has been averaged over 48 different GAs, we conclude that a mutationChance greater or equal to 0.20 introduces, for this specific dataset at least, a sufficient degree of flexibility into the GA. Broadly speaking, we envisage the occurrence of a compromise between accuracy and computational effort, as lower and higher values results in terms of mutationChance might result in inferior accuracy and substantially higher number of generations, respectively. However, it is important to note that – except for very low mutationChance – the extent of mutation has a relatively minor impact on the performance of SOAP_GAS in this case.
A similar compromise in terms of accuracy vs. computational effort can be observed when varying popSize, i.e. the size of the GA population. As illustrated in Fig. 4b), increasing popSize results in an improvement in terms of the score. As a larger population size allows the GA to explore the search space more effectively, the number of generations needed to converge SOAP_GAS tends to shrink as popSize increases. However, in terms of computational time we need to consider that the total number of machine learning models evaluated within the GA is equal to the number of generations multiplied by popSize. As such, increasing popSize appears to be a feasible strategy to improve the overall accuracy of the SOAP descriptors – bearing in mind the associated increase in computational effort.
Interestingly, we have found that the early stopping criteria (i.e. earlyStop and earlyNum) have a negligible impact on the performance of SOAP_GAS. This is encouraging, as it serves to highlight the robustness of the algorithm. On the other hand, the ratio between numChildren and luckyFew can have a significant impact as illustrated in the heat map reported in Fig. 4d). In principle, increasing the fraction of luckyFew relative to numChildren equates to increase the flexibility of the GA, by introducing an element of randomness that should be akin to the effect of the mutation process. However, we have found that this particular parameter behaves much more erratically than mutationChance, in that specific numChildren/luckyFew ratios seems to lead to fairly different accuracy. Further data relative to the impact of the GA parameters on the performance of SOAP_GAS can be found in the ESI.† Note that as many as 96 statistically independent GAs (i.e. started with different random combinations of SOAP parameters for each individual within the initial population) have been used to obtain the heat map in Fig. 4d). Thus, while the impact of this parameter is not drastic, different choices are certainly worth exploring.
In light of these findings, we can conclude that SOAP_GAS is rather robust with respect to the choice of the GA parameters.
C. SOAP_GAS timing & accuracy: comparison with grid search
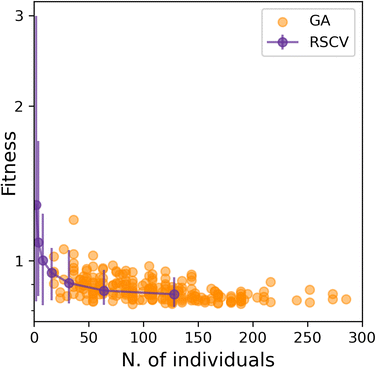
Having established that SOAP_GAS provides robust results, notwithstanding the specific choice of the GA parameters discussed in the previous section, we can now attempt to make a comparison between SOAP_GAS and potentially the most straightforward alternative to optimising SOAP parameters, namely a randomised grid search (RSCV). The latter simply involves a trial-and-error procedure whereby a certain number of SOAPs characterised by randomly chosen SOAP parameters are evaluated and scored.To offer a fair comparison, we have used the same search space for both RSCV and SOAP_GAS (see sec. IIIA). In terms of centres and neighbors, we have used C atoms exclusively, and we have not applied any compression. The results are summarised in Fig. 5, where we report the score for both RSCV and SOAP_GAS as a function of the number of individuals. In the case of SOAP_GAS, the number of individuals corresponds to the total number of SOAP descriptors evaluated across all the generations needed to converge the algorithm. As the time needed to obtain the score for a given SOAP vector (which is the computational intensive step for both approaches) is exactly the same for either RSCV or SOAP_GAS, we can compare directly the interplay between accuracy and computational effort for the two methodologies. We have accumulated 84 and 96 statistically independent instances of RSCV and SOAP_GAS respectively to obtain a robust statistics. Whilst the SOAP_GAS results are reported as a scatter plot (as different GAs require different number of individuals to converge), the nature of the RSCV results allows us to assign (min–max, in this particular case) error bars to the accuracy corresponding to specific numbers of individuals.
The results for both RSCV and SOAP_GAS show a substantial degree of variability, thus strengthening the concept that multiple combinations of potentially even quite dissimilar SOAP parameters can provide similar results in terms of the accuracy of the SOAP vector. The number of individuals required to achieve a significant improvement in terms of accuracy is similar for RSCV and SOAP_GAS, albeit we found that in some cases SOAP_GAS manages to outperform the RSCV results, given the same number of individuals. This suggests that, overall, SOAP_GAS provides a framework which is equally efficient to the RSCV approach, but with the potential to identify combinations of SOAP parameters which lead to greater accuracy.
D. Working with multiple SOAPs
We would expect the accuracy of multiple SOAPs optimised at the same time (Conc. in Table 4) to be higher than that of multiple SOAPs optimised individually and subsequently concatenated (Ind. in Table 4). This is indeed the case, as illustrated by the results summarised in Table 4. In particular, we have chosen to focus on 5 different combinations of the ten![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) -ten SOAP vectors (where
-ten SOAP vectors (where ![[scr X, script letter X]](https://www.rsc.org/images/entities/char_e14a.gif) stand for one of the most abundant atomic species in the dataset, see Table 1) analysed in Table 2. The gains in terms of accuracy are small, but suggest that the “best” parameters for each SOAP vector in a concatenated descriptor does depend to some extent on whether the SOAP vector was considered in isolation. To strengthen this claim, it appears that the accuracy gains increase when considering longer combinations of SOAP vectors – which in turn offer a larger parameter space to be optimised as a whole.
stand for one of the most abundant atomic species in the dataset, see Table 1) analysed in Table 2. The gains in terms of accuracy are small, but suggest that the “best” parameters for each SOAP vector in a concatenated descriptor does depend to some extent on whether the SOAP vector was considered in isolation. To strengthen this claim, it appears that the accuracy gains increase when considering longer combinations of SOAP vectors – which in turn offer a larger parameter space to be optimised as a whole.
| Performance | ||||||
|---|---|---|---|---|---|---|
| Ind. | Conc. | |||||
| Score | Time (s) | Gens. | Score | Time (s) | Gens. | |
| [C, H] | 0.297 | 6061 | 8 | 0.291 | 1302 | 5.3 |
| [C, H, O] | 0.287 | 7201 | 11 | 0.29 | 1305 | 5 |
| [C, H, O, Cl] | 0.289 | 7966 | 14 | 0.281 | 1452 | 5.2 |
| [C, H, O, Cl, N] | 0.282 | 9019 | 17 | 0.271 | 1454 | 5.4 |
| [Br, C, Cl, F, H, I, N, O, P, S] | 0.283 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 121 121 |
32 | 0.268 | 3655 | 4 |
| MSE | ||||
|---|---|---|---|---|
| Ind. | Conc. | |||
| Test | Train | Test | Train | |
| [C, H] | 1.144 ± 0.067 | 0.905 ± 0.014 | 1.14 ± 0.07 | 0.898 ± 0.013 |
| [C, H, O] | 1.138 ± 0.061 | 0.883 ± 0.011 | 1.141 ± 0.062 | 0.89 ± 0.011 |
| [C, H, O, Cl] | 1.139 ± 0.058 | 0.889 ± 0.01 | 1.165 ± 0.070 | 0.926 ± 0.013 |
| [C, H, O, Cl, N] | 1.125 ± 0.051 | 0.880 ± 0.011 | 1.105 ± 0.07 | 0.866 ± 0.011 |
| [Br, C, Cl, F, H, I, N, O, P, S] | 1.125 ± 0.051 | 0.88 ± 0.011 | 1.113 ± 0.067 | 0.872 ± 0.016 |
| PCC | ||||
|---|---|---|---|---|
| Ind. | Conc. | |||
| Test | Train | Test | Train | |
| [C, H] | 0.883 ± 0.002 | 0.91 ± 0.001 | 0.884 ± 0.002 | 0.911 ± 0.001 |
| [C, H, O] | 0.884 ± 0.002 | 0.913 ± 0.001 | 0.883 ± 0.001 | 0.912 ± 0.001 |
| [C, H, O, Cl] | 0.883 ± 0.001 | 0.912 ± 0.001 | 0.885 ± 0.002 | 0.913 ± 0.001 |
| [C, H, O, Cl, N] | 0.885 ± 0.002 | 0.913 ± 0.001 | 0.888 ± 0.003 | 0.915 ± 0.001 |
| [Br, C, Cl, F, H, I, N, O, P, S] | 0.885 ± 0.002 | 0.913 ± 0.001 | 0.887 ± 0.003 | 0.915 ± 0.002 |
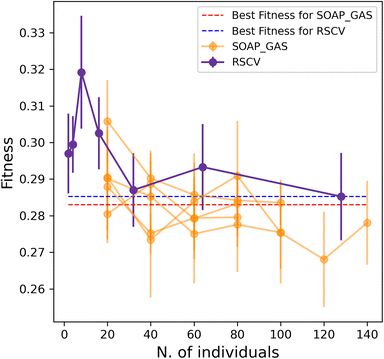
Importantly, the optimisation of multiple SOAP vectors at the same time is a situation where SOAP_GAS outperforms the RSCV approach, as illustrated in Fig. 6. Not only are the results of SOAP_GAS consistently more accurate than the RSCV ones, but it turns out that in this case the RSCV can barely manage to improve on the accuracy of the individual (concatenated) SOAP (obtained via RSCV), which corresponds to the blue, dashed line in Fig. 6. Conversely, SOAP_GAS pushes well below the red dashed line corresponding to the accuracy of the individual (concatenated) SOAP obtained via SOAP_GAS.
This finding is not entirely surprising, as when attempting to optimise multiple SOAPs at the same time via RSCV the number of grid points needed to converge increases massively. On the other hand, SOAP_GAS is inherently better equipped to explore the search space in a more clever fashion, steering the SOAP parameters toward different local minima without wasting time in probing regions of the search space that result in very low accuracy.
In addition, we have found that, when using SOAP_GAS, optimising multiple SOAP vectors at the same time is less computationally expensive than optimising each SOAP vector individually. This is illustrated in Table 4, where we compare the number of generations (“Gens.” column – or, equivalently, the time) needed for the SOAP_GAS to converge in these two distinct scenarios. Crucially, the more SOAP vectors we include, the larger the difference in terms of computational cost between individual and concurrent optimisations. For instance, a total of 32 generations are needed to converge the [Br, C, Cl, F, H, I, N, O, P, S] SOAP vectors individually, whilst only 4 generations are – on average – required to converge this combination of SOAP vectors concurrently. Note that the same number of individuals per generation has been used to craft this comparison. This is important as it demonstrates that the SOAP_GAS framework can be used to efficiently optimise combinations of different SOAP vectors at the same time, which, as we have seen, also typically leads to further (if rather small) gains in terms of the overall accuracy of the descriptor as well.
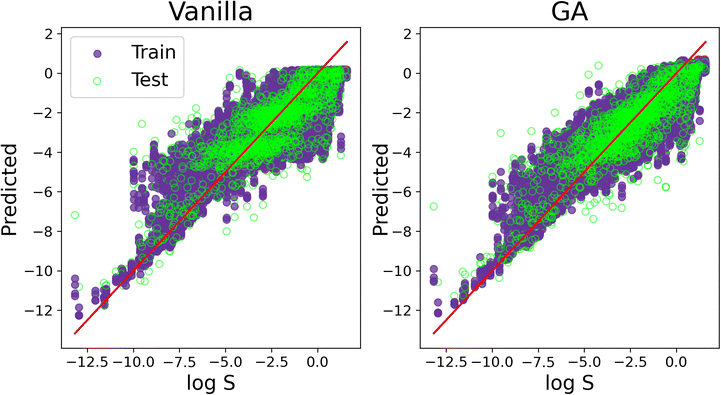
We conclude our discussion by offering a visual comparison of the improvement, in terms of accuracy, obtained by applying SOAP_GAS to this particular dataset. The result in Fig. 7 have been obtained with the C-ten SOAP, μ = 0, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) = 1, ν = 1 and
= 1, ν = 1 and ![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif) = 0 compression. The initial SOAP parameters were cutoff = 8, lmax = 6, nmax = 2 and atom_sigma = 0.5, which upon optimisation changed to cutoff = 12, lmax = 8, nmax = 5 and atom_sigma = 1.1. The MSE(PCC) for the test set improved from 1.515(0.839) to 1.209(0.875).
= 0 compression. The initial SOAP parameters were cutoff = 8, lmax = 6, nmax = 2 and atom_sigma = 0.5, which upon optimisation changed to cutoff = 12, lmax = 8, nmax = 5 and atom_sigma = 1.1. The MSE(PCC) for the test set improved from 1.515(0.839) to 1.209(0.875).
Solubility measurements found in literature are usually characterised by experimental uncertainties of the order of ±0.5–0.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S.62 On account of that, ML models for predicting solubility having MSEs (for the test set) in the range of 0.5–1.2 are generally considered to be good.51 Additionally, recent solubility models leveraging ML algorithms, including random forest regression, have produced PCCs (again, for the test set) in the range of 0.81–0.95.14,15,48,63 As shown in Table 4, the SOAP_GAS solubility model resulted in MSE and PCC values that lie in those ranges for both the training and test sets. Although our model MSE values may fall in the upper range of what is favourable, we highlight that most of the models cited used comparatively much smaller test sets (less than 100 molecules, compared with ∼2000 in our case) than the ones we have considered in this work.
S.62 On account of that, ML models for predicting solubility having MSEs (for the test set) in the range of 0.5–1.2 are generally considered to be good.51 Additionally, recent solubility models leveraging ML algorithms, including random forest regression, have produced PCCs (again, for the test set) in the range of 0.81–0.95.14,15,48,63 As shown in Table 4, the SOAP_GAS solubility model resulted in MSE and PCC values that lie in those ranges for both the training and test sets. Although our model MSE values may fall in the upper range of what is favourable, we highlight that most of the models cited used comparatively much smaller test sets (less than 100 molecules, compared with ∼2000 in our case) than the ones we have considered in this work.
IV. Conclusions
The SOAP vector has been gaining popularity in the context of machine learning for physical chemistry applications as a general-purpose descriptor to extract information from a variety of systems – ranging from small drug-like molecules to semiconducting alloys. Aside from the key consideration involving the choice of which atomic species to use in order to describe the relevant local atomic environments, four parameters need to be chosen when building any given SOAP vector.In this work, we demonstrate that this choice is not trivial, and cannot be guided entirely by physical intuition. To address this issue, we have developed SOAP_GAS, a computational framework based on genetic algorithms that offers a reliable alternative to e.g. the grid search approaches commonly used to identify well-performing combinations of SOAP parameters.
SOAP_GAS is freely available on GitHub at https://github.com/gcsosso/SOAP_GAS.git, and leverages the recent developments described in ref. 26 to enable the efficient description of heterogeneous datasets containing different molecules characterised by different number of atoms and different atomic species, as either isolated molecules or within condensed phases. It also uses the compression options described in ref. 46 to minimise the computational cost needed to deal with large datasets. SOAP_GAS offers full control over the flexibility of the underlying GA and can benefit from parallel computing as well.
We have chosen to explore the capabilities of SOAP_GAS by focusing on the prototypical machine learning-base challenge of predicting the solubility of a relatively small (∼6000) dataset small drug-like molecules. We reiterate that this work does not aim to further the state-of-the-art in terms of this specific application, but rather we seek to showcase the capabilities of the SOAP_GAS algorithm when deployed in the context of a fairly standard ML problem for drug design and discovery. We show that SOAP_GAS consistently improves the accuracy of a given non-optimised SOAP vector which parameters have been taken “off-the-shelf”. An analysis of the reproducibility of our results revealed that multiple combinations of very different SOAP parameters can yield equally accurate predictions, thus highlighting the need for a robust optimisation strategy as opposed to relying on physical intuition when it comes to the choice of the SOAP parameters. In addition, we found only very weak correlations between the SOAP parameters. This was unexpected in that one might intuitively think that expanding the spatial extent of the atomic environment under consideration would necessitate an increase in the number of angular, but even more so radial basis functions utilised to specify the SOAP vector of interest. However, this is not the case, and in fact simply utilising longer cutoffs does not result in improved accuracy.
The SOAP_GAS algorithm itself relies on the specification of a few parameters, aimed at tailoring the flexibility of the underlying GA. We have explored the impact of the different choices in terms of said parameters, and found SOAP_GAS to offer rather robust results notwithstanding the specific choice of GA parameters. Of these, the mutation chance is perhaps the most prominent one, in that it has to be sufficiently high for the GA to manage to escape local minima of the search space.
We have also compared the efficiency of SOAP_GAS to that of the customarily used randomised grid search (RSCV) approach, particularly in terms of the interplay between computational effort and resulting SOAP accuracy. Overall, RSCV and SOAP_GAS offer similar performance, with the latter yielding marginally better results. However, SOAP_GAS consistently outperforms the RSCV when dealing with the concurrent optimisation of multiple SOAP vectors at the same time – a scenario that does lead, in the case of SOAP_GAS, to further (if on average rather small) improvements in terms of accuracy. This result is not entirely unexpected, in that the number of grid points for the RSCV substantially increase when dealing with multiple SOAP vectors, whilst the SOAP_GAS algorithm is inherently designed to avoid non-relevant region of the search space to converge onto the well-performing combinations of SOAP parameters. Importantly, we found that optimising multiple combinations of SOAP vectors at the same time via the SOAP_GAS algorithm not only leads to further improvements in terms of accuracy, but it is also more computationally efficient than optimising each SOAP vector individually.
In the future, it would be interesting to expand the SOAP_GAS framework to include other descriptors requiring parameter optimisation. For the time being, we hope that this simple tool might facilitate the usage of the SOAP descriptor for machine learning applications in physical chemistry, and we are looking forward to exploring the capabilities of the algorithm when applied to more challenging datasets/problems in, e.g., the realm of drug design and discovery.
Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
A. P. B. is listed as an inventor on a patent filed by Cambridge Enterprise Ltd. related to SOAP and GAP (US patent 8843509, filed on 5 June 2009 and published on 23 September 2014).Acknowledgements
T. B. thanks EPSRC for a PhD studentship through the Mathematics for Real-World Systems Centre for Doctoral Training (MathSys, EPSRC grant number EP/S022244/1). S. T. thanks EPSRC for a PhD studentship through the Centre for Doctoral Training in Modeling of Heterogeneous Systems (HetSys, EPSRC Grant No. EP/S022848/1). A. P. B. is supported by the NOMAD Centre of Excellence (European Commission grant agreement ID 951786) and the CASTEP-USER project, funded by the Engineering and Physical Sciences Research Council under the grant agreement EP/W030438/1. We gratefully acknowledge the use of Athena at HPC Midlands+, which was funded by the EPSRC through Grant No. EP/P020232/1, through the HPC Midlands+ consortium, as well as the high-performance computing facilities provided by the Scientific Computing Research Technology Platform at the University of Warwick.Notes and references
- O. V. Prezhdo, Advancing Physical Chemistry with Machine Learning, J. Phys. Chem. Lett., 2020, 11, 9656–9658 CrossRef CAS PubMed.
- F. Noé, A. Tkatchenko, K.-R. Müller and C. Clementi, Machine Learning for Molecular Simulation, Annu. Rev. Phys. Chem., 2020, 71, 361–390, DOI:10.1146/annurev-physchem-042018-052331.
- M. Ceriotti, C. Clementi and O. Anatole von Lilienfeld, Machine learning meets chemical physics, J. Chem. Phys., 2021, 154, 160401 CrossRef CAS PubMed.
- J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Combining Machine Learning and Computational Chemistry for Predictive Insights Into Chemical Systems, Chem. Rev., 2021, 121, 9816–9872 CrossRef CAS.
- A. Karthikeyan and U. D. Priyakumar, Artificial intelligence: machine learning for chemical sciences, J. Chem. Sci., 2022, 134, 2 CrossRef CAS PubMed.
- M. R. Dobbelaere, P. P. Plehiers, R. Van de Vijver, C. V. Stevens and K. M. Van Geem, Machine Learning in Chemical Engineering: Strengths, Weaknesses, Opportunities, and Threats, Engineering, 2021, 7, 1201–1211 CrossRef CAS.
- G. C. Sosso, V. L. Deringer, S. R. Elliott and G. Csányi, Understanding the thermal properties of amorphous solids using machine-learning-based interatomic potentials, Mol. Simul., 2018, 44, 866–880, DOI:10.1080/08927022.2018.1447107.
- X. Gu and C. Zhao, Thermal conductivity of single-layer mos2 (1-x) se2x alloys from molecular dynamics simulations with a machine-learning based interatomic potential, Comput. Mater. Sci., 2019, 165, 74–81 CrossRef CAS.
- D. Visaria and A. Jain, Machine-learning-assisted space-transformation accelerates discovery of high thermal conductivity alloys, Appl. Phys. Lett., 2020, 117, 202107 CrossRef CAS.
- J. Xiong, S.-Q. Shi and T.-Y. Zhang, A machine-learning approach to predicting and understanding the properties of amorphous metallic alloys, Mater. Des., 2020, 187, 108378 CrossRef CAS.
- H. Miyazaki, T. Tamura, M. Mikami, K. Watanabe, N. Ide, O. M. Ozkendir and Y. Nishino, Machine learning based prediction of lattice thermal conductivity for half-Heusler compounds using atomic information, Sci. Rep., 2021, 11, 13410 CrossRef CAS.
- T. S. Schroeter, A. Schwaighofer, S. Mika, A. Ter Laak, D. Suelzle, U. Ganzer, N. Heinrich and K.-R. Müller, Estimating the domain of applicability for machine learning qsar models: a study on aqueous solubility of drug discovery molecules, J. Comput.-Aided Mol. Des., 2007, 21, 485–498 CrossRef CAS.
- Q. Cui, S. Lu, B. Ni, X. Zeng, Y. Tan, Y. D. Chen and H. Zhao, Improved Prediction of Aqueous Solubility of Novel Compounds by Going Deeper With Deep Learning, Front. Oncol., 2020, 10, 121 CrossRef.
- S. Boobier, D. R. Hose, A. J. Blacker and B. N. Nguyen, Machine learning with physicochemical relationships: solubility prediction in organic solvents and water, Nat. Commun., 2020, 11, 1–10 CrossRef.
- M. Lovrić, K. Pavlović, P. Žuvela, A. Spataru, B. Lučić, R. Kern and M. W. Wong, Machine learning in prediction of intrinsic aqueous solubility of drug-like compounds: Generalization, complexity, or predictive ability?, J. Chemom., 2021, 35, e3349 CrossRef.
- K. Ge and Y. Ji, Novel Computational Approach by Combining Machine Learning with Molecular Thermodynamics for Predicting Drug Solubility in Solvents, Ind. Eng. Chem. Res., 2021, 60, 9259–9268 CrossRef CAS.
- Z. Ye and D. Ouyang, Prediction of small-molecule compound solubility in organic solvents by machine learning algorithms, J. Cheminf., 2021, 13, 98 CAS.
- Y. Ma, Z. Gao, P. Shi, M. Chen, S. Wu, C. Yang, J. Wang, J. Cheng and J. Gong, Machine learning-based solubility prediction and methodology evaluation of active pharmaceutical ingredients in industrial crystallization, Front. Chem. Sci. Eng., 2022, 16, 523–535 CrossRef CAS.
- H. Chen, O. Engkvist, Y. Wang, M. Olivecrona and T. Blaschke, The rise of deep learning in drug discovery, Drug Discovery Today, 2018, 23, 1241–1250 CrossRef PubMed.
- L. Deng, The mnist database of handwritten digit images for machine learning research, IEEE Signal Processing Magazine, 2012, vol. 29, pp. 141–142 Search PubMed.
- D. Dua and C. Graff, UCI machine learning repository, 2017.
- T. Barnard, H. Hagan, S. Tseng and G. C. Sosso, Less may be more: an informed reflection on molecular descriptors for drug design and discovery, Mol. Syst. Des. Eng., 2020, 5, 317–329 RSC.
- C. R. Collins, G. J. Gordon, O. A. von Lilienfeld and D. J. Yaron, Constant size molecular descriptors for use with machine learning, arXiv, 2017, preprint, arXiv:1701.06649, DOI:10.48550/arXiv.1701.06649.
- E. M. Collins and K. Raghavachari, Effective molecular descriptors for chemical accuracy at dft cost: Fragmentation, error-cancellation, and machine learning, J. Chem. Theory Comput., 2020, 16, 4938–4950 CrossRef CAS PubMed.
- M. J. Martínez, M. Razuc and I. Ponzoni, Modesus: A machine learning tool for selection of molecular descriptors in qsar studies applied to molecular informatics, BioMed Res. Int., 2019, 2019, 2905203 Search PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, On representing chemical environments, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- S. N. Pozdnyakov, M. J. Willatt, A. P. Bartok, C. Ortner, G. Csanyi and M. Ceriotti, Incompleteness of Atomic Structure Representations, Phys. Rev. Lett., 2020, 125, 166001 CrossRef CAS.
- M. O. Jäger, E. V. Morooka, F. Federici Canova, L. Himanen and A. S. Foster, Machine learning hydrogen adsorption on nanoclusters through structural descriptors, npj Comput. Mater., 2018, 4, 1–8 CrossRef.
- J. L. Priedeman, C. W. Rosenbrock, O. K. Johnson and E. R. Homer, Quantifying and connecting atomic and crystallographic grain boundary structure using local environment representation and dimensionality reduction techniques, Acta Mater., 2018, 161, 431–443 CrossRef CAS.
- M. A. Caro, Optimizing many-body atomic descriptors for enhanced computational performance of machine learning based interatomic potentials, Phys. Rev. B, 2019, 100, 024112 CrossRef CAS.
- S. De, A. P. Bartók, G. Csányi and M. Ceriotti, Comparing molecules and solids across structural and alchemical space, Phys. Chem. Chem. Phys., 2016, 18, 13754 RSC.
- R. Todeschini and P. Gramatica, New 3d molecular descriptors: the whim theory and qsar applications, in 3D QSAR in drug design, Springer, 2002, pp. 355–380 Search PubMed.
- V. Zaverkin and J. Kästner, Gaussian moments as physically inspired molecular descriptors for accurate and scalable machine learning potentials, J. Chem. Theory Comput., 2020, 16, 5410–5421 CrossRef CAS PubMed.
- M. Gastegger, L. Schwiedrzik, M. Bittermann, F. Berzsenyi and P. Marquetand, wacsf—weighted atom-centered symmetry functions as descriptors in machine learning potentials, J. Chem. Phys., 2018, 148, 241709 CrossRef CAS PubMed.
- M. O. J. Jäger, E. V. Morooka, F. F. Canova, L. Himanen and A. S. Foster, Machine learning hydrogen adsorption on nanoclusters through structural descriptors, npj Comput. Mater., 2018, 1–8 Search PubMed.
- A. Goscinski, F. Musil, S. Pozdnyakov, J. Nigam and M. Ceriotti, Optimal radial basis for density-based atomic representations, J. Chem. Phys., 2021, 1–12 Search PubMed.
- V. Fung, J. Zhang, E. Juarez and B. G. Sumpter, Benchmarking graph neural networks for materials chemistry, npj Comput. Mater., 2021, 7, 1–8 CrossRef.
- A. S. Rosen, S. M. Iyer, D. Ray, Z. Yao, A. Aspuru-Guzik, L. Gagliardi, J. M. Notestein and R. Q. Snurr, Machine learning the quantum-chemical properties of metal–organic frameworks for accelerated materials discovery, Matter, 2021, 4, 1578–1597 CrossRef CAS.
- Y. Zuo, C. Chen, X. Li, Z. Deng, Y. Chen, J. Behler, G. Csányi, A. V. Shapeev, A. P. Thompson and M. A. Wood, et al., Performance and cost assessment of machine learning interatomic potentials, J. Phys. Chem. A, 2020, 124, 731–745 CrossRef CAS PubMed.
- M. F. Langer, A. Goeßmann and M. Rupp, Representations of molecules and materials for interpolation of quantum-mechanical simulations via machine learning, npj Comput. Mater., 2022, 8, 1–14 CrossRef.
- F. Musil, A. Grisafi, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Physics-inspired structural representations for molecules and materials, Chem. Rev., 2021, 121, 9759–9815 CrossRef CAS PubMed.
- S. K. Natarajan and M. A. Caro, Particle swarm based hyper-parameter optimization for machine learned interatomic potentials, arXiv, 2020, preprint, arXiv:2101.00049, DOI:10.48550/arXiv.2101.00049.
- K. De Jong, Genetic-algorithm-based learning, in Machine learning, Elsevier, 1990, pp. 611–638 Search PubMed.
- J. J. Grefenstette, Genetic algorithms and machine learning, in Proceedings of the sixth annual conference on Computational learning theory, 1993, pp. 3–4 Search PubMed.
- J. Mavračič, F. C. Mocanu, V. L. Deringer, G. Csányi and S. R. Elliott, Similarity between amorphous and crystalline phases: The case of tio2, J. Phys. Chem. Lett., 2018, 9, 2985–2990 CrossRef PubMed.
- J. P. Darby, J. R. Kermode and G. Csányi, Compressing local atomic neighbourhood descriptors, npj Comput. Mater., 2022, 8, 166 CrossRef.
- M. C. Sorkun, J. V. A. Koelman and S. Er, Pushing the limits of solubility prediction via quality-oriented data selection, iScience, 2021, 24, 101961 CrossRef CAS.
- S. Boobier, A. Osbourn and J. B. Mitchell, Can human experts predict solubility better than computers?, J. Cheminf., 2017, 9, 1–14 Search PubMed.
- C. Saal and A. Nair, Solubility in pharmaceutical chemistry, Walter de Gruyter GmbH & Co KG, 2020 Search PubMed.
- A. Llinàs, R. C. Glen and J. M. Goodman, Solubility Challenge: Can You Predict Solubilities of 32 Molecules Using a Database of 100 Reliable Measurements?, J. Chem. Inf. Model., 2008, 48, 1289–1303 CrossRef PubMed.
- A. Llinas, I. Oprisiu and A. Avdeef, Findings of the second challenge to predict aqueous solubility, J. Chem. Inf. Model., 2020, 60, 4791–4803 CrossRef CAS.
- N. M. O'Boyle, C. Morley and G. R. Hutchison, Pybel: a python wrapper for the openbabel cheminformatics toolkit, Chem. Cent. J., 2008, 2, 1–7 CrossRef.
- K. Chen, C. Kunkel, K. Reuter and J. T. Margraf, Reorganization energies of flexible organic molecules as a challenging target for machine learning enhanced virtual screening, Digital Discovery, 2022, 1, 147–157 RSC.
- S. Axelrod and R. Gomez-Bombarelli, Molecular machine learning with conformer ensembles, arXiv, 2021, preprint, arXiv:2012.08452 [physics], DOI:10.48550/arXiv.2012.08452.
- L. Breiman, Random forests, Mach. Learn., 2001, 45, 5–32 CrossRef.
- M. Olson, A. Wyner and R. Berk, Modern neural networks generalize on small data sets, Adv. Neural Inf. Process. Syst., 2018, 31, 1–10 Search PubMed.
- T. Shaikhina, D. Lowe, S. Daga, D. Briggs, R. Higgins and N. Khovanova, Decision tree and random forest models for outcome prediction in antibody incompatible kidney transplantation, Biomed. Signal Process Control, 2019, 52, 456–462 CrossRef.
- A. P. Bartók, N. Bernstein, G. Csányi and J. Kermode, GAP and SOAP documentation, https://libatoms.github.io/GAP/, accessed November 2022 Search PubMed.
- H. Doll and S. Carney, Statistical approaches to uncertainty: p values and confidence intervals unpacked, Equine Vet. J., 2007, 39, 275–276 CrossRef CAS.
- L. C. Blum and J.-L. Reymond, 970 Million Druglike Small Molecules for Virtual Screening in the Chemical Universe Database GDB-13, J. Am. Chem. Soc., 2009, 131, 8732–8733 CrossRef CAS PubMed.
- G. Montavon, M. Rupp, V. Gobre, A. Vazquez-Mayagoitia, K. Hansen, A. Tkatchenko, K.-R. Müller and O. A. V. Lilienfeld, Machine learning of molecular electronic properties in chemical compound space, New J. Phys., 2013, 15, 095003 CrossRef CAS.
- D. S. Palmer and J. B. Mitchell, Is experimental data quality the limiting factor in predicting the aqueous solubility of druglike molecules?, Mol. Pharmaceutics, 2014, 11, 2962–2972 CrossRef CAS.
- A. Avdeef, Prediction of aqueous intrinsic solubility of druglike molecules using random forest regression trained with wiki-ps0 database, ADMET and DMPK, 2020, 8, 29–77 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2me00149g |
| This journal is © The Royal Society of Chemistry 2023 |