 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Applications of magnetic and electromagnetic forces in micro-analytical systems
M.
Suwa
 *a,
S.
Tsukahara
*a,
S.
Tsukahara
 a and
H.
Watarai
a and
H.
Watarai
 *b
*b
aDepartment of Chemistry, Graduate School of Science, Osaka University, Toyonaka, Osaka 560-0043, Japan. E-mail: msuwa@chem.sci.osaka-u.ac.jp
bR3 Institute for Newly-Emerging Science Design, Osaka University, Toyonaka, Osaka 560-8531, Japan. E-mail: watarai@chem.sci.osaka-u.ac.jp
First published on 13th January 2023
Abstract
Novel applications of magnetic fields in analytical chemistry have become a remarkable trend in the last two decades. Various magnetic forces have been employed for the migration, orientation, manipulation, and trapping of microparticles, and new analytical platforms for separating and detecting molecules have been proposed. Magnetic materials such as functional magnetic nanoparticles, magnetic nanocomposites, and specially designed magnetic solids and liquids have also been developed for analytical purposes. Numerous attractive applications of magnetic and electromagnetic forces on magnetic and non-magnetic materials have been studied, but fundamental studies to understand the working principles of magnetic forces have been challenging. These studies will form a new field of magneto-analytical science, which should be developed as an interdisciplinary field. In this review, essential pioneering works and recent attractive developments are presented.
1. Introduction
The book “Unified Separation Science”, written by J. C. Giddings in 1991 not only introduced his original method of field-flow-fractionation but also greatly helped to understand the fundamental science behind various types of traditional separation methods by showing the concept of general driving forces in separation mechanisms of molecules and particles.1 His basic idea is that the fundamental meaning of separation is physical displacement through space, which includes flow displacement that is powerful and nonselective and relative displacement that is relatively weak but selective for analytes.2 Relative displacement needs a driving force, F, which is derived from the total chemical potential, μ*, composed of physical interaction with an external field, μext, and chemical interaction between a solute and solvent molecules, μ = μ° + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c, where μ° is the standard chemical potential in the standard state and c is the concentration of the solute,
c, where μ° is the standard chemical potential in the standard state and c is the concentration of the solute,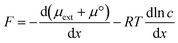 | (1) |
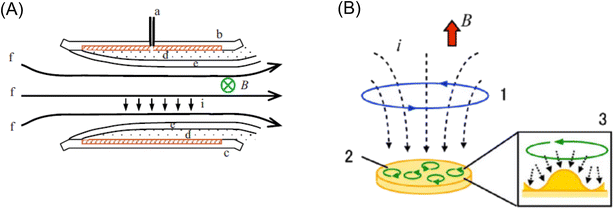
According to magnetism, materials can be roughly classified into diamagnetic and paramagnetic materials, which are characterized by different magnetization profiles and magnetic susceptibilities.6 Almost all organic and biological materials are diamagnetic and have negative magnetic susceptibilities, while some transition metals and lanthanides and their compounds are paramagnetic, having positive magnetic susceptibilities. The major forces exerted on a substance by the application of a magnetic field are shown in Fig. 1. The first one is Kelvin force (Fig. 1A), FK, which is also known as the magnetic field-gradient force, given by the following equation, when it works on a spherical particle with volume, V:
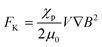 | (2) |
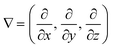 is a vector differential operator, B is the magnetic flux density (T) and ∇B2 = 2(B·∇)B. This force is used as the driving force of magnetophoresis. The second one is the torque (Fig. 1B), T, or magnetic orientation force, which is represented by,
is a vector differential operator, B is the magnetic flux density (T) and ∇B2 = 2(B·∇)B. This force is used as the driving force of magnetophoresis. The second one is the torque (Fig. 1B), T, or magnetic orientation force, which is represented by,| T = m × B | (3) |
| FL = qv × B | (4) |
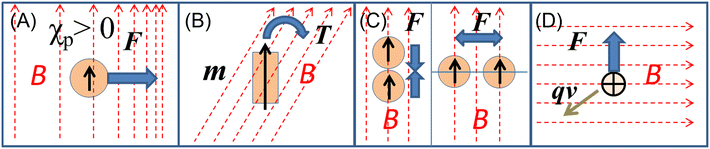 | ||
| Fig. 1 Illustration of (A) Kelvin force, (B) magnetic torque, (C) typical magnetic dipole–dipole interactions and (D) Lorentz force. | ||
2. Application of magnetic field-gradient force
2.1 Magnetophoresis
Magnetophoresis is the phenomenon in which a particle migrates with translational motion under a magnetic field gradient. Understanding the magnetophoretic behavior of individual particles is crucial for microfluidic magnetic separation, magnetic manipulation, magnetic drug targeting, etc. Here, we briefly introduce the fundamental principle of magnetophoresis.Under a magnetic field gradient, ∇H, a magnetic force, Fmag, works on a particle,23 as follows:
| Fmag = μmm·∇H, | (5) |
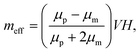 | (6) |
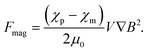 | (7) |
| Fdrag = 6πηrvmag, | (8) |
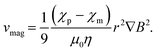 | (9) |
The development of image processing techniques and strong magnets made it easy to directly measure the magnetophoretic velocity of microparticles. In the late 1990s and 2000s, fundamental and feasibility studies on magnetophoresis have been actively conducted. The research group of Zborowski and Chalmers played an important role in the development of magnetophoretic velocity analysis. Chalmers et al.26,27 applied a computer algorithm, “cell tracking velocimetry (CTV)”, to measure the magnetophoretic velocity of microparticles.28–31 To estimate the magnetic susceptibility from the magnetophoretic velocity, the size of the migrating particle should be measured. However, the precise size measurement is difficult because of the displacement of the particles from the focal plane of the microscope or the variation in the intensity of the illumination light. Thus, to solve this problem, Jin et al.32 simultaneously measured the magnetophoretic velocity, vmag, and sedimentation velocity, vsed, with CTV. As shown in Fig. 2A, the magnetic force is perpendicular to the gravity in their setup, and thus vmag and vsed can be independently measured. Dividing vmag by vsed yields
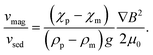 | (10) |
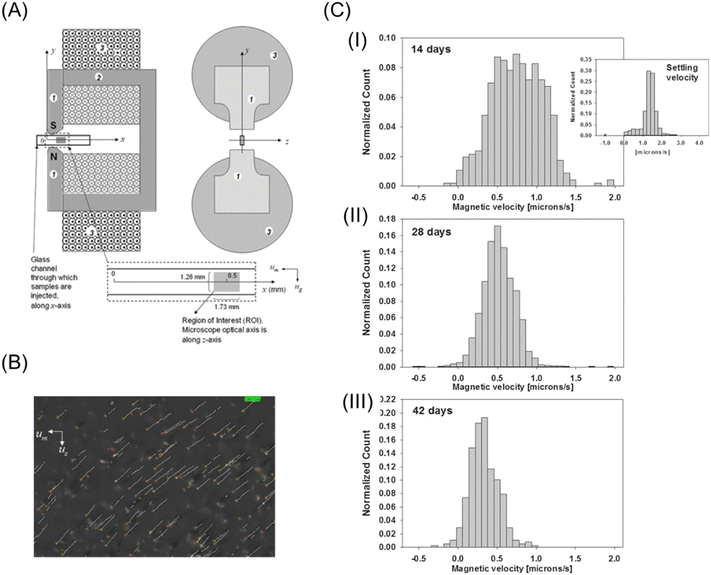 | ||
| Fig. 2 (A) Schematic drawing of magnets and migration channel for the CTV system. 1 and 2 pole pieces and flux return yolk and 3 coil of the electromagnets. Reproduced from ref. 32 with permission from the Royal Society of Chemistry. (B) Screen output of CTV software of metHb RBC. Reproduced with permission from ref. 41 from the Royal Society of Chemistry. (C) Histograms of the magnetophoretic velocity of deoxygenated RBCs for the same specific donor after 14 (I), 28 (II), and 42 (III) days of storage. For comparison, the right panel of (I) shows a histogram of the settling velocity of RBCs at 14 days reprinted with permission from ref. 42. Copyright © 2017, the American Chemical Society. | ||
Watarai's group also contributed to the development of analytical techniques utilizing magnetophoresis. They investigated the magnetophoretic velocities of diamagnetic polystyrene microparticles in paramagnetic manganese(II) aqueous solution, i.e., χp < χm.43 As predicted by eqn (9), the reverse of the migration direction was experimentally observed for the first time. In this study, a capillary cell was set between a pair of Nd–Fe–B magnets. From the magnetophoretic velocity of a polystyrene microparticle, the complex profile of ∇B2 at the edge of the magnet could be determined. Suwa and Watarai constructed an apparatus for the sensitive measurement of the magnetophoretic velocity utilizing a superconducting magnet (10 T). By placing a silica capillary cell between a pair of iron pole pieces in the bore of the superconducting magnet, a very large gradient field (maximum of ∇B2 ∼ 9 × 104 T2 m−1) could be generated.44 They measured the magnetophoretic velocities of individual emulsion droplets and determined the extraction ratio of an Mn(II)–TTA complex44 and the interfacial concentration of Dy(III) alkylcarboxylate.45,46 The detection limit of Mn(II) attained the attomole level. Further, Suwa and Watarai succeeded in measuring the rapid photo-induced spin transition of a single crystal of cobalt–iron polycyanide47,48 from the change in the magnetophoretic velocity just after the irradiation of a pulse laser light of 532 nm.49,50 Egami and Watarai51 showed the usefulness of a magnetic circuit, which was an assembly of permanent magnets and could generate a strong magnetic field (max. 2.8 T) and a gradient (max. ∇B2 = 7.8 × 103 T2 m−1). They could measure the interfacial magnetic susceptibility and interfacial concentration of Prussian blue on a single toluene droplet. The magnetophoresis of a single microbubble in an organic liquid was measured together with laser-thermophoresis.52 The bubble behaved like a paramagnetic particle in a diamagnetic organic liquid, and the magnetophoretic velocity of the bubble was used to estimate the magnetic susceptibility of the organic liquid. Their works indicated that the magnetophoretic velocity analysis is a potential tool for the basic study of microscale chemistry and materials science.
Recently, Watarai and Chen53 showed the feasibility of the mole-ratio method utilizing magnetophoretic velocimetry. The mole-ratio method has been widely used to determine the composition of metal complexes, commonly utilizing spectroscopic measurement. The diamagnetic C-18 silica particles adsorbed with a hydrophobic phosphate ligand (L) were dispersed in an aqueous solution of a paramagnetic metal ion (M), whose concentration was not very high to affect χm. The metal complex (MLq) was formed on the hydrophobic pore surface of the silica particle, and thus χp increased. Fig. 3B shows the plots of the normalized velocity of vmag, which was obtained as the ratio of the magnetophoretic velocity to the maximum velocity at the fixed magnetic field gradient position, against the mole-ratio of the metal to ligand. Similar to the traditional mole-ratio method, the plots were approximated by two straight lines, and the intersection of these lines corresponded to 1/q. The device of this method is simple and inexpensive, as shown in Fig. 3A. This method was also applied to micro-solvent extraction systems.54 The magnetic mole-ratio method can detect picomoles of paramagnetic ions and is especially advantageous for systems with no characteristic absorption bands.
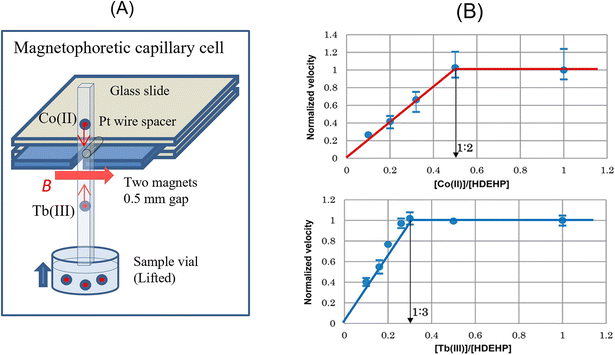 | ||
| Fig. 3 (A) Schematic drawing of the cell to measure the magnetophoretic velocity of a C18-silica particle adsorbed by a metal complex with bis(2-ethylhexyl)hydrogen phosphate (HDEHP). (B) Magnetophoretic mole-ratio plots determining Co(DEHP)2 and Tb(DEHP)3. Reprinted with permission from ref. 53. Copyright © 2017, the American Chemical Society. | ||
The measurement of the magnetophoretic velocity of sub-micrometer-sized fluorescent polystyrene spheres was demonstrated in 0.5 M MnCl2 aqueous solution.55 Given that it was hard to directly measure their diameter (0.5–5 μm) with an optical microscope, the size of the particles was estimated from the Brownian motion perpendicular to the field gradient. Watarai et al. also proposed an alternative way to avoid the problem of the size measurement in magnetophoretic velocity analysis, which is regarded as zero-velocity magnetophoresis.56 The magnetophoretic velocity of a particle in a liquid medium must be zero at χp = χm when the influence of gravity force is removed. In this feasibility study, the χm of the aqueous medium was varied by adding DyCl3, or the χm of the nonaqueous medium was changed by using different organic solvents. The magnetophoretic velocity normalized by ∇B2 against χm had a linear relationship, and the extrapolation of χm to vmag = 0 yielded χp. This method not only can be applied to smaller particles but also to non-spherical particles or the measurement of the magnetic susceptibility of the medium.
It is of great interest how small MNPs are moved by a magnetic force. Lim et al.57 studied the magnetophoretic behavior of individual iron oxide MNPs (38 nm magnetic core and a 67 nm thick polymer/Au nanoparticle plasmonic shell) using a dark-field optical microscope. The magnetic field gradient of 100–1000 T m−1 was produced by an electromagnet and a thin (5 μm) pole piece of mu-metal as a magnetic tweezer. They observed the magnetophoretic displacement of an iron oxide MNP located at a distance of less than 10 μm under a magnetic field gradient, which was sufficient to dominate the Brownian motion. Zhang et al.58 also measured the magnetophoretic velocities of single MNPs in a microchip with a permanent magnet, which were found to be 2.73 μm s−1 for 160 nm diameter MNPs and 23.6 μm s−1 for diameter 500 nm MNP. Their studies suggested that this type of larger single MNP can be moved by an Nd–Fe–B magnet, and the migration velocity of MNPs can be utilized for viscoelastic force measurements in living cells.
MNPs were used for solid-phase extraction because they are easily collected with a permanent magnet from a sample solution. However, in this type of system, MNPs tend to form complex aggregates and agglomerates. Therefore, the separation behavior cannot be explained by the magnetophoresis of simple individual MNPs. According to the fundamental studies by Lim et al.,59 to account for the separation with weak magnetic field gradients, two physical effects should be considered, i.e., cooperative magnetophoresis and magnetophoresis-induced convection. The former means the magnetophoresis of strongly interactive particles or chain-like aggregates formed by dipole–dipole interaction induced by a magnetic field.60 The aggregation of MNPs dramatically enhances the magnetophoretic velocity.61 Alternatively, the latter indicates a fluid dynamic instability due to an inhomogeneous magnetic field.62 As depicted in Fig. 4A and B, the magnetic force near the magnet is stronger than far from it. Therefore, the inhomogeneous motion of MNPs causes convection in a cuvette by momentum transfer between MNPs and the surrounding fluid, as shown in Fig. 4C. This convective motion boosts the magnetophoretic capture of MNPs. Their study provides insights into the design of MNPs and magnetic separation systems.
 | ||
| Fig. 4 (A) Time-lapse images of the capture of MNPs (ca. 30 nm) in diluted suspension with a permanent magnet. (B) Illustration of the convection induced in a MNP suspension by an inhomogeneous magnetic field. (C) Time-lapse images of macroscopic convection visualized using a dye (methylene blue). Reproduced from ref. 62 with permission from The Royal Society of Chemistry. | ||
2.2 Magnetic manipulation of micro/nano particles
Instead of gravity, Namba and Watarai combined the vertical flow of the medium with magnetic buoyancy to trap a particle depending on the size and magnetic susceptibility.65 They demonstrated the magnetic trapping of human blood cells suspended in 0.1 M MnCl2 aqueous solution under a gradient of 1800 T2 m−1 generated by permanent magnets in a square capillary tube (100 μm × 100 μm in the inner section). The blood cells could be trapped at the edge of the pole pieces, and complete trapping could be performed when the flow rate was less than 1 μL h−1 (∼30 μm s−1).
Whitesides and colleagues have developed an analytical separation technique that utilizes the levitation principle (called “MagLev”).66 They made a minimal point of B2 between a pair of permanent magnets with a like-pole-facing configuration (N–N or S–S). After putting a powder sample in a paramagnetic liquid (for example, MnCl2 or Gd(III) complex aqueous solution) between the magnets, the sample started moving to the equilibrium position, which depended on its density and magnetic susceptibility. They especially focused on the difference in density as a characteristic parameter for separation rather than magnetic susceptibility. This method has comprehensive applicability with various diamagnetic samples, such as polymers,67 foods,68 crystal polymorphs,69 and illicit drugs.70
Using magnetophoretic buoyancy, Rodríguez-Villarreal et al.71 demonstrated the continuous focusing of diamagnetic particles in a capillary flow system. The capillary cell was placed at the gap (300 μm) between two Nd–Fe–B permanent magnets with a like-pole-facing configuration. The suspension of diamagnetic particles in a paramagnetic aqueous solution flowed in the capillary. The diamagnetic particles were repelled from both magnets and continuously focused on the center of the capillary. They examined different types of particles (polystyrene microspheres and HaCaT cells) and paramagnetic solutions (MnCl2, GdCl3, and gadolinium(III)-diethylenetriaminepentaacetic acid (DTPA)).
Graphite is strongly diamagnetic and has magnetic anisotropy. For highly oriented pyrolytic graphite (HOPG), the magnetic susceptibility along its out-of-plane direction (perpendicular to the graphene plane) is −5.82 × 10−4, whereas that along the in-plane direction is −8.2 × 10−5. Given that the magnetic susceptibility of water is −9.0 × 10−6, the magnetophoretic buoyancy could be subjected to HOPG in water. Nguyen et al.72 investigated the magnetophoretic behavior of a HOPG flask with full sizes of 4.6 μm × 3.4 μm × 1.2 μm on average. A pair of permanent magnets produced the magnetic field (>1 T) and the field gradient of ∇B2 = 2300 T2 m−1, which was strong enough to align the HOPG flask with the graphene planes parallel to the magnetic field. They successfully measured the magnetophoretic velocity of lipid-coated graphite in NaCl aqueous solution, suggesting a way for previously undiscovered biomedical applications.
Dunne et al.73 reported an interesting attempt to make a microfluidic channel in a magnetic fluid by utilizing magnetic buoyancy. They fabricated a quadrupolar magnet consisting of four bar magnets, as shown in Fig. 5. A null magnetic field at the center of the quadrupolar magnet was created. Diamagnetic water in ferrofluid was confined at the null magnetic line, and then a “water antitube” was formed. This liquid-in-liquid channel showed remarkable advantages including self-healing, non-clogging, near-frictionless, and adjustable thickness. A blanched antitube can be created by shaping two stacked magnets with waterjet-cutting. For example, the Y-junction of the antitube was successfully formed in ferrofluid. Furthermore, flow control, such as pumping and valving, in the antitube could be done by manipulating the field.
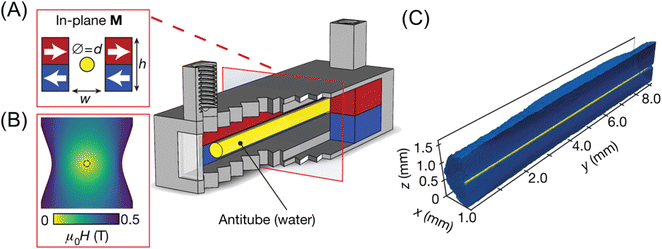 | ||
| Fig. 5 (A) Permanent magnets (red, blue) in an in-plane quadrupolar configuration. The yellow area shows a low-field zone created at the centre, where an antitube of water is stabilized inside an immiscible magnetic liquid. (B) Contour plot of the magnetic field. (C) Synchrotron X-ray tomographic reconstruction of a water antitube (yellow) with a diameter of 81 μm, surrounded by ferrofluid (blue). Reproduced from ref. 73 with permission. Copyright © 2020, Springer Nature. | ||
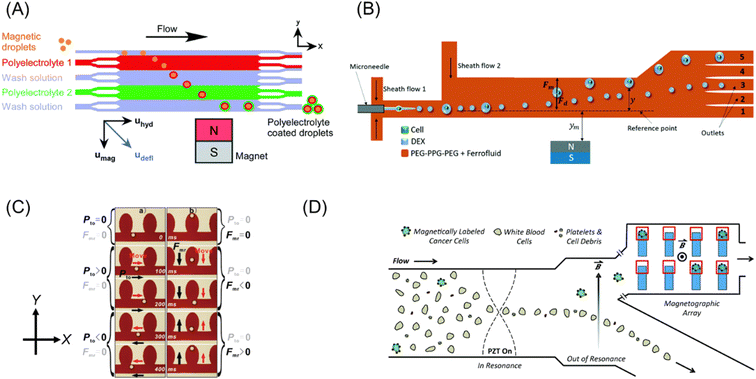 | ||
| Fig. 6 (A) Concept of continuous flow particle coating and washing via the deflection of magnetic templates through multi-laminar flow streams of polyelectrolyte and washing solutions. Reproduced from ref. 81 with permission from the Royal Society of Chemistry. (B) Schematic illustration of the selective separation of cell-containing droplets utilizing ATPS. Reproduced from ref. 82 with permission from The Royal Society of Chemistry. (C) Microscopic images of droplet motion in microstructures. Black and red arrows indicate the direction of the applied forces and droplet motion. Reprinted with permission from ref. 83. Copyright © 2011, the American Chemical Society. (D) Illustration of microfluidic system for the separation of rare cells, which uses acoustic and magnetic fields. Reproduced from ref. 84 with permission from The Royal Society of Chemistry. | ||
Navi et al.82 fabricated a continuous cell separation platform using an aqueous two-phase system (ATPS), which consisted of a dextran (DEX)-rich lower phase and polyethylene glycol–polypropylene glycol–polyethylene glycol (PEG–PPG–PEG) triblock copolymer-rich upper phase. As shown in Fig. 6B, the microchip was filled with ferrofluid in the PEG–PPG–PEG phase, whereas the cell suspension in the DEX phase was injected through a microneedle. Due to the cell-triggered Rayleigh–Plateau instability, the cell-encapsulated droplets were larger than the empty droplets. Then, the difference in magnetic buoyancy on these droplets resulted in distinguishable deflection in the microchip. This technique does not require a cumbersome procedure of magnetic labeling.
Zhang et al.83 demonstrated comprehensive two-dimensional manipulation of diamagnetic microdroplets in ferrofluid by hydrostatic pressure and magnetophoretic buoyancy. Fig. 6C summarizes the concept of manipulation. A diamagnetic oil droplet is individually generated at a T-junction by controlling the hydrostatic pressure of the ferrofluid and the oil. The droplet is transported to the microwell array region by the ferrofluid flow. The motion of a droplet can be controlled in the ±X-direction and ±Y-direction by hydrostatic pressure and magnetophoretic buoyancy, respectively (Fig. 6C). They demonstrated the trapping of a droplet in a preferred microwell, exchange of the droplet positions, and contact and fusion of the droplets. This manipulation strategy can perform four essential steps in chemical experiments including sampling, dilution, reaction, and detection.
Complex microfluidic devices that combine a magnetic field with other external fields were fabricated to achieve precise cell sorting. A rare cell (such as circulating tumor cells, CTCs) sorting method, which combined acoustic field, flow field and magnetic field, was demonstrated.84 As shown in Fig. 6D, on-chip analysis of individual cells was carried out using a microchip composed of three zones: as follows: (1) the focusing zone by acoustic standing wave, (2) separation zone by the combination of flow and magnetic field, and (3) capturing zone by microwell array with micro-magnets. As a demonstration, a small amount of adherent human prostate cancer (LNCaP), which served as surrogates for CTC, was spiked in a suspension of leukocytes, followed by selective magnetic labeling to LNCaP. The initial ratio of LNCaP to leukocytes was ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150. After passing the magnetic separation zone of this microchip, the LNCaP cells were enriched over 100-fold. Further, the microwell array could capture the magnetically labeled cancer cells with an accuracy exceeding 80%. Thus, this system is promising for liquid biopsies, single-cell biology, and immunology.
150. After passing the magnetic separation zone of this microchip, the LNCaP cells were enriched over 100-fold. Further, the microwell array could capture the magnetically labeled cancer cells with an accuracy exceeding 80%. Thus, this system is promising for liquid biopsies, single-cell biology, and immunology.
Digital microfluidics (DMF) is liquid-handling technology that manipulates liquids in discrete droplets in integrated microfluidic devices, usually by the force of an electric field gradient.85 In the case of a ferrofluidic droplet, a magnetic force was employed to actuate the droplet by moving a magnet under the flat substrate.86 Wheeler's group demonstrated the flexibility of DMF by combining biosensor-based electrochemical measurement of glucose with a chemiluminescent magnetic bead-based sandwich immunoassay for insulin.87 In direct blood loading for plasma separation and diagnostic assays by paramagnetic particle DMF, they demonstrated a 21-step rubella virus (RV) IgG immunoassay, yielding a detection limit of 1.9 IU mL−1, below the diagnostic cut-off.88 Further, they demonstrated portable sample-processing DMF molecular assays for the detection of the Zika virus from a 5 μL sample using RNA captured on magnetic beads.89
Oleschuk's group showed that the combination of low-friction superhydrophobic surfaces and droplets containing superparamagnetic particles could reliably dispense droplets with high precision (≤6%). Droplets ranging in size from 5 to 20 μL were used for an EDTA-based on-chip complexometric colorimetric titration for water hardness.90 Furthermore, precise control of droplets in magnetically driven DMF platforms was achieved using a low-friction surface, magnetically susceptible material/droplet(s), and an applied magnetic field. The optimized platforms were applied in a quantitative fluorescence-based DNA assay under 2 min.91
2.3 Magnetic force and chemical interaction
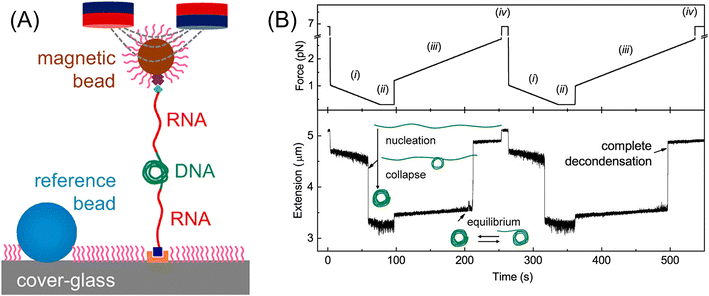 | ||
| Fig. 7 (A) Setup of magnetic tweezers. (B) Time-extension course recorded during repeated force-cycles obtained at 0.2 mM Co(NH3)63+ using nonmethylated DNA: (i) force-decreasing region with −0.01 pN s−1, leading to nucleation and condensation, (ii) low constant force is kept for 20 s, (iii) force-increasing region with 0.01 pN s−1, where through equilibrium state DNA completely decondensed, and (iv) high constant force is kept for 10 s. Reprinted with permission from ref. 98. Copyright © 2020, the American Chemical Society. | ||
Applying an external pulling force to individual molecules can change their equilibrium structure and dissociate their bonds in some cases, as reported in the studies of dynamic force spectroscopy, though major subjects of magnetic tweezers were DNA.99–101 Cysteamine molecules were tethered to Ag nanoparticles on a glass slide with SH end and to magnetic beads with NH2 end forming an amide group. With an increase in the pulling force from 0 to 100 pN per magnetic bead, the surface-enhanced Raman scattering (SERS) intensity ratio of ν(C–S) trans/ν(C–S) gauche, corresponding to the equilibrium isomer ratio of cysteamine, increased from 0.6 to 1.08, indicating an increase in the trans form from 37% to 52%.102 This result suggested that the trans form, which has a longer molecular structure than the gauche form, is stabilized under the pulled condition. A quartz crystal microbalance (QCM) is known as an extremely sensitive device for the measurement of very small weight changes in the order of ng. Yu et al. fabricated a conductive polyaniline-coated QCM and detected the weight increase due to the HCl vapor absorption when a magnetic field (0–3.1 T) was applied.103 Imai and Watarai prepared a QCM (9 MHz) electrode adsorbed with magnetic beads (200 nm in diameter, modified by poly-glycidyl methacrylate) on the Au electrode surface, forming a layered structure. Then, the interaction energy between the layers was measured by changing the environmental temperature under the application of pulling force by a magnetic circuit (3.5 T). The desorption rate of magnetic beads under a high magnetic field gradient was measured from the frequency shift of the QCM. The activation energy of 21 kJ mol−1 was obtained, corresponding to the hydrogen bonding enthalpy (10–30 kJ mol−1) between the polar groups of S–H, N–H, and O–H on the surface of the magnetic beads.104
Bishop et al. demonstrated the rapid motion of a magnetic Janus particle (4 μm in diameter), composed of a hydrophobic polystyrene hemisphere and a hydrophilic magnetic hemisphere of 3-mercaptopropionic acid on 20 nm Au/25 nm Ni/5 nm Ti layers on the curved liquid–liquid interface of a water droplet (291 μm in radius) in decane.108 The application of a static homogeneous vertical field of 15 mT drove particle motion to the drop equator, where the particle magnetic moment could align parallel to the field (Fig. 8A). Furthermore, they demonstrated that time-varying (spatially uniform) magnetic fields could drive a variety of steady particle motions on the interface of a water droplet in decane. Upon the application of a precessing field, the magnetic Janus particles moved either along circular orbits at the drop poles or along zigzag paths at the drop equator (Fig. 8B). They suggested that the observed magneto-capillary particle motions can be used to enhance the mass transfer in emulsions stabilized by magnetic particles.109
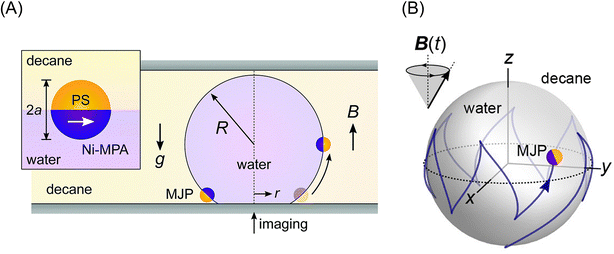 | ||
| Fig. 8 (A) Schematic illustration of a magnetic Janus particle (MJP) moving on the curved interface of a water droplet in decane due to a homogeneous magnetic field B. The inset shows the preferred orientation of the MJP at the interface and its magnetic moment (white arrow). Reproduced from ref. 108 with permission from The Royal Society of Chemistry. (B) Simulation of zig-zag motion of MJP in the interface due to a precessing magnetic field. Reprinted with permission from ref. 110. Copyright © 2020, the American Chemical Society. | ||
2.4 Application of magnetic force to separation methods
Solid-phase extraction (SPE) and liquid–liquid extraction (LLE) are fundamental separation techniques in analytical chemistry. However, traditional extraction methods require organic solvents or solid adsorbate, which are often not eco-friendly. Thus, to solve this problem, many attempts to impart magnetism to the extraction media have recently been reported.The extraction particles in SPE are commonly packed in cartridges and used with high performance because a large specific area is preferable for the rapid adsorption of the analytes. Recently, surface-modified MNPs have been recognized as potential materials for SPE because they can be collected with a magnetic field in a non-contact manner from a dispersed mixture with the sample solution. Also, it can be functionalized with various molecules to offer high selectivity of a target analyte. There have been many reports on the use of magnetic beads in SPE for a wide variety of analytes.111–118
Further, it is possible to decorate MNPs with a layer of metal–organic frameworks (MOFs) for use in SPE. MOFs are porous polymeric materials composed of metal ions as cross-linking points and organic ligands as bridges. The analytes are adsorbed in the pores due to hydrophobic interactions, π–π stacking with aromatic rings in ligands, hydrogen bonding, ionic interactions, dipole–dipole interactions, and Lewis acid–base interactions with uncoordinated sites of linking metals. Hence, MOFs can have excellent molecular selectivity and absorption capacity, and their combination with MNP enables the separation and enrichment of low-abundant species, such as toxic metal ions in water,119–122 peptides in body fluids,123,124 and dyes from contaminated water.125,126 Recently, the enrichment of exosomes,127 which is promising as a biomarker for cancer, in a urine sample was performed with a Zr-MOF-functionalized MNP. Exosomes specifically adsorbed on the pores of this magnetic MOF due to the bond between the Zr–O unit and the phospholipid bilayer, and then magnetically separated from the complex biological fluid. They achieved a high recovery rate of exosomes (>95%) with 10 min incubation.
Ionic liquids (ILs),128 which are room-temperature molten salts, are a promising extraction solvent due to their low toxicity, low vapor pressure, and high thermal stability. Their physical and chemical properties, such as hydrophobicity, power to dissolve chemical and biological compounds, and viscosity, can be tuned by replacing their organic cations and/or organic/inorganic anions. Recently, magnetic property was added by using paramagnetic metal complex anions such as FeCl4−, GdCl63−, and Ni(II) hexafluoroacetylacetonate.128,129 These materials are called magnetic ionic liquid (MIL), which possess high magnetic susceptibility and can easily be recovered with a permanent magnet. Several research groups showed the potential of MILs as an extraction solvent for drugs,130 environmental pollutants,131 hormones,132 bacteria,133etc. A notable application of MILs is DNA purification and preconcentration.134–139 Traditionally, LLE is used for DNA isolation, but it needs a large amount of organic solvent, which causes the loss of the DNA. Further, the multiple centrifugation steps to remove cellular residue are time-consuming and a significant bottleneck in DNA analysis. Thus, to improve this situation, Wang et al.135 studied DNA extraction in a hydrophobic MIL, which consisted of a hexaalkylguanidinium cation and paramagnetic metal complex anion (Fig. 9A). An aliquot (20 μL) of MIL was added in 1.0 mL aqueous solution of DNA, and then stirred by vortexing. The dispersed MIL, which extracted DNA, was gathered by applying a magnetic field (Fig. 9B). At a lower pH, satellite DNA (stDNA) was well extracted into the MIL phase, while proteins remained in the aqueous phase (Fig. 9C). Therefore, stDNA could be purified and enriched before PCR assay.
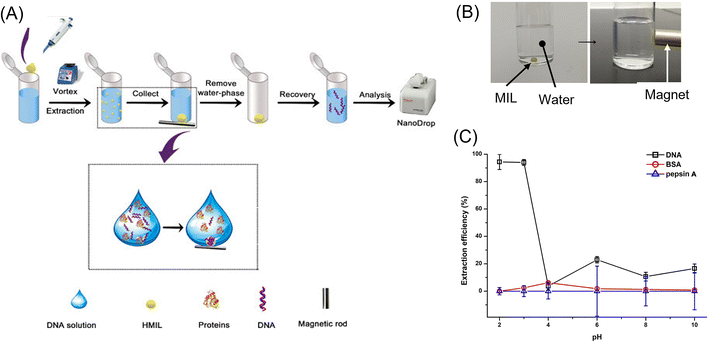 | ||
| Fig. 9 Scheme of the extraction procedure (A), attractive behavior of an MIL droplet in water to a magnet (B), and extraction efficiency of stDNA, BSA, and pepsin A as a function of pH (C) for demonstration of the performance of the DNA extraction from complex samples. Reprinted with permission from ref. 135. Copyright © 2021, the American Chemical Society. | ||
The effect of a magnetic field on solvent extraction equilibria has not been reported, but Tsukahara et al.140 discovered the influence of magnetic force on the extraction rate of paramagnetic Eu3+ with 2-thenoyltrifluoroacetonate (tta−) anion from oxalate (ox−) solution to the dodecane phase. By microscopic observation of the dodecane/water interface sandwiched with permanent magnets, they observed random flashing spots due to the extraction of fluorescent Eu(tta)3 in the dodecane side of the interface (Fig. 10A). Further, when the magnetic field gradient applied to the interface increased, the flash frequency increased (Fig. 10B). The mechanism of random flashing was thought to be the formation of micro-aggregates of non-fluorescent and paramagnetic Eu(tta)(ox)+ complex in the aqueous phase, which migrated to the interface by magnetophoretic attraction and reacted with excess Htta in dodecane to form fluorescent Eu(tta)3 at the interface141 (Fig. 10C).
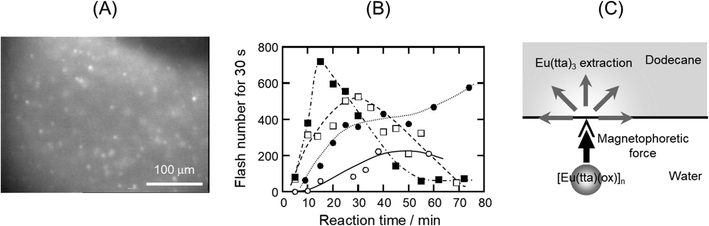 | ||
| Fig. 10 (A) Random fluorescent flashing at the dodecane/water interface, showing the extraction of Eu(tta)3. (B) Increase in the extraction rate of Eu(tta)3 with a magnetic field; ○ no magnets, ● 2 magnets, □ 6 magnets, and ■ 8 magnets. (C) Illustration of the magnetophoresis of the micro-aggregates of [Eu(tta)(ox)+]n. Reprinted from ref. 140. | ||
Fuh et al. developed analytical magnetapheresis and applied it to blood typing.142 They also developed the magnetic thin channel method to trap and concentrate functional magnetic particles and used it for the immunological analysis of C-reactive protein,143 hepatitis B surface antigen,144 and tumor necrosis factor-α.145,146
Studies of the magnetic field effect on chromatography are limited. Mukherjee et al. reported in 1980 on the magneto-paper electrophoresis of inorganic ions using 1.5 T electromagnet.147 They observed that the migration distance of trivalent lanthanide ions spotted on a 1 cm × 35 cm paper strip was retarded by a magnetic field, and the magnetic retardation effect was proportional to the effective magnetic moments of the ions. Nomizu et al. studied magnetic chromatography to separate a mixed suspension of hematite (0.2 μm φ × 1.0 μm long) and magnetite (ca. 0.6 μm in diameter) particles in a PTFE tube (1.5 mm o.d. × 0.5 mm i.d.) and successfully separated them by controlling the magnetic field application time.148 Fujiwara et al. studied the migration of metal ions on silica gel under a magnetic field gradient of 410 T2 m−1 and observed that their mobilities depended on the magnetic susceptibilities.149,150 In the case of Cu2+, they thought that the Cu2+ ions moved in a large group of Cu2+ ions and H2O molecules with a diameter of 4.6 μm, not in a single Cu2+ ion.151 Barrado and Rodríguez reported “high-performance liquid magneto-chromatography” in 2006.152 They stated that its distinctive features are (a) a stationary phase with a high specific surface area of fine Fe3O4 particles supported on silica gel and (b) a variable intensity magnetic field with 0–5.5 mT. The effect of magnetic field on the retention time of amino acid after forming a Cu(II) complex was observed, but the separation performance was less than expected. Thus, fundamental studies on the packing materials and design of a magnetic field are required.
2.5 Micro-composites and magnetic force
Magnetic force can be used to arrange or organize microparticles in 2D or 3D structures, depending on their magnetic properties. They can sometimes exhibit unique properties, as found in photonic crystals. Also, magnetic force can actuate micro-subjects that were designed to generate expected mechanical motion. This section reviews some works relating to magnetic photonic crystals and magnetic soft robots, given that they will suggest valuable hints for analytical applications.A typical example of magnetic photonic crystals was reported by Yin et al. in 2007.155 They prepared polyacrylate-capped superparamagnetic magnetite nanoparticles with diameters ranging from 30 to 180 nm via a high-temperature hydrolysis method. The diffraction color of a dispersion of these particles (120 nm in diameter) in water changed drastically from red to blue by the application of an external magnetic field in the range of 8.78 to 35.2 mT, where the diffraction peak shifted from 740 nm to below 450 nm, as shown in Fig. 11A. The application of magnetic photonic crystals to a humidity sensor has been reported by Ge et al.156 They fabricated a thin film containing superparamagnetic Fe3O4@SiO2 colloids (97 nm in core diameter) and a liquid precursor of poly(ethylene glycol)acrylate on an Nd–Fe–B magnet, followed by instant polymerization with UV-curable resin (NOA61) to fix the photonic structures formed through the magnetic assembly. The composite film contained hygroscopic poly(ethylene glycol) methacrylate (PEGMA) and crosslinker poly(ethylene glycol) diacrylate (PEGDA), which can strongly absorb water vapor, and therefore swelled upon contact with humid air, which led to visual color changes due to the increase or decrease in the lattice constant of the fixed ordered photonic structure (Fig. 11B). By optimizing the cross-linking level and the thickness of the polymer film, the reflection wavelength of the humidity sensor shifted by 160 nm within several minutes. Its intensity was readable with the naked eye. In addition, the photonic humidity sensor showed good reversibility and durability. Other applications including magnetically responsive photonic watermarks on banknotes,157 magnetically switchable plasmonic nanorods,158 and magnetically aligned layer-by-layer assembly for noble optical materials159 were reported. However, to date, the application of magnetic photonic crystals to micro-analytical systems has not been reported. A future trial concerning this subject is anticipated.
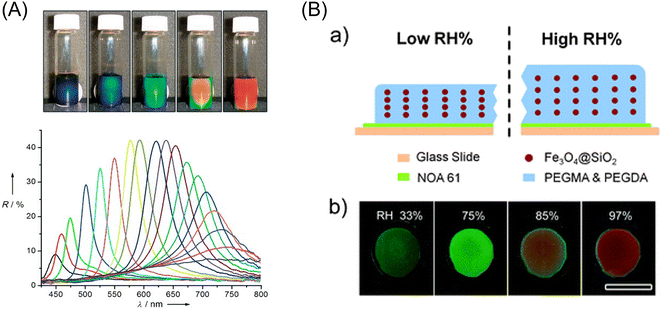 | ||
| Fig. 11 (A) (Top) Photographs of colloidal crystals formed in response to an external magnetic field: the magnet–sample distance decreases gradually from right to left. (Bottom) Dependence of the reflection spectra at normal incidence of the colloidal crystals on the distance of the sample from the magnet. Diffraction peaks blue-shift (from right to left) as the distance decreases from 3.7 to 2.0 cm with a step size of 0.1 cm. Reprinted with permission from ref. 155. Copyright © 2007, WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. (B) (a) Schematic illustration of the structure of the humidity sensing film and the mechanism of color switching between low and high relative humidity (RH) environments. (b) Digital photos of a typical film with a 50% crosslink level in different humidity environments, showing blueish-green, green, yellow, and red. The scale bar is 1 cm. Reproduced from ref. 156 with permission from The Royal Society of Chemistry. | ||
3. Application of magnetic torque
3.1 Orientation of diamagnetic substances under a dc magnetic field
Magnetic orientation occurs when a particle with magnetic anisotropy is exposed to an applied magnetic field (Fig. 1B). The magnetic anisotropy of a particle can be represented by the magnetic susceptibilities of χ1, χ2, and χ3 (Fig. 13A). For simplification, a uniaxially anisotropic diamagnetic particle, where χ1 > χ2 = χ3, is considered. Under a static magnetic field, the magnetic torque on the particle can be expressed by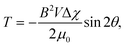 | (11) |
Generally, the magnetic susceptibility of a molecule is anisotropic. Taking benzene as an example, the magnetic susceptibility differs between the in-plane and out-of-plane directions of the aromatic ring, where the latter is more diamagnetic because of the induced ring current. Therefore, the benzene ring tends to align parallel to the field. Unfortunately, this diamagnetic anisotropic energy is negligibly smaller than the thermal energy of room temperature, and it is impossible to orient a single molecule with a magnetic field. When molecules form a μm-sized particle with ordered structure, such as aggregates and microcrystals, the magnetic energy becomes larger than the thermal energy.
Owing to the development of superconducting magnets in the 1990s, the magnetic orientation of various weak magnetic micrometer-sized objects can be observed. Higashi et al.168,169 showed the magnetic orientation of red blood cells with their disk plane parallel to the magnetic field direction, and the dependence on the field strength up to 8 T suggested that their magnetic anisotropy was attributed to the molecular alignment of the lipid bilayer of cell membrane.170 There are other reports on the magnetic orientation of diamagnetic micro/nano objects including porphyrin aggregates,171,172 single-wall carbon nanotubes,173 conducting polymer nanowires,174,175 and gold nanorods.176,177
There are highly anisotropic diamagnetic particles, which can be aligned with an electromagnet or permanent magnet. For example, the needle-shaped monosodium urate (MSU) crystal has large magnetic anisotropy and can be oriented with a low magnetic field of 0.5 T.178,179 MSU crystals develop in the joint and cause gout. Takeuchi et al.180 reported a technique to detect MSU crystals by utilizing the magnetic orientation, aiming to develop a non-invasive diagnostic method for gout. They observed the angle distribution of the scattered near-infrared (NIR) light (785 nm) from a suspension of MSU needle crystals (12 μm in length, ∼1 μm in width) induced by the application of a static magnetic field. Due to the magnetic orientation of the crystal, the angle distribution significantly changed.
Iwasaka and Mizukawa181 showed the orientation of guanine crystals contained in fish scales under a weak magnetic field (<0.5 T). The guanine crystals were platy (20–30 μm in length, 5 μm in width, and 70 nm in thickness) and their planes oriented parallel to the magnetic field. The guanine crystal has a relatively high refractive index of 1.83, and thus it exhibits strong light reflection at the surface of the crystal. Iwasaka et al.182 demonstrated the control of the direction of the reflection by a magnetic field. This crystal can be used as a controllable mirror for analyzing microscale objects.
Liquid crystals (LCs) also have high magnetic anisotropy, and it is well known that their direction can be controlled by a low magnetic field, especially when the LCs are in the nematic phase.183 Nematic LCs are widely utilized in displays, projectors, variable optical retarders, etc. The interaction between the LC and the substrate is vital to increasing the performance of these devices. The anchoring energy is a parameter to measure how the LC molecules are fixed at the interface, but the relationship between the anchoring energy and the chemical property of the substrate is not well known. Abbott et al. showed the behavior of LC molecules in contact with the water phase.184,185 Depending on the solute in the aqueous phase, the preferable direction of the LC molecule at the interface changed. Yesil et al.186 developed anchoring energy measurement at the LC/water interface using the magnetic orientation of LCs. The experimental setup is shown in Fig. 12A. An electromagnet (<0.5 T) was attached to a polarization microscope with a crossed-Nicol configuration. A similar optical cell to that Abbott reported was placed between the poles of the electromagnet. Then, an aqueous solution of surfactant, dodecyltrimethylammonium bromide (C12TAB) or tetradecyltrimethylammonium bromide (C14TAB), was added to the cell. The adsorption of the surfactant at the water/LC interface also caused homeotropic alignment. Therefore, the director of the LCs aligned to the direction of observation, and the light did not transmit to the polarization microscope (top microphotograph of Fig. 12B). Then, an external magnetic field was swept from 0 to 0.5 T. When the field strength was attained at a certain threshold, the LC alignment began. This phenomenon is the so-called Fréedericksz transition. The anchoring energy (WAQ|LC) can be determined from the threshold magnetic field, as shown in Fig. 12C. This is the first report of the quantitative determination of WAQ|LC, and this method will help reveal the relationship between the surface chemistry and the anchoring energy of LCs.
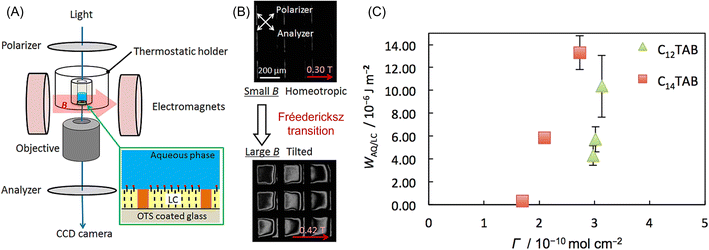 | ||
| Fig. 12 (A) Experimental setup for the observation of the Fréedericksz transition of a LC thin layer in contact with an aqueous solution. LC thin layer (∼20 μm) was supported by a Cu TEM grid and an octadecyl trichlorosilane (OTS)-coated glass, which induced homeotropic alignment. (B) Changes in polarized light microscope images with an increase in the magnetic field from 0.3 T to 0.42 T. (C) Plots of the anchoring energy (WAQ/LC) against the surfactant concentration in the aqueous phase. Reprinted with permission from ref. 186. Copyright © 2018, the American Chemical Society. | ||
3.2 Alignment of diamagnetic microcrystals under a modulated rotating magnetic field
Kimura et al.187 proposed a method to align diamagnetic micro-crystals three-dimensionally using a time-dependent elliptic magnetic field. They considered the magnetic alignment of a biaxial crystal, which has three different principal values, i.e., χ1 > χ2 > χ3 (Fig. 13A bottom), in a viscous medium under a static and rotational magnetic field. When a static magnetic field is applied along the x-direction of the laboratory axis (Fig. 13B), the χ1-axis of the crystal aligns along the x-axis, whereas the χ2 and χ3-axes are randomly distributed in the yz-plane. Alternatively, where a rotational magnetic field is imposed (Fig. 13C), the χ3-axis is oriented along the z-direction to minimize the magnetic potential energy, while the χ1 and χ2-axes are not fixed. Three-dimensional alignment can be performed by a temporally modulated rotational magnetic field (Fig. 13D), where the rotational speed is slow near the x-axis and fast near the y-axis. A detailed mathematical study of this three-dimensional orientation has been reported by Yamaguchi et al.,188,189 and the optimal strength and frequency of the modulating magnetic field have been systematically discussed.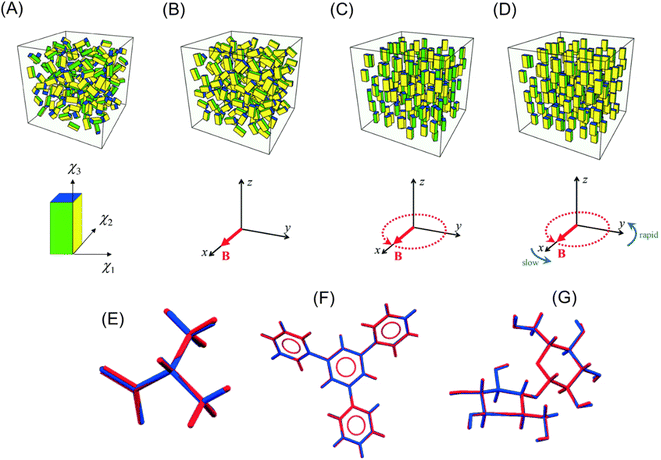 | ||
| Fig. 13 Concept of the 3D-orientation by a magnetic field. The definition of three different principal values of a biaxial crystal, χ1 > χ2 > χ3, is shown in (A). (A) Random orientation under no magnetic field, (B) χ1 axes align uniaxially in the x-axis under a static magnetic field, (C) χ3 axes align uniaxially along the z-axis under a rotating magnetic field applied in the xy plane, and (D) three axes align in 3D (χ1//x-axis, χ2//y-axis, and χ3//z-axis) under a frequency-modulated rotating magnetic field. Reproduced from ref. 197 with permission from The Royal Society of Chemistry. Comparison of the structures determined from MOMA (blue) and the structures reported previously (red): (E) L-alanine, (F) 1,3,5-triphyenilbenzene, and (G) cellobiose. Reproduced from ref. 190 with permission from The Royal Society of Chemistry. | ||
Kimura et al. prepared pseudo-single crystals called MOMA, which denoted a magnetically oriented microcrystal array. A suspension of microcrystals in polymer solution or UV curable resin was exposed to an elliptically rotating magnetic field. After reaching sufficient orientation, the microcrystals were immobilized by the solidification of the medium, i.e., gelation or photo-curing. The MOMA sample could be handled as a single crystal. They demonstrated X-ray structure analyses of MOMAs of organic190,191 and inorganic192 compounds and proteins,193–195 which were too fine to be analyzed by ordinary X-ray diffraction. Fig. 13E–G show the structure of the organic compounds determined from X-ray diffraction measurement of MOMA, which contained microcrystals of less than 50 μm. For comparison, the corresponding structures determined by using single crystals were overlapped. In each compound, the determined structures were in excellent agreement. Furthermore, they demonstrated that MOMA is applicable to solid-state NMR spectroscopy.196
Given that the solidification process often disarranges the microcrystals due to the anisotropic shrinkage of a gel or resin, it is preferable to measure the aligning microcrystals in situ in a highly viscous fluid under a modulated rotational magnetic field. Kimura and co-workers developed a technique for collecting single-crystal X-ray diffraction data from a liquid suspension, which was termed a magnetically oriented microcrystal suspension (MOMS). A magnetic orientation attachment was mounted on an in-house X-ray diffractometer to prepare the MOMS sample. Several measurement modes were proposed for the MOMS samples, such as the adjustment of the collection timing with a rotating shutter,198 continuous rotational method,199 and an intermittent rotation method.200 These developments allowed the structure determination of microcrystals less than 5 μm without a synchrotron X-ray source.
3.3 Orientation of magnetic nanoparticles: observation with light
Given that MNPs have a large magnetic moment, they can be oriented in liquid by a lower magnetic field than the anisotropic diamagnetic objects. A conventional method to characterize MNPs is magnetization measurement, which is sensitive to the rotational motion of the magnetic moment due to Néel and Brownian rotations. If Néel rotation, which is the rotation of magnetic moment inside the MNP, is negligible, only Brownian rotation, which is the rotation of the particle itself, can be monitored by the magnetization measurement. It is known that a magnetic field can induce linear dichroism and birefringence in MNP samples.201–203 The induced optical anisotropy can measure the orientation of the individual MNPs204 along the direction of the magnetic field and the formation of chain-like aggregation.202Watarai and Sakurai205 observed that the magnetic orientational linear dichroism (MOLD) is very sensitive to the formation of small aggregates such as dimers and other oligomers of MNPs in solution. They measured the change in the MOLD spectra and shift in the maximum wavelength of COOH-modified MNP suspension by adding cationic surfactants or metal ions under a static magnetic field. The primer MNPs started to form oligomers at the critical concentration, as indicated by red arrows in Fig. 14A and B, which was defined as the “critical association concentration”. The apparent association number at the cation concentration giving the maximum MOLD was evaluated for each cation from the magnetic field dependence of MOLD according to Langevin analysis. The apparent association numbers were, for example, 1.98 for Co(II) and 6.25 for Dy(III) (Fig. 14C). Then, the increase in MOLD value and the red shift in the wavelength with the addition of cation was ascribed to the formation of dimers and other oligomers, which had higher optical and magnetic anisotropy than the individual MNPs. The further addition of metal ions caused the migration and precipitation of the MNP aggregates in an optical cell. The use of the MOLD spectra of MNPs is a promising technique for detecting the association of MNPs in solution, which is valuable for the determination of the stability of colloidal systems and the design of magnetic immunoassays.
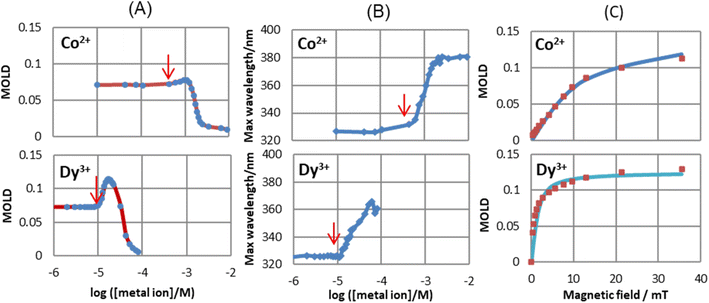 | ||
| Fig. 14 Effect of metal ion concentrations of Co2+ and Dy3+ on (A) max. MOLD values and (B) max. wavelength of MOLD spectra (35.6 mT). The red arrows show the critical association concentrations. (C) Langevin analysis in [Co2+] = 9.24 × 10−4 M and [Dy3+] = 1.67 × 10−5 M, 0.00165 wt% MNPs. Reproduced with permission from ref. 205. Copyright © 2020, the American Chemical Society. | ||
The dimerization of nanoparticles in solution is thought to be the first step in the aggregation of nanoparticles.206 The formation of dimers is known to be highly sensitive to the zeta potential of the particle surface or immunological interactions at the surface. Prins et al. reported a study to use the formation of dimers of nanoparticles as two-particle nanoactuators for the rapid and sensitive detection of biomolecules.207 Initially, biologically activated MNPs (500 nm in diameter) were incubated with the target proteins. Thereafter, a rotating magnetic field was applied to drive the formation of MNP chains. Finally, the magnetic field was removed to allow unbound nanoparticles to redisperse and the optical scattering from monomers and dimers was detected under a frequency-selective rotating magnetic field (3.5 mT, 1–5 Hz). They demonstrated a limit of detection lower than 5 pM for biotinylated BSA in human plasma in an assay time of less than 3 min. This method was applied for the analysis of prostate-specific antigen (PSA),208 the detection of conformation switching of single native proteins,209 and fundamental research of the kinetic mechanisms of aggregation210 and inter-particle biomolecular reactivity.211
The response of MNPs to an alternating magnetic field ranging from kHz to MHz has been used for recent biomedical applications and nanoscale measurement techniques, such as magnetic particle imaging (MPI),212,213 magnetic hyperthermia therapy (MHT),214,215 magnetic particle nanorheology (MPN),216–218 and homogeneous bio-sensing method.219,220 MPI and MHT utilize Néel rotation under an ac magnetic field, whereas Brownian rotation is observed in MPN and biosensors. However, recent studies221–227 suggest that these rotational behaviors are not independent, where the Néel rotation affects the Brownian rotation and vice versa. Therefore, Brownian rotation causes an unexpected signal in MPI and a change in the heat efficiency in MHT. Alternatively, Néel rotation produces a systematic error in MPN because it is assumed that the dynamic magnetization signal is completely attributed to Brownian rotation. Ota and Takemura measured the two-step magnetization response of MNPs dispersed in water by applying a fast responding pulse magnetic field, where the Brownian regime occurred after the Néel regime.228
Suwa et al. demonstrated that Brownian rotation could be measured with light under an oscillating magnetic field. They found that when a pulsed magnetic field was applied to a suspension of maghemite MNPs of 10 nm in diameter, its absorbance parallel to the magnetic field decreased.229 For a more detailed investigation, they observed the absorbance change (ΔA) under a damped oscillating magnetic field (DOMF) in the frequency (f) range of 28.1 to 92.0 kHz.230Fig. 15A shows the typical waveform of ΔA, which is different from that of the DOMF (bottom panel of Fig. 15A). Specifically, ΔA has a linear relation with the degree of alignment 〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉, where θ is the angle between the optic axis (easy axis) and the direction of light (magnetic field) and the angle bracket indicates the ensemble average. As shown in Fig. 15C, 〈cos2
θ〉, where θ is the angle between the optic axis (easy axis) and the direction of light (magnetic field) and the angle bracket indicates the ensemble average. As shown in Fig. 15C, 〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉 is plotted against B. This dynamic hysteresis curve directly indicates the Brownian rotation behavior of iron oxide MNPs under an oscillating magnetic field, where the MNPs keep aligning to some extent and oscillate small with 2f. This behavior is consistent with the “magnetic mode”, a predicted orientational mode for superparamagnetic nanoparticles by Usov and Liubimov222 with a numerical simulation. Suwa et al. studied the size-dependence of the Brownian rotation, and they observed the “viscous mode”, which is another orientational mode predicted by Usov, for the larger particles (25 nm in diameter).231 Thus, this optical method can characterize MNPs based on the Brownian rotation in liquid. In addition, a recent study showed that this method will be useful for measuring the local viscous environment around the MNPs.232
θ〉 is plotted against B. This dynamic hysteresis curve directly indicates the Brownian rotation behavior of iron oxide MNPs under an oscillating magnetic field, where the MNPs keep aligning to some extent and oscillate small with 2f. This behavior is consistent with the “magnetic mode”, a predicted orientational mode for superparamagnetic nanoparticles by Usov and Liubimov222 with a numerical simulation. Suwa et al. studied the size-dependence of the Brownian rotation, and they observed the “viscous mode”, which is another orientational mode predicted by Usov, for the larger particles (25 nm in diameter).231 Thus, this optical method can characterize MNPs based on the Brownian rotation in liquid. In addition, a recent study showed that this method will be useful for measuring the local viscous environment around the MNPs.232
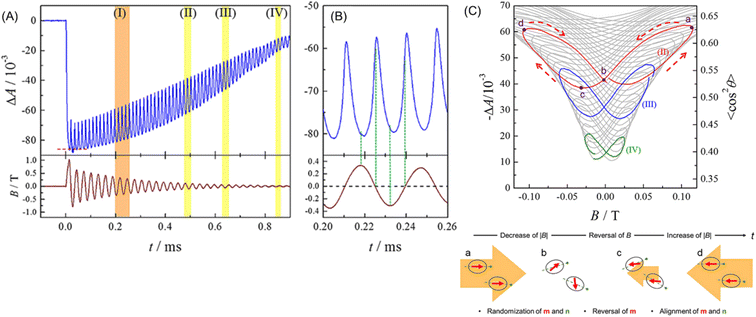 | ||
Fig. 15 (A) Typical waveform of absorbance change of MNP suspension (upper) and DOMF (bottom). (B) Enlargement of region I in (A). (C) Plots of ΔA (〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ〉) against B. The colored lines show the region highlighted in (A). Temporal direction of the curve is depicted by dashed arrows. The bottom figure illustrates the speculated behavior of magnetic moment (red arrows) and the easy axis (green dashed line) during the half period of field oscillation. Reprinted with permission from ref. 230. Copyright © 2019, American Institute of Physics. θ〉) against B. The colored lines show the region highlighted in (A). Temporal direction of the curve is depicted by dashed arrows. The bottom figure illustrates the speculated behavior of magnetic moment (red arrows) and the easy axis (green dashed line) during the half period of field oscillation. Reprinted with permission from ref. 230. Copyright © 2019, American Institute of Physics. | ||
4. Application of electromagnetic force
4.1 Application of electromagnetophoretic force
Kolin formulated the electromagnetophoretic (EMP) force on a particle in an electrolyte solution in 1953.233,234 When a homogeneous electric current is applied through a closed conductive solution containing a particle under a homogeneous magnetic field perpendicularly applied to the electric current, the force is exerted on both the medium and the particle. Here, two forces act on the particle. The Lorentz force directly working on a particle is called the electromagnetic weight (EMW), FEMW. The Lorentz force on the medium that works on the particle as an equal magnitude and opposite directional force is called the electromagnetic buoyancy (EMB), FEMB. The electromagnetophoretic force, FEMP, exerted on a particle having a volume, V (m3), in a closed cell with an inner sectional area of S (m2) is expressed as the sum of FEMW and FEMB, as follows: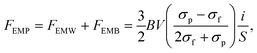 | (12) |
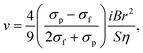 | (13) |
Iiguni and Ohtani determined the surface conductivity of an organic droplet in an aqueous solution of cetyltrimethylammonium bromide (CTAB) from the measurement of the electromagnetophoretic velocity of the droplet under a magnetic field of 1 T and electric current of 40–110 μA. An increase in CTAB concentration resulted in an increase in the surface conductivity.237 It will be interesting to investigate the relationship between the surface conductivity observed by electromagnetophoretic velocimetry and zeta potential of the droplet.
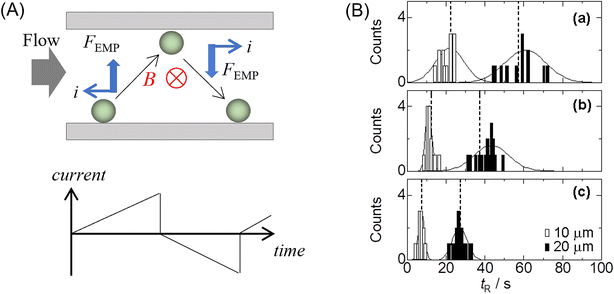
Chromatographic application of EMP force to a particle separation was investigated by Iiguni and Watarai, which was called electromagnetophoretic adsorption–desorption chromatography in a capillary flow system.238 The principle is the combination of the Stokes viscous force generated by the liquid flow and the adsorption–desorption migration across the inside of the capillary caused by the electromagnetophoretic buoyancy induced by the applications of an alternative current and a homogenous magnetic field (Fig. 16A). When the electric current direction was switched periodically, the test polystyrene particles showed “zigzag” migration behavior, mainly depending on the particle size and desorption force from the capillary wall. Employing this method, the polystyrene particles of 10 μm and 20 μm in diameter dispersed in 1 M KCl solution containing 0.01% Triton X-100 were separated using only a 1 mm long fused-silica capillary with the inner diameter of 200 μm under a homogeneous magnetic field of 10 T. The best resolution of 1.90 was attained under the conditions of maximum current of 2000 μA switched with 0.5 Hz and flow rate of 100 μL h−1 (Fig. 16B).
 | ||
| Fig. 16 (A) Schematic drawing of the concept of adsorption–desorption EMP chromatography working under a switched electric current, i. (B) Chromatograms of polystyrene particles under the flow rates of (a) 60, (b) 80, and (c) 100 μL h−1 with 2000 max μA (0.5 Hz) and 10 T. Reproduced with permission from ref. 238. Copyright © 2005 m Elsevier B.V. | ||
Iiguni et al. studied electromagnetophoresis in microchip systems using hydrodynamic focusing in the sample inlet part to separate different-sized polystyrene particles (3, 6, and 10 μm in diameters) and between yeast cells and polystyrene particles. However, the hydrodynamic focusing required a large amount of sheath solution.239 To overcome this disadvantage and improve the separation efficiency, they fabricated a microchip system composed of a 7 mm EMP focusing segment and 3 mm EMP separation segment, where the two EMP forces were applied inversely.240 To keep the sample particles in a single flow channel, a micro-dialysis hollow fiber (o.d. 220 μm, i.d. 200 μm, molecular cut-off: 13 kDa) was used in the microchip. An injected mixture of particles was focused to one side in the focusing segment of the hollow fiber channel, and then the particles were migrated in opposite direction, with the velocity depending on the size, and finally fractionated by the Y-shaped outlet channels. Consequently, 87% of 3 μm polystyrene particles was isolated from a mixture of 3 and 10 μm particles.201
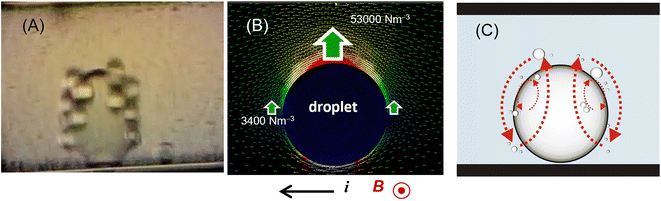
A magnetic field and an electric current were postulated to be uniform in a simple analysis of the EMP velocity, but the uniformity of the electric current density changed when the micro-flow system included non-conductive microparticles or emulsions in a conductive medium. The ionic current density profile inside the channel was greatly changed by the presence of this droplet, and the EMP force around the droplet became complicated. Funaki et al. observed a curious micro-convection of smaller organic droplets around a larger organic droplet in a capillary electromagnetophoretic system.241 When the electric current of 0.5 or 1.0 mA was applied at 3.5 T or 2.7 T, larger droplets became arranged at regular intervals on the capillary wall, and smaller droplets circulated around the larger droplets (Fig. 17). This behavior was explained by the difference in the local electric current density around a larger droplet, which was lowest on both electrode sides of the droplet, leading to the circulation of the medium due to the inhomogeneity of the Lorentz-force around the larger droplet.
 | ||
| Fig. 17 Behavior of organic droplets in a capillary (100 μm i.d.) in a superconducting bulk magnet system (3.5 T) observed from the direction parallel to the magnetic field. (A) Rotation of smaller droplets around a larger droplet at 500 μA. (B) Simulation of Lorentz forces exerted to the top and side regions of a 10 μm droplet at 1 mA. (C) Schematic illustration of the orbitals of smaller droplets due to local electromagnetophoretic convection. Dodecane was 20% in volume with 0.2 mM Triton X-100 in 1 M KCl solution. Reprinted from ref. 241. | ||
Kato et al. developed electromagnetophoretic dynamic force measurement for the detachment dynamics of microparticles adsorbed on the inner wall of a silica capillary. Especially, the COOH-modified polystyrene particle–wall interaction in electrolyte solutions was studied by changing the pH and the concentration of coexisting metal ions of Cu2+, Ni2+, Fe3+, or Al3+ on the desorption dynamics under a 10 T magnetic field.245 They derived the equation for the dynamic force analysis based on the model of Bell,246 as follows:
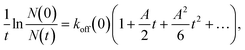 | (14) |
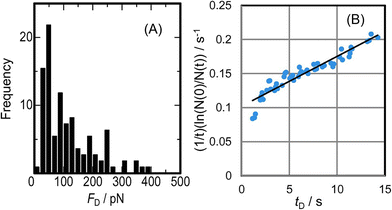 | ||
| Fig. 18 (A) Histogram of the desorption events of 10 μm COOH-modified polystyrene particles by electromagnetophoretic pulling force at a rate of 16.1 pN s−1 at pH 7.1. (B) Dynamic force analysis of the detaching event shown in (A) by eqn (14), giving the values of Δx/Nb = 0.03 nm and koff(0) = 0.10 s−1. Reprinted with permission from ref. 245. Copyright © 2016, The Chemical Society of Japan. | ||
The effect of an external force on the structural equilibrium of a biological molecule was investigated by Wakiyama and Watarai.247 The pulling force due to the electromagnetophoretic buoyancy was applied to stretch cysteamine molecules bound between a polystyrene particle and Ag nanoparticles on a glass substrate. The SERS spectra of cysteamine observed under the pulling force of 81 pN showed an increase in the trans/gauche ratio, suggesting a shift in the conformational equilibrium to the trans form side by the pulling force, as observed in the magnetophoretic dynamic force measurement.90
4.2 Electrochemical systems
 | ||
| Fig. 19 (A) Schematic configuration of the MHD electrode where the magnetic field is applied parallel to the electrode. a: Luggin capillary, b: working electrode, c: counter electrode, d: diffusion layer, e: hydrodynamic boundary layer, and f: streaming. Reprinted with permission from ref. 250. Copyright © 2009 Elsevier B.V. (B) MHD electrode where the magnetic field was applied vertically to the electrode. 1: vertical MHD flow around the electrode edge, 2: micro-MHD vortices and 3: schematic of the micro-MHD vortex around the non-equilibrium fluctuations (humps) on the deposit surface.254 Reprinted with permission from ref. 259. Copyright © 2014, The Polish Physical Society. | ||
The MHD effect was also studied on electrodeposition in a vertical magnetic field configuration, where a magnetic field, B, and current, i, were applied perpendicularly to the electrode surface.253,254 Two types of MHD flows were proposed by Aogaki's group, as shown in Fig. 19B. One is the macroscopic MHD flow around the electrode edge, where the ionic currents are not parallel to the magnetic fields. This is termed vertical MHD flow (Fig. 19B1). The other is the micro-MHD vortex around the local bumps and micro-dents formed by nonequilibrium fluctuation in electrodeposition (Fig. 19B2). Then, the surface morphologies of the magneto-electrodeposition films exhibited micro-circular structures, suggesting the existence of micro-MHD vortices.248,254,255 Recently, the dominant role of the global (vertical) MHD flow compared to the micro-local MHD flow has been shown in the formation of nm-sized cones in the electrodeposition of nickel layers on a copper working electrode.256 In addition to the importance of Lorentz force in electrochemical systems, the role of Kelvin force has been clarified in the electrodeposition of micro-structured copper layers.257,258
The earlier applications of MHD force in analytical chemistry were reviewed by Fritsch et al. in 2010.266
Recently, this group successfully eliminated the need to add redox species to the solution for the MHD pumping by the use of the electrode modified with a conductive polymer, thus removing interferences with detection, sample, and reagents for lab-on-a-chip applications.267,268 A conductive polymer, poly(3,4-ethylenedioxythiophene) (PEDOT), was electropolymerized on microband gold electrodes in a solution consisting of 0.010 M EDOT, 0.010 M SDS, and 0.100 M KCl (ref. 267) or in solutions containing 0.010 M EDOT and 0.100 M TBAPF6 or LiClO4 electrolyte, respectively, in propylene carbonate.268 At the anode, PEDOT was changed from the neutral to oxidized state, which was associated with ions moving into or out of the film from the surrounding solution to compensate for the change in charge. At the cathode, PEDOT was converted from its oxidized state to its neutral state, causing the anions to leave the PEDOT film and enter the surrounding solution. This redox reaction generated an ionic current in the solution, leading to the MHD flow of the solution, as shown in Fig. 20A. When a 0.37 T magnet was used, fluid speeds of 590 μm s−1 were observed immediately after applying a potential step.267 The conductive polymer redox MHD pumping was combined with an epitaxial light sheet confocal microscope to observe three types of leukocyte samples.269 Recently, their redox magnetohydrodynamics (RMHD) microfluidics was coupled with dark-field microscopy to offer high-throughput single-nanoparticle (NP) differentiation in a flowing mixture of 82 nm Ag and 140 nm Au-coated silica particles by localized surface plasmon resonance and tracking of NPs (Fig. 20B). The well-controlled RMHD pumping enabled a continuous, reversible, and uniform flow for precise and simultaneous NP tracking of the Brownian motion.270
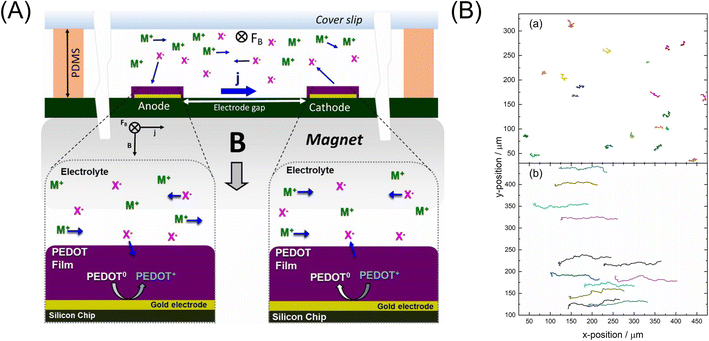 | ||
| Fig. 20 (A) Illustration of the generation of MHD fluid flow by PEDOT-modified electrodes, which produced an ionic current, j, between anode and cathode upon application of an electronic current, and in a chamber containing electrolyte of M+ and X− ions over a permanent magnet, providing B. M+ and X− refer to cations and anions, respectively. Reprinted from ref. 268. (B) Effect of 1-D MHD flowing in the tracking of the mixed NP suspension in 50 mM KNO3 over 74 frames (7.4 s) during an applied current of +50 μA and in the (a) absence and (b) presence of a magnet (flow direction to positive x-positions). Reprinted from ref. 270. | ||
Naaman et al. synthesized chiral Fe3O4 NPs by adsorbing chiral molecules on the surface of NPs to induce chiral catalytic activity and used them as a spin selective anode in photoelectrochemical water splitting with visible light.272 The water splitting could be performed with an electric current as high as 10 mA cm−2, and the H2O2 evolution was reduced. The role of chiral molecules, which were D- and L-tryptophan and L-alanine peptides, was explained as the spin filter. Recently, the effect of a magnetic field on the oxygen evolution reaction was quantitatively studied using a cobalt oxide|fluorine-doped tin oxide-coated glass anode, and a 4.7% increase in the anodic current at 1.5 V was observed at the magnetic field of 371 mT.273 The magnetic field effect was separated into two distinct regions, depending on if the magnetic flux density was lower or higher than 40 mT, but the physical origin of the two regions was not clear. Suda et al. prepared a spin-selective and high-conductive chiral MoS2 electrode by intercalating (R)-(+)-α-methylbenzylamine or (S)-(−)-α-methylbenzylamine. The chiral molecule-intercalated multilayers could achieve spin polarization as high as 75%. The spin selectivity suppressed the production of H2O2 and promoted the formation of ground-state O2 molecules.274 Hydrogen production from water splitting is a recent hot subject related to the global Carbon Neutral Project.
4.3 Chiral selectivity in magneto-electrochemistry
The electromagnetic force or Lorentz force induces rotational motion, as observed in the cyclotron motion of charged particles in a magnetic field. On the surface of the working electrode, electromagnetic force generates hydrodynamic helical motion of electrolyte solution depending on the direction of the magnetic field and the current, which are both applied vertically to the electrode (Fig. 19B of 4.2). Mogi et al. discovered that a polyaniline film prepared on a Pt working electrode by magneto-electropolymerization (MEP) under the conditions of a magnetic field of 5 T and a passing charge of 0.1 C cm−2 exhibited enantioselectivity when the polyaniline film electrode was used in the cyclic voltammetry measurement of L- and D-ascorbic acids (AA).275 The current of the oxidation peak of L-AA at 0.4 V was larger than that for D-AA on the film electrode prepared at +5 T. The result was the opposite on the −5 T-film electrode, where the peak current for D-AA was larger than that for L-AA. The ability of enantioselective recognition of the polyaniline film depended on the direction of the magnetic field. They thought that the Lorentz force may act on the currents in the polymer chains and induce helically coiled structures of the polymer chains. They also observed that the Cu film produced by magneto-electrodeposition under 5 T showed chiral selectivity in the cyclic voltammetry of tartaric acid (TA) (Fig. 21A).259 The enantiomeric excess (ee) ratio in the voltammograms, which is defined as ee = (iLp − iDp)/(iLp + iDp), where iLp and iDp represent the peak currents of L- and D-TA, respectively, gave positive values during 30–50 s deposition time (with a maximum value of 0.5 at 40 s), where the steady self-organized state of the MHD flows formed on the surface of the Cu film electrode. These facts implied that the self-organized state of the micro-MHD and the vertical MHD flows are crucial for the formation of chiral Cu film surfaces (Fig. 21B).259 Furthermore, they found that the specific adsorption of chloride ions on the film surfaces and the direction of the magnetic field of 5 T had a drastic influence on the chiral property of the Cu film, which was measured by the voltammetric ee ratio of L- and D-alanine. They suggested that not only the micro-MHD vortices but also the rate-limiting steps of Cu dislocation are responsible for the chiral surface formation.276 Recently, they investigated the effect of the working electrode diameters of 25, 100, and 3000 μm on the chiral selectivity of a Cu film prepared under the magnetic fields of 1–5 T. The results suggested that the strong vertical MHD flows can induce the breaking of the chiral structure of the Cu film through the fluctuation of the micro-MHD vortices.277 Further studies are anticipated on the fabrication of other chiral electrodes and the relationship between the nanostructure of the electrode and the chiral selectivity in the electrode reaction.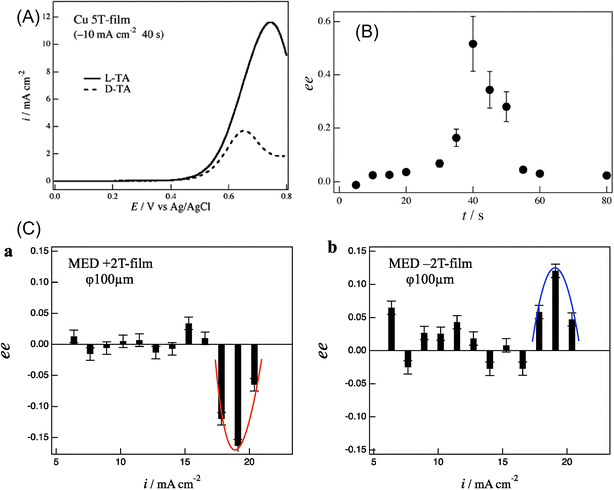 | ||
| Fig. 21 (A) Voltammograms of 20 mM L- and D-tartaric acid (TA) under 50 mV s−1 in Cu 5 T-film electrode in 0.1 M NaOH with 40 s deposition time.259 (B) Enantioexcess (ee) vs. magneto-electrodeposition time. Reprinted with permission from ref. 259. Copyright © 2014, The Polish Physical Society. (C) ee ratio vs. deposition current on a 100 μm electrode: (a) +2 T film and (b) −2 T film. Reprinted from ref. 277. | ||
Besides the micro-MHD vortex mechanism for chiral electrodeposition, Naaman's group reported another principle to generate enantio-selective interaction between chiral molecules and a perpendicularly magnetized ferromagnetic electrode, which is known as the chirality-induced spin selectivity (CISS) effect.278,279 When electrons move through chiral molecules, their transport velocity is spin-dependent given that the preferred spin orientation is determined by the handedness of the molecule and the direction of motion.279 They demonstrated the enantioselective adsorption of L- or D-polyalanine (PAL)-based oligomer (thiolated α-helix oligopeptide) when its solution was exposed for 2 s in 0.3 T to a ferromagnetic (FM) cobalt film covered with 5 nm of gold.280 In one magnetization direction, the L-PAL adsorption rate was 8-times faster than that of D-PAL. In contrast, in the other magnetization direction, the D-PAL adsorption rate was 4 times faster than that of L-PAL (Fig. 22A). However, the D-PAL purification level was lower than that of L-PAL, indicating the asymmetry in adsorption rate ratios. A longer adsorption time of 2 min resulted in a reduction in the enantio-selectivity of adsorption, suggesting that the process includes substantial kinetic differences. When a racemic PAL mixture was exposed to a magnetized substrate (1 cm × 1 cm), upon sequential exposure to 100 substrates with up- or down-pointing magnetization (0.3 T), a clear CD spectrum corresponding to D- or L-PAL, respectively, was obtained from the residual solution. The results indicated that the L-enantiomer favors the surface that is magnetized up, whereas the D-enantiomer favors the down magnetization. The spin-selective interaction between the enantiomer and the substrate was explained using DFT calculation (Fig. 22C and D). Naaman's group extended their study to the enantio-selective separation of small molecules. An ultrathin Ni (5 nm)/Au (10 nm) film coated with an achiral self-assembled monolayer (SAM) of carboxyl-terminated alkanethiols [HS–(CH2)x−1–COO−] was exposed to 1 mM solution of both (R)- or (S)-1-amino-2-propanol for different interaction times under magnetized either parallel (up) or antiparallel (down) with respect to the substrates. The OH-stretching band of the 1-amino-2-propanol-SAM adduct formed on the surface of Ni film was monitored by infrared (IR) spectroscopy as a function of the substrate magnetization (either up or down by 0.5 T magnet), and the incubation time. Maximum adsorption of (S)-1-amino-2-propanol was observed after 2 min for the down magnetization, but that of (R)-1-amino-2-propanol adsorbed more strongly after 10 min for the up magnetization. This selectivity was effective for 30–40 min, and no discernible difference was found for longer adsorption times. According to the study by changing the number of CH2 groups, it was found that the spin-exchange interaction decays at a distance of 0.75 nm from the ferromagnet-gold-covered surface. A gold (10 nm)-coated Ni (120 nm) electrode with a 1.0 nm SAM of 1-hexanethiol was used as the working electrode for the electrochemical oxidation and reduction of (R)- and (S)-ferrocene in solution, injecting electrons with their spin-polarized parallel (down magnetization) or antiparallel (up magnetization). The cyclic voltammogram showed a clear dependence of the direction of the magnetization, suggesting the enantio-selectivity associated with the helicity of the electron. The effect of spin injection was also observed in the electrochemical reduction of camphor sulfonic acid.281 Based on the two principles of (1) chiral-induced spin selectivity, which allowed the selective adsorption of one enantiomer on a perpendicularly magnetized substrate, and (2) the release of the adsorbates electrochemically, the enantioselective separation method of a racemic mixture of thiolated molecules was developed by applying ferromagnetic surfaces (Fig. 22B).282
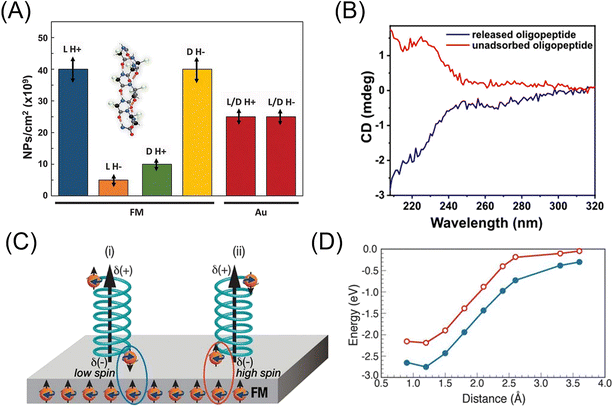 | ||
| Fig. 22 (A) Enantio-specific adsorption from L- and D-oligopeptide solutions after exposure for 2 s shown by the SiO2 nanoparticle adsorption density, which was compared with the adsorption density on Au with an applied external magnetic field of up (H+) or down (H−). Reprinted with permission from ref. 280. Copyright © 2018, The American Association for the Advancement of Science. (B) CD spectra of the racemic oligopeptide after passing through the separation system (red line) and the electrochemically desorbed oligopeptide from the ferromagnetic surfaces (blue line). Reprinted from ref. 282. (C) Electrical polarization of the molecule is accompanied by spin polarization. The spin alignment at each electric pole depends on the specific enantiomer. Therefore, the interaction between the magnetized Ni surface and the molecule (circled in blue and red) follows either a low-spin (i) or a high-spin (ii) potential, depending on the direction of magnetization of the substrate. Reprinted with permission from ref. 280. Copyright © 2018, The American Association for the Advancement of Science. (D) Interaction energies between Ni substrate and H atom calculated by DFT as a function of the distance between a hydrogen atom and a surface. In the calculation, all spins of the Ni atoms are aligned parallel to each other, and the H atom spin is aligned either parallel (red curve) or antiparallel (blue curve) to the spin of the Ni atoms. Reprinted with permission from ref. 280. Copyright © 2018, The American Association for the Advancement of Science. | ||
Both phenomena, the micro-MHD vortex-induced chiral selectivity reported by Mogi et al. and the spin-induced chiral selectivity reported by Naaman's group, have provided exciting subjects in the field of magneto-electrochemistry and chiral materials science. Future research on the in situ measurement of the surface chiral reactions will clarify the mechanism of the spin-selective effect in the enantio-selectivity of an electrodeposited film fabricated under micro-MHD conditions. Besides, enantio-selective separation using an electromagnetic field or spin selective interaction will be valuable for constructing novel micro-flow analytical systems.
5. Conclusion and perspective
In the last two decades, magnetophoretic force, magnetic orientation force, and electromagnetophoretic force have been applied to various analytical systems. However, the utility of these forces is not well understood in the field of analytical chemistry, and thus it should be further investigated in future studies. The unique feature of magnetic gradient force and magnetic orientation force is that these forces depend on the magnetic susceptibility of the analytical samples, which can be used for the determination of their components. However, to date, the development of this feature is in its infancy. Another important feature is that any of three forces can work more effectively on a microparticle than on molecules or ions in solution because the forces are proportional to the volume of the samples. Therefore, biological particles such as cells and DNA can be directly migrated or manipulated by these forces. For the separation and detection of molecules and ions, nano/micrometer-sized particles or composites need to be used as chemical mediators. In this regard, functional MNPs have been designed and synthesized as highly sensitive analytical probes for biosensing.22A high magnetic field and/or high magnetic field gradient are generally preferred to attain high performance in magneto-analytical methods. Electromagnets (<1 T) or superconducting magnets (5–15 T) are suitable to serve a homogeneous magnetic field, but small permanent magnets (<0.5 T) are commonly used for micro-analytical and electrochemical systems because of their excellent usability in small instruments. However, it should be noted that the magnetic field generated by a permanent magnet is inherently inhomogeneous. Therefore, not only the Lorentz force but also the magnetic gradient force should be carefully considered in electrochemical systems. In addition, the magnetic field dependence of the analytical performance is not always investigated, especially in studies using permanent magnets. The measurement of magnetic field dependency should be recommended to understand the mechanism of magnetic field effect and to determine the optimum magnetic field. A magnetic circuit composed of permanent magnets, which can generate a high magnetic field of more than 3 T (ref. 51) and a one-dimensional uniform magnetic field283 should be used more widely, combined with microscopic observations. Permanent magnets also provide a high magnetic field gradient to levitate a micro-water droplet.65,284 Furthermore, a rotating magnetic field by quadratic electromagnets15 and a frequency-modulated rotating magnetic field192 were used to rotate and orient submicron- and micro-particles. Electromagnets are especially suitable for providing an ac magnetic field. A pulsed magnetic field higher than 10 T and shorter than 1 ms can be generated by a rather simple electromagnet with a power supply. A pulsed magnet is recommended for observing magneto-optical effects such as Faraday rotation of solution samples285–287 and can be used to measure the magnetic moment of a microparticle from the relaxation experiment in the air.288,289 An extremely high magnetic field of 100 T was used for the phase transition studies.290 Alternatively, the effect of the extremely low magnetic field of the Earth (<50 μT) was studied in relation to the mechanism of magnetoreception of bees, birds, and fishes.291 Hore's group reported the radical-pair mechanism of light-sensitive cryptochrome proteins as a key reaction of magnetoreception,292 but some researchers293 proposed the role of magnetite in magnetoreception. Thus, the analytical applications of a geomagnetic field will be a fantastic future subject.
A magnetic gradient force was employed for the magnetophoretic velocity analysis of single microparticles, which attained attomole sensitivity for Mn(II). It is a unique advantage that the sensitivity of this method depends on the magnetic susceptibility of the analyte. Therefore, MNP can be recognized as an extremely sensitive tag in analyzing targeted bio-molecules and cells. When MNPs are used for migration or separation, the magnetic moment determined by the size and aggregation state of MNPs are crucially important, given that a single superparamagnetic MNP smaller than 10 nm is difficult to migrate in liquids by a magnetic gradient force. The study of dynamic force measurements by magnetic tweezers has been limited to DNA and proteins, but it should also be applied to the characterization of small molecules. Magneto-chromatography has not been improved to date, and thus substantial effort is required in the design of magnetic fields. The magneto-capillary effect, magnetic photonic crystals, and magnetic soft robots suggest valuable hints for future analytical applications.
Magnetic torque was utilized for the orientation of diamagnetic microcrystals by a static magnetic field and the alignment of microcrystals by a modulated magnetic field, which served for X-ray diffraction analysis.187 The magnetic orientation of MNPs was studied by linear dichroism spectroscopy205 and Sagnac interferometry.294 Here, again, the aggregation state of MNPs will severely affect the interpretation of the observation. Optical polarization measurements of the magnetic orientation of MNPs will become a promising method to measure the viscosity of the nano-environment,232 the stability of MNPs in solution, and the aggregation dynamics of nanoparticles given that the optical transition moment of MNPs is parallel to the easy axis of the magnetic moment of MNP295 and highly sensitive to the rotational relaxation dynamics.228
Electromagnetophoretic force was applied for the size separation and adsorption–desorption chromatography of microparticles,238 but more applications should be investigated. The electromagnetophoretic buoyancy was shown to be useful for dynamic force measurement and manipulation of diamagnetic particles.244 The local Lorentz force, which can be changed by the inhomogeneous current density around micro-subjects,241,254 will be useful to fabricate micro-structured flow systems. In a Cu magneto-electrodeposition surface, its chiral selectivity was observed.254 The chiral selectivity of the electrodeposited polymer and metal films needs to be studied more extensively. Alternatively, the contribution of electron spin orientation in the chiral molecule selectivity on ferromagnetic substrates was reported.278 The role of electron spin in the adsorption and electrochemical reactions of chiral molecules is the hottest topic in magneto-electrochemistry given that it may bridge between spintronics and molecular chirality. Recently, chiral-induced spin selectivity in the formation and recombination of radical pairs in the cryptochrome magnetoreception was discussed.296
The migration and rotation of magnetic subjects were usually measured by microscopic, optical, and electrochemical methods. However, extremely sensitive magnetic sensors such as nitrogen-vacancy (NV) centers297 and optically pumped magnetometers298,299 have been developed and commercially available. These sensors will be applied in micro-analytical systems in the near future. In conclusion, we can say that the future of “magneto-analytical science” is very attractive.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by JSPS KAKENHI grant numbers 21K05112 and 20K05551.References
- J. C. Giddings, Unified Separation Science, John Wiley & Sons, Ltd, New York, Chichester, Brisbane, Toronto, Singapore, 1991 Search PubMed.
- J. C. Giddings, Anal. Chem., 1981, 53, 945A–952A CrossRef CAS.
- E. Maxwell, Cryogenics, 1975, 15, 179–184 CrossRef.
- M. Sagawa, S. Fujimura, H. Yamamoto, Y. Matsuura and K. Hiraga, IEEE Trans. Magn., 1984, 20, 1584–1589 CrossRef.
- M. Hoenig, IEEE Trans. Magn., 1983, 19, 880–883 CrossRef.
- J. M. D. Coey, Magnetism and Magnetic Materials, Cambridge University Press, Cambridge, 2010 Search PubMed.
- H. Watarai, M. Suwa and Y. Iiguni, Anal. Bioanal. Chem., 2004, 378, 1693–1699 CrossRef CAS PubMed.
- M. Suwa and H. Watarai, Anal. Chim. Acta, 2011, 690, 137–147 CrossRef CAS PubMed.
- H. Watarai, Annu. Rev. Anal. Chem., 2013, 6, 353–378 CrossRef CAS PubMed.
- N. Pamme, Lab Chip, 2007, 7, 1644–1659 RSC.
- A. Munaz, M. J. A. Shiddiky and N.-T. Nguyen, Biomicrofluidics, 2018, 12, 031501 CrossRef PubMed.
- K. Aguilar-Arteaga, J. A. A. Rodriguez and E. Barrado, Anal. Chim. Acta, 2010, 674, 157–165 CrossRef CAS PubMed.
- J. S. Beveridge, J. R. Stephens and M. E. Williams, Annu. Rev. Anal. Chem., 2011, 4, 251–273 CrossRef CAS PubMed.
- S. Wang, J. Xu, W. Li, S. Sun, S. Gao and Y. Hou, Chem. Rev., 2022, 122, 5411–5475 CrossRef CAS PubMed.
- A. van Reenen, A. M. de Jong, J. M. J. den Toonder and M. W. J. Prins, Lab Chip, 2014, 14, 1966–1986 RSC.
- K. R. Hurley, H. L. Ring, H. Kang, N. D. Klein and C. L. Haynes, Anal. Chem., 2015, 87, 11611–11619 CrossRef CAS PubMed.
- M. Faraji, Nanochem. Res., 2016, 1, 264–290 CAS.
- C. P. Moerland, L. J. van IJzendoorn and M. W. J. Prins, Lab Chip, 2019, 19, 919–933 RSC.
- R. Soares, V. C. Martins, R. Macedo, F. A. Cardoso, S. A. M. Martins, D. M. Caetano, P. H. Fonseca, V. Silvério, S. Cardoso and P. P. Freitas, Anal. Bioanal. Chem., 2019, 411, 1839–1862 CrossRef CAS PubMed.
- X. Xuan, Micromachines, 2019, 10, 744 CrossRef PubMed.
- X. Liu, Y. Tian and L. Jiang, Nano Lett., 2021, 21, 2699–2708 CrossRef CAS PubMed.
- O. Civelekoglu, A. B. Frazier and A. F. Sarioglu, Magnetochemistry, 2022, 8, 10 CrossRef CAS.
- T. B. Jones, Electromechanisc of Particles, Cambridge University Press, Cambridge, 1995 Search PubMed.
- S. J. Gill, C. P. Malone and M. Downing, Rev. Sci. Instrum., 1960, 31, 1299–1303 CrossRef.
- M. Zborowski, C. B. Fuh, L. Sun, J. J. Chalmers and R. Green, Anal. Chem., 1995, 67, 3702–3712 CrossRef CAS PubMed.
- J. J. Chalmers, Y. Zhao, M. Nakamura, K. Melnik, L. Lasky, L. Moore and M. Zborowski, J. Magn. Magn. Mater., 1999, 194, 231–241 CrossRef CAS.
- J. J. Chalmers, S. Haam, Y. Zhao, K. McCloskey, L. Moore, M. Zborowski and P. S. Williams, Biotechnol. Bioeng., 1999, 64, 519–526 CrossRef CAS PubMed.
- M. Zborowski, G. R. Ostera, L. R. Moore, S. Milliron, J. J. Chalmers and A. N. Schechter, Biophys. J., 2003, 84, 2638–2645 CrossRef CAS PubMed.
- H. Zhang, L. R. Moore, M. Zborowski, P. S. Williams, S. Margel and J. J. Chalmers, Analyst, 2005, 130, 514–527 RSC.
- E. J. Chosy, M. Nakamura, K. Melnik, K. Comella, L. C. Lasky, M. Zborowski and J. J. Chalmers, Biotechnol. Bioeng., 2003, 82, 340–351 CrossRef CAS PubMed.
- D. R. Leigh, S. Steinert, L. R. Moore, J. J. Chalmers and M. Zborowski, Cytometry, Part A, 2005, 66, 103–108 CrossRef PubMed.
- X. Jin, Y. Zhao, A. Richardson, L. Moore, P. S. Williams, M. Zborowski and J. J. Chalmers, Analyst, 2008, 133, 1767 RSC.
- W. Xue, L. R. Moore, N. Nakano, J. J. Chalmers and M. Zborowski, J. Magn. Magn. Mater., 2019, 474, 152–160 CrossRef CAS PubMed.
- J. Kim, J. Gómez-Pastora, M. Weigand, M. Potgieter, N. A. Walters, E. Reátegui, A. F. Palmer, M. Yazer, M. Zborowski and J. J. Chalmers, Cytometry, Part A, 2019, 95, 478–487 CrossRef CAS PubMed.
- J. Gómez-Pastora, J. Kim, V. Multanen, M. Weigand, N. A. Walters, E. Reátegui, A. F. Palmer, M. H. Yazer, M. Zborowski and J. J. Chalmers, Exp. Hematol., 2021, 99, 21–31 CrossRef PubMed , e5.
- J. Kim, M. Weigand, A. F. Palmer, M. Zborowski, M. H. Yazer and J. J. Chalmers, Analyst, 2019, 144, 935–942 RSC.
- M. R. H. Weigand, J. Gómez-Pastora, J. Kim, M. T. Kurek, R. J. Hickey, D. C. Irwin, P. W. Buehler, M. Zborowski, A. F. Palmer and J. J. Chalmers, PLoS One, 2021, 16, 1–14 Search PubMed.
- X. Jin, J. J. Chalmers and M. Zborowski, Anal. Chem., 2012, 84, 4520–4526 CrossRef CAS PubMed.
- J. Kim, J. Gómez-Pastora, C. J. Gilbert, M. Weigand, N. A. Walters, E. Reátegui, A. F. Palmer, M. Yazer, M. Zborowski and J. J. Chalmers, Anal. Chem., 2020, 92, 1956–1962 CrossRef CAS PubMed.
- J. Gómez-Pastora, M. Weigand, J. Kim, A. F. Palmer, M. Yazer, P. C. Desai, M. Zborowski and J. J. Chalmers, Sci. Rep., 2022, 12, 1–12 CrossRef PubMed.
- X. Jin, M. H. Yazer, J. J. Chalmers and M. Zborowski, Analyst, 2011, 136, 2996 RSC.
- J. J. Chalmers, X. Jin, A. F. Palmer, M. H. Yazer, L. Moore, P. Amaya, K. Park, X. Pan and M. Zborowski, Anal. Chem., 2017, 89, 3702–3709 CrossRef CAS PubMed.
- H. Watarai and M. Namba, Anal. Sci., 2001, 17, 1233–1236 CrossRef CAS PubMed.
- M. Suwa and H. Watarai, Anal. Chem., 2002, 74(19), 5027–5032 CrossRef CAS PubMed.
- M. Suwa and H. Watarai, J. Chromatogr. A, 2003, 1013, 3–8 CrossRef CAS PubMed.
- M. Suwa and H. Watarai, Anal. Sci., 2008, 24, 133–137 CrossRef CAS PubMed.
- N. Shimamoto, S. Ohkoshi, O. Sato and K. Hashimoto, Chem. Lett., 2002, 31, 486–487 CrossRef.
- N. Shimamoto, S. Ohkoshi, O. Sato and K. Hashimoto, Inorg. Chem., 2002, 41, 678–684 CrossRef CAS PubMed.
- M. Suwa and H. Watarai, Chem. Commun., 2004, 1656 RSC.
- M. Suwa and H. Watarai, Sci. Technol. Adv. Mater., 2006, 7, 373–379 CrossRef CAS.
- S. Egami and H. Watarai, Analyst, 2009, 134, 278–282 RSC.
- Y. Urabe, H. Monjushiro and H. Watarai, AIP Adv., 2020, 10, 2–5 Search PubMed.
- H. Watarai and J. Chen, Anal. Chem., 2017, 89, 10141–10146 CrossRef CAS PubMed.
- H. Watarai and M. Kurahashi, Anal. Chim. Acta, 2020, 1111, 60–66 CrossRef CAS PubMed.
- M. Kawano and H. Watarai, Analyst, 2012, 137, 4123 RSC.
- H. Watarai, H. T. T. Duc, T. T. N. Lan, T. Zhang and S. Tsukahara, Anal. Sci., 2014, 30, 745–749 CrossRef CAS PubMed.
- J. Lim, C. Lanni, E. R. Evarts, F. Lanni, R. D. Tilton and S. A. Majetich, ACS Nano, 2011, 5, 217–226 CrossRef CAS PubMed.
- P. Zhang, S. Park and S. H. Kang, Chem. Commun., 2013, 49, 7298 RSC.
- S. S. Leong, Z. Ahmad, S. C. Low, J. Camacho, J. Faraudo and J. Lim, Langmuir, 2020, 36, 8033–8055 CrossRef CAS PubMed.
- J. Faraudo, J. S. Andreu and J. Camacho, Soft Matter, 2013, 9, 6654 RSC.
- J. S. Andreu, J. Camacho, J. Faraudo, M. Benelmekki, C. Rebollo and L. M. Martínez, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 1–8 CrossRef PubMed.
- S. S. Leong, Z. Ahmad and J. Lim, Soft Matter, 2015, 11, 6968–6980 RSC.
- Y. Ikezoe, N. Hirota, J. Nakagawa and K. Kitazawa, Nature, 1998, 393, 749–750 CrossRef CAS.
- Y. Ikezoe, T. Kaihatsu, S. Sakae, H. Uetake, N. Hirota and K. Kitazawa, Energy Convers. Manage., 2002, 43, 417–425 CrossRef CAS.
- H. Watarai and M. Namba, J. Chromatogr. A, 2002, 961, 3–8 CrossRef CAS PubMed.
- S. Ge, A. Nemiroski, K. A. Mirica, C. R. Mace, J. W. Hennek, A. A. Kumar and G. M. Whitesides, Angew. Chem., Int. Ed, 2020, 59, 17810–17855 CrossRef CAS PubMed.
- A. Winkleman, R. Perez-Castillejos, K. L. Gudiksen, S. T. Phillips, M. Prentiss and G. M. Whitesides, Anal. Chem., 2007, 79, 6542–6550 CrossRef CAS PubMed.
- K. A. Mirica, S. T. Phillips, C. R. MacE and G. M. Whitesides, J. Agric. Food Chem., 2010, 58, 6565–6569 CrossRef CAS PubMed.
- M. B. J. Atkinson, D. K. Bwambok, J. Chen, P. D. Chopade, M. M. Thuo, C. R. Mace, K. A. Mirica, A. A. Kumar, A. S. Myerson and G. M. Whitesides, Angew. Chem., Int. Ed., 2013, 52, 10208–10211 CrossRef CAS PubMed.
- C. K. Abrahamsson, A. Nagarkar, M. J. Fink, D. J. Preston, S. Ge, J. S. Bozenko and G. M. Whitesides, Angew. Chem., Int. Ed., 2020, 59, 874–881 CrossRef CAS PubMed.
- A. I. Rodríguez-Villarreal, M. D. Tarn, L. A. Madden, J. B. Lutz, J. Greenman, J. Samitier and N. Pamme, Lab Chip, 2011, 11, 1240–1248 RSC.
- J. Nguyen, D. V. Conca, J. Stein, L. Bovo, C. A. Howard and I. Llorente Garcia, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 2425–2434 CrossRef CAS PubMed.
- P. Dunne, T. Adachi, A. A. Dev, A. Sorrenti, L. Giacchetti, A. Bonnin, C. Bourdon, P. H. Mangin, J. M. D. Coey, B. Doudin and T. M. Hermans, Nature, 2020, 581, 58–62 CrossRef CAS PubMed.
- B. Ngamsom, E. A. Wandera, A. Iles, R. Kimani, F. Muregi, J. Gitaka and N. Pamme, Analyst, 2019, 144, 6889–6897 RSC.
- F. Shen, H. Hwang, Y. K. Hahn and J. K. Park, Anal. Chem., 2012, 84, 3075–3081 CrossRef CAS PubMed.
- Y. Jo, Y. K. Hahn and J. K. Park, Microfluid. Nanofluid., 2017, 21, 1–11 CrossRef CAS.
- F. Shen and J. K. Park, Anal. Chem., 2018, 90, 920–927 CrossRef CAS PubMed.
- G. P. Zhu, M. Hejiazan, X. Huang and N. T. Nguyen, Lab Chip, 2014, 14, 4609–4615 RSC.
- Z. D. Call, C. S. Carrell, I. Jang, B. J. Geiss, D. S. Dandy and C. S. Henry, Anal. Methods, 2020, 12, 5177–5185 RSC.
- N. Pamme and A. Manz, Anal. Chem., 2004, 76, 7250–7256 CrossRef CAS PubMed.
- A. Q. Alorabi, M. D. Tarn, J. Gómez-Pastora, E. Bringas, I. Ortiz, V. N. Paunov and N. Pamme, Lab Chip, 2017, 17, 3785–3795 RSC.
- M. Navi, N. Abbasi, M. Jeyhani, V. Gnyawali and S. S. H. Tsai, Lab Chip, 2018, 18, 3361–3370 RSC.
- K. Zhang, Q. Liang, X. Ai, P. Hu, Y. Wang and G. Luo, Anal. Chem., 2011, 83, 8029–8034 CrossRef CAS PubMed.
- C. W. Shields IV, J. L. Wang, K. A. Ohiri, E. D. Essoyan, B. B. Yellen, A. J. Armstrong and G. P. López, Lab Chip, 2016, 16, 3833–3844 RSC.
- K. Choi, A. H. C. Ng, R. Fobel and A. R. Wheeler, Annu. Rev. Anal. Chem., 2012, 5, 413–440 CrossRef CAS PubMed.
- Z.-G. Guo, W.-M. Liu and B.-L. Su, Appl. Phys. Lett., 2008, 92, 063104 CrossRef.
- R. P. S. De Campos, D. G. Rackus, R. Shih, C. Zhao, X. Liu and A. R. Wheeler, Anal. Chem., 2019, 91, 2506–2515 CrossRef CAS PubMed.
- C. Dixon, J. Lamanna and A. R. Wheeler, Lab Chip, 2020, 20, 1845–1855 RSC.
- T. Narahari, J. Dahmer, A. Sklavounos, T. Kim, M. Satkauskas, I. Clotea, M. Ho, J. Lamanna, C. Dixon, D. G. Rackus, S. J. R. da Silva, L. Pena, K. Pardee and A. R. Wheeler, Lab Chip, 2022, 22, 1748–1763 RSC.
- T. J. Hutama and R. D. Oleschuk, Lab Chip, 2017, 17, 2640–2649 RSC.
- P. Agrawal, K. J. Bachus, G. Carriere, P. Grouse and R. D. Oleschuk, Anal. Bioanal. Chem., 2019, 411, 5393–5403 CrossRef CAS PubMed.
- S. B. Smith, L. Finzi and C. Bustamante, Science, 1992, 258, 1122–1126 CrossRef CAS PubMed.
- T. R. Strick, J. F. Allemand, D. Bensimon, A. Bensimon and V. Croquette, Science, 1996, 271, 1835–1837 CrossRef CAS PubMed.
- C. Haber and D. Wirtz, Rev. Sci. Instrum., 2000, 71, 4561 CrossRef CAS.
- C. Gosse and V. Croquette, Biophys. J., 2002, 82, 3314–3329 CrossRef CAS PubMed.
- I. Vilfan, B. Startup, J. Lipfert, D. A. Koster and N. Dekker, Handbook of Single-Molecule Biophysics, Springer, US, New York, NY, 2009 Search PubMed.
- X. Zhang, H. Chen, H. Fu, P. S. Doyle and J. Yan, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 8103–8108 CrossRef CAS PubMed.
- Y.-J. Yang, H.-L. Dong, X.-W. Qiang, H. Fu, E.-C. Zhou, C. Zhang, L. Yin, X.-F. Chen, F.-C. Jia, L. Dai, Z.-J. Tan and X.-H. Zhang, J. Am. Chem. Soc., 2020, 142, 9203–9209 CrossRef CAS PubMed.
- E. Evans, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 105–128 CrossRef CAS PubMed.
- V. Vogel, Annu. Rev. Biophys. Biomol. Struct., 2006, 35, 459–488 CrossRef CAS PubMed.
- M. Kruithof, F. Chien, M. De Jager and J. Van Noort, Biophys. J., 2008, 94, 2343–2348 CrossRef CAS PubMed.
- T. Goto and H. Watarai, Langmuir, 2010, 26, 4848–4853 CrossRef CAS PubMed.
- G. Y. Yu, W. D. Hunt, M. Josowicz and J. Janata, Rev. Sci. Instrum., 2007, 78, 065111 CrossRef PubMed.
- S. Imai and H. Watarai, Anal. Sci., 2012, 28, 833–836 CrossRef CAS PubMed.
- D. Vella and L. Mahadevan, Am. J. Phys., 2005, 73, 817–825 CrossRef.
- N. Vandewalle, L. Clermont, D. Terwagne, S. Dorbolo, E. Mersch and G. Lumay, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 041402 CrossRef CAS PubMed.
- N. Vandewalle, N. Obara and G. Lumay, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 127 CrossRef CAS PubMed.
- W. Fei, M. M. Driscoll, P. M. Chaikin and K. J. M. Bishop, Soft Matter, 2018, 14, 4661–4665 RSC.
- F. Liu, Y. Li, Y. Huang, A. Tsyrenova, K. Miller, L. Zhou, H. Qin and S. Jiang, Nano Lett., 2020, 20, 8773–8780 CrossRef CAS PubMed.
- W. Fei, P. M. Tzelios and K. J. M. Bishop, Langmuir, 2020, 36, 6977–6983 CrossRef CAS PubMed.
- S. Ghosh, T. H. Fang, M. S. Uddin and K. Hidajat, Colloids Surf., B, 2013, 105, 267–277 CrossRef CAS PubMed.
- R. Kaur, P. Khullar, A. Gupta and M. S. Bakshi, Langmuir, 2021, 37, 14558–14570 CrossRef CAS PubMed.
- L.-L. Wu, M. Tang, Z.-L. Zhang, C.-B. Qi, J. Hu, X.-Y. Ma and D.-W. Pang, Anal. Chem., 2018, 90, 10518–10526 CrossRef CAS PubMed.
- S.-L. Hong, Y.-N. Zhang, Y.-H. Liu, M. Tang, D.-W. Pang, G. Wong, J. Chen, X. Qiu, G. F. Gao, W. Liu, Y. Bi and Z.-L. Zhang, Anal. Chem., 2018, 90, 7310–7317 CrossRef CAS PubMed.
- H. Y. Tsai, S. Y. Li and C. B. Fuh, Anal. Bioanal. Chem., 2018, 410, 1923–1929 CrossRef CAS PubMed.
- Q. Zhang, Y. Huang, B. Jiang, Y. Hu, J. Xie, X. Gao, B. Jia, H. Shen, W. Zhang and P. Yang, Anal. Chem., 2018, 90, 7357–7363 CrossRef CAS PubMed.
- H. Zhang, H. Lai, X. Wu, G. Li and Y. Hu, Anal. Chem., 2020, 92, 4607–4613 CrossRef CAS PubMed.
- J. Kang, D. Kang, G. Yeom and C.-J. Park, Anal. Chem., 2021, 93, 16804–16812 CrossRef CAS PubMed.
- A. Bagheri, M. Taghizadeh, M. Behbahani, A. Akbar Asgharinezhad, M. Salarian, A. Dehghani, H. Ebrahimzadeh and M. M. Amini, Talanta, 2012, 99, 132–139 CrossRef CAS PubMed.
- M. Esmaeilzadeh, Microchim. Acta, 2019, 186, 14 CrossRef PubMed.
- L. Huang, M. He, B. Chen and B. Hu, J. Mater. Chem. A, 2015, 3, 11587–11595 RSC.
- S. Rezabeyk and M. Manoochehri, RSC Adv., 2020, 10, 36897–36905 RSC.
- M. Zhao, C. Deng, X. Zhang and P. Yang, Proteomics, 2013, 13, 3387–3392 CrossRef CAS PubMed.
- J.-P. Wei, H. Wang, T. Luo, Z.-J. Zhou, Y.-F. Huang and B. Qiao, Anal. Bioanal. Chem., 2017, 409, 1895–1904 CrossRef CAS PubMed.
- Y. Xu, J. Jin, X. Li, Y. Han, H. Meng, C. Song and X. Zhang, Microchim. Acta, 2015, 182, 2313–2320 CrossRef CAS.
- Y. Xu, J. Jin, X. Li, Y. Han, H. Meng, J. Wu and X. Zhang, J. Sep. Sci., 2016, 39, 3647–3654 CrossRef CAS PubMed.
- N. Zhang, N. Sun and C. Deng, Chem. Commun., 2020, 56, 13999–14002 RSC.
- K. D. Clark, M. N. Emaus, M. Varona, A. N. Bowers and J. L. Anderson, J. Sep. Sci., 2018, 41, 209–235 CrossRef CAS PubMed.
- S. A. Pierson, O. Nacham, K. D. Clark, H. Nan, Y. Mudryk and J. L. Anderson, New J. Chem., 2017, 41, 5498–5505 RSC.
- M. A. Abdelaziz, F. R. Mansour and N. D. Danielson, Anal. Bioanal. Chem., 2021, 413, 205–214 CrossRef CAS PubMed.
- E. Fernández, L. Vidal and A. Canals, Anal. Bioanal. Chem., 2018, 410, 4679–4687 CrossRef PubMed.
- J. Merib, D. A. Spudeit, G. Corazza, E. Carasek and J. L. Anderson, Anal. Bioanal. Chem., 2018, 410, 4689–4699 CrossRef CAS PubMed.
- K. D. Clark, J. A. Purslow, S. A. Pierson, O. Nacham and J. L. Anderson, Anal. Bioanal. Chem., 2017, 409, 4983–4991 CrossRef CAS PubMed.
- K. D. Clark, O. Nacham, H. Yu, T. Li, M. M. Yamsek, D. R. Ronning and J. L. Anderson, Anal. Chem., 2015, 87, 1552–1559 CrossRef CAS PubMed.
- X. Wang, M. Liu and X. Ding, Langmuir, 2021, 37, 11665–11675 CrossRef CAS PubMed.
- A. Marengo, M. N. Emaus, C. M. Bertea, C. Bicchi, P. Rubiolo, C. Cagliero and J. L. Anderson, Anal. Bioanal. Chem., 2019, 411, 6583–6590 CrossRef CAS PubMed.
- A. N. Bowers, M. J. Trujillo-Rodríguez, M. Q. Farooq and J. L. Anderson, Anal. Bioanal. Chem., 2019, 411, 7375–7385 CrossRef CAS PubMed.
- M. N. Emaus and J. L. Anderson, Anal. Bioanal. Chem., 2020, 412, 8039–8049 CrossRef CAS PubMed.
- M. N. Emaus, K. D. Clark, P. Hinners and J. L. Anderson, Anal. Bioanal. Chem., 2018, 410, 4135–4144 CrossRef CAS PubMed.
- S. Tsukahara, A. Takata and H. Watarai, Anal. Sci., 2004, 20, 1515–1521 CrossRef CAS PubMed.
- A. Takata, S. Tsukahara and H. Watarai, Chem. Lett., 2004, 33, 518–519 CrossRef CAS.
- H. Y. Tsai, C. Yin, Y. P. Lin and C. B. Fuh, J. Chromatogr. A, 2006, 1120, 35–37 CrossRef CAS PubMed.
- H. Y. Tsai, C. F. Hsu, I. W. Chiu and C. Bor Fuh, Anal. Chem., 2007, 79, 8416–8419 CrossRef CAS PubMed.
- H. Y. Tsai, J. R. Chan, Y. C. Li, F. C. Cheng and C. B. Fuh, Biosens. Bioelectron., 2010, 25, 2701–2705 CrossRef CAS PubMed.
- C. S. Li, S. H. Chen, H. Y. Tsai and C. B. Fuh, Sens. Actuators, B, 2012, 166–167, 819–823 CrossRef CAS.
- H. Y. Tsai, M. J. Chuang, B. C. Chou, S. F. Yang and C. Bor Fuh, Sens. Actuators, B, 2016, 223, 834–838 CrossRef CAS.
- H. G. Mukherjee, D. Majumder and N. K. Srimani, J. Indian Chem. Soc., 1980, 11, 939–941 Search PubMed.
- T. Nomizu, K. Yamamoto and M. Watanabe, Anal. Sci., 2001, 17, 177–180 Search PubMed.
- M. Fujiwara, D. Kodoi, W. Duan and Y. Tanimoto, J. Phys. Chem. B, 2001, 105, 3343–3345 CrossRef CAS.
- M. Fujiwara, K. Chie, J. Sawai, D. Shimizu and Y. Tanimoto, J. Phys. Chem. B, 2004, 108, 3531–3534 CrossRef CAS.
- M. Fujiwara, K. Mitsuda and Y. Tanimoto, J. Phys. Chem. B, 2006, 110, 13965–13969 CrossRef CAS PubMed.
- E. Barrado and J. A. Rodríguez, J. Chromatogr. A, 2006, 1128, 189–193 CrossRef CAS PubMed.
- Z. Cai, N. L. Smith, J.-T. Zhang and S. A. Asher, Anal. Chem., 2015, 87, 5013–5025 CrossRef CAS PubMed.
- H. Hu, C. Chen and Q. Chen, J. Mater. Chem. C, 2013, 1, 6013 RSC.
- J. Ge, Y. Hu and Y. Yin, Angew. Chem., Int. Ed., 2007, 46, 7428–7431 CrossRef CAS PubMed.
- R. Xuan, Q. Wu, Y. Yin and J. Ge, J. Mater. Chem., 2011, 21, 3672–3676 RSC.
- H. Hu, H. Zhong, C. Chen and Q. Chen, J. Mater. Chem. C, 2014, 2, 3695 RSC.
- M. Zhang, D. J. Magagnosc, I. Liberal, Y. Yu, H. Yun, H. Yang, Y. Wu, J. Guo, W. Chen, Y. J. Shin, A. Stein, J. M. Kikkawa, N. Engheta, D. S. Gianola, C. B. Murray and C. R. Kagan, Nat. Nanotechnol., 2017, 12, 228–232 CrossRef CAS PubMed.
- V. T. Tran, D. K. Lee, J. Kim, K.-J. Jeong, C.-S. Kim and J. Lee, ACS Appl. Mater. Interfaces, 2020, 12, 16584–16591 CrossRef CAS PubMed.
- Y. Kim and X. Zhao, Chem. Rev., 2022, 122, 5317–5364 CrossRef CAS PubMed.
- X. Zhao, J. Kim, C. A. Cezar, N. Huebsch, K. Lee, K. Bouhadir and D. J. Mooney, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 67–72 CrossRef CAS PubMed.
- J. Zhang, Z. Ren, W. Hu, R. H. Soon, I. C. Yasa, Z. Liu and M. Sitti, Sci. Robot., 2021, 6, eabf0112 CrossRef PubMed.
- R. María-Hormigos, B. Jurado-Sánchez and A. Escarpa, Anal. Chem., 2018, 90, 9830–9837 CrossRef PubMed.
- J. Yu, D. Jin, K.-F. Chan, Q. Wang, K. Yuan and L. Zhang, Nat. Commun., 2019, 10, 5631 CrossRef CAS PubMed.
- Q. Wang, K. F. Chan, K. Schweizer, X. Du, D. Jin, S. C. H. Yu, B. J. Nelson and L. Zhang, Sci. Adv., 2021, 7, 1–13 Search PubMed.
- B. Wang, K. F. Chan, K. Yuan, Q. Wang, X. Xia, L. Yang, H. Ko, Y.-X. J. Wang, J. J. Y. Sung, P. W. Y. Chiu and L. Zhang, Sci. Robot., 2021, 6, eabd2813 CrossRef PubMed.
- D. Jin and L. Zhang, Acc. Chem. Res., 2022, 55, 98–109 CrossRef CAS PubMed.
- T. Takeuchi, T. Mizuno, T. Higashi, A. Yamagishi and M. Date, J. Magn. Magn. Mater., 1995, 140–144, 1462–1463 CrossRef.
- T. Takeuchi, T. Mizuno, T. Higashi, A. Yamagishi and M. Date, Phys. B, 1994, 201, 601–605 CrossRef CAS.
- T. Higashi, A. Yamagishi, T. Takeuchi, N. Kawaguchi, S. Sagawa, S. Onishi and M. Date, Blood, 1993, 82, 1328–1334 CrossRef CAS PubMed.
- Y. Kitahama, Y. Kimura and K. Takazawa, Langmuir, 2006, 22, 7600–7604 CrossRef CAS PubMed.
- Y. Fujiwara, N. Shibata, Y. Matsumoto and Y. Tanimoto, J. Magn. Magn. Mater., 2007, 310, 2859–2861 CrossRef CAS.
- H. Yonemura, Y. Yamamoto, S. Yamada, Y. Fujiwara and Y. Tanimoto, Sci. Technol. Adv. Mater., 2008, 9, 024213 CrossRef PubMed.
- H. Yonemura, K. Yuno, Y. Yamamoto, S. Yamada, Y. Fujiwara and Y. Tanimoto, Synth. Met., 2009, 159, 955–960 CrossRef CAS.
- H. Yonemura, K. Yuno and S. Yamada, Jpn. J. Appl. Phys., 2010, 49, 01AE06 Search PubMed.
- H. Yonemura, J. Suyama, T. Arakawa and S. Yamada, Thin Solid Films, 2009, 518, 668–673 CrossRef CAS.
- H. Yonemura, S. Natsuko, J. Suyama and S. Yamada, J. Photochem. Photobiol., A, 2011, 220, 179–187 CrossRef CAS.
- Y. Takeuchi, Y. Sugawara, T. Sugawara and M. Iwasaka, IEEE Trans. Magn., 2014, 50, 1–4 Search PubMed.
- Y. Takeuchi, M. Sekiya, A. Hamasaki, M. Iwasaka and M. Matsuda, IEEE Trans. Magn., 2017, 57, 5100105 Search PubMed.
- Y. Takeuchi, M. Iwasaka, M. Matsuda and A. Hamasaki, IEEE Trans. Magn., 2021, 57, 1–5 Search PubMed.
- M. Iwasaka and Y. Mizukawa, Langmuir, 2013, 29, 4328–4334 CrossRef CAS PubMed.
- M. Iwasaka, Y. Mizukawa and N. W. Roberts, Langmuir, 2016, 32, 180–187 CrossRef CAS PubMed.
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Oxford University Press, Oxford, 2nd edn, 1993 Search PubMed.
- Y.-K. Kim, J. Noh, K. Nayani and N. L. Abbott, Soft Matter, 2019, 15, 6913–6929 RSC.
- N. L. Abbott, Eng. Sci. Fundam. - Core Program. Top. 2011 AIChE Annu. Meet., 2011, 1, pp. 27–28.
- F. Yesil, M. Suwa and S. Tsukahara, Langmuir, 2018, 34, 81–87 CrossRef CAS PubMed.
- T. Kimura and M. Yoshino, Langmuir, 2005, 21, 4805–4808 CrossRef CAS PubMed.
- M. Yamaguchi, S. Ozawa and I. Yamamoto, Jpn. J. Appl. Phys., 2010, 49, 6–9 Search PubMed.
- M. Yamaguchi, I. Yamamoto and T. Kimura, Jpn. J. Appl. Phys., 2013, 52, 6–9 Search PubMed.
- F. Kimura, W. Oshima, H. Matsumoto, H. Uekusa, K. Aburaya, M. Maeyama and T. Kimura, CrystEngComm, 2014, 16, 6630–6634 RSC.
- F. Kimura, T. Kimura, W. Oshima, M. Maeyama and K. Aburaya, J. Appl. Crystallogr., 2010, 43, 151–153 CrossRef CAS.
- T. Kimura, C. Chang, F. Kimura and M. Maeyama, J. Appl. Crystallogr., 2009, 42, 535–537 CrossRef CAS PubMed.
- F. Kimura, K. Mizutani, B. Mikami and T. Kimura, Cryst. Growth Des., 2011, 11, 12–15 CrossRef CAS.
- S. Tsukui, F. Kimura, E. F. Garman, S. Baba, N. Mizuno, B. Mikami and T. Kimura, J. Appl. Crystallogr., 2016, 49, 457–461 CrossRef CAS.
- S. Tsukui, F. Kimura, K. Kusaka, S. Baba, N. Mizuno and T. Kimura, Acta Crystallogr., Sect. D: Struct. Biol., 2016, 72, 823–829 CrossRef CAS PubMed.
- R. Kusumi, F. Kimura, G. Song and T. Kimura, J. Magn. Reson., 2012, 223, 68–72 CrossRef CAS PubMed.
- F. Kimura and T. Kimura, CrystEngComm, 2018, 20, 861–872 RSC.
- C. Tsuboi, K. Aburaya, F. Kimura, M. Maeyama and T. Kimura, CrystEngComm, 2016, 18, 2404–2407 RSC.
- C. Tsuboi, S. Tsukui, F. Kimura, T. Kimura, K. Hasegawa, S. Baba and N. Mizuno, J. Appl. Crystallogr., 2016, 49, 2100–2105 CrossRef CAS.
- C. Tsuboi, F. Kimura, T. Tanaka and T. Kimura, Cryst. Growth Des., 2016, 16, 2810–2813 CrossRef CAS.
- J. P. Llewellyn, J. Phys. D: Appl. Phys., 1983, 16, 95 CrossRef CAS.
- M. Xu and P. J. Ridler, J. Appl. Phys., 1997, 82, 326–332 CrossRef CAS.
- F. Bentivegna, J. Ferré, M. Nývlt, J. P. Jamet, D. Imhoff, M. Canva, A. Brun, P. Veillet, Š. Višňovský, F. Chaput and J. P. Boilot, J. Appl. Phys., 1998, 83, 7776–7788 CrossRef CAS.
- E. Hasmonay, E. Dubois, S. Neveu, J. C. Bacri and R. Perzynski, Eur. Phys. J. B, 2001, 21, 19–29 CrossRef CAS.
- H. Watarai and S. S. M. Sakurai, Langmuir, 2020, 36, 12414–12422 CrossRef CAS PubMed.
- G. Trefalt, I. Szilagyi, T. Oncsik, A. Sadeghpour and M. Borkovec, Chimia, 2013, 67, 772 CrossRef CAS PubMed.
- A. Ranzoni, J. J. H. B. Schleipen, L. J. van IJzendoorn and M. W. J. Prins, Nano Lett., 2011, 11, 2017–2022 CrossRef CAS PubMed.
- A. Ranzoni, G. Sabatte, L. J. van IJzendoorn and M. W. J. Prins, ACS Nano, 2012, 6, 3134–3141 CrossRef CAS PubMed.
- F. A. Gutiérrez-Mejiá, C. P. Moerland, L. J. Van Ijzendoorn and M. W. J. Prins, Nanoscale, 2019, 11, 19933–19942 RSC.
- M. R. W. Scheepers, A. R. Romijn, L. J. Van Ijzendoorn and M. W. J. Prins, Langmuir, 2019, 35, 10533–10541 CrossRef CAS PubMed.
- M. R. W. Scheepers, S. R. R. Haenen, J. M. Coers, L. J. van IJzendoorn and M. W. J. Prins, Nanoscale, 2020, 12, 14605–14614 RSC.
- B. Gleich and J. Weizenecker, Nature, 2005, 435, 1214–1217 CrossRef CAS PubMed.
- E. Y. Yu, M. Bishop, B. Zheng, R. M. Ferguson, A. P. Khandhar, S. J. Kemp, K. M. Krishnan, P. W. Goodwill and S. M. Conolly, Nano Lett., 2017, 17, 1648–1654 CrossRef CAS PubMed.
- F. J. Teran, C. Casado, N. Mikuszeit, G. Salas, A. Bollero, M. P. Morales, J. Camarero and R. Miranda, Appl. Phys. Lett., 2012, 101, 62413 CrossRef.
- D. Cabrera, A. Coene, J. Leliaert, E. J. Artés-Ibáñez, L. Dupré, N. D. Telling and F. J. Teran, ACS Nano, 2018, 12, 2741–2752 CrossRef CAS PubMed.
- M. Hess, E. Roeben, A. Habicht, S. Seiffert and A. M. Schmidt, Soft Matter, 2019, 15, 842–850 RSC.
- A. C. Bohórquez, M. Unni, S. Belsare, A. Chiu-Lam, L. Rice, C. Pampo, D. Siemann and C. Rinaldi, Bioconjugate Chem., 2018, 29, 2793–2805 CrossRef PubMed.
- M. Hess, M. Gratz, H. Remmer, S. Webers, J. Landers, D. Borin, F. Ludwig, H. Wende, S. Odenbach, A. Tschöpe and A. M. Schmidt, Soft Matter, 2020, 16, 7562–7575 RSC.
- M. Donolato, P. Antunes, R. S. Bejhed, T. Zardán Gómez de la Torre, F. W. Østerberg, M. Strömberg, M. Nilsson, M. Strømme, P. Svedlindh, M. F. Hansen and P. Vavassori, Anal. Chem., 2015, 87, 1622–1629 CrossRef CAS PubMed.
- B. Tian, J. Fock, G. A. S. Minero, F. Garbarino and M. F. Hansen, Anal. Chem., 2019, 91, 10102–10109 CrossRef CAS PubMed.
- J. Carrey, B. Mehdaoui and M. Respaud, J. Appl. Phys., 2011, 109, 83921 CrossRef.
- N. A. Usov and B. Y. Liubimov, J. Appl. Phys., 2012, 112, 23901 CrossRef.
- S. Ota, Y. Matsugi, T. Nakamura, R. Takeda, Y. Takemura, I. Kato, S. Nohara, T. Sasayama, T. Yoshida and K. Enpuku, J. Magn. Magn. Mater., 2019, 474, 311–318 CrossRef CAS.
- H. Mamiya and B. Jeyadevan, Sci. Rep., 2011, 1, 157 CrossRef PubMed.
- S. A. Shah, D. B. Reeves, R. M. Ferguson, J. B. Weaver and K. M. Krishnan, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 94438 CrossRef PubMed.
- S. B. Trisnanto, S. Ota and Y. Takemura, Appl. Phys. Express, 2018, 11, 75001 CrossRef.
- L. M. Bauer, S. F. Situ, M. A. Griswold and A. C. S. Samia, J. Phys. Chem. Lett., 2015, 6, 2509–2517 CrossRef CAS PubMed.
- S. Ota and Y. Takemura, J. Phys. Chem. C, 2019, 123, 28859–28866 CrossRef.
- M. Suwa and H. Watarai, J. Phys.: Conf. Ser., 2009, 156, 012025 CrossRef.
- M. Suwa, A. Uotani and S. Tsukahara, J. Appl. Phys., 2019, 125, 123901 CrossRef.
- M. Suwa, A. Uotani and S. Tsukahara, Appl. Phys. Lett., 2020, 116, 262403 CrossRef CAS.
- M. Suwa, A. Uotani, Y. Tojo, R. Onodera and S. Tsukahara, Langmuir, 2022, 38, 9708–9719 CrossRef CAS PubMed.
- A. Kolin, Science, 1953, 117, 134–137 CrossRef CAS PubMed.
- A. Kolin and R. T. Kado, Nature, 1958, 182, 510–512 CrossRef CAS PubMed.
- S. Ozawa, D. Kurosaka, I. Yamamoto and T. Takamasu, Jpn. J. Appl. Phys., 2011, 50, 070212 CrossRef.
- M. Namba, H. Watarai and T. Takeuchi, Anal. Sci., 2000, 16, 5–9 CrossRef CAS.
- Y. Iiguni and H. Ohtani, Anal. Sci., 2013, 29, 35–39 CrossRef CAS PubMed.
- Y. Iiguni and H. Watarai, J. Chromatogr. A, 2005, 1073, 93–98 CrossRef CAS PubMed.
- Y. Fukui, Y. Iiguni, S. Kitagawa and H. Ohtani, Anal. Sci., 2015, 31, 197–203 CrossRef CAS PubMed.
- Y. Iiguni, A. Tanaka, S. Kitagawa and H. Ohtani, Anal. Sci., 2016, 32, 41–48 CrossRef CAS PubMed.
- M. Funaki, M. Suwa and H. Watarai, Anal. Sci., 2017, 33, 1013–1019 CrossRef CAS PubMed.
- Y. Iiguni and H. Watarai, Anal. Sci., 2003, 19, 33–37 CrossRef CAS PubMed.
- Y. Iiguni and H. Watarai, Bull. Chem. Soc. Jpn., 2006, 79, 47–52 CrossRef CAS.
- Y. Iiguni and H. Watarai, Analyst, 2010, 135, 1426–1432 RSC.
- T. Kato, Y. Iiguni and H. Watarai, Bull. Chem. Soc. Jpn., 2016, 89, 1487–1492 CrossRef CAS.
- G. I. Bell, Science, 1978, 200, 618–627 CrossRef CAS PubMed.
- S. Wakiyama and H. Watarai, Anal. Sci., 2017, 33, 399–401 CrossRef CAS PubMed.
- L. M. A. Monzon and J. M. D. Coey, Electrochem. Commun., 2014, 42, 38–41 CrossRef CAS.
- R. Aogaki, K. Fueki and T. Mukaibo, Denki Kagaku oyobi Kogyo Butsuri Kagaku, 1975, 43, 504–508 CrossRef CAS.
- R. Aogaki, R. Morimoto and M. Asanuma, J. Magn. Magn. Mater., 2010, 322, 1664–1668 CrossRef CAS.
- R. Morimoto, M. Miura, A. Sugiyama, M. Miura, Y. Oshikiri, Y. Kim, I. Mogi, S. Takagi, Y. Yamauchi and R. Aogaki, J. Phys. Chem. B, 2020, 124, 11854–11869 CrossRef CAS PubMed.
- R. Morimoto, M. Miura, A. Sugiyama, M. Miura, Y. Oshikiri, Y. Kim, I. Mogi, S. Takagi, Y. Yamauchi and R. Aogaki, J. Phys. Chem. B, 2020, 124, 11870–11881 CrossRef CAS PubMed.
- R. Aogaki, Magnetohydrodynamics, 2003, 39, 453–460 CrossRef.
- I. Mogi, R. Morimoto, R. Aogaki and K. Watanabe, Sci. Rep., 2013, 3, 2574 CrossRef PubMed.
- I. Mogi, R. Morimoto and R. Aogaki, Curr. Opin. Electrochem., 2018, 7, 1–6 CrossRef CAS.
- M. Huang, K. Skibinska, P. Zabinski, M. Wojnicki, G. Włoch, K. Eckert and G. Mutschke, Electrochim. Acta, 2022, 420, 140422 CrossRef CAS.
- G. Mutschke, K. Tschulik, T. Weier, M. Uhlemann, A. Bund and J. Fröhlich, Electrochim. Acta, 2010, 55, 9060–9066 CrossRef CAS.
- G. Mutschke, K. Tschulik, M. Uhlemann, A. Bund and J. Fröhlich, Phys. Rev. Lett., 2012, 109, 229401 CrossRef PubMed.
- I. Mogi, R. Aogaki, R. Morimoto and K. Watanabe, Acta Phys. Pol., A, 2014, 126, 380–381 CrossRef.
- N. Leventis and X. Gao, Anal. Chem., 2001, 73, 3981–3992 CrossRef CAS PubMed.
- J. West, B. Karamata, B. Lillis, J. P. Gleeson, J. Alderman, J. K. Collins, W. Lane, A. Mathewson and H. Berney, Lab Chip, 2002, 2, 224–230 RSC.
- S. Qian and H. H. Bau, Mech. Res. Commun., 2009, 36, 10–21 CrossRef PubMed.
- E. A. Clark and I. Fritsch, Anal. Chem., 2004, 76, 2415–2418 CrossRef CAS PubMed.
- P. U. Arumugam, E. S. Fakunle, E. C. Anderson, S. R. Evans, K. G. King, Z. P. Aguilar, C. S. Carter and I. Fritsch, J. Electrochem. Soc., 2006, 153, E185 CrossRef CAS.
- Z. P. Aguilar, P. Arumugam and I. Fritsch, J. Electroanal. Chem., 2006, 591, 201–209 CrossRef CAS.
- M. C. Weston, M. D. Gerner and I. Fritsch, Anal. Chem., 2010, 82, 3411–3418 CrossRef CAS PubMed.
- C. K. Nash and I. Fritsch, Anal. Chem., 2016, 88, 1601–1609 CrossRef CAS PubMed.
- F. Z. Khan and I. Fritsch, J. Electrochem. Soc., 2019, 166, H615–H627 CrossRef CAS.
- F. Z. Khan, J. A. Hutcheson, C. J. Hunter, A. J. Powless, D. Benson, I. Fritsch and T. J. Muldoon, Anal. Chem., 2018, 90, 7862–7870 CrossRef CAS PubMed.
- J. C. Sikes, K. Wonner, A. Nicholson, P. Cignoni, I. Fritsch and K. Tschulik, ACS Phys. Chem. Au, 2022, 2, 289–298 CrossRef CAS PubMed.
- T. Cesin-AbouAtme, C. G. Lopez-Almeida, G. Molina-Labastida and J. G. Ibanez, J. Chem. Educ., 2021, 98, 3045–3049 CrossRef CAS.
- W. Zhang, K. Banerjee-Ghosh, F. Tassinari and R. Naaman, ACS Energy Lett., 2018, 3, 2308–2313 CrossRef CAS.
- C. Hunt, Z. Zhang, K. Ocean, R. P. Jansonius, M. Abbas, D. J. Dvorak, A. Kurimoto, E. W. Lees, S. Ghosh, A. Turkiewicz, F. A. Garcés Pineda, D. K. Fork and C. P. Berlinguette, J. Am. Chem. Soc., 2022, 144, 733–739 CrossRef CAS PubMed.
- Z. Bian, K. Kato, T. Ogoshi, Z. Cui, B. Sa, Y. Tsutsui, S. Seki and M. Suda, Adv. Sci., 2022, 9, 2201063 CrossRef CAS PubMed.
- I. Mogi and K. Watanabe, Jpn. J. Appl. Phys., 2005, 44, L199–L201 CrossRef CAS.
- I. Mogi, R. Aogaki and K. Watanabe, Bull. Chem. Soc. Jpn., 2015, 88, 1479–1485 CrossRef CAS.
- I. Mogi, R. Aogaki and K. Takahashi, Magnetochemistry, 2021, 7, 142 CrossRef CAS.
- R. A. Rosenberg, D. Mishra and R. Naaman, Angew. Chem., Int. Ed., 2015, 54, 7295–7298 CrossRef CAS PubMed.
- R. Naaman and D. H. Waldeck, Annu. Rev. Phys. Chem., 2015, 66, 263–281 CrossRef CAS PubMed.
- K. Banerjee-Ghosh, O. Ben Dor, F. Tassinari, E. Capua, S. Yochelis, A. Capua, S.-H. Yang, S. S. P. Parkin, S. Sarkar, L. Kronik, L. T. Baczewski, R. Naaman and Y. Paltiel, Science, 2018, 360, 1331–1334 CrossRef CAS PubMed.
- T. S. Metzger, S. Mishra, B. P. Bloom, N. Goren, A. Neubauer, G. Shmul, J. Wei, S. Yochelis, F. Tassinari, C. Fontanesi, D. H. Waldeck, Y. Paltiel and R. Naaman, Angew. Chem., Int. Ed., 2020, 59, 1653–1658 CrossRef CAS PubMed.
- K. Santra, D. Bhowmick, Q. Zhu, T. Bendikov and R. Naaman, J. Phys. Chem. C, 2021, 125, 17530–17536 CrossRef CAS.
- H. Lee, H. Han and S. Jeon, Anal. Chem., 2021, 93, 12237–12242 CrossRef CAS PubMed.
- Y. Ikezoe and M. Sugaya, US20220181054, 2022.
- K. Isai, M. Suwa and H. Watarai, Anal. Sci., 2009, 25, 1–3 CrossRef CAS PubMed.
- K. Miyamoto, K. Isai, M. Suwa and H. Watarai, J. Am. Chem. Soc., 2009, 131, 6328–6329 CrossRef CAS PubMed.
- M. Suwa, Y. Nakano, S. Tsukahara and H. Watarai, Anal. Chem., 2013, 85, 5176–5183 CrossRef CAS PubMed.
- M. Arase, M. Suwa and H. Watarai, Anal. Chem., 2006, 78, 6660–6663 CrossRef CAS PubMed.
- M. Arase, M. Suwa and H. Watarai, Anal. Bioanal. Chem., 2008, 391, 701–707 CrossRef CAS PubMed.
- Y. H. Matsuda, Crystals, 2020, 10, 866 CrossRef CAS.
- S. Nimpf and D. A. Keays, iScience, 2022, 25, 104454 CrossRef PubMed.
- P. J. Hore and H. Mouritsen, Annu. Rev. Biophys., 2016, 45, 299–344 CrossRef CAS PubMed.
- G. Bao, J. Appl. Mech., 2021, 88, 1–7 CrossRef PubMed.
- H. Watarai and Z. Chen, Bull. Chem. Soc. Jpn., 2019, 92, 949–951 CrossRef CAS.
- H. Watarai, S. Subhan Memon Sakurai and H. Subhan Memon Sakurai, Anal. Sci., 2019, 35, 951–954 CrossRef CAS PubMed.
- J. Luo and P. J. Hore, New J. Phys., 2021, 23, 043032 CrossRef CAS.
- V. Radu, J. C. Price, S. J. Levett, K. K. Narayanasamy, T. D. Bateman-Price, P. B. Wilson and M. L. Mather, ACS Sens., 2020, 5, 703–710 CrossRef CAS PubMed.
- S. Knappe, T. H. Sander, O. Kosch, F. Wiekhorst, J. Kitching and L. Trahms, Appl. Phys. Lett., 2010, 97, 133703 CrossRef.
- O. Baffa, R. H. Matsuda, S. Arsalani, A. Prospero, J. R. A. Miranda and R. T. Wakai, J. Magn. Magn. Mater., 2019, 475, 533–538 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |



