Recent progress on the effects of impurities and defects on the properties of Ga₂O₃

Abstract

Ga₂O₃ is attractive for power devices and solar-blind ultraviolet photodetectors due to its ultra-wide bandgap, large breakdown field, and favorable stability. However, it is difficult to prepare the ideal Ga₂O₃ since there are plenty of defects (e.g., vacancies and interstitial atoms) in the bulk and films which can affect the physical properties of Ga₂O₃. Besides, the deep level defects act as trapped centers and have influence on the sensitivity and responsivity of optoelectronic devices. It has been discovered that doping is an effective strategy to modulate the properties of Ga₂O₃. In this review, the effects of defects and impurities on the material properties of Ga₂O₃ are mainly discussed. Considering that β-Ga₂O₃ is the most stable and the most studied currently, it is the main focus of this review. Firstly, the intrinsic properties (e.g., electronic, absorption, thermal and mechanical properties) of β-Ga₂O₃ are introduced, and then the influence of impurities (e.g., dopants and passivators) and defects on the electronic properties of β-Ga₂O₃ is discussed emphatically. Besides, the other properties (e.g., luminescence, magnetic, and piezoelectric properties) of β-Ga₂O₃ modulated by defects and impurities are also briefly discussed. Meanwhile, some new research directions are also worth exploring. These problems and potential directions are summarized and discussed in the last section.

---

Yifei Wang

Yifei Wang obtained his BS in microelectronics science and engineering from Xidian University in 2019. From 2019 to the present, he studies in the State Key Discipline Laboratory of Wide Band Gap Semiconductor Technology at Xidian University, under the supervision of Prof. Jingjing Chang and Prof. Yue Hao. His current research focuses on the preparation of metal oxide-based thin-film transistors and photoelectric devices, and the materials simulation of wide bandgap semiconductors.

Jingjing Chang

Prof. Jingjing Chang received his PhD degree from the National University of Singapore in 2014. After graduation, he worked as a Research Fellow in Materials Science & Engineering, National University of Singapore, from 2014 to 2015. Then he joined Xidian University, where he is currently a professor. His research interests include perovskite and metal oxide materials, electronic devices (transistors and RRAM devices) and optoelectronic devices (solar cells, photodetectors, and X-ray detectors).

Yue Hao

Prof. Yue Hao received his PhD degree in computational mathematics from Xi’an Jiaotong University in 1991. He is the Vice president of Xidian University, professor, doctor, advisor of PhD candidates, a senior member of the IEEE, executive director of the Chinese Association of Electronics, chairman of the executive councils of the Shaanxi Provincial Association of Electronics, the Trade Association of Integrated Circuits, and the Shaanxi Provincial Semiconductor Illumination Association. His research interests include wide bandgap semiconductor materials and devices, reliability of ultra-deep submicron small-sized devices, SoC design, and its design methodology.

---

I. Introduction

Gallium oxide (Ga₂O₃), one of the ultra-wide bandgap (UWBG) semiconductors, has attracted more and more attention in recent years, as shown in Fig. 1.^1–5 The literature on Ga₂O₃ exploded in the beginning of this century. Ga₂O₃ possesses many superior characteristics compared with other foregone semiconductors (e.g., SiC, GaN, GaAs, Si, and so on). For example, Ga₂O₃ single wafers with large areas can be prepared by scalable and low-cost melt growth techniques. Moreover, its large bandgap (E_g) ranges from 4.6 eV to 5.3 eV, and its breakdown field is up to 8 MV cm⁻¹, which further improves its applications in high voltage devices, as shown in Fig. 2(a).^6,7 The relationship between the on-resistance and breakdown voltage of common semiconductors is shown in Fig. 2(b). Such log–log plots represent Baliga's figure of merit (BFOM) of semiconductors which is a typical FOM for the low-frequency unipolar vertical power switch. Generally, the high voltage and low on-resistance properties of semiconductors facilitate generation of less heat and help obtain a similarly ideal situation at high voltage for the switch-type power device.⁷ Such characteristics are beneficial for developing efficient manufacturing processes and reducing the size and cost in the field of power switching devices. The ultra-wide bandgap semiconductor Ga₂O₃ possesses a higher BFOM than the traditional semiconductor so that Ga₂O₃ based devices provide more efficient power switching and energy savings than the devices based on Si, GaAs, SiC, and GaN.⁸ In addition, the large bandgap leads to its cut-off wavelength located in the deep ultraviolet region. The cut-off wavelength of Ga₂O₃-based photodetectors ranges from 250 nm to 280 nm, which meets the requirements of deep ultraviolet light (DUV) detection, as shown in Fig. 2(c).⁹ Meanwhile, the photodetectors based on Ga₂O₃ are insensitive to visible and infrared light, which improves the sensitivity of ultraviolet (UV) detection. In addition, the solar-blind photodetectors based on Ga₂O₃ can also overcome the shortcomings of other semiconductor-based photodetectors, e.g. Al_xGa_1−xN and Mg_xZn_1−xO. That is, high temperatures are required when the Al component to be incorporated is high in photodetectors based on Al_xGa_1−xN (T > 1350 °C). The phase separation from wurtzite to the rock-salt structure occurs in photodetectors based on Mg_xZn_1−xO when the Mg component is high.^10–14 Besides, Ga₂O₃ has a relatively high density (6.44 g cm⁻³) and radiation resistance, as well as rapid scintillation and decay time constant of several nanoseconds, which makes it a promising candidate for nuclear radiation detection.^15,16 Therefore, the applications of Ga₂O₃ are more and more extensive with the development of science and technology. Fig. 3 summarizes the frequently applied devices based on Ga₂O₃. The main application areas of Ga₂O₃ are photoelectronic detection, power devices, and some other applications (e.g., radiation detection, flame detectors, gas sensors, memory devices, and photocatalysts). The successful applications of these areas are related to the unique properties of Ga₂O₃ closely. To obtain high-performance devices based on Ga₂O₃, understanding the basic properties of Ga₂O₃ is indispensable in the process of device preparation and application.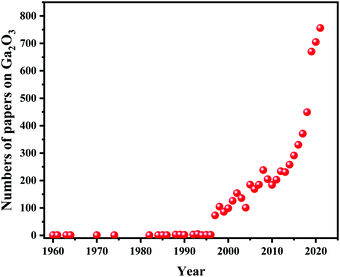

Fig. 1 Number of research studies on Ga₂O₃ as a function of time (data derived from Web of Science).

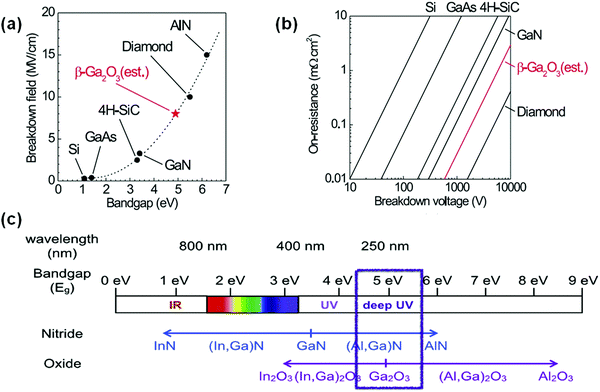Fig. 2 (a) Relationship between the breakdown fields and the bandgaps of different generation semiconductors. Reproduced with permission.⁶ Copyright 2012, American Institute of Physics Publishing. (b) Relationship between the breakdown voltages and switching resistances of different generation semiconductors. Reproduced with permission.²³⁵ Copyright 2014, WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. (c) The bandgap and wavelength range of GaN and Ga₂O₃ modulated by varying the alloy's composition. Reproduced with permission.³⁷⁷ Copyright 2017, Elsevier Ltd.

Fig. 3 Schematic illustration of various device applications based on Ga₂O₃.

Ga₂O₃ has six phases (i.e., β-Ga₂O₃, ε-Ga₂O₃, α-Ga₂O₃, δ-Ga₂O₃, γ-Ga₂O₃, and κ-Ga₂O₃) and β-Ga₂O₃ is the most stable phase under ambient conditions. That is, the rest of the phases can be transformed into β-Ga₂O₃ under specific temperature, pressure, or other conditions. Therefore, most devices are based on β-Ga₂O₃ up to now. Note that Ga₂O₃ behaves as an insulator if it satisfies the stoichiometric ratio. However, the Ga₂O₃ prepared in the experiments behaves as an electron-rich (i.e., n-type) semiconductor instead of the so-called insulator. For example, intrinsic β-Ga₂O₃ contains a certain electron concentration (n = 10¹⁷–10¹⁸ cm⁻³) and mobility (μ < 200 cm² V⁻¹ s⁻¹). However, the electron concentration is low and the mobility is far from the theoretical value (μ = 300 cm² V⁻¹ s⁻¹).^5,17–19 These cannot meet the criteria of high-performance devices. Besides, due to the unique Ga–O arrangement configuration, β-Ga₂O₃ can be exfoliated to obtain low-dimensional Ga₂O₃ which is considered to have potential applications in flexible electronic and optoelectronic devices.^20–25 However, freshly exfoliated low-dimensional Ga₂O₃ is unstable and has no obvious quantum confinement effects, which will negatively affect the electronic performance and reliability of the devices. Therefore, it will hinder further applications based on low-dimensional Ga₂O₃ greatly.^26,27 It has been found that the main reason for these unsatisfactory results is the defects in Ga₂O₃, e.g., vacancies, interstitial atoms, dangling bonds, and deep level defects, which are usually introduced in the preparation process. Therefore, it is very crucial to understand the mechanism of these defects and modulate the defects to design and obtain high-performance Ga₂O₃ materials and devices. Doping engineering and passivation engineering are important methods to modulate the material properties of semiconductors. On the one hand, substituting host atoms with suitable impurity atoms can modulate the electronic properties of the doping systems, e.g., the electronic structure, carrier concentrations, and carrier mobility. On the other hand, it has a certain influence on the defects. It has been discovered that passivating the surface dangling bonds is essential for achieving high stability and excellent electronic properties of low-dimensional Ga₂O₃. Meanwhile, other material properties (e.g., magnetic, luminescence, scintillation, and piezoelectric) can also be modulated by doping engineering for application in other areas.

Herein, we summarize the recent progress on the effects of impurities and defects on the properties of Ga₂O₃. Because β-Ga₂O₃ is the most stable structure under ambient conditions, it is the focus of the present review, supplemented by the situations of low-dimensional Ga₂O₃ and other metastable Ga₂O₃. The basic properties of Ga₂O₃ are introduced firstly, and then other properties (e.g., electronic, magnetic, luminescence, scintillation, and piezoelectric) based on the host β-Ga₂O₃ modulated by impurities and defects are described in depth. Finally, the issues to be solved in this area and prospects in the future are given.

II. Basic properties

1. Polymorphs of Ga₂O₃

There are five commonly identified polymorphs of Ga₂O₃ including hexagonal phase (α-Ga₂O₃), monoclinic phase (β-Ga₂O₃), cubic defective spinel phase (γ-Ga₂O₃), cubic bixbyite phase (δ-Ga₂O₃), and hexagonal wurtzite phase (ε-Ga₂O₃).^28–30 The formation energy coupled with the thermodynamic stability of these five polymorphs is ranked as β < ε < α < δ < γ.⁵ In recent years, another new phase, the metastable κ-Ga₂O₃, is also synthesized on sapphire.^31–33 Note that any other metastable phases can be converted into β-Ga₂O₃ at high temperatures (400–700 °C) under special conditions, as shown in Fig. 4 schematically. Only β-Ga₂O₃ can be grown as bulk crystals from melts, fluxes, or gas phases, while other phases can be obtained as thin films or thick layers.³⁴ Theoretically, the opinion that these metastable phases could not be transformed from β-Ga₂O₃ has been accepted for a long time. However, a recent study discovered that β-Ga₂O₃ could convert into α-Ga₂O₃ under high pressure by shock compression experiments.³⁵ The phase transition condition between α-Ga₂O₃ and β-Ga₂O₃ was estimated to be 2.0–3.0 GPa, 1200–1500 K. In addition, the phase transition was also observed at high temperature and pressure, i.e. 19.2 GPa³⁶ and 20–22 GPa³⁷ or 21 GPa, 1873 K.³⁸ It was reported that phase transitions initialized at relatively low pressures and then expanded to higher pressures, e.g., from about 6 GPa³⁹ to 40 GPa,⁴⁰ or from 13.6–16.4 GPa to 39.2 GPa.⁴¹ Note that the temperature increases the regrowth of β-Ga₂O₃; thus complete phase transition into pure α-Ga₂O₃ is almost impossible. Therefore, mixtures of the two phases are usually prepared under high pressure experimentally. The structure and properties of these phases of Ga₂O₃ will be discussed in detail in the subsequent sections. The intrinsic structural parameters and fundamental physical constants of these Ga₂O₃ polymorphs are summarized in Table 1.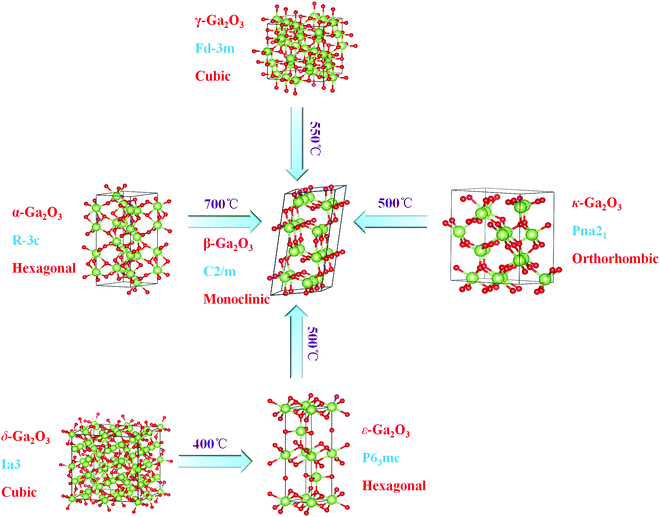

Fig. 4 Schematic diagram of six phase structures and their phase transition relationships in Ga₂O₃ (α-Ga₂O₃, β-Ga₂O₃, δ-Ga₂O₃, γ-Ga₂O₃, ε-Ga₂O₃, and κ-Ga₂O₃). Reproduced with permission.⁴ Copyright 2019, Elsevier Ltd.

Table 1 Crystal structures, lattice parameters, bandgaps, and electron effective masses of the Ga₂O₃ family

Phase	Structure	Space group	Lattice parameters	Bandgap (eV)	Electron effective mass (me)	Ref.
α	Hexagonal	R3̄c	a = b = 4.98 Å, c = 13.43 Å, α = β = 90°, γ = 120°	5.2–5.3	0.276m0	80 and 81
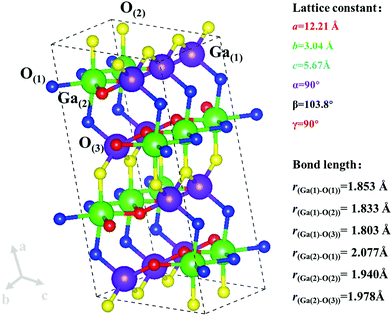
β	Monoclinic	C2/m	a = 12.23 Å, b = 3.04 Å, c = 5.80 Å, α = γ = 90°, β = 103.8°	E g(indirect) = 4.69 eV	0.27m0–0.34m0	101–103
				E g(direct) = 4.66 eV
Γ	Cubic	Fd3̄m	a = b = c = 8.24 Å, α = β = γ = 90°	5.0(direct), 4.4(indirect)	—	45
δ	Cubic	Ia3	a = b = c = 9.52 Å, α = β = γ = 90°	—	—	45
ε	Hexagonal	P63mc	a = b = 2.90 Å, c = 9.26 Å, α = β = 90°, γ = 120°	4.9–5.0	0.24m0	90 and 93
κ	Orthorhombic	Pna21	a = 5.05 Å, b = 8.70 Å, c = 9.28 Å, α = β = γ = 90°	4.62	—	31

---

β-Ga₂O₃. It is a typical monoclinic structure with the space group C2/m whose lattice constants are a = 12.21 Å, b = 3.04 Å, c = 5.67 Å, α = γ = 90°, β = 103.8°.^42,43 β-Ga₂O₃ is a kind of anion-dense accumulation structure. The b-axis of the centrosymmetric unit cell is the two-fold rotational axis in the β-Ga₂O₃ cell. Each β-Ga₂O₃ unit cell has two inequivalent Ga sites (Ga₍₁₎ and Ga₍₂₎) and three inequivalent O sites (O₍₁₎, O₍₂₎, and O₍₃₎). Half of the Ga atoms are at Ga₍₁₎ sites, forming a slightly distorted tetrahedron with four O ions. The other half of the Ga atoms are located at Ga₍₂₎ sites, forming a highly distorted octahedron with six O ions. Each O₍₁₎ is threefold-coordinated, located at the intersection point of two octahedra and one tetrahedron. Each O₍₂₎ is threefold-coordinated, shared by an octahedron and two tetrahedra. Each O₍₃₎ is fourfold-coordinated, located at the corner of three octahedra and one tetrahedron.^44–48 In the bulk β-Ga₂O₃, the Ga–O bond lengths are Ga₍₁₎–O₍₁₎ = 1.853 Å, Ga₍₁₎–O₍₂₎ = 1.833 Å, Ga₍₁₎–O₍₃₎ = 1.803 Å, Ga₍₂₎–O₍₁₎ = 2.077 Å, Ga₍₂₎–O₍₂₎ = 1.940 Å, and Ga₍₂₎–O₍₃₎ = 1.978 Å. The structure and lattice parameters of β-Ga₂O₃ are shown in detail in Fig. 5.⁴⁸ These structural characteristics lead to low symmetry for β-Ga₂O₃, which leads to significant anisotropy in structural, optical, and electronic properties. Besides, β-Ga₂O₃ can be grown by the low-cost melt methods, e.g., Czochralski method (CZ method),^49,50 edge-defined film-fed growth method (EFG method),⁵¹ floating-zone method (FZ method),⁵² and vertical Bridgman method.⁵³ Meanwhile, the β-Ga₂O₃ film can also be realized by epitaxial methods, e.g., metal–organic chemical vapor deposition (MOCVD),^54–58 mist-chemical vapor deposition (mist-CVD),⁵⁹ halide vapor phase epitaxy (HVPE),^60–62 laser molecular beam epitaxy (LMBE),^63,64 pulsed laser deposition (PLD)^65–69 and magnetron sputtering.^70–73 Compared with the expensive costs of crystal growth of other wide bandgap semiconductors (e.g., GaN and SiC) and irrealizable wafer of other phases, β-Ga₂O₃ has advantages in crystal growth and large-scale applications. Therefore, state-of-the-art microelectronic and optoelectronic devices are almost based on β-Ga₂O₃ in Ga₂O₃'s family.

Fig. 5 Schematic diagram of the structure of the unit cell of β-Ga₂O₃.

α-Ga₂O₃. The formation of metastable Ga₂O₃ depends on the lattice structure of the substrate and the growth temperature. Since the metastable phase α-Ga₂O₃ possesses a similar structure and little lattice mismatches to sapphire, the high-quality metastable phase α-Ga₂O₃ can be deposited on sapphire substrates by heteroepitaxial methods, e.g., pulsed laser deposition (PLD),⁷⁴ halide vapor phase epitaxy (HVPE),⁷⁵ metal–organic chemical vapor deposition (MOCVD),⁷⁶ low-temperature atomic layer deposition (ALD),⁷⁷ and mist-CVD.^78,79 α-Ga₂O₃ is a typical hexagonal crystal with the space group R3̄c, whose lattice constants are a = b = 4.98 Å, c = 13.43 Å, α = γ = 90°, β = 120°.^80,81 Compared with β-Ga₂O₃, α-Ga₂O₃ has a larger bandgap (E_g = 5.2–5.3 eV). Meanwhile, α-Ga₂O₃ can form tunable component alloys with In₂O₃ and Al₂O₃, for example, α-(In_xGa_1−x)₂O₃ and α-(Al_xGa_1−x)₂O₃. Note that the α-(Al_xGa_1−x)₂O₃ alloy will not undergo phase transition when the Al component (x) varies in the range of 0–100%.⁸² Besides, the carrier concentrations in α-Ga₂O₃ can be modulated effortlessly. Thus, α-Ga₂O₃ has remarkable potential applications. In recent years, Sn or Si doped α-Ga₂O₃ is applied in the Schottky barrier diode (SBD) and metal–semiconductor field-effect transistors (MESFETs). For example, Shiojima et al. investigated the effects of annealing temperature on the interface contact properties of the doped α-Ga₂O₃ SBD.⁸³ They found that both forward and reverse currents increased with 400 °C annealing due to thermal degradation and different electrode materials. Dang et al. proposed a cost-effective strategy to realize high-performance Sn doped α-Ga₂O₃ MESFETs.⁸⁴ By optimizing the dimension of MESFETs, the on/off ratio could reach up to 2 × 10⁷, and the rectification ratio and reverse breakdown voltage were 6 × 10⁶ and ∼20 V, respectively. Compared with β-Ga₂O₃-based power devices, the performance of α-Ga₂O₃-based power devices has been improved summarily.

γ-Ga₂O₃. The space group of γ-Ga₂O₃ is Fd3̄m. Its lattice parameters are a = b = c = 8.24 Å, α = β = γ = 90°.⁴⁵ It has a crystal structure similar to that of an ideal spinel (e.g., MgAl₂O₄). Different from the ideal spinel structure, Ga atoms in γ-Ga₂O₃ only occupy the octahedral sites. γ-Ga₂O₃ can be epitaxially grown on sapphire and spinel substrates by mist-CVD,⁸⁵ molecular beam epitaxy (MBE),⁸⁶ and PLD.^87–89

δ-Ga₂O₃. It is a metastable phase with a body-centered cubic structure and the space group is Ia3. It is isomorphous with some bixbyite crystals (e.g., In₂O₃, and Mn₂O₃).^4,90,91 The lattice parameters of δ-Ga₂O₃ are a = b = c = 9.52 Å, α = β = γ = 90°.⁴⁵ Although Sharma et al. synthesized nano-structured δ-Ga₂O₃ by the chemical precipitation method, there were still some β-Ga₂O₃ components in the nano-film, which made it impure.⁹² Therefore, a relevant in-depth research study is still needed to prepare pure δ-Ga₂O₃ films.

ε-Ga₂O₃. Hexagonal ε-Ga₂O₃ is prepared by heteroepitaxial growth normally. The lattice parameters of ε-Ga₂O₃ are a = b = 2.90 Å, c = 9.26 Å, α = β = 90°, γ = 120°.^90,93 Note that hexagonal ε-Ga₂O₃ has a larger spontaneous polarization (P_(ε-Ga2O3) = 24.44 μC cm⁻²) compared with GaN.^33,94 Inspired by the previous work on the Al_xGa_1−xN/GaN heterojunctions, high-density two-dimensional electron gas (2DEG) can be formed at the ε-(Al_xGa_1−x)₂O₃/ε-Ga₂O₃ interface without any intentional doping. It has been discovered that the 2DEG charge densities at the ε-(Al_xGa_1−x)₂O₃/ε-Ga₂O₃ interface can reach up to 1.4 × 10¹⁴ cm⁻² by varying the barrier type and ε-AlGaO₃ thickness.⁹⁵ Meanwhile, charge contrast ratios over 1500 can be realized by the thick ε-Ga₂O₃ cap layer and thin ε-AlGaO₃ layers. This phenomenon reveals its potential applications in modulation-doped field effect transistors (MODFETs), non-volatile memory, and neuromorphic applications.^95,96

κ-Ga₂O₃. Orthorhombic κ-Ga₂O₃ has attracted scholars in recent years. κ-Ga₂O₃ was considered to be the orthorhombic ε-Ga₂O₃ incorrectly due to their similar crystal structure in the previous research. In 2017, Cora et al. investigated the real structure of the Ga₂O₃ film deposited by MOVPE on the α-Al₂O₃ substrate in detail.³¹ They discovered that the layer had a columnar structure perpendicular to the interface and its origin was related to the formation of small domains. By transmission electron microscopy (TEM), it was observed that O atoms of the Ga₂O₃ layer formed a densely packed structure along the c-axis, while Ga atoms and these O atoms formed tetrahedral and octahedral structures, respectively. Meanwhile, these two different geometric structures formed two types of polyhedral layers. The oxygen positions are similar with 4H-SiC (ABAC) type close-packed stacking. Furthermore, the detailed TEM results revealed that the microstructure was ordered in 5–10 nm large domains and each domain was found to belong to the orthorhombic (Pna2₁) structure, which was regarded as the structure of κ-Ga₂O₃. This phenomenon was different from that discovered in ε-Ga₂O₃, so this work laid a foundation for in-depth understanding of the correct structure of κ-Ga₂O₃. The lattice parameters of κ-Ga₂O₃ are a = 5.05 Å, b = 8.70 Å, c = 9.28 Å, α = β = γ = 90°.³¹ Furthermore, it has been discovered that κ-Ga₂O₃ can be prepared by pulsed-laser deposition (PLD),⁹⁷ metal–organic vapor phase epitaxy (MOVPE),^31,76 and HVPE.^98,99 Note that recent research discovered that κ-Ga₂O₃ was expected to exhibit a larger spontaneous polarization (P_(κ-Ga2O3) = 26.39 μC cm⁻²) along the c-axis compared with GaN and ε-Ga₂O₃. κ-Ga₂O₃ with expected spontaneous polarization and piezoelectric effects will be applied in high-performance power devices to form two-dimensional electron gas at the hetero-interface. Such features are expected to further improve the performance of HEMTs.

2. Electronic properties of β-Ga₂O₃

In terms of the electronic properties of β-Ga₂O₃, band structure, density of states (DOS) and transport properties are the focus, because they are related to device performance closely. The electronic structures of β-Ga₂O₃ calculated by density functional theory (DFT) are illustrated in Fig. 6(a). Here, the GGA functional and the HSE06 hybrid functional are applied to obtain the band structure of β-Ga₂O₃, respectively. Note that the bandgap derived from HSE06 is closer to the experimental bandgap, while the bandgap obtained from GGA is underestimated because the exchange–correlation terms of the two functionals are different. As shown in Fig. 6(a), the conduction band minimum (CBM) and the valence band maximum (VBM) are located at the Γ and M points, respectively, which leads to the indirect bandgap in β-Ga₂O₃. On the other hand, in most previous publications, β-Ga₂O₃ exhibits the direct bandgap in which both CBM and VBM are located at the Γ point.^59,100 Since the difference of the VBM between the M and Γ points is less than 100 meV, the measured indirect bandgap (E_g(indirect) = 4.69 eV) is a little larger than the measured direct bandgap (E_g(direct) = 4.66 eV). Furthermore, it can be observed that the CBM is mainly contributed by the Ga 4s orbital in the DOS diagram (see Fig. 6(b and c)), and the dispersive degree is large. The electron effective mass of β-Ga₂O₃ is small, which is in the range of 0.27m₀–0.34m₀ obtained by first-principles calculations.^101–103 The band structure and conclusions are in good agreement with the experimental results.^104–106 Note that both theoretical and experimental valence bands of β-Ga₂O₃ show weak band dispersion. As shown in Fig. 6(b–d), combined with the relevant partial density of states (PDOS), the valence band maximum is mainly composed of O 2p orbitals, and the dispersive degree is small, thus it is flat. Although the VBM of β-Ga₂O₃ is mainly composed of p orbitals, the contribution of each p orbital component is not equal. The VBM is mainly contributed by the 2p_x and 2p_z orbitals of O atoms. In general, the p shell contains three p orbitals, that is, p_x, p_y, and p_z, which are dumbbell-shaped but in different stretching directions. Therefore, the three different components of p orbitals show anisotropy. The characteristics of orbital contributions connected with the band structure reveal the anisotropy of electronic properties from another perspective. Similar experimental and theoretical methods have also measured the bandgaps (E_g) and electron effective masses of other phases, as listed in Table 1.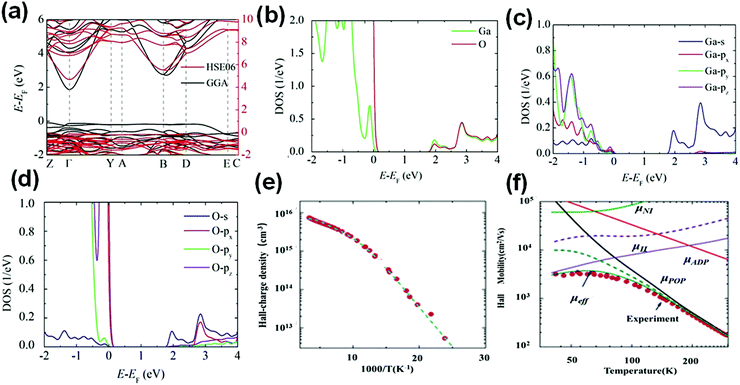

Fig. 6 (a) Band structure of bulk β-Ga₂O₃ obtained by the HSE06 functional (red solid line) and GGA functional (black solid line). (b–d) Partial density of states (PDOS) of bulk β-Ga₂O₃. Reproduced with permission.²¹ Copyright 2018, American Chemical Society. (e) Measured Hall-charge density as a function of 1000/T (the dashed line presents the fitting of the charge density calculated based on the charge neutrality equation). (f) Experimental and calculated dependence of the Hall mobility in different scattering mechanisms on the temperature. Reproduced with permission.³⁷⁸ Copyright 2019, American Institute of Physics Publishing.

As mentioned above, the electron clouds of the Ga 4s orbital are spherically symmetric so that the band dispersion of the CBM in the Brillouin zone is symmetrical. In other words, the electron effective masses of β-Ga₂O₃ obtained from the CBM exhibit the isotropic character. Note that the electron clouds of the s orbital have a large radius, which results in the large overlapping electronic conduction path. It is thought that the mean free path of electrons in β-Ga₂O₃ is greater than the chemical bond length of β-Ga₂O₃. As a result, the small electron effective masses of β-Ga₂O₃ suggest the high electron mobility in β-Ga₂O₃.⁴ However, such electron mobility is far lower than that of other wide bandgap semiconductors, such as 4H-SiC (∼1000 cm² V⁻¹ s⁻¹) and GaN (∼1200 cm² V⁻¹ s⁻¹).^5,107 Moreover, the electron mobility of β-Ga₂O₃ (μ_experiment = 20–170 cm² V⁻¹ s⁻¹) is much lower than the theoretical expectation (μ_theory = 300 cm² V⁻¹ s⁻¹) in the experiments.^{17,18,108–111} On the one hand, the low mobility is attributed to a large number of internal defects in β-Ga₂O₃. Therefore, the modulations of defects are very urgent and vital to realizing high-performance β-Ga₂O₃ based devices. On the other hand, the reasons are attributed to the different scattering mechanisms of electrons within different temperature ranges and the complex vibration modes of phonons in β-Ga₂O₃. It has been discovered by exploring of the influence of temperature on the mobility of β-Ga₂O₃ that β-Ga₂O₃ is affected by strong electron–phonon interaction (EPI) effects. Unlike the traditional notions of carrier transport in Si and GaAs, the low symmetry β-Ga₂O₃ crystal contains a variety of phonon modes generally and the carrier transport mechanism is quite different. The lattice vibration will disturb the potential field of the periodic crystal with the variation of temperature in the low symmetry crystal. Thus, the phonon vibration modes will combine with electron motion. This results in that the mobility of electrons is affected by electron–phonon interaction effects. This EPI effect plays a pivotal role in controlling the mobility of intrinsic semiconductors, and the interaction is a long-range Coulomb interaction essentially. Unfortunately, this phenomenon cannot be avoided in a semiconductor with a low symmetry structure. Among them, the polarized optical phonon (POP) scattering which is one of the representatives of EPI effects has been investigated a lot because it is an important scattering mechanism at medium temperature (e.g., room temperature). Besides, as shown in Fig. 6(e and f), other mechanisms also affect the carrier mobility in β-Ga₂O₃, e.g., ionized (μ_II) scattering, neutral impurity (μ_NI) scattering, and acoustic deformation potential scattering (μ_ADP). Through theoretical analysis, the values of the Hall mobility at different temperatures after being affected by these scattering mechanisms are listed in detail.

In the bulk β-Ga₂O₃, the long-range interaction controls the intrinsic electron transport. In this condition, the same dipole moment is produced by transverse optical (TO) and longitudinal optical (LO) vibrational mode splitting at the long-wavelength limit. The LO modes gain slightly higher energy than their TO counterparts. The electron and LO modes are coupled in the long-range EPI effect. This coupling is polar and the scattering resulting from this coupling is regarded as POP scattering. At low temperatures, the POP scattering effect in β-Ga₂O₃ is weak and the impurity scattering plays a dominant role. As the temperature increases gradually, the electrons’ energy also increases and the ionized impurity scattering decreases, which increases the bulk electron mobility. In addition, POP scattering attempts to dominate with a further increase in temperature. The rate of POP scattering increases with increasing temperature due to the increase in the Bose occupancy number. Therefore, the bulk electron mobility begins to drop. As mentioned earlier, the bulk mobility in β-Ga₂O₃ at moderate temperature is also affected by other scattering mechanisms. However, according to the Fermi-Golden rule, the effects of these scatterings on bulk electron mobility are small compared with that of POP scattering. They can be ignored when investigating the transport problems in β-Ga₂O₃ generally. It is discovered that the POP scattering effect is the main culprit in reducing the bulk electron mobility in bulk β-Ga₂O₃ in the range of moderate temperatures. To suppress the POP scattering, one possible solution is to screen the POP modes. This strategy needs higher carrier concentrations in the bulk β-Ga₂O₃.

Unfortunately, the carrier concentrations in intrinsic β-Ga₂O₃ are so low that the POP scattering is unable to be suppressed. Low carrier concentrations and mobility result in low electrical conductivity (σ) so that it limits the device performance of β-Ga₂O₃. Doping is an available strategy to tune the properties of semiconductors. In general, substitution doping with external atoms different from host valence electrons will modulate the properties of semiconductors. In β-Ga₂O₃, the incorporation of some electron-rich metals (e.g., Sn, Si) can increase the carrier concentrations by orders of magnitude. Nevertheless, electron mobility still fails to reach the theoretical value (less than half of the theoretical value).¹¹² To obtain electrons with high mobility, the electron transport path needs to be optimized to satisfy the features of less scattering, and the two-dimensional electron gas (2DEG) matches these conditions. Therefore, the device performance can be improved by obtaining two-dimensional electron gas to improve carrier mobility. It has been discovered that two-dimensional electron gas with high mobility can be formed by modulation doping at the (Al_xGa_1−x)₂O₃/Ga₂O₃ heterojunction interface. Therefore, the mobility of 2DEG (>100 cm² V⁻¹ s⁻¹, μ_max = 1000 cm² V⁻¹ s⁻¹) will be higher than that in the bulk through reasonable modulated doping and band matching of the heterojunction interface; then electrons with high mobility are expected to be realized in Ga₂O₃.^{18,110,113,114}

3. Absorption and transmittance properties

As an ultra-wide bandgap semiconductor, β-Ga₂O₃ has high transmittance and low absorption in the visible and near-infrared regions of the solar spectrum, and hence it can be applied in transparent conductive electrodes in some areas.^115,116 Meanwhile, the absorption cutoff edge and the maximum absorption peak are located in the ultraviolet region, and it has strong absorption in the solar-blind ultraviolet region. It is noted by polarized optical absorption and reflectance measurements that the light absorption of β-Ga₂O₃ in three different directions of [100], [010], and [001] is also different, as shown in Fig. 7(a), suggesting anisotropy in the optical properties of β-Ga₂O₃. Although the absorption situations are different in the three different directions, the absorption intensity is weaker in the low-energy region and greater in the high-energy region. According to the absorption coefficient curve derived from the Tauc plot method, the optical bandgaps of β-Ga₂O₃ are different in three different directions. Fig. 7(a) shows that the bandgap along the [010] orientation is the largest (E_g[010] = 4.850 eV), while the optical bandgap along the other two directions ([100] and [001]) is 4.585 eV and 4.560 eV, respectively. Onuma et al. applied a 300 W Xe lamp to measure the optical absorption and transmittance at room temperature.¹¹⁷ In addition to the anisotropic light absorption, the transmittance of β-Ga₂O₃ in different directions was also investigated (see Fig. 7(b)). The transmittance of E‖b orientation is higher than that of E‖a and unpolarized orientation. Furthermore, they revealed the absorption and transmittance mechanism by using experimental results coupled with theoretical calculations, as shown in Fig. 7(c). Such anisotropic optical absorption and transmittance can be explained by the inconsistent band-to-band transition. Each primitive cell contains the following bands, called Γ₁⁺, Γ₂⁺, Γ₁⁻, and Γ₂⁺ bands. The CBM is isotropic and is expressed as the Γ₁⁺ band. Except for the transitions from the Γ₁⁺ and Γ₂⁺ bands to the Γ₁⁺ band of the CBM which are dipole forbidden, the other band-to-band transitions are dipole allowed. Therefore, the transitions from the rest of the different bands of the VBM to the Γ₁⁺ band of the CBM represent optical properties in different directions.^46,117–119 This explains the anisotropy in the optical properties of β-Ga₂O₃ reasonably.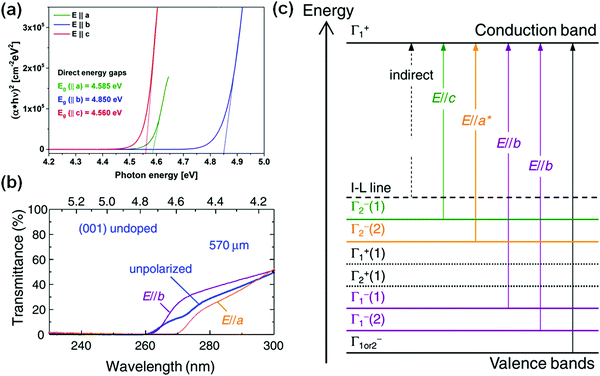

Fig. 7 (a) Polarization-dependent absorption edge of bulk β-Ga₂O₃ crystal samples obtained by the Czochralski method. Reproduced with permission.⁴² Copyright 2018, IOP Publishing Ltd. (b) Unpolarized (blue solid line) and polarized (purple and orange solid lines) transmittance spectra of the (001) undoped β-Ga₂O₃ substrate at room temperature. (c) Irreducible representations and rough transition process of the band structure in β-Ga₂O₃. The horizontal solid and dotted lines represent the valence bands for the dipole allowed and forbidden transitions at Γ, respectively. The vertical solid lines represent the rough transition process. Reproduced with permission.¹¹⁷ Copyright 2015, The Japan Society of Applied Physics.

4. Thermal and mechanical properties

Although β-Ga₂O₃ has many excellent properties that have attracted scholars, there are still many troublesome problems which need to be overcome. Thermal conductivity (κ) is an important parameter that severely affects the performance and reliability of devices including both power devices and optoelectronic devices. There are several methods to obtain the thermal conductivity of β-Ga₂O₃. The theoretical method may involve independent first-principles calculations or could be coupled with machine learning.¹²⁰ The experimental methods are the 3ω method and the time domain thermo-reflectance (TDTR) method.^121,122 Due to the continuous optimizations and updates of calculation methods, the theoretical thermal conductivity (e.g., κ_[010] = 20.00 W m⁻¹ K⁻¹,¹²³ 21.54 W m⁻¹ K^−1 124) has been very close to the experimental value (e.g., κ_[010] = 21.00 W m⁻¹ K^−1 125). Therefore, the scholars use theoretical calculations to predict and then evaluate the thermal properties rather than complex experiments. Note that the thermal conductivity of β-Ga₂O₃ is lower than that of some semiconductors commonly applied up to now, e.g. κ_GaN = 240.00 W m⁻¹ K⁻¹,^126–128κ_Si = 140.00 W m⁻¹ K⁻¹,¹²⁹ and κ_SiC = 350.00 W m⁻¹ K⁻¹.¹²⁹ The low thermal conductivity of β-Ga₂O₃ needs more in-depth research on the internal mechanism, which should be noticed in device applications. Galazka et al. measured the thermal conductivity of β-Ga₂O₃ along the [010] direction by applying the laser flash diffusivity method, where the thermal conductivity decreased with increasing temperature in the range of 20–1200 °C.¹²⁵ They found that the point defect scattering played a major role in the thermal conductivity at low temperature, while the phonon–phonon Umklapp scattering gradually dominated at high temperatures (above 150 K). Note that the thermal conductivity of β-Ga₂O₃ is anisotropic due to the low symmetry structure. Guo et al. investigated the four different orientations in the β-Ga₂O₃ bulk by the time domain thermo-reflectance (TDTR) method.¹²² They measured the thermal conductivity of different orientations by varying the temperature and found that the thermal conductivity decreased as the temperature increased in general, as shown in Fig. 8(a and b). Based on the verification of previous studies, they also found that the reason for anisotropic thermal conductivity was due to the discrepancies in the speed of sound along different crystal orientations.

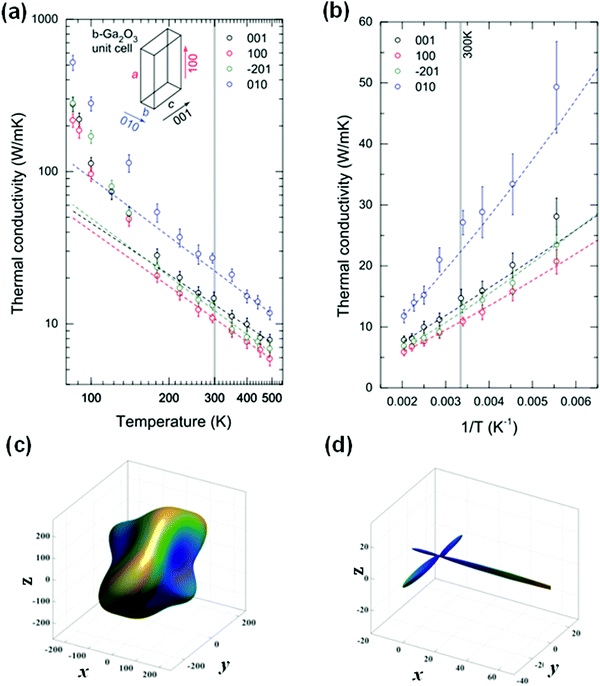Fig. 8 (a) Temperature-dependent thermal conductivity in the log scale along different crystal orientations of β-Ga₂O₃ by the TDTR approach as a function of temperature (K). (b) Temperature-dependent thermal conductivity in the linear scale along different crystal orientations of β-Ga₂O₃ by the TDTR approach as a function of 1/T (K⁻¹). Reproduced with permission.¹²² Copyright 2015, American Institute of Physics Publishing. The direction-dependent (c) Young's modulus and (d) shear modulus of bulk β-Ga₂O₃ in 3D representation surfaces. Reproduced with permission.¹³² Copyright 2019, Elsevier Ltd.

The thermal coefficients are related to the mechanical coefficients in the process of investigating other crystal properties. As for monoclinic β-Ga₂O₃, it has 13 kinds of elastic constants (C₁₁, C₂₂, C₃₃, C₄₄, C₅₅, C₆₆, C₁₂, C₁₃, C₁₅, C₂₃, C₂₅, C₃₅, and C₄₆).^23,130–132 They are usually obtained by first-principles calculations, as well as Young's modulus E, bulk modulus B, shear modulus G, and other mechanical constants. Note that the obvious differences of these mechanical constants in different orientations indicate that the mechanical properties of the bulk β-Ga₂O₃ are anisotropic obviously. Fig. 8(c and d) displays the 3D representation surfaces of direction-dependent Young's and shear moduli of bulk β-Ga₂O₃, respectively. It is not a common sphere and has different values in different directions, that is, it is anisotropic. Meanwhile, the minimum thermal conductivity κ_min is closely related to the above elastic properties and can be obtained by the following formula: 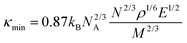, where k_B, N_A, N, ρ, E, and M are the Boltzmann constants, Avogadro's number, the number of atoms in the unit cell, density, Young's modulus, and the weight of the unit cell, respectively.^23,133,134 Therefore, this also explains the reasons for the different thermal conductivity of bulk β-Ga₂O₃ in different directions observed in the experiment from another aspect.

In addition, it has been found that C₁₁ is less than C₂₂ and C₃₃, while C₅₅ and C₆₆ are greater than C₄₄, suggesting that the bond strength along the [100] direction of bulk β-Ga₂O₃ is weaker than that in other directions. Thus, it can be sliced into quasi two-dimensional flakes along the (100) surface. The exfoliation energy of β-Ga₂O₃ along the (100) surface is calculated by the DFT method, as shown in Fig. 9(a).²¹ The mechanical properties of low-dimensional Ga₂O₃ after exfoliation also have great variations compared with that of bulk. For example, the anisotropies in the compressive and shear behaviors in the monolayer Ga₂O₃ are enhanced as shown in Fig. 9(b and c). Their shapes are far from sphere shapes. Meanwhile, the modulus B, G, and E of monolayer Ga₂O₃ decrease (see Fig. 9(d)) while the thermal constant κ increases up to 49 W m⁻¹ K⁻¹.²³ It is expected to alleviate the heat dissipation problem caused by the poor thermal conductivity in the bulk Ga₂O₃.

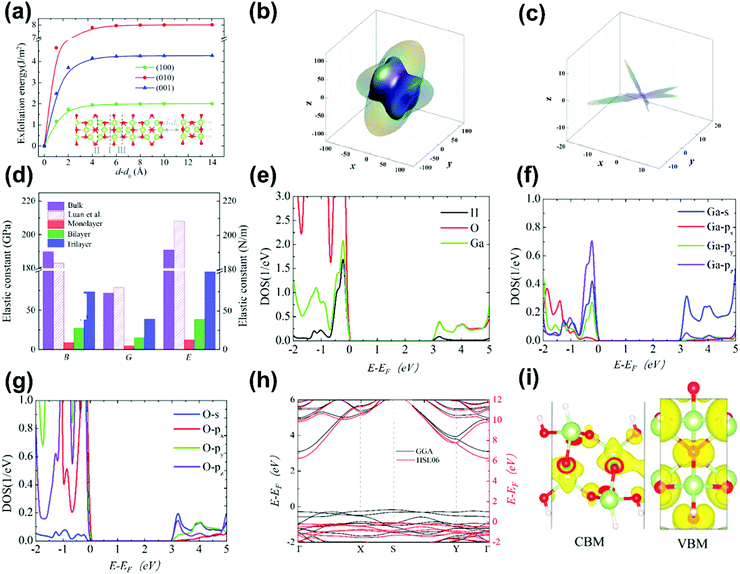Fig. 9 (a) Calculated exfoliation energy in different crystal planes as a function of d − d₀. Reproduced with permission.²¹ Copyright 2018, American Chemical Society. The direction-dependent (b) Young's modulus and (c) shear modulus of low-dimensional Ga₂O₃ in 3D representation surfaces. (d) Bulk modulus (B), shear modulus (G), and Young's modulus (E) of the bulk and different layers of low-dimensional Ga₂O₃. Reproduced with permission.¹³² Copyright 2019, Elsevier Ltd. (e–g) PDOS of H passivated low-dimensional Ga₂O₃. (h) Band structure of monolayer low-dimensional β-Ga₂O₃ obtained by the HSE06 functional (red solid line) and GGA functional (black solid line). (i) Projected charge densities of the CBM and VBM of H passivated low-dimensional Ga₂O₃. Reproduced with permission.²¹ Copyright 2018, American Chemical Society.

Unluckily, this exfoliation property is not observed in other metastable Ga₂O₃ up to now. As mentioned above, β-Ga₂O₃ is composed of a chain structure in which [GaO₄] tetrahedra intersect with [GaO₆] octahedra. Because the atoms in the crystal need to meet the rule of the dense packing properties, the O atoms and Ga atoms at the interface between [GaO₄] tetrahedra and [GaO₆] octahedra often have long bond lengths. This is the unique feature of this crossed chain structure. In contrast, the lattice structures of other phases are composed of only [GaO₆] octahedra, which are not easy to exfoliate into the low-dimensional structure. Thus, the subsequent research is mainly based on the low-dimensional Ga₂O₃ obtained from exfoliated β-Ga₂O₃.

5. Low-dimensional Ga₂O₃

Due to the unique structure of β-Ga₂O₃, the low-dimensional structure can be obtained by exfoliating the bulk β-Ga₂O₃. As the thickness of the material decreases to the atomic thickness, the properties change accordingly. However, since β-Ga₂O₃ is not a van der Waals material, obtaining ultra-thin flakes with a thickness of less than 100 nm is a huge challenge. Kwon et al. solved this problem in 2017.¹³⁵ They mechanically exfoliated the bulk β-Ga₂O₃ with tape and then applied plasma etching to tune the thickness of exfoliated Ga₂O₃. Combined with the SF₆ atmosphere, the thickness of the β-Ga₂O₃ flake could be tuned from 300 nm down to ∼60 nm. Because the reaction between SF₆ and Ga₂O₃ generated oxygen and volatile oxyfluoride compounds, and non-volatile compounds (e.g., GaF_x) that can be moved by ion bombardment, the thickness of exfoliated Ga₂O₃ can be reduced. Meanwhile, Van de Walle et al. and Bermudez attempted to thin the thickness of β-Ga₂O₃ along the [100] orientation down to half to attain the monolayer β-Ga₂O₃ theoretically and then investigated the properties of monolayer β-Ga₂O₃ briefly.^48,136 In the process of exploring the transport properties of low-dimensional Ga₂O₃, the carrier mobility (∼130 cm² V⁻¹ s⁻¹) of β-Ga₂O₃ membranes exfoliated by Hwang et al. was found to be close to that of the bulk.²² However, the mobility value is still not comparable to those of other wide bandgap semiconductors. The lack of quantum confinement effects has been observed in the unpassivated β-Ga₂O₃ flake. What's more, the exfoliated Ga₂O₃ is unstable under ambient conditions because of the dangling bonds on the surface. It is found that surface passivation technology is one of the good solutions to the instability of low-dimensional wide bandgap semiconductors.¹³⁷ Based on previous research results, Su et al. did further research on exfoliated Ga₂O₃ by surface passivation engineering.^{21,27,132,138} They put forward a new strategy for applying hydrogen to passivate the surface of low-dimensional Ga₂O₃, which further enhanced the quantum confinement effects. They found that the H passivated structure demonstrated a larger bandgap (5–6 eV) and higher carrier mobility (∼25 000 cm² V⁻¹ s⁻¹), which led to its application in optoelectronic devices. Meanwhile, samples with hydrogen passivation had a long electron relaxation time (∼4 ps) and larger exciton binding energy (1–2 eV) than the bulk. Although some theoretical studies have been carried out on low-dimensional Ga₂O₃, it still needs to be confirmed by subsequent related experiments. In addition to the mechanical exfoliation mentioned above, it should be noticed that the low-dimensional Ga₂O₃ monolayer can also be obtained by the chemical synthesis method and MBE, but the exfoliation method is widely applied because of its simple process.^139,140

Although H passivated monolayer Ga₂O₃ has many excellent properties, there are still some problems that need to be solved, e.g., many defects in the parent bulk Ga₂O₃ are also accompanied by the monolayer Ga₂O₃ during the exfoliation. Besides, similar to the bulk Ga₂O₃, the VBM of monolayer Ga₂O₃ is still mainly contributed by the 2p orbitals of O, as shown in Fig. 9(e and g). The dispersion degree of monolayer Ga₂O₃'s valence band is low (see Fig. 9(h)), and the effective mass of the hole is large, which affects the hole transport. Meanwhile, the generated holes do not become free holes instead of the localized holes formed near the O atoms (see Fig. 9(i)). Effective p-type doping is difficult to be obtained. Therefore, investigating the effects of impurities and defects on the properties of low-dimensional Ga₂O₃ is similar to the situation in the bulk Ga₂O₃ to a degree.

III. Effects of defects and impurities on electronic properties

Although β-Ga₂O₃ has been fabricated by several methods, there are inevitable defects (e.g., vacancies, deep level defects, etc.) in β-Ga₂O₃ which significantly affect the properties of β-Ga₂O₃ and the performance of β-Ga₂O₃ based devices.^52,141 On the one hand, defects can serve as scatter centers to affect the carrier mobility and then affect the device output characteristics and responsive characteristics. On the other hand, they can also serve as trapped centers which affect sensitivity in the photodetectors. In addition to the bulk defects, the surface and interface defects of β-Ga₂O₃ are also associated with poor device performance, such as threshold voltage instability, reduced channel carrier mobility, and poor device reliability. Therefore, the defects including vacancies and interstitial atoms in the β-Ga₂O₃ host material are worth to be studied.

Metal oxides are insulators under the condition of meeting the stoichiometric ratio, but their growth has a great relationship with the composition of the ambient atmosphere in the actual process. The insufficiency or excess of O atoms in the chemical composition results in oxygen vacancies (V_O) or oxygen interstitials (O_i), respectively.^142,143 V_O and O_i play the roles of donor and acceptor, respectively, thus making the conductivity of oxides vary with the oxygen content at room temperature, as shown in Fig. 10(a). Meanwhile, considering the differences of growth environments such as Ga rich and O rich, other single defects (V_Ga and Ga_i) and double defects also exist in β-Ga₂O₃.¹⁴⁴ Besides, some impurities inevitably enter β-Ga₂O₃ crystals and act as impurities in the actual growth process of bulk β-Ga₂O₃; for example, hydrogen (H) and Si impurities, etc., even form complexes with the vacancies in the host.^{105,145–147} Meanwhile, the Ir ions are observed in the bulk β-Ga₂O₃ due to the utilization of crucible in the melt method in recent years.¹⁴⁸ These dopants introduced unintentionally during the preparation are deemed unintentional dopants. The unintentional dopants are related to the raw materials and vessels applied in the preparation closely, and they are generally unavoidable. Therefore, they are considered to be another origin of n-type performance in intrinsic β-Ga₂O₃.

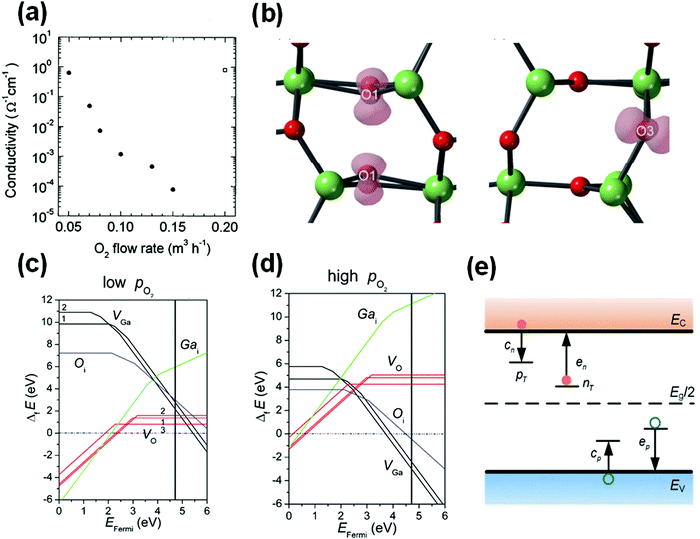Fig. 10 (a) The electrical conductivity of the β-Ga₂O₃ single crystals along the b axis as a function of the O₂ flow rate. The closed circles and the open square refer to samples grown from undoped and Sn-doped Ga₂O₃, respectively. Reproduced with permission.⁴⁶ Copyright 1997, American Institute of Physics Publishing. (b) Relaxed atomic configurations and iso-surfaces of the squared wave functions of the STHs on the O₁ and the O₃ site in β-Ga₂O₃. Reproduced with permission.³⁷⁹ Copyright 2019, American Physical Society. Formation energies of point defects (e.g., V_Ga, V_O, Ga_i, and O_i) in β-Ga₂O₃ as a function of the Fermi energies in (c) O-poor and (d) O-rich conditions. Reproduced with permission.¹⁴⁶ Copyright 2013, American Physical Society. (e) Four processes of capture and emission of carriers between deep-level defects and the valence band (VB) or the conduction band (CB) in terms of the well-known Shockley–Read–Hall model. Reproduced with permission.³⁸⁰ Copyright 2021, IOP Publishing Ltd.

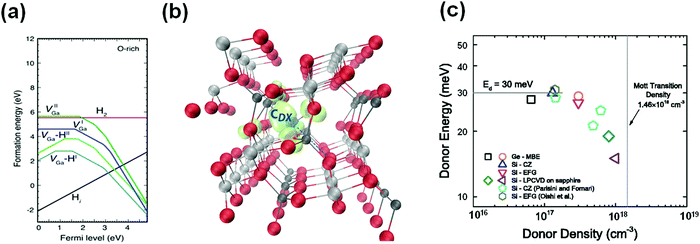
The electronic performance of devices needs to be further modulated in the applications of β-Ga₂O₃ devices. Doping engineering is an effective method. The available dopants, e.g., Si,¹⁴⁹ Ge,¹⁵⁰ Sn,¹⁴¹etc., are commonly applied in β-Ga₂O₃. These dopants tune the electron concentrations of β-Ga₂O₃ ranging from 10¹⁵ to 10²¹ cm⁻³, which meet the basic requirements of high-performance devices. However, effective p-type doping, the troublesome question, is difficult to be realized in β-Ga₂O₃ due to the flat valence band, self-trapped effects, and so on.^151,152 The self-trapped effects in β-Ga₂O₃ are generally induced by the lattice distortion.¹⁵³ Self-trapped charges are localized and the wave function of the electrons is only localized around the O atoms but not involved in the whole crystal, as shown in Fig. 10(b). This has also been confirmed by some characterization methods, e.g., deep-level transient spectroscopy (DLTS) and deep-level optical spectroscopy (DLOS). The conditions are also observed in other wide bandgap oxides such as ZnO, SnO₂, and In₂O₃.¹⁵⁴ Since the existent defects and impurities have significant effects on the fabrication and application of β-Ga₂O₃, understanding the physical properties of defects and impurities of β-Ga₂O₃ is of great significance. Meanwhile, the significance of obtaining p-type Ga₂O₃ is not only to overcome the problems of Ga₂O₃ itself but also to some extent to provide guidance for effective p-type doping of other wide bandgap oxide semiconductors.

In the following section, the common defects and impurities in β-Ga₂O₃ are summarized, e.g., vacancies and interstitial atoms, deep level defects, unintentional doping impurities, available doping impurities, and surface passivators. The intrinsic defects of bulk β-Ga₂O₃ and the effects of donors, acceptors, and passivators on the electronic properties are described. Meanwhile, the effects of defects and impurities on the electronic properties of low-dimensional β-Ga₂O₃ are comparatively reviewed here.

1. Intrinsic defects

1.1 Oxygen vacancy (V_O). Note that both bulk β-Ga₂O₃ grown by the melt method and epitaxial film obtained by vapor deposition often show a certain conductivity after the growth process or subsequent heat treatment in the atmosphere of N₂, H₂, or vacuum. Moreover, the conductivity (σ) of β-Ga₂O₃ varies with the oxygen flow conditions, as shown in Fig. 10(a).⁵² Specifically, β-Ga₂O₃ has high conductivity at a low O₂ flow rate and it decreases with increasing O₂ content. These treatments significantly tune the concentrations of oxygen vacancies (V_O) in β-Ga₂O₃. Therefore, the conductivity of β-Ga₂O₃ is related to the O₂ content in the atmosphere, which is related to the oxygen vacancy (V_O) concentrations in β-Ga₂O₃. The V_O is regarded as the donor, and the carriers ionized by V_Os will further increase the background carrier concentrations in the undoped Ga₂O₃ bulk or film. For example, Lee et al. prepared β-Ga₂O₃ thin films by magnetron sputtering, and then annealed them in the O₂ and N₂ atmosphere, respectively.¹⁵⁵ Dong et al. annealed the sputtered β-Ga₂O₃ thin film in an atmosphere of O₂ of different volume percentage.¹⁵⁶ They all found that the conductivity of the as-grown Ga₂O₃ film also varied with the variation of O₂ content in the annealed atmosphere. They suggested that V_O which played the role of a donor provided additional carriers based on X-ray photoelectron spectroscopy (XPS). In the O 1s XPS spectra, two main peaks can be obtained by the fitting of the O 1s peak by Gaussian fitting. The strongest peaks with binding energies of 531.6–531.9 eV were assigned to lattice oxygen (i.e., Ga–O bond), and the peaks with the highest binding energy around 532 eV were assigned to oxygen vacancy (V_O) in general.^157–167 The as-grown Ga₂O₃ films were post-annealed in the O₂ and N₂ atmospheres respectively in Lee et al.'s research. The O content increased more in the O₂ environment (O/Ga = 1.43) than in the N₂ environment (O/Ga = 1.42). Meanwhile, the carrier concentrations of the films obtained by the C–V measurement in O₂ and N₂ atmospheres were 1.62 × 10¹⁶ cm⁻³ and 2.01 × 10¹⁶ cm⁻³, respectively. Thus, it can be derived from the experiments that the variation of carrier concentrations and electrical conductivity was commonly caused by oxygen vacancies (V_Os). The related mechanism is that an oxygen vacancy (V_O) often captures two electrons to maintain its neutral oxygen vacancy. Free electrons can be ionized by single or double neutral oxygen vacancies in β-Ga₂O₃. This mechanism allows β-Ga₂O₃ to produce excess electrons to behave as an electron-rich oxide. Thus, β-Ga₂O₃ shows conductivity upon annealing in the absence of an oxygen atmosphere. The V_O is presumed to introduce a shallow donor level, which will provide electrons to increase the carrier concentrations and further increase the conductivity. Meanwhile, it is found that the V_O is a shallow donor level located at about ∼0.02–0.03 eV below the CBM in the experiment.¹⁶⁸ However, the viewpoint that the conductivity of β-Ga₂O₃ is induced by V_Os is refuted by other results. Zacherle et al. found the related phenomena.^{143,169–171} Although V_Os were easily formed at the low oxygen partial pressure, the transition level from the neutral state to the +2 state was the deep level in the bandgap whether in the O-rich or O-poor ambient condition, as shown in Fig. 10(c and d). One of the three types of V_Os (V_O(2)) in β-Ga₂O₃ was close to the CBM, and the other two (V_O(1) and V_O(3)) were far away in the ΔE_form − E_Fermi diagram. However, the defect level E_(0/+2) introduced by V_O(2) close to the conduction band was still more than 1 eV (i.e., E_c − E_(0/+2) > 1 eV), which had also been obtained in other literature.^171–173 This indicated that the V_O was a deep-level defect. Moreover, Onuma et al. found that the blue emission was observed in β-Ga₂O₃, which was attributed to the recombination between the deep local donor and the trapped hole.^174,175 The deep-level donor states here were speculated to be derived from V_Os. The deep defects may not increase the electron concentrations.^105,143,172 This phenomenon is similar to the case in other oxides, e.g., ZnO and In₂O₃.¹⁷⁶ In addition, the deep V_O states are also confirmed by deep level transient spectroscopy (DLTS), deep resolution cathodoluminescence spectroscopy, and surface photoelectric voltage spectroscopy.^177,178 The results show that the distance from the defect level related to V_O to the CBM is over 1 eV. Thus, whether the oxygen vacancy (V_O) is the main source of n-type conductivity for β-Ga₂O₃ is still worth discussing and investigating.

As discussed in the previous section, the intrinsic defects (e.g., V_Os) cannot be avoided in the low-dimensional Ga₂O₃ due to the direct exfoliation from the parent β-Ga₂O₃ bulk, which will have significant impact on the electronic properties of low-dimensional Ga₂O₃. To explore the effects of ordinary vacancies and explain the mechanism of defective low-dimensional Ga₂O₃, defective low-dimensional Ga₂O₃ models were constructed and explained theoretically by Sun et al.¹⁷⁹ They found that the effects of defects on the low-dimensional Ga₂O₃ were similar to that in the bulk. For example, the V_Os introduced impurity states into the bandgap, which further reduced the bandgap and affected the performance of low-dimensional Ga₂O₃.

In general, V_Os existing in the bulk β-Ga₂O₃ are considered as annoying defects in the power and optoelectronic devices. V_O hinders the fabrication of bipolar devices because the p-type Ga₂O₃ is difficult to obtain as mentioned before. That is, V_O has been regarded as the donor in much research, especially in devices based on thin films grown by physical vapor phase epitaxy. It ionizes several electrons to increase the background carrier concentrations in Ga₂O₃ and then compensates the acceptor dopants which have a low ionization rate to decrease the hole concentrations. Therefore, researchers have to consider applying a combination of heterogeneous p/n-type semiconductor materials in forming bipolar transistors or field-effect transistors in complementary devices and circuits technology. Besides, V_Os as the trapped centers affect the sensitivity and responsivity in optoelectronic detectors, which should be noticed in the actual applications.

Effective ohmic-type metal–semiconductor contacts are important steps in the fabrication of transistors. In field-effect transistors based on metal-oxides, ohmic contact is often expected to be realized by the production of many V_Os in the semiconductor at the interface of field-effect transistors. In the fabrication of β-Ga₂O₃ based transistors, Ti is chosen as the direct contact layer with β-Ga₂O₃, and Au is deposited upon Ti. The ohmic contact between Ti/Au and Ga₂O₃ is formed by rapid thermal annealing (RTA) in a N₂ atmosphere in the range of 450–500 °C.^107,180,181 Because the O atoms located at the Ti–Ga₂O₃ interface upon annealing in the absence of oxygen can spread into Ti contacted with Ga₂O₃ to form TiO_x, the interface at Ga₂O₃ forms lots of V_Os. This reduces the contact barrier located at the interface of Ga₂O₃, enabling easy formation of the ohmic contact. As for the non-volatile storage area, e.g., resistance random access memory (RRAM), V_Os are of great benefit for device applications.^182–184 The conductive filament model composed of the oxygen vacancies is the main conduction mechanism of RRAM. The switching between low and high resistance states (LRS and HRS) in the resistive memory is carried out by the formation and disconnection of V_O conductive filaments in the Ga₂O₃ layer, which is expected to update the existing von Neumann architecture of memory.

1.2 Gallium vacancy (V_Ga). Different from the V_O, gallium vacancy (V_Ga) is a p-type acceptor defect which may be formed in β-Ga₂O₃ under the O-rich condition in theory. In recent years, Zacherle et al. obtained the formation energy and defect levels of V_Ga by first-principles calculations, as shown in Fig. 10(c and d).¹⁸⁵ Gallium vacancy (V_Ga) promotes β-Ga₂O₃ to form a p-type semiconductor theoretically, that is, the Fermi level (E_F) is close to the valence band. However, the formation energy of V_Ga is very large in this situation, indicating that V_Ga is not easy to form. Although the formation energy of V_Ga decreases significantly as the Fermi level approaches the CBM of Ga₂O₃, the expected p-type Ga₂O₃ is not observed in the experiments. The phenomenon that the formation energies of cation vacancies are too high to realize p-type semiconductors can be discovered in other oxides, e.g., ZnO and In₂O₃.^143,186,187 In order to further determine the existence of V_Ga and its possible compensation effects in Ga₂O₃, positron annihilation spectroscopy is applied to explore the compensation of vacancy defects in Ga₂O₃ films in terms of experiments.¹⁸⁸ The conclusion reveals that the compensation is not constrained by cation vacancy. Similar results can be obtained by other research.^{105,170,189,190} Moreover, advanced detection methods of defects in the materials provide convenience for locating deep defect levels in materials. Polyakov et al. discovered the deep acceptor level by low-temperature photo-capacitance and capacitance–voltage measurement. The acceptor level was regarded as V_Ga and it was located at the position of E_v + 2.5–2.8 eV.^178,191,192 Meanwhile, they found another V_Ga in the gap located at the position of E_v + 1.3 eV by deep level transient spectroscopy with electrical and optical excitation (DLTS and ODLTS).¹⁹³ Therefore, V_Ga is a deep acceptor defect and does not contribute to the p-type conduction in Ga₂O₃. It is difficult to realize p-type Ga₂O₃ by V_Ga in the host material. Although the formation energy of a single V_Ga is very high and it is hard to realize, the formation of other defects will induce the V_Ga generated in the experiments, for example, the H treatment discussed in the “Unintentional doping mechanism” section.

1.3 Oxygen and gallium interstitials (O_i and Ga_i). Gallium and oxygen interstitials (Ga_i and O_i) play the roles of donor and acceptor respectively in principle. They have some effects on n-type conduction and p-type conduction. However, the theoretical calculations show that their formation energies are higher than that of other defects, and therefore the concentrations of these defects are less in β-Ga₂O₃ crystals, as shown in Fig. 10(c and d).^143,146 Their effects on the whole defective systems' properties can be ignored normally.

1.4 Deep-level defects. Deep-level defects are noteworthy defects in semiconductors because they have strong effects on carriers’ capture and recombination although they have weak influence on carrier concentrations and conductivity. These deep-level defects are investigated by deep-level transient spectroscopy (DLTS) and deep-level optical spectroscopy (DLOS). The detective fundamental is the Shockley–Read–Hall model which contains the excitation and capture of the carriers at the defect level, as shown in Fig. 10(e). The excitation and recombination of carriers can occur not only between the conduction band and the valence band but also between the conduction band/valence band and defect levels in the bandgap. Five kinds of deep levels (viz. E1,…,E5) have been reported in the Ga₂O₃ bulk and films, as shown in Fig. 11(a). By using DLTS, Zhang et al. observed that the E1, E2, and E3 levels were located at 0.62 eV, 0.82 eV, and 1.00 eV from the CBM, respectively.¹⁷⁸ Similar positions of these deep levels were also found by Irmscher et al. and Farzana et al.^192,194 The other two deep defect levels named E4 and E5 respectively were observed by DLOS. They were located at 2.16 eV and 4.40 eV from the CBM, respectively. These deep levels were often located in the bandgap as compensation levels or trapped centers. Other researchers have also observed deep defect levels in bulk or thin film Ga₂O₃. The positions of these deep defect levels are listed in Table 2. There are many speculations about the origin of these deep levels. It is inferred that the source of deep level E1 may be assigned to transition metal (such as Fe and Co) doping, while the source of E2 may be caused by Sn doping or Fe doping. In addition, it may also be attributed to V_O. The source of the E3 level may be related to transition metal doping or V_O. Moreover, the results detected in the epitaxial layer suggest that it may also be related to the complex formed by H and intrinsic defects. E4 is related to the intrinsic defects or V_Ga coupling with H. The concentrations of E5 in bulk materials are high up to 10¹⁶ cm⁻³, which is considered to be related to V_Gas or self-trapped holes (STHs). 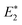Besides, it is interesting to find that there is an level at 0.72 eV below the conduction band, which may originate from V_Gas or their complexes. It should be noticed that the concentrations of these defects are different in bulk and epitaxial films, as shown in Table 2. Meanwhile, the concentrations of E2 and E4 levels increase under the proton irradiation condition, which proves that the origin of these two deep levels is related to the intrinsic defects in Ga₂O₃. This character can be also applied to examine the damage of proton irradiation.

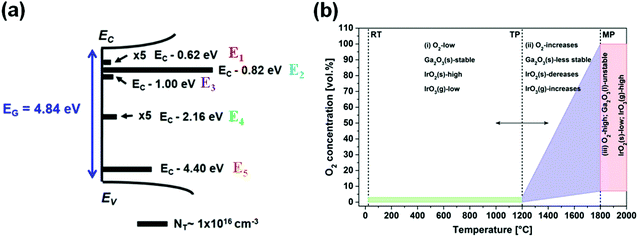Fig. 11 (a) Summary of the distribution of deep level defect states detected by both DLTS and DLOS in the same EFG-grown β-Ga₂O₃(010) materials. Reproduced with permission.¹⁷⁸ Copyright 2016, American Institute of Physics Publishing. (b) Schematic diagram of O₂ delivery to the growth furnace for growing large diameter β-Ga₂O₃ single crystals from an Ir crucible as a function of temperature by the melt-grown method. Reproduced with permission.³⁸¹ Copyright 2017, The Electrochemical Society.

Table 2 Summary of the ionization energy and concentrations of deep level defects in bulk β-Ga₂O₃ crystals and films

Deep trap level	Type	Ionization energy referenced to CBM (Ea, eV)	Concentrations (cm^−3)	Ref.
E1	Bulk	0.62	10^14–10^15	178
	Bulk	0.55	10^14–10^15	192
	Film	0.60	∼10^13	387
E2	Bulk	0.82	∼10^16	192
	Bulk	0.74	∼10^16	192
	Film	0.78	—	148 and 388
	Film	0.80	∼10^16	191 and 253
E2*	Bulk	0.75	—	388
	Film	0.72–0.78	10^13–10^14	387 and 389
E3	Bulk	1.00–1.04	10^15–10^16	178, 192 and 194
	Bulk	0.95	—	390
	Film	0.98	∼10^15	391
	Film	1.05	∼10^15	392
	Film	1.10	∼10^16	191
E4	Bulk	1.30	∼10^16	194
	Bulk	1.48	—	388
	Film	1.20	∼10^14	389
E5	Film	1.35	—	389

---

2. Unintentional doping mechanism

The preparation of β-Ga₂O₃ by the melt-grown method or epitaxial methods is subject to contamination introduced by some external elements which are often referred to as unintentional dopants. In addition to V_O, the unintentional dopants are generally regarded as another influencing factor on the intrinsic conductivity of β-Ga₂O₃ because these unintentional dopants provide high background carrier concentrations by ionization in the β-Ga₂O₃ single crystal or epitaxial film, thus making it an n-type semiconductor. As shown in Table 3, these unintentional dopants make β-Ga₂O₃ grown by the melt process and epitaxial methods exhibit high carrier concentrations (10¹⁴–10¹⁸ cm⁻³). Besides, the background carriers introduced by these unintentional dopants compensate these low concentration holes which are induced by the low solubility and high ionization energy of the acceptor in the experiments of β-Ga₂O₃ doped by the acceptors. Consequently, effective p-type Ga₂O₃ is difficult to realize. In addition, the background carriers introduced by these unintentional dopants have important effects on the effective doping concentrations and the breakdown field in the field of power devices. The accurate control of doping concentrations in the β-Ga₂O₃ drift layer can lead to a significant increase in the breakdown field in general. However, there are unintentional impurities in the drift layer which not only compensate the background carriers induced by the unintentional dopants but also act as the scattering centers to affect the mobility of the carriers. Therefore, the doping mechanism of these unintentional dopants should not be ignored.

Table 3 Summary of electronic properties (electron concentration (n), mobility (μ), and conductivity (σ)) of Ga₂O₃ bulk materials and thin films with unintentional doping prepared by different methods

Type	Preparation method	Carrier concentration n (cm^−3)	Carrier mobility μ (cm^2 V^−1 s^−1)	Conductivity σ (S cm^−1)	Ref.
Thin film	MOVPE	10^14–10^17	100–140	0.001–10	393
Bulk	CZ	2.5 × 10^16–5 × 10^17	110–150	—	365
Bulk	CZ	10^17–10^18	80–127	∼0.87–25	125
Bulk	CZ	∼10^18	—	—	195
Bulk	CZ	2.5 × 10^16–2 × 10^18	80–152	—	232
Bulk	CZ	1.8 × 10^17	—	—	394
Bulk	FZ	2 × 10^18	100	—	168
Bulk	FZ	10^17–10^18	20–200	—	395
Bulk	VB	5.1 × 10^16	90.5	∼0.74	396
Bulk	EFG	1 × 10^17	150	—	397
Bulk	EFG	3.92 × 10^16	107	∼0.67	398
Bulk	EFG	2.0 × 10^17	—	—	265
Bulk	OFZ	10^18	—	10^−4–1	52
Bulk	OFZ	10^17–10^18	50–180	6.82–16.67	399
Bulk	OFZ	4.99 × 10^17	87.5	6.99	231

---

At present, melt-grown β-Ga₂O₃ still inevitably introduces these unintentional dopants. The source of these unintentional dopants is often related to the purity of the raw material, of which Ir element is the most common impurity.^195–197Fig. 11(b) shows the effects of the growth atmosphere and temperature on the formation of β-Ga₂O₃ single crystals by the Czochralski method. It is identified that the Ga atoms, O atoms, and Ir atoms satisfy a certain thermodynamic equilibrium relationship. The β-Ga₂O₃ powder gradually becomes unstable near 1200 °C, and the Ir element gradually begins to be oxidized to IrO_3(g) at this time. When the growth temperature increases to the melting point of β-Ga₂O₃ (∼1800 °C), IrO_3(g) becomes stable and mixes into the Ga₂O₃ melt as an unintentional dopant gradually. In other words, Ir atoms will mix into the Ga₂O₃ melt and they can substitute some Ga atoms through the growth atmosphere and temperature modulation, which promotes Ga₂O₃ to become an electron-rich system. Besides, other unintentional doping impurities, e.g., Fe and Si, mostly come from raw materials. The mechanism is similar to the intentional doping mechanism with impurities; thus the only way to suppress the influence of these impurities is to further purify the raw material. As for the chemical vapor deposition methods (e.g., MOCVD), the raw materials are synthesized from trimethylgallium (TMGa) or triethylgallium (TEGa) which inevitably introduces H atoms into Ga₂O₃. Note that hydrogen can be introduced in the Ga₂O₃ host material by two ways: substitution (H_O) and interstitial (H_i). It is discovered that some annealed Ga₂O₃ materials contain more carrier concentrations, which may be due to the introduction of H_i^198,199 because H_i has low formation energy whether in O-rich conditions or O-poor conditions. Differently, H_O has low formation energy only in O-poor conditions. Both H_O and H_i are predicted to be shallow donors.¹⁰⁵ Interestingly, H can bind to the V_Ga to form the V_Ga–H complex, and then impedes the formation of p-type Ga₂O₃.^{170,190,197,200–202} The V_Ga–H complex defects have high thermal stability in β-Ga₂O₃.^203,204 Meanwhile, the formation energy of H-vacancy complexes can be lower than that of single vacancy, as shown in Fig. 12(a). When the Fermi level becomes closer to the conduction band, that is, the semiconductor becomes more and more degenerate, although the formation energy of V_Ga also decreases, the formation energy of V_Ga–H decreases much faster. The V_Ga–H complex is often considered to introduce a shallow donor level, thus resulting in increasing background carriers of Ga₂O₃. Meanwhile, H can stabilize the presence of negatively charged cation vacancies, and reduce their charge state by passivation. In addition, H is more likely to combine with other acceptor dopants to form complexes, such as Mg,¹⁹⁷ which should be paid attention to in the actual doping process.

Fig. 12 (a) Formation energies of vacancies (V_Ga), interstitial atoms (H_i), and H-vacancy complexes (V_Ga–H) in β-Ga₂O₃, shown in the O-rich conditions. Reproduced with permission.¹⁹⁰ Copyright 2011, IOP Publishing Ltd. (b) Localization of the negatively charged C_DX⁻ defect state in Ga₂O₃, illustrated by the iso-surface (green) of the corresponding electron density. Reproduced with permission.²¹³ Copyright 2018, American Institute of Physics Publishing. (c) Summary of the donor energies as a function of donor concentration. Reproduced with permission.²¹⁰ Copyright 2018, American Institute of Physics Publishing.

As for low-dimensional Ga₂O₃, it is directly obtained from the bulk Ga₂O₃ by mechanical exfoliation. Therefore, it is also affected by the unintentional doping mechanism, which increases the carrier concentrations without intentional doping. The mechanism is similar to that in the bulk material.

3. Hetero-valence impurities

3.1 Donors. β-Ga₂O₃ with an ideal stoichiometric ratio is a strong insulator. However, the prepared β-Ga₂O₃ in practice tends to behave as an n-type semiconductor. The reason for the n-type conductivity of Ga₂O₃ remains controversial. A widely accepted view is that the electric conductivity of Ga₂O₃ is larger in an O-poor environment than that in an O-rich environment due to the negative correlation between conductivity and oxygen pressure p(O₂).^205,206 This explanation seems to make sense in the physical vapor deposition method such as magnetron sputtering and pulsed laser deposition. On the other hand, in the chemical vapor deposition and melt method, some electron-rich impurities as unintentional dopants enter into the host material as substitutions or interstitials during the preparation process, which can be regarded as the dopant.²⁰⁷ Such dopants increase the carrier concentrations and then properly achieve high conductivity. Ir and H as unintentional dopants have been discussed in the previous section.

Although there is a certain concentration of electrons in undoped β-Ga₂O₃, such concentrations cannot meet the requirements of high-performance devices. Doping engineering has been regarded as an effective way to modulate the electronic properties of semiconductors. The dopant atom whose radius is close to that of the host atom is selected for substitution doping generally. If the dopant atom differs greatly from the host atom, interstitial atoms will be introduced or lattice distortion will be produced in the systems. According to this principle, many atoms (e.g., Si, Sn, Ge, Zn, Cu, etc.) with a radius close to that of Ga can be applied to substitute the lattice position of the Ga host atom. Many atoms (e.g., N, F, Cl, C, etc.) with a radius similar to that of O can be applied to substitute the lattice position of O in the same way. In the process of doping, the numbers of valence electrons of an impurity atom are compared with that of the host atom to define the electron-rich dopant or electron-poor dopant generally.^208,209 Among all the researched dopants of β-Ga₂O₃ up to now, the group IV_A elements (i.e., C, Si, Ge, and Sn), the group VII_A elements (i.e., F, Cl, Br, and I) and some transition metals (e.g., V, W, Mo, Re, Nb, etc.) are often applied to substitute the host atoms of β-Ga₂O₃. It is noticed that these donor dopants introduce shallow levels relatively. That is, the electron transition from the impurity level to the conduction band requires no more energy so that the carrier concentrations increase by orders of magnitude. So far, electron-rich dopants are available and easy to come into play, mainly because Ga₂O₃ prefers n-type conductivity. Ga atoms have more spherical s orbital overlaps which make them more suitable for electron transport in the conduction band.^{105,207,210–218}

In this section, some of the most commonly applied electron-rich dopants are summarized. The influence of these dopants on the electronic properties (e.g., electron mobility and carrier concentrations) of Ga₂O₃ is vital because these parameters reflect the merits and demerits of Ga₂O₃ doped with these impurities. This will guide the selection of the dopants for material and device engineers. The carrier concentrations, mobility, and conductivity of different electron-rich element doped Ga₂O₃ bulk and films are listed in Table 4.

Table 4 Summary of electronic properties (electron concentration (n), mobility (μ), and conductivity (σ)) of Ga₂O₃ bulk materials and thin films with intentional doping prepared by different methods

Type	Preparation method	Dopant	Carrier concentration n (cm^−3)	Carrier mobility μ (cm^2 V^−1 s^−1)	Conductivity σ (S cm^−1)	Ref.
Bulk	CZ	Hf	7.5 × 10^18–1.9 × 10^19	65–80	93.46–192.31	250
Bulk	CZ	Li	1.9 × 10^16–2.9 × 10^20	106–118	—	232
Bulk	CZ	Sn	2.5 × 10^18–10^19	50–84	—	232
Bulk	CZ	Sn	3 × 10^18–10^19	35–52	∼16.67–100	125
Bulk	CZ	Mg	—	—	—	125
Bulk	CZ	Cu	∼7 × 10^17	∼79	—	232
Bulk	CZ	Mg, Co, Ni, Al	<10^15	—	—	232
Bulk	CZ	Cr	4.0 × 10^17–10^18	76–120	—	232
Bulk	CZ	Ce	3.3 × 10^16–2.7 × 10^17	95–120	—	232
Bulk	CZ	Cu	—	—	10^−10–10^−7	284
Bulk	CZ	Si	10^18–10^19	—	—	232
Bulk	CZ	Si + Ce/Al	1.0 × 10^18–3.0 × 10^18	—	—	232
Bulk	CZ	Sn	10^18–10^19	—	—	232
Bulk	CZ	Zr	6.5 × 10^17–5 × 10^18	∼73–112	11.628–58.82	250
Bulk	CZ	Zr	1.5 × 10^18, 5.0 × 10^18	—	—	394
Bulk	VB	Sn	4.7 × 10^17–3.6 × 10^18	60–111	8.40–34.48	396
Bulk	Verneuil	Mg	—	—	10^−10–10^−6	400
Bulk	Verneuil	Zr	—	—	10^−7–10^−3	400
Bulk	EFG	Sn	4 × 10^18	110	—	401
Bulk	EFG	Si	4.9 × 10^18	93	∼71.43	352
Bulk	EFG	Fe	∼10^16	—	—	265
Bulk	OFZ	Nb	9.55 × 10^16–1.8 × 10^19	40–80	2.78 × 10^−3–181.82	246
Bulk	OFZ	Ta	3.6 × 10^16–3.0 × 10^19	50–100	∼0.60–250	402
Bulk	OFZ	Sn	2.26 × 10^18–7.12 × 10^18	49.3–64.7	23.42–56.18	231
Bulk	OFZ	Si	10^16–10^18	∼100	0.03–50	149
Bulk	OFZ	Mg	—	—	1.67 × 10^−12	117
Thin film	PLD	Si	10^15–10^20	—	10^−4–1	382
Thin film	PLD	Si	2.24 × 10^20	64.5	2323	266
Thin film	PLD	Si	2.61 × 10^19–1.74 × 10^20	18.6–26.5	78–732	403
Thin film	PLD	Zn	7.16 × 10^11–6.35 × 10^12	0.52–6.67	1.43 × 10^−7–1.41 × 10^−4	404
Thin film	PLD	N	—	—	10^−5–10^3	405
Thin film	PLD	Sn	2.9 × 10^20	—	—	401
Thin film	PLD	Sn	1.4 × 10^19	0.44	1	406
Thin film	PLD	Fe	0.99 × 10^11	9.3	4.42 × 10^−12	407
Thin film	PLD	Sn	2.01 × 10^20	62.3	0.60	407
Thin film	PLD	Sn	2.0 × 10^17–1.0 × 10^18	—	—	216
Thin film	MOVPE	Sn	1 × 10^18	41	—	408
Thin film	MOVPE	Si	10^12–10^13	<100	—	409
Thin film	MOVPE	Si	4 × 10^17–5 × 10^19	—	—	410
Thin film	Sputter	Si	—	—	4.8 × 10^−3–1	411
Thin film	Sputter	Mg	—	—	∼10^−3	412
Thin film	Sputter	Zr	—	—	∼10^−3–0.1	412
Thin film	Sputter	Ti	—	—	∼0.01–0.1	412
Thin film	Sputter	V	∼10^15–9.3 × 10^18	0.45–0.56	1 × 10^−5–1	244
Thin film	Sputter	N	1.01 × 10^12	—	2.1 × 10^−3	291
Thin film	Sputter	Ta	5.4 × 10^15–2.4 × 10^19	11.4–84.8	∼0.11 to ∼3.86	413
Thin film	MOCVD	Sn	—	—	10^−9–10^−4	414
Thin film	MOCVD	Ge	2.0 × 10^16–3.0 × 10^20	38–140	—	236
Thin film	MOCVD	Mg	—	—	∼8 × 10^−8	415
Thin film	ALD	Sn	2.3 × 10^20	—	—	401
Thin film	MBE	Ge	10^16–10^20	40–120	∼1–630	150
Thin film	MBE	Ge	4.0 × 10^17	111	—	416
Thin film	MBE	Si	Up to 10^19	90–100	—	417
Thin film	Mist-CVD	F	Up to 1.3 × 10^19	Up to 4.6	∼10.4–16.13	240
Thin film	LPCVD	Ge	10^17–10^19	—	—	237

---

IV_A – C, Si, Ge, and Sn. The elements in group IV_A have one more valence electron than that of the Ga element so that they can act as donors theoretically. Typical representatives of the IV_A elements are C, Si, Sn, and Ge, and they have been proved to be n-type dopants.^{105,108,145,219,220} C is easy to form positive charges. It has a radius close to that of the O atom, while it has a disparity with the radius of the Ga atom. C can not only substitute the Ga site (C_Ga) to form a deep impurity level, but can also substitute O (C_O) to produce a shallow level. Of the two situations, C_O is the most favorable situation. Interestingly, C_Ga can form a DX center, which is mainly caused by the off-site configuration of C_Ga due to the lattice distortion, as shown in Fig. 12(b).²¹³ The DX center is the common deep-level defect. It causes the charge state of the system to change from a positive state to a negative state directly without the experience of the neutral state. Thus, β-Ga₂O₃ containing C_Ga has a promising application prospect in high-density data storage devices and optoelectronic switches. The potential applications have been proved in II–V compounds and alloys, e.g., GaAs and Al_xGa_1−xAs, previously.^221–227

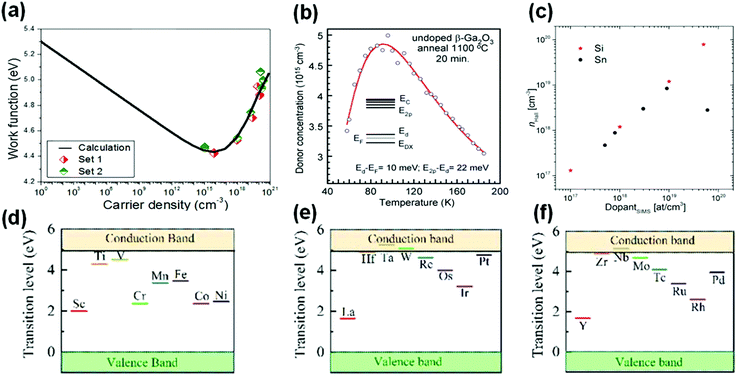
Si, Sn, and Ge prefer to form shallow donor levels when substituting the Ga site.^105,217 Si-Doped Ga₂O₃ was acquired by ion implantation by Sasaki et al. successfully.²²⁸ It is noticed that the activation efficiency which is above 60% can be obtained after annealing, with the concentration of the Si dopant varying from 1 × 10¹⁹ to 5 × 10¹⁹ cm⁻³. Due to the small ionization energy of Si, the maximum carrier concentrations of Si doped β-Ga₂O₃ can reach up in the range of 10¹⁹–10²⁰ cm⁻³. In addition, it has been discovered that the donor energy of Si decreases gradually with the increase of donor density, as shown in Fig. 12(c). This principle has been verified in Si doped β-Ga₂O₃ samples prepared by different methods, e.g., CZ, EFG, and low-pressure chemical vapor deposition (LPCVD). Therefore, it is easy to ionize the doped Si atoms and then increase the electron concentrations in β-Ga₂O₃. Meanwhile, high carrier concentrations promote the Burstein–Moss (B–M) effect that occurs in β-Ga₂O₃, which results in the absorption edge moving towards the high-energy direction.²²⁹ The Tauc plot method can be applied to analyze Ga₂O₃ samples with different carrier concentrations and it is discovered that the optical bandgap of samples with high carrier concentrations caused by Si increase. In addition, the mobility of the doped β-Ga₂O₃ thin films on the native substrate by homoepitaxy can reach up to 72 cm² V⁻¹ s⁻¹, which is still less than the theoretical value. The reason may be that the carriers are scattered more by ionized impurities. In addition, the contact resistance decreases significantly if the electrode contacts the Si doped β-Ga₂O₃. Zhang et al. investigated the Si doped β-Ga₂O₃ film grown on the sapphire by PLD. The Si composition in the epitaxial films was controlled by varying the target composition. It has been discovered that the carrier concentrations varied in the range of 10¹⁵–10²⁰ cm⁻³. Furthermore, they obtained the variation of the work function of β-Ga₂O₃ under the condition of varied carrier concentrations by Kelvin force microscopy (KFM), as shown in Fig. 13(a). The work function of Si doped β-Ga₂O₃ grown by PLD increased gradually when the carrier concentrations exceeded 10¹⁵ cm⁻³. After analysis, Si doped β-Ga₂O₃ (N_d ≈ 5 × 10¹⁹ cm⁻³) showed low contact resistance commonly. In general, dopants incorporated into the host system need to be activated to make dopants manifest good performance. In the same year, Son et al. investigated the donors' activated situations of Si doped β-Ga₂O₃ substrates treated at different annealing temperatures.²³⁰ They applied electron paramagnetic resonance (EPR) to study the donors’ behavior and revealed that Si doped β-Ga₂O₃ may also possess the DX⁻ state, as shown in Fig. 13(b). The donors in the substrates annealed at ∼1100–1110 °C were partially activated and were shown to behave as the negative charge state DX⁻ locating at ∼28–29 meV below the CBM. When the annealed temperature increased up to 1150 °C, the donors were fully activated and the ionized electrons were partially delocalized. Meanwhile, the electron concentrations also increased from 10¹⁶ cm⁻³ to ∼9 × 10¹⁷ cm⁻³ and the activation energy decreased from 49 meV to ∼17 meV remarkably. It follows that the low cost and easy availability make Si one of the most common n-type dopants.

Fig. 13 (a) Work function as a function of carrier density by calculation and KFM measurement in Si doped Ga₂O₃. Reproduced with permission.³⁸² Copyright 2016, American Institute of Physics Publishing. (b) Temperature dependence of the donor concentrations in the neutral charge state measured by EPR. The inset shows the schematic energy level of the DX center in this condition. Reproduced with permission.²³⁰ Copyright 2016, AIP Publishing. (c) Hall free carrier concentrations as a function of the concentrations of Si and Sn doped β-Ga₂O₃ single crystalline epitaxial layers obtained by secondary-ion mass spectrometry (SIMS). Reproduced with permission.³⁸³ Copyright 2017, IOP Publishing. The transition level positions of (d) fourth, (e) fifth and (f) sixth period transition metal doped α-Ga₂O₃. Reproduced with permission.²⁰⁸ Copyright 2021, IOP Publishing Ltd.

As for another commonly applied n-type dopant in β-Ga₂O₃, Sn is of great significance to obtain materials with high electron concentrations in practical applications. Sn is an effective dopant in the preparation of conductive Ga₂O₃ single-crystals or epitaxial films. Sn prefers to replace Ga₍₂₎ and there are also localized defect states existing within the bandgap.^231,232 In the aspect of experiments, Du et al. obtained Sn-doped Ga₂O₃ epitaxial film on β-Ga₂O₃(100) substrates by MOCVD.²³³ They found that the Sn content affected the structural, Raman, and photoelectric properties of homoepitaxial thin films. That is, the films with varied Sn contents changed the electrical conductivity indeed. The lowest resistivity (1.20 × 10⁻¹ Ω cm) and the highest Hall mobility (∼12.03 cm² V⁻¹ s⁻¹) of these homoepitaxial thin films were obtained for the 10% Sn-doped sample. Meanwhile, the bandgaps of these samples varied from 4.16 eV to 4.69 eV by tuning the Sn content from 1% to 12%. It has potential applications in the mainstream optoelectronic devices. Note that the carrier concentrations introduced by Sn show the maximum value in a certain range, which is different from the Si dopant, as shown in Fig. 13(c). The measured effective Sn doping limits by secondary ion mass spectrometry (SIMS) are limited to 10¹⁷–10¹⁹ cm⁻³. It is found that the addition of Sn atoms deteriorates the crystallization quality of the β-Ga₂O₃ film constantly, thus reducing the efficiency of doping and having the doping limit.²¹⁰ This indicates that the doping concentrations will be limited when the ion radius of the dopant is larger than the radius of the host ion. Moreover, although the doping concentrations increase monotonously, the electron concentrations decrease so that the electronic properties of the film deviate from the expected situation. This phenomenon has also been observed in In₂O₃:Sn and SnO₂:Sb thin films.²³⁴ Notably, recent studies revealed that the Sn dopant did not exist only in the form of Sn⁴⁺. Sn exhibited two modes which were active mode and inactive mode in the Ga₂O₃ film grown by MBE.²³⁵ That is, Sn existed in the active mode as Sn⁴⁺, while it existed in the inactive mode as Sn²⁺, which has been investigated by X-ray absorption spectroscopy (XAS). This fresh phenomenon is worthy of further study.

Although Si, Sn, and Ge are all n-type dopants of Ga₂O₃, the host atom sites they substitute are not the same. Sn substitutes Ga₍₂₎ priorly when they are incorporated in Ga₂O₃ as the donors, while Si and Ge will substitute Ga₍₁₎ sites. Therefore, Si and Ge introduce the relatively shallow level which results in the efficient activation at room temperature, while Sn introduces the deep level.²³⁶ Although Si has a high activation rate, Ge will produce more carriers than Si to further increase the carrier concentrations in the systems when the doping concentration of Ge is similar to that of Si. Meanwhile, the ionized Ge has a greater radius than that of the ionized Si, which matches the sizes of tetrahedrally coordinated Ga₍₁₎ in β-Ga₂O₃. Since Ge does not cause extra lattice distortion and leads to good crystal uniformity of β-Ga₂O₃, Ge also has a potential application in n-type doping in β-Ga₂O₃. In the actual doping engineering, Ahmadi et al. applied MBE to realize Ge doping in β-Ga₂O₃. The carrier concentrations could be increased up to 10²⁰ cm⁻³, and the carrier mobility was up to 120 cm² V⁻¹ s⁻¹.¹⁵⁰ Besides, Ranga et al. and Alema et al. incorporated Ge into β-Ga₂O₃ by LPCVD and MOCVD, respectively.^236,237 The carrier concentrations of Ge doped β-Ga₂O₃ prepared by CVD reached up to 10²⁰ cm⁻³, and the carrier mobility was about 140 cm² V⁻¹ s⁻¹, which indicated that the performance of the Ge doped β-Ga₂O₃ epitaxial film prepared by the CVD method was comparable to that prepared by MBE. Although Ge has many advantages, Si and Sn are more preferred dopants in realizing n-type doped β-Ga₂O₃ by using group IV_A elements due to the low-cost and convenient doping technology.

In low-dimensional Ga₂O₃, Si, Ge, and Sn can also be used to increase the carrier concentrations. Since low-dimensional Ga₂O₃ is mostly obtained by slicing it directly from the parent bulk Ga₂O₃ by mechanical exfoliation, the variation of carrier concentrations after doping is closely related to that in the parent bulk Ga₂O₃. Meanwhile, Liu et al. confirmed that the Si, Ge, and Sn doping caused low-dimensional Ga₂O₃ to behave as n-type Ga₂O₃ by first-principles calculations.²³⁸ Si, Sn, and Ge doped two-dimensional Ga₂O₃ shifted the Fermi levels into the conduction band, indicating that these elements show donor behaviors. Meanwhile, no impurity levels existed in the bandgaps of these systems. Note that, unlike the situations in bulk Ga₂O₃, Si, Ge, and Sn doping induced indirect-to-direct bandgap transition in low-dimensional Ga₂O₃. This transition arose from dopant-induced charge redistribution. The interaction between the dopant and neighboring O atoms affected the states’ distribution of the highest valence level, thereby shifting the position of the VBM and leading to this phenomenon.

VII_A – F, Cl, Br, and I. Halogens that can substitute oxygen (F_O, Cl_O, Br_O, and I_O) have been identified as shallow donor impurities. Konishi et al. discovered that the Ga₂O₃ Schottky diode treated by HF had a high breakdown voltage and a relatively high barrier height (∼1.5 eV).²³⁹ Before depositing the metal, fluorine was incorporated into Ga₂O₃ by HF treatment coupling with the post-annealing treatment. Then, F atoms tended to bond to the semiconductor surface and also tended to diffuse into the material during annealing. Because F tended to react with the ionized donor to form neutral complexes or act as negative ions to compensate n-type doping and further caused the surface loss. The surface depletion area was broadened to increase the breakdown voltage of the device. Besides, Shu et al. and Morimoto et al. proved that F could improve the conductivity of α-Ga₂O₃ by first-principles calculations and experiments, respectively.^240,241 It was found that the conductivity could reach up to 16.13 S cm; thus it had potential applications in devices.

The halogen doped β-Ga₂O₃ has potential applications in the area of photocatalytic decomposition of water.²⁴² The essence of this application is to modulate the energy position of the band edge in halogen atom doped β-Ga₂O₃ so that it can better match the O₂/H₂O potential and H⁺/H₂ potential of H₂O. It should be noted that the CBM of pure β-Ga₂O₃ is lower than the H⁺/H₂ potential (0 eV) and the VBM is higher than the O₂/H₂O potential (1.23 eV). Compared with the intrinsic position of the CBM and VBM in β-Ga₂O₃, the F element does not modulate the intrinsic positions of the CBM and VBM. The Cl element reduces the CBM to 0.35 eV, and the VBM is increased by 0.13 eV. The CBM and VBM of Br doped β-Ga₂O₃ are further reduced and elevated, respectively. The VBM of I-doped β-Ga₂O₃ further decreases to close to the O₂/H₂O potential, while the CBM increases. Meanwhile, the bandgaps of these doped systems decrease from 4.50 eV to 2.64 eV with the increase of the number of periods. In conclusion, the photocatalytic reduction and/or oxidation abilities of Cl, Br and I doped β-Ga₂O₃ are improved compared with pure Ga₂O₃ and F doped Ga₂O₃, which has potential applications in the photocatalytic areas.

Transition metals. Transition metals can introduce more than one energy level into the semiconductors by doping due to multiple states of charge.^208,243 Much progress has been made in the research of transition metal doped β-Ga₂O₃ in recent years. In addition to the unintentional dopants (e.g., Ir) as mentioned before, the researchers have studied the transition metal by intentional doping to further improve the carrier concentrations expected in β-Ga₂O₃. Huang et al. investigated β-Ga₂O₃ doped with V, W, Mo, Re, and Nb. They found that the electronic properties of doped β-Ga₂O₃ were altered.^244,245 Particularly, it was found that Nb would form the shallow donor level in β-Ga₂O₃. Zhou et al. proposed that the carrier concentrations could be modulated over the range of 9.55 × 10¹⁶–1.8 × 10¹⁹ cm⁻³ in Nb-doped β-Ga₂O₃.²⁴⁶ The maximum mobility of the Nb-doped β-Ga₂O₃ bulk was 182 cm² V⁻¹ s⁻¹, which revealed the high transport properties. Shi et al. and Zhang et al. studied the effects of Nb doping on the properties of β-Ga₂O₃ films by magnetron sputtering.^246,247 Furthermore, Shi et al. focused on the charge-trapping properties of Nb doped β-Ga₂O₃ by obtaining the metal-oxide–nitride-oxide–silicon (MONOS) structure capacitor; they found that it had better charge-trapping properties with light doping concentrations.²⁴⁷ However, the performance of the capacitor was deteriorative in heavy doping Nb concentrations. This was mainly related to the Nb out-diffusion degree and interface traps. Light Nb doping could generate more electron traps, while there were more hole traps at the interface with heavy doping. The increase of hole traps would lead to the decrease of the charge trapping capacity of the capacitors, which was reflected in the case of heavy Nb doping. In 2020, Chen et al. obtained the Nb-doped β-Ga₂O₃ nanobelt by a mechanical exfoliation method and the bottom-gate FET was fabricated successfully. The concentration was ∼10¹⁸ cm⁻³ and the mobility was in the range of 32.11–71.54 cm² V⁻¹ s⁻¹. Therefore, the FET showed excellent performance. In addition to Nb, Ta doping was explored in 2019. The concentration and mobility of the Ta doped β-Ga₂O₃ bulk were 3.6 × 10¹⁶–3.0 × 10¹⁹ cm⁻³ and 50–100 cm² V⁻¹ s⁻¹, respectively. Besides, the d²s² group (e.g., Hf and Zr) doped β-Ga₂O₃ has also been studied in recent years. Zr tends to substitute octahedral Ga, and Zr doped β-Ga₂O₃ has satisfactory mobility in degenerate systems. The mobility of Zr-doped β-Ga₂O₃ is further improved to 112 cm² V⁻¹ s⁻¹, while the maximum carrier concentration is only 10¹⁸ cm⁻³.^248,249 Proper Hf can increase the carrier concentration in β-Ga₂O₃ up to 10¹⁹ cm⁻³, and the conductivity can reach about 200 cm² V⁻¹ s⁻¹.²⁵⁰ However, Hf and Zr are more expensive than Si; thus Hf and Zr are not optimal selection to obtain β-Ga₂O₃ with high carrier concentrations normally.²⁵¹ Besides, it has been discovered that there are two defect levels located at E_c – 0.55–0.60 eV (E₁) and E_c – 0.90–1.1 eV (E₃) by DLTS and other measurements, respectively.^{191,192,252,253} The origin of the defect levels at these two positions is speculated to be the transition metals. The deep levels do not play an obvious role in improving the conductivity in Ga₂O₃, and they may act as the trapped centers as discussed before.

Transition metals have also been applied in the doping engineering of metastable Ga₂O₃ (e.g., α-Ga₂O₃). For example, Wang et al. predicted variation laws of defect levels of electron-rich transition metal doped α-Ga₂O₃ by first-principles calculations, and their positions are shown in Fig. 13(d–f).²⁰⁸ They summarized that the transition level positions of electron-rich dopants selected from group III_B to VIII_B of the Periodic Table almost showed the “N”-shaped variation rule. That is, the transition levels went from deep to shallow at first, and then went into deep levels again. Finally, they went to relatively shallow levels again. This was mainly due to the different types of chemical bonds between different subgroups and O atoms. If the dopants were selected from group IV_B to V_B, the ionic bonds were formed between O and the dopants with raised d-orbitals. On the other hand, if the dopants were selected from group VI_B to VIII_B, the covalent characteristics were observed between O and dopants with evident d-orbital splitting, because d orbitals contributed to the levels that were introduced. This was the main reason for the variation of the introduced levels. Note that the anomalous variation of Cr and Mn doped β-Ga₂O₃ in the fourth period was mainly due to the strong orbitals spin effect.

Besides, the transition metal atoms containing d orbitals can hybridize with O atoms, which makes the doped β-Ga₂O₃ exhibit special properties.^{208,254–256} Due to the unique properties (e.g., multi-orbitals and special d-orbitals), the magnetic and luminescence properties of β-Ga₂O₃ will be affected, which will be described later.

3.2 Deep acceptors. Although the availability of n-type doping in β-Ga₂O₃ can be fulfilled and succeeded, p-type doping has been a troublesome problem in β-Ga₂O₃ doping engineering. There are three kinds of important issues that should be faced in p-type doping in Ga₂O₃. On the one hand, holes are always predicted to be self-trap holes, resulting in the holes that prefer to form small polarons at O sites rather than free carriers. On the other hand, the dispersion degree of the valence band is small and the energy distribution of the VBM is flat; thus the effective mass of the hole is large. In addition, the high concentrations of background carriers in Ga₂O₃ make even the small number of holes introduced by the ionized acceptor immediately compensated. Thus, it is difficult to obtain the effective p-type Ga₂O₃ by doping with potential acceptors, which can also be discovered in other wide bandgap oxide semiconductors.²⁵⁷ Furthermore, this is becoming one of the factors which hinder the further applications of Ga₂O₃ as the basis for high-quality semiconductor materials in complementary metal-oxide-semiconductor (CMOS) technology.

In this section, the research progress of some potential acceptor dopants is reviewed, and the effects of some electron-poor metal or non-metal dopants are mainly introduced here. Since effective p-type low-dimensional Ga₂O₃ cannot be realized by substitution doping, the internal mechanism is similar to that in bulk materials. Therefore, this section mainly discusses the situation in bulk Ga₂O₃, while it will not be repeated in low-dimensional Ga₂O₃.

Mg. Magnesium, which has one less valence electron than Ga, can be an acceptor dopant theoretically. Mg has been proved to be an effective acceptor dopant in other wide bandgap semiconductors (e.g., GaN) in the early research. Although Mg formed complexes with H easily, Hiroshi Amano et al. realized Mg doped p-type GaN materials by low-energy electron beam irradiation (LEEEBI) successfully.^258–260 Inspired by this, Mg doped β-Ga₂O₃ was synthesized by Qian et al.²⁶¹ Combined with the post-annealing treatment, the doped β-Ga₂O₃ thin films with various Mg concentrations (i.e., 4.92 at%, 6.88 at%, and 8.58 at%) were fabricated by magnetron sputtering. The Fermi level of the Mg doped β-Ga₂O₃ thin film was close to the valence band, indicating a weak p-type characteristic. However, Chikoidze et al. proposed that the acceptor level introduced by Mg was more than 1 eV away from the VBM, indicating that it may be a deep level impurity by Hall and photoemission measurements.²⁶² To understand the internal mechanism of the Mg's effects, the polaron model was built to explain this phenomenon theoretically.²⁶³ By the results of the Koopmans-compliant hybrid functional analysis of the defect levels, Mg would introduce an acceptor level corresponding to a small polaron, which would be formed at the O₍₁₎ site near the Mg atom. In addition, it has been found that Mg compensates the background carriers of Ga₂O₃ to reduce the background carrier concentrations. Therefore, the resistivity of the Mg doped Ga₂O₃ substrate will be further increased, thus transforming into an insulating substrate gradually.
Fe. Fe is considered to be the effective compensation dopant in group-III semiconductors, and especially Fe doped β-Ga₂O₃ is expected to increase the resistance of the β-Ga₂O₃ bulk and film. Because Fe and Ga₍₂₎ have the same valence state and their ionic radii are very close (r_(Ga³⁺) = 0.062 nm ≈ r_(Fe³⁺) = 0.064 nm), Fe will substitute Ga₍₂₎ preferentially.²⁶⁴ The defect level of Fe acts as the recombination center or capture center to compensate the unintentional electrons and holes. The mechanism of trap centers capturing carriers is shown in Fig. 14(a).²⁶⁴ By capturing electrons (holes), the valence state of Fe³⁺ is lowered to Fe²⁺ (raised to Fe⁴⁺), which affects the background carrier concentrations. Meanwhile, the behavior of Fe doping does not promote the generation of other dense traps associated with Fe.^265,266 Therefore, Fe doped β-Ga₂O₃ realizes the semi-insulating substrate and the current blocking layer. The carrier concentrations of Fe doped β-Ga₂O₃ are decreased to 10¹⁵–10¹⁶cm⁻³ gravely, and thus it can be applied as a semi-insulating substrate in power devices.²⁶⁵ The semi-insulating substrates of Fe doped β-Ga₂O₃ are commercially available nowadays. The Fe dopant concentrations are about 10¹⁸ cm⁻³ in these substrates to compensate background carriers and pin the Fermi level.^265,267,268

Fig. 14 (a) Schematic diagram of variations of the valence state of Fe in Fe doped β-Ga₂O₃. Reproduced with permission.²⁶⁴ Copyright 2021, Springer Science and Business Media, LLC, part of Springer Nature 2021. (b) The transition levels of N, Be, Mg, Ca, Sr, Zn, and Cd doped β-Ga₂O₃. Reproduced with permission.²⁷⁶ Copyright 2018, IOP Publishing Ltd. (c) The transition levels of I_B and II_B group transition metal doped α-Ga₂O₃. Reproduced with permission.²⁰⁸ Copyright 2021, IOP Publishing Ltd.

Based on this, homogeneous epitaxial doped β-Ga₂O₃ films on Fe doped semi-insulating substrates have many advantages compared with heterogeneous epitaxial doped β-Ga₂O₃ films, e.g., smooth surface (RMS < 0.5), high carrier concentrations (∼10²⁰ cm⁻³) and electrical conductivity (μ_max = 2323 cm² V⁻¹ s⁻¹), low defects, good lattice match with the substrates, etc.²⁶⁹ Therefore, homogeneous epitaxial thin films based on Fe doped semi-insulating substrates are widely applied in power devices. In addition, selecting the appropriate gate oxide dielectric material is crucial in the applications of FETs, because the lattice mismatch existing between the gate dielectric layer and the Ga₂O₃ channel layer may further deteriorate the electronic performance of the interface. Huang et al. proposed that the homoepitaxial Fe doped β-Ga₂O₃ layer had the potential to be a high-insulated gate dielectric material, which improved the electronic performance of Ga₂O₃ FETs.²⁷⁰ They grew Fe-doped β-Ga₂O₃ films on sapphire substrates by Laser-MBE and investigated the resistance of the samples at different substrate temperatures. The resistances of these samples were on the order of GΩ. The variation of resistance was modulated by the Fe³⁺/Fe²⁺ ratio, that is, when the Fe³⁺/Fe²⁺ ratio decreased, the resistance would increase. Compared with pure β-Ga₂O₃, the resistance of Fe doped Ga₂O₃ increased significantly, showing the properties of high insulation. Therefore, it was expected that this approach would be worth trying in the fabrication of dielectric layers in the FETs in the future.

Zn and Cu. Zn has one less valence electron than Ga, and thus it can be used as an acceptor dopant. Zn-doped β-Ga₂O₃ has been extensively studied because the radius of Zn²⁺ is close to that of Ga³⁺; thus large lattice distortion will not be introduced during doping.^{209,271–275} Therefore, Zn is an ideal dopant for obtaining p-type β-Ga₂O₃. However, theoretical research seems to refuse this conclusion. Lyons et al. obtained the positions of the Zn-doped β-Ga₂O₃'s defect levels by first-principles calculations, as shown in Fig. 14(b).²⁷⁶ Obviously, the position of the defect level was far from the VBM (ΔE > 1 eV). Therefore, the defect level introduced by Zn was a deep level, which had little effect on the acquisition of p-type β-Ga₂O₃. Considering the difficulty of realizing effective p-type β-Ga₂O₃ discussed before, Chikoidze et al. proposed a new method.²⁷⁷ They reduced the mean free path of the carriers by incorporating Zn and then obtained p-type β-Ga₂O₃ with an ultra-high breakdown electric field (13.2 MV cm⁻¹), which provided an important reference for the acquisition of homogeneous bipolar devices with high breakdown electric field subsequently.

In general, considering that the low doping concentrations will introduce the deep level in the bandgap, the high accepter-doping concentrations promote the introduced acceptor level close to the valence band. This is considered to be another strategy to realize effective p-Ga₂O₃. Nevertheless, such a method is unsuccessful in the Zn doped β-Ga₂O₃. When the concentration of Zn decreases to ∼1.5%, deep levels are introduced and p-Ga₂O₃ cannot be obtained.^218,278 When the doping concentration increases up to ∼2%, Zn has negligible change in the basic band structure. It just reduces the bandgap and introduces impurity absorption peaks in the longwave range.²⁷⁹ The p-Ga₂O₃ is not realized again. When the concentration of Zn increases up to ∼4%, Zn introduces a shallow level of ∼0.3 eV up to the valence band.¹⁰⁸ The reason is that the concentrations of V_O decrease when the concentration of the Zn component increases.²⁸⁰ The introduction of Zn into β-Ga₂O₃ as the acceptor dopant compensates the background electrons and reduces the electron concentrations. Although the acceptor level is shallower than that in the condition of low doping concentrations, effective p-type β-Ga₂O₃ has not been obtained yet. This is mainly due to the large background carrier concentrations caused by unintentional doping. Moreover, with the increase of the Zn component concentration, the Burstein–Moss effect will occur, which modulates the optoelectronic properties.

Compared with Zn, the valence electrons of Cu are fewer, which may be easy to realize p-type doping in Ga₂O₃. Yan et al. found that Cu introduced two acceptor impurity levels near the VBM and produced 100% spin polarization near the Fermi level.²⁸¹ P-Ga₂O₃ could be realized by Cu in this research. On the other hand, Kyrtsos et al. found that Cu was not an effective acceptor, which was different from the previous research.²¹⁸ It would introduce deep acceptor levels in β-Ga₂O₃, which was not beneficial to practical device applications. Meanwhile, it should be noticed that Cu-doped β-Ga₂O₃ will hinder the grain growth, thus deteriorating the crystallinity of the doping systems.^282,283 In order to realize a high-quality Cu doped Ga₂O₃ single wafer, Galazka et al. recently attempted to synthesize Cu doped Ga₂O₃ by the CZ method but it was in vain.²³² The failure of the experiment was caused by excess Cu evaporation. After analyzing the reasons for the failure, Jesenovec et al. improved the CZ method and the VGF method to fabricate the high-quality Cu doped Ga₂O₃ single crystal successfully.²⁸⁴ Then they discovered the fresh phenomenon that Cu-doped β-Ga₂O₃ had a photodarkening effect. They combined theoretical results with experimental conclusions to reveal the internal mechanism. That is, the EPR results revealed that Cu²⁺ would transform to Cu³⁺ under light exposure, which was a rare oxidation state of Cu. After Cu was introduced into the Ga₂O₃ single crystal, it would form complexes with unintentional dopants (i.e., H_i or H_O). When the Cu_Ga–H_O complex absorbed external light, H would be released resulting in the formation of Cu³⁺ and O–H modes.

In addition to more research in Zn and Cu doping in β-Ga₂O₃, related studies have also been carried out in other metastable phases, but they are few. Recently, aiming to further reveal the effects of the transition metals (I_B and II_B) on the electronic properties of α-Ga₂O₃, Wang et al. made theoretical predictions on Zn and Cu group doped α-Ga₂O₃.²⁰⁸ Different from the traditional deep level defects, they found that Cu and Zn would form an AX center in α-Ga₂O₃, as shown in Fig. 14(c). As a deep-level defect similar to the DX center, the AX center limits the maximum free carrier concentrations in the host material.^285–287 The AX centers are the first found in doped α-Ga₂O₃, and it is considered to be an important reason for hindering the acquisition of p-type α-Ga₂O₃.

Bi. As mentioned above, effective p-type doping in Ga₂O₃ by general acceptor dopants is difficult to form, and they tend to form localized holes. Traditionally, the acceptor dopant is considered according to its outer electrons, that is, the element with fewer extranuclear electrons than the host element is generally selected as the acceptor dopant. However, the appearance of Bi₂O₃ provides a new idea for p-type doping in semiconductors.²⁸⁸ The feature of this p-type oxide is that the s orbitals of Bi will hybridize with the O orbitals when the compound is formed. Then as a consequence of hybridization a low accepter level is introduced in the bandgap. Inspired by this, Sabino et al. studied β-Ga₂O₃ doped by Bi with filled s orbitals systematically.^289,290 By increasing the concentrations of the Bi element, they found that the accepter level further decreased, as shown in Fig. 15(a). The specific feasibility needs to be confirmed by subsequent related experiments.

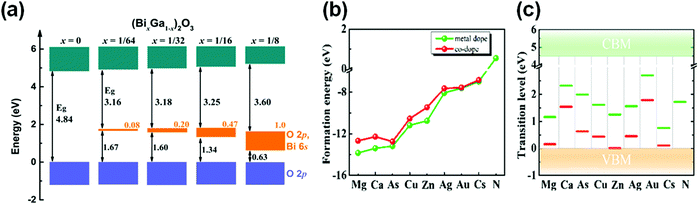Fig. 15 (a) Schematic representation of the effects of Bi concentrations (x = 1/48, 1/24, 1/16, and 1/8) on the defect level position in (Ga_1−xBi_x)₂O₃. Reproduced with permission.²⁹⁰ Copyright 2021, American Physical Society. (b) The formation energies and (c) the acceptor levels of single metal doped and (electron-poor metal, N) co-doped β-Ga₂O₃. Reproduced with permission.²⁰⁹ Copyright 2021, Elsevier Ltd.

N. The number of valence electrons of N is one less than that of O, and the radius of N^3- is close to that of O²⁻. The lattice distortion degree caused by the addition of N is small. Therefore, it is considered as an ideal non-metallic acceptor. The realization of p-Ga₂O₃ doped by N has been one of the hot topics that scholars are interested in. Early studies focused more on the optimized preparation and luminescence characteristics in N-doped Ga₂O₃ nanowires, because the N element can modulate the electronic structure of β-Ga₂O₃ and introduce defect levels in the bandgap, thus achieving tunable light emission. Meanwhile, good crystal quality, smooth surface, variable bandgap (4.75–4.88 eV), and high visible light transmittance (>80%) Ga₂O₃ nanowires can be obtained by optimizing the film thickness and annealing conditions.^291–294 These characteristics can make N-doped Ga₂O₃ applied in transparent electronics such as transparent conductive electrodes. Although the N atom is considered as a potential acceptor, it is found that the defect levels which the N substituted O host atom introduces are deep levels (ΔE > 2 eV).¹⁰⁴ In addition, the p-type characteristics of the N doped β-Ga₂O₃ are not obvious, and the main reason is that N doping often couples with some vacancies. Dong et al. found that the defects of N_OV_O were stable under Ga-rich conditions.²⁹⁵ These donor defects converted N-doped β-Ga₂O₃ into a weak n-type β-Ga₂O₃. That is, even if holes were generated after N incorporation, these excess holes would be compounded by electrons generated due to intrinsic defects (i.e., V_O). Meanwhile, they found that the intrinsic absorption edge would red-shift in N-doped β-Ga₂O₃ coupling with vacancies. Moreover, an extra peak was generated in the low-energy region (1.23 eV). The origin of this peak was related to the recombination of electrons trapped by donors due to V_O and holes trapped by acceptors due to N doping, which verified the red-light emission observed in the early experiments.²⁹⁶ Recently, Fang et al. proposed a new approach to obtain p-type Ga₂O₃ by N-doping, and they prepared a solar-blind photodetector based on this.^297,298 That is, they proposed that GaN on the sapphire was oxidized into different components of GaN_xO_3(1−x)/2 thermally in a modified CVD system. This was caused by an energy-driven multi-step structural phase transition mechanism. It led to partial oxidation and phase transition in GaN, which was equivalent to doping Ga₂O₃ with N. Based on this process, the hole concentrations and mobility of GaN_xO_3(1−x)/2 reached up to 10¹⁶ cm⁻³ and 41.4 cm² V⁻¹ s⁻¹, respectively. However, the hole concentrations and conductivity were still very low, and the electronic performance was far less than that in n-type Ga₂O₃. In addition, it was difficult to control the phase transition and doping concentrations of N atoms accurately, which led to complex process implementation. Therefore, it still needs more work to carry out and optimize in this aspect.

Besides, N-doped β-Ga₂O₃ has also been widely applied in power devices. The β-Ga₂O₃ layer implanted with N is annealed at a temperature over 1100 °C because such a temperature helps activate the implanted N atoms. The holes generated by N atom incorporation can compensate the background carriers in β-Ga₂O₃. This gives rise to the energy barrier in electron movement, which further blocks the vertical flow of current effectively. Therefore, N-doped β-Ga₂O₃ acts as a current blocking layer in depletion-mode vertical Metal-Oxide–Semiconductor Field Effect Transistors (MOSFETs) and as a field-plate (or guard ring) in vertical β-Ga₂O₃ Schottky barrier diodes.^299–301

The defect levels introduced by Be, Ca, Sr, and Cd have also been investigated by DFT.²⁷⁶ Compared with N, these defect levels are relatively close to the valence band but they are still deep levels as shown in Fig. 14(b).

3.3 Co-doping. The solubility and activation rate of the dopants are also the fundamental factors which determine the doping effectiveness. The concentrations and activation rates of dopants in Ga₂O₃ are often limited, especially in the p-type doping process as discussed in the previous section. At the same time, some doped atoms couple with the defects, which further hinders the realization of p-type doping. The solubility of acceptor dopants in host crystals is generally low. The co-doping strategy is proposed in this situation. Partial co-doping methods have increased the dopant solubility and the activation rate and lowered the ionization energy. For example, the maximum hole concentration in Mg doped GaN is about 10¹⁷ cm⁻³.³⁰² The hole concentrations increase by an order of magnitude when O atoms are co-doped with Mg atoms. Inspired by this phenomenon, several co-doping approaches, in particular, electron-poor metal dopant co-doping with the N dopant, have been tried in β-Ga₂O₃.²⁰⁹ Zhang et al. found that the formation energy of N-doped β-Ga₂O₃ could be reduced by (Zn, N) co-doping. This confirms that the co-doping method improves the solubility of N-doping, which is similar to that in GaN. Meanwhile, compared with only one acceptor level in N doped β-Ga₂O₃ (E − E_VBM = 0.761 eV), two acceptor levels are introduced in the bandgap in N–Zn co-doped β-Ga₂O₃ (E₁ − E_VBM = 0.149 eV, E₂ − E_VBM = 0.483 eV).³⁰³ However, the underlying mechanism was not unveiled yet. Inspired by previous studies on ZnO, the shallow acceptor level of ZnO can be obtained by co-doping (electron-rich cation, electron-poor anion) due to the donor–acceptor level rejection.³⁰⁴ Meanwhile the acceptor level position can be reduced by co-doping from the perspective of molecular orbital theory. Yan et al. used some electron-poor cations containing p and d orbitals to replace Ga, and they used an N atom to substitute O in β-Ga₂O₃, as shown in Fig. 15(b and c).²⁰⁹ The acceptor levels reduced significantly because co-doping further moved the Ga–O bonding orbitals up and moved the dopant–O antibonding orbitals coupling with the unoccupied p orbitals of N and O ions down by using the (metal, N) co-doping method instead of pure metal doping.³⁰⁵ Besides, Ma et al. investigated the co-doping of Al–N and In–N, and found that the formation energy was reduced and the acceptor levels were close to the valence band.³⁰⁶ Since the acceptor level of the In–N co-doping system was closer to the VBM, they further used the In atom for co-doping with more N atoms, and found that the acceptor levels were closer to the valence band compared with the single N atom. That is, increasing the concentration of N is more favorable for obtaining p-type β-Ga₂O₃. In the case of non-metallic doping only, N–P co-doping has also been found theoretically to be possible to form p-type β-Ga₂O₃ with high hole concentrations.³⁰⁷ From this, the co-doping research studies in β-Ga₂O₃ are not only beneficial for obtaining p-type β-Ga₂O₃, but can also provide a guideline for obtaining other phases of p-type Ga₂O₃. Therefore, the research on co-doping is worthy of further related theoretical and experimental research in-depth.

3.4 Surface passivation. The Ga₂O₃ bulk is a three-dimensional material, and it has a large number of internal defects and surface defects. Although it is different from materials with a layered structure, Ga₂O₃ can be easily exfoliated into a quasi two-dimensional (quasi 2D) structure with a large surface area. Note that the dangling bonds existing on the surface of exfoliated Ga₂O₃ form surface states. These surface states will affect the performance of Ga₂O₃ materials and devices seriously. For example, they affect the carriers’ transport around the surface and the injection of carriers by limiting the interface resistance due to the Fermi pinning effect. Meanwhile, the quasi 2D Ga₂O₃ without passivation has other disadvantages, e.g., inconspicuous quantum confinement effects, inconspicuous bandgap variation, instability, etc. Therefore, some impurity atoms should be selected for surface treatment to saturate the dangling bonds on the surface of unpassivated quasi 2D Ga₂O₃.

It is found that the electronic properties of the bulk Ga₂O₃ will be modulated by the surface treatment and impurity absorption in the research of surface treatment on the bulk Ga₂O₃ material. For example, Yang et al. investigated the bulk Ga₂O₃ materials after surface treatment such as plasma treatment (CF₄ and O₂), gaseous treatment (ultraviolet/O₃), and liquid treatment (HCl, H₂O₂, etc.).^308,309 The experimental results about the surface of Ga₂O₃ absorbed by the different impurities showed that different surface treatments had different effects on the electronic properties (e.g., Schottky barrier height, etc.) of bulk Ga₂O₃. The results of I–V and C–V tests showed that the Schottky barrier height decreased and the ideal factor increased under plasma treatment, and the reverse characteristics of diodes based on Ga₂O₃ deteriorated. The other two treatments did not deteriorate the electronic properties of the near-surface in Ga₂O₃. Considering that low-dimensional materials will be sensitive to surface treatment, it is significant to investigate the surface passivation of the unpassivated Ga₂O₃ for the preparation of high-performance devices based on Ga₂O₃.

As for low-dimensional wide bandgap semiconductors, the common approach is to use hydrogen or halogen functional groups for passivation to modulate the electronic properties. This strategy can further improve optoelectronic properties and material stability.^26,60In addition, the semi-saturated and full saturated functionalization can enhance thermodynamic stability and electron transport performance. As discussed in the previous section, Fig. 9(e–g) shows the PDOS of H passivated low-dimensional monolayer Ga₂O₃. Note that the VBM is mainly contributed by O 2p orbitals coupling with Ga 4p and H 1s orbitals.^21,27 It is obvious that the charges are still localized near the O atom in the VBM of the H passivated low-dimensional Ga₂O₃, as shown in Fig. 9(i). The charges at the CBM are delocalized, which is the same condition in bulk Ga₂O₃. Meanwhile, it can be concluded that the contribution of the H 1s orbital to the VBM is larger than that of the CBM by comparing the contribution of adsorbed H atoms to the CBM and VBM of low-dimensional Ga₂O₃. That is, the surface passivated impurity atoms have taken part in the formation and modulation of the band structure of low dimensional Ga₂O₃. Considering this, one inspiration is that surface functionalization can modulate the electronic properties by passivating different atoms for application in low-dimensional Ga₂O₃. It is similar to passivation modification of surface functional groups. Meanwhile, in realizing the modulating properties of impurity doping in low-dimensional materials, surface passivation is first applied because doping methods such as ion implantation cannot accurately control the doping concentrations when materials are exfoliated to the low-dimensional structure.³¹⁰ The general process of passivation is shown in Fig. 16(a) schematically. The sliced monolayer Ga₂O₃ is exposed to a halogen-rich ambient condition for surface absorption and passivation. The schematic structures after passivation by halogen atoms are shown in Fig. 16(b). Then, Guo et al. investigated the effects of passivation with F, Cl, and H separately and in pair combinations (F–F, F–Cl, F–H, Cl–H, and Cl–Cl) on the electronic properties of monolayer Ga₂O₃.^63,108Fig. 16(c) shows that halogen atom (F and Cl) passivation can change the band structure of monolayer Ga₂O₃ directly from the indirect bandgap to the direct bandgap compared with H passivation. Meanwhile, the electronic properties of low dimensional Ga₂O₃ passivated by F and Cl are also different. Although F-passivated low dimensional Ga₂O₃ has higher stability than Cl-passivated Ga₂O₃, it is unfortunate that the transport properties of low dimensional Ga₂O₃ passivated by F further deteriorate. It has been discovered that the monolayer ClGa₂O₃H shows a hole mobility of 3913.52 cm² V⁻¹ s⁻¹ along the b direction, which is the highest value among the passivated samples (as shown in Fig. 17(a and b)). Although Cl passivation can reduce the electron effective mass of low dimensional Ga₂O₃ effectively, the anisotropy in material properties makes the transport situations disparate in different directions. It is noticed that the electron mobility along the b direction is reduced, while the electron mobility along the c direction is increased. Cl passivated monolayer Ga₂O₃ demonstrates high hole and electron mobility and a direct band structure, which can be the theoretical guideline to obtain the higher performance devices compared with F and H passivated monolayer Ga₂O₃.

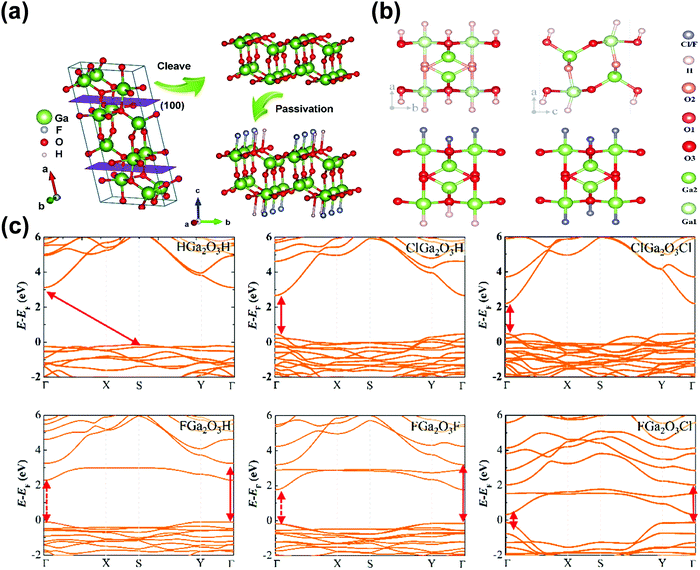Fig. 16 (a) The schematic diagram of exfoliated and passivated processes to obtain low-dimensional Ga₂O₃. Reproduced with permission.³⁸⁴ Copyright 2020, the Royal Society of Chemistry. (b) The geometric structures of monolayer HGa₂O₃H, ClGa₂O₃H/FGa₂O₃H, and ClGa₂O₃Cl/FGa₂O₃F/ClGa₂O₃F. (c) The band structure of hydrogen- and halogen-passivated monolayer β-Ga₂O₃. Reproduced with permission.²⁷ Copyright 2020, Elsevier Ltd.

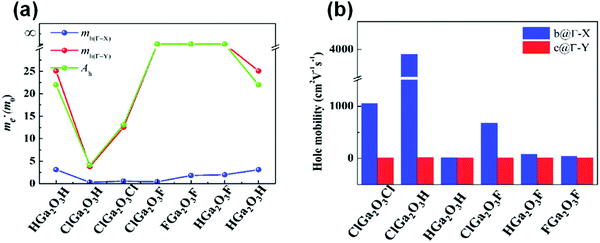Fig. 17 (a) Effective hole masses and (b) hole mobility of different H/halogen passivated monolayer Ga₂O₃ along b (Γ–X) and c (Γ–Y) directions. Reproduced with permission.²⁷ Copyright 2020, Elsevier Ltd.

4. Homo-valence impurities (Al and In)

In addition to the hetero-valence doping methods mentioned above, the same group elements (i.e., homo-valence elements) incorporated into semiconductors to form alloys have special phenomena and applications, e.g., Al_xGa_1−xN (x = 0–100%), In_xGa_1−xN (x = 0–100%) and GaN. The crystal structure of AlN and InN applied in GaN alloy engineering is the same as that of GaN, which will not lead to phase separation during doping. Meanwhile, the valence electrons of Al, Ga, and In atoms are equal so that no impurity states will be introduced into the systems during doping. Besides, the bandgap can also be modulated when GaN is alloyed with AlN and/or InN. Since the E_g of AlN is 6.2 eV (∼200 nm) and that of InN is 0.7 eV (∼1771 nm), the luminescence area of the Al_xGa_1−xN and In_xGa_1−xN alloys can cover from the infrared region to the deep ultraviolet region by controlling the proportion of the doping component.³¹¹ GaN alloy engineering has been applied to HEMTs, ultraviolet photodetectors, and LEDs by modulating bandgap and energy level matching to improve device performance. Inspired by this research, the Ga₂O₃ alloy engineering, i.e., (Al_xGa_1−x)₂O₃ and (In_xGa_1−x)₂O₃, can also be realized, which will provide a new idea for the application of Ga₂O₃ in heterojunction modulation doped field effect transistors (MODFETs) and solar-blind ultraviolet photodetectors.

In this section, (Al_xGa_1−x)₂O₃ and (In_xGa_1−x)₂O₃ alloys are discussed here. The effects of the contents of homo-valence elements on the lattice parameters and bandgap of the alloys and the phase separation phenomenon in the alloys are discussed. Finally, the applications of the (Al_xGa_1−x)₂O₃ and (In_xGa_1−x)₂O₃ alloys in power devices and optoelectronic devices are introduced briefly to further illustrate the value of alloy engineering realized in Ga₂O₃.

4.1 (Al_xGa_1−x)₂O₃. The stable phase of Al₂O₃ is a corundum structure rather than a monoclinic structure. In corundum Al₂O₃, both Al and O atoms form the [AlO₆] octahedral configurations. Different from that, the positions occupied by [AlO₆] octahedral configurations and [AlO₄] tetrahedral configurations are bisected in the monoclinic Al₂O₃. The Al atom will occupy the octahedral position preferentially to form β-(Al_xGa_1−x)₂O₃ when Al atoms are incorporated into β-Ga₂O₃. Note that phase separation will occur because the most stable structure of Al₂O₃ is not the same as that of β-Ga₂O₃. Therefore, the related Al content is worth noting when the phase separation appears. Although the critical components obtained by different preparation methods are different, the substitution mechanism and varied tendency of Al doped β-Ga₂O₃ are the same. Fig. 18(a) shows the formation enthalpy variation of different structures of the β-(Al_xGa_1−x)₂O₃ alloy with different Al contents (x = 0–100%). The monoclinic structure of the β-(Al_xGa_1−x)₂O₃ alloy remains at low Al content (x < 0.5). Note that the formation enthalpy of the (Al_xGa_1−x)₂O₃ alloy is the lowest under the monoclinic structure when x = 0.5. Al has substituted all the Ga₍₂₎ in β-Ga₂O₃ in this condition. The arrangement minimizes its associated energy cost and enables the ordered alloy to have a very low formation enthalpy. Al atoms begin to occupy tetrahedral configurations if Al component x is over 0.5. Because corundum Al₂O₃ is stable under ambient conditions, the β-(Al_xGa_1−x)₂O₃ alloy no longer maintains a monoclinic structure when the Al component x is greater than 0.7. The monoclinic phase could transform into the corundum structure gradually because the radius of the Al atom is smaller than that of the Ga atom. The lattice constant decreases with the increase of Al components; thus the volumes of the β-(Al_xGa_1−x)₂O₃ alloy will decrease linearly, as shown in Fig. 18(b). The trend of lattice parameters follows Vegard's law. Besides, the bandgap of the β-(Al_xGa_1−x)₂O₃ alloy can be modulated from 4.9 eV to 7 eV, as shown in Fig. 18(c).^312,313 The bandgap of Al₂O₃ is larger than that of β-Ga₂O₃ so that the bandgap will increase with the increase of Al content. Furthermore, the energy positions of the CBM and VBM of the β-(Al_xGa_1−x)₂O₃ alloy vary with the alloy component x. The variations of x have apparent effects on the positions of the CBM (ΔE_CBM > 3 eV), while the energy positions of the VBM change little (ΔE_VBM < 0.5 eV). As mentioned in the previous section, the CBM of β-Ga₂O₃ is contributed by the 4s orbitals of Ga, while the VBM is contributed by the 2p orbitals of O. Similarly, the CBM of Al₂O₃ is contributed by Al 3s orbitals, and the VBM is contributed by O 2p orbitals. When the Al content increases, the orbital contribution of the CBM of the alloy gradually changes from the Ga 4s orbital to the Al 3s orbital, while the VBM is only contributed by the O 2p orbitals. The metal cation s orbital interacts with O orbitals to form bonding orbitals and anti-bonding orbitals. The overlap of high energy anti-bonding orbitals mainly forms the conduction band of the alloy, while the overlap of low energy bonding orbitals forms the valence band of the alloy. Therefore, with the increase of Al components, the anti-bonding orbitals formed by interaction with O orbitals gradually raise the CBM energy of β-Ga₂O₃ upward, and thus this tendency appears.^312,314,315

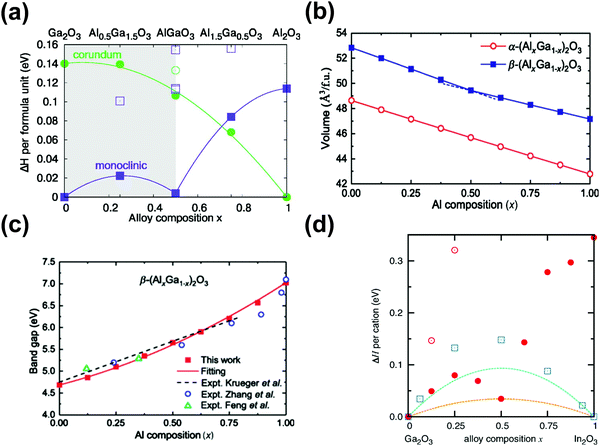Fig. 18 (a) Enthalpy of formation as a function of alloy concentration x in the corundum and monoclinic structures β-(Al_xGa_1−x)₂O₃. The lowest energy structures are represented by the solid symbols and higher energy structures are represented by open symbols under the same condition. Reproduced with permission.³¹² Copyright 2018, American Institute of Physics Publishing. (b) The variations of α-(Al_xGa_1−x)₂O₃'s and β-(Al_xGa_1−x)₂O₃'s volumes as a function of Al composition x. (c) The variations of β-(Al_xGa_1−x)₂O₃'s bandgap as a function of Al composition x obtained from many scholars’ research. Reproduced with permission.³¹⁴ Copyright 2018, American Physical Society. (d) Enthalpy of formation as a function of alloy concentration x for Ga₂O₃ alloying with In₂O₃ in the bixbyite (blue squares) and monoclinic (red solid circles) crystal structure. The red open circles are higher-energy metastable alloys’ configurations. Reproduced with permission.³²⁸ Copyright 2015, American Physical Society.

β-(Al_xGa_1−x)₂O₃ films have been widely studied recently. The β-(Al_xGa_1−x)₂O₃ film extends the range of potential applications and further optimizes device performance successfully, especially in power devices and optoelectronic devices. One of the advantages of the β-(Al_xGa_1−x)₂O₃ bandgap engineering is to achieve high breakdown voltage of materials and achieve high response photodetectors. For example, although the dark current of the β-(Al_xGa_1−x)₂O₃-based solar-blind photodetector (0.356 nA) is higher than that of pure Ga₂O₃ (35.8 pA), the responsivity is 15.7 times higher than that of pure Ga₂O₃-based solar-blind photodetector.³¹⁶ However, because the (Al_xGa_1−x)₂O₃ alloy is still subject to bulk phonon scattering, the mobility of the alloy (4 cm² V⁻¹ s⁻¹) is not as good as that of pure Ga₂O₃, so it is not feasible to prepare devices based on the single alloy. At the same time, (Al_xGa_1−x)₂O₃ with a large bandgap can form the heterojunction with pure Ga₂O₃, and the large band-offset promotes the formation of the two-dimensional electron gas at the interface. This overcomes the influence of phonon scattering in the bulk on semiconductor mobility and can be applied to MODFET coupling with a Si δ-doped Ga₂O₃ layer. Inspired by this, Krishnamoorthy et al. researched the performance and carrier mobility of MODFETs based on the β-(Al_xGa_1−x)₂O₃/β-Ga₂O₃ heterojunction.^{96,113,317–319} In their studies, the devices showed excellent switching characteristics and the mobility was up to 180 cm² V⁻¹ s⁻¹ by Hall measurements at room temperature, which is higher than that of bulk materials but still lower than the theoretical mobility. It is found in the experiments that the defects of the (Al_xGa_1−x)₂O₃ alloy also increase with the increase of Al components.^320–322 Thus, it is still necessary to optimize the defects to achieve higher carrier mobility continuously.

In alloy engineering based on other phases, the bandgap of the alloy increases with the increase of Al composition, while the lattice parameters decrease further. Both of them are similar to the situations in β-(Al_xGa_1−x)₂O₃ alloy engineering. For example, the bandgap can be tuned from 5.3 eV to 8.5 eV with the variation of the Al component in α-(Al_xGa_1−x)₂O₃. The variations of x also have effects on the positions of the CBM (ΔE_CBM > 3 eV), while the energy positions of the VBM change little (ΔE_VBM < 0.1 eV). Note that α-(Al_xGa_1−x)₂O₃ still maintains the single corundum structure (x = 0–100%)⁸² because the structures of Al₂O₃ and α-Ga₂O₃ are all corundum structures consisting of octahedral structures. This provides convenience for α-(Al_xGa_1−x)₂O₃ alloy engineering realized in α-Ga₂O₃.

4.2 (In_xGa_1−x)₂O₃. The ground-state structure of In₂O₃ is the body-centered cubic bixbyite structure. In this structure, all the In atoms are octahedrally coordinated. The fundamental direct bandgap of In₂O₃ is about 2.9 eV by XPS measurements and DFT calculations.^323–326 However, its optical bandgap is large (3.73 eV). Due to the inversion center of the bixbyite crystal structure, the electrons' transition from the VBM to the CBM is dipole forbidden.³²⁷ Only transitions from states lower in the valence band are allowed and lead to strong absorption. Therefore, the optical bandgap is relatively large. In addition, it is found that the CBM of In₂O₃ is contributed by the In 5s orbital, which has a large radius and wave function overlap degree compared with the Ga 4s orbital by the analysis of DOS. Therefore, In doping is more helpful for the conduction of electrons.

In atoms prefer to substitute the octahedral Ga site (Ga₍₂₎) in β-(In_xGa_1−x)₂O₃ alloy because the atomic radius of In is larger than that of Ga. The lattice parameters of the (In_xGa_1−x)₂O₃ alloy keep increasing with the increase of the In composition, which makes the volume of the (In_xGa_1−x)₂O₃ alloy system keep increasing. This trend increases linearly and meets Vegard's law, too. By incorporating different components of In, the bandgap of β-(In_xGa_1−x)₂O₃ can vary from 2.9 eV to 4.9 eV. Note that the bandgap of β-(In_xGa_1−x)₂O₃ will decrease when the In content increases because the bandgap of In₂O₃ is smaller than that of Ga₂O₃. The phase separation occurs when In is added with a certain concentration due to the different stable lattice structures between In₂O₃ and β-Ga₂O₃. The critical point of phase separation is related to many factors, e.g., different substrates and temperatures. The results of first-principles calculations can reveal the insight mechanism involved. Peelaers et al. further revealed the phase transition mechanism by calculating the formation enthalpy under different In components, as shown in Fig. 18(d).³²⁸ The monoclinic structure of β-(In_xGa_1−x)₂O₃ will be energetically favorable when x < 0.5. This trend can be explained by considering the cationic configuration of different crystal structures. In the monoclinic structure, octahedral Ga and tetrahedral Ga account for half respectively. The In atom tends to occupy an octahedral position and form In–O octahedral configurations. This configuration has the lowest energy. If x is over 0.5, In occupies the Ga₍₁₎ atom gradually because all Ga₍₂₎ atoms have been occupied by In atoms. This will introduce local strain and require extra energy, which results in energy enlargement. Therefore, this tendency leads to phase instability, which leads to the phase transition from the monoclinic structure to the cubic bixbyite structure gradually. In other metastable phases of Ga₂O₃, the variable rules of bandgap and lattice parameters after doping In are the same as those in β-(In_xGa_1−x)₂O₃, and the existence of phase separation still needs to be paid attention in practical applications.^329–331

(In_xGa_1−x)₂O₃ alloys also have potential applications in power and optoelectronic devices. In 2015, Wenckstern et al. investigated the SBD based on the (In_xGa_1−x)₂O₃ alloy.³²⁵ In the absence of phase transition, the series resistances of the diodes based on (In_xGa_1−x)₂O₃ decreased with the increase of the In content. Moreover, it limited the forward current of the diode, increased the reverse current, and had a great influence on the rectifier characteristics of the diode. Then they also fabricated the SBD based on the Si-doped (In_xGa_1−x)₂O₃ alloy. The forward current of the diode based on (In_xGa_1−x)₂O₃ doped by Si became larger than that of the undoped (In_xGa_1−x)₂O₃ diode, while the reverse current and series resistance varied little. It can be concluded that the reverse current and series resistance are more dependent on the In content. In addition, the rectification ratio was still very low. In the field of optoelectronic devices, Vasyltsiv et al. found that the dark conductivity and the photoconductivity decreased with increasing In composition under the condition that the monoclinic structure of the (In_xGa_1−x)₂O₃ alloy remains unchanged.³³² The responsivity of the photodetectors increased with the increase of the In component gradually; thus this is an advantage of the detectors based on the (In_xGa_1−x)₂O₃ alloy.

IV. Effects of impurities and defects on other properties

In addition to their influence on electronic properties, defects and impurities also have significant influence on the magnetic, piezoelectric, luminescence, and scintillation properties of β-Ga₂O₃. The variations and mechanisms of other physical properties induced by defects and impurities are summarized in this section. The defects and impurities induced modulation of these properties broadens the application range of Ga₂O₃, such as spintronic devices, piezoelectric devices, scintillators, radiation detectors, etc.

1. Magnetic properties

Spin manipulation in semiconductors, that is spintronics, provides a new development path for the functional materials. β-Ga₂O₃ with an ideal stoichiometric ratio does not exhibit good magnetic properties because of the 3d¹⁰ configuration of Ga³⁺ ions. In 2007, Sridharan et al. discovered the ferromagnetism existing in β-Ga₂O₃.³³³ They found by PL measurements that the photoluminescence intensity varied greatly with the variation of the magnetic field. They believed that this magnetism could form locally around the specific locations of V_Os. With further research, the magnetic moment of β-Ga₂O₃ appeared obviously when V_Ga was introduced. Although it is still difficult to realize p-type β-Ga₂O₃ by introducing many V_Gas as discussed previously, this phenomenon means that V_Ga is of great significance for expanding the applications of β-Ga₂O₃ in spin electronic devices. In general, charged V_Gas exist mainly in three forms, i.e., V_Ga⁻, V_Ga²⁻ and V_Ga³⁻. Among them, V_Ga⁻ and V_Ga²⁻ discovered by electron paramagnetic resonance (EPR) under high neutron irradiation exhibit magnetic properties. The origin of magnetism in Ga₂O₃ is mainly caused by the localization effects of the surrounding oxygen negative ions as revealed by reported research, i.e., due to the presence of unpaired electrons in the 2p orbitals of O ions.³³⁴ In addition, the highly localized holes around oxygen ions and the lattice relaxation due to the presence of charged cation vacancies further confirm that the defect levels introduced by V_Ga are not shallow. In addition, Son et al. performed EPR studies on β-Ga₂O₃ annealed in an O₂ environment.³³⁵ They found that the annealing process also induced an electron paramagnetic resonance center named IR1. The IR1 was speculated from V_Ga(1)²⁻ or the V_Ga(1)–Ga_i–V_Ga(1) complex. Although intrinsic β-Ga₂O₃ is a non-magnetic material, the magnetic β-Ga₂O₃ can be realized in different experimental environments, such as annealing, irradiation to create Ga vacancies in the host crystal, doping with some magnetic impurities, etc. Therefore, the specific environments make β-Ga₂O₃ magnetic, which has potential in the application of spintronic devices, e.g., spin-glass, magnetic random access memory (MRAM), etc.^336,337

According to the previous theoretical predictions, doping transition metals, especially Mn, in wide bandgap semiconductors can enable the semiconductors to have a high Curie temperature (T_C) exceeding room temperature.³³⁸ Besides, it is found that magnetic impurity doping can achieve good dilute magnetic semiconductor characteristics in wide bandgap oxide semiconductors. Typically, this means replacing a few percent of host atoms with transition metal impurities which carry large spin magnetization in the host ligand field. If these magnetic impurities exhibit ferromagnetic interactions, the entire system may exhibit bulk ferromagnetism as long as the ferromagnetic interactions extend beyond the impurity distance of typical impurities. These are the prerequisites for obtaining spintronic materials. Previously, Mn^339–342 and Cr^{339,343–345} have been incorporated into other wide bandgap semiconductors (e.g., ZnO, GaN, and GaAs) and the doped semiconductors show good magnetism. Inspired by these research phenomena, the magnetic properties of Mn and Cr doped β-Ga₂O₃ are also studied in many kinds of research.

To realize Mn-doped Ga₂O₃ successfully, Minami et al. prepared it by the sol–gel method, and Kim et al. obtained Mn-doped Ga₂O₃ at an annealing temperature exceeding 100 °C by magnetron sputtering.^346,347 However, the quality of the films prepared by these two methods is not very good. The ferromagnetic properties in their research are not very obvious. Subsequently, Guo et al. realized high-quality β-(Ga_1−xMn_x)₂O₃ on sapphire by the laser molecular beam epitaxy technique.^348,349 The β-(Ga_1−xMn_x)₂O₃ alloy showed ferromagnetism at room temperature when x ≥ 0.11. Furthermore, the magnetization and coercivity of the β-(Ga_1−xMn_x)₂O₃ alloy enhanced significantly with the increasing Mn content. That is, as x increases, the saturation magnetization (M_s) monotonically increases from 5.5 emu cm⁻³ to the maximum of 33.1 emu cm⁻³, and the coercivity and remanence (M_r) also increase. Although they applied the bound magnetic polaron (BMP) model to explain the experimental results, they still did not get reasonable results. Wang et al. further revealed the internal mechanism of the ferromagnetic phenomenon and variations caused by Mn doping in Ga₂O₃ by the first-principles calculations method in 2019. They revealed that the spatial delocalization of O 2p orbitals and the strong overlap of p–d orbitals led to a stable ferromagnetic state at room temperature, as discovered in the early experiment.³⁴⁸ Besides, Guo et al. obtained Cr doped Ga₂O₃ vermicular nanowires and further explored the magnetic properties.³⁵⁰ They found that the nanostructured Ga₂O₃:Cr exhibited anisotropic magnetic behavior. Derived from the M–H curve diagram, the largest saturation magnetization and coercivity in the Ga₂O₃:Cr nanostructure are 62.2 emu cm⁻³ and 115 Oe, respectively.

Additionally, it is found that Zn-doped Ga₂O₃ may show spin properties as investigated by first-principles calculations in recent years. The formation energy of Zn doped Ga₂O₃ which is a ferromagnetic (FM) semiconductor with 100% spin polarization is lower than that of the undoped and non-spin Ga₂O₃ system, which reveals that the ferromagnetic Zn doped system is easy to form. Meanwhile, the spin effects in Zn doped Ga₂O₃ are affected by the p–d hybridization of O and Zn atoms.^272,351 The magnetic moment of Zn-doped Ga₂O₃ is 1.0μ_B per cell. It is noticed that the magnetic moment of the system will drop to 0.49μ_B per cell with the introduction of V_Os. Therefore, a large number of V_Os should be avoided to obtain Zn-doped Ga₂O₃ with excellent magnetic properties.

2. Luminescence properties

The doping control of β-Ga₂O₃ is complicated due to self-compensation and defects, especially point defects. Meanwhile, the research of electronic transitions during light emission provides a deep understanding of the related mechanism of defects. The luminescence properties of β-Ga₂O₃ have also attracted extensive attention because they can indirectly reflect the behavior of intrinsic and/or external defects and impurities in β-Ga₂O₃. According to recent research, there are no emission peaks in the near band edge of β-Ga₂O₃. They nearly exist in the ultraviolet (UVL, 3.2–3.6 eV), blue (BL, 2.8–3.0 eV), and green (GL, 2.4 eV) band regions of the emission spectra of β-Ga₂O₃, as shown in Fig. 19(a).^{206,352–355} The origins of these different band regions have also been studied in depth by some measurements. In summary, the UVL band is due to the carriers' (electron–hole) recombination, as shown in Fig. 19(b). The BL band is caused by self-trapped holes or electrons trapped by V_Os and the GL band is caused by the interaction between self-trapped holes and electrons trapped by a cluster of V_Os. Note that the cathodoluminescence (CL) spectrum is affected by some factors, e.g., temperature. The measurement of the temperature-dependent CL spectrum of the (001) undoped β-Ga₂O₃ substrate by the FZ method is shown in Fig. 19(a). At low temperatures (<200 K), the intensity of the UVL band is more obvious in the undoped Ga₂O₃ single crystal. However, the intensities of the GL band and the BL band increase gradually as the temperature increases, while the intensity of the UVL band decreases. This may be due to the gradual strengthening of recombination caused by deep-level defects at high temperatures.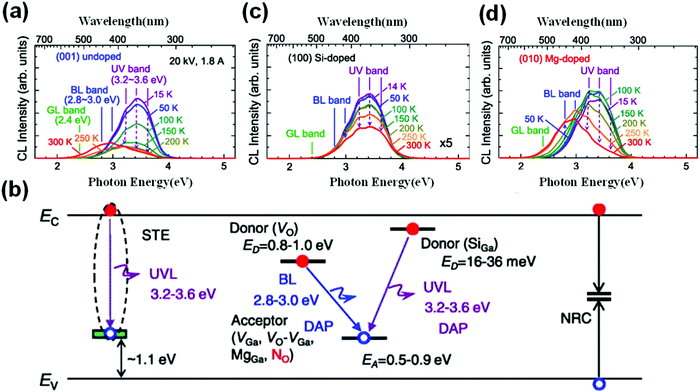

Fig. 19 (a) Temperature-dependent CL spectra of (001) undoped β-Ga₂O₃ crystal samples. Reproduced with permission.¹⁷⁴ Copyright 2013, American Institute of Physics Publishing. (b) The schematic diagram of emission mechanism models of UVL and BL bands in β-Ga₂O₃. Reproduced with permission.³⁸⁵ Copyright 2018, American Institute of Physics Publishing. Temperature-dependent CL spectrum of (c) (100) Si-doped (enlarged by a factor of 5) and (d) (010) Mg-doped β-Ga₂O₃ crystal samples. Reproduced with permission.¹⁷⁴ Copyright 2013, American Institute of Physics Publishing.

Besides temperature, doping can also have certain effects on the CL spectrum so that it can reveal the influence of impurities and defects. Luminescence measurements are considered to be a very effective tool to detect and identify impurities or intrinsic defects by the recombination of generated excess carriers at the defect levels. In order to discover the intrinsic mechanism, Ouma et al. studied the donor Si and the compensating acceptor Mg doped β-Ga₂O₃ substrates in detail, and the CL spectrum measurements were carried out, as shown in Fig. 19(c and d).³⁵² In the Si-doped sample, the intensity was only in the ultraviolet region as the temperature varies, while in the Mg-doped sample, the intensity was similar to that of the undoped sample, but the intensity of the GL band and the BL band became strong under the high-temperature condition. It can be concluded that the UVL band is independent of impurities. The more detailed origins of the UVL band can be attributed to the recombination of free electrons and STHs or STEs. The BL band is attributed to the donor–acceptor pair (DAP) transition including deep donors and acceptors as shown in Fig. 19(b). As mentioned previously, the V_O is a deep-level donor impurity, while the V_Ga is a deep-level acceptor impurity in the conclusions obtained from first-principles calculations. The formation energies of charged defects and impurities depend on the position of the Fermi level (E_f). In general, the formation energy of charged V_Os decreases when E_f is close to the VBM. In the Mg-doped β-Ga₂O₃ sample, E_f shifts toward the VBM in a degree. In the Si-doped β-Ga₂O₃ sample, the formation energy gradually increases as E_f approaches the CBM. The variations of Fermi levels and formation energies in these two systems can reflect the variations of resistivity indirectly. It is known that the resistivity of intrinsic Ga₂O₃ is related to vacancies. The variation of resistivity after doping is related to BL intensity in terms of spectrum. Therefore, V_Ga and V_O, especially V_O, have a strong correlation to the BL band. It has been inferred that the possible deep donors are V_O and Ga_i, and the possible acceptors are V_Ga, V_O–V_Ga complex, and Mg_Ga. Besides, the effects of doping on intrinsic defects in β-Ga₂O₃ can be reflected by the change of the BL band indirectly. For example, the suppression of the BL band in heavy N-doped β-Ga₂O₃ epitaxial films is evidence that N-doping in β-Ga₂O₃ leads to a decrease in V_O concentrations and the resulting high resistivity in N-doped epitaxial films.^104,356 In addition, transition metals such as Cr, Fe, Co, Ni, Mn, and Ti (except Cu) have been incorporated into Ga₂O₃ for further exploration.^357–360 The results are that the BL bands of these elements doped Ga₂O₃ become suppressed. As for the GL band, it has been discovered that it is related to O₂ partial pressure in FZ growth, but its particular mechanism has not been discovered.³⁵⁴

3. Piezoelectric properties

The piezoelectric effect is an important phenomenon in semiconductor research. The causes of this phenomenon are that ionic polarization generates a piezoelectric potential in the presence of external strain due to the asymmetric structure of crystals especially, for example, ZnO, GaN, and InN. Because of its structural similarity to GaN, ε-Ga₂O₃ has also been found to have piezoelectric properties, as mentioned previously.^{7,214,361,362} Although monoclinic β-Ga₂O₃ has a low symmetry, no piezoelectric properties are found in it. In recent years, it has been discovered that doped β-Ga₂O₃ has piezoelectric properties. Different from the previous research focusing on electronic properties by doping, Li et al. further found that β-Ga₂O₃ doped with unique elements manifested piezoelectricity and the positions of doping elements in the Periodic Table were related to the magnitude of the piezoelectric coefficient recently, as shown in Fig. 20(a).³⁶³ The impurities (e.g., Ni, Cu, Zn, In, and Sn) away from Ga made the doped β-Ga₂O₃ exhibit strong piezoelectric properties, that is, the values of e₁₁ in different doping systems increase more or less compared with that of intrinsic β-Ga₂O₃ (e₁₁ = 0.02–11.24 C m⁻²). The piezoelectric potential of the β-Ga₂O₃ crystal can be applied to modulate the carrier behavior at the metal–semiconductor or p–n junction interface, thus optimizing the device performance. Relative studies open new fields for other applications of the family of Ga₂O₃.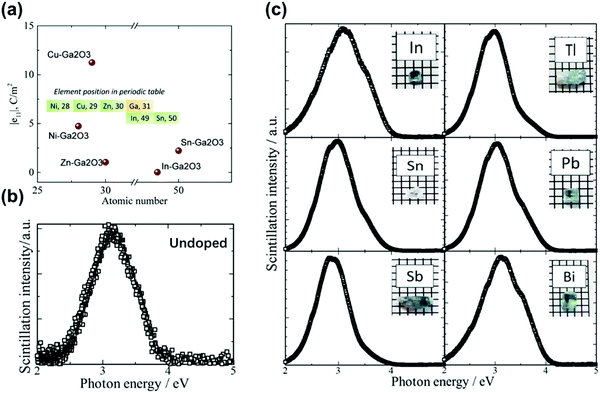

Fig. 20 (a) Piezoelectric coefficients of Ni, Cu, Zn, In, and Sn doped β-Ga₂O₃. The inset graph shows dopants’ positions in the Periodic Table. Reproduced with permission.³⁸⁶ Copyright 2021, American Institute of Physics Publishing. Scintillation spectra of (b) undoped and (c) In, Tl, Sn, Pb, Sb, and Bi doped bulk Ga₂O₃ under X-ray irradiation. Reproduced with permission.³⁷⁴ Copyright 2017, Elsevier Ltd.

4. Scintillation properties

A scintillator is a kind of material applied for radiation detectors, which plays an important role in the detection of medical imaging, safety, astrophysics and logging, and other fields. In general, scintillators are made of insulators and semiconductors. In recent years, β-Ga₂O₃ has been considered as a potential candidate for fast scintillation detection devices.³⁶⁴ Some elements are selected as dopants and the doping behaviors (e.g., single doping, double doping, and triple doping) will affect the scintillator characteristics.^{232,365–370} It has been discovered that the crystal β-Ga₂O₃ is doped by various dopants such as Ce,^365,370,371 Al,^365,370 Mg,³⁷² Pr,³⁷³ Be,³⁷² Ba,³⁷² Bi,³⁷⁴ Sn,^367,374 and Si coupled with Ce^375,376 to obtain excellent scintillation properties. The dopants affect the position and shape of the scintillation spectra. For example, Usui et al. investigated the scintillation spectra of undoped β-Ga₂O₃ and that of the β-Ga₂O₃ bulk doped with some elements (In, Tl, Sn, Pd, Sb, and Bi) under X-ray irradiation, as shown in Fig. 20(b and c).³⁷⁴ The spectrum of the doped β-Ga₂O₃ was similar to that of the undoped β-Ga₂O₃, but there were still some differences in the shape and position. Generally, these dopants are divided into three groups for scintillation doping: electron-rich and electron-poor elements in main group elements, and rare earth elements. Compared with the undoped β-Ga₂O₃, the scintillation properties of Ga₂O₃ doped with rare earth elements can be observed obviously. In addition, the emission peaks in β-Ga₂O₃ doped with electron-poor dopants have different positions, while the β-Ga₂O₃ doped with electron-rich dopants show fewer changes in the emission shape. These research studies bring significance to the further applications of optoelectronic and radiation detection devices, and thus relative research is deeply being carried out.

V. Summary and outlook

In this review, we have summarized the recent advances in the effects of doping, defects, and passivation on the material properties (e.g., electronic, optical, magnetic, etc.) of Ga₂O₃, especially common β-Ga₂O₃. First, the basic properties (electronic, absorption, thermal and mechanical) of intrinsic β-Ga₂O₃ were summarized. Considering the uniqueness of the monoclinic β-Ga₂O₃ structure, it was successfully transformed into low-dimensional Ga₂O₃ by the mechanical exfoliation method, thereby expanding the research areas of Ga₂O₃. Therefore, the intrinsic properties of the new semiconductor, i.e., low-dimensional Ga₂O₃, were also discussed. Then, some defects (e.g., V_O, V_Ga, Ga_i, O_i, and deep-level defects) in undoped β-Ga₂O₃ were discussed in detail. Note that the intrinsic β-Ga₂O₃ manifested n-type semiconductor behavior which was considered to be caused by the effects of V_Os or defect complexes. Besides, the unintentional doping mechanism had also been accepted to be another reason. Although intrinsic β-Ga₂O₃ behaved as an electron-rich semiconductor, its low carrier concentrations and high defects cannot meet the requirements of high-performance devices. Doping was a common strategy to modulate semiconductor properties.^379,386 Then, the mechanism of the electronic properties of β-Ga₂O₃ tuned by single doping (donors and deep acceptors), co-doping, and surface passivation of hetero-valence elements was discussed. Meanwhile, the situations of homo-valence elements (Al and In) substituting Ga to form alloys were also discussed. Note that it was relatively easy to achieve n-type doping in bulk β-Ga₂O₃, while the troublesome problem is how to achieve effective p-type doping. No reasonable solutions have been found so far. Besides, considering that it is difficult to precisely control the substitution doping in low-dimensional Ga₂O₃ by ion implantation, the properties of low-dimensional Ga₂O₃ are usually tuned by surface passivation. The related research is briefly summarized in this review. Lastly, the effects of defects and impurities on other properties (i.e., magnetic, luminescence, scintillation, and piezoelectric) of β-Ga₂O₃ are discussed briefly.

The intrinsic properties of Ga₂O₃ have been studied in detail for a long time, and their advantages have been gradually understood. Subsequently, Ga₂O₃ with modulated properties by defects and impurities is considered to further optimize semiconductor and microelectronics technology. It should be realized that there are still some obstacles which need to be overcome and the directions worthy of being further researched so that large-scale and deep applications of β-Ga₂O₃ are realized in the future:

(1) The true reasons for undoped β-Ga₂O₃ manifesting n-type semiconductor behavior: although the fabrication of β-Ga₂O₃ is relatively mature at present, β-Ga₂O₃ prepared by either melting method or epitaxy method manifests the features of an n-type semiconductor. There are still controversial opinions about this phenomenon. At present, the generally accepted viewpoints are (a) the effects of intrinsic defects and complexes of impurities coupling with defects, e.g., V_O and V_Ga–H complex; (b) the effects of unintentional dopants such as H and Ir introduced in the process. The n-type feature of β-Ga₂O₃ deposited by physical vapor deposition is mainly due to V_O and that prepared by chemical vapor deposition and the melting method is mainly due to V_O and unintentional dopants; this opinion is widely accepted in the experiments. However, through first-principles calculations, it is found that the defect level position introduced by V_O is deep. Therefore, it does not play a crucial role in the n-type conduction in undoped β-Ga₂O₃. Thus, subsequent research is urgent to further reveal the internal mechanism of undoped β-Ga₂O₃ depicted as an n-type semiconductor in order to unify the theoretical and experimental results.

(2) The suitable acceptors and the realization of effective p-type β-Ga₂O₃: despite continuous explorations of suitable acceptors in β-Ga₂O₃, there are still no effective p-type dopants reported. It is reported that effective p-type β-Ga₂O₃ is difficult to obtain due to the following factors: (a) the VBM of β-Ga₂O₃ is relatively flat and the dispersion degree is small, and thus the hole effective mass is large and the mobility is low; (b) ionized holes in β-Ga₂O₃ are easy to form self-trapped holes (STHs), and thus the holes cannot move freely. These affect the holes’ transport in β-Ga₂O₃; (c) the acceptors have low solubility and ionization rates, and they will introduce deep levels in the bandgap. The deep level has a little contribution to the p-type conduction in β-Ga₂O₃; (d) the background carriers in β-Ga₂O₃ are high due to the unintentional doping effects, and a small number of holes ionized by the acceptors are quickly compensated. Considering the above reasons, the optimizations that should further reduce the effects of defects and unintentional impurities in β-Ga₂O₃ can be adapted, thereby reducing the background carrier concentrations. Meanwhile, co-doping can further improve the solubility of dopants, and thus it can be attempted to achieve p-type β-Ga₂O₃ by co-doping acceptors instead of single doping in experiments in the future.

(3) The in-depth exploration of the effects of defects and impurities on other properties of β-Ga₂O₃: impurities and defects can modulate not only the electronic properties of β-Ga₂O₃ but also other material properties. As mentioned in this review, impurities and defects can make β-Ga₂O₃ have magnetic, piezoelectric, photocatalytic, and scintillator properties, which will further expand the applications of β-Ga₂O₃ beyond optoelectronics and power devices. Relevant studies have established a certain theoretical basis in recent years, and many scholars have also carried out relevant experimental exploration. Therefore, more in-depth studies are needed to reveal the deeper value of β-Ga₂O₃ in these fields.

(4) The related research (defects and impurities) in other phases of Ga₂O₃: because β-Ga₂O₃ is the most stable among the six phases of Ga₂O₃ under ambient conditions, most of the current research is based on β-Ga₂O₃. Other phases of Ga₂O₃ are also worth researching because other phases of Ga₂O₃ have better performance or novel performance compared with β-Ga₂O₃ in some areas. For example, α-Ga₂O₃ has a larger bandgap, and thus it has a larger breakdown field compared with β-Ga₂O₃, which is expected to further improve the performance of Ga₂O₃ based power devices such as breakdown voltage. Besides, hexagonal ε-Ga₂O₃ has a larger spontaneous polarization compared with GaN. By combining ε-Ga₂O₃ with ε-(Al_xGa_1−x)₂O₃ to form a heterojunction, more two-dimensional electron gas (2DEG) will be generated due to large spontaneous polarization at the ε-(Al_xGa_1−x)₂O₃/ε-Ga₂O₃ interface. Therefore, the charges increase resulting in the increment of current density under the condition of the same cross-section. The output performance of MODFETs based on ε-(Al_xGa_1−x)₂O₃/ε-Ga₂O₃ will be improved. Therefore, the research should be extended to other phases of Ga₂O₃ appropriately in the future. Surprising results may be obtained in these research studies.

(5) Deep research on the appropriate passivation atoms modulating the properties of low-dimensional Ga₂O₃: in recent years, with the deepening research of β-Ga₂O₃, the scholars find that β-Ga₂O₃ can be mechanically exfoliated to obtain low-dimensional Ga₂O₃. Due to the presence of dangling bonds at the surface, scholars apply atoms such as H and halogen elements (F and Cl) to passivate the surface. In addition to achieving stability, they find that the band structure and orbital contribution of low dimensional Ga₂O₃ are affected by the passivation atoms. This discovery provides a new avenue to modulate the internal properties of low-dimensional Ga₂O₃, that is, surface passivation. Therefore, it is necessary to find appropriate passivation atoms to passivate the dangling bonds on the surface of low-dimensional Ga₂O₃ in order to obtain stability coupled with improved properties of low-dimensional Ga₂O₃. In addition to the theoretical prediction, experiments are needed to confirm it.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the National Key Research and Development Program of China (Grant 2021YFA0715600, 2018YFB2202900), the National Natural Science Foundation of China (52192610), the Key Research and Development Program of Shaanxi Province (Grant 2020GY-310), Wuhu and Xidian University special fund for industry-university-research cooperation (XWYCXY-012021004), the Fundamental Research Funds for the Central Universities and the Innovation Fund of Xidian University.

References

1. Y. Hao and F. Jiang, Fundam. Res., 2021, 1, 655.
2. Y. Yuan, W. Hao, W. Mu, Z. Wang, X. Chen, Q. Liu, G. Xu, C. Wang, H. Zhou, Y. Zou, X. Zhao, Z. Jia, J. Ye, J. Zhang, S. Long, X. Tao, R. Zhang and Y. Hao, Fundam. Res., 2021, 1, 697–716.
3. Y. Hao, J. Semicond., 2019, 40, 010301.
4. D. Guo, Q. Guo, Z. Chen, Z. Wu, P. Li and W. Tang, Mater. Today Phys., 2019, 11, 100157.
5. J. Zhang, J. Shi, D. C. Qi, L. Chen and K. H.-L. Zhang, APL Mater., 2020, 8, 020906.
6. M. Higashiwaki, K. Sasaki, A. Kuramata, T. Masui and S. Yamakoshi, Appl. Phys. Lett., 2012, 100, 2010–2013.
7. B. Fu, Z. Jia, W. Mu, Y. Yin, J. Zhang and X. Tao, J. Semicond., 2019, 40, 011804.
8. R. Sharma, M. E. Law, F. Ren, A. Y. Polyakov and S. J. Pearton, J. Vac. Sci. Technol., A, 2021, 39, 060801.
9. J. Xu, W. Zheng and F. Huang, J. Mater. Chem. C, 2019, 7, 8753–8770.
10. S. Oh, Y. Jung, M. A. Mastro, J. K. Hite, C. R. Eddy and J. Kim, Opt. Express, 2015, 23, 28300.
11. K. Balakrishnan, A. Bandoh, M. Iwaya, S. Kamiyama, H. Amano and I. Akasaki, Jpn. J. Appl. Phys., 2007, 46, 307–310.
12. M. Imura, K. Nakano, N. Fujimoto, N. Okada, K. Balakrishnan, M. Iwaya, S. Kamiyama, H. Amano, I. Akasaki, T. Noro, T. Takagi and A. Bandoh, Jpn. J. Appl. Phys., 2006, 45, 8639–8643.
13. W. Yang, S. S. Hullavarad, B. Nagaraj, I. Takeuchi, R. P. Sharma, T. Venkatesan, R. D. Vispute and H. Shen, Appl. Phys. Lett., 2003, 82, 3424–3426.
14. H. Bae, A. Charnas, X. Sun, J. Noh, M. Si, W. Chung, G. Qiu, X. Lyu, S. Alghamdi, H. Wang, D. Zemlyanov and P. D. Ye, ACS Omega, 2019, 4, 20756–20761.
15. D. A. Bauman, A. I. Borodkin, A. A. Petrenko, D. I. Panov, A. V. Kremleva, V. A. Spiridonov, D. A. Zakgeim, M. V. Silnikov, M. A. Odnoblyudov, A. E. Romanov and V. E. Bougrov, Acta Astronaut., 2021, 180, 125–129.
16. H. Liang, S. Cui, R. Su, P. Guan, Y. He, L. Yang, L. Chen, Y. Zhang, Z. Mei and X. Du, ACS Photonics, 2019, 6, 351–359.
17. Z. C. Zhang, Y. Wu, C. Lu and S. Ahmed, Appl. Phys. A: Mater. Sci. Process., 2018, 124, 637.
18. N. Ma, N. Tanen, A. Verma, Z. Guo, T. Luo, H. (Grace) Xing and D. Jena, Appl. Phys. Lett., 2016, 109, 1–6.
19. Y. Park, J. Ma, G. Yoo and J. Heo, Nanomaterials, 2021, 11, 1–10.
20. Z. Li, Y. Liu, A. Zhang, Q. Liu, C. Shen, F. Wu, C. Xu, M. Chen, H. Fu and C. Zhou, Nano Res., 2019, 12, 143–148.
21. J. Su, R. Guo, Z. Lin, S. Zhang, J. Zhang, J. Chang and Y. Hao, J. Phys. Chem. C, 2018, 122, 24592–24599.
22. W. S. Hwang, A. Verma, H. Peelaers, V. Protasenko, S. Rouvimov, H. Xing, A. Seabaugh, W. Haensch, C. Van De Walle, Z. Galazka, M. Albrecht, R. Fornari and D. Jena, Appl. Phys. Lett., 2014, 104, 3–8.
23. H. Yuan, J. Su, R. Guo, K. Tian, Z. Lin, J. Zhang, J. Chang and Y. Hao, Appl. Surf. Sci., 2020, 527, 146740.
24. G. Shin, H. Y. Kim and J. Kim, Korean J. Chem. Eng., 2018, 35, 574–578.
25. W. Wang, J. Lu and Z. Ni, Nano Res., 2021, 14, 1889–1900.
26. L. Dong, S. Zhou, B. Xin, C. Yang, J. Zhang, H. Liu, L. Zhang, C. Yang and W. Liu, Appl. Surf. Sci., 2021, 537, 147883.
27. R. Guo, J. Su, H. Yuan, P. Zhang, Z. Lin, J. Zhang, J. Chang and Y. Hao, Mater. Today Phys., 2020, 12, 100192.
28. M. Jędrzejczyk, K. Zbudniewek, J. Rynkowski, V. Keller, J. Grams, A. M. Ruppert and N. Keller, Environ. Sci. Pollut. Res., 2017, 24, 26792–26805.
29. Y. W. Huan, S. M. Sun, C. J. Gu, W. J. Liu, S. J. Ding, H. Y. Yu, C. T. Xia and D. W. Zhang, Nanoscale Res. Lett., 2018, 13, 246.
30. R. Fornari, M. Pavesi, V. Montedoro, D. Klimm, F. Mezzadri, I. Cora, B. Pécz, F. Boschi, A. Parisini, A. Baraldi, C. Ferrari, E. Gombia and M. Bosi, Acta Mater., 2017, 140, 411–416.
31. I. Cora, F. Mezzadri, F. Boschi, M. Bosi, M. Čaplovičová, G. Calestani, I. Dódony, B. Pécz and R. Fornari, CrystEngComm, 2017, 19, 1509–1516.
32. I. Cora, Z. Fogarassy, R. Fornari, M. Bosi, A. Rečnik and B. Pécz, Acta Mater., 2020, 183, 216–227.
33. J. Kim, D. Tahara, Y. Miura and B. G. Kim, Appl. Phys. Express, 2018, 11, 061101.
34. S. I. Stepanov, V. I. Nikolaev, V. E. Bougrov and A. E. Romanov, Rev. Adv. Mater. Sci., 2016, 44, 63–86.
35. H. Yusa, T. Tsuchiya, N. Sata and Y. Ohishi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 1–9.
36. Y. M. Ma, H. Y. Chen, K. F. Yang, M. Li, Q. L. Cui, J. Liu and G. T. Zou, Chinese Phys. Lett., 2008, 25, 1603–1605.
37. D. Machon, P. F. McMillan, B. Xu and J. Dong, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 1–9.
38. S. V. Ovsyannikov and L. S. Dubrovinsky, High Press. Res., 2011, 31, 23–29.
39. E. Lipinska-Kalita, B. Chen, B. Kruger, Y. Ohki, J. Murowchick and P. Gogol, Phys. Rev. B, 2003, 68, 352091.
40. K. E. Lipinska-Kalita, P. E. Kalita, O. A. Hemmers and T. Hartmann, Phys. Rev. B, 2008, 77, 1–9.
41. H. Wang, Y. He, W. Chen, Y. W. Zeng, K. Stahl, T. Kikegawa and J. Z. Jiang, J. Appl. Phys., 2010, 107, 033520.
42. Z. Galazka, Semicond. Sci. Technol., 2018, 33, 113001.
43. J. Åhman, G. Svensson and J. Albertsson, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1996, 52, 1336–1338.
44. C. Janowitz, V. Scherer, M. Mohamed, A. Krapf, H. Dwelk, R. Manzke, Z. Galazka, R. Uecker, K. Irmscher, R. Fornari, M. Michling, D. Schmeier, J. R. Weber, J. B. Varley and C. G. Van De Walle, New J. Phys., 2011, 13, 085014.
45. S. Yoshioka, H. Hayashi, A. Kuwabara, F. Oba, K. Matsunaga and I. Tanaka, J. Phys.: Condens. Matter, 2007, 19, 346211.
46. N. Ueda, H. Hosono, R. Waseda and H. Kawazoe, Appl. Phys. Lett., 1997, 71, 933–935.
47. E. A. Albanesi, S. J. Sferco, I. Lefebvre, G. Allan and G. Hollinger, Phys. Rev. B, 1992, 46, 13260–13267.
48. V. M. Bermudez, Chem. Phys., 2006, 323, 193–203.
49. Z. Galazka, J. Appl. Phys., 2022, 131, 031103.
50. V. I. Vasil’tsiv and Y. M. Zakarko, J. Appl. Spectrosc., 1983, 39, 1037–1041.
51. H. Aida, K. Nishiguchi, H. Takeda, N. Aota, K. Sunakawa and Y. Yaguchi, Jpn. J. Appl. Phys., 2008, 47, 8506–8509.
52. N. Ueda, H. Hosono, R. Waseda and H. Kawazoe, Appl. Phys. Lett., 1997, 70, 3561–3563.
53. K. Hoshikawa, E. Ohba, T. Kobayashi, J. Yanagisawa, C. Miyagawa and Y. Nakamura, J. Cryst. Growth, 2016, 447, 36–41.
54. Z. Feng, A. F.-M. A.-U. Bhuiyan, N. K. Kalarickal, S. Rajan and H. Zhao, Appl. Phys. Lett., 2020, 117, 222106.
55. F. Alema, Y. Zhang, A. Osinsky, N. Orishchin, N. Valente, A. Mauze and J. S. Speck, APL Mater., 2020, 8, 021110.
56. H. Ghadi, J. F. McGlone, C. M. Jackson, E. Farzana, Z. Feng, A. F.-M. A.-U. Bhuiyan, H. Zhao, A. R. Arehart and S. A. Ringel, APL Mater., 2020, 8, 021111.
57. Z. (Ashley) Jian, I. Sayed, W. Liu, S. Mohanty and E. Ahmadi, Appl. Phys. Lett., 2021, 118, 172102.
58. Z. Feng, A. F.-M. Anhar Uddin Bhuiyan, M. R. Karim and H. Zhao, Appl. Phys. Lett., 2019, 114, 250601.
59. V. I. Vasyltsiv, Y. I. Rym and Y. M. Zakharko, Phys. Status Solidi Basic Res., 1996, 195, 653–658.
60. M. Lee, M. Yang, H. Y. Lee, H. U. Lee, H. Lee, H. Son and U. J. Kim, Mater. Sci. Semicond. Process., 2021, 123, 105565.
61. S. H. Kim, M. Yang, H. Y. Lee, J. S. Choi, H. U. Lee, U. J. Kim and M. Lee, Mater. Sci. Semicond. Process., 2021, 123, 105534.
62. Q. Liu, L. Chen, Z. Tao and X. Xiu, Bandaoti Guangdian/Semicond. Optoelectron., 2021, 42, 252–258.
63. J. Guo, A. Liu, B. Man, M. Liu, S. Jiang, J. Hou and D. Kong, Optoelectron. Adv. Mater. Rapid Commun., 2011, 5, 964–968.
64. D. Kong, A. Liu, J. Guo, B. Man, M. Liu, S. Jiang and J. Hou, Optoelectron. Adv. Mater. Rapid Commun., 2012, 6, 1004–1008.
65. H. Shen, K. Baskaran, Y. Yin, K. Tian, L. Duan, X. Zhao and A. Tiwari, J. Alloys Compd., 2020, 822, 153419.
66. M. K. Yadav, A. Mondal, S. Das, S. K. Sharma and A. Bag, J. Alloys Compd., 2020, 819, 153052.
67. Q. Wang, J. Chen, P. Huang, M. Li, Y. Lu, K. P. Homewood, G. Chang, H. Chen and Y. He, Appl. Surf. Sci., 2019, 489, 101–109.
68. R. Wakabayashi, T. Oshima, M. Hattori, K. Sasaki, T. Masui, A. Kuramata, S. Yamakoshi, K. Yoshimatsu and A. Ohtomo, J. Cryst. Growth, 2015, 424, 77–79.
69. X. H. Chen, S. Han, Y. M. Lu, P. J. Cao, W. J. Liu, Y. X. Zeng, F. Jia, W. Y. Xu, X. K. Liu and D. L. Zhu, J. Alloys Compd., 2018, 747, 869–878.
70. P. Schurig, M. Couturier, M. Becker, A. Polity and P. J. Klar, Phys. Status Solidi Appl. Mater. Sci., 2019, 216, 1900385.
71. C. V. Ramana, Gallium Oxide: Technology, Devices and Applications, 2019, pp. 47–66.
72. J. Castillo, R. Garcia-Perez and H. Huq, J. Electron. Mater., 2019, 48, 536–541.
73. S. S. Kumar, E. J. Rubio, M. Noor-A-Alam, G. Martinez, S. Manandhar, V. Shutthanandan, S. Thevuthasan and C. V. Ramana, J. Phys. Chem. C, 2013, 117, 4194–4200.
74. D. Y. Guo, X. L. Zhao, Y. S. Zhi, W. Cui, Y. Q. Huang, Y. H. An, P. G. Li, Z. P. Wu and W. H. Tang, Mater. Lett., 2015, 164, 364–367.
75. Y. Oshima, E. G. Víllora and K. Shimamura, Appl. Phys. Express, 2015, 8, 4–8.
76. V. Gottschalch, S. Merker, S. Blaurock, M. Kneiß, U. Teschner, M. Grundmann and H. Krautscheid, J. Cryst. Growth, 2019, 510, 76–84.
77. J. W. Roberts, J. C. Jarman, D. N. Johnstone, P. A. Midgley, P. R. Chalker, R. A. Oliver and F. C.-P. Massabuau, J. Cryst. Growth, 2018, 487, 23–27.
78. H. Nishinaka, D. Tahara, S. Morimoto and M. Yoshimoto, Mater. Lett., 2017, 205, 28–31.
79. T. Ma, X. Chen, F. Ren, S. Zhu, S. Gu, R. Zhang, Y. Zheng and J. Ye, J. Semicond., 2019, 40, 012804.
80. M. Marezuo and J. P. Remeika, J. Chem. Phys., 1967, 46, 1862–1865.
81. M. Feneberg, J. Bläsing, T. Sekiyama, K. Ota, K. Akaiwa, K. Ichino and R. Goldhahn, Appl. Phys. Lett., 2019, 114, 142102.
82. E. Ahmadi and Y. Oshima, J. Appl. Phys., 2019, 126, 160901.
83. K. Shiojima, H. Kambara, T. Matsuda and T. Shinohe, Thin Solid Films, 2019, 685, 17–25.
84. G. T. Dang, T. Kawaharamura, M. Furuta and M. W. Allen, IEEE Trans. Electron Devices, 2015, 62, 3640–3644.
85. R. Horie, H. Nishinaka, D. Tahara and M. Yoshimoto, J. Alloys Compd., 2021, 851, 156927.
86. T. Hadamek, A. B. Posadas, F. Al-Quaiti, D. J. Smith, M. R. McCartney and A. A. Demkov, AIP Adv., 2021, 11, 045209.
87. T. Oshima, K. Matsuyama, K. Yoshimatsu and A. Ohtomo, J. Cryst. Growth, 2015, 421, 23–26.
88. H. Hayashi, R. Huang, F. Oba, T. Hirayama and I. Tanaka, J. Mater. Res., 2011, 26, 578–583.
89. R. Huang, H. Hayashi, F. Oba and I. Tanaka, J. Appl. Phys., 2007, 101, 063526.
90. H. Y. Playford, A. C. Hannon, E. R. Barney and R. I. Walton, Chem. – Eur. J., 2013, 19, 2803–2813.
91. S. Yoshioka, H. Hayashi, A. Kuwabara, F. Oba, K. Matsunaga and I. Tanaka, J. Phys.: Condens. Matter, 2007, 19, 346211.
92. A. Sharma, M. Varshney, H. Saraswat, S. Chaudhary, J. Parkash, H.-J. Shin, K.-H. Chae and S.-O. Won, Int. Nano Lett., 2020, 10, 71–79.
93. X. Wang, M. Faizan, G. Na, X. He, Y. H. Fu and L. Zhang, Adv. Electron. Mater., 2020, 6, 1–7.
94. J. Wang, H. Guo, C. Zhu, Q. Cai, G. Yang, J. Xue, D.-J. Chen, Y. Tong, B. Liu, H. Lu, R. Zhang and Y.-D. Zheng, IEEE Electron Device Lett., 2020, 38, 1.
95. P. Ranga, S. B. Cho, R. Mishra and S. Krishnamoorthy, Appl. Phys. Express, 2020, 13, 061009.
96. S. Krishnamoorthy, Z. Xia, C. Joishi, Y. Zhang, J. McGlone, J. Johnson, M. Brenner, A. R. Arehart, J. Hwang, S. Lodha and S. Rajan, Appl. Phys. Lett., 2017, 111, 3–7.
97. M. Knei, A. Hassa, D. Splith, C. Sturm, H. Von Wenckstern, T. Schultz, N. Koch, M. Lorenz and M. Grundmann, APL Mater., 2019, 7, 022516.
98. Y. Li, X. Xiu, W. Xu, L. Zhang, H. Zhao, Z. Xie, T. Tao, P. Chen, B. Liu, R. Zhang and Y. Zheng, Superlattices Microstruct., 2021, 152, 106845.
99. Y. Zhang, Y. Gong, X. Chen, Y. Kuang, J. Hao, F. F. Ren, S. Gu, R. Zhang and J. Ye, ACS Appl. Electron. Mater., 2022, 4, 461–468.
100. H. He, R. Orlando, M. A. Blanco, R. Pandey, E. Amzallag, I. Baraille and M. Rérat, Phys. Rev. B: Condens. Matter Mater. Phys, 2006, 74, 1–8.
101. S. Geller, J. Chem. Phys., 1960, 33, 676–684.
102. B. G. Pfrommer, M. Cote, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233–240.
103. A. Mock, R. Korlacki, C. Briley, V. Darakchieva, B. Monemar, Y. Kumagai, K. Goto, M. Higashiwaki and M. Schubert, Phys. Rev. B, 2017, 96, 1–14.
104. H. Peelaers, J. L. Lyons, J. B. Varley and C. G. Van De Walle, APL Mater., 2019, 7, 022519.
105. J. B. Varley, J. R. Weber, A. Janotti and C. G. Van De Walle, Appl. Phys. Lett., 2010, 97, 97–100.
106. C. Janowitz, V. Scherer, M. Mohamed, A. Krapf, H. Dwelk, R. Manzke, Z. Galazka, R. Uecker, K. Irmscher, R. Fornari, M. Michling, D. Schmeier, J. R. Weber, J. B. Varley and C. G. Van De Walle, New J. Phys., 2011, 13, 085014.
107. Y. Guo, J. Zhang, F. Zhu, Z. X. Yang, J. Xu and J. Yu, Appl. Surf. Sci., 2008, 254, 5124–5128.
108. C. Zhang, F. Liao, X. Liang, H. Gong, Q. Liu, L. Li, X. Qin, X. Huang and C. Huang, Phys. B, 2019, 562, 124–130.
109. Y. Kang, K. Krishnaswamy, H. Peelaers and C. G. Van De Walle, J. Phys.: Condens. Matter, 2017, 29, 234001.
110. K. Ghosh and U. Singisetti, J. Mater. Res., 2017, 32, 4142–4152.
111. F. Alema, Y. Zhang, A. Osinsky, N. Valente, A. Mauze, T. Itoh and J. S. Speck, APL Mater., 2019, 7, 121110.
112. N. Ma, N. Tanen, A. Verma, Z. Guo, T. Luo, H. (Grace) Xing and D. Jena, Appl. Phys. Lett., 2016, 109, 212101.
113. Y. Zhang, C. Joishi, Z. Xia, M. Brenner, S. Lodha and S. Rajan, Appl. Phys. Lett., 2018, 112, 233503.
114. Z. Xia, C. Joishi, S. Krishnamoorthy, S. Bajaj, Y. Zhang, M. Brenner, S. Lodha and S. Rajan, IEEE Electron Device Lett., 2018, 39, 568–571.
115. H. Hosono, Thin Solid Films, 2007, 515, 6000–6014.
116. D. D. Edwards, T. O. Mason, F. Goutenoire and K. R. Poeppelmeier, Appl. Phys. Lett., 1997, 70, 1706–1708.
117. T. Onuma, S. Saito, K. Sasaki, T. Masui, T. Yamaguchi, T. Honda and M. Higashiwaki, Jpn. J. Appl. Phys., 2015, 54, 112601.
118. T. Onuma, K. Tanaka, K. Sasaki, T. Yamaguchi, T. Honda, A. Kuramata, S. Yamakoshi and M. Higashiwaki, Appl. Phys. Lett., 2019, 115, 231102.
119. F. Ricci, F. Boschi, A. Baraldi, A. Filippetti, M. Higashiwaki, A. Kuramata, V. Fiorentini and R. Fornari, J. Phys.: Condens. Matter, 2016, 28, 224005.
120. Y. Bin Liu, J. Y. Yang, G. M. Xin, L. H. Liu, G. Csányi and B. Y. Cao, J. Chem. Phys., 2020, 153, 144501.
121. M. Handwerg, R. Mitdank, Z. Galazka and S. F. Fischer, Semicond. Sci. Technol., 2015, 30, 024006.
122. Z. Guo, A. Verma, X. Wu, F. Sun, A. Hickman, T. Masui, A. Kuramata, M. Higashiwaki, D. Jena and T. Luo, Appl. Phys. Lett., 2015, 106, 111909.
123. Z. Yan and S. Kumar, Phys. Chem. Chem. Phys., 2018, 20, 29236–29242.
124. M. D. Santia, N. Tandon and J. D. Albrecht, Appl. Phys. Lett., 2015, 107, 041907.
125. Z. Galazka, K. Irmscher, R. Uecker, R. Bertram, M. Pietsch, A. Kwasniewski, M. Naumann, T. Schulz, R. Schewski, D. Klimm and M. Bickermann, J. Cryst. Growth, 2014, 404, 184–191.
126. Y. Zhang, Q. Su, J. Zhu, S. Koirala, S. J. Koester and X. Wang, Appl. Phys. Lett., 2020, 116, 202101.
127. D. S. Tang, Y. C. Hua, Y. G. Zhou and B. Y. Cao, Acta Phys. Sin., 2021, 70, 045101.
128. M. D. Kamatagi, N. S. Sankeshwar and B. G. Mulimani, Diam. Relat. Mater., 2007, 16, 98–106.
129. Q. Zheng, C. Li, A. Rai, J. H. Leach, D. A. Broido and D. G. Cahill, Phys. Rev. Mater., 2019, 3, 014601.
130. K. Adachi, H. Ogi, N. Takeuchi, N. Nakamura, H. Watanabe, T. Ito and Y. Ozaki, J. Appl. Phys., 2018, 124, 085102.
131. J. Furthmüller and F. Bechstedt, Phys. Rev. B, 2016, 93, 1–16.
132. J. Su, J. Zhang, R. Guo, Z. Lin, M. Liu, J. Zhang, J. Chang and Y. Hao, Mater. Des., 2019, 184, 108197.
133. S. Luan, L. Dong and R. Jia, J. Cryst. Growth, 2019, 505, 74–81.
134. L. B. Drissi, K. Sadki, M. H. Kourra and M. Bousmina, J. Appl. Phys., 2018, 123, 185106.
135. Y. Liao, Z. Zhang, Z. Gao, Q. Qian and M. Hua, ACS Appl. Mater. Interfaces, 2020, 12, 30659–30669.
136. H. Peelaers and C. G. Van De Walle, Phys. Rev. B, 2017, 96, 1–5.
137. Z. Wang, G. Wang, X. Liu, S. Wang, T. Wang, S. Zhang, J. Yu, G. Zhao and L. Zhang, J. Mater. Chem. C, 2021, 9, 17201–17232.
138. R. Guo, J. Su, Z. Lin, J. Zhang, Y. Qin, J. Zhang, J. Chang and Y. Hao, Adv. Theory Simul., 2019, 2, 1900106.
139. Z. Wu, Z. Jiang, P. Song, P. Tian, L. Hu, R. Liu, Z. Fang, J. Kang and T. Y. Zhang, Small, 2019, 15, 2–7.
140. J. Kim, J. Kim, S. Oh and M. A. Mastro, Phys. Chem. Chem. Phys., 2016, 18, 15760–15764.
141. A. Kuramata, K. Koshi, S. Watanabe, Y. Yamaoka, T. Masui and S. Yamakoshi, Jpn. J. Appl. Phys., 2016, 55, 1202A2.
142. J. Yao, T. Liu and B. Wang, Mater. Res. Express, 2019, 6, 075913.
143. P. De, Q. D. Ho, F. Seemann, M. Lorke and T. Frauenheim, Phys. Rev. B, 2017, 95, 075208.
144. T. Kobayashi, T. Gake, Y. Kumagai, F. Oba and Y. I. Matsushita, 2019, arXiv, pp. 1–5.
145. M. Yamaga, E. Víllora, K. Shimamura, N. Ichinose and M. Honda, Phys. Rev. B, 2003, 68, 1–9.
146. T. Zacherle, P. C. Schmidt and M. Martin, Phys. Rev. B, 2013, 87, 1–10.
147. A. Kyrtsos, M. Matsubara and E. Bellotti, Phys. Rev. B, 2017, 95, 245202.
148. M. E. Ingebrigtsen, J. B. Varley, A. Y. Kuznetsov, B. G. Svensson, G. Alfieri, A. Mihaila, U. Badstübner and L. Vines, Appl. Phys. Lett., 2018, 112, 042104.
149. E. G. Víllora, K. Shimamura, Y. Yoshikawa, T. Ujiie and K. Aoki, Appl. Phys. Lett., 2008, 92, 202120.
150. E. Ahmadi, O. S. Koksaldi, S. W. Kaun, Y. Oshima, D. B. Short, U. K. Mishra and J. S. Speck, Appl. Phys. Express, 2017, 10, 041102.
151. A. Kyrtsos, M. Matsubara and E. Bellotti, Appl. Phys. Lett., 2018, 112, 032108.
152. S. B. Zhang, S. H. Wei and A. Zunger, Phys. Rev. B, 2001, 63, 075205.
153. T. Gake, Y. Kumagai and F. Oba, Phys. Rev. Mater., 2019, 3, 44603.
154. S. Lany and A. Zunger, Phys. Rev. B, 2009, 80, 085202.
155. Y.-J. Lee, M. A. Schweitz, S.-K. Lee, J.-H. Koh and S.-M. Koo, J. Nanoelectron. Optoelectron., 2020, 15, 561–565.
156. L. Dong, R. Jia, B. Xin and Y. Zhang, J. Vac. Sci. Technol., A: Vac., Surf., Film, 2016, 34, 060602.
157. S. H. Lee, K. M. Lee, Y. Bin Kim, Y. J. Moon, S. Bin Kim, D. Bae, T. J. Kim, Y. D. Kim, S. K. Kim and S. W. Lee, J. Alloys Compd., 2019, 780, 400–407.
158. S. Rafique, L. Han and H. Zhao, Phys. Status Solidi Appl. Mater. Sci., 2017, 214, 1–6.
159. L. Su, S. Y. Chen, L. Zhao, Y. Zuo and J. Xie, Appl. Phys. Lett., 2020, 117, 211101.
160. P. Mukhopadhyay, I. Hatipoglu, T. S. Sakthivel, D. A. Hunter, P. R. Edwards, R. W. Martin, G. Naresh-Kumar, S. Seal and W. V. Schoenfeld, Adv. Photonics Res., 2021, 2, 2000067.
161. M. Dong, W. Zheng, C. Xu, R. Lin, D. Zhang, Z. Zhang and F. Huang, Adv. Opt. Mater., 2019, 7, 1–8.
162. D. Y. Guo, Z. P. Wu, Y. H. An, X. C. Guo, X. L. Chu, C. L. Sun, L. H. Li, P. G. Li and W. H. Tang, Appl. Phys. Lett., 2014, 105, 023507.
163. H. T. Zhou, L. J. Cong, J. G. Ma, M. Z. Chen, D. Y. Song, H. B. Wang, P. Li, B. S. Li, H. Y. Xu and Y. C. Liu, J. Alloys Compd., 2020, 847, 156536.
164. Y. Cai, K. Zhang, Q. Feng, Y. Zuo, Z. Hu, Z. Feng, H. Zhou, X. Lu, C. Zhang, W. Tang, J. Zhang and Y. Hao, Opt. Mater. Express, 2018, 8, 3506.
165. H. Zhou, L. Cong, J. Ma, B. Li, M. Chen, H. Xu and Y. Liu, J. Mater. Chem. C, 2019, 7, 13149–13155.
166. Y. Wang, C. Wu, D. Guo, P. Li, S. Wang, A. Liu, C. Li, F. Wu and W. Tang, ACS Appl. Electron. Mater., 2020, 2, 2032–2038.
167. S. Ghose, S. Rahman, L. Hong, J. S. Rojas-Ramirez, H. Jin, K. Park, R. Klie and R. Droopad, J. Appl. Phys., 2017, 122, 095302.
168. M. R. Lorenz, J. F. Woods and R. J. Gambino, J. Phys. Chem. Solids, 1967, 28, 403–404.
169. T. Zacherle, P. C. Schmidt and M. Martin, Phys. Rev. B, 2013, 87, 235206.
170. M. D. McCluskey, J. Appl. Phys., 2020, 127, 190401.
171. A. Usseinov, Z. Koishybayeva, A. Platonenko, A. Akilbekov, J. Purans, V. Pankratov, Y. Suchikova and A. I. Popov, Latv. J. Phys. Tech. Sci., 2021, 14, 7384.
172. L. Dong, R. Jia, B. Xin, B. Peng and Y. Zhang, Sci. Rep., 2017, 7, 1–12.
173. D. Sun, Y. Gao, J. Xue and J. Zhao, J. Mater. Sci., 2020, 55, 9343–9353.
174. T. Onuma, S. Fujioka, T. Yamaguchi, M. Higashiwaki, K. Sasaki, T. Masui and T. Honda, Appl. Phys. Lett., 2013, 103, 2011–2014.
175. T. Harwig and F. Kellendonk, J. Solid State Chem., 1978, 24, 255–263.
176. C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van De Walle, Rev. Mod. Phys., 2014, 86, 253–305.
177. H. Gao, S. Muralidharan, N. Pronin, M. R. Karim, S. M. White, T. Asel, G. Foster, S. Krishnamoorthy, S. Rajan, L. R. Cao, M. Higashiwaki, H. Von Wenckstern, M. Grundmann, H. Zhao, D. C. Look and L. J. Brillson, Appl. Phys. Lett., 2018, 112, 1–6.
178. Z. Zhang, E. Farzana, A. R. Arehart and S. A. Ringel, Appl. Phys. Lett., 2016, 108, 2–7.
179. J. Sun and J. Leng, Phys. B, 2019, 552, 195–201.
180. W. Xiong, X. Zhou, G. Xu, Q. He, G. Jian, C. Chen, Y. Yu, W. Hao, X. Xiang, X. Zhao, W. Mu, Z. Jia, X. Tao and S. Long, IEEE Electron Device Lett., 2021, 42, 430–433.
181. M. H. Lee and R. L. Peterson, APL Mater., 2019, 7, 022524.
182. J. Hou, R. Guo, J. Su, Y. Du, Z. Lin, J. Zhang, Y. Hao and J. Chang, Phys. Chem. Chem. Phys., 2021, 23, 5975–5983.
183. W. Li, J. Wan, Z. Tu, H. Li, H. Wu and C. Liu, Ceram. Int., 2022, 48, 3185–3191.
184. C. C. Yang, J. Q. Huang, K. Y. Chen, P. H. Chiu, H. T. Vu and Y. K. Su, IEEE Access, 2019, 7, 175186–175191.
185. T. Zacherle, P. C. Schmidt and M. Martin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 1–10.
186. A. Kyrtsos, M. Matsubara and E. Bellotti, Phys. Rev. B, 2017, 95, 1–9.
187. Y. Kang and C. G. Van De Walle, Appl. Phys. Lett., 2017, 111, 152107.
188. E. Korhonen, F. Tuomisto, D. Gogova, G. Wagner, M. Baldini, Z. Galazka, R. Schewski and M. Albrecht, Appl. Phys. Lett., 2015, 106, 242103.
189. S. Krishnakumar, N. Shanthi, P. Mahadevan and D. Sarma, Phys. Rev. B, 2000, 61, 16370–16376.
190. J. B. Varley, H. Peelaers, A. Janotti and C. G. Van De Walle, J. Phys.: Condens. Matter, 2011, 23, 334212.
191. A. Y. Polyakov, N. B. Smirnov, I. V. Shchemerov, D. Gogova, S. A. Tarelkin and S. J. Pearton, J. Appl. Phys., 2018, 123, 115702.
192. K. Irmscher, Z. Galazka, M. Pietsch, R. Uecker and R. Fornari, J. Appl. Phys., 2011, 110, 063720.
193. A. Y. Polyakov, N. B. Smirnov, I. V. Shchemerov, S. J. Pearton, F. Ren, A. V. Chernykh, P. B. Lagov and T. V. Kulevoy, APL Mater., 2018, 6, 096102.
194. E. Farzana, M. F. Chaiken, T. E. Blue, A. R. Arehart and S. A. Ringel, APL Mater., 2019, 7, 022502.
195. C. A. Lenyk, N. C. Giles, E. M. Scherrer, B. E. Kananen, L. E. Halliburton, K. T. Stevens, G. K. Foundos, J. D. Blevins, D. L. Dorsey and S. Mou, J. Appl. Phys., 2019, 125, 045703.
196. J. R. Ritter, K. G. Lynn and M. D. McCluskey, J. Appl. Phys., 2019, 126, 225705.
197. J. R. Ritter, J. Huso, P. T. Dickens, J. B. Varley, K. G. Lynn and M. D. McCluskey, Appl. Phys. Lett., 2018, 113, 052101.
198. P. D.-C. King, I. McKenzie and T. D. Veal, Appl. Phys. Lett., 2010, 96, 10–13.
199. P. D.-C. King, R. L. Lichti, Y. G. Celebi, J. M. Gil, R. C. Vilão, H. V. Alberto, J. Piroto Duarte, D. J. Payne, R. G. Egdell, I. McKenzie, C. F. McConville, S. F.-J. Cox and T. D. Veal, Phys. Rev. B, 2009, 80, 081201.
200. M. Stavola, W. B. Fowler, Y. Qin, P. Weiser and S. Pearton, Gallium Oxide: Technology, Devices and Applications, 2018, pp. 191–210.
201. Y. Wei, X. Li, J. Yang, C. Liu, J. Zhao, Y. Liu and S. Dong, Sci. Rep., 2018, 8, 1–8.
202. D. P. Butt, Y. Park and T. N. Taylor, J. Nucl. Mater., 1999, 264, 71–77.
203. S. Ahn, F. Ren, E. Patrick, M. E. Law and S. J. Pearton, ECS J. Solid State Sci. Technol., 2017, 6, 3026–3029.
204. Y. G. Celebi, R. L. Lichti, B. B. Baker, P. W. Mengyan, H. N. Bani-Salameh and E. Catak, Phys. B, 2012, 407, 2879–2882.
205. G. J. Exarhos and X. D. Zhou, Thin Solid Films, 2007, 515, 7025–7052.
206. L. Binet and D. Gourier, J. Phys. Chem. Solids, 1998, 59, 1241–1249.
207. J. N. Dang, S. W. Zheng, L. Chen and T. Zheng, Chinese Phys. B, 2019, 28, 016301.
208. Y. Wang, J. Su, H. Yuan, Z. Lin, J. Zhang, Y. Hao and J. Chang, Semicond. Sci. Technol., 2021, 36, 095026.
209. C. Yan, J. Su, Y. Wang, Z. Lin, J. Zhang, J. Chang and Y. Hao, J. Alloys Compd., 2021, 854, 157247.
210. A. T. Neal, S. Mou, S. Rafique, H. Zhao, E. Ahmadi, J. S. Speck, K. T. Stevens, J. D. Blevins, D. B. Thomson, N. Moser, K. D. Chabak and G. H. Jessen, Appl. Phys. Lett., 2018, 113, 1–6.
211. D. Sun, Y. Gao, J. Xue and J. Zhao, J. Alloys Compd., 2019, 794, 374–384.
212. Y. Li, C. Yang, L. Wu and R. Zhang, Mod. Phys. Lett. B, 2017, 31, 1–11.
213. S. Lany, APL Mater., 2018, 6, 046103.
214. S. J. Pearton, J. Yang, P. H. Cary, F. Ren, J. Kim, M. J. Tadjer, M. A. Mastro and P. H. Cary IV, Cit. Appl. Phys. Rev. Appl. Phys. Lett. J. Chem. Phys. Appl. Phys. Lett. Appl. Phys. Lett. Appl. Phys. Lett., 2018, 51, 11301–13504.
215. A. Bouzid and A. Pasquarello, Phys. Status Solidi, 2019, 13, 2–6.
216. M. D. Heinemann, J. Berry, G. Teeter, T. Unold and D. Ginley, Appl. Phys. Lett., 2016, 108, 1–5.
217. Y. Zhang, J. Yan, G. Zhao and W. Xie, Phys. B Condens. Matter, 2010, 405, 3899–3903.
218. A. Kyrtsos, M. Matsubara and E. Bellotti, Appl. Phys. Lett., 2018, 112, 032108.
219. D. Verma Atul, Certain distance degree based Topol. indices Zeolite LTA Fram., 2018, pp. 11–14.
220. M. A. Blanco, M. B. Sahariah, H. Jiang, A. Costales and R. Pandey, Phys. Rev. B, 2005, 72, 184103.
221. D. J. Chadi and K. J. Chang, Phys. Rev. Lett., 1988, 61, 873–876.
222. D. J. Chadi and K. J. Chang, Phys. Rev. B, 1989, 39, 10063–10074.
223. J. Li, S.-H. Wei and L.-W. Wang, Phys. Rev. Lett., 2005, 94, 185501.
224. L. Gordon, J. L. Lyons, A. Janotti and C. G. Van De Walle, Phys. Rev. B, 2014, 89, 1–6.
225. N. T. Son, M. Bickermann and E. Janzén, Appl. Phys. Lett., 2011, 98, 092104.
226. T. N. Morgan, Phys. Rev. B, 1986, 34, 2664–2669.
227. M.-H. Du and S. B. Zhang, Phys. Rev. B, 2005, 72, 075210.
228. K. Sasaki, M. Higashiwaki, A. Kuramata, T. Masui and S. Yamakoshi, Appl. Phys. Express, 2013, 6, 086502.
229. L. Zr and O. Nb, Ceram. Int., 2017, 43, 11879–11884.
230. N. T. Son, K. Goto, K. Nomura, Q. T. Thieu, R. Togashi, H. Murakami, Y. Kumagai, A. Kuramata, M. Higashiwaki, A. Koukitu, S. Yamakoshi, B. Monemar and E. Janzén, J. Appl. Phys., 2016, 120, 235703.
231. N. Suzuki, S. Ohira, M. Tanaka, T. Sugawara, K. Nakajima and T. Shishido, Phys. Status Solidi Curr. Top. Solid State Phys., 2007, 4, 2310–2313.
232. Z. Galazka, K. Irmscher, R. Schewski, I. M. Hanke, M. Pietsch, S. Ganschow, D. Klimm, A. Dittmar, A. Fiedler, T. Schroeder and M. Bickermann, J. Cryst. Growth, 2020, 529, 125297.
233. X. Du, Z. Li, C. Luan, W. Wang, M. Wang, X. Feng, H. Xiao and J. Ma, J. Mater. Sci., 2015, 50, 3252–3257.
234. J. C. Manifacier, L. Szepessy, J. F. Bresse, M. Perotin and R. Stuck, Mater. Res. Bull., 1979, 14, 163–175.
235. M. Higashiwaki, K. Sasaki, A. Kuramata, T. Masui and S. Yamakoshi, Phys. Status Solidi, 2014, 211, 21–26.
236. F. Alema, G. Seryogin, A. Osinsky and A. Osinsky, APL Mater., 2021, 9, 091102.
237. P. Ranga, A. Bhattacharyya, L. Whittaker-Brooks, M. A. Scarpulla and S. Krishnamoorthy, J. Vac. Sci. Technol., A, 2021, 39, 030404.
238. X. Liu, K. Cheng, R. Li, Y. Jia, Q. Lu, S. Wang, H. Chen and F. Ma, Appl. Surf. Sci., 2021, 553, 149458.
239. K. Konishi, K. Goto, H. Murakami, Y. Kumagai, A. Kuramata, S. Yamakoshi and M. Higashiwaki, Appl. Phys. Lett., 2017, 110, 103506.
240. S. Morimoto, H. Nishinaka and M. Yoshimoto, Thin Solid Films, 2019, 682, 18–23.
241. T. K. Shu, R. X. Miao, S. D. Guo, S. Q. Wang, C. H. Zhao and X. L. Zhang, Chinese Phys. B, 2020, 29, 126301.
242. W. Guo, Y. Guo, H. Dong and X. Zhou, Phys. Chem. Chem. Phys., 2015, 17, 5817–5825.
243. S. Mirov, V. Fedorov, I. Moskalev, M. Mirov and D. Martyshkin, J. Lumin., 2013, 133, 268–275.
244. J. Huang, Y. Hu, T. Zou, K. Tang, Z. Zhang, Y. Ma, B. Li, L. Wang and Y. Lu, Surf. Coat. Technol., 2019, 366, 70–74.
245. H. Peelaers and C. G. Van De Walle, Phys. Rev. B, 2016, 94, 1–4.
246. H. Zhang, J. Deng, Z. Pan, Z. Bai, L. Kong and J. Wang, Vacuum, 2017, 146, 93–96.
247. R. P. Shi, X. D. Huang, J. K.-O. Sin and P. T. Lai, Microelectron. Reliab., 2016, 65, 64–68.
248. M. Saleh, A. Bhattacharyya, J. B. Varley, S. Swain, J. Jesenovec, S. Krishnamoorthy and K. Lynn, Appl. Phys. Express, 2019, 12, 3–7.
249. J. Guo, M. Ma, Y. Li, D. Zhang, Y. Liu and W. Zheng, IEEE Electron Device Lett., 2021, 42, 895–898.
250. M. Saleh, J. B. Varley and J. Jesenovec, Semicond. Sci. Technol., 2020, 35, 04LT01.
251. S. Chen, K. C. Lukas, W. Liu, C. P. Opeil, G. Chen and Z. Ren, Adv. Energy Mater., 2013, 3, 1210–1214.
252. J. F. McGlone, Z. Xia, Y. Zhang, C. Joishi, S. Lodha, S. Rajan, S. A. Ringel and A. R. Arehart, IEEE Electron Device Lett., 2018, 39, 1042–1045.
253. J. F. McGlone, Z. Xia, C. Joishi, S. Lodha, S. Rajan, S. Ringel and A. R. Arehart, Appl. Phys. Lett., 2019, 115, 153501.
254. C. C. Chueh, C. Z. Li and A. K.-Y. Jen, Energy Environ. Sci., 2015, 8, 1160–1189.
255. T. Liu, S. Liu, K. H. Tu, H. Schmidt, L. Chu, D. Xiang, J. Martin, G. Eda, C. A. Ross and S. Garaj, Nat. Nanotechnol., 2019, 14, 223–226.
256. K. T. Chan, J. B. Neaton and M. L. Cohen, Phys. Rev. B, 2008, 77, 1–12.
257. J. B. Varley, A. Janotti, C. Franchini and C. G. Van De Walle, Phys. Rev. B, 2012, 85, 2–5.
258. H. Amano, M. Kito, K. Hiramatsu and I. Akasaki, Jpn. J. Appl. Phys., 1989, 28, 2112–2114.
259. S. Nakamura, N. Iwasa, M. Senoh and T. Mukai, Jpn. J. Appl. Phys., 1992, 31, 1258–1266.
260. S. Nakamura, T. Mukai, M. Senoh and N. Iwasa, Jpn. J. Appl. Phys., 1992, 31, 139–142.
261. Y. P. Qian, D. Y. Guo, X. L. Chu, H. Z. Shi, W. K. Zhu, K. Wang, X. K. Huang, H. Wang, S. L. Wang, P. G. Li, X. H. Zhang and W. H. Tang, Mater. Lett., 2017, 209, 558–561.
262. E. Chikoidze, A. Fellous, A. Perez-Tomas, G. Sauthier, T. Tchelidze, C. Ton-That, T. T. Huynh, M. Phillips, S. Russell, M. Jennings, B. Berini, F. Jomard and Y. Dumont, Mater. Today Phys., 2017, 3, 118–126.
263. Q. D. Ho, T. Frauenheim and P. Deák, J. Appl. Phys., 2018, 124, 3.
264. N. Zhang, H. Liu, Q. Sai, C. Shao, C. Xia, L. Wan, Z. C. Feng and H. F. Mohamed, J. Mater. Sci., 2021, 56, 13178–13189.
265. A. Y. Polyakov, N. B. Smirnov, I. V. Shchemerov, D. Gogova, S. A. Tarelkin and S. J. Pearton, J. Appl. Phys., 2018, 123, 115702.
266. X. Chu, Z. Liu, S. Zhang, P. Li and W. Tang, Phys. Scr., 2021, 96, 1–6.
267. A. Mauze, Y. Zhang, T. Mates, F. Wu and J. S. Speck, Appl. Phys. Lett., 2019, 115, 052102.
268. R. Sun, Y. K. Ooi, P. T. Dickens, K. G. Lynn and M. A. Scarpulla, Appl. Phys. Lett., 2020, 117, 052101.
269. H. M. Jeon, K. D. Leedy, D. C. Look, C. S. Chang, D. A. Muller, S. Badescu, V. Vasilyev, J. L. Brown, A. J. Green and K. D. Chabak, APL Mater., 2021, 9, 1–9.
270. Y. Huang, H. Wu, Y. Zhi, Y. Huang, D. Guo, Z. Wu, P. Li, Z. Chen and W. Tang, Appl. Phys. A: Mater. Sci. Process., 2018, 124, 1–9.
271. W. Yue, J. Yan, J. Wu and L. Zhang, J. Semicond., 2012, 33, 3–7.
272. Y. Guo, H. Yan, Q. Song, Y. Chen and S. Guo, Comput. Mater. Sci., 2014, 87, 198–201.
273. D. Skachkov and W. R.-L. Lambrecht, Appl. Phys. Lett., 2019, 114, 202102.
274. J. Jesenovec, J. Varley, S. E. Karcher and J. S. McCloy, J. Appl. Phys., 2021, 129, 225702.
275. Y. Su, D. Guo, J. Ye, H. Zhao, Z. Wang, S. Wang, P. Li and W. Tang, J. Alloys Compd., 2019, 782, 299–303.
276. J. L. Lyons, Semicond. Sci. Technol., 2018, 33, 05LT02.
277. E. Chikoidze, T. Tchelidze, C. Sartel, Z. Chi, R. Kabouche, I. Madaci, C. Rubio, H. Mohamed, V. Sallet, F. Medjdoub, A. Perez-Tomas and Y. Dumont, Mater. Today Phys., 2020, 15, 100263.
278. C. Tang, J. Sun, N. Lin, Z. Jia, W. Mu, X. Tao and X. Zhao, RSC Adv., 2016, 6, 78322–78334.
279. V. Vasanthi, M. Kottaisamy and V. Ramakrishnan, AIP Conf. Proc., 2017, 1832, 10–13.
280. D. Guo, X. Qin, M. Lv, H. Shi, Y. Su, G. Yao, S. Wang, C. Li, P. Li and W. Tang, Electron. Mater. Lett., 2017, 13, 483–488.
281. H. Yan, Y. Guo, Q. Song and Y. Chen, Phys. B, 2014, 434, 181–184.
282. A. A. Dakhel, Solid State Sci., 2013, 20, 54–58.
283. Y. Zhang, J. Yan, Q. Li, C. Qu, L. Zhang and W. Xie, Mater. Sci. Eng. B Solid-State Mater. Adv. Technol., 2011, 176, 846–849.
284. J. Jesenovec, C. Remple, J. Huso, B. Dutton, P. Toews, M. D. McCluskey and J. S. McCloy, J. Cryst. Growth, 2022, 578, 126419.
285. T. S. Jeong, J. H. Yu, H. S. Mo, T. S. Kim, C. J. Youn and K. J. Hong, J. Appl. Phys., 2013, 114, 053504.
286. D. J. Chadi, Phys. Rev. B, 1999, 59, 15181–15183.
287. S. B. Zhang, J. Phys.: Condens. Matter, 2002, 14, 881–903.
288. T. Kim and J. K. Jeong, Phys. Status Solidi, 2022, 16, 2100394.
289. F. P. Sabino, X. Cai, S.-H. Wei and A. Janotti, 2019, arXiv:1906.00840v1.
290. X. Cai, F. P. Sabino, A. Janotti and S. H. Wei, Phys. Rev. B, 2021, 103, 1–6.
291. R. Sun, H. Y. Zhang, G. G. Wang, J. C. Han, X. Z. Wang, L. Cui, X. P. Kuang, C. Zhu and L. Jin, Superlattices Microstruct., 2014, 65, 146–151.
292. R. Sun, H. Y. Zhang, G. G. Wang, J. C. Han, X. Z. Wang, X. P. Kuang, L. Cui, L. Jin and J. L. Tian, Superlattices Microstruct., 2013, 60, 257–262.
293. Y. Zhang, J. Yan, Q. Li, C. Qu, L. Zhang and T. Li, Phys. B, 2011, 406, 3079–3082.
294. S. C. Vanithakumari and K. K. Nanda, Bull. Mater. Sci., 2011, 34, 1331–1338.
295. L. Dong, R. Jia, C. Li, B. Xin and Y. Zhang, J. Alloys Compd., 2017, 712, 379–385.
296. Y. P. Song, H. Z. Zhang, C. Lin, Y. W. Zhu, G. H. Li, F. H. Yang and D. P. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 1–7.
297. Z. X. Jiang, Z. Y. Wu, C. C. Ma, J. N. Deng, H. Zhang, Y. Xu, J. D. Ye, Z. L. Fang, G. Q. Zhang, J. Y. Kang and T. Y. Zhang, Mater. Today Phys., 2020, 14, 100226.
298. Z. Y. Wu, Z. X. Jiang, C. C. Ma, W. Ruan, Y. Chen, H. Zhang, G. Q. Zhang, Z. L. Fang, J. Y. Kang and T. Y. Zhang, Mater. Today Phys., 2021, 17, 100356.
299. T. Kamimura, Y. Nakata, M. H. Wong and M. Higashiwaki, IEEE Electron Device Lett., 2019, 40, 1064–1067.
300. M. H. Wong, K. Goto, H. Murakami, Y. Kumagai and M. Higashiwaki, IEEE Electron Device Lett., 2019, 40, 431–434.
301. C.-H. Lin, Y. Yuda, M. H. Wong, M. Sato, N. Takekawa, K. Konishi, T. Watahiki, M. Yamamuka, H. Murakami, Y. Kumagai and M. Higashiwaki, IEEE Electron Device Lett., 2019, 40, 1487–1490.
302. U. Kaufmann, P. Schlotter, H. Obloh, K. Köhler and M. Maier, Phys. Rev. B, 2000, 62, 10867–10872.
303. L. Zhang, J. Yan, Y. Zhang, T. Li and X. Ding, Phys. B, 2012, 407, 1227–1231.
304. T. Yamamoto and H. Katayama-Yoshida, Phys. B, 2001, 302, 155–162.
305. J. Chang, Z. Lin, M. Lin, C. Zhu, J. Zhang and J. Wu, J. Mater. Chem. C, 2015, 3, 1787–1793.
306. J. Ma, J. Lin, J. Liu, F. Li, Y. Liu and G. Yang, Chem. Phys. Lett., 2020, 746, 137308.
307. L. Li, F. Liao and X. Hu, Superlattices Microstruct., 2020, 141, 106502.
308. J. Yang, Z. Sparks, F. Ren, S. J. Pearton and M. Tadjer, J. Vac. Sci. Technol., B, 2018, 36, 061201.
309. J. Yang, C. Fares, F. Ren, R. Sharma, E. Patrick, M. E. Law, S. J. Pearton and A. Kuramata, J. Appl. Phys., 2018, 123, 165706.
310. W. Chen, D. Qi, X. Gao and A. T.-S. Wee, Prog. Surf. Sci., 2009, 84, 279–321.
311. Z. Dridi, B. Bouhafs, P. Ruterana and B. Mar, Semicond. Sci. Technol., 2013, 18, 850–856.
312. H. Peelaers, J. B. Varley, J. S. Speck and C. G. Van De Walle, Appl. Phys. Lett., 2018, 112, 242101.
313. F. He, Y. Wang, Z. Lin, J. Su, J. Zhang, J. Chang and Y. Hao, Appl. Phys. Lett., 2021, 119, 112102.
314. T. Wang, W. Li, C. Ni and A. Janotti, Phys. Rev. Appl., 2018, 10, 1–7.
315. A. K. Saikumar, S. D. Nehate and K. B. Sundaram, Crit. Rev. Solid State Mater. Sci., 2021, 0, 1–32.
316. Q. Feng, X. Li, G. Han, L. Huang, F. Li, W. Tang, J. Zhang and Y. Hao, Opt. Mater. Express, 2017, 7, 1240.
317. Y. Zhang, A. Neal, Z. Xia, C. Joishi, J. M. Johnson, Y. Zheng, S. Bajaj, M. Brenner, D. Dorsey, K. Chabak, G. Jessen, J. Hwang, S. Mou, J. P. Heremans and S. Rajan, Appl. Phys. Lett., 2018, 112, 1–6.
318. Y. Zhang, Z. Xia, J. McGlone, W. Sun, C. Joishi, A. R. Arehart, S. A. Ringel and S. Rajan, IEEE Trans. Electron Devices, 2019, 66, 1574–1578.
319. E. Ahmadi, O. S. Koksaldi, X. Zheng, T. Mates, Y. Oshima, U. K. Mishra and J. S. Speck, Appl. Phys. Express, 2017, 10, 071101.
320. H. Peelaers, J. B. Varley, J. S. Speck and C. G. de Walle, Appl. Phys. Lett., 2018, 112, 242101.
321. A. Vaidya, C. N. Saha and U. Singisetti, IEEE Electron Device Lett., 2021, 42, 1444–1447.
322. R. Miller, F. Alema and A. Osinsky, in CS MANTECH 2018 - 2018 International Conference on Compound Semiconductor Manufacturing Technology, 2018.
323. A. Walsh, J. L.-F. Da Silva, S. H. Wei, C. Körber, A. Klein, L. F.-J. Piper, A. Demasi, K. E. Smith, G. Panaccione, P. Torelli, D. J. Payne, A. Bourlange and R. G. Egdell, Phys. Rev. Lett., 2008, 100, 167402.
324. R. L. Weiher and R. P. Ley, J. Appl. Phys., 1966, 37, 299–302.
325. H. Von Wenckstern, D. Splith, M. Purfürst, Z. Zhang, C. Kranert, S. Müller, M. Lorenz and M. Grundmann, Semicond. Sci. Technol., 2015, 30, 024005.
326. W. He, Z. Wang, T. Zheng, L. Wang and S. Zheng, J. Electron. Mater., 2021, 50, 3856–3861.
327. A. Walsh, J. L.-F. Da Silva, S. H. Wei, C. Körber, A. Klein, L. F.-J. Piper, A. Demasi, K. E. Smith, G. Panaccione, P. Torelli, D. J. Payne, A. Bourlange and R. G. Egdell, Phys. Rev. Lett., 2008, 100, 2–5.
328. H. Peelaers, D. Steiauf, J. B. Varley, A. Janotti and C. G. Van De Walle, Phys. Rev. B, 2015, 92, 1–6.
329. N. Suzuki, K. Kaneko and S. Fujita, J. Cryst. Growth, 2014, 401, 670–672.
330. H. Nishinaka, N. Miyauchi, D. Tahara, S. Morimoto and M. Yoshimoto, CrystEngComm, 2018, 20, 1882–1888.
331. V. Prozheeva, R. Hölldobler, H. Von Wenckstern, M. Grundmann and F. Tuomisto, J. Appl. Phys., 2018, 123, 125705.
332. H. H. Tippins, Phys. Rev., 1965, 140, 653–658.
333. V. Sridharan, S. Banerjee, M. Sardar, S. Dhara, N. Gayathri and V. S. Sastry, 2007, arXiv:cond-mat/0701232v1.
334. Y. Yang, J. Zhang, S. Hu, Y. Wu, J. Zhang, W. Ren and S. Cao, Phys. Chem. Chem. Phys., 2017, 19, 28928–28935.
335. N. T. Son, Q. D. Ho, K. Goto, H. Abe, T. Ohshima, B. Monemar, Y. Kumagai, T. Frauenheim and P. Deák, Appl. Phys. Lett., 2020, 117, 032101.
336. X. Lin, J. Wang, Z. Fu, Q. Huang and Y. Lu, J. Am. Ceram. Soc., 2021, 104, 4679–4686.
337. Z. Chen, T. Li, T. Yang, H. Xu, R. Khenata, Y. Gao and X. Wang, Nanomaterials, 2019, 9, 1342.
338. D. J. Heinzen, R. H. Wynar, P. D. Kheruntsyan, P. D. Drummond, T. Dietl, H. Ohno, F. Matsukura, J. Cibert and D. Ferrand, Chem. Phys. Lett., 1995, 269, 2657.
339. K. Ueda, H. Tabata and T. Kawai, Appl. Phys. Lett., 2001, 79, 988–990.
340. R. Ullah and J. Dutta, J. Hazard. Mater., 2008, 156, 194–200.
341. O. D. Jayakumar, H. G. Salunke, R. M. Kadam, M. Mohapatra, G. Yaswant and S. K. Kulshreshtha, Nanotechnology, 2006, 17, 1278–1285.
342. T. Fukumura, Z. Jin, M. Kawasaki, T. Shono, T. Hasegawa, S. Koshihara and H. Koinuma, Appl. Phys. Lett., 2001, 78, 958–960.
343. Y. Liu, J. Yang, Q. Guan, L. Yang, Y. Zhang, Y. Wang, B. Feng, J. Cao, X. Liu, Y. Yang and M. Wei, J. Alloys Compd., 2009, 486, 835–838.
344. B. Wang, J. Iqbal, X. Shan, G. Huang, H. Fu, R. Yu and D. Yu, Mater. Chem. Phys., 2009, 113, 103–106.
345. K. Sato and H. Katayama-Yoshida, Phys. E, 2001, 10, 251–255.
346. T. Minami, T. Shirai, T. Nakatani and T. Miyata, Jpn. J. Appl. Phys., 2000, 39, L524.
347. J. H. Kim and K. H. Yoon, J. Mater. Sci.: Mater. Electron., 2009, 20, 879–884.
348. X. Wang, R. Quhe, Y. Zhi, Z. Liu, Y. Huang, X. Dai, Y. Tang, Z. Wu and W. Tang, Superlattices Microstruct., 2019, 125, 330–337.
349. Y. Huang, Z. Chen, X. Zhang, X. Wang, Y. Zhi, Z. Wu and W. Tang, J. Semicond., 2018, 39, 1–6.
350. D. Guo, Z. Wu, P. Li, Q. Wang, M. Lei, L. Li and W. Tang, RSC Adv., 2015, 5, 12894–12898.
351. X. H. Wang, F. B. Zhang, K. Saito, T. Tanaka, M. Nishio and Q. X. Guo, J. Phys. Chem. Solids, 2014, 75, 1201–1204.
352. T. Onuma, S. Fujioka, T. Yamaguchi, M. Higashiwaki, K. Sasaki, T. Masui and T. Honda, Appl. Phys. Lett., 2013, 103, 3–6.
353. T. Harwig, F. Kellendonk and S. Slappendel, J. Phys. Chem. Solids, 1978, 39, 675–680.
354. E. G. Víllora, T. Atou, T. Sekiguchi, T. Sugawara, M. Kikuchi and T. Fukuda, Solid State Commun., 2001, 120, 455–458.
355. T. Zhang, J. Lin, X. Zhang, Y. Huang, X. Xu, Y. Xue, J. Zou and C. Tang, J. Lumin., 2013, 140, 30–37.
356. Y. Nakano, ECS J. Solid State Sci. Technol., 2017, 6, 615–617.
357. J. Zhang, C. Xia, Q. Deng, W. Xu, H. Shi, F. Wu and J. Xu, J. Phys. Chem. Solids, 2006, 67, 1656–1659.
358. A. Nakazawa, D. Yasukawa, H. Wakai, H. Oda and A. Yamanaka, Phys. Status Solidi, 2013, 10, 1584–1587.
359. W. Zhou, C. Xia, Q. Sai and H. Zhang, Appl. Phys. Lett., 2017, 111, 242103.
360. J. Zhang, B. Li, C. Xia, J. Xu, Q. Deng, X. Xu, F. Wu, W. Xu, H. Shi, G. Pei and Y. Wu, Sci. China, Ser. E: Technol. Sci., 2007, 50, 51–56.
361. M. Mulazzi, F. Reichmann, A. Becker, W. M. Klesse, P. Alippi, V. Fiorentini, A. Parisini, M. Bosi and R. Fornari, APL Mater., 2019, 7, 1–7.
362. F. Mezzadri, G. Calestani, F. Boschi, D. Delmonte, M. Bosi and R. Fornari, Inorg. Chem., 2016, 55, 12079–12084.
363. L. Li, AIP Adv., 2021, 11, 1–7.
364. S. E. Derenzo, E. Bourret-Courshesne, G. Bizarri and A. Canning, Nucl. Instruments Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip., 2016, 805, 36–40.
365. Z. Galazka, R. Schewski, K. Irmscher, W. Drozdowski, M. E. Witkowski, M. Makowski, A. J. Wojtowicz, I. M. Hanke, M. Pietsch, T. Schulz, D. Klimm, S. Ganschow, A. Dittmar, A. Fiedler, T. Schroeder and M. Bickermann, J. Alloys Compd., 2020, 818, 152842.
366. N. He, H. Tang, B. Liu, Z. Zhu, Q. Li, C. Guo, M. Gu, J. Xu, J. Liu, M. Xu, L. Chen and X. Ouyang, Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers, Detect. Assoc. Equip., 2018, 888, 9–12.
367. Y. Usui, D. Nakauchi, N. Kawano, G. Okada, N. Kawaguchi and T. Yanagida, J. Phys. Chem. Solids, 2018, 117, 36–41.
368. Y. Usui, T. Kato, N. Kawano, G. Okada, N. Kawaguchi and T. Yanagida, J. Lumin., 2018, 200, 81–86.
369. N. He, X. Ouyang, M. Xu, H. Tang, B. Liu, Z. Zhu, M. Gu, J. Xu, J. Liu and L. Chen, IEEE Trans. Nucl. Sci., 2020, 67, 400–404.
370. Z. Galazka, S. Ganschow, A. Fiedler, R. Bertram, D. Klimm, K. Irmscher, R. Schewski, M. Pietsch, M. Albrecht and M. Bickermann, J. Cryst. Growth, 2018, 486, 82–90.
371. Y. Usui, T. Oya, G. Okada, N. Kawaguchi and T. Yanagida, Optik, 2017, 143, 150–157.
372. T. Yanagida and N. Kawaguchi, Jpn. J. Appl. Phys., 2020, 59, SCCB20.
373. W. Li, Y. Peng, C. Wang, X. Zhao, Y. Zhi, H. Yan, L. Li, P. Li, H. Yang, Z. Wu and W. Tang, J. Alloys Compd., 2017, 697, 388–391.
374. Y. Usui, T. Oya, G. Okada, N. Kawaguchi and T. Yanagida, Mater. Res. Bull., 2017, 90, 266–272.
375. M. Makowski, W. Drozdowski, M. E. Witkowski, A. J. Wojtowicz, K. Irmscher, R. Schewski and Z. Galazka, Opt. Mater. Express, 2019, 9(9), 3738–3743.
376. W. Drozdowski, M. Makowski, M. E. Witkowski, A. J. Wojtowicz, R. Schewski, K. Irmscher and Z. Galazka, Opt. Mater., 2020, 105, 109856.
377. M. Choi and J. Son, Curr. Appl. Phys., 2017, 17, 713–716.
378. Y. Zhang, F. Alema, A. Mauze, O. S. Koksaldi, R. Miller, A. Osinsky and J. S. Speck, APL Mater., 2019, 7, 022506.
379. F. He, Y. Qin, Y. Wang, Z. Lin, J. Su, J. Zhang, J. Chang and Y. Hao, IEEE J. Electron Devices Soc., 2021, 9, 373–377.
380. Z. Wang, X. Chen, F. F. Ren, S. Gu and J. Ye, J. Phys. D: Appl. Phys., 2021, 54, 043002.
381. Z. Galazka, R. Uecker, D. Klimm, K. Irmscher, M. Naumann, M. Pietsch, A. Kwasniewski, R. Bertram, S. Ganschow and M. Bickermann, ECS J. Solid State Sci. Technol., 2017, 6, 3007–3011.
382. F. Zhang, M. Arita, X. Wang, Z. Chen, K. Saito, T. Tanaka, M. Nishio, T. Motooka and Q. Guo, Appl. Phys. Lett., 2016, 109, 102105.
383. M. Baldini, M. Albrecht, A. Fiedler, K. Irmscher, R. Schewski and G. Wagner, ECS J. Solid State Sci. Technol., 2017, 6, 3040–3044.
384. L. Dong, S. Zhou, L. Gong, W. Wang, L. Zhang, C. Yang, J. Yu and W. Liu, J. Mater. Chem. C, 2020, 8, 12551–12559.
385. T. Onuma, Y. Nakata, K. Sasaki, T. Masui, T. Yamaguchi, T. Honda, A. Kuramata, S. Yamakoshi and M. Higashiwaki, J. Appl. Phys., 2018, 124, 075103.
386. F. He, Y. Wang, H. Yuan, Z. Lin, J. Su, J. Zhang, J. Chang and Y. Hao, Ceram. Int., 2021, 47, 35029–35036.
387. A. Y. Polyakov, N. B. Smirnov, I. V. Shchemerov, E. B. Yakimov, J. Yang, F. Ren, G. Yang, J. Kim, A. Kuramata and S. J. Pearton, Appl. Phys. Lett., 2018, 112, 032107.
388. M. E. Ingebrigtsen, A. Y. Kuznetsov, B. G. Svensson, G. Alfieri, A. Mihaila, U. Badstübner, A. Perron, L. Vines and J. B. Varley, APL Mater., 2019, 7, 022510.
389. A. Y. Polyakov, N. B. Smirnov, I. V. Shchemerov, E. B. Yakimov, S. J. Pearton, C. Fares, J. Yang, F. Ren, J. Kim, P. B. Lagov, V. S. Stolbunov and A. Kochkova, Appl. Phys. Lett., 2018, 113, 1–6.
390. C. Zimmermann, Y. K. Frodason, A. W. Barnard, J. B. Varley, K. Irmscher, Z. Galazka, A. Karjalainen, W. E. Meyer, F. D. Auret and L. Vines, Appl. Phys. Lett., 2020, 116, 072101.
391. E. Farzana, E. Ahmadi, J. S. Speck, A. R. Arehart and S. A. Ringel, J. Appl. Phys., 2018, 123, 161410.
392. A. Y. Polyakov, I. H. Lee, N. B. Smirnov, E. B. Yakimov, I. V. Shchemerov, A. V. Chernykh, A. I. Kochkova, A. A. Vasilev, F. Ren, P. H. Carey and S. J. Pearton, Appl. Phys. Lett., 2019, 115, 1–6.
393. R. Ahrling, J. Boy, M. Handwerg, O. Chiatti, R. Mitdank, G. Wagner, Z. Galazka and S. F. Fischer, Sci. Rep., 2019, 9, 1–9.
394. R. Sun, Y. K. Ooi, A. Bhattacharyya, M. Saleh, S. Krishnamoorthy, K. G. Lynn and M. A. Scarpulla, Appl. Phys. Lett., 2020, 117, 212104.
395. E. G. Víllora, K. Shimamura, T. Ujiie and K. Aoki, Appl. Phys. Lett., 2008, 92, 9–12.
396. K. Hoshikawa, T. Kobayashi and E. Ohba, J. Cryst. Growth, 2020, 546, 125778.
397. T. Oishi, Y. Koga, K. Harada and M. Kasu, Appl. Phys. Express, 2015, 8, 031101.
398. W. Mu, Z. Jia, Y. Yin, Q. Hu, Y. Li, B. Wu, J. Zhang and X. Tao, J. Alloys Compd., 2017, 714, 453–458.
399. E. G. Víllora, Y. Morioka, T. Atou, T. Sugawara, M. Kikuchi and T. Fukuda, Phys. Status Solidi, 2002, 193, 187–195.
400. T. Harwig and J. Schoonman, Solid State Commun., 1976, 18, 1223–1225.
401. S. C. Siah, R. E. Brandt, K. Lim, L. T. Schelhas, R. Jaramillo, M. D. Heinemann, D. Chua, J. Wright, J. D. Perkins, C. U. Segre, R. G. Gordon, M. F. Toney and T. Buonassisi, Appl. Phys. Lett., 2015, 107, 252103.
402. H. Cui, H. F. Mohamed, C. Xia, Q. Sai, W. Zhou, H. Qi, J. Zhao, J. Si and X. Ji, J. Alloys Compd., 2019, 788, 925–928.
403. K. D. Leedy, K. D. Chabak, V. Vasilyev, D. C. Look, J. J. Boeckl, J. L. Brown, S. E. Tetlak, A. J. Green, N. A. Moser, A. Crespo, D. B. Thomson, R. C. Fitch, J. P. McCandless and G. H. Jessen, Appl. Phys. Lett., 2017, 111, 2–6.
404. X. H. Wang, F. B. Zhang, K. Saito, T. Tanaka, M. Nishio and Q. X. Guo, J. Phys. Chem. Solids, 2014, 75, 1201–1204.
405. L. Nagarajan, R. A. De Souza, D. Samuelis, I. Valov, A. Börger, J. Janek, K. D. Becker, P. C. Schmidt and M. Martin, Nat. Mater., 2008, 7, 391–398.
406. M. Orita, H. Ohta, M. Hirano and H. Hosono, Appl. Phys. Lett., 2000, 77, 4166–4168.
407. D. Wang, J. Li, A. Jiao, X. Zhang, X. Lu, X. Ma and Y. Hao, J. Alloys Compd., 2021, 855, 157296.
408. M. Baldini, M. Albrecht, A. Fiedler, K. Irmscher, D. Klimm, R. Schewski and G. Wagner, J. Mater. Sci., 2016, 51, 3650–3656.
409. F. Zhang, K. Saito, T. Tanaka, X. Wang and Q. Guo, AIP Adv., 2020, 10, 1–7.
410. D. Gogova, G. Wagner, M. Baldini, M. Schmidbauer, K. Irmscher, R. Schewski, Z. Galazka, M. Albrecht and R. Fornari, J. Cryst. Growth, 2014, 401, 665–669.
411. C. V. Ramana, E. J. Rubio, C. D. Barraza, A. Miranda Gallardo, S. McPeak, S. Kotru and J. T. Grant, J. Appl. Phys., 2014, 115, 043508.
412. J. Frank, M. Fleischer and H. Meixner, Sens. Actuators, B, 1996, 34, 373–377.
413. Y. Shang, K. Tang, Z. Chen, Z. Zhang, J. Deng, Y. Hu, K. Gu, M. Cao, L. Wang and J. Huang, Mater. Sci. Semicond. Process., 2021, 134, 106040.
414. W. Mi, J. Ma, Z. Li, C. Luan and H. Xiao, J. Mater. Sci.: Mater. Electron., 2015, 26, 7889–7894.
415. X. Feng, Z. Li, W. Mi, Y. Luo and J. Ma, Mater. Sci. Semicond. Process., 2015, 34, 52–57.
416. N. Moser, J. McCandless, A. Crespo, K. Leedy, A. Green, A. Neal, S. Mou, E. Ahmadi, J. Speck, K. Chabak, N. Peixoto and G. Jessen, IEEE Electron Device Lett., 2017, 38, 775–778.
417. M. H. Wong, K. Sasaki, A. Kuramata, S. Yamakoshi and M. Higashiwaki, Jpn. J. Appl. Phys., 2016, 55, 1202B9.

---