Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Na2.4Al0.4Mn2.6O7 anionic redox cathode material for sodium-ion batteries – a combined experimental and theoretical approach to elucidate its charge storage mechanism†
Cindy
Soares‡
a,
Begoña
Silván‡
 ac,
Yong-Seok
Choi‡
ac,
Yong-Seok
Choi‡
 bcd,
Veronica
Celorrio
bcd,
Veronica
Celorrio
 e,
Valerie R.
Seymour
e,
Valerie R.
Seymour
 ac,
Giannantonio
Cibin
e,
John M.
Griffin
ac,
Giannantonio
Cibin
e,
John M.
Griffin
 ac,
David O.
Scanlon
ac,
David O.
Scanlon
 bcde and
Nuria
Tapia-Ruiz
bcde and
Nuria
Tapia-Ruiz
 *ac
*ac
aDepartment of Chemistry, Lancaster University, Lancaster, LA1 4YB, UK. E-mail: n.tapiaruiz@lancaster.ac.uk
bDepartment of Chemistry, University College London, 20 Gordon Street, London WC1H 0AJ, UK
cThe Faraday Institution, Quad One, Harwell Science and Innovation Campus, Didcot OX11 0RA, UK
dThomas Young Centre, University College London, Gower Street, London WC1E 6BT, UK
eDiamond Light Source Ltd, Diamond House, Harwell Science and Innovation Campus, Didcot OX11 0DE, UK
First published on 16th December 2021
Abstract
Here we report the synthesis via ceramic methods of the high-performance Mn-rich Na2.4Al0.4Mn2.6O7 oxygen-redox cathode material for Na-ion batteries, which we use as a testbed material to study the effects of Al substitution and subsequent Na excess in the high-capacity, anionic redox-based cathode material, Na2Mn3O7. The material shows a stable electrochemical performance, with a specific capacity of 215 mA h g−1 in the 1.5–4.7 V voltage range at C/20 and a capacity retention of 90% after 40 cycles. Using a combination of electrochemical and structural analysis together with hybrid density functional theory calculations we explain the behaviour of this material with changes in Mn/anionic redox reactions and associated O2 release reactions occurring during electrochemical cycling (Na+ ion insertion/extraction), and compare these findings to Na2Mn3O7. We expect that these results will advance understanding of the effect of dopants in Mn-rich cathode materials with oxygen redox activity to pave their way towards high-performance sodium-ion batteries.
Introduction
Sodium-ion batteries (SIBs) are a promising candidate for next-generation batteries, as sodium is an abundant element with an easy-access source, which translates into a low-cost and sustainable alternative energy storage technology. Moreover, the chemical similarities of Li and Na coupled with the already well-established knowledge in lithium-ion battery (LIB) technology allow for rapid implementation of SIBs in applications such as the grid or low-cost transportation.1,2 Among the cathode materials researched in the field of SIBs, layered Na–Mn–O ternary compounds have been particularly relevant due to their high capacity, abundance, non-toxicity and low cost. The NaxMnO2 (x > 0.5) composition has been the most studied, showing a maximum theoretical capacity of 244 mA h g−1 based on the Mn3+/4+ redox-active couple. Nonetheless, these materials generally present low capacity retention, e.g., β-NaMnO2 shows 53% capacity retention at C/20 after 100 cycles, with an initial capacity of 175 mA h g−1 (when cycled between 4.2 V and 2.0 V);3 and α-NaMnO2 shows 70% capacity retention at C/30 after 20 cycles, with an initial capacity of 185 mA h g−1 (when cycled between 3.8 V and 2.0 V).4 The poor cycling stability of Mn-based compounds is generally attributed to structural instabilities associated with the Jahn–Teller (JT) effect of the Mn3+ ions formed during cycling, particularly under a low working voltage range (1.5–2.1 V).5Na2Mn3O7 (or Na0.57Mn0.86[ ]0.14O2) (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group) has been extensively studied in the past years due to the large anionic redox contribution (75 mA h g−1 above 4.0 V vs. Na+/Na) to the overall charge stored in the material (theoretical capacity = 155 mA h g−1), which results in high energy densities.6,7 This large anionic redox capacity arises from non-bonding 2p orbitals of the oxygen atoms neighbouring the unoccupied Mn site in the transition metal (TM) layers.8–11 Despite its large anionic redox capacity, Na2Mn3O7 does not fully use its redox-active oxygen ions. Earlier studies on Na2Mn3O7 revealed that three non-bonding oxygen atoms per formula unit are redox-active, where theoretically, a maximum of only two of them can be oxidized/reduced during cycling.6,8 This shows that, once all non-bonding oxygen atoms of Na2Mn3O7 become active, its anionic redox capacity can be increased by ≈50%. One effective way to further use the redox-active oxygen atoms is by aliovalent substitution, using elements with oxidation states lower than Mn4+, such as Mg2+, B3+, Al3+, etc. Thus, to satisfy charge neutrality, the aliovalent-doped Na2+αMyMn3−yO7 (M = elements with oxidation states lower than 4+) should have a greater number of Na+ ions or, equivalently, higher anionic redox capacity. Another approach to enhance anionic redox reactions is by substitution of TMs with more electronegative elements.12,13 This concept stems from the fact that highly electronegative dopants can weaken the ionicity of Mn–O bonds and destabilize the energy of non-bonding O 2p bands, enabling anionic redox reactions.
space group) has been extensively studied in the past years due to the large anionic redox contribution (75 mA h g−1 above 4.0 V vs. Na+/Na) to the overall charge stored in the material (theoretical capacity = 155 mA h g−1), which results in high energy densities.6,7 This large anionic redox capacity arises from non-bonding 2p orbitals of the oxygen atoms neighbouring the unoccupied Mn site in the transition metal (TM) layers.8–11 Despite its large anionic redox capacity, Na2Mn3O7 does not fully use its redox-active oxygen ions. Earlier studies on Na2Mn3O7 revealed that three non-bonding oxygen atoms per formula unit are redox-active, where theoretically, a maximum of only two of them can be oxidized/reduced during cycling.6,8 This shows that, once all non-bonding oxygen atoms of Na2Mn3O7 become active, its anionic redox capacity can be increased by ≈50%. One effective way to further use the redox-active oxygen atoms is by aliovalent substitution, using elements with oxidation states lower than Mn4+, such as Mg2+, B3+, Al3+, etc. Thus, to satisfy charge neutrality, the aliovalent-doped Na2+αMyMn3−yO7 (M = elements with oxidation states lower than 4+) should have a greater number of Na+ ions or, equivalently, higher anionic redox capacity. Another approach to enhance anionic redox reactions is by substitution of TMs with more electronegative elements.12,13 This concept stems from the fact that highly electronegative dopants can weaken the ionicity of Mn–O bonds and destabilize the energy of non-bonding O 2p bands, enabling anionic redox reactions.
In this regard, Al3+ ions, with low oxidation state and high electronegativity compared to Mn4+ ions, are ideal substituents to improve anionic redox reactions occurring in Na2Mn3O7. Al3+ ions have been shown to improve ionic diffusion kinetics in compounds by widening the d spacing between TM layers.14–17 Despite the promising aspects of Al3+ ion substitution, this strategy has been mostly employed in LiTMO2 and NaTMO2, where cationic redox reactions prevail over anionic redox reactions.18–21 This causes a lack of understanding of the effect of Al3+ ion substitution on the electrochemical performance of cathode materials with anionic redox reactions. In this regard, partial substitution of Mn ions with Al3+ ions may be a prevalent strategy to improve the electrochemical properties of these materials, by bestowing multiple characteristics, such as increasing Na+ ion mobility and long-cycling stability, and unlocking anionic redox activity to increase energy density.22–25
In this work, we aim to investigate the role of Al substitution in the charge storage mechanism of the Na2Mn3O7 cathode. To this end, using Na2.4Al0.4Mn2.6O7 as a testbed material, we study the effect of Al3+ ion substitution on structural changes, such as the interlayer spacing and Na+ ion insertion sequences. Using electrochemical, structural and hybrid density functional theory (DFT) calculations, we analyse the changes in Mn/oxygen redox reactions and associated O2 release during battery cycling. Based on these findings, we discuss the role of Al on the electrochemical behaviour of Mn-based cathodes and its potential application for developing high-performance cathodes for SIBs.
Experimental section
Material synthesis and structure characterisation
Na2.4Al0.4Mn2.6O7 was synthesised by a solid-state method using stoichiometric amounts of Na2CO3 (99%, Sigma Aldrich), Al2(CO3)3 (99%, Alfa Aesar) and MnO2 (99%, Alfa Aesar). The mixture was ball-milled at 350 rpm for 4 h using a planetary ball-mill machine (Tob Energy). Na2Mn3O7 was synthesised by mixing stoichiometric amounts of NaNO3 (99%, Alfa Aesar) and MnCO3 (99.99%, Sigma Aldrich) using a mortar and a pestle.Powders were pressed into 13 mm pellets at 5 tones per cm2 and calcined under an oxygen flow at 700 °C for 12 h followed by 1000 °C for 6 h, with an intermediate ball-milling step at 400 rpm for 1 h for the Na2.4Al0.4Mn2.6O7 synthesis, and under an oxygen flow at 600 °C for 4 h for the Na2Mn3O7 synthesis. The heating and cooling rate used during the annealing process was 10 °C min−1.
Powder X-ray diffraction (PXRD) data for Na2.4Al0.4Mn2.6O7 and Na2Mn3O7 pristine materials, and cast Na2.4Al0.4Mn2.6O7 electrodes at different states of charge were collected at ambient temperature from 10° to 90° 2θ degrees in a θ/2θ Bragg–Brentano geometry using an X-ray diffractometer (Miniflex, Rigaku) with a Cu X-ray source (0.6 kW) (λ Kα1 = 1.5406 Å, λ Kα2 = 1.5444 Å) equipped with a D/teX-ULTRA 250 high-speed position sensitive detector system. The X-ray diffractometer was enclosed in an N2-filled MBraun glovebox. For the ex situ measurements, electrodes were galvanostatically cycled at 10 mA g−1 to selected voltages, extracted from the coin cells, rinsed three times with diethyl carbonate (DEC), and dried at 80 °C under vacuum in the antechamber of an argon-filled glovebox (MBraun) ([H2O] and [O2] ≤ 0.1 ppm). To disregard any preferred orientation in the as-prepared Na2.4Al0.4Mn2.6O7 material, XRD data were also acquired in transmission mode, using a spinning borosilicate capillary (0.5 mm diameter) placed in a 4-circle Kappa precision goniometer in an Agilent Supernova diffractometer with a Mo X-ray source and an Atlas S2 135 mm CCD area detector. XRD data were fit with the Le Bail method, using the FullProf Suite software.26 VESTA 3.5.7 software was used to visualise the crystal structures.27
Sample microstructure was analysed using field emission scanning electron microscopy (FE-SEM) with a JEOL JSM-7800F operating at 5.0 kV. Elemental analysis was performed at 10 kV using X-ray Energy Dispersive Spectrometer (EDS) (X-Max50, large area 50 mm2 Silicon Drift Detector (SDD) from Oxford Instruments). Sample preparation consisted of uniformly coating the samples onto carbon tabs (G3348N, Agar Scientific).
X-ray fluorescence (XRF) spectrometry was carried out using an EDXRF Shimadzu EDX 8000 spectrometer with an SSD detector and an Rh X-ray source. The sample was pelletized and manipulated under an argon atmosphere without air exposure. Quantification of elemental Na was not possible due to the overlapping signal with Rh escape peaks originating from the X-ray source.
Electrochemical characterisation
The electrochemical properties of Na2.4Al0.4Mn2.6O7 and Na2Mn3O7 were assessed in sodium half-cells using stainless steel 2032-type coin-cells (Tob New Energy). Electrode preparation and coin-cell assembly were carried out in an argon-filled glovebox (MBraun) ([H2O] and [O2] ≤ 0.1 ppm). Electrode slurries were first prepared by mixing a homogenous powdered mixture (500 mg) consisting of 80 wt% active material (Na2.4Al0.4Mn2.6O7), 10 wt% carbon black (>99.0%, Alfa Aesar) and 10 wt% polyvinylidene fluoride (PVDF) (>99.0%, Alfa Aesar) with a mortar and pestle. Then, the powdered mixture was dissolved in ca. 1.2 mL N-methyl-2-pyrrolidone (NMP) (anhydrous, >99.0%, Alfa Aesar) and the homogeneous slurry mixture was cast onto an aluminium foil using a doctor blade and then dried under vacuum at 80 °C for 12 h in the glovebox antechamber. Once dried, the 12 mm diameter electrodes were cut and pressed under ≈174 MPa, with a typical active material mass loading of 2.4–3.0 mg cm−2. Sodium metal disks (15 mm in diameter) (Alfa Aesar Merck) were used as reference electrodes, and 1 M NaPF6 (99%, Alfa Aesar) in the anhydrous organic solution of ethylene carbonate/diethylene carbonate (EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC 1
DEC 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 w/w%, Gotion) as electrolyte. The electrolyte was dried under molecular sieves for a week before use.
1 w/w%, Gotion) as electrolyte. The electrolyte was dried under molecular sieves for a week before use.
Galvanostatic measurements were carried out on a battery tester (Neware) in the voltage range of 1.5–4.7 V vs. Na+/Na at selected current rates (C/20 to 5/C, 1C = 160 and 155 mA g−1 for Na2.4Al0.4Mn2.6O7 and Na2Mn3O7, respectively).
Cyclic voltammetry (CV) experiments were conducted using an IviumStat potentiostat (Alvatek), at a scan rate of 0.1 mV s−1 in the voltage range of 1.5–4.7 V vs. Na+/Na.
Galvanostatic intermittent titration technique (GITT) measurements during charge/discharge were carried out by applying a pulse of ±1.7 µA for 1 h followed by an open circuit relaxation of 2 h. The procedure was carried out in the voltage range of 1.5–4.7 V vs. Na+/Na. The diffusion coefficient for Na2.4Al0.4Mn2.6O7, D, was calculated using eqn (S1),† where we assumed a constant molar mass (320.81 g mol−1) and cell volume (169.81 cm3 mol−1) during the cycling process. The surface area was calculated using two different approaches: (1) using the average particle size value obtained from SEM images (0.77 µm diameter particles), whereby we assumed that particles were spherical and had a smooth surface and an intimate contact with the electrolyte; and (2) considering a flat surface contact area (electrode area).
Electrochemical impedance spectroscopy (EIS) studies were carried out on Na2.4Al0.4Mn2.6O2 and Na2Mn3O7 with two different electrochemical cell set-ups. EIS data were collected in the 100 kHz to 10 mHz frequency range with an amplitude of 10 mV and after a 1 h voltage pulse using a Biologic VMP-300 potentiostat and an Ivium Octostat potentiostat. EIS data on the first cycle were collected using a three-electrode cell (EL-cell), where the active electrode materials were cycled using metallic Na disks as counter and reference electrodes. The referece is a pre-assembled and commercial Na ring (El-cell) enclosed in the cell around the glass fibre separator. On the other hand, EIS data on the 100th cycle were collected using two-electrode coin cells.
All the electrochemical testing was conducted at room temperature.
Nuclear magnetic resonance (NMR)
23Na magic-angle spinning (MAS) NMR spectra of pristine Na2.4Mn2.6Al0.4O7 and Na2Mn3O7 materials were obtained at 9.4 T on a Bruker Avance III 400 MHz spectrometer working at a Larmor frequency of 105.8 MHz. Powdered samples were packed into 2.5 mm rotors, in an argon-filled MBraun glovebox ([H2O] and [O2] ≤ 0.1 ppm) and kept static or spun up to 30 kHz. 23Na MAS NMR spectra were acquired using a single pulse or Hahn echo pulse sequence, with a recycle delay of 0.5 s. Spectra referencing was done using a secondary solid reference of NaCl (δiso = 7.2 ppm). Due to the nature of the samples and the experimental parameters used, the relative intensities may not match contributions in the materials and therefore spectra are not quantitative. Additionally, the distorted baseline of the single pulse experiments can affect the observed position of peaks compared to the flatter baseline of the Hahn echo experiments. Ex situ23Na MAS NMR spectra were obtained at 9.4 T, using a Hahn echo pulse sequence and 30 kHz MAS. 1 kHz line broadening was used in spectra processing. Ex situ samples were run in powder form in coin cells (active material![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) carbon black weight ratio of 80
carbon black weight ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20) using around 8 mg of active material per cell. Na metal was used as a counter and reference electrode and 1 M NaPF6 in EC
20) using around 8 mg of active material per cell. Na metal was used as a counter and reference electrode and 1 M NaPF6 in EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DEC (1
DEC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 vol%) as the electrolyte. After cycling the cells to a defined voltage, the cells were opened, and powder was recovered. Powders were washed three times with DEC inside an argon-filled glovebox (MBraun), followed by the removal of excess solvent and drying under vacuum at room temperature in the glovebox antechamber before the NMR measurement.
1 vol%) as the electrolyte. After cycling the cells to a defined voltage, the cells were opened, and powder was recovered. Powders were washed three times with DEC inside an argon-filled glovebox (MBraun), followed by the removal of excess solvent and drying under vacuum at room temperature in the glovebox antechamber before the NMR measurement.
Ex situ synchrotron X-ray absorption near-edge spectroscopy (XANES)
X-ray absorption near edge structure (XANES) data were collected at the B18 beamline at Diamond Light Source (Harwell, UK). For the measurement, cast electrodes were cycled at different states of charge, and then, extracted from the coin cells and rinsed three times with DEC in an argon-filled glovebox (MBraun) ([H2O] and [O2] ≤ 0.1 ppm). After this, electrodes were dried at 80 °C under vacuum in the glovebox antechamber and sealed in individual aluminium laminated pouches under vacuum to minimise air exposure during data acquisition. Measurements were performed at the Mn K-edge energies above and below the absorption edges (ca. 6540 eV) and electrode data were collected in fluorescence mode, using a 36-element Ge detector. Mn metal foil was used as an internal standard and reference data for MnO, Mn3O2 and MnO2 powders were collected on transmission mode using gas-filled ionisation chambers to measure both incident and transmitted intensities. Three repetitions of each sample were measured, totalling a 15 min measurement. Athena software in the Demeter package was used to perform energy calibration, background subtraction and normalization.28,29 Linear combination fitting (LCF) was performed using the Athena software within an energy range of −20 eV below to +30 eV above the edge. Each sample spectra were fitted for every combination of the standard spectra. The combination of standards that resulted in the best fit (smallest R-factor and reduced χ2) was chosen as the most likely representation of the sample.Ab initio calculations
All the calculations performed in this work employed DFT as implemented in the Vienna Ab initio Simulation Package code.30,31 Interactions between core and valence electrons were described using the projector augmented wave (PAW) method.32 Na (2p63s1), Mn (3p63d54s2), Al (3s23p1), and O (2s22p4) electron configurations were treated as the valence electrons. Convergence to plane wave energy was checked, with a cut-off of 500 eV found to be sufficient to converge the total energy to within 0.01 eV atom−1. Brillouin zones for all compounds were sampled such that the k-points were converged with an accuracy of the total energy in 0.001 eV per atom, which corresponds to k-grids of 3 × 3 × 3 and 2 × 2 × 2 for primitive (24 atoms) and supercell (120 atoms) structures.To analyse the Na+ ion insertion sequences and theoretical voltages of Na2Mn3O7 and Na2.4Al0.4Mn2.6O7 upon cycling, we predicted the optimized geometries of partially and fully sodiated NaxMn3O7 and NaxAl0.4Mn2.6O7 using the PBEsol+U method.33 This method provides computationally cost-effective corrections on highly correlated Mn d orbitals, which allows rapid modeling of materials with TMs. The detailed procedures are described in two sections of the ESI,†i.e., Computational details for the construction of model structures (Fig. S1 and S2†) and Computational details for the theoretical voltage calculations (Fig. S3†).
While the PBEsol+U method has been shown to provide an accurate geometry for a wide variety of solid systems with a relatively low computational cost, it can result in quantitatively incorrect descriptions of electronic structures, especially when predicting the defect state of highly localized electrons.34,35 Therefore, to better simulate O loss behaviour during desodiation of Na2Mn3O7 and Na2.4Al0.4Mn2.6O7, we used the screened hybrid functional (HSE06),36 with 25% of exact non-local Fock exchange added to the PBE37 functional, that consistently produces more accurate electronic structures than standard DFT approaches.38 The systems before O2 gas release were first modelled by selecting four different structures of Na2Mn3O7, Na2.4Al0.4Mn2.6O7, NaMn3O7 and Na1.4Al0.4Mn2.6O7 from PBEsol+U optimized supercells, and relaxing their structures again with HSE06 functional. The desodiation and associated O loss were then simulated by creating Na and O vacancies in each supercell, followed by the structural relaxations of defective structures. Calculations for defective structures were also done with HSE06 functional to make total energies consistent with host supercells. All Na and O sites of host supercells were classified based on their local bonding environment (Tables 1 and 2). The energy required for desodiation, Ef(D), was estimated by calculating defect formation energies for Na vacancies for individual Na sites according to:
| Ef(D) = Etot(D) − Etot(bulk) + nNaEtot(Na) | (1) |
To calculate the minimum energy path and corresponding activation barrier for O2 dimer formation after desodiation, climbing image nudged elastic band calculations were carried out for partially desodiated NaMn3O7 using HSE06 functional. For this purpose, we first optimized the geometry of NaMn3O7 before and after O2 dimer formation. Using the optimized geometries as initial and final states, five intermediate images were then generated using linear interpolation. Lastly, the minimum energy path was searched by minimizing the spring forces parallel to the transition pathways and real forces projected perpendicular to the strings. For all HSE06 calculations, the Brillouin zone was sampled using only the Γ point.
Results and discussion
Crystal structure and microstructure
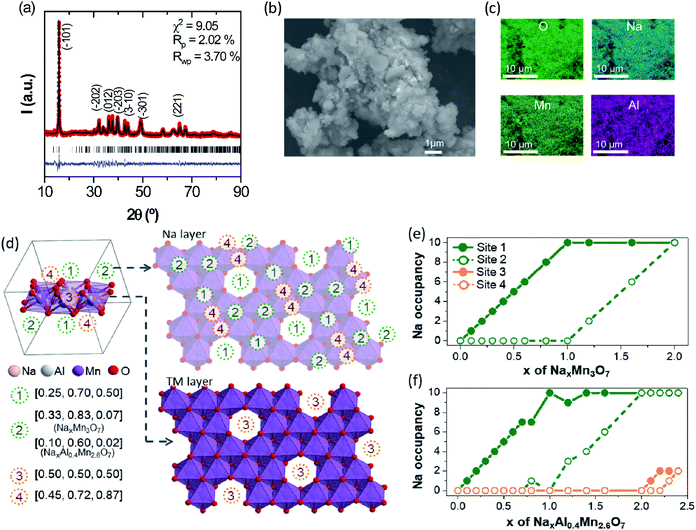
The TM-deficient layered compound Na2.4Mn2.6Al0.4O7 (Na0.68Mn0.74Al0.11[ ]0.15O2 in conventional NaxMO2 notation) was synthesised by solid-state reaction methods, as detailed in the Experimental section. Powder X-ray diffraction (XRD) data of as-prepared Na2.4Mn2.6Al0.4O7 show a sharp and well-defined (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01) reflection at 2θ = 15.9° and broader and less intense reflections at higher 2θ values (Fig. 1a). The latter implies a high level of long-range layer stacking disorder combined with poor crystallinity, hindering an accurate structural refinement using the Rietveld method. Neutron and X-ray diffraction studies on the Na2Mn3O7 parent structure have shown that the [Mn3O7]2− layers are not perfectly aligned throughout the structure, losing the stacking sequence across the c direction.39 XRD data were fit with the Le Bail method, using published crystallographic data on Na2Mn3O7.6 As a result, XRD data were indexed in the triclinic P
01) reflection at 2θ = 15.9° and broader and less intense reflections at higher 2θ values (Fig. 1a). The latter implies a high level of long-range layer stacking disorder combined with poor crystallinity, hindering an accurate structural refinement using the Rietveld method. Neutron and X-ray diffraction studies on the Na2Mn3O7 parent structure have shown that the [Mn3O7]2− layers are not perfectly aligned throughout the structure, losing the stacking sequence across the c direction.39 XRD data were fit with the Le Bail method, using published crystallographic data on Na2Mn3O7.6 As a result, XRD data were indexed in the triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group, with cell parameters a = 6.587(2) Å, b = 6.984(2) Å and c = 7.540(3) Å, and α = 106.07(2)°, β = 107.32(2)°, and γ = 110.39(3)°. Rwp and Rp agreement factors are 3.70 and 2.02%, respectively, indicating a good quality fit. No secondary phases were observed in the X-ray diffractogram, suggesting high sample purity. Na2.4Mn2.6Al0.4O7 shows a slightly larger cell volume of 280.94(9) Å3 compared to experimental and literature values obtained for Na2Mn3O7 (Fig. S4†).6,40–42 The presence of Al3+ ions does not affect the volume of the crystallographic unit cell since both Al3+ and Mn4+ ions have a very similar ionic radius when they are octahedrally coordinated with oxygen (≈0.53 Å).43 Subsequently, we attribute these differences to the extra Na+ ions per formula unit (0.4 Na+) in Na2.4Mn2.6Al0.4O7. These additional Na+ ions are required to charge-balance the material, due to the aliovalent substitution of Mn4+ ions by Al3+ ions. For comparison purposes, only a 0.3% increase in volume per formula unit was observed in a similar layered material, LiNi0.7Co0.3O2, when substituting Co3+ ions (≈0.54 Å) with 10% Al3+ ions.20 XRD data were also collected in a spinning capillary to discard any preferred orientation in the sample attributed to the flat sample holder used (Fig. S5†). Similar relative X-ray diffraction peak intensities were observed in both datasets, suggesting limited preferred orientation. The FE-SEM image of pristine Na2.4Mn2.6Al0.4O7 shows a mixture of lamellar and irregular primary particles with an average diameter size of 0.77 µm that aggregate into larger irregular-shaped secondary particles with a broad size distribution between 4.2 and 18.1 µm (average of 9.1 µm) (Fig. 1b). EDS elemental mapping on selected particles shows a homogeneous distribution of sodium, aluminium, manganese, and oxygen atoms (Fig. 1c and S6†), which confirms the presence of a single-phase product, as observed in the X-ray diffraction data (Fig. 1a). A Mn
space group, with cell parameters a = 6.587(2) Å, b = 6.984(2) Å and c = 7.540(3) Å, and α = 106.07(2)°, β = 107.32(2)°, and γ = 110.39(3)°. Rwp and Rp agreement factors are 3.70 and 2.02%, respectively, indicating a good quality fit. No secondary phases were observed in the X-ray diffractogram, suggesting high sample purity. Na2.4Mn2.6Al0.4O7 shows a slightly larger cell volume of 280.94(9) Å3 compared to experimental and literature values obtained for Na2Mn3O7 (Fig. S4†).6,40–42 The presence of Al3+ ions does not affect the volume of the crystallographic unit cell since both Al3+ and Mn4+ ions have a very similar ionic radius when they are octahedrally coordinated with oxygen (≈0.53 Å).43 Subsequently, we attribute these differences to the extra Na+ ions per formula unit (0.4 Na+) in Na2.4Mn2.6Al0.4O7. These additional Na+ ions are required to charge-balance the material, due to the aliovalent substitution of Mn4+ ions by Al3+ ions. For comparison purposes, only a 0.3% increase in volume per formula unit was observed in a similar layered material, LiNi0.7Co0.3O2, when substituting Co3+ ions (≈0.54 Å) with 10% Al3+ ions.20 XRD data were also collected in a spinning capillary to discard any preferred orientation in the sample attributed to the flat sample holder used (Fig. S5†). Similar relative X-ray diffraction peak intensities were observed in both datasets, suggesting limited preferred orientation. The FE-SEM image of pristine Na2.4Mn2.6Al0.4O7 shows a mixture of lamellar and irregular primary particles with an average diameter size of 0.77 µm that aggregate into larger irregular-shaped secondary particles with a broad size distribution between 4.2 and 18.1 µm (average of 9.1 µm) (Fig. 1b). EDS elemental mapping on selected particles shows a homogeneous distribution of sodium, aluminium, manganese, and oxygen atoms (Fig. 1c and S6†), which confirms the presence of a single-phase product, as observed in the X-ray diffraction data (Fig. 1a). A Mn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio of 2.58
Al ratio of 2.58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.42 was determined from XRF spectrometry in the sample, which is close to the expected nominal stoichiometry.
0.42 was determined from XRF spectrometry in the sample, which is close to the expected nominal stoichiometry.
23Na solid-state NMR spectra were obtained to examine local Na environments of Na2.4Al0.4Mn2.6O7 and Na2Mn3O7, for comparison. 23Na MAS NMR spectra for Na–Mn–M–O materials (where M = e.g., Mg and Al) typically show peaks that can be assigned to details such as layering arrangements, defects, and Mn oxidation states.3,6,4423Na MAS NMR spectra of Na2.4Al0.4Mn2.6O7 and Na2Mn3O7 are shown in Fig. S7.† The spectrum for Na2Mn3O7 (Fig. S7a†) shows an isotropic peak at ∼1500 ppm. This is consistent with a large Fermi contact interaction that is expected for Na within a predominately Mn4+ setting, as expected for this material.3,44 Two sharp peaks close to 0 ppm surrounded by a spinning sideband manifold are also observed. Resonances close to 0 ppm suggest the presence of Na environments within a diamagnetic impurity phase.3 Although no secondary phases were observed in the XRD data, one explanation could be a low-level amorphous phase. The 23Na MAS NMR spectrum for Na2.4Al0.4Mn2.6O7 (Fig. S7b†) shows a wide spectral envelope, consisting of broadened intensity centred around 1000 ppm, and spinning sideband manifolds centred around 500 and 0 ppm, the latter again showing the presence of a diamagnetic impurity. Comparison of spectra recorded at variable MAS rate (Fig. S8†) shows that the broad sideband manifold has isotropic peaks at 730 ppm, 500 ppm and 330 ppm. Comparison of both static NMR spectra (Fig. S9†) confirms the lower shifts for Na2.4Al0.4Mn2.6O7 and the presence of two main groups at ∼1000 and ∼500 ppm. The lower shifts observed for Na2.4Al0.4Mn2.6O7 indicate a weaker Fermi contact interaction and the isotropic peaks at 500 and 330 ppm are consistent with the shift range for Na+ ions within a local Mn3+ setting. In summary, the comparison of the 23Na spectra for both materials shows the extra local environments for Na+ ions and lower shifts corresponding to Mn3+ upon Al3+ ion substitution, where the former and latter results corroborate our DFT data (Fig. 1e, f and 4) and XANES data (Fig. S10†), respectively. However, the spectral broadening prevents more detailed analysis.
To gain further insight into the crystal structure of Na2.4Mn2.6Al0.4O7, DFT calculations were used to determine the atomic positions of additional Na+ ions within the structure, assuming a disordered distribution of Al3+ and Mn4+ ions within the 2i sites (0.07, 0.07, 0.22) in the vacancy-ordered TM layer.8,42 The insertion sequences of Na2.4Al0.4Mn2.6O7 upon discharge were then predicted by modelling partially desodiated NaxAl0.4Mn2.6O7 (see Computational details for the construction of model structures, Fig. S1 and S2 in ESI†). Fig. 1d displays the symmetrically inequivalent Na sites predicted from Na2.4Al0.4Mn2.6O7, represented in the unit cell and supercell with ten formula units. In the supercell, four different Na sites were observed: three different 2i sites in the Na layer (Na1 (0.25, 0.70 and 0.50), Na2 (0.10, 0.6, 0.02) and Na4 (0.45, 0.72 and 0.87)), which may accommodate up to ten Na+ ions per site; and one 1 h site in the TM layer, Na3 (0.5, 0.5, 0.5), which may uptake five Na+ ions. These sites are identical to those observed in Na2Mn3O7,6,39 except for the Na2 site which is found in a slightly different position i.e., Na2 (0.33, 0.83, 0.07) due to excess Na in sites Na3 and Na4, which may repel some pre-existing Na+ ions in the Na2 site.
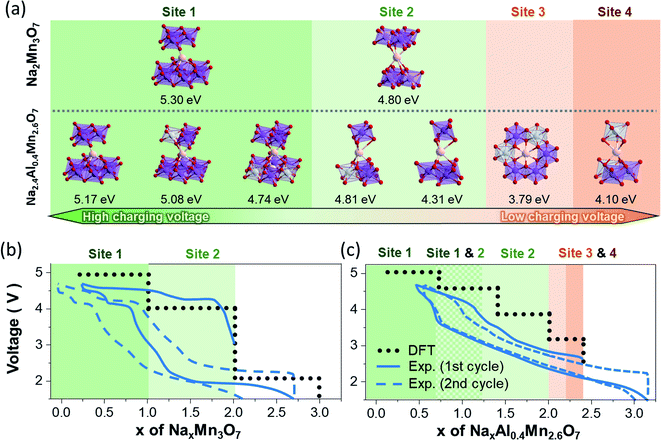
Further computational studies show that Na1 and Na2 sites of NaxAl0.4Mn2.6O7 are occupied sequentially until x = 2, with a slight difference in Na active sites near x = 1 compared to NaxMn3O7 (Fig. 1e and f). Further Na+ ion insertion occurs into the vacancy sites in the TM layer (Na3 site) until Na content reaches x = 2.2. Na+ ion insertion into vacancies in the TM layer may increase the TM–Na repulsion within layers and Na–Na repulsion between adjacent layers, increasing the cell volume, as observed in the XRD data (Fig. 1a). Last, Na+ ion insertion occurs into site Na4 up to x = 2.4. The presence of Na in sites Na3 and Na4 causes slight displacements of Na sites such that the Td (site Na1) and Oh (site Na2) sites become trigonal prismatic (Table 1). The structure of Na2.4Al0.4Mn2.6O7, with Na+ ions (ca. 0.2 Na) located in the TM layer resembles that of other cathode materials with demonstrated oxygen redox activity such as Li-rich layered oxides45–47 and other Na layered compounds.48,49
| Na site | Na2Mn3O7 | Na2.4Al0.4Mn2.6O7 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 1′ | 1″ | 1‴ | 2′ | 2″ | 3 | 4 | |
| Neighbouring structures | 9 MnO6 octahedra | 6 MnO6 octahedra | 9 MnO6 octahedra | 7 MnO6 and 2 AlO6 octahedra | 8 MnO6 and AlO6 octahedra | 4 MnO6 octahedra | 3 MnO6 and AlO6 octahedra | 4 MnO6 and 2 AlO6 octahedra | 2 MnO6 and 2 AlO6 octahedra |
| Coordination | Tetrahedral | Octahedral | Prismatic | Prismatic | Prismatic | Prismatic | Prismatic | Octahedral | Prismatic |
| Vacancy formation energy (eV) | 5.30 | 4.80 | 5.17 | 4.74 | 5.08 | 4.31 | 4.81 | 3.79 | 4.10 |
Charge carrier pathways and structural changes
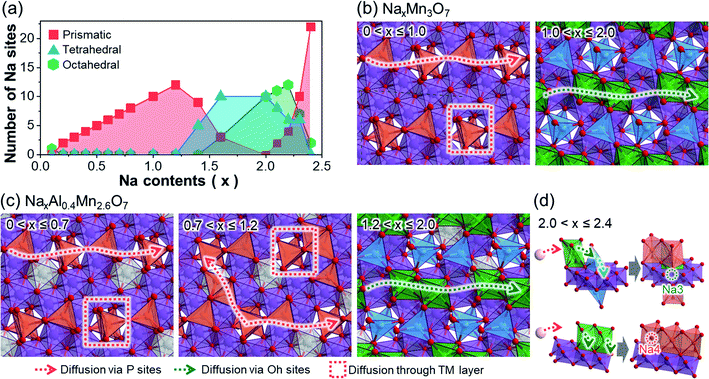
To provide a better insight into the changes in diffusion pathways after Al3+ ion substitution, we represented the potential Na+ ion diffusion pathways of both NaxMn3O7 and NaxAl0.4Mn2.6O7. This was done by classifying the active Na sites in terms of their shape and displaying them on the TM layer (Fig. 2). In NaxMn3O7, active Na sites at low sodiation levels (0 < x ≤ 1.0) are characterized by prismatic Na1 sites above unoccupied Mn sites (Fig. 2a and b). Based on the distribution of active Na sites, two diffusion pathways can be suggested: in-plane 1D diffusion along with the prismatic Na1 sites, and interplanar diffusion through unoccupied Mn sites. As Na+ ions continue to intercalate into NaxMn3O7 (1.0 < x ≤ 2.0), repulsion between Na+ ions increases and pushes Na1 sites toward unoccupied Mn sites, changing their coordination to tetrahedral. The so-formed tetrahedral Na1 sites are likely to be fixed under x ≥ 1.0 (Fig. 1e) and block the diffusion pathways, which slows down the diffusion kinetics. Na+ ion diffusion in highly sodiated NaxMn3O7, therefore, tends to follow 1D diffusion pathways through octahedral Na2 sites, which is expected to be more sluggish than prismatic–prismatic Na+ ion diffusion at low sodiation content (0 < x ≤ 1.0).50In the case of NaxAl0.4Mn2.6O7, Na+ ion diffusion at high voltages (0 < x ≤ 0.7) follows two diffusion pathways, similar to NaxMn3O7 under 0 < x ≤ 1.0 (Fig. 2c). However, with an additional supply of Na+ ions (0.7 < x ≤ 1.2), both prismatic Na1 and Na2 sites become active, unlike in NaxMn3O7 (Fig. 1f). This is speculated to be due to the higher electronegativity of Al compared to Mn, which destabilizes O 2p orbitals of Al–O bonds and, in turn, makes Na+ ions stable on site 2 above AlO6 octahedra. These active Na2 sites bridge 1D diffusion pathways between Na1 sites and allow a broader range of diffusion along the in-planar direction, resulting in enhanced rate performance of NaxAl0.4Mn2.6O7. Under highly sodiated conditions (1.2 < x ≤ 2.0), similar to NaxMn3O7, Na1 sites are fixed as tetrahedral sites near unoccupied Mn sites, causing Na+ ion diffusion to occur via octahedral Na2 sites. Once all Na1 and Na2 sites are occupied, excess Na+ ions intercalate into the unoccupied Mn site (i.e., Na3) and nearby Na2 site (i.e., Na4) (Fig. 2d). This process is speculated to occur with the cooperative motion of pre-existing Na1 or Na2 as most free spaces are already occupied by Na1 and Na2.
The above discussion suggests that Na+ ion diffusion pathways are widened due to the high electronegativity of Al3+ ions. Moreover, subsequent structural analysis on the Al-substituted Na2Mn3O7 cathode revealed that Al shortens the lattice along the in-planar direction of the TM layers, while increasing the interlayer spacing of these TM layers (see Discussion on the structural changes after Al substitution section and Fig. S11 and S12 in ESI†). Since most Na+ ion diffusion pathways of Na2Mn3O7 and Na2.4Al0.4Mn2.6O7 cathodes are aligned along the in-planar direction, these structural changes will shorten the diffusion pathways while widening the diffusion channels, further improving the Na+ ion diffusion kinetics. This may explain the enhanced rate performance observed for Na2.4Al0.4Mn2.6O7 during rate capability tests, as it will be later discussed (Fig. 3d), and agrees with experimental DNa+ values obtained from GITT data (Fig. S13 and S14†), which are among the largest reported for sodium layered oxides (e.g., D ≈ 10−11 cm2 s−1 for P2-Na7/9Cu2/9Fe1/9Mn2/3O2 and D ≈ 10−12 to 10−11 cm2 s−1 for Na0.7Mn0.7Ni0.3−xCoxO2, x = 0, 0.1, 0.3).51,52
Electrochemical performance
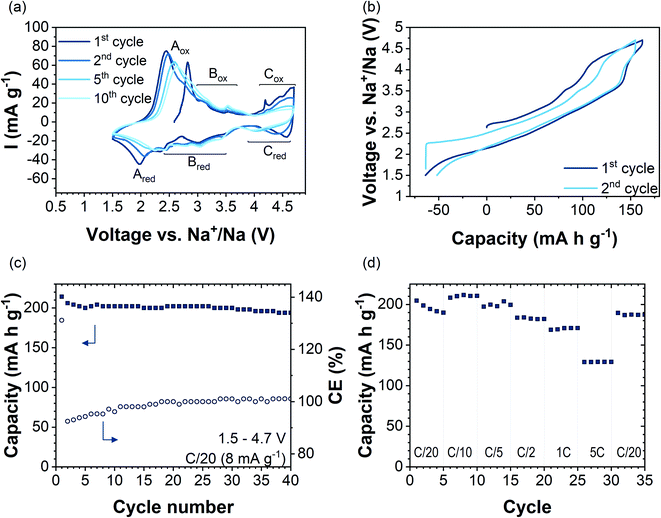
Fig. 3a shows cyclic voltammetry data of Na2.4Mn2.6Al0.4O7 in the 1st, 2nd, 5th, and 10th cycles in the voltage range of 1.5–4.7 V vs. Na+/Na at a scan rate of 0.1 mV s−1. Several redox peaks are observed in the CV data, indicating a multistep Na+ insertion/extraction process. The first anodic sweep shows three distinct regions with oxidation peaks at potentials of 2.8 V (Aox), 3.2 V and 3.6 V (Box region), and above 4 V (Cox region). By direct comparison with other manganese-based systems such as P2-Na2/3Mn1−xAlxO2,16 Na0.67[Fe0.5Mn0.5]O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 53 and P2-Na2/3Mn0.9Mg0.1O2,44 the first anodic peak (Aox) can be related to the oxidation reaction of Mn3+/Mn4+ ions in the structure. Data are in accordance with NMR and XANES data, which show Mn3+/Mn4+ cation mixing in the pristine sample (Fig. S9 and S10c†). In subsequent cycles, Aox shifts to higher potentials upon cycling (by ≈0.15 V) and its maximum peak current intensity decreases upon cycling from 75 mA g−1 in the 2nd cycle to 58 mA g−1 in the 10th cycle. On the cathodic sweep, the corresponding Ared reduction peak appears at 1.9 V and shifts to higher potentials upon cycling, occurring at 2.2 V at the 10th cycle. The increased polarisation could be attributed to structural changes occurring upon cycling.54 Anodic and cathodic peaks in the 2.5–3.7 V voltage range (region B in Fig. 3a) did not change in potential over the first 10 cycles. GITT data in this voltage range showed a decrease in DNa+ values by two orders of magnitude, which might be attributed to sodium/vacancy ordering structural arrangements (Fig. S14†). The observed anodic peaks in region C (Cox) are similar to those attributed to an oxygen redox reaction arising from the presence of non-bonding O 2p orbitals in Na2Mn3O7 (Fig. S15a†).6,8 The fast loss of peak current intensity upon cycling together with an increase in voltage polarization reflects the partial irreversibility of the process due to phenomena such as oxygen gas formation from the particle surface.55 Nevertheless, earlier works on cathode materials with oxygen-redox activity, e.g.,56–58 have shown oxygen redox activity, even though the associated anionic redox-related plateaus (in galvanostatic data) or current peaks (in CV data) are not discernible anymore. Therefore, we cannot rule out oxygen redox activity in Na2.4Al0.4Mn2.6O7 after the first cycle by the absence of the high-voltage redox peaks in the CV data.
53 and P2-Na2/3Mn0.9Mg0.1O2,44 the first anodic peak (Aox) can be related to the oxidation reaction of Mn3+/Mn4+ ions in the structure. Data are in accordance with NMR and XANES data, which show Mn3+/Mn4+ cation mixing in the pristine sample (Fig. S9 and S10c†). In subsequent cycles, Aox shifts to higher potentials upon cycling (by ≈0.15 V) and its maximum peak current intensity decreases upon cycling from 75 mA g−1 in the 2nd cycle to 58 mA g−1 in the 10th cycle. On the cathodic sweep, the corresponding Ared reduction peak appears at 1.9 V and shifts to higher potentials upon cycling, occurring at 2.2 V at the 10th cycle. The increased polarisation could be attributed to structural changes occurring upon cycling.54 Anodic and cathodic peaks in the 2.5–3.7 V voltage range (region B in Fig. 3a) did not change in potential over the first 10 cycles. GITT data in this voltage range showed a decrease in DNa+ values by two orders of magnitude, which might be attributed to sodium/vacancy ordering structural arrangements (Fig. S14†). The observed anodic peaks in region C (Cox) are similar to those attributed to an oxygen redox reaction arising from the presence of non-bonding O 2p orbitals in Na2Mn3O7 (Fig. S15a†).6,8 The fast loss of peak current intensity upon cycling together with an increase in voltage polarization reflects the partial irreversibility of the process due to phenomena such as oxygen gas formation from the particle surface.55 Nevertheless, earlier works on cathode materials with oxygen-redox activity, e.g.,56–58 have shown oxygen redox activity, even though the associated anionic redox-related plateaus (in galvanostatic data) or current peaks (in CV data) are not discernible anymore. Therefore, we cannot rule out oxygen redox activity in Na2.4Al0.4Mn2.6O7 after the first cycle by the absence of the high-voltage redox peaks in the CV data.
Galvanostatic charge/discharge profiles of the first two cycles of Na2.4Mn2.6Al0.4O7 in the voltage range 1.5–4.7 V vs. Na+/Na at a constant current of 8 mA g−1 (C/20 rate) are shown in Fig. 3b. The material was initially charged from its open-circuit value (OCV) (≈2.65 V) to 4.7 V, showing a capacity of 163 mA h g−1 which corresponds to the extraction of two Na+ ions per formula unit to yield Na0.4Mn2.6Al0.4O7. The voltage profile starts with a moderate slope from 2.8 V to 4 V followed by a plateau that terminates at 4.7 V. The voltage profiles are significantly different to our experimental (Fig. S15b†) and literature data on Na2Mn3O7, which shows two high-voltage plateaus during charge.6,8
Galvanostatic data for Na2.4Mn2.6Al0.4O7 match the cyclic voltammetry data, which shows the oxidation of Mn3+ ions to Mn4+ starting at low potentials (≈2.8 V), followed by the oxidation of oxygen anions at high-potentials (V > 4.0 V) (Fig. 3a). The sloppy load profile of Na2.4Mn2.6Al0.4O7 compared to reported load curves for Na2Mn3O7 indicates that Al3+ ion substitution for Mn4+ ions in the TM layer alleviates the structural transitions occurring upon cycling in Na2Mn3O7.8,59 On the subsequent discharge cycle, the same processes are observed: the reduction of oxygen anions above 4.0 V, reflected as a short plateau, and the reduction of Mn4+ to Mn3+ ions below this voltage. A higher discharge capacity (i.e., 215 mA h g−1) compared to the first charge capacity, which results in a coulombic efficiency (CE) of 130%, was observed (see Fig. 3c). This can be explained by the surplus of Mn3+ ions formed and the ability of uptaking a higher sodium content compared to the as-synthesised material, due to the low cut-off potential choice. The charge capacity above 4 V is reduced from the first cycle (55 mA h g−1) to the second cycle (26 mA h g−1), indicating that the high-voltage redox processes are not fully reversible, most likely reflecting the irreversibility of the oxygen redox process and/or oxygen evolution reaction. The reversibility of the reaction will be further discussed with the help of ab initio calculations. Overall, a capacity retention of 90% with respect to the first discharge cycle and a CE of ca. 100% was achieved after 40 cycles (Fig. 3c). For comparison, as-synthesised Na2Mn3O7 was galvanostatically cycled using an identical protocol (i.e., 40 cycles at C/20 in the voltage range 1.5–4.7 V), showing a capacity retention of 59% with a CE of 96% (Fig. S15b†). These data agree with previous reports on Na2Mn3O6.85, where a capacity retention of 50% with a CE of 90% after 50 cycles in the 1.5–4.5 V voltage range was observed.59
Rate capability tests were carried out at different current densities from C/20 to 5C (i.e., 8 mA g−1 to 800 mA g−1) in the 1.5–4.7 V vs. Na+/Na potential window, acquiring data for five consecutive cycles at each rate. Fig. 3d shows discharge capacities at different applied rates (solid squares), together with the CE (open circles). The first discharge cycle shows a capacity of 205 mA h g−1 when applying a current of C/20 to the electrode. Increasing the applied current to C/10, C/5, C/2, 1C, and 5C, and back to C/20 leads to specific capacities (at the 5th cycle) of 210, 200, 182, 171, 130 and 187 mA h g−1, respectively. The discharge capacity of 130 mA h g−1 observed at 5C corresponds to 64% of the first discharge capacity obtained at C/20. By contrast, at 5C the capacity for Na2Mn3O7 was 51% of that obtained in the first cycle at C/20 (Fig. S15d†). When the current returns to C/20, a reversible discharge capacity of 187 mA h g−1 was achieved. This corresponds to a capacity retention of 92% with respect to the initial discharge cycle. As the charge–discharge rate increased from C/5 to 5C, the voltage profile curves changed slightly, shortening the charge/discharge plateau at 4.0 V (Fig. S16†). Therefore, the kinetically limited process seems to be related to the high voltage oxygen redox activity, which has been described as a rate-determining step in the charge/discharge process.60 Nyquist plots for Na2.4Al0.4Mn2.6O2 and Na2Mn3O7 showed larger charge-transfer resistance values for the former, becoming even more evident after 100 cycles (Fig. S17 and S18†). EIS data for other Al-substituted compounds, such as P2-Na0.5Mn0.5−xAlxCo0.5O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 and Al-doped LiNi0.5Mn1.5O4
15 and Al-doped LiNi0.5Mn1.5O4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 61 have also shown an increase in charge transfer resistance with Al3+ ion substitution, which has been attributed to the formation of a thicker cathode-electrolyte interface (CEI) layer at high states of charge and/or a more unstable surface.15,61,62
61 have also shown an increase in charge transfer resistance with Al3+ ion substitution, which has been attributed to the formation of a thicker cathode-electrolyte interface (CEI) layer at high states of charge and/or a more unstable surface.15,61,62
Charge compensation mechanism
Ex situ XRD data were collected on cycled electrodes at different states of charge during the first cycle, to examine the structural arrangements occurring in Na2.4Al0.4Mn2.6O2 (Fig. S19†). XRD data on the electrode charged to 4.7 V (red data) shows broadened peaks and changes in the relative intensities, suggesting an increase in disorder and atomic occupations with respect to the pristine electrode. Furthermore, an increase in the cell volume parameters attributed to an increase of the interlayer distance was observed. This behaviour is typical in layered oxides, and it is ascribed to the increased repulsion of the oxygen ions in adjacent layers in the absence of shielding effect of Na+ ions in the Na-layer.63–65 No extra phases were observed, indicating a solid-solution behaviour. On the other hand, XRD data on the electrode that was charged and discharged (4.7–1.5 V voltage range) shows two extra peaks at ≈38.5° and 42.8° 2θ (indicated with a diamond symbol in Fig. S19†). These are in good agreement with the orthorhombic Na0.44MnO2 phase (Pbma space group), previously observed during discharge in Na2Mn3O7 (Fig. S20†).66 Table S2† summarises the crystallographic data obtained by indexing the XRD data shown in Fig. S19† using the Le Bail method.Ex situ 23Na solid-state NMR spectra for Na2.4Al0.4Mn2.6O7 electrodes (pristine, charged and discharged) are shown in Fig. S21.† The spectrum for the pristine cathode is similar to that of the Na2.4Al0.4Mn2.6O7 powder with distinct features at ∼500 ppm and ∼730 ppm, and with an added intensity around 0 ppm due to residual electrolyte. The resonance at 330 ppm is hidden by a spinning sideband. In the charged electrode material, the 500 and 730 ppm features are not observed, and the spectrum instead shows intensity at a higher shift of 910 ppm. Although this shift is lower than the 1500 ppm observed for the undoped material, the increase in shift compared to the pristine doped material is consistent with the removal of Na+ ions from the structure, resulting in a more Mn4+ ion rich local environment.3,44 The spectrum for the discharged material, whilst broadened, is similar to the pristine electrode material. For comparison, ex situ23Na SSNMR spectra were also obtained for Na2Mn3O7 electrode materials (Fig. S22†). As for the Na2.4Al0.4Mn2.6O7 materials, there is an intense peak close to 0 ppm in the spectra, due to residual electrolyte and the diamagnetic component discussed previously. The pristine electrode material shows a main peak at ∼1500 ppm, consistent with the Na2Mn3O7 powder. Spectra obtained at different MAS rates show that the shift of this peak may be temperature-dependent. The spectrum of the charged electrode material shows small added features at 930 ppm and 650 ppm (with one peak a spinning sideband of the other). The spectrum for the discharged electrode is different with the peak at ∼1500 ppm not observed and the spinning sideband pattern of the broader component of the spectrum shifted to lower ppm and over a wider shift range. This is consistent with the discharged material having an increased sodium content, and therefore different local Na environments when compared to the pristine material.
Although new Na environments can be detected with NMR, it has not been possible to decide their nature. Therefore, to gain further understanding of the charge/discharge behaviour in Na2.4Al0.4Mn2.6O7 and its Na2Mn3O7 parent material, we examined via computational methods the insertion sequences of Na atoms and relate the results to the voltage profiles of the cathode materials upon cycling.
For this purpose, the Na sites of Na2Mn3O7 and Na2Al0.4Mn2.6O7 occupied during charging/discharging were predicted by optimizing the geometries of partially sodiated NaxMn3O7 and NaxAl0.4Mn2.6O7 supercells. Upon cycling of the sodium layered electrodes, the local bonding between Na atoms and TM changes largely, whereas TM–O bonds mostly maintain their octahedral coordination. For such systems, the electrochemical potentials are primarily determined by the bond dissociation energy between active Na atoms and TM layers. From this perspective, the difference in Na+ ion insertion sequences between Na2Mn3O7 and Na2.4Al0.4Mn2.6O7 and their differing Na bonding environment during sodiation can result in differing voltage profiles. To verify this relationship, we first summarized all local bonding environments of Na sites in Na2Mn3O7 and Na2.4Al0.4Mn2.6O7 structures (Table 1) and assessed how strongly Na+ ions are bounded in each coordination environment by comparing their Na vacancy formation energies (Fig. 4a). Comparison in Na vacancy formation energies reveals that, of two Na sites in Na2Mn3O7, Na+ ions in site Na1 are more strongly bonded to TM layers, requiring higher potentials to remove them compared to those in site Na2. This matches the two voltage plateaus observed, where Na+ ions from site Na2 are first removed at low voltage (Na2Mn3O7 → NaMn3O7), followed by the removal of Na+ ions from site Na1 at high voltage (NaMn3O7 → Mn3O7).
For Na2.4Al0.4Mn2.6O7, the presence of Al3+ ions and Na+ ion excess changes the structure such that Na+ ions in Na1 and Na2 sites have three and two different variations of local bonding environment, respectively (represented by prime symbols in Table 1). Consequently, Na vacancy formation energies may vary even for the same Na site: 4.74–5.17 eV for Na1 site and 4.31–4.81 eV for Na2 site. This shows that Na+ ion extraction from these sites during charging occurs throughout various voltage values, resulting in sloping voltage profiles of NaxAl0.4Mn2.6O7 in the range of 0.4 < x < 2.0 (Fig. 3b). The relatively high Na vacancy formation energies from Na1 and Na2 indicate that the removal of these Na sites will require high charge voltages (4.2–5 V), which corresponds to the high voltage plateau in Fig. 3b and redox peaks in region C in the CV data (Fig. 3a). On the other hand, the Na vacancy formation energies of sites Na3 and Na4 are lower than those of sites Na1 and Na2, which is due to electrostatic repulsions with adjacent Na atoms in Na1 and Na2 sites. Such weakly bonded Na atoms are likely to be removed first during charging, which is represented as the low voltage anodic peaks in region B of the cyclic voltammetry data (Fig. 3a). Additional theoretical voltage calculations reveal that the model structures resemble well the first charge curves of Na2Mn3O7 and Na2.4Al0.4Mn2.6O7 (Fig. 4b and c): (1) predicted voltage profiles agree with the overall shape of the charging curves, including the two-stepwise profiles of Na2Mn3O7 and the sloping curves in the 0.4 ≤ x ≤ 2.0 region and the distinct low voltage plateau in the 2.0 ≤ x ≤ 2.4 region of NaxAl0.4Mn2.6O7. (2) When experimental voltage values are averaged over the x range of each voltage plateau, the averaged voltage values are close to the predicted voltages by less than 0.5 V. However, the above predictions are no longer consistent with the experimental data as charging and discharging processes proceed, due to structural changes which are not considered in these calculations.
Furthermore, we simulated the first desodiation process of Na2Mn3O7 and Na2.4Al0.4Mn2.6O7 and analysed its effect on electronic and atomic structures. Before desodiation, the valence band maxima (VBM) of both materials are predominantly formed by O 2p states and the conduction band minima are occupied by p–d hybridized states of O and Mn atoms (Fig. S23†).
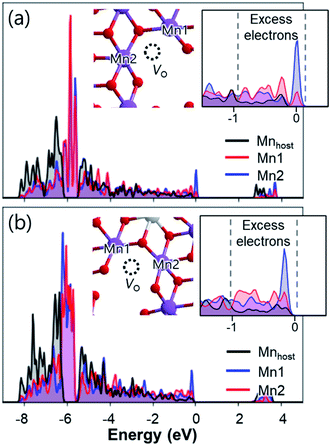
Density of states calculations show that, after removing Na atoms, electron holes are likely to be centred on the 2p states of oxygen. Additional analysis of the local Madelung potentials of O revealed that O atoms from Mn–O–Mn or Mn–O–Al near the unoccupied Mn sites in the TM layers (also referred to as non-bonding oxygen atoms8) have lower Madelung potentials (23.93–25.88 V) than those of other O atoms (27.39–29.86 V) (Table S3†). Considering that the energy to generate a positive hole is lower for lower Madelung energy,38,67 electron holes tend to be localized on 2p states of O near the unoccupied Mn sites. Such hole localizations can also be predicted from the partial density of states of O atoms (Fig. S24†), where high-energy electrons are concentrated on the non-bonding O atoms. As a result, the desodiation of Na2Mn3O7 and Na2.4Al0.4Mn2.6O7 causes the localized holes at 2p states of non-bonding O atoms, which can be observed after removing a Na atom from Na2Mn3O7 and Na2.4Al0.4Mn2.6O7 (Fig. 5a–d). Such hole localization behaviours occur for all Na vacancies in Na2Mn3O7 and Na2.4Al0.4Mn2.6O7, regardless of the type of Na sites (Fig. S25 and S26†). The above results indicate that the desodiation of Na2Mn3O7 and Na2.4Al0.4Mn2.6O7 proceeds by redox reactions from 2p states of non-bonding O atoms,68 which is in good agreement with previous reports on Na2Mn3O7.8,59
 | ||
| Fig. 5 Projected density of states calculated for (a) Na1.9Mn3O7 and (b) Na2.3Al0.4Mn2.6O7. Insets show the magnified density of states near hole levels. Partial charge densities (green isosurfaces) of (c) Na1.9Mn3O7 and (d) Na2.3Al0.4Mn2.6O7 calculated for the hole bands located ≈1.5 eV above the VBM. (e) Distributions of O–O bond lengths near the unoccupied Mn sites before and after the desodiation of Na2Mn3O7 and Na2.4Al0.4Mn2.6O7. Distribution of hole polarons after desodiation are shown as insets, with labels for the corresponding types of O listed in Table 2. In the insets, the lengths of contracted O–O bonds are indicated by numbers. | ||
Upon further desodiation, electron holes continuously accumulate in non-bonding O atoms and, in turn, induce some structural distortion in the lattice of Na2Mn3O7 and Na2.4Al0.4Mn2.6O7. To understand this coupling between excess holes and structural changes, we first analysed the structural changes near the non-bonding O atoms. Fig. 5e shows the changes in bond length between non-bonding O atoms in Na2Mn3O7 and Na2.4Al0.4Mn2.6O7 before and after desodiation. In the case of Na2Mn3O7, all O–O bonds near the unoccupied Mn sites have similar bond lengths of ∼2.8 Å. However, after the weakly bounded Na atoms in site Na2 (see Fig. 4a) are extracted upon charge, the resultant NaMn3O7 shows contracted O–O bonds with bond lengths ranging from 2.46 to 2.80 Å. Subsequent calculations on the localized holes of NaMn3O7 reveal that, of four different O sites in Na2Mn3O7 (Table 2), the three-coordinated O2 (O coordinated by two Mn and one Na) is the most preferential hole site because of its low Madelung potential (Tables S3 and S4†) and its proximity to Na vacancies. Such selective partial oxidization of O2− to On− causes the contraction of bond distance to occur locally near O2 atoms (Fig. 5e and S27†). Additional calculations showed that the partially oxidized On− acted as main sites for the formation of O–O dimer species: (1) the vacancy formation energies of O sites showed that the partially oxidized On− required the lowest energy to be removed compared to other O sites (Table 2); and (2) nudged elastic band calculations showed that the formation of the O2 dimer from the non-bonding On− species was a thermodynamically driven process (with reaction enthalpy of −0.29 eV), with a low activation barrier of 0.78 eV (Fig. S28†). Together with Mn ion migration to the Na layer, the kinetic barrier for O–O dimerization can be further lowered.69 The above findings, i.e., shortened bond distances of O2–O2 bonds, their low vacancy formation energies, and low activation barriers for O2 dimer formation, suggest the formation of “peroxo-like” O–O dimers (and associated O2 gas release) after the first charge of Na2Mn3O7. The formation of peroxo-like dimers has been demonstrated with resonant inelastic X-ray scattering (RIXS) in other layered oxides such as P2-NaxLiyMn1−yO2 (y = 0.2, 0.25) with non-bonding O atoms.70
| O site | Na2Mn3O7 | NaMn3O7 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 1 | 2 | 2′ | 3 | 5 | |
| Adjacent atoms | 2 Mn and 2 Na | 2 Mn and Na | 3 Mn and Na | 3 Mn and 2 Na | 2 Mn and 2 Na | 2 Mn and Na | 2 Mn and Na | 3 Mn and Na | 3 Mn |
| Oxidation state | 2− | 2− | 2− | 2− | 2− | 2− | n-(oxidized) | 2− | 2− |
| Vacancy formation energy (eV) | 0.143 | 0.0 | 1.372 | 1.297 | 0.54 | 0.39 | 0.0 | 1.07 | 1.10 |
| O site | Na2.4Al0.4Mn2.6O7 | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| Adjacent atoms | 2 Mn and 2 Na | 2 Mn and 3 Na | Mn, Al and 3 Na | 2 Mn, Al, and Na | 2 Mn, Al, and 2 Na | 3 Mn and Na | 3 Mn and 2 Na | 3 Mn and 3 Na |
| Oxidation state | 2− | 2− | 2− | 2− | 2− | 2− | 2− | 2− |
| Vacancy formation energy (eV) | 0.0 | 0.152 | 0.504 | 0.811 | 1.244 | 1.133 | 1.228 | 1.275 |
| O site | Na1.4Al0.4Mn2.6O7 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 2′ | 3 | 4 | 5 | 5′ | 6 | 7 | 8 | 9 | 10 | |
| Adjacent atoms | 2 Mn and 2 Na | 2 Mn and Na | 2 Mn and Na | Mn, Al, and Na | 2 Mn, Al, and Na | Mn, Al, and 2 Na | Mn, Al, and 2 Na | 2 Mn and Al | 3 Mn | 3 Mn and Na | 2 Mn, Al, and 2 Na | 3 Mn and 2 Na |
| Oxidation state | 2− | 2− | n-(oxidized) | n-(oxidized) | 2− | 2− | n-(oxidized) | 2− | 2− | 2− | 2− | 2− |
| Vacancy formation energy (eV) | 0.174 | 0.636 | 0.482 | 0 | 0.535 | 0.31 | 0.061 | 0.52 | 1.845 | 1.141 | 0.972 | 1.694 |
The partial oxidation of non-bonding O atoms and associated O–O bond shortening can also be observed in Na2.4Al0.4Mn2.6O7 (Fig. 5e). Overall, O–O bonds near the unoccupied Mn sites are slightly distorted compared to Na2Mn3O7 such that the O–O bond lengths vary from 2.78 to 2.84 Å. After desodiation, the O–O bonds of Na1.4Al0.4Mn2.6O7 are shortened to the lowest length of 2.42 Å. Such contraction in O–O bonds arise mainly from their partially oxidized O sites, i.e., O2′, O3, and O5′ (Table 2 and Fig. 5e), where each oxygen atom has differing coordination environment; two Mn and Na atoms for O2′; Mn, Al and Na atoms for O3; and Mn, Al, and two Na atoms for O5′. Madelung potentials of Al-coordinated O (17.37 and 20.85 V for O3 and O5, respectively) are lower than that of two-Mn-coordinated O2′ (20.86 V), indicating that, upon further charging, excess holes are likely to be localized in O atoms adjacent to Al. Additional calculations on the O vacancy formation energies show that among all O atoms nearby the unoccupied Mn sites (O1, O2, O2′, O3, O5′ and O5), partially oxidized O atoms, especially those coordinated by Al (O3 and O5′), are more readily removed upon charging. This suggests that owing to the preferential hole formation excess in Al-coordinated O atoms during charging, Na2.4Al0.4Mn2.6O7 can also suffer from the formation of O–O dimers and associated O loss upon charging.
Calculations on the Na and O vacancies of Na2Mn3O7 and Na2.4Al0.4Mn2.6O7 enabled us to reveal the early stage of the anionic redox reactions during charge. Na+ ion extraction during charging partially oxidizes non-bonding oxygen atoms adjacent to the unoccupied Mn sites, causing the oxygen atoms to have localized excess holes (Fig. 5a–d). The distribution of excess holes can be modified by external dopants, such as Al, where holes are preferentially located on non-bonding oxygen atoms coordinated by Al. Next, the so-formed electron holes in oxygen atoms shorten the O–O bond distance up to 2.4 Å (Fig. 5e). Compared to other oxygen atoms, those comprising the shortened O–O bonds can be readily removed from their original sites (Table 2), which suggest the formation of oxygen dimers with shorter bond lengths, e.g., peroxo-like O–O dimers, and O2 gas. Song et al. hypothesised on the possibility of O2 gas evolution from mostly surface but also bulk Na2Mn3O7 particles together with a decrease of crystallinity and increase of particle stress, although without providing any further experimental evidence.6
The above findings of contracted O–O bonds and their weak binding to the TM layer were observed in both Na2Mn3O7 and Na2.4Al0.4Mn2.6O7, suggesting that these are susceptible to O loss upon the first charge. Such O loss can also be supported from experiments: both cathodes display shortened high voltage plateaus during the first discharge process and subsequent charge–discharge cycles (Fig. 4b and c), which indirectly indicates a decrease in the amount of redox-active O. Furthermore, additional calculations on the electronic structures of Na2Mn3O7 and Na2.4Al0.4Mn2.6O7 show that the removal of non-bonding O atoms leads to the formation of localized excess electrons on two adjacent Mn4+ ions (Fig. 6). The so-formed excess electrons reduce both Mn4+ ions to Mn3+, where excess electrons positioned in Mn with lower Madelung potentials exhibit higher energy (Table S4 and Fig. S29–S31†). This suggests that O loss at high voltages causes the reduction of Mn4+ to Mn3+ to maintain charge neutrality, which can explain the mixed oxidation states of Mn at high voltages observed in XANES spectra. Fig. S10a and b† illustrates XANES spectra of Mn K-edge at various states of charge, together with the MnO (Mn2+), Mn2O3 (Mn3+) and MnO2 (Mn4+) references. Linear combination fit analyses (LCF) were used to semi-quantify the oxidation state of Mn at the different points of charge and discharge and the results are shown in Fig. S10c.† A report of the goodness of fit parameters (R-factor and reduced χ2) along with the per cent that each model contributes to the fit is summarised in Table S5.† A similar reduction of the TM at highly charged states due to the oxygen redox activity has also been observed for Ni4+/3+ in Li1.2Ni0.4Ru0.4O2.71 Considering that the Mn3+O6 octahedra are Jahn–Teller active,72 such reduction of Mn4+ ions might have detrimental effects on the cycling stability of the studied cathodes.
Although the above analyses have focused on O loss and subsequent effect on Mn reduction, electron holes formed in O atoms upon desodiation can cause other structural changes. In addition to O2 gas release, these excess holes can shorten the O–O bond lengths to form various O2 dimer species, such as peroxo-like O2n− or peroxide O22−-species.10 Previous studies on Li-ion layered cathodes have reported that the shortened O–O bond can trigger TM migration to octahedral sites in the Li layer and subsequent formation of spinel-like phases.73 Other studies have also suggested the possibility of cation dopant migration to the tetrahedral site of the Na layer in layered oxides, which prevents further TM migration and stabilizes cyclability of cathodes.74
Conclusions
In summary, we have studied the effects of Al3+ ion substitution and Na+ ion excess in the Mn-rich, Na2Mn3O7 cathode material with triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group. We synthesised Na2.4Al0.4Mn2.6O7 (Na0.68Mn0.74Al0.11[ ]0.15O2 in conventional NaxMO2 notation) as a reference compound by a ceramic method and its crystal structure was characterised with X-ray diffraction. Given the highly disordered nature of the cathode material, we used DFT calculations to provide an accurate crystallographic model of the structure. We then assessed the electrochemical properties of the Na2.4Al0.4Mn2.6O7 cathode in Na half-cells using different electrochemical methods, including galvanostatic cycling, cyclic voltammetry, electrochemical impedance spectroscopy, and galvanostatic intermittent titration. Cyclic voltammetric data showed the presence of both Mn3+/Mn4+ and O2−/On− redox-active species in the material during Na cycling, which were further confirmed using XANES spectroscopy and computational studies. On the other hand, galvanostatic measurements showed an initial specific capacity of 215 mA h g−1 in the 1.5–4.7 voltage range at C/20 and a capacity retention of 90% after 40 cycles. Experimental load curves were compared to computationally generated ones to gain insight into the Na+ ion insertion/extraction sequences generated upon cycling. Subsequent examinations on the modelled structures revealed that owing to the high electronegativity of Al3+ compared to the Mn4+ counterpart, Na2.4Al0.4Mn2.6O7 allows Na+ ions to diffuse throughout various directions, parallel to the TM layers. The shorter Al–O bond lengths and lower oxidation state of Al3+ ions distort the Na+ ion migration pathways such that these are shorter and have wider diffusion channels, which further improve Na+ ion diffusion kinetics. These results suggest selection criteria of dopants for high-rate performance layered oxides cathodes, where these should have: (1) higher electronegativity, (2) smaller ionic radius, and (3) lower oxidation states than TM elements. Therefore, we expect that this concept can be extended for developing future fast charging layered oxide cathodes.
space group. We synthesised Na2.4Al0.4Mn2.6O7 (Na0.68Mn0.74Al0.11[ ]0.15O2 in conventional NaxMO2 notation) as a reference compound by a ceramic method and its crystal structure was characterised with X-ray diffraction. Given the highly disordered nature of the cathode material, we used DFT calculations to provide an accurate crystallographic model of the structure. We then assessed the electrochemical properties of the Na2.4Al0.4Mn2.6O7 cathode in Na half-cells using different electrochemical methods, including galvanostatic cycling, cyclic voltammetry, electrochemical impedance spectroscopy, and galvanostatic intermittent titration. Cyclic voltammetric data showed the presence of both Mn3+/Mn4+ and O2−/On− redox-active species in the material during Na cycling, which were further confirmed using XANES spectroscopy and computational studies. On the other hand, galvanostatic measurements showed an initial specific capacity of 215 mA h g−1 in the 1.5–4.7 voltage range at C/20 and a capacity retention of 90% after 40 cycles. Experimental load curves were compared to computationally generated ones to gain insight into the Na+ ion insertion/extraction sequences generated upon cycling. Subsequent examinations on the modelled structures revealed that owing to the high electronegativity of Al3+ compared to the Mn4+ counterpart, Na2.4Al0.4Mn2.6O7 allows Na+ ions to diffuse throughout various directions, parallel to the TM layers. The shorter Al–O bond lengths and lower oxidation state of Al3+ ions distort the Na+ ion migration pathways such that these are shorter and have wider diffusion channels, which further improve Na+ ion diffusion kinetics. These results suggest selection criteria of dopants for high-rate performance layered oxides cathodes, where these should have: (1) higher electronegativity, (2) smaller ionic radius, and (3) lower oxidation states than TM elements. Therefore, we expect that this concept can be extended for developing future fast charging layered oxide cathodes.
To understand the underlying chemistry under oxygen loss and capacity fading, we performed partial charge density calculations on electron holes of desodiated Na2.4Al0.4Mn2.6O7, and confirmed oxygen redox reactions to stem from 2p states of non-bonding O atoms, analogously to Na2Mn3O7. In conjunction with O vacancy formation energies, energy barrier calculations suggested that the O atoms with electron holes during desodiation form “peroxo-like” O–O dimer species by O–O bond shortening. Furthermore, we showed that the preferential positions for O–O dimer formation can be adjusted by Al3+ ion substitution in the TM layer. Such behaviour arises from the change in electrostatic energy (Madelung potential) of O atoms neighbouring Al atoms. This suggests that one can adjust the O–O dimer distribution of desodiated cathodes by careful dopant selection, i.e., by using dopants with low oxidation states and large ionic radii that lower the Madelung potential of adjacent oxygen atoms, one can force O–O dimer species to form nearby dopants, and vice versa. Considering that O–O dimers are a major cause of O2 gas release10 and TM migration into the alkali metal layer,73 these studies may guide future studies on developing cathode materials that are resistive to oxygen loss and structural degradation. In conjunction with future calculations on structural changes during anionic redox (e.g., O, cation, and dopant migration), these findings may enable researchers to uncover the effect of dopants on anionic redox reactions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
NTR would like to thank Lancaster University, the Royal Society (RG170150) and the Faraday Institution (FIRG018) for financial support. We acknowledge the Science and Technology Facilities Council (STFC) for access to B18 beamtime at the Diamond Light Source (SP21847). YC and DOS are grateful to the Faraday Institution for funding the MICHAEL computing cluster hosted at University College London (UCL). The calculations have been also carried out on the Myriad (Myriad@UCL), Young (Young@UCL), and Kathleen (Kathleen@UCL) High Performance Computing Facility provisioned by UCL. Via our membership of the UKs HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202, EP/R029431), this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk). We are also grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1 and EP/T022213/1).References
- V. Palomares, M. Casas-Cabanas, E. Castillo-Martínez, M. H. Han and T. Rojo, Update on Na-based battery materials. A growing research path, Energy Environ. Sci., 2013, 6(8), 2312–2337, 10.1039/c3ee41031e.
- N. Tapia-Ruiz, et al., 2021 roadmap for sodium-ion batteries, JPhys Energy, 2021, 3(3), 031503, DOI:10.1088/2515-7655/AC01EF.
- J. Billaud, et al., β-NaMnO2: a high-performance cathode for sodium-ion batteries, J. Am. Chem. Soc., 2014, 136(49), 17243–17248, DOI:10.1021/ja509704t.
- X. Ma, H. Chen and G. Ceder, Electrochemical Properties of Monoclinic NaMnO2, J. Electrochem. Soc., 2011, 158(12), A1307, DOI:10.1149/2.035112jes.
- E. Gonzalo, M. Zarrabeitia, N. E. Drewett, J. Miguel and T. Rojo, Sodium manganese-rich layered oxides: potential candidates as positive electrode for sodium-ion batteries, Energy Storage Mater., 2021, 34, 682–707, DOI:10.1016/j.ensm.2020.10.010.
- B. Song, et al., Understanding the Low-Voltage Hysteresis of Anionic Redox in Na2Mn3O7, Chem. Mater., 2019, 31(10), 3756–3765, DOI:10.1021/acs.chemmater.9b00772.
- F. M. Chang and M. Jansen, Darstellung und Kristallstruktur von Na2Mn3O7, Z. Anorg. Allg. Chem., 1985, 531(12), 177–182, DOI:10.1002/zaac.19855311224.
- B. Mortemard de Boisse, et al., Highly Reversible Oxygen-Redox Chemistry at 4.1 V in Na4/7−x[□1/7Mn6/7]O2(□: Mn Vacancy), Adv. Energy Mater., 2018, 2, 1800409, DOI:10.1002/aenm.201800409.
- Y. Xie, M. Saubanère and M. L. Doublet, Requirements for reversible extra-capacity in Li-rich layered oxides for Li-ion batteries, Energy Environ. Sci., 2017, 10(1), 266–274, 10.1039/c6ee02328b.
- G. Assat and J. M. Tarascon, Fundamental understanding and practical challenges of anionic redox activity in Li-ion batteries, Nat. Energy, 2018, 3(5), 373–386, DOI:10.1038/s41560-018-0097-0.
- A. J. Perez, et al., Approaching the limits of cationic and anionic electrochemical activity with the Li-rich layered rocksalt Li3IrO4, Nat. Energy, 2017, 2(12), 954–962, DOI:10.1038/s41560-017-0042-7.
- X. Bai, et al., Anionic Redox Activity in a Newly Zn-Doped Sodium Layered Oxide P2-Na2/3Mn1−yZnyO2 (0 < y < 0.23), Adv. Energy Mater., 2018, 8(32), 1–12, DOI:10.1002/aenm.201802379.
- Y. Yu, et al., Towards controlling the reversibility of anionic redox in transition metal oxides for high-energy Li-ion positive electrodes, Energy Environ. Sci., 2021, 14(4), 2322–2334, 10.1039/d0ee03765f.
- D. Yuan, et al., Synthesis and electrochemical behaviors of layered Na0.67[Mn0.65Co0.2Ni0.15]O2 microflakes as a stable cathode material for sodium-ion batteries, J. Mater. Chem. A, 2013, 1(12), 3895–3899, 10.1039/c3ta01430d.
- H. V. Ramasamy, et al., Efficient Method of Designing Stable Layered Cathode Material for Sodium Ion Batteries Using Aluminum Doping, J. Phys. Chem. Lett., 2017, 8(20), 5021–5030, DOI:10.1021/acs.jpclett.7b02012.
- W. L. Pang, et al., P2-type Na2/3Mn1-xAlxO2 cathode material for sodium-ion batteries: Al-doped enhanced electrochemical properties and studies on the electrode kinetics, J. Power Sources, 2017, 356, 80–88, DOI:10.1016/j.jpowsour.2017.04.076.
- L. G. Chagas, S. Jeong, I. Hasa and S. Passerini, Ionic Liquid-Based Electrolytes for Sodium-Ion Batteries: Tuning Properties To Enhance the Electrochemical Performance of Manganese-Based Layered Oxide Cathode, Appl. Mater. Interfaces, 2019, 11(1), 22278–22289, DOI:10.1038/s41467-021-22527-z.
- W. Li, et al., High-Nickel NMA: A Cobalt-Free Alternative to NMC and NCA Cathodes for Lithium-Ion Batteries, Adv. Mater., 2020, 32(33), 2002718, DOI:10.1002/ADMA.202002718.
- K. Zhou, Q. Xie, B. Li and A. Manthiram, An in-depth understanding of the effect of aluminum doping in high-nickel cathodes for lithium-ion batteries, Energy Storage Mater., 2021, 34, 229–240, DOI:10.1016/J.ENSM.2020.09.015.
- S. Madhavi, G. V. Subba Rao, B. V. R. Chowdari and S. F. Y. Li, Effect of aluminum doping on cathodic behaviour of LiNi0.7Co0.3O2, J. Power Sources, 2001, 93(1–2), 156–162, DOI:10.1016/S0378-7753(00)00559-0.
- B. Wang, et al., Which of the nickel-rich NCM and NCA is structurally superior as a cathode material for lithium-ion batteries?, J. Mater. Chem. A, 2021, 9(23), 13540–13551, 10.1039/D1TA01128F.
- Y. Kee, N. Dimov, S. Champet and D. H. Gregory, Investigation of Al-doping effects on the NaFe0.5Mn0.5O2 cathode for Na-ion batteries, Ionics, 2016, 2245–2248, DOI:10.1007/s11581-016-1839-2.
- A. Dianat, N. Seriani, M. Bobeth and G. Cuniberti, Effects of Al-doping on the properties of Li-Mn-Ni-O cathode materials for Li-ion batteries: An ab initio study, J. Mater. Chem. A, 2013, 1(32), 9273–9280, 10.1039/c3ta11598d.
- K. Hoang, Doping Li-rich cathode material Li2MnO3: interplay between lattice site preference, electronic structure, and delithiation mechanism, Phys. Rev. Mater., 2017, 1(7), 1–10, DOI:10.1103/PhysRevMaterials.1.075404.
- E. Gonzalo, et al., P2 manganese rich sodium layered oxides: rational stoichiometries for enhanced performance, J. Power Sources, 2018, 401, 117–125, DOI:10.1016/j.jpowsour.2018.08.068.
- J. Rodríguez-Carvajal, Recent advances in magnetic structure determination by neutron powder diffraction, Phys. B, 1993, 192(1–2), 55–69, DOI:10.1016/0921-4526(93)90108-I.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44(6), 1272–1276, DOI:10.1107/S0021889811038970.
- B. Ravel and M. Newville, ATHENA, ARTEMIS, HEPHAESTUS: Data analysis for X-ray absorption spectroscopy using IFEFFIT, J. Synchrotron Radiat., 2005, 12(4), 537–541, DOI:10.1107/S0909049505012719.
- M. Newville, IFEFFIT: Interactive XAFS analysis and FEFF fitting, J. Synchrotron Radiat., 2001, 8(2), 322–324, DOI:10.1107/S0909049500016964.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for open-shell transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48(17), 13115–13118, DOI:10.1103/PhysRevB.48.13115.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979, DOI:10.1103/PhysRevB.50.17953.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Band theory and Mott insulators: Hubbard U instead of Stoner I, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(3), 943–954, DOI:10.1103/PhysRevB.44.943.
- A. B. Kehoe, D. O. Scanlon and G. W. Watson, Modelling potential photovoltaic absorbers Cu3MCh4 (M = V, Nb, Ta; Ch = S, Se, Te) using density functional theory, J. Phys.: Condens. Matter, 2016, 28(1), 175801, DOI:10.1038/s41467-021-22527-z.
- A. G. Squires, D. O. Scanlon and B. J. Morgan, Native Defects and Their Doping Response in the Lithium Solid Electrolyte Li7La3Zr2O12, Chem. Mater., 2020, 32(5), 1876–1886, DOI:10.1021/acs.chemmater.9b04319.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125(22), 224106, DOI:10.1063/1.2404663.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- D. O. Scanlon, et al., Band alignment of rutile and anatase TiO2, Nat. Mater., 2013, 12(9), 798–801, DOI:10.1038/nmat3697.
- E. A. Raekelboom, A. L. Hector, J. Owen, G. Vitins and M. T. Weller, Syntheses, structures, and preliminary electrochemistry of the layered lithium and sodium manganese(IV) oxides, A2Mn3O7, Chem. Mater., 2001, 13(12), 4618–4623, DOI:10.1021/cm011105j.
- C. Venkatesh, B. Bandyopadhyay, A. Midya, K. Mahalingam, V. Ganesan and P. Mandal, Magnetic properties of the one-dimensional S = 2 Heisenberg antiferromagnetic spin-chain compound Na2Mn3O7, Phys. Rev. B, 2020, 101(18), 184429, DOI:10.1103/PhysRevB.101.184429.
- E. Adamczyk and V. Pralong, Na2Mn3O7: A Suitable Electrode Material for Na-Ion Batteries?, Chem. Mater., 2017, 29(11), 4645–4648, DOI:10.1021/acs.chemmater.7b01390.
- K. Sada, B. Senthilkumar and P. Barpanda, Layered Na2Mn3O7 as a 3.1 V Insertion Material for Li-Ion Batteries, ACS Appl. Mater. Interfaces, 2018, 1, 67191–67246, DOI:10.1021/acsami.9b03813.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32(5), 751–767, DOI:10.1107/S0567739476001551.
- R. J. Clément, et al., Structurally stable Mg-doped P2-Na2/3Mn1-YMgyO2 sodium-ion battery cathodes with high rate performance: Insights from electrochemical, NMR and diffraction studies, Energy Environ. Sci., 2016, 9(10), 3240–3251, 10.1039/c6ee01750a.
- J. Lee, et al., Fully Exploited Oxygen Redox Reaction by the Inter-Diffused Cations in Co-Free Li-Rich Materials for High Performance Li-Ion Batteries, Adv. Sci., 2020, 7(17), 2001658, DOI:10.1002/advs.202001658.
- M. Sathiya, et al., Li4NiTeO6 as a positive electrode for Li-ion batteries, Chem. Commun., 2013, 49(97), 11376–11378, 10.1039/c3cc46842a.
- B. Qiu, et al., Gas-solid interfacial modification of oxygen activity in layered oxide cathodes for lithium-ion batteries, Nat. Commun., 2016, 7(1), 1–10, DOI:10.1038/ncomms12108.
- M. Otoyama, Q. Jacquet, A. Iadecola, M. Saubanère, G. Rousse and J. M. Tarascon, Synthesis and Electrochemical Activity of Some Na(Li)-Rich Ruthenium Oxides with the Feasibility to Stabilize Ru 6+, Adv. Energy Mater., 2019, 9(15), 1–12, DOI:10.1002/aenm.201803674.
- D. P. Siriwardena, et al., Effect of Fe3+ for Ru4+ substitution in disordered Na1.33Ru0.67O2 cathode for sodium-ion batteries: Structural and electrochemical characterizations, Electrochim. Acta, 2019, 325, 134926, DOI:10.1016/j.electacta.2019.134926.
- D. H. Lee, J. Xu and Y. S. Meng, An advanced cathode for Na-ion batteries with high rate and excellent structural stability, Phys. Chem. Chem. Phys., 2013, 15(9), 3304–3312, 10.1039/C2CP44467D.
- Y. Li, et al., Air-Stable Copper-Based P2-Na7/9Cu2/9Fe1/9Mn2/3O2 as a New Positive Electrode Material for Sodium-Ion Batteries, Adv. Sci., 2015, 2(6), 1500031, DOI:10.1002/ADVS.201500031.
- Z. Y. Li, J. Zhang, R. Gao, H. Zhang, Z. Hu and X. Liu, Unveiling the Role of Co in Improving the High-Rate Capability and Cycling Performance of Layered Na0.7Mn0.7Ni0.3-xCoxO2 Cathode Materials for Sodium-Ion Batteries, ACS Appl. Mater. Interfaces, 2016, 8(24), 15439–15448, DOI:10.1021/ACSAMI.6B04073/SUPPL_FILE/AM6B04073_SI_001.PDF.
- H. Wang, R. Gao, Z. Li, L. Sun, Z. Hu and X. Liu, Different Effects of Al Substitution for Mn or Fe on the Structure and Electrochemical Properties of Na0.67Mn0.5Fe0.5O2 as a Sodium Ion Battery Cathode Material, Inorg. Chem., 2018, 57(9), 5249–5257, DOI:10.1021/acs.inorgchem.8b00284.
- X. Lu, et al., Rate-dependent phase transitions in Li2FeSiO4 cathode nanocrystals, Sci. Rep., 2015, 5, 1–9, DOI:10.1038/srep08599.
- Y. Sun, et al., Study on Potassium Doped Modification of Li1.2Ni0.13Co0.13Mn0.54O2 Materials Synthesized by Novel Method for Lithium Ion Battery, J. Electrochem. Soc., 2018, 165(2), A333–A338, DOI:10.1149/2.1001802jes.
- G. Assat, A. Iadecola, D. Foix, R. Dedryvere and J. M. Tarascon, Direct quantification of anionic redox over long cycling of li-rich nmc via hard X-ray photoemission spectroscopy, ACS Energy Lett., 2018, 3(11), 2721–2728, DOI:10.1021/ACSENERGYLETT.8B01798/SUPPL_FILE/NZ8B01798_SI_001.PDF.
- W. E. Gent, et al., Coupling between oxygen redox and cation migration explains unusual electrochemistry in lithium-rich layered oxides, Nat. Commun., 2017, 8(2091), 1–12, DOI:10.1038/s41467-017-02041-x.
- K. Dai, et al., High Reversibility of Lattice Oxygen Redox Quantified by Direct Bulk Probes of Both Anionic and Cationic Redox Reactions, Joule, 2019, 3, 518–541, DOI:10.1016/j.joule.2018.11.014.
- Q. Wang, W. Yang, F. Kang and B. Li, Na2Mn0.33+Mn2.74+O6.85: a cathode with simultaneous cationic and anionic redox in Na-ion battery, Energy Storage Mater., 2018, 24, DOI:10.1016/j.ensm.2018.06.003.
- M. M. Rahman and F. Lin, Oxygen Redox Chemistry in Rechargeable Li-Ion and Na-Ion Batteries, Matter, 2021, 4(2), 490–527, DOI:10.1016/j.matt.2020.12.004.
- P. Sun, Y. Ma, T. Zhai and H. Li, High performance LiNi0.5Mn1.5O4 cathode by Al-coating and Al3+-doping through a physical vapor deposition method, Electrochim. Acta, 2016, 191, 237–246, DOI:10.1016/J.ELECTACTA.2016.01.087.
- Z. W. Lebens-Higgins, et al., Surface Chemistry Dependence on Aluminum Doping in Ni-rich LiNi0.8Co0.2−yAlyO2 Cathodes, Sci. Rep., 2019, 9(1), 1–12, DOI:10.1038/s41598-019-53932-6.
- E. Gonzalo, M. H. Han, J. M. L. del Amo, B. Acebedo, M. Casas-Cabanas and T. Rojo, Synthesis and characterization of pure P2- and O3-Na2/3Fe2/3Mn1/3O2 as cathode materials for Na ion batteries, J. Mater. Chem. A, 2014, 2(43), 18523–18530, 10.1039/C4TA03991B.
- P.-F. Wang, et al., Layered Oxide Cathodes for Sodium-Ion Batteries: Phase Transition, Air Stability, and Performance, Adv. Energy Mater., 2018, 8(8), 1701912, DOI:10.1002/AENM.201701912.
- B. Mortemard de Boisse, et al., Coulombic self-ordering upon charging a large-capacity layered cathode material for rechargeable batteries, Nat. Commun., 2019, 10(1), 1–7, DOI:10.1038/s41467-019-09409-1.
- N. Muralidharan and K. Nallathamby, Strategy to Qualify Layered Family Na2Mn3O7 Anode for Use in Sodium-Ion Batteries, Energy Fuels, 2021, 35(14), 11545–11550, DOI:10.1021/ACS.ENERGYFUELS.1C01080/SUPPL_FILE/EF1C01080_SI_001.PDF.
- J. Buckeridge, et al., Polymorph Engineering of TiO2: Demonstrating How Absolute Reference Potentials Are Determined by Local Coordination, Chem. Mater., 2015, 27(11), 3844–3851, DOI:10.1021/acs.chemmater.5b00230.
- D. H. Seo, J. Lee, A. Urban, R. Malik, S. Kang and G. Ceder, The structural and chemical origin of the oxygen redox activity in layered and cation-disordered Li-excess cathode materials, Nat. Chem., 2016, 8(7), 692–697, DOI:10.1038/nchem.2524.
- H. Chen and M. S. Islam, Lithium extraction mechanism in Li-rich Li2MnO3 involving oxygen hole formation and dimerization, Chem. Mater., 2016, 28(18), 6656–6663, DOI:10.1021/acs.chemmater.6b02870.
- R. A. House, et al., Superstructure control of first-cycle voltage hysteresis in oxygen-redox cathodes, Nature, 2020, 577, 502–508, DOI:10.1038/s41586-019-1854-3.
- N. Li, et al., Layered-rocksalt intergrown cathode for high-capacity zero-strain battery operation, Nat. Commun., 2021, 12(1), 4–13, DOI:10.1038/s41467-021-22527-z.
- X. Li, et al., Direct visualization of the Jahn-Teller effect coupled to Na ordering in Na5/8MnO2, Nat. Mater., 2014, 13(6), 586–592, DOI:10.1038/nmat3964.
- J. Hong, et al., Metal–oxygen decoordination stabilizes anion redox in Li-rich oxides, Nat. Mater., 2019, 18(3), 256–265, DOI:10.1038/s41563-018-0276-1.
- M. Guilmard, L. Croguennec and C. Delmas, Thermal Stability of Lithium Nickel Oxide Derivatives. Part I, Chem. Mater., 2003, 15(23), 4476–4483, DOI:10.1021/cm030340u.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ta05137g |
| ‡ Contributed equally to the work. |
| This journal is © The Royal Society of Chemistry 2022 |