Quantifying the trade-off between stiffness and permeability in hydrogels†
Yiwei
Gao
 and
H. Jeremy
Cho
and
H. Jeremy
Cho
 *
*
Department of Mechanical Engineering, University of Nevada, Las Vegas, Las Vegas, NV 89154, USA. E-mail: jeremy.cho@unlv.edu
First published on 27th September 2022
Abstract
Hydrogels have a distinct combination of mechanical and water-transport behaviors. As hydrogels stiffen when they de-swell, they become less permeable. Here, we combine de Gennes' semi-dilute polymer theory with the Kozeny-Carman equation to develop a simple, succinct scaling law describing the relationship between mechanical stiffness and hydraulic permeability where permeability scales with stiffness to the −8/9 power. We find a remarkably close agreement between the scaling law and experimental results across four different polymer families with varied crosslinkings. This inverse relationship establishes a fundamental trade-off between permeability and stiffness.
Hydrogels are polymer networks with an interconnected, water-filled porous structure. Water can be absorbed within these pores or permeate through them. The polymer network provides mechanical structure to hydrogels. This leads to hydrogels having a distinct combination of mechanical and water-transport behaviors, making them advantageous for a wide variety of applications. Much of the application-focused studies either study the mechanics in detail (e.g., stimuli-responsive water flow materials, soft robotics, and artificial tissues1–6) or transport behavior (e.g., contact lenses, drug delivery, wastewater purification, and solar distillation7–13). Currently, there is little understanding of how mechanics and transport behavior could be coupled.
An overarching conclusion from previous studies is that the mesh size in polymer networks dictates the properties of hydrogels.14 For instance, mesh size controls hydrogel friction, modulus, and permeability.14–18 One way to control mesh size and thereby change hydrogel properties is to add crosslinking. Naturally, without crosslinking, the polymer network structure has no solid-like rigidity and the polymer solution will flow as a viscous liquid.19 Crosslinking, by constraining the movement of polymer strands, adds solid-like elasticity, rendering the hydrogel a viscoelastic material.20–23 With extremely high crosslinking, the polymer will gain significant brittleness.24 In our work, we focus on crosslinked hydrogels that behave as solids as we probe their elastic properties at shorter timescales rather than their long-timescale viscous creep behaviors. The feasibility of varying crosslinking density to modify stiffness, permeability, as well as a multitude of other properties has been widely confirmed. Stiffness-focused studies25–27 have found that higher crosslinking densities generally result in stiffer gels, which is due to a reduced mesh size of the polymer and a denser network structure.15,16,28,29 Transport-focused studies have found that crosslinking can modify gas or solute permeability7,30–33 where lower crosslinking densities generally result in higher permeable gels,34–37 which is due to the enlarged mesh size and enhanced porosity of the network.14–16 Inspired by the great volume of work establishing the importance of mesh size, we seek to provide a succinct relationship between mechanical stiffness and water permeability of hydrogels as mesh size is varied by crosslinking.
Here, we adopt de Gennes' semi-dilute polymer solution theory38 as a basis for understanding the influence of mesh size on mechanical stiffness. Previously, we adopted this theory to successfully characterize changes in stiffness, osmotic pressure, and swelling by varying crosslinking density.27 The semi-dilute theory is a simple, elegant, and experimentally proven description that produces results that are indistinguishable from the more thorough, but complex Flory–Rehner theory that combines Flory–Huggins solution thermodynamics with Gaussian-chain (rubber-like elasticity effects) due to crosslinking.17,39,40 While the semi-dilute theory does not strictly consider crosslinks, we can assume that the mesh size and corresponding swelling state is set by crosslinking and the osmotic pressure of the environment. The semi-dilute theory provides an illustrative molecular perspective of the most essential part of polymer mixtures, and the properties of polymer networks in a good solvent (like water) are universal and do not depend on how the networks are prepared.41 With this perspective, the gel is considered to be a solution of polymer chains that are long and the spacing between the chains, ξ, is what ultimately dictates the properties of the gel. This spacing between polymer chains is related to the polymer volume fraction as
| ξ = a7/4v−1/4ϕpoly−3/4 | (1) |
 | (2) |
| v = a3(1 − 2χ). | (3) |
Thus, monomers that “dislike” solvent (more positive χ42) have smaller effective volumes compared to those that “like” solvent (more negative χ). From eqn (2), we highlight how stiffness scales with polymer volume fraction as K ∝ ϕpoly9/4, quantifying the effect that gels soften (K decreases) as they swell with water (ϕpoly decreases). We and others previously verified this 9/4 scaling,27,43–45 validating the semi-dilute description for hydrogels. Furthermore, for pure polyacrylamide gels, we verify this 9/4 scaling through a comparison of mechanical stiffness versus polymer mass fraction (Fig. S7a, ESI†).
Inspired by the fact that ϕpoly is an important controlling parameter of gels, we investigate whether ϕpoly also controls the water transport behavior of hydrogels as quantified by the hydraulic permeability. Intuitively, we should expect that by increasing crosslinking, the mesh size, ξ, decreases, causing the polymer volume fraction to increase (decreasing swelling), and the porosity of the polymer network to decrease. As a result, the polymeric network becomes more constrained, with less porous space.46–49 Here, we investigate whether this more constrained polymer network increases the difficulty to flow water through it as quantified by the Darcy hydraulic permeability, κ:
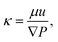 | (4) |
To test whether higher ϕpoly indeed results in lower permeability, we need a way to independently control ϕpoly without changing other properties of the gel. One way to only change ϕpoly is to alter the osmotic pressure of the environment (e.g., changing the ambient solution environment or humidity). The other way is to vary the crosslinking. We and others have shown that changing crosslinking simply changes ϕpoly (or the equilibrium swelling state) and minimally affects other molecular properties.27,50 That is, in eqn (2), the monomer size, a, and excluded volume, v, do not change with crosslinker amount—only ϕpoly changes. As such, hydrogels that differ only by crosslinking can be viewed as being a part of the same polymer family. To provide a comprehensive understanding, in this study, we consider 21 different hydrogels spanning across four different polymer families: (1) pure polyacrylamide (PAAm) hydrogels, (2) hydrolyzed PAAm hydrogels,51,52 (3) PAAm hydrogels with N,N-dimethylacrylamide (DMA) as a filler,53,54 and (4) PAAm hydrogels copolymerized with N-Isopropylacrylamide (PNI-co-AAm).55,56 Within each family, we have five to six different hydrogels differing by crosslinking amount where we use N,N′-methylene(bis)acrylamide (MBA) as a crosslinker. The molar crosslinker-to-monomer ratios span 0.5% to 7%. Fourier-transform infrared (FTIR) spectroscopy analysis confirms that significant changes in spectra are observed across different families, but insignificant changes are observed across different crosslinker ratios within the same families (Fig. 2a), consistent with our previous work.27
After establishing that crosslinking can be used to independently vary ϕpoly, we test the idea of higher ϕpoly leading to lower hydraulic permeability by performing water transport experiments using a custom-built permeability cell controlled by a microfluidic pressure regulator (Elveflow OB1) and flow rate sensor (see Fig. S1, ESI†). Using Darcy's law (eqn (4)), we find that in the limit of a small pressure difference, ΔP, applied across the gel, the experimentally measurable permeability is
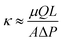 | (5) |
As expected, the permeability of the tested hydrogels decreases as the crosslinker ratio generally increases from 0.5% to 7% (Fig. 2b, red). However, there are a few notable complications. Increasing crosslinker ratio between 3% to 5% results in very little change (plateau-like trend) or even an increase in permeability (PAAm with DMA). As shown in the hydrolyzed PAAm samples above 5%, the permeability decreases in contrast to the plateau-like behavior at slightly lower crosslinker ratios. Thus, the relationship between permeability and crosslinker ratio is highly polymer-family-specific and would likely need a complicated model to describe accurately. As discussed earlier and in accordance with previous work on mesh size theory,14–18 polymer volume fraction more directly controls permeability as it does with stiffness. If this were the case, then any changes in permeability should have corresponding inverse changes in stiffness. Therefore, we also measure the stiffness of the tested samples using a custom-built indentation tester (see ESI,† Fig. S3) in accordance with previous testing procedures.27 Indeed, the stiffness of the hydrogels increases as crosslinker ratio increases (Fig. 2b, blue). Similar to our measurements with permeability, the dependence on crosslinker ratio is highly polymer-family-specific. However, as expected, any changes in permeability have corresponding inverse changes in stiffness. This coupling between permeability and stiffness is highlighted by the fact that while increasing crosslinker ratio from 3% to 5% for PAAm with DMA results in an anomalous increase in permeability, this is complemented by an anomalous decrease in stiffness. Furthermore, any plateau-like trends in permeability also exist in stiffness. This suggests that both permeability and stiffness are governed by the more fundamental polymer volume fraction and mesh spacing between polymer chains as opposed to the crosslinker ratio (Fig. 1).
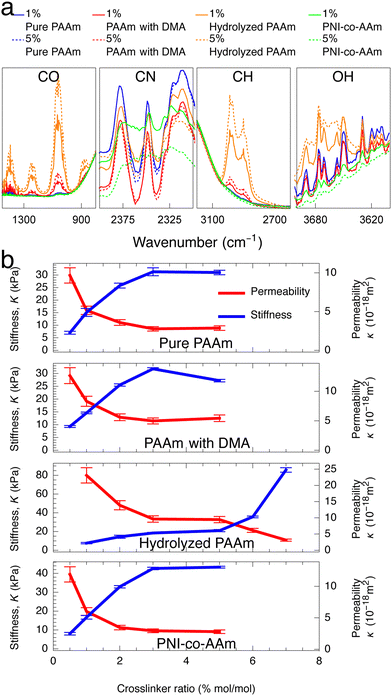 | ||
| Fig. 2 (a) Significant changes in FTIR spectra are only observed across polymer families and not by varied crosslinker ratio. (Complete FTIR test results of all samples are shown in ESI,† Fig. S5) (b) In all four hydrogel families, increasing crosslinker ratio generally increases stiffness and decreases hydraulic permeability with a few polymer-family-specific exceptions. Crosslinker ratios above 5% are not tested for some hydrogels due to high sample brittleness precluding accurate stiffness characterization. | ||
If mesh size controls permeability, then we need to incorporate a description of permeability that depends on polymer volume fraction. Assuming the space between polymer strands, 1 − ϕpoly is fully wetted by the flowing liquid, then we can define this space as the porosity, ε. This porosity, as confirmed by dissipative particle dynamics simulations,58 can be related to the permeability. While there are several descriptions relating κ to ε,18,59 the Kozeny-Carman equation is a simple and widely used model that explicitly defines a relationship between κ and ε and has been used to describe permeability through soft gel materials.60–63 Here, we take the Kozeny-Carman equation of permeability, substitute ε = 1 − ϕpoly, and treat monomer units of the polymer mesh as effective “grains”:
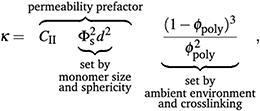 | (6) |
The swelling-dependent term in the Kozeny-Carman equation can be expanded as  . In the limit of small ϕpoly—applicable to highly swollen gels—the magnitude of the leading-order term, 1/ϕpoly2, is much greater than the other terms. Thus, for small ϕpoly the permeability can be approximated by the leading-order term as
. In the limit of small ϕpoly—applicable to highly swollen gels—the magnitude of the leading-order term, 1/ϕpoly2, is much greater than the other terms. Thus, for small ϕpoly the permeability can be approximated by the leading-order term as
| κ ≈ CIIΦs2d2ϕpoly−2. | (7) |
If this approximation is valid, then the slope of κ using eqn (6) when plotted on a log–log scale should be close to −2 as this is the exponent of the simplified scaling relationship in eqn (7). Indeed, as long as ϕpoly < 0.05, the difference in values of log–log slope between eqn (6) and (7) is within 8% (see ESI,† Fig. S6). Since, for many swollen hydrogels, ϕpoly is often much smaller than 0.05,64–67 the relationship in eqn (7) is a very reasonable simplification, providing single-digit-percentage uncertainty or less. Furthermore, for pure PAAm gels, we verify this −2 scaling through a comparison of hydraulic permeability versus polymer mass fraction (Fig. S7b, ESI†).
Combining the scaling relationships between stiffness to ϕpoly (eqn (2)) and permeability to ϕpoly (eqn (7)) through the elimination of ϕpoly, we obtain a scaling law that directly relates stiffness, K, to the hydraulic permeability, κ:
 | (8) |
| κ ∝ K−8/9. | (9) |
To verify this simple scaling law, we plot the permeability against the stiffness for the 21 hydrogels across four different polymer families with varied crosslinking from 0.5% to 7% tested earlier on log–log scaling (Fig. 3). In accordance with Eq. 8, each polymer family has data points corresponding to different crosslinker ratios that lie on a slope of −8/9. The close agreement within 3.7% uncertainty across a wide range of hydrogel crosslinker ratios provides strong validation of the scaling law (eqn (8)). As mentioned previously, we chose to use the Kozeny-Carman description in accordance with other works involving gels;60–63 however, we can also generalize the scaling law result (eqn (9)) as κ ∝ K−4α/9 where α scales ϕpoly to κ as κ ∝ ϕ−αpoly. According to Kapur et al.,18α can be the range of 1.4 to 3.3. When explicitly fitting our experimental results to an arbitrary α, we find that α = 1.8 ± 0.2, a result that is within 10% of the Kozeny-Carman exponent of α = −2. Nonetheless, we find that setting α = −2 (eqn (7)) describes the four tested hydrogel families accurately as we separately verify in Fig. S7b (ESI†), thereby validating the Kozeny-Carman description for hydrogels. We highlight the fact that for hydrolyzed PAAm gels, we are able to obtain more than a decade range of stiffness and find that the scaling still holds. Thus, the scaling law allows one to determine the permeability of gels based on its stiffness as long as the prefactor in eqn (8) has been determined from a reference sample in the same polymer family. Interestingly, the prefactor in eqn (8) suggests that monomers that are rendered more hydrophilic (decreasing χ), κ should increase. This is in agreement with our results where the more hydrophilic hydrolyzed PAAm (Fig. 3, red) has a higher permeability than its more hydrophobic pure PAAm counterpart (Fig. 3, blue) at the same stiffness.
 | ||
| Fig. 3 Plotting permeability and stiffness of 21 hydrogels with varying crosslinker ratio across four polymer families shows a close agreement with eqn (8) where the log–log slope is −8/9. | ||
In conclusion, our work confirms that combining de Gennes’ semi-dilute polymer theory and the Kozeny-Carman equation provides an accurate scaling law relating permeability to the stiffness of hydrogels. Our resulting scaling law between permeability and stiffness (1) reconfirms the importance mesh size (and therefore, degree of swelling and polymer volume fraction) on hydrogel properties, and (2) provides a simple, succinct, and experimentally testable relationship between mechanical stiffness and water permeability of hydrogels. Future studies could investigate whether the scaling law can be applied to hydrogels with high entanglement68,69 or sliding crosslinkers70–72 to alter polymer volume fraction. Future studies could also investigate the validity of the scaling law for gas permeability or liquid solution permeabilities where polymer volume fraction is modified through osmotic pressure rather than crosslinking. We anticipate that our work will guide the informed synthesis of hydrogels tuned by crosslinker amount for applications in a wide variety of fields.
Author contributions
Y. G. performed data curation, investigation, methodology, and validation. H. J. C. performed supervision and project administration. Both Y. G. and H. J. C. performed conceptualization, formal analysis, visualization, and writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
It is a pleasure to acknowledge Mario Mata, Bianca Navarro, Stone Wachs, Brandon Ortiz, and Ryan Phung for helpful discussions and assistance in experiments. We also acknowledge Nicholas K. K. Chai for the design and build of the custom indentation tester, as well as Vesper Evereux for graphical illustrations. We also thank Suraj V. Pochampally and Jaeyun Moon for assistance with FTIR spectroscopy. This work was supported by the University of Nevada, Las Vegas through start-up funds, the Faculty Opportunity Award, the Top Tier Doctoral Graduate Research Assistantship program, and the Technology Commercialization Award.Notes and references
- H.-L. Tan, S.-Y. Teow and J. Pushpamalar, Bioengineering, 2019, 6, 17 CrossRef CAS PubMed.
- Y. Zhou, C. Wan, Y. Yang, H. Yang, S. Wang, Z. Dai, K. Ji, H. Jiang, X. Chen and Y. Long, Adv. Funct. Mater., 2019, 29, 1806220 CrossRef.
- R. Subramani, A. Izquierdo-Alvarez, P. Bhattacharya, M. Meerts, P. Moldenaers, H. Ramon and H. Van Oosterwyck, Front. Mater., 2020, 7, 212 CrossRef.
- K. Liu, Y. Zhang, H. Cao, H. Liu, Y. Geng, W. Yuan, J. Zhou, Z. L. Wu, G. Shan and Y. Bao, et al. , Adv. Mater., 2020, 32, 2001693 CrossRef CAS PubMed.
- S. Lin, H. Yuk, T. Zhang, G. A. Parada, H. Koo, C. Yu and X. Zhao, Adv. Mater., 2016, 28, 4497–4505 CrossRef CAS PubMed.
- S. Jiang, S. Liu and W. Feng, J. Mech. Behav. Biomed. Mater., 2011, 4, 1228–1233 CrossRef CAS PubMed.
- N. Efron, P. B. Morgan, I. D. Cameron, N. A. Brennan and M. Goodwin, Optom. Vis. Sci., 2007, 84, E328–E337 CrossRef.
- J. Kim, A. Conway and A. Chauhan, Biomaterials, 2008, 29, 2259–2269 CrossRef CAS PubMed.
- L. Zhao, P. Wang, J. Tian, J. Wang, L. Li, L. Xu, Y. Wang, X. Fei and Y. Li, Sci. Total Environ., 2019, 668, 153–160 CrossRef CAS PubMed.
- V. Sinha and S. Chakma, J. Environ. Chem. Eng., 2019, 7, 103295 CrossRef CAS.
- H. Lu, W. Shi, F. Zhao, W. Zhang, P. Zhang, C. Zhao and G. Yu, Adv. Funct. Mater., 2021, 31, 2101036 CrossRef CAS.
- V. Van Tran, D. Park and Y.-C. Lee, Environ. Sci. Pollut. Res., 2018, 25, 24569–24599 CrossRef CAS PubMed.
- D. S. Jones, C. P. Lorimer, C. P. McCoy and S. P. Gorman, J. Biomed. Mater. Res., Part B, 2008, 85, 417–426 CrossRef PubMed.
- N. R. Richbourg and N. A. Peppas, Prog. Polym. Sci., 2020, 105, 101243 CrossRef CAS.
- Y. Gombert, R. Simič, F. Roncoroni, M. Dübner, T. Geue and N. D. Spencer, Adv. Mater. Interfaces, 2019, 6, 1901320 CrossRef CAS.
- A. A. Pitenis and W. G. Sawyer, Tribol. Lett., 2018, 66, 1–7 CrossRef CAS.
- S. P. Obukhov, M. Rubinstein and R. H. Colby, Macromolecules, 1994, 27, 3191–3198 CrossRef CAS.
- V. Kapur, J. C. Charkoudian, S. B. Kessler and J. L. Anderson, Ind. Eng. Chem. Res., 1996, 35, 3179–3185 CrossRef CAS.
- M. Huang, H. Furukawa, Y. Tanaka, T. Nakajima, Y. Osada and J. P. Gong, Macromolecules, 2007, 40, 6658–6664 CrossRef CAS.
- L. Cacopardo, N. Guazzelli, R. Nossa, G. Mattei and A. Ahluwalia, J. Mech. Behav. Biomed. Mater., 2019, 89, 162–167 CrossRef CAS PubMed.
- T. L. Sun, T. Kurokawa, S. Kuroda, A. B. Ihsan, T. Akasaki, K. Sato, M. Haque, T. Nakajima and J. P. Gong, et al. , Nat. Mater., 2013, 12, 932–937 CrossRef CAS PubMed.
- O. Chaudhuri, Biomater. Sci., 2017, 5, 1480–1490 RSC.
- D. Huang, Y. Huang, Y. Xiao, X. Yang, H. Lin, G. Feng, X. Zhu and X. Zhang, Acta Biomater., 2019, 97, 74–92 CrossRef CAS PubMed.
- Y. Kawauchi, Y. Tanaka, H. Furukawa, T. Kurokawa, T. Nakajima, Y. Osada and J. P. Gong, J. Phys.: Conf. Ser., 2009, 012016 CrossRef.
- S. Lin and L. Gu, Materials, 2015, 8, 551–560 CrossRef.
- S. P. Pilipchuk, M. K. Vaicik, J. C. Larson, E. Gazyakan, M.-H. Cheng and E. M. Brey, J. Biomed. Mater. Res., Part A, 2013, 101, 2883–2895 CrossRef PubMed.
- Y. Gao, N. K. Chai, N. Garakani, S. S. Datta and H. J. Cho, Soft Matter, 2021, 17, 9893–9900 RSC.
- Y. Tanaka, M. Seii, J. Sui and M. Doi, J. Chem. Phys., 2020, 152, 184901 CrossRef CAS PubMed.
- H. J. Kwon, A. Kakugo, T. Ura, T. Okajima, Y. Tanaka, H. Furukawa, Y. Osada and J. P. Gong, Langmuir, 2007, 23, 6257–6262 CrossRef CAS PubMed.
- H. Ju, A. C. Sagle, B. D. Freeman, J. I. Mardel and A. J. Hill, J. Membr. Sci., 2010, 358, 131–141 CrossRef CAS.
- C.-C. Peng and A. Chauhan, J. Membr. Sci., 2012, 399, 95–105 CrossRef.
- J. Pozuelo, V. Compañ, J. M. González-Méijome, M. González and S. Mollá, J. Membr. Sci., 2014, 452, 62–72 CrossRef CAS.
- L. Liu, A. Chakma and X. Feng, J. Membr. Sci., 2008, 310, 66–75 CrossRef CAS.
- H. Matsuyama, M. Teramoto and H. Urano, J. Membr. Sci., 1997, 126, 151–160 CrossRef CAS.
- M. K. Yazdi, V. Vatanpour, A. Taghizadeh, M. Taghizadeh, M. R. Ganjali, M. T. Munir, S. Habibzadeh, M. R. Saeb and M. Ghaedi, Mater. Sci. Eng., C, 2020, 114, 111023 CrossRef CAS PubMed.
- A. C. Sagle, H. Ju, B. D. Freeman and M. M. Sharma, Polymer, 2009, 50, 756–766 CrossRef CAS.
- M. J. Tavera-Quiroz, J. J. F. Daz and A. Pinotti, Int. J. Appl. Eng. Res., 2018, 13, 13302–13307 Search PubMed.
- P.-G. De Gennes, Scaling concepts in polymer physics, Cornell university press, 1979 Search PubMed.
- R. van der Sman, Food Hydrocolloids, 2015, 48, 94–101 CrossRef CAS.
- A. Fernandez-Nieves, H. Wyss, J. Mattsson and D. A. Weitz, Microgel suspensions: fundamentals and applications, John Wiley & Sons, 2011 Search PubMed.
- S. Panyukov, Sov. Phys. JETP, 1990, 71, 372–379 Search PubMed.
- E. Nagy, Basic Equations of Mass Transport through a Membrane Layer, 2019, vol. 2, pp. 457–481 Search PubMed.
- M. Zrinyi and F. Horkay, Polymer, 1987, 28, 1139–1143 CrossRef CAS.
- S. P. Obukhov, M. Rubinstein and R. H. Colby, Macromolecules, 1994, 27, 3191–3198 CrossRef CAS.
- C. L. Bell and N. A. Peppas, Biopolymers II, Berlin, Heidelberg, 1995, pp. 125–175 Search PubMed.
- R. da Silva and M. G. de Oliveira, Polymer, 2007, 48, 4114–4122 CrossRef CAS.
- N. E. Ben Ammar, T. Saied, M. Barbouche, F. Hosni, A. H. Hamzaoui and M. Şen, Polym. Bull., 2018, 75, 3825–3841 CrossRef CAS.
- M. N. Collins and C. Birkinshaw, J. Appl. Polym. Sci., 2011, 120, 1040–1049 CrossRef CAS.
- S. J. Bryant, K. S. Anseth, D. A. Lee and D. L. Bader, J. Orthop. Res., 2004, 22, 1143–1149 CrossRef CAS.
- J. Li, Y. Hu, J. J. Vlassak and Z. Suo, Soft Matter, 2012, 8, 8121–8128 RSC.
- S. Saber-Samandari, M. Gazi and E. Yilmaz, Polym. Bull., 2012, 68, 1623–1639 CrossRef CAS.
- J. Aalaie and A. Rahmatpour, J. Macromol. Sci., Part B: Phys., 2007, 47, 98–108 CrossRef.
- S. Skelton, M. Bostwick, K. O'Connor, S. Konst, S. Casey and B. P. Lee, Soft Matter, 2013, 9, 3825–3833 RSC.
- E. A. Kuru, N. Orakdogen and O. Okay, Eur. Polym. J., 2007, 43, 2913–2921 CrossRef CAS.
- B. Manjula, K. Varaprasad, R. Sadiku and K. M. Raju, Adv. Polym. Technol., 2013, 32(2), 21340 CrossRef.
- L. Yang, X. Fan, J. Zhang and J. Ju, Polymers, 2020, 12, 389 CrossRef CAS.
- J.-F. Louf, N. B. Lu, M. G. O’Connell, H. J. Cho and S. S. Datta, Sci. Adv., 2021, 7, eabd2711 CrossRef PubMed.
- B. Hertzberg, A. Alexeev and G. Yushin, J. Am. Chem. Soc., 2010, 132, 8548–8549 CrossRef CAS PubMed.
- L. Spielman and S. L. Goren, Environ. Sci. Technol., 1968, 2, 279–287 CrossRef.
- S.-I. Nakao, T. Nomura and S. Kimura, AIChE J., 1979, 25, 615–622 CrossRef CAS.
- S. Zaidi and A. Kumar, Desalination, 2005, 172, 107–117 CrossRef CAS.
- E. Iritani, N. Katagiri, K. Yamaguchi and J.-H. Cho, Drying Technol., 2006, 24, 1243–1249 CrossRef CAS.
- N. Isobe, S. Kimura, M. Wada and S. Deguchi, J. Taiwan Inst. Chem. Eng., 2018, 92, 118–122 CrossRef CAS.
- W. Zhang, Y. Liu, M. Zhu, Y. Zhang, X. Liu, H. Yu, Y. Jiang, Y. Chen, D. Kuckling and H.-J. P. Adler, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 6640–6645 CrossRef CAS.
- Q. Lv, M. Wu and Y. Shen, Colloids Surf., A, 2019, 583, 123972 CrossRef CAS.
- S. J. Kim, S. J. Park and S. I. Kim, React. Funct. Polym., 2003, 55, 53–59 CrossRef CAS.
- A. Kumar, M. Pandey, M. Koshy and S. A. Saraf, Int. J. Drug Delivery, 2010, 2, 135–140 CrossRef.
- J. Kim, G. Zhang, M. Shi and Z. Suo, Science, 2021, 374, 212–216 CrossRef CAS PubMed.
- K. Chen, Y. Feng, Y. Zhang, L. Yu, X. Hao, F. Shao, Z. Dou, C. An, Z. Zhuang and Y. Luo, et al. , ACS Appl. Mater. Interfaces, 2019, 11, 36458–36468 CrossRef CAS PubMed.
- J. P. Gong, Soft Matter, 2010, 6, 2583–2590 RSC.
- R. Du, Z. Xu, C. Zhu, Y. Jiang, H. Yan, H.-C. Wu, O. Vardoulis, Y. Cai, X. Zhu and Z. Bao, et al. , Adv. Funct. Mater., 2020, 30, 1907139 CrossRef CAS.
- C.-Y. Shi, Q. Zhang, C.-Y. Yu, S.-J. Rao, S. Yang, H. Tian and D.-H. Qu, Adv. Mater., 2020, 32, 2000345 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01215d |
| This journal is © The Royal Society of Chemistry 2022 |

